Piloting for Scale-Up—An Ancient Technology Only for Non-Chemical Engineering Trained Investors

Abstract

Investors demand risk minimization references or at least demonstrator plant operations that are scaled down by a factor of about 25 times less than the manufacturing scale. This causes increased investments of about 30% and a time delay of about 3–5 years. Nevertheless, modern process simulation studies based on experimental model parameter determination at a reduced laboratory scale and process model validation by mini-plant operations with risk assessment studies based on a statistically sound quality by design (QbD) approach should be able to substitute existing methods with less effort in terms of time and cost. This approach is used for a risk assessment study based on an industrial-scale simulated moving bed chromatography separation of m- and p-isomers, including potential enrichment cycles of the simulated moving bed’s (SMB) internal desorbent and the corresponding raffinate and extract distillation columns, and well-documented experimental literature data. The results quantify potential risks within probability ranges for investor decisions quite sufficiently. The benefits of ROI across various annual capacity scales and product magnitudes are evident through reductions of about 30% regarding investment and 3–8 years in terms of time to market, which should motivate the desire to implement these innovative methods more strategically in industrial daily work instead of piloting demonstrator-scale construction and operation.

1. Introduction

In order to build large-scale manufacturing plants based on chemical or biotechnology laboratory studies, piloting is a necessary step to verify the scale-up from laboratory-scale to manufacturing-scale operations. The objective is, on the one hand, to supply sufficient amounts of the technology for product quality testing and application studies and/or, on the other hand, to verify the prediction of the technical readiness level for investment decisions from laboratory-scale operations (TRL 3–4) to prototyping (TRL 6–8) [1]. Plants of a global scale are of significant economic and ecological importance for reducing COGs and GWP [2].

Typical interest rates for loans in plant construction in the chemical industry vary depending on risk and market conditions, residing between approx. 6 and 15% [3].

Studies show that interest rates for construction loans are influenced by risk factors such as losses, debt, and common equity ratios [4]. In the chemical industry, interest rates for long-term loans can also be affected by external factors such as energy prices. Elevated natural gas prices may reduce investment activity, thereby increasing firms’ reliance on long-term financing [5]. If large test amount quantities are needed, either a CDMO or piloting is necessary to supply them. Piloting is a necessary condition. But, if only the scalability of a project has to be proven, the technical risk has to be defined a priori in order to evaluate the efforts and benefits of piloting.

Normally, piloting is conducted for fluid dynamic studies to define throughput and capacity based on the normal operation point and high- and low-load conditions. This can be performed without the mass transfer of the real feed mixture.

Investors make decisions based on a triangle of product quality, profit and risk. Whereas product quality may differ in scale and assessing the technical maturity of the manufacturing scale depends on quantitative criteria, risk is often sensed. But risk assessment methods can quantify criteria as well, and moreover, the final judgement in calculating risks is often left to the entrepreneur. The amount of time, resources and budget required increases in order to minimize the risk. For example, the highest amount of effort that entails the lowest risk is the construction and operation of a production-scale plant—which is linked to the demand for references. Investors who do not come from the chemical engineering sector require at least a scale factor of around 20 to a maximum of 30 in order to demonstrate technical maturity for investment decisions with lower/low risk. This necessitates demonstration plants and no longer plants constructed at the pilot scale. It should be kept in mind that such low scale factors are not the state of the art in chemical engineering but apply to scales of 10,000 to 100,000 tons per year, depending on the degree of heterogeneity of the individual operating units [6].

Therefore, such excessive pilot-scale studies were substituted, with the introduction of process simulation methods, by mini-plant technology about 30–40 years ago in order to reduce time, effort, budget and resources from years to months and tens of EUR mil. to few EUR mil. [7]. A comparison of the sizes of the pilot and mini plant can be found in the

Table 1. Time comparison between pilot plant and mini-plant [8].

Component	Pilot Plant	Mini-Plant
Planning time	1 year	3–4 months
Order/creation time	1 year	max. 3 months *
Start-up time	3 months	1 month
Test time	6–9 months	6–9 months
Total time	approx. 3 years	approx. 1 year
Ratio of plant costs	10 to 1

* Incl. ordering of special components.

.

Investors demand risk minimization with the help of a demonstrator and innovative technologies like process simulations based on laboratory-scale model parameter determination and final model validation with the aid of mini-plant experiments in order to define risks a priori using any risk assessment without piloting and the use of a demonstrator, leading to evident benefits in terms of time and cost.

The knowledge base differences for various unit operations are large. The more heterogeneity is involved, the more scale-dependent studies are needed, which makes distillation the best unit to predict performance. Such a mini-plant should verify scale factors for low-, high- and medium-throughput operation points and reveal any non-ideal behavior under a technical operation that cannot be predicted by process simulations like foam, mulm, fouling, mechanical and chemical aging, as well as any issues that affect side components, such as contaminant enrichment [9]. A risk analysis can be useful for classifying and evaluating such effects.

This will be exemplified in the following paragraphs in detail, using a typical bulk/fine chemical process like m-/p-isomer separation with simulated moving bed chromatography combined with two distillation columns for the eluent recycling of raffinate and extract. The example combines two interconnected recycle loops of chromatography eluent recycling and distillation top eluent recycling. Moreover, any good predictable homogeneous distillation column with a supposedly less-investigated chromatography step requires a heterogeneous zeolite adsorbent.

Is an investment of approximately EUR 20 million, including pilot costs of around EUR 5 million, justified by the additional effort required for piloting, which increases the investment cost by approximately 25%? Does the same apply for an investment of EUR 200 million with pilot expenses amounting to EUR 50 million? It should be noted that offers from certain international engineering firms, which are often state-subsidized or at least “guided”, have the potential to reduce the investment cost by a factor of three. Nevertheless, the minimal optimized operating costs may not be achieved through this approach; however, the investment risk is significantly mitigated, even without the delays and expenses associated with piloting.

It remains an open question as to whether modern risk assessment methodologies based on process simulation studies can effectively bridge this gap. Traditionally, process simulations focus on the principal components as key species, while certain physical property predictions inherently involve uncertainties [10]. Since the 1990s, mini-plant technology has substituted classical pilot plants to validate process simulations with key components and show real chemical component effects and, with representatively scaled-down reference equipment, achievable throughput with upper and lower limits. Nowadays, process simulation with risk assessment and laboratory-scale studies can answer the questions above. In addition, risk is quantified by the most sensitive parameters.

1.1. Isomer Separation for Bulk/Fine Chemical Process

The separation of isomers by SMB processes has long been used on a large industrial scale. The most well-known separation of isomers by SMB technology is the Parex process from UOP. In 1971, UOP first introduced the Parex process for the recovery of p-xylene from a mixture of C8 aromatics, one of several adsorption processes that make up UOP’s Sorbex SMB adsorption technology [11].

Due to its commercial success, further variants were developed, and currently, four main industrial processes exist: Parex from UOP [12], Aromax from Toray [13], Eluxyl from IFP [14] and VARICOL from Novasep [15]. The global p-xylene capacity at the end of 2001 was 21.4 million tons per year, while the industrial capacity of these plants can be up to 750,000 tons per year [16].

Isomers that have been more rarely been produced than xylene by SMB technology at the commercial scale that offer potential for further SMB separation are, e.g., cresols, more precisely, entailing the separation between meta- and para-cresol. Both p-cresol and m-cresol are primarily used for the production of light-resistant antioxidants [17]. The separation of m-cresol/p-cresol mixtures is difficult using conventional distillation due to their close boiling points. Several reactive separation methods have been proposed for the separation and purification of these mixtures, such as dissociation extraction, reactive crystallization and reactive distillation in the presence of amines, etc., which are efficient but costly methods [18]. Adsorption is a method that has the potential to separate such mixtures economically. The separation of m-/p-cresols by adsorption on Ba-X and Ca-X zeolites has already been investigated and high-purity p-cresol was obtained in good yields [17].

The separation of cresol isomers using zeolites as adsorbents is known in principle [17]. In particular, wide-pored zeolites have been used, which also include faujasite types exchanged with cations. Phenols, primary alcohols and aromatic hydrocarbons are used as desorbents. However, a sharp separation of these isomers can only be achieved by pre-loading the adsorbent with 4 to 8% water. However, as water is bound more strongly than cresols, this greatly reduces the adsorption capacity of the zeolite [19,20]. Zinnen was able to determine an optimum water level of 4.5 wt% (LOI) in 1992 [20].

Monitoring and controlling the water content in the SMB process as an inline method is possible using NIR (near infrared). A near-infrared spectrum of the liquid phase is recorded by a spectroscopic online analysis device using at least one fixed measurement point in a column (e.g., between the feed and extract). The water content in the process can be controlled and regulated using multivariate regression models. An additional measurement of the water content using the Karl Fischer method via an additional sampling point is optional [21].

A principle for concentration analysis in the SMB system for the separation of isomers is possible with a Raman spectrum concentration measuring device [22]. The RAMAN analysis method described in US 8,194,245 enables the continuous monitoring and detection of any failures with a very small time delay [23].

1.2. Process Development in Chemical (or Process) Industry and Risk Assessment

In the development of large-scale industrial plants, criteria must be met within an economically acceptable risk framework. This includes product purity as a specification essential for marketability. In this regard, the vendor or operator may have an obligation to implement corrective measures until the specification is satisfied. This represents a significant risk that must be managed through relatively high safety margins and potential mitigation strategies.

A more robust approach would be re-chromatography within the process; however, this measure would proportionally reduce throughput capacity based on the amount reprocessed, making it feasible only for rare extreme cases. Typically, a conservative assumption is made that the separation factor between isomers is approximately 10% lower than ideal.

Potential impurities are also taken into account by setting maximum allowable limits in the feed. Together, these considerations usually result in columns that are oversized by about 10% in length, which translates proportionally to a reduced feed volume based on the maximum adsorbent loading. This means that roughly a 10% reduction in adsorbent loading at the operating point is included as a safety margin.

An additional safety margin of about 10% adsorbent capacity loss is incorporated to cover potential irreversible accumulations. This provides considerable protection against this risk and allows us to establish limits on irreversible adsorbent capacity loss due to impurities in the feed or components potentially formed through reactions or degradation. Typically, these impurities are limited to a few ppm at most.

Furthermore, fluctuations in temperature, pressure, concentration, and residence time distribution can be realistically defined and methodically examined. These variations can be excluded or quantified at the laboratory scale with minimal effort and would subsequently be included in a comprehensive risk assessment.

The theoretically optimal operating point for SMB chromatography is derived from the operating/triangle diagram theory [24]. However, this considers only phase equilibrium and does not account for non-ideal phenomena such as axial dispersion, hold-ups in the apparatus, non-uniform packing (void fraction), or inaccuracies and delays in pump and valve switching [25].

When a dynamic process model is used for design, the achievable throughput is typically reduced by 5–20% compared to the theoretical optimum to reflect a realistic operating point. This reduction can be well quantified for each specific system using the dynamic process model [26].

Additionally, to account for potential variations in feed concentrations of the main binary components and fluctuations in feed flow rates, a chromatographic safety margin of about 10% unused bed length is included. This margin forms part of the previously mentioned reduction in throughput capacity. The operating point must be experimentally validated using a mini-plant setup. Following this approach, plant capacity can be reliably achieved at 100% with at least a 5% safety margin.

2. Materials and Methods

2.1. SMB Process Model

A rigorous SMB process model is used to describe the behavior of the SMB unit using a mathematical model [25,27]. The similarity of cresols and xylenes with regard to the separation of the para-isomer is based on their similar chemical structures and the resulting physical and chemical properties. Therefore, the development and design of an SMB unit for p-cresol separation is carried out on the basis of well-studied p-xylene separations. The patent literature offers parameters for the experimental separation of p-DMP in SMB plants, which have already been summarized by Minceva et al. [28]. Therefore, a study based exclusively on experiments documented in the literature, which are cited below, is possible.

Considering the previous information and space limitations, a 1:1-scale SMB plant and operating conditions are selected. Faujasite-type BaX zeolites, e.g., 1-pentanol, are used as adsorbents and desorbents based on Zinnen et al. [20]. The feed is considered as a typical cresol mixture containing, e.g., 40% p-cresol and 60% m-cresol. The equilibrium data for p-, m- and 1-pentanol at 150 °C are based on Zinnen et al. [20]. The SMB data, operating conditions and model parameters used in the simulation study are summarized in

Table 2. SMB geometry, operating conditions and model parameters used for SMB model.

SMB Geometry	Operating Conditions	Model Parameters
Lc = 2.00 m	T = 150 °C	Pe = 2000
dc = 4.5 m	LOI = 4.5 wt%	dp = 0.04 cm
VC = 33 m3	QF = 22.59 m3/h	εb = 0.36
Column nr. = 16	QD = 50.22 m3/h	εp = 0.43
Configuration: 3-6-4-3	QE = 37.81 m3/h
	QR = 35.00 m3/h
	QRec. = 292.07 m3/h

visualized in Figure 1 in order to imitate a typical scale of about 100,000 mt per year for any realistic cost discussions. The design of the SMB process is initially based on the work diagram theory, with the assumption of medium desorbency [23,27,28], and is then optimized in the strict SMB process model [24,25].

The optimization of the process is based on various performance parameters. On the one hand, this comprises the extract and raffinate purity of the respective cresols.

$$P_E^{PK}={\displaystyle \frac{c_E^{PK}}{c_E^{MK}+c_E^{PK}}}\cdot 100;P_R^{MK}={\displaystyle \frac{c_R^{MK}}{c_R^{MK}+c_R^{PX}}}\cdot 100$$

(1)

Desorbent consumption for extract and raffinate:

$${DC}_E={\displaystyle \frac{Q_D}{c_E^{PK}{Q}_E}};{DC}_R={\displaystyle \frac{Q_D}{c_R^{MK}{Q}_R}}$$

(2)

Adsorbent productivity for cresols:

$${PR}_{Ads}^{PK}={\displaystyle \frac{c_E^{PK}{Q}_E}{V_s}}{;PR}_{Ads}^{MK}={\displaystyle \frac{c_E^{MK}{Q}_R}{V_s}}$$

(3)

A pure cresol mixture is used in the calculation for the design and optimization of the SMB process. In further development, the level of detail will be increased to reflect the actual real phenomena of the SMB configuration. Therefore, for the task of risk assessment, all possible—but, not necessarily real or existing—impurities (o-cresol [20], 2,4–2,6 Xylenol, o-Ethylphenol [20], and benzoic acid [29]) can be found in the literature and added to the feed in a total concentration of 1000 ppm with an additional water content of 150 ppm. The data used for the physical properties are listed in

Table 3. Physical properties of single components.

Components	Vmolar,i [m3/mol] 10−4	Mi [g/mol]	ρi [kg/m3] (150 °C)	dmolec [A°]	Ts [°C]
1-Pentanol	1.257	88.15	622.16	-	138.00
m-cresol	1.163	108.1	80,722	6.5 [17]	201.81
p-cresol	1.163	108.1	916.15	6.0 [17]	203.02
o-cresol	1.158	108.1	890.09	6.5 *	190.83
2,4 Xylenol	1.331	122.17	882.84	7.3 *	210.43
2,5 Xylenol	1.344	122.17	987.00	7.38 *	210.49
2,6 Xylenol	1.501	122.17	861.22	7.38 [17]	201.25
o-Etph.	1.364	122.16	861.79	7.4 *	204.52
BA	1.154	122.12	873.52	7.8 [30]	247.77
Water	0.196	18.02	671.41	2.7 [31]	100

* Estimated values based on known diameters.

based on the literature data. The multicomponent Langmuir isotherm is used to describe the equilibrium of multicomponent adsorption.

2.2. Desorbent Recycling–Distillation

In this study, a steady-state simulation is used to design and optimize two distillation columns. The distillation column was simulated based on the rate-based modeling approach using packed stages. The rate-based approach balances gas and liquid phases separately by considering mass and heat flows across the interface [32]. The Peng–Rob model is used as a thermodynamic model for process simulation.

The design is based on the results of the rigorous SMB process model of the optimized operating point, which is based on an overall yearly production of 100 kt m-cresol. In order to recycle the desorbent in the highest possible yield and purity, the number of stages, reflux ratios and flow rates are iteratively optimized. The diameter is designed depending on the throughput and the resulting flooding factor. The general conditions used are summarized in

Table 4. Configuration of internal column—packing.

Characteristic	Model Parameter
Packing type	SULZER Mellapack 500Y (Sulzer, Ltd., Winterthur, Switzerland)
Height of packing	50 cm
Specific area	5.08 m2/m3
Porosity	0.975

.

To ensure sufficiently good separation, the sump products (Ts > 140 °C) should be present in a maximum concentration of 100 ppm at the head fraction.

2.3. Impact Assessment and Statistical Analysis

For the planning of process characterization and control studies, a risk assessment approach as presented in the A-mab case study by the CMC (chemical, manufacturing and control) working group is applied [33]. The workflow for selecting the parameters to be included in OFAT (one-factor-at-a-time), DoE, and finally, control studies consists of the following steps:

• The identification of parameters for OFAT studies in the Ishikawa analysis.
• The ranking of the main effect based on effect attributes according to OFAT studies and an assessment of the possible effects of interactions.
• The calculation of severity levels and implementation of control studies. The calculation of severity levels and implementation of derived statistical experimental designs.
• An analysis of the study results to quantify parameter effect levels, identify CPP (critical process parameter), KPP (key process parameters) and process optima, and define the design space, control space and PAR (proven acceptable range).

The impact and interaction score obtained is then multiplied, and either a univariate or multivariate analysis of the parameter is performed based on the scores given in

Table 5. Ratings for the impact and interaction assessment of potential variables on the process attributes and the CQAs [33].

Impact	CQA	PA
No Impact/Interaction	1	1
Minor Impact/Interaction	4	2
Major Impact/Interaction	8	4

. Variables with a score of ≤2 are not analyzed, those with scores of 4–8 can be analyzed via univariate or multivariate analyses, and those with higher scores are analyzed via multivariate analyses. The decision as to whether variables with scores of 4–8 must be analyzed univariately or multivariately must be appropriately justified.

The resulting multivariate study is the design space for the SMB process. The endpoints of this multidimensional space are modeled in a full factorial DoE and the resulting design space can be statistically analyzed.

3. Results

3.1. Simulation Results and Discussion

The operating temperature of the p-cresol-SMB separation unit is between 140 and 160 °C, preferably 150 °C [34]. The ratio between the desorbent and feed stream is between 1.20 and 2.5, Ref. [35], the ratio between recycling and feed stream is between 5 and 12 [35]. The zeolite is used in the form of spherical particles with a diameter of 0.25 to 1 mm [35]. The water content of the zeolite should be less than 5 wt%, preferably 4.5 wt% [19,32].

3.2. Modeling Competitive Adsorption Isotherms

The experimental adsorption equilibrium data, based on experimental feed pulse tests from Zinnen et al. [20], were fitted by the multicomponent Langmuir isotherm model

$$q_i={\displaystyle \frac{H_i{c}_i}{1+{\sum }_{j=1}^{NC}{K}_j{c}_j^F}}$$

(4)

where K_i (L/g) represents the Langmuir constants and q_max,i represents the saturation capacities expressed in g/(l of adsorbent).

The maximal loading of the individual components was determined by iteration on the basis of the material properties in Table 3. The Langmuir isotherm curves of the main components are shown in Figure 2. It should be noted that the isotherm curves of components 1-pentanol and m-cresol overlap due to their slightly differing isotherm parameters. In addition, the separation factor of m/p-cresol and 1-pentanol/p-cresol was shown as a function of the concentration.

3.3. Prediction of the Separation and Regeneration Regions

The successful design and operation of SMB systems depends on the correct choice of operating conditions, in particular, the flow rates in each zone and the switching time. The group of Mazzotti, Storti and Morbidelli derived a graphical methodology for the design of shortcuts, known as triangular theory, and extended the theory to systems with nonlinear adsorption isotherms [23,27,28,34]. This methodology is currently the state of the art and has been applied to a large number of separations.

It involves simultaneously adjusting the value of the switching time and the values of the flow rates in zones 1–4, resulting in a pure extract and refined fractions. The flow rates in zones 1–4 are selected so that they are sufficiently high or low to fulfill the boundary conditions for the production quantity and requirement. The feed quantity is left constant and all other flows are adjusted.

Figure 3 shows the separation range obtained for the 60 wt% m-cresol mixture when using 1-pentanol in a desorbent to feed stream ratio of 2.2. The shape of the separation regions corresponds to that resulting from equilibrium theory for a medium-strength desorbent [36,37]. The black solid line represents pure extract and raffinate fractions. In addition, the regeneration areas zones I and IV are implemented as a green solid line for m_I -m_IV [35,38].

The simplest form of calculating the operating point is based on the flow rates of the respective zones, the switching time and the column characteristics.

$$m_j={\displaystyle \frac{Q_j^{SMB}·t^{*}-V_c·{\epsilon }_t}{V_c(1-{\epsilon }_t)}}$$

(5)

Including the number of columns per zone with an influence on the dimensionless flow ratios, this means that a higher number of columns is equivalent to a higher dimensionless flow ratio. This is shown by the solid points shown in red (filled symbols: square for working point, triangle for regeneration point) in Figure 3.

This shifts the operating point into the operating range and the regeneration point closer to the regeneration range. This result is used as the basis for the following rigorous process modeling.

3.4. Dynamic Modeling of SMB Process

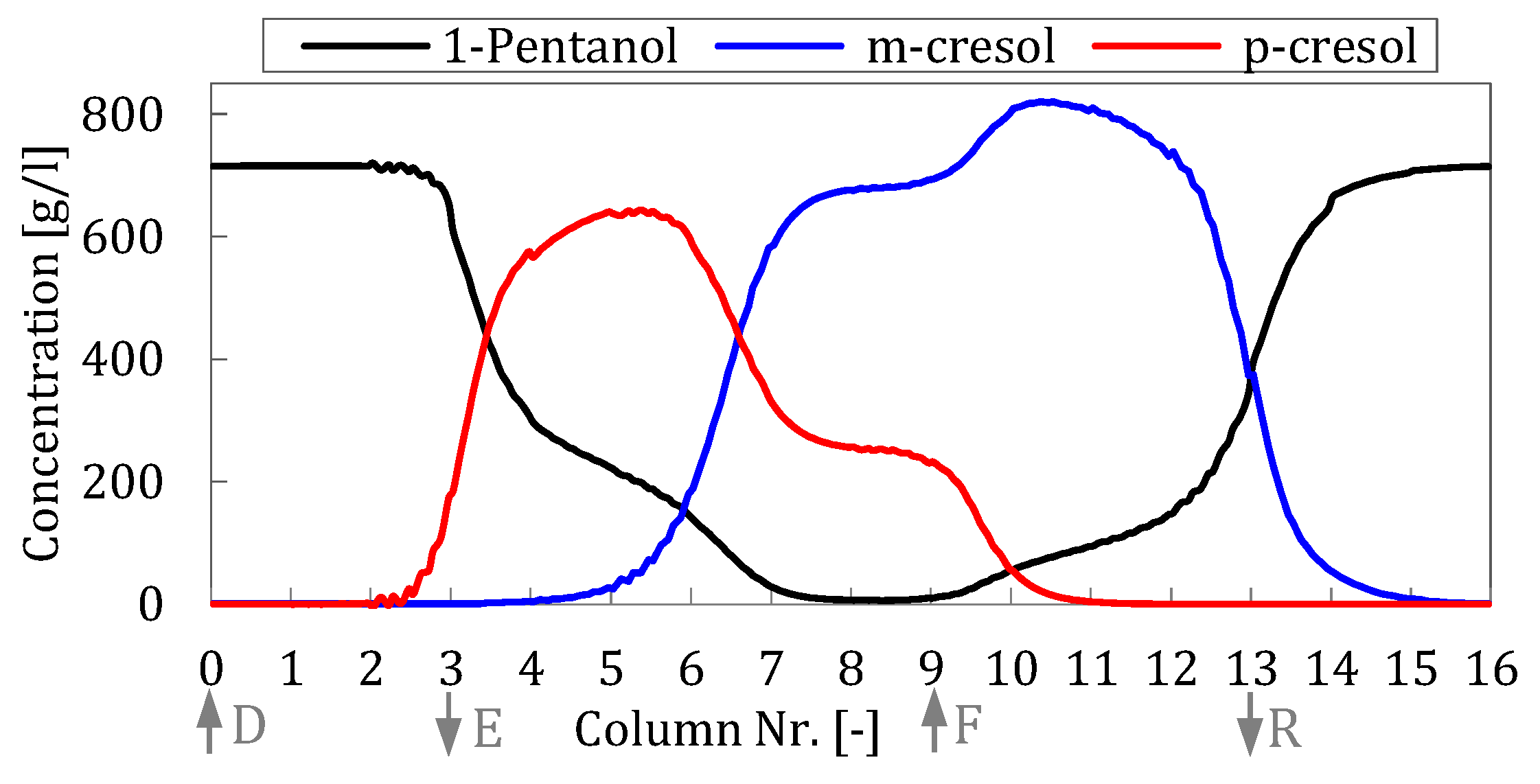
The model parameters used in the simulation are given in Table 2, and the isotherm parameters presented in Figure 4 show detailed simulation concentration profiles.

The system reached a cyclic steady state after 16 cycles. The extract performances calculated by using the SMB model were purity = 99.81%, DC = 2.91 L/kg, and PR = 22.70 kg/m³h. The raffinate performance results are purity = 99.99%, DC = 1.93 L/kg, and PR = 34.26 kg/m³h.

In terms of the solid results of the optimized operating point, which show both high purity and low desorbent consumption with simultaneously high productivity, they can serve as a basis for further calculations.

3.5. Column Reduction Studies

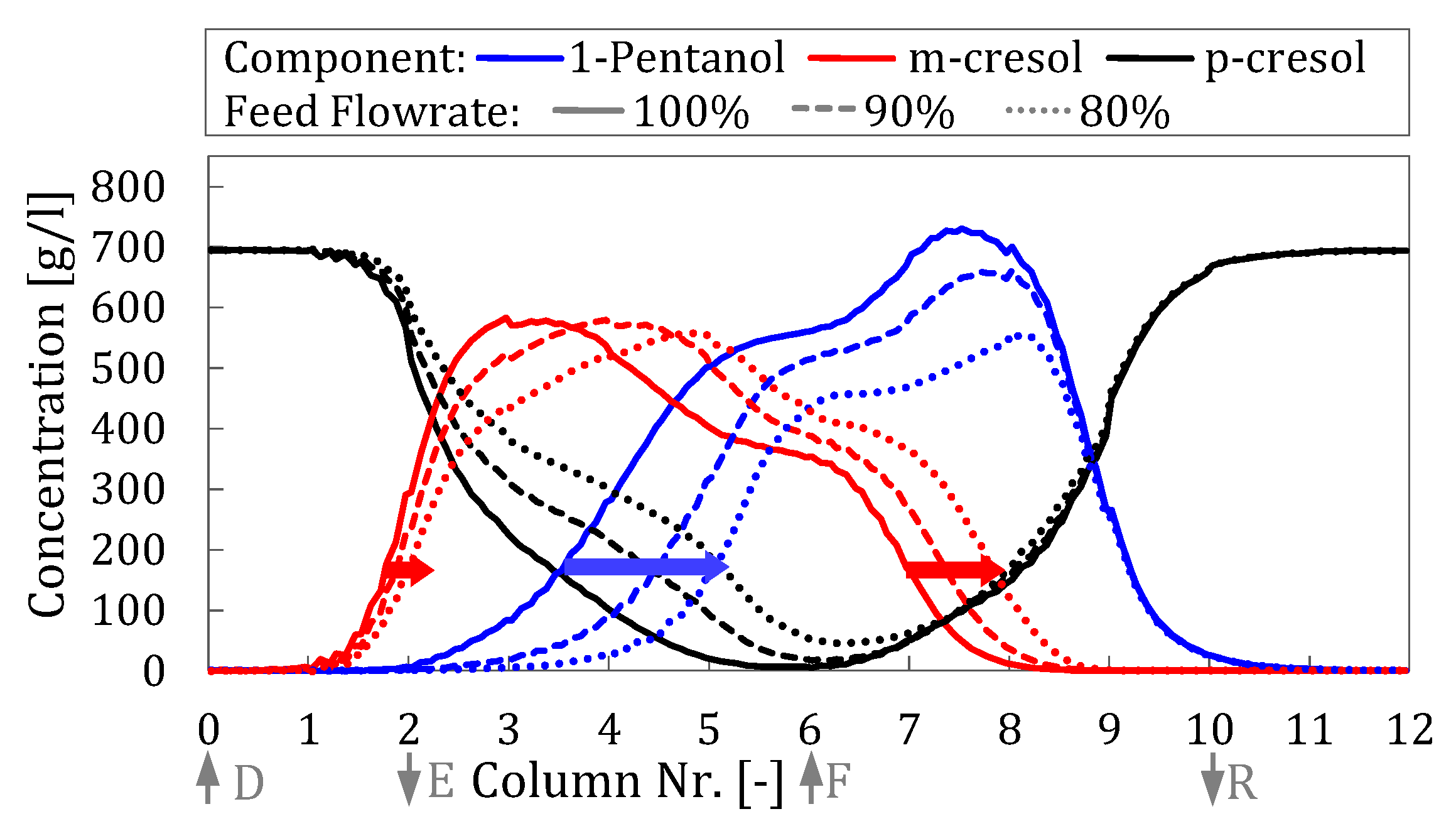
For further process optimization, it is recommended to remove potentially redundant columns. In this context, a total of four columns were classified as redundant: one column from zone I, two columns from zone II and one column from zone III. The removal of these columns enables an improvement in efficiency while keeping the feed flow constant.

Reducing the number of columns without adjusting the flow rates leads to a shift in the desorption front of the m-cresol to the left (shown in Figure 5). This occurs to such an extent that this has a significant effect on the purity of the separated products and leads to a decrease in the purity of the extract by 0.390 and 0.028% m-cresol purity in the raffinate.

Reducing the amount of feed has a positive effect on the separation of the cresols in zone II by shifting the desorption front of the m-cresol to the right. However, this shift also leads to a corresponding shift in the adsorption front of the p-cresol in zone III to the right, which results in the contamination of the raffinate phase. The influence of the feed quantity is summarized in

Table 6. Process performance for 12-column SMB process in case of reduced feed stream.

Performance Parameter	Feed Stream
	100%	90%	80%
Purity [%]	97.78	99.42	99.81
PR [kg/(m3h)]	33.32	26.02	19.23
DC [L/kg]	1.98	2.29	2.75
Purity [%]	99.97	99.90	99.50
PR [kg/(m3h)]	26.49	26.17	25.21
DC [L/kg]	2.50	2.27	2.10

for the most important performance parameters.

In order to obtain a sufficient level of purity of p-cresol, it is necessary to reduce the feed flowrate by 20%. However, the purity drops to 99.81% p-cresol in the extract and 99.50% m-cresol in the raffinate and thus falls below the required specification. These results illustrate the complex interactions between feed quantity, desorption and adsorption, which affect both the purity and the efficiency of the separation.

The results fit into the range of known large-scale SMB systems, which include up to 24 columns. For the cresol separation, the process simulation identifies an optimum process with 16 columns, and downsizing by a further 4 columns leads to a decline in the product specifications. The fact that this system operates in particularly high concentration ranges means that the SMB concentration profiles are broader than in classic SMB separations, which often operate in areas of low concentration and thus in the range of the initial gradients. The broadening of the concentration profiles requires a minimum number of columns in the individual zones in order to ensure sufficiently good separation.

3.6. Side Component Analysis

The adsorption behavior of the impurities was classified on the bases of the molecular diameter and the pKs value. Former studies have been able to establish a correspondence between the size of the molecule and the adsorption speed. The size of the molecules relates directly to the diffusion speed within the zeolite, which means that they are significantly hindered by the limitations of the pore structure [30].

Most of the secondary components can be classified as weakly absorbing components, similar to m-cresol. This behavior can be modeled in the simulation process using suitable isotherm parameters. As in the case of m-cresol, the concentration profiles of the minor components increase in zones III and IV. They accumulate in the raffinate phase due to their weak or slow adsorption.

If water is also considered a minor component, it can be described as having similar adsorption behavior to p-cresol. Therefore, water adsorption takes place in the extract. However, it is known from the literature that water adsorbs much more strongly than all other components and that a certain proportion of water is already present on the zeolite in bound form at the start of the process. A proposal for taking this effect into account for the process model was therefore made.

3.7. Water Loading

Until now, the effect of pre-adsorbed water has not been considered in SMB process models. However, it is known that the adsorption of a p-cresol/m-cresol mixture on partially hydrated Ba-X zeolites has different selectivities when the adsorbed water content is changed and 16 columns are used with a total amount of 464.024 tons of zeolite material, containing an initial water loading of 64.27 g_water/kg_Ads at an ideal water content of 4.5 wt%.

Due to the high-concentration operation point range, it can be validly assumed that the breakthrough curves are measured under the same operating conditions as in an SMB column. In this case, the zeolites are already loaded with water (LOI = 4.5 wt%) and the observed loading capacity is lower than the actual loading capacity (‘water-free’ zeolite). To take this into account, the values for q_max,i of all components were increased by the value of the initially loaded water of 64.27 g_H2O/kg_Ads.

In addition, the initial conditions of the column are changed so that all columns have a constant loading of desorbent and water. The final isotherm parameters and the SMB concentration profile are shown in Figure 6. The similar adsorption behavior of components 2,5 and 2,6 Xylenol causes an overlap between the isothermal curve and the concentration profiles in Figure 6.

The central result is that separation efficiency can be achieved despite any of the potential impurities. Therefore, the purity of the extract phase remains at 99.71%, DC = 2.59 L/kg and PR = 25.52 kg/m³h. The results of the raffinate fraction show a slight decrease in purity of 0.02% and DC of 0.09 L/kg or more. The productivity amounts to 32.72 kg/m³h.

The enrichment of the minor components is shown in

Table 7. Enrichment of minor components in product fractions.

Component	Mass Fraction in wt%
	Extract	Raffinate
1-Pentanol	72.406	53.440
p-cresol	27.374	0.0083
m-cresol	0.0786	46.358
Water	0.1392	0.1103
Impurities (total)	0.0028	0.0837

in the form of mass fractions. As can already be seen in the SMB profile, most of the enrichment of all minor components takes place in the raffinate fraction, where it amounts to 837 ppm.

By implementing water in the SMB process model as an influential component in the SMB process, the effect of constant water loading in the liquid phase and the solid phase can be described for the first time. This serves as a risk assessment based on the worst-case scenario including the effects of water, which have not yet been documented sufficiently in any experimentally investigated SMB process or their models in the literature. Nevertheless, this study points out the risks and necessary operation tasks.

3.8. Desorbent Recycling

Two rectification columns were designed for the recycling of the desorbent, in which 1-pentanol was recovered at the top and the cresol phase in the bottom. The composition of the feed is based on the results of the SMB modeling process and is summarized in Table 7.

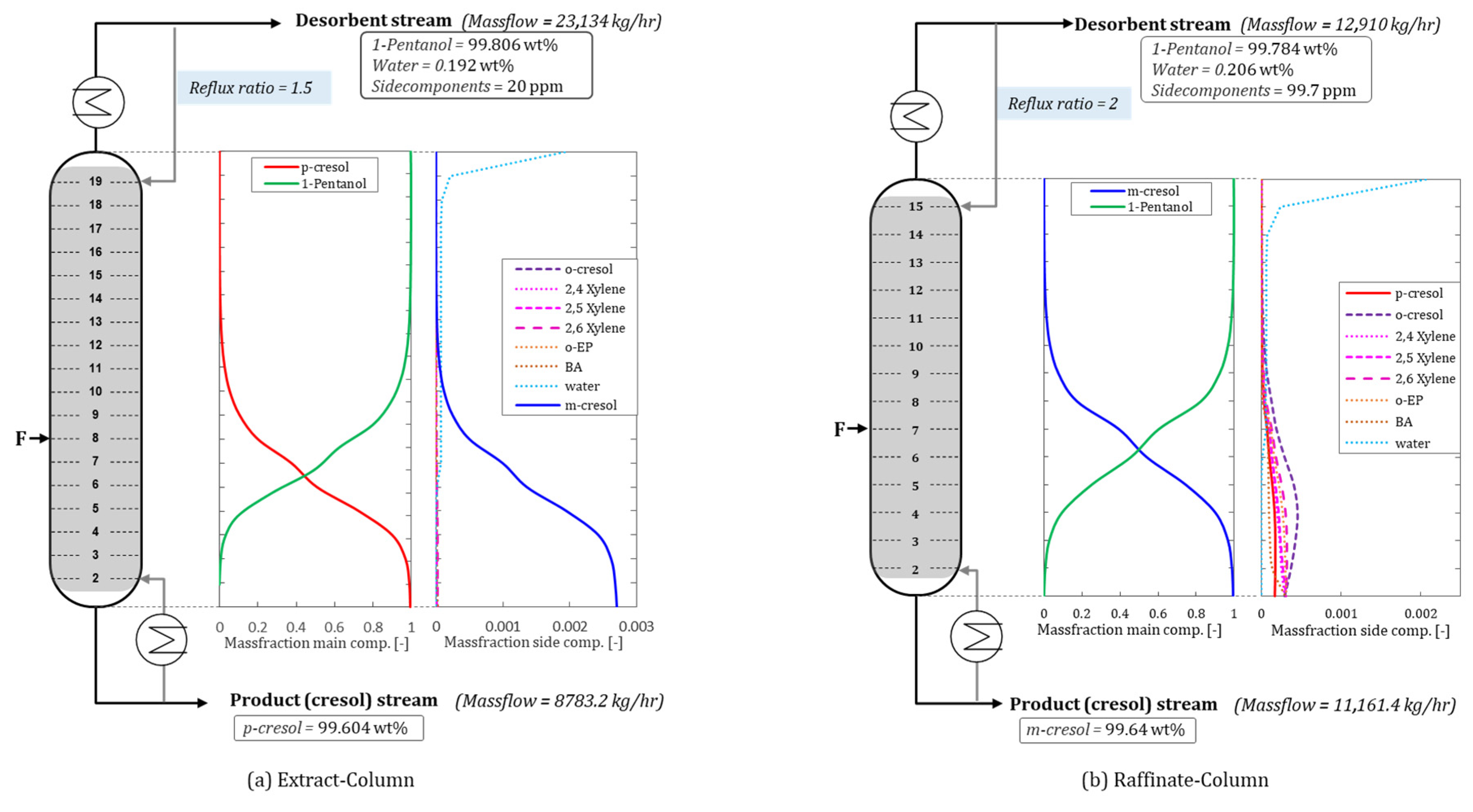
For the recycling of 1-pentanol in the extract fraction, the specifications for impurities in the overhead product are complied with at 20 ppm, whereby the permissibility limit of 100 ppm is not exceeded. The largest impurity in the overhead product is water, with a mass fraction of 1920 ppm. A packed column with 18 packed elements with a diameter of 2.5 m is required for this separation. This means that the separation takes place at a total height of 9 m. The width of the packing elements ensures a constant flood load (shown in Figure 7).

As a result of the lower feed volume flow for the raffinate stream, a rectification column with 14 packed elements is required for effective separation (d_packing = 2.2 m, h_packing = 0.5 m). The flood load of the column is also below 80% on average, which leads to a stable process operation. The specifications regarding impurities in the top product of 99.7 ppm are sufficiently well met. With this separation, an overhead product with a water content of 2060 ppm is achieved.

Both specified rectification columns achieve the required purity standards, while impurities in the overhead product can be reduced.

In particular, the process variables shown in Figure 8 relevant to long-term effects are of interest. In the experimental setting, these can only be determined by complex long-term experiments.

On the one hand, we investigate the deactivation of the adsorbent due to the availability of an irreversible bonding component in the feed, which causes a decrease in the maximum loading capacity. The adsorbent used in industrial SMB plants is traditionally designed for a long service life (10–20 years). It is known that a slow deactivation of the adsorbent occurs, and this leads to a loss of process performance. It is interesting to see how the adsorbent capacity affects the process performance and at which point the specification can no longer be maintained.

On the other hand, the effect of the amount of possible secondary components in the feed and in the desorbent that is afterwards recycled is also investigated. The intention is to determine which secondary components are to be considered critical and in what concentration. For this purpose, a qualitative quantity of 0 to 2000 ppm of impurities in the feed is assumed to be equally distributed. According to the OFAT analysis, the process and model parameters used have hardly any effect on raffinate purity if only one parameter fluctuates (see

Table 8. Final impact assessment after OFAT studies and overview of main effect, interaction, and overall severity score. Green: no impact. Yellow: minor impact. Red: major impact.

		Main Effect Ranking					Interaction Effect Ranking					Severity
Function		Impact CQA (Purity E)	Impact CQA (Purity R)	Impact PA (Extract)	Impact PA (Raffinate)	Highest Main Effect	Interaction CQA (Purity E)	Interaction CQA (Purity R)	Impact PA (Extract)	Impact PA (Raffinate)	Highest Interaction Effect
Fluid dynamic	QE	1	1	1	1	1
	QF	4	1	2	1	2
	QR	4	1	1	2	1	4	4	1	1	4	4
	QIV	8	4	4	4	8	8	8	2	2	8	64
	dp	1	1	1	2	1
	εb	8	1	4	4	8	8	8	2	2	8	64
	εp	4	4	2	1	4	4	4	1	1	4	16
	Pe	1	1	1	1	1
Equilibrium	qmax,i	8	4	4	2	8	8	8	4	4	8	64
	αij	4	4	2	2	8
Kinetic	kg,i	1	1	1	1	1
Process parameter	wFpara	1	1	1	1	1	4	1	4	4	4	4
	wFimpur.	1	4	1	1	4	4	4	1	1	4	16
	xDimpur	1	1	2	1	4	4	4	1	1	1	4
	wDwater	1	1	1	1	1
	T	4	2	4	4	4	8	8	4	4	8	32

). This was expected for raffinate purity, as the operating point for the raffinate fraction is more stable than for the extract fraction. In contrast, the adsorption of p-cresol is more sensitively influenced by several parameters. The adsorption equilibrium is influenced by the maximum loading and the separation factor.

This is first reflected in the interactions between the parameters, which is the reason why these variables are investigated via multivariate analysis in the statistical design of experiments. Furthermore, the adsorption behavior depends on the temperature. The volume flow of the recycling process, which is responsible for regeneration and significantly influences the flow rates of the zones, has a major influence on the purity of the extract. In addition, to analyze the long-term effects, the impurities in the extract and feed and the concentration fluctuations in the feed are further investigated.

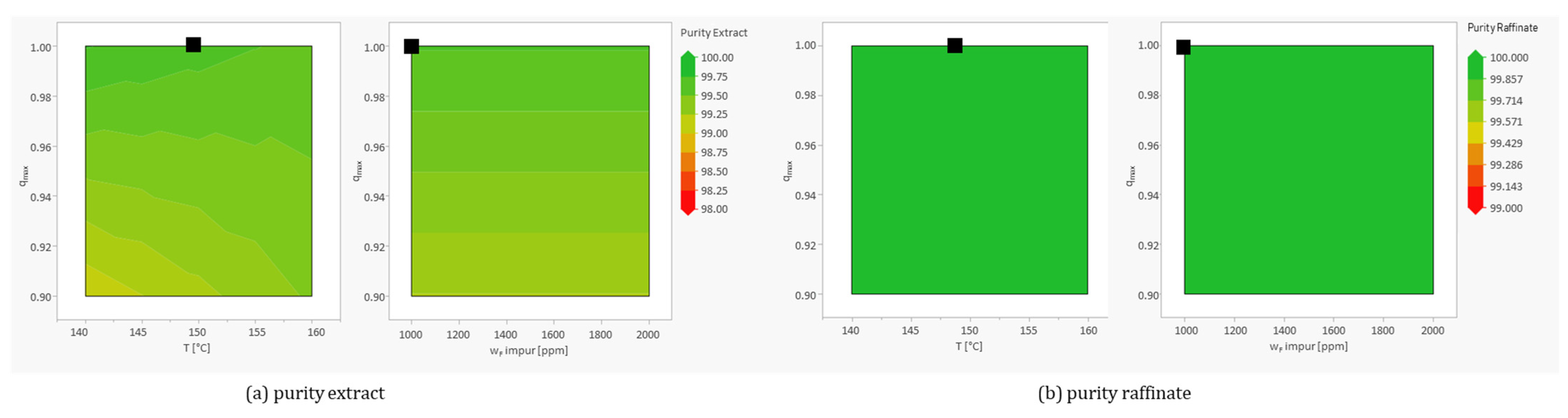
The main effect on purity is the decrease in maximum load and temperature, as well as their interactions with each other. This agrees with the results from the OFAT study. The significant importance of temperature only emerges through its interaction with other parameters (see Figure 9). Other significant factors are the fluctuating recycling flow rate and the increase in void volume.

No significant deterioration can be observed for the investigated areas of the parameters shown in Figure 9. Thus, the uninvestigated areas that represent a deterioration for maximum loading and feed contamination are not considered critical.

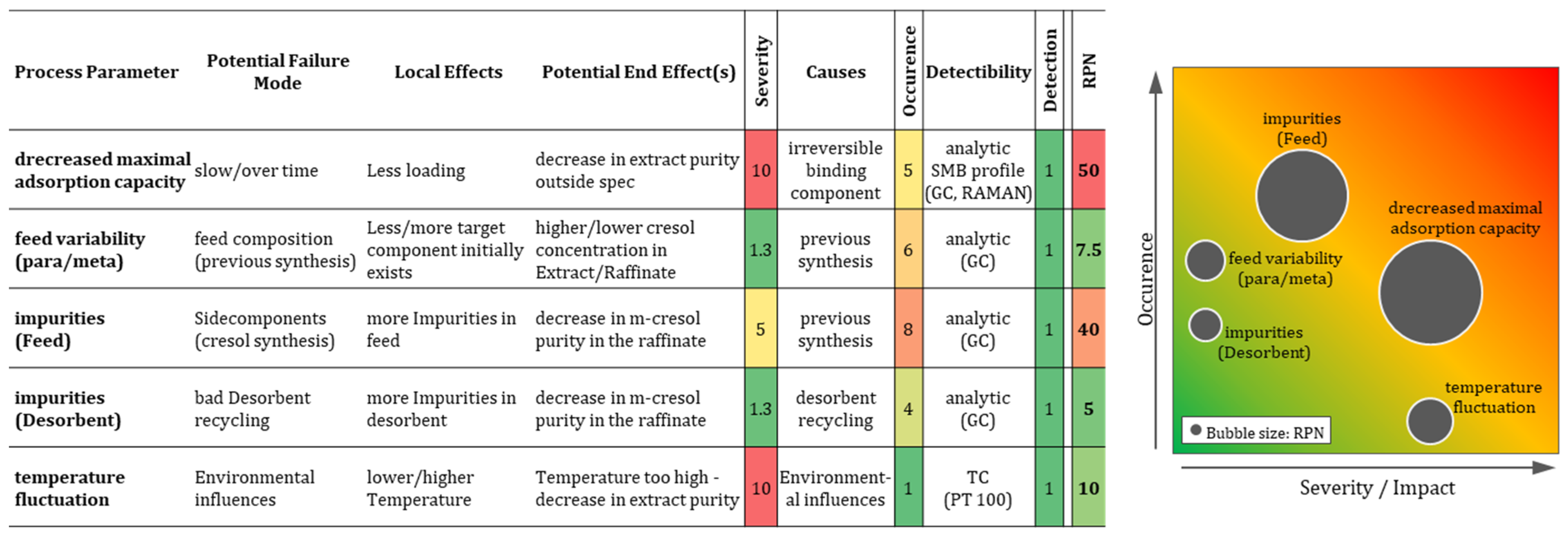
3.9. Failure Mode and Effect Analysis

Using the data from the characterization studies, an FMEA risk classification was made. Figure 10 shows the results of the process parameter risk analysis for the SMB process.

In this analysis, the effects on the product purity (m- and p-cresol) and on the PAs were taken into account. Process parameters that have a severity level ≥ 8 or an RPN > 72 are classified as CPPs (loading capacity and temperature) based on the explained approach in the Introduction. The risks determined during this assessment can be controlled by implementing the strategies listed in Figure 10. As a result, these CPPs can be classified as WC-CPPs (well-controlled critical process parameters). The RPN describes the significance of the development of suitable control mechanisms. Therefore, a worst-case scenario in relation to irreversible bonding (highest RPN) is shown.

The scenario shows that a significant decrease in loading capacity of 10% with irreversible bonding occurs after 8000 operating hours if the proportion of contamination is present in the feed at up to 7.25 ppm and is continuously transported into the SMB system in an uncontrolled way.

The lowest risk is posed by the impurities in the desorbent, which can return to the SMB process via desorbent recycling from the SMB unit. As the impurities investigated are heavier and are separated in the distillation sump, an accumulation of these components in the recycling stream can only be caused by an incorrect or insufficient operation of the distillation process. Possible temperature fluctuations have an influence on the adsorption behavior of the cresols. However, fluctuations of 10 °C are not to be considered critical as simple monitoring in real time using simple temperature sensors (Pt100) is possible and a sufficiently fast temperature adjustment can be realized.

The fluctuation in the composition of the feed in relation to the cresols can be considered uncritical in the range of 5% (m-cresol) fluctuation. While the considered amount of impurities in the feed represents a medium risk for the process quality, as the probability of occurrence cannot be directly influenced by previous syntheses, it is assumed that more impurities are quite realistic. Analyzing the feed by GC once a day is fast enough to detect these impurities as this effect occurs slowly. If it is not possible to eliminate the cause of the contamination, a timely regeneration of the zeolite can be scheduled. Alternatively, the number of columns can be increased according to the amount of adsorbent required for capacity adjustment.

As this is associated with higher operating costs and low productivity per column, the elimination of the source of contamination should be prioritized. Corresponding impurities, which are not described in the literature and are only examined here as a theoretical possibility, can, in any case, only originate from the upstream synthesis stages and should be avoided there accordingly.

The measurement technology required for this is more than fast enough in view of the long-term changes over thousands of operating hours of the CPPs through GC analysis (a few hours).

3.10. Process Simulation in Development Phase

When discussing these safety margins in terms of the accuracy and predictive reliability of simulation studies integrated with risk assessments, it becomes evident that, for a dependable conclusion, the accuracy of these simulations must fall within the defined safety margins. Only then can they serve as a decision-making criterion and potentially replace piloting and demonstration phases. It is important to note that, when comparing predictions from experimentally validated process models, the so-called “real conditions” in both pilot plant and demonstration operations—including error analysis and reproducibility at the manufacturing scale—typically lie within approximately ±5%.

In order to assess the applicability of simulation studies in risk assessment, it is essential to critically consider the main scales involved and the impacts that manifest themselves at each stage. In the development of a large-scale process, the different scales ensure an adequate process understanding during the development of new processes, minimizing risks and supporting a time- and cost-efficient project execution (see Figure 11).

Mini-plant experiments are conducted using real process streams and technical media. Separation behavior and sensitivities related to product purity—which carries the highest risk priority—are determined at this stage.

The mini-plant enables an experimental validation of the process model, quantification of model accuracy and predictive reliability [39] and identification of potential process enrichments occurring in recycle loops with original technical media. In this case, these include both the internal SMB desorbent recycle stream and desorbent recycling through one or both distillation columns where applicable. Such phenomena can be quantified and subsequently integrated into the process model, allowing it to correctly represent and predict these effects, provided they experimentally occur in reality. For accurate experimental quantification, sufficiently precise analytical methods tailored to these quantities are required. Effects that cannot be experimentally measured cannot be detected in mini-plant trials.

If the potential risk of accumulations is known at the industrial scale, it is necessary to track potential trace impurities from feedstocks or undesired reaction and decomposition products that may form during the process using advanced analytical tools such as mass spectrometry (MS) and nuclear magnetic resonance (NMR) during early lab-scale trials. These experiments must be performed with genuine technical media of industrial quality. Subsequently, mass and component balances can be conducted at an early stage using scales capable of handling volumes on the order of a few hundred milliliters.

To evaluate the necessity of this additional analytical effort, risk assessment based on a priori simulations—including all hypothetical components as representatives—is the method of choice. It is inefficient to pilot several hundred kilograms aiming to detect every minor impurity with standard coarse analytics or to be confronted by unexpected impurities at the production scale. Nevertheless, many approaches exist at the production scale to manage these challenges, especially if, guided by the results of the risk assessment, the prioritization of flushing, regeneration, or cleaning is implemented. Should test quantities of impurities be required for regulatory purposes, operations at the mini-plant scale are sufficient to generate the necessary amounts—ranging from a few milligrams to grams—of trace components. From a risk management perspective, it is also possible to evaluate hypothetical quantities and components and discuss their probabilities to determine whether prolonged enrichment studies in a mini-plant—spanning several months—would be justified and deliver added value.

The accuracy and predictive reliability of the process model lie within the experimental error margin of the mini-plant when the mini-plant trial errors are considered as a worst-case scenario in the simulated risk analysis. The fluid dynamics of the mini-plant unit are well characterized and incorporated as residence time distributions into the dynamic process model, including equipment hold-ups, based on the apparatus dimensions to describe the mini-plant experiments. Mass transfer/reaction kinetics and phase equilibrium/reaction equilibrium are scale-independent and have previously been determined with maximum accuracy at the laboratory scale. Consequently, the only scale-dependent aspect in a dynamic process model is fluid dynamics—provided that a physico-chemical mechanistic modeling approach, rather than a purely statistical one, is applied that correctly separates the individual effects.

Pilot Plant: Subsequent piloting primarily serves to investigate the scale-up behavior concerning fluid dynamics. This means operating, without the separation of substances, only the main phases without transient components to establish the operating range between the flooding and loading limits of the apparatus’ fluid dynamic performance. These reference values are scaled up to the large-scale plant using internal benchmark data from historically realized full-scale installations relative to the pilot plant scale. The known fluid dynamic and residence time distribution characteristics of the large-scale plant are used to adjust parameters such as equipment dimensions, hold-ups, and dispersion/back-mixing within the process model, enabling an accurate prediction of the industrial plant’s performance in terms of product purity and throughput.

Considering additionally that, at a larger scale, packing quality is generally lower and apparatus control and regulation inaccuracies, as well as hold-up and residence time distribution fluctuations, tend to increase, the operating point may shift by up to 1–3% relative to the mini-plant conditions. However, this deviation is still covered by the previously mentioned 5% throughput margin without added risk [25].

For assessing the risk associated with prediction accuracy and reliability, the most methodologically sound approach is to quantify them in a data-driven way, for example, through Monte Carlo simulation studies. This approach is analogous to methods utilized in financial investor banking, where it has been successfully applied and accepted for decades in the context of large investment sums and risks. Therefore, it is equally acceptable for investment decisions in the chemical–pharmaceutical process engineering sector.

Aging effects in particular can be efficiently investigated on a laboratory scale. The use of smaller quantities of auxiliary materials minimizes both costs and effort. In just a few weeks in a laboratory, an operation can imitate over several years of production. To achieve this, a stable and safe operating point is first determined, which is designed through studies with low, medium and high throughput or load. At this operating point, all necessary enrichments can then be integrated as they depend directly on the flow conditions.

Experimental enrichment studies also require a few months in a mini-plant, which makes a longer operation necessary to imitate a 1–5-year production cycle before typical revision cycles occur. In a continuous operation, for example, with five shifts and at least two operators per shift for safety reasons, a considerable amount of time, work and cost is required, which can quickly rise to an additional EUR 1–3 million.

However, this high expenditure is often not in proportion to the potential benefits of risk reduction. Through careful risk assessment, supported by laboratory-scale experiments and process simulations, the entire process can be better understood and optimized. Good process simulation can be used as a tool to replace pilot and demonstrator phases. As a result, subsequent steps in process development can be made more efficient, which ultimately leads to greater efficiency and reliability of the entire process

4. Conclusions

In order to include enrichment studies for risk assessment, for the model-based design and optimization of the total SMB process including raffinate and extract desorbent recycling distillation columns with a closed desorbent cycle and an SMB internal desorbent recycling cycle, the necessary design and operating parameters were at first determined based on the literature data. Possible impurities from cresol synthesis were divided into weak bonding impurities, which were to be found in the raffinate, and strong bonding impurities, which were found in the extract, based on their material properties (size and pKs value). These effects could be implemented in the total process simulations using suitable model parameters.

For desorbent recovery, two rectification columns were designed on the basis of de-tailed rate-based modeling. The raffinate and extract column can ensure the continuous recovery of the desorbent with a maximum of 100 ppm impurity of the high boilers in the overhead product and a throughput of 1785 kgDes./h (extract) and 1202 kgDes./h (raffinate). The concentration of any hypothetical impurity in the recycled desorbent was determined to be max. 49 ppm. The types of potential impurities are realistically assumed based on the literature, but the impurity concentrations are not documented in the literature; as has been seen and measured, their maximal limit is defined by risk assessment studies.

The FMEA revealed that in a hypothetical worst-case scenario, irreversible contamination reduces the loading capacity of the zeolite by blocking bonding areas and reducing the maximum loading for the cresols. It is demonstrated that at 8000 operating hours, an irreversible bonding component, which leads to a capacity loss of 10%, can only be considered critical from a feed concentration over 7.25 ppm. If any accumulation was detected, a technically straightforward measure would be to successively replenish the adsorbent in the last column—typically installed as an additional safety column in zone 1 (adsorbent cleaning function) —with a fresh adsorbent for each cycle, reintegrating it into the SMB sequence until all 16 columns are completely renewed, without interrupting the continuous process. In a worst-case scenario, this approach would increase operating costs by approximately 5% due to the somewhat earlier adsorbent replacement than initially planned. This presents no significant risk and can be considered a feasible solution.

Potential accumulations in the SMB desorbent recycle loops or in the two distillation columns, if they do occur, could be mitigated by implementing a purge. A straightforward technical measure would be to design a purge option for the system beforehand. This would not noticeably increase investment costs and would raise operating costs in proportion to the amount of desorbent replaced—typically 5–10%—resulting in an approximate 1–2% increase in operational expenses. This also poses no significant risk and may be a viable solution. The risk analysis demonstrated that product purity can be assured within a margin of ±5% in the m/p ratios, thus ensuring a reliably predictable and realistically safe operation. The impurity concentration of 1000–2000 ppm is not risk-relevant with regard to the specifications required.

The simulation studies completed as part of the FMEA identify critical process parameters and can be used in statistically robust regression models to define the design space. Corresponding polynomials were developed to evaluate product quality. With all results of the simulation study, a certain residual risk remains based on the process model. Despite extensive model validation, it cannot be ruled out that all real effects are captured. Even with this consideration, no critical loss of capacity could be identified, and all specifications remain within the required framework.

While the results based on rigorous process modeling and laboratory- or mini-plant-scale model parameter determination provide strong evidence that piloting trials for the total process, including desorbent recycling cycles, may often be unnecessary and uneconomical, it should be emphasized that this conclusion may not be universally applicable. The redundancy of pilot plants depends on the robustness of the applied modeling approach, the certainty of parameter determination, and the complexity or novelty of the process in question. In situations where there remain significant unknowns or the potential for unexpected scale-dependent effects, piloting may still play a crucial role in risk management and final validation. Thus, although process simulation studies and risk assessments based on established QbD methods can substantially reduce the reliance on piloting, a case-by-case evaluation is required to ensure that process safety and performance criteria are fully met.

This is exemplified for different manufacturing plant scales of 10,000, 100,000 and 1,000,000 mt per year, with corresponding investments of approximately EUR 20, 200 and 2000 million achieved by realistic piloting and demonstrator costs and timelines, as shown in Figure 12. It is important to note that these ROI estimates are based on the literature values and model assumptions rather than comprehensive empirical data or detailed case studies. The absence of primary, industry-based empirical validation is recognized as a limitation of the present work and an important avenue for future research.

Scenarios 2 and 3 demonstrate, for varying scales, the potential advantages of risk assessment through process simulation studies, which are based on parameter determination for miniaturized laboratory models and subsequent validation by mini-plant technology, allowing for the possibility of skipping pilot and demonstration plant operations. These advantages are most evident at a small scale: here, the time to market can be reduced to 73% by replacing the demonstrator with a simulation and even to 47% when both the pilot plant and the demonstrator are replaced by simulations. Investment costs, under these model-based assumptions, may be reduced by 30% to 63%. The subjective and scenario-based nature of these estimates, however, underscores the need for further empirical study and validation using detailed real-world industry data.

This study is based on the literature laboratory-scale experiments for the model parameter determination of a process model. A validation of the proposed operation point will be performed as the next step on a mini-plant, e.g., one with a 10 mm column diameter. It is not worth following this up with multi-month and costly enrichment studies as the risk assessment points out, with 99% certainty, that the level of risk will remain within the 5% capacity safety margin. Moreover, it is still feasible to implement purges in the recycling streams of the SMB and for distillation units to copy any unpredictable worst-case scenario. Therefore, while piloting and demonstrators can often be omitted within an acceptable risk margin, this decision should always consider any residual uncertainty and the specific context of the process.

The advantages in terms of the break-even point are obvious over a wide range and should motivate the industry to use these innovative, documented methods more strategically in its daily work. The responsible lead project engineer is thus given a cost-efficient and fast tool to quantify risk transparently in order to support their technical decisions towards management investor decisions.