Experimental Study on Water-Hammer-Effect Fracturing Based on High-Frequency Pressure Monitoring
Abstract
1. Introduction
2. Methods
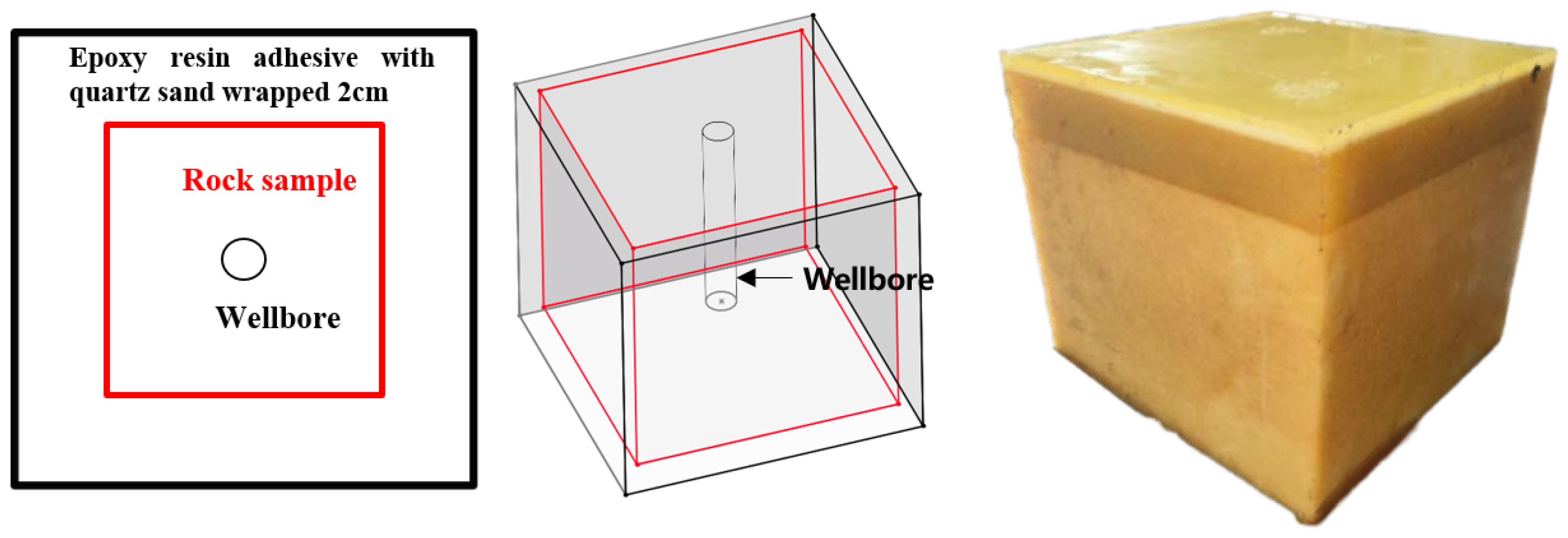
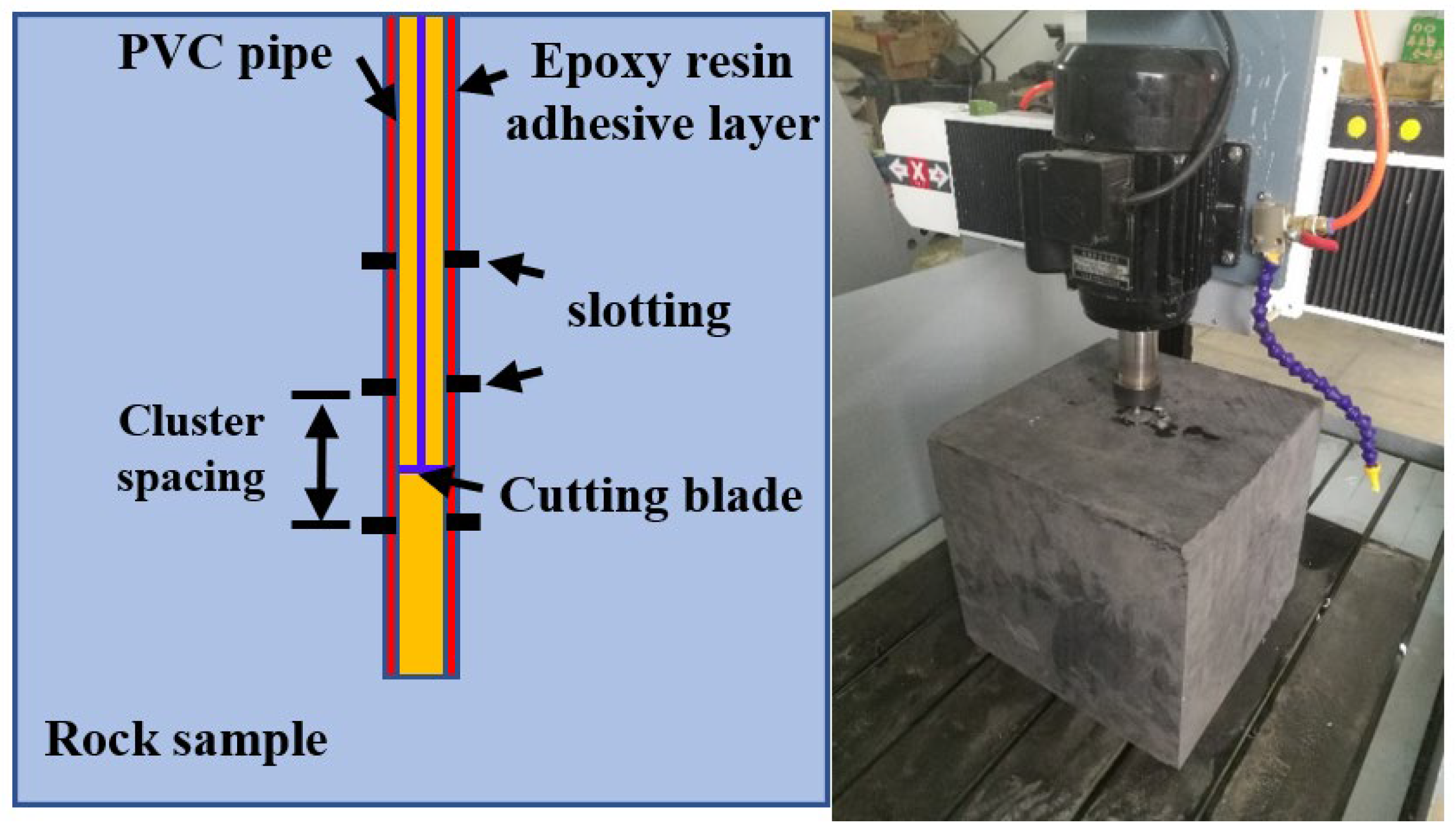
2.1. Fracturing Sample Preparation
2.2. Experimental Parameter Design
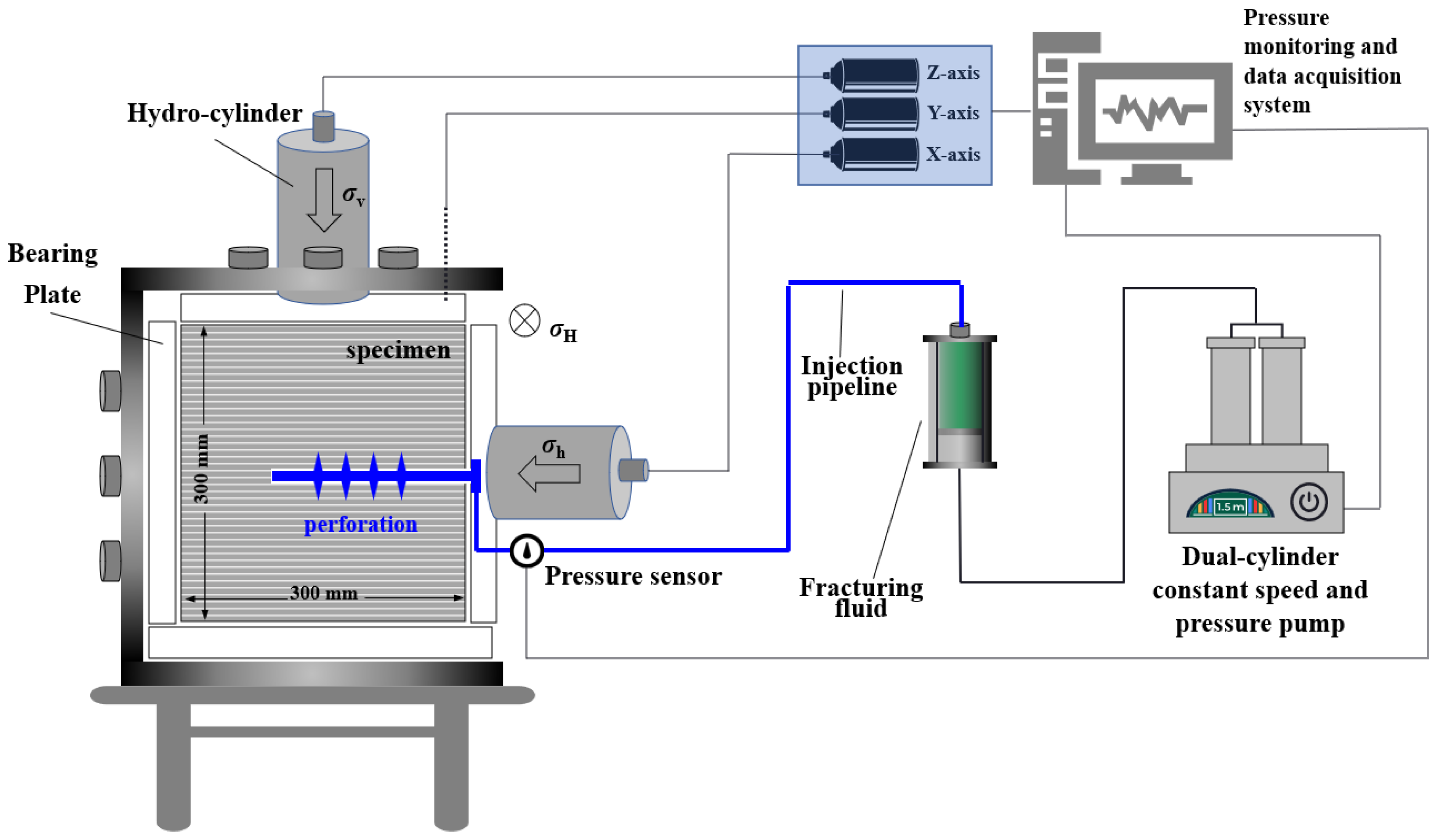
2.3. Experimental Equipment
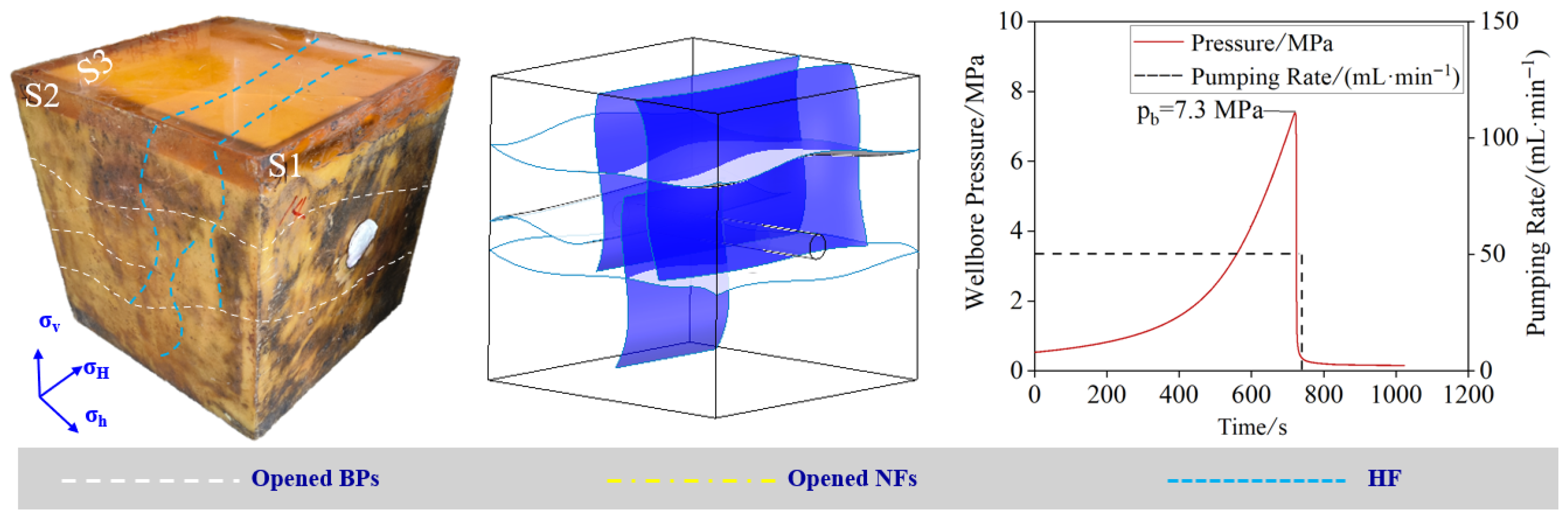
2.4. Experimental Procedures and Methodology
3. Results and Discussion
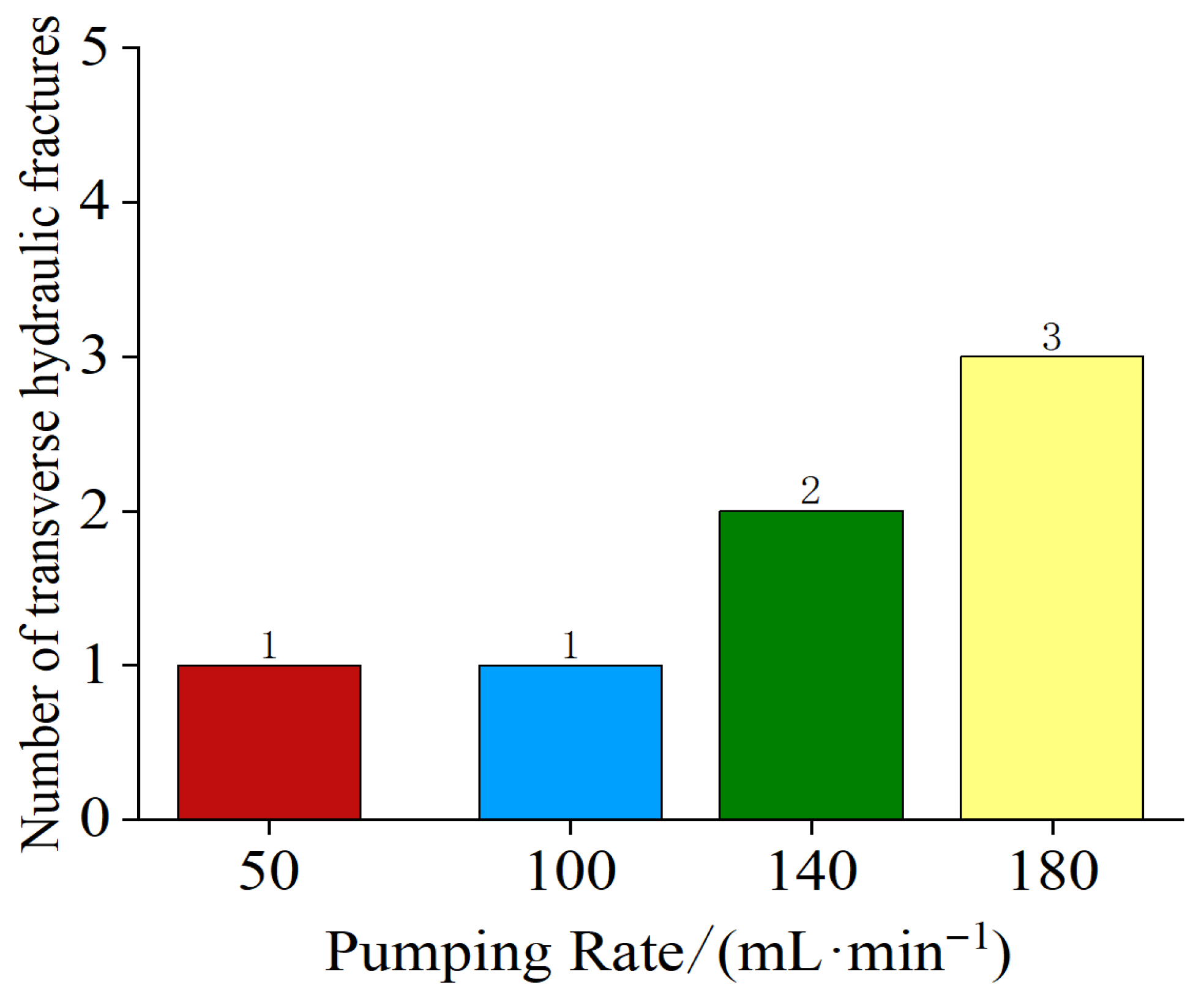
3.1. Influence of Flow Rate
3.2. Influence of Fracturing Fluid Viscosity
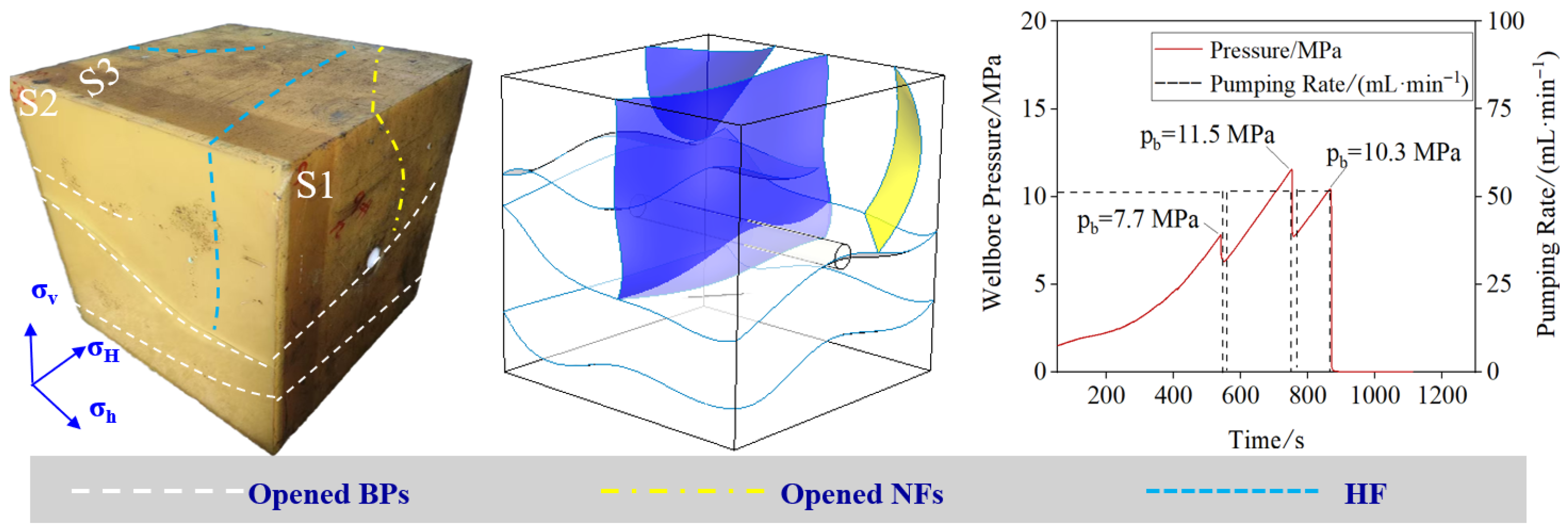
3.3. Relationship Between Water Hammer Curves and Fracture Morphology
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.N.; Yang, Z.; Cui, J.W.; Zhu, R.K.; Hou, L.H.; Tao, S.Z.; Yuan, X.J.; Wu, S.T.; Lin, S.H.; Wang, L.; et al. Formation mechanism, geological characteristics, and development strategy of nonmarine shale oil in China. Pet. Explor. Dev. 2013, 40, 15–27. [Google Scholar] [CrossRef]
- Zhao, W.Z.; Hu, S.Y.; Hou, L.H.; Yang, T.; Li, X.; Guo, B.C.; Yang, Z. Types and resource potential of continental shale oil in China and its boundary with tight oil. Pet. Explor. Dev. 2020, 47, 1–11. [Google Scholar] [CrossRef]
- Li, G.X.; Wang, F.; Pi, X.J.; Liu, H. Optimized application of geology-engineering integration data of unconventional oil and gas reservoirs. China Pet. Explor. 2019, 24, 147–152. [Google Scholar] [CrossRef]
- Jiao, F.Z. Re-recognition of “unconventional” in unconventional oil and gas. Pet. Explor. Dev. 2019, 46, 847–855. [Google Scholar] [CrossRef]
- Lei, Q.; Xu, Y.; Cai, B.; Guan, B.; Wang, X.; Bi, G.; Li, H.; Li, S.; Ding, B.; Fu, H.; et al. Progress and prospects of horizontal well fracturing technology for shale oil and gas reservoirs. Pet. Explor. Dev. 2022, 49, 191–199. [Google Scholar] [CrossRef]
- Carey, M.A.; Mondal, S.; Sharma, M.M. Analysis of water hammer signatures for fracture diagnostics. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; SPE: Richardson, TX, USA, 2015. No. SPE-174866-MS. [Google Scholar] [CrossRef]
- Carey, M.A.; Mondal, S.; Sharma, M.M.; Hebert, D.B. Correlating water hammer signatures with production log and microseismic data in fractured horizontal wells. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016; SPE: Richardson, TX, USA, 2016. No. SPE-179108-MS. [Google Scholar] [CrossRef]
- Hwang, J.; Szabian, M.J.; Sharma, M.M. Hydraulic fracture diagnostics and stress interference analysis by water hammer signatures in multi-stage pumping data. In Proceedings of the Unconventional Resources Technology Conference (URTeC), Austin, TX, USA, 24–26 July 2017; URTEC: Austin, TX, USA, 2017. No. URTEC-2687423-MS. [Google Scholar] [CrossRef]
- Panjaitan, M.L.; Moriyama, A.; McMillan, D.; Dunaeva, A.; Rutledge, L.; Xu, J.; Parkhonyuk, S.; Kabannik, A.; Korkin, R.; Warren, M. Qualifying diversion in multi clusters horizontal well hydraulic fracturing in haynesville shale using water hammer analysis, step-down test and microseismic data. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018; SPE: Richardson, TX, USA, 2018. No. SPE-189850-MS. [Google Scholar] [CrossRef]
- Dung, N.; David, C.; Tom, D.; Jon, S.; Nico, R.; Annie, O. Practical applications of water hammer analysis from hydraulic fracturing treatments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 May 2021; SPE: Richardson, TX, USA, 2021. No. SPE-204154-MS. [Google Scholar] [CrossRef]
- Ma, X.; Zhou, F.; Andrade, J.A.O.; Gosavi, S.V.; Burch, D. Evaluation of water hammer analysis as diagnostic tool for hydraulic fracturing. In Proceedings of the Unconventional Resources Technology Conference (URTeC), Denver, CO, USA, 22–24 July 2019; URTEC: Denver, CO, USA, 2019. No. URTEC-2019-935-MS. [Google Scholar] [CrossRef]
- Bergant, A.; Tijsseling, A.S.; Vítkovský, J.P.; Covas, D.I.C.; Simpson, A.R.; Lambert, M.F. Parameters affecting water-hammer wave attenuation, shape and timing—Part 2: Case studies. J. Hydraul. Res. 2008, 46, 382–391. [Google Scholar] [CrossRef]
- Saldungaray, P.; Duenckel, R.; Palisch, T. Reducing hydraulic fracturing HSE footprint through the application of a non-radioactive method for proppant placement and propped fracture height assessment. In Proceedings of the SPE Middle East Health, Safety, Security, and Environment Conference and Exhibition, Doha, Qatar, 22–24 September 2014; SPE: Richardson, TX, USA, 2014; p. SPE-170333-MS. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Xu, Y.; Zhang, J.J.; Su, J.F. Apply relief valve against surge to protect long-distance pipeline. Oil Gas Storage Transp. 2006, 25, 58–61. [Google Scholar] [CrossRef]
- Zhao, B.L.; Xu, S.R.; Yu, T.C.; Shao, Y. Variation of transient pressure in leaking water pipe network. China Water Wastewater 2019, 35, 40–45. [Google Scholar] [CrossRef]
- Guo, X.L.; Yang, K.L.; Guo, Y.X.; Wang, T.; Fu, H. Transient pressure rise method for leak detection in pipeline systems. J. Basic Sci. Eng. 2011, 19, 20–28. [Google Scholar] [CrossRef]
- Hu, X.D.; Li, Z.L.; Zhou, F.J.; Qiu, Y.; Li, Y.J.; Luo, Y.H. Water hammer waveform-based experimental study on wave velocity inversion method. Water Resour. Hydropower Eng. 2022, 53, 106–118. [Google Scholar] [CrossRef]
- Qiu, Y.; Hu, X.D.; Zhou, F.J.; Jiang, Z.S.; Wang, Y.J.; Lu, X.T.; Li, J.Y.; Yi, P.K. Study on influence factors of wellhead water hammer response characteristics after fracturing pumps shutdown. Chin. J. Hydrodyn. 2023, 38, 965–973. [Google Scholar] [CrossRef]
- Iriarte, J.; Merritt, J.; Kreyche, B. Using water hammer characteristics as a fracture treatment diagnostic. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium, Oklahoma City, OK, USA, 27–31 March 2017; SPE: Richardson, TX, USA, 2017. No. SPE-185087-MS. [Google Scholar] [CrossRef]
- Qiu, Y.; Hu, X.; Zhou, F.; Yi, P.; Wang, Y.; Jiang, Z. A New Investigation of Wellbore Parameters Influence on Shut-In Pressure Transient Signatures from Water Hammer Fracture Diagnostics. In Proceedings of the SPE International Hydraulic Fracturing Technology Conference and Exhibition, Muscat, Oman, 12–14 September 2023. [Google Scholar]
- Mondal, S. Pressure Transients in Wellbores: Water Hammer Effects and Implications for Fracture Diagnostics. Master’s Thesis, The University of Texas at Austin, Austin, TX, USA, 2010. [Google Scholar]
- Haustveit, K.; Dahlgren, K.; Greenwood, H.; Peryam, T.; Kennedy, B.; Dawson, M. New age fracture mapping diagnostic tools-A STACK case study. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 24–26 January 2017; SPE: Richardson, TX, USA, 2017. No. SPE-184862-MS. [Google Scholar] [CrossRef]
- Luo, Y.H.; Hu, X.D.; Zhou, F.J.; Qiu, Y.; Lu, X.T.; Li, J.Y.; Wang, Y.J. A new water hammer decay model: Analyzing the interference of multiple fractures and perforations on decay rate. SPE J. 2023, 28, 1973–1985. [Google Scholar] [CrossRef]
- Shen, J.G.; He, H.Y.; Li, Y.C.; Zou, L.Q.; Wang, Y.X.; Zhu, Z.Y.; Guo, L.K.; Fu, S.R. An investigation of data analysis method for hydraulic fracturing based on the water hammer effect. Unconv. Resour. 2023, 3, 284–290. [Google Scholar] [CrossRef]
- Parkhonyuk, S.; Fedorov, A.; Kabannik, A.; Korkin, R.; Nikolaev, M.; Tsygulev, I. Measurements while fracturing: Nonintrusive method of hydraulic fracturing monitoring. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018; SPE: Richardson, TX, USA, 2018. No. SPE-189866-MS. [Google Scholar] [CrossRef]
- Wang, X.Q.; Dong, Y.; Li, P.C.; Jin, J.; Lu, D.T. Location estimation of subsurface fluid-filled fractures: Cepstral predominant peak analysis and numerical study. Phys. Fluids 2022, 34, 043102. [Google Scholar] [CrossRef]
- Wang, X.Q.; Zhao, L.; Wang, Z.Y.; Xiu, C.H.; Jia, G.L.; Dong, Y.; Lu, D.T. Data analysis method of pump shutdown pressure based on water hammer effect and cepstrum transformation. Reserv. Eval. Dev. 2023, 13, 108–116. [Google Scholar] [CrossRef]
- Korkin, R.; Parkhonyuk, S.; Fedorov, A.; Badazhkov, D.; Kabannik, A. High frequency pressure monitoring and data analytics for stimulation efficiency determination: New perspectives or potential limits. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 4–6 February 2020; SPE: Richardson, TX, USA, 2020. No. SPE-199762-MS. [Google Scholar] [CrossRef]
- Yong, R.; Qiu, Y.; Zhou, F.J.; Hu, X.D.; Song, Y.; Zhou, X.J. The evaluation of temporary plugging effect in shale gas wells based on high-frequency water hammer pressure. Pet. Sci. Bull. 2024, 9, 789–797. [Google Scholar] [CrossRef]
- Qiu, Y.; Hu, X.D.; Zhou, F.J.; Li, Z.L.; Li, Y.J.; Luo, Y.H. Water hammer response characteristics of wellbore-fracture system: Multi-dimensional analysis in time, frequency and quefrency domain. J. Pet. Sci. Eng. 2022, 213, 110425. [Google Scholar] [CrossRef]
- Sun, S.; He, Y.; Li, Y.; Liu, L.; Liu, Y.; Zou, L.; Ma, H. A Novel Comprehensive Water Hammer Pressure Model for Fracture Geometry Evaluation. SPE J. 2025, 30, 5350–5366. [Google Scholar] [CrossRef]
- Detournay, E. Mechanics of hydraulic fractures. Annu. Rev. Fluid Mech. 2016, 48, 311–339. [Google Scholar] [CrossRef]
- Dontsov, E.V. An approximate solution for a penny-shaped hydraulic fracture that accounts for fracture toughness, fluid viscosity and leak-off. Roy. Soc. Open Sci. 2016, 3, 160737. [Google Scholar] [CrossRef] [PubMed]
- Madyarov, A.; Prioul, R.; Zutshi, A.; Seprodi, N.; Groves, D.; Pei, J.; Wong, S. Understanding the impact of completion designs on multi-stage fracturing via block test experiments. In Proceedings of the 55th US Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 18–25 June 2021; ARMA: Alexandria, VA, USA, 2021. No. ARMA-2021-1309. [Google Scholar]
- Bunger, A.P.; Jeffrey, R.G.; Detournay, E. Application of scaling laws to laboratory-scale hydraulic fractures. In Proceedings of the 40th US Symposium on Rock Mechanics (USRMS), Anchorage, AK, USA, 25–29 June 2005; ARMA: Alexandria, VA, USA, 2005. No. ARMA-05-818. [Google Scholar]
- Zhang, S.C.; Li, S.H.; Zou, Y.S.; Li, J.M.; Ma, X.F.; Zhang, X.H.; Wang, Z.F.; Wu, S. Experimental study on fracture height propagation during multi-stage fracturing of horizontal wells in shale oil reservoirs. J. China Univ. Pet. 2021, 45, 77–86. [Google Scholar] [CrossRef]
- Zou, Y.S.; Gao, B.D.; Zhang, S.C.; Ma, X.F.; Sun, Z.Y.; Wang, F.; Liu, C.Y. Multi-fracture nonuniform initiation and vertical propagation behavior in thin interbedded tight sandstone: An experimental study. J. Pet. Sci. Eng. 2022, 213, 110417. [Google Scholar] [CrossRef]
- Ishida, T.; Chen, Q.; Mizuta, Y. Influence of fluid viscosity on the hydraulic fracturing mechanism. J. Energy Resour. Technol. 2004, 126, 190–195. [Google Scholar] [CrossRef]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 1023–1034. [Google Scholar] [CrossRef]

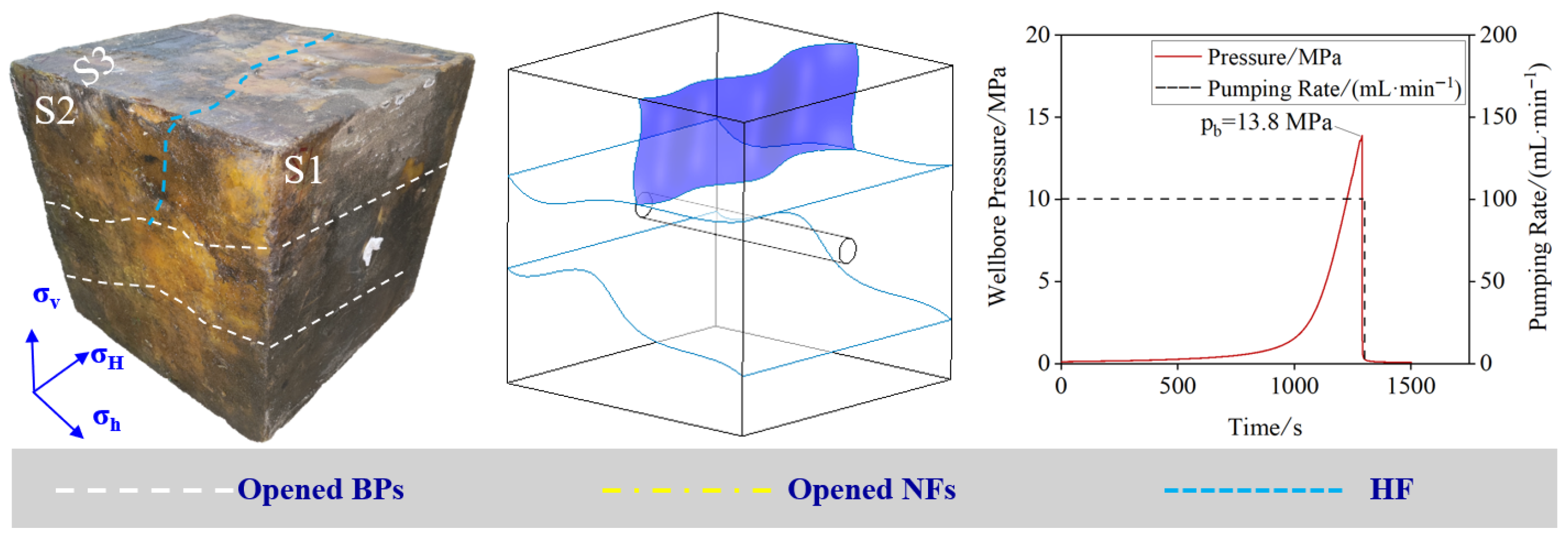
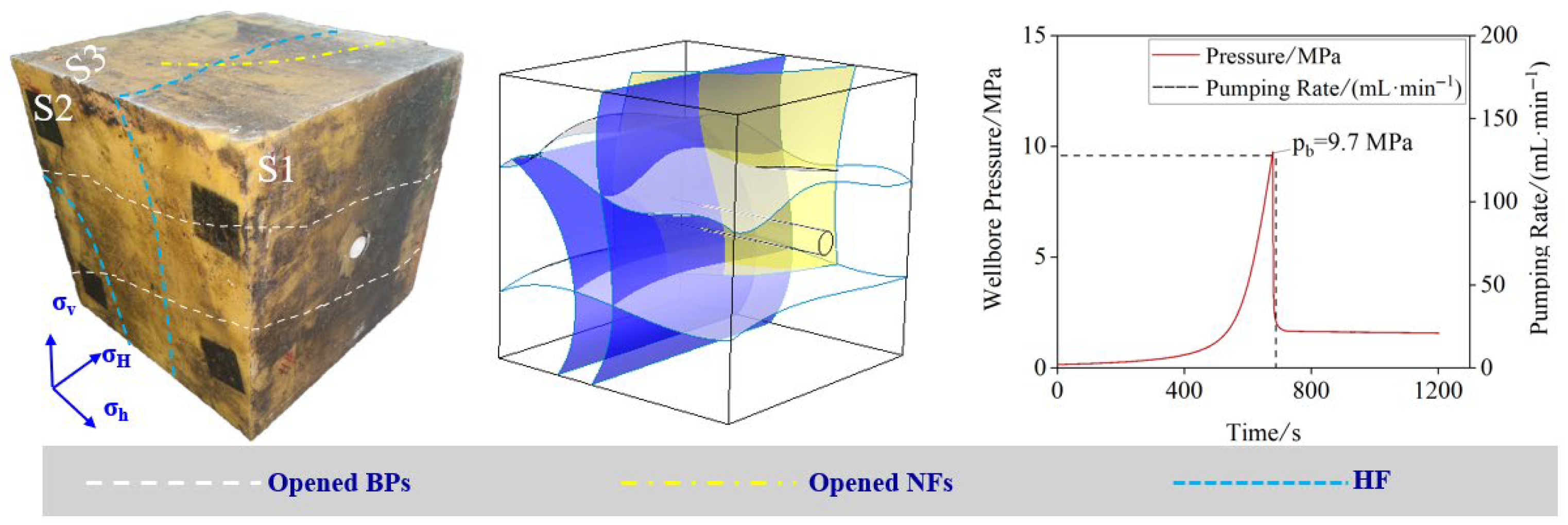
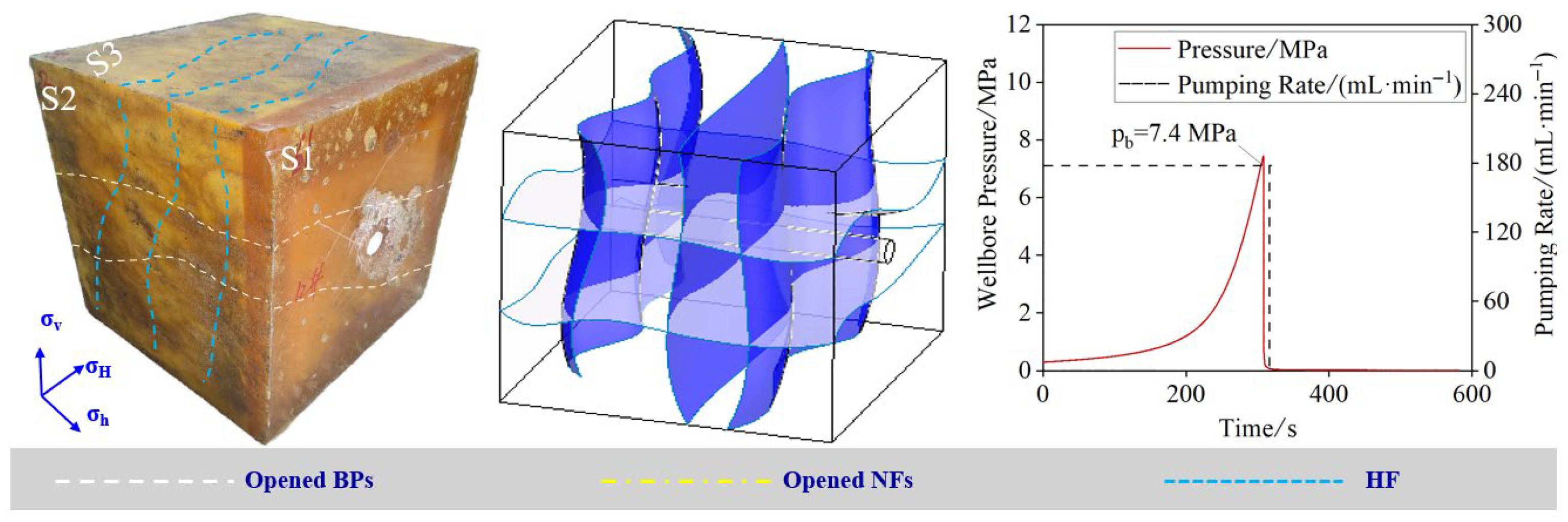



| Core Direction | Elastic Modulus/GPa | Compressive Strength/MPa | Tensile Strength/MPa |
|---|---|---|---|
| Parallel to bedding | 49.1 | 244.1 | 6.5 |
| Vertical to bedding | 40.3 | 300.9 | 9.3 |
| Rock Sample Number | 1# | 2# | 3# | 4# | 5# | 6# |
|---|---|---|---|---|---|---|
| Pre-fracturing Characteristics of Rock Samples | A bedding plane opened 5 cm below the wellbore | One bedding plane noticeably opened 5 cm above the wellbore, and another 5 cm below the wellbore | One bedding plane opened 6 cm above the wellbore, and another opened 5 cm below the wellbore | One bedding plane opened 3 cm above the wellbore, and another opened 4 cm below the wellbore | One bedding plane opened 3 cm below the wellbore | One bedding plane opened 7 cm above the wellbore |
| Rock Sample Number | Horizontal Stress Difference/MPa (σH-σh) | Displacement/(mL·min−1) | Fracturing Fluid Viscosity/mPa·s | Number of Clusters | Cluster Spacing/cm |
|---|---|---|---|---|---|
| 1 | 14 | 50 | 3–5 | 7 | 3 |
| 2 | 14 | 100 | 3–5 | 7 | 3 |
| 3 | 14 | 140 | 3–5 | 7 | 3 |
| 4 | 14 | 180 | 3–5 | 3 | 3 |
| 5 | 14 | 50 | 8–10 | 7 | 3 |
| 6 | 14 | 50 | 12–15 | 7 | 3 |
| Rock Sample Number | 1# | 3# | 5# | 6# |
| Decay Rate | 2.03 | 5.28 | 6.77 | 6.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Sun, H.; Zou, L.; Yang, L.; Jiang, H.; Zhao, Z.; Sun, R.; Zou, Y. Experimental Study on Water-Hammer-Effect Fracturing Based on High-Frequency Pressure Monitoring. Processes 2025, 13, 2900. https://doi.org/10.3390/pr13092900
Li Y, Sun H, Zou L, Yang L, Jiang H, Zhao Z, Sun R, Zou Y. Experimental Study on Water-Hammer-Effect Fracturing Based on High-Frequency Pressure Monitoring. Processes. 2025; 13(9):2900. https://doi.org/10.3390/pr13092900
Chicago/Turabian StyleLi, Yanchao, Hu Sun, Longqing Zou, Liang Yang, Hao Jiang, Zhiming Zhao, Ruchao Sun, and Yushi Zou. 2025. "Experimental Study on Water-Hammer-Effect Fracturing Based on High-Frequency Pressure Monitoring" Processes 13, no. 9: 2900. https://doi.org/10.3390/pr13092900
APA StyleLi, Y., Sun, H., Zou, L., Yang, L., Jiang, H., Zhao, Z., Sun, R., & Zou, Y. (2025). Experimental Study on Water-Hammer-Effect Fracturing Based on High-Frequency Pressure Monitoring. Processes, 13(9), 2900. https://doi.org/10.3390/pr13092900






