Mass Transfer Mechanism and Process Parameters in Glycerol Using Resonant Acoustic Mixing Technology
Abstract
1. Introduction
2. Methods and Theory
3. Numerical Simulation
4. Results and Discussion
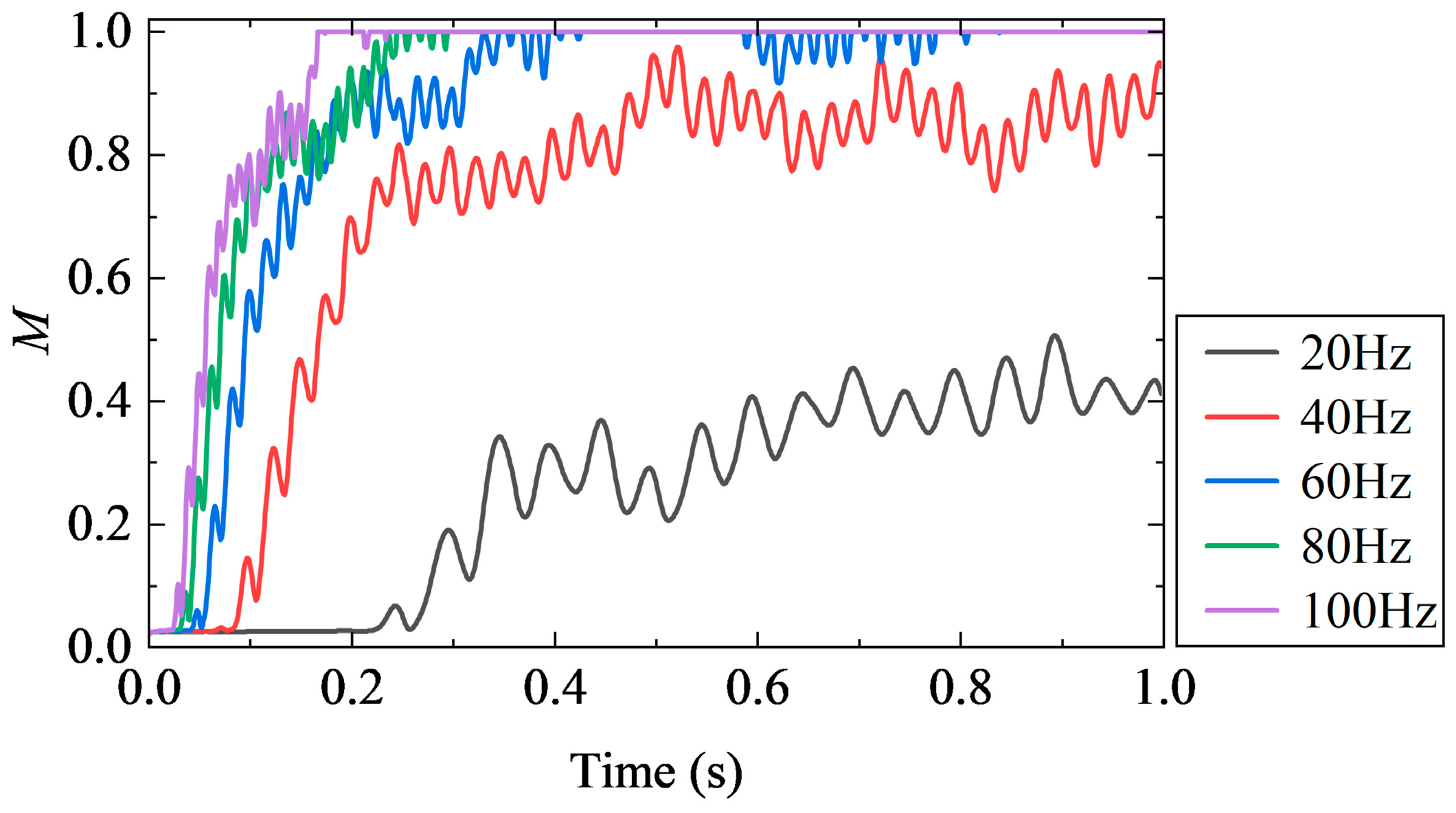
4.1. Mass Transfer Mechanism
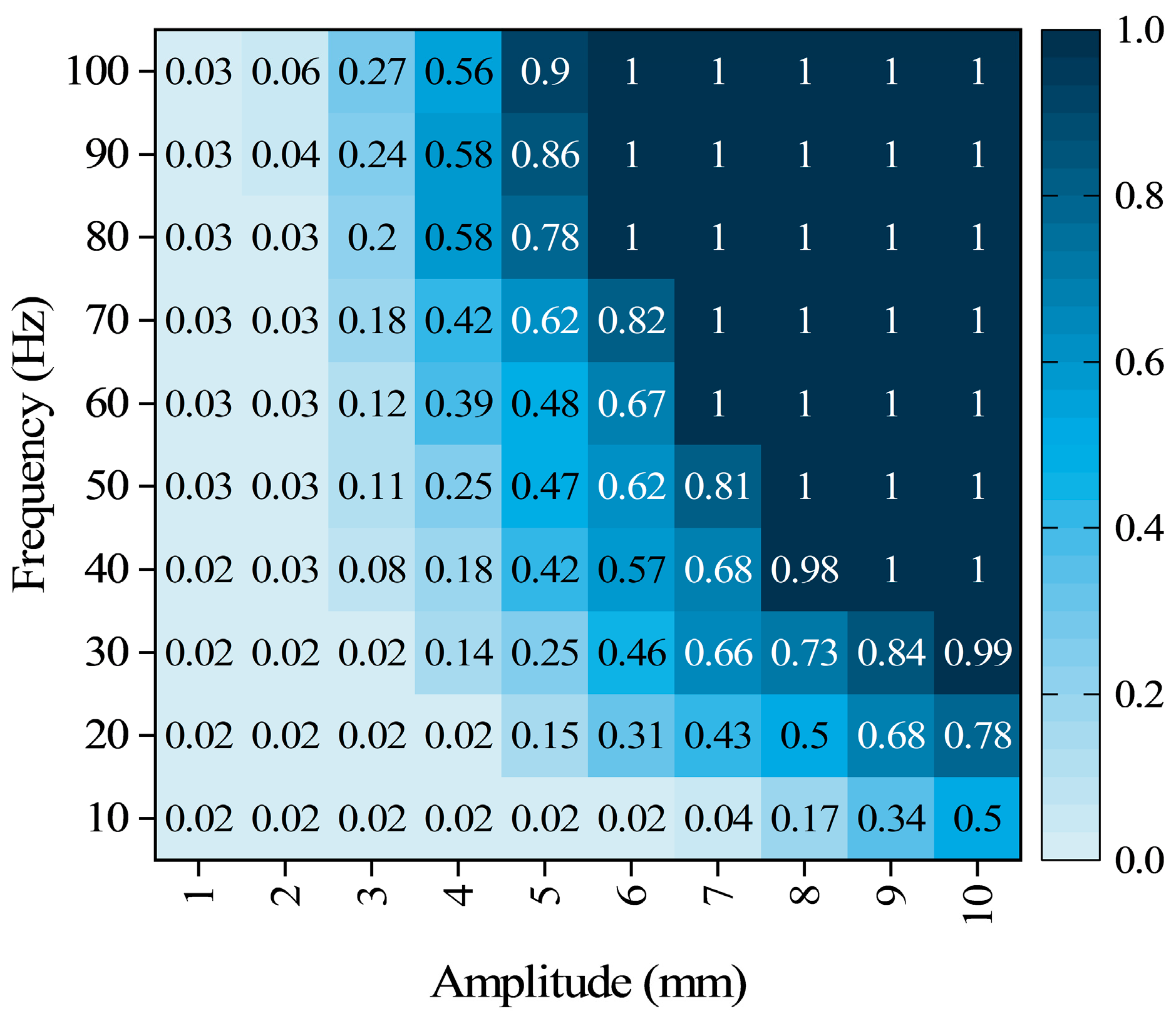
4.2. Effects of Vibration Frequency and Amplitude on Flow Field Mass Transfer
5. Conclusions and Perspectives
- (1)
- The mass transfer mechanism of glycerol in resonant acoustic mixing proceeds through three distinct phases: (i) initial development of Faraday instability at the fluid surface, (ii) subsequent generation of large-scale vortices driven by Faraday waves enabling whole-field mass transport, and (iii) final achievement of localized mixing through small-scale vortices.
- (2)
- The transport process of glycerol in resonant acoustic mixing evolves through three characteristic stages: (i) stable Faraday wave oscillation, (ii) rapid mass transfer during flow instability, and (iii) localized mixing upon reaching steady state.
- (3)
- Both increasing vibrations’ frequency and amplitude effectively enhance the mass transfer rate and efficiency. The critical curve derived from parametric studies follows a power-law function.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abiev, R.S.; Vdovets, M.; Romashchenkova, N.; Maslikov, A. Intensification of mass transfer processes with the chemical reaction in multi-phase systems using the resonance pulsating mixing. Russ. J. Appl. Chem. 2019, 92, 1399–1409. [Google Scholar] [CrossRef]
- Karpacheva, S.; Zakharov, E.; Raginsky, L.; Muratov, V. Pul’siruyushchiye Ekstraktory; Atomizdat Moscow: Moscow, Russia, 1964. [Google Scholar]
- Karpacheva, S.; Zakharov, E. Osnovy Teorii i Rascheta Pul’satsionnykh Kolonnykh Reaktorov (Fundamentals of the Theory and Design of Pulsed Columnar Reactors); Atomizdat: Moscow, Russia, 1980. [Google Scholar]
- Karpacheva, S.; Ryabchikov, B. Pul’satsionnaya Apparatura v Khimicheskoi Tekhnologii; Khimiya Moscow: Moscow, Russia, 1983. [Google Scholar]
- Coguill, S.; Martineau, Z.; Martineau, Z. Vessel Geometry and Fluid Properties Influencing Mix Behavior for ResonantAcoustic Mixing Processes. In Proceedings of the 38th International Pyrotechnics Seminar, Denver, CO, USA, 10–15 June 2012; pp. 10–15. [Google Scholar]
- Park, J.H.; Bae, K.T.; Kim, K.J.; Joh, D.W.; Kim, D.; Myung, J.-H.; Lee, K.T. Ultra-fast fabrication of tape-cast anode supports for solid oxide fuel cells via resonant acoustic mixing technology. Ceram. Int. 2019, 45, 12154–12161. [Google Scholar] [CrossRef]
- Kevadiya, B.D.; Zhang, L.; Davé, R.N. Sustained Release of Poorly Water-Soluble Drug from Hydrophilic Polymeric Film Sandwiched Between Hydrophobic Layers. AAPS Pharmscitech 2018, 19, 2572–2584. [Google Scholar] [CrossRef] [PubMed]
- Effaty, F.; Gonnet, L.; Koenig, S.G.; Nagapudi, K.; Ottenwaelder, X.; Friscic, T. Resonant acoustic mixing (RAM) for efficient mechanoredox catalysis without grinding or impact media. Chem. Commun. 2023, 59, 1010–1013. [Google Scholar] [CrossRef]
- Gonnet, L.; Lennox, C.B.; Do, J.L.; Malvestiti, I.; Koenig, S.G.; Nagapudi, K.; Friscic, T. Metal-Catalyzed Organic Reactions by Resonant Acoustic Mixing. Angew. Chem. Int. Ed. Engl. 2022, 61, e202115030. [Google Scholar] [CrossRef]
- Liao, D.; Liu, Q.; Li, C.; Liu, N.; Wang, M.; An, C. RDX crystals with high sphericity prepared by resonance acoustic mixing assisted solvent etching technology. Def. Technol. 2023, 28, 23–32. [Google Scholar] [CrossRef]
- Zhang, S.; Zhan, L.; Zhang, Y.; Hou, J.; Li, B. Continuous flow resonance acoustic mixing technology: A novel and efficient strategy for preparation of nano energetic materials. FirePhysChem 2023, 3, 29–36. [Google Scholar] [CrossRef]
- Andrews, M.R.; Collet, C.; Wolff, A.; Hollands, C. Resonant Acoustic® Mixing: Processing and Safety, Propellants, Explosives. Pyrotechnics 2019, 45, 77–86. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X. Effect of vibration parameters and wall friction on the mixing characteristics of binary particles in a vertical vibrating container subject to cohesive forces. Powder Technol. 2023, 413, 118078. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X. Convection of granular matter in a frequency-domain perspective and an endogenous low-frequency excitation perturbation. Powder Technol. 2024, 442, 119849. [Google Scholar] [CrossRef]
- Liu, B.; Wang, X. Deagglomeration of fine granular materials under low-frequency vertical harmonic vibration. Powder Technol. 2022, 396, 754–764. [Google Scholar] [CrossRef]
- Wright, C.J.; Wilkinson, P.J.; Gaulter, S.E.; Fossey, D.; Burn, A.O.; Gill, P.P. Is ResonantAcoustic Mixing® (RAM) a Game Changer for Manufacturing Solid Composite Rocket Propellants? Propellants Explos. Pyrotech. 2021, 47, e202100146. [Google Scholar] [CrossRef]
- Zhan, X.; Shen, B.; Sun, Z.; He, Y.; Shi, T.; Li, X. Numerical study on the flow of high viscous fluids out of conical vessels under low-frequency vibration. Chem. Eng. Res. Des. 2018, 132, 226–234. [Google Scholar] [CrossRef]
- Zhan, X.; Yu, L.; Jiang, Q.; Shi, T. Flow pattern and power consumption of mixing highly viscous fluids under vertical acoustic vibration. Chem. Eng. Res. Des. 2023, 199, 438–449. [Google Scholar] [CrossRef]
- Claydon, A.J. Resonant Acoustic Mixing of Polymer Bonded Explosives. Ph.D. Dissertation, Cranfield University, Bedford, UK, 2021. [Google Scholar]
- Claydon, A.J.; Patil, A.N.; Gaulter, S.; Kister, G.; Gill, P.P. Determination and optimisation of Resonant Acoustic Mixing (RAM) efficiency in Polymer Bonded eXplosive (PBX) processing. Chem. Eng. Process.—Process Intensif. 2022, 173, 108806. [Google Scholar] [CrossRef]
- Huo, Q.; Wang, X. Dynamic analysis of power-law non-Newtonian fluids under low-frequency vertical harmonic vibration by dynamic mode decomposition. Phys. Fluids 2023, 35, 044114. [Google Scholar] [CrossRef]
- Huo, Q.; Wang, X. Faraday instability of non-Newtonian fluids under low-frequency vertical harmonic vibration. Phys. Fluids 2022, 34, 094107. [Google Scholar] [CrossRef]
- Huo, Q.; Wang, X. Mixing mechanism of power-law non-Newtonian fluids in resonant acoustic mixing. Phys. Fluids 2024, 36, 024121. [Google Scholar] [CrossRef]
- Xue, X.; Yao, H.-D.; Davidson, L. Synthetic turbulence generator for lattice Boltzmann method at the interface between RANS and LES. Phys. Fluids 2022, 34, 055118. [Google Scholar] [CrossRef]
- Ambekar, A.S.; Schwarzmeier, C.; Rüde, U.; Buwa, V.V. Particle-resolved turbulent flow in a packed bed: RANS, LES, and DNS simulations. AIChE J. 2023, 69, e17615. [Google Scholar] [CrossRef]
- Zhu, C.-S.; Zhao, B.-R.; Lei, Y.; Guo, X.-T. Simulation of single bubble dynamic process in pool boiling process under microgravity based on phase field method. Chin. Phys. B 2023, 32, 044702. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- van Hooff, T.; Blocken, B.; Tominaga, Y. On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments. Build. Environ. 2017, 114, 148–165. [Google Scholar] [CrossRef]
- Li, L.; Gu, Z.; Xu, W.; Tan, Y.; Fan, X.; Tan, D. Mixing mass transfer mechanism and dynamic control of gas-liquid-solid multiphase flow based on VOF-DEM coupling. Energy 2023, 272, 127015. [Google Scholar] [CrossRef]
- Ertesvåg, I.S.; Magnussen, B.F. The eddy dissipation turbulence energy cascade model. Combust. Sci. Technol. 2000, 159, 213–235. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Dissipation of energy in the locally isotropic turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 434, 15–17. [Google Scholar]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 434, 9–13. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Li, Y.; Umemura, A. Two-dimensional numerical investigation on the dynamics of ligament formation by Faraday instability. Int. J. Multiph. Flow 2014, 60, 64–75. [Google Scholar] [CrossRef]
- Heijnen, J.; Van, K. Mass transfer, mixing and heat transfer phenomena in low viscosity bubble column reactors. Chem. Eng. J. 1984, 28, B21–B42. [Google Scholar] [CrossRef]
- Mehta, S.K.; Pati, S.; Mondal, P.K. Numerical study of the vortex-induced electroosmotic mixing of non-Newtonian biofluids in a nonuniformly charged wavy microchannel: Effect of finite ion size. Electrophoresis 2021, 42, 2498–2510. [Google Scholar] [CrossRef] [PubMed]
- Zhan, X.; Yu, L.; Jiang, Y.; Jiang, Q.; Shi, T. Mixing Characteristics and Parameter Effects on the Mixing Efficiency of High-Viscosity Solid–Liquid Mixtures under High-Intensity Acoustic Vibration. Processes 2023, 11, 2367. [Google Scholar] [CrossRef]
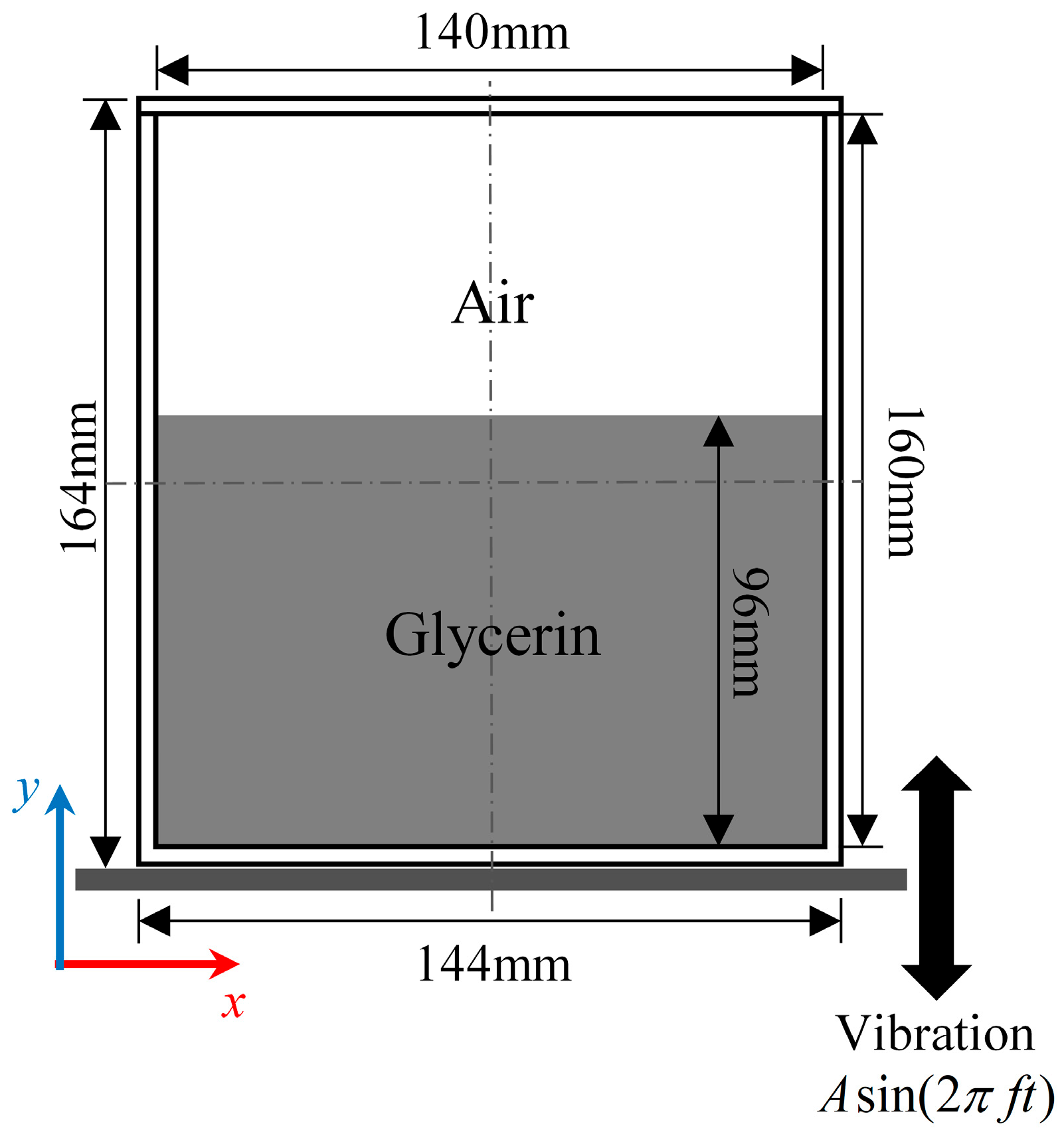











| Project | Parameter |
|---|---|
| Density of glycerin | ρG = 1260 kg·m−3 |
| Viscosity of glycerin | η = 0.8 Ρa·s |
| Density of air | ρA = 1.225 kg·m−3 |
| Viscosity of air | η = 1.79 × 10−5 Ρa·s |
| Surface tension | 0.07 N·m−1 |
| Wall boundary | No-slip wall |
| Pressure–velocity coupling | SIMPLE |
| Time step | 0.001 s |
| Simulation time | 1 s |
| Residual | 10−5 |
| Computer configuration | Intel(R) Core(TM) i9-14900KF 3.20 GHz 192 GB RAM |
| 1 mm | 2 mm | 3 mm | 4 mm | 5 mm | 6 mm | 7 mm | 8 mm | 9 mm | 10 mm | |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 Hz | 0.06 | 0.13 | 0.19 | 0.25 | 0.31 | 0.38 | 0.44 | 0.5 | 0.57 | 0.63 |
| 20 Hz | 0.13 | 0.25 | 0.38 | 0.5 | 0.63 | 0.75 | 0.88 | 1 | 1.13 | 1.27 |
| 30 Hz | 0.19 | 0.38 | 0.57 | 0.75 | 0.94 | 1.13 | 1.32 | 1.51 | 1.7 | 1.88 |
| 40 Hz | 0.25 | 0.5 | 0.75 | 1.01 | 1.26 | 1.51 | 1.76 | 2.01 | 2.26 | 2.51 |
| 50 Hz | 0.31 | 0.63 | 0.94 | 1.26 | 1.57 | 1.88 | 2.2 | 2.51 | 2.83 | 3.14 |
| 60 Hz | 0.38 | 0.75 | 1.13 | 1.51 | 1.88 | 2.26 | 2.64 | 3.02 | 3.39 | 3.77 |
| 70 Hz | 0.44 | 0.88 | 1.32 | 1.76 | 2.20 | 2.64 | 3.08 | 3.52 | 3.96 | 4.4 |
| 80 Hz | 0.5 | 1.01 | 1.51 | 2.01 | 2.51 | 3.02 | 3.52 | 4.02 | 4.52 | 5.03 |
| 90 Hz | 0.57 | 1.13 | 1.7 | 2.26 | 2.83 | 3.39 | 3.96 | 4.52 | 5.09 | 5.65 |
| 100 Hz | 0.63 | 1.26 | 1.88 | 2.51 | 3.14 | 3.77 | 4.4 | 5.03 | 5.65 | 6.28 |
| 1 mm | 2 mm | 3 mm | 4 mm | 5 mm | 6 mm | 7 mm | 8 mm | 9 mm | 10 mm | |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 Hz | 4 | 7.9 | 11.8 | 15.8 | 19.7 | 23.7 | 27.6 | 31.6 | 35.5 | 39.5 |
| 20 Hz | 15.8 | 31.6 | 47.4 | 63.2 | 79 | 94.7 | 110.5 | 126.3 | 142.1 | 157.9 |
| 30 Hz | 35.5 | 71.1 | 106.6 | 142.2 | 177.7 | 213.2 | 248.8 | 284.3 | 319.8 | 355.4 |
| 40 Hz | 63.2 | 126.3 | 190 | 252.7 | 315.8 | 379 | 442.2 | 505.3 | 568.5 | 631.7 |
| 50 Hz | 98.7 | 197.4 | 296.1 | 394.8 | 493.5 | 592.2 | 690.9 | 789.6 | 888.3 | 987 |
| 60 Hz | 142.1 | 284.2 | 426.4 | 568.5 | 710.6 | 852.7 | 994.8 | 1137 | 1279.1 | 1421.2 |
| 70 Hz | 193.4 | 386.9 | 580.3 | 773.7 | 967.2 | 1160.6 | 1354 | 1547.4 | 1740.9 | 1934.3 |
| 80 Hz | 253.7 | 505.3 | 758 | 1010.6 | 1263.3 | 1516 | 1768.6 | 2021.3 | 2273.9 | 2526.6 |
| 90 Hz | 319.8 | 639.7 | 959.5 | 1279.3 | 1599.2 | 1919 | 2238.8 | 2558.6 | 2878.5 | 3198.3 |
| 100 Hz | 394.8 | 789.6 | 1184.4 | 1579.1 | 1973.9 | 2368.7 | 2763.5 | 2763.5 | 3553.1 | 3947.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, N.; Zhang, G.; Zhang, X.; Gao, Y.; Zhu, S. Mass Transfer Mechanism and Process Parameters in Glycerol Using Resonant Acoustic Mixing Technology. Processes 2025, 13, 2845. https://doi.org/10.3390/pr13092845
Ma N, Zhang G, Zhang X, Gao Y, Zhu S. Mass Transfer Mechanism and Process Parameters in Glycerol Using Resonant Acoustic Mixing Technology. Processes. 2025; 13(9):2845. https://doi.org/10.3390/pr13092845
Chicago/Turabian StyleMa, Ning, Guangbin Zhang, Xiaofeng Zhang, Yuqi Gao, and Shifu Zhu. 2025. "Mass Transfer Mechanism and Process Parameters in Glycerol Using Resonant Acoustic Mixing Technology" Processes 13, no. 9: 2845. https://doi.org/10.3390/pr13092845
APA StyleMa, N., Zhang, G., Zhang, X., Gao, Y., & Zhu, S. (2025). Mass Transfer Mechanism and Process Parameters in Glycerol Using Resonant Acoustic Mixing Technology. Processes, 13(9), 2845. https://doi.org/10.3390/pr13092845






