A Novel Terminal Sliding Mode Control with Robust Prescribed-Time Stability
Abstract
1. Introduction
1.1. Motivation and Background
1.2. Related Works
1.3. Contributions
- A novel prescribed-time Lyapunov stability theorem is established, providing a rigorous foundation that guarantees convergence within a fixed, user-defined time, independent of initial conditions.
- An integral terminal sliding mode controller (ITSMC) with bounded, time-varying gains is proposed, which eliminates the traditional reaching phase of sliding mode control and avoids the singularity problem.
- A new terminal sliding mode control scheme is developed for a class of second-order nonlinear systems, extending the ITSMC framework to broader system classes.
- The proposed controllers guarantee that system trajectories reach both the sliding manifold and the desired equilibrium point within the prescribed time, ensuring robustness and high tracking accuracy under matched perturbations and uncertainties.
1.4. Paper Organization
1.5. Notation
2. Preliminaries
- 1.
- Globally finite-time stableif it is globally asymptotically stable and there exists a settling time function such that for all, ;
- 2.
- Globally fixed-time stable if it is globally finite-time stable and there exists a constant such that for all initial conditions , indicating that the convergence time is finite and has a known upper bound.
- 1.
- it is globally finite-time stable and
- 2.
- for every prescribed constant , chosen independently of , the settling time satisfies .
3. Robust Prescribed-Time Stability
- 1.
- The function is strictly decreasing and remains strictly positive within the entire interval.
- 2.
- It converges to zero if and only if t tends to T.
- 3.
- The limit is equal to zero.
4. Application to SMC
4.1. Integral TSMC
4.2. Non-Singular Terminal Sliding Mode Control
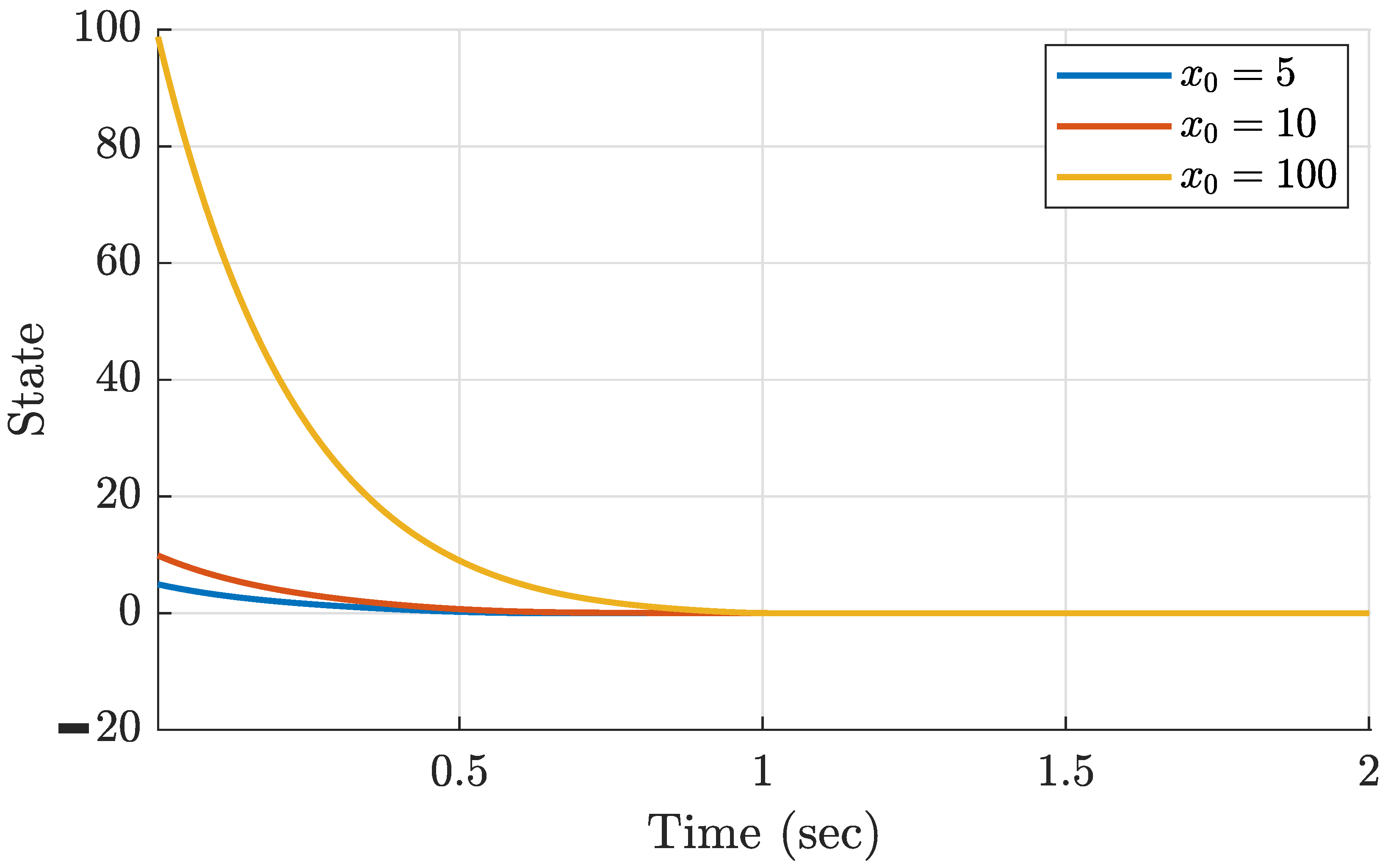
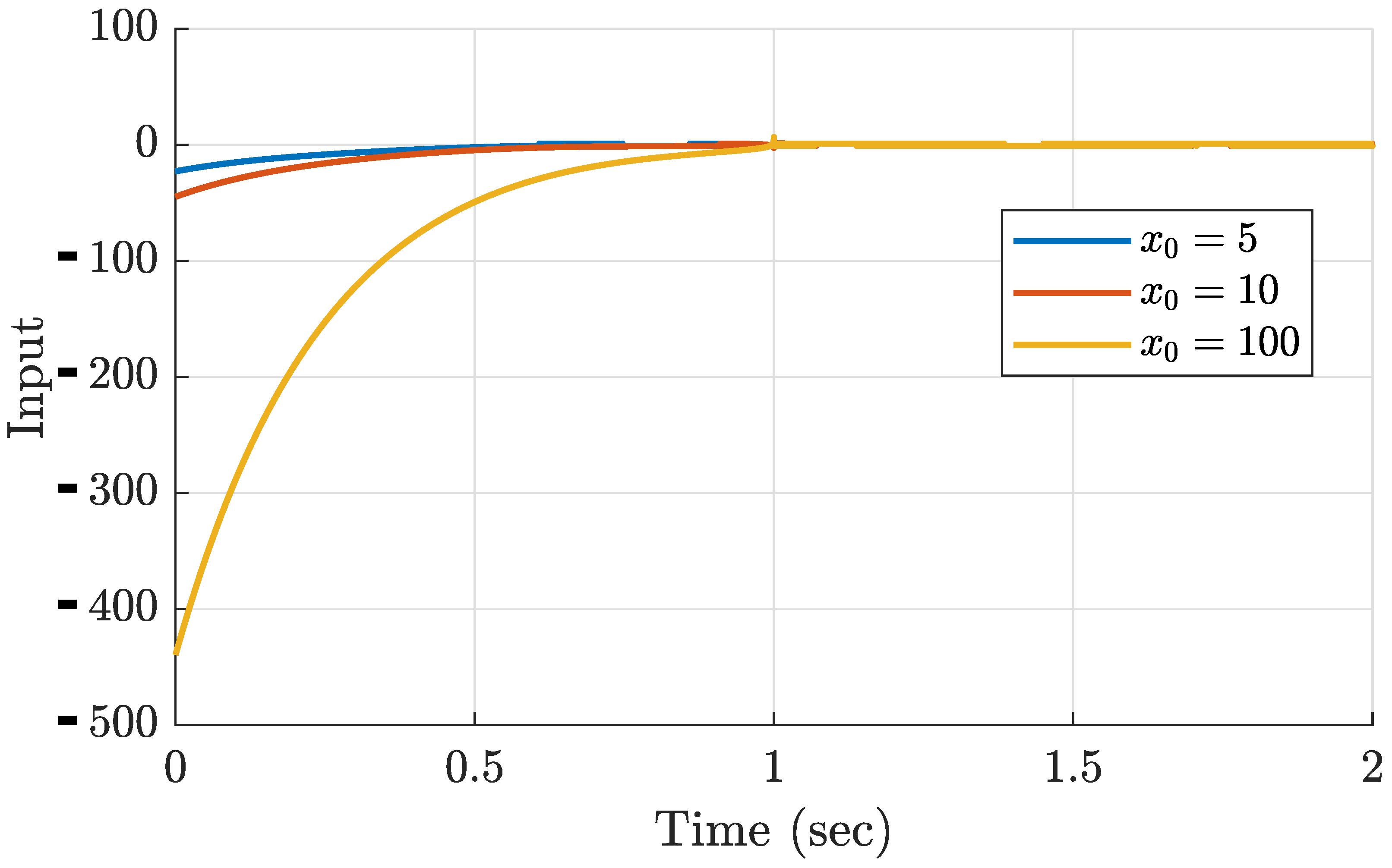
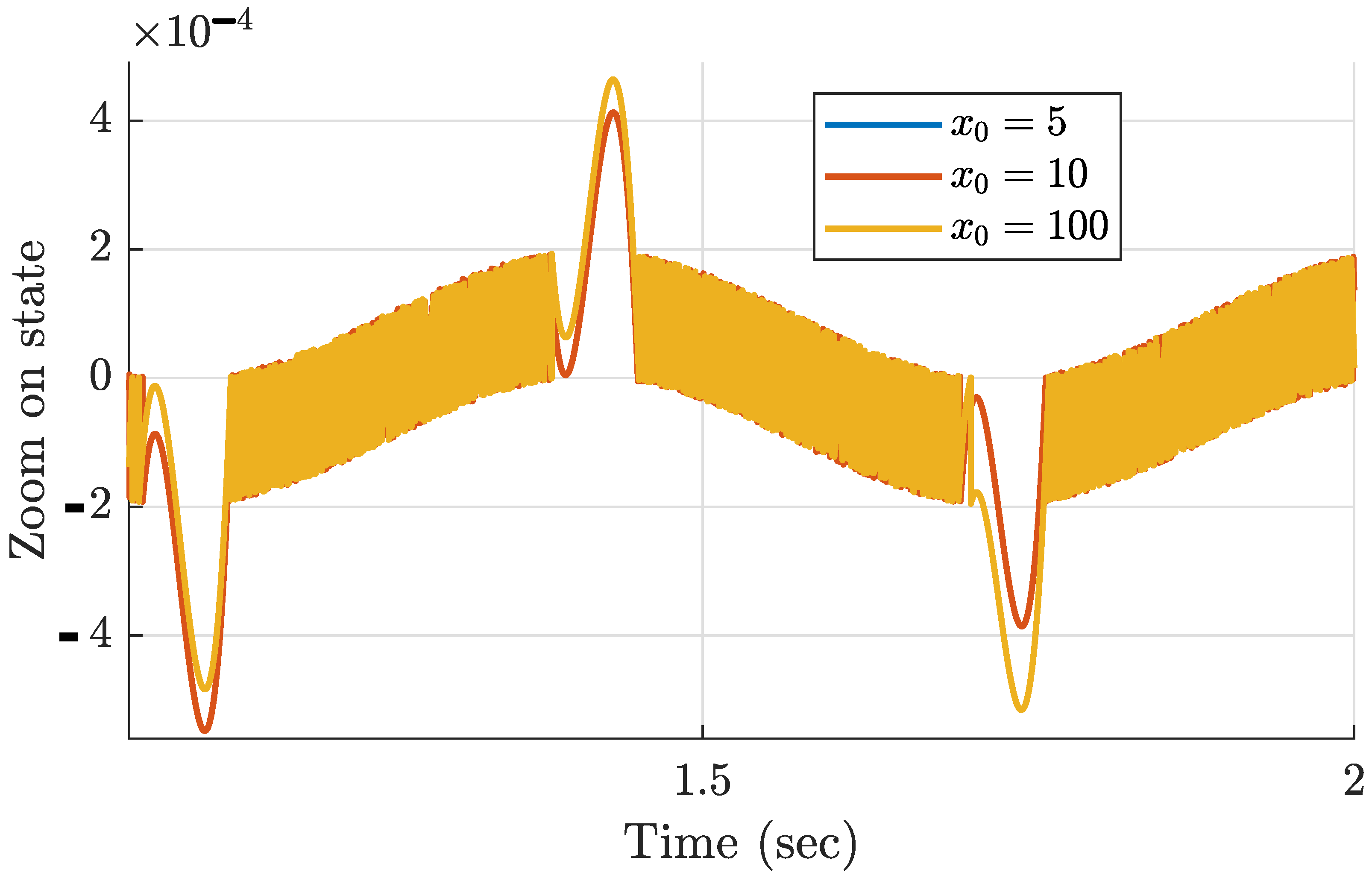
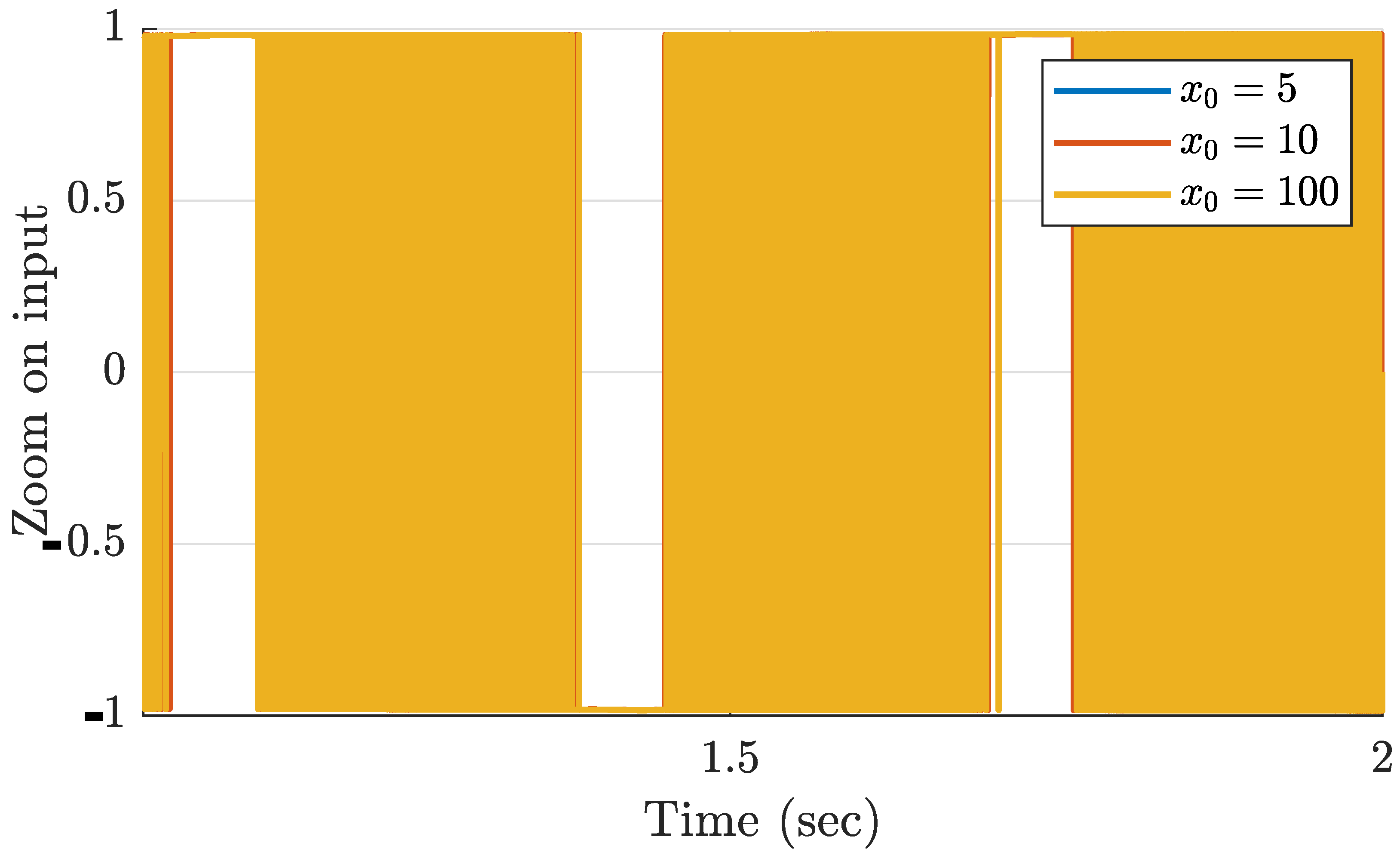
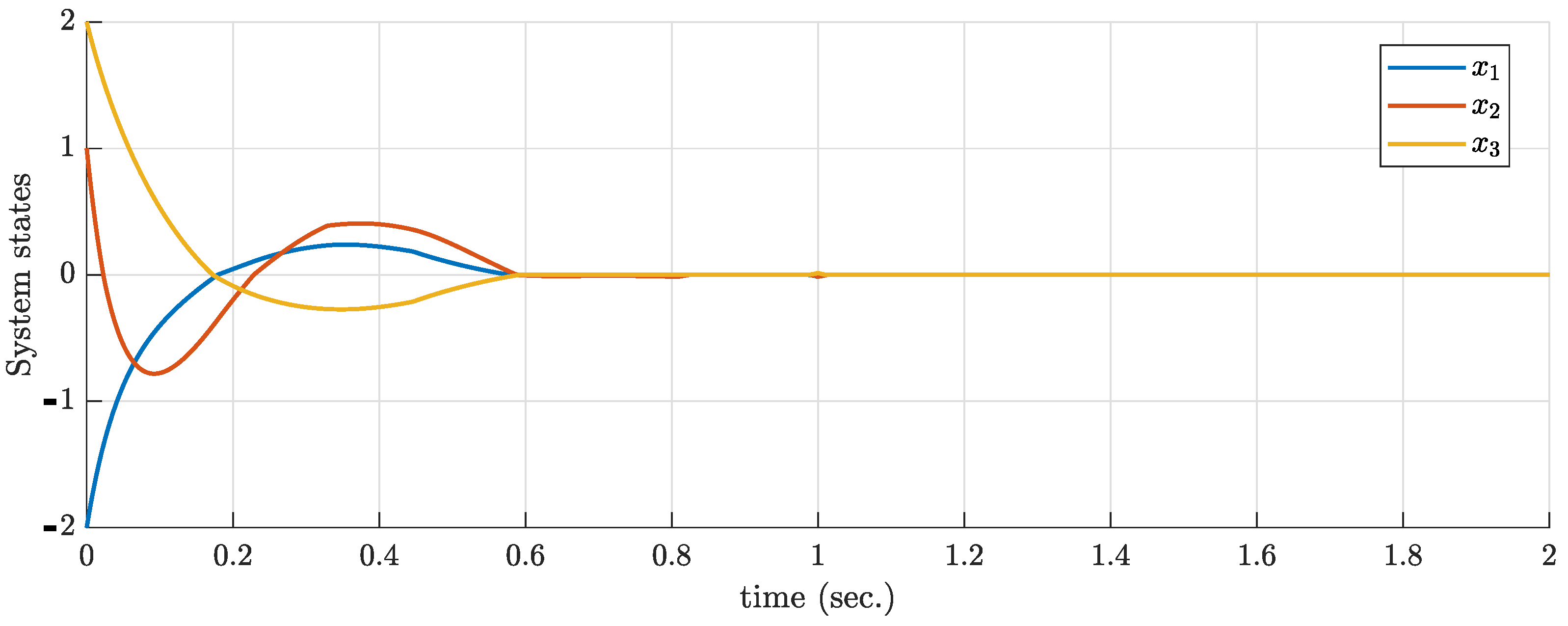
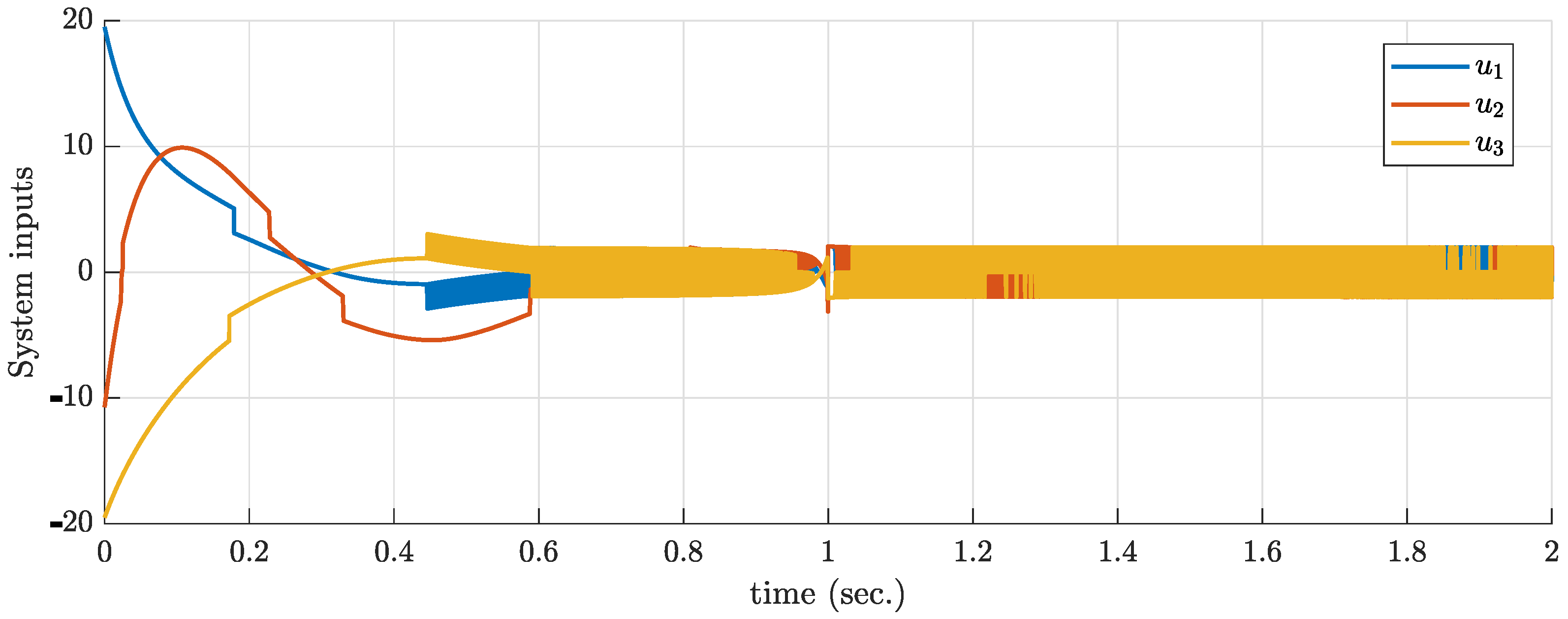
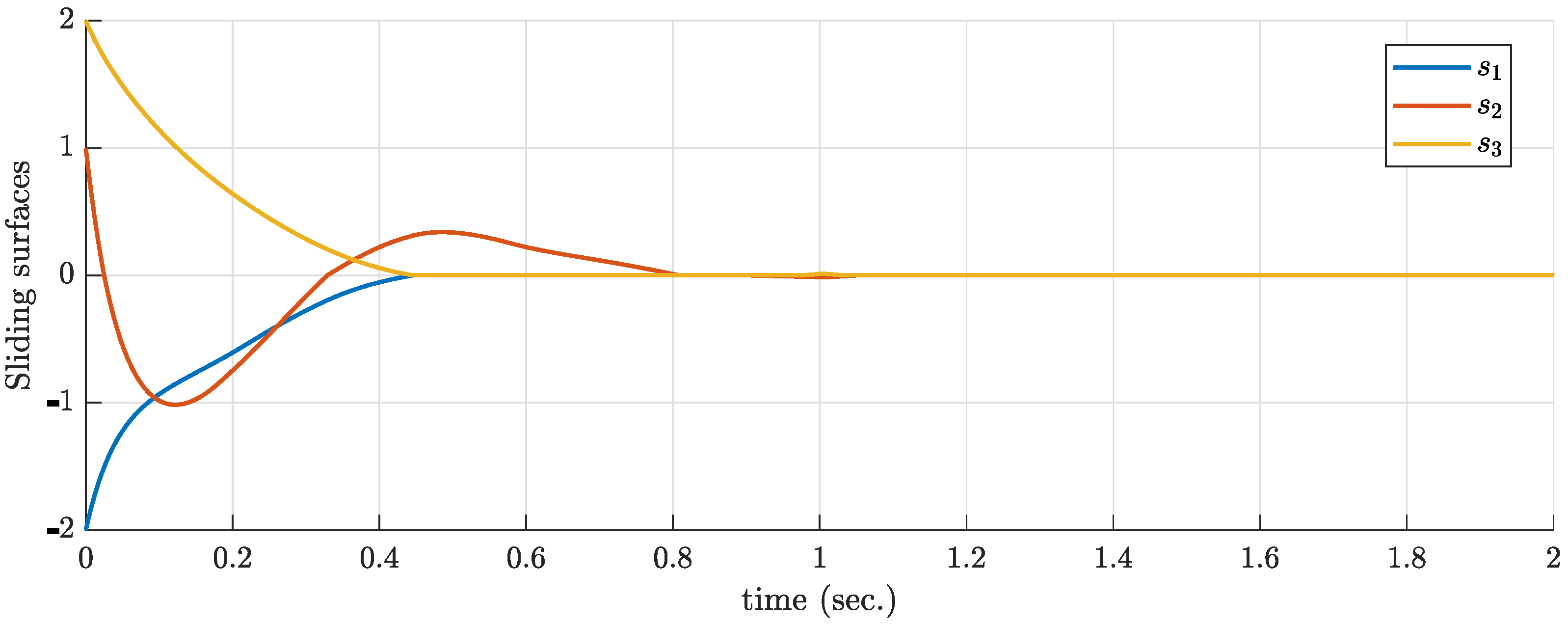
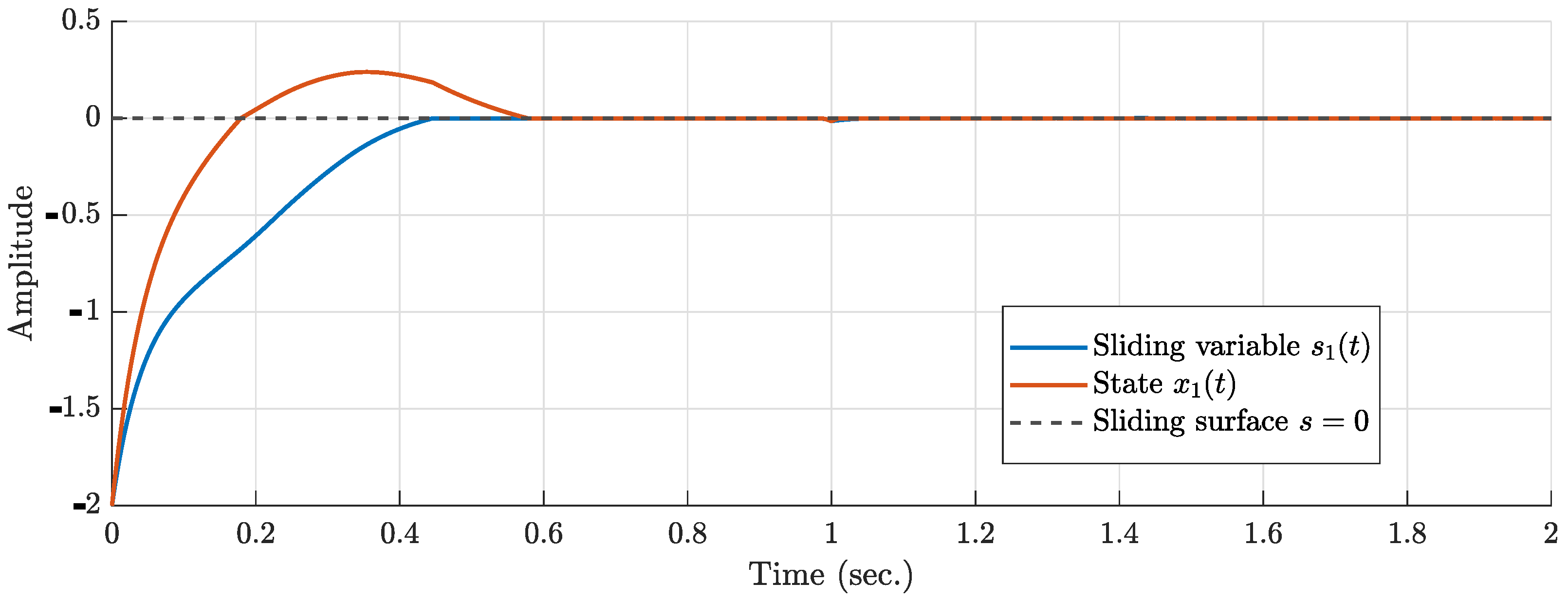
5. Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Gao, Y.; Zhao, Y.; Liu, Z.; Wang, J.; Kuang, J.; Yan, F.; Liu, J. Neural Network-Based Tracking Control of Uncertain Robotic Systems: Predefined-Time Nonsingular Terminal Sliding-Mode Approach. IEEE Trans. Ind. Electron. 2022, 69, 10510–10520. [Google Scholar] [CrossRef]
- Yun, Q.; Wang, X.; Yao, C.; Zhuang, W.; Shao, M.; Gao, H. A Second-Order Sliding Mode Voltage Controller with Fast Convergence for a Permanent Magnet Synchronous Generator System. Processes 2023, 12, 71. [Google Scholar] [CrossRef]
- Zhihong, M.; Yu, X.H. Terminal sliding mode control of MIMO linear systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 1065–1070. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Holloway, J.; Krstic, M. Time-varying feedback for regulation of normal-form nonlinear systems in prescribed finite time. Automatica 2017, 83, 243–251. [Google Scholar] [CrossRef]
- Wang, Z.; Lam, H.K.; Guo, Y.; Xiao, B.; Li, Y.; Su, X.; Yeatman, E.M.; Burdet, E. Adaptive event-triggered control for nonlinear systems with asymmetric state constraints: A prescribed-time approach. IEEE Trans. Autom. Control 2022, 68, 3625–3632. [Google Scholar] [CrossRef]
- Benaddy, A.; Labbadi, M.; Elyaalaoui, K.; Bouzi, M. Fixed-Time Fractional-Order Sliding Mode Control for UAVs under External Disturbances. Fractal Fract. 2023, 7, 775. [Google Scholar] [CrossRef]
- Song, Y.; Ye, H.; Lewis, F.L. Prescribed-Time Control and Its Latest Developments. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4102–4116. [Google Scholar] [CrossRef]
- Shi, S.; Dai, L.; Min, H.; Hu, Y. Non-singular terminal sliding mode controller design for nonlinear systems with prescribed convergence time guarantees. Int. J. Robust Nonlinear Control 2023, 34, 2597–2613. [Google Scholar] [CrossRef]
- Efimov, D.; Polyakov, A. Finite-Time Stability Tools for Control and Estimation. Found. Trends Syst. Control 2021, 9, 171–364. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Krstic, M. Time-varying feedback for stabilization in prescribed finite time. Int. J. Robust Nonlinear Control 2019, 29, 618–633. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y. A general approach to precise tracking of nonlinear systems subject to non-vanishing uncertainties. Automatica 2019, 106, 306–314. [Google Scholar] [CrossRef]
- Tran, D.; Yucelen, T. Finite-time control of perturbed dynamical systems based on a generalized time transformation approach. Syst. Control Lett. 2020, 136, 104605. [Google Scholar] [CrossRef]
- Arabi, E.; Yucelen, T.; Singler, J.R. Robustness of finite-time distributed control algorithm with time transformation. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 108–113. [Google Scholar]
- Krishnamurthy, P.; Khorrami, F.; Krstic, M. A dynamic high-gain design for prescribed-time regulation of nonlinear systems. Automatica 2020, 115, 108860. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F. Prescribed-time stabilization of nonlinear systems with uncertain input gain and non-vanishing disturbances. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; pp. 1859–1864. [Google Scholar]
- Jiménez-Rodríguez, E.; Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Defoort, M.; Loukianov, A.G. A Lyapunov-like characterization of predefined-time stability. IEEE Trans. Autom. Control 2020, 65, 4922–4927. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, D. On the design of nonautonomous fixed-time controllers with a predefined upper bound of the settling time. Int. J. Robust Nonlinear Control 2020, 30, 3871–3885. [Google Scholar] [CrossRef]
- Orlov, Y.; Kairuz, R.I.V. Autonomous output feedback stabilization with prescribed settling-time bound. IEEE Trans. Autom. Control 2022, 68, 2452–2459. [Google Scholar] [CrossRef]
- Aldana-López, R.; Seeber, R.; Haimovich, H.; Gómez-Gutiérrez, D. On inherent limitations in robustness and performance for a class of prescribed-time algorithms. Automatica 2023, 158, 111284. [Google Scholar] [CrossRef]
- Orlov, Y.; Kairuz, R.I.V.; Aguilar, L.T. Prescribed-time robust differentiator design using finite varying gains. IEEE Control Syst. Lett. 2021, 6, 620–625. [Google Scholar] [CrossRef]
- Kairuz, R.I.V.; Orlov, Y.; Aguilar, L.T. Robust observer design with prescribed settling-time bound and finite varying gains. Eur. J. Control 2022, 68, 100667. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y. Prescribed-time exact tracking for a class of nonlinear systems. IEEE Control Syst. Lett. 2023, 7, 1351–1356. [Google Scholar] [CrossRef]
- Hong, Y. Finite-time stabilization and stabilizability of a class of controllable systems. Syst. Control Lett. 2002, 46, 231–236. [Google Scholar] [CrossRef]
- Moulay, E.; Perruquetti, W. Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 2006, 323, 1430–1443. [Google Scholar] [CrossRef]
- Shakouri, A.; Assadian, N. Prescribed-time control with linear decay for nonlinear systems. IEEE Control Syst. Lett. 2021, 6, 313–318. [Google Scholar] [CrossRef]
- Chitour, Y.; Ushirobira, R.; Bouhemou, H. Stabilization for a perturbed chain of integrators in prescribed time. SIAM J. Control Optim. 2020, 58, 1022–1048. [Google Scholar] [CrossRef]
- Defoort, M.; Polyakov, A.; Demesure, G.; Djemai, M.; Veluvolu, K. Leader-follower fixed-time consensus for multi-agent systems with unknown non-linear inherent dynamics. IET Control Theory Appl. 2015, 9, 2165–2170. [Google Scholar] [CrossRef]
- Yang, X.; Lam, J.; Ho, D.W.; Feng, Z. Fixed-time synchronization of complex networks with impulsive effects via nonchattering control. IEEE Trans. Autom. Control 2017, 62, 5511–5521. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Z.; Hu, J.; Wang, X. Controller design for global fixed-time synchronization of delayed neural networks with discontinuous activations. Neural Netw. 2017, 87, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Khanzadeh, A.; Mohammadzaman, I. Fixed-time integral sliding mode control design for a class of uncertain nonlinear systems based on a novel fixed-time stability condition. Eur. J. Control 2023, 69, 100753. [Google Scholar] [CrossRef]
| Parameter | Symbol | Value |
|---|---|---|
| Resistance of the stator | 0.148 | |
| Inductance of the d-q-axis | 0.192 mH | |
| Flux linkage | 0.0082 Wb | |
| Inertia moment | J | 12 kg·mm2 |
| Coefficient of damping | B | N·m·s/rad |
| Number of pole pairs | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Mortajine, C.; Bouzi, M.; Benaddy, A. A Novel Terminal Sliding Mode Control with Robust Prescribed-Time Stability. Processes 2025, 13, 2728. https://doi.org/10.3390/pr13092728
El Mortajine C, Bouzi M, Benaddy A. A Novel Terminal Sliding Mode Control with Robust Prescribed-Time Stability. Processes. 2025; 13(9):2728. https://doi.org/10.3390/pr13092728
Chicago/Turabian StyleEl Mortajine, Chaimae, Mostafa Bouzi, and Abdellah Benaddy. 2025. "A Novel Terminal Sliding Mode Control with Robust Prescribed-Time Stability" Processes 13, no. 9: 2728. https://doi.org/10.3390/pr13092728
APA StyleEl Mortajine, C., Bouzi, M., & Benaddy, A. (2025). A Novel Terminal Sliding Mode Control with Robust Prescribed-Time Stability. Processes, 13(9), 2728. https://doi.org/10.3390/pr13092728







