The Effect of Jet Deviation on the Stability of Pelton Turbine
Abstract
1. Introduction
2. Numerical Simulation Method
2.1. Turbine Geometric Parameters
2.2. Mathematical Model
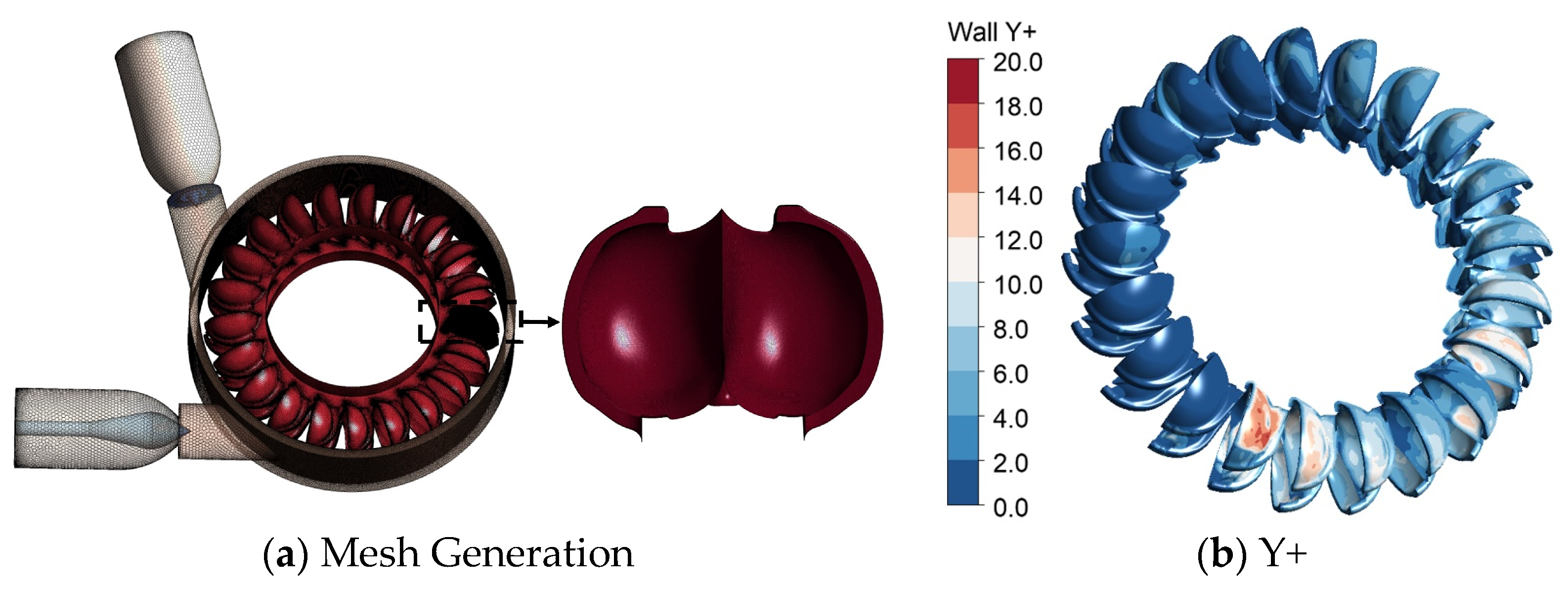
2.3. Mesh Generation and Independence Verification
2.4. Boundary Conditions
2.5. Comparison of Experimental and Numerical Calculations
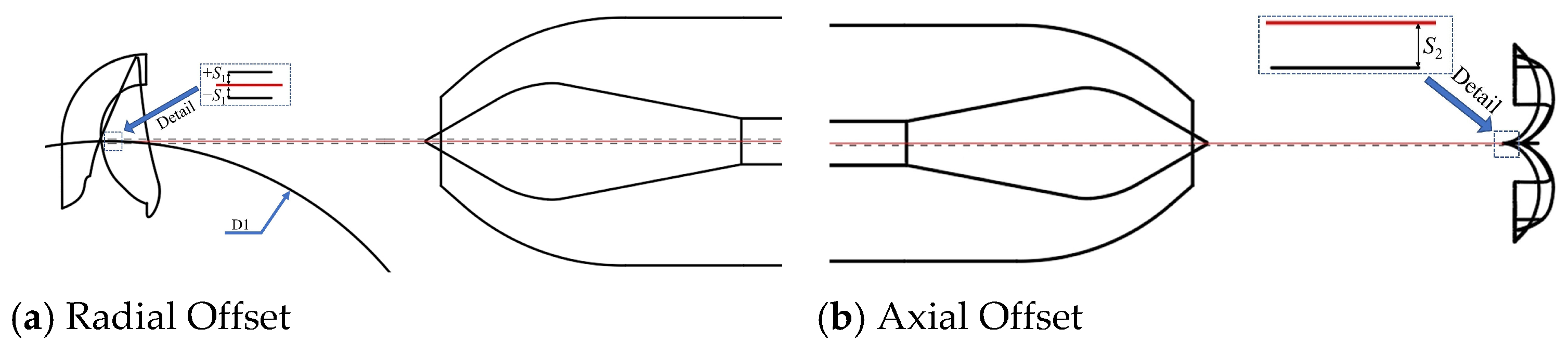
3. Numerical Calculation of Bucket Offset Working Conditions Results and Discussion
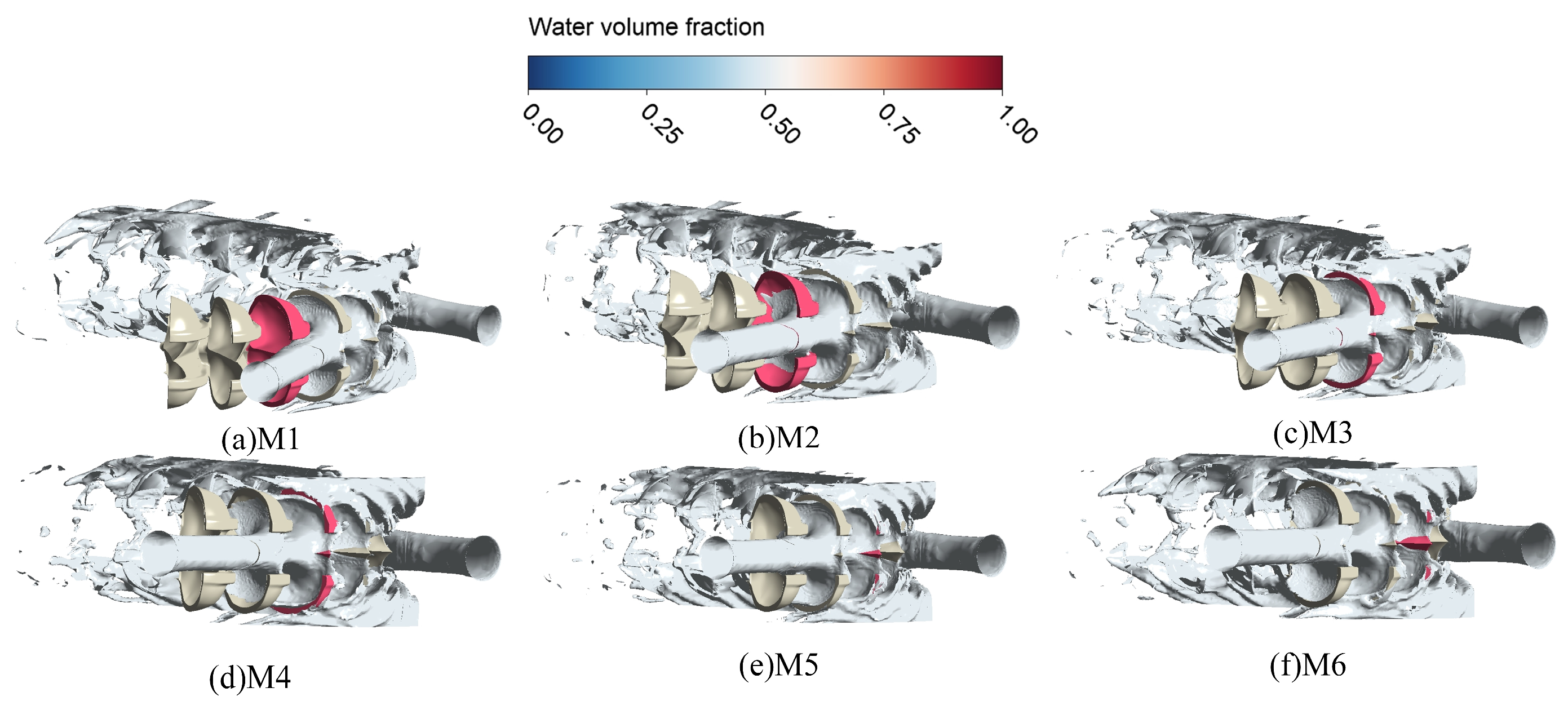
3.1. Numerical Calculation of the Internal Flow Characteristics of Buckets
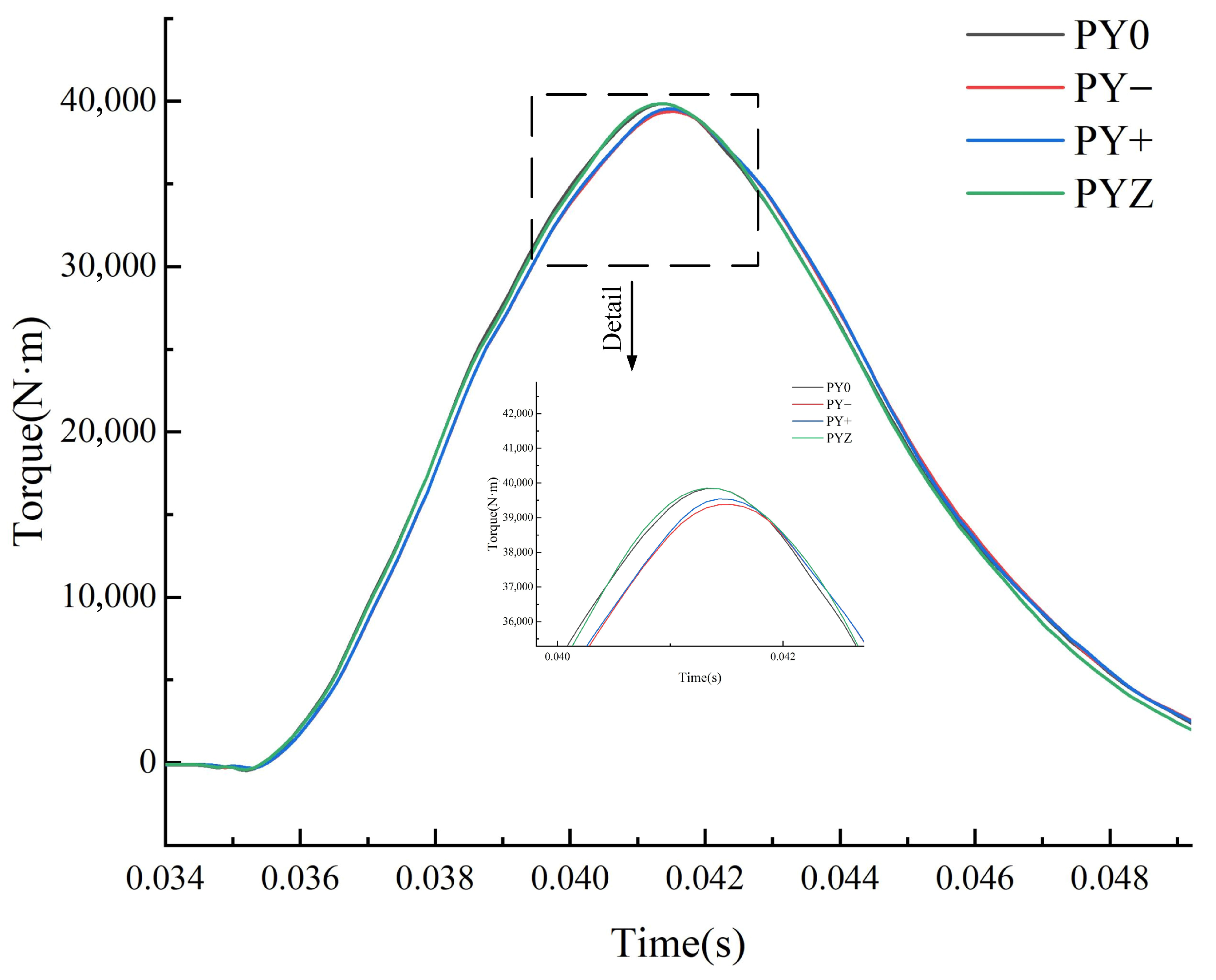
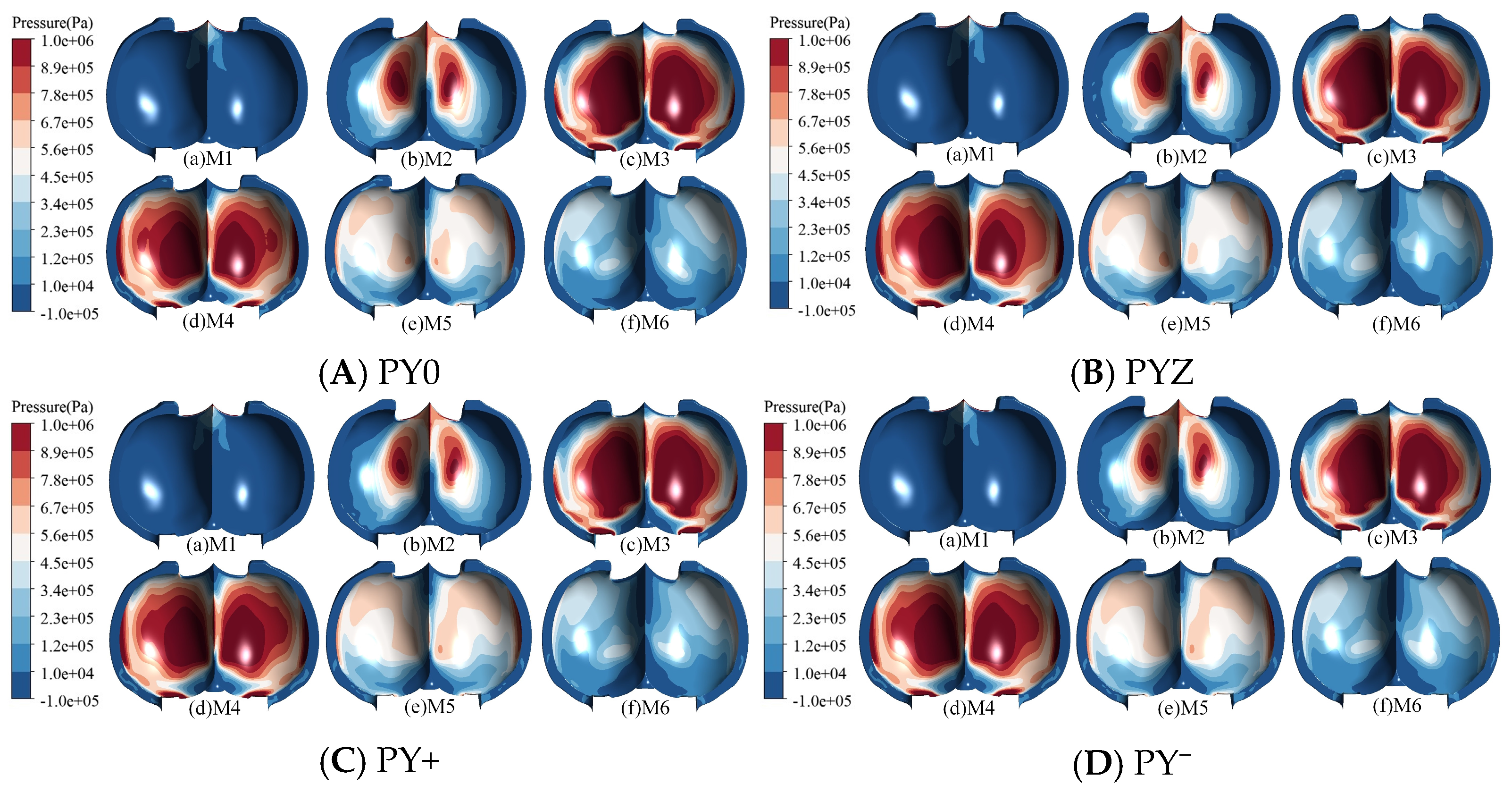
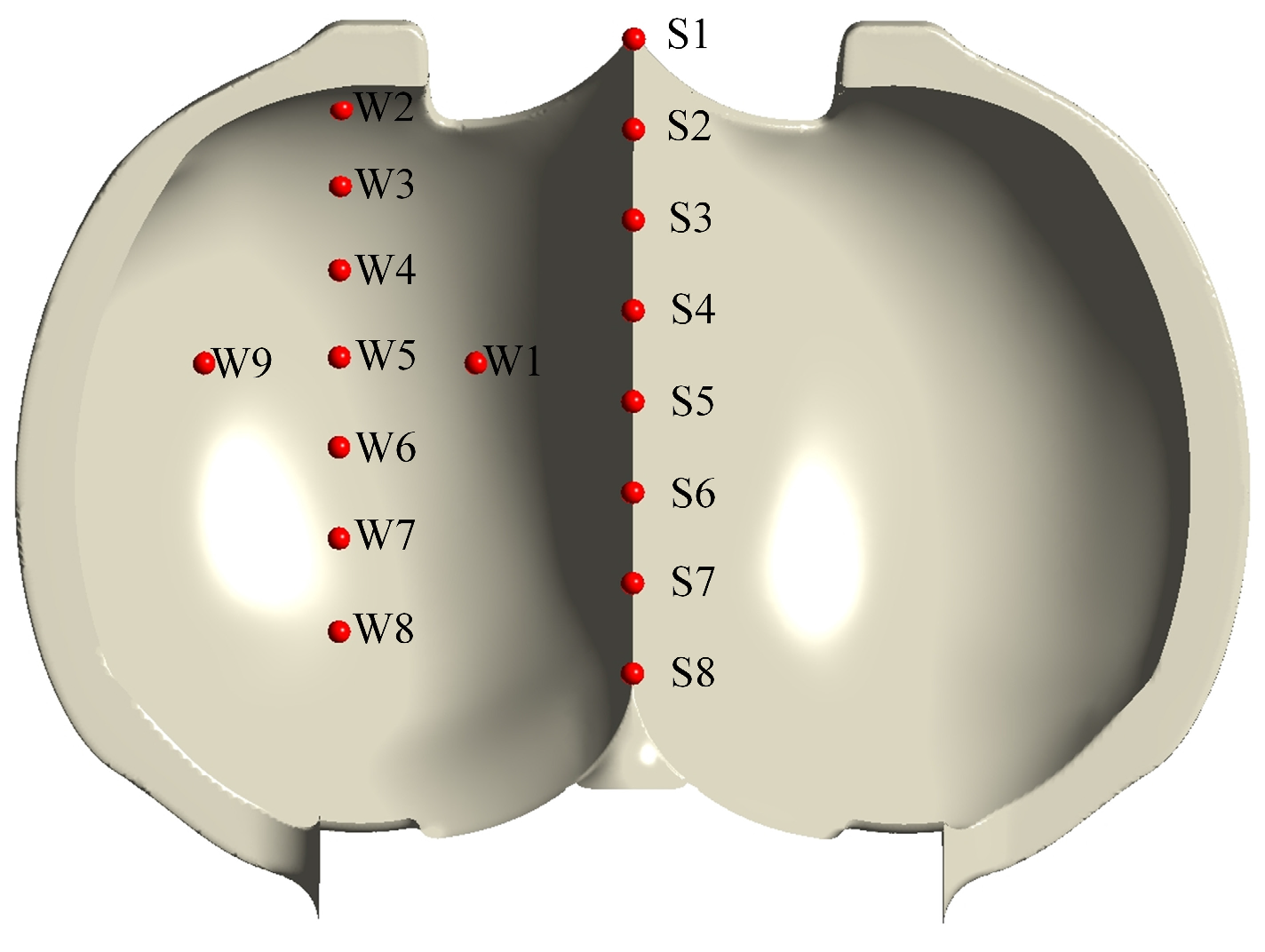
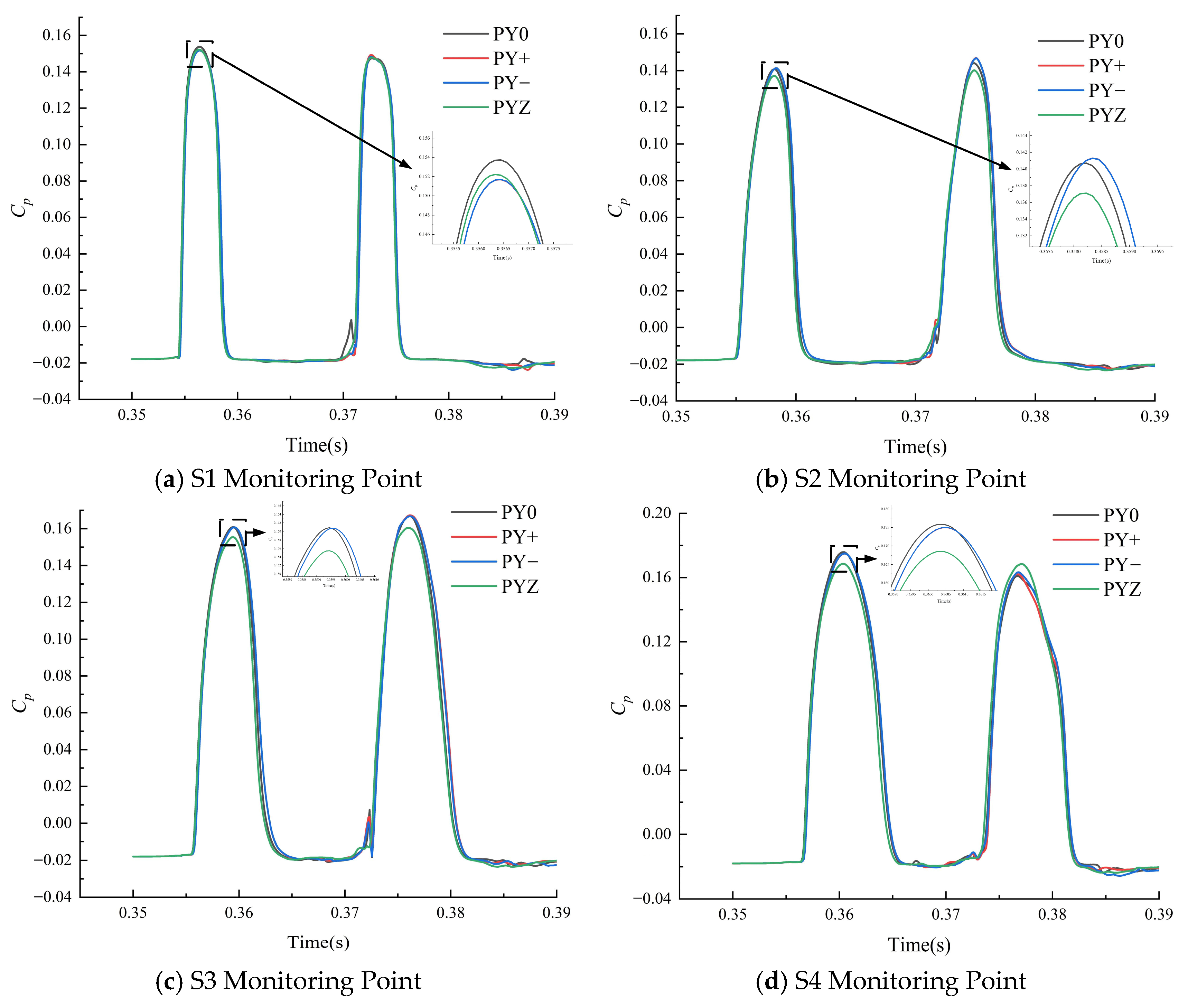
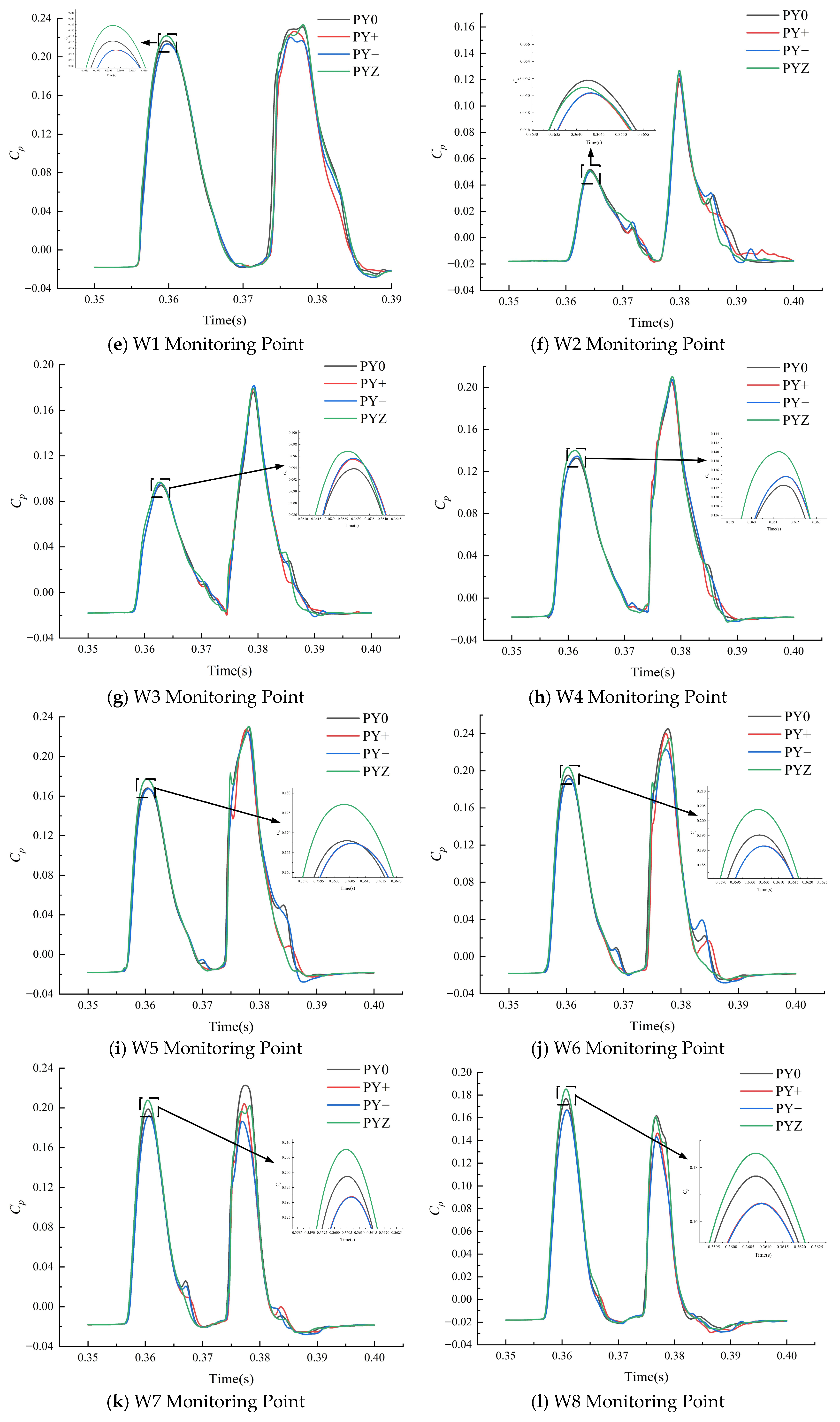
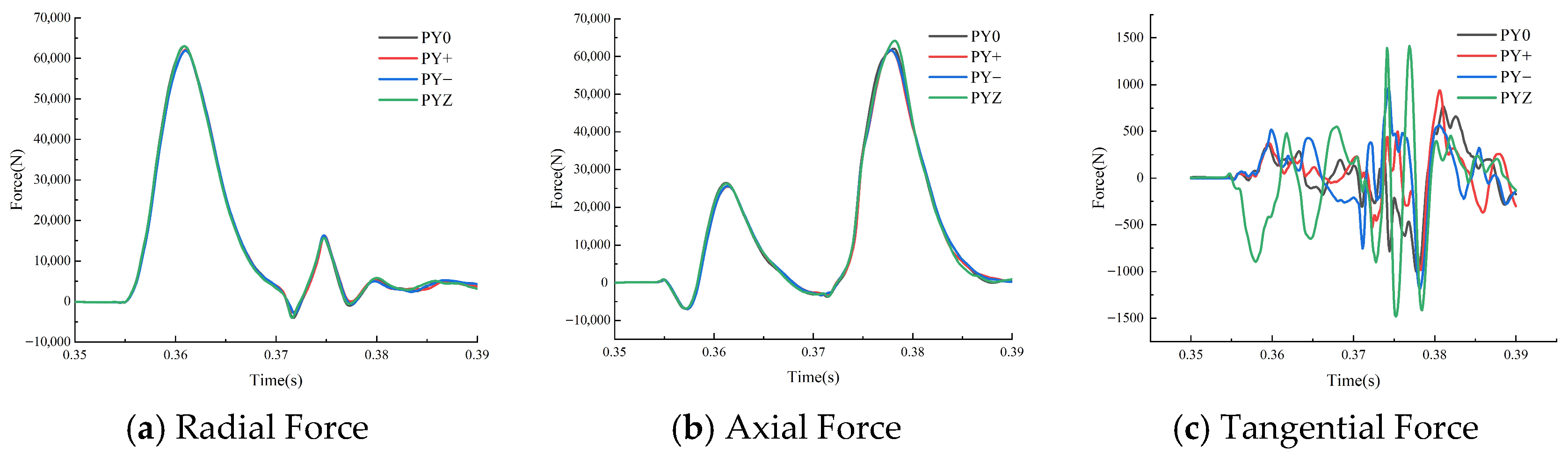
3.2. Stability Calculation of the Bucket Offset Working Conditions
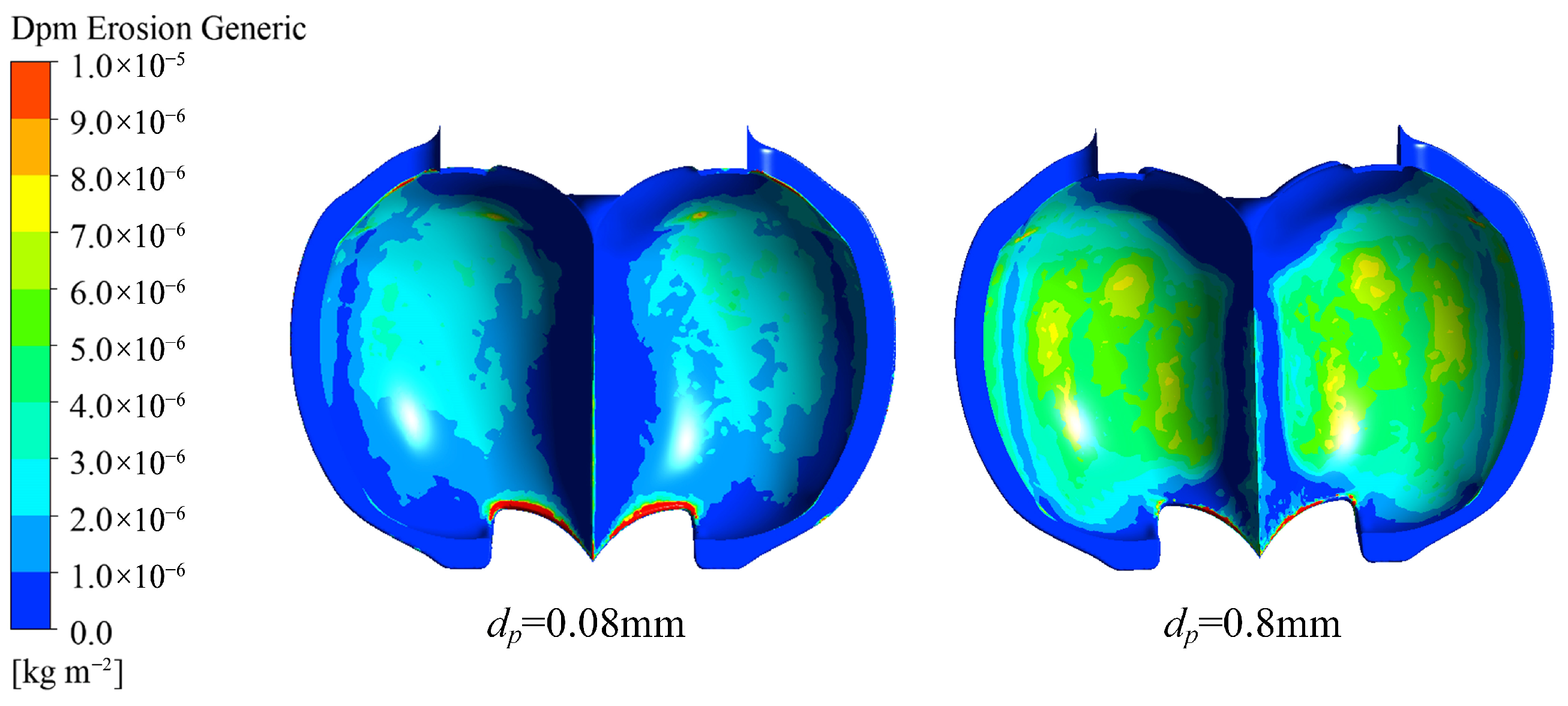
3.3. Erosion Analysis for Different Particle Sizes
4. Conclusions
- (1)
- Radial offset causes the jet to enter the bucket later when deflected outward and earlier when deflected inward.
- (2)
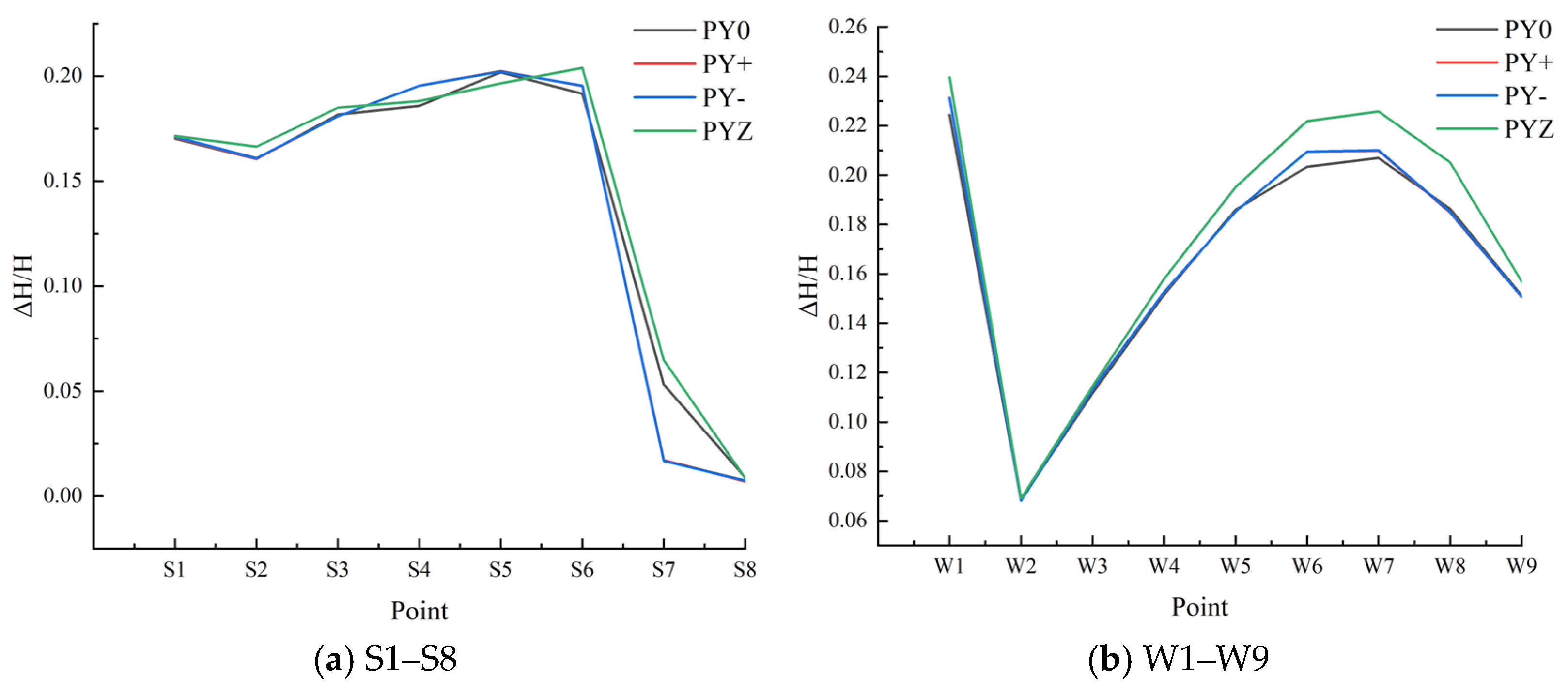
- Radial offset increases the relative pressure pulsation amplitude, with the most pronounced effects observed near the bucket root and along the division blade. The maximum amplitude reaches 20% at point S5. On the working face, the increase in pressure pulsation amplitude is more substantial under the PY+ condition compared to the PY− condition, with the most significant relative amplitude change observed at point W1, reaching 23%. The highest absolute pressure pulsation amplitude is recorded at point W6, reaching 24%.
- (3)
- Axial offset results in an uneven pressure distribution and elevated relative pressure pulsation amplitudes. The most notable change is observed at point W1, with an amplitude reaching 23.97%. This condition increases the likelihood of bucket vibration and fatigue damage.
- (4)
- Erosion is more severe for large particle sizes than for small particle sizes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VOF | volume of fluid |
| GCI | grid convergence index |
| SST | shear stress transport |
Nomenclature
| PY0 | no offset |
| PY+ | radial offset of the jet toward the outer edge of bucket |
| PY− | radial offset toward the bucket root |
| PYZ | axial offset |
| Cp | pressure coefficient |
References
- Bhattarai, S.; Vichare, P.; Dahal, K.; Al, M.A.; Olabi, A.G. Novel trends in modelling techniques of Pelton Turbine bucket for increased renewable energy production. Renew. Sustain. Energy Rev. 2019, 112, 87–101. [Google Scholar] [CrossRef]
- Yang, Z.; Li, C.; Zhou, X. Global hydropower development status and potential analysis in 2021. Adv. Sci. Technol. Water Resour. 2022, 42, 39–44+56. [Google Scholar]
- Liu, X. Hydraulic Turbine Sand and Water Flow and Erosion; Water Conservancy and Hydropower Press: Beijing, China, 2020. [Google Scholar]
- Han, L.; Zhang, G.; Wang, Y.; Wei, X.Z. Investigation of erosion influence in distribution system and nozzle structure of Pelton turbine. Renew. Energy 2021, 178, 1119–1128. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Chang, X.; Qin, B.; Pang, J.; Lai, Z.; Jiang, D.; Qin, M.; Yao, B.; Zeng, Y. Research on the mechanism of sediment erosion in the bucket of a large-scale Pelton turbine at a hydropower station. Powder Technol. 2025, 455, 120805. [Google Scholar] [CrossRef]
- Yao, B.; Zhou, Y.; Wu, B.; Pang, J.; Jiang, D.; Zhang, H.; Liu, J.; Qin, B.; Liu, X. Effect of sediment erosion on pressure pulsations in a large Pelton turbine. Energy Sci. Eng. 2024, 12, 4040–4056. [Google Scholar] [CrossRef]
- Qin, M.; Yu, Z.; Wu, B.; Pang, J.; Jiang, D.; Zhang, H.; Liu, J.; Hua, H.; Liu, X. Numerical simulation of multiphase flow and prediction of sediment wear in a large Pelton turbine. Energy Sci. Eng. 2024, 12, 5031–5044. [Google Scholar] [CrossRef]
- Santolin, A.; Cavazzini, G.; Ardizzon, G.; Pavesi, G. Numerical investigation of the interaction between jet and bucket in a Pelton turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 721–728. [Google Scholar] [CrossRef]
- Anagnostopoulos, J.S.; Papantonis, D.E. A fast Lagrangian simulation method for flow analysis and runner design in Pelton turbines. J. Hydrodyn. 2012, 24, 930–941. [Google Scholar] [CrossRef]
- Han, L.; Duan, X.L.; Gong, R.Z.; Zhang, G.F.; Wang, H.J.; Wei, X.Z. Physic of secondary flow phenomenon in distributor and bifurcation pipe of Pelton turbine. Renew. Energy 2019, 131, 159–167. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Q.; Zhang, B.; Xu, Y. Old wine in a new bottle: Energy loss evaluation in a six-nozzle Pelton turbine with entropy production theory. Energy 2025, 319, 135132. [Google Scholar] [CrossRef]
- Jung, I.H.; Kim, Y.S.; Shin, D.H.; Chung, J.T.; Shin, Y. Influence of spear needle eccentricity on jet quality in micro Pelton turbine for power generation. Energy 2019, 175, 58–65. [Google Scholar] [CrossRef]
- Zeng, C.; Xiao, Y.; Luo, Y.; Zhang, J.; Wang, Z.; Fan, H.; Ahn, S.-H. Hydraulic performance prediction of a prototype four-nozzle Pelton turbine by entire flow path simulation. Renew. Energy 2018, 125, 270–282. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Z.; Zhou, H.; Wang, Z.; Guo, P. Numerical assessment of transient flow and energy dissipation in a Pelton turbine during startup. Phys. Fluids 2024, 36, 094119. [Google Scholar] [CrossRef]
- Fan, W.; Sun, L.; Guo, P. Investigation on unstable flow characteristics and energy dissipation in Pelton turbine. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2304643. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, B.; Xu, B.; Tang, P.; Guo, N.; Zhang, W. Investigation on the influence of bucket’s flow patterns on energy conversion characteristics of Pelton turbine. Eng. Appl. Comput. Fluid. Mech. 2023, 17, 2234435. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, B.; Tang, P.; Guo, N.; Zhu, B. Generation mechanism and control method of counter torque in the bucket of a Pelton turbine. Phys. Fluids 2023, 35, 105133. [Google Scholar] [CrossRef]
- GB/T 8564-2003; Installation Code for Hydraulic Turbine Generators. China Standards Press: Beijing, China, 2003.
- Li, L.; Lu, J.; Gong, Y.; Zhao, H.; Liu, X.; Zhu, B. Sediment erosion characteristics of Pelton turbine runner: Effects of sediment concentration and diameter. Renew. Energy 2024, 220. [Google Scholar] [CrossRef]
- Ge, X.; Sun, J.; Zhou, Y.; Cai, J.; Zhang, H.; Zhang, L.; Ding, M.; Deng, C.; Binama, M.; Zheng, Y. Experimental and numerical studies on opening and velocity influence on sediment erosion of Pelton turbine buckets. Renew. Energy 2021, 173, 1040–1056. [Google Scholar] [CrossRef]
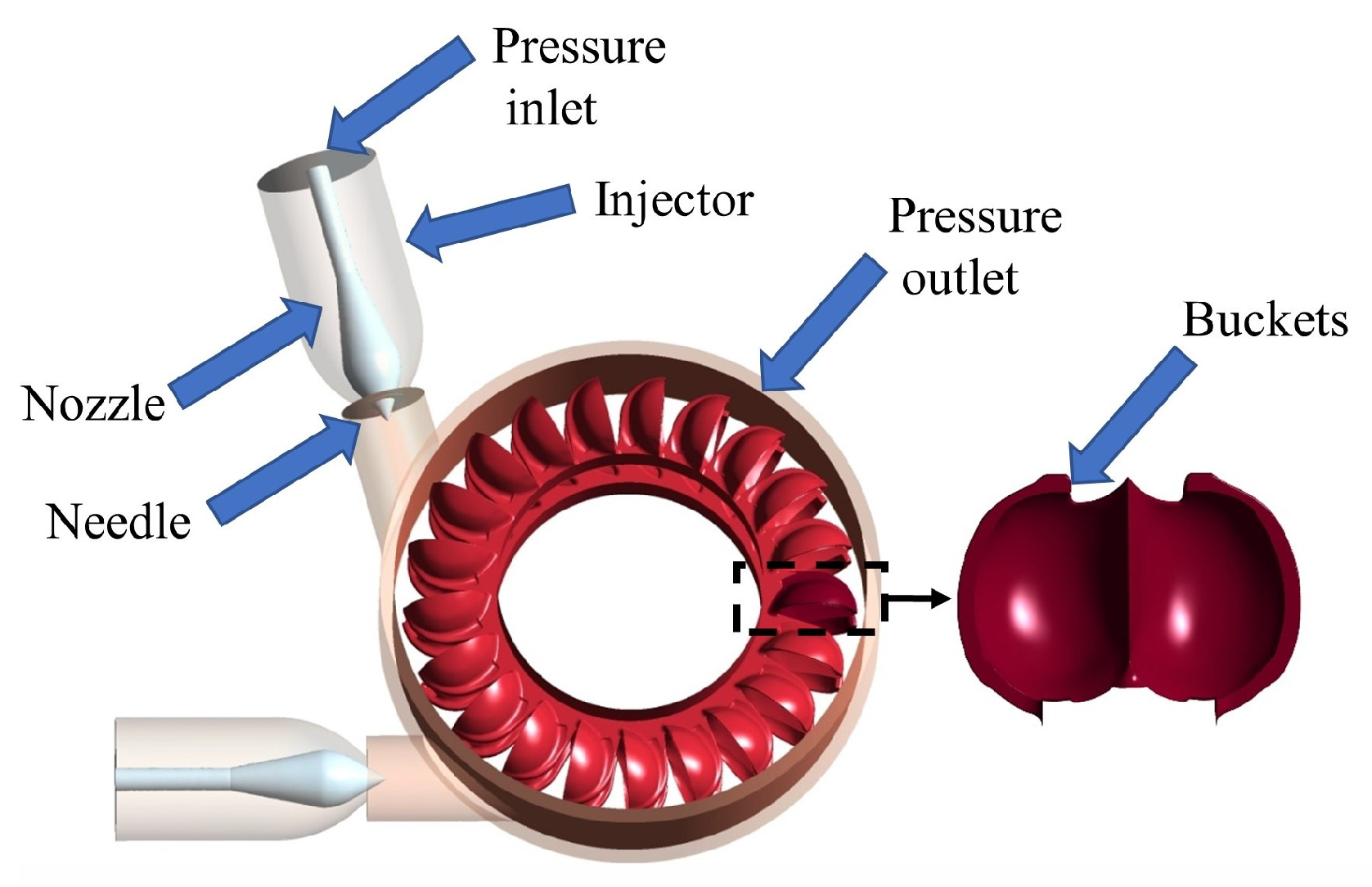

| Design Parameters | Value | Design Parameters | Value |
|---|---|---|---|
| Head (m) | 578 | Flow (m3/s) | 2.09 |
| Rated speed (r/min) | 750 | Number of nozzles | 2 |
| Number of buckets | 21 | Runner pitch circle diameter (mm) | 1280 |
| Bucket width (mm) | 382.3 | Nozzle inlet diameter (mm) | 430 |
| Component | G1 | G2 | G3 |
|---|---|---|---|
| Number of grids | 12,489,710 | 9,580,455 | 6,943,521 |
| Parameter | φ1 | φ2 | φ3 | pr | GCI |
|---|---|---|---|---|---|
| φ | 39,972.8 | 39,836.11688 | 39,643.5 | 3.45 | 1.15% |
| Flow Q | Efficiency η | |
|---|---|---|
| experimental | 2.09 m3/s | 86.7% |
| numerical calculation | 2.04 m3/s | 84.3% |
| errors | 2.39% | 2.77% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Z.; Liu, J.; Pang, J.; Zhang, J.; Gang, Y.; Cai, Y.; Li, J.; Wang, H.; Xu, K.; Liu, X. The Effect of Jet Deviation on the Stability of Pelton Turbine. Processes 2025, 13, 2683. https://doi.org/10.3390/pr13092683
Yuan Z, Liu J, Pang J, Zhang J, Gang Y, Cai Y, Li J, Wang H, Xu K, Liu X. The Effect of Jet Deviation on the Stability of Pelton Turbine. Processes. 2025; 13(9):2683. https://doi.org/10.3390/pr13092683
Chicago/Turabian StyleYuan, Zhiqiang, Jitao Liu, Jiayang Pang, Jian Zhang, Yuanyuan Gang, Yinhui Cai, Jianan Li, Haoyu Wang, Kang Xu, and Xiaobing Liu. 2025. "The Effect of Jet Deviation on the Stability of Pelton Turbine" Processes 13, no. 9: 2683. https://doi.org/10.3390/pr13092683
APA StyleYuan, Z., Liu, J., Pang, J., Zhang, J., Gang, Y., Cai, Y., Li, J., Wang, H., Xu, K., & Liu, X. (2025). The Effect of Jet Deviation on the Stability of Pelton Turbine. Processes, 13(9), 2683. https://doi.org/10.3390/pr13092683






