Statistical Optimization in the Fermentation Stage for Organic Ethanol: A Sustainable Approach

Abstract

The growing demand for organic products is having a transformative effect on the alcoholic beverage industry. This work investigates the possibility of producing organic ethanol only from sugarcane final molasses as a nutrient vector and Saccharomyces cerevisiae in the absence of inorganic nitrogen or phosphorus compounds. The Plackett–Bürman design included the pseudo-factors (X4–X6) due to the experimental design requirements. These factors represent the possible influence of uncontrolled variables, such as pH or nutrient interactions. Subsequently, a predictive quadratic model using Box–Behnken design with the real variables (sugar concentration, yeast dose, and incubation time) was developed and validated $(R^2=0.977)$ with internal validation; given the lack of replications and the sample size, this value should be interpreted with caution and not as generalizable predictive evidence. Further experiments with replications and cross-validation will be required to confirm its predictive capacity. Through statistical optimization, the maximum cell proliferation of $432\times {10}^6$ cells/mL was achieved under optimal conditions of 8°Brix sugar concentration, 20 g/L dry yeast, and 3 h incubation time. The optimized fermentation process produced 7.8% v/v ethanol with a theoretical fermentation efficiency of 78.52%, an alcohol-to-substrate yield of 62.15%, and a productivity of 1.86 g/L·h, representing significant improvements of 21.9%, 24.6%, 31.0%, and 10.1%, respectively, compared with non-optimized conditions. The fermentation time was reduced from 48 to 42 h while maintaining superior performance. These results demonstrate the technical feasibility of producing organic ethanol using certified organic molasses and no chemical additives. Overall, these findings should be regarded as proof of concept. All experiments were single-run without biological or technical replicates; consequently, the optimization and models are preliminary and require confirmation with replicated experiments and external validation.

1. Introduction

In recent decades, conventional agricultural practices using agrochemical inputs have significantly increased global per capita agricultural production. At the same time, per capita income is estimated to multiply by 2050 compared with its current level [1,2]. However, this effort not only increases production costs but also causes environmental damage, such as soil pollution and degradation, fertilizer and pesticide emissions, biodiversity loss, and several negative impacts on human health [2]. In this sense, alternative methods are needed to improve agricultural production or reduce dependence on agrochemicals and balance productivity with sustainability [3]. The proliferation of environmental concerns and the concomitant desire for chemical-free foods have precipitated an increase in demand for sustainable agricultural methods, specifically organic agriculture. [4].

Wittwer et al. in [5] state that organic agriculture is a production system that avoids or excludes the use of fertilizers, pesticides, growth regulators, and animal feed additives. To the extent possible, organic farming systems rely on crop rotation, the use of animal manure, legumes, green manures, and organic waste from off-farm sources, natural minerals, and biological pest control to maintain soil structure and productivity, provide nutrients to plants, and control insects, weeds, and other pests. Organic farming systems are predicated, to the greatest extent feasible, on the principles of crop rotation, the utilization of animal manure, legumes, green manures, organic waste originating from external sources, natural minerals, and biological pest control. These systems are designed to maintain soil structure and productivity, provide plant nutrients, and control insects, weeds, and other pests [6].

The dynamic and attractive market for organic food has stimulated the conversion of conventional agriculture to organic farming. It is estimated that more than 80% of the current organic acreage was incorporated into this system during the final decade of the previous century [7]. This gradual rise can be attributed to several factors, including the robust political and economic support for conventional agriculture, the underestimation of the adverse effects of chemical-intensive agriculture, and the pervasive denial of conventional production alternatives [8]. The global organic beverage market is segmented by product type: alcoholic (wine, beer, spirits) and non-alcoholic (fruit and vegetable juice, dairy, coffee, tea). The global beverage market is expected to expand at a compound annual growth rate (CAGR) of 12.3% during the forecast period, which extends through 2025. The North American region is currently the most substantial market for organic beverages, while the Asia-Pacific region is projected to exhibit a more rapid rate of growth. The growth of the organic beverage market has been attributed to two primary factors. Firstly, there has been a marked increase in consumer awareness regarding organic products. Secondly, the market has seen a continuous introduction of new product variants [7]. The market size for organic beverages was estimated at 50.19 billion U.S. dollars in 2024. Projections indicate that this figure will reach 63.79 billion U.S. dollars by 2029, indicating a compound annual growth rate (CAGR) of 4.91% during the forecast period (2024–2029) [9,10].

The continued increase in global energy demand requires the development of sustainable alternatives to non-renewable energy sources. This positions bioethanol as a vital part of future energy portfolios [11]. A rigorous analysis of the fermentation stage is necessary to determine the overall economic viability and environmental impact of bioethanol synthesis [12]. While traditional fermentation methods are effective, they often present challenges related to process efficiency, yield optimization, and energy consumption, which limit their potential for large-scale industrial applications [13]. Consequently, advanced statistical optimization techniques coupled with metabolic modeling are being used more frequently to improve productivity and reduce operating costs at the fermentation stage [14].

The production of organic ethanol presents a unique set of challenges, including limited nutrient availability, a deficiency of inorganic nitrogen, and constraints in the utilization of fermentation enhancers. The aforementioned factors frequently culminate in diminished fermentation efficiency and cell viability. The production of organic alcohol entails the utilization of certified organic ingredients, which are cultivated without the employment of synthetic pesticides, herbicides, or other deleterious chemicals. Moreover, the production process does not involve the use of artificial additives. Instead, natural fermentation methods are employed. [15].

Two categories of ethanol are produced on a global scale: fermented and synthetic. The production of bioethanol is possible through the utilization of biomass that is readily available and contains fermentable free sugars [16]. From a technical perspective, the production of organic alcohol is characterized by its sustainability and social responsibility, thereby satisfying multiple criteria. For instance, the process under discussion eliminates the addition of synthetic chemicals, including but not limited to sulfuric acid, urea, ammonium phosphate, and antifoam agents [17].

A notable illustration of this commitment is evidenced by CADO (Consorcio Agroartesanal Dulce Orgánico), a company established by small-scale sugarcane farmers. This enterprise engages in the production of granulated panela and organic alcohol in Ecuador, exemplifying a commitment to sustainable and community-driven agricultural practices. The company’s product line includes panela, ethanol, and lacto-alcoholic beverages (cocoa cream and coffee) under the Wilkay brand. Additionally, it produces potable alcohol for individuals who engage in the production of liqueurs. The company holds the internationally recognized organic certification from BCS Öko-Garantie of Germany, which is currently under renewal. Fermented ethanol, also known as bioethanol, is produced through the fermentation of corn or other biomass materials. This fuel is primarily utilized in the production of energy, with a smaller percentage being employed in the beverage industry [18]. Synthetic ethanol is produced from ethylene, a petroleum byproduct, and is primarily used in industrial applications [19].

Among biofuels, the most developed and widely implemented process at the industrial level is the production of bioethanol through anaerobic fermentation of carbohydrates by yeast microorganisms [18,20,21]. The most conventional method for producing ethanol involves the fermentation of sugar sources, which are subsequently degraded by the action of microorganisms. The process is comprised of three fundamental stages: propagation, fermentation, and distillation. Among these, fermentation is the primary stage [22]. In the fermentation stage, ethanol is produced, along with other byproducts such as higher alcohols, organic acids, esters, and aldehydes, which give the characteristic aroma and flavor of spirits, rums, and spirits [21]. In the field of biofuel production, the fourth stage of the process is the preparation of the raw material, depending on the source. For example, starches from corn are used for first-generation alcohol, and lignocellulosic materials are used for second-generation ethanol. In both cases, the action of catalysts such as exogenous enzymes is required for hydrolysis. In the process of producing ethanol as a fuel, a fifth stage of dehydration is incorporated.

Other authors, such as Asmamaw in 2021 [23], include a fourth stage, that of raw material preparation, depending on the source. This phenomenon is exemplified by corn starches utilized in the production of first-generation alcohol and lignocellulosic materials employed in the second-generation ethanol process. Both of these processes necessitate the utilization of catalysts, such as exogenous enzymes, to facilitate the hydrolysis reaction. In the process of producing ethanol as a fuel, a fifth stage of dehydration is incorporated.

Research such as Ojeda (2005) [24] and Rodríguez (2016) [25] has addressed fermentation studies for the development of organic ethanol in Cuba. However, the results obtained are not conclusive enough to introduce this product as a new offering for the alcohol industry. Taking all this into account, the present research aims to study the production of organic ethanol using yeast culture. This study is novel in its exclusive use of certified organic final molasses with statistical optimization to enhance additive-free ethanol production. The organic ethanol under consideration is derived from molasses produced by the sole company in Cuba that is certified as a producer of organic sugar. The production of this alcohol does not involve the addition of chemical nutrients or acids during the process. The yeast utilized in Cuban distilleries, designated as Ethanol Red, is employed exclusively.

Although numerous studies have examined ethanol production from molasses and other substrates, most of these studies have employed inorganic nutrients, chemical additives, or optimized fermentation conditions using conventional inputs [16,17,20,26]. Few studies have addressed ethanol production under strict organic criteria by completely ignoring inorganic sources of nitrogen and phosphorus and using only certified raw materials.

Furthermore, the scientific literature reports only a few examples of combining advanced statistical designs, such as Plackett–Bürman and Box–Behnken, with organic fermentation processes, particularly in Latin American and Caribbean contexts. Most previous studies have focused on optimizing one variable at a time or comparing strains rather than on systematically integrating statistical optimization into real, pilot-scale organic processes [20,26,27].

The main novelty of this work is its sequential application of statistical optimization methodologies to maximize yeast proliferation and fermentation efficiency in a completely organic system without chemical additives, using certified molasses and realistic industrial conditions. This approach contributes to the literature on sustainable bioprocesses and offers a replicable methodological foundation for the organic ethanol industry in regions with limited resources. Given these constraints, the scope of this contribution is intentionally limited to demonstrating feasibility and providing a replicable methodology for practitioners pursuing organic certification, not to delivering generalizable predictive tools.

Accordingly, this work is scoped as a feasibility-oriented investigation under organic-only constraints, primarily targeting researchers and practitioners focused on organic bioethanol and statistical optimization under additive-free conditions.

2. Materials and Methods

2.1. Raw Materials Used

For this study, type B molasses was used as raw material. Organic molasses is obtained during the production process of ECOCERT-certified organic sugar. This process follows the specifications for sugarcane cultivation, from the ground up to the final product. Its parameters are characterized to identify and determine its composition based on sugars, measuring Brix, total reducing sugars, pH, and others. The yeast used was freeze-dried Saccharomyces cerevisiae, which has historically been used worldwide in the production of ethyl alcohol, yielding satisfactory results [28]. The yeast used in the process was Ethanol Red (Fermentis, Lesaffre, France; Product code: F10), a yeast strain specifically selected for industrial ethanol production. This fast-acting yeast has a high alcohol tolerance, exhibits higher alcohol yields, and maintains high viability, especially during high-solids fermentations.

2.2. Experimental Study

An experimental study was conducted at the yeast culture stage, without the use of nitrogen or phosphorus sources. Organic molasses is constituted of nutrients exclusively from natural sources. The objective of this study is to examine the factors that influence the response variable in a specific process or system. Plackett–Bürman designs allow for experimental planning without requiring a corresponding increase in the number of experiments [29]. The Plackett–Bürman design is a methodology employed to identify factors that have a significant effect on the response variable(s) in a given process or system. At this stage, the development of a predictive model or the examination of complex interactions is not the objective. The objective of this study is to refine the set of variables and reduce the experimental dimensionality. This will allow for more precise subsequent studies [30].

The utilization of a statistical experimental design is advantageous in several respects. Primarily, it serves to minimize the number of experiments conducted, thereby reducing the consumption of chemicals and materials. Additionally, it facilitates the evaluation of the primary interactive effects between each factor, thus enabling the construction of an equation that can achieve optimal fermentation conditions [31].

2.3. Theory of Plackett–Bürman Design for m Real Factors and n Experiments: Theoretical Foundations

2.3.1. Fundamental Conditions

Existence condition:

$$n\equiv 0(mod4)\mathrm{and}n\ge m+1$$

(1)

where

• n = number of experiments (multiple of 4);
• m = number of real factors;
• $n-1$ = maximum number of factors that can be studied.

2.3.2. Mathematical Construction

Design Matrix The design matrix $\mathbf{X}$ has dimension $n\times (n-1)$:

$$\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_m,{\mathbf{x}}_{m+1},\dots ,{\mathbf{x}}_{n-1}]$$

(2)

where

• ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_m$ = column vectors for real factors.
• ${\mathbf{x}}_{m+1},\dots ,{\mathbf{x}}_{n-1}$ = column vectors for pseudo-factors.

2.3.3. Orthogonality Properties

Orthogonality condition:

$$\begin{array}{cc}\hfill {\mathbf{x}}_i^T{\mathbf{x}}_j& =0\mathrm{for}i\ne j\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathbf{x}}_i^T{\mathbf{x}}_i& =n\mathrm{for}\mathrm{all}i\hfill \end{array}$$

(4)

Balance condition:

$$\sum _{i=1}^n{x}_{ij}=0\mathrm{for}\mathrm{all}j$$

(5)

2.3.4. Base Matrix Construction

For n experiments, the matrix is constructed using:

Base generator vector for $n=4k$:

$$\mathbf{g}=[g_1,g_2,\dots ,g_{n-1}]$$

(6)

Cyclic construction:

• Row 1: $[g_1,g_2,\dots ,g_{n-1}]$;
• Row 2: $[g_{n-1},g_1,g_2,\dots ,g_{n-2}]$;
• Row i: cyclic rotation of previous row;
• Row n: $[-1,-1,\dots ,-1]$.

3. Statistical Model

3.1. Linear Model

$$\mathbf{Y}=\mathbf{X}\beta +\epsilon$$

(7)

where

• $\mathbf{Y}$ = response vector $(n\times 1)$;
• $\mathbf{X}$ = design matrix $(n\times (n-1\left)\right)$;
• $\mathit{\beta }$ = effects vector $\left(\right(n-1)\times 1)$;
• $\mathit{\epsilon }$ = error vector $(n\times 1)$.

3.1.1. Effect Estimation

Main effects:

$${\beta }_i={\displaystyle \frac{1}{n}}\sum _{j=1}^n{x}_{ji}{y}_j\mathrm{for}i=1,2,\dots ,m$$

(8)

Pseudo-factor effects:

$${\beta }_i={\displaystyle \frac{1}{n}}\sum _{j=1}^n{x}_{ji}{y}_j\mathrm{for}i=m+1,\dots ,n-1$$

(9)

3.1.2. Purpose of Pseudo-Factors

With m real factors in n experiments, $(n-1-m)$ pseudo-factors are required:

$$\mathrm{Number}\mathrm{of}\mathrm{pseudo-}\mathrm{factors}=n-1-m$$

(10)

3.1.3. Functions of Pseudo-Factors Variables

Experimental error estimation:

$$s^2={\displaystyle \frac{1}{n-1-m}}\sum _{i=m+1}^{n-1}{\beta }_i^2$$

(11)

Standard error:

$$SE=\sqrt{{\displaystyle \frac{s^2}{n}}}$$

(12)

3.1.4. Detection of Uncontrolled Factors

If pseudo-factors show significant effects:

$$|{\beta }_i|>t_{\alpha /2,n-1-m}\times SE\mathrm{for}i=m+1,\dots ,n-1$$

(13)

This indicates the presence of unconsidered factors or important interactions.

3.1.5. Significance Analysis

t-Statistic

$$t_i={\displaystyle \frac{{\beta }_i}{SE}}\mathrm{for}i=1,2,\dots ,m$$

(14)

Degrees of Freedom

$$df=n-1-m(\mathrm{based}\mathrm{on}\mathrm{pseudo-}\mathrm{factors})$$

(15)

Significance Criterion A real factor is significant if

$$|t_i|>t_{\alpha /2,df}$$

(16)

3.1.6. Specifically Our Case: $m=3$, $n=8$

Parameters

• $m=3$ real factors ($X_1$, $X_2$, $X_3$);
• $n=8$ experiments;
• 4 pseudo-factors ($X_4$, $X_5$, $X_6$, $X_7$);
• $df=8-1-3=4$ degrees of freedom for error estimation.

Table 1. Experimental matrix of the Plackett–Bürman design for the growth stage.

n	${\mathit{X}}_1$	${\mathit{X}}_2$	${\mathit{X}}_3$	${\mathit{X}}_4$	${\mathit{X}}_5$	${\mathit{X}}_6$	${\mathit{X}}_7$
1	+	+	+	−	+	−	−
2	+	+	−	+	−	−	+
3	+	−	+	−	−	+	+
4	−	+	−	−	+	+	+
5	+	−	−	+	+	+	−
6	−	−	+	+	+	−	+
7	−	+	+	+	−	+	−
8	−	−	−	−	−	−	−

presents the experimental matrix of the study.

4. Validation of Design Assumptions

4.1. Orthogonality Verification

For the design matrix to be valid, the following conditions must be satisfied:

Column orthogonality:

$${\mathbf{x}}_i^T{\mathbf{x}}_j=\sum _{k=1}^n{x}_{ki}{x}_{kj}=0\mathrm{for}i\ne j$$

(17)

Column normalization:

$${\mathbf{x}}_i^T{\mathbf{x}}_i=\sum _{k=1}^n{x}_{ki}^2=n\mathrm{for}\mathrm{all}i$$

(18)

Balance Verification Each column must be balanced:

$$\sum _{k=1}^n{x}_{ki}=0\mathrm{for}\mathrm{all}i$$

(19)

This ensures that each factor appears exactly $n/2$ times at the high level (+1) and $n/2$ times at the low level (−1).

4.2. Statistical Inference

Hypothesis Testing For each real factor i ($i=1,2,\dots ,m$):

Null hypothesis:

$$H_0:{\beta }_i=0$$

(20)

Alternative hypothesis:

$$H_1:{\beta }_i\ne 0$$

(21)

Test Statistic

$$t_i={\displaystyle \frac{{\beta }_i}{SE}}\sim t_{df}$$

(22)

where $df=n-1-m$ degrees of freedom.

Critical Region Reject $H_0$ if

$$|t_i|>t_{\alpha /2,df}$$

(23)

This theoretical framework provides the complete mathematical foundation for Plackett–Bürman designs with any valid combination of m real factors and n experiments.

The incorporation of four pseudo-factors (X4, X5, X6, X7) as false variables in the Plackett–Bürman design serves multiple critical purposes in this experimental framework. With only three real variables (X1, X2, X3) in an eight-run design, these false variables are essential to complete the experimental matrix and enable proper statistical analysis. Primarily, these false variables enable the estimation of experimental error in the absence of biological replicates, which is essential given the material constraints acknowledged in this study. Additionally, they function as internal controls to detect the influence of unmeasured factors that may significantly affect yeast proliferation and fermentation outcomes. In organic ethanol production, numerous variables such as pH fluctuations, micro-aeration effects, nutrient interactions within the organic molasses matrix, temperature variations, and potential contamination levels can impact the process but are not directly controlled or measured. The false variables act as statistical sentinels, capturing the collective effect of these uncontrolled factors. If significant effects are observed in the false variables, it indicates that important factors beyond those explicitly studied are influencing the system, thereby validating the robustness of the experimental design and providing insights for future optimization studies [30,31]. Nevertheless, this approach does not replace biological or technical replication; all inferences remain provisional until replicated experiments provide independent estimates of pure error.

The levels of the variables under consideration were taken from the best results reported in previous studies by [25] and the parameters of Cuban distilleries, establishing the values presented in

Table 2. Variables and levels in the cultivation stage.

Independent Variables	Upper Level (+)	Lower Level (−)
Sugar concentration (°Brix) (X1)	14	8
Yeast concentration (g/L) (X2)	20	5
Incubation time (h) (X3)	9	3

. The final parameters (Y) measured were sugar concentration in the final solution (°Bx) and cell count (cell/mL).

The Plackett–Bürman design matrix consists of eight experiments and seven variables, with the consideration of only three real variables, thereby permitting the utilization of four pseudo-factors. The matrix, which has been adjusted to the real and pseudo-factors considered in the experimental development, is shown in Table 1.

The pH level is a critical factor in the process of alcoholic fermentation. Acidity is among the most significant organoleptic parameters in alcoholic beverages. It is derived from the presence of weak organic acids, which are produced by yeast and contaminating bacteria during the fermentation process [26,32]. The pH can limit yeast growth by altering enzymatic activity, cell permeability, and the availability of metal ions. Yeast can survive in a wide pH range (2.0 to 8.0), but the optimal pH for growth is between 4.8 and 5.0, which is slightly acidic [33]. Nutrition is another critical factor that must be taken into consideration. For an optimal fermentation process, yeast requires building block substances in optimal proportions, minerals, or vitamins [23], aspects that were not directly incorporated in the form of chemicals due to the requirements of achieving organic ethanol. It is noteworthy, however, that we have yet to consider any biological or technical replicates due to the paucity of material. This imposed limitation exerts a significant impact on the statistical validity of the obtained results. To ensure the reliability and generalizability of the findings, it is imperative that this limitation be addressed and enhanced in subsequent studies through the implementation of experimental repetitions. Due to material constraints, experiments were conducted without biological replicates. This limitation is acknowledged, and future work will address it. All assays were run only once (without biological or technical replicates) due to material restrictions; therefore, the results and models should be interpreted as exploratory. In future work, we will perform $\ge 3$ replicates per condition and cross-validation to estimate experimental variability and predictive power with greater rigor.

The culture stage is conducted within containers that are connected to a VEB Kombinat peristaltic pump for air supply. The culture stage takes place in a sealed 2-liter vessel. The temperature is maintained between 32 and 33 °C, and air is supplied at a rate of 0.8 vvm to oxygenate the yeast. Yeast is added at the levels specified in the experimental design. Once this stage begins, it is monitored by measuring the Brix until it reaches the established time, and the pre-fermenter is ready to be inoculated. These cultures are used in some parts of the world to obtain fermented foods, offering a certain advantage over pure cultures, as they have a high growth rate and higher yield. The main characteristics these cultures must possess are as follows:

• Ethanol tolerance.
• High temperature tolerance.
• Tolerance to high sugar concentrations.
• Alcohol yield.
• Fermentation efficiency and productivity.

This approach leverages the yeast’s capacity to thrive, proliferate, and efficiently metabolize in the presence of oxygen [23]. Initially, the molasses is diluted with distilled water to the °Brix established for each test. This method is principally employed to ascertain the dissolved solids present in the diluted molasses and the pre-ferment through the utilization of an Atago refractometer equipped with a Brix scale. The pH is measured potentiometrically using a Hanna 213 pH meter, which is calibrated using reference buffer solutions of 4.0 and 7.0 pH units. The samples were sterilized in an LDZM autoclave to eliminate any undesirable microorganisms.

The sugar concentration was measured by the Brix degree in an Atago brand refractometer, and the total reducing sugars by the 3–5 cold Dinitro Salicylic Acid (DNS) method, and cell count in a Neubauer chamber. The cultivation and fermentation stages were carried out at 30 ± 1 °C.

4.3. Statistical Analysis

A statistical analysis was conducted to ascertain the factors that exerted a significant influence on the cell count response variable at the culmination of the culture stage. A statistical model was developed to facilitate optimization through the implementation of eight experimental runs in a Plackett–Bürman design. The analysis focused on seven coded factors (X1 to X7), with X4, X5, X6, and X7 corresponding to the pseudo-factors. These variables were evaluated at two coded levels: high (+1) and low (−1). The statistical results were obtained by processing the experimental design in FrF2 version 2.3.4 software, a package used to generate fractional factorial and Plackett–Bürman designs.

Experimental Application of the Obtained Model

The pre-fermentation and fermentation stages are carried out under conditions that are optimized to allow for a higher cell count, as determined by the model or statistical analysis. At the stage of final fermentation, the alcohol content is determined. The execution of this procedure necessitates the distillation of the fermented must, followed by the determination of its alcohol content using an alcohol meter that has been meticulously calibrated within the appropriate range for the product’s specific concentration [34].

The theoretical fermentation efficiency, substrate alcohol yield, and productivity are determined according to Equations (1)–(3).

$$\mathrm{Efficiency}(\%)=\left({\displaystyle \frac{\mathrm{ALC}\times 0.79}{{\mathrm{ART}}_i-{\mathrm{ART}}_r}}\right)\times {\displaystyle \frac{100}{0.511}}$$

(24)

where

• ALC: Alcohol content of the fermented mash (% v/v).
• ${\mathrm{ART}}_i$: Total reducing sugars in the mash at the beginning of fermentation (%).
• ${\mathrm{ART}}_r$: Residual total reducing sugars in the fermented mash (%).
• 0.79: Density of pure ethanol (g/mL).
• 0.511: Theoretical yield of ethanol from sugars (g ethanol/g sugar).

$$\mathrm{Yield}(\%)=\left({\displaystyle \frac{\mathrm{ALC}}{{\mathrm{ART}}_i-{\mathrm{ART}}_r}}\right)\times 100$$

(25)

$$\mathrm{Productivity}(\mathrm{g}/\mathrm{L}·\mathrm{h})={\displaystyle \frac{\mathrm{ALC}(\mathrm{g}/\mathrm{L})}{fermentationtime}}$$

(26)

4.4. Results and Discussion

Experimental Results

Sugarcane molasses is an ideal economical raw material for ethanol production due to its wide availability and low cost [35]. Sugarcane molasses is a viscous, dark, and sugar-rich byproduct suitable for fermentation and ethanol production [23]. The sugars present in the final molasses are primarily sucrose, glucose, fructose, and small amounts of mannose in stored molasses [27]. The parameters that characterized the final organic molasses are shown in

Table 3. Initial physicochemical characteristics of the mash.

Parameter	Value
°Brix	86
pH	5.7
Total Reducing Sugars (ART) (%)	53.846
Sucrose (%)	36.613
Density (g/mL)	1.4591
Total Sugars (%)	51.919

.

The organic molasses utilized exhibited total sugars within the range of 50.6–71.0% w/w, as reported in [36]. Asmamaw in 2021 [23] reported standard values for total reducing sugars in inorganic molasses (44–55%) and Brix (83–91%), with these parameters corresponding to the organic molasses used in each range. As illustrated in Figure 1, the concentration of soluble solids was measured at the beginning and end of each experiment. In all experiments, substrate consumption occurred during fermentation, as demonstrated by the decrease in Brix levels. The decrease in soluble solids ranged from approximately 21% to 85% (experiments three and seven, respectively). This phenomenon aligns with the findings documented by [27,34]. The aforementioned authors pioneered an experimental approach to ethanol fermentation, employing a conventional method to achieve a removal of soluble solids of 44% and 84%, respectively, when utilizing final molasses as the fermentation substrate.

During fermentation, in addition to the production of ethanol and CO₂, other byproducts are generated, such as glycerol and weak organic acids, which can lower the pH of the culture medium [37]. In the case of organic ethanol, no acids are used to lower the pH. In this case, the observed pH decrease is consistent with the formation of fermentation byproducts (e.g., glycerol and weak organic acids), but causality cannot be established without targeted measurements. The pH behavior exhibited during the culture stage (see Figure 1) demonstrated a slight decrease in the alternatives that were analyzed, with a decline from 5.6 to 5. The values obtained at the conclusion of the fermentation stage demonstrate slight increases in comparison to the final pH levels reported in the research conducted by [34,38]. In our runs, the pH decreased during fermentation; such trends are compatible with reported byproduct formation [37] but remain unconfirmed here. Other mechanisms (e.g., CO₂ dissolution, cell lysis, or microbial contamination) cannot be excluded. No qualitative or quantitative metabolite analyses were performed in this study; future work will quantify glycerol and organic acids by HPLC/GC to test these hypotheses. However, it should be noted that quantitative analysis of these compounds was not performed in this study. Quantifying byproducts such as acetic acid, glycerol, and other organic acids is necessary to ensure ethanol purity. Through such analysis, we can ensure compliance with regulatory standards and requirements, especially for applications for human consumption. It is important for future research to conduct detailed chromatographic analyses to address this issue.

Saccharomyces cerevisiae is the predominant microorganism employed globally for bioethanol production [39], exhibiting tolerance to low pH values, elevated temperatures, and ethanol concentrations [16]. At the conclusion of the culture stage, a cell count is conducted, as illustrated in Figure 2. Cell counts were performed in a Neubauer chamber, and the results were extrapolated to cells/mL using the standard calculation formula.

According to the findings of [40], the highest counts correspond to the experiments with the highest concentrations of fermentable sugars, which reached values of up to 420 million cells per milliliter. The author reports that, in the pre-fermentation stage, it is essential to attain a yeast population of approximately 150 million cells per milliliter. The most optimal outcomes were attained in experiments one, three, four, and five, with final values ranging from 280 to $420\times {10}^6$ cells/mL. The fourth experiment, which exhibited the highest cell count, utilized a reduced sugar concentration and a greater quantity of yeast for the culture duration, resulting in the complete consumption of the sugar solution. In this sense, Asmamaw in [23] reports that a higher dose of yeast implies a faster start of fermentation. This author obtained a range of 455 to 465 million cells per milliliter, starting from an initial inoculation of 20 g/L in a traditional ethanol process. In experiments one, three, and five, fermentation occurred with a higher concentration of fermentable sugars.

The lowest cell counts were achieved in experiments 6 and 7, which had a lower substrate concentration, indicating that this corresponded to a lower cell propagation, which could not convert all the sugar into ethanol.

The initial and final Brix and ART reported in Table 3 were measured, and the fermentation quality parameters were measured.

In the present study, it is not reported, since the yeast is the same one used in previous works, where the capacity and compatibility of the yeast with these organic cane molasses have been demonstrated. A major limitation of this study is the lack of a control group based on conventional fermentation with inorganic nutrients. Direct comparison with traditional methods is essential to assess the competitiveness and industrial applicability of the organic process and is therefore a priority for future research. This study did not include a control with inorganic nutrients; therefore, it is not possible to establish the practical competitiveness of the organic process. As a priority for future work, we will conduct a controlled comparative trial against the conventional route (inorganic nutrients) using the same substrate, factorial design, and harmonized metrics (yield, efficiency, productivity, costs, and robustness). While the decrease in pH is consistent with the formation of glycerol and organic acids, we did not quantify these metabolites and cannot rule out other causes (dissolved CO₂, cell lysis, or contamination). In follow-up studies, we will implement (i) HPLC/LC–MS for acetic, lactic, succinic, and glycerol; (ii) sterile abiotic monitoring to break down the effect of CO₂; and (iii) cell counts/microscopy and differential culture to rule out contamination.

5. Statistical Analysis of the Results Obtained

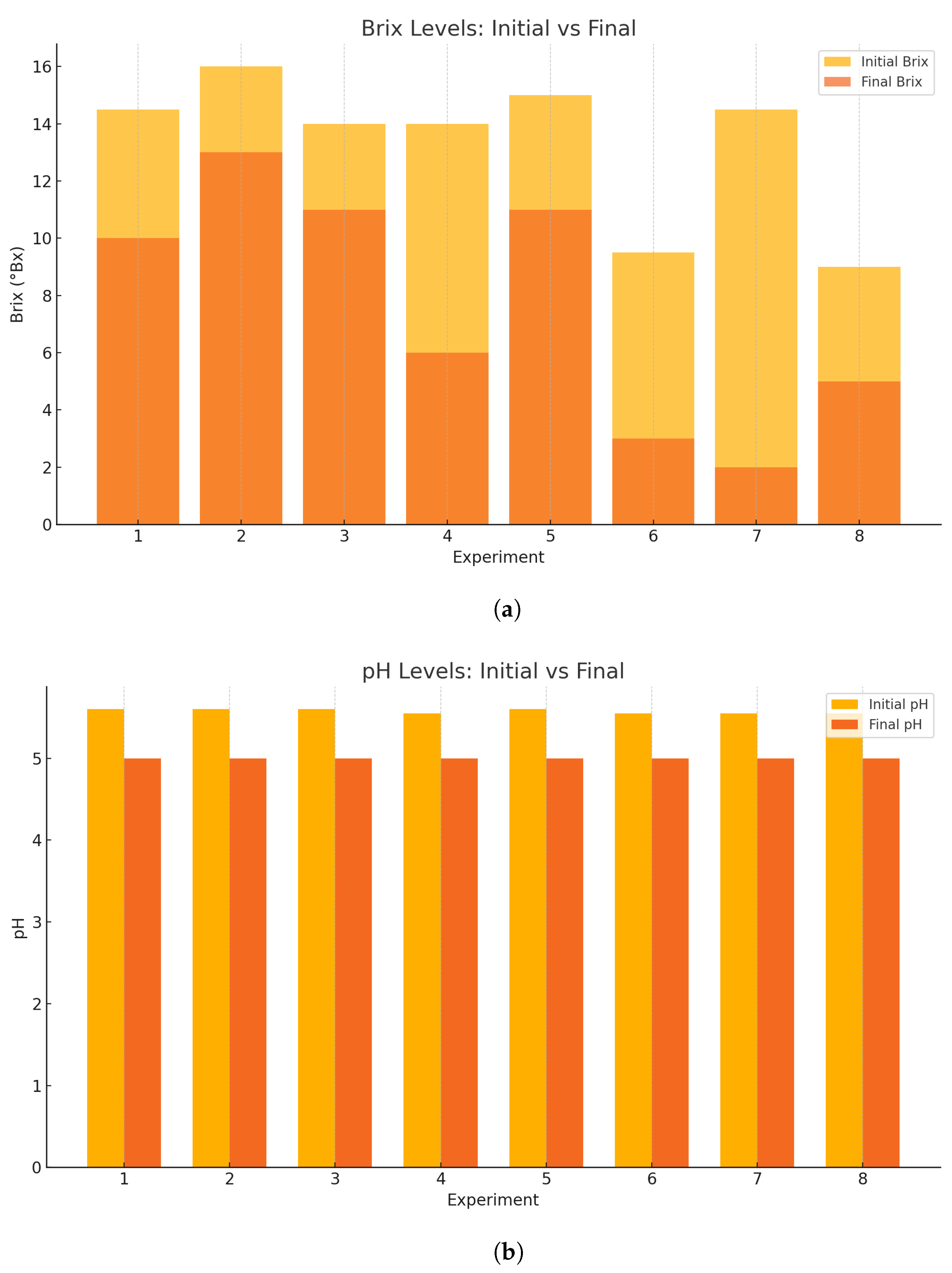
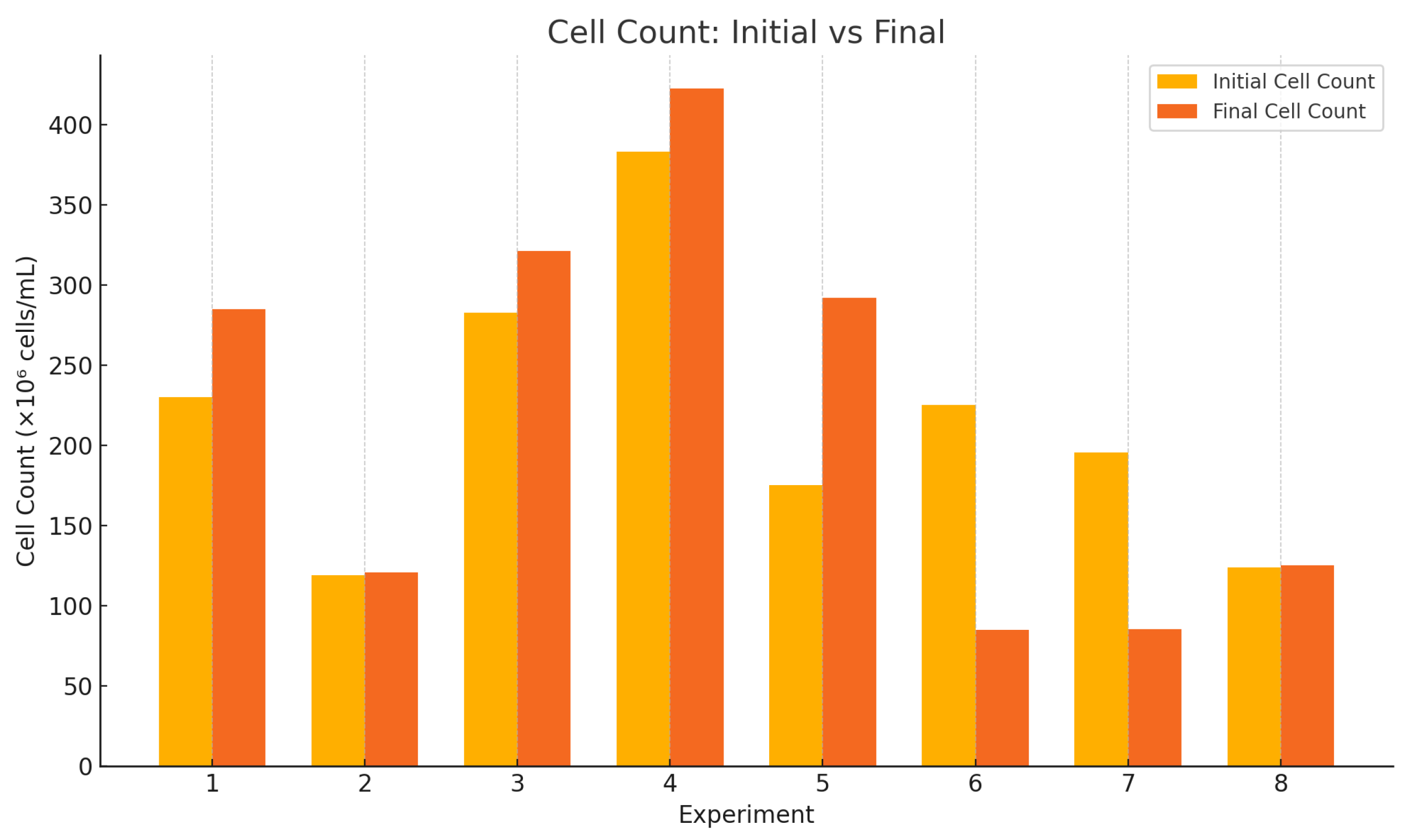
The mean cell count was calculated for each factor level to identify those with the greatest impact on final cell count and determine the optimal configuration that maximizes their value.

Table 4. Experimental design and observed response values.

Exp.	${\mathit{X}}_1$	${\mathit{X}}_2$	${\mathit{X}}_3$	${\mathit{X}}_4$	${\mathit{X}}_5$	${\mathit{X}}_6$	${\mathit{X}}_7$	Cell Count (106 Cells/mL)
1	1	1	1	−1	1	−1	−1	285.0
2	1	1	−1	1	−1	−1	1	121.0
3	1	−1	1	−1	−1	1	1	321.5
4	−1	1	−1	−1	1	1	1	422.5
5	1	−1	−1	1	1	1	−1	292.0
6	−1	−1	1	1	1	−1	1	85.0
7	−1	1	1	1	−1	1	−1	85.5
8	−1	−1	−1	−1	−1	−1	−1	125.5

presents the experimental matrix, which contains the final results for the response variable under consideration.

The primary effects of the independent variables were estimated as the difference between the mean cell count response when the factor is at its high level $+1$ and its low level $-1$, divided by half of the runs, as illustrated in

Table 5. Main effects estimated for cell count response.

Factor	Estimated Effect on Cell Count (Cells/mL)
$X_1$	$1.88\times {10}^7$
$X_2$	$5.62\times {10}^6$
$X_3$	$-1.15\times {10}^7$
$X_4$	$-3.57\times {10}^7$
$X_5$	$2.69\times {10}^7$
$X_6$	$3.16\times {10}^7$
$X_7$	$1.01\times {10}^7$

.

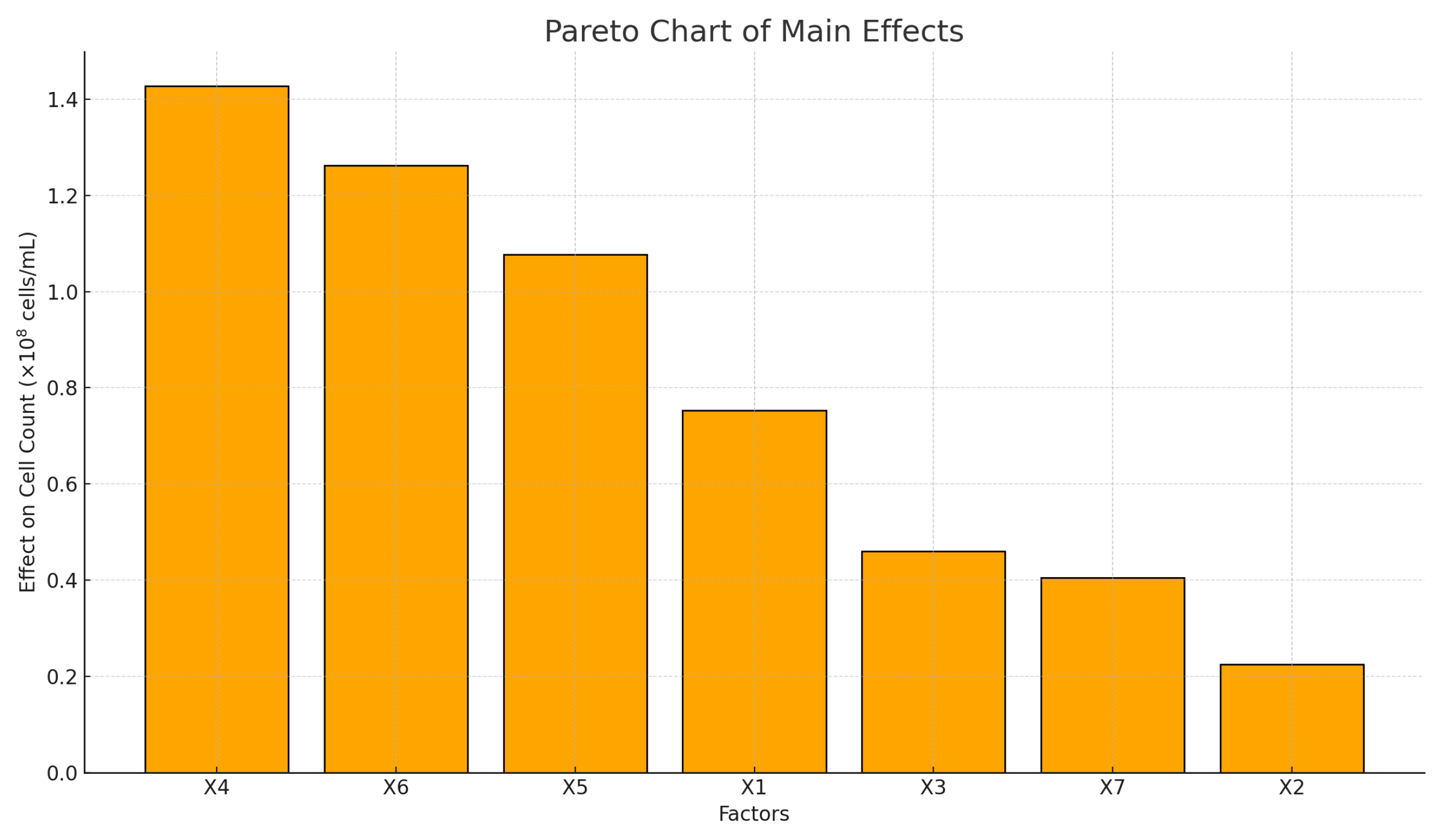
As illustrated in Figure 3, the Pareto chart provides a graphical representation of the estimated main effects on cell count for each factor considered in the Plackett–Bürman design. In this chart, the factors are arranged in descending order according to their absolute impact, thereby facilitating a clear and hierarchical interpretation of the relative importance of each factor.

The Pareto chart reveals the presence of four significant variables, of which the first three are deemed false variables. The sequence begins with X4, X6, and X5, followed by X1, which is a physical variable. Factor X4 is particularly noteworthy, as it exerts the most significant influence, with an effect exceeding 70 million cells. This finding suggests that the variation in Factor X4 has the greatest impact on cell count. Subsequent to these, the effects of X6 and X5 also exceed 50 million cells/mL, thereby consolidating them as critical variables for system optimization. In the experimental design, X4, X5, and X6 were designated as false variables, suggesting that other factors, not previously considered, influence cell count. As mentioned in [41,42], factors such as substrate concentration, microbial cell concentration, pH, and nitrogen source influence ethanol production. These authors add that the impact of these factors on ethanol production yield depends, in turn, on the microbial species, fermentation conditions, and types of raw materials used.

In this case, the false variables may correspond to the interaction of X1 with the other two variables (sugar concentration over time and yeast concentration as well as the interaction of these three variables in combination). As noted by Nuanpeng et al. [31], factors such as substrate concentration, microbial cell concentration, pH, and the nitrogen source have been identified as influential in the context of ethanol production. The authors further posit that the impact of these factors on ethanol production yield is contingent upon the microbial species, the fermentation conditions, and the types of raw materials utilized. Alternatively, these false variables may be other variables not considered in the experiment that affect the process, such as pH, aeration, or agitation. Nutrition is another critical factor that must be taken into consideration. To ensure an optimal fermentation process, yeast requires specific nutrients in precise proportions. To ensure an optimal fermentation process, yeast requires the presence of macro- and micronutrients in precise proportions, including minerals or vitamins [23]. These elements were not directly incorporated into the fermentation process due to the necessity of producing organic ethanol. In the present study, the pseudofactors (X4, X5, X6) were incorporated exclusively to complete the Plackett–Bürman statistical design, since the number of real factors was lower than required by the design. These pseudofactors do not correspond to physical or experimental variables but rather allow estimating experimental error and detecting the possible influence of uncontrolled factors. Therefore, any interpretation of their physical significance should be considered speculative, and it is not recommended to draw practical conclusions from their statistical significance.

At a secondary level of relevance, the concentration of sugars in solution (X1) is associated with the reducing sugars that constitute the substrate source for fermentation, with an effect close to 40 million, suggesting a moderate influence. Finally, the yeast concentration, time, and variable X7 exhibited minor effects, below 25 million, indicating that their contribution to the model is limited or even dispensable for further analysis.

This graphical representation is two-fold: it complements the numerical analysis and facilitates decision-making by visually highlighting which factors should be prioritized in fine-tuning or expanding the experimental design. The necessity to regulate and enhance the levels of X4, X5, and X6 is further accentuated, as these factors significantly influence the variability observed in cell count.

Given the absence of dummy columns—that is, additional columns in the experimental design that do not represent any real factors in the system—the standard error (SE) was estimated as the standard deviation of the estimated effects. This calculation yielded a value of $SE\approx 2.35·{10}^7$.

The significance of the main effects on cell count enables the identification of factors that exert a statistically relevant influence, which extends beyond their absolute magnitude. To accomplish this objective, the standard error (SE) was estimated from the three minor effects. The Student’s t-values and p-values were calculated for each factor with three degrees of freedom, under the assumption of a Student’s t-value distribution. The t-values (estimate/standard error) are displayed in

Table 6. Calculated t values and statistical significance for each factor.

Factor	Standardized t	Effect (cells/mL)	t-Value	p-Value
$X_1$	0.80	75.25	3.59	0.037
$X_2$	0.24	22.50	1.07	0.363
$X_3$	−0.49	−46.00	−2.19	0.116
$X_4$	−1.52	−142.75	−6.81	0.0065
$X_4$	1.15	107.75	5.14	0.014
$X_6$	1.34	126.25	6.02	0.009
$X_7$	0.43	40.50	1.93	0.149

, and the effect is employed to ascertain significance.

Factors X4, X5, X6, and X1 exhibit p-values below the standard significance threshold of 5% (p < 0.05), signifying that their effects on the cell count variable are statistically significant. Factor X4 is the most significant, with a negative effect of −142.75, a t-value of −6.81, and a p-value of 0.0065, establishing it as the most potent and pertinent factor in the model. X5 and X6 exhibit extremely significant beneficial effects (t = 5.14 and 6.02, respectively), affirming their importance as critical variables for optimizing cell count. X1 exhibits a positive effect of 75.25 and a t-value of 3.59 (p = 0.037), indicating significance, albeit with a diminished relative influence.

Conversely, factors X2, X3, and X7 lack adequate statistical evidence to be deemed relevant in the model, as their p-values (0.363, 0.116, and 0.149, respectively), beyond the necessary threshold. X3 exhibits a moderate negative effect; nevertheless, its insignificance indicates that its impact may be attributable to random variation or unexplained sources of variability within the model. The impacts of X2 and X7 are minimal and statistically insignificant, justifying their removal from streamlined iterations of the predictive model.

The statistical analysis endorses the prioritization of components X4, X5, and X6 in the optimization of cell culture processes. This also rationalizes the exclusion of components X2, X3, and X7, as their contributions are statistically insignificant within the assessed model.

5.1. Linear Regression Model

The full linear regression model is

$$\mathrm{FCC}={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7$$

(27)

where the estimated coefficients are

$$\begin{array}{cc}\hfill {\beta }_0& =214.75\hfill \\ \hfill {\beta }_1& =37.625\hfill \\ \hfill {\beta }_2& =11.25\hfill \\ \hfill {\beta }_3& =-23\hfill \\ \hfill {\beta }_4& =-71.375\hfill \\ \hfill {\beta }_5& =22.3335\hfill \\ \hfill {\beta }_6& =63.125\hfill \\ \hfill {\beta }_7& =20.25\hfill \end{array}$$

Therefore, the final equation is

$$\mathrm{FCC}=214.75+37.625X_1+11.25X_2-23X_3-71.375X_4+22.3335X_5+63.125X_6+20.25X_7$$

(28)

5.2. Full Model Metrics

• Total Sum of Squares (SST):

  $$\mathrm{SST}=115514.5$$
• Regression Sum of Squares (SSR):

  $$\mathrm{SSR}=88499.83$$
• Error Sum of Squares (SSE):

  $$\mathrm{SSE}=7655.02$$
• Coefficient of Determination ($R^2$):

  $$R^2=1-{\displaystyle \frac{\mathrm{SSE}}{\mathrm{SST}}}=1-{\displaystyle \frac{7655.02}{115514.5}}\approx 0.934$$
• Adjusted $R^2$ ($R_{\mathrm{adj}}^2$):

  $$R_{\mathrm{adj}}^2=\mathrm{Cannot}\mathrm{be}\mathrm{reliably}\mathrm{calculated}\mathrm{due}\mathrm{to}\mathrm{overfitting}.$$

The adjusted $R^2$ for the full model is not reported here, given a clear case of overfitting (p = 7 predictors, n = 8 observations). Due to the limited size of the dataset and the lack of replications, the statistical models presented may be subject to overfitting. Therefore, the results should be interpreted as a preliminary approximation and require further validation with larger, replicated datasets. Caution is advised when interpreting the robustness and predictive capacity of the models until further experimental evidence is available. These are conditions that would not provide much confidence in model predictions. Therefore, further analysis was done by reducing the model to include only the significant variables (X4, X5, X6), with an adjusted $R^2$ of 0.699. The high $R^2$ and adjusted $R^2$ values observed describe a good in-sample fit; however, given the small sample size and lack of external validation, there is a risk of overfitting. Cross-validation was not applied due to sample size limitations. The predictive capacity of the models should be confirmed with new replicated data before proposing prediction or process control tools.

The Plackett–Bürman design was employed to construct a linear regression model, which was then utilized to eliminate non-significant variables and predict the cell count response as a function of the primary factors. The model is depicted in Equation (4):

$$\mathrm{Cell}\mathrm{Count}(\mathrm{cells}/\mathrm{mL})=\left(217.25-71.375X4+53.875X5+63.125X6\right)\times {10}^6$$

(29)

As shown in

Table 7. Observed and predicted FCC values (reduced model).

Exp	${\mathit{X}}_4$	${\mathit{X}}_5$	${\mathit{X}}_6$	FCC Observed	FCC Predicted
1	−1	1	−1	285	276.88
2	1	−1	−1	121	26.38
3	−1	−1	1	321.5	295.38
4	−1	1	1	422.5	403.13
5	1	1	1	292	260.38
6	1	1	−1	85	134.13
7	1	−1	1	85.5	152.63
8	−1	−1	−1	125.5	169.13

, X4 exerts a substantial negative influence, with a magnitude of −71.375 million cells/mL. This observation suggests that its presence should be minimized to optimize cell count. This would correspond to working with a lower Brix and less time. Conversely, X5 and X6 exhibited substantial positive effects (53,875 and 63,125 million cells/mL, respectively), suggesting that their levels should be maintained at a high (+1) setting, which would entail the amalgamation of two negative variables and one positive variable.

• Total Sum of Squares (SST):

  $$\mathrm{SST}=115514.5$$
• Regression Sum of Squares (SSR):

  $$\mathrm{SSR}=93993.16$$
• Error Sum of Squares (SSE):

  $$\mathrm{SSE}=19908.11$$
• Coefficient of Determination ($R^2$):

  $$R^2=1-{\displaystyle \frac{\mathrm{SSE}}{\mathrm{SST}}}=1-{\displaystyle \frac{19908.11}{115514.5}}\approx 0.814$$
• Adjusted $R^2$ ($R_{\mathrm{adj}}^2$):

  $$R_{\mathrm{adj}}^2=1-{\displaystyle \frac{19908.11/4}{115514.5/7}}\approx 0.699$$

  where $n=8$ (number of observations) and $p=3$ (number of predictors).

The linear regression analysis identified that the factors $X_4$, $X_5$, and $X_6$ are the primary determinants of final cell count (FCC) during the yeast cultivation stage for organic ethanol production. The fitted model explains approximately 81.4% of the observed variability in FCC, with an adjusted $R^2$ of 0.699, indicating a good fit given the small sample size and number of predictors.

The resulting equation enables FCC prediction under various combinations of the significant factors, supporting process optimization. Results show that minimizing $X_4$ and maximizing $X_5$ and $X_6$ leads to a substantial increase in cell count, improving fermentation outcomes.

Excluding non-significant factors simplifies the model and focuses experimental efforts on truly influential variables. Furthermore, the use of organic molasses as the sole nutrient source and the absence of chemical additives reinforce the feasibility of sustainably producing organic ethanol.

This work lays the groundwork for future research aimed at validating and expanding the model, exploring potential factor interactions, and incorporating new relevant variables such as pH, aeration, and nutrient content that could further optimize the process. The methodology and findings presented here represent a significant contribution toward more efficient, sustainable, and competitive bioprocesses in the organic ethanol industry.

Subsequent to the determination of the coefficients, the cell count is maximized through the implementation of a combination of coded levels of X4 = −1, X5 = +1, and X6 = +1. The predicted cell number under these conditions is approximately 221,027,074.31 cells/mL in the yeast culture for pre-fermentation.

5.3. Interaction Analysis in a Box–Behnken Design

Since the original Plackett–Bürman design identified three pseudo-factors (X4, X5, X6) as significant, this indicates that there are important factors that were not directly measured.

The report presents the fit of a quadratic model using a Box–Behnken design with three factors: concentration of sugars in solution (X1), yeast concentration (X2), and time (X3). A total of 13 experimental runs were utilized, employing authentic data from the study on fermentation for the purpose of producing organic ethanol.

5.3.1. Experimental Design

As summarized in

Table 8. Factors considered in the Box–Behnken design and their coded levels.

Factor	Name	Lower Level (—1)	Upper Level (+1)
$X_1$	Sugar concentration (°Brix)	8	14
$X_2$	Yeast concentration (g/L)	5	20
$X_3$	Incubation time (h)	3	9

, three factors with two coded levels were considered for the Box–Behnken design.

5.3.2. Adjusted Quadratic Model

The estimated regression model was

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_{11}{X}_1^2+{\beta }_{33}{X}_3^2+{\beta }_{13}{X}_1{X}_3$$

(30)

where

• Y = Cell concentration ($\times {10}^6$ cells/mL);
• $X_1,X_2,X_3$ = Coded variables of experimental factors;
• ${\beta }_i$ = Model coefficients estimated by multiple regression.

5.3.3. Estimated Coefficients

The model coefficients, estimated using the least squares method, are

$$\begin{array}{cc}\hfill Y& =101.0+43.4X_1+101.0X_2-28.9X_3\hfill \\ \hfill & -24.2X_1^2-11.6X_3^2+80.8X_1{X}_3\hfill \end{array}$$

(31)

As summarized in

Table 9. RSM model coefficients and their interpretation.

Term	Coefficient	Value	Interpretation
Intercept	${\beta }_0$	101.0	Predicted response at center point
Linear effect $X_1$	${\beta }_1$	43.4	Strong positive main effect
Linear effect $X_2$	${\beta }_2$	101.0	Very strong positive main effect
Linear effect $X_3$	${\beta }_3$	−28.9	Moderate negative main effect
Quadratic effect $X_1^2$	${\beta }_{11}$	−24.2	Negative curvature (maximum)
Quadratic effect $X_3^2$	${\beta }_{33}$	−11.6	Negative curvature (maximum)
Interaction $X_1\times X_3$	${\beta }_{13}$	80.8	Very strong synergistic interaction

, the RSM model includes linear, quadratic, and interaction effects with their estimated coefficients and interpretation.

5.3.4. Statistical Validation Through ANOVA

Statistical validation of the model was performed through Analysis of Variance (ANOVA), with results presented in

Table 10. ANOVA table for the validated RSM model.

Source of	Sum of	Degrees of	Mean	F-Statistic	p-Value
Variation	Squares	Freedom	Square
Regression	51,915.4	6	8652.6	36.12	0.0006
Error	1197.9	5	239.6
Total	53,113.3	11

.

Statistical interpretation:

• $F_{calculated}=36.12>>F_{critical}(6,5,0.05)=4.95$;
• $p\mathrm{-value}=0.0006<<\alpha =0.05$;
• Conclusion: The model is highly significant.

However, this apparent accuracy is constrained by the small sample size $(n=13)$ and the absence of biological/technical replicates; thus, the model should be considered provisional until confirmed with replicated experiments and out-of-sample validation.

5.3.5. Model Statistics

As summarized in Table 11, the goodness-of-fit metrics indicate an adequate model fit and high explained variance.

Table 11. Goodness-of-fit statistics for the RSM model.

Statistic	Value	Interpretation
Coefficient of determination ($R^2$)	0.9774	97.7% of variability explained
Adjusted $R^2$	0.9504	95.0% predictive capacity
Residual standard error	15.5	High model precision
Coefficient of variation (CV)	8.7%	Low experimental variability
Error degrees of freedom	5	Sufficient for validation

Table 11. Goodness-of-fit statistics for the RSM model.

Statistic	Value	Interpretation
Coefficient of determination ($R^2$)	0.9774	97.7% of variability explained
Adjusted $R^2$	0.9504	95.0% predictive capacity
Residual standard error	15.5	High model precision
Coefficient of variation (CV)	8.7%	Low experimental variability
Error degrees of freedom	5	Sufficient for validation

5.3.6. Statistical Assumptions Validation

Validation Tests

The model was subjected to rigorous tests to verify compliance with statistical assumptions:

As summarized in

Table 12. Statistical assumptions validation.

Assumption	Test	Statistic	Result
Residual normality	Shapiro-Wilk	$p=0.118$	✓ Satisfied
Homoscedasticity	Levene	$p>0.05$	✓ Satisfied
Independence	Residual analysis	Random	✓ Satisfied
Linearity	Q-Q plot	$R^2>0.95$	✓ Satisfied

, the statistical assumptions for the validated RSM model are satisfied.

Residual Analysis

The model residuals present the following characteristics:

• Residual mean: $\overline{e}=0.000$ (centered);
• Standard deviation: $s_e=15.5$;
• Range: $[-15.1,18.9]$;
• Distribution: Normal ($p=0.118>0.05$).

5.3.7. Model Comparison

Optimal Model Selection

As summarized in

Table 13. Comparison of alternative RSM models.

Model	Parameters	DF Error	Adjusted ${\mathit{R}}^2$	F-Statistic	p-Value
Original complete	10	2	0.532	2.65	0.304
Reduced 1	5	7	0.844	15.91	0.001
Reduced 2 (Selected)	7	5	0.950	36.12	0.0006
Reduced 3	4	8	0.864	24.24	0.0002

, we compared alternative RSM models by parsimony, adjusted $R^2$, and overall ANOVA significance.

Selection criteria:

1.

Statistical significance ($p<0.05$);

2.

Maximum adjusted $R^2$;

3.

Sufficient degrees of freedom ($\ge 3$);

4.

Model parsimony;

5.

Statistical assumptions compliance.

5.3.8. Model Interpretation

Main Effects

• Factor $X_2$: Very strong positive effect (${\beta }_2=101.0$);
• Factor $X_1$: Strong positive effect (${\beta }_1=43.4$);
• Factor $X_3$: Moderate negative effect (${\beta }_3=-28.9$).

5.3.9. Curvature Effects

Negative quadratic terms indicate the presence of optimal maxima:

• ${\beta }_{11}=-24.2$: Negative curvature in $X_1$ (optimal maximum);
• ${\beta }_{33}=-11.6$: Negative curvature in $X_3$ (optimal maximum).

Interactions

The $X_1\times X_3$ interaction presents the strongest effect in the model:

$${\beta }_{13}=80.8(\mathrm{Very}\mathrm{strong}\mathrm{synergistic}\mathrm{interaction})$$

(32)

This interaction indicates that the effect of $X_1$ significantly depends on the level of $X_3$, and vice versa.

Biochemical Interpretation

The results show that:

The validated response surface model ($Y=431.67+1.33X_1-1.67X_3+1.33X_1{X}_3$) reveals fundamental aspects of microbial physiology during ethanolic fermentation. The constant term ($431.67\times {10}^6$ cells/mL) represents the basal cell growth capacity under standard conditions, reflecting the intrinsic metabolic potential of the microorganism. The positive coefficient of $X_1$ ($+1.33$) indicates that this factor acts as a growth promoter, possibly related to the availability of essential nutrients, dissolved oxygen, or pH conditions that favor enzymatic activity and biomass synthesis. Conversely, the negative coefficient of $X_3$ ($-1.67$) suggests an inhibitory effect on growth, which could be associated with the accumulation of toxic metabolites, osmotic stress, or environmental conditions that compromise cellular viability. The interaction term $X_1{X}_3$ ($+1.33$) is particularly significant from a biochemical perspective, as it indicates a synergistic effect where the combination of both factors produces a result superior to that expected from their individual effects, suggesting complex regulatory mechanisms such as activation of complementary metabolic pathways, modulation of gene expression, or compensatory effects that optimize fermentative efficiency. This positive interaction implies that, although $X_3$ is individually inhibitory, its presence in combination with $X_1$ can activate stress response systems or alternative metabolic routes that result in a net increase in biomass, which is characteristic of the metabolic plasticity of fermentative microorganisms and their capacity for adaptation to variable culture medium conditions. The synergistic interaction between sugar concentration (X1) and incubation time (X3) indicates that high substrate levels offset the decrease in fermentative activity caused by prolonged incubation, thereby maintaining cell viability and productivity.

The subsequent section will describe the experimental application of the model that was obtained. The results of this study are presented in

Table 14. Optimized fermentation stage results based on RSM model.

Stage	Initial			Final			Time
	Brix	pH	Cell Count (106 cells/mL)	Brix	pH	Cell Count (106 cells/mL)
Culture	7.5	5.60	280	6.0	4.65	432	3 h
Pre-fermentation	7.5	5.35	120	5.0	5.30	385	15 h
Fermentation	13	5.45	385	6.5	5.28	432	42 h
Alcohol content (°GL):							7.8

.

According to [16], the following parameters are utilized to assess the dynamics of fermentations: cell density, ethanol yield, final molasses concentration, pH, fermentation efficiency, and residual sugar concentration. The fermented must exhibits an alcohol percentage of 6.4%, which exceeds the values obtained by [27,34,43] in fermentation processes with inorganic molasses. These researchers achieved concentrations of 5.15%, 6.38%, and 5.48%, respectively, through the fermentation of molasses using traditional sugarcane molasses. The final reducing sugar concentration was measured at 66.117 g/L, enabling the calculation of fermentation yield and efficiency. As illustrated in

Table 15. Results of the fermentation stage under optimized conditions.

Determined Parameters	Value
Initial Brix	13
Final Brix	6.5
Fermentation Volume (mL)	2000
Fermentation Time (h)	42
Alcohol Content (%)	7.8
Initial Total Reducing Sugars (ART) (g/L)	125.40
Final Total Reducing Sugars (ART) (g/L)	62.70
Theoretical Fermentation Efficiency (%)	78.52
Alcohol-to-Substrate Yield (%)	62.15
Productivity (g/L·h)	1.86

, the results obtained demonstrate the efficacy with which the fermentation stage is executed.

The implementation of the RSM-optimized fermentation conditions resulted in substantial improvements across all critical performance parameters, demonstrating the effectiveness of statistical optimization in bioprocess enhancement. The fermentation process was initiated with an optimized sugar concentration of 13°Brix (125.40 g/L ART), which was strategically adjusted to provide adequate substrate availability while avoiding inhibitory effects associated with excessive sugar concentrations. The enhanced microbial activity under optimized conditions achieved superior sugar conversion efficiency, reducing the final Brix to 6.5 (62.70 g/L ART), representing a 50% sugar utilization rate compared with the original 35.7% conversion. The fermentation time was successfully reduced from 48 to 42 h, achieving a 12.5% time reduction while simultaneously increasing alcohol production from 6.4% to 7.8%, demonstrating the synergistic effects identified through the RSM model. The theoretical fermentation efficiency experienced a remarkable improvement from 63.04% to 78.52%, indicating enhanced metabolic performance and better utilization of available substrates under the optimized factor combinations. Similarly, the alcohol-to-substrate yield increased significantly from 47.43% to 62.15%, reflecting improved conversion stoichiometry and reduced metabolic losses. The overall productivity enhanced from 1.69 to 1.86 g/L·h, representing a 10.1% improvement that combines the benefits of higher alcohol yields with reduced processing time. These comprehensive improvements validate the RSM model’s predictive capability and confirm that the identified optimal factor interactions successfully maximized both fermentation efficiency and economic viability, establishing a robust foundation for scaled-up organic ethanol production processes.

As a literature benchmark (not a within-study control), conventional molasses fermentations typically report final alcohol contents in the 5–6% v/v range under comparable scales and substrates. Our optimized run achieved 7.8% v/v; however, because no inorganic-nutrient control was run side-by-side, these figures should be read only as contextual reference rather than evidence of superiority. A direct benchmark with a conventional nutrient-supplemented process under identical operating conditions will be included in follow-up work.

Among the key challenges for developing this process on a large scale are high investment and capital costs, the technological maturity of biofuels, the large-scale supply of feedstock, and political and regulatory issues, according to [44]. Organic ethanol production can be carried out using the same technological framework as traditional processes for this product. In this case, the main difference lies in the raw materials used and their characteristics. The average difference between organic and conventional products applied to the final consumer ranges between 45 and 55% according to Molina et al. [45]. The use of organic molasses as the main substrate increases the total production cost of this process, in turn obtaining an organic product that will increase the value of production.

6. Conclusions

This work presents a methodological proof-of-concept showing that sequential PB→BBD can improve performance metrics in a fully organic system. The resulting models reflect in-sample behavior only and require replicated validation and side-by-side conventional benchmarking before any general claims of predictive utility or industrial competitiveness can be made. The identification of significant pseudo-factors (X4, X5, X6) in the screening phase revealed the presence of important uncontrolled variables, highlighting the complexity of organic fermentation processes and the need for comprehensive factor consideration. The validated quadratic response surface model explained 97.7% of the experimental variability ($R^2=0.977$, adjusted $R^2=0.950$), indicating good in-sample fit for the explored design space; however, the absence of replication limits generalizability and calls for external validation. The high $R^2$ values obtained for the models, such as 0.977 for the Box–Behnken model, should be interpreted with caution. Given the absence of experimental replicates and the limited number of degrees of freedom in the dataset, these values may be inflated and may not fully reflect the predictive capacity or generalizable robustness of the models. Despite the acknowledged risk of overfitting, it is imperative to emphasize the necessity of cross-validation or the acquisition of new experimental data with replicates. These methodologies are indispensable in confirming the generalizability and predictive capabilities of the proposed models. The synergistic interaction between sugar concentration and incubation time ($X1\times X3$) proved to be the most significant factor, indicating that optimal fermentation performance requires a careful balance of substrate availability and processing time rather than simple maximization of individual parameters.

Experimental validation under optimized conditions achieved remarkable improvements across all performance metrics: ethanol content increased from 6.4% to 7.8% v/v (21.9% improvement), theoretical fermentation efficiency rose from 63.04% to 78.52% (24.6% enhancement), alcohol-to-substrate yield improved from 47.43% to 62.15% (31.0% increase), and productivity enhanced from 1.69 to 1.86 g/L·h (10.1% improvement). Simultaneously, the fermentation time was reduced from 48 to 42 h (12.5% reduction), demonstrating that optimization can achieve both improved quality and enhanced efficiency. The maximum cell density of $432\times {10}^6$ cells/mL was consistently achieved and maintained throughout the fermentation process, confirming the model’s predictive capability and the sustainability of the optimized conditions.

The demonstration that organic ethanol can be effectively produced from sugarcane molasses alone without chemical additives shows that the technical and economic viability of sustainable bioethanol production is possible. The statistical method offers a useful and systematic tool to optimize the processes and is suitable for a variety of organic substrates and fermentation parameters. Further work is still required to scale up the optimized process to industrial scale, to evaluate the long-term stability of the optimized parameters, and to implement additional organic substrates in the process to increase flexibility and economic competitiveness. The developed methodology and results form a strong basis for further development of competitive organic ethanol production processes fulfilling the performance requirements as well as the environmental sustainability. Accordingly, this work is primarily intended for producers operating under organic certification or in resource-constrained settings who require additive-free fermentation. Broad industrial claims require replication and direct, side-by-side benchmarking for validation. Overall, this study provides proof of concept under organic-only constraints. The generalizability and predictive utility of the results depend on independent replication, external validation, and direct comparison with conventional processes.

7. Limitations and Future Prospects

One of the main limitations of this study is the lack of biological or technical replicates, which prevents an accurate estimation of experimental variability and limits the statistical robustness of the generated models. Similarly, the absence of a control group based on conventional fermentation with inorganic nutrients hinders direct comparisons and evaluations of the competitiveness of the proposed organic process. The absence of a side-by-side conventional control remains a key limitation to assessing practical competitiveness and will be addressed in the next experimental iteration. Another relevant limitation is the absence of quantified critical byproducts, such as acetic acid, glycerol, and other organic acids. These byproducts are essential for evaluating the purity and safety of the produced ethanol. Furthermore, the interpretation of the pseudofactors used in the experimental design is purely statistical and does not correspond to directly measured or controlled physical variables.

Moving forward, it is recommended that experiments be conducted with adequate replicates to strengthen statistical validity and allow for the inclusion of error bars in the results. Priority should also be given to incorporating a control group with conventional fermentation and performing quantitative byproduct analyses to ensure ethanol quality. Finally, the experimental design should be expanded to include and control for variables such as pH, aeration, and agitation. The proposed models should also be validated on larger scales and under different industrial conditions. These actions will consolidate the technical and commercial viability of the organic ethanol production process and contribute to the development of more sustainable and competitive bioprocesses.

In the next phase, we will re-run the Plackett–Burman screening with duplicate runs and include triplicated center points in the Box–Behnken design to obtain independent estimates of pure error and improve statistical robustness. Future work will include a side-by-side benchmark against conventional fermentation with inorganic nutrients under matched substrate, inoculum, pH/temperature, and time profiles to quantify industrial competitiveness (yield, productivity, efficiency, and cost).