Mechanisms and Optimization of Critical Parameters Governing Solid-Phase Transport in Jet Pumps for Vacuum Sand Cleanout
Abstract
1. Introduction
2. Principles
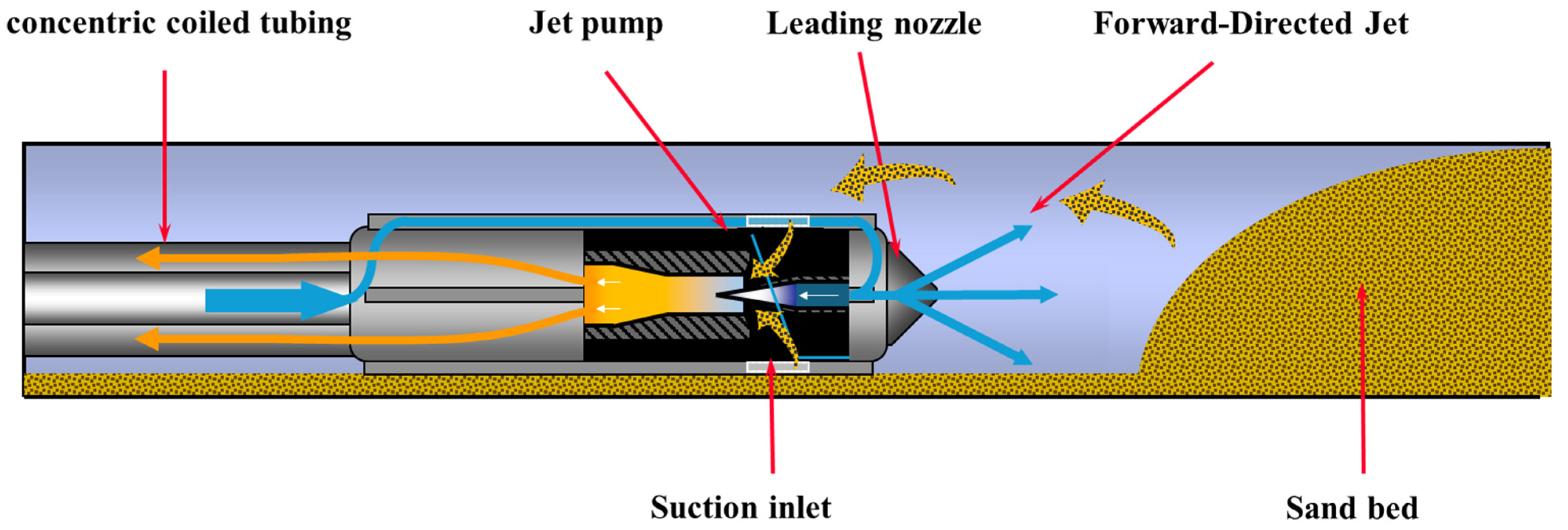
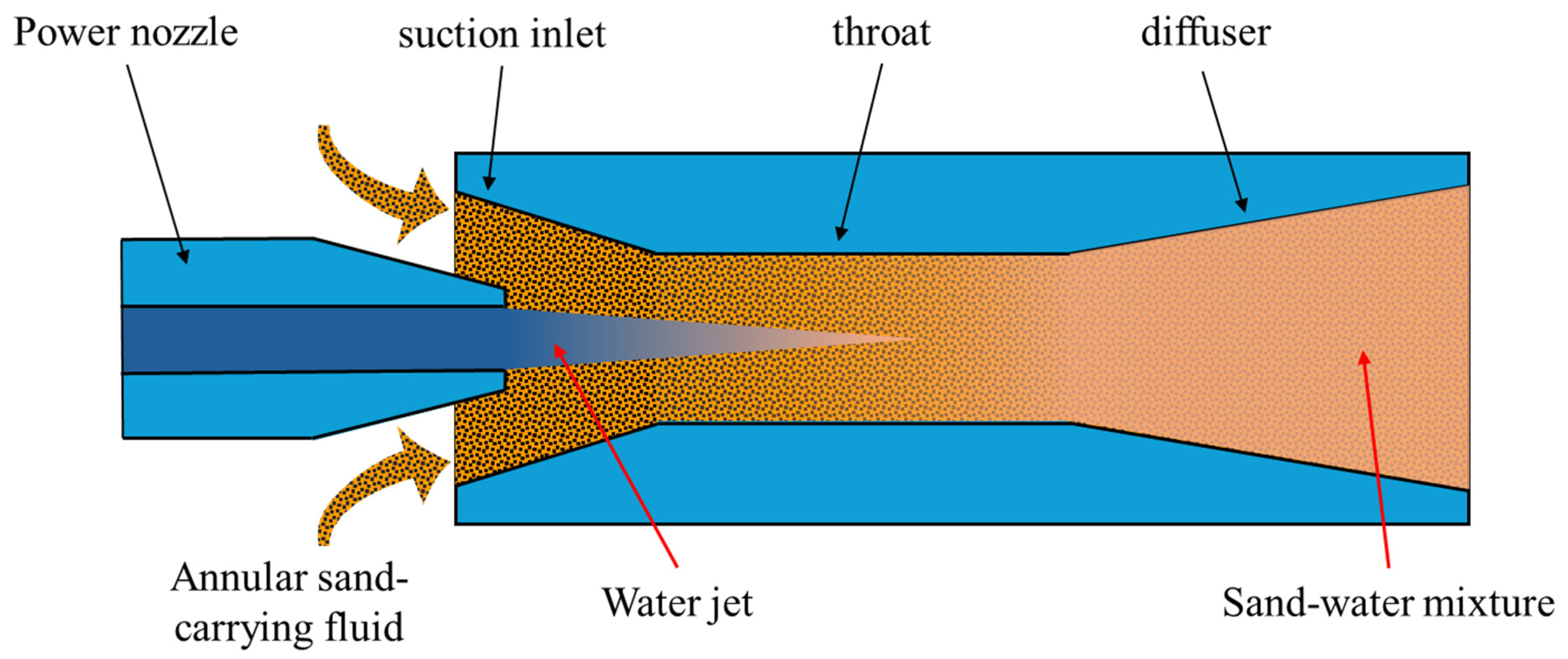
2.1. Technical Principle
2.2. Evaluation Metrics for Solid-Phase Suction Capacity
3. Methodology
3.1. Governing Equations
- (1)
- Continuity equation for the mixture phase:
- (2)
- Momentum conservation equation:
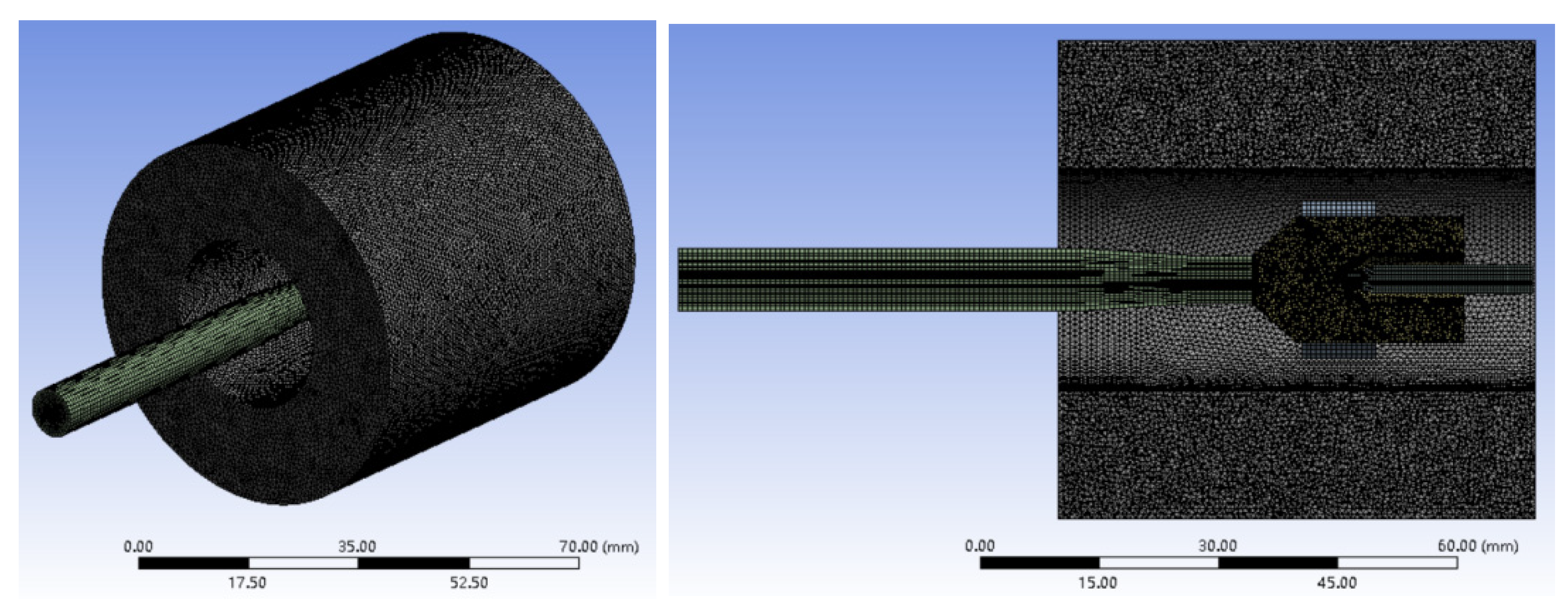
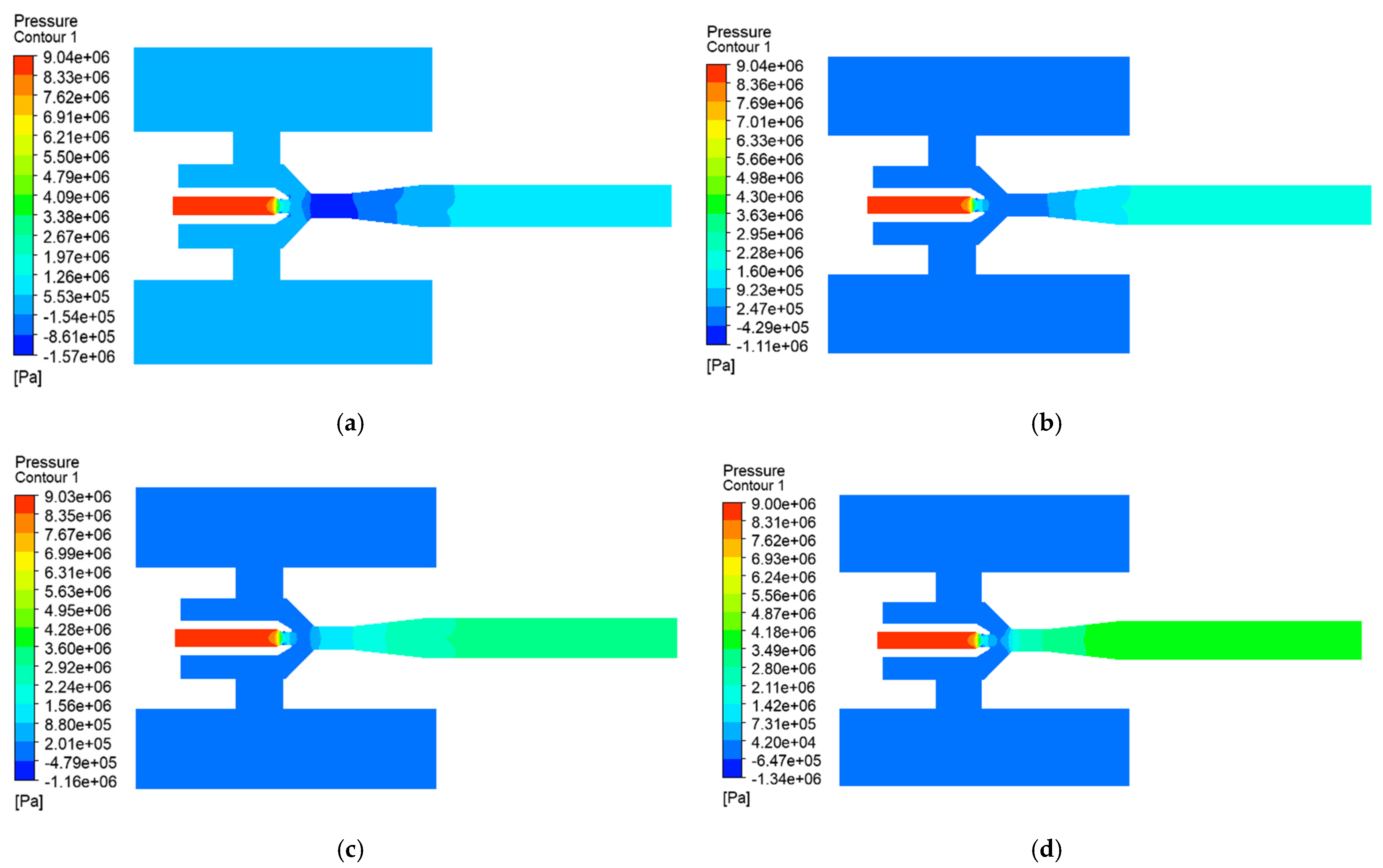
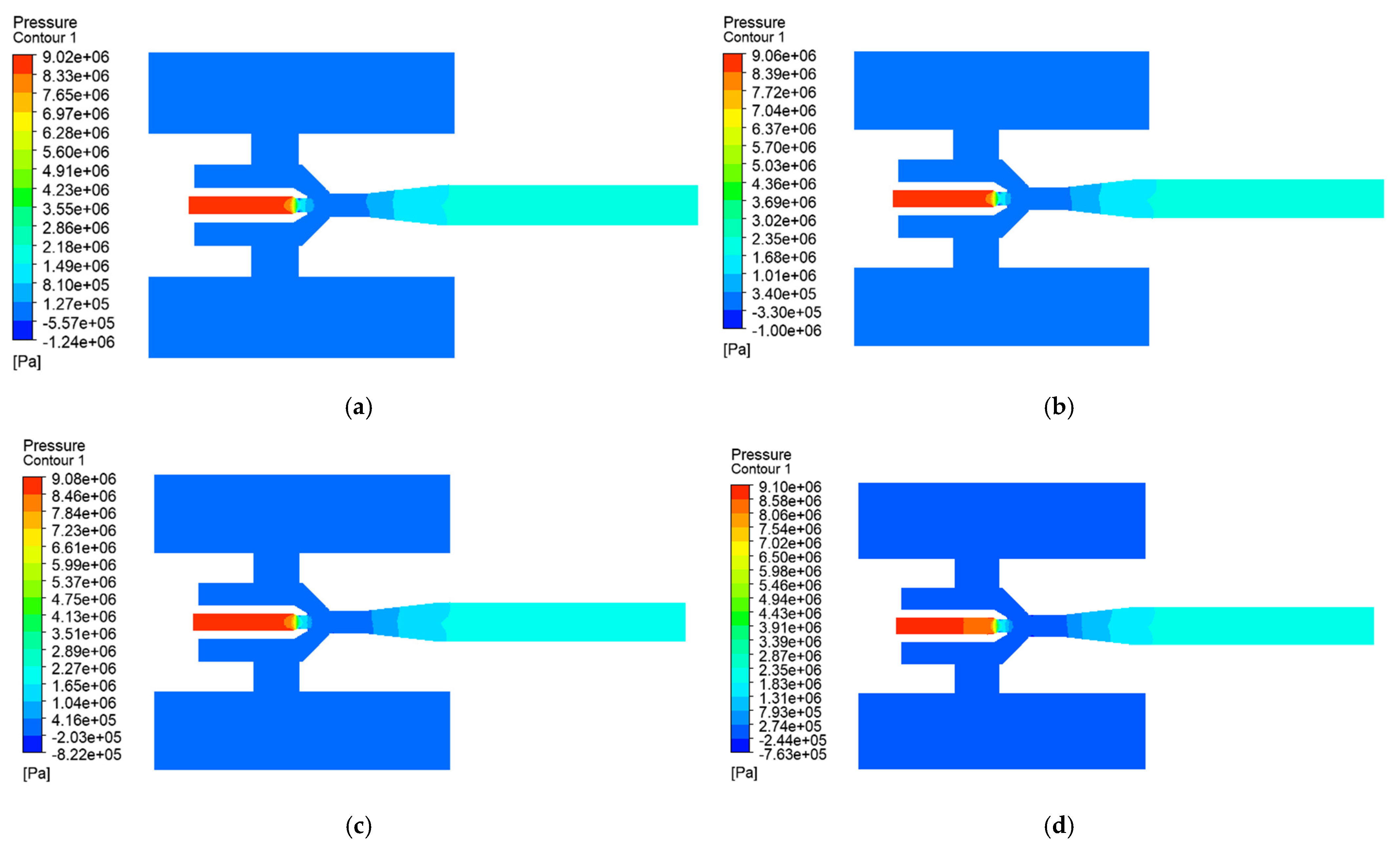
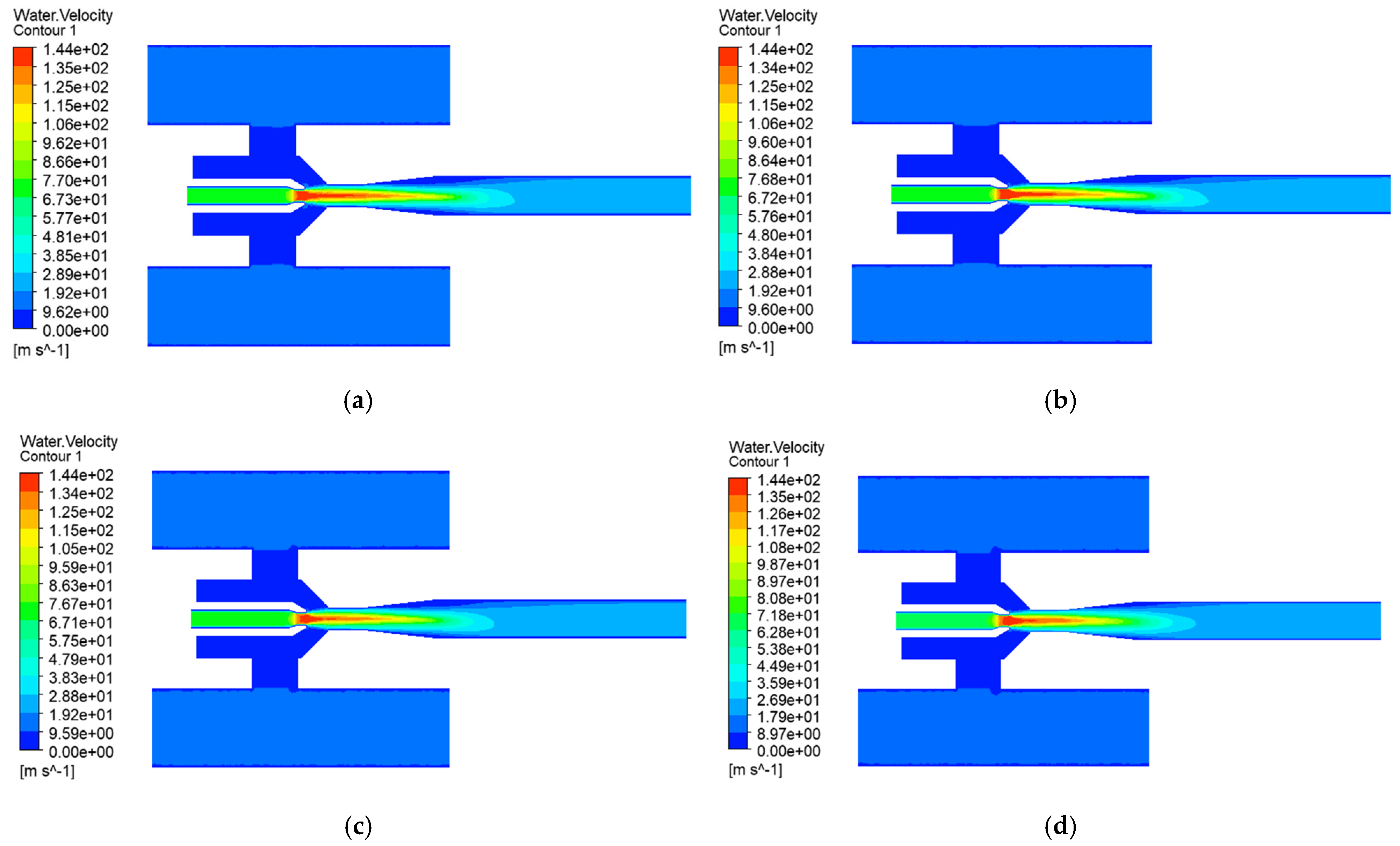
3.2. Computational Domain and Grid Division
3.3. Boundary Conditions and Solution Method
- Driving pressure differential (governs kinetic energy generation at the nozzle): ΔPmotive = P1 − P3;
- Resistance pressure differential (dictates flow resistance in the diffusion section): ΔPback = P2 − P3.
4. Simulation Results and Discussion
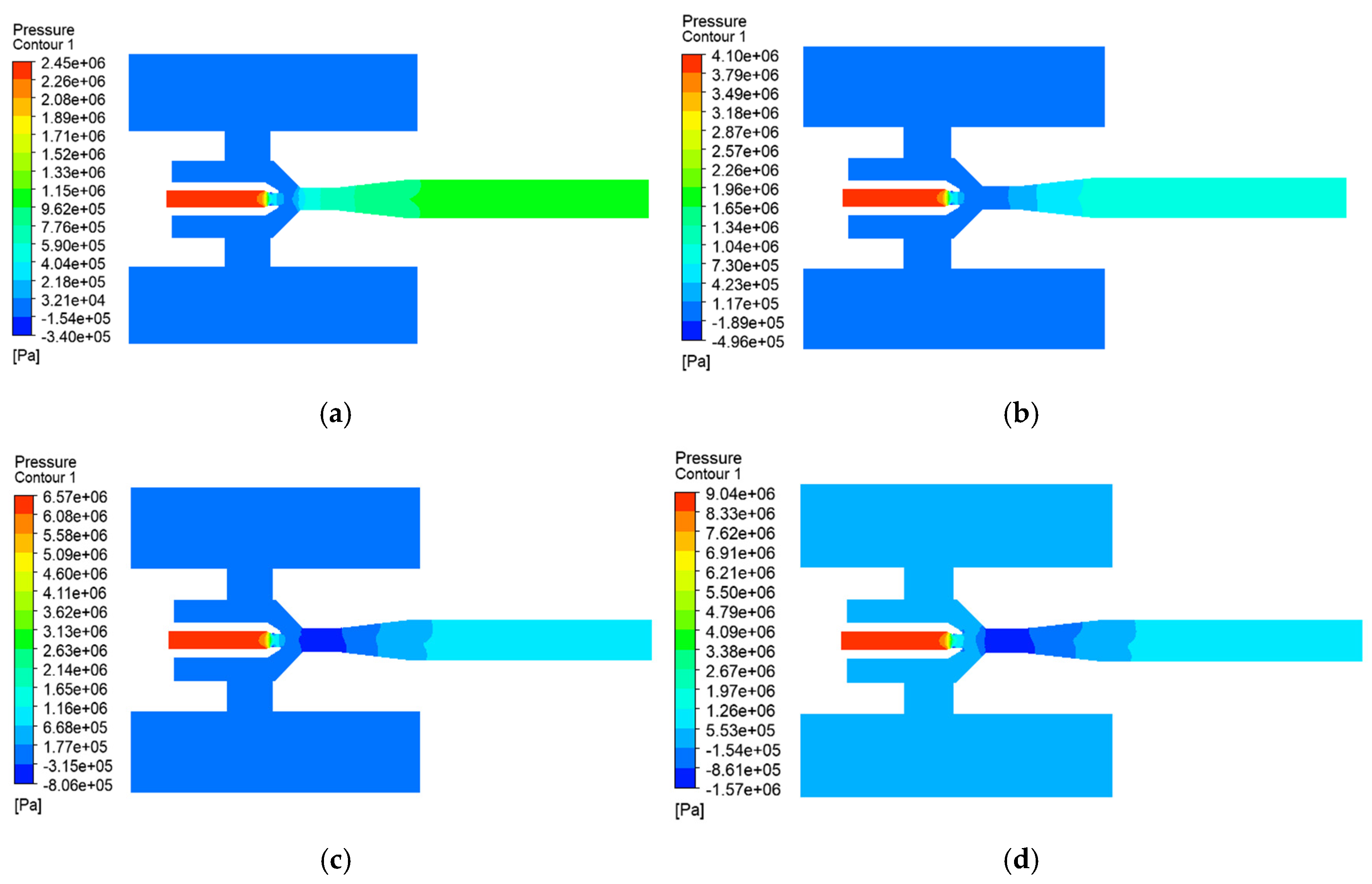
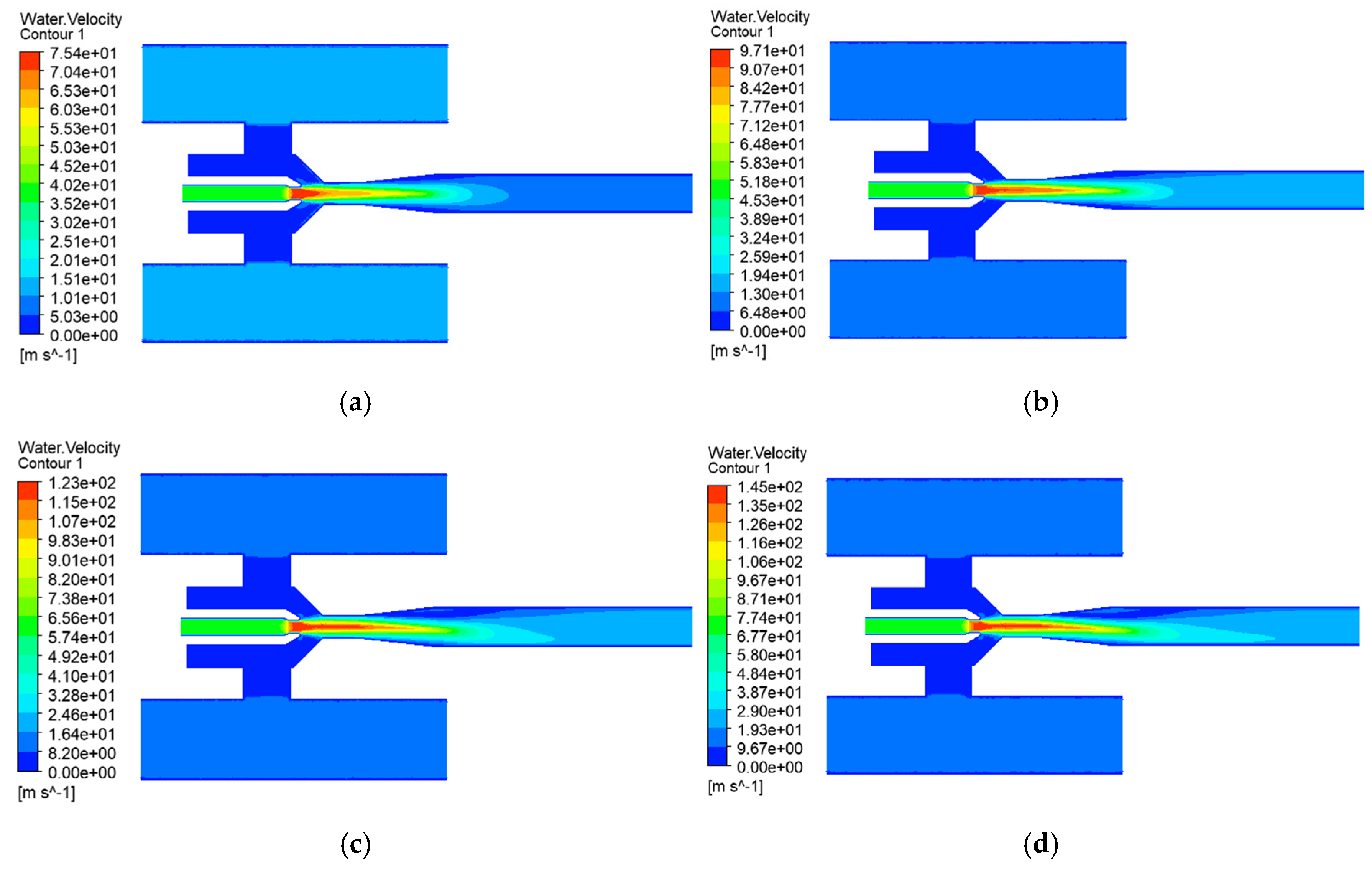
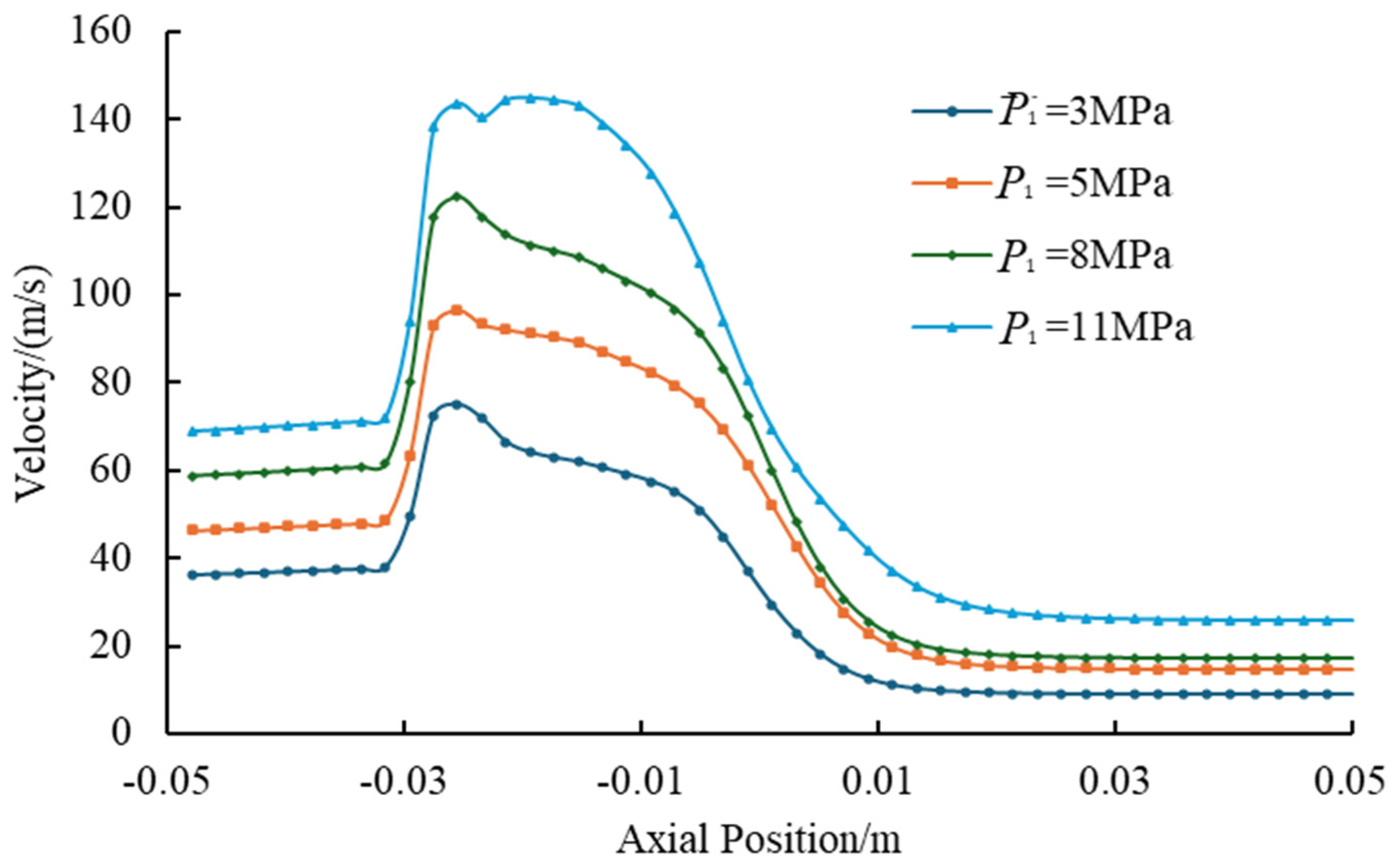
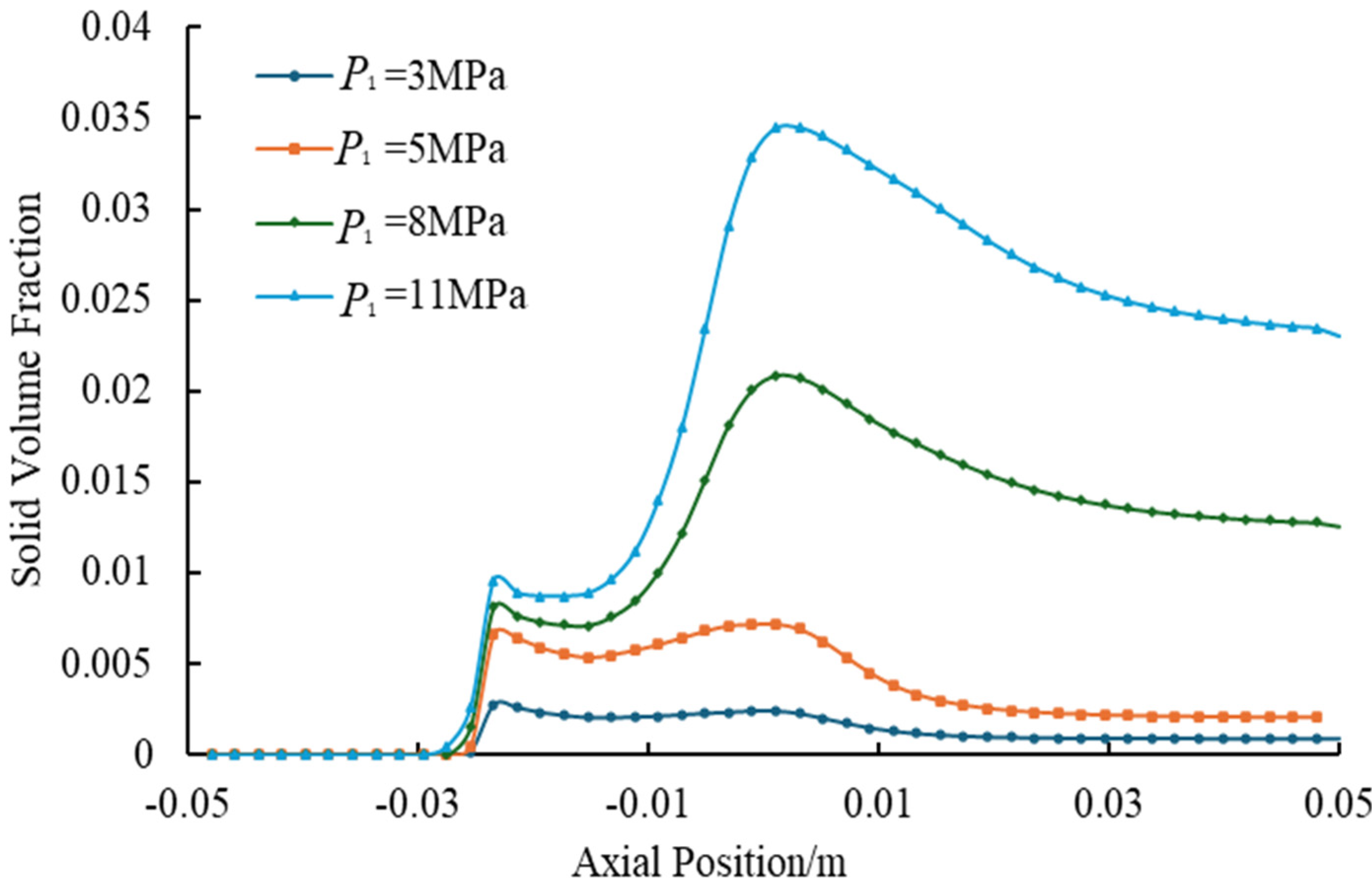
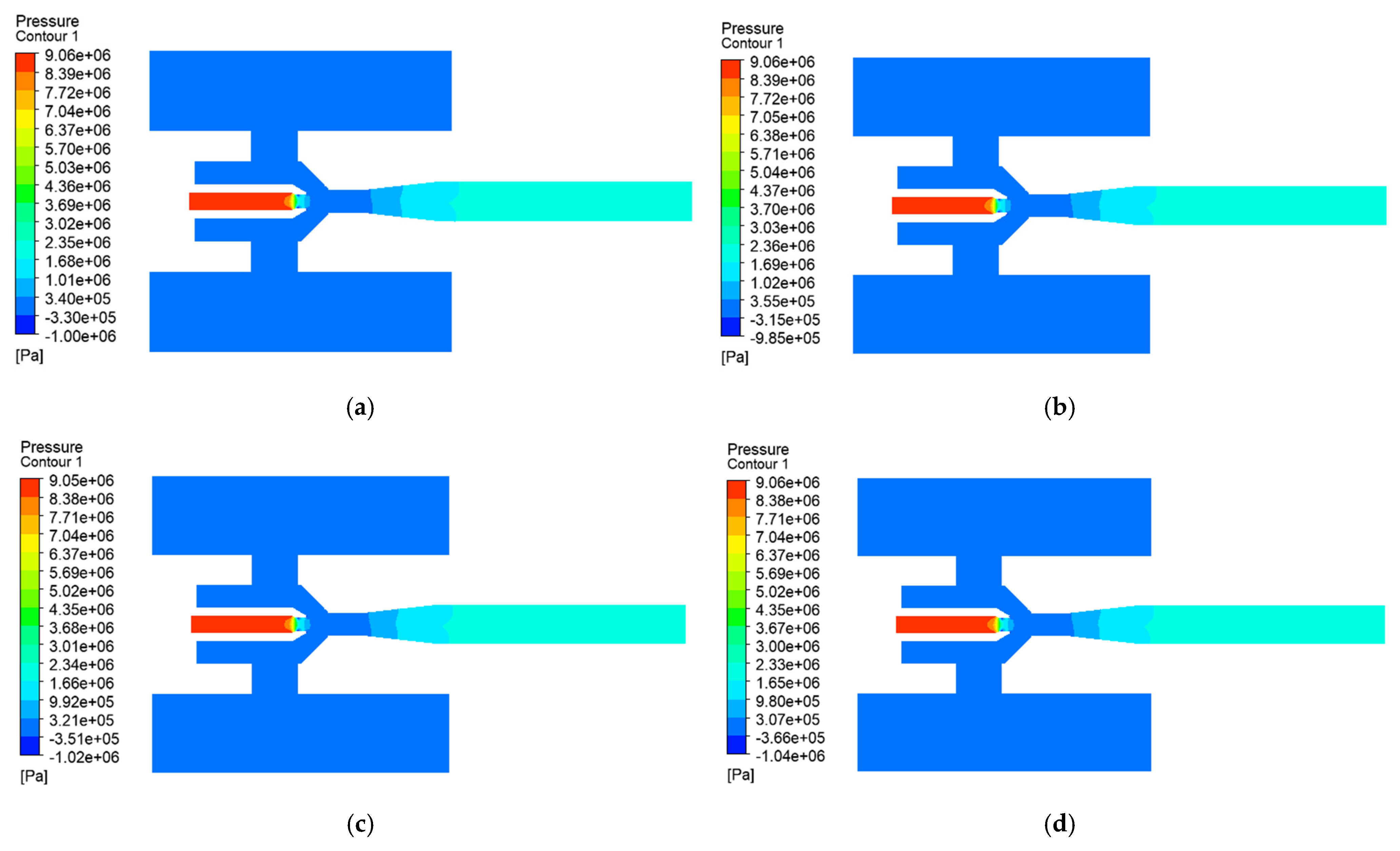
4.1. Effect of Working Pressure on Solid-Phase Transport Capacity of Jet Pump
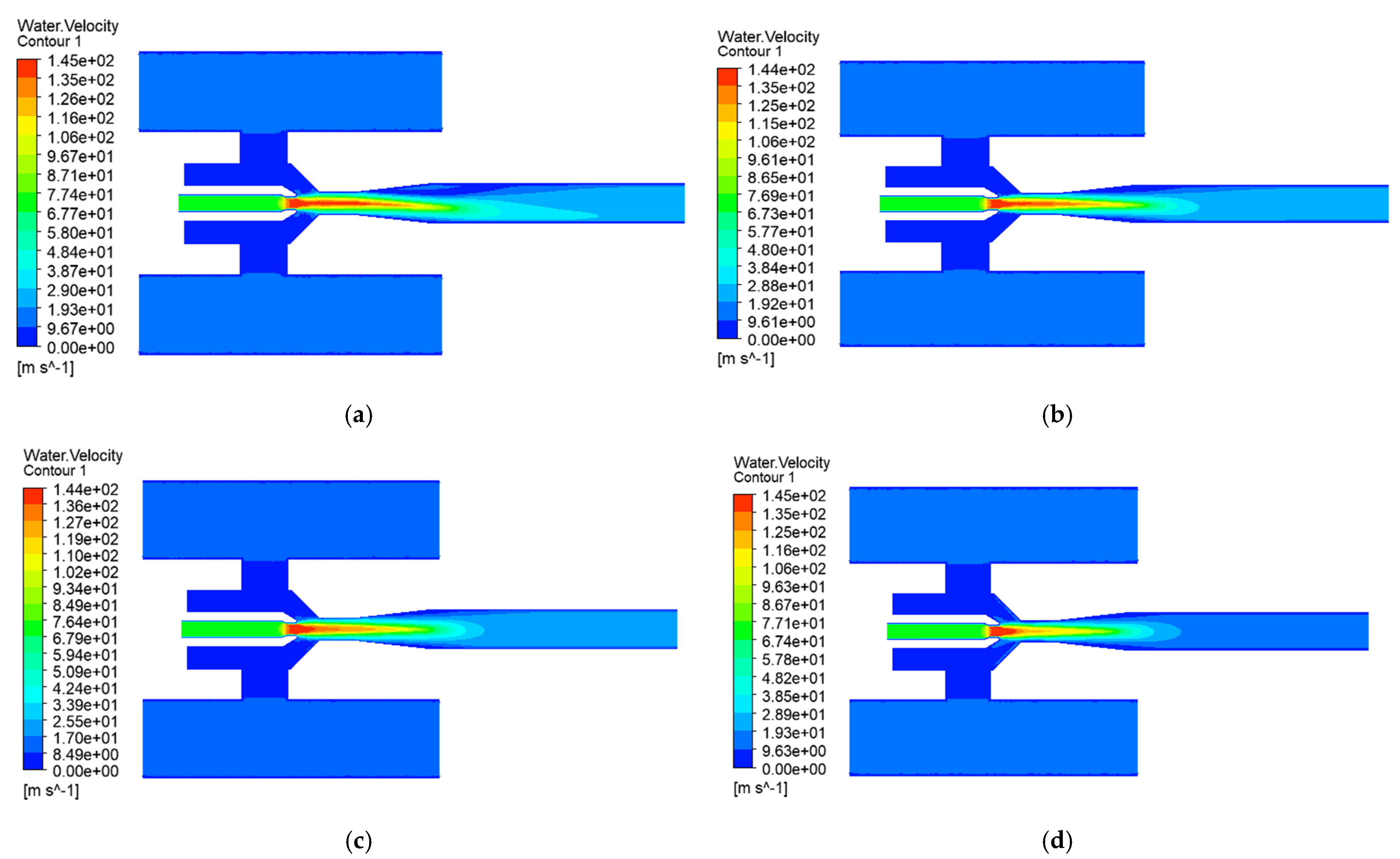
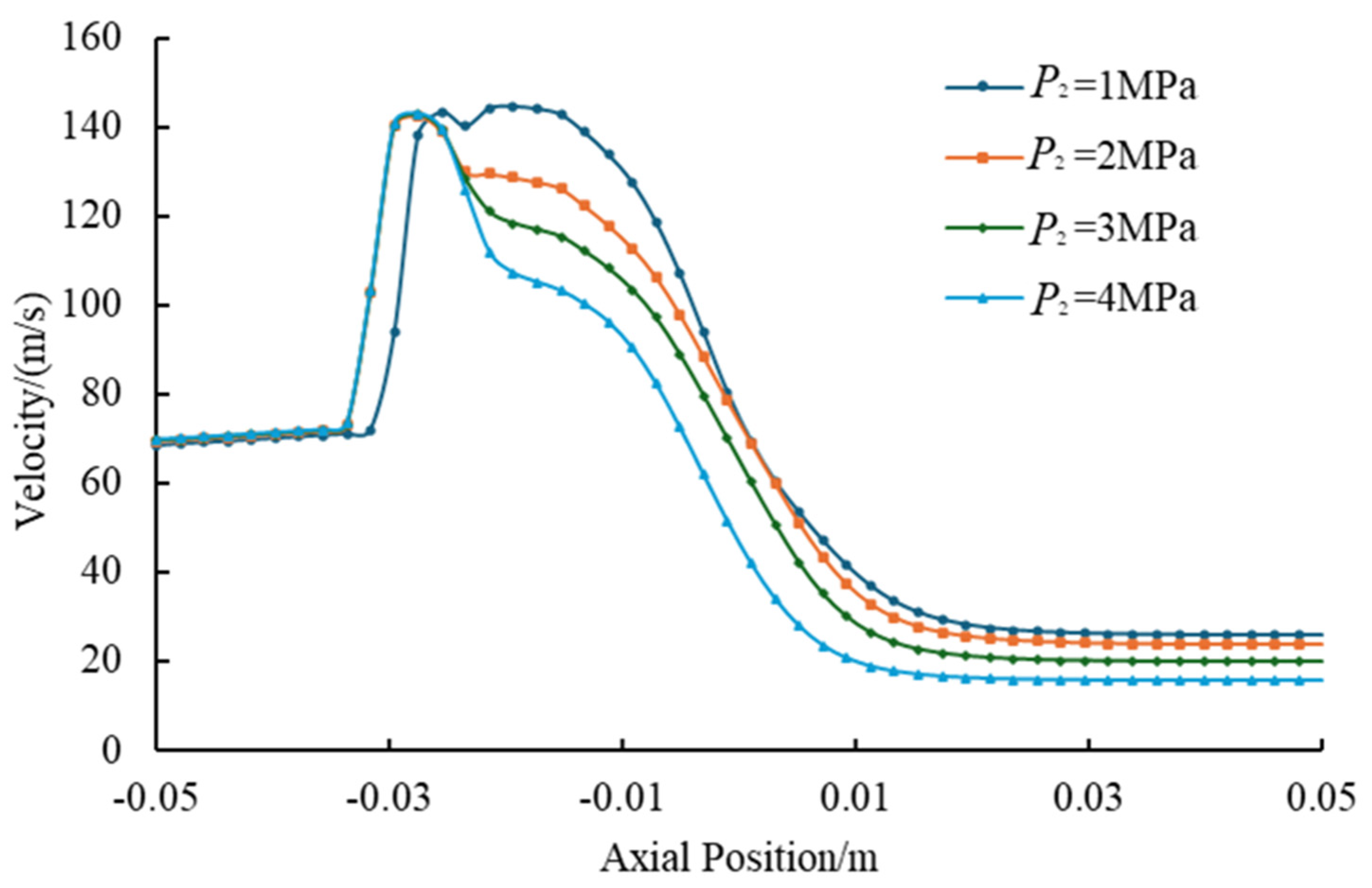
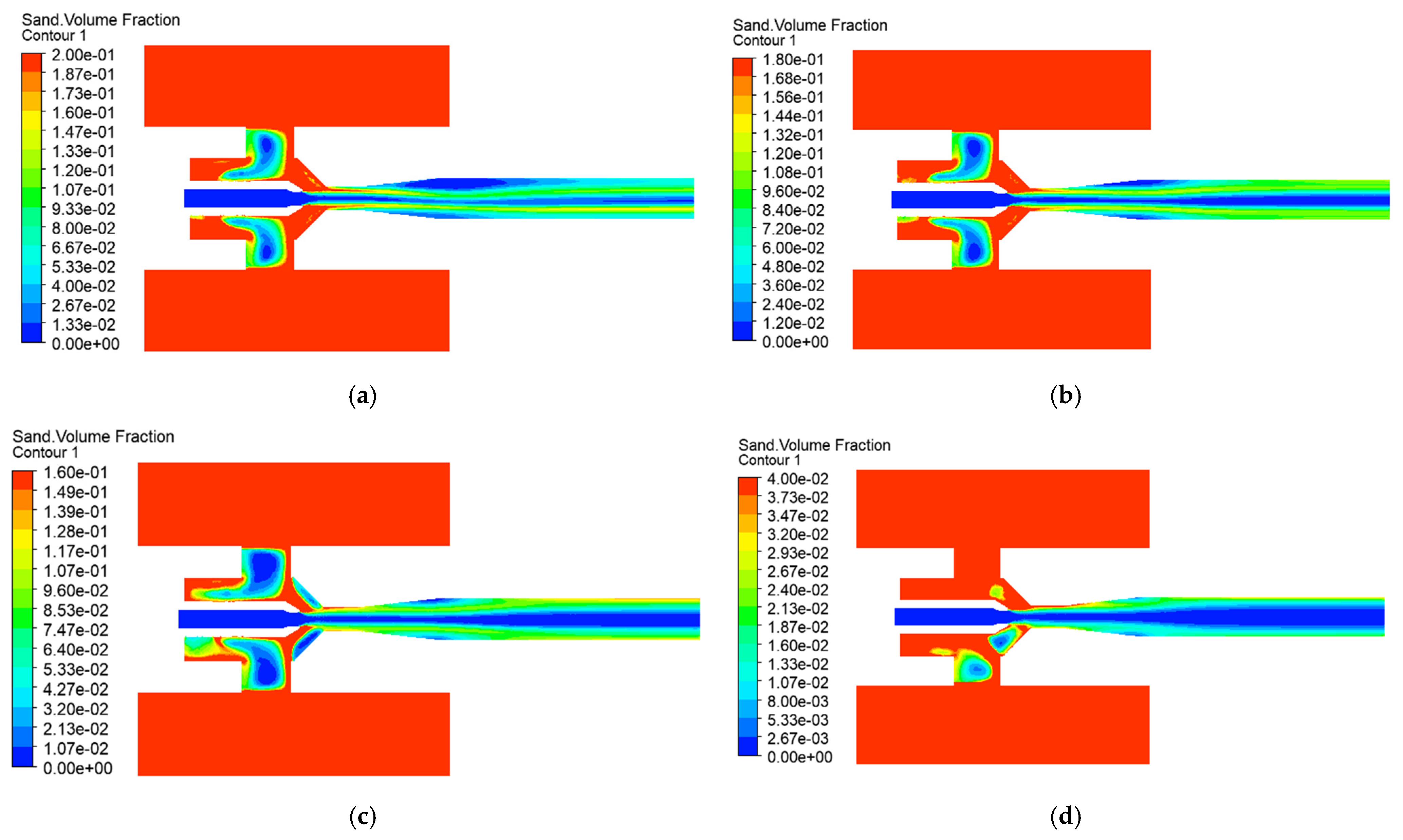
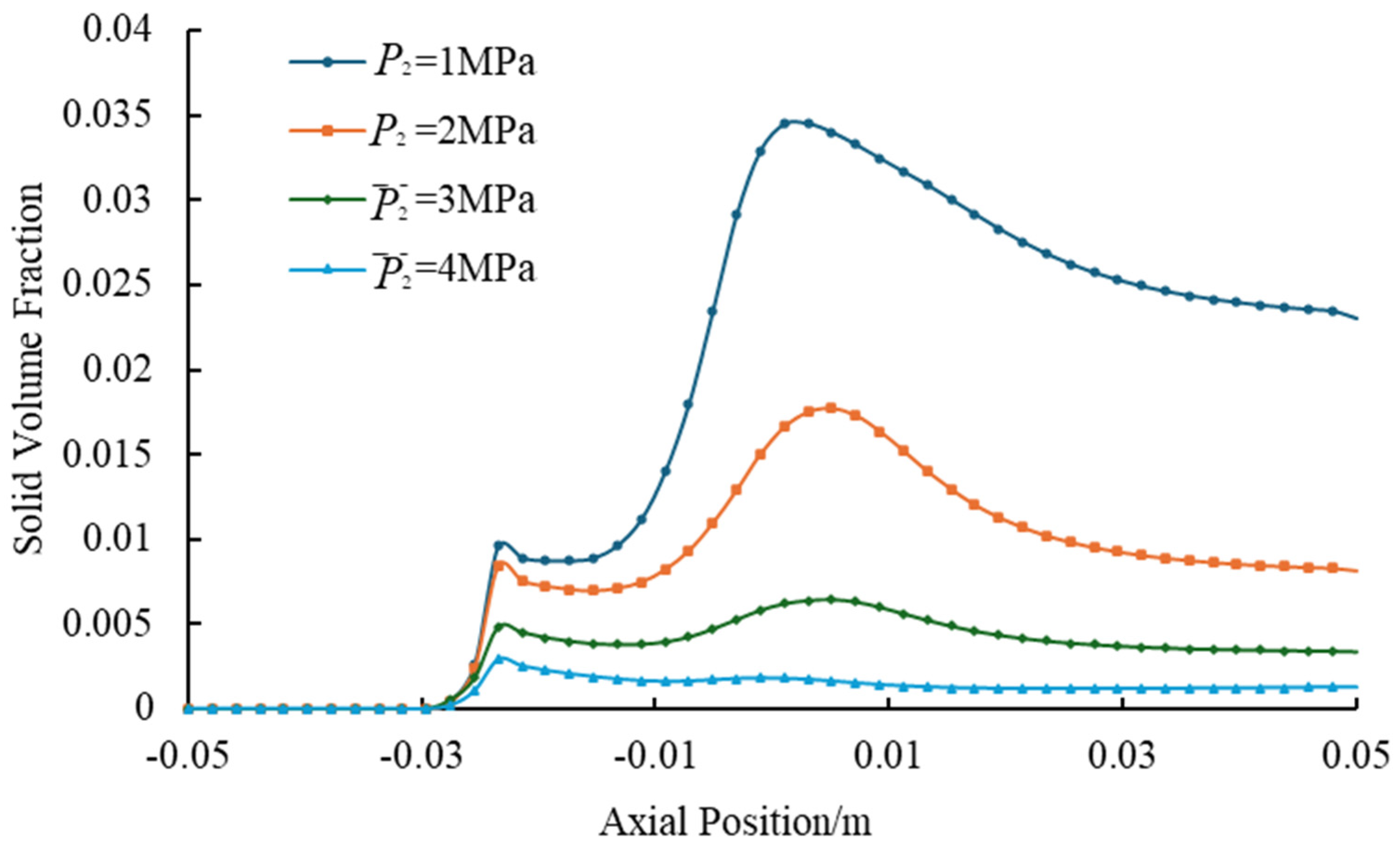
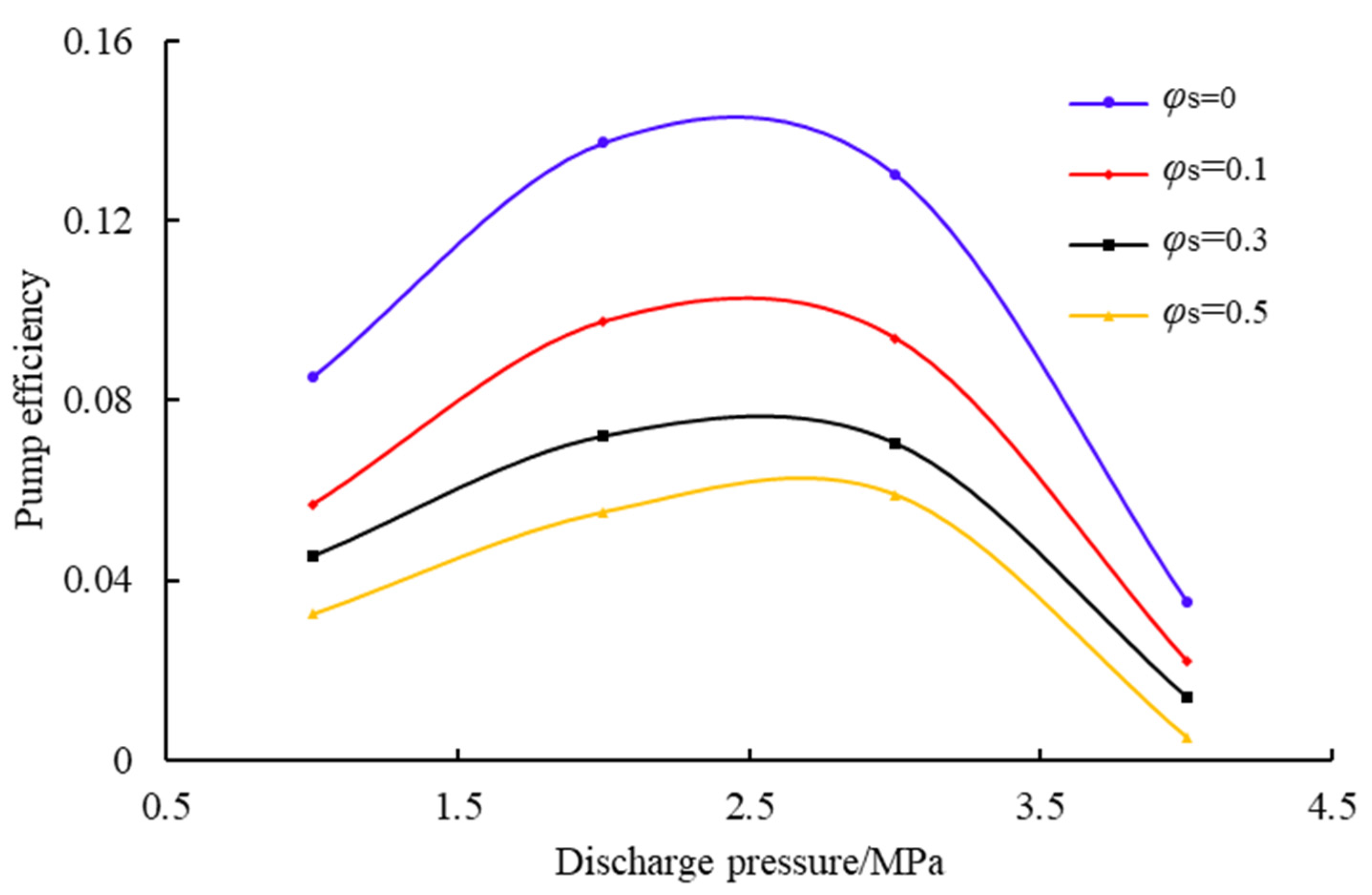
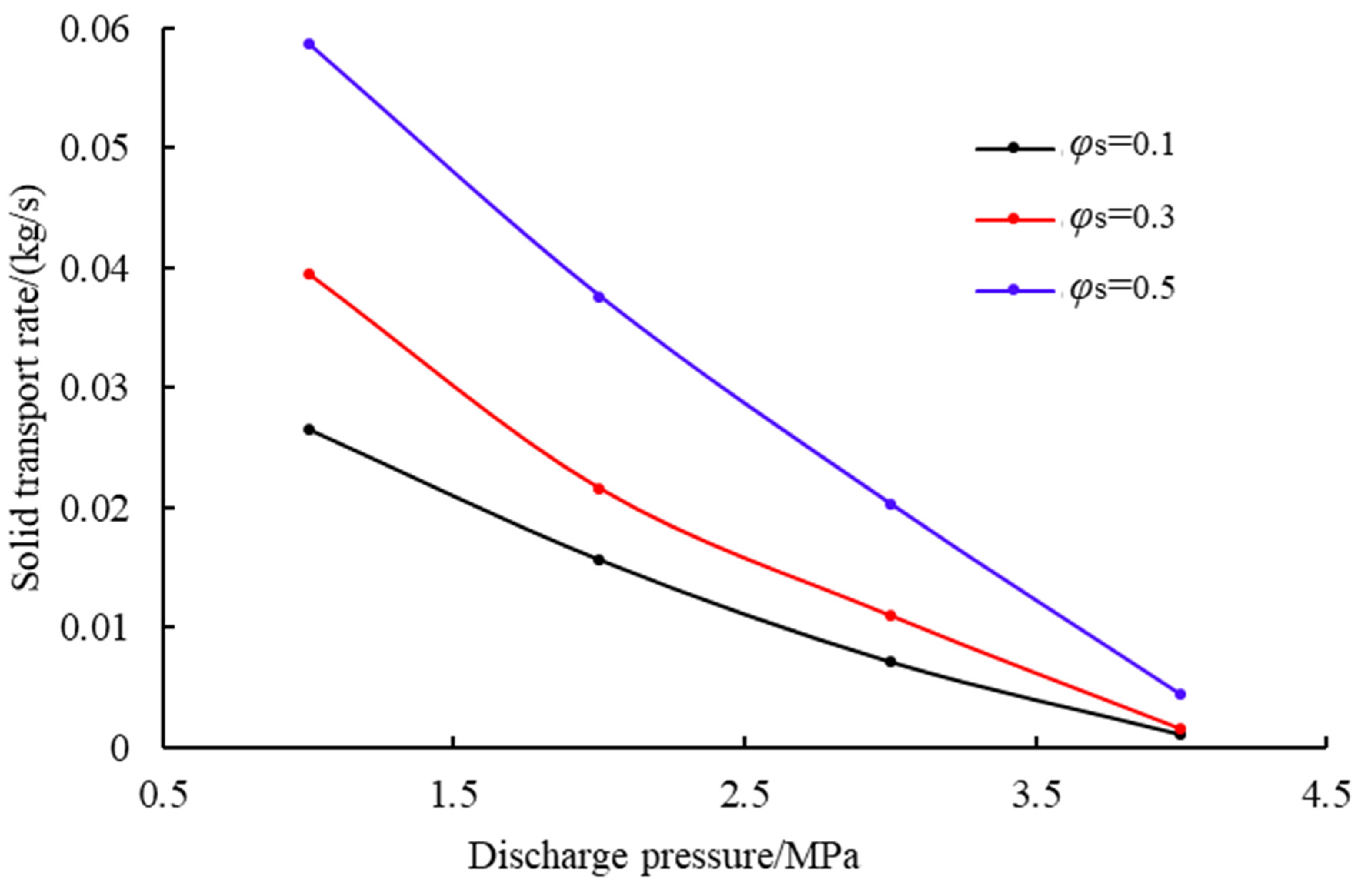
4.2. Effect of Discharge Pressure on Jet Pump Solid-Phase Transport Capacity
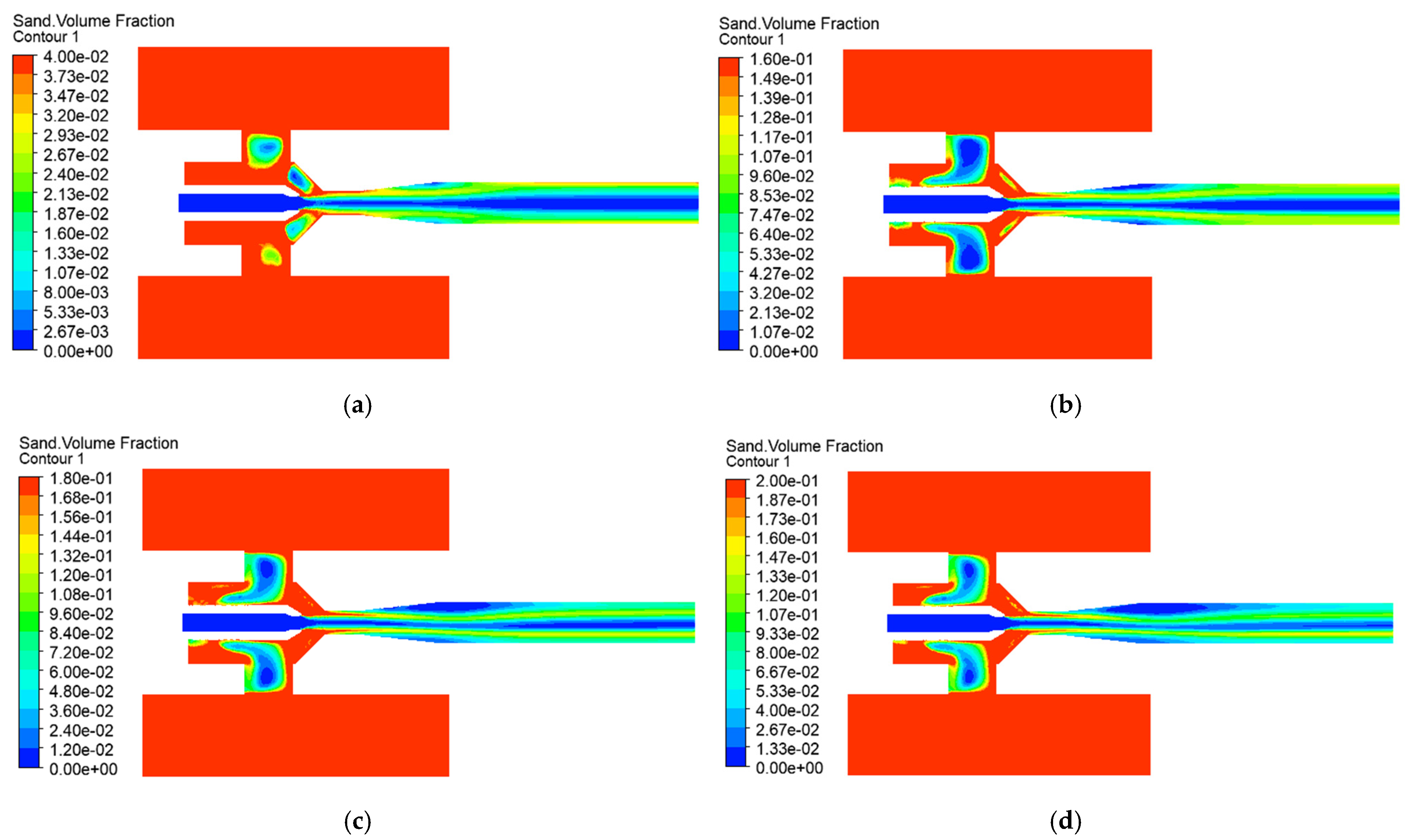
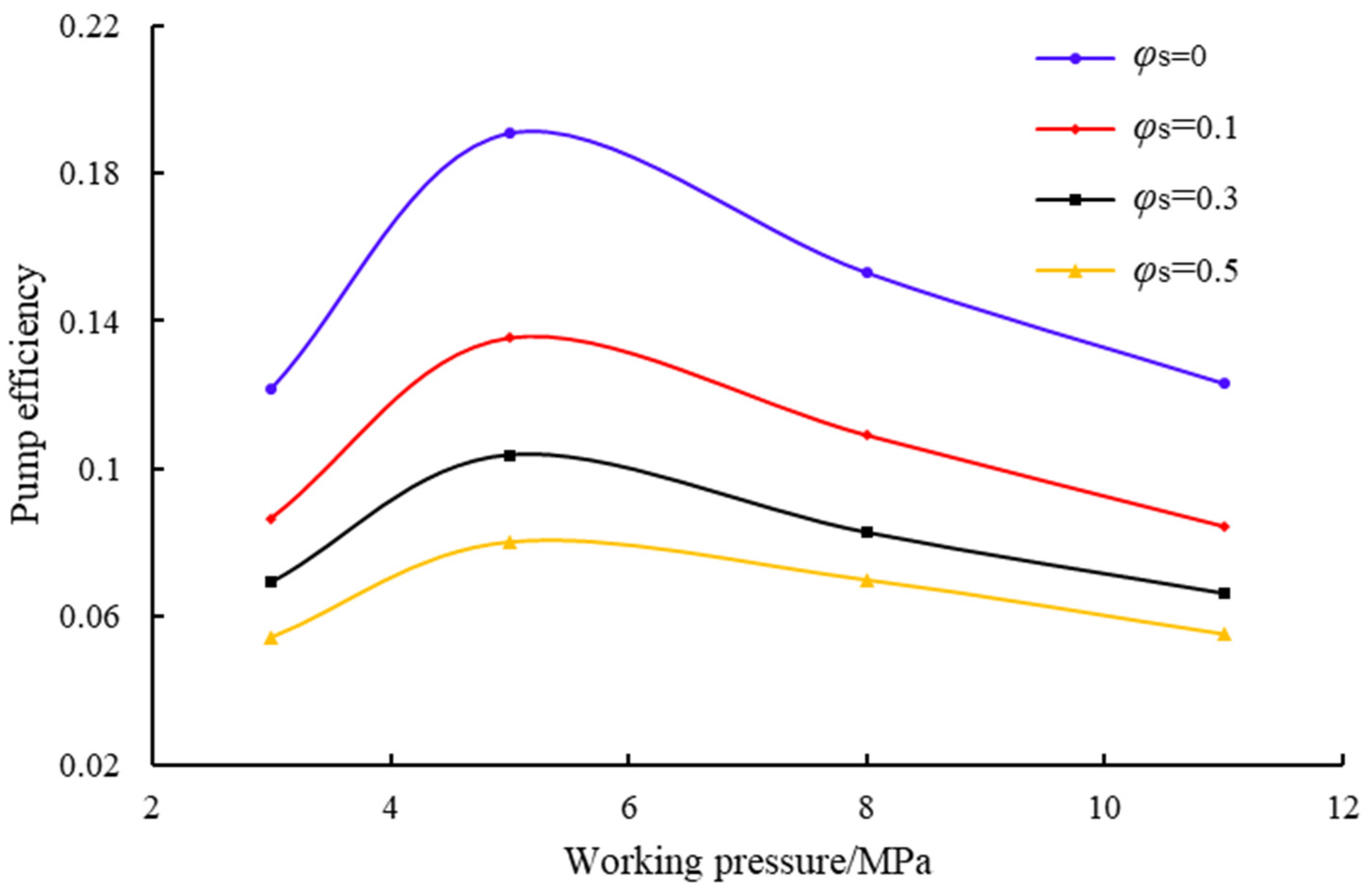
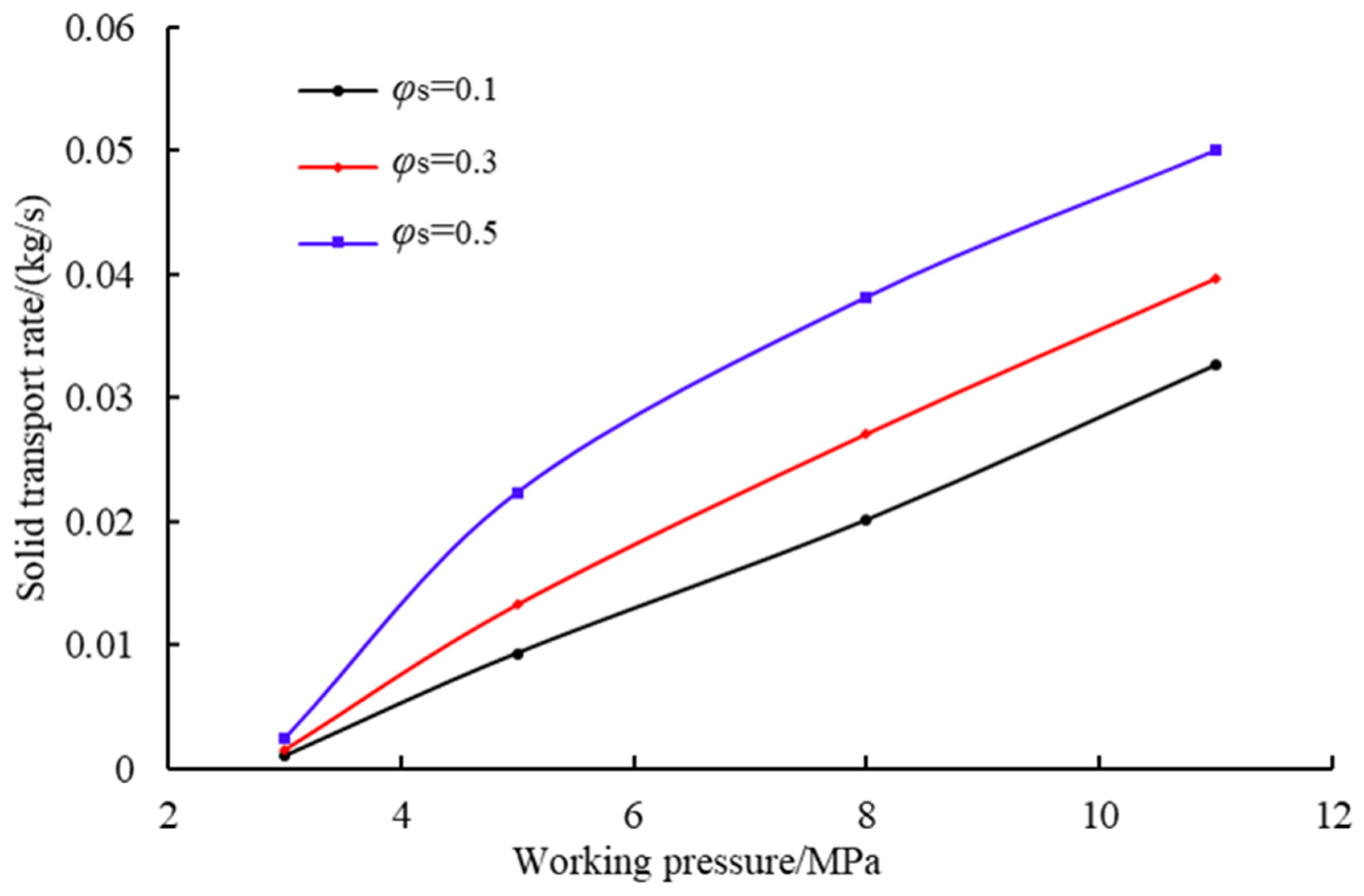
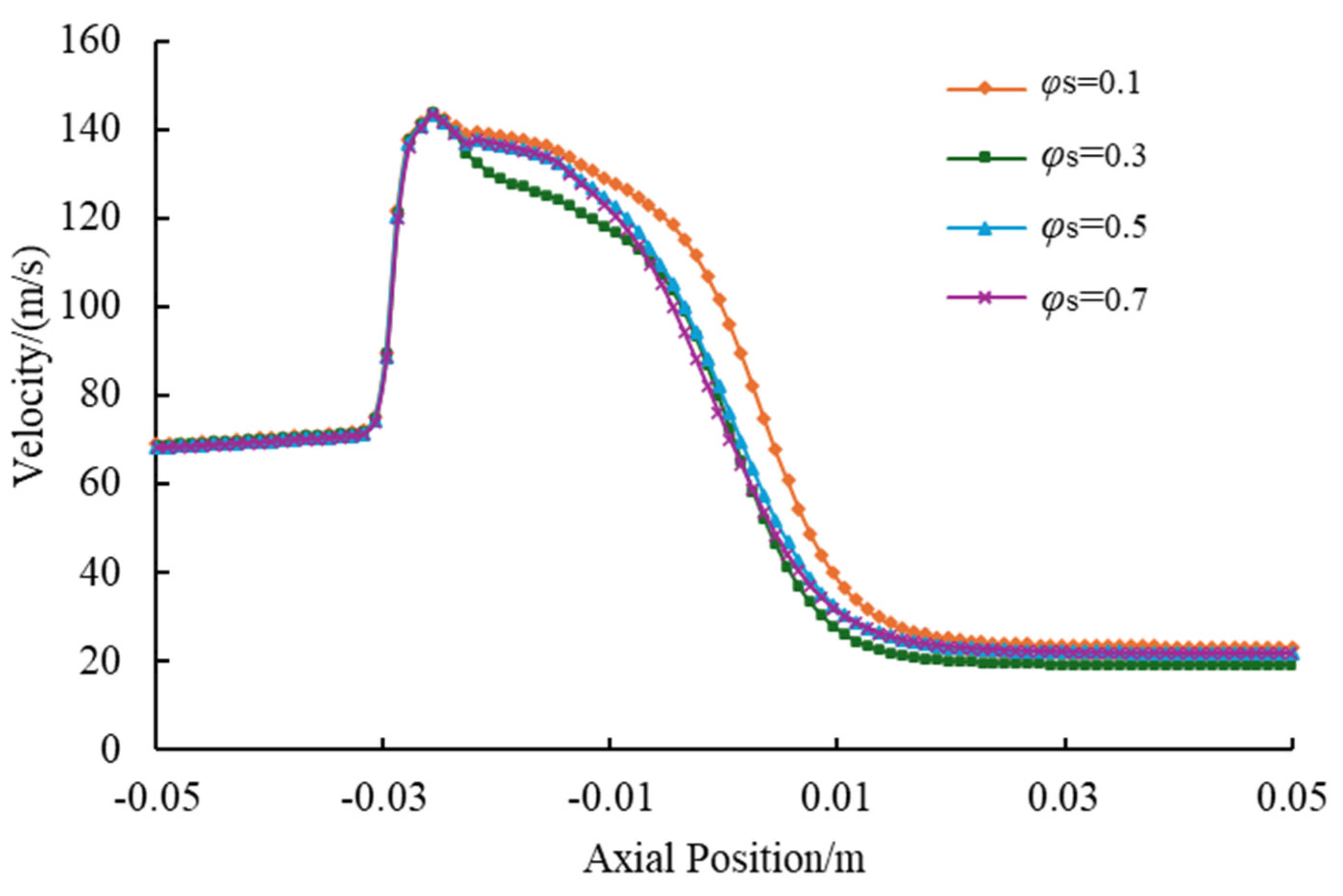
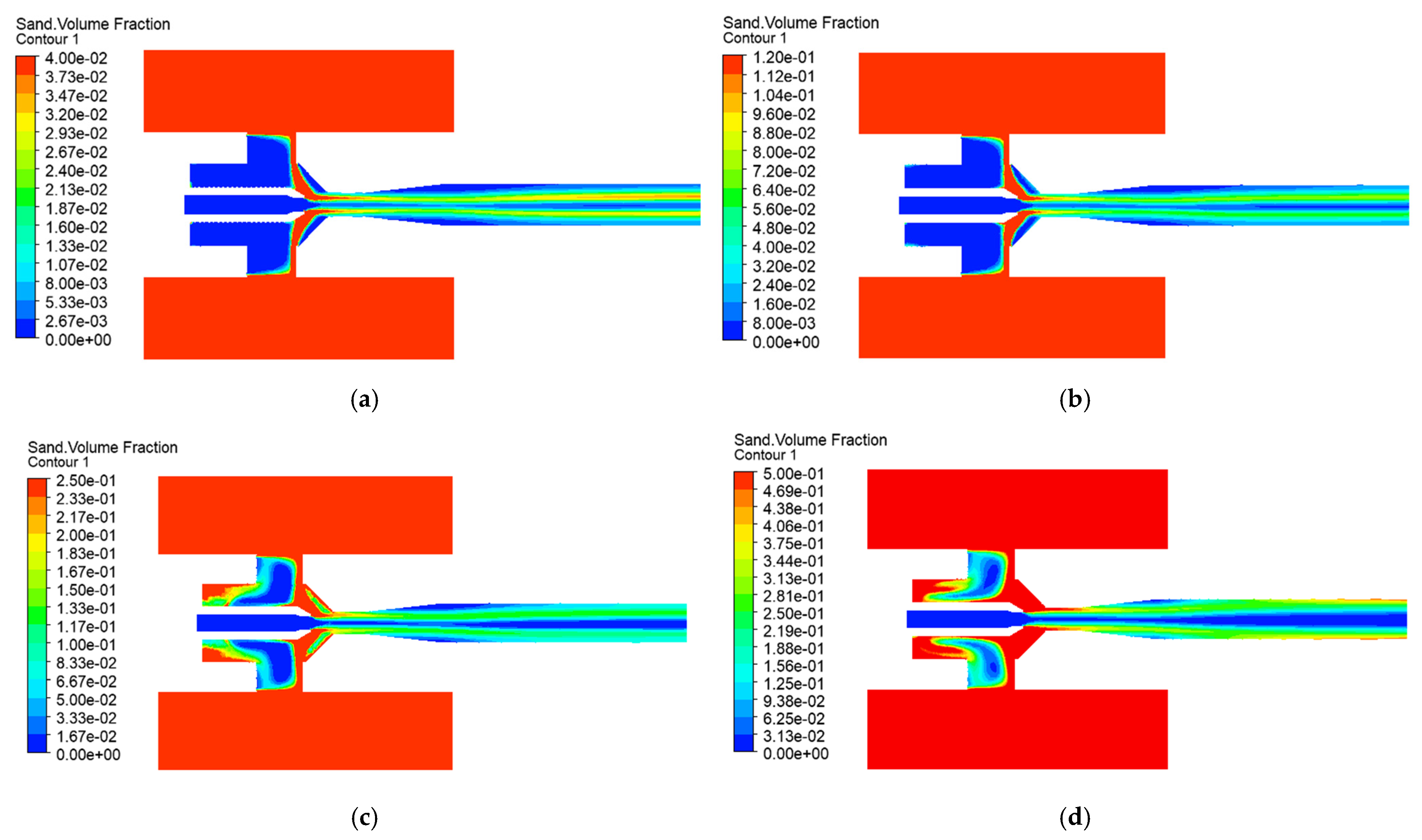
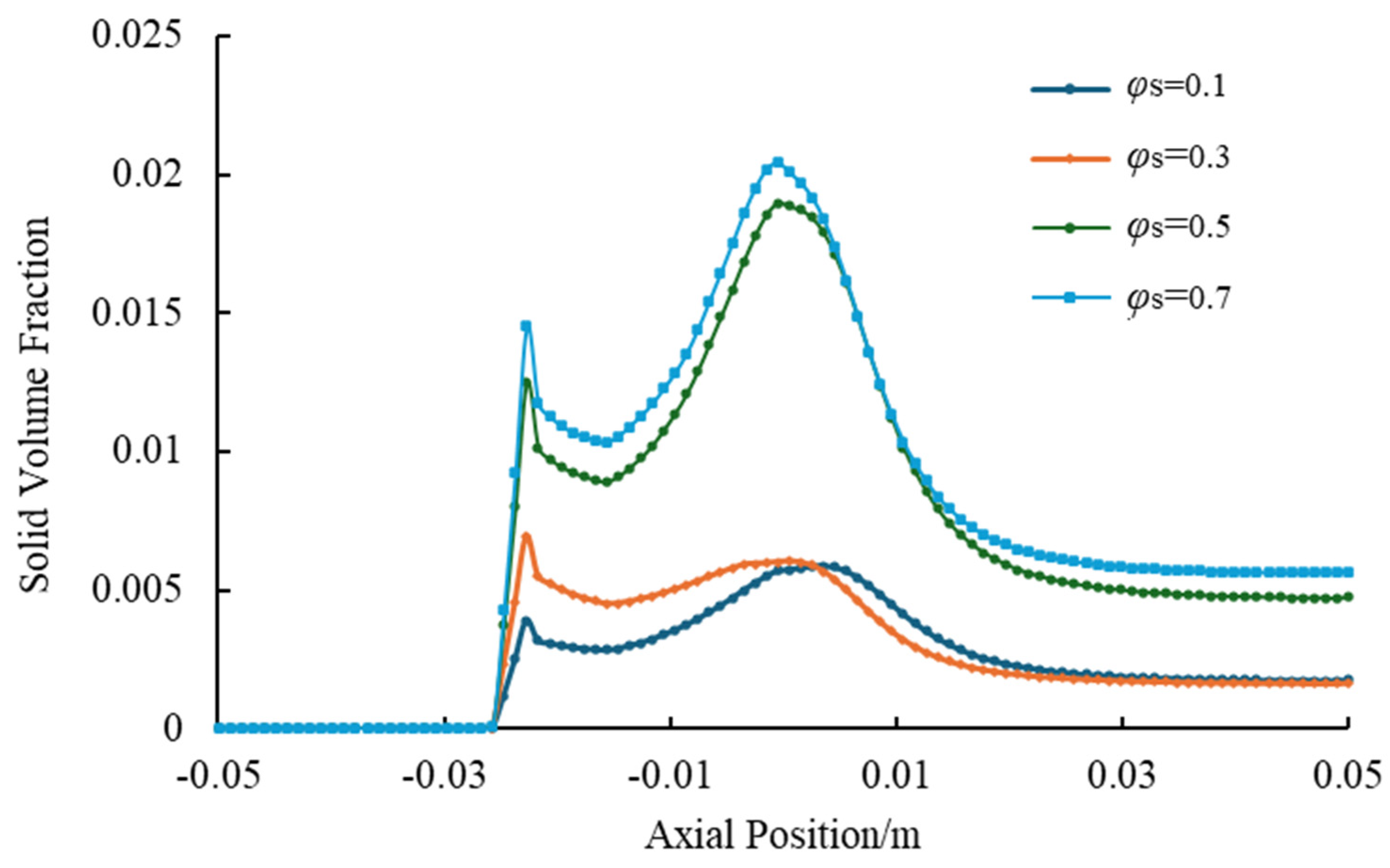
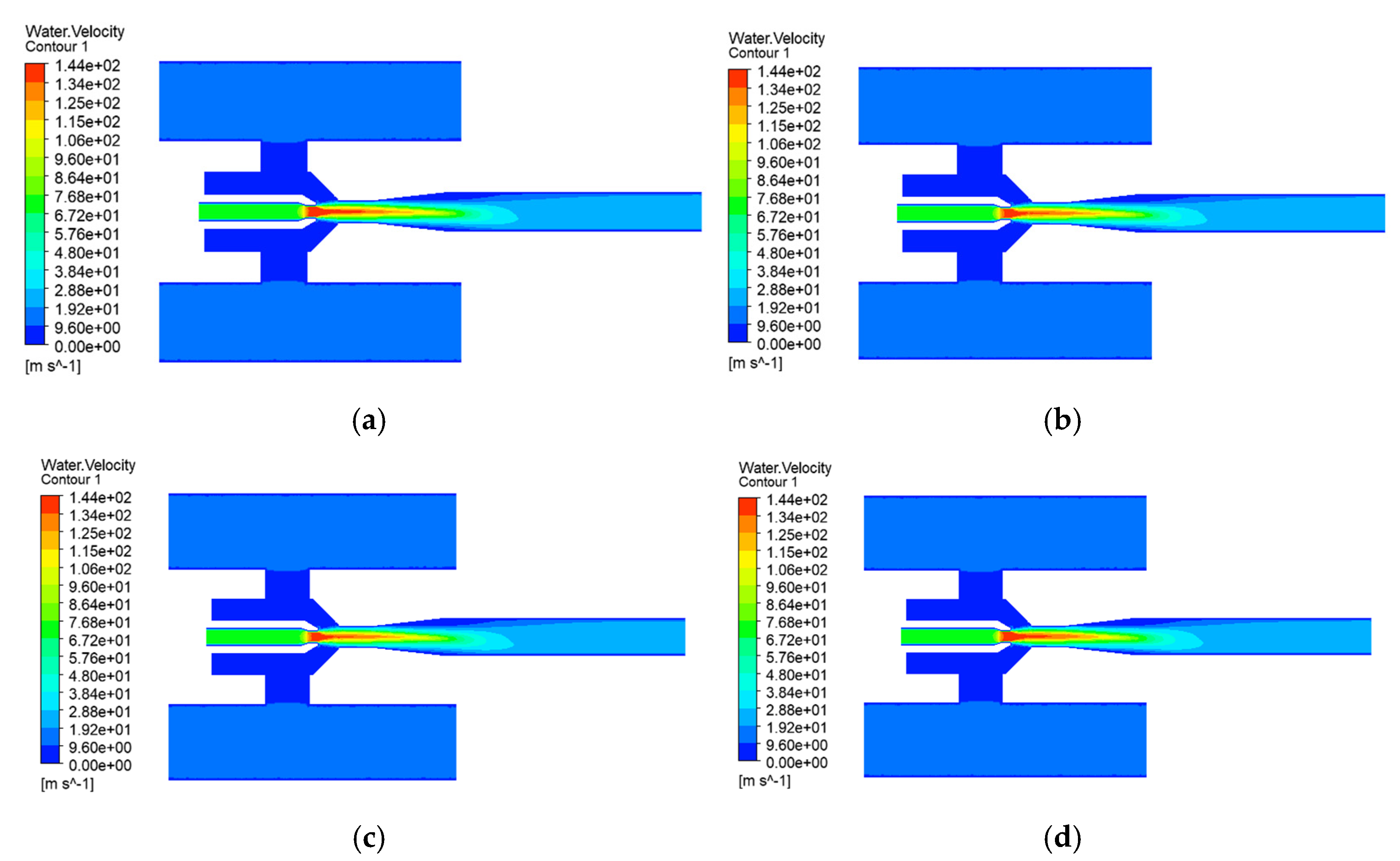
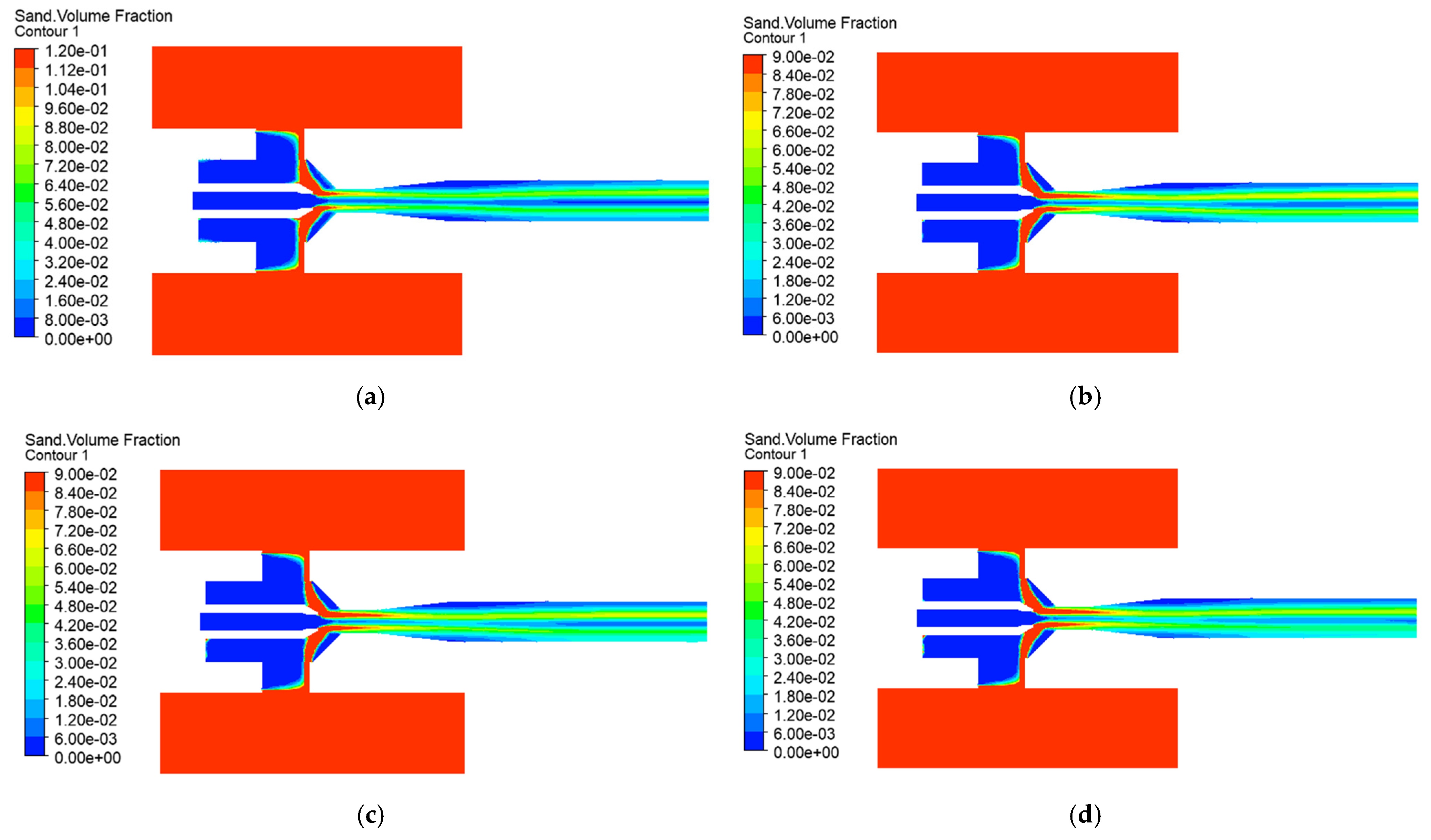
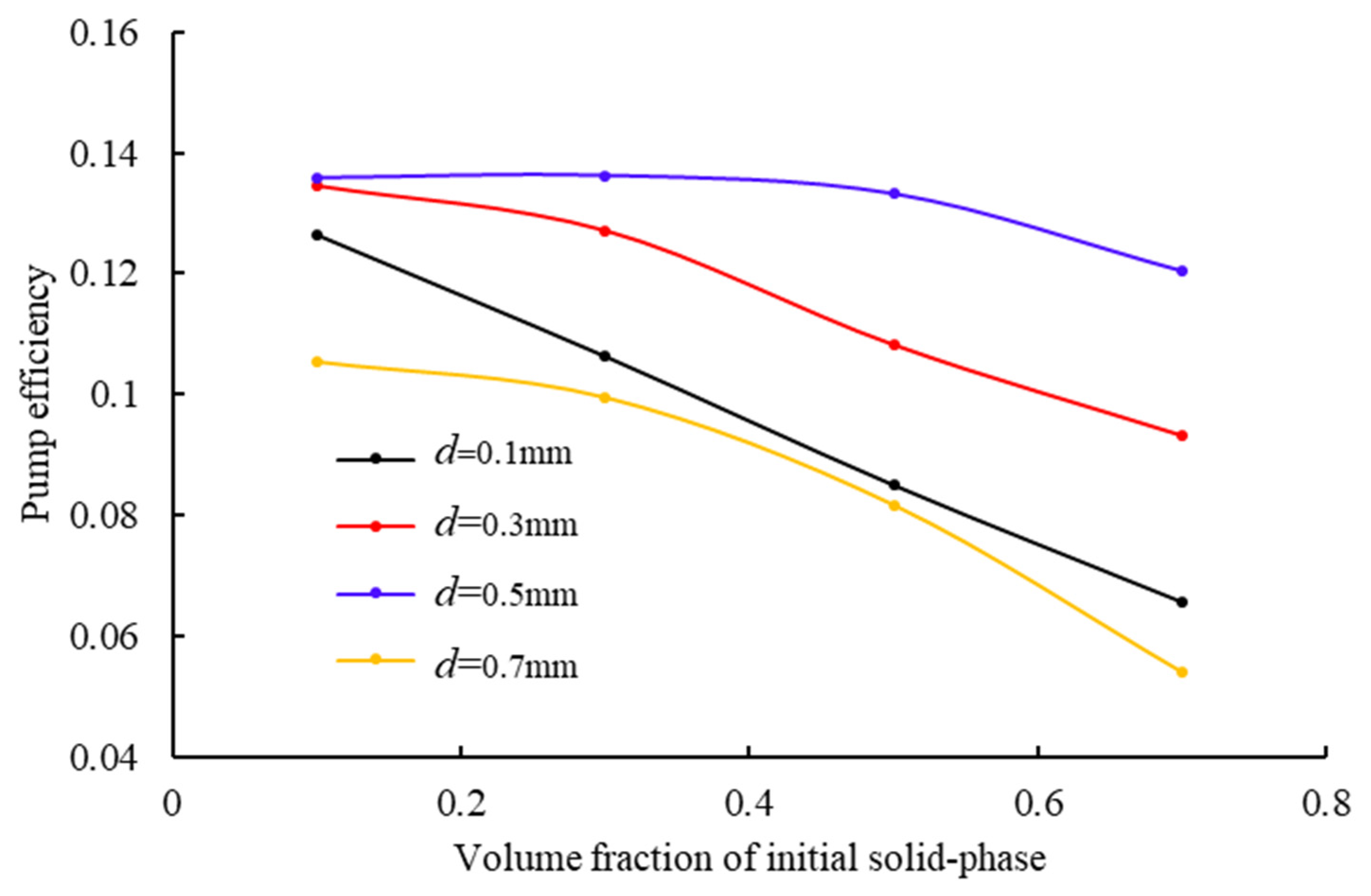
4.3. Effects of Solid-Phase Parameters on Jet Pump Solid-Phase Transport Capacity
- (1)
- Initial Solid Volume Fraction
- (2)
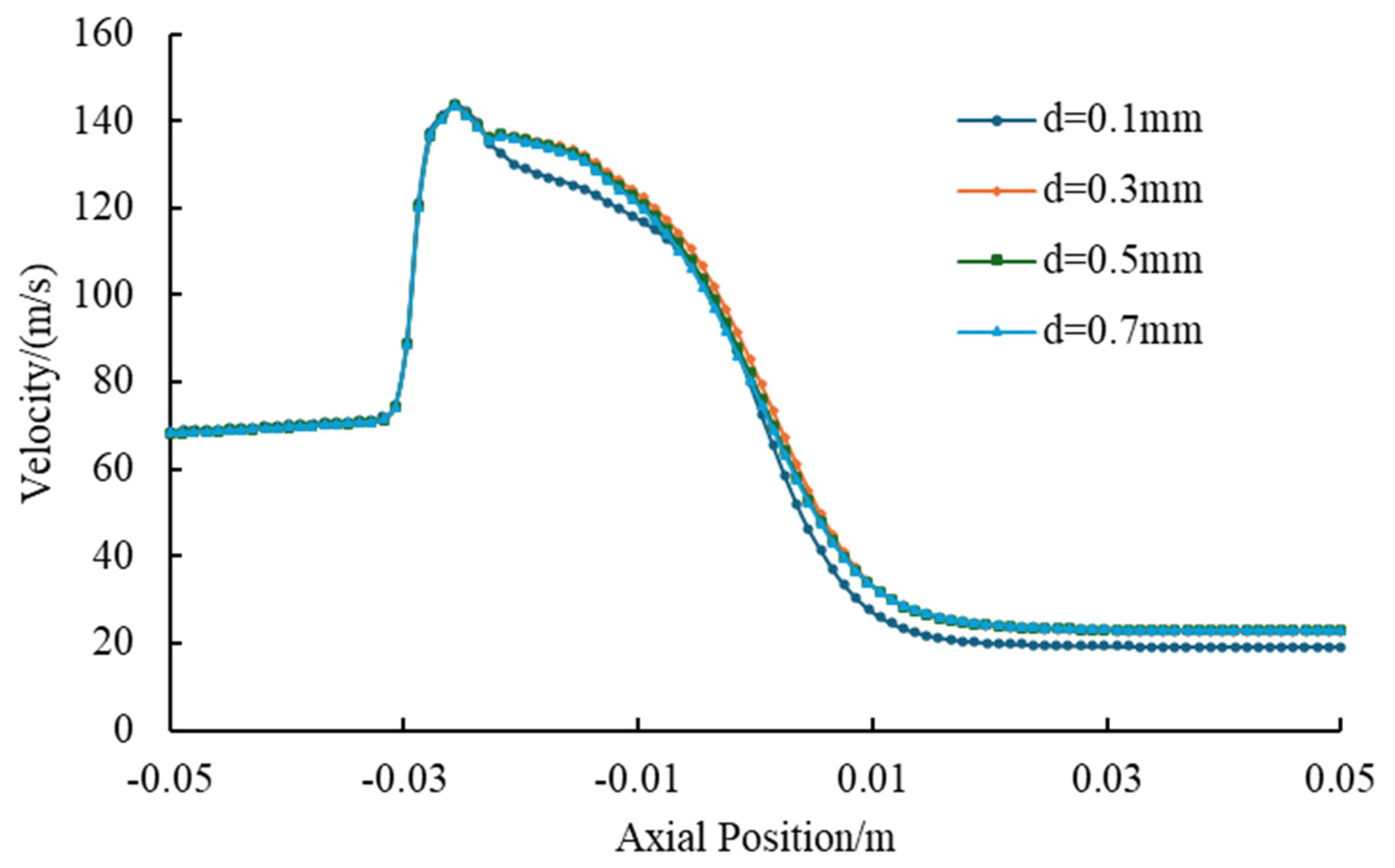
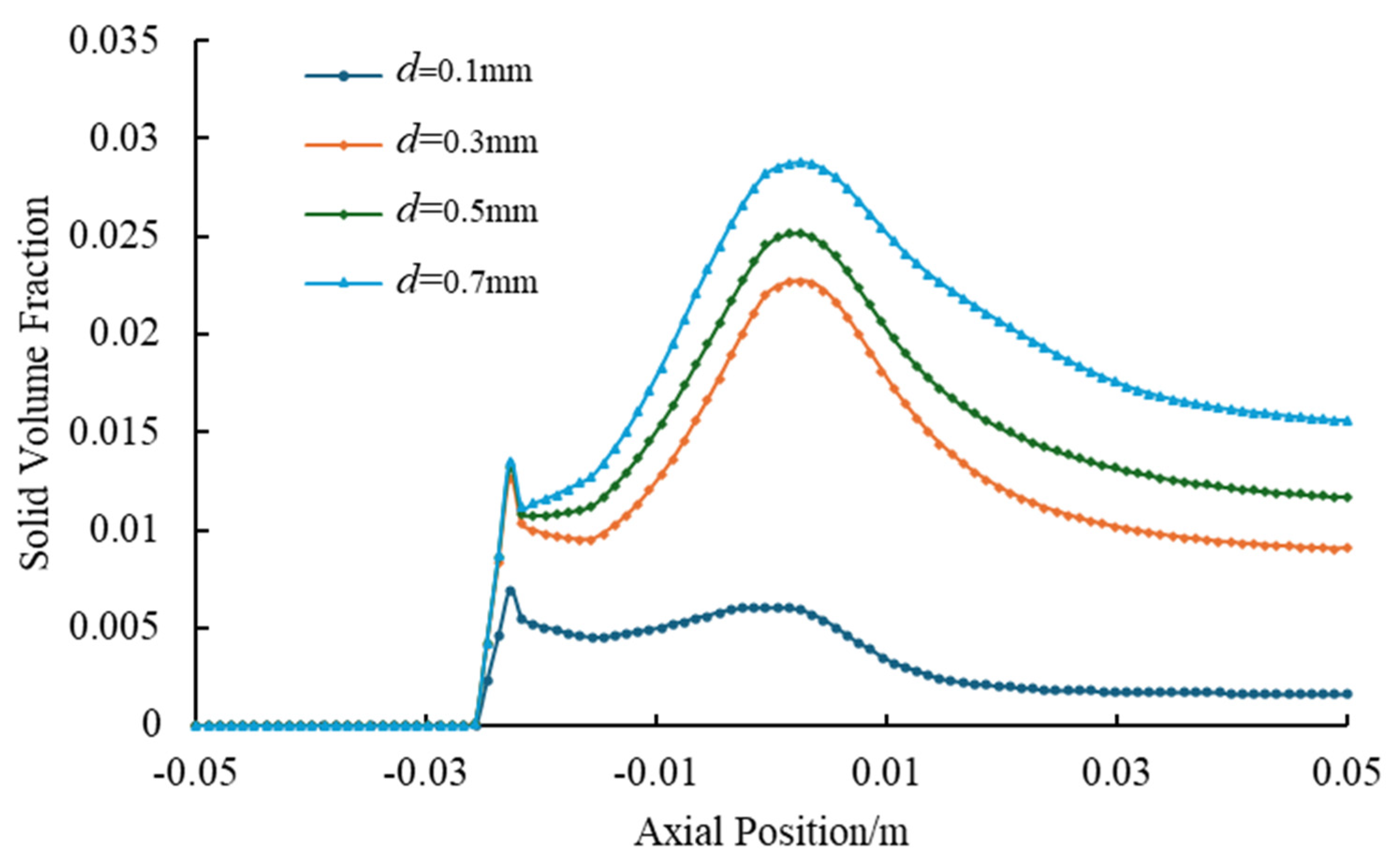
- Solid Particle Diameter
- (3)
- Performance Analysis and Critical Efficiency
5. Experimental Analysis
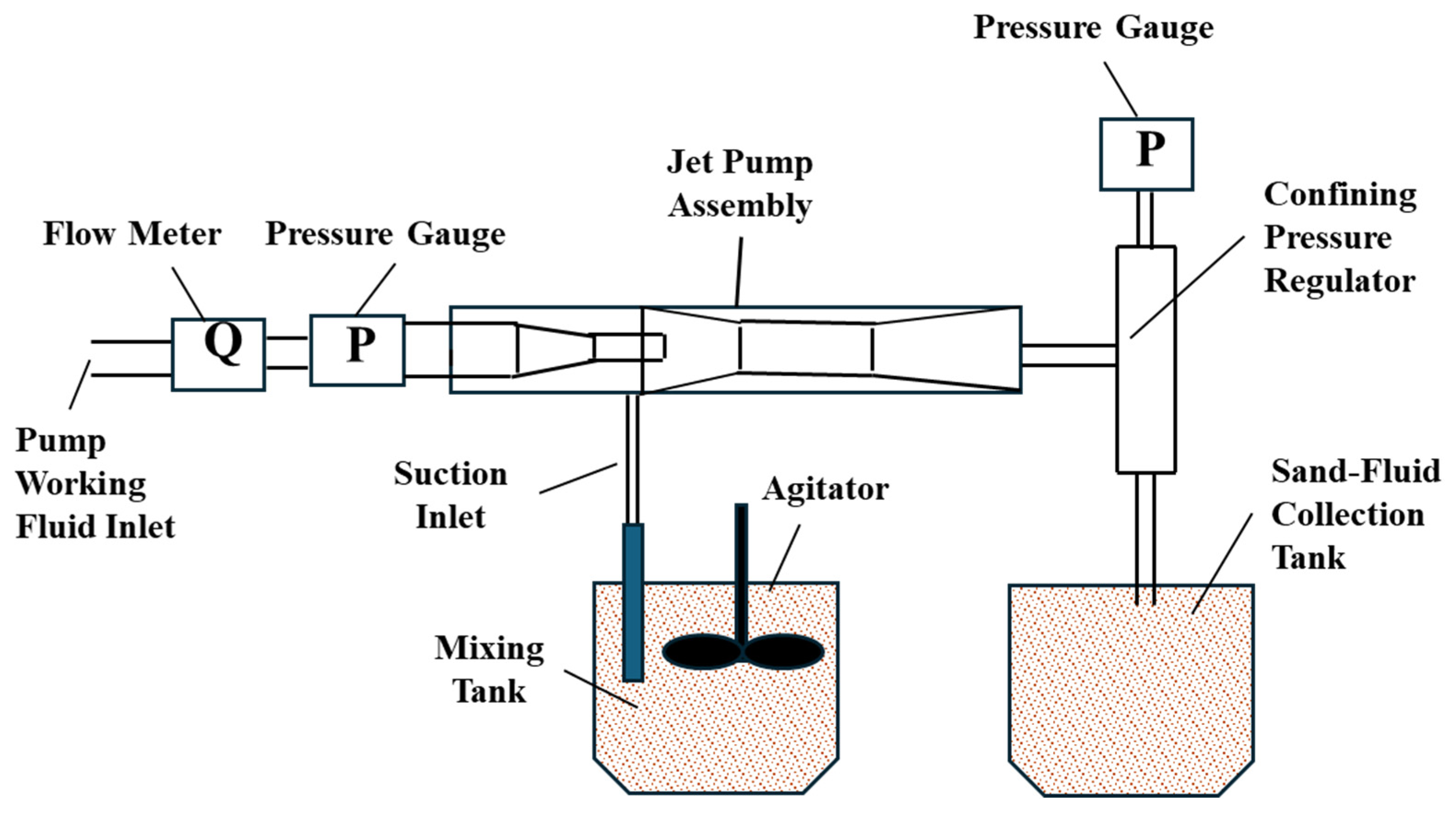
5.1. Experimental Apparatus
- Power system: High-pressure pump array (0–25 MPa operating range);
- Flow loop: Precision-controlled concentric tubing circuit;
- Test section: Instrumented jet pump assembly with replaceable components;
- Data acquisition: Real-time monitoring system with ±0.25% FS accuracy;
- Sand-fluid collection tank: Functionally critical component for solid-phase capture and volumetric quantification.
5.2. Experimental Method
- Install a jet pump with a 2.6 mm nozzle, 6 mm throat diameter, and 9 mm nozzle-throat distance.
- Verify the liquid levels in the suction line buffer tank (>80% capacity).
- Mix quartz sand and water at a 2:8 volume in the mixing tank. The density of the mixed sand–fluid slurry (ρmix) can be determined as follows:
- Maintain the solid concentration at φ = 0.1 using a helical propeller mixer (300 rpm), and distribute the mixture uniformly through a wellbore simulator.
- Start the pump and gradually ramp up to the target flow rate.
- Adjust the discharge pressure to P2 = 1 MPa by confining the pressure regulator.
- Sequentially increase the working pressure from 3 to 11 MPa.
- Record the parameters at a steady state: working flow rate (q1); working pressure (P1).
- After stabilization, initiate a 30 s timed collection.
- Capture discharged solids in the sand–fluid collection tank. Measure the dry sand mass (msand) and suction sand–fluid mixture volume (Vsuction).
- Calculate the performance parameters:
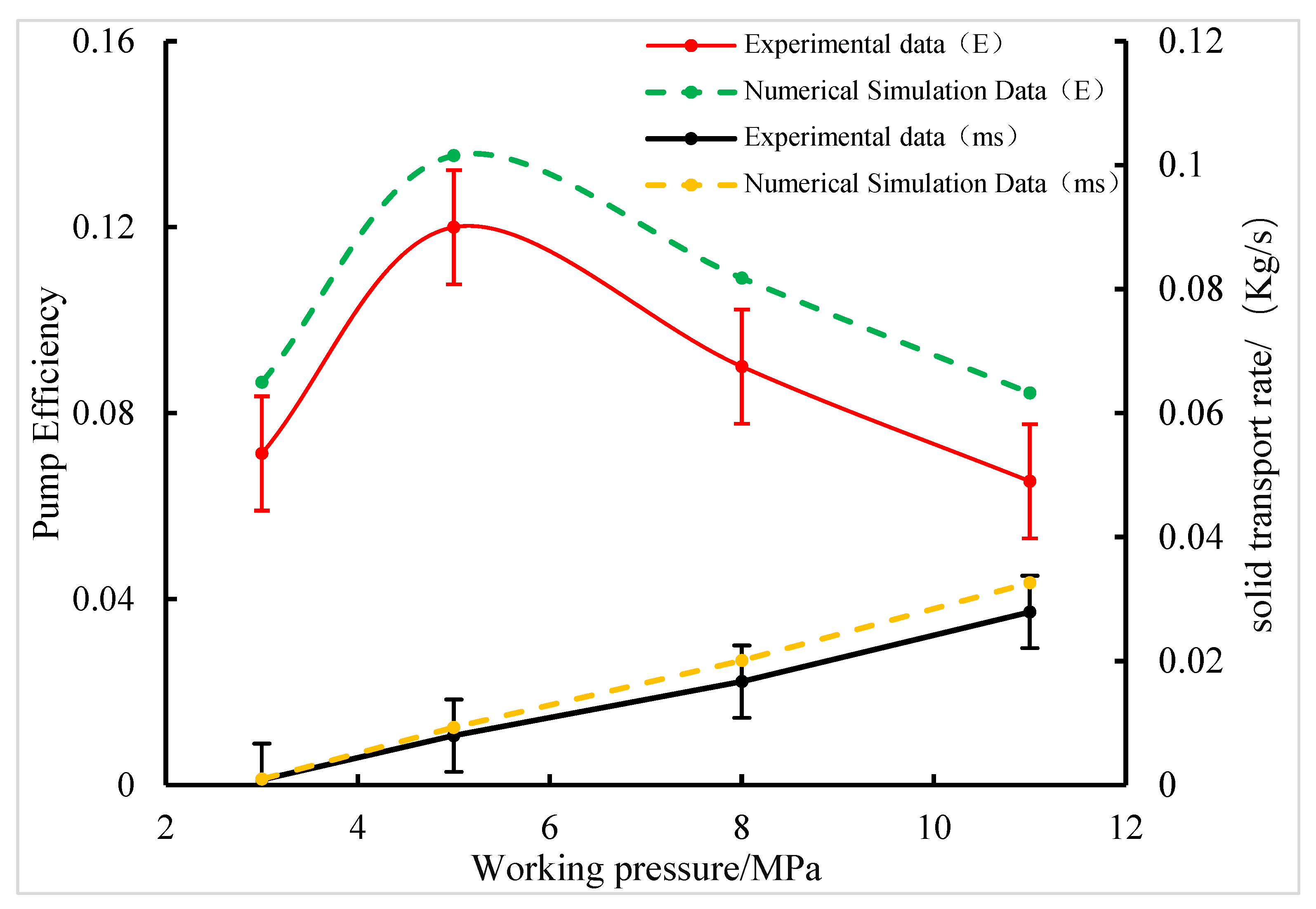
5.3. Experimental Data Comparison
6. Conclusions
- (1)
- Working pressure optimization reveals a critical trade-off: increasing the working pressure to 8 MPa enhances the solid transport rate by 116% compared to the operation condition of 5 MPa, while the turbulent dissipation beyond 5 MPa reduces the pump efficiency by 19.5%. Operational balance is achieved within a range of 5–8 MPa, with 5 MPa maximizing the energy efficiency (peak efficiency 13.5%) and 8 MPa prioritizing the sand clearance capacity, which is particularly essential for deep-well applications.
- (2)
- The discharge pressure thresholds dictate transport viability: While the pressure in the inlet exceeds 2.5 MPa, the throat pressure difference may decrease by over 90% and the transmission rate of the solid phase decreased by 50%. Engineering protocols mandate discharge pressure at or below 2.5 MPa, with the proportional increase in working pressure compensating for energy loss in unavoidable high-discharge scenarios.
- (3)
- Solid-phase constraints demonstrate particle-size-dominated failure: diameters beyond 0.5 mm induce a 68.3% efficiency reduction and 42% transport rate decline through inertial collision dominance, while the volume fraction beyond 0.3 reduces efficiency by 35% despite marginal transport gains near 11% due to viscous energy losses. Stringent limits require a maximum particle diameter of 0.5 mm and a maximum solid volume fraction of 0.3 to prevent performance degradation.
- (4)
- The dual-metric framework validates operational superiority, increasing sand-clearance efficiency under optimized parameters: working pressure of 5–8 MPa, a maximum discharge pressure of 2.5 MPa, a maximum particle diameter of 0.5 mm, and a maximum solid volume fraction of 0.3.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pineda, R.; Lindsey, B.J.; Taggart, M. A Chronological Review of Concentric Coiled Tubing Vacuum Technology: Past, Present and Future; Technical Report; SPE: Houston, TX, USA, 2010. [Google Scholar]
- Davies, A.; Dunning, M.; Kuchel, M.; Roberts, T.; Taggart, M. Pushing the Boundaries of Concentric-Coiled-Tubing Technology to Resurrect Subhydrostatic Gas Wells on an Unmanned Offshore Installation. SPE Prod. Oper. 2012, 27, 67–77. [Google Scholar] [CrossRef]
- Li, J.; Bayfield, I.; Paton, G. Effective Heavy Oil Post-Fracturing Proppant Cleanout with Coiled Tubing: Experimental Study and Field Case History. In Proceedings of the 2006 SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2006. Paper SPE 101235. [Google Scholar]
- Rafferty, P.; Ennis, J.; Skufca, J.; Craig, S. Enhanced Solids Removal Techniques from Ultra Low Pressure Wells Using Concentric Coiled Tubing Vacuum Technology. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007; SPE: Richardson, TX, USA, 2007. Paper SPE-107010. [Google Scholar]
- Dong, P.; Lang, Z.; Xu, X. The Fully Coupled Fluid-Solid Analysis for the Reservoir Rock Deformations Due to Oil Withdrawal. J. Geomech. 2000, 6, 5. [Google Scholar]
- Wu, J.; Yu, D.; Wu, G.; Liu, J. Current Situation and Prospect of Jet Pumps. J. Drain. Irrig. Mach. Eng. 2007, 25, 65–68. [Google Scholar]
- Liu, B.; Du, J.; Qi, Y.; Zhang, F.; Yu, Y.; Zhao, H. A New Coal Particles Cleanout Technology in Coalbed Methane Wells in China. J. Pet. Sci. Eng. 2015, 127, 445–451. [Google Scholar] [CrossRef]
- Sun, W.; Li, M.; Zhu, F.B. Exploration of the Mechanism and Prediction of Jet Pump Feature Structure Optimization for the Enhanced Pumping Performance. Proc. Inst. Mech. Eng. Part A J. Power Energy 2023, 237, 1775–1789. [Google Scholar] [CrossRef]
- Deng, H.; Liu, X.; Ma, W. Flow Field Analysis at the Diffuser Outlet of Jet Sand Discharge Pump for Oil Wells. J. Jilin Univ. (Earth Sci. Ed.) 2010, 40, 689–693. [Google Scholar]
- Xiao, L.; Long, X.; Li, X.; Zeng, Q.; Yang, X. Numerical Investigation on the Recirculation in Annular Jet Pumps. J. Mech. Sci. Technol. 2013, 27, 1603–1609. [Google Scholar] [CrossRef]
- Meakhail, T.; Teaima, I. Experimental and Numerical Studies of the Effect of Area Ratio and Driving Pressure on the Performance of Water and Slurry Jet Pumps. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2250–2266. [Google Scholar] [CrossRef]
- Zhou, L.; Yuan, L. 3D Large Eddy Simulation of Liquid-Solid Two-Phase Flow Characteristics in Jet Pumps. J. Drain. Irrig. Mach. Eng. 2012, 30, 522–526. [Google Scholar]
- Itoh, K.; Nishigaki, S.; Honda, I.; Yoshida, T.; Boda, A.; Kumamaru, H.; Shimogonya, Y. Performance of Solid-Liquid Two Phase Jet Pump Vacuuming Up Beach Sand. In Proceedings of the ASME 2010 International Mechanical Engineering Congress and Exposition, Vancouver, BC, Canada, 12–18 November 2010; ASME: New York, NY, USA, 2010; pp. 503–509. [Google Scholar]
- Liu, B.; Sun, W.; Wu, J.; Wang, H.; Xu, L.; Qi, Y.; Zhang, F. Influence of Initial Solid Concentration on the Performance of Jet Pump for Fracturing Flowback Fluid. J. China Coal Soc. 2018, 43 (Suppl. S2), 634–640. [Google Scholar]
- Shen, J. Flow Field Characteristic Analysis of Double-Tube Sand-Carrying Jet Pump. Master’s Thesis, Yangtze University, Jingzhou, China, 2021. [Google Scholar]
- Fan, L.; Mao, Z.; Yang, C. Numerical Simulation of Laminar Solid-Liquid Two-Phase Flow in Stirred Tanks. Chem. Eng. Commun. 2007, 194, 291–308. [Google Scholar] [CrossRef]
- Ge, Y.; Ge, Q.; Yu, J. Numerical Simulation and Confirming of Optimal Range on the Nozzle-to-Throat Clearance of Liquid-Gas Jet Pump. Fluid Mach. 2012, 40, 21–24. [Google Scholar]
- Jia, X.; Liao, H.; Hu, Q.; He, Y.; Wang, Y.; Niu, W. Optimization Method of Jet Pump Process Parameters and Experimental Study on Optimal Parameter Combinations. Processes 2023, 11, 2841. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Shen, X. Numerical Simulation and Experiment on the Turbulent Flow in the Jet Pump. J. Chem. Eng. Chin. Univ. 2006, 20, 175–179. [Google Scholar]
- Wibisono, K.; Sitaresmi, R. Evaluation of Hydraulic Jet Pump Application in Sembakung Field. J. Earth Energy Sci. Eng. Technol. 2020, 3, 75–83. [Google Scholar] [CrossRef]
- Falk, K.; Fraser, B. Concentric Coiled Tubing Application for Sand Cleanouts in Horizontal Wells. J. Can. Pet. Technol. 1998, 37, 46–50. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Luft, H.B.; Wilde, G.; Alingig, G.; Jumawid, F. Cleanouts with Coiled Tubing in Low Bottom Hole Pressure Wellbores. In Proceedings of the 2008 SPE/ICoTA Coiled Tubing and Well Intervention Conference and Exhibition, The Woodlands, TX, USA, 1–2 April 2008. Paper SPE 113841. [Google Scholar]
- Mann, J.A.; Young, R.J. A Theoretical and Experimental Study of Ejector Performance with Two-Phase Flow. J. Fluids Eng. 1972, 94, 301–310. [Google Scholar]
- ANSYS, Inc. ANSYS Fluent Theory Guide, Release 2021R1, Section 16.3: Multiphase Mixture Model; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
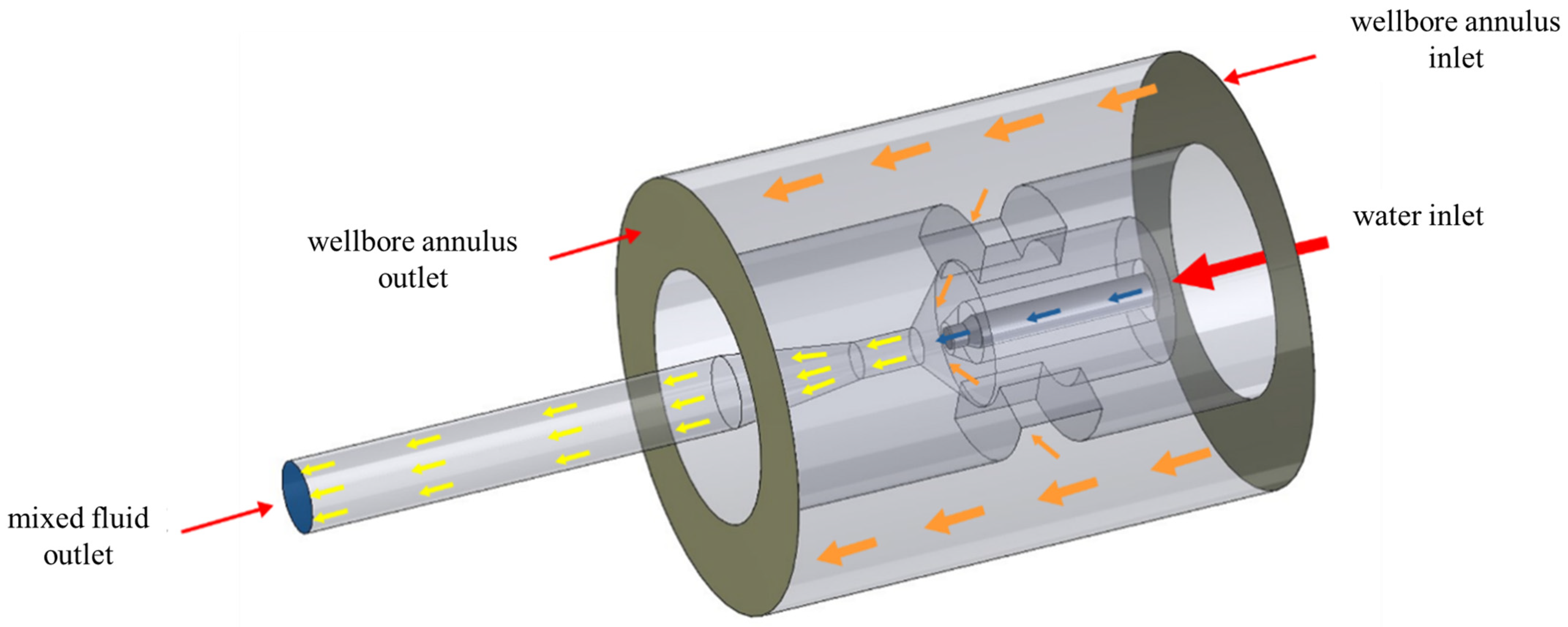

| Boundary Name | Type | Phase Association | Value |
|---|---|---|---|
| Water inlet | Pressure inlet | Liquid phase | P1 = 3–11 MPa |
| Wellbore annulus inlet | Pressure inlet | Solid–liquid mixture | φs = 0.1–0.4; d = 0.1–0.7 mm |
| Mixed fluid outlet | Pressure outlet | Solid–liquid mixture | P2 = 1–4 MPa |
| Wellbore annulus outlet | Pressure outlet | Solid–liquid mixture | P3 = 0.1 MPa |
| Wall | No-slip wall (turbulent flow) | / | Standard wall function (turbulent flow) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Liao, H.; Zhang, L.; Zhang, Y.; Liu, J. Mechanisms and Optimization of Critical Parameters Governing Solid-Phase Transport in Jet Pumps for Vacuum Sand Cleanout. Processes 2025, 13, 2639. https://doi.org/10.3390/pr13082639
Jia X, Liao H, Zhang L, Zhang Y, Liu J. Mechanisms and Optimization of Critical Parameters Governing Solid-Phase Transport in Jet Pumps for Vacuum Sand Cleanout. Processes. 2025; 13(8):2639. https://doi.org/10.3390/pr13082639
Chicago/Turabian StyleJia, Xia, Hualin Liao, Lei Zhang, Yan Zhang, and Jiawei Liu. 2025. "Mechanisms and Optimization of Critical Parameters Governing Solid-Phase Transport in Jet Pumps for Vacuum Sand Cleanout" Processes 13, no. 8: 2639. https://doi.org/10.3390/pr13082639
APA StyleJia, X., Liao, H., Zhang, L., Zhang, Y., & Liu, J. (2025). Mechanisms and Optimization of Critical Parameters Governing Solid-Phase Transport in Jet Pumps for Vacuum Sand Cleanout. Processes, 13(8), 2639. https://doi.org/10.3390/pr13082639






