Thermodynamic Modeling of Multilayer Insulation Schemes Coupling Liquid Nitrogen Cooled Shield and Vapour Hydrogen Cooled Shield for LH2 Tank
Abstract
1. Introduction
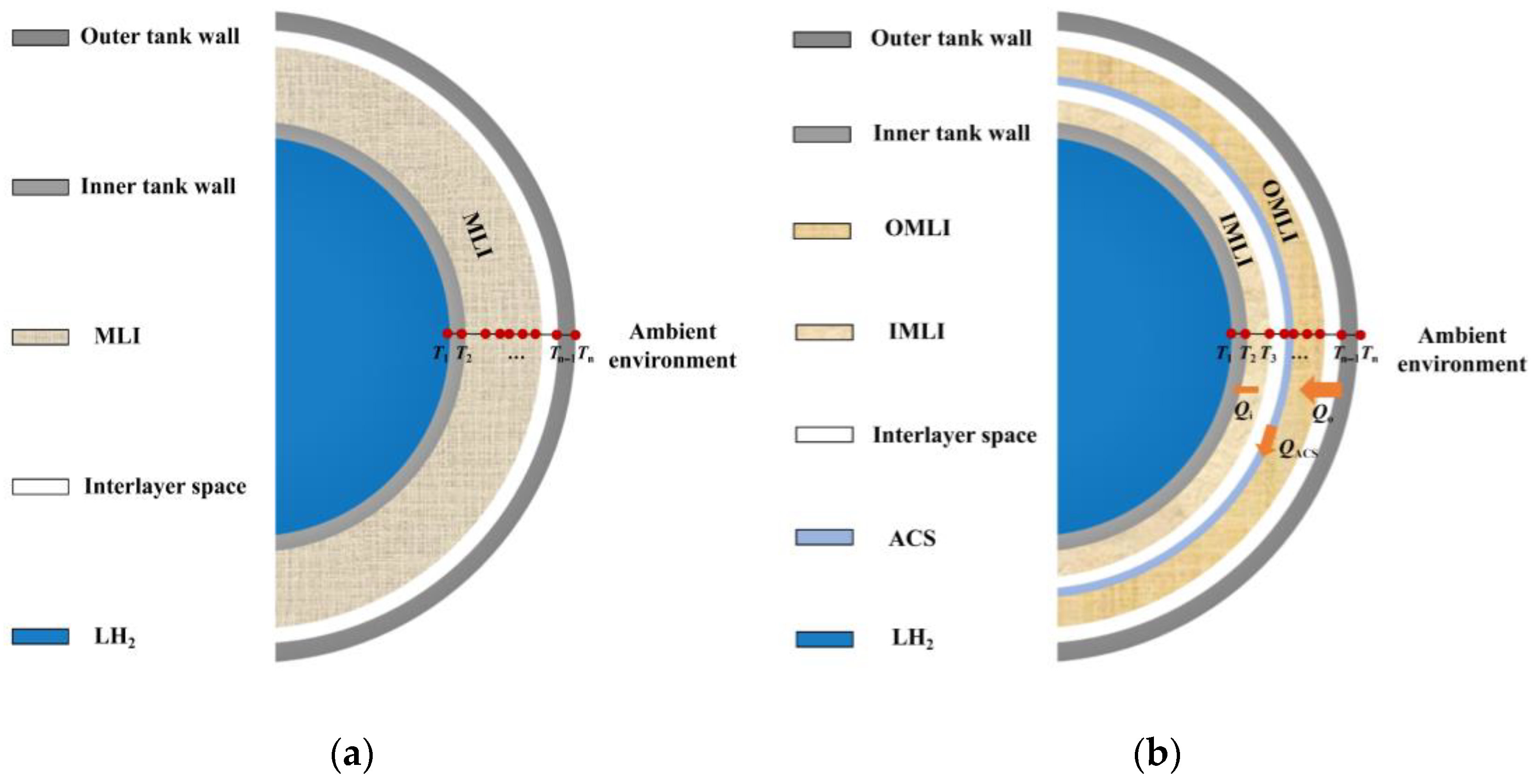
2. LH2 Storage Tank and Insulation System
3. Thermodynamic Model and Experimental Verification
3.1. Assumptions
- (1)
- The absorption effect of spacers in MLI materials on radiative heat transfer was neglected.
- (2)
- Due to the high vacuum level within the MLI, convection caused by residual gas was neglected.
- (3)
- Thermal expansion and delamination between the MLI materials were not considered.
- (4)
- The internal pressure of the LH2 storage tank was maintained at 0.1 MPa with a temperature stabilized at 20 K.
- (5)
- The paper mainly focused on the condition where the ACS and coil reach steady state; that is, the temperature of the ACS was equal everywhere, without considering the temperature difference in ACS.
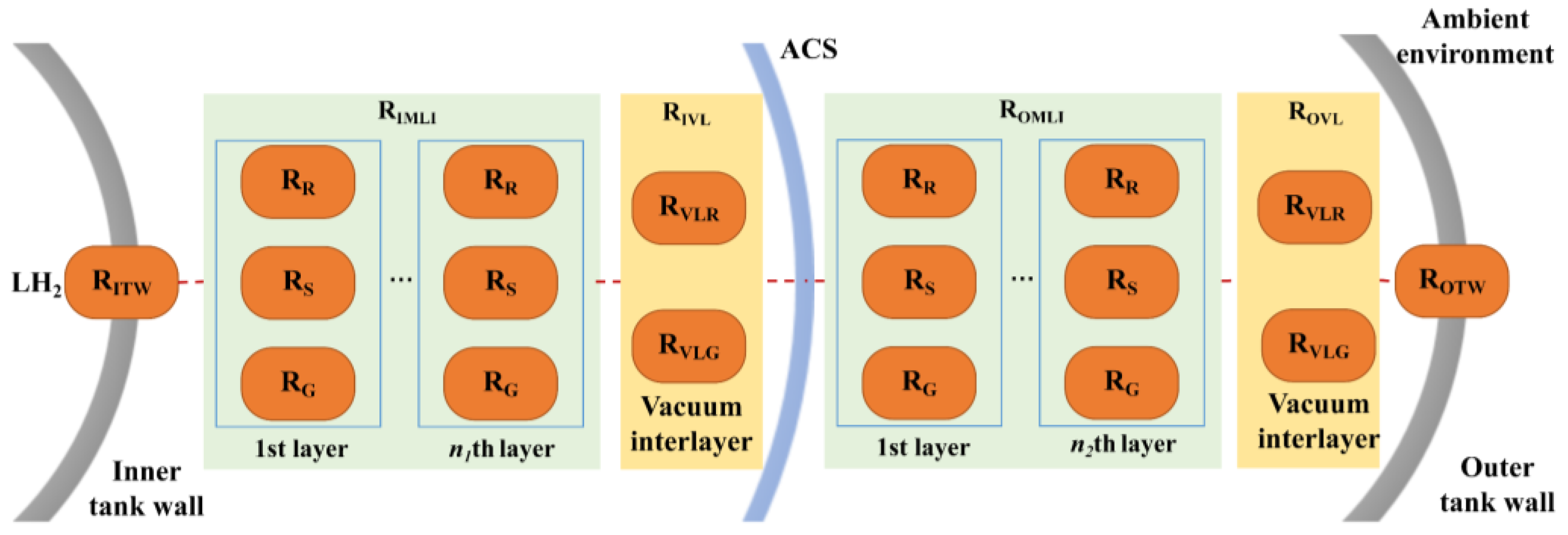
3.2. Thermodynamic Model of MLI and MLI-ACS
3.2.1. Thermodynamic Model of MLI
- (1)
- Heat transfer model of tank wall
- (2)
- Heat transfer model of MLI
- -
- Radiative heat transfer
- -
- Solid conduction
- -
- Residual gas conduction
- (3)
- Heat transfer model of interlayer
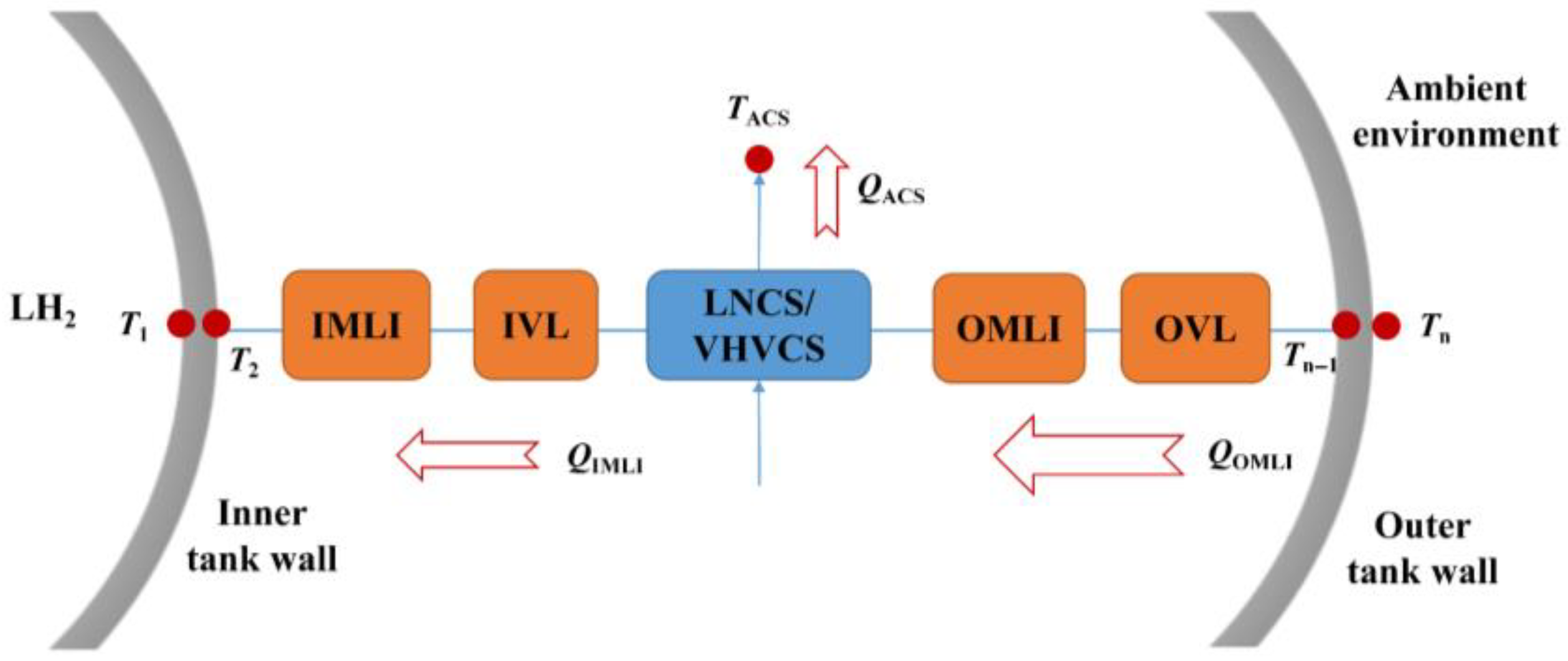
3.2.2. Thermodynamic Model of MLI-LNCS/MLI-VHVCS
- (1)
- Heat transfer in OMLI
- (2)
- Heat leakage through IMLI
- (3)
- Heat absorption by LNCS
- (4)
- Heat absorption by VHVCS
3.2.3. Thermodynamic Model of Thermal Bridge
- (1)
- Thermal bridge model of support system
- (2)
- Thermal bridge model of piping system
3.3. Boundary Conditions and Calculation Procedure
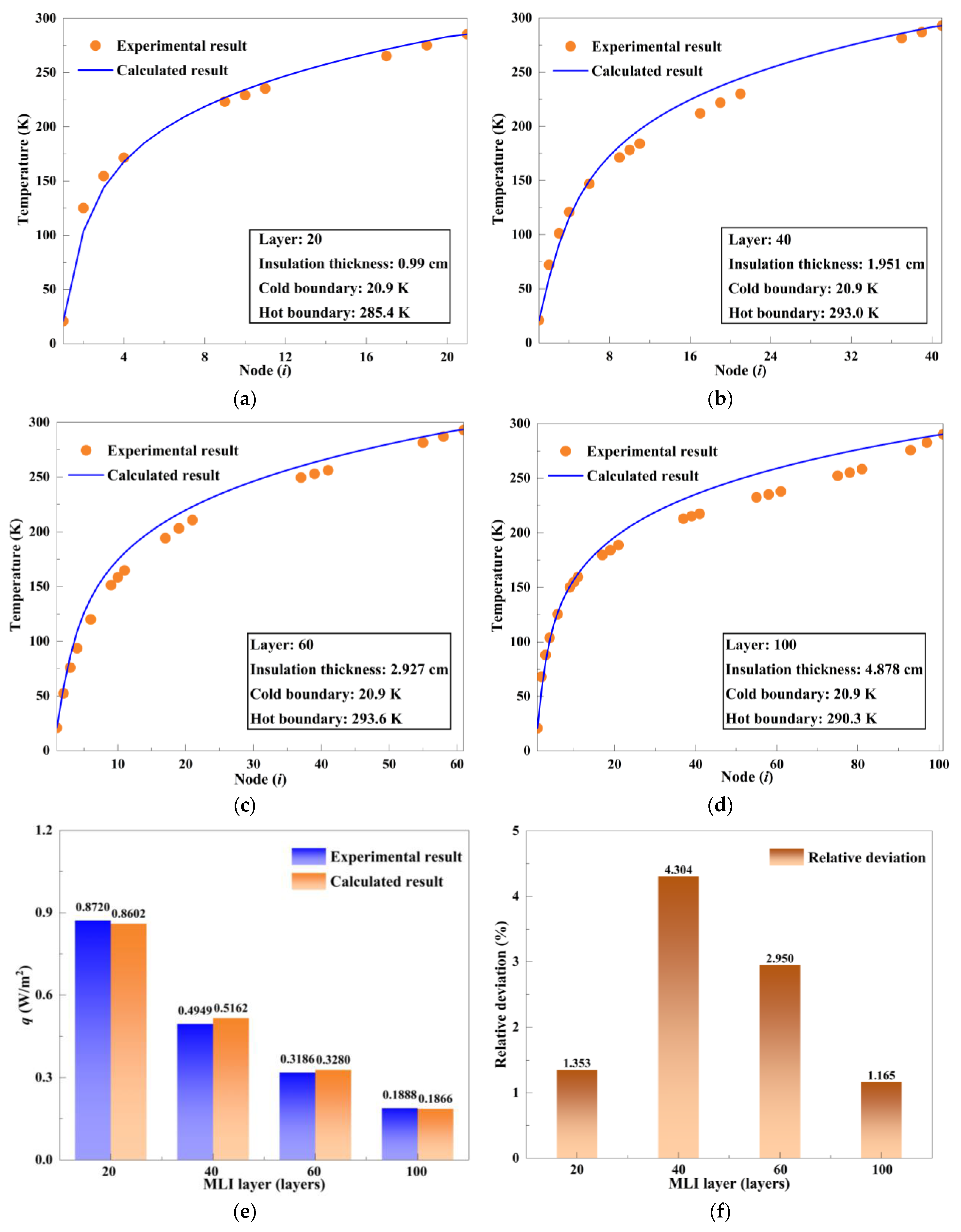
3.4. Experimental Validation
4. Results and Discussion
4.1. Heat Transfer in MLI
4.1.1. Temperature Distribution and Heat Leakage
4.1.2. Heat Leakage Distribution and Proportion in MLI
4.2. Co-Optimization of MLI-LNCS Scheme
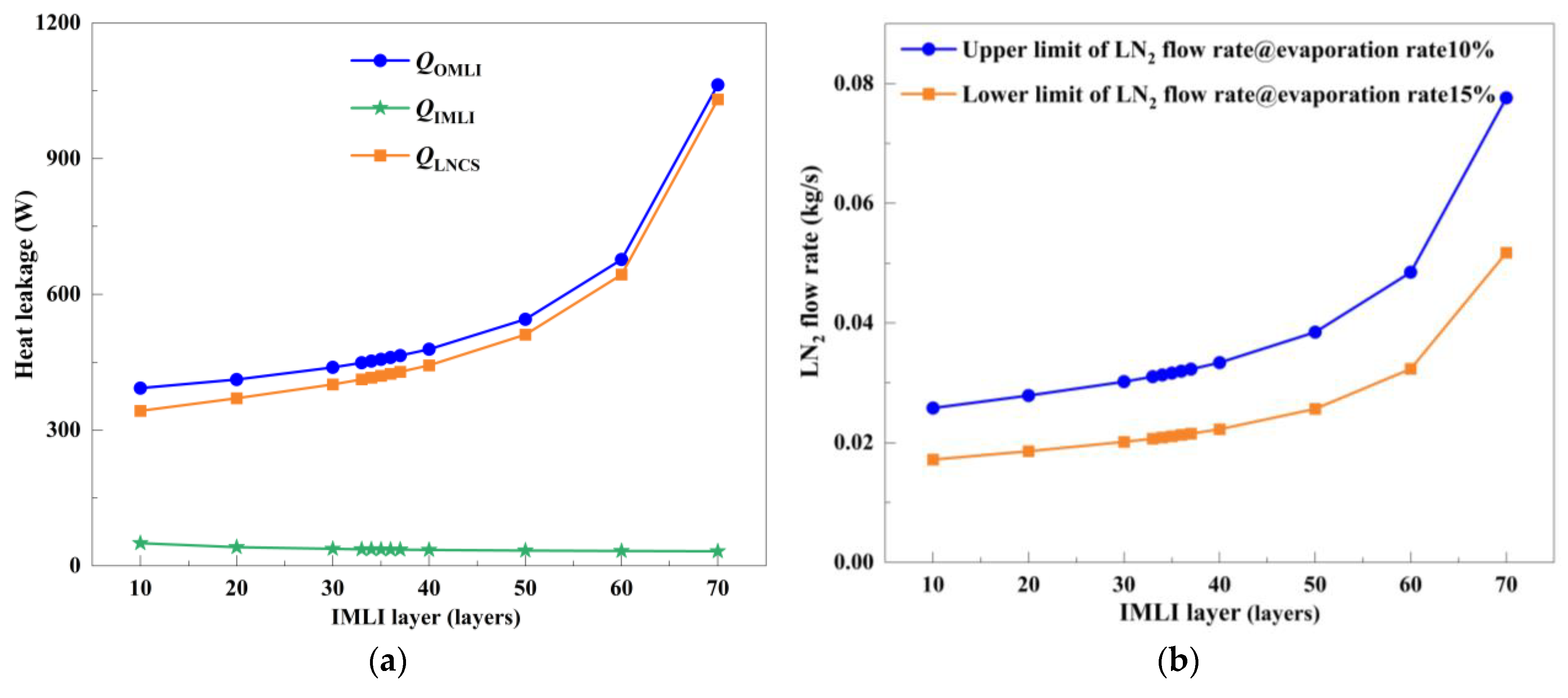
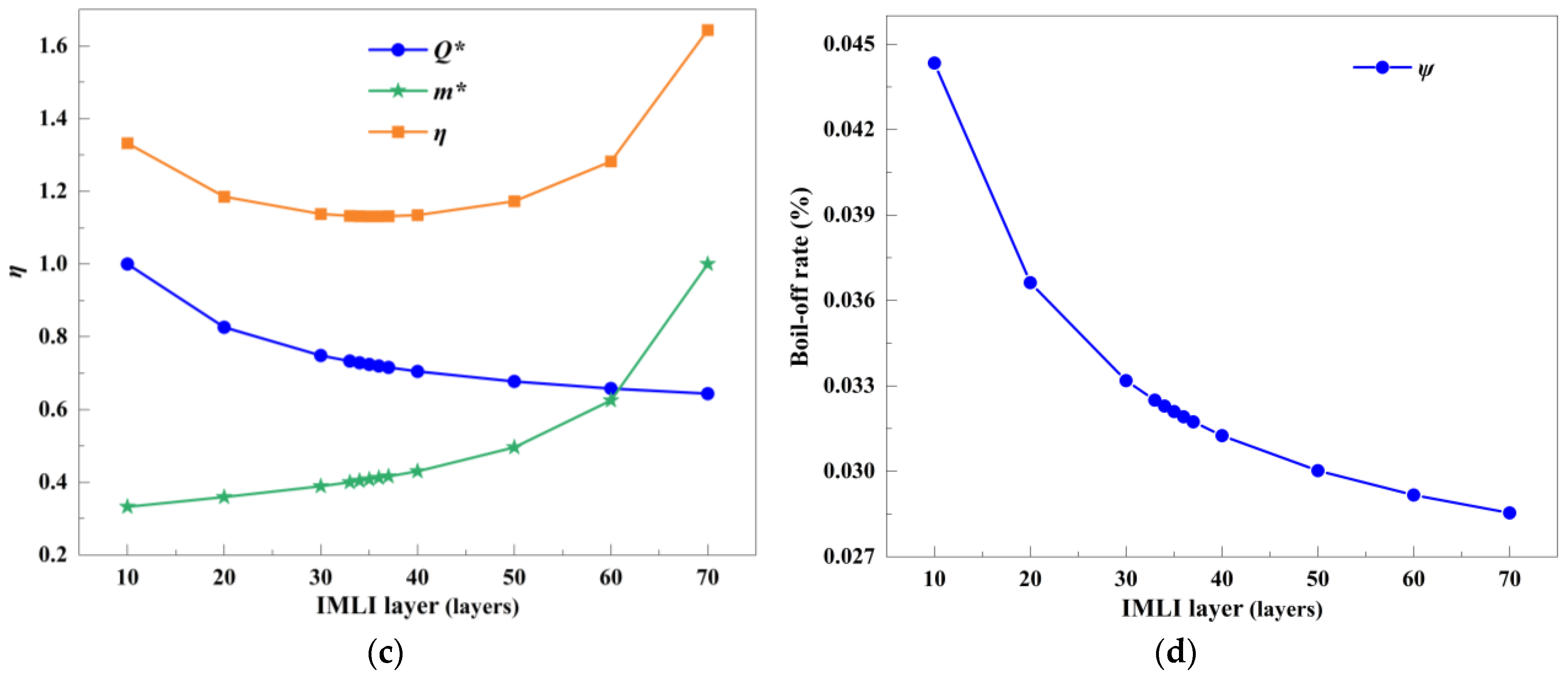
4.2.1. Optimization of IMLI-Layer Count Based on Initial LNCS Position
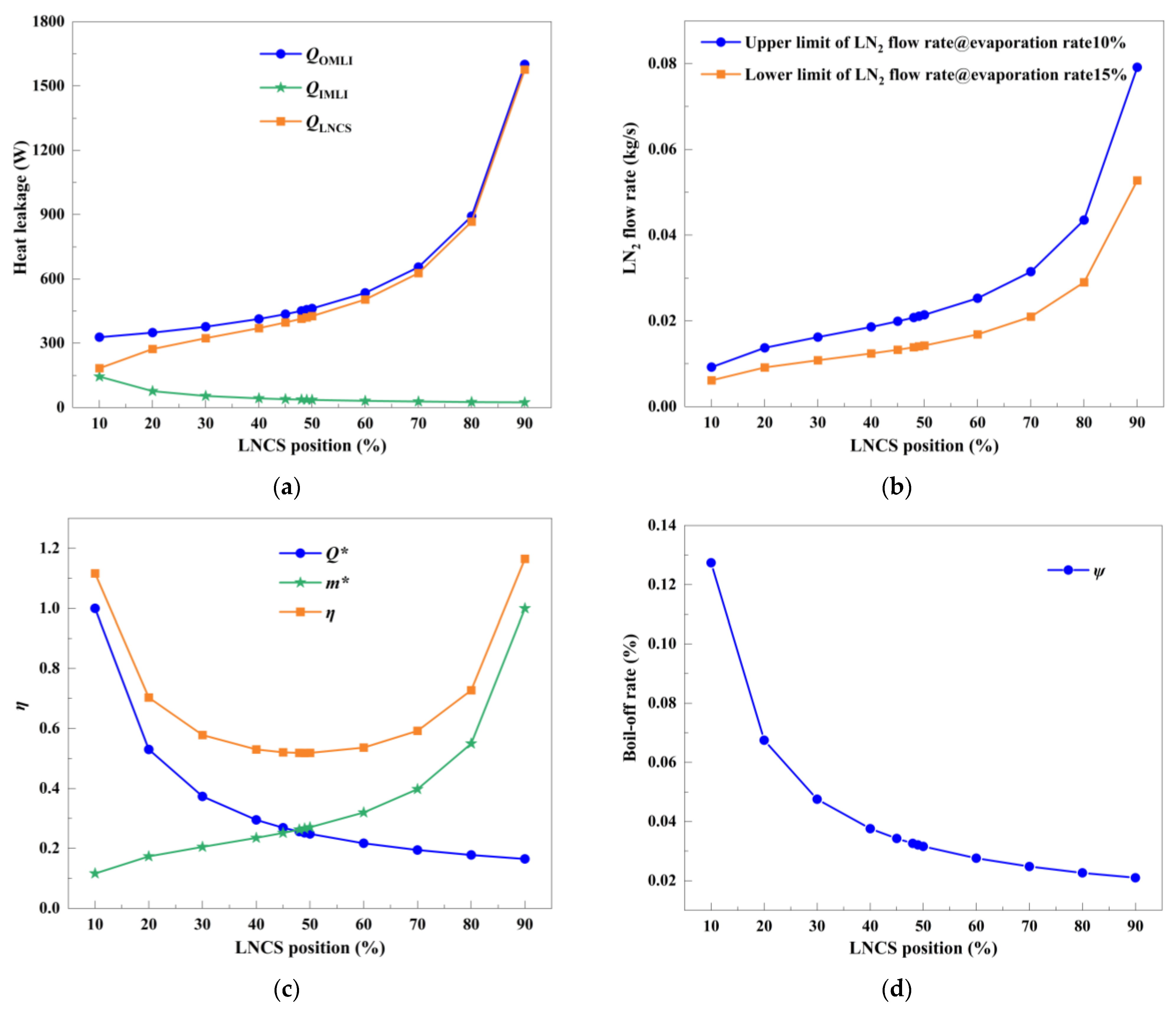
4.2.2. Optimization of LNCS Position Based on IMLI Layer Count
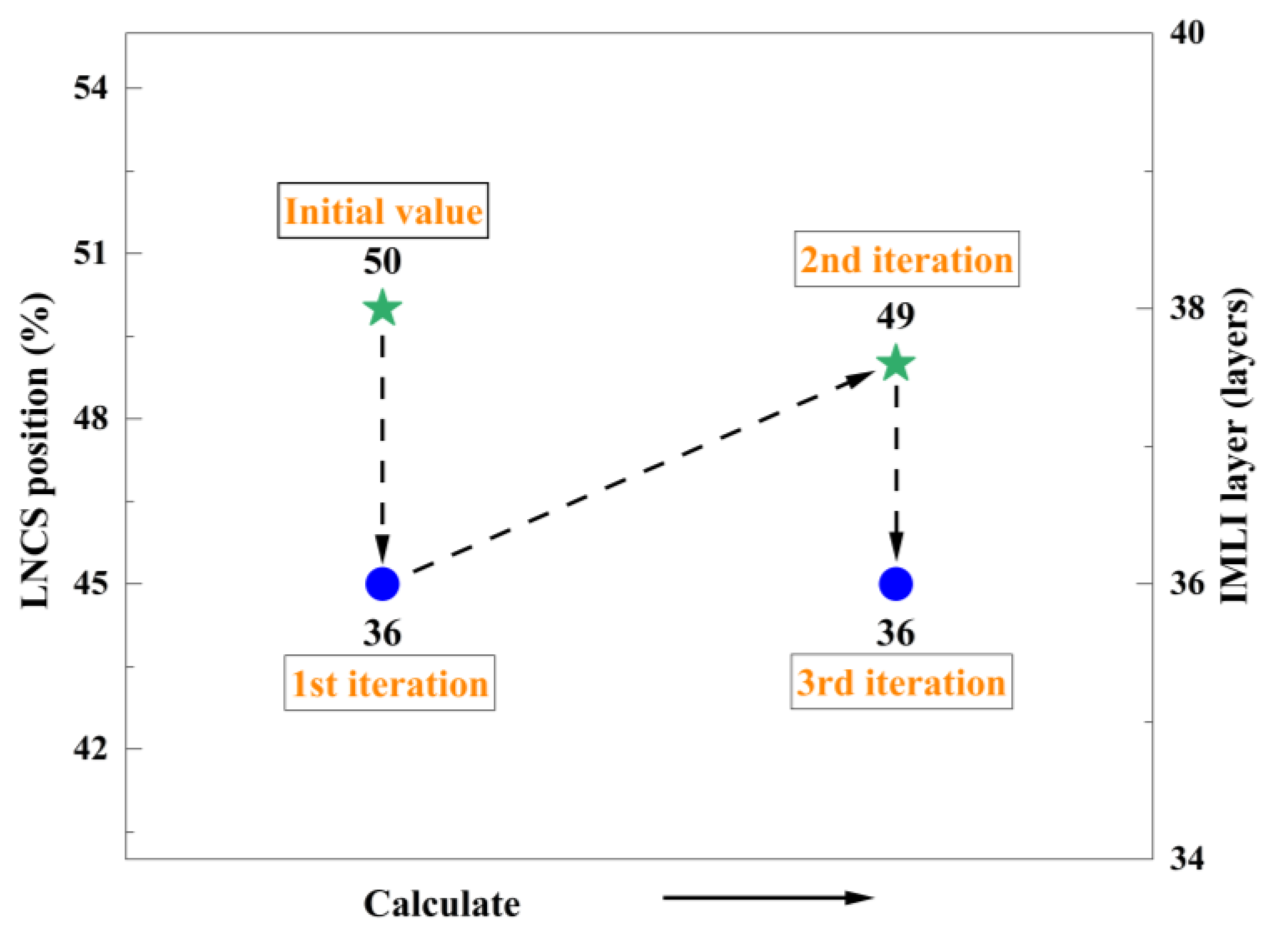
4.2.3. Co-Optimization of IMLI Layer Count and LNCS Position
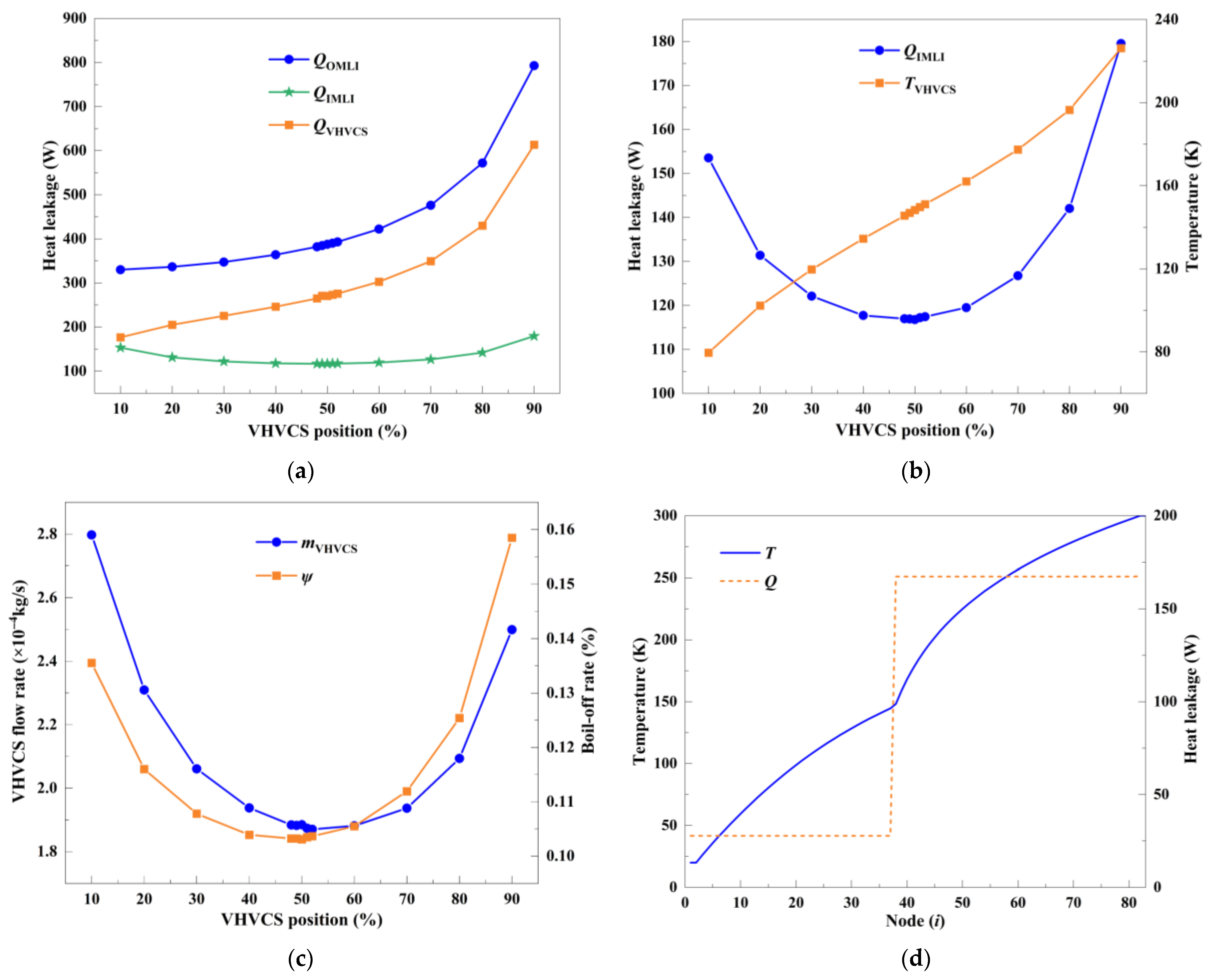
4.3. Co-Optimization of MLI-VHVCS Scheme
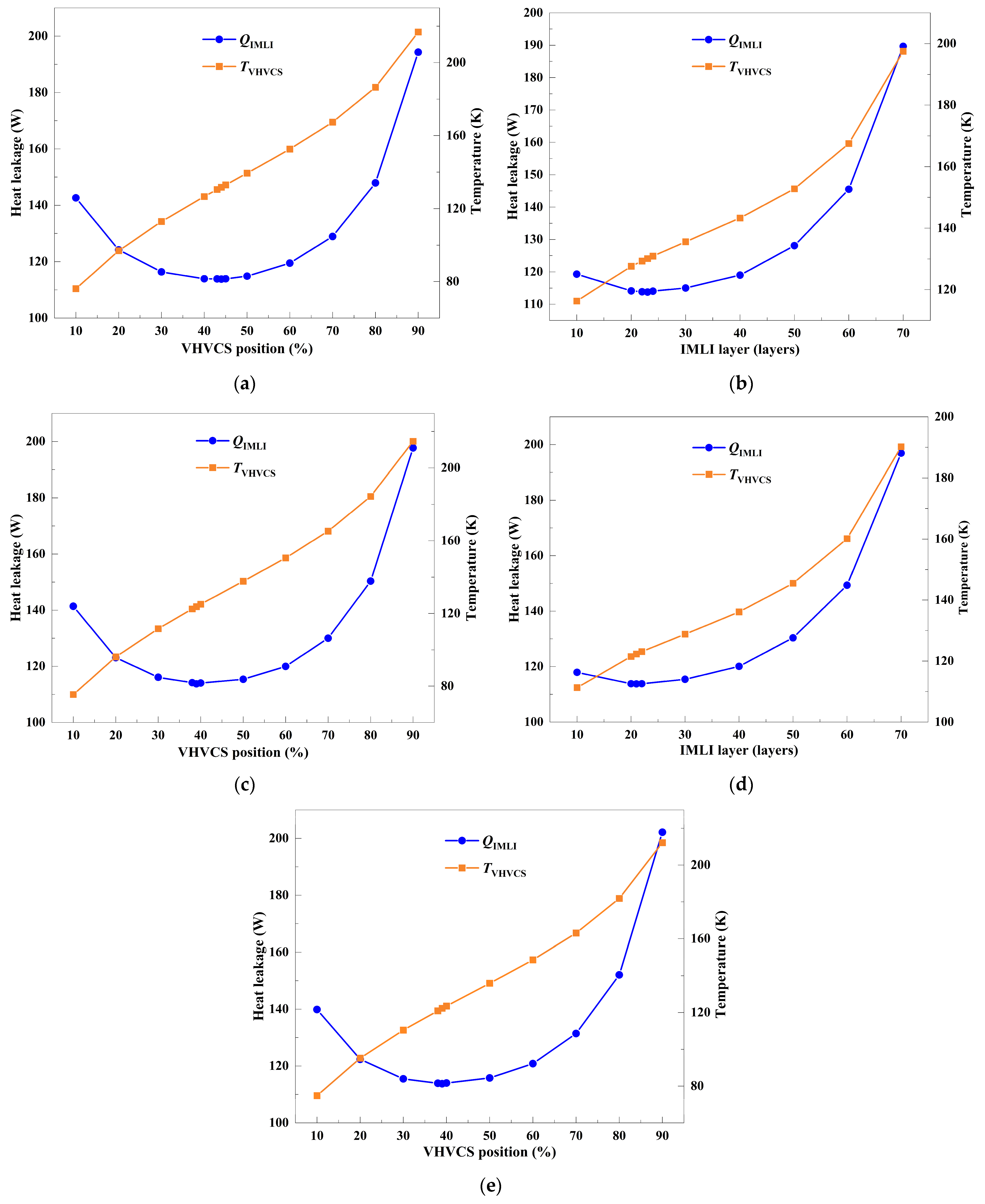
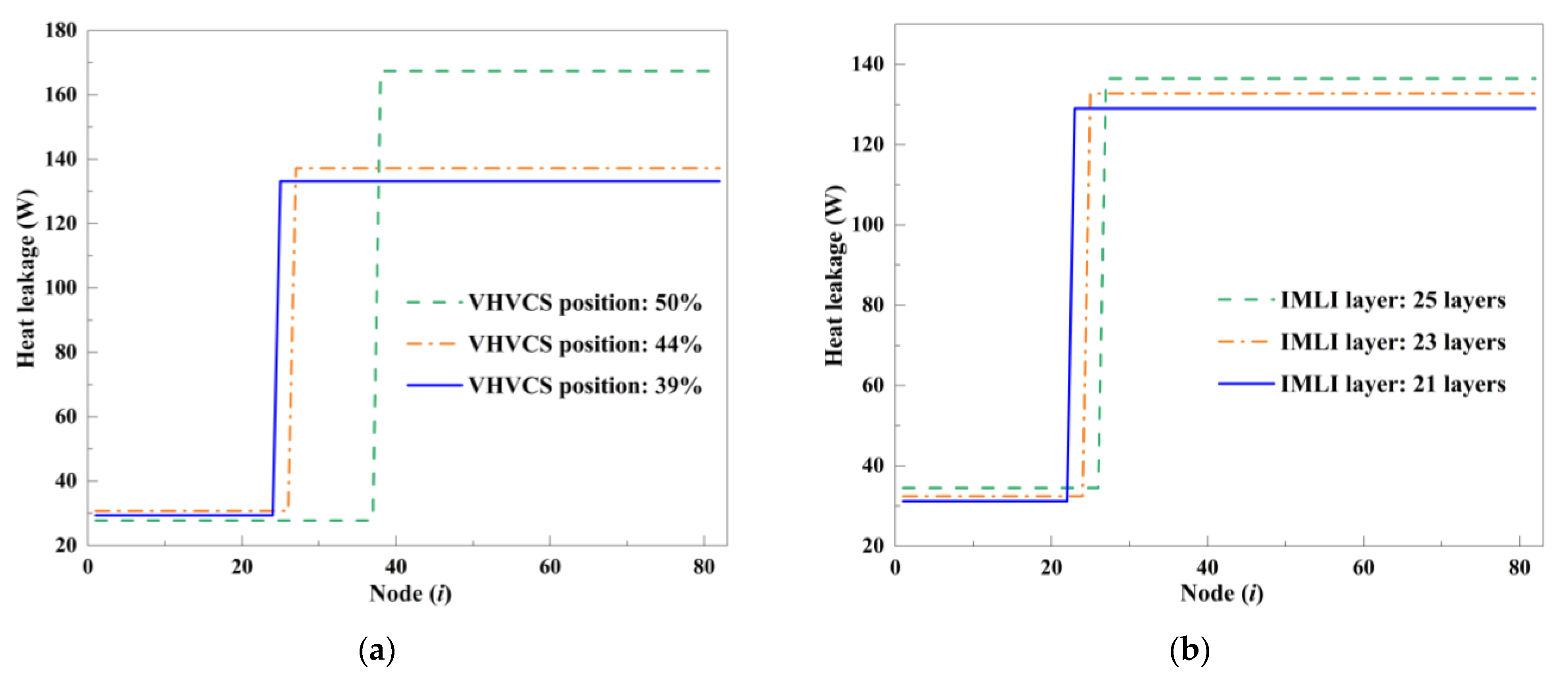
4.3.1. Iterative Co-Optimization of VHVCS Position and IMLI Layer Count
- (1)
- First iteration step
- (2)
- Second iteration step
- (3)
- Iteration steps three to seven
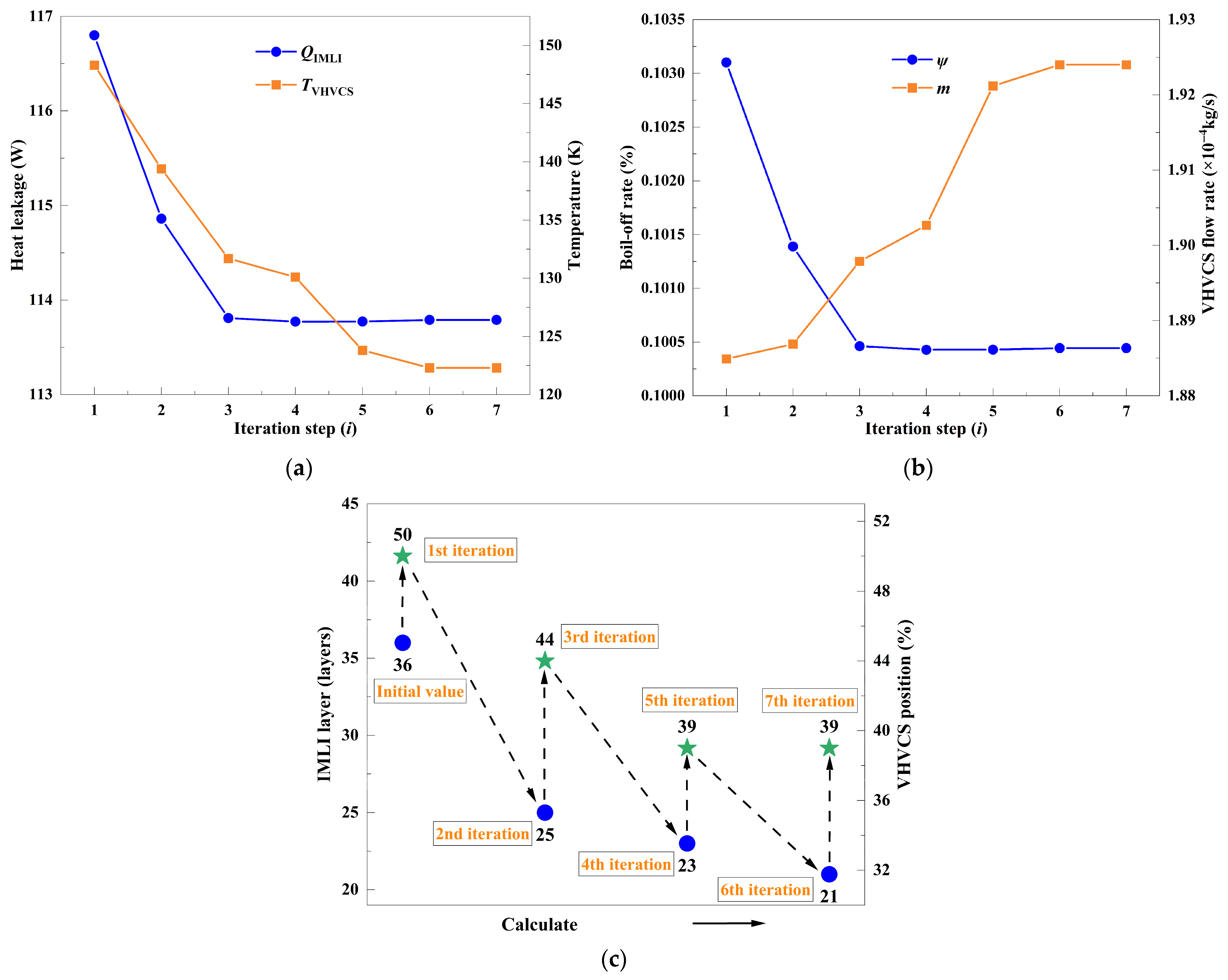
4.3.2. Convergence Characteristics of Co-Optimization Process
4.3.3. Evolution of Heat Leakage and MLI Temperature Distribution
4.4. Comparison of Three Insulation Schemes
5. Conclusions
- (1)
- The established model demonstrated good performance in predicting the thermal performance of MLI insulation under LH2 temperature conditions. The relative deviations between the calculated values and experimental values are within 5%. The thermal resistance of the insulation scheme gradually decreases from the inner side to the outer side. A significant temperature gradient is observed near the cold boundary, while the gradient becomes more moderate near the warm boundary.
- (2)
- For the MLI-LNCS scheme, the optimal number of IMLI layers is 36, with the optimal LNCS position installed at 49% of the interlayer space. For the MLI-VHVCS scheme, the optimal number of IMLI layers is 21, and the corresponding optimal VHVCS installation position is identified at 39%.
- (3)
- Compared to the conventional MLI scheme, the MLI-LNCS scheme reduces heat leakage by 88.09%. However, the LN2 circulation system results in high operational costs. The MLI-VHVCS scheme achieves a 62.74% reduction in heat leakage, demonstrating that harnessing the sensible cooling capacity of cryogenic vapor effectively enhances the thermal insulation performance of LH2 storage tanks. Although the MLI-LNCS scheme provides a 68.04% reduction in heat leakage compared to the MLI-VHVCS scheme, the latter proves more favorable when considering economic considerations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| LT | length of the tank, m | Q* | dimensionless heat leakage |
| QMLI | heat leakage through the MLI, W | m* | dimensionless mass flow rate |
| σ | Stephan–Boltsman constant | η | dimensionless evaluation parameter |
| ε(T) | emissivity of the radiation shield | λH | conductivity at hot boundary, W/(m·K) |
| T1 | inner-surface temperature of inner tank, K | λL | conductivity at cold boundary, W/(m·K) |
| T2 | outer-surface temperature of inner tank, K | TACS | ACS temperature, K |
| Tn−1 | inner-surface temperature of outer tank, K | λACS | conductivity of acs, W/(m·K) |
| Tn | outer-surface temperature of outer tank, K | λamb | conductivity of air, W/(m·K) |
| C | empirical constant, 0.008 | Nu | Nusselt number |
| f | relative solid density | Re | Reynolds number |
| k | conductivity of spacer, W/(m·K) | Pr | Prandtl number |
| Ta | ambient temperature, 300 K | ψ | daily boil-off rate |
| p | vacuum pressure, Pa | ρ | LH2 density, kg/m3 |
| γ | specific heat ratio, γ = cp/cv | V | tank capacity, m3 |
| α | accommodation coefficient, 0.9 | LH2 | liquid hydrogen |
| RT | total thermal resistance, K/W | LN2 | liquid nitrogen |
| QOMLI | heat leakage through OMLI, W | MLI | multilayer insulation |
| QIMLI | heat leakage through IMLI, W | OMLI | outer-multilayer insulation |
| QACS | heat absorbed by ACS, W | IMLI | inner-multilayer insulation |
| m | mass flow rate, kg/s | ACS | active cooled shield |
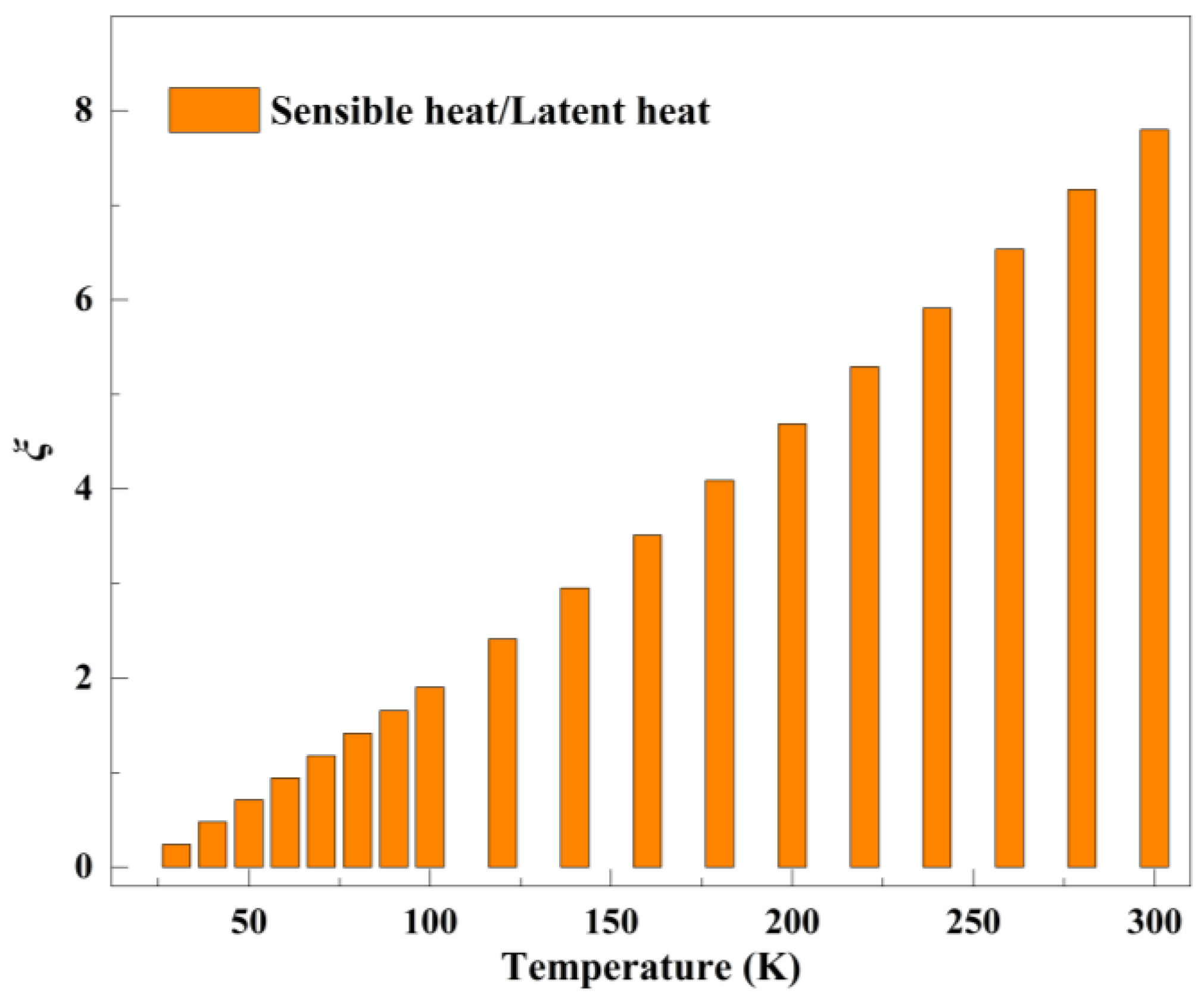
| ∆H | latent heat of vaporization, kJ/kg | LNCS | liquid-nitrogen cooled shield |
| QSEN | sensible heat of cryogenic vapor, J/kg | VHVCS | vapor-hydrogen cooled shield |
References
- Labidine Messaoudani, Z.; Rigas, F.; Hamid, M.D.B.; Hassan, C.R.C. Hazards, safety and knowledge gaps on hydrogen transmission via natural gas grid: A critical review. Int. J. Hydrogen Energy 2016, 41, 17511–17525. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y. IPCC 2021: Summary for policymakers. In Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Chen, C.; Li, C.; Reniers, G.; Yang, F. Safety and security of oil and gas pipeline transportation: A systematic analysis of research trends and future needs using WoS. J. Clean. Prod. 2021, 279, 123583. [Google Scholar] [CrossRef]
- Mahajan, D.; Tan, K.; Venkatesh, T.; Kileti, P.; Clayton, C.R. Hydrogen Blending in Gas Pipeline Networks: A Review. Energies 2022, 15, 3582. [Google Scholar] [CrossRef]
- Qadrdan, M.; Abeysekera, M.; Wu, J.; Jenkins, N.; Winter, B. The Future of Gas Networks. In The Role of Gas Networks in a Low Carbon Energy System; SpringerBriefs in Energy; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Kong, M.; Feng, S.; Xia, Q.; Chen, C.; Pan, Z.; Gao, Z. Investigation of mixing behavior of hydrogen blended to natural gas in gas network. Sustainability 2021, 13, 4255. [Google Scholar] [CrossRef]
- Seyam, S.; Dincer, I.; Agelin-Chaab, M. Economic and environmental impact assessments of hybridized aircraft engines with hydrogen and other fuels. Int. J. Hydrogen Energy 2022, 47, 11669–11685. [Google Scholar] [CrossRef]
- Harichandan, S.; Kar, S.K.; Bansal, R.; Mishra, S.K. Achieving sustainable development goals through adoption of hydrogen fuel cell vehicles in India: An empirical analysis. Int. J. Hydrogen Energy 2023, 48, 4845–4859. [Google Scholar] [CrossRef]
- Li, C.; Li, M.; Zheng, Y.; Fang, B.; Lin, J.; Ni, J.; Lin, B.; Jiang, L. Revealing hydrogen migration effect on ammonia synthesis activity over ceria-supported Ru catalysts. Appl. Catal. B Environ. 2023, 320, 121982. [Google Scholar] [CrossRef]
- Cherrad, N. Pumping of hydrogen by free heating for buildings supply from a safe storage bed. Therm. Sci. Eng. Prog. 2019, 13, 100370. [Google Scholar] [CrossRef]
- Cunnington, G.R.; Tien, G.L. A study of heat-transfer process in multiplayer insulation. In Progress in Astronautics and Aeronautics; Academic Press: New York, NY, USA, 1970; Volume 23, pp. 111–126. [Google Scholar]
- Jacob, S.; Kasthurirengan, S.; Karunanithi, R. Investigations into the thermal performance of multilayer insulation (300-77 K) Part 1: Calorimetric studies. Cryogenics 1992, 32, 1137–1146. [Google Scholar] [CrossRef]
- McIntosh, G.E. Layer by Layer MLI calculation using a seperated mode equation. In Advance in Cryogenic Engineering; Springer: Berlin/Heidelberg, Germany, 1994; Volume 39, pp. 1683–1690. [Google Scholar]
- Bapat, S.L.; Narayankhedkar, K.G.; Lukose, T.P. Performance prediction of multilayer insulation. Cryogenics 1990, 30, 700–710. [Google Scholar] [CrossRef]
- Krishnaprakas, C.K.; Narayana, K.B.; Dutta, P. Heat transfer correlations for multilayer insulation systems. Cryogenics 2000, 40, 431–435. [Google Scholar] [CrossRef]
- Daryabeigi, K. Heat transfer in high-temperature fibrous insulation. J. Thermophys. Heat Transf. 2003, 17, 10–20. [Google Scholar] [CrossRef]
- Johnson, W.L. Thermal Performance of Cryogenic Multilayer Insulation at Various Layer Spacings. Master’s Thesis, University of Central Florida Orlando, Orlando, FL, USA, 2010. [Google Scholar]
- Johnson, W. Thermal analysis of low layer density multilayer insulation test results. Adv. Cryog. Eng. 2012, 1314, 1519–1526. [Google Scholar]
- Wang, B.; Wang, H.; Gao, Y.; Yu, J.; He, Y.; Xiong, Z.; Lu, H.; Pan, Q.; Gan, Z. Theoretical analysis of entropy generation in multilayer insulations: A casestudy of performance optimization of variable density multilayerinsulations for liquid hydrogen storage systems. Int. J. Hydrogen Energy 2024, 85, 175–190. [Google Scholar] [CrossRef]
- Hastings, L.J.; Martin, J.J. Experimental testing of a foam/multilayer insulation (FMLI) thermal control system (TCS) for use on a cryogenic upper stage. Space Technol. Appl. Int. Forum. 1998, 420, 331–341. [Google Scholar]
- Li, K.; Chen, J.; Tian, X.; He, Y. Study on the performance of variable density multilayer insulation in liquid hydrogen temperature region. Energies 2022, 15, 9267. [Google Scholar] [CrossRef]
- Camplese, D.; Scarponi, G.E.; Chianese, C.; Hajhariri, A.; Eberwein, R.; Otremba, F.; Cozzani, V. Modeling the performance of multilayer insulation in cryogenic tanks undergoing external fire scenarios. Process Saf. Environ. Prot. 2024, 186, 1169–1182. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Hu, X.; Yang, S.; Zhang, C.; Guo, A.; Du, H. Validation of heat transfer models and optimization of heat shielding performance of high-temperature multilayer insulations for hypersonic vehicles. Appl. Therm. Eng. 2025, 258, 124840. [Google Scholar] [CrossRef]
- Rahman, A.A.; Wang, B.; Yu, J.; Gao, Y.; He, Y.; Jin, T.; Gan, Z. Machine learning approaches for the prediction of thermal performance of multilayer insulation materials at low temperatures. Appl. Therm. Eng. 2025, 264, 125527. [Google Scholar] [CrossRef]
- Yin, L.; Yang, H.; Ju, Y. Review on the key technologies and future development of insulation structure for liquid hydrogen storage tanks. Int. J. Hydrogen Energy 2024, 57, 1302–1315. [Google Scholar] [CrossRef]
- Tanaka, S. Transport of Liquid Helium. Low Temp. Eng. 1977, 5, 52–53. Available online: https://www.semanticscholar.org/paper/The-Transport-of-Liquid-Helium-Tanaka/87916b61ce707406b149662343498fb3aa85b317 (accessed on 20 September 2024). [CrossRef]
- Zheng, J.; Chen, L.; Wang, J.; Zhou, Y.; Wang, J. Thermodynamic modelling and optimization of self-evaporation vapor cooled shield for liquid hydrogen storage tank. Energy Convers. Manag. 2019, 184, 74–82. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Wang, P.; Zhang, J.; Wang, J.; Zhou, Y. A novel cryogenic insulation system of hollow glass microspheres and self-evaporation vapor-cooled shield for liquid hydrogen storage. Front. Energy 2019, 14, 570–577. [Google Scholar] [CrossRef]
- Jiang, W.B.; Zuo, Z.Q.; Huang, Y.H.; Wang, B.; Sun, P.J.; Li, P. Coupling optimization of composite insulation and vapor-cooled shield for onorbit cryogenic storage tank. Cryogenics 2018, 96, 90–98. [Google Scholar] [CrossRef]
- Syed, S.; Goyal, M.; Atrey, M.D. Optimum Design of Liquid Helium Dewar with Vapour Cooled Shields. Indian J. Cryog. 2016, 41, 63. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Wang, J.; Xi, X.; Zhu, H.; Zhou, Y.; Wang, J. Thermodynamic analysis and comparison of four insulation schemes for liquid hydrogen storage tank. Energy Convers. Manag. 2019, 186, 526–534. [Google Scholar] [CrossRef]
- Chen, L.B.; Zheng, J.P.; Wu, X.L.; Cui, C.; Zhou, Y.; Wang, J.J. Research of the cold shield in cryogenic liquid storage. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 278, p. 012194. [Google Scholar] [CrossRef]
- Chato, J.C.; Khodadadi, J.M. Optimization of cooled shields in cryogenic insulations. J. Heat Transfer. 1984, 106, 871–875. [Google Scholar] [CrossRef]
- Babac, G.; Sisman, A.; Cimen, T. Two-dimensional thermal analysis of liquid hydrogen tank insulation. Int. J. Hydrogen Energy 2009, 34, 6357–6363. [Google Scholar] [CrossRef]
- Kim, S.Y.; Kang, B.H. Thermal design analysis of a liquid hydrogen vessel. Int. J. Hydrogen Energy 2000, 25, 133–141. [Google Scholar] [CrossRef]
- Xu, Z.; Tan, H.; Wu, H. Performance comparison of multilayer insulation coupled with vapor cooled shield and different para-ortho hydrogen conversion types. Appl. Therm. Eng. 2023, 234, 12125. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Lee, J.H.; Kim, K.H.; Lim, C.H.; Lee, S.H. Coupled CFD modeling and thermal analysis of multi-layered insulation structures in liquid hydrogen storage tanks for various vapor-cooled shield. Case Stud. Therm. Eng. 2024, 63, 105317. [Google Scholar] [CrossRef]
- Sun, Z.; Li, M.; Qu, Z.; Tian, D.; Zhang, J. A quasi-2D thermodynamic model for performance analysis and optimization of liquid hydrogen storage system with multilayer insulation and vapor-cooled shield. J. Energy Storage 2023, 73, 109128. [Google Scholar] [CrossRef]
- Li, K.; Wen, J.; Wang, S. Insulation and cost optimization of vapor-cooled shield coupled with para-to-ortho hydrogen conversion based on self-pressurization model of liquid hydrogen tank and NSGA-II. J. Energy Storage 2024, 99, 113229. [Google Scholar] [CrossRef]
- Lv, H.; Zhang, Z.; Chen, L.; Zhang, Z.; Chen, S.; Hou, Y. Thermodynamic analysis of vapor-cooled shield with para-to-ortho hydrogen conversion in composite multilayer insulation structure for liquid hydrogen tank. Int. J. Hydrogen Energy 2024, 50, 1448–1462. [Google Scholar] [CrossRef]
- Li, K.; Wen, J.; Xin, B.; Zhou, A.; Wang, S. Transient-state modeling and thermodynamic analysis of self-pressurization liquid hydrogen tank considering effect of vacuum multi-layer insulation coupled with vapor-cooled shield. Energy 2024, 286, 129450. [Google Scholar] [CrossRef]
- Liang, J.; Li, C.; Ma, Y.; Liu, X.; Zhang, S.; Zhou, Z.; Li, Y. Study on transient thermal performance of coupled vapor-cooled shield insulation for liquid hydrogen tank during the on-orbit period. Appl. Therm. Eng. 2025, 266, 125665. [Google Scholar] [CrossRef]
- Leng, Y.; Zhang, S.; Wang, X.; Pu, L.; Xu, P. Comparative study on thermodynamic performance of liquid hydrogen storage insulation system incorporating vapor-cooled shield with para-ortho hydrogen conversion by one-dimensional and quasi-two-dimensional model. Energy Convers. Manag. 2024, 321, 119068. [Google Scholar] [CrossRef]
- Jiang, W.; Zuo, Z.; Sun, P.; Li, P.; Huang, Y. Thermal analysis of coupled vapor-cooling-shield insulation for liquid hydrogen-oxygen pair storage. Int. J. Hydrogen Energy 2022, 47, 8000–8014. [Google Scholar] [CrossRef]
- Shi, C.; Zhu, S.; Wan, C.; Bao, S.; Zhi, X.; Qiu, L.; Wang, K. Performance analysis of vapor-cooled shield insulation integrated with para-ortho hydrogen conversion for liquid hydrogen tanks. Int. J. Hydrogen Energy 2023, 48, 3078–3090. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, M.; Han, W.; Wu, Z.; Chen, S. Cold energy utilization analysis of cryogenic dual-energy heavy-duty trucks coupled LH2/LNG cooled shield. Int. J. Hydrogen Energy 2024, 71, 387–399. [Google Scholar] [CrossRef]
- Chen, C. Development of 300 m3 Liquid Hydrogen Storage Tank for Transportation Vehicle; Harbin Industrial University: Harbin, China, 2014. [Google Scholar]
- Corruccini, R.J. Gaseous heat conduction at low pressures and temperatures. Vacuum 1959, 7, 19–29. [Google Scholar] [CrossRef]
- Xu, J.; Liu, F.A.; Zhang, J.; Li, C.; Liu, Q.; Li, C.; Jia, W.; Fu, S.; Li, L. Numerical Study on Heat Leakage, Thermal Stratification, and Self-Pressurization Characteristics in Liquid Helium Storage Tanks. Energies 2024, 17, 6254. [Google Scholar] [CrossRef]
- Stochl, R.J. Basic Performance of a Multilayer Insulation System Containing 20 to 160 Layers; NASA TN D-7659; National Aeronautics and Space Administration: Washington, DC, USA, 1974.







| Basic Parameters | Cold-Boundary Temperature (K) | Hot-Boundary Temperature (K) | Wind Speed (m/s) | MLI Layer Count (Layers) | MLI Layer Density (Layers/cm) |
|---|---|---|---|---|---|
| 20 | 300 | 7.717 | 80 | 25 |
| Path | Literature—Chen | Emissivity: 0.05 | Emissivity: Exponential Equation |
|---|---|---|---|
| Insulation heat leakage (%) | 29.92 | 30.43 | 39.21 |
| Support-structure heat leakage (%) | 68.59 | 68.11 | 59.52 |
| Pipeline-system heat leakage (%) | 1.49 | 1.46 | 1.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Chen, L.; Zhou, X. Thermodynamic Modeling of Multilayer Insulation Schemes Coupling Liquid Nitrogen Cooled Shield and Vapour Hydrogen Cooled Shield for LH2 Tank. Processes 2025, 13, 2574. https://doi.org/10.3390/pr13082574
Lu J, Chen L, Zhou X. Thermodynamic Modeling of Multilayer Insulation Schemes Coupling Liquid Nitrogen Cooled Shield and Vapour Hydrogen Cooled Shield for LH2 Tank. Processes. 2025; 13(8):2574. https://doi.org/10.3390/pr13082574
Chicago/Turabian StyleLu, Jingyang, Liqiong Chen, and Xingyu Zhou. 2025. "Thermodynamic Modeling of Multilayer Insulation Schemes Coupling Liquid Nitrogen Cooled Shield and Vapour Hydrogen Cooled Shield for LH2 Tank" Processes 13, no. 8: 2574. https://doi.org/10.3390/pr13082574
APA StyleLu, J., Chen, L., & Zhou, X. (2025). Thermodynamic Modeling of Multilayer Insulation Schemes Coupling Liquid Nitrogen Cooled Shield and Vapour Hydrogen Cooled Shield for LH2 Tank. Processes, 13(8), 2574. https://doi.org/10.3390/pr13082574





