Analytical Prediction of Fatigue Life for Roller Bearings Considering Impact Loading
Abstract
1. Introduction
2. Theoretical Analysis
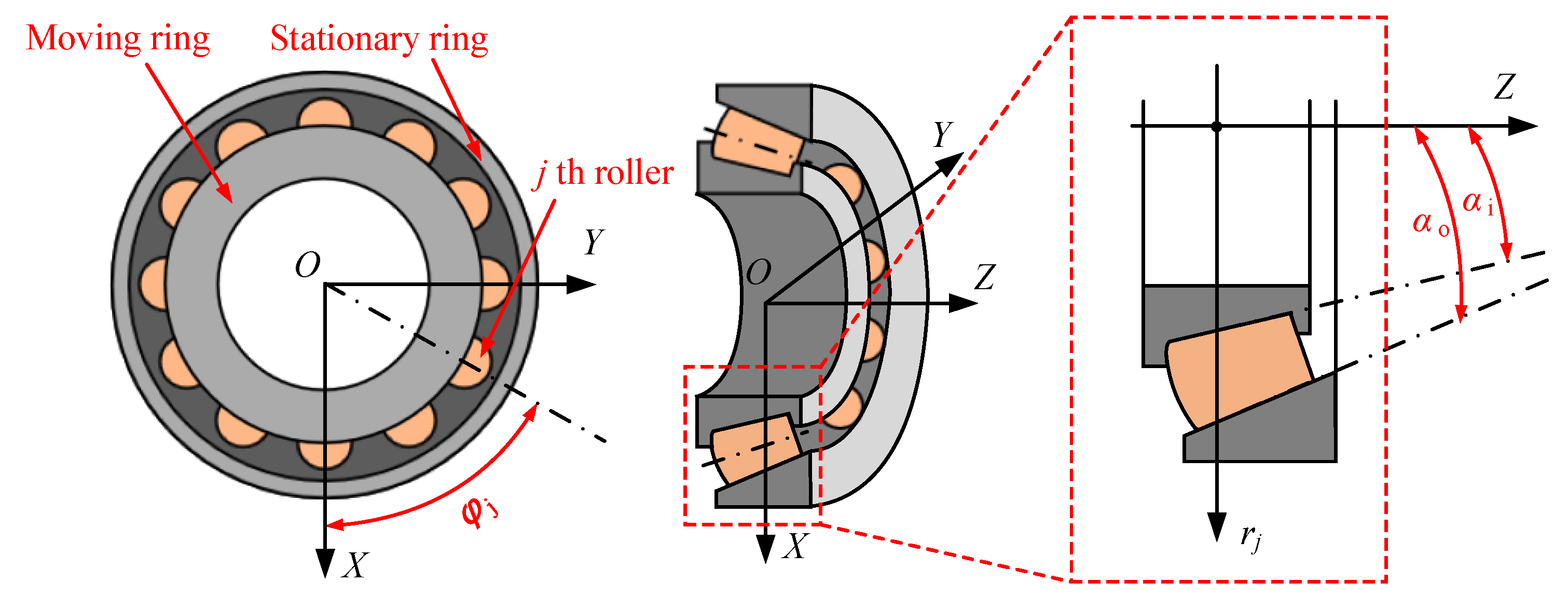
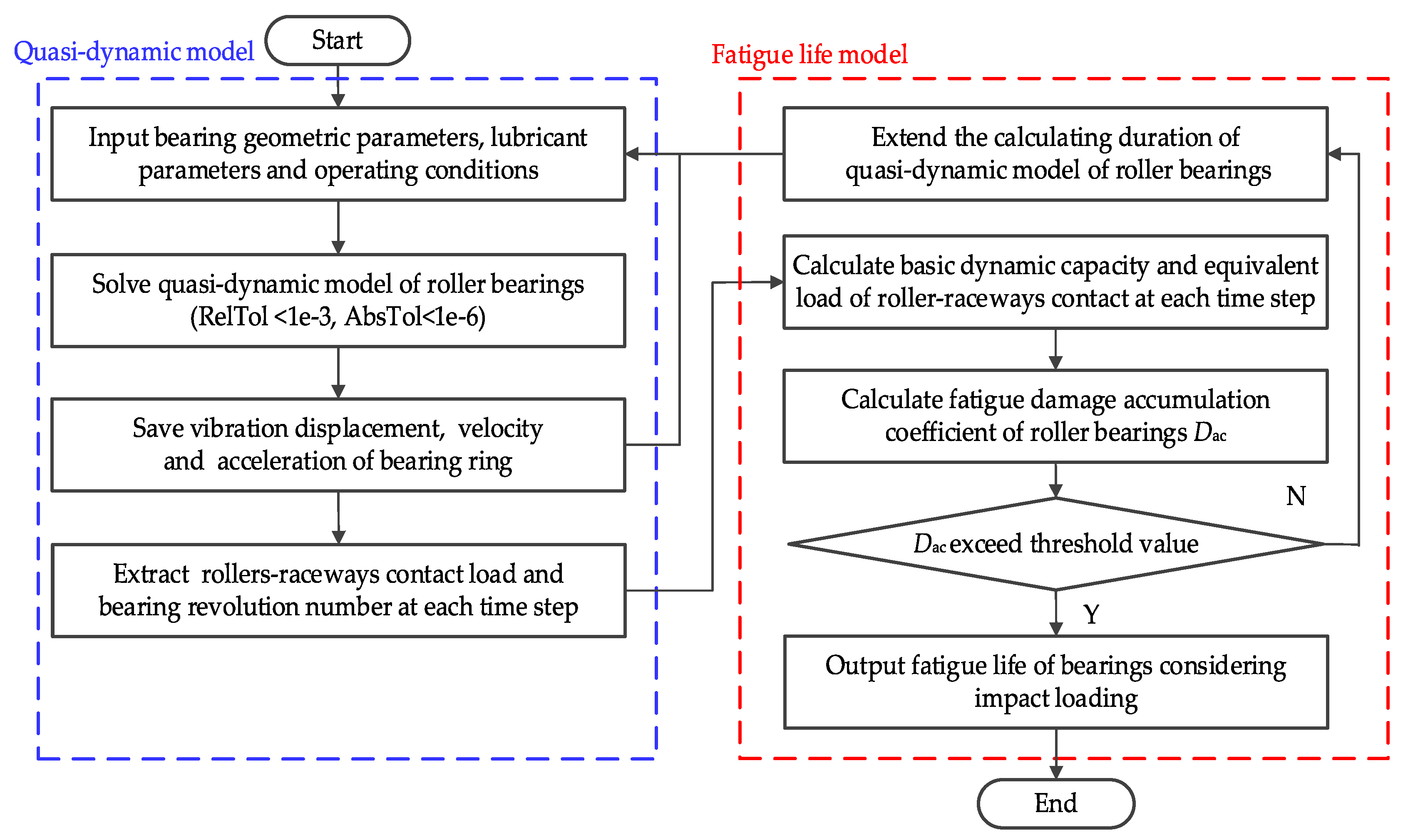
2.1. Quasi-Dynamic Model of Roller Bearings
2.2. Fatigue Life Model of Roller Bearings
3. Results and Discussion
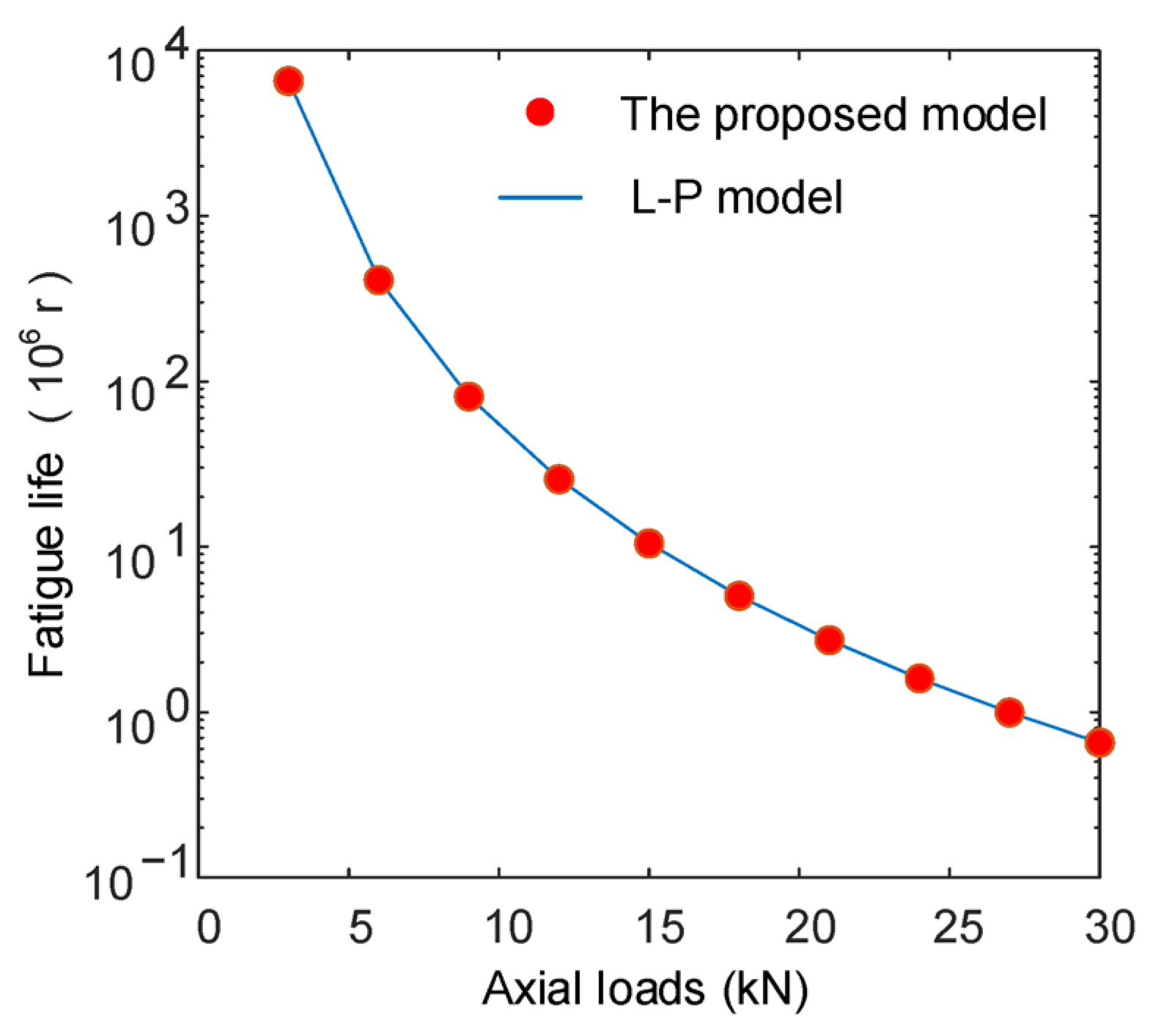
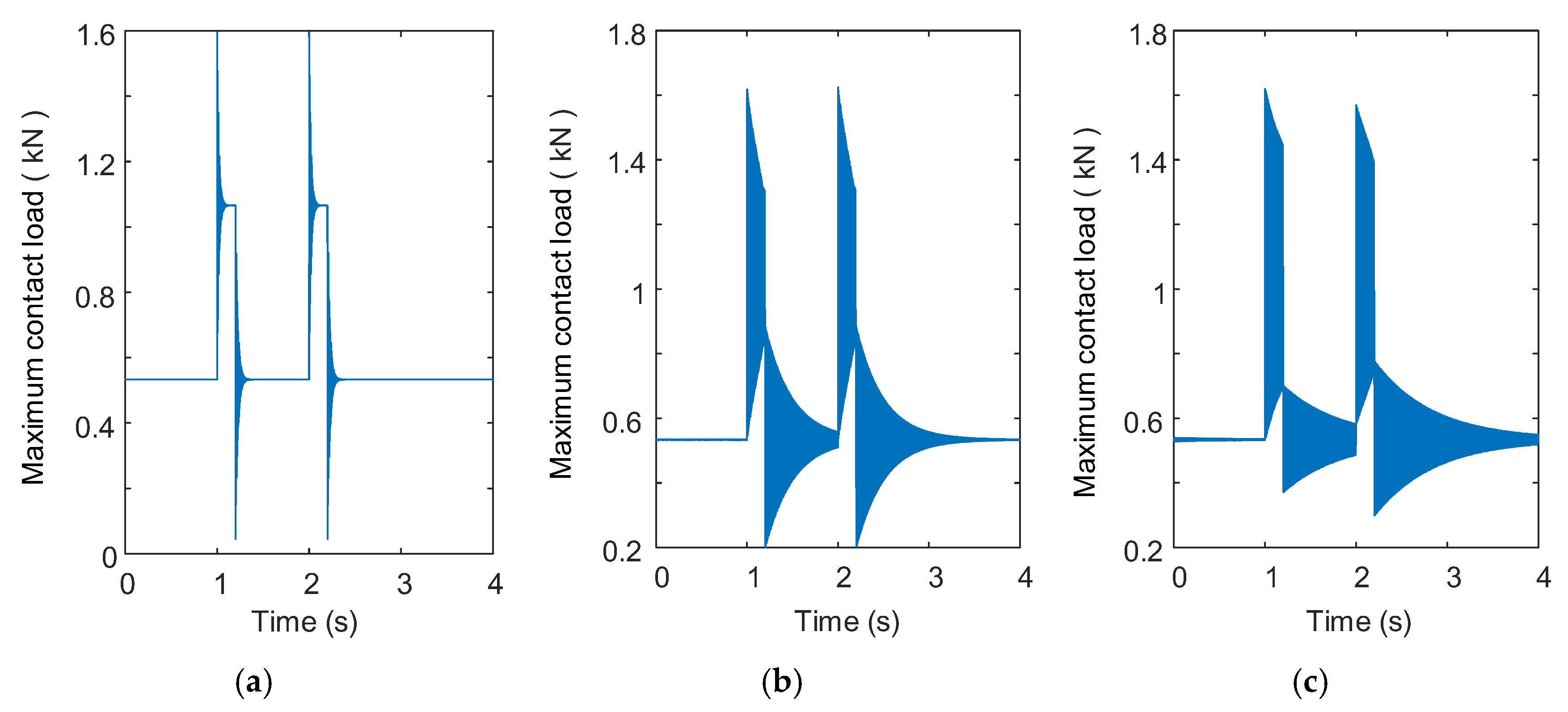
3.1. Comparison Analysis and Model Validation
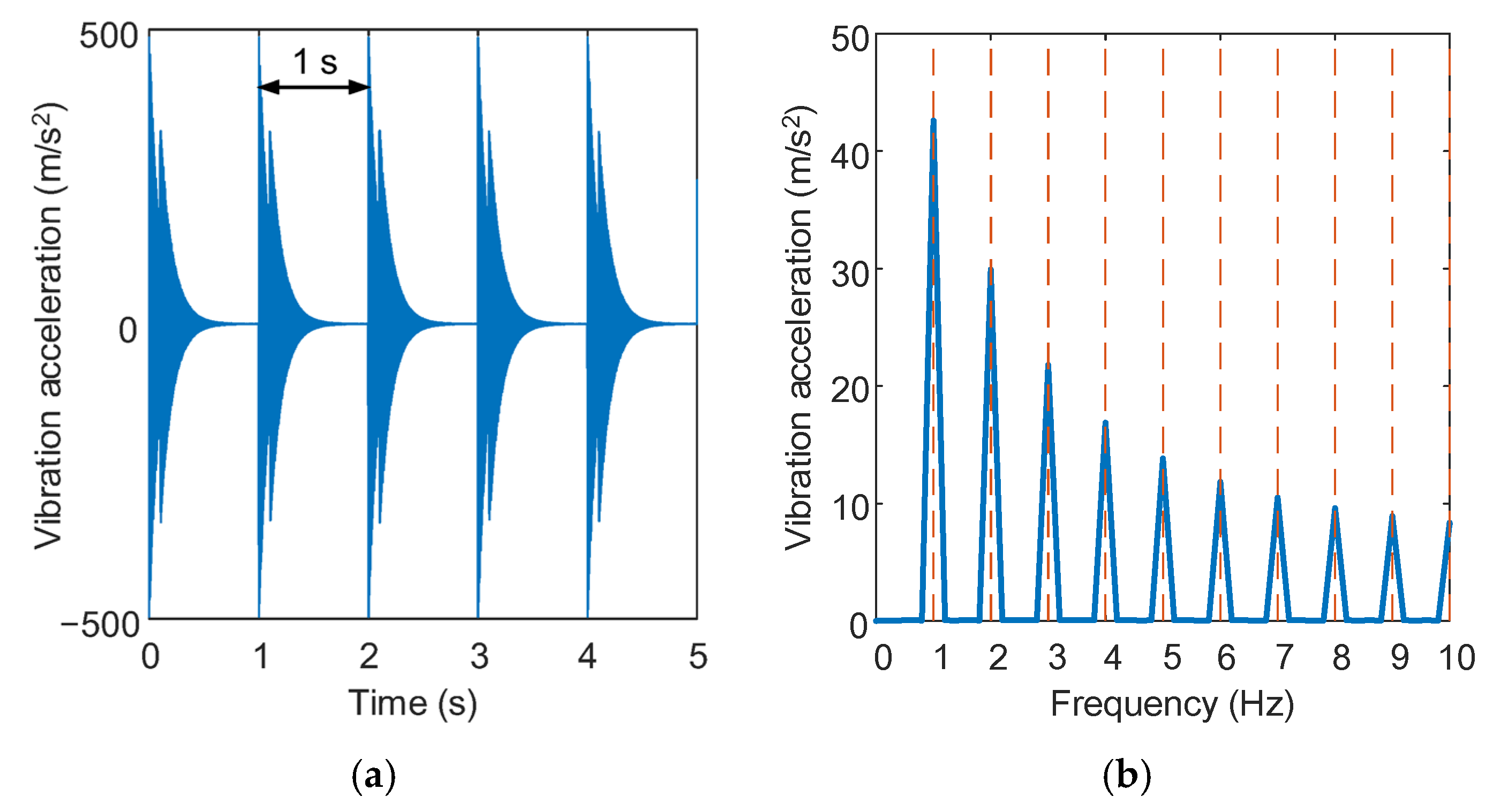
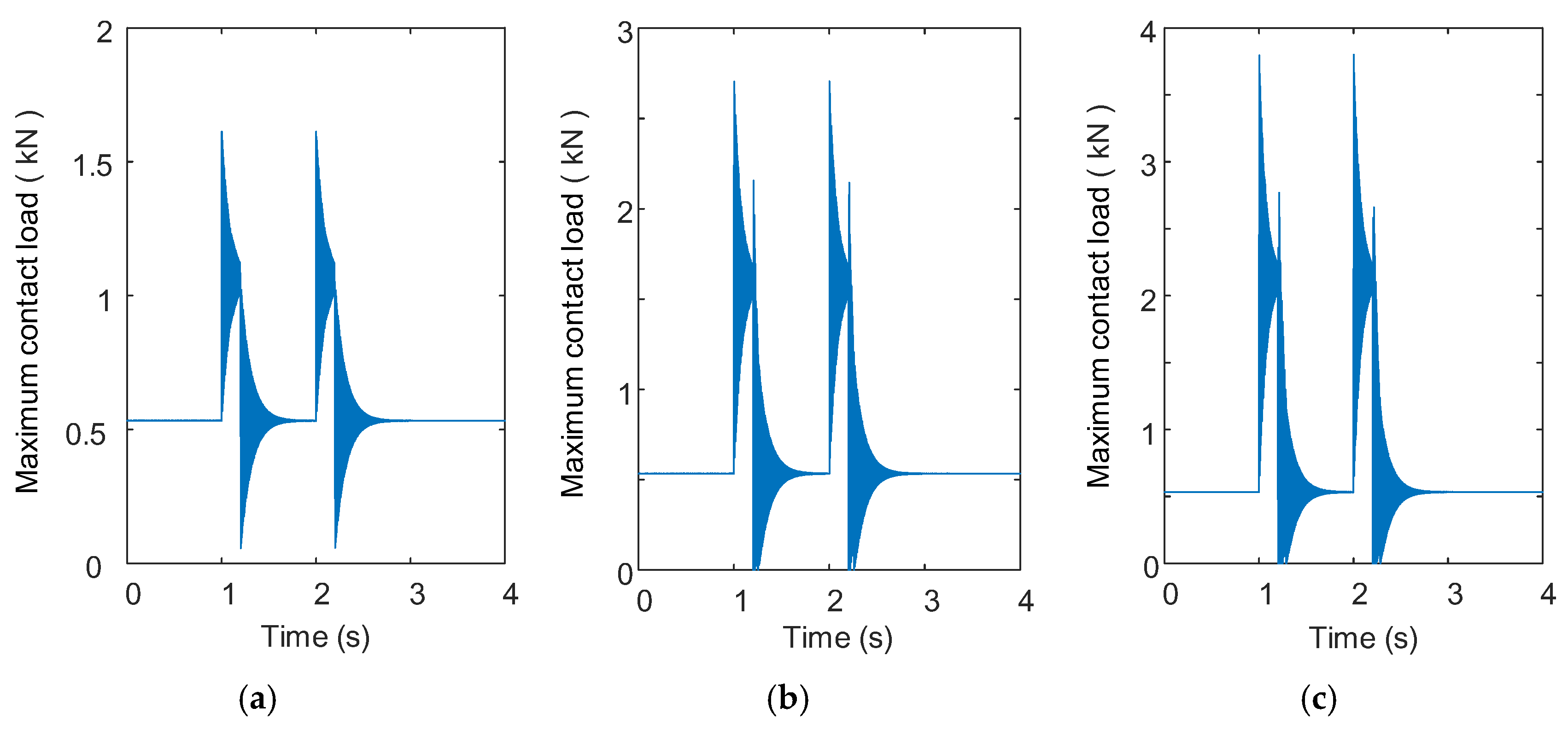
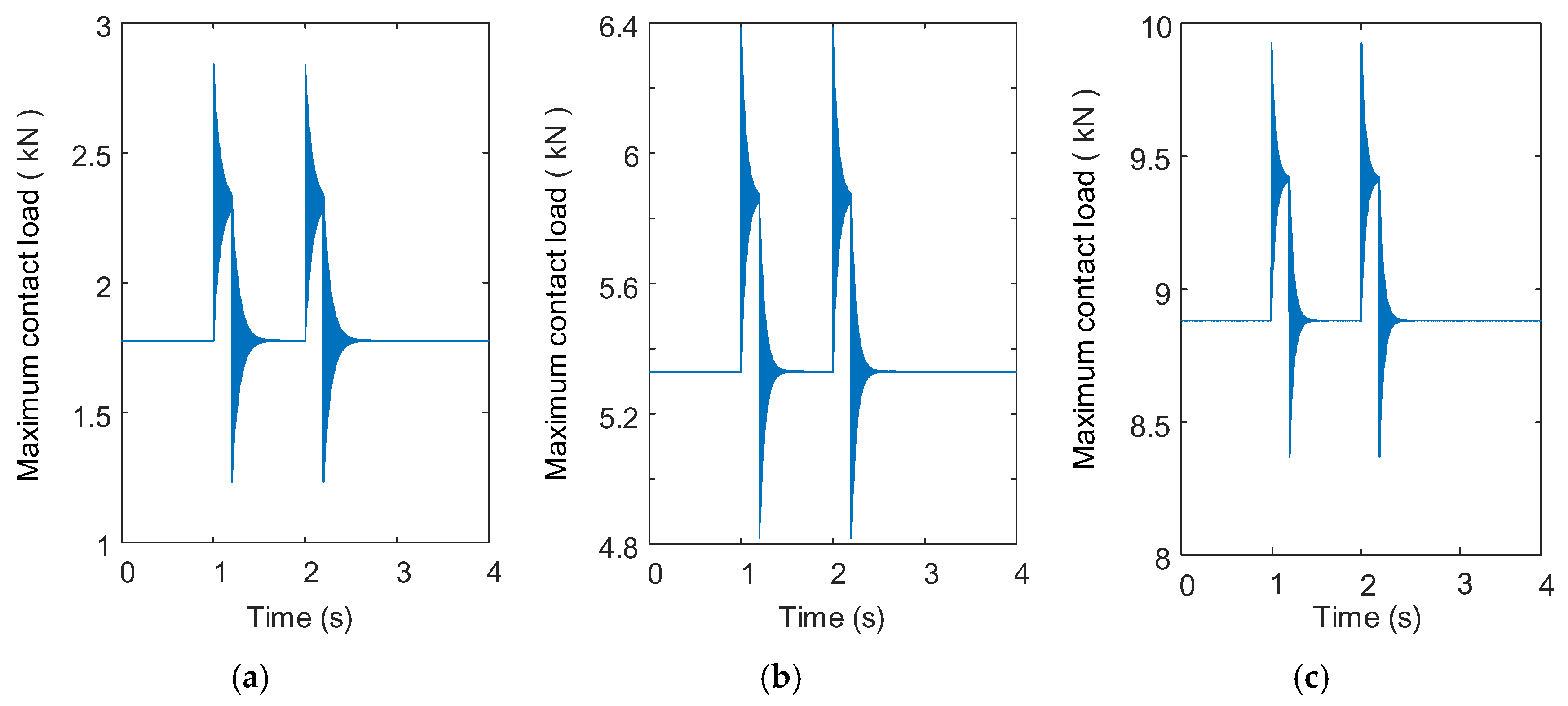
3.2. Instantaneous Fluctuation in Contact Load Considering Impact Loading
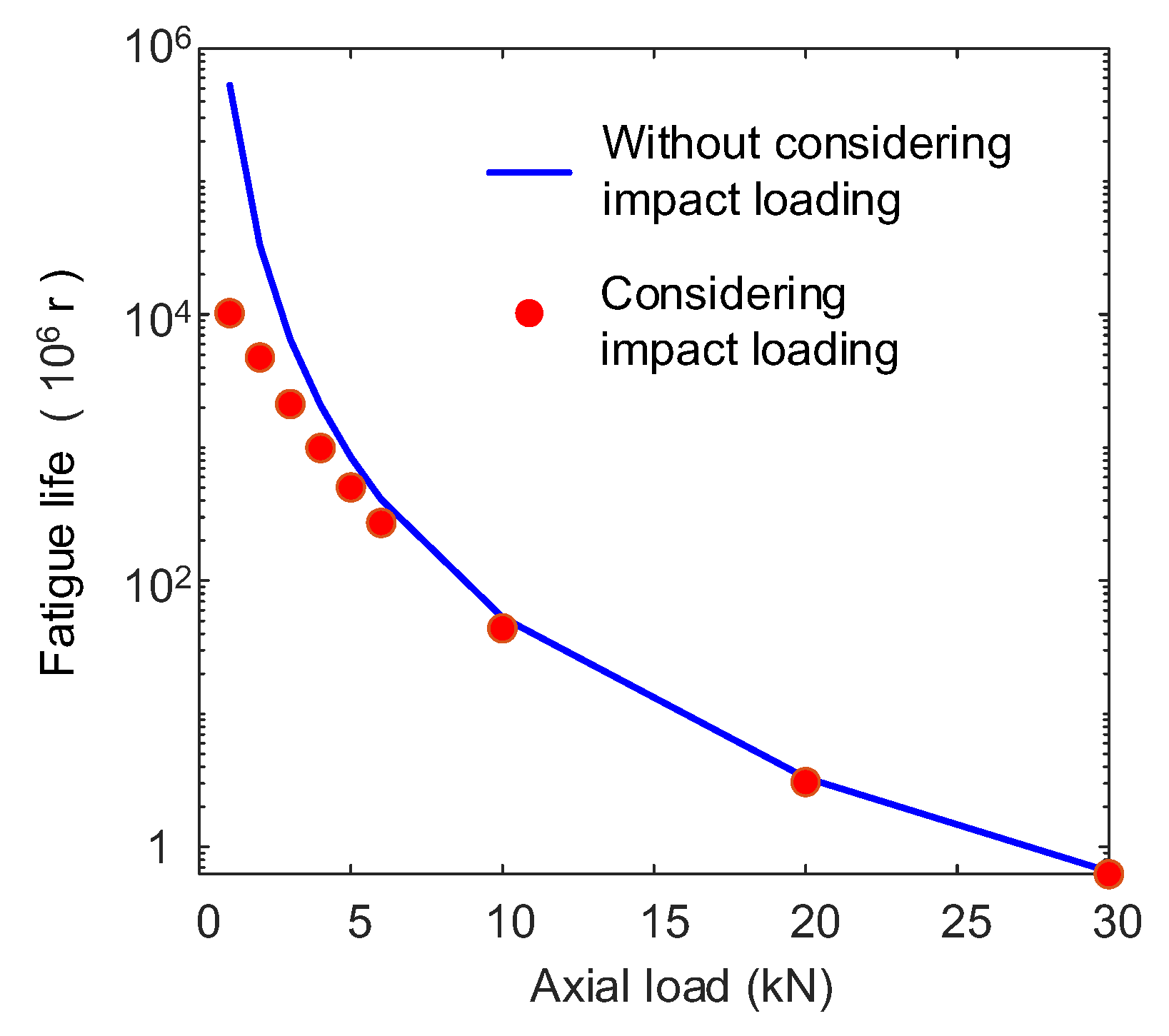
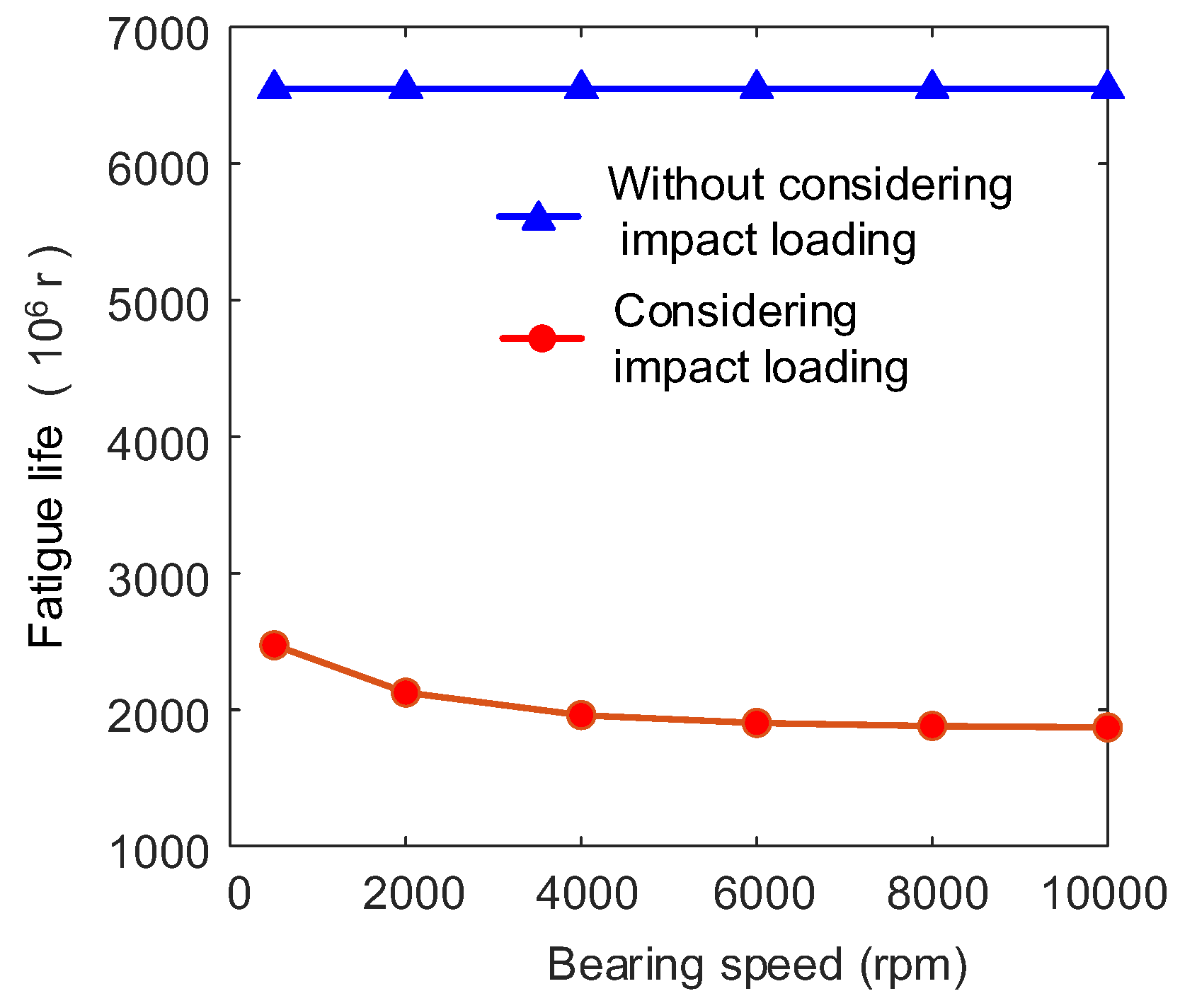
3.3. Fatigue Life of Roller Bearings Considering Impact Loading
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | Oil film damping factor between roller and raceways (N·s/m) |
| cx, cy, cz | Integrated damping of bearing (N·s/m) |
| dm | Pitch diameter of bearing (m) |
| D | Mean diameter of roller (m) |
| Dac | Fatigue damage accumulation coefficient (1) |
| E′ | Equivalent elastic modulus between roller and raceway (N/m2) |
| Fdjo | Oil film damping force between jth roller and outer ring (N) |
| Fx, Fy, Fz | External loads acting on bearing (N) |
| hc | Center oil film thickness between roller and raceway (m) |
| kx, ky, kz | Integrated stiffness of bearing (N/mm) |
| K | Contact stiffness factor between roller and raceways (N/mm10/9) |
| Lk | Potential fatigue life corresponding to the roller–raceways contact load in kth time step (r) |
| Lo, Li | Roller and outer raceway contact fatigue life (r) |
| Li | Roller and inner raceway contact fatigue life (r) |
| m | Quality of inner ring (kg) |
| n | Bearing speed (r/min) |
| nk | Bearing speed in kth time step (r/min) |
| nr | Number of rollers inside bearing (1) |
| Qc | Basic dynamic capacity for roller–raceway contact (N) |
| Qe | Equivalent load for roller–raceway contact (N) |
| Qei | Equivalent load for roller–inner raceway contact (N) |
| Qeo | Equivalent load for roller–outer raceway contact (N) |
| Qji | Contact load between jth roller and inner raceway (N) |
| Qjo | Contact load between jth roller and outer ring (N) |
| R | Equivalent curvature radius between roller and raceway (m) |
| u | Entrainment velocity between roller and raceway (m/s) |
| ui | Entrainment velocity between roller and inner raceway (m/s) |
| uo | Entrainment velocity between roller and outer raceway (m/s) |
| vjo | Normal oil film extrusion speed between jth roller and outer raceway (m/s) |
| w | Contact load per unit length between roller and raceway (N/m) |
| x, y, z | Displacement of inner ring (m) |
| Velocity of inner ring (m/s) | |
| Acceleration of inner rings (m/s2) | |
| α | Mean contact angle between roller and raceways (rad) |
| αi | Roller–inner raceway contact angle (rad) |
| αo | Roller–outer raceway contact angle (rad) |
| α0 | Pressure–viscosity coefficient of the lubricant (m2/N) |
| γ | Geometry coefficients (1) |
| δjo | Elastic deformation between jth roller and outer raceway (mm) |
| Δt | Time step size (s) |
| η0 | Lubricant viscosity in atmospheric conditions (Pa·s) |
| λ | Reduction factor for basic dynamic capacity (1) |
| φj | Angular position of jth roller after running time t (rad) |
| φj0 | Initial angular position of jth roller (rad) |
References
- Lundberg, G.; Palmgren, A. Dynamic capacity of rolling bearings. J. Appl. Mech. 1949, 16, 165–172. [Google Scholar] [CrossRef]
- Chiu, Y.P.; Tallian, T.E.; McCool, J.I. An engineering model of spalling fatigue failure in rolling contact: I. The subsurface model. Wear 1971, 17, 433–446. [Google Scholar] [CrossRef]
- Tallian, T. Weibull distribution of rolling contact fatigue life and deviations therefrom. A S L E Trans. 1962, 5, 183–196. [Google Scholar] [CrossRef]
- Ioannides, E.; Harris, T.A. A new fatigue life model for rolling bearings. J. Tribol. 1985, 107, 367–377. [Google Scholar] [CrossRef]
- Harris, T.A.; Mccool, J.I. On the accuracy of rolling bearing fatigue life prediction. J. Tribol. 1996, 118, 297–309. [Google Scholar] [CrossRef]
- ANSI/ABMA 9-2020; Load Ratings and Fatigue Life for Ball Bearings. American National Standards Institute (ANSI)/American Bearing Manufacturers Association (ABMA): New York, NY, USA, 2020.
- ANSI/ABMA 11-2020; Load Ratings and Fatigue Life for Roller Bearings. American National Standards Institute (ANSI)/American Bearing Manufacturers Association (ABMA): New York, NY, USA, 2020.
- ISO/TR 1281-1:2008; Rolling Bearings—Explanatory Notes on ISO 281—Part 1: Basic Dynamic Load Rating and Basic Rating Life. International Organization for Standardization (ISO): Geneva, Switzerland, 2008.
- ISO/TS 16281:2008; Rolling Bearings—Methods for Calculating the Modified Reference Rating Life for Universally Loaded Bearings. International Organization for Standardization (ISO): Geneva, Switzerland, 2008.
- ISO 281:2007; Rolling Bearings—Dynamic Load Ratings and Rating Life. International Organization for Standardization (ISO): Geneva, Switzerland, 2007.
- Oswald, F.B.; Zaretsky, E.V.; Poplawski, J.V. Effect of internal clearance on load distribution and life of radially loaded ball and roller bearings. Tribol. Trans. 2012, 55, 245–265. [Google Scholar] [CrossRef]
- Takahashi, K.; Nagatomo, T. Effects of axial clearance on surface initiated flaking in tapered roller bearings. J. Tribol. 2023, 145, 054301. [Google Scholar] [CrossRef]
- Fang, B.; Zhang, J. Analytical determination of the optimal clearance for the fatigue life of ball bearing under different load conditions. J. Tribol. 2022, 144, 021203. [Google Scholar] [CrossRef]
- Tong, V.C.; Hong, S.W. Fatigue life of tapered roller bearing subject to angular misalignment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 147–158. [Google Scholar] [CrossRef]
- Tong, V.C.; Hong, S.W. Analysis of the stiffness and fatigue life of double-row angular contact ball bearings. J. Korean Soc. Precis. Eng. 2017, 34, 813–821. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Wang, Y.; Xie, L. Fatigue life analysis of ball bearings and a shaft system considering the combined bearing preload and angular misalignment. Appl. Sci. 2020, 10, 2750. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, B.; Hong, J.; Zhu, Y. Effect of preload on ball-raceway contact state and fatigue life of angular contact ball bearing. Tribol. Int. 2017, 114, 365–372. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, T.; Deng, S. Combined analysis of stiffness and fatigue life of deep groove ball bearings under interference fits, preloads and tilting moments. J. Mech. Sci. Technol. 2023, 37, 539–553. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E.; Gabelli, A. A model for rolling bearing life with surface and subsurface survival: Surface thermal effects. Wear 2020, 460, 203446. [Google Scholar] [CrossRef]
- Kim, T.; Suh, J.; Lee, J.; Lee, B.; Yu, Y. Fatigue life prediction of double-row tapered roller bearings considering thermal effect. Adv. Mech. Eng. 2023, 15, 16878132231154099. [Google Scholar] [CrossRef]
- Zaretsky, E.V. Rolling Bearing Life Prediction, Theory, and Application. US Patent 1234567B1, 27 August 2020. [Google Scholar]
- Lee, J.G.; Palazzolo, A. Catcher bearing life prediction using a rainflow counting approach. J. Tribol. 2012, 134, 031101. [Google Scholar] [CrossRef]
- Yu, A.; Huang, H.; Li, Y.; Yang, W.; Deng, Z. A modified nonlinear fatigue damage accumulation model for life prediction of rolling bearing under variable loading conditions. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 852–864. [Google Scholar] [CrossRef]
- Cui, L. A new fatigue damage accumulation rating life model of ball bearings under vibration load. Ind. Lubr. Tribol. 2020, 72, 1205–1215. [Google Scholar] [CrossRef]
- Lei, Y.; Han, D.; Lin, J.; He, Z. Planetary gearbox fault diagnosis using an adaptive stochastic resonance method. Mech. Syst. Signal Process. 2013, 38, 113–124. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, W.; Yuan, L. Nonlinear vibroimpact characteristics of a planetary gear transmission system. Shock. Vib. 2016, 1, 4304525. [Google Scholar] [CrossRef]
- Li, X.; Gong, F.; Tao, M.; Dong, L.; Du, K.; Ma, C.; Zhou, Z.; Yin, T. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Bian, J.; Gu, Y.; Murray, M.H. A dynamic wheel–rail impact analysis of railway track under wheel flat by finite element analysis. Veh. Syst. Dyn. 2013, 51, 784–797. [Google Scholar] [CrossRef]
- Kwofie, S.; Rahbar, N. A fatigue driving stress approach to damage and life prediction under variable amplitude loading. Int. J. Damage Mech. 2013, 22, 393–404. [Google Scholar] [CrossRef]
- Harris, T.A. Essential Concepts of Bearing Technology, 5th ed.; Taylor & Francis: New York, NY, USA, 2008; pp. 134–136, 213–223. [Google Scholar]
- Dowson, D.; Higginson, G.R.; Nielsen, K.W. Elasto-hydrodynamic lubrication (International series in material, science and technology). J. Tribol. 1978, 100, 447. [Google Scholar] [CrossRef]
- Wen, S. Elastohydrodynamic Lubrication; Tsinghua University Press: Beijing, China, 1992; pp. 122–126. [Google Scholar]
- Harris, T.A. Advanced Concepts of Bearing Technology, 5th ed.; Taylor & Francis: New York, NY, USA, 2008; pp. 16–18. [Google Scholar]



| Geometrical Parameters | Value |
|---|---|
| Mean diameter of taper roller (m) | 6.49 × 10−3 |
| Pitch diameter of bearing (m) | 0.1872 |
| Effective length of roller (m) | 1.366 × 10−2 |
| Number of rollers | 23 |
| Contact angle between roller and outer raceway (rad) | 0.245 |
| Contact angle between roller and inner raceway (rad) | 0.195 |
| Contact angle between roller and flange (rad) | 1.562 |
| Taper angle of roller (rad) | 0.026 |
| Lubricant Parameters | Value |
| Viscosity in atmospheric conditions (Pa·s) | 3.7 × 10−2 |
| Pressure–viscosity coefficient (m2/N) | 2.2 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gong, H.; Li, Y.; Gao, Z.; Zhao, T. Analytical Prediction of Fatigue Life for Roller Bearings Considering Impact Loading. Processes 2025, 13, 2545. https://doi.org/10.3390/pr13082545
Liu Y, Gong H, Li Y, Gao Z, Zhao T. Analytical Prediction of Fatigue Life for Roller Bearings Considering Impact Loading. Processes. 2025; 13(8):2545. https://doi.org/10.3390/pr13082545
Chicago/Turabian StyleLiu, Yuwei, Haosen Gong, Yufei Li, Zehai Gao, and Tong Zhao. 2025. "Analytical Prediction of Fatigue Life for Roller Bearings Considering Impact Loading" Processes 13, no. 8: 2545. https://doi.org/10.3390/pr13082545
APA StyleLiu, Y., Gong, H., Li, Y., Gao, Z., & Zhao, T. (2025). Analytical Prediction of Fatigue Life for Roller Bearings Considering Impact Loading. Processes, 13(8), 2545. https://doi.org/10.3390/pr13082545






