1. Introduction
The evolution of robotic systems from structured industrial settings to unstructured and unknown environments—ranging from collaborative manufacturing to minimally invasive surgery—has necessitated advanced control paradigms capable of reconciling motion precision with safe, adaptive physical interaction. Traditional force control methods, such as impedance control (IC) and hybrid position/force control, have enabled robots to interact with partially modeled environments well by regulating contact forces through stiffness/damping adjustments. However, their fixed-parameter architectures are likely to fail when confronted with dynamic uncertainties inherent to real-world applications: composite materials with time-varying stiffness [
1,
2], collaborative tasks requiring human-like adaptability [
3], or biological tissues with nonlinear viscoelasticity [
4].
Adaptive impedance control (AIC) has emerged as a promising solution by allowing real-time tuning of impedance parameters—stiffness (K), damping (B), and inertia (M)—based on sensory feedback. Bridging classical impedance control with modern adaptive control theory [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15], AIC improves robustness and adaptability in uncertain environments.
In the realm of model-based AIC (MBAIC), many notable contributions have been made. For example, regressor-based adaptive control for manipulator–environment dynamics and model reference adaptive control for human–robot interaction scenarios targeted structured uncertainties in [
5,
6,
7], while regressor-free approaches employed function approximation techniques in [
8,
9] or disturbance observers in [
10] to handle nonlinearities and unknown external inputs. Notably, ref. [
9] addressed both model uncertainties and contact disturbances using universal approximators. More recently, adaptive laws with error iterative mechanisms in [
11] dynamically adjusted damping parameters, yielding promising steady-state tracking results. Recent studies evolved to address contact discontinuities, time-varying parameters, and unstructured environment uncertainties. For example, in [
12], adaptive force-based control was represented to manage unknown terrain reaction forces, payload variations, and unmodeled dynamics in real time. In [
13], an iterative stiffness adaptive method was developed for unknown terrain stiffness and geometry. Additionally, finite-time backstepping in [
14] handled time-varying disturbances, fast convergence, unknown environments, and abrupt force transitions. Ref. [
15] handled human-induced uncertainties, time-varying motion intentions, and interaction force variations in assistive tasks.
Despite these advances, MBAIC methods still face challenges in highly unstructured or dynamically evolving environments due to their reliance on accurate system models and sensitivity to parameter uncertainty. In particular, achieving both robust transient response and steady-state accuracy under unknown, time-varying contact conditions remains a critical open problem. These limitations have prompted a growing shift toward data-driven approaches, such as reinforcement learning and deep neural networks, which offer real-time adaptability without explicit model knowledge. This fusion of adaptive control theory and machine learning is expected to underpin the next generation of robotic systems, enabling greater versatility in domains ranging from autonomous assembly [
16] to limb rehabilitation [
17].
Several studies have explored hybrid architectures that combine model-based control principles with data-driven learning techniques to enhance adaptation in unknown environments. For instance, trajectory learning via iterative control [
18], reinforcement learning for endpoint tracking [
19], and impedance adaptation using integral reinforcement learning [
20] have shown promising results. Gradient-based impedance learning schemes were also explored in [
21]. However, these methods typically address either trajectory or force adaptation in isolation, offer limited analysis of force control performance, and often require manual tuning or are restricted to specific tasks. To some extent, these issues hinder their generalization to diverse or unseen contact scenarios. To further enhance adaptability in both free and constrained motion tasks, ref. [
22] introduced a fuzzy neural network within a broad learning framework, while [
23] proposed a reference adaptation approach using trajectory parameterization and iterative learning to balance tracking accuracy and force minimization. Although effective, these works often rely on partially known dynamics or require explicit modeling of environmental stiffness and damping, limiting their adaptability and maintaining a degree of model dependency. Meanwhile, recent reinforcement-learning-based approaches [
24,
25] show promise but generally demand extensive exploration or rely on predefined movement primitives to a certain degree, which can still hinder real-time adaptation and pose safety risks in physical human–robot interaction scenarios. More recently, ref. [
26] developed a DRL-based adaptive variable impedance control strategy that ensures provable stability while improving sample efficiency, generalization capability, and robust force tracking under uncertain conditions. These recent advances demonstrate the potential of hybrid control architectures that combine the stability and interpretability of model-based approaches with the adaptability and flexibility of data-driven learning. By leveraging the strengths of both paradigms, such methods accelerate the realization of robust and intelligent robotic systems capable of operating effectively in complex, dynamic, and uncertain environments.
Building on the above analyses, this study seeks to enhance robotic force–motion control in unknown, time-varying contact environments, with a focus on accompanied force tracking and exploratory contact motions. Emphasis is placed on improving contact dynamics, steady state force–motion performance, and learning efficiency by reducing exploration demands. The main contributions of this work are as follows:
- (i)
To enable intelligent and robust impedance adaptation in unknown environments, we propose a reinforcement learning framework that integrates a model-based expert to mitigate key limitations of DRL in continuous control domains. Unlike conventional approaches, our core innovation lies in reformulating the decoupled force–position interaction as a continuous Markov Decision Process (MDP). Within this formulation, a Deep Deterministic Policy Gradient (DDPG) algorithm, combined with expert-guided exploration, optimizes impedance parameters through an actor–critic architecture by leveraging a tailored reward function that reflects impedance regulation objectives.
- (ii)
To accelerate policy convergence and ensure initial contact stability, a warm-start strategy is employed using behavior cloning from a conventional adaptive variable impedance control law. This expert controller, based on force error feedback, serves as a demonstrator that provides prior knowledge for early-stage DDPG training. As a result, our method significantly enhances learning efficiency, achieving a 37.5% faster convergence rate—requiring only 125 episodes compared to 200 in the vanilla DDPG baseline—for complex force–motion coordination tasks involving transitions from flat to curved surfaces.
- (iii)
A comprehensive time- and frequency-domain performance analysis is conducted to evaluate both the dynamic and steady-state behavior of the system under various sources of uncertainty, including variations in reference force, reference trajectory, and surface material and geometry. Quantitative results confirm that the theoretical analysis is in good agreement with the outcomes of simulation experiments. Moreover, the proposed IIC approach demonstrates strong generalization and robust stability across diverse simulated conditions, delivering superior performance in the presence of changing material properties, environmental stiffness, and external disturbances.
The remainder of this paper is organized as follows: In
Section 2, the preliminaries are presented, including the dynamic modeling of the robot–environment interaction and the formulation of impedance control under uncertain conditions.
Section 3 details the proposed intelligent impedance control strategy, which incorporates expert guidance with a reinforcement learning framework. In
Section 4, a comprehensive performance evaluation is provided, analyzing both dynamic and steady-state behaviors through time- and frequency-domain methods.
Section 5 demonstrates the effectiveness of the proposed approach through simulation studies under a high-fidelity IIC simulation framework with various unknown task scenarios. Finally,
Section 6 concludes the paper and indicates potential directions for future research.
3. Expert-Guided DRL for IIC Strategy
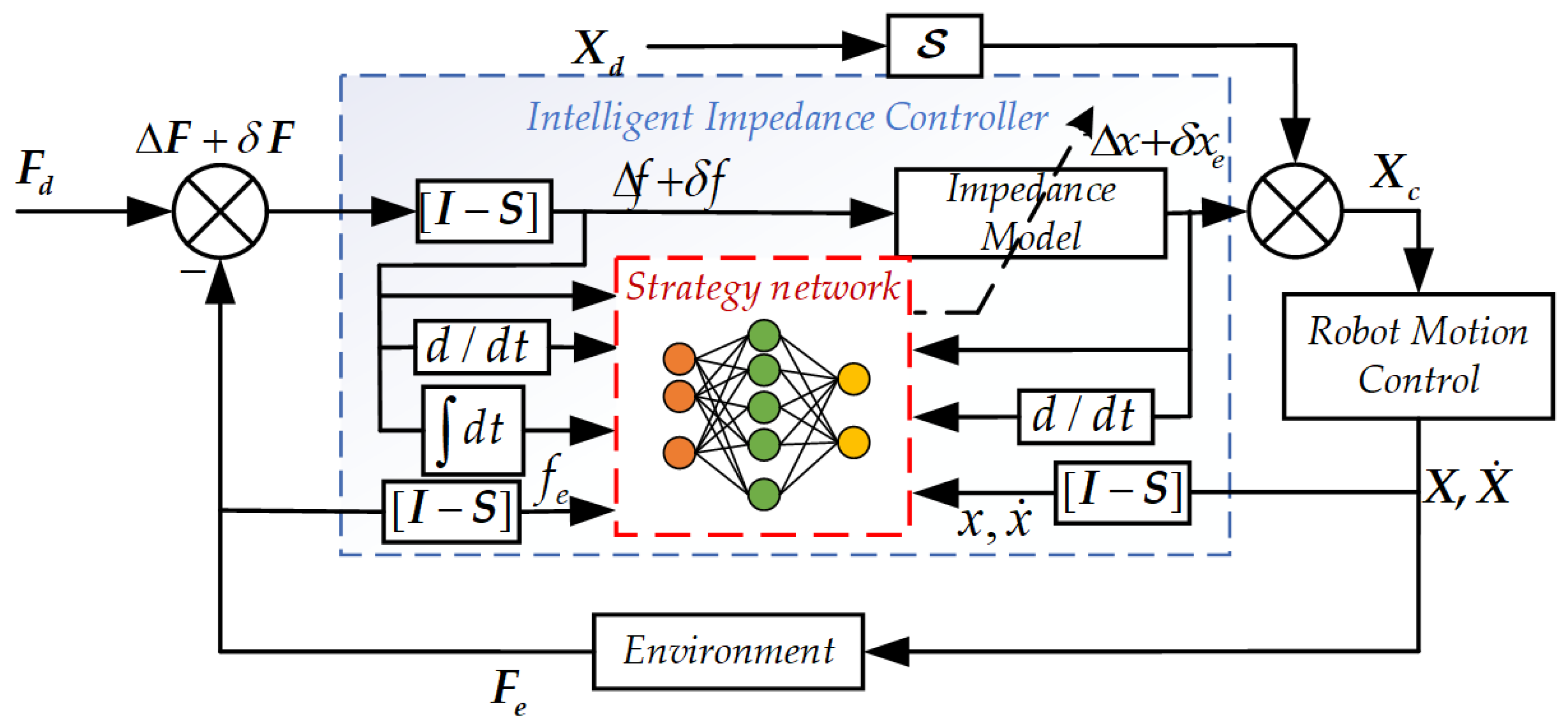
To combine the advantages of both traditional model-based and entirely learning-based approaches discussed in prior sections, we propose a position/force-decoupled intelligent impedance control framework incorporating a strategy network, as illustrated in
Figure 3. This architecture achieves closed-loop adaptation of impedance parameters through trial-and-error interaction with various unknown environmental dynamics. The core innovation lies in the integration of a DRL policy with an expert-guided strategy network that makes it autonomously tune impedance parameters, thereby enabling robust and sample-efficient force tracking in environments characterized by time-varying and uncertain contact properties.
To decouple motion control along the x and y directions from force control along the
z-axis (the force-constrained direction), a selection matrix is introduced:
This matrix facilitates orthogonal decomposition of the task space while preserving dynamic consistency. Focusing on the force-constrained direction allows the multidimensional impedance adaptation problem to be reduced to a one-dimensional formulation, simplifying controller training while retaining key system dynamics. In this simplified setting, Equation (5) can be reformulated as
where
,
, and
represent the nominal inertia, damping, and stiffness parameters, and
and
are compensation terms from the adjustable impedance strategies
and
learned through the DRL agent under uncertain conditions. By substituting the predicted environmental deformation as expressed in Equation (4) into Equation (7), we obtain
Here,
and
denote the environmental uncertainties and the corresponding adjustable compensation term, respectively. As illustrated in Equation (8) and
Figure 3, the impedance adaptation process can be achieved through the policy network that autonomously tunes the damping and stiffness parameters. This policy adjustment is performed by iterative trial-and-error exploration in response to force–motion tasks with the unknown interaction dynamics, using only the initial contact point as prior information. By doing so, the estimated force
progressively converges to unknown dynamics
, effectively attenuating the influence of unmodeled environmental variations and dynamic disturbances. The closed-loop structure shown in
Figure 3 also highlights the integration of real-time sensory feedback into the learning process, allowing the learned policy to adapt impedance parameters dynamically, enabling robust force tracking and adaptive and generalized behavior in complex and uncertain contact scenarios. To model dynamic agent–environment interactions for persistent contact operation, the robotic force control problem under environmental variability is formally framed as a Markov Decision Process (MDP), necessitating systematic design of state observables, action policies, and reward function topologies.
3.1. Design of State Space
To promote adaptive impedance control under unknown interaction dynamics, the state space is carefully constructed to capture the nonlinear coupling between the robot’s end-effector motion and contact force behavior in uncertain environments. The state vector
at time t is defined as
Here, denotes the contact force in the force-constrained direction. The vector represents the force tracking error, its time derivative, and accumulated integral, forming a proportional–integral–derivative (PID)-like representation that enhances robustness to fluctuating force disturbances. The terms correspond to the measured end-effector position and velocity in the same direction, while capture the environment deformation and its rate of change.
This multidimensional state formulation enables the policy network to perceive and respond to key dynamic indicators, including real-time force deviation, motion tracking accuracy, and the system’s transient behavior. By embedding both force regulation and kinematic feedback into the state space, this design ensures observability and supports stable impedance adaptation in contact tasks involving time-varying, uncertain environments. It forms the foundation for real-time policy optimization after learning described in subsequent sections.
3.2. Design of Action Space
In the proposed IIC framework, the design of the action space plays a critical role in enabling the learning agent to effectively modulate the robot’s dynamic behavior during interaction with unknown environments. Rather than directly commanding the joint torques or position trajectories, the action space
is defined in terms of the impedance parameters—specifically, the damping and stiffness coefficients within the force-constrained direction as follows:
where
A denotes a bounded set of admissible impedance parameter variations. This formulation ensures that the learned policy adheres to the physical structure of impedance control, thereby maintaining system stability while allowing adaptive behavior.
To ensure both training efficiency and control safety, the action space A must be carefully constrained. If the permissible range is too narrow, the agent may be unable to explore effective parameter configurations. Conversely, an overly broad action space not only increases the risk of instability but also leads to inefficient exploration and elevated control energy consumption.
Remark 1. The design of the action space is governed by two critical principles:
(i) Stability Assurance: The bounds of A are derived through time- and frequency-domain stability analysis (see
Section 4.2), ensuring that all learned impedance profiles yield asymptotic convergence in force tracking and maintain system passivity under nominal operating conditions. (ii) Exploration Efficiency: Empirical evidence [31,32] shows that action spaces with excessively large ranges introduce high-dimensional exploration burdens [33,34] without proportionate gains in control performance. Hence, constraining A within theoretically justified and empirically effective limits is key to balancing learning efficiency with physical stability. 3.3. Reward Function
During each training episode, the robotic arm executes continuous force tracking tasks while interacting with unknown and possibly time-varying environmental surface profiles. The design of the reward function plays a pivotal role in shaping the learning trajectory of the agent and directly affects its ability to achieve robust and adaptive control. Traditional sparse-reward schemes—based on binary success or failure signals—often fail to provide sufficient learning gradients in complex contact-rich environments. This results in slow convergence and suboptimal control performance, particularly when precise force regulation and rapid adaptation are required simultaneously. On the other hand, excessively complex or over-engineered reward formulations can obscure the learning objective due to competing criteria and ill-defined trade-offs.
To address these limitations, the proposed reward function is explicitly designed to capture key performance objectives in uncertain environments, namely rapid dynamic response, minimal overshoot, and high steady-state tracking accuracy. The total reward is decomposed into multiple sub-components as follows:
where
is the dynamic reward,
represents steady-state reward,
denotes safety-based task termination reward. The weighting factors
are hyperparameters selected based on specific task requirements and system characteristics, balancing stability, responsiveness, and long-term precision.
3.3.1. Dynamic Reward
The dynamic reward is specifically designed to encourage fast convergence and suppress force overshoot during the transient response phase. It leverages an exponential decay mechanism to penalize large deviations from the desired contact force, while partitioning the error space into intervals that reflect performance thresholds. The reward function is defined as
where m is the number of intervals dividing the error magnitude domain,
is the desired contact force,
is the reward coefficient for the
i-th interval,
is the corresponding exponential decay rate, and
denotes the
i-th partitioned region of the force deviation space.
This formulation allows dynamic sensitivity tuning across different error ranges. Larger errors invoke harsher penalties, encouraging the agent to swiftly reduce force deviation in early transient phases, while finer rewards in near-zero-error regions promote high precision during convergence. Compared to standard reward shaping methods, this interval-based decay approach provides several advantages:
It enables task-specific sensitivity adjustment via interval-wise tuning;
It offers robustness to sensor noise by grouping small deviations within thresholds, preventing reward instability due to measurement fluctuations [
35];
It supports generalization across surface types, as tuning the number of intervals and decay constants enables adaptation to various material properties and dynamics.
Overall, the dynamic reward incentivizes the agent to minimize contact force errors efficiently and stabilize interaction dynamics, thereby supporting both responsiveness and robustness in unpredictable environments.
3.3.2. Steady-State Reward
The steady-state reward is designed to encourage precise force tracking by reinforcing small steady-state deviations and promoting consistent accuracy during sustained contact. It is mathematically defined as
where
is a small positive constant introduced to avoid singularity as the tracking error approaches zero. The use of a logarithmic function provides a continuous and smooth reward gradient, which increases sharply as the contact force error
diminishes. This characteristic inherently motivates the agent to minimize long-term deviations and fine-tune its behavior around the desired force target.
The logarithmic reward structure also contributes to learning stability. Unlike linear or quadratic penalties, which may excessively punish large errors and destabilize learning, the logarithmic compression scales the penalty more moderately. This nonlinearity allows the agent to maintain learning progress even in the presence of occasional transient disturbances or sensing noise, making the training process more robust to outliers and irregularities in contact dynamics. As a result, it is expected that the steady-state reward supports both high-precision regulation and stable convergence in uncertain and variable environments.
3.3.3. Task Termination Reward
The task termination reward incorporates a safety-oriented learning mechanism to ensure that the agent develops both stable and safe behaviors during force-interaction tasks. If any predefined safety constraint is violated during the training process, the episode is immediately terminated and penalized, effectively discouraging unsafe exploration and promoting policy robustness. Specifically, the agent’s behavior is evaluated at each time step based on the following two critical safety conditions:
The commanded end-effector position must correspond to a valid inverse kinematic solution, ensuring that the resulting joint configuration q remains within the allowable joint range . This condition prevents physically infeasible or potentially damaging commands.
The actual contact force must remain below a predefined safe threshold , thereby avoiding excessive interaction forces that could compromise the mechanical integrity of the robot or its environment.
The task termination reward is defined as
where
is a fixed positive reward granted for safe task completion, and
is a fixed negative penalty assigned upon safety violation or instability.
This reward component plays a dual role: it strengthens adherence to physical and safety constraints while guiding the agent toward reliable and responsible behavior in uncertain contact environments. By embedding safety directly into the reward structure, this mechanism enhances training stability and accelerates convergence toward viable control policies, especially in safety-critical or real-world applications [
31,
32,
35].
3.4. DDPG with Expert Strategy
The strategy network architecture, detailed in
Figure 4, is built upon an expert-guided Deep Deterministic Policy Gradient (DDPG) framework—a policy-based deep reinforcement learning algorithm tailored for continuous action spaces. By incorporating expert knowledge into the learning loop, this approach enhances stability and accelerates convergence, making it particularly suitable for addressing complex force control tasks in robotic arms interacting with uncertain and dynamic environments.
3.4.1. DDPG Algorithm [36,37]
As shown in
Figure 4, the DDPG algorithm operates within an actor–critic architecture and is adapted here to support real-time impedance parameter adjustment. To improve sample efficiency and training stability, an experience replay buffer is employed to store state transitions collected from each complete contact episode during surface interaction. During each training iteration, a minibatch of N state transitions
is randomly sampled from this buffer to update the neural networks. Let
,
, and
denote the state, action, and reward at time step
i, respectively, and let
represent the next state at time step
i + 1. The critic network parameters are updated by minimizing the mean-squared Bellman error (MSBE) loss, which integrates two critical components: L2 regularization to prevent overfitting, and temporal-difference (TD) targets calculated via bootstrapping. Simultaneously, the actor network is updated by applying deterministic policy gradient ascent, where gradients are backpropagated to optimize the parameters of the current policy network. To balance exploration and exploitation in the continuous action space, the selected action is perturbed with Ornstein–Uhlenbeck (OU) noise. This temporally correlated noise facilitates smooth exploration trajectories, enhancing interaction efficiency in physical systems. To stabilize learning and reduce the risk of policy oscillation, target networks
and
are updated using a soft update mechanism by incrementally blending target network parameters with those of the current networks. This gradual synchronization technique prevents conflicting interactions between the actor’s policy adjustments and the critic’s value predictions, thereby stabilizing the learning process.
3.4.2. Expert Strategy
Despite its advantages, the DDPG algorithm faces persistent challenges in balancing exploration and exploitation of unknown dynamics, particularly during initial training stages when excessive random exploration substantially delays policy convergence. To mitigate this inefficiency in early-phase exploration, an expert-guided control strategy that enables accelerated acquisition of meaningful control experiences by providing structured prior knowledge to the agent is designed. This approach is especially pertinent in impedance control tasks, where conventional methods often struggle to adapt effectively to environmental uncertainties. To this end, our solution introduces an adaptive variable impedance law to obtain an expert-guided strategy, allowing the agent to rapidly acquire meaningful control behaviors without relying solely on gradient-based updates. By responding to dynamic interaction states with minimal computational overhead, the expert-guided process significantly accelerates the convergence of the DDPG learning algorithm.
The expert strategy iteratively refines the intelligent impedance strategy based on real-time tracking error feedback, starting from initially set impedance parameters derived from a weak-model-based approach. The stiffness and damping are adjusted according to both the rate of the error change and its accumulated history, enabling robust and stable adaptation under uncertain conditions. The actions selected by the expert strategy are defined as
where
and
represent the expert-determined adaptive stiffness and damping coefficients at time t. These coefficients are updated using the following iterative laws:
where
is the sampling interval,
and
are the update rates, and
represents a small constant induced to prevent singularity at
and provide numerical robustness.
During the expert-guided phase, the current policy network
is trained by minimizing the mean squared error between its output and the expert-generated strategy:
where
M is the number of state transition samples randomly selected during the expert-guided period. Meanwhile, the critic network
Q of the value function is updated using the standard DDPG loss based on the Bellman equation. During this phase, the target critic network
parameters are synchronized directly with those of the current critic to ensure consistency.
In this expert-guided learning period, the agent primarily mimics the behavior of the expert controller, allowing it to quickly learn feasible and stable policies. Once this phase concludes, the expert strategy is deactivated, and the strategy parameters of the agent will continue to be updated by employing the trained policy network, thereby preserving the architecture and dynamics of the original DDPG framework.
By embedding expert knowledge into the early training process, the agent benefits from a well-informed initialization. This pre-trained policy serves as a strong foundation for subsequent reinforcement learning, allowing the actor–critic architecture to progressively refine the control strategy. Ultimately, the agent acquires an optimal policy that exhibits both fast convergence and high adaptability in contact-rich and uncertain environments.
4. Performance Analysis
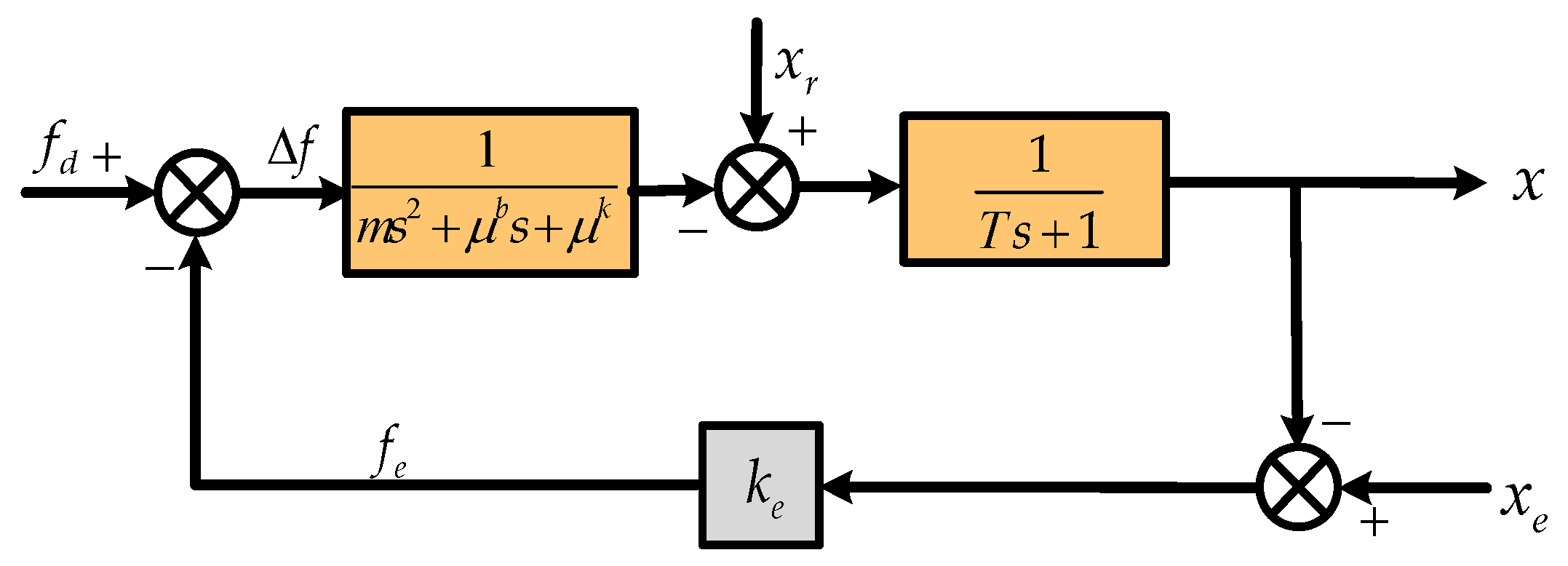
In this section, a time- and frequency-domain analysis approach is employed to evaluate the system’s performance. As illustrated in
Figure 5, a unidimensional force-constrained contact model is considered to assess the impact of the proposed intelligent impedance strategy on both the dynamic and steady-state behavior of force tracking under unknown environmental conditions. In this framework, the inner position control loop is approximated as a first-order inertial system with a time constant
T, which includes position tracking error and modeling uncertainties. The outer impedance control loop modulates the desired force response based on this inner loop. Within the impedance control block, the parameters
and
represent the adjustable damping and stiffness coefficients, respectively, which are adaptively generated by the strategy network. This model allows for analytical insights into how the impedance adjustment influences system stability, transient response, and robustness in uncertain contact environments.
4.1. Dynamics Performance Analysis
Considering learning convergent system, although stability analysis is not provided, methods such as the Routh–Hurwitz criterion remain theoretically applicable. To simplify the dynamic analysis, we assume the time constant is sufficiently small, allowing the first-order term in Equation (22) to be neglected. Under this assumption, the system’s damping ratio
and natural frequency
can be expressed as
This formulation reveals that the adjustable parameters and output by the impedance strategy network directly affect the system’s damping and dynamic response characteristics. Specifically, increasing or decreasing enhances damping, thereby suppressing oscillatory behavior and reducing overshoot; adjusting by increasing modifies the system’s transient response time. These findings indicate that in dynamic interaction scenarios involving rapidly varying or uncertain environments, the intelligent impedance controller should increase damping to improve vibration attenuation and tune to adapt the response rate according to contact dynamics. Moreover, in combination with the system’s analysis in Equation (8), it becomes clear that optimal impedance parameter tuning effectively mitigates the destabilizing effects of environmental uncertainties, promoting robust and adaptive force control.
4.2. Steady-State Performance Analysis
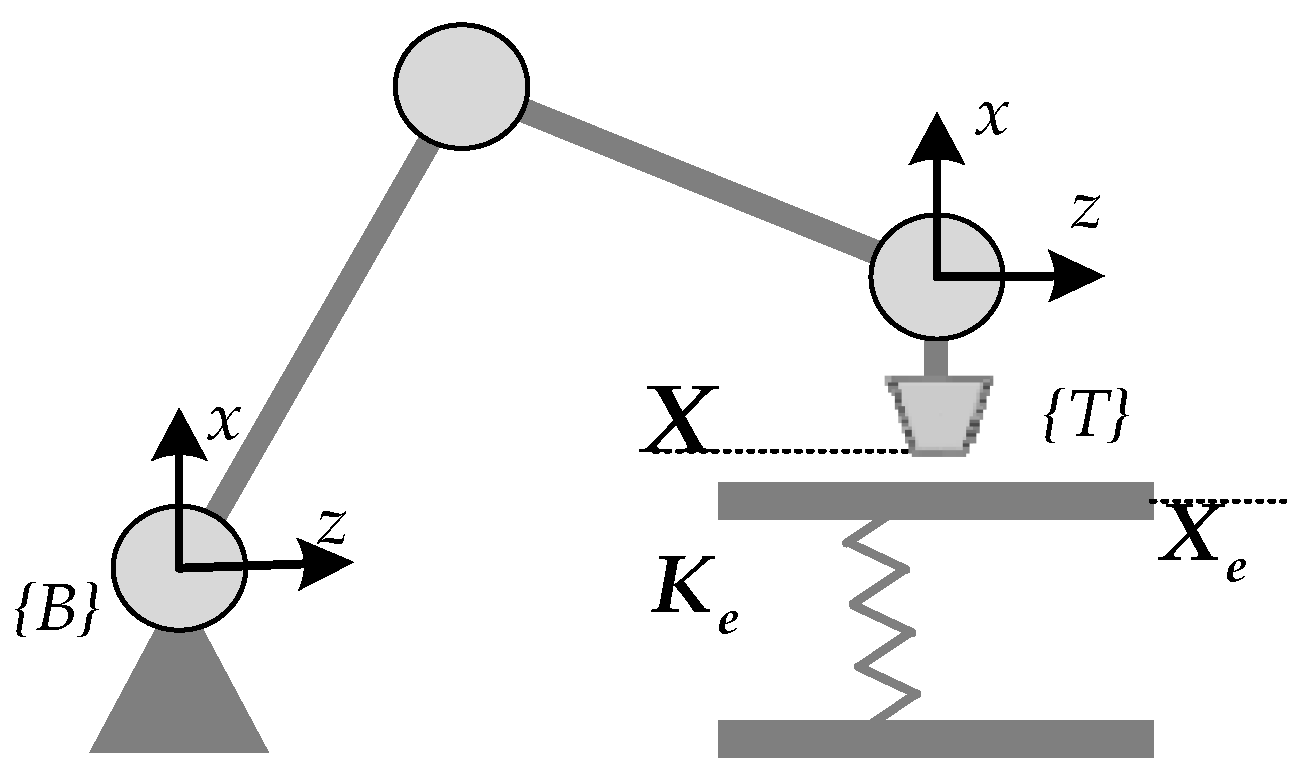
It is assumed that the system is subject to modeling uncertainties from the position loop and external disturbances originating from three primary sources: the contact environment
, the reference trajectory
, and the reference force
. When the system remains stable, the corresponding error transfer functions for each component, denoted as
and
, can be derived as follows:
Then, the lumped steady-state error (SSE) can be derived using the Final Value Theorem and the principle of linear superposition, as follows:
Different contact surface profiles are detailed as follows:
- (i)
Planar Surface Contact
When the contact surface in the force-constrained direction is planar and the initial contact point can be treated as constant, force–motion control keeps a constant force tracking, and all inputs
,
, and
behave as step inputs. Let
, and
denote the amplitudes of these step signals. Under these conditions, SSE can be obtained as follows:
It is evident that SSE → 0 as . Thus, by regulating the impedance stiffness to zero, ideal steady-state force tracking performance can be achieved on a planar surface.
- (ii)
Sloped Surface Contact
For a sloped contact surface with an inclination angle, the SSE depends on the geometric profile of the environment. Besides the effects from
and
, the corresponding steady-state error expression of
becomes
In this scenario, as long as the stiffness coefficient k remains nonzero, the cumulative tracking error increases progressively. Therefore, for optimal performance, the impedance strategy should dynamically reduce during interaction with inclined surfaces.
- (iii)
Sinusoidal Surface Contact
Since
and
remain unchanged,
is analyzed as below. If the contact surface exhibits a sinusoidal profile, i.e.,
, the frequency-domain analysis is performed by substituting
into Equation (22). The resulting transfer function exhibits the following characteristics:
The steady-state error contains a sinusoidal component at the same frequency as the environmental curvature, indicating that surface topology directly influences the periodic tracking error. Therefore, frequency-domain characteristics can be utilized to analyze how intelligent impedance regulation suppresses such errors.
5. Simulation Verification and Analysis
This section presents a high-fidelity IIC simulation framework developed within the MATLAB 2021b/Simulink environment, as depicted in
Figure 6. To accurately replicate the dynamic behavior of the manipulator—including realistic contact interactions and control performance—a multi-toolbox co-simulation architecture is employed. Specifically, the virtual testbed is built using the Simscape Multibody physics simulation toolbox, which perfectly integrates the Unified Robot Description Format (URDF) model of the EFORT serial robotic manipulator as a benchmark robot system. The topological structure of this model is illustrated in
Figure 6b.
The platform offers a robust and high-fidelity testbed for evaluating system-level performance under complex and uncertain conditions. The simulation experiments are designed to evaluate dynamic interactions with a single predefined touch-point under multi-source uncertainty, including variations in contact conditions and environmental compliance, all within a uniform motion trajectory. The simulation environment is parametrically aligned with the physical properties of the real system. Systematic comparisons are conducted against conventional IC and AIC as shown in Equation (16) to quantitatively evaluate performance in handling undetermined contact dynamics.
The adaptive impedance controller is trained using the Deep Learning Toolbox and Reinforcement Learning Toolbox, implementing the DDPG algorithm with expert-guided initialization. Training is conducted on a benchmarking platform featuring an Intel Core i7-7700K processor, utilizing the MATLAB Parallel Computing Toolbox in local worker mode to accelerate batch training and simulation cycles.
5.1. Training Simulation
5.1.1. Learning Settings
The neural architectures underpinning the actor–critic framework, schematically illustrated in
Figure 7, adopt distinct yet complementary feedforward designs. The actor network of policy π comprises two hidden layers, while the critic network of value function Q features a deeper structure with four hidden layers. Each layer contains 64 neurons, initialized with random parameters to encourage exploration in early training.
The actor network receives an eight-dimensional state vector as input, whereas the critic network adopts a skip connection structure. Specifically, the action vector is element-wise summed with the output of the second hidden layer via trainable projection matrices. This residual integration mitigates gradient conflict during temporal-difference (TD) backpropagation, stabilizing convergence and improving learning robustness.
The output layers employ task-specific activation strategies to enforce meaningful constraints. The critic network uses rectified linear unit (ReLU) activations to ensure non-negative Q-value outputs, consistent with the Bellman equation’s theoretical assumptions. In contrast, the actor network applies a hyperbolic tangent (tanh) activation function followed by a scaling layer to constrain continuous control outputs within a predefined range. This bounded action representation not only reduces excessive control effort through saturation but also enhances policy generalization.
To prevent overfitting, L2 regularization with a scaling factor is applied, and all network parameters are optimized using the Adam optimizer, which improves convergence speed while reducing training latency and computational cost [
37]. The specific training hyperparameters are summarized in
Table 1. Each training episode corresponds to a 1.5 s interaction trajectory consisting of 1500 sampled transitions. These transitions are stored in a replay buffer of size 10
6. During training, a minibatch of 64 samples is drawn randomly from the buffer to update the actor and critic networks. Over the course of training 300 episodes with trial-and-error mode, approximately 450,000 unique transitions can be collected. Depending on the update frequency, once per time step, the agent performs up to 1500 gradient updates per episode. This cumulative data volume ensures sufficient experience diversity while maintaining the efficiency of the learning process.
5.1.2. Training Process
During training, the robotic arm autonomously explores unstructured contact environments through directionally guided interaction, executing adaptive contact motions at a constant velocity across unmodeled surface geometries. The simulation framework includes a variety of environmental profiles
, both planar and curved, to enhance generalization under force-controlled conditions, as illustrated in
Figure 8. And the system predicts trajectory
in the force constraint direction by adjusting control actions accordingly.
On the force control axis, the initial contact point with the environment is set at , with initial nominal impedance parameters defined as and . A change in the surface profile is introduced at t = 0.5 s to emulate dynamic environmental transitions. The environment stiffness is configured as , and the target contact force is maintained at , serving as the reference for force-tracking behavior throughout the training process.
The Intelligent Impedance controller Is trained under two distinct modalities: the baseline DDPG algorithm and the expert-integrated variant (EXPERT_DDPG). The comparative learning performance is visualized through the reward evolution profiles presented in
Figure 9. The instantaneous reward trajectories for the IC, AIC, and IIC are computed using the policy optimization metric defined in Equation (11), while the average reward values of IIC are depicted as a statistical aggregation over 20 training rounds.
As shown in
Figure 9a,b, the reward performance of traditional IC and AIC remains constant throughout the training process, as these controllers are not driven by reward-based optimization. In contrast, agents trained using the IIC framework exhibit a steadily increasing reward trend as the number of training episodes progresses. Although the reward curves display fluctuations due to exploration noise, both IIC variants eventually converge after approximately 200 and 125 training episodes, respectively. Notably, the EXPERT_DDPG algorithm achieves a 37.5% improvement in convergence efficiency over the baseline DDPG approach. These findings validate both the effectiveness and the enhanced training efficiency of the proposed IIC method cooperating with expert-guided strategies.
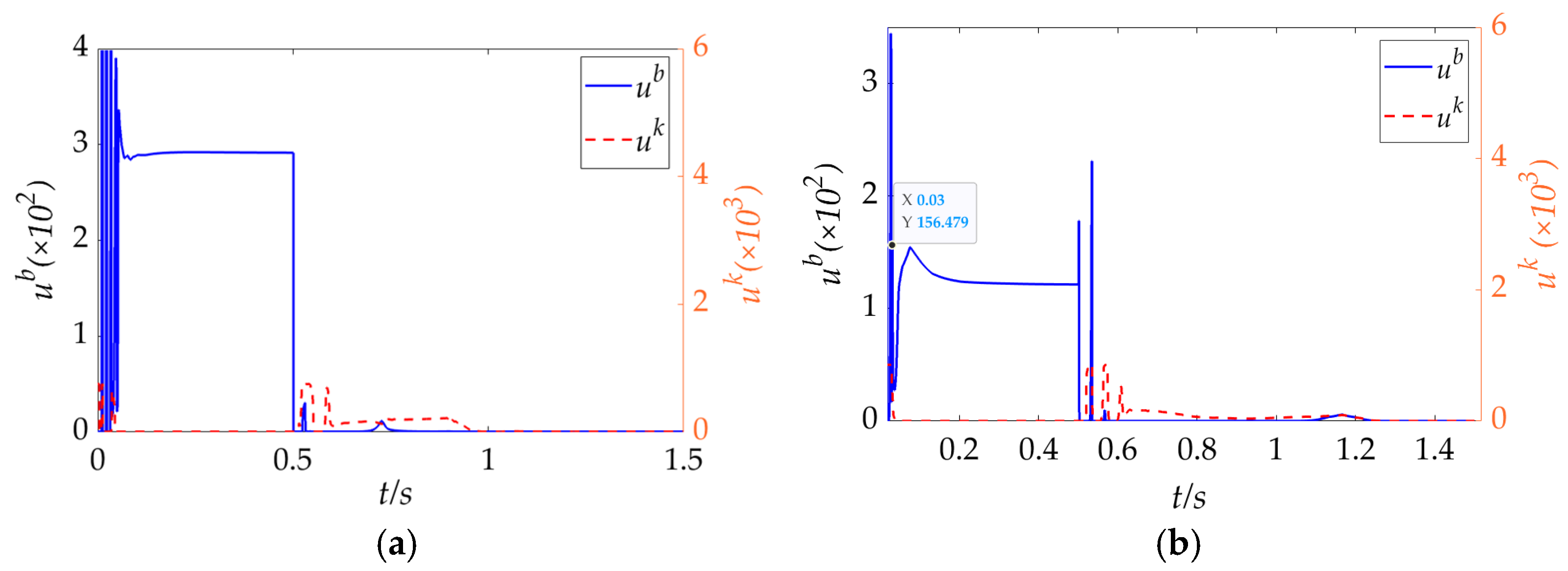
The Impedance parameter adjustment strategies learned by the IIC framework under both training paradigms are illustrated in
Figure 10. In conjunction with the position trajectory variation depicted in
Figure 8, it is evident that the action parameters undergo rapid changes when the robotic arm transitions into contact with the environment or encounters abrupt variations in surface profile. Notably, during step changes in the reference force, the stiffness
and damping coefficient
increase under the proposed strategy, effectively suppressing overshoot and improving response, which aligns well with the dynamic analysis presented in
Section 4.2. These behaviors indicate that during the transient phase of force tracking control, the IIC framework successfully generates impedance control strategies that strike a balance between rapid response and effective damping. Consequently, the system achieves optimal dynamic performance throughout the interaction.
As the robotic arm transitions into steady-state contact, the impedance control strategy
produced by the IIC method continuously fine-tunes the action parameters to minimize tracking error within a narrow margin. This adaptive behavior is consistent with the learning objectives outlined in
Section 2.2, demonstrating the framework’s ability to sustain high-precision control in uncertain and dynamic environments.
5.2. Comparative Evaluation in Uncertain Scenarios
To rigorously evaluate the force control performance of the IIC framework in diverse uncertain environments, a series of comparative experiments is conducted against IC and AIC methods. In these comparisons, IC uses appropriately selected fixed impedance parameters
,
, and
, while AIC adopts the initial values described in
Section 5.1.2 along with
. Additionally, the parameters
and
in Equation (16) are both set to 0.05.
The simulations encompass five representative uncertain contact scenarios, designed to reflect realistic and challenging operational conditions: (i) time-varying reference force, (ii) variable environmental stiffness, (iii) sloped surface contact, (iv) curved surface contact, and (v) contact environments subjected to external disturbances. These scenarios collectively test the adaptability, robustness, and dynamic response of each control strategy under dynamically changing conditions.
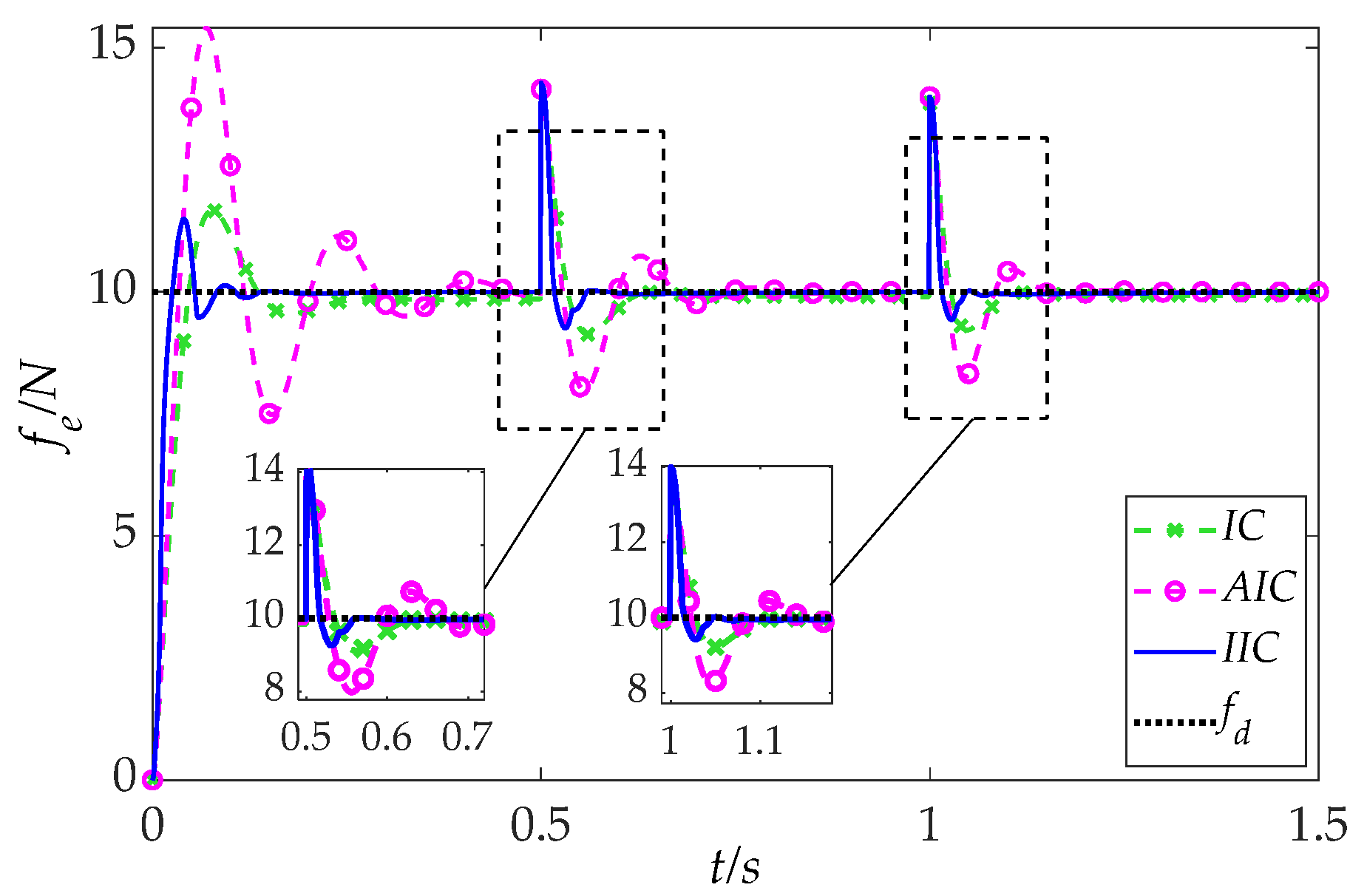
5.2.1. Time-Varying Reference Force
To evaluate the robustness of the IIC framework under dynamic task requirements, a basic planar contact environment is established, where the desired contact force in the force control direction varies over time as follows:
The resulting force tracking performance is illustrated in
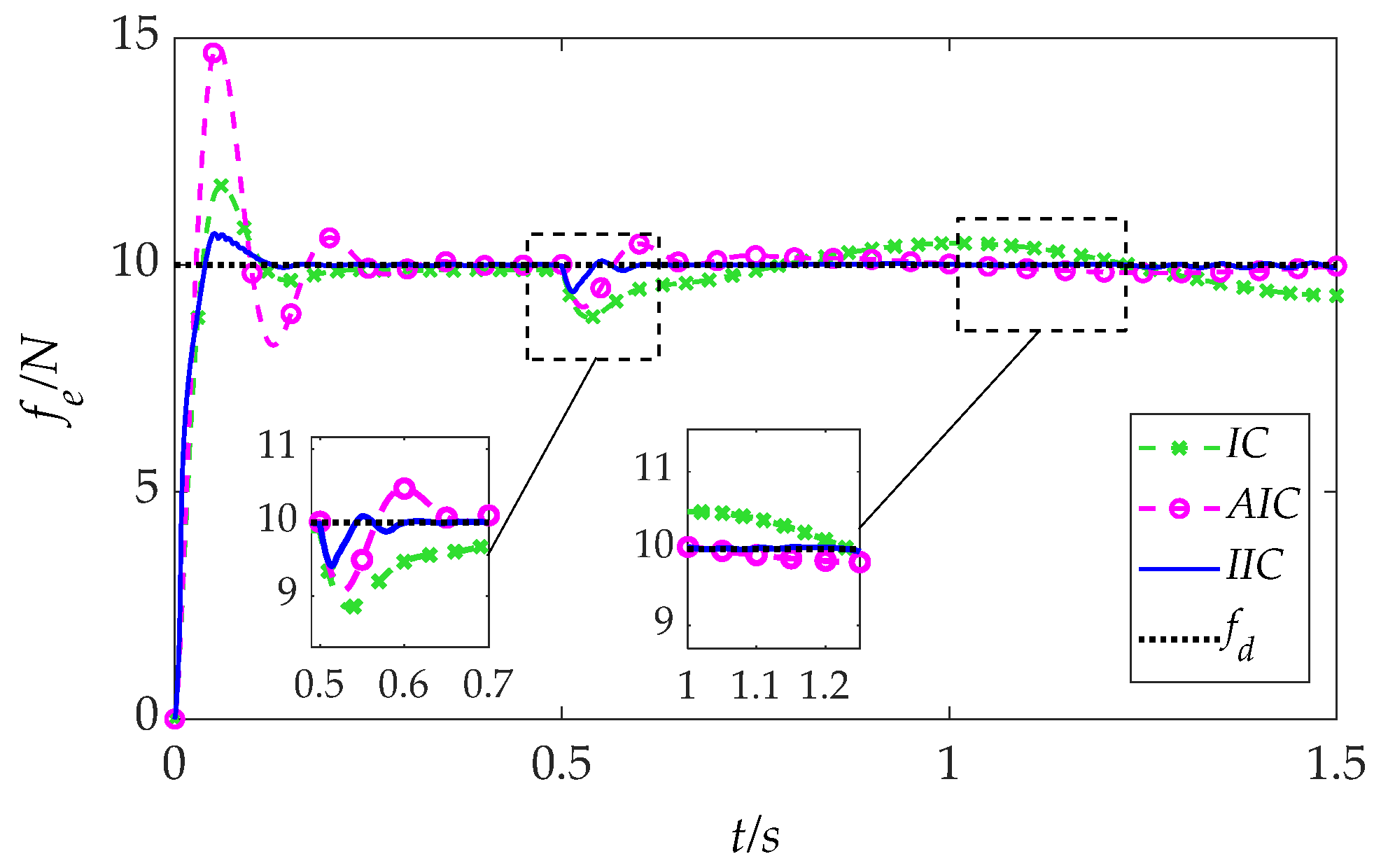
Figure 11. As shown, the conventional IC method exhibits relatively large tracking errors throughout the task. The AIC method, while maintaining good steady-state accuracy, suffers from pronounced overshoots and prolonged settling times following each step change in the reference force. In contrast, the proposed IIC approach achieves marked improvements in both transient and steady-state behaviors. Specifically, the IIC method demonstrates minimal overshoot and significantly reduced tracking error under the same conditions, thereby offering superior overall control performance.
Quantitative control metrics including initial overshoot, settling time, undershoot during falling transitions, and steady-state error (SSE) are summarized in
Table 2. Compared to the baseline IC method, the IIC framework reduces overshoot and settling time by 74% and 44%, respectively, and reduces undershoot by 28%, while maintaining an SSE on the order of O(10
−2). These results confirm that the IIC method consistently delivers enhanced dynamic responsiveness and tracking precision for both rising and falling reference forces.
5.2.2. Variable Environmental Stiffness
In this scenario, the end-effector contact configuration of the robotic arm follows the setup described in
Section 5.2.1, with the reference contact force maintained at a constant value. To quantitatively evaluate the proposed controller’s adaptability to environmental stiffness variations, simulations are conducted to emulate real-world scenarios where stiffness changes abruptly through successive step transitions. The time-varying stiffness is defined as
The resulting force tracking responses for the IC, AIC, and IIC methods are presented in
Figure 12. As illustrated, abrupt changes in environmental stiffness lead to significant degradation in the AIC method, with prolonged adjustment times and substantial oscillations characterized by longer settling times and larger undershoots. In contrast, although the peak oscillation amplitude remains roughly constant across methods, the IIC controller demonstrates rapidly enhanced adaptability to stiffness uncertainties. Following the first stiffness change, the IIC method reduces undershoot by 12% and settling time by 48% compared to the IC baseline. Similar improvements are observed after the second increase in stiffness. Overall, the IIC approach outperforms both IC and AIC by achieving faster response times and maintaining stable force tracking with minimal undershoot across all transitions. Detailed performance comparisons are summarized in
Table 3.
These results confirm that the IIC method offers superior robustness to dynamic variations in environmental stiffness and consistently delivers high-precision force tracking performance under these uncertain contact conditions.
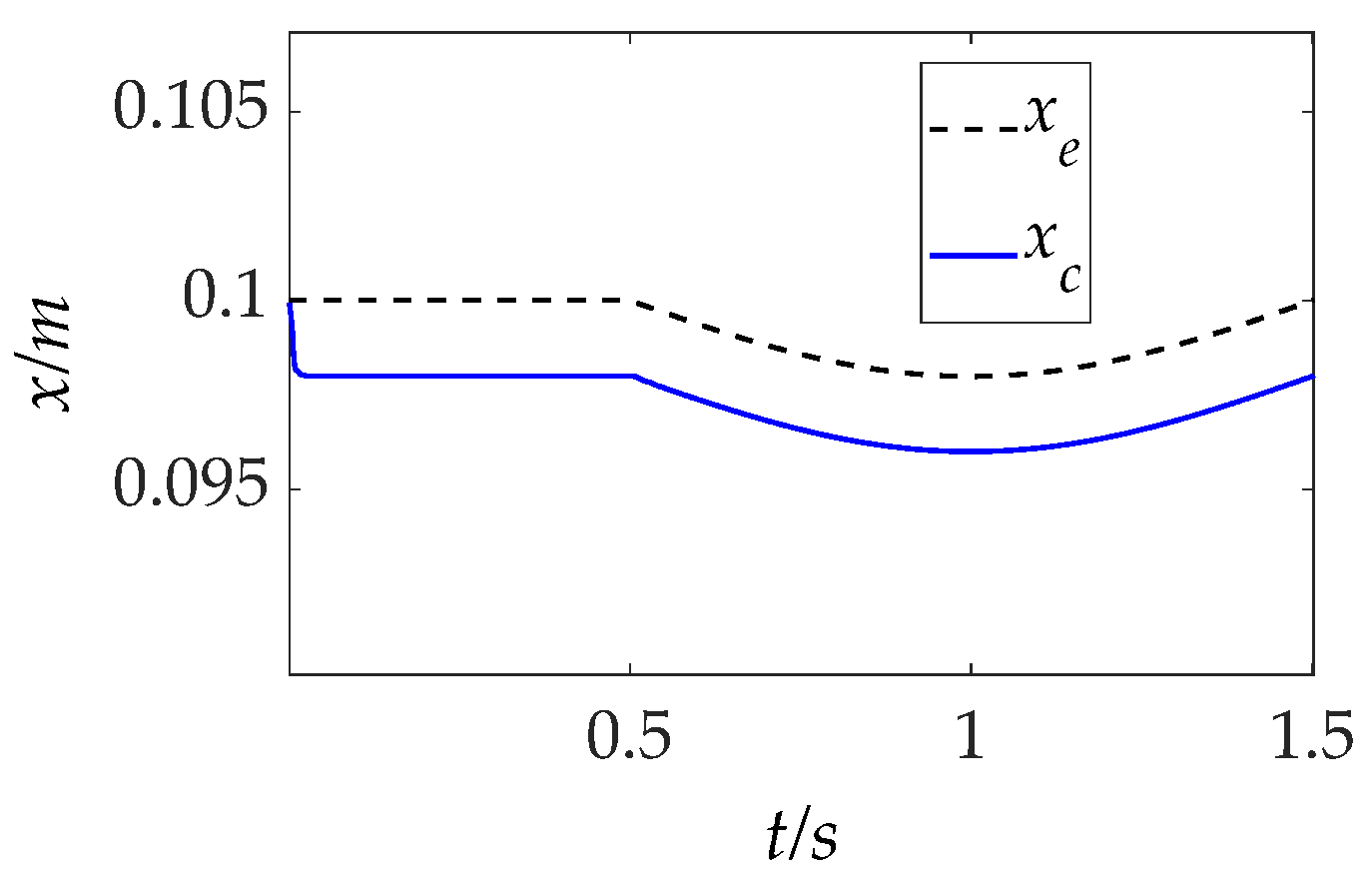
5.2.3. Sloped Surface Contact
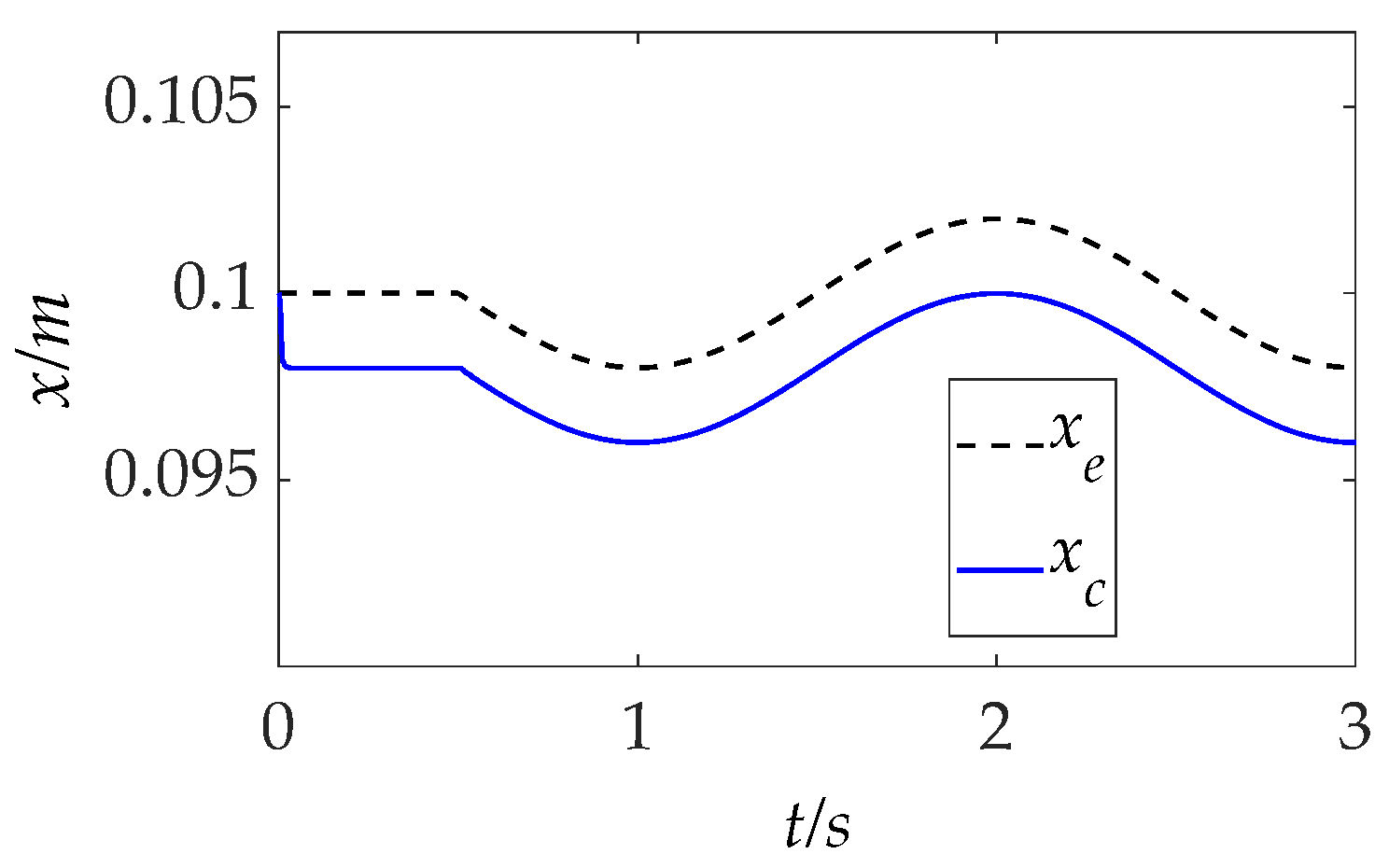
To assess the adaptability of the IIC method to dynamic positional variations in the environment, the robotic arm is tasked with operating in a composite terrain comprising both flat and sloped surfaces. The corresponding trajectory variations along the force control axis are illustrated in
Figure 13.
Force tracking results for this scenario are shown in
Figure 14, with key performance metrics including overshoot, settling time, and SSE summarized in
Table 4, aligned with changes in surface profile.
As the robotic arm transitions from a flat to an inclined region, the IC method exhibits a gradual increase in force tracking error, consistent with the SSE analysis presented in
Section 4.1 (ii). When a sudden geometric variation occurs at t = 0.5 s, the IC and AIC methods display similar dynamic performance, characterized by overshoot and prolonged settling time. In contrast, the IIC method maintains significantly improved tracking performance throughout the transition, exhibiting almost negligible minimal oscillation and relatively low SSE even when subjected to abrupt changes in surface inclination.
These results demonstrate the IIC controller’s strong ability to adapt to positional uncertainties induced by inclined geometries, validating its robustness and effectiveness in unstructured or previously unknown sloped environments.
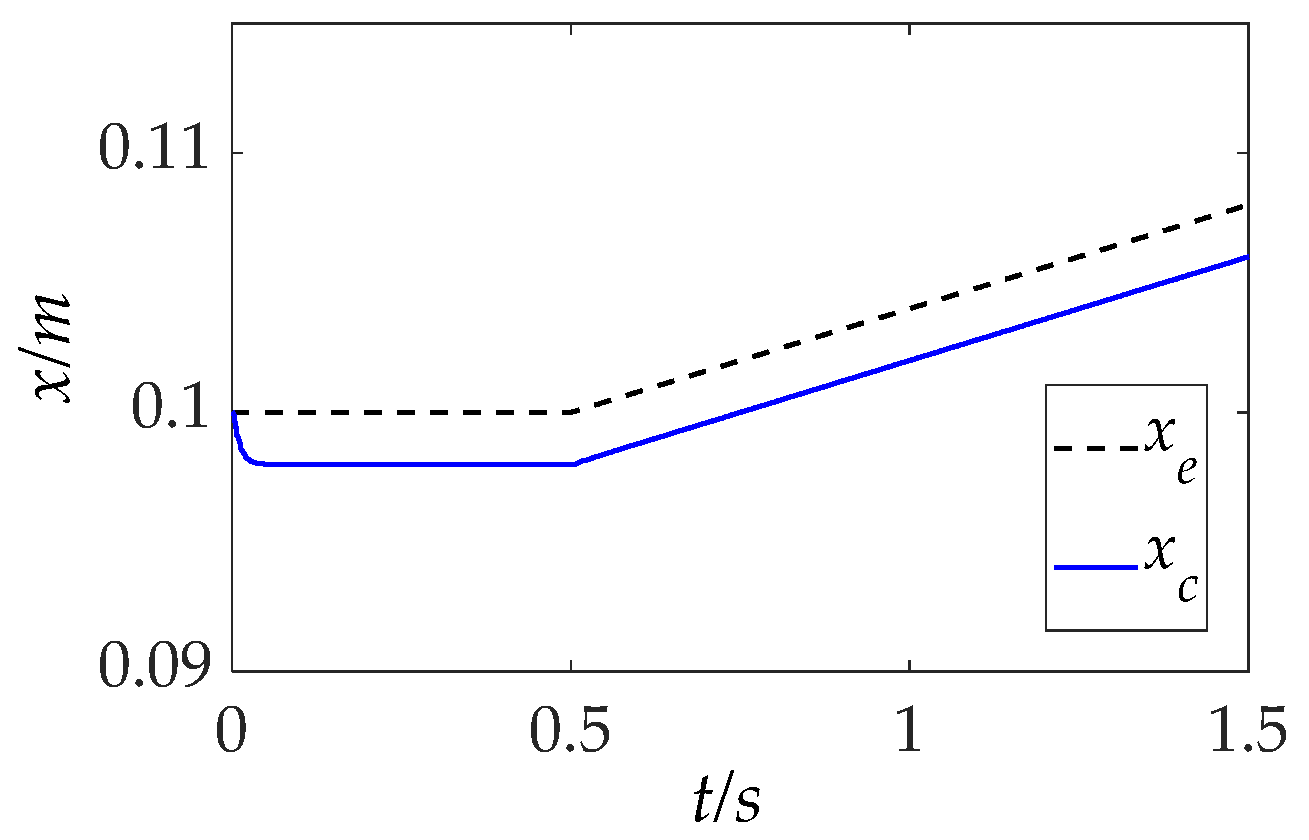
5.2.4. Curved Surface Contact
As in the training scenario described in
Section 5.1.2, another representative complex surface composed of both flat and curved segments is introduced. The manipulator’s trajectory variations along the normal contact direction in this environment are shown in
Figure 15. The corresponding force tracking responses using the IC, AIC, and IIC methods are presented in
Figure 16.
As shown, when the environment undergoes positional variations due to the curved geometry, initial force oscillations manifest as undershoot caused by the concave contact region. The IC method exhibits sinusoidal-like fluctuations in tracking error, remaining within 5% but failing to reach within 2% tolerance. Although the AIC method achieves a relatively low SSE, it suffers from pronounced undershoot and oscillatory behavior, indicating less favorable dynamic characteristics. In contrast, the IIC method outperforms both baselines in terms of dynamic response and steady-state accuracy. It effectively suppresses overshoot and undershoot while improving overall tracking precision, as corroborated by the quantitative results in
Table 5. Notably, at t = 0.5 s, when positional uncertainty is introduced by the curved surface, the IIC method achieves the smallest oscillation amplitude, reducing undershoot by 50% compared to the IC method through adaptive impedance adjustment. These results further validate the robustness and effectiveness of the IIC framework in handling dynamically varying contact conditions on complex curved surfaces.
5.2.5. Disturbance Rejection Under External Perturbations
To further evaluate the system’s robustness against external force disturbances, a transient external perturbation with a specified amplitude of 3 N is applied in the normal direction between 0.5 s and 1.0 s. During this period, the robotic arm maintains constant motion along a flat surface while sustaining a target contact force under the same environmental stiffness conditions as described in
Section 5.2.1. The resulting force tracking responses using IC, AIC, and IIC methods are shown in
Figure 17, with quantitative performance metrics summarized in
Table 6.
Simulation results indicate that although all control strategies suppress the peak disturbance to a similar amplitude, the IIC framework exhibits superior dynamic convergence properties, achieving the smallest undershoot, shortest settling time, and lowest SSE in the presence of disturbances. Specifically, it achieves faster stabilization with a 41% reduction in settling time compared to the conventional IC method under identical disturbance conditions.
It is important to note that the contact dynamics with uncertainties, as described by Equation (5), pose significant challenges in simultaneously achieving satisfactory transient response and steady state performance to robustness. Any variation in operating conditions can lead to substantial parameter uncertainties, which represent a major control challenge. Nevertheless, the IIC method demonstrates strong disturbance rejection capability in the presence of force uncertainties induced by environmental perturbations. This effectively verifies the robustness and adaptability of the IIC approach in unknown and unstructured environments.
6. Conclusions and Future Scope
6.1. Conclusions
This study proposed an Intelligent Impedance Control (IIC) framework that integrates model-based insights with a data-driven adaptive strategy using Deep Reinforcement Learning (DRL) to address the challenges of force control in robotic manipulators operating under uncertain environmental conditions. By formulating the control problem as a Markov Decision Process (MDP) and employing the Deep Deterministic Policy Gradient (DDPG) algorithm, the proposed method enables the autonomous learning of impedance control policies that adapt to a wide range of contact scenarios.
To enhance training efficiency, particularly during the early learning phase, an expert-guided adaptive impedance strategy with a conventional error-feedback iterative updating mechanism was introduced. This pre-trained policy effectively accelerates convergence and steers the learning process toward more stable and efficient control policies.
Comprehensive simulations conducted across a variety of uncertain contact environments—characterized by diverse surface profiles, varying material stiffness, and transient disturbances—demonstrated the superior generalization and adaptability of the IIC approach. Compared to conventional impedance control (IC) and adaptive impedance control (AIC), the IIC method consistently outperformed in terms of reduced overshoot, faster settling time, and lower steady-state error under unknown and complex environmental conditions.
6.2. Future Scope
The current evaluation is conducted entirely in high-fidelity simulation, which allows contact task adaptation within a certain range of environmental dynamic changes, especially where robot and environment dynamics can be realistically captured. These findings highlight the potential of DRL-based impedance control strategies in improving the robustness and adaptability of robotic manipulators in dynamic and unstructured environments.
Nevertheless, while the proposed hybrid adaptive impedance strategy demonstrates a degree of generalization capabilities, further research is needed to enhance its applicability to more complex and uncertain contact scenarios. Future studies could explore environments with greater variability, such as pronounced surface concavity, steeper inclination angles, and a broader spectrum of material stiffness. In addition, the real-world deployment may introduce additional factors such as sensor noise, complex unmodeled dynamics, and hardware constraints. Therefore, future work could focus on transferring the learned policy to real hardware, potentially using sim-to-real techniques such as domain randomization or fine-tuning with real-world data.
Furthermore, we plan to incorporate formal verification methods by integrating model-based reasoning with data-driven learning to improve the interpretability, stability, and reliability of control strategies in unstructured, time-varying environments. Comprehensive ablation studies will also be conducted to isolate and quantify the contributions of key components, including the impedance regulation, expert guidance, and the DRL framework itself.
While integrating DRL, expert guidance for impedance control may increase system complexity, challenging real-time implementation. Modular design, adaptability–real-time balance, computational advances, and dynamic environment demands jointly create compelling research opportunities worthy of exploration. Ultimately, we hope our efforts can provide a solid foundation for robust policy learning and contribute to advancing sim-to-real transfer for complex robotic manipulation tasks.