The Influence of the Geometric Configuration of the Drive System on the Motion Dynamics of Jaw Crushers
Abstract
1. Introduction
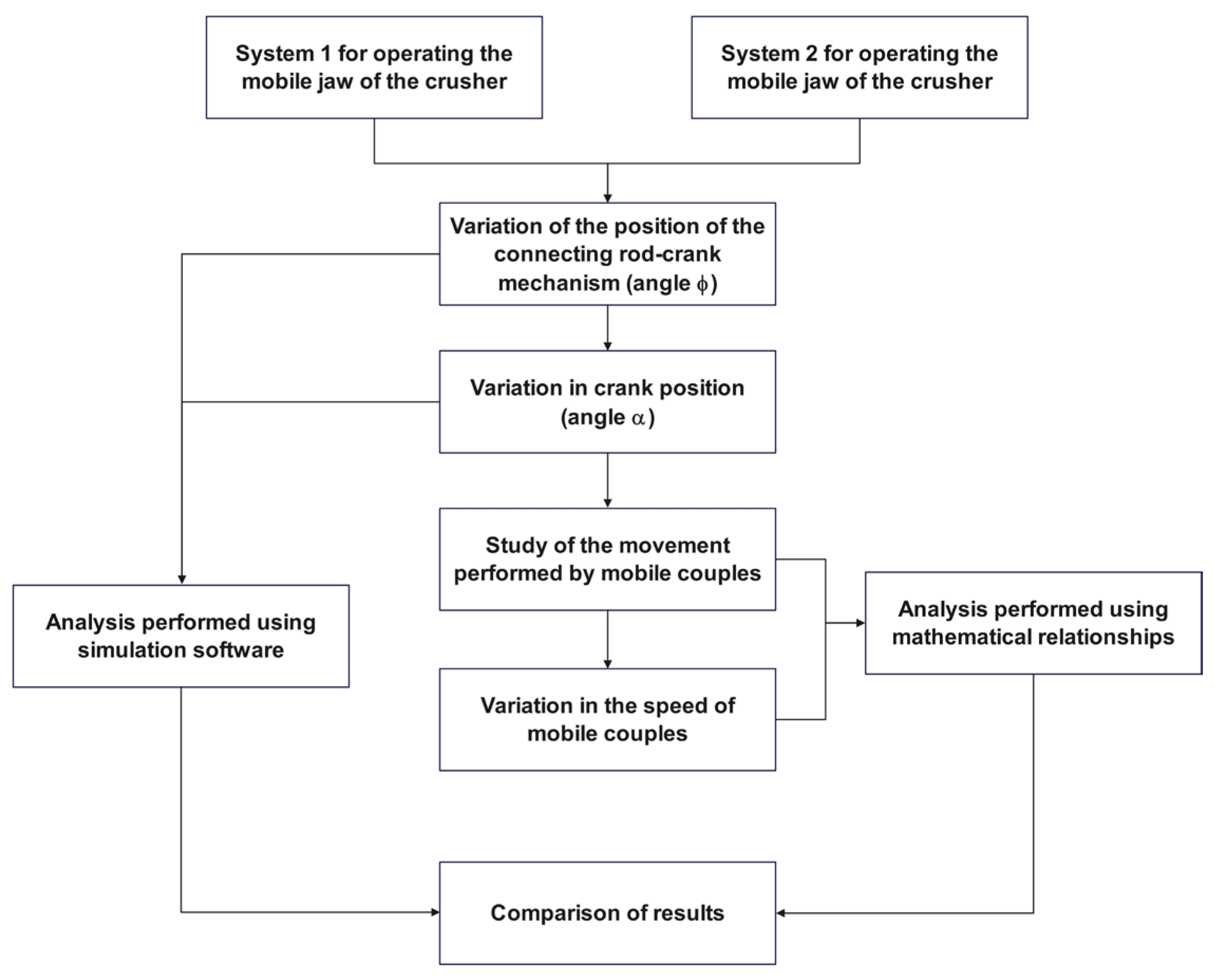
2. Methodology
3. Theoretical Considerations
- The Equations corresponding to joint B are expressed as follows:
- 2.
- The calculation relationships corresponding to joint C can be determined using the following Equations:
- 3.
- The calculation formulas required to determine the coordinates of joint E are as follows:
4. Results
- Component lengths of the jaw crusher’s drive system:
- Length of element AB: 42 mm;
- Length of element BC: 2165 mm;
- Length of element DC: 1099 mm;
- Length of element CD: 1839 mm;
- Length of element FE: 2885 mm.
- Coordinates of the mechanism’s fixed joints:
- Fixed joint D: xD = 1190 mm, yD = −1800 mm;
- Fixed joint F: xF = −1625 mm, yF = 1011 mm.
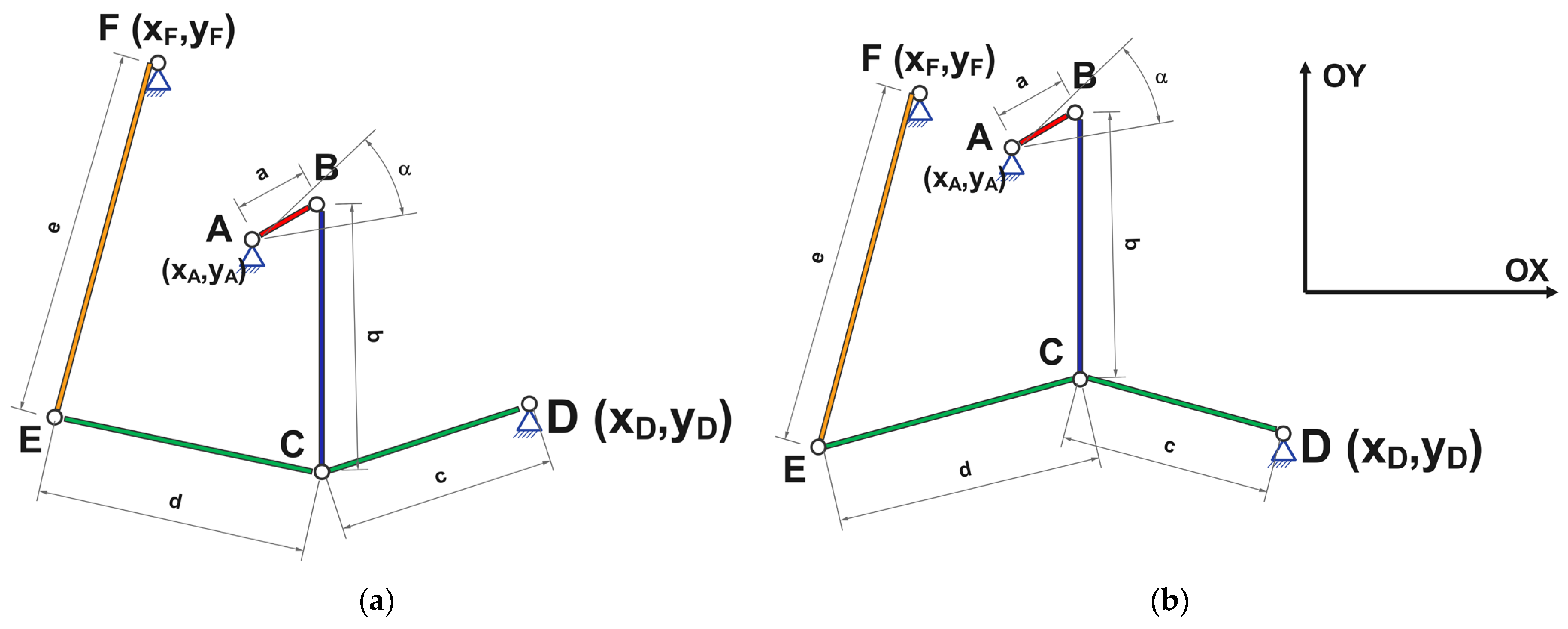
- The mechanism is constructed by respecting the fixed positions of joints D and F.
- Initially, joint A is positioned at the origin of the coordinate system XOY, with xA = 0 mm and yA = 0 mm.
- Based on the location of the fixed joints, the mechanism’s elements are then positioned.
- For the initial crank position (α = 0°), the coordinates of mobile joint C are determined.
- Considering that the study evaluates two types of drive systems for the movable jaw, two coordinate sets for joint C were obtained:
- These procedural steps were used to identify the coordinates of joint C, which serve as reference points in the kinematic analysis.
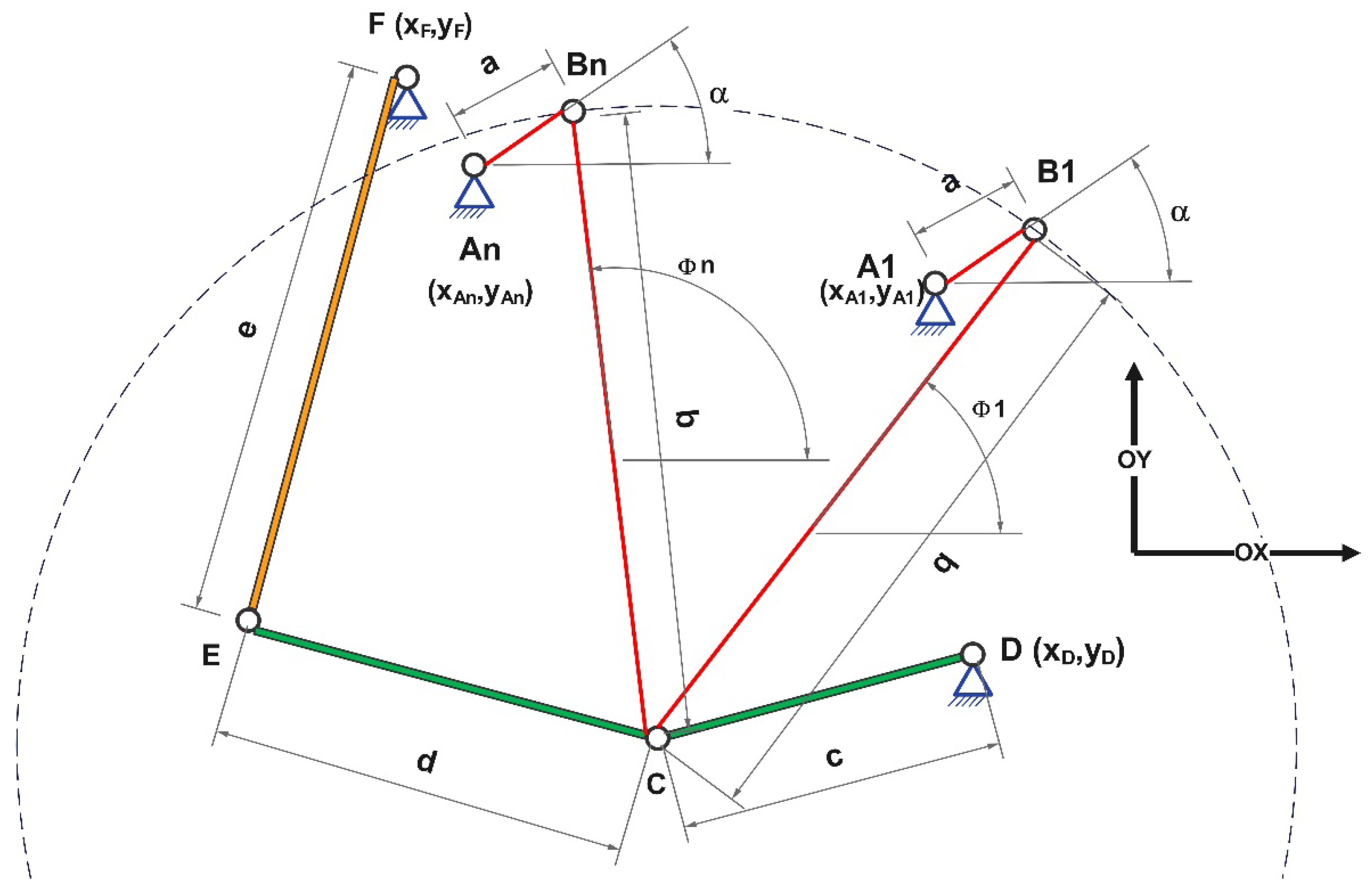
- The fixed joints F, E, C, and D are positioned within the coordinate system;
- The connecting rod CB is placed at an angle ϕ relative to the horizontal axis;
- Crank AB is positioned with an initial angle α = 0°. From this configuration, the coordinates of fixed joint A (xA and yA) are determined mathematically using the following calculation formula:
- d.
- Both the coordinates of fixed joints A, D, and F, as well as the dimensional values of the mechanism’s elements (a, b, c, d and e), will be substituted into calculation Equations (1)–(10).
- e.
- As previously stated, the mathematical computations were performed using Mathcad 15, a software platform that is capable of handling complex mathematical operations involving numerous parameters and extensive value ranges for each parameter. The following working parameters were varied during the study:
- i.
- The angle described by the crank, denoted as α, represents the rotation of the crank with respect to the horizontal axis. This angle was varied within the range of 0° to 360°, using an increment of 1.125°, resulting in a total of 321 discrete values generated by the corresponding calculation formulas.
- ii.
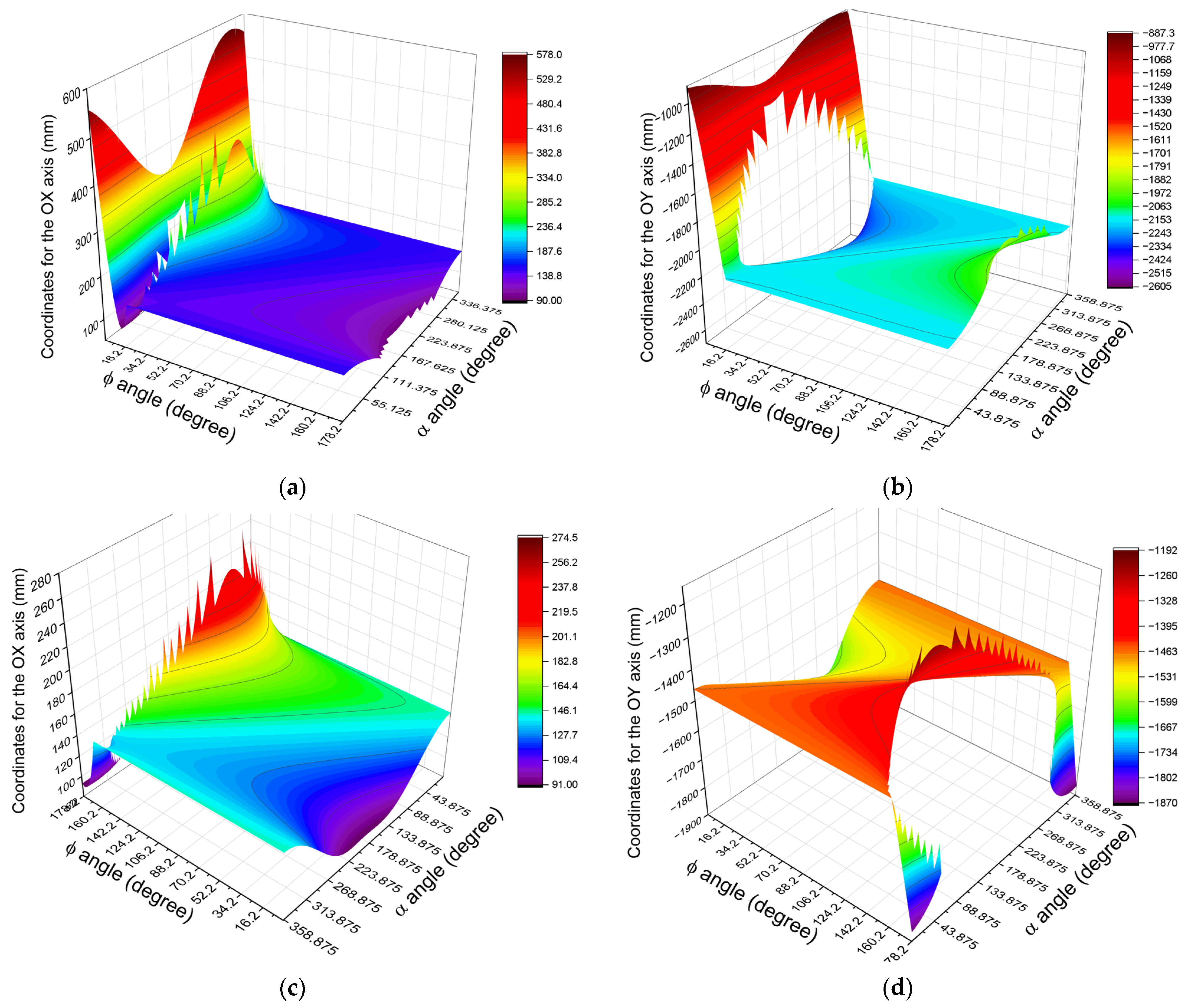
- The angle described by the connecting rod relative to the horizontal axis, denoted as ϕ, was selected based on the graphical representation presented in Figure 4. This figure illustrates the trajectory traced by fixed joint C as the angle ϕ varies between 0° and 180°. This analysis was conducted for both drive system configurations.
- Drive system corresponding to Figure 1a:
- Angle ϕ varies within the interval of 34.2° to 171° for the coordinates along the OX axis.
- For the OY axis, the valid range of angle ϕ is also 34.2° to 171°.
- Drive system corresponding to Figure 1b:
- Angle ϕ varies within the interval of 0° to 133° for coordinates along the OX axis.
- For the OY axis, the angle ϕ varies between 0° and 135°.
- The step size for angle α is 1.125°. This value was chosen arbitrarily; there is no mathematical or logical basis for this choice. It is entirely up to the person conducting the study and depends on how fine or coarse they wish the mathematical analysis to be.
- Similarly, the step size used for varying angle ϕ was also selected arbitrarily, just like in the case of angle α.
- -
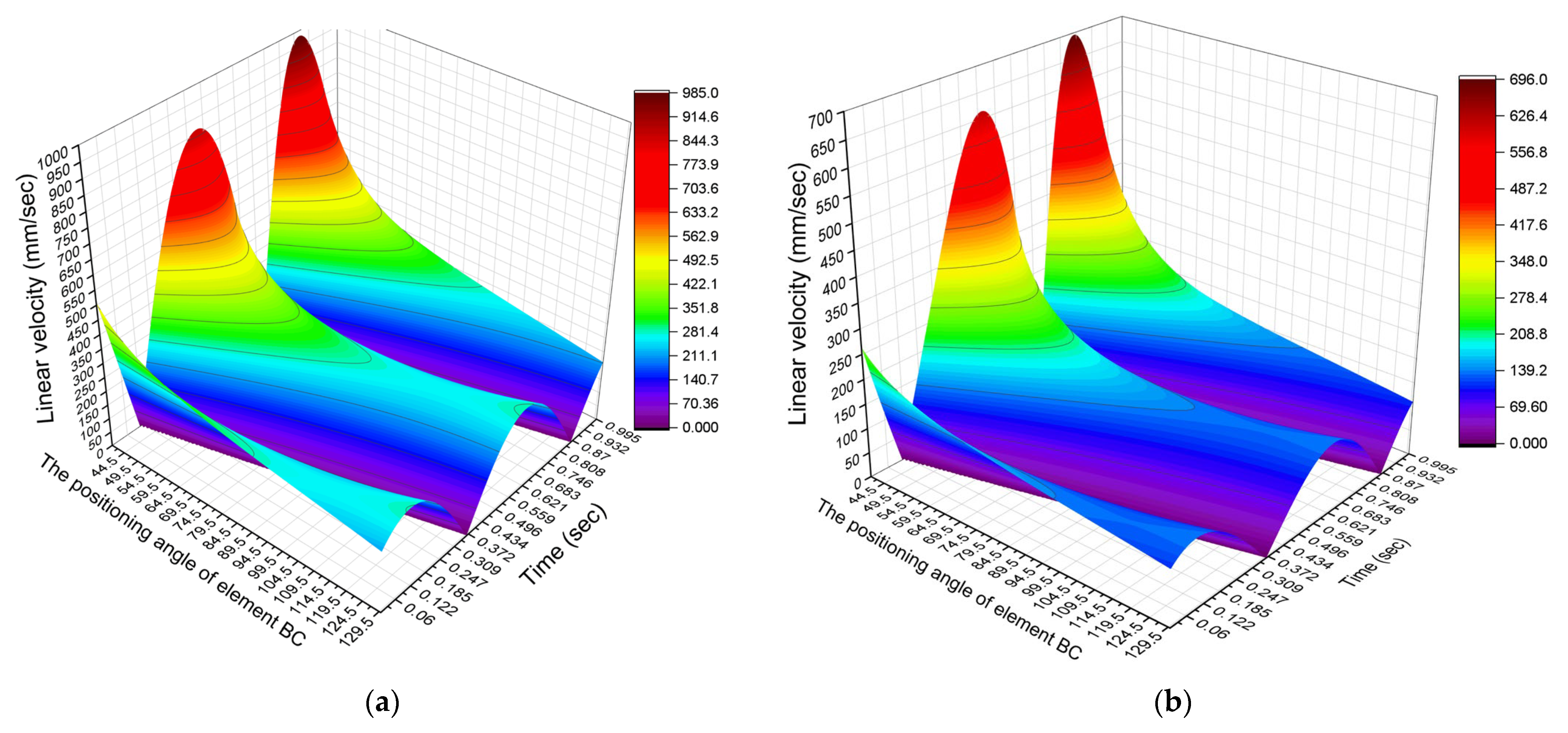
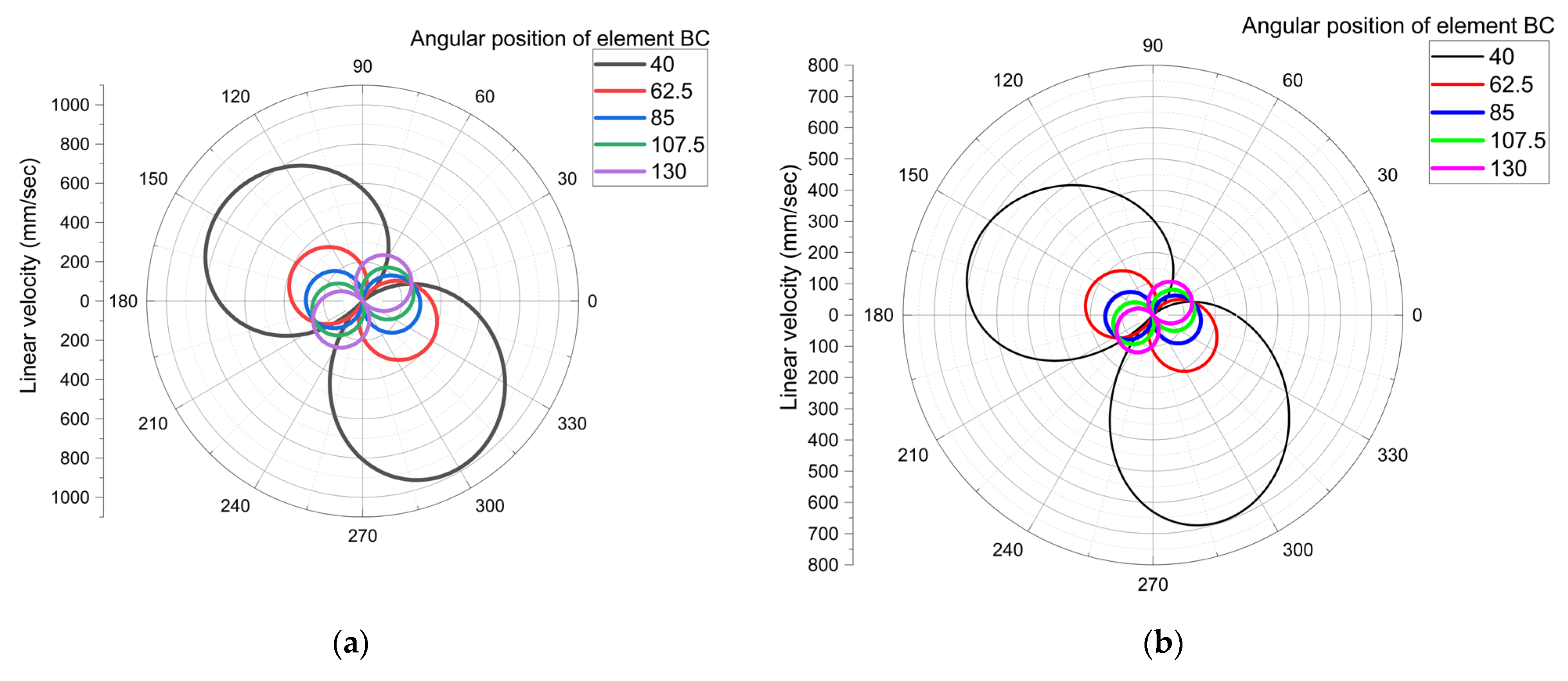
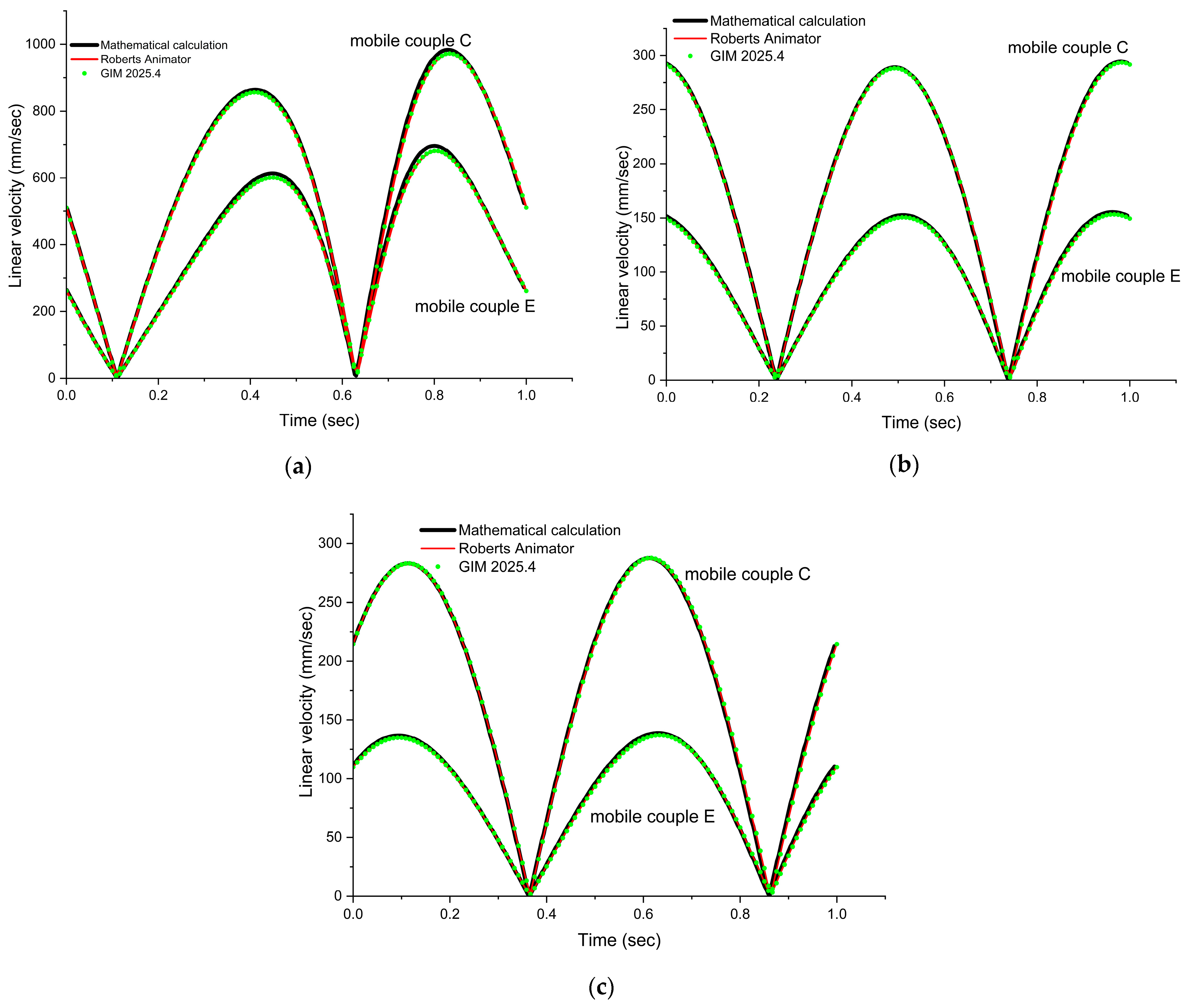
- For Figure 5a, the linear velocity varies between 0.01 mm/sand 983.241 mm/s;
- -
- For Figure 5b, the linear velocity varies between 0.0004 mm/s and 695.974 mm/s;
- -
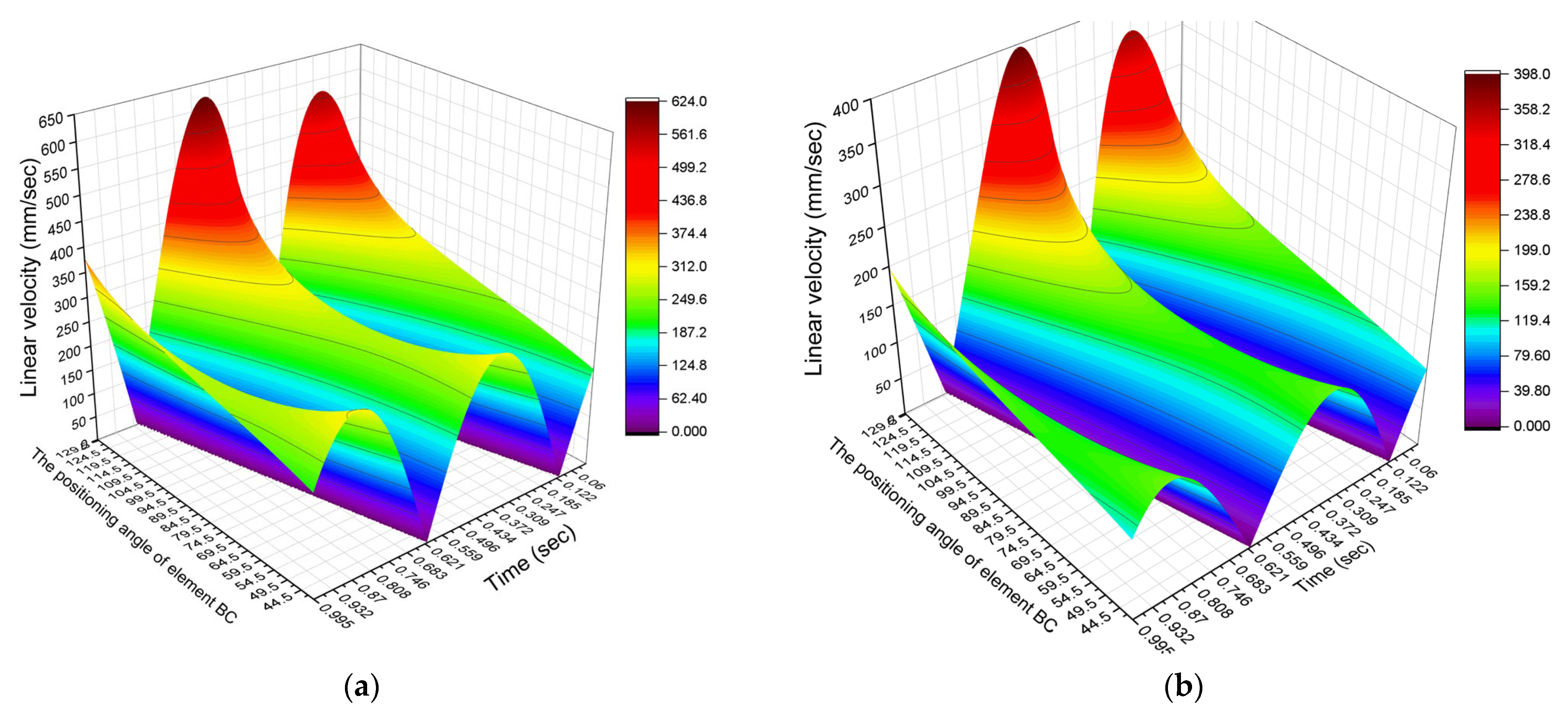
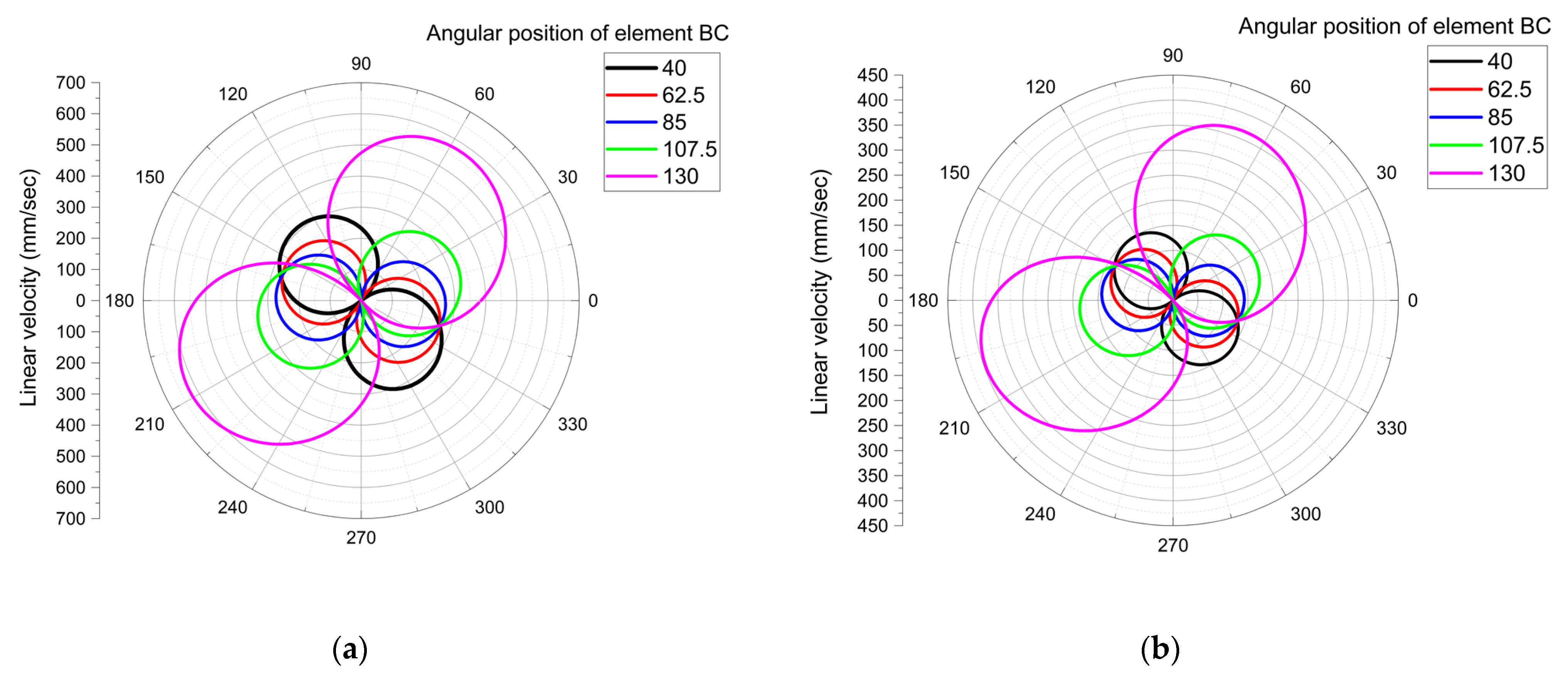
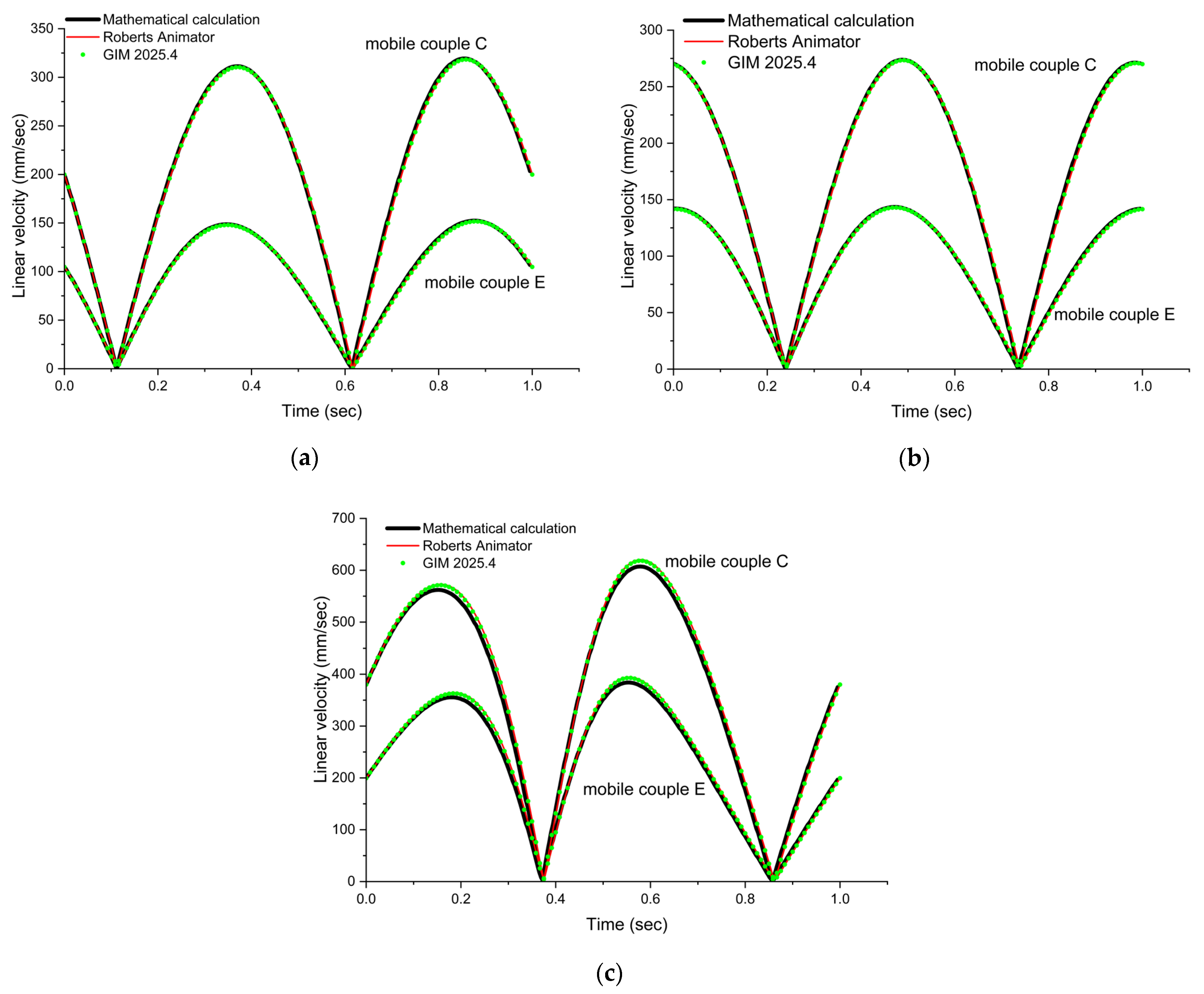
- For Figure 6a, the linear velocity varies between 0.005 mm/s and 622.66 mm/s;
- -
- For Figure 6b, the linear velocity varies between 0.002 mm/sand 396.52 mm/s.
- -
- The velocity variation follows a sinusoidal pattern.
- -
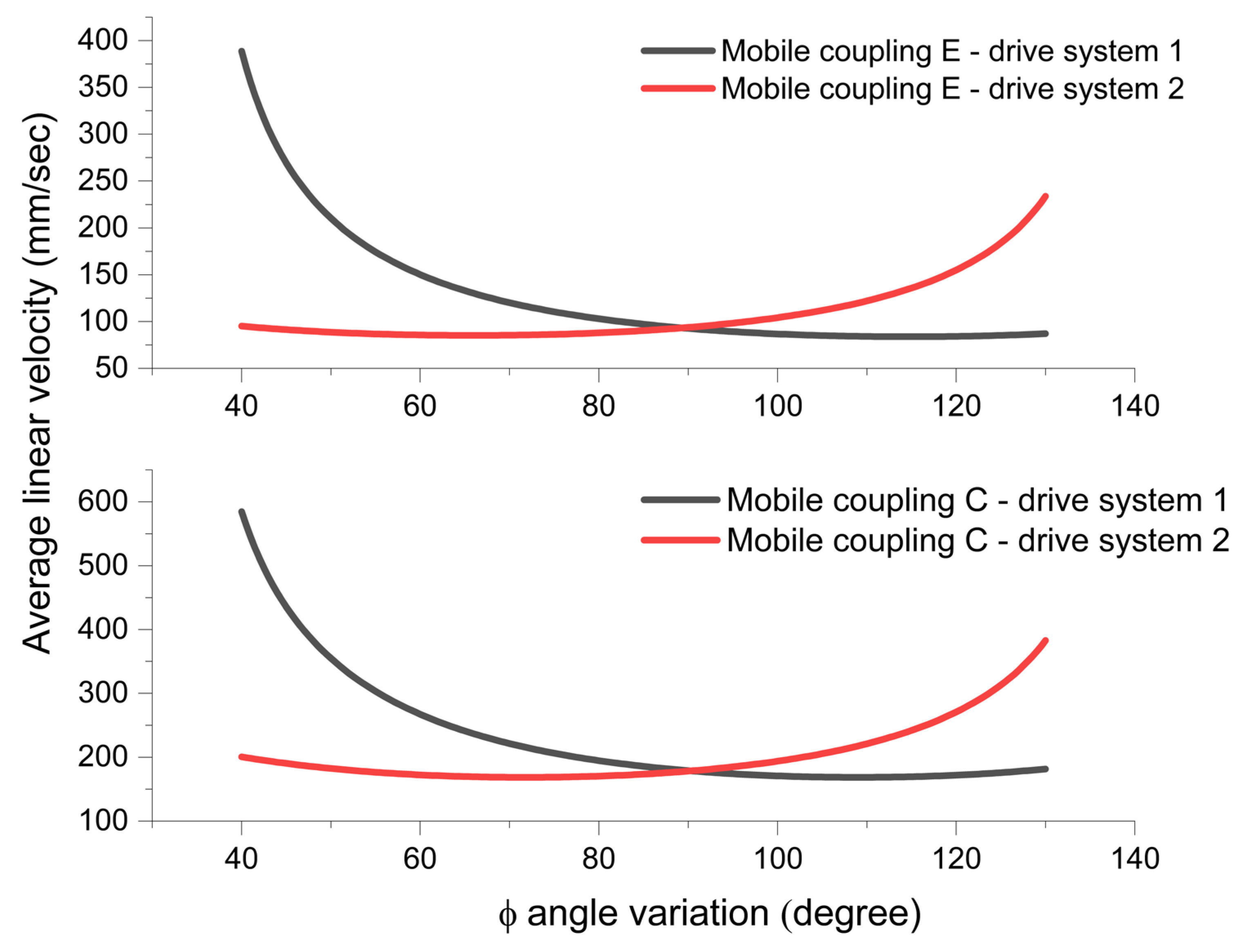
- The maximum values of the studied parameter are observed at moving joint C. For moving joint E, a decrease in linear velocity is observed. This decrease is consistent across both drive systems and amounts to approximately 64%.
- -
- For the initial value of angle ϕ = 40°, the highest linear velocity values are obtained for both moving joints C and E. As the value of angle ϕ increases, the linear velocity decreases, reaching a minimum peak of 264.789 mm/s for joint C and 132.8 mm/s for joint E. These minimum values occur within the angle range ϕ = 105–111°. Beyond this interval, the linear velocity values begin to increase again. This pattern of variation is characteristic of the first drive system.
- -
- In contrast, for the second drive system of the crusher, the variation in linear velocity is inverted compared to the first system. Specifically, the maximum linear velocity values are obtained at ϕ = 130°, and they decrease to a minimum peak of 264.801 mm/sec (for joint C) and 134.79 mm/s (for joint E). These minimum values are observed within the angle range ϕ = 64.5–69.5°. As with the first system, the parameter values begin to increase again after this interval.
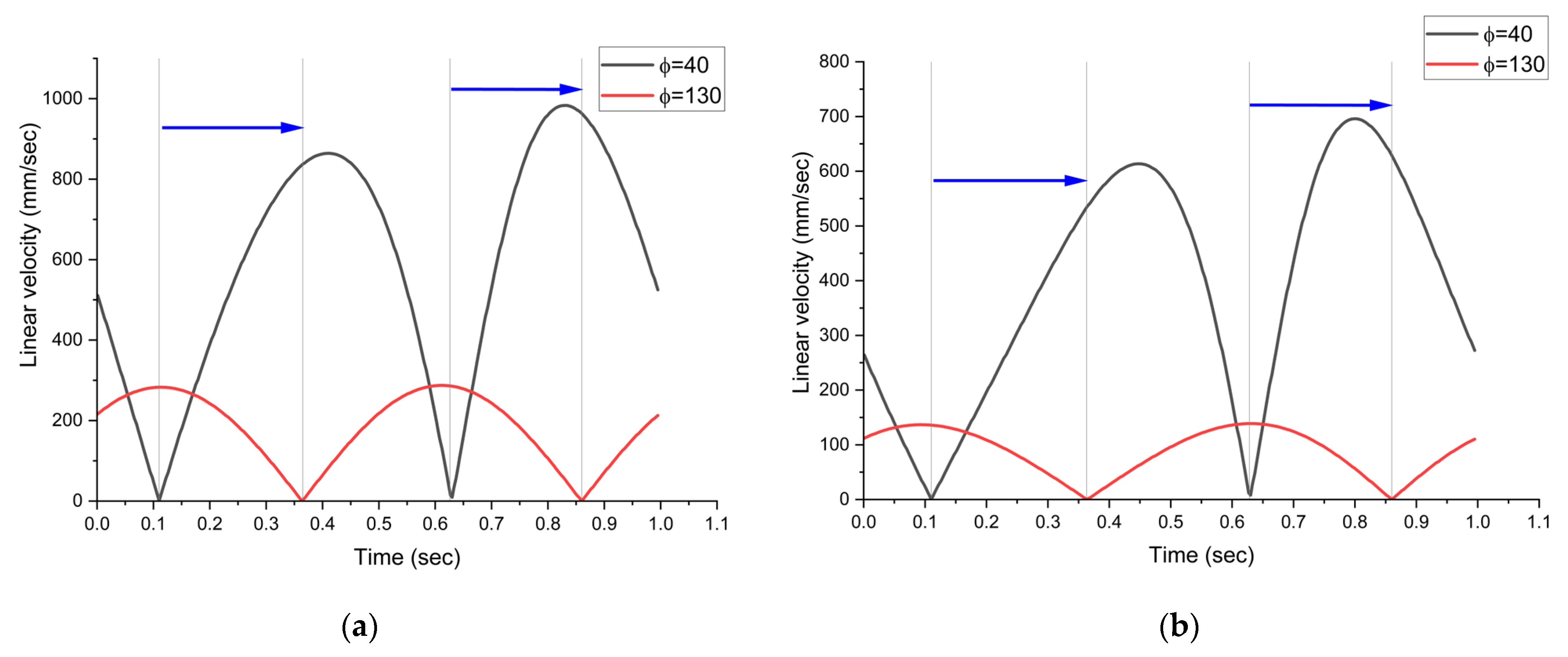
- 1. Regarding the drive system corresponding to Figure 1a, for the five selected values of angle ϕ, the maximum linear velocity values were obtained as follows:
- For joint C:
- ○
- ϕ = 40° → maximum linear velocity at α = 144° and 306°;
- ○
- ϕ = 62.5° → maximum linear velocity at α = 157° and 330°;
- ○
- ϕ = 80° → maximum linear velocity at α = 177° and 350°;
- ○
- ϕ = 107.5° → maximum linear velocity at α = 199° and 16.8°;
- ○
- ϕ = 130° → maximum linear velocity at α = 220° and 40.8°.
- For joint E:
- ○
- ϕ = 40° → maximum linear velocity at α = 158.6° and 292°;
- ○
- ϕ = 62.5° → maximum linear velocity at α = 165° and 322°;
- ○
- ϕ = 80° → maximum linear velocity at α = 184.5° and 347°;
- ○
- ϕ = 107.5° → maximum linear velocity at α = 206° and 10.1°;
- ○
- ϕ = 130° → maximum linear velocity at α = 228° and 33.7°.
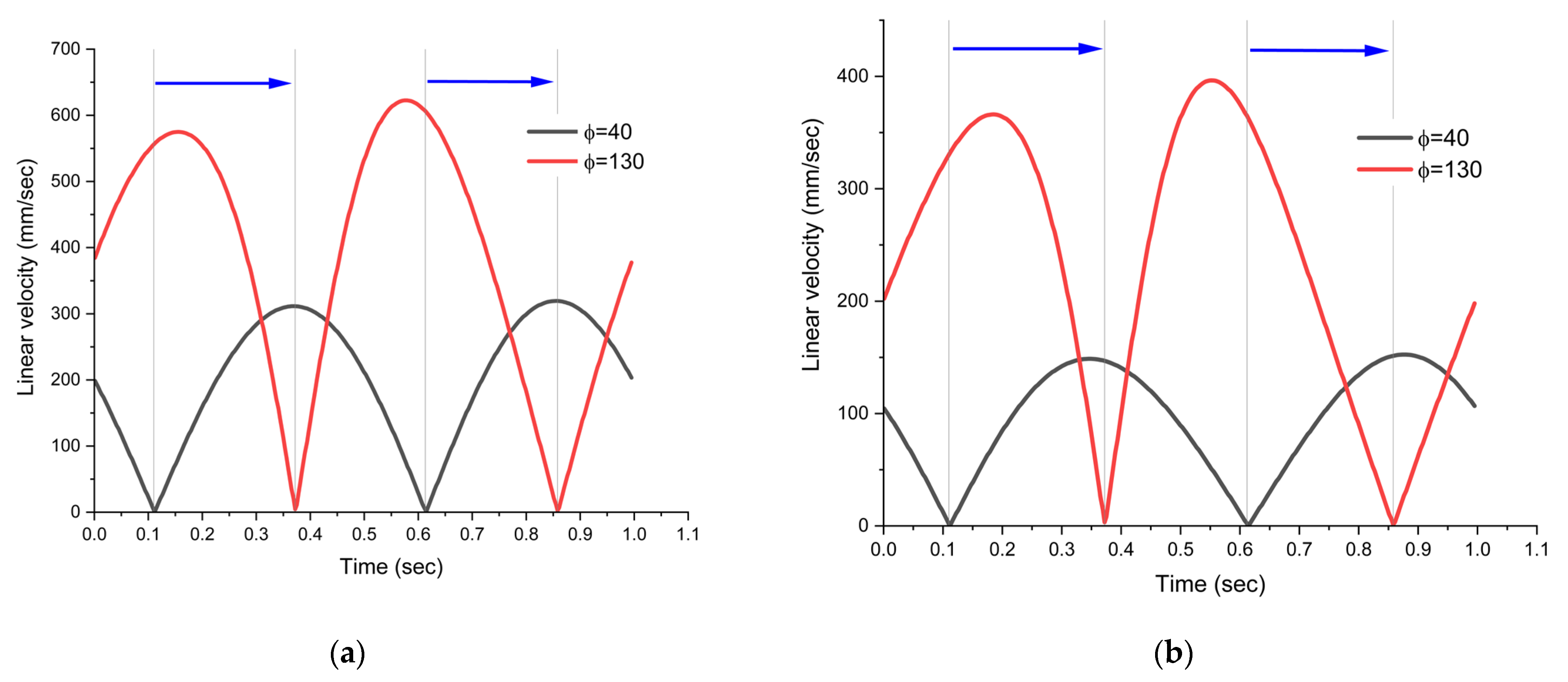
- 2. Regarding the drive system illustrated in Figure 1b, the analysis conducted for the five selected values of angle ϕ revealed the angular positions α at which the linear velocity reaches its maximum, for both joint C and joint E:
- For joint C, the following results were obtained:
- ○
- ϕ = 40° → maximum linear velocity at α = 134° and 309°;
- ○
- ϕ = 62.5° → maximum linear velocity at α = 154° and 332°;
- ○
- ϕ = 80° → velocity peaks at α = 176° and 353°;
- ○
- ϕ = 107.5° → maximum velocity at α = 196.8° and 20.2°;
- ○
- ϕ = 130° → maximum values at α = 207° and 56.2°.
- For joint E, the angular positions α corresponding to the maximum velocities are as follows:
- ○
- ϕ = 40° → maximum velocity at α = 125° and 316°;
- ○
- ϕ = 62.5° → maximum values at α = 148.5° and 337°;
- ○
- ϕ = 80° → peaks located at α = 169.8° and 2.25°;
- ○
- ϕ = 107.5° → maximum velocity at α = 190.1° and 28.1°;
- ○
- ϕ = 130° → maximum values recorded at α = 200.2° and 65°.
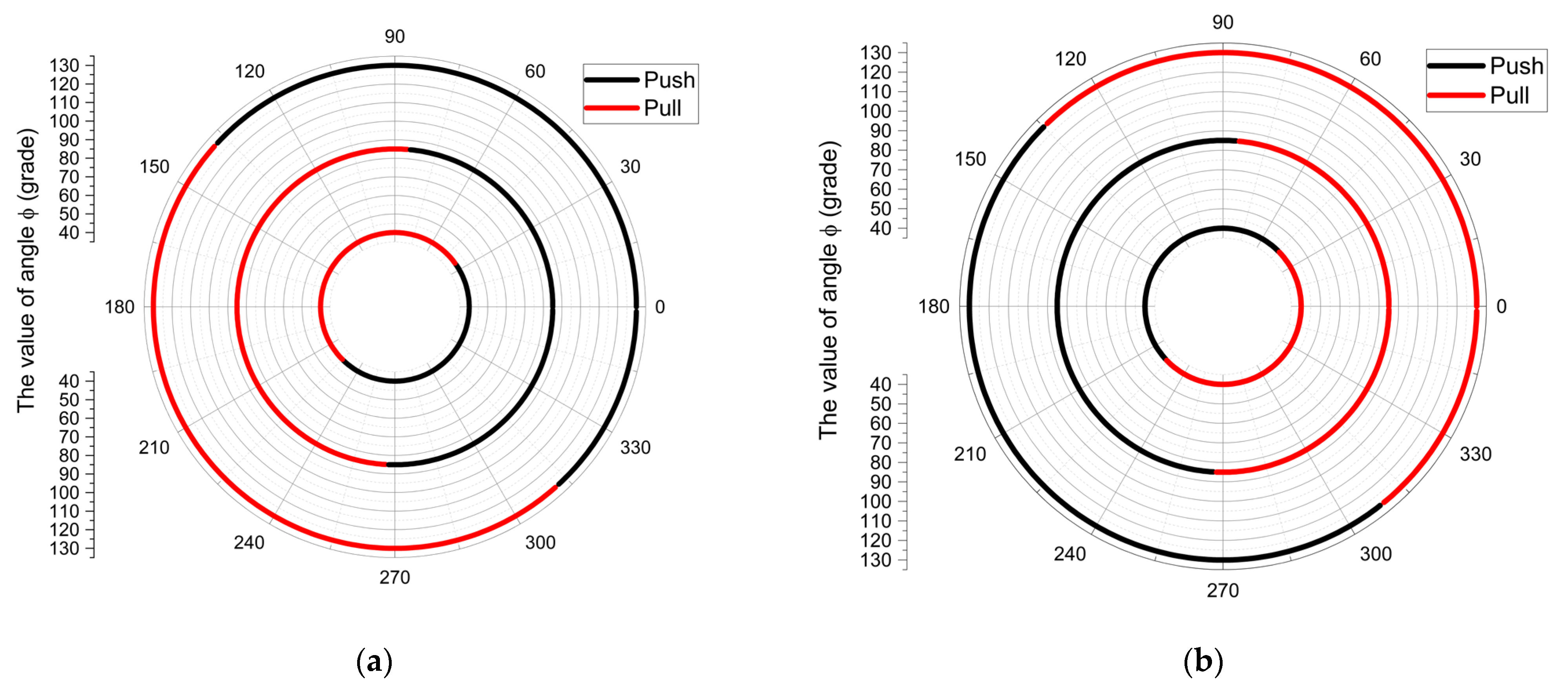
- 3. By analyzing all the values corresponding to the linear velocity peaks, the following observations can be made:
- For the drive system illustrated in Figure 1a, it is observed that angle α shifted by 76° and 94.8° from its initial value (corresponding to ϕ = 40°) for joint C, and by 69.4° and 101.7° for joint E.
- For the second drive system, presented in Figure 1b, a similar variation in angle α is observed: it changes by 73° and 116.6° for joint C, and by 75.2° and 109° for joint E, relative to the initial value corresponding to ϕ = 40°.
- -
- -
- Furthermore, from the comparative analysis of the aforementioned graphs, the following is observed:
- The highest velocity value in Drive System 1 occurs during the pushing phase (i.e., high velocity during the crushing process, the active stroke).
- The same conclusion applies to Drive System 2, based on the analysis of its linear velocity variation.
5. Discussion
6. Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okechukwu, C.; Dahunsi, O.A.; Oke, P.K.; Oladele, I.O.; Dauda, M.; Olaleye, B.M. Design and operations challenges of a single toggle jaw crusher: A review. Niger. J. Technol. 2017, 36, 814–821. [Google Scholar] [CrossRef]
- Gurway, S.; Gadge, P. Stone Crushers: A Technical Review on Significant Part of Construction Industry. In Recent Advances in Civil Engineering; Springer: Singapore, 2022; pp. 365–383. [Google Scholar]
- Patel, G.; Kumar, D. Study of Kinematic and Dynamic Analysis of Jaw Crusher—A Review. 2016. Available online: https://www.academia.edu/127781687/Study_of_Kinematic_and_Dynamic_Analysis_of_Jaw_Crusher_A_Review (accessed on 30 May 2025).
- Mining Equipment Maintenance. In Mining Equipment Reliability, Maintainability, and Safety; Dhillon, B.S., Ed.; Springer: London, UK, 2008; pp. 115–133. [Google Scholar]
- Toryanik, E.I.; Gryzlov, A.V.; Zhuravsky, A.A.; Kubrak, S.S. Determining the Strength of Coke under Crushing Forces. Coke Chem. 2017, 60, 102–107. [Google Scholar] [CrossRef]
- Wu, J.J.; Wu, S.L.; You, X.X. PHM for complex mining and metallurgy equipment multi-state system based optimal multivariate Bayesian model. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Selangor Darul Ehsan, Malaysia, 9–12 December 2014; pp. 1042–1046. [Google Scholar]
- Ciężkowski, P.; Lubikowski, K.; Łosiewicz, A.; Bąk, S.; Caban, J.; Dumała, S.; Grabowski, P. Investigation effect of the process parameters in mechanical comminution on ceramic materials. Adv. Sci. Technol. Res. J. 2025, 19, 223–238. [Google Scholar] [CrossRef]
- Deb, M.; Sen, D. Parametric study of the behavior of double toggle switching mechanisms. Mech. Mach. Theory 2013, 63, 8–27. [Google Scholar] [CrossRef]
- Deb, M.; Sen, D. Design of double toggle switching mechanisms. Mech. Mach. Theory 2014, 71, 163–190. [Google Scholar] [CrossRef]
- Hafeez, I.; Juniad, F.; Kamal, M.A.; Hussain, J. Influence of single-and two-stage aggregate manufacturing mechanisms on asphalt mixture performance. J. Mater. Civ. Eng. 2016, 28, 04015180. [Google Scholar] [CrossRef]
- Korman, T.; Bedekovic, G.; Kujundzic, T.; Kuhinek, D. Impact of physical and mechanical properties of rocks on energy consumption of Jaw Crusher. Physicochem. Probl. Miner. Process. 2015, 51, 461–475. [Google Scholar] [CrossRef]
- Leich, L.; Röttger, A.; Krengel, M.; Theisen, W. Recycling of NdFeB Magnets by Electrodischarge Sintering—Microstructure, Magnetic, and Mechanical Properties. J. Sustain. Met. 2019, 5, 107–117. [Google Scholar] [CrossRef]
- Pasaribu, M.A.H.; Adhitya, B.B.; Costa, A.; Nayobi, B. Effect of Curing Time and Variations in Na2SiO3: NaOH Ratio on the Mechanical Properties of Fly Ash-based Geopolymer Artificial Aggregates using the Crushing Method. J. Adv. Res. Appl. Mech. 2024, 117, 107–117. [Google Scholar] [CrossRef]
- Arsenault, M.; Tremblay, L.F.; Zeinali, M. Optimization of trajectory durations based on flow rate scaling for a 4-DoF semi-automated hydraulic rockreaker. Mech. Mach. Theory 2020, 143, 103632. [Google Scholar] [CrossRef]
- Bello, S.K.; Bajela, G.G.; Lamidi, S.; Oshinlaja, S. Design and Fabrication of Pneumatic Can Crushing Machine. Int. J. Adv. Sci. Res. Eng. 2020, 6, 154–161. [Google Scholar] [CrossRef]
- Klinzing, G.E.; Rizk, F.; Marcus, R.; Leung, L.S. Principles of Pneumatic Conveying. In Pneumatic Conveying of Solids: A Theoretical and Practical Approach; Klinzing, G.E., Rizk, F., Marcus, R., Leung, L.S., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 193–235. [Google Scholar]
- Nikitin, A.G.; Abramov, A.V.; Zhivago, E.Y.; Dvornikov, L.T.; Saruev, L.A. Improvement of jaw crushers reliability using elastic pneumatic elements in the connection of kinematic pairs. IOP Conf. Ser. Mater. Sci. Eng. 2018, 411, 012054. [Google Scholar] [CrossRef]
- Han, B.; Chakraborty, A. Ligand extension of aluminum fumarate metal-organic framework in transferring higher water for adsorption desalination. Desalination 2024, 592, 118135. [Google Scholar] [CrossRef]
- Han, B.; Chakraborty, A. Synergistic ionic liquid encapsulated MIL-101 (Cr) metal-organic frameworks for an innovative adsorption desalination system. J. Clean. Prod. 2024, 474, 143565. [Google Scholar] [CrossRef]
- Altshul, G.M.; Gouskov, A.M.; Panovko, G.Y.; Shokhin, A.E. Interaction model of one jaw of a vibrating jaw crusher with the processed rock, taking into account the properties of the electric motor. IOP Conf. Ser. Mater. Sci. Eng. 2020, 747, 012047. [Google Scholar] [CrossRef]
- Bru, K.; Beaulieu, M.; Sousa, R.; Leite, M.M.; de Sousa, A.B.; Kol, E.; Rosenkranz, J.; Parvaz, D.B. Comparative laboratory study of conventional and Electric Pulse Fragmentation (EPF) technologies on the performances of the comminution and concentration steps for the beneficiation of a scheelite skarn ore. Min. Eng. 2020, 150, 106302. [Google Scholar] [CrossRef]
- Gavrilov, Y.A.; Zagrivniy, E.A. The Autoresonant Electric Drive of the Swinging Movement Pendular Vibration Exciter Vibration Jaw Crushers. J. Min. Inst. 2010, 186, 116–119. [Google Scholar]
- Huang, J.; Zong, Y.; Liu, Y.; Hu, K.; Wang, B.; Zhao, X.; Jiang, T.; Hong, Z.; Wang, Z.L. Feature-Reinforced Strategy for Enhancing the Accuracy of Triboelectric Vibration Sensing Toward Mechanical Equipment Monitoring. Small 2025, 21, 2503997. [Google Scholar] [CrossRef]
- Mohammadi, V.S.; Noaparast, M.; Aslani, S. The effect of high voltage electrical pulses on iron ore comminution to improve desulfurization flotation recovery. Physicochem. Probl. Miner. Process. 2022, 58, 150264. [Google Scholar] [CrossRef]
- Chen, Y.H.; Zhang, G.S.; Zhang, R.L.; Gupta, T.; Katayama, A. Finite element study on the wear performance of movable jaw plates of jaw crushers after a symmetrical laser cladding path. Symmetry 2020, 12, 1126. [Google Scholar] [CrossRef]
- Pedro, D.; de Brito, J.; Evangelista, L. Performance of concrete made with aggregates recycled from precasting industry waste: Influence of the crushing process. Mater. Struct. Mater. Constr. 2015, 48, 3965–3978. [Google Scholar] [CrossRef]
- Xu, P.Y.; Li, J.; Hu, C.; Chen, Z.; Ye, H.Q.; Yuan, Z.Q.; Cai, W.J. Surface property variations in flotation performance of calcite particles under different grinding patterns. J. Cent. South Univ. 2018, 25, 1306–1316. [Google Scholar] [CrossRef]
- Sastri, S.R.S. Capacities and performance characteristics of jaw crushers. Min. Metall. Explor. 1994, 11, 80–86. [Google Scholar] [CrossRef]
- Rajan, B.; Singh, D. Comparison of Shape Parameters and Laboratory Performance of Coarse Aggregates Produced from Different Types of Crushing Operations. J. Mater. Civ. Eng. 2017, 29, 04017044. [Google Scholar] [CrossRef]
- Olaleye, B.M. Influence of some rock strength properties on jaw crusher performance in granite quarry. Min. Sci. Technol. 2010, 20, 204–208. [Google Scholar] [CrossRef]
- Maleki-Moghaddam, M.; Zare, S. Investigating the chamber filling effect on the jaw crusher, cone crusher and HPGR performance. Can. Met. Q. 2025, 64, 1403–1412. [Google Scholar] [CrossRef]
- Abhilash Kumar, K.A.; Kiran, K.S.; Gopal, B.B. Optimization study and material properties of angular artificial aggregates. Emergent Mater. 2025. [Google Scholar] [CrossRef]
- Lal Chauhan, B.; Jail Singh, G. Sustainable development of recycled concrete aggregate through optimized acid-mechanical treatment: A simplified approach. Constr. Build. Mater. 2023, 399, 132559. [Google Scholar] [CrossRef]
- Chen, L.; Xue, J.; Zhang, X.; Wang, Y. Optimization and reliability analysis of movable jaw structure of jaw crusher based on response surface. Int. J. Perform. Eng. 2019, 15, 1408–1416. [Google Scholar] [CrossRef]
- Balasubramanyam, C.; Spandana, K.R.; Ajay, M.S.; Shetty, A.B.; Seetharamu, K.N. Optimization approach for synthesis of 5 point double toggle mechanism. Int. J. Interact. Des. Manuf. 2017, 11, 839–850. [Google Scholar] [CrossRef]
- Chen, Z.R.; Wang, G.Q.; Xue, D.M.; Bi, Q.S. Simulation and optimization of gyratory crusher performance based on the discrete element method. Powder Technol. 2020, 376, 93–103. [Google Scholar] [CrossRef]
- Datta, S.; Roy, S.; Davim, J.P. Optimization Techniques: An Overview. In Optimization in Industry: Present Practices and Future Scopes; Datta, S., Davim, J.P., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–11. [Google Scholar]
- Gurway, S.; Gadge, P. Optimizing processing parameters of stone crushers through Taguchi method. Mater. Today Proc. 2022, 65, 3512–3518. [Google Scholar] [CrossRef]
- Laciak, M.; Šofranko, M. Optimization of device selection in design of technological lines for the aggregates production. Appl. Mech. Mater. 2014, 611, 387–394. [Google Scholar] [CrossRef]
- Luo, Z.; Li, S. Optimization design for crushing mechanism of double toggle jaw crusher. Appl. Mech. Mater. 2012, 201–202, 312–316. [Google Scholar] [CrossRef]
- Murithi, M.; Keraita, J.N.; Obiko, J.O.; Mwema, F.M.; Wambua, J.M.; Jen, T.-C. Optimisation of the swinging jaw design for a single toggle jaw crusher using finite element analysis. Int. J. Interact. Des. Manuf. 2024, 18, 6351–6358. [Google Scholar] [CrossRef]
- Li, S.J.; Wan, X.H.; Dong, Z.W.; Hou, W.Z. Optimization designing of jaw crusher teeth plate shape based on the FEM method. Adv. Mater. Res. 2013, 614, 333–336. [Google Scholar] [CrossRef]
- Zhang, J.C.; Wang, L.C. Optimization design of vibratory jaw crusher with double cavities based on matlab. Adv. Mater. Res. 2014, 945–949, 596–599. [Google Scholar] [CrossRef]
- Baruti, B.; Peci, N.; Vitaku, A.; Malollari, I.; Zeqiri, R.; Kelmendi, M. Analysis of the Possibilities of Decreasing the Impact of Crushing Operations on Environment. J. Environ. Prot. Ecol. 2011, 12, 2056–2061. [Google Scholar]
- Bo, S.J.; Wang, X.; Ye, Q.H. Dynamic simulation research of jaw crusher with multi-joint clearance. Appl. Mech. Mater. 2014, 644–650, 2678–2681. [Google Scholar] [CrossRef]
- Muscalu, M.; Ghica, V.G.; Iacob, G.; Petrescu, M.I.; Buzatu, M. Studies and research on waste mosi2 heating elements. UPB Sci. Bull. Ser. B Chem. Mater. Sci. 2021, 83, 239–248. [Google Scholar]
- Zhao, Z.; Li, Y.; Li, W.; Xian, Z.; Zhu, X.; Zhong, J. Research on the biaxial compound pendulum jaw crusher based on seven-bar mechanism. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 1876–1889. [Google Scholar] [CrossRef]
- Ciezkowski, P.; Maciejewski, J.; Bak, S. Analysis of Energy Consumption of Crushing Processes—Comparison of One-Stage and Two-Stage Processes. Stud. Geotech. Mech. 2017, 39, 17–24. [Google Scholar] [CrossRef][Green Version]
- Mishchuk, Y.; Mishchuk, D.; Kapusta, O. Mathematical modeling kinematics of double toggle jaw crusher. Girnichi Budivelni Dorozhni Ta Meliorativni Mashini 2023, 102, 5–16. [Google Scholar] [CrossRef]
- Sinha, R.S.; Mukhopadhyay, A.K. Failure rate analysis of Jaw Crusher: A case study. Sadhana 2019, 44, 17. [Google Scholar] [CrossRef]
- Hroncová, D.; Delyova, I.; Frankovský, P.; Neumann, V.; Čech, D. Kinematic motion analysis of the members of a double jaw crusher. Acta Mechatronica 2022, 7, 1–7. [Google Scholar] [CrossRef]
- Sinha, R.S.; Mukhopadhyay, A.K. Failure rate analysis of jaw crusher using Weibull mode. J. Process Mech. Eng. 2016, 231, 760–772. [Google Scholar] [CrossRef]
- Erry, S.; Partama, M.; Fahrudinoor. Size distribution of jaw crusher crushing products for rounded material. KURVATEK 2024, 9, 95–100. [Google Scholar] [CrossRef]
- Shrivastava, A.K.; Sharma, A.K. A review on study of jaw crusher. Int. J. Mod. Eng. Res. 2012, 2, 885–888. [Google Scholar]
- Tufan, B.; Tufan, E. Evaluating the impacts of jaw crusher design parameters by simulation. In Proceedings of the 10th International Conference on Advances in Science, Engineering and Technology (ICASET-18), Paris, France, 20–21 June 2018. [Google Scholar]
- PaweŁ, C. Correlation of energy consumption and shape of crushing plates. J. Min. Geoengin. 2012, 2012, 91–100. [Google Scholar]
- Gupta, A.; Yan, D. Mineral Processing Design and Operation; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Peter, N.M. Optimisation of Energy Efficiency and Comminution Process of a Single Toggle Jaw Crusher Using Discrete Element Method. Ph.D. Thesis, Jomo Kenyatta University of Agriculture And Technology, Juja, Kenya, 2021. [Google Scholar]
- Shrivastava, A.K.; Sharma, A.K. Dynamic Analysis of Double Toggle Jaw Crusher Using Pro- Mechanica. Int. J. Eng. Res. Appl. 2012, 2, 1132–1135. [Google Scholar]
- Gaesenngwe, G.; Gwiranai, D.; Shephered, B. Assessing Efficiency in a unified size reduction plant when reducing large ore into powder particulate matter. Procedia Manuf. 2019, 35, 808–813. [Google Scholar] [CrossRef]
- Cao, J.; Rong, X.; Yang, S.C. Jaw plate kinematical analysis for single toggle jaw crusher design. In Proceedings of the International Technology and Innovation Conference 2006 (ITIC 2006), London, UK, 11–12 October 2006. [Google Scholar]
- Guan, Y.; Zhang, Q.; Zhang, Z.; Xiao, Y. Modeling simulation and kinematic analysis based on Pro/Engineer for jaw crusher mechanism. In Proceedings of the 2011 2nd International Conference on Mechanic Automation and Control Engineering, MACE 2011—Proceedings, Hohhot, China, 15–17 July 2011; pp. 1407–1409. [Google Scholar]
- Oduori, M.; Mutuli, S.; Munyasi, D. The kinematics and mechanical advantage of the double-toggle jaw crusher. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 095440621773555. [Google Scholar] [CrossRef]
- Yong, J. Resrarch on the Kinematics simulation of out-moving jaw crusher based on Nastran. Appl. Mech. Mater. 2013, 433–435, 63–66. [Google Scholar] [CrossRef]
- Liang, J.T.; Zhao, S.D.; Zhao, Y.Q.; Zhu, M.Z. Hybrid-loop servo control system of double toggle mechanical press for flexible forming process based on sliding mode control and neural network techniques. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2016, 230, 35–45. [Google Scholar] [CrossRef]
- Legendre, D.; Zevenhoven, R. Assessing the energy efficiency of a jaw crusher. Energy 2014, 74, 119–130. [Google Scholar] [CrossRef]
- Bhatawdekar, R.M.; Singh, T.N.; Tonnizam Mohamad, E.; Armaghani, D.J.; Binti Abang Hasbollah, D.Z. River Sand Mining Vis a Vis Manufactured Sand for Sustainability. In Proceedings of the International Conference on Innovations for Sustainable and Responsible Mining; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2021; pp. 143–169. [Google Scholar]
- Eddie, G.-H.; Ahmed, S.; Semaan, A. Design and modeling of a six-bar mechanism for repetitive tasks with symmetrical end effector motion. Eng. Technol. Appl. Sci. Res. 2024, 14, 16302–16310. [Google Scholar] [CrossRef]
- Figliolini, G.; Lanni, C.; Tomassi, L. First- and Second-Order Centrodes of Both Coupler Links of Stephenson III Six-Bar Mechanisms. Machines 2025, 13, 93. [Google Scholar] [CrossRef]
- Rishmany, J.; Imad, R. Finite Element and Multibody Dynamics Analysis of a Ball Mill Glass Crusher. Model. Simul. Eng. 2023, 2023, 1–17. [Google Scholar] [CrossRef]
- Xiong, Y.; Gan, J.; Chen, W.; Ou, T.; Zhao, G.; Wu, D. Application of Multibody Dynamics and Bonded-Particle GPU Discrete Element Method in Modelling of a Gyratory Crusher. Minerals 2024, 14, 774. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, K.; Zhang, Y.; An, J. Discrete Element Method–Multibody Dynamics Coupling Simulation and Experiment of Rotary Tillage and Ridging Process for Chili Pepper Cultivation. Agronomy 2024, 14, 446. [Google Scholar] [CrossRef]
- Plamadeala, O. Studiul și analiza procesului tehnologic de concasare pentru determinarea parametrilor optimali de lucru ai concasorului. Ph.D. Thesis, Universitatea Tehnică a Moldovei Republica Moldova, Chişinău, Moldova, 2022. [Google Scholar]
- Frank, O.M.; Mwenje, M.S.; Masinde, M.D. Analysis of the single toggle jaw crusher kinematics. J. Eng. Des. Technol. 2015, 13, 213–239. [Google Scholar] [CrossRef]
- Golikov, N.S.; Timofeev, I.P. Determination of capacity of single-toggle jaw crusher, taking into account parameters of kinematics of its working mechanism. Int. Conf. Inf. Technol. Bus. Ind. 2018, 2018 Pt 1–4, 1015. [Google Scholar] [CrossRef]
- Kemper, D.; Fimbinger, E.; Antretter, T.; Egger, M.; Flachberger, H. Impact crusher kinematics: The dynamics of an impact swing mechanism as an analytical-mathematical model. Results Eng. 2024, 21, 101694. [Google Scholar] [CrossRef]
- Technologies, H. Roberts Animator. Available online: http://www.aes.nu/1-5softprod.htm (accessed on 30 May 2025).
- Macho, E.; Urízar, M.; Petuya, V.; Hernández, A. Improving Skills in Mechanism and Machine Science Using GIM Software. Appl. Sci. 2021, 11, 7850. [Google Scholar] [CrossRef]
- Petuya, V.; Macho, E.; Altuzarra, O.; Pinto, C.; Hernandez, A. Educational software tools for the kinematic analysis of mechanisms. Comput. Appl. Eng. Educ. 2014, 22, 72–86. [Google Scholar] [CrossRef]
- Mosnegutu, E.; Barsan, N.; Chitimus, D.; Ciubotariu, V.; Bibire, L.; Mirilă, D.; Jasiński, M.; Sporea, N.; Petre, I.C. Kinematic Analysis of the Jaw Crusher Drive Mechanism: A Different Mathematical Approach. Processes 2025, 13, 2226. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mosnegutu, E.; Tomozei, C.; Irimia, O.; Ciubotariu, V.; Mirila, D.; Panainte-Lehadus, M.; Jasiński, M.; Sporea, N.; Petre, I.C. The Influence of the Geometric Configuration of the Drive System on the Motion Dynamics of Jaw Crushers. Processes 2025, 13, 2498. https://doi.org/10.3390/pr13082498
Mosnegutu E, Tomozei C, Irimia O, Ciubotariu V, Mirila D, Panainte-Lehadus M, Jasiński M, Sporea N, Petre IC. The Influence of the Geometric Configuration of the Drive System on the Motion Dynamics of Jaw Crushers. Processes. 2025; 13(8):2498. https://doi.org/10.3390/pr13082498
Chicago/Turabian StyleMosnegutu, Emilian, Claudia Tomozei, Oana Irimia, Vlad Ciubotariu, Diana Mirila, Mirela Panainte-Lehadus, Marcin Jasiński, Nicoleta Sporea, and Ivona Camelia Petre. 2025. "The Influence of the Geometric Configuration of the Drive System on the Motion Dynamics of Jaw Crushers" Processes 13, no. 8: 2498. https://doi.org/10.3390/pr13082498
APA StyleMosnegutu, E., Tomozei, C., Irimia, O., Ciubotariu, V., Mirila, D., Panainte-Lehadus, M., Jasiński, M., Sporea, N., & Petre, I. C. (2025). The Influence of the Geometric Configuration of the Drive System on the Motion Dynamics of Jaw Crushers. Processes, 13(8), 2498. https://doi.org/10.3390/pr13082498










