Investigation of Temperature Drop Characteristics During the Throttling Process of Ultra-High-Pressure Condensate Gas

Abstract

The southern margin block of the Xinjiang Oilfield represents a typical ultra-high-pressure condensate gas field. Existing surface throttling practices rely heavily on empirical experience, with the underlying throttling mechanisms remaining unclear and lacking systematic theoretical support. In this study, the TW1 Well is selected as the research subject. Based on the principle of equal total enthalpy before and after throttling—and with particular attention to the effects of condensate gas heavy components and water on enthalpy calculations—a mathematical model for throttling-induced temperature drop, tailored to ultra-high-pressure condensate gas, is developed. The model enables a systematic analysis of temperature variations throughout the throttling process. Results indicate that the pre-throttle temperature is the primary factor controlling the magnitude of temperature change, and that post-throttle temperature rise may occur due to the Joule–Thomson coefficient becoming negative under ultra-high-pressure conditions. By integrating hydrate-formation prediction with differential pressure calculations across the throttling valve, a rational production scheme is proposed. This study provides a theoretical basis for understanding the mechanisms of ultra-high-pressure condensate gas well throttling and delivers critical technical support for the scientific design and optimization of surface throttling operations.

1. Introduction

With the acceleration of natural gas exploration and development, the Xinjiang Oilfield has made substantial progress in the southern margin of the Junggar Basin. The first 100-billion-cubic-meter natural gas area in the Hutubi structural belt is undergoing rapid appraisal and development [1]. Among them, three wells in the HT1 Well Area have shown long-term stable production performance, marking a significant breakthrough for the Xinjiang Oilfield in the field of natural gas exploration and development [2,3].

The southern margin block of the Xinjiang Oilfield is characterized as a typical ultra-deep, high-temperature, and high-pressure condensate gas reservoir, with wellhead pressures reaching up to 130 MPa. To ensure the safe operation of pipelines, a multi-stage throttling method is used on-site to reduce the wellhead pressure. The post-throttling temperature and pressure at the wellhead are key parameters in the entire gathering and transportation system, critically influencing hydrate prediction, pipeline material selection, and production regime design [4]. However, due to the presence of heavy components in high-pressure condensate gas, there are large deviations in critical parameters, resulting in complex throttling behavior and an unclear throttling mechanism [5]. Therefore, there is an urgent need to study the temperature drop characteristics of ultra-high-pressure condensate gas during throttling to reveal the changing laws of key parameters, such as pressure and temperature, in the throttling system during production. This will provide the necessary theoretical basis for the design of high-pressure throttling processes at the wellhead of ultra-high-pressure gas wells.

Many scholars have conducted fruitful research on the throttling mechanism at the wellhead of high-pressure gas wells. Jiang et al. [6] developed a three-dimensional cage-and-sleeve throttling valve model to predict temperature and pressure fields within the valve, thereby preventing hydrate formation and ensuring safe production. Li et al. [7] used numerical simulation to investigate the cooling and condensation temperature drop characteristics of natural gas inside the throttling valve. Shoghl et al. [8] used CFD modeling to study the single-phase flow of hydrocarbons during throttling, predicting the Joule–Thomson behavior and the associated temperature and pressure changes of natural gas and various pure gases. Li et al. [9] developed a condensation model for the throttling process using CFD, examining the temperature variations and condensation characteristics during throttling, as well as the influence of condensation latent heat on the flow, thereby ensuring the safety of natural gas transmission systems. Tay et al. [10] used numerical simulation methods to study the potential of the Joule–Thomson cooling effect in natural gas dehydration. Zhang et al. [11] employed CFD numerical simulation to investigate the throttling characteristics of natural gas in a throttling valve, discussing its throttling performance and the hydrate formation resulting from temperature variations. He et al. [12] employed numerical simulation to model the gas–liquid two-phase flow in a nozzle, investigating how upstream temperature and pressure, as well as the gas–liquid ratio, affect the flow characteristics. However, due to the complex composition of ultra-high-pressure condensate gas, the aforementioned numerical simulation methods struggle to accurately characterize each component’s concentration, which significantly impairs the accuracy of predicted throttling temperature and pressure.

To improve the precision of natural-gas throttling temperature-drop calculations, some researchers have proposed constructing mathematical models to compute the temperature drop after throttling. Tarom et al. [13] constructed an analytical model based on correction factors, considering the effects of gas specific gravity, temperature, and pressure, to predict the JT coefficient with high accuracy under unknown component conditions, thereby indirectly solving for the throttling temperature drop. Sokovnin et al. [14] established a two-stage pressure reduction mathematical model, derived the gas temperature variation at key sections, and proposed an optimal control method to prevent hydrate formation. Li et al. [15] conducted a numerical study on the Joule–Thomson (JT) coefficient of natural gas under different hydrogen blending ratios, investigating the throttling temperature drop characteristics of natural gas with varying hydrogen content. Luo et al. [16] proposed a method for predicting the temperature drop of superhigh-pressure sulfur-containing natural gas, combining the enthalpy-conserved throttling model with the mixing rule of the Lee-Kesler Equation of state (EoS). Li et al. [17] selected the LK equation to calculate the enthalpy of natural gas, which is more accurate compared to the BWRS, PR, and SRK equations. Compared with numerical simulation methods, constructing a mathematical model based on the principle of equal total enthalpy before and after throttling yields a more accurate calculation of the post-throttling temperature. In the cited literature, Luo et al. [16] and Li et al. [17] both calculate the throttling temperature drop of wellhead natural gas; however, they do not account for the effects of ultra-high pressure or for the heavy fractions and water content in condensate oil. As a result, their models deviate when predicting the throttling temperature drop of ultra-high-pressure condensate gas. The present study incorporates these heavy-fraction and water-content effects to improve the model’s accuracy.

In summary, this study not only characterizes the throttling-induced temperature drop but also demonstrates how the resulting data can guide field operating practices. First, by fully accounting for the effects of heavy fractions and water content under ultra-high-pressure conditions, we develop and validate a mathematical model that quantitatively describes the evolution of wellhead temperature. Second, we subject the model outputs to systematic statistical and sensitivity analyses, identifying inlet pressure, inlet temperature, and gas-production rate as the primary controlling factors. On this basis, we offer engineering recommendations for choke-step optimisation, hydrate mitigation strategies, and production-parameter tuning, thereby providing a robust scientific basis for the safe and efficient operation of ultra-high-pressure gas wells.

2. Methodology

Key thermophysical properties of ultra-high-pressure condensate gas, such as the compressibility factor and enthalpy, can be calculated using equations of state. However, due to the presence of heavy components in condensate gas, the critical parameters often deviate significantly, leading to limitations in the predictive accuracy of existing equations of state. Therefore, it is necessary to introduce an enthalpy calculation method that accounts for the influence of heavy components and water under ultra-high-pressure conditions. Additionally, an optimal mixing rule should be selected to establish a numerical model for calculating the throttling temperature drop in ultra-high-pressure condensate gas, incorporating the effects of both heavy components and water.

2.1. Selection of Equation of State

The ultra-high-pressure condensate-gas throttling model is founded on the equality of total enthalpy before and after throttling. Studies [16,17] show that the gas compressibility factor—by accounting for real gas non-idealities—is essential for accurate enthalpy calculations, and its precise determination refines thermodynamic predictions. Accordingly, this work prioritizes the accuracy of compressibility-factor computation when selecting the equation of state to ensure the model’s predictive precision.

The compressibility factor of natural gas is commonly calculated using four types of equations of state: Redlich–Kwong (RK), Peng–Robinson (PR), Lee–Kesler (LK), and Soave–Redlich–Kwong (SRK) [18]. When applying the RK, PR, and SRK equations, the cubic equation of state approach is used. In contrast, the application of the LK Equation requires incorporation of the three-parameter corresponding states principle [19].

The RK, SRK, and PR equations are all cubic equations of state and can be uniformly expressed as follows [20]:

$$Z^3-\left(1+B^{\ast }-u{B}^{\ast }\right)Z^2+\left(A^{\ast }+w{B}^{\ast }-u{B}^{\ast }-u{B}^{\ast 2}\right)Z-A^{\ast }{B}^{\ast }-w{B}^{\ast 2}-w{B}^{\ast 3}=0$$

(1)

$$A^{\ast }={\displaystyle \frac{ap}{R^2{T}^2}} B^{\ast }={\displaystyle \frac{bp}{RT}}$$

(2)

In Equations (1) and (2), Z is the compressibility factor, dimensionless; R is the gas constant, 8314 J/(kg·mol); p_c is the critical pressure of the fluid, Pa; T_c is the critical temperature, K; w is the acentric factor; T_r is the reduced temperature, T/T_c; and f_ω is the correction factor, as referenced in literature [21,22]. The coefficients for the three cubic equations of state are shown in

Table 1. Coefficients in the three cubic equations of state.

Equation	u	w	b	a
RK	1	0	${\displaystyle \frac{0.08664R{T}_c}{p_c}}$	${\displaystyle \frac{0.077796R{T}_c}{p_c}}$
SRK	1	0	${\displaystyle \frac{0.08664R{T}_c}{p_c}}$	${\displaystyle \frac{0.42748R^2{T}_c^2}{p_c}}{\left[1+f_{\omega }\left(1-T_r^{0.5}\right)\right]}^2$
PR	2	−1	${\displaystyle \frac{0.077796R{T}_c}{p_c}}$	${\displaystyle \frac{0.457235R^2{T}_c^2}{p_c}}{\left[1+f_{\omega }\left(1-T_r^{0.5}\right)\right]}^2$

.

The form of the LK Equation is as follows [23]:

$$z^{\left(i\right)}={\displaystyle \frac{p_r{\nu }_r}{T_r}}=1+{\displaystyle \frac{B}{{\nu }_r}}+{\displaystyle \frac{C}{{\nu }_r^2}}+{\displaystyle \frac{D}{{\nu }_r^5}}+{\displaystyle \frac{c_4}{T_r^3{\nu }_r^2}}\left(\beta +{\displaystyle \frac{\gamma }{{\nu }_r^2}}\right)\mathit{exp}\left({\displaystyle \frac{-\gamma }{{\nu }_r^2}}\right)$$

(3)

where v_r represents the specific volume of the reference fluid, and v represents the molar volume of the reference fluid, in m³/mol.

$$B=b_1-b_2/T_r-b_3/T_r^2-b_4/T_r^3$$

(4)

$$C=c_1-c_2/T_r+c_3/T_r^3$$

(5)

$$D=d_1+d_2/T_r$$

(6)

where b₁, b₂, b₃, c₁, c₂, c₃, c₄, d₁, d₂, β, and γ are parameters obtained from experiments, and their values need to be referenced from the literature [23].

The condensate gas samples from HT1 and TW1 Wells were calculated using four equations of state, RK, PR, LK, and SRK, with pressures and temperatures of 145.15 MPa, 159.63 °C and 171.78 MPa, 170.1 °C, respectively.

Table 2. Natural gas composition of Well TW1.

Component Name	Mole Fraction/%	Component Name	Mole Fraction/%	Component Name	Mole Fraction/%
N2	0.4600	iC5	0.3058	C11	0.0108
CO2	0.0000	nC5	0.0904	C12	0.0008
C1	93.6421	C6	0.0817	C13	0.0005
C2	4.0160	C7	0.0802	C14	0.0002
C3	0.6800	C8	0.0587	C15	0.0002
iC4	0.2013	C9	0.0446	C16	0.0002
nC4	0.3030	C10	0.0235	C17	0.0000

and

Table 3. Natural gas composition of Well HT1.

Component Name	Mole Fraction/%	Component Name	Mole Fraction/%	Component Name	Mole Fraction/%
N2	0.9670	iC5	0.1037	C11	0.0008
CO2	0.5835	nC5	0.0700	C12	0.0003
C1	92.5559	C6	0.0916	C13	0.0003
C2	4.1094	C7	0.0902	C14	0.0002
C3	0.8949	C8	0.0587	C15	0.0002
iC4	0.2480	C9	0.0146	C16	0.0001
nC4	0.2070	C10	0.0035	C17	0.0001

present the natural gas compositions for wells HT1 and TW1, respectively.

The calculated results of the compressibility factor were compared with the measured results, as shown in

Table 4. Comparison results of the HT 1 equation of state (145.15 MPa, 159.63 °C).

Comparison of Results	RK	SRK	PR	LK
calculated value	2.028	2.051	1.854	2.126
measured value	2.230	2.230	2.230	2.230
relative error%	9.06	7.66	16.85	4.65

and

Table 5. Comparison results of the TW 1 Well equation of state (171.78 MPa, 170.1 °C).

Comparison of Results	RK	SRK	PR	LK
calculated value	2.249	2.278	1.994	2.362
measured value	2.335	2.335	2.335	2.335
relative error%	5.03	3.63	13.27	1.52

.

By comprehensively comparing the measured PVT compressibility factor values and the calculation results from the four equations of state for both wells, the LK Equation exhibited the smallest calculation error, with relative errors of only 4.65% and 1.52%. Therefore, the LK Equation was selected to calculate the physical property parameters of ultrahigh-pressure condensate gas.

2.2. Enthalpy Calculation Method for Ultra-High-Pressure Condensate Gas

Many researchers have shown that the LK Equation, proposed by Lee B.I. and Kesler M.G. [24] based on the corresponding states principle, is the most accurate equation for calculating enthalpy differences. This equation is also recommended by the API Data Handbook [17] as the standard method for enthalpy difference calculation. Based on the three-parameter corresponding states principle, the enthalpy calculation method represented by the LK Equation is shown in Equation (7) [25]:

$$h=h_0-{\displaystyle \frac{R{T}_c}{M}}{F}_h$$

(7)

where h₀ represents the enthalpy of the ideal gas, in J/kg; M is the molar mass of the gas, in g/mol; and F_h is the effect of pressure on the enthalpy of the actual fluid, dimensionless.

$$F_h=F_h^{\left(0\right)}+{\displaystyle \frac{\omega }{{\omega }^{\left(h\right)}}}\left(F_h^{\left(h\right)}-F_h^{\left(0\right)}\right)$$

(8)

where $F_{\mathrm{h}}^{\left(0\right)}$ represents the effect of pressure on the enthalpy of a simple fluid, dimensionless; and $F_{\mathrm{h}}^{\left(\mathrm{h}\right)}$ represents the effect of pressure on the enthalpy of the reference fluid, dimensionless.

$$F_h^{\left(i\right)}=-T_r\left\{z^{\left(i\right)}-1-{\displaystyle \frac{b_2+2b_3/T_r+3b_4/T_r^2}{T_r{V}_r}}-{\displaystyle \frac{c_2-3c_3/T_r^2}{2T_r{V}_r^2}}+{\displaystyle \frac{d_2}{5T_R{V}_r^5}}+3E\right\}$$

(9)

$$E={\displaystyle \frac{c_4}{2T_r^3\gamma }}\left\{\beta +1-\left(\beta +1+{\displaystyle \frac{\gamma }{V_r^2}}\right)\mathit{exp}\left(-{\displaystyle \frac{\gamma }{V_r^2}}\right)\right\}$$

(10)

where, when Equation (9) is applied to a simple fluid, i = 0; and when Equation (9) is applied to the reference fluid, i = h.

$$h_0=A_h+B_{h}T+C_h{T}^2+D_h{T}^3+E_h{T}^4+F_h{T}^5$$

(11)

where h₀ represents the enthalpy of the ideal gas in J/kg; A_h, B_h, C_h, D_h, E_h, and F_h are the correlation coefficients.

For the heavy components C_n⁺ in condensate gas, if their physical property parameters cannot be measured, they need to be characterized by treating them as multiple components and then calculating the required physical property parameters. If the physical property parameters are measured, the following method can be used for calculation.

For the liquid phase composition of the heavy components in condensate gas, the enthalpy calculation method is shown in Equation (12) [25]:

$$H_L=1291.36\left[A_1\left(T-144.3\right)+A_2\left(T^2-{144.3}^2\right)+A_3\left(T^3-{144.3}^3\right)\right]$$

(12)

In Equation (12), H_L represents the liquid phase enthalpy, in J/kg.

$$\left\{\begin{array}{c}{A}_1={10}^{-3}\left(-1171.26+\left(23.722+24.907\gamma \right)K+{\displaystyle \frac{1149.82-46.535}{\gamma }}\right)\\ A_2={10}^{-6}\left(1.0+0.82463K\left({\displaystyle \frac{56.086-13.817}{\gamma }}\right)\right)\\ A_3={10}^{-9}\left(1.0+0.82463K\left({\displaystyle \frac{9.6757-2.3653}{\gamma }}\right)\right)\end{array}\right.$$

(13)

where K is the characteristic coefficient of the component, dimensionless; and γ is the relative density of the component, in kg/m³.

For the gas phase composition of the heavy components in condensate gas, the enthalpy calculation method is shown in Equation (14) [24].

$$\begin{array}{c}H=H_L^{\ast }+1291.36\left[B_1\left(T-0.8T_c\right)+B_2\left(T^2+0.64T_c^2\right)+B_3\left(T^3-0.512T_c^3\right)\right]\\ +{\displaystyle \frac{R{T}_c}{M}}\left(4.507+5.266\omega -F_H\right)\end{array}$$

(14)

where H represents the gas phase enthalpy, in J/kg; H* is the liquid phase enthalpy at T_r = 0.8, in J/kg; and F_H is the pressure-related enthalpy factor, dimensionless.

$$\begin{array}{c}{B}_1={10}^{-3}\left[-356.44+29.71K+B_4\left(295.02-{\displaystyle \frac{248.46}{\gamma }}\right)\right]\\ B_2={10}^{-6}\left[-146.24+\left(77.62-2.772K\right)K-B_4\left(301.42-{\displaystyle \frac{253.87}{\gamma }}\right)\right]\\ B_3={10}^{-9}\left(-56.487-2.95B_4\right)\\ B_4={\left[\left({\displaystyle \frac{12.8}{K}}-1.0\right)\left(1.0-{\displaystyle \frac{10.0}{K}}\right)\left(\gamma -0.885\right)\left(\gamma -0.70\right)\left({10}^4\right)\right]}^2\end{array}$$

(15)

For the enthalpy calculation of water in super-high-pressure condensate gas, this paper applies the IAPWS-IF97 equation, which provides methods for calculating parameters such as the specific enthalpy, saturation vapor pressure, and heat capacity of water and steam [26]. This equation has become the international standard for calculating the thermophysical properties of water. The enthalpy calculation method under high-pressure conditions is shown in Equations (16)–(18) [27].

$${\displaystyle \frac{h\left(T,P\right)}{RT}}=\tau {\gamma }_{\tau }$$

(16)

$${\gamma }_{\tau }={\left({\displaystyle \frac{\partial \gamma }{\partial \tau }}\right)}_{\pi }={\displaystyle \sum }_{i=1}^{34}{n}_i{\left(7.1-\pi \right)}^{I_i}{J}_i{\left(\tau -1.222\right)}^{\left(J_i-1\right)}$$

(17)

$$\tau ={\displaystyle \frac{1386}{T}} \pi ={\displaystyle \frac{P}{16.53}}$$

(18)

where n, I, J, n_i, and J_i are characteristic values obtained from reference [27], dimensionless.

2.3. Calculation of Virtual Critical Parameters for Mixtures

The enthalpy is typically calculated based on the LK Equation by first determining the enthalpy of an ideal gas and then using a pseudo-critical method to correct the enthalpy of the mixed gas. When calculating, virtual critical parameters are used to replace the actual critical parameters of the fluid, and mixing rules are applied for the calculation. This paper optimizes four mixing rules: Van der Waals, Wong–Sandler, Plocker–Knapp, and Lee–Kesler, and introduces the Prausnitz–Gunn virtual critical pressure calculation rule to improve calculation accuracy [28]. Among these, the Wong–Sandler and Prausnitz–Gunn mixing calculation methods are shown in Equations (19)–(21) [18].

$$T_{cm}={\displaystyle \frac{1}{8V_c}}{\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^n{x}_i{x}_j{({\nu }_{ci}^{1/3}+{\nu }_{cj}^{1/3})}^3{(T_{ci}{T}_{cj})}^{1/2}$$

(19)

$${\nu }_{cm}={\displaystyle \frac{1}{8}}{\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{j=1}^n{x}_i{x}_j{\left({\nu }_{ci}^{1/3}+{\nu }_{cj}^{1/3}\right)}^3$$

(20)

$$P_{cm}={\displaystyle \frac{\left(0.2905-0.085{{\displaystyle \sum }}_{i=1}^n{x}_i{\omega }_i\right)R{T}_{cm}}{V_{cm}}}$$

(21)

where y_i represents the mole fraction of component i; T_cm is the virtual critical temperature of the mixture, in K; P_cm is the virtual critical pressure of the mixture, in Pa; v_cm is the virtual critical molar volume of the mixture, in m³/mol; and v_ci is the critical molar volume of component i, in m³.

$${\omega }_m={\displaystyle \sum }_{i=1}{y}_i{\omega }_i$$

(22)

where w_i represents the acentric factor of component i; and w_m is the acentric factor of the mixture.

The Prausnitz–Gunn virtual critical pressure calculation method is shown in Equation (23) [29].

$$p_{mc}={\displaystyle \frac{R{T}_{mc}{{\displaystyle \sum }}_{i=1}^n{z}_{ci}}{{{\displaystyle \sum }}_{i=1}^n{y}_i{V}_{ci}{M}_i}}$$

(23)

where z_ci represents the critical compressibility factor of component i, dimensionless; and M_i is the molar mass of component i, in g/mol.

Using the four mixing rules and introducing the virtual critical pressure to calculate the temperature after throttling at TW1 Well, the results are shown in

Table 6. Throttling temperature calculation using different mixing rules.

Mixing Rules	Pseudocritical Pressure/MPa	Pseudocritical Temperature/°C	Post-Throttle Temperature/°C	Relative Error
Van der Waals + Prausnitz-Gunn	4.11	−65.04	62.82	6.1%
Wong-Sandler + Prausnitz-Gunn	4.29	−57.88	67.05	0.3%
Plocker-Knapp + Prausnitz-Gunn	4.63	−64.14	59.94	10.3%
Lee-Kesler + Prausnitz-Gunn	4.42	−48.68	57.02	14.7%
field measured value	\	\	66.87	\

.

Table 6 lists the pseudocritical temperatures and pseudocritical pressures calculated using various mixing rules. It was found that the pseudocritical temperature T_cm directly affects the compressibility factor and the Joule–Thomson coefficient, and that the Prausnitz–Gunn pseudocritical pressure must be determined based on T_cm. Consequently, the cooling model is highly sensitive to T_cm; a ±5% deviation in T_cm leads to an approximately ±3.2% change in the throttled temperature.

Moreover, Table 6 shows that the throttled temperature calculated using the Wong–Sandler + Prausnitz–Gunn mixing rule exhibits the smallest relative error compared to experimental values—only 0.27%. Therefore, the Wong–Sandler + Prausnitz–Gunn mixing rule was selected in this study for its superior predictive accuracy.

2.4. Model Solution

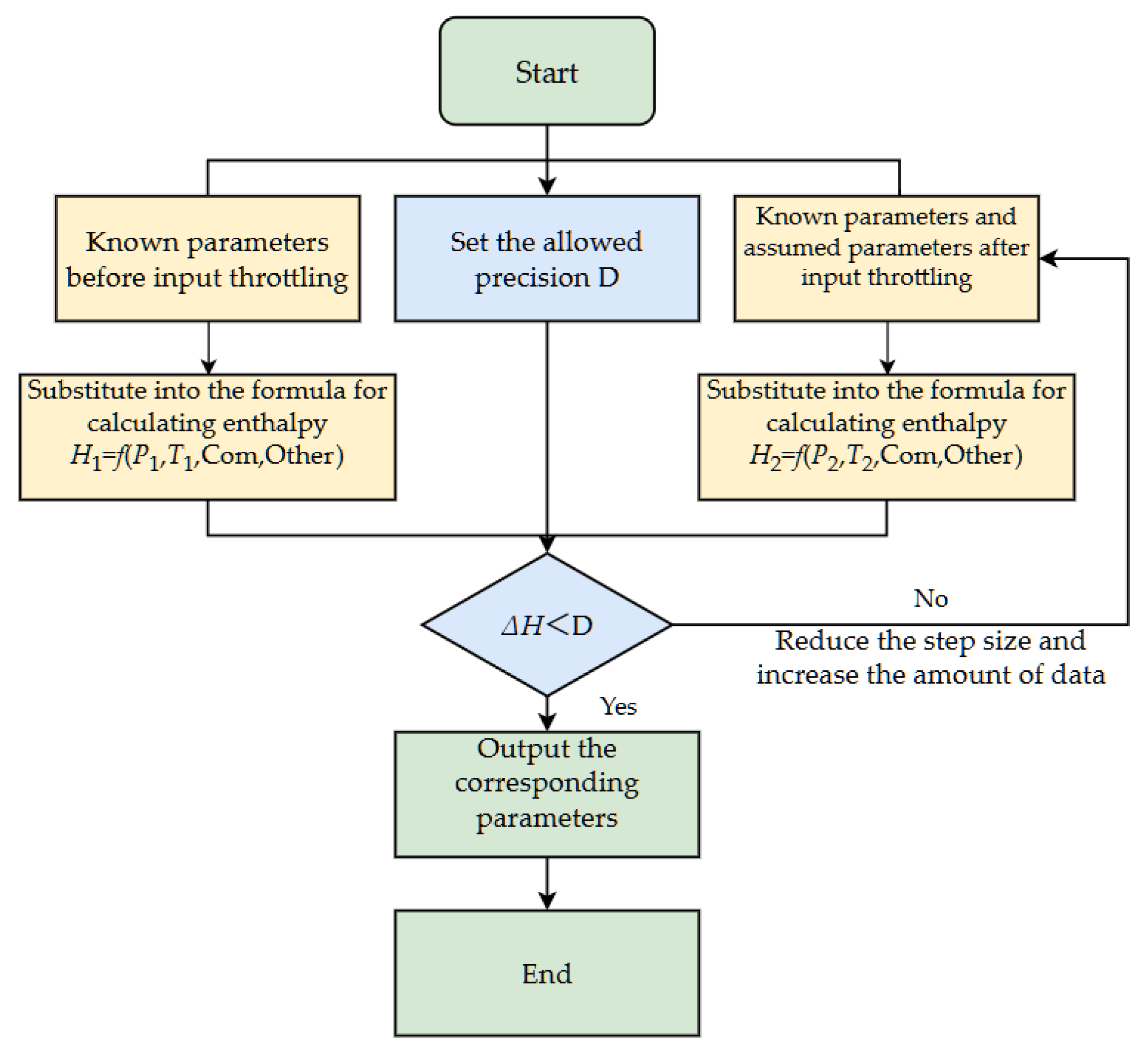
As mentioned above, the mathematical model for solving the temperature drop during throttling of super-high-pressure condensate gas is mainly based on the equation of state for super-high-pressure condensate gas, enthalpy calculation of super-high-pressure condensate gas, enthalpy calculation of condensate gas heavy components and water, and the principle of equal total enthalpy before and after throttling. The solution must follow specific steps. The specific solution steps are as follows:

Step 1: Input the temperature and pressure of the super-high-pressure condensate gas before throttling.

Step 2: Input the gas, oil, and water production rates before throttling. If these parameters are unknown, they can be calculated based on the temperature and pressure before throttling.

Step 3: Calculate the enthalpy values of each component before throttling and compute the total enthalpy H₁ using the mixing rule.

Step 4: Input the estimated temperature value and the pressure after throttling.

Step 5: Based on the temperature and pressure after throttling, calculate the mass fractions of the gas and liquid phases.

Step 6: Calculate the enthalpy values of each component after throttling and compute the total enthalpy H₂ using the mixing rule.

Step 7: Compare the total enthalpies before and after throttling, H₁ and H₂. If H₁ > H₂, increase the estimated temperature after throttling; if H₁ < H₂, decrease the estimated temperature after throttling.

Step 8: If ΔH = (H₁ − H₂) < 0.1, output the result, which is the temperature after throttling.

To facilitate understanding of the entire solving process, a calculation flowchart is provided as shown in Figure 1.

2.5. Verification of Model Calculation Accuracy

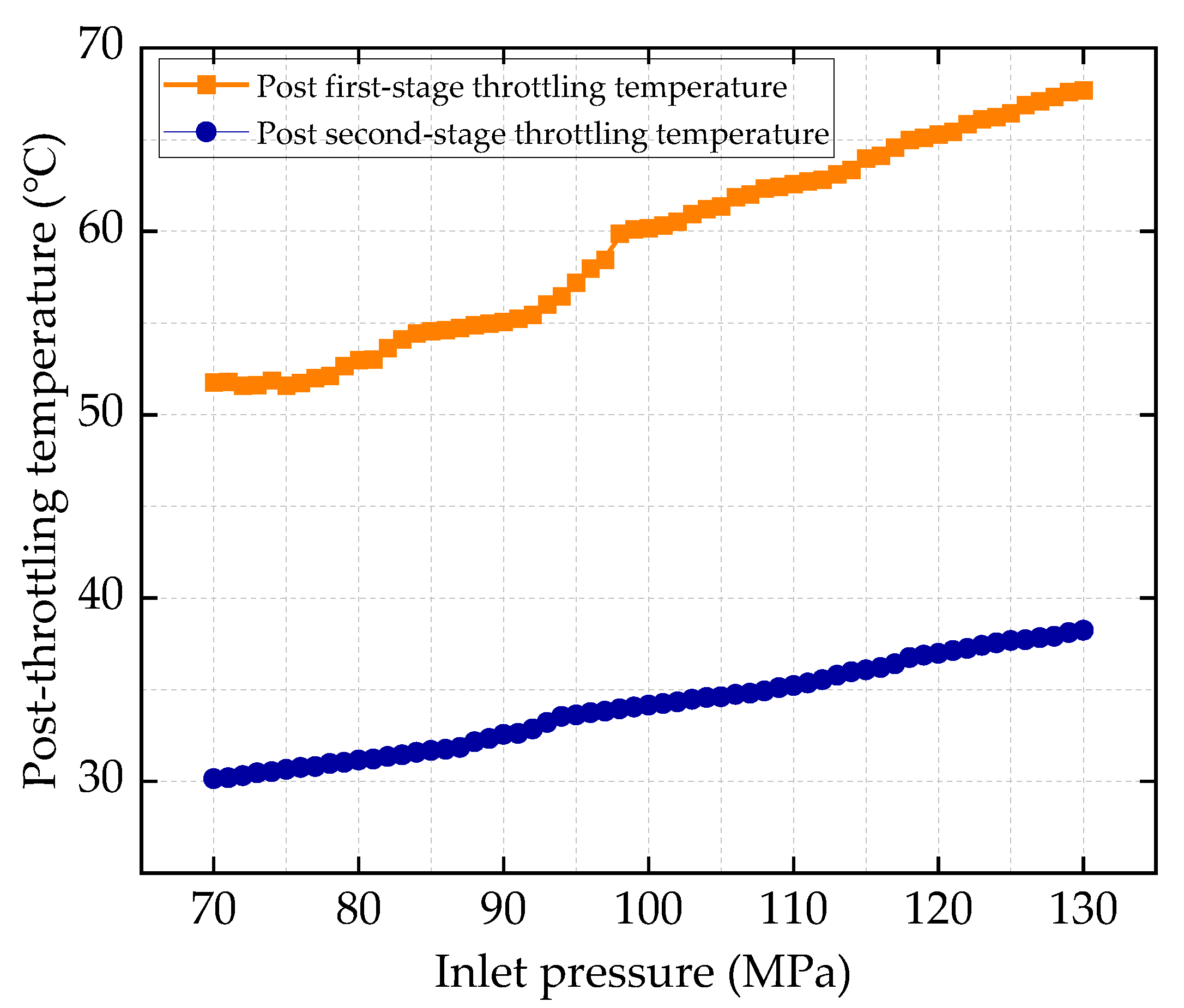
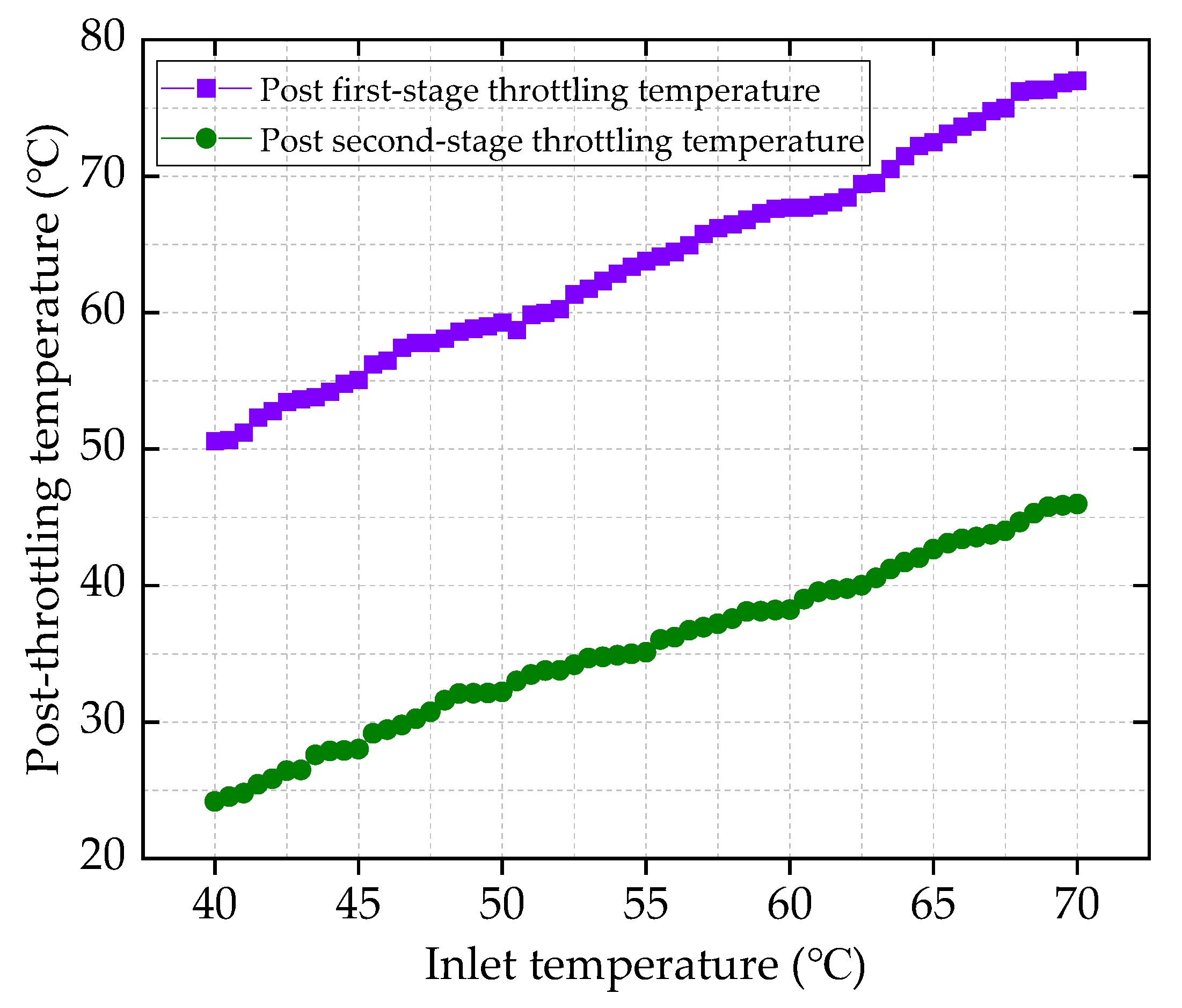
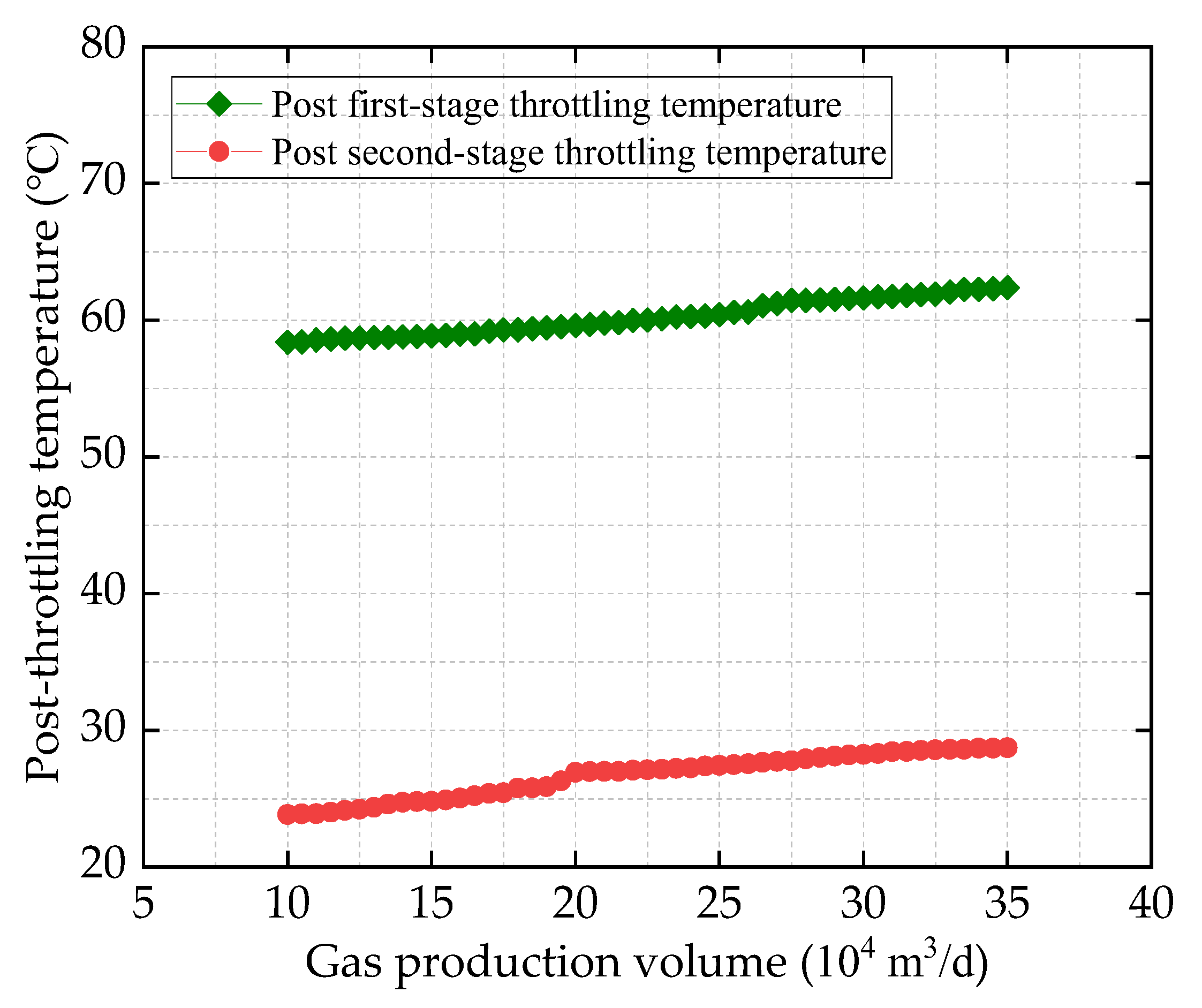
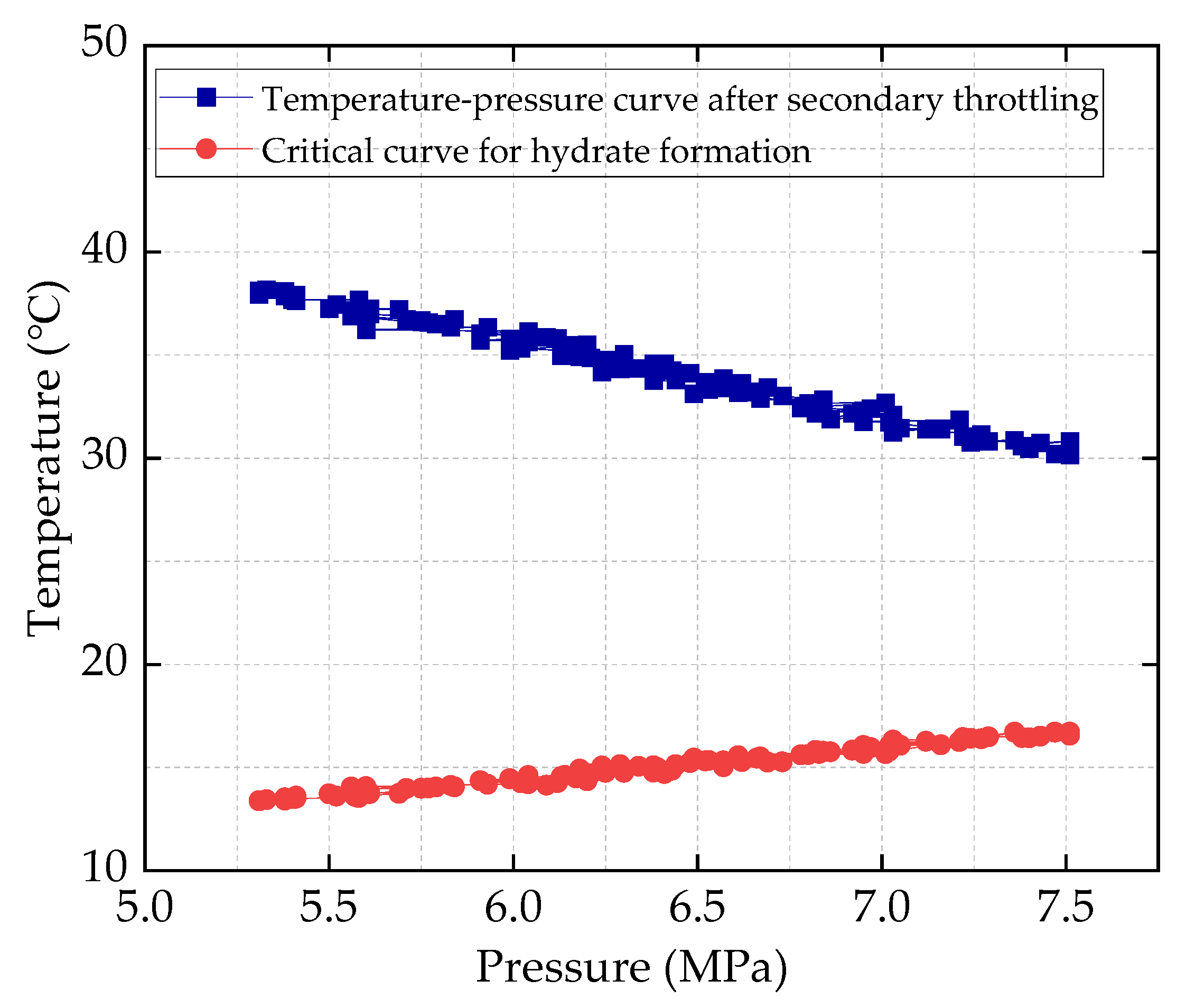
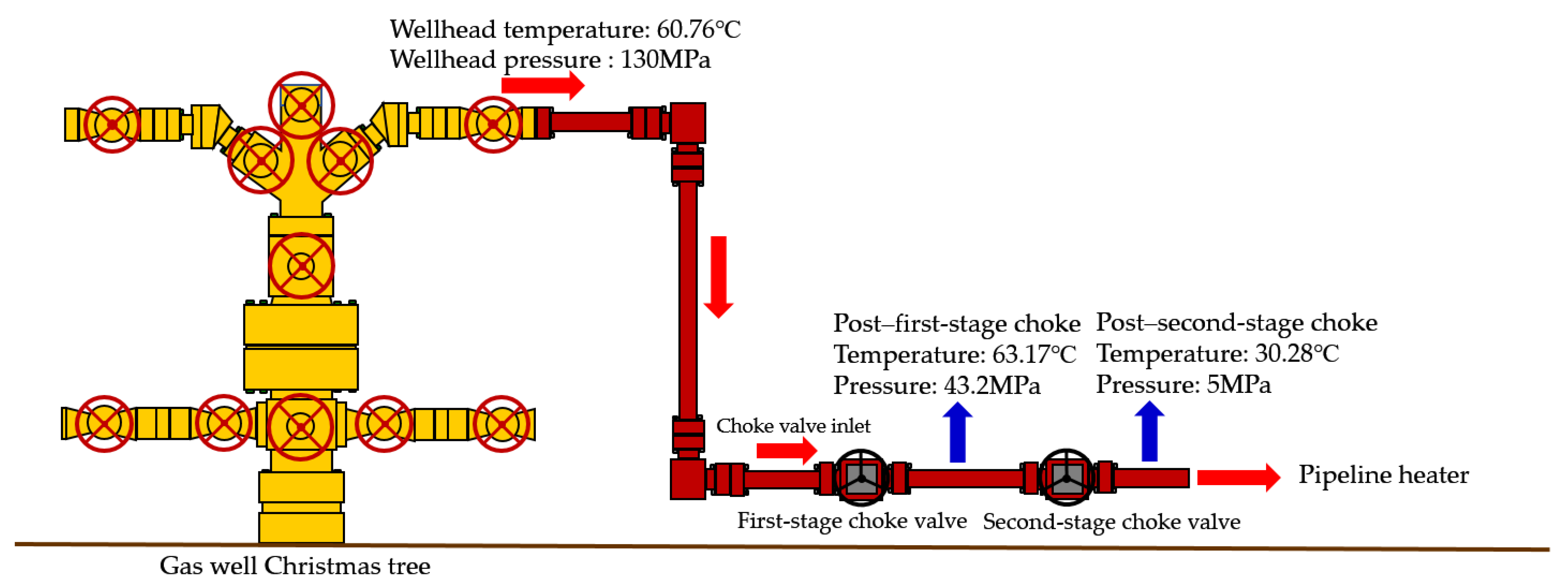
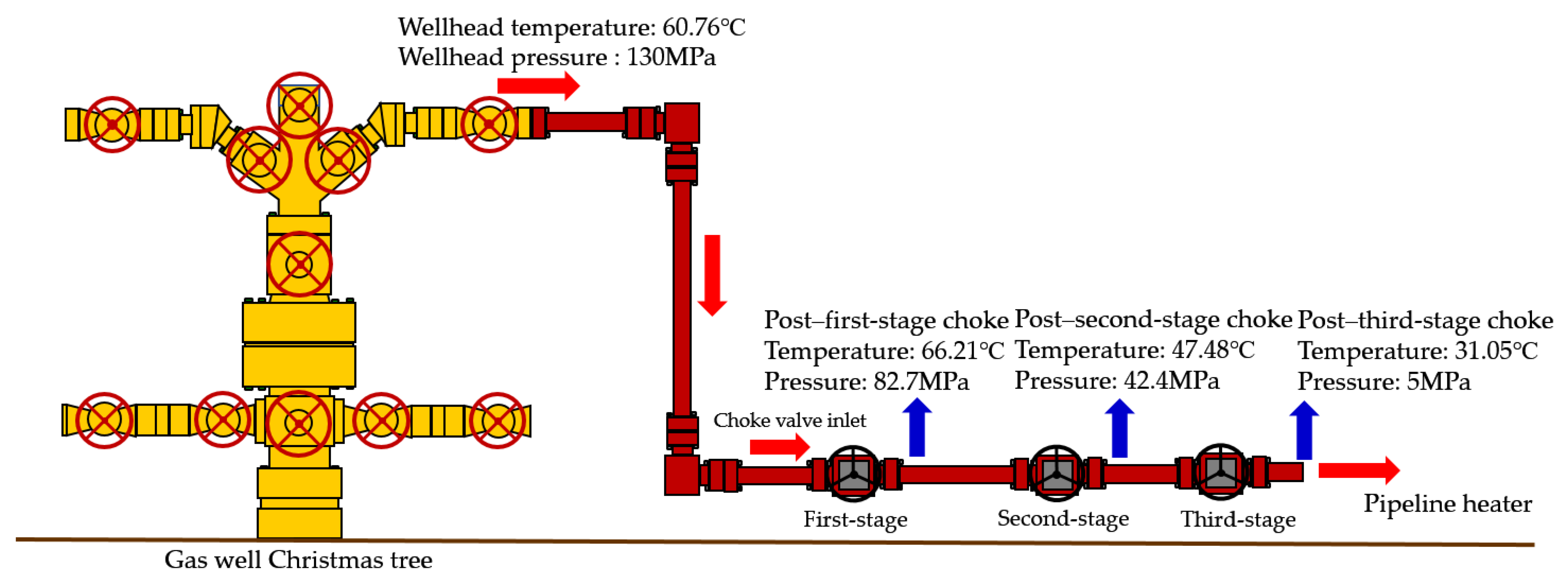
HT1 Well is a typical ultra-high-pressure condensate gas well. A two-stage throttling process is employed on site to reduce the gas pressure. The pressure before throttling exceeds 80 MPa, with a temperature above 70 °C. After the first-stage throttling, the pressure is approximately 40 MPa, and after the second-stage throttling, it is around 11 MPa. To characterize the accuracy of the calculation results, the relative error between the calculated value and the field-measured value is defined as shown in Equation (24):

$$\epsilon =\left|{\displaystyle \frac{{\eta }_c-{\eta }_e}{{\eta }_e}}\right|$$

(24)

where ε represents the relative error; and η_c and η_e denote the calculated and experimental temperatures after throttling, respectively.

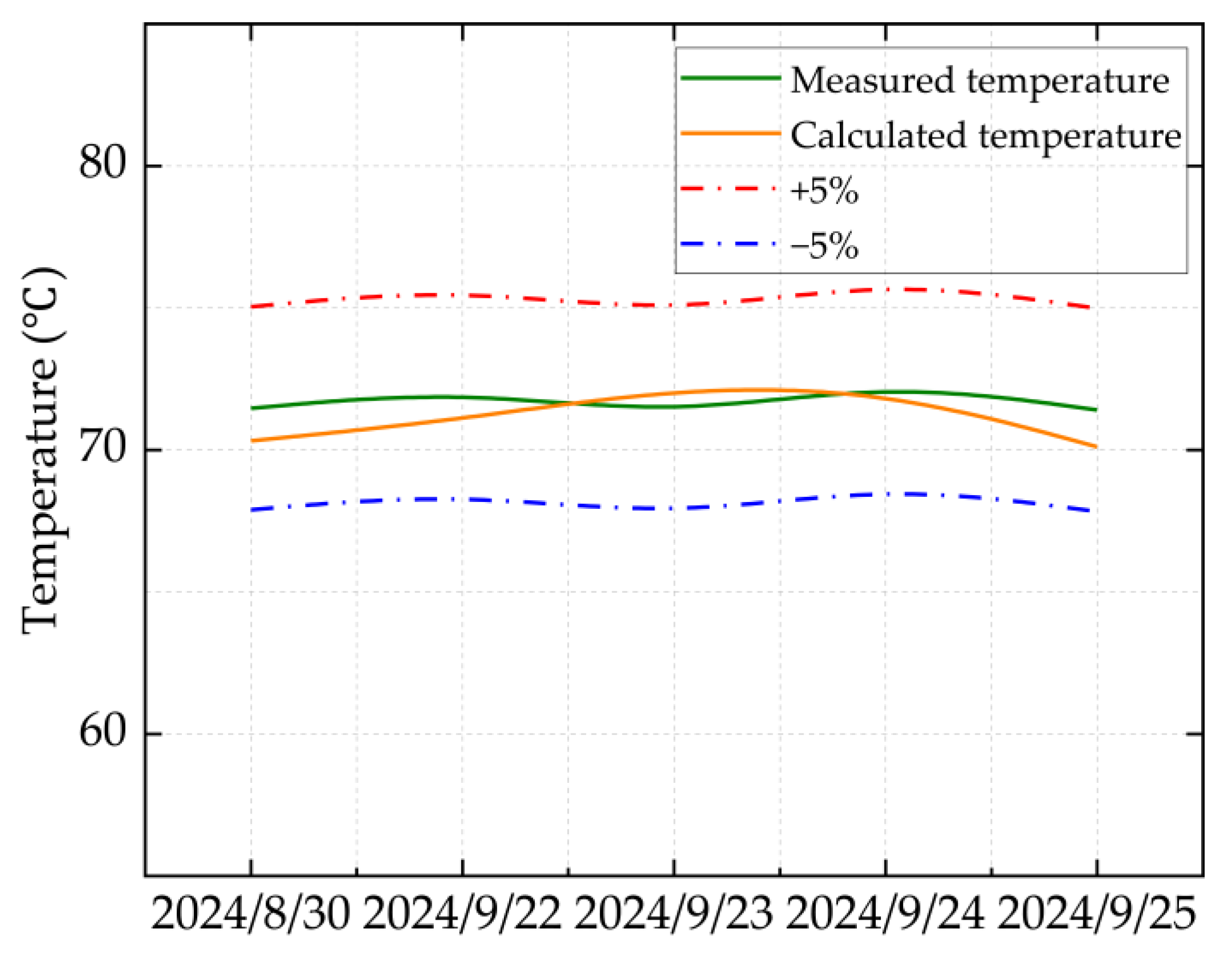
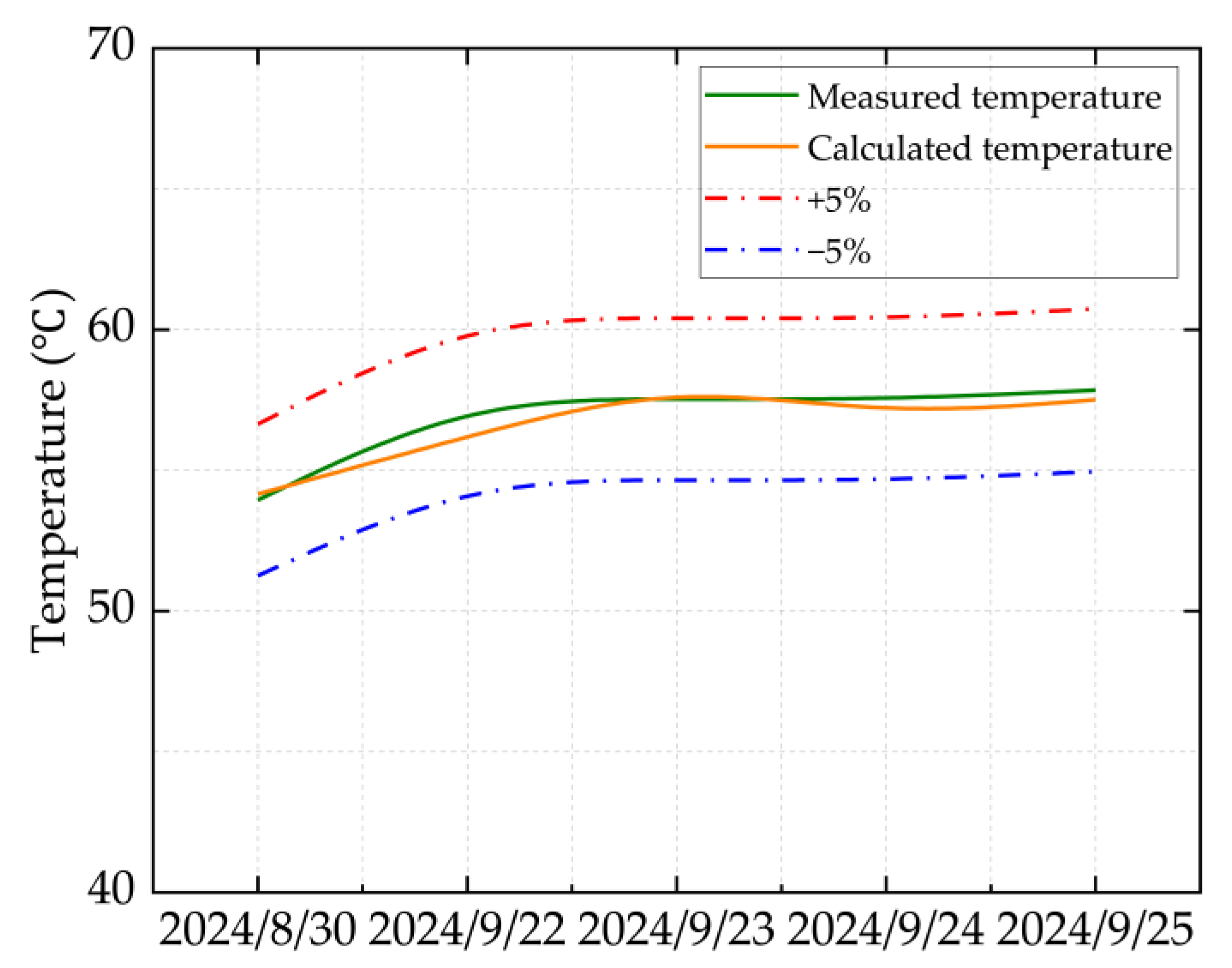
Based on the production reports of HT1 Well from 30 August to 25 September 2024, the field-measured values are compared with the calculated values. The comparison results are illustrated in Figure 2 and Figure 3.

Figure 2 and Figure 3 show that the calculation error under all operating conditions is less than 2%, indicating that the ultra-high-pressure condensate gas throttling temperature-drop model developed in this study is highly accurate. In particular, under ultra-high-pressure conditions (wellhead pressure above 100 MPa), the calculated results are especially precise.

Meanwhile, to demonstrate that the model proposed herein is equally applicable to calculating the temperature drop caused by throttling in other high-pressure condensate gas wells, this study adopts the condensate gas sample from Reference [17] as the baseline parameters and computes its post-throttling temperature drop. The results are presented in

Table 7. Comparison of measured and calculated values for high-pressure condensate gas wells.

Pressure/Mpa		Temperature/°C
Before Throttling/MPa	After Throttling/MPa	Before Throttling/°C	After Throttling/°C	Calculated Values/°C
74.05	12.07	89.37	73.98	74.88
82.95	11.17	79.87	66.71	64.12
73.34	11.66	93.23	74.50	72.11
79.50	10.68	84.25	69.00	71.25
85.30	10.83	90.21	72.98	74.03

.

From Table 7, using the gas sample from Reference [17] as the baseline parameters produces a maximum relative error of no more than 3.5% in the calculated post-throttling temperature drop, demonstrating high accuracy. This accuracy results from the fact that the ultra-high-pressure condensate gas throttling temperature-drop model developed in this paper is governed primarily by gas composition. Since most high-pressure and ultra-high-pressure condensate gas wells share similar compositions, consisting mainly of methane and light hydrocarbons with a small amount of heavy components, the model is applicable to the majority of condensate gas wells.

3. Results and Discussion

3.1. Calculation and Analysis of the Throttling-Induced Temperature Drop in Ultra-High-Pressure Condensate Gas

3.1.1. Sensitivity Analysis of Factors Influencing Throttling-Induced Temperature Drop

(1)

Different inlet pressures

Based on field measurements for well TW1, the pre-throttling temperature was set at 60 °C, and the inlet pressure ranged from 70 MPa to 130 MPa. Using the ultra-high-pressure condensate gas throttling temperature-drop model, the temperature-drop behavior at different pressures was calculated, as illustrated in Figure 4.

As shown in Figure 4, for TW1 Well, as the pre-throttling pressure increases, the temperature drop across the throttling decreases. When the pre-throttling pressure exceeds 90 MPa, the post-throttling temperature actually begins to rise. Moreover, for every 10 MPa increase in pre-throttling pressure, the temperature difference before and after throttling for the TW1 Well decreases by an average of 1.2 °C.

(2)

Different inlet temperatures

To investigate the temperature-drop characteristics at different inlet temperatures, based on field measurements, the inlet temperature of the TW1 Well was set from 40 °C to 70 °C, and the temperature difference before and after throttling was calculated for each inlet temperature, as illustrated in Figure 5.

As shown in Figure 5, for TW1 Well, as the pre-throttling temperature increases, the temperature drop across the throttling decreases. Compared to the effect of pre-throttling pressure, the temperature difference before and after throttling is more strongly influenced by the inlet temperature. For every 5 °C increase in pre-throttling temperature, the temperature difference for the TW1 Well decreases by an average of 3.1 °C, indicating that in ultra-high-pressure condensate gas, the throttling temperature drop is more sensitive to temperature.

(3)

Different gas production rates

Based on field measurements, to investigate the effect of different gas production rates on the throttling temperature drop, the gas production rate of the TW1 Well was set from 100,000 m³/d to 350,000 m³/d, and the temperature difference before and after throttling was calculated for each rate, as illustrated in Figure 6.

Figure 6 shows that the temperature after throttling in the TW1 Well is only slightly affected by the gas production rate. When the daily gas production increases by 20,000 m³, the temperature after throttling increases by only about 0.3 °C. This paper suggests that this phenomenon may be due to the small change in pressure differential before and after throttling. Despite the increase in gas production, if the pressure differential before and after throttling does not significantly expand, the Joule–Thomson effect during the throttling process is not significant, resulting in a relatively small temperature drop.

3.1.2. Influence of the Joule–Thomson Effect on Throttling Temperature Drop

In the calculation process of this study, it was found that the TW1 Well exhibited a temperature increase during the throttling process. This phenomenon is reflected in both the field-measured data and the results, with a high degree of consistency between the two. According to the monitoring data from 26 September 2024 to 7 October 2024, the average temperature at the TW1 Well wellhead was 56 °C, and the temperature increased by approximately 10 °C after the first stage of throttling.

According to the principle that the total enthalpy of the gas before and after throttling remains constant and the characteristics of the gas pressure drop, the temperature change before and after throttling can be expressed by Equation (25) shown below [30]:

$$dT={\left({\displaystyle \frac{\partial T}{\partial p}}\right)}_{H}dp$$

(25)

where ${\left({\displaystyle \frac{\partial T}{\partial p}}\right)}_H$ is referred to as the Joule–Thomson coefficient and is represented by μ, i.e.,:

$$\mu ={\left({\displaystyle \frac{\partial T}{\partial p}}\right)}_H$$

(26)

Using thermodynamic relations and the derivation of gas enthalpy, it can be derived that

$$\mu ={\displaystyle \frac{1}{C_P}}\left(T{\left({\displaystyle \frac{\partial v}{\partial T}}\right)}_P-v\right)$$

(27)

where C_p is the specific heat capacity of the gas at constant pressure, J/(kg·K).

Substituting Equation (27) into Equation (25) and integrating them, we can obtain

$$\mathrm{\Delta }T=T_2-T_1={{\displaystyle \int }}_{p_1}^{p_2}{\displaystyle \frac{T{\left(\frac{\partial v}{\partial T}\right)}_p-v}{C_p}}dp$$

(28)

From Equation (28), it can be concluded that the throttling temperature change of real gases is closely related to the Joule–Thomson coefficient, requiring specific consideration of three different cases. When ΔT < 0, the temperature decreases after throttling. When ΔT > 0, the temperature increases after throttling. When ΔT = 0, the temperature remains unchanged after throttling [31].

Regarding this phenomenon, this paper suggests that the direct cause is due to the change in the Joule–Thomson coefficient under ultra-high-pressure conditions. Based on the above derivation, the temperature increase during throttling in the TW1 Well is caused by the Joule–Thomson coefficient μ < 0. Since μ < 0 under ultra-high-pressure conditions, the pressure drop after throttling dp < 0, and substituting this into Equation (28) results in ΔT > 0. Therefore, the throttling temperature increases under this working condition.

To gain a clearer understanding of the temperature change after throttling in the TW1 Well, this paper uses the developed ultra-high-pressure condensate gas throttling calculation software. Based on the TW1 Well’s production report from 26 September 2024 to 7 October 2024, the throttling pressure is set to 35 MPa, and the wellhead temperature is 63 °C. The temperature variation under different inlet pressures during throttling is calculated, as illustrated in Figure 7.

As shown in Figure 7, for the TW1 Well, the temperature after throttling may either increase or decrease with changes in the pressure before throttling. When the pressure before throttling is 92 MPa, μ = 0, and the temperature remains unchanged before and after throttling. When the pressure before throttling is less than 92 MPa, a cooling effect occurs, and the temperature decreases after throttling. When the pressure is greater than 92 MPa, a heating effect occurs, and the temperature increases after throttling.

3.2. Design of Production System for Ultra-High-Pressure Condensate Gas Wells

3.2.1. Basis for Production System Design

Based on the calculation method for the throttling temperature drop of ultra-high-pressure condensate gas, a production system plan for the TW1 Well is proposed for the wellhead process. The wellhead equipment should be designed based on high-pressure and high-temperature conditions, with the selection of appropriate throttling valves, oil nozzles, and other facilities. Due to the gas flow characteristics under ultra-high-pressure conditions, high-pressure-resistant pipelines and valves must be selected, while also considering potential issues such as hydrates and wax formation in the condensate gas. The main bases for the design are as follows:

(1)

Hydrate formation prediction

This study focuses on hydrate formation in the downstream pipeline following throttling. In the post-throttle section, the flow velocity is low, residence time is ample, and the system remains in a deeply supersaturated state, allowing it to be treated as a series of quasi-steady-state processes. Consequently, nucleation induction time and mass/heat transfer resistances are neglected, and hydrate formation at each temperature–pressure point is predicted solely using the thermodynamic statistical method [32].

Figure 8 and Figure 9 show that the critical temperature for hydrate formation is approximately between 10 °C and 28 °C. The temperatures after the first and second throttling at well TW1 are much higher than the critical temperature for hydrate formation, so no hydrates will form in either the throttling section or the section before throttling. The temperature difference between the temperature after secondary throttling and the hydrate formation temperature is even smaller, making hydrate formation more likely.

(2)

Throttling pressure difference design basis

The TW1 Well adopts a two-stage throttling process. Reasonably determining the pressure drop between each stage not only ensures the safe operation of the pipeline but also stabilizes production, maintaining good production conditions. This paper, based on the critical flow theory, calculates the critical pressure for the super-high-pressure condensate gas two-phase gas-liquid flow and establishes a reasonable throttling pressure difference.

This paper applies the HNE-DS model, which is based on the improved PR Equation of state, to calculate the throttling pressure difference [33].

Where the critical compressibility factor w_c is given by Equation (29) [33]:

$$w_c=-{\eta }_c{\displaystyle \frac{p_1}{v_1}}\left[w_0{\displaystyle \frac{d{v}_{g1}}{d{p}_1}}+\left(1-x\right){\displaystyle \frac{d{v}_{L1}}{d{p}_1}}\right]-{\displaystyle \frac{c_{p,L1}}{\mathrm{\Delta }h}}\left(v_{g1}-v_{L1}\right)N{\displaystyle \frac{d{T}_1}{d{p}_1}}$$

(29)

where η_c is the critical exit pressure ratio, dimensionless; x is the gas phase component fraction, dimensionless; C_p,L1 is the specific heat capacity at constant pressure for the liquid phase, J/(kg·K); Δh is the latent heat of vaporization, J/kg; p₁ is the stagnation pressure, Pa; and v_g1 and v_L are the gas and liquid phase volume fractions, respectively. N is the boiling delay coefficient.

The calculation method for the critical pressure ratio η_c is shown in Equation (30) [33]:

$${\eta }_c={\displaystyle \frac{0.036203+2.74652w+0.45113w_c}{1+4.89524x-2.317001w_c+2.6859w_c^2-0.81197w_c^2}}$$

(30)

3.2.2. Production System Plan

Based on the production conditions of the TW1 Well and the aforementioned design basis, the production system plan for the surface process is as follows.

(1)

Hydrate Control Plan

The hydrate formation conditions under different temperatures and pressures were predicted using the thermodynamic statistical method. According to the prediction results, the temperature after the first and second-stage throttling in TW1 Well is much higher than the critical temperature for hydrate formation, so hydrates will not form under normal operating conditions. However, under extremely low temperatures (the lowest temperature in 2024 being −52.3 °C), based on the super-high-pressure condensate gas throttling temperature drop characteristics, the throttling temperature drop is most affected by the temperature before throttling, and there is a significant risk of hydrate formation after throttling due to the influence of external temperatures. Therefore, it is recommended to install heating systems at the wellhead and pipeline facilities or add methanol injection pipelines to ensure gas flow in the pipelines at extremely low temperatures and prevent production stoppages due to ice blockage or hydrate formation.

(2)

Throttling Pressure Differential Design

Based on the production characteristics of the TW1 Well, the appropriate throttling pressure differential is calculated using Equations (29) and (30). The inlet pressure is set at 130 MPa, and the calculation results are shown in

Table 8. Setting of throttling pressure drop at each level.

Throttling Stages	First and Second-Stage Pressure Differential/MPa	Second and Third-Stage Pressure Differential/MPa	Gathering Station Inlet Pressure/MPa
two-stage throttling	38.2	\	5
three-stage throttling	40.3	37.4	5

.

Figure 10 and Figure 11 show the process designs for the two-stage and three-stage throttling methods, respectively. The throttling temperatures between each stage were calculated using the mathematical model established in this paper, and the throttling pressure differences between each stage were designed based on critical flow theory.

As shown in Table 8, when two-stage throttling is used, the first and second-stage throttling pressure differential is controlled at approximately 38.2 MPa, with the pressure after the second-stage throttling controlled at approximately 5 MPa. When three-stage throttling is used, it is recommended to use a fixed nozzle for the first and second stages and an adjustable nozzle for the third stage. The first and second-stage throttling pressure differential is controlled at approximately 40.3 MPa, while the second and third-stage throttling pressure differential is controlled at approximately 37.4 MPa. This ensures that the first and second-stage throttling will not reach a critical flow state, and the third-stage adjustable nozzle can adjust the well production rate by changing the opening.

In summary, the ultra-high-pressure condensate gas throttling temperature-drop model can provide effective guidance for designing production schemes in condensate gas wells. At the same time, significant residual pressure and heat remain available during wellhead throttling in ultra-high-pressure gas wells. To further enhance energy efficiency and reduce emissions, one can exploit the temperature and pressure drop characteristics of the throttling process by treating the throttling valve and its immediately adjacent upstream and downstream pipeline segments as a control volume, calculating the specific exergy at the inlet and outlet, and performing an exergy balance to quantify the irreversibilities occurring in throttling and downstream flow. By comparing the actual process with an ideal isothermal reversible expansion, the respective contributions of the temperature drop and pressure drop to exergy destruction can be distinguished [34]. In the future, this methodology could be extended to a segmented exergy distribution analysis across the entire pipeline network, coupled with dynamic hydrate-formation models and online monitoring data, to optimize valve selection, pipeline insulation design, and real-time energy-saving and emission-reduction control—thereby providing a robust scientific basis for the efficient, low-carbon operation of oil and gas production systems.

4. Conclusions

Through the study of the throttling temperature drop characteristics of ultra-high-pressure condensate gas wells, the following conclusions are drawn:

(1)

Under ultra-high-pressure conditions, selecting the LK Equation provides higher accuracy for calculating the compressibility factor. The relative error when calculating for the TW1 Well is only 1.5%. The Wong–Sandler + Prausnitz–Gunn mixing rule provides the highest calculation accuracy, with the relative error compared to field measurements being only 0.27%. Considering the impact of the enthalpy of the condensate gas, heavy components and water, the calculation error compared to the measured value is less than 2%. In the future, once additional wells have complete PVT datasets, we will conduct further robustness testing.

(2)

The study found that the temperature before throttling has the greatest impact on the temperature drop. For every 5 °C increase in the temperature before throttling, the average temperature difference before and after throttling for the TW1 Well decreases by 3.1 °C. The increase in temperature after throttling in TW1 Well is due to changes in pressure, which result in a negative Joule–Thomson coefficient (μ < 0), causing the temperature to rise after throttling. When the wellhead pressure is less than 92 MPa, the temperature after throttling decreases, but when it is greater than 92 MPa, the temperature increases after throttling. In future work, we will address the inherent limitations of our ultra-high-pressure throttling-temperature-drop model, which is rooted in classical thermodynamics and therefore cannot fully capture energy-dissipation mechanisms, microscopic temperature perturbations, or process-specific influences. To improve the model, we intend to implement zonal corrections that integrate a high-precision equation of state, non-equilibrium CFD, and multiphase experimental data.

(3)

Under normal operating conditions, the TW1 Well will not generate hydrates. However, with the lowest temperature of −52.3 °C for the whole year in 2024, it is recommended to install heating systems at the wellhead and pipeline facilities or add methanol injection pipelines. Regarding pressure differential design, for two-stage throttling, it is recommended to control the first and second-stage throttling pressure differential at approximately 38.2 MPa, with the pressure after the second-stage throttling controlled at approximately 5 MPa. For three-stage throttling, it is recommended to control the first and second-stage throttling pressure differential at approximately 40.3 MPa, with the second and third-stage throttling pressure differential controlled at approximately 37.4 MPa.

However, ultra-high-pressure condensate gas wells still face potential risks of erosion effects in practical applications. On one hand, the wellhead throttling devices are subject to erosion from sand particles; on the other hand, the severe pressure gradient across the throttling valve can cause local fluid pressure to rapidly drop below the vaporization pressure, triggering flash evaporation. At the same time, the sharp temperature drop may lead to the formation of cavitation bubbles. The collapse of these bubbles generates microjets and shockwaves that can cause material fatigue and micro-crack propagation on the valve surface, resulting in erosive damage. The risk of cavitation erosion increases further in the presence of liquid-phase hydrocarbons or hydrate formation. Future research is needed to better understand the erosion phenomena under ultra-high-pressure conditions and to implement effective protective measures.