Creep Deformation Mechanisms of Gas-Bearing Coal in Deep Mining Environments: Experimental Characterization and Constitutive Modeling

Abstract

The impact mechanism of long-term creep in gas-containing coal on coal and gas outbursts has not been fully elucidated and remains insufficiently understood for the purpose of disaster engineering control. This investigation conducted triaxial creep experiments on raw coal specimens under controlled confining pressures, axial stresses, and gas pressures. Through systematic analysis of coal’s physical responses across different loading conditions, we developed and validated a novel creep damage constitutive model for gas-saturated coal through laboratory data calibration. The key findings reveal three characteristic creep regimes: (1) a decelerating phase dominates under low stress conditions, (2) progressive transitions to combined decelerating–steady-state creep with increasing stress, and (3) triphasic decelerating–steady–accelerating behavior at critical stress levels. Comparative analysis shows that gas-free specimens exhibit lower cumulative strain than the 0.5 MPa gas-saturated counterparts, with gas presence accelerating creep progression and reducing the time to failure. Measured creep rates demonstrate stress-dependent behavior: primary creep progresses at 0.002–0.011%/min, decaying exponentially to secondary creep rates below 0.001%/min. Steady-state creep rates follow a power law relationship when subject to deviatoric stress (R² = 0.96). Through the integration of Burgers viscoelastic model with the effective stress principle for porous media, we propose an enhanced constitutive model, incorporating gas adsorption-induced dilatational stresses. This advancement provides a theoretical foundation for predicting time-dependent deformation in deep coal reservoirs and informs monitoring strategies concerning gas-bearing strata stability. This study contributes to the theoretical understanding and engineering monitoring of creep behavior in deep coal rocks.

1. Introductory

With the development of deep coal resource mining, the mining and treatment of deep high-gas mines has become a research hotspot in coal mine engineering research [1,2]. During the process of deep coal mining, the coal rock body may undergo progressive destruction of coal pillars and coal seams under high stress, which leads to serious safety hazards, resulting in the fracture of coal rock seams and gas protrusion [3]. During this process, the creep of the coal body undergoes little changes in the short term, but it seriously affects the stability of the roadway as a result of the long-term mechanical action [4]. Therefore, a comprehensive understanding of the creep characteristics of gas-containing coal bodies is crucial for safe production and disaster prevention in terms of deep gas-containing coal seams.

Creep is a phenomenon in which a coal rock body continues to deform slowly under high stress [5,6]. Stress transfer and redistribution of internal stresses in coal bodies affected by mining occurs after mining, which leads to internal structural changes and, thus, affects long-term creep behavior [6]. Yang et al. [7] found that coal specimens under high confining pressures have typical three-stage creep characteristics, and with the increase in confining pressure, the creep threshold increases, whereas the creep threshold coefficient decreases. Guo et al. [5] improved the viscoelastic member with an hourglass component and time step function, established a fractional-order creep damage constitutive model and accurately captured the nonlinear decelerating and accelerating creep phases, explaining the hysteresis characteristics observed during the creep failure process. Zhang et al. [8] carried out triaxial creep experiments and established a nonlinear creep model. Zhou et al. [9] carried out creep experiments on soft rock and found that the creep had a strong mutation characteristic, and concluded that the destruction of the rock mass and the hardening effect competed with each other during the creep process. Li et al. [10] modified Nishihara’s model by adding an accelerating element to characterize the creep of sandstone, and assessed the accelerated creep stage. Yin et al. [11] explored the effect of insufficient creep on the deformation energy of tectonic coals under hydrostatic pressure and found that insufficient or no creep leads to a bending decrease in the deformation energy curve when 76.41~82.45% of the maximum stress is exceeded. Li et al. [12] established an intrinsic model of coal–rock assemblage creep considering the effect of the water content, based on the Hamburg creep model, and found that the stress environment and water content had a significant effect on the creep characteristics of the coal–rock assemblage. Zhou et al. [13] established a new model considering the effect of the matrix–fracture interaction and creep deformation on the permeability of deep coal under triaxial stress, and found that the permeability decreased gradually during the stage of primary creep.

The rheological hypothesis of coal and gas outburst suggests that such outbursts are the result of a sudden change in the rheological properties of coal containing gas, which has been repeatedly verified during the process of deep coal mining [14,15]. To achieve a quantitative evaluation of the stability of prominent coal seams, it is necessary to conduct in-depth research on the rheological properties of gas containing coal and establish a quantitative mathematical model. Gas action further induced changes in the creep characteristics of the coal body. Li et al. [16] analyzed the creep behavior of gas-containing coal bodies, and found that the deformation of 0.5 MPa gas was greater than that of coal specimens without gas pressure (0 MPa) under the same axial stress, which gradually decreases. This indicates that gas has a positive effect on the deformation process of coal, which accelerates the creep process, reduces the strength of the coal, and changes the creep properties of the coal. At the same time, creep leads to coal seam stress and microporous structure destruction and closure, which in turn leads to a reduction in coal seam permeability [17,18]. However, in deep gas-containing coal seams, the coal body is in a gas–solid coupling state, resulting in a creep phenomenon that is different from that of conventional coal bodies. The above model gives less consideration to the expansion force of adsorbed gas during the creep process of a coal body, which has some limitations in regard to characterizing the creep of gas-bearing coal.

To examine the creep behavior of deep coal seams containing gas and conduct a quantitative characterization of deformation damage under high-stress conditions, this study performed triaxial creep tests on raw coal specimens under varying confining, axial, and gas pressure conditions, using an RMT-150C electro-hydraulic servo mechanics experimental machine from Wuhan, China. The investigation analyzed variations in the physical characteristics under each loading configuration. Incorporating coal matrix adsorption-induced expansion effects, we modified the Burgers creep model to develop a damage-coupled constitutive model of gas-bearing coal creep. The proposed model underwent iterative optimization and experimental validation using laboratory data. These findings provide important theoretical references for stability assessments of deep gas-bearing coal strata, the monitoring of dynamic hazards, and engineering support design in coal seams.

2. Experimental Methods

2.1. Experiment Procedure

The coal briquettes used in this study were obtained from Wangpo Coal Mine, Shanxi, China. Coal briquettes with dimensions of 400 × 300 × 300 mm were selected from the working face, sealed and packed, and transported to the laboratory. According to International Society for Rock Mechanics (IRSM) standards [19], six coal samples were taken from the coal blocks, with diameters and lengths of 50 mm and 100 mm, respectively.

The Triaxial Loading Test System uses the RMT-150C electro-hydraulic servo mechanics experimental machine (Figure 1), which consists of a host computer, control system, triaxial test system, shear test system, indirect tensile device, and a hydraulic source, etc. The maximum output force of the vertical hydraulic cylinder is 1000 kN, and the maximum confining pressure is 50 MPa. The vertical hydraulic cylinder’s maximum force is 1000 kN, the piston stroke is 50 mm, the deformation rate is 0.0001~1 mm/s, the loading rate is 0.01~100 kN/s, the maximum confining pressure is 50 MPa, and the confining pressure rate is 0.001~1 MPa/s. A triaxial clamping device diagram is shown in Figure 1. The gripper was developed in-house. Methane gas was used as the experimental gas. The gripper can be used for φ50×70~100 mm sized coal rock specimens; the maximum confining pressure under loading conditions is 35 MPa; the maximum axial pressure under loading conditions is 75 MPa; the maximum inlet pressure is 30 MPa. The gas transmission control device consists of high-pressure gas cylinders, pressure-reducing valves, gas leakage monitors, vacuum pumps, an inlet pipe, outlet pipe inlet valves, a gas pressure digital display meter, and other components.

2.2. Experimental Procedures

To mine the coal seam safely, it is necessary to extract the original gas before mining the coal seam. To analyze the creep change in the original coal seam in the deep coal seam over a long period of time, creep infiltration experiments were carried out on the gas-containing coal body under the in situ stress state. The experimental steps are as follows:

(1)

Assemble and place the three-axis gripper on the operating table and connect the pressure system, sonic collector, and gas transmission unit.

(2)

Create a new loading control file, select the pressure control system–rock triaxial test module, and select manual control. Input the initial axial pressure and confining pressure parameters and start loading until the stress reaches the initial values. The confining pressure and gas pressure conditions of each coal sample are shown in

Table 1. Experimental conditions of each specimen.

Number	Confining Pressure σ3 (MPa)	Gas Pressure pg (MPa)	Number	Confining Pressure σ3 (MPa)	Gas Pressure pg (MPa)
No. 1	6	0	No. 2	6	0.5
No. 3	8	0	No. 4	8	0.5
No. 5	10	0	No. 6	10	0.5

.

(3)

Open the outlet valve, close the inlet valve, and evacuate for 15 min.

(4)

Close the outlet valve, open the inlet valves and the cylinder valve and fill with gas. Adjust the gas cylinder pressure, reducing the valve to the set value, inflate for 2 h; let the coal sample and gas achieve full adsorption, to achieve an adsorption equilibrium.

(5)

According to the site conditions of the coal seam, load the samples up to an axial pressure of 20 MPa, a loading rate of 2 MPa/min, and a constant loading time of 60 min. After that, increase the loading pressure by 2 MPa at each stage.

(6)

At the end of the experiment, make a record. Then, close the gas cylinder, the pressure reducing valve and the inlet valve of the gripper, and open the outlet valve until the gas pressure in the gripper drops to 0, and then stop the press loading.

(7)

According to different experimental programs, change the gas pressure, loading mode, repeat steps (1)~(6), to apply different conditions to the stress–gas coupling damage experiments.

3. Experimental Results

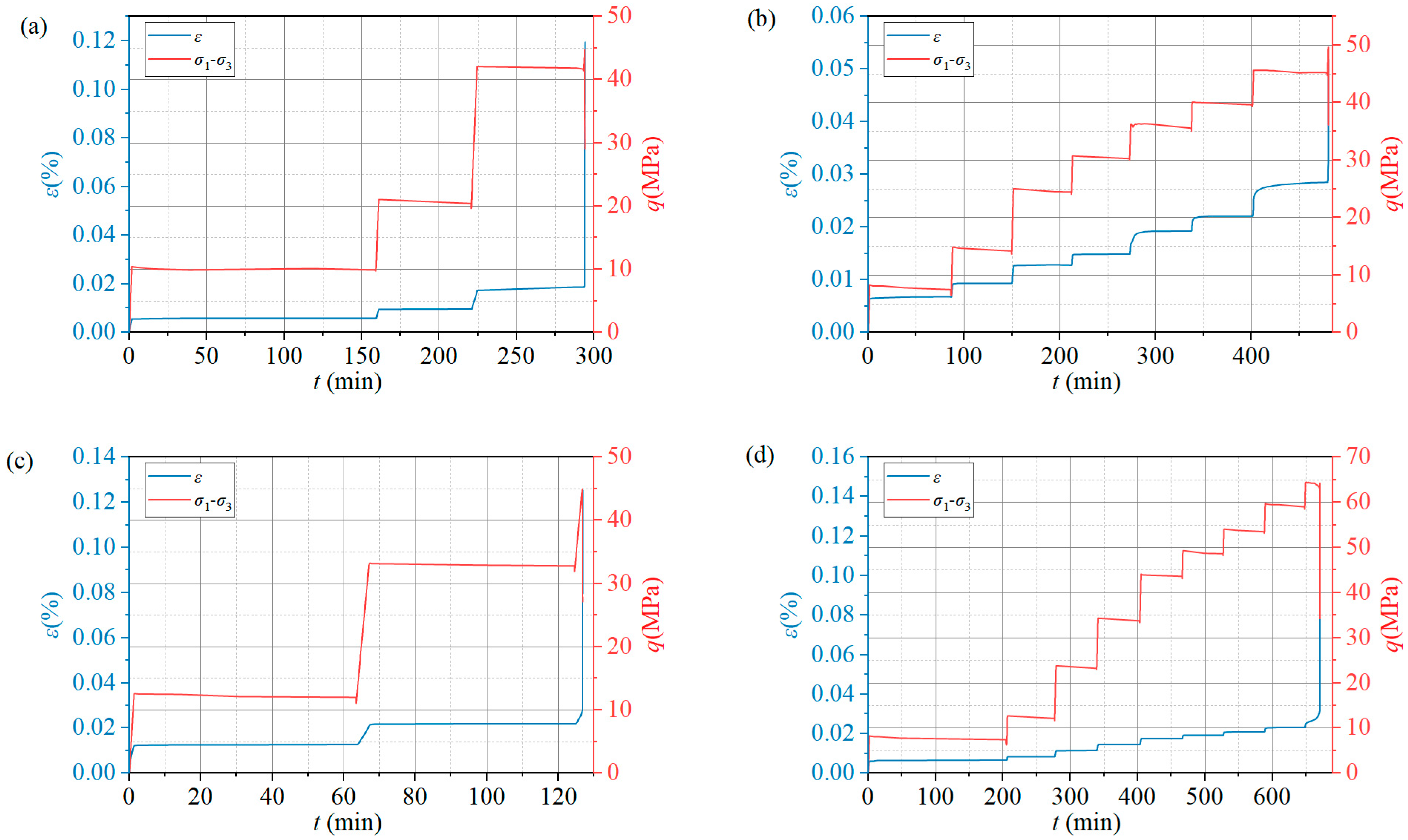
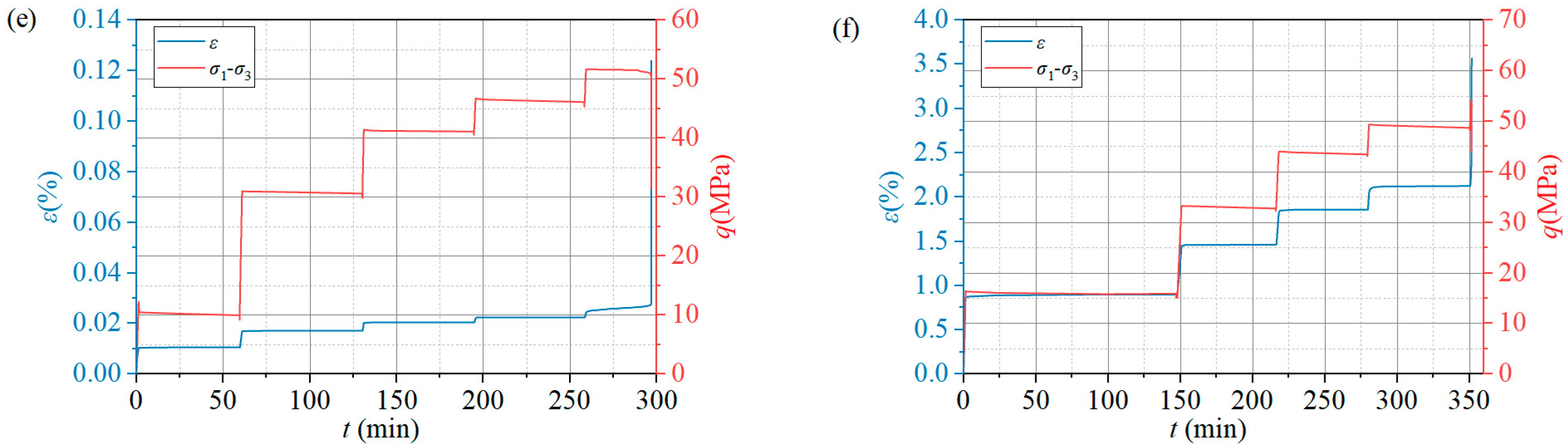
3.1. Mechanical Loading Results

Figure 2 shows the stress–strain loading curves during the loading of each coal sample, and Figure 3 shows the creep curves and bias stress curves of each coal sample. From Figure 2, it can be seen that as the strain–stress curves are consistent with the uniaxial stress–strain curves, the difference is that the stress remains constant during the creep stage, while the strain gradually increases. Meanwhile, the curves do not change consistently under different gas-containing pressures and confining pressure environments. At the lower stress level, the creep behavior is relatively small; the creep behavior is more obvious under high stress, as shown in regard to specimen No. 4.

From Figure 3, it can be seen that as loading proceeds, the creep change in the coal body at each stress level is not consistent. The creep phenomenon is not clear under low stress. Stable creep phenomena, with different major and minor forms, appear under a medium level of stress. However, some coal samples (e.g., Figure 3d,e) show unstable tertiary creep phenomena at high stresses, characterized by acceleration after secondary creep. The No. 4 coal samples exemplify stress-controlled transitions at 60 MPa below the axial level, and the creep rate decreases as the time stabilizes. Beyond 60 MPa, the creep rate increases significantly after the secondary stage, indicating the onset of tertiary creep.

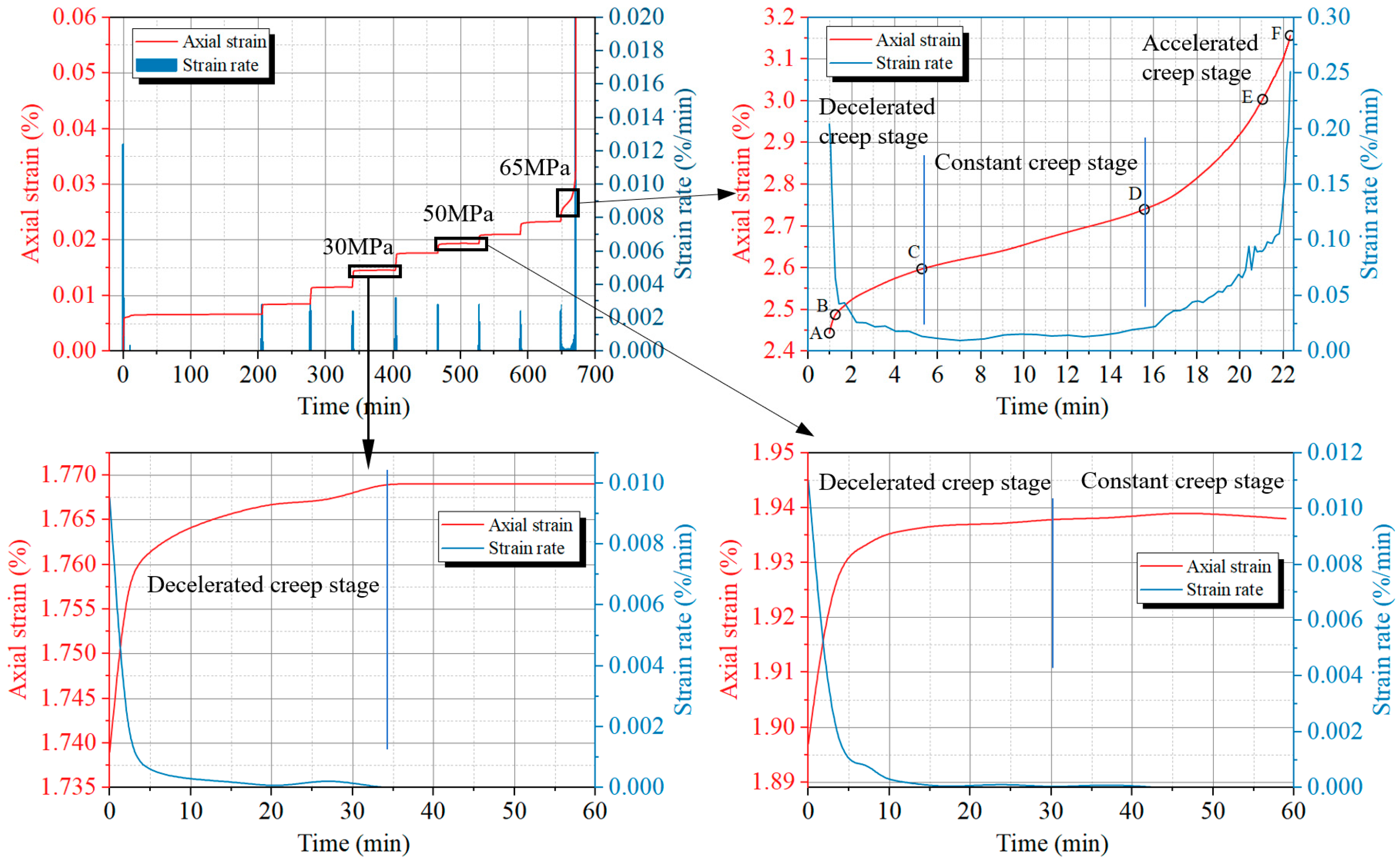
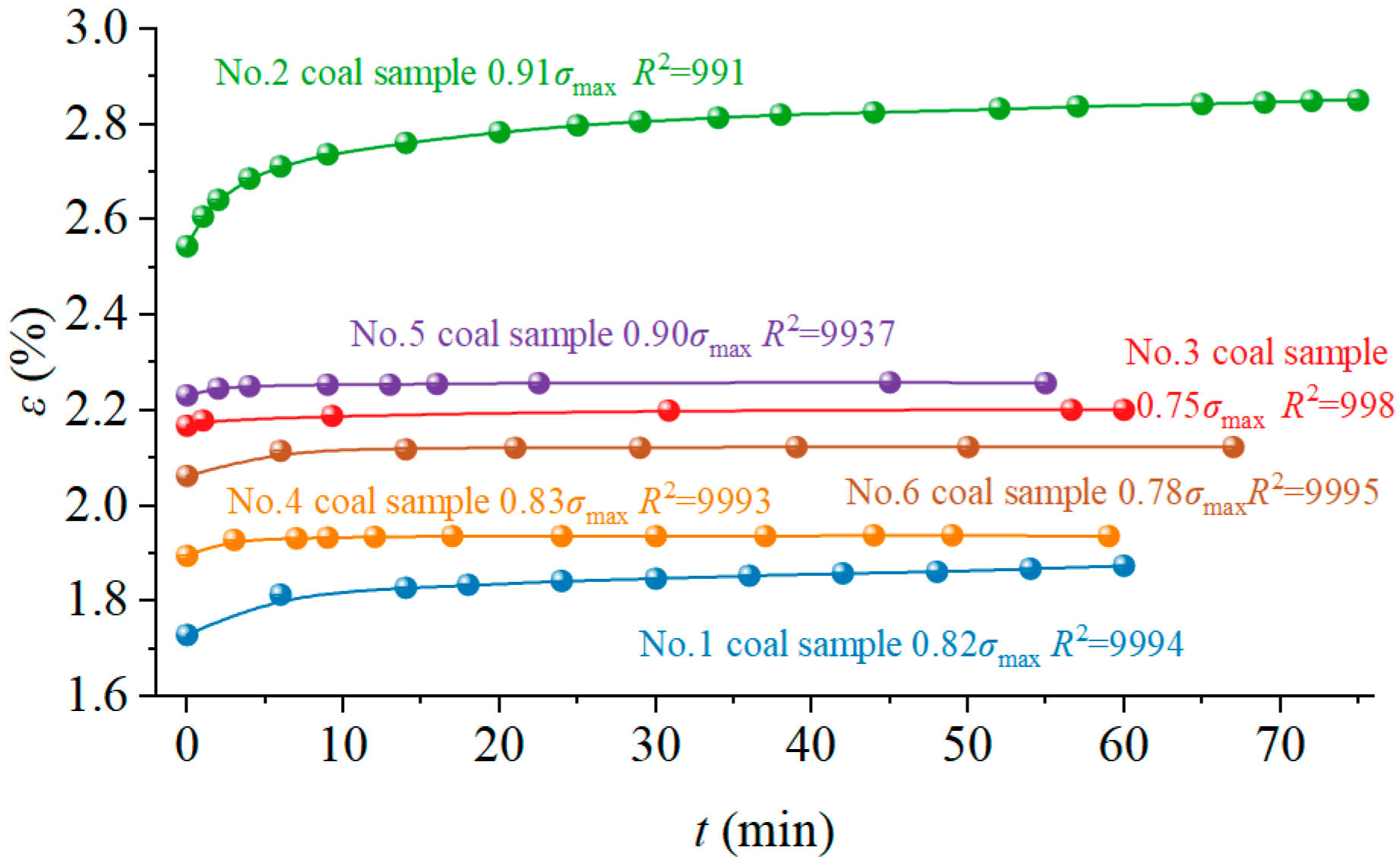
3.2. Characteristics of Loading Creep Damage

Creep instability failure of the coal body needs to satisfy two conditions in terms of the loading stress level and creep time at the same time. The creep curves of each coal sample under different stress levels are shown in Figure 4. The failure characteristics of the coal samples before creep are obvious. The coal samples have different degrees of instantaneous axial strain when applying various levels of axial stress. The deformation decreases gradually with time, indicating that the coal specimens have obvious time-varying deformation characteristics under a constant load. Under first order axial stress, the axial strain increases rapidly during the initial hour of stress application, but the deformation stabilizes over time. As shown in Figure 4d, there is a hysteresis in the final failure of the coal samples, i.e., when the final stress is applied, the coal samples do not fail instantaneously, but undergo a period of accelerated creep.

Comparing the creep curves of each specimen at different stress levels, the strain curves only show a decelerated creep phase at low stress levels. As the stress level increases, the strain curve begins to show a decelerated and constant creep phase. The creep rate gradually decelerates and does reach a constant rate. Finally, at the highest stress level, the strain curves show the obvious characteristics of decelerating, constant, and accelerating stages (No. 4 coal sample at 65 MPa stress level).

Under the same axial stress conditions, the strains also differed. The strain values for the coal specimens without gas pressure (0 MPa) were lower than those for 0.5 MPa gas-filled coal. This phenomenon indicates that gas causes unequal time to failure and gas accelerates the creep process. Gas pressure and migration, such as adsorption, diffusion, and flow within the coal, exacerbate the extension and penetration of internal cracks, which indirectly affects the creep behavior of the coal and increases the strain values of the coal.

3.3. Analysis of Typical Creep Phenomena

Taking Figure 5 as an example, when the stress level of the No. 4 coal sample reaches 30 MPa, the initial strain creep rate is small as 0.002–0.009%/min, and then decreases to 0 after 30 min. This stage is obviously characterized by decelerated creep. When the stress level reaches 50 MPa, the initial creep rate is 0.002–0.011%/min, and then gradually decreases to below 0.001%/min. For the strain curves of the corresponding stages, the axial strain keeps increasing, i.e., it has a constant creep characteristic.

Comparing the creep curves of the coal samples at different stress levels, at low stress levels, the strain curves show only a decelerating creep phase. At this point the strain rate tends toward 0. However, as the stress level increases, the strain curves begin to show a decelerated and constant creep phase. The creep rate gradually decelerates and does not reach a constant rate. Finally, at the highest stress level, the strain curve exhibits the distinctive characteristics of the decelerating, constant, and accelerating phases: the gradual acceleration of the creep rate. If there is only one decelerating creep phase in the creep curve, it is called stable creep. If the creep curve contains decelerating, constant, or accelerating creep, it is called non-stationary creep.

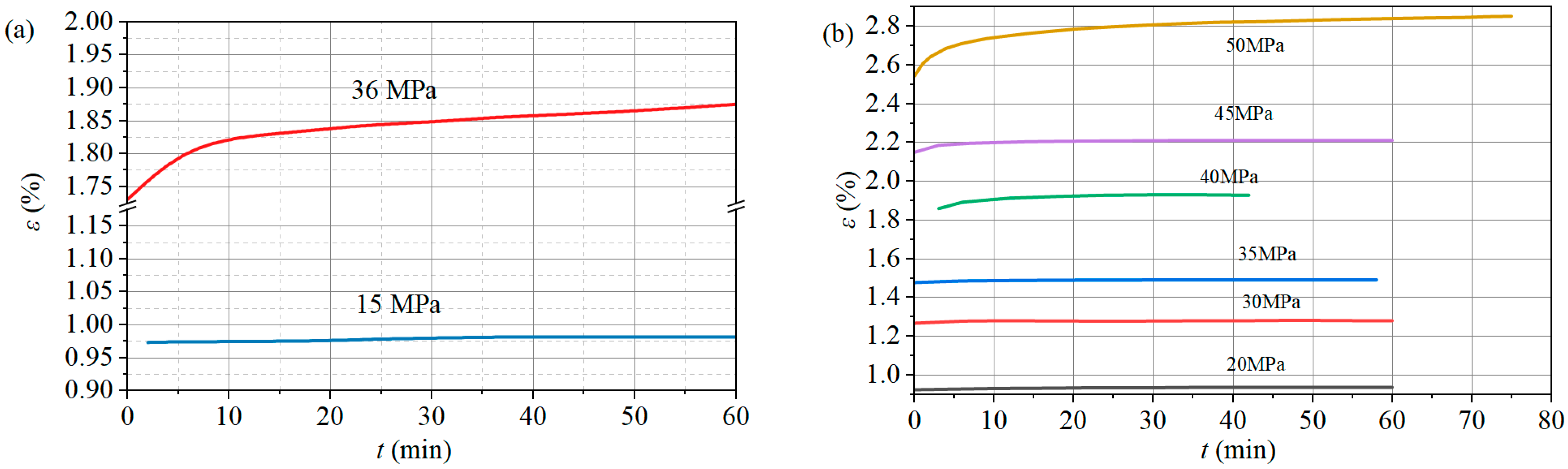
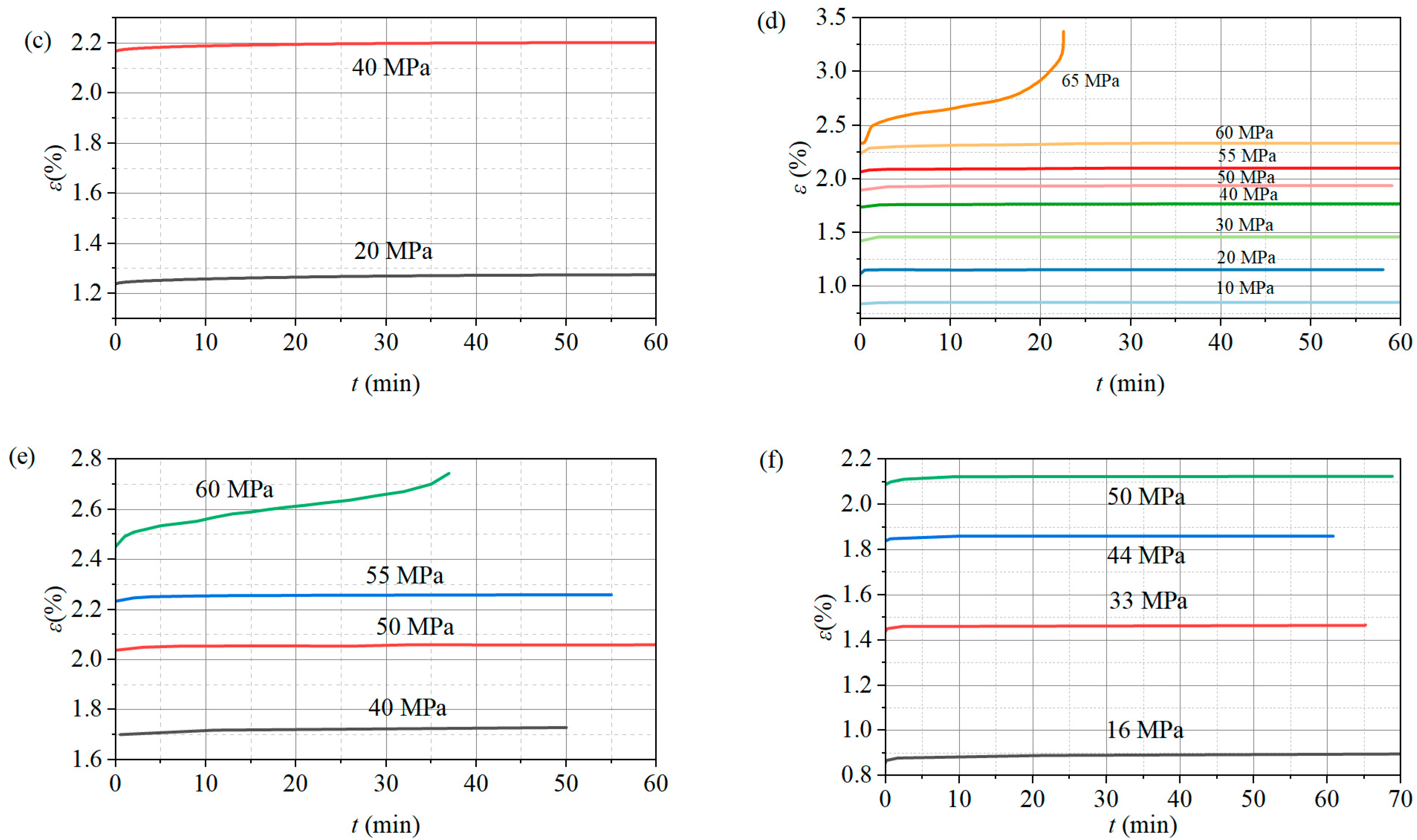
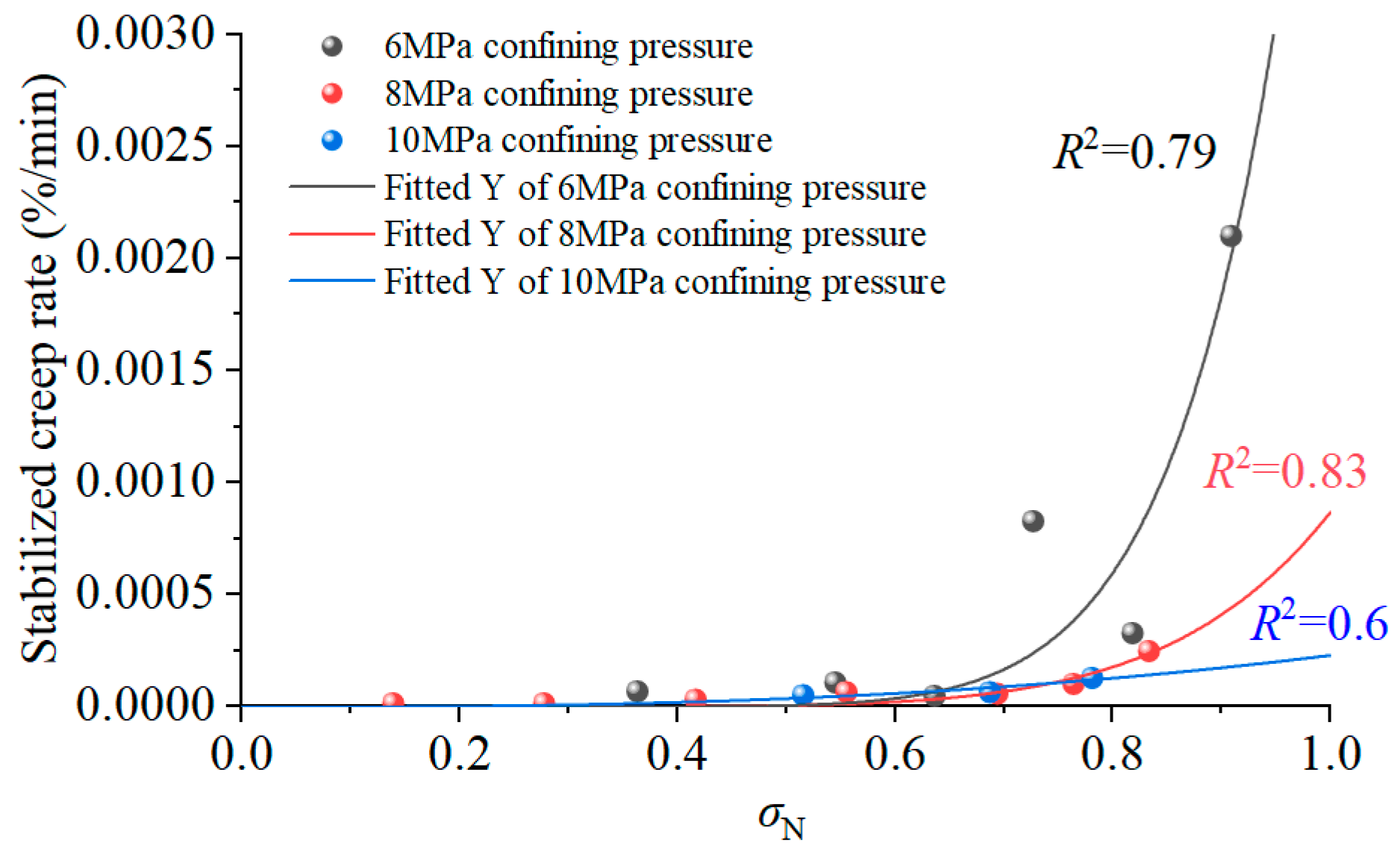
3.4. Variation in Creep Rate of Gas-Bearing Coal Bodies

The strain rate (${\epsilon }_{\mathrm{steady}}^{\prime }$) of the stable creep stage for each stress stage of the gas-containing gas was analyzed to determine the effect of stress on the creep rate. At the same time, in order to reflect the role of stress, each stress level is normalized and the normalized stress is expressed as ${\sigma }_N$. The stable creep of the gas-containing coal samples at each stress stage is shown in Figure 6.

As shown in Figure 6, the stabilized creep of the gas-bearing coal body at each stress stage is smaller at the low stress stage and gradually becomes larger at the high stress stage. It is noted that there is a tendency to decrease with the increase in the enclosing pressure at the same stress level. Numerical fitting of the stabilized creep rate at each stage was carried out, and the fitting results are as follows:

The variation in the creep rate with stress for a 6 MPa perimeter pressure is:

$${\mathit{\epsilon }}_{\mathbf{steady}}^{\prime }=\mathbf{0.005}\mathbf{\cdot }{\mathit{\sigma }}_N^{9.52}$$

(1)

The variation in the creep rate with stress for an 8 MPa perimeter pressure is:

$${\mathit{\epsilon }}_{\mathbf{steady}}^{\prime }=\mathbf{0.00075}\mathbf{\cdot }{\mathit{\sigma }}_N^{7.09}$$

(2)

The variation in the creep rate with stress for a 10 MPa perimeter pressure is:

$${\mathit{\epsilon }}_{\mathbf{steady}}^{\prime }=\mathbf{0.000235}\mathbf{\cdot }{\mathit{\sigma }}_N^{2.6}$$

(3)

The fitting accuracies of 0.79, 0.83, and 0.60 were obtained, which indicates that the power function format was used for better fitting. This indicates that the relationship between the stabilized creep rate and the bias stress is in accordance with the power function law, which has similar conclusions in regard to other rock materials, such as sandstone [6].

4. Discussion

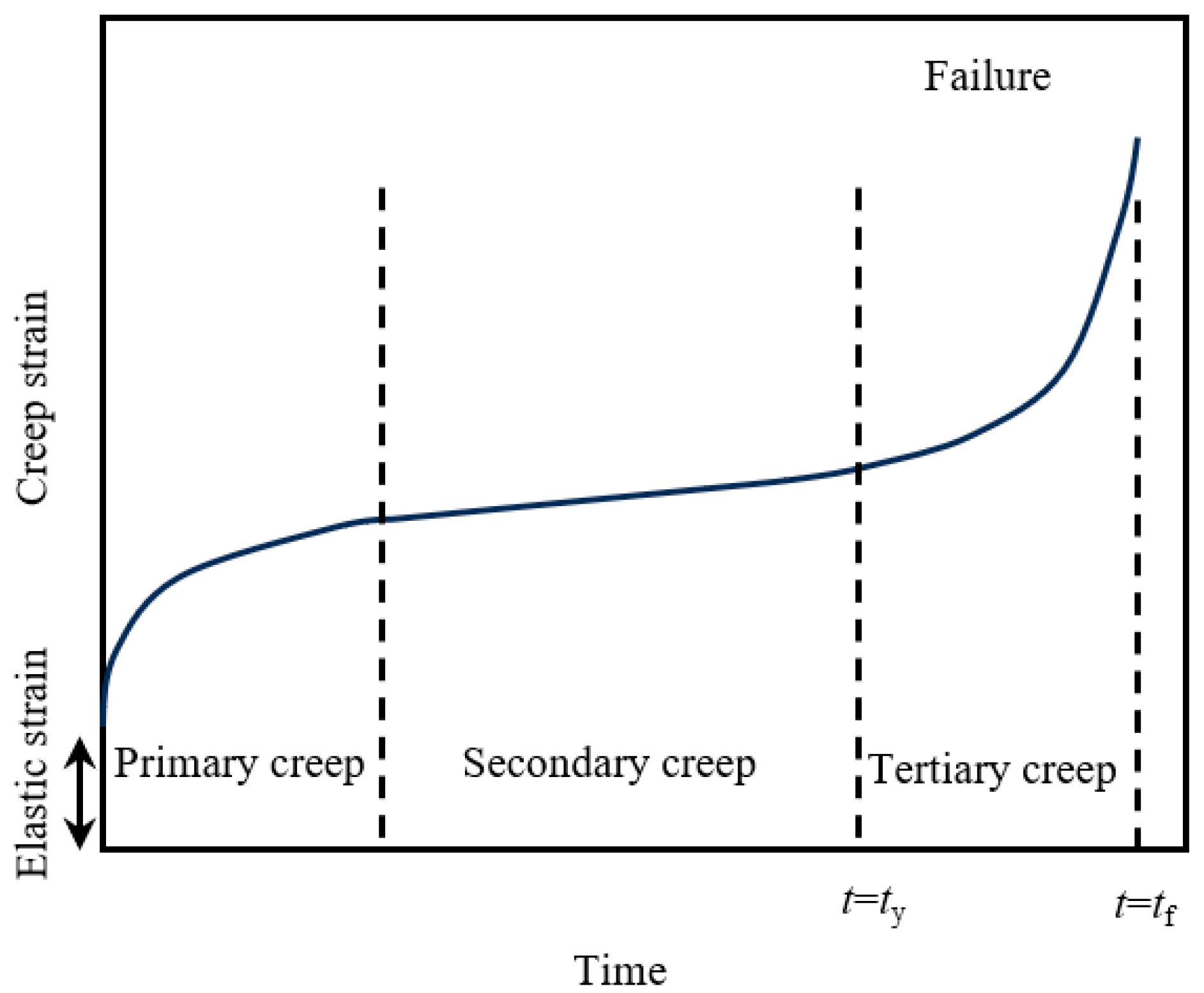
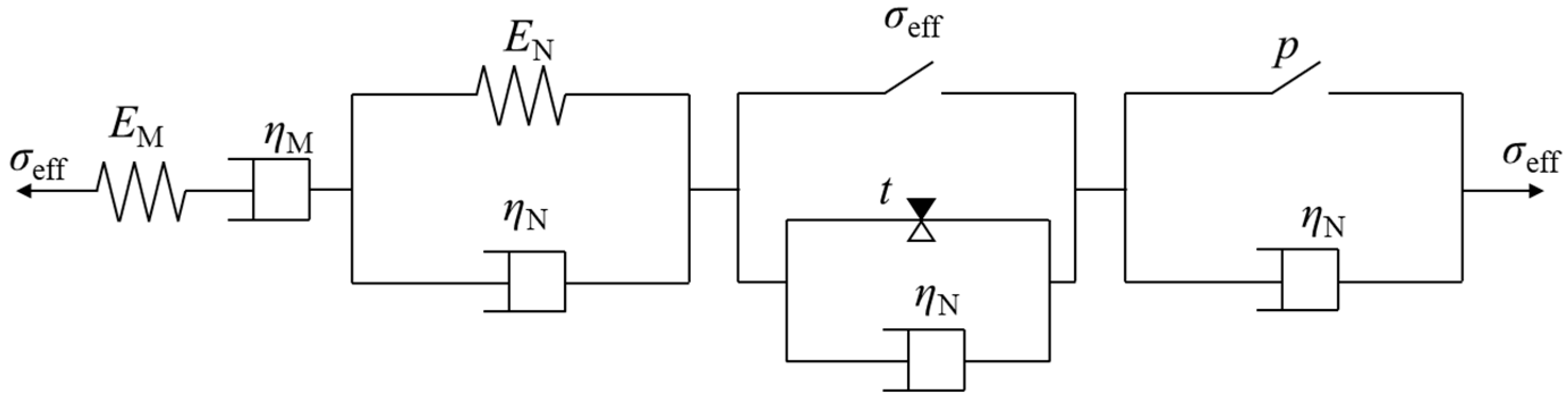
4.1. Creep Strain in Coal

The deformation of the coal body mainly relies on the change in stress and time. Among them, the rapid change in stress induces destabilization damage of the coal body, while the change in time under high stress induces the creep behavior of the coal body. Figure 7 shows a typical creep curve of coal under partial stress conditions [17,20,21]. It consists of three stages: (1) primary creep; (2) secondary creep; and (3) tertiary creep. The strain rate during primary creep decreases with time, becomes zero during steady-state creep and, finally, increases with time during tertiary creep.

In general, the general equation for creep [22] can be written as:

$$\epsilon ={\epsilon }^e+{\epsilon }^c$$

(4)

where $\epsilon$ is the total strain; ${\epsilon }^e$ is the elastic strain of the coal body, obeying Hooke’s law; and ${\epsilon }^c$ is the creep strain.

Among the traditional creep models, the Burgers model has creep characteristics, such as transient elasticity, creep, and stress relaxation. It can effectively reflect the creep characteristics of coal–rock assemblages. The creep characteristics of all rock materials can be obtained by modeling the shear modulus and viscosity coefficient of the Kelvin body and the shear modulus and viscosity coefficient of the Maxwell body [12]. The creep model is shown in Figure 8. In Figure 8, σ is the stress, E_M and E_N are the elastic moduli of Kelvin’s body and Maxwell’s body, η_M and η_N are the viscosity coefficient of Kelvin’s body and Maxwell’s body, and ω is the moisture content.

Burgers creep equation [10] is known as:

$${\mathit{\epsilon }}_{\mathbf{ve}}^c={\displaystyle \frac{{\mathit{\sigma }}_{\mathbf{eff}}}{{\mathit{E}}_M}}+{\displaystyle \frac{{\mathit{\sigma }}_{\mathbf{eff}}}{{\mathit{\eta }}_M}}t+{\displaystyle \frac{{\mathit{\sigma }}_{\mathbf{eff}}}{{\mathit{\eta }}_N}}\left[1-e^{-{\displaystyle \frac{t}{\tau }}}\right]$$

(5)

where $E_M,{\eta }_M$ is the modulus of elasticity and coefficient of viscosity of the Maxwell body; and $E_N,{\tau }_N$ is the modulus of elasticity and relaxation time of the Kelvin body.

Under low stress, the material still has weak creep behavior. However, in fact, for coal seam excavation in the field, the coal body creep time under the action of low stress is much longer than the coal seam excavation time. Therefore, this paper does not need to consider the creep behavior under low stress.

The creep characteristics of the coal rock body are affected by the gas action, and the creep characteristics become very complicated under long-term ground stress and gas action. It is difficult to explain the creep phenomenon of the gas-containing coal body using the existing creep constitutive model; one of the reasons for this is that the key mechanical parameters in the constitutive model are generally constant constants, and the rock parameters do not change with the gas participation, which is a linear type of creep. However, in practice, this does not reflect the real situation of coal rock creep. The Burgers model is improved on a traditional basis, and the intrinsic model of the creep effect of gas action on the coal body can be obtained by comprehensively considering the effect of gas action on each parameter.

In regard to the deformation process of the coal body, its total strain can be decomposed into elastic strain, plastic strain, creep strain, and adsorption–expansion strain under the action of gas; therefore, Equation (4) can be modified as:

$$\epsilon ={\epsilon }^e+{\epsilon }^c+{\epsilon }^s$$

(6)

where ${\epsilon }^s$ is the adsorption–expansion strain.

4.2. The Effect of Gas Action on the Creep of Coal Bodies

Coal body properties are regarded as a viscoelastic–plastic porous medium [23]; containing gas action will cause expansion strain; gas action is mainly manifested in regard to the following: (1) gas pressure affects the effective stress; (2) gas adsorption leads to expansion strain of the coal body; and (3) gas seepage coupled with the deformation of the coal body.

To assess the effective stress caused by gas expansion of the coal body, the Terzaghi effective stress principle was used to correct [24] as:

$${\mathit{\sigma }}_{\mathbf{eff}}=\sigma -\alpha pI$$

(7)

where α is the Biot coefficient and I is the unit tensor. Where the elastic strain ${\epsilon }^e$ is:

$${\mathit{\epsilon }}^e={\displaystyle \frac{1}{2G}}{\sigma }_{{\mathbf{eff}}^{\prime }}+{\displaystyle \frac{1}{3K}}{\sigma }_{\mathbf{eff},m}I$$

(8)

where G, K are the shear modulus and bulk modulus, ${\mathit{\sigma }}_{{\mathbf{eff}}^{\prime }}$ is the bias tensor, and ${\mathit{\sigma }}_{\mathbf{eff},m}$ is the average effective stress.

In considering viscoelastic–plastic simulation, the traditional model cannot describe the accelerated creep phase, so an improved Burgers model was obtained by connecting a nonlinear visco-plastic body in parallel with the traditional model and superimposing the effect of gas on the coefficient of viscosity:

$${\mathit{\epsilon }}^c={\mathit{\epsilon }}_{\mathbf{ve}}^c+{\mathit{\epsilon }}_{\mathbf{vp}}^c$$

(9)

where ${\mathit{\epsilon }}_{\mathbf{ve}}^c$ is the strain provided by the conventional Burgers model, called the viscoelastic strain, and ${\mathit{\epsilon }}_{\mathbf{vp}}^c$ is the visco-plastic strain considering the effect of gas.

The visco-plastic strain considering the gas weakening effect is:

$${\dot{\mathit{\epsilon }}}_{\mathbf{vp}}^c=\left\{\begin{array}{l}0,\sigma \le {\sigma }_y\\ A{\left({\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{{\sigma }_y(p)}}\right)}^n{e}^{-Q/(RT)},\sigma >{\sigma }_y\end{array}\right.$$

(10)

where ${\sigma }_y(p)={\sigma }_{y0}\cdot \exp (-kp)$, the gas pressure p reduces the yield strength; A, n, Q, R, T are material constants and temperature parameters.

Based on the Langmuir adsorption equation [24], the expansion strain is related to the gas pressure and the coal body gas adsorption–expansion strain is:

$${\epsilon }^s={\displaystyle \frac{{\epsilon }_{\max }p}{p+p_L}}I$$

(11)

where ${\mathit{\epsilon }}_{\max }$ is the maximum expansion strain and p_L is the Langmuir pressure constant.

In a coal body, gas flow satisfies Darcy’s law. Darcy’s law is modified by the gas seepage equation [2,25,26]:

$${\displaystyle \frac{\partial (\varphi {\rho }_g)}{\partial t}}+\nabla \cdot ({\rho }_g{\mathbf{v}}_g)=Q_s$$

(12)

where φ is the porosity; ρ_g is the gas density; ${\mathbf{v}}_g=-{\displaystyle \frac{k_1}{\mu }}\nabla p$ is the seepage rate; and Q_S is the gas source term (adsorption/desorption rate).

Changes in porosity due to creep action and gas action, etc., are considered:

$$k_1=k_0{\left(1+\beta {\epsilon }_v^c\right)}^3$$

(13)

where k₀ is the initial permeability, $\beta$ is the fracture compression coefficient, and ${\mathit{\epsilon }}_v^c$ is the creep volumetric strain.

Assuming a uniaxial state of stress, a one-dimensional simplified form of the completed intrinsic model was obtained using the total strain expression:

$$\epsilon (t)=\underset{\mathrm{Maxwell}}{\underbrace{{\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{E_M}}+{\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{{\eta }_M}}}}+\underset{\mathrm{Kelvin}}{\underbrace{{\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{{\eta }_K}}\left[1-e^{-{\displaystyle \frac{t}{\tau }}}\right]}}+\underset{\mathrm{Viscoplasticity}}{\underbrace{A{\left({\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{{\sigma }_y(p)}}\right)}^n}}t+\underset{\mathrm{Adsorption} \mathrm{expansion}}{\underbrace{{\displaystyle \frac{{\epsilon }_{\max }p}{p+p_L}}}}$$

(14)

where ${\mathit{\eta }}_M,{\mathit{\eta }}_K$ is the viscosity coefficient associated with the gas pressure (according to which $\mathit{\eta }={\mathit{\eta }}_0{\mathit{e}}^{bp}\mathbf{,}\mathit{b}$ can be assumed to be the fitting parameter).

During the specific analysis process, for the deceleration creep stage, the visco-plastic term can be neglected, so the equation can be simplified as:

$$\epsilon (t)={\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{E_M}}+{\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{{\eta }_M}}+{\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{{\eta }_K}}\left[1-e^{-{\displaystyle \frac{t}{\tau }}}\right]+{\displaystyle \frac{{\epsilon }_{\max }p}{p+p_L}}$$

(15)

For the stable creep phase, the Kelvin body strain region is saturated, when 1 − e^−t/τK = 0 at which point the equation can be simplified to:

$$\epsilon (t)={\displaystyle \frac{{\mathit{\sigma }}_{\mathbf{eff}}}{E_M}}+{\displaystyle \frac{{\mathit{\sigma }}_{\mathbf{eff}}}{{\eta }_M}}+{\displaystyle \frac{{\epsilon }_{\max }p}{p+p_L}}$$

(16)

For the accelerated creep phase, when the cumulative and visco-plastic flow of coal damage needs to be considered, the equation can be simplified as:

$$\epsilon (t)={\epsilon }_{\mathrm{steady}}+A{\left({\displaystyle \frac{{\sigma }_{\mathbf{eff}}}{{\sigma }_y(p)}}\right)}^n\left(t-t_{accel}\right)$$

(17)

where ε_steady is the strain during the stabilization phase for the stabilization phase, and t_accel is the moment during the accelerated change.

A schematic diagram of the model is shown in Figure 9.

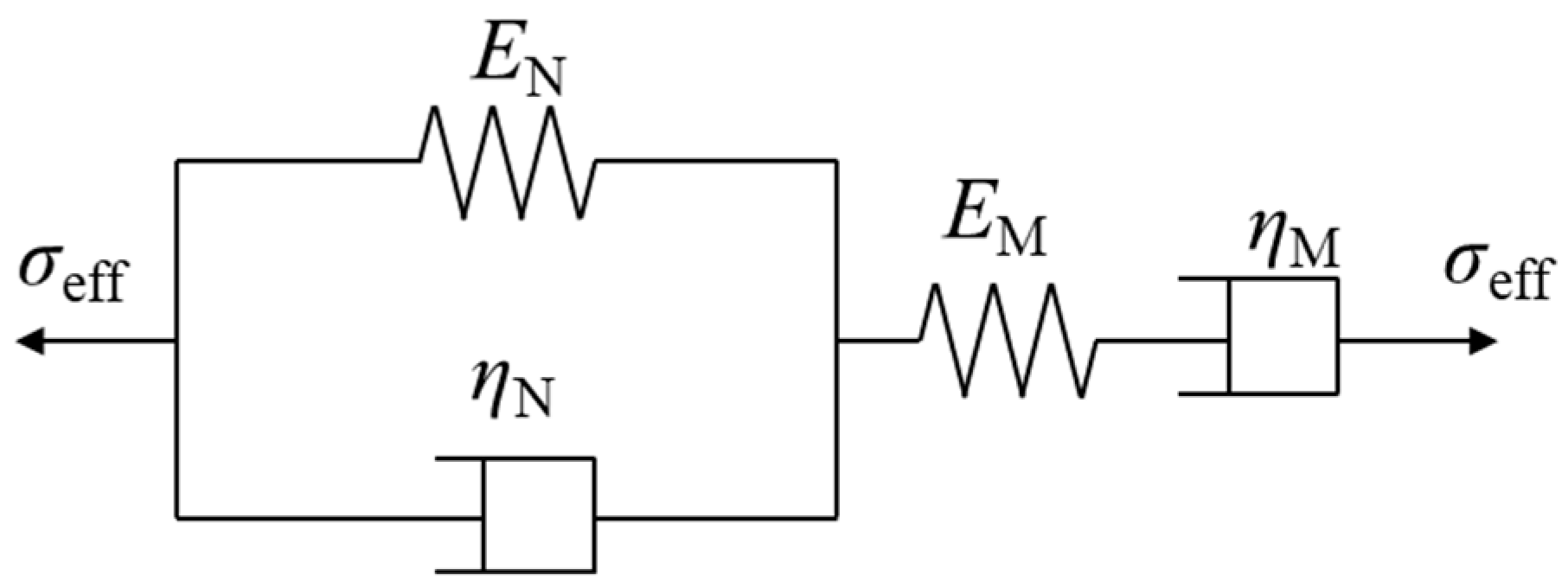
4.3. Validation of the Model

To assess the validity of the formula and the experimental data, the creep results for different perimeter pressures at different stress levels are fitted using Equations (15)–(17), and the fitting equations are realized by using the Python 3.8 SciPy library. The SciPy library has powerful numerical calculations and nonlinear fitting functions, and the built-in curve_fit module and other modules of multiple optimization algorithms make it more adaptable. The parameter values for each experimental condition are obtained using calculations. The codes for the calculations in this paper are shown in Appendix A. The results are shown in

Table 2. Simulation parameters after fitting.

Parameter	EM/MPa	EK/MPa	ηM	ηK	εmax	pL	α	σy0	k	ε0
No. 1	2987.35	6.98 × 104	1.97 × 106	1984	0.00395	0.079	1.19	49.8	0.049	0.00183
No. 2	2850.12	7.23 × 104	1.85 × 106	2107	0.00428	0.067	1.32	48.6	0.053	0.00175
No. 3	4125.37	4.86 × 104	3.15 × 106	1472	0.00297	0.048	1.53	55.2	0.038	0.00185
No. 4	3278.54	6.23 × 104	1.78 × 106	1865	0.00431	0.076	1.15	52.4	0.047	0.0019
No. 5	3562.84	5.78 × 104	2.41 × 106	1823	0.00265	0.061	1.38	52.4	0.044	0.00178
No. 6	3256.71	6.24 × 104	2.78 × 106	2015	0.00352	0.059	1.27	51.9	0.047	0.00181

:

The creep deformation and catastrophic damage results were fitted using the creep model of gas-containing coal established in this study. The elastic and viscous moduli at different creep stress levels were obtained. To verify the correctness of the present model, the test data were inverted using the model parameters for the No. 4 coal samples under 50 MPa circumferential pressure conditions. The inversion test data were compared with the original test data, as shown in Figure 10. This result shows the rapid increase in each creep strain during the initial stage, while the creep curve gradually stabilizes with the increase in time. The comparison results show that the experimental data after inversion using the above model parameters do not differ much from the original experimental data, and the correlation coefficient R² is 0.991, which verifies the correctness of the present model.

At high stress levels, the strain rate also increases during the steady-state creep phase. After the long-term strength is exceeded, the change in the strain rate is significant, even if the stress increases slightly. The resistance to deformation of the coal body gradually decreases under the continuous action of high stress levels, until failure occurs. When the coal body is loaded beyond a certain stress level, the viscosity decreases gradually with the increase in the applied stress. Therefore, the fitting parameters of the intrinsic model’s viscosity established in this study are consistent with the rheological properties of gas-containing coal bodies.

5. Conclusions

In this study, triaxial creep tests were carried out on raw coal samples under different confining pressures, axial pressures, and gas pressures, and the physical characteristics of the coal samples under each condition were analyzed, and the intrinsic model of gas-containing creep damage was established and optimized and verified based on laboratory data. The main conclusions are as follows:

(1)

Coal body creep appears as a decelerating creep stage at low stress levels, begins to show decelerating and constant creep stages as stress levels increase, and shows distinctive features of decelerating, constant, and accelerating stages at the highest stress levels. The strain values for coal specimens without gas pressure (0 MPa) are lower than those for gas-filled coal of 0.5 MPa, and the gas causes unequal time to failure, and the gas accelerates the creep process.

(2)

The primary creep rate is 0.002–0.011%/min and, then, secondary creep gradually decreases to below 0.001%/min. The stable creep rate of gas-containing coals at each stress stage is small at the low stress stage and gradually becomes larger at the high stress stage. The relationship between the stable creep rate and partial stress is in accordance with the power function law.

(3)

On the basis of the Burgers model, the creep damage constitutive model of gas-containing coal considering the role of adsorption–expansion stress was established according to the principle of effective stress in porous media. The comparison results show that the experimental data after inversion using the above model parameters do not differ much from the original experimental data, and the R² of the correlation coefficients are all greater than 0.991, which verifies the correctness of the constitutive model.