Production Capacity and Temperature–Pressure Variation Laws in Depressurization Exploitation of Unconsolidated Hydrate Reservoir in Shenhu Sea Area
Abstract
1. Introduction
2. Mathematical Model of NGH Exploitation
3. Establishment of Numerical Model for Hydrate in Shenhu Sea Area
3.1. Model Development for Hydrate Depressurization Production
- (1)
- The heat exchange behaviors between fluid and solid, as well as between different fluid phases in the model, only include thermal convection and thermal conduction, while thermal radiation is not considered.
- (2)
- There is an aqueous phase, gas phase, and hydrate phase in the formation pore space. It is assumed that the hydrate phase and gas phase are methane hydrate and methane gas, respectively, and the formation pores are completely filled by the three phases of water, methane hydrate, and methane gas.
- (3)
- The hydrate phase in the model has no seepage behavior in the reservoir, meaning there is no relative displacement between the hydrate phase and solid particles.
- (4)
- Only the aqueous phase and gas phase exist as seepage phases in the formation pore space, and their seepage behaviors follow the generalized Darcy’s law, with the gas slippage effect ignored.
- (5)
- The formation deformation during the depressurization exploitation of natural gas hydrates conforms to the small deformation theory of solid mechanics.
- (6)
- The physical parameters such as density, thermal conductivity, and specific heat of hydrates and rocks are set as constant values during the hydrate exploitation process.
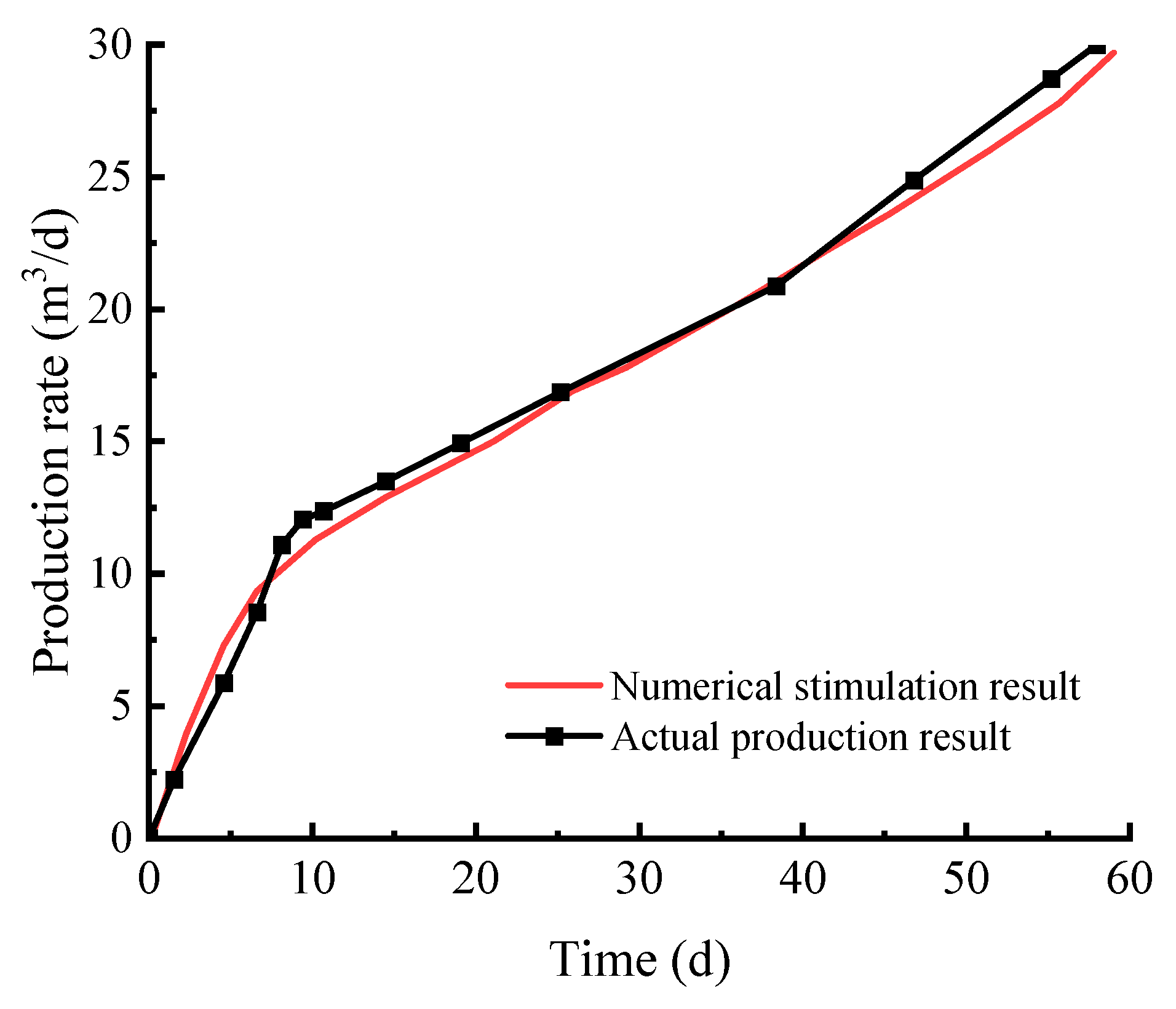
3.2. Model Verification for Hydrate Depressurization Production
4. Analysis of Numerical Simulation Results for Depressurization Production
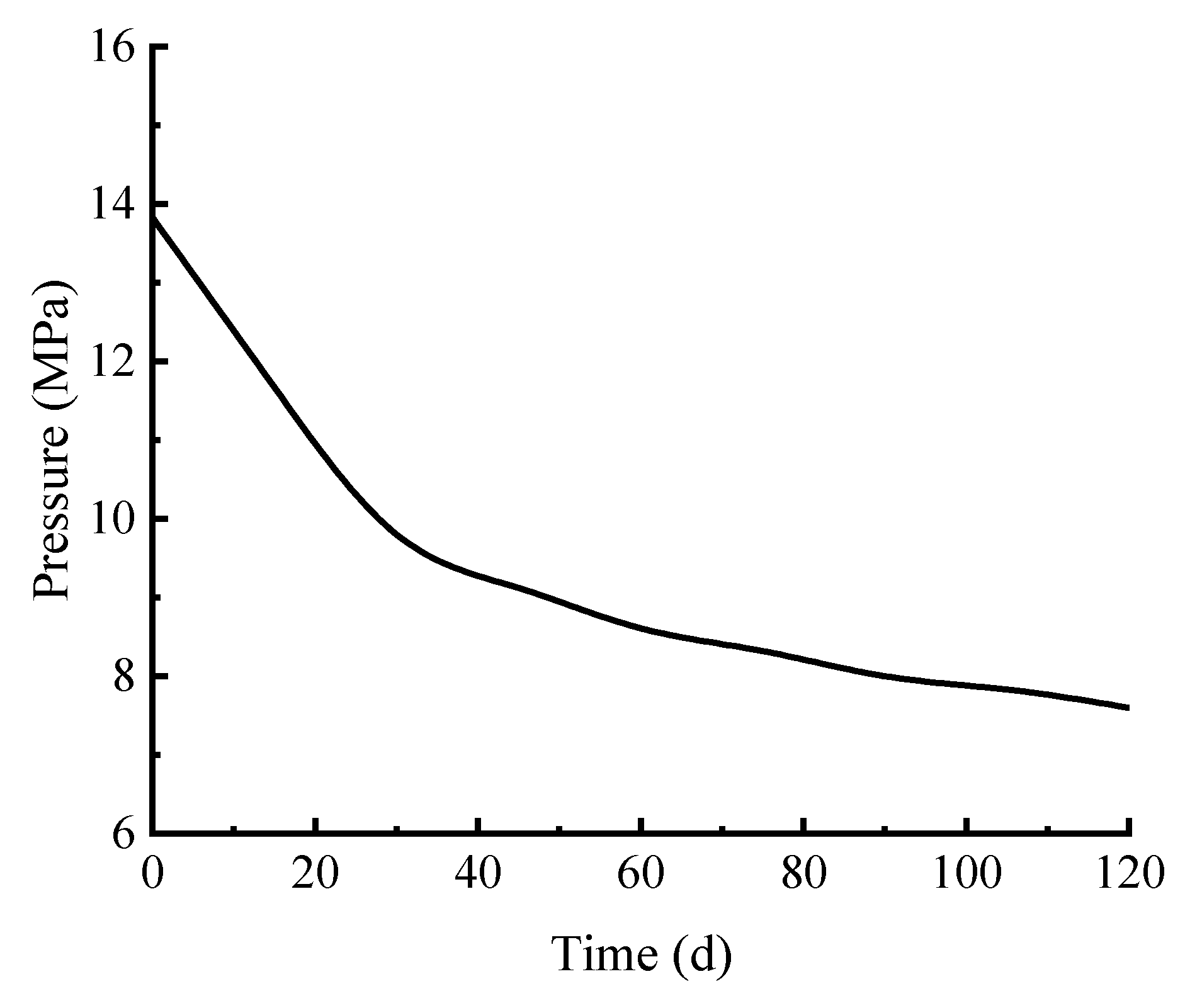
4.1. Analysis of Reservoir Pressure Change
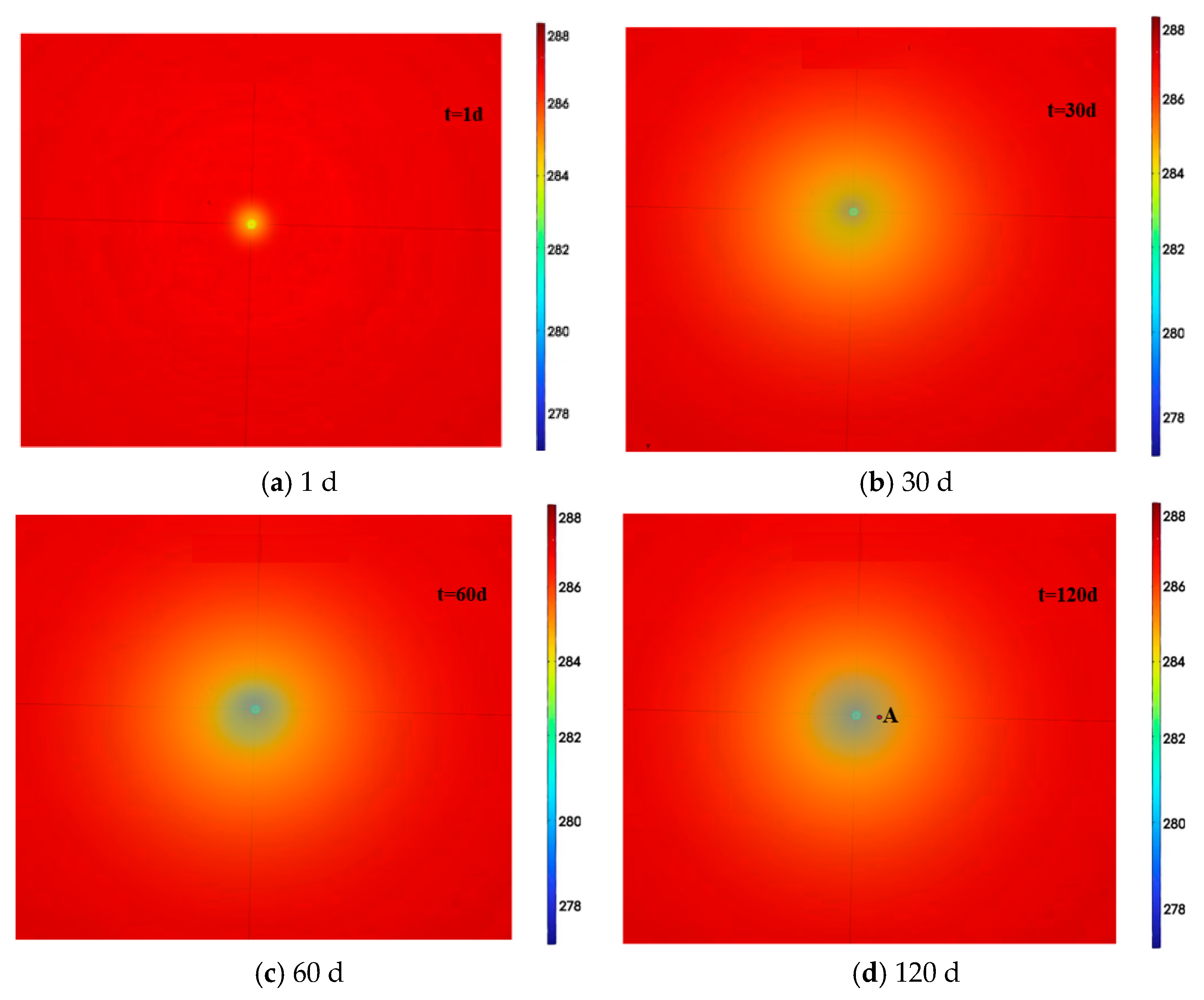
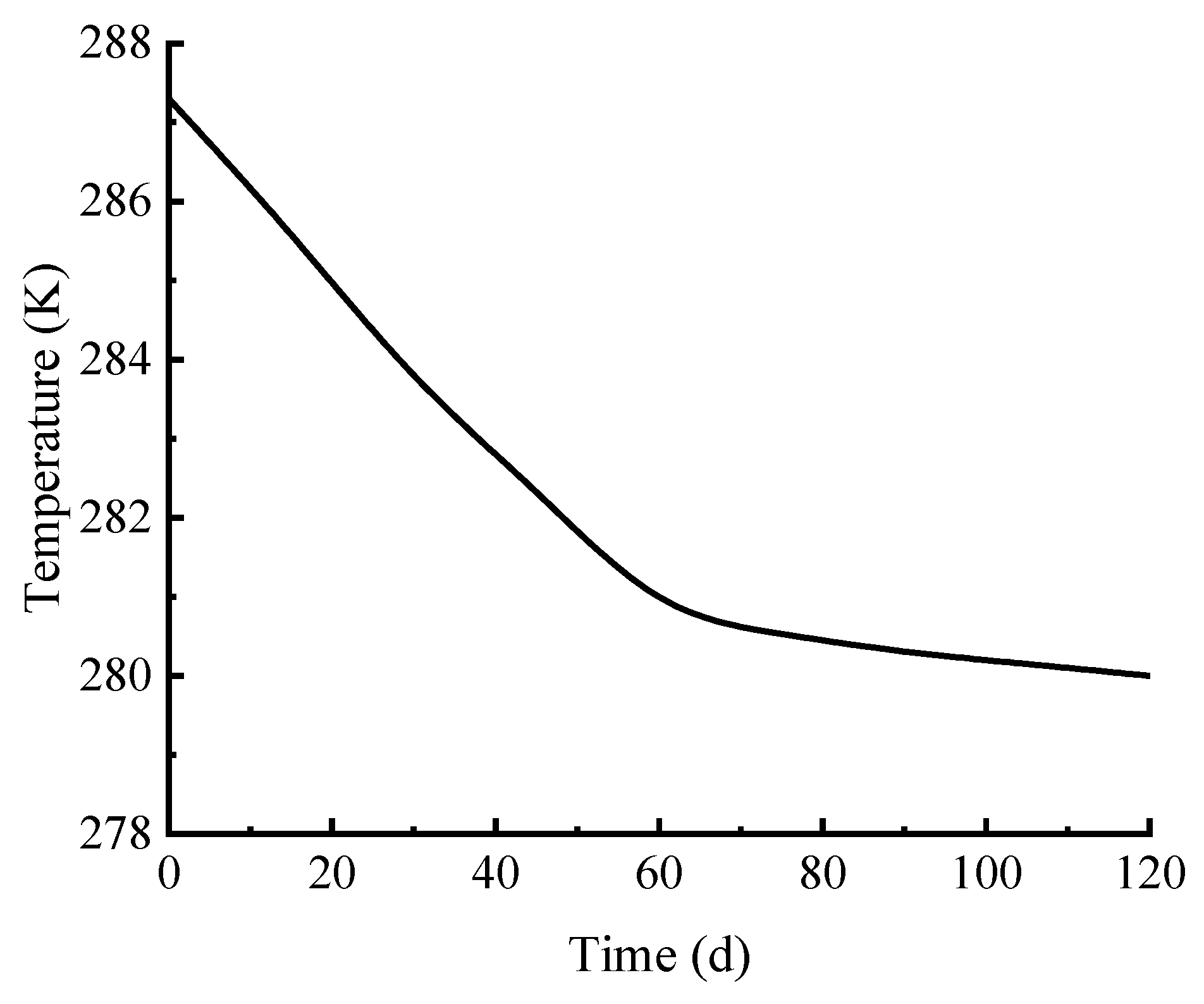
4.2. Analysis of Reservoir Temperature Change
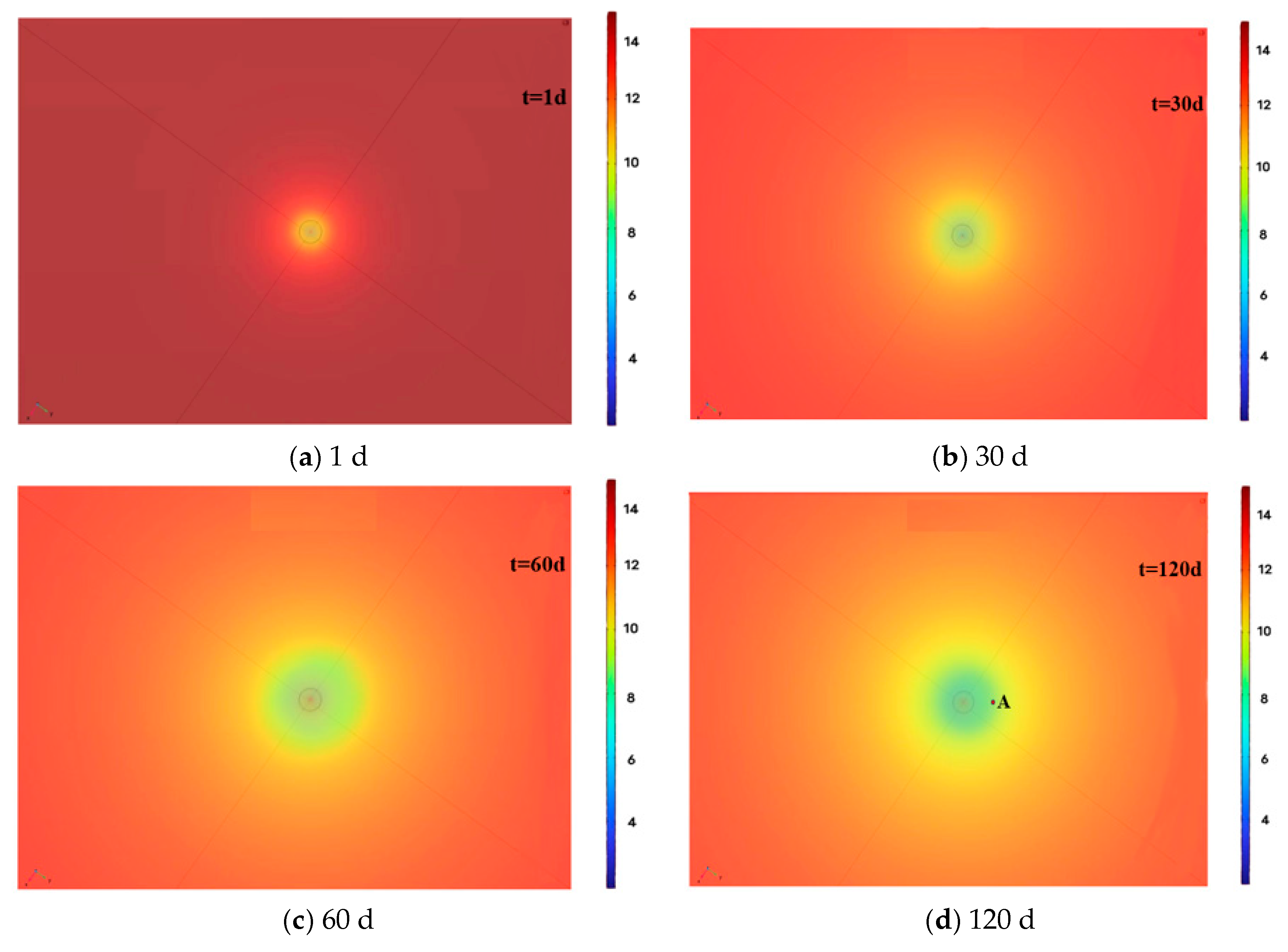
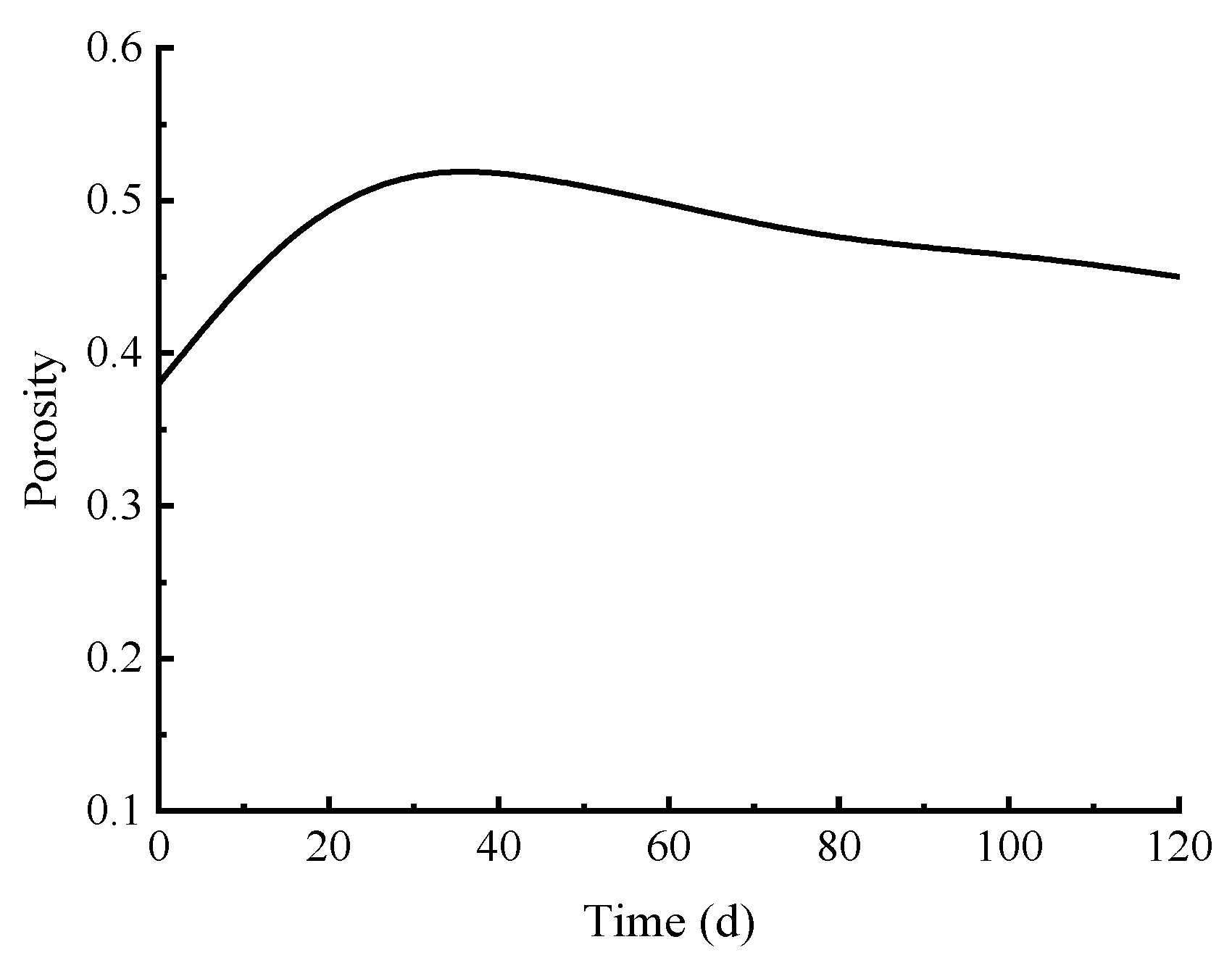
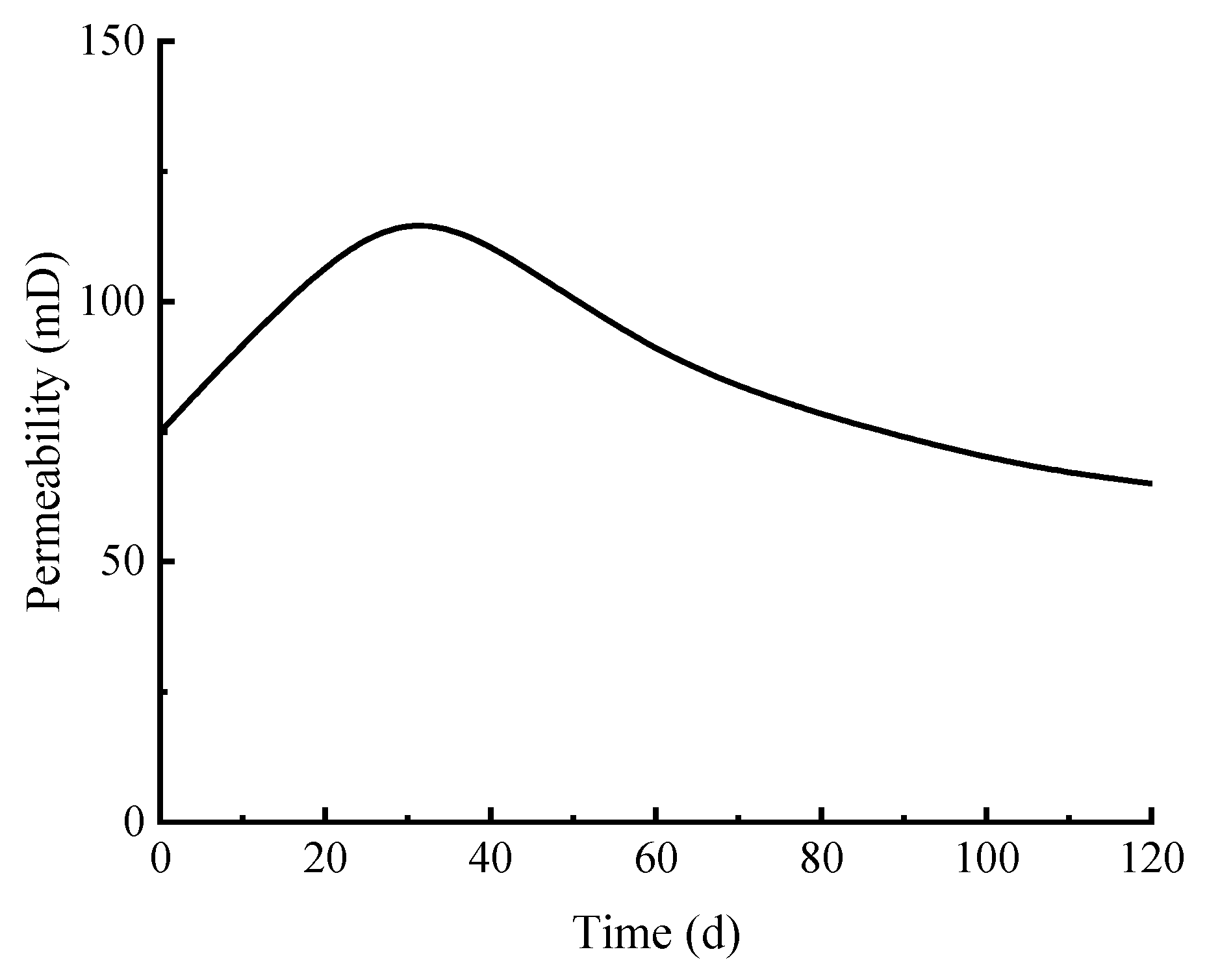
4.3. Analysis of Physical Property Parameters Change
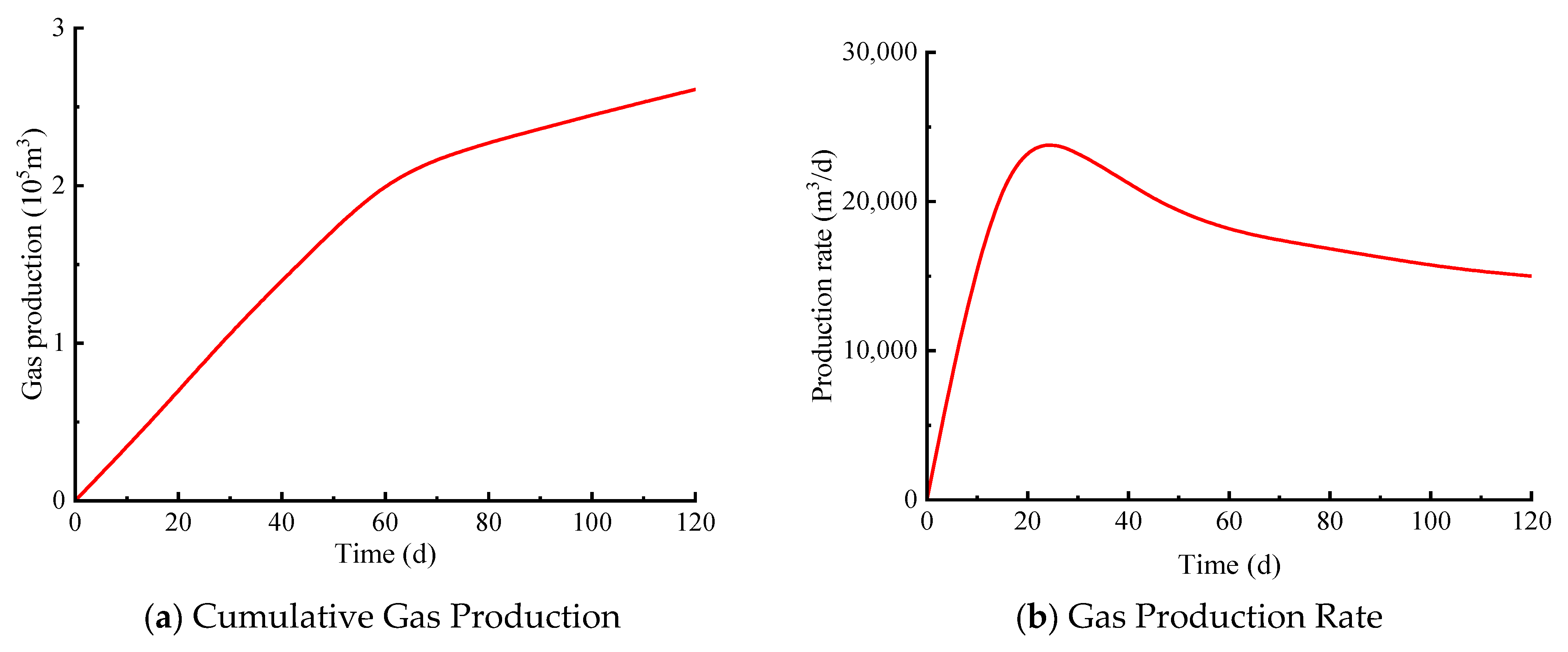
4.4. Analysis of Production Capacity Change
5. Conclusions
- (1)
- During the vertical well depressurization exploitation, within 0–30 days, rapid near-well pressure drop (13.83→9.8 MPa, 36.37%) drives peak gas production (25,000 m3/d) via hydrate dissociation, with porosity (0.41→0.52) and permeability (75→100 mD) increasing. Within 30–60 days, slower pressure decline (9.8→8.6 MPa, 12.24%) and fines migration cause permeability fluctuations (120→90 mD), reducing gas production to 20,000 m3/d. Within 60–120 days, pressure stabilizes (~7.6 MPa) with residual hydrate saturation < 0.1, leading to stable low permeability (60 mD) and gas production (15,000 m3/d), with cumulative production reaching 2.2 × 106 m3.
- (2)
- Key Mechanisms: Productivity changes are governed by coupled processes: rapid initial dissociation driven by pressure drops and heat absorption; subsequent productivity decline due to reduced heat supply, fines migration, and porosity compression; and eventual stabilization as hydrate saturation and fluid flow reach dynamic equilibrium.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Cheng, Y.; Li, C. Mechanical properties research of unconsolidated hydrate-bearing sediments under the effect of clay minerals. PLoS ONE 2025, 20, e0319772. [Google Scholar] [CrossRef]
- Li, Q.C.; Wu, J.J.; Li, Q.; Wang, F.L.; Cheng, Y. Sediment Instability Caused by Gas Production from Hydrate-bearing Sediment in Northern South China Sea by Horizontal Wellbore: Sensitivity Analysis. Nat. Resour. Res. 2025, 34, 1667–1699. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.C.; Wang, F.L.; Ning, X.; Wang, Y.L.; Bai, B.J. Settling behavior and mechanism analysis of kaolinite as a fracture proppant of hydrocarbon reservoirs in CO2 fracturing fluid. Colloids Surf. A Physicochem. Eng. Asp. 2025, 724, 137463. [Google Scholar] [CrossRef]
- Hui, C.Y.; Zhang, Y.Q.; Zhang, P.P. Numerical simulation of natural gas hydrate exploitation productivity based on radial well fracturing combined with depressurization method. Nat. Gas Ind. 2022, 42, 12–16. [Google Scholar] [CrossRef]
- Wan, Y.Z.; Wu, N.Y.; Hu, G.W. Reservoir stability during depressurization exploitation of natural gas hydrates in Shenhu Sea Area, South China Sea. Nat. Gas Ind. 2018, 38, 17–20. [Google Scholar]
- Mao, P.X. Numerical Simulation Study on Multi-Branch Well Exploitation of Argillaceous Silt Hydrate Reservoir in Shenhu Sea Area, South China Sea; China University of Geosciences: Wuhan, China, 2023; pp. 14–18. [Google Scholar]
- Wei, N.; Li, C.; Zhao, X. Numerical simulation of depressurization exploitation in class 1 hydrate reservoirs under different development factors in Shenhu area, South China sea. Front. Earth Sci. 2024, 12, 20–24. [Google Scholar] [CrossRef]
- Wang, T.H.; Liu, Z.Z.; Yang, Y.J. Depressurization-induced gas production from hydrate reservoirs in the Shenhu sea area using horizontal well: Numerical simulation on horizontal well section deployment for gas production enhancement. Front. Earth Sci. 2023, 15, 49–57. [Google Scholar] [CrossRef]
- Wan, C.Y.; Zhang, H.; Li, L. Current status and technical discussion of depressurization exploitation equipment for marine natural gas hydrates. Pet. Mach. 2024, 52, 23–27. [Google Scholar]
- Jin, G.R.; Xu, T.F.; Liu, X. Optimization study on simulation exploitation scheme of natural gas hydrate depressurization thermal stimulation method. J. Cent. South Univ. (Nat. Sci. Ed.) 2015, 46, 34–43. [Google Scholar]
- Li, G.; Li, X.S. Numerical Simulation of Single-Well Thermal Huff and Puff Exploitation for Natural Gas Hydrates in Shenhu Sea Area, South China Sea. Chem. Ind. Eng. Prog. 2011, 30, 45–48. [Google Scholar]
- Su, Z.; He, Y.; Wu, N. Evaluation on gas production potential from laminar hydrate deposits in Shenhu Area of South China Sea through depressurization using vertical wells. J. Pet. Sci. Eng. 2012, 86, 87–98. [Google Scholar] [CrossRef]
- Almenningen, S.; Flatlandsmo, J.; Fernø, M. Production of Sedimentary Methane Hydrates by Depressurization. In Proceedings of the SPE Bergen One Day Seminar, Bergen, Norway, 20 April 2016; SPE-180015-MS. Volume 87, pp. 59–67. [Google Scholar]
- Song, Y.C.; Liang, H.F.; Wang, Z. Analysis of heat transfer characteristics of natural gas hydrate depressurization decomposition. J. Petrochem. Coll. 2008, 21, 45–49. [Google Scholar]
- Oyama, H.; Konno, Y.; Masuda, Y. Dependence of Depressurization-Induced Dissociation of Methane Hydrate Bearing Laboratory Cores on Heat Transfer. Energy Fuels 2009, 23, 46–50. [Google Scholar] [CrossRef]
- Shahbazi, A.; Poladi-Darvish, M. Behavior of depressurization in type III hydrate reservoirs. SPE J. 2014, 19, 19–25. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, D.; Yang, M. Analysis of heat transfer effects on gas production from methane hydrate by depressurization. Int. J. Heat Mass Transf. 2014, 77, 29–31. [Google Scholar] [CrossRef]
- Liu, D. Heat Transfer Analysis of Natural Gas Hydrate Decomposition Process in Porous Media. Master’s Thesis, Dalian University of Technology, Dalian, China, 2014; pp. 12–19. [Google Scholar]
- Li, B.; Li, X.S.; Li, G. Depressurization induced gas production from hydrate deposits with low gas saturation in a pilot-scale hydrate simulator. Appl. Energy 2014, 129, 24–28. [Google Scholar] [CrossRef]
- Cheng, C.X. Study on Heat Transfer Characteristics of Natural Gas Hydrate Sediments and Its Influence on Exploitation. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2015; pp. 11–17. [Google Scholar]
- Liu, L.Q.; Xu, J.; Li, Y. Parameter sensitivity analysis of TOUGH+HYDRATE hydrate model. Mar. Sci. 2014, 38, 22–29. [Google Scholar]
- Sun, J.; Ning, F.; Li, S. Numerical simulation of gas production from hydrate-bearing sediments in the Shenhu area by depressurizing: The effect of burden permeability. J. Unconv. Oil Gas Resour. 2015, 12, 23–33. [Google Scholar] [CrossRef]
- Cui, W.; Xiao, J.Q. Application of numerical simulation to study the first test production data of hydrates in Shenhu Sea Area. Earth Sci. 2022, 47, 18–20. [Google Scholar]
- Yang, Z.Y.; Wu, X.M. Numerical simulation study on combined exploitation of multiple layers in natural gas hydrate reservoirs. Reserv. Eval. Dev. 2023, 13, 39–40. [Google Scholar]
- Han, H. Study on Pore Seepage Characteristics of Natural Gas Hydrate Reservoirs in Shenhu Sea Area, South China Sea. Master’s Thesis, China University of Petroleum, Beijing, China, 2023; pp. 16–21. [Google Scholar]
- Zhang, Y.F.; Xu, S.Y.; Lu, Y.C. Study on the influence of reservoir physical property changes on natural gas hydrate decomposition. Pet. Ind. Technol. Superv. 2024, 40, 40–46. [Google Scholar]
- Liu, J.L. Numerical Simulation Study on Optimized Test Production Scheme of Hydrate Reservoir in Shenhu Sea Area. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2018; pp. 21–28. [Google Scholar]
- Cui, Y.D.; Lu, C.; Guan, Z.Y. Influence of reservoir creep on gas well productivity during depressurization exploitation of natural gas hydrates in South China Sea. Reserv. Eval. Dev. 2023, 13, 19–28. [Google Scholar]
- Jia, R.; Hao, D.H.; Xu, J.M. Experimental study on influencing factors of sand production in hydrate exploitation reservoirs. J. Undergr. Space Eng. 2024, 20, 28–31. [Google Scholar]
- Wang, R.; Wang, T.J. Production dynamic analysis and parameter optimization of depressurization-injection thermal exploitation of hydrates in Shenhu Sea Area. Petrochem. Technol. 2020, 27, 46–49. [Google Scholar]
- Kun, X.; Yu, L.; Tao, Y. Numerical simulation of gas hydrate production in Shenhu area using depressurization: The effect of reservoir permeability heterogeneity. Energy 2023, 29, 27–30. [Google Scholar]
- Adisasmito, S.; Frank, R.; Sloan, J. Hydrates of carbon dioxide and methane mixtures. J. Chem. Eng. Data 1991, 36, 48–51. [Google Scholar] [CrossRef]
- Liu, J.J.; Shao, Z.L.; Zheng, Y.X. Numerical simulation of natural gas hydrate depressurization decomposition process. J. Southwest Pet. Univ. (Nat. Sci. Ed.) 2017, 39, 38–49. [Google Scholar]
- Sun, Y.; Meng, M.; Dai, X. Large-scale experiments of the borehole instability on shale formation influenced by drill pipe rotation. Energy Sci. Eng. 2019, 7, 2895–2920. [Google Scholar] [CrossRef]
- Sun, Y.W.; Cheng, Y.F. Research on Strengthening Technology of Horizontal Well with Ridge Fractures in Shenhu Unconsolidated Hydrate Reservoir. In Proceedings of the 11th Academic Conference of Geology Resource Management and Sustainable Development, Beijing, China, 16–17 December 2023; Elsevier: Engineering Village: Amsterdam, The Netherlands, 2023; pp. 7–15. [Google Scholar]
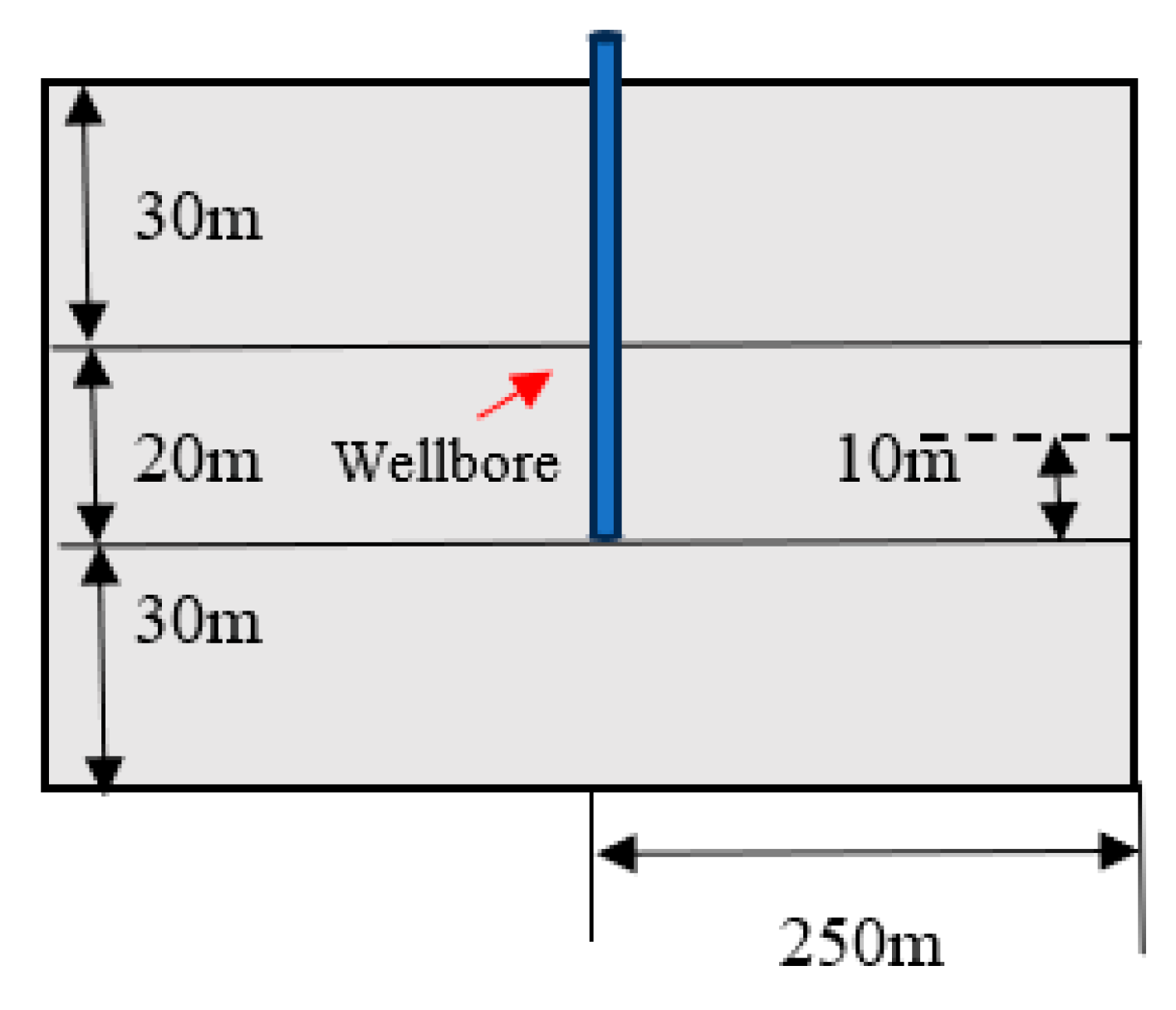
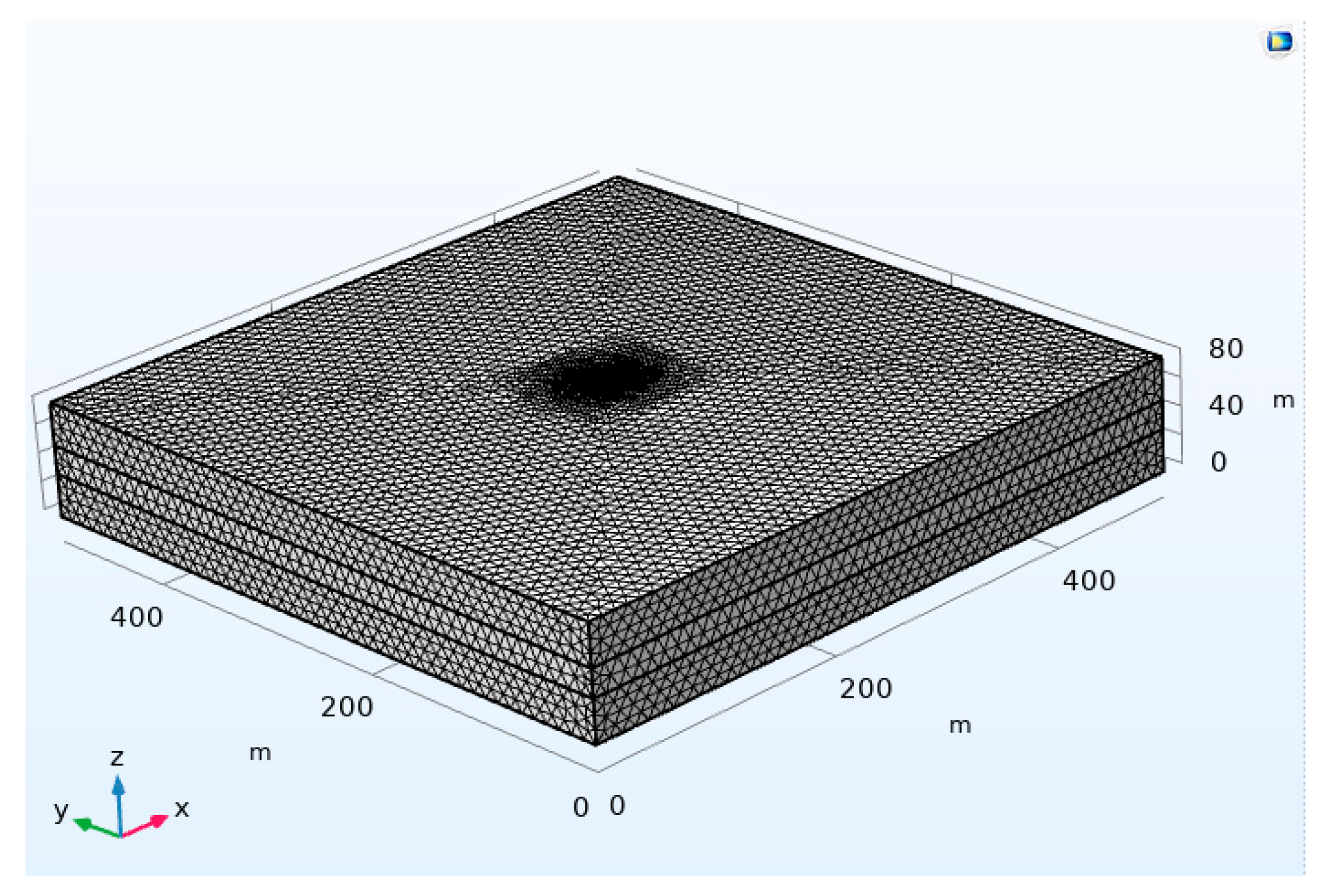
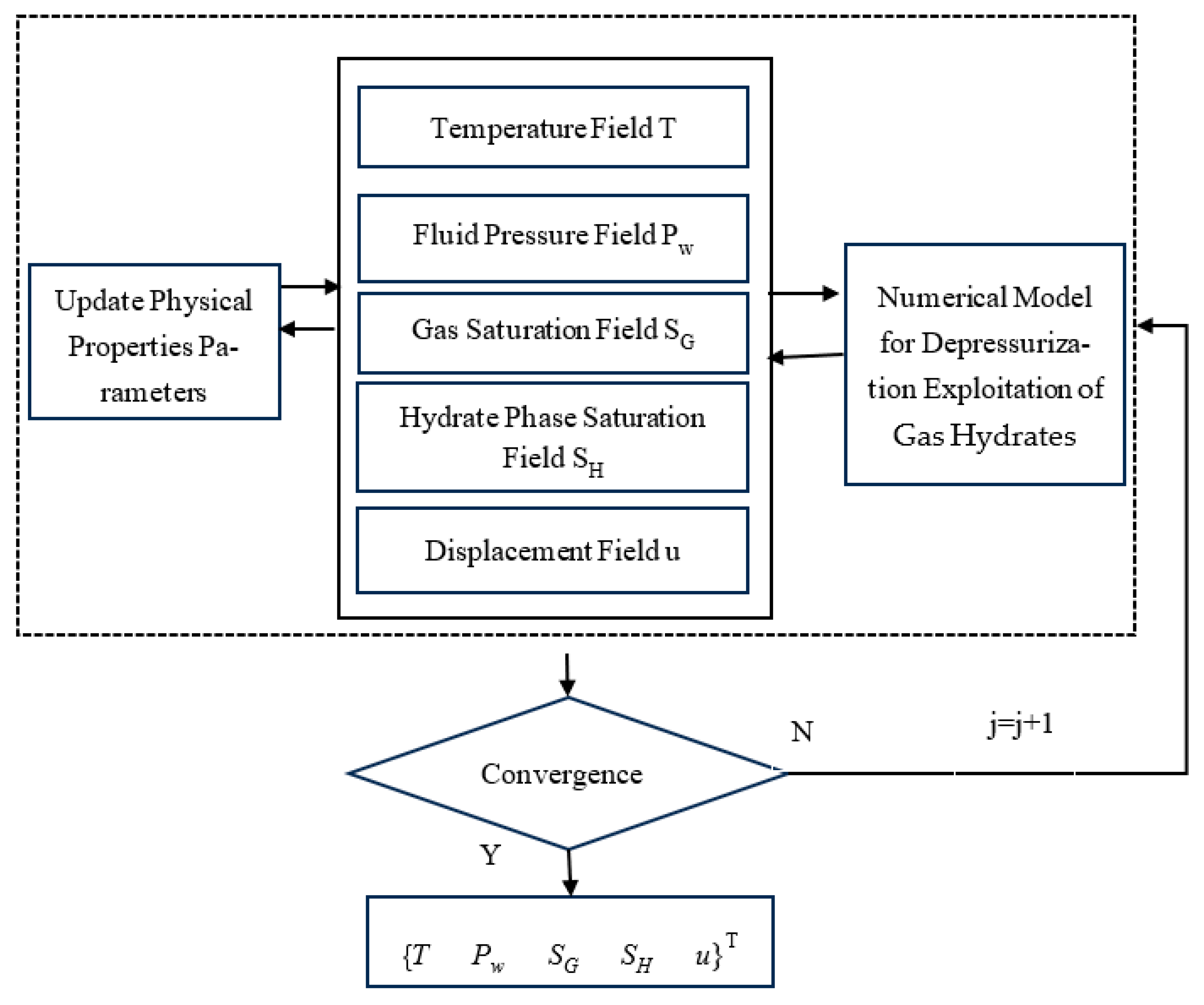

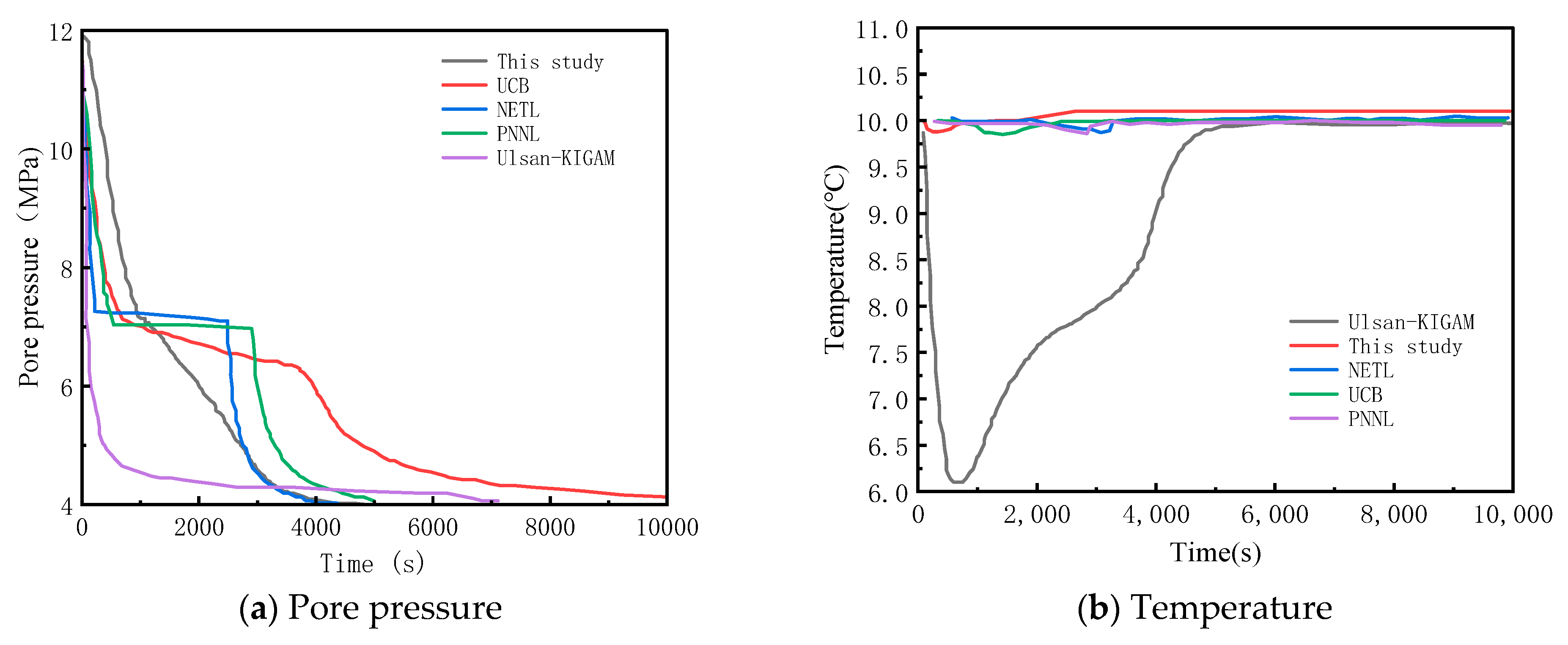



| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| Depth from Top of Hydrate Layer to Mud Line | 165 | m | Seawater Depth | 1225 | m |
| Pore Pressure (Bottom of Hydrate Layer) | 13.83 | MPa | Temperature (Bottom of Hydrate Layer) | 287.3 | K |
| Geothermal Gradient | 0.0433 | K·m−1 | Porosity | 0.41 | - |
| Intrinsic Permeability (Hydrate Layer) | 75 | mD | Intrinsic Permeability (Overlying and Underlying Strata) | 5 | mD |
| Initial Hydrate Saturation (Hydrate Layer) | 0.438 | - | Initial Water Saturation (Hydrate Layer) | 0.512 | - |
| Irreducible Gas Saturation (Hydrate Layer) | 0.05 | - | Irreducible Water Saturation (Hydrate Layer) | 0.30 | - |
| Thermal Conductivity (Water) | 0.6 | W·m−1·K−1 | Density(water) | 1000 | kg·m−3 |
| Viscosity (Water) | 1.14 | mPa·s | Thermal Conductivity (CH4) | 0.044 | W·m−1·K−1 |
| Viscosity (CH4) | 0.01 | mPa·s | Thermal Conductivity (Hydrate) | 0.393 | W·m−1·K−1 |
| Specific Heat Capacity (Water) | 4200 | J·kg−1·K−1 | Density (Seawater) | 1030 | kg·m−3 |
| Specific Heat Capacity (Hydrate) | 2200 | J·kg−1·K−1 | Density (Gas Hydrate) | 910 | kg·m−3 |
| Thermal Conductivity | 1.5 | W·m−1·K−1 | Specific Heat Capacity (Formation) | 1000 | J·kg−1·K−1 |
| Density of Formation | 2600 | kg·m−3 | Poisson’s Ratio | 0.3 | - |
| Reference Pressure (Gas Inflow) | 0.1 | MPa | Fitting Parameter | 0.45 | - |
| Borehole Radius | 0.1 | m | Rock Shear Modulus | 200 | MPa |
| Drainage Radius | 100 | m | Rock Internal Friction Angle | 30 | ° |
| Vertical In situ Stress | 20.25 | MPa | Maximum Horizontal Principal Stress | 24.7 | MPa |
| Minimum Horizontal Principal Stress | 19.5 | MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Cheng, Y.; Wang, Y.; Zhao, J.; Shi, X.; Dai, X.; Shi, F. Production Capacity and Temperature–Pressure Variation Laws in Depressurization Exploitation of Unconsolidated Hydrate Reservoir in Shenhu Sea Area. Processes 2025, 13, 2418. https://doi.org/10.3390/pr13082418
Sun Y, Cheng Y, Wang Y, Zhao J, Shi X, Dai X, Shi F. Production Capacity and Temperature–Pressure Variation Laws in Depressurization Exploitation of Unconsolidated Hydrate Reservoir in Shenhu Sea Area. Processes. 2025; 13(8):2418. https://doi.org/10.3390/pr13082418
Chicago/Turabian StyleSun, Yuanwei, Yuanfang Cheng, Yanli Wang, Jian Zhao, Xian Shi, Xiaodong Dai, and Fengxia Shi. 2025. "Production Capacity and Temperature–Pressure Variation Laws in Depressurization Exploitation of Unconsolidated Hydrate Reservoir in Shenhu Sea Area" Processes 13, no. 8: 2418. https://doi.org/10.3390/pr13082418
APA StyleSun, Y., Cheng, Y., Wang, Y., Zhao, J., Shi, X., Dai, X., & Shi, F. (2025). Production Capacity and Temperature–Pressure Variation Laws in Depressurization Exploitation of Unconsolidated Hydrate Reservoir in Shenhu Sea Area. Processes, 13(8), 2418. https://doi.org/10.3390/pr13082418






