Design and Experimentation of Variable-Density Damping Materials Based on Topology Optimization
Abstract
1. Introduction
2. Analysis of Optimization Methods for Vibration Reduction Performance
2.1. Modal Frequency Response Analysis Method
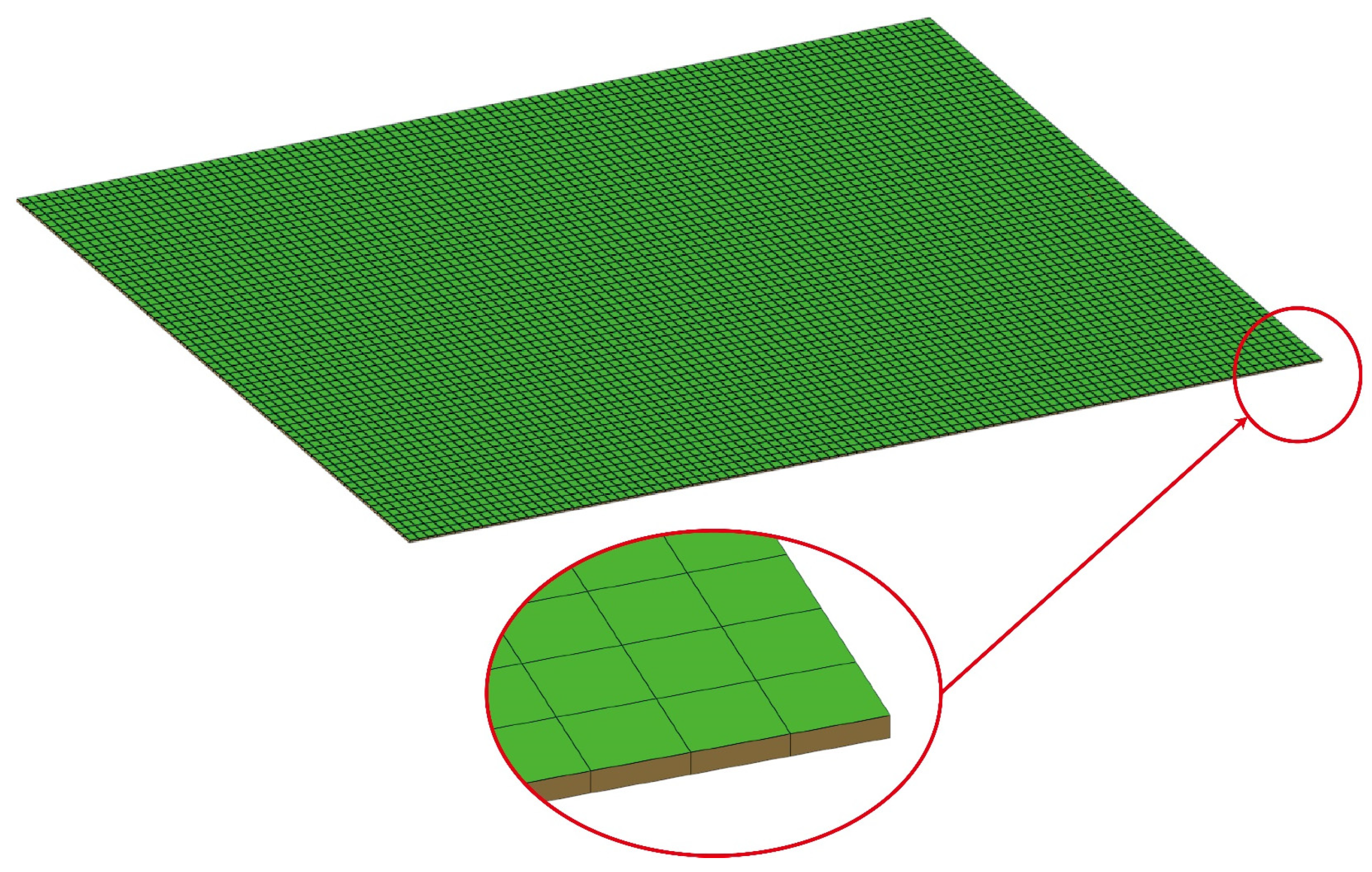
2.2. Finite Element Model
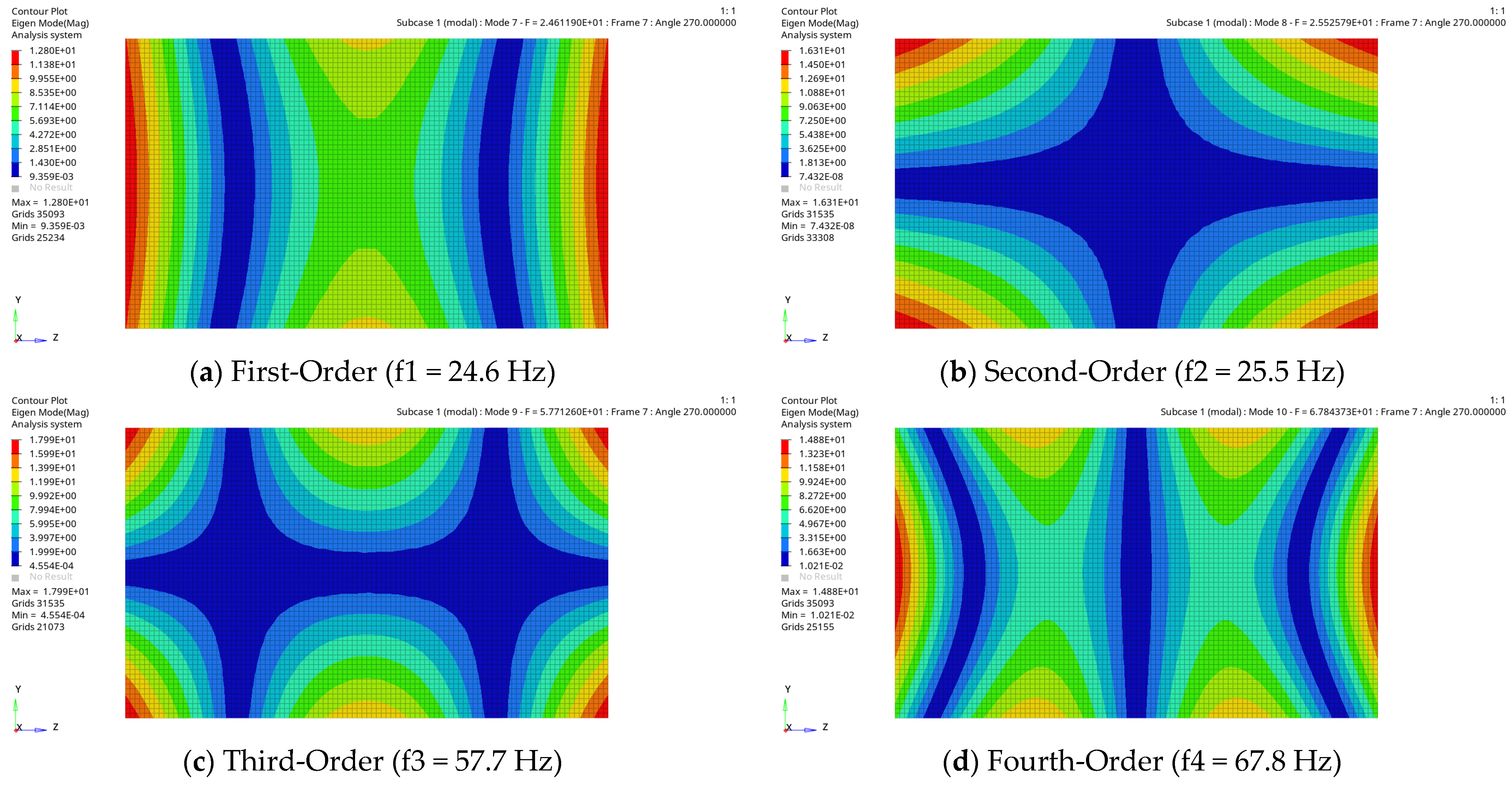
2.3. Modal Frequency Response Analysis
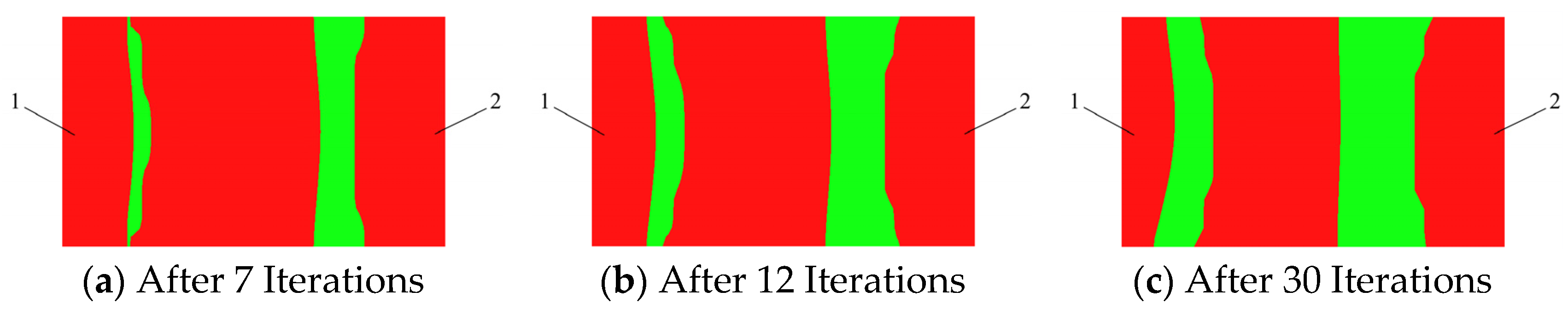
3. Topology Optimization Method Based on Variable Density
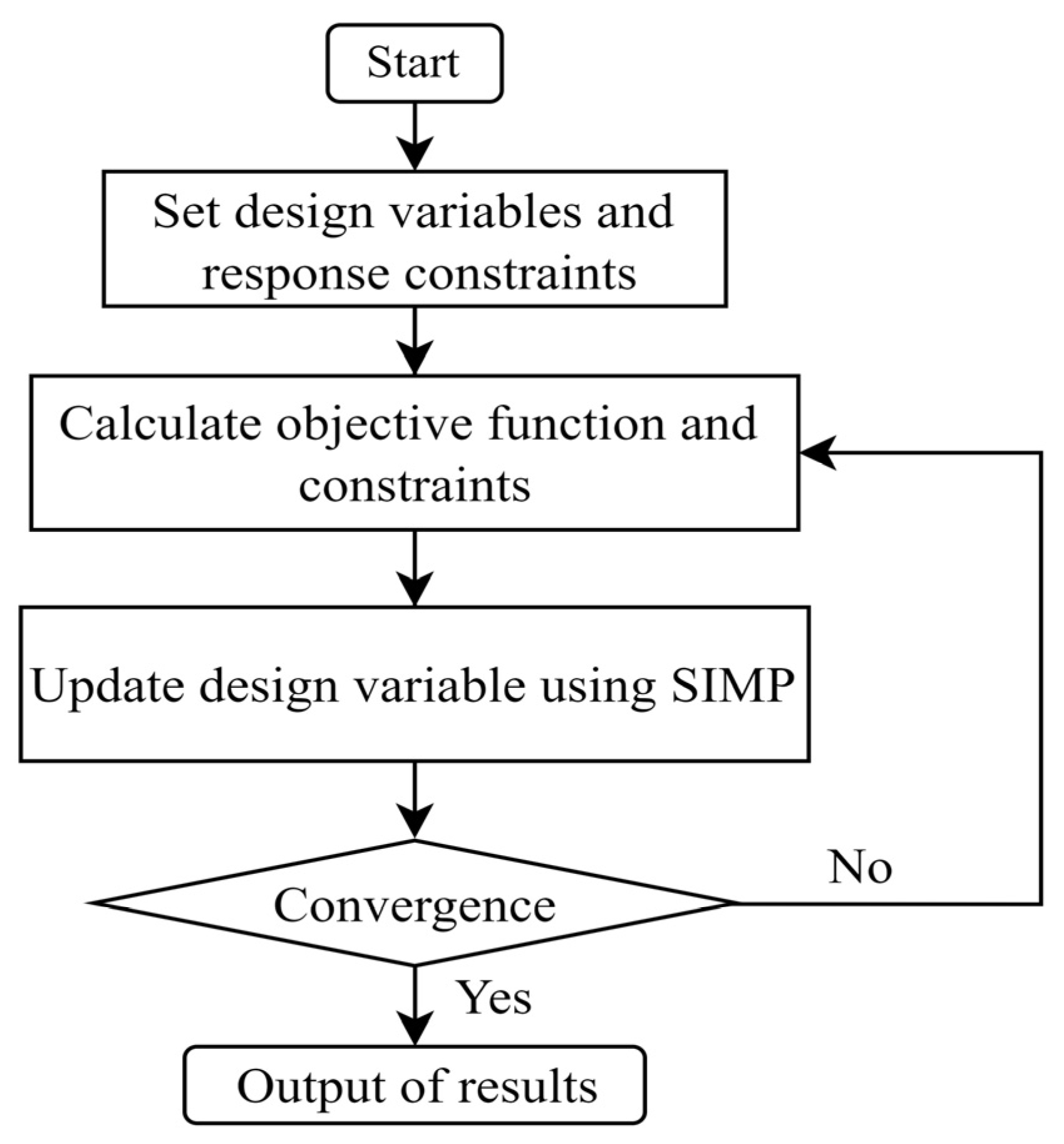
3.1. Design of Topology Optimization Model
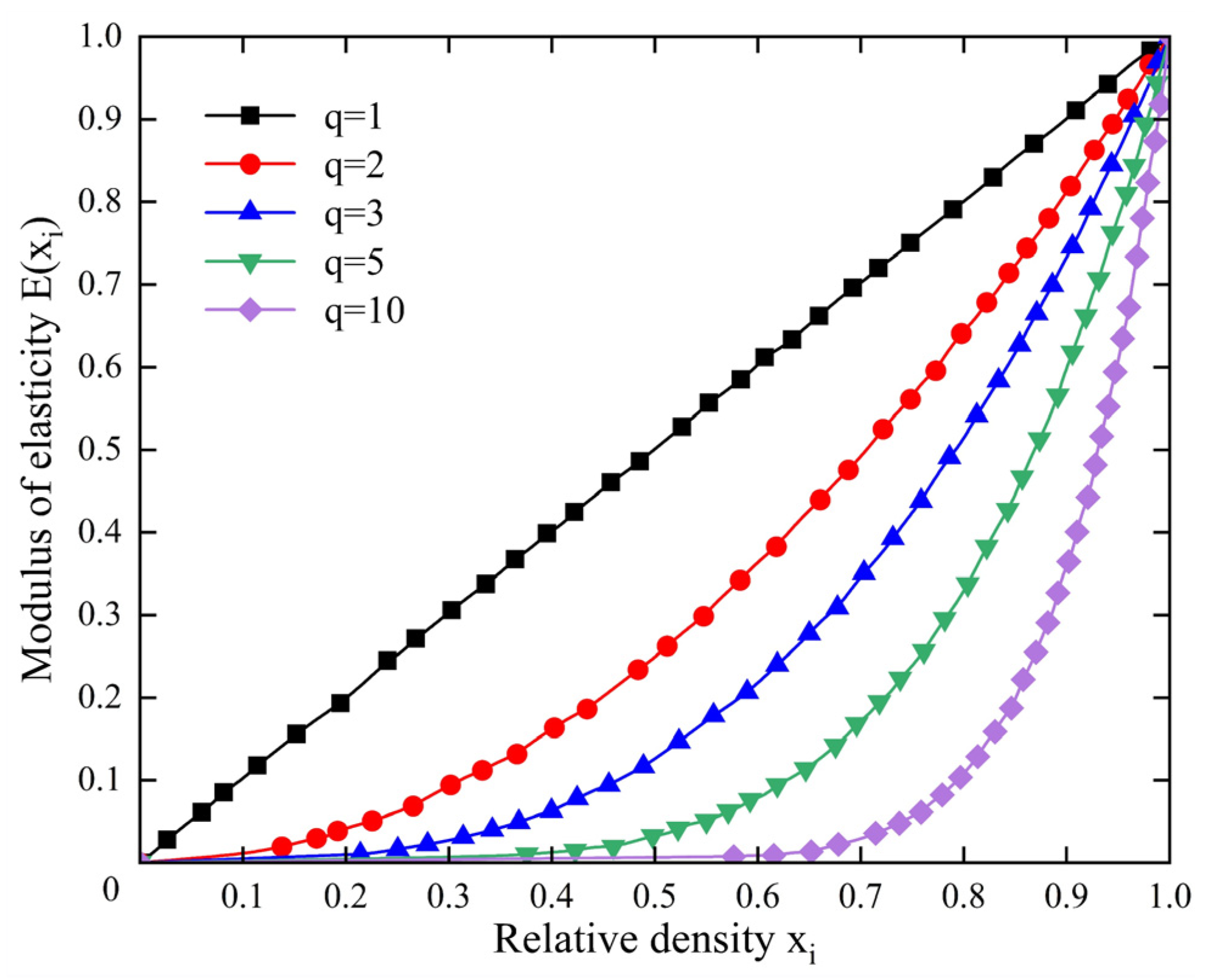
3.2. Variable Density Method
4. Experimental Analysis
4.1. Experimental Equipment
4.2. Test Setup Construction
4.3. Test Results and Analysis
5. Conclusions
- (A)
- The SIMP (Solid Isotropic Material with Penalization) variable density topology optimization algorithm adopted in this paper was able to finely regulate the microstructure of materials to achieve optimal material layout design for superior damping performance.
- (B)
- By combining finite element simulation and experimental validation, this paper not only conducted theoretical design optimization but also verified the effectiveness of the design through experiments, ensuring the validity and correctness of simulated and practical effects. The optimized design reduced the amount of damping material used by 31.2%, with an equal percentage of reduction in structural mass and material costs, while achieving a significant reduction in vibration response, which has important practical significance in engineering applications, especially in terms of cost control and structural lightweighting.
- (C)
- This method can be widely applied in fields such as automobiles, aerospace, and civil engineering, and has important practical significance for achieving structural lightweighting and cost optimization. The application of optimization algorithms can significantly improve design efficiency, reduce the number of design iterations, and shorten the design cycle. By reducing the amount of damping material used, engineering costs can be effectively lowered, economic benefits can be improved, and resource consumption and environmental pollution can be reduced, aligning with sustainable development requirements.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Liao, J.; Huang, C.; Yu, H.; Yan, J.; Li, H. Study on the Damping Dynamics Characteristics of a Viscoelastic Damping Material. Processes 2022, 10, 635. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, B.; Lai, S.-K.; Liu, W.; Zhong, H. Topology optimization of proportionally damped structures under harmonic excitations: Analysis of velocity and acceleration responses. Eng. Struct. 2022, 258, 114140. [Google Scholar] [CrossRef]
- Bai, C.; Chen, T.; Wang, X.; Sun, X. Optimization layout of damping material using vibration energy-based finite element analysis method. J. Sound Vib. 2021, 504, 116117. [Google Scholar] [CrossRef]
- Chen, B.; Dai, J.; Song, T.; Guan, Q. Research and Development of High-Performance High-Damping Rubber Materials for High-Damping Rubber Isolation Bearings: A Review. Polymers 2022, 14, 2427. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Ding, X.; Wang, Q.; Ni, W.; Li, H. Topology optimization of composite material with high broadband damping. Comput. Struct. 2020, 239, 106331. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, B.; Li, Z.; Zhong, H. A method for topology optimization of structures under harmonic excitations. Struct. Multidiscip. Optim. 2018, 58, 475–487. [Google Scholar] [CrossRef]
- El-Sabbagh, A.; Baz, A. Topology optimization of unconstrained damping treatments for plates. Eng. Optim. 2013, 46, 1153–1168. [Google Scholar] [CrossRef]
- Allaire, G.; Michailidis, G. Modal basis approaches in shape and topology optimization of frequency response problems. Int. J. Numer. Methods Eng. 2018, 113, 1258–1299. [Google Scholar] [CrossRef]
- Wan, C.; Jiao, H.; Lv, L.; Lu, C. Multi-material topology optimization based on multiple simp of variable density method. J. Mech. Sci. Technol. 2024, 38, 749–759. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, Y.; Ge, M.; Zhao, Y. Topology optimization of heat sink based on variable density method. Energy Rep. 2022, 8, 718–726. [Google Scholar] [CrossRef]
- Höke, Ö.; Bozca, M. Topology Optimisation of Engine Cross Members for Lightweight Structure in Light Commercial Vehicles. Int. J. Precis. Eng. Manuf. 2020, 21, 465–482. [Google Scholar] [CrossRef]
- Steffensen, M.T.; Tcherniak, D.; Thomsen, J.J. Accurate frequency response function estimation using noise measurements in experimental modal analysis. J. Phys. Conf. Ser. 2024, 2647, 212003. [Google Scholar] [CrossRef]
- Mudahemuka, E.; Miyagi, M.; Shin, R.; Kaneko, N.; Okada, Y.; Yamamoto, K. Estimating Bridge Natural Frequencies Based on Modal Analysis of Vehicle–Bridge Synchronized Vibration Data. Sensors 2024, 24, 1060. [Google Scholar] [CrossRef] [PubMed]
- Sestieri, A.; D’Ambrogio, W. Frequency response function versus output-only modal testing identification. In Proceedings of the 21st International Modal Analysis Conference (IMAC XXI), Kissimmee, FL, USA, 3–6 February 2003; pp. 41–46. [Google Scholar]
- De Carolis, S.; Messina, A.; Soria, L. Modal analysis through response-based FRFs: Additional modes for local diagnoses. J. Sound Vib. 2023, 549, 117574. [Google Scholar] [CrossRef]
- Abdullah, N.; Fouzi, M.; Sani, M.M. Computational Modal Analysis on Finite Element Model of Body-in-white Structure and Its Correlation with Experimental Data. Int. J. Automot. Mech. Eng. 2020, 17, 7915–7926. [Google Scholar] [CrossRef]
- Katsurayama, Y.; Deng, M.; Jiang, C. Operator-based experimental studies on nonlinear vibration control for an aircraft vertical tail with considering low-order modes. Trans. Inst. Meas. Control 2016, 38, 1421–1433. [Google Scholar] [CrossRef]
- Brincker, R.; Skafte, A.; López-Aenlle, M.; Sestieri, A.; D’Ambrogio, W.; Canteli, A. A local correspondence principle for mode shapes in structural dynamics. Mech. Syst. Signal Process. 2014, 45, 91–104. [Google Scholar] [CrossRef]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology optimization of multi-scale structures: A review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Du, B.; Chen, X.; Yao, W. Topology optimization of hyperelastic structures using a modified evolutionary topology optimization method. Struct. Multidiscip. Optim. 2020, 62, 3071–3088. [Google Scholar] [CrossRef]
- Yamamoto, T.; Yamada, T.; Izui, K.; Nishiwaki, S. Topology optimization of free-layer damping material on a thin panel for maximizing modal loss factors expressed by only real eigenvalues. J. Sound Vib. 2015, 358, 84–96. [Google Scholar] [CrossRef]
- Ma, L.; Cheng, L. Topological optimization of damping layout for minimized sound radiation of an acoustic black hole plate. J. Sound Vib. 2019, 458, 349–364. [Google Scholar] [CrossRef]
- Costa, G.; Montemurro, M. Eigen-frequencies and harmonic responses in topology optimisation: A CAD-compatible algorithm. Eng. Struct. 2020, 214, 110602. [Google Scholar] [CrossRef]
- Zuo, W.; Saitou, K. Multi-material topology optimization using ordered SIMP interpolation. Struct. Multidiscip. Optim. 2017, 55, 477–491. [Google Scholar] [CrossRef]
- Zargham, S.; Ward, T.A.; Ramli, R.; Badruddin, I.A. Topology optimization: A review for structural designs under vibration problems. Struct. Multidiscip. Optim. 2016, 53, 1157–1177. [Google Scholar] [CrossRef]
- Martinez, J.M. A note on the theoretical convergence properties of the SIMP method. Struct. Multidiscip. Optim. 2005, 29, 319–323. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Huang, Y. An improved multi-objective topology optimization model based on SIMP method for continuum structures including self-weight. Struct. Multidiscip. Optim. 2021, 63, 211–230. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, X.; Zhu, B.; Wang, R.; Cui, C.; Zhang, H. Topology Optimization of Geometrically Nonlinear Structures Based on a Self-Adaptive Material Interpolation Scheme. Machines 2023, 11, 1047. [Google Scholar] [CrossRef]
- Lian, R.; Jing, S.; He, Z.; Shi, Z. A Hierarchical Double Penalty Method of Gray-Scale Elements for SIMP in Topology Optimization. J. Comput.-Aided Des. Comput. Graph. 2020, 32, 1349–1356. [Google Scholar]
- Wang, F.; Bollen, M. Frequency-Response Characteristics and Error Estimation in RMS Measurement. IEEE Trans. Power Deliv. 2004, 19, 1569–1578. [Google Scholar] [CrossRef]





| Name | Dimensions (L* W* H)/mm | Mesh Element Count | Mesh Size/mm | Mesh Nodes | Element Type |
|---|---|---|---|---|---|
| Steel Plate | 1000 × 600 × 5 | 6000 | 10 × 10 | 6161 | PSHELL |
| Damping Plate | 1000 × 600 × 2.5 | 6000 | 10 × 10 × 2.5 | 12,322 | PSOLID |
| Name | Elastic Modulus/MPa | Density/(kg/m3) | Poisson’s Ratio | Thickness/mm | Damping Ratio |
|---|---|---|---|---|---|
| Steel Plate | 200,000 | 7800 | 0.3 | 5 | - |
| Damping Plate | 7 | 2000 | 0.4 | 2.5 | 0.12 |
| Name | Model | Sensitivity/(mV/ms−2) |
|---|---|---|
| Exciter | KDJ-2 | - |
| Signal Acquisition and Analysis Instrument | INV3062 | - |
| Accelerometer-1 | IEPE | 1.01 |
| Accelerometer-2 | IEPE | 1.04 |
| Accelerometer-3 | IEPE | 1.04 |
| Accelerometer-4 | IEPE | 1.02 |
| Frequency/Hz | Amplitude of Undamped Steel Plate/(mm/s2/N) | Amplitude of Fully Damped Steel Plate/(mm/s2/N) | Amplitude of Optimized Damped Steel Plate/(mm/s2/N) |
|---|---|---|---|
| 30 | 1.4150 | 0.2584 | 0.30508 |
| 75 | 8.1521 | 0.9882 | 1.2947 |
| 140 | 14.1966 | 1.1242 | 1.13825 |
| 200 | 2.9179 | 1.6678 | 1.9760 |
| 285 | 14.8517 | 0.8904 | 0.9649 |
| 380 | 3.1106 | 0.9272 | 1.0900 |
| 410 | 19.2416 | 2.2876 | 2.62454 |
| 540 | 29.3070 | 0.6975 | 0.7508 |
| 635 | 6.6144 | 0.9707 | 1.1177 |
| 680 | 13.1889 | 0.54016 | 0.05472 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Han, B.; Kuang, Z.; Ding, H.; Wang, K.; Du, C.; Wu, W.; Li, H.; Wang, J. Design and Experimentation of Variable-Density Damping Materials Based on Topology Optimization. Processes 2025, 13, 2276. https://doi.org/10.3390/pr13072276
Zeng X, Han B, Kuang Z, Ding H, Wang K, Du C, Wu W, Li H, Wang J. Design and Experimentation of Variable-Density Damping Materials Based on Topology Optimization. Processes. 2025; 13(7):2276. https://doi.org/10.3390/pr13072276
Chicago/Turabian StyleZeng, Xiangkun, Biaojie Han, Ziheng Kuang, Han Ding, Kaixin Wang, Canyi Du, Wei Wu, Hongluo Li, and Jiangang Wang. 2025. "Design and Experimentation of Variable-Density Damping Materials Based on Topology Optimization" Processes 13, no. 7: 2276. https://doi.org/10.3390/pr13072276
APA StyleZeng, X., Han, B., Kuang, Z., Ding, H., Wang, K., Du, C., Wu, W., Li, H., & Wang, J. (2025). Design and Experimentation of Variable-Density Damping Materials Based on Topology Optimization. Processes, 13(7), 2276. https://doi.org/10.3390/pr13072276







