Economic Operation Optimization for Electric Heavy-Duty Truck Battery Swapping Stations Considering Time-of-Use Pricing

Abstract

Battery-swapping stations (BSSs) are pivotal for supplying energy to electric heavy-duty trucks. However, their operations face challenges in accurate demand forecasting for battery-swapping and fair revenue allocation. This study proposes an optimization strategy for the economic operation of BSSs that optimizes revenue allocation and load balancing to enhance financial viability and grid stability. First, factors including geographical environment, traffic conditions, and truck characteristics are incorporated to simulate swapping behaviors, supporting the construction of an accurate demand-forecasting model. Second, an optimization problem is formulated to maximize the weighted difference between BSS revenue and squared load deviations. An economic operations strategy is proposed based on an adaptive Shapley value. It enables precise evaluation of differentiated member contributions through dynamic adjustment of bias weights in revenue allocation for a strategy that aligns with the interests of multiple stakeholders and market dynamics. Simulation results validate the superior performance of the proposed algorithm in revenue maximization, peak shaving, and valley filling.

1. Introduction

Electric heavy-duty trucks, which have the advantages of being environmentally friendly and easily rechargeable, have become a key choice for transportation under the policy-driven goals of carbon peaking and carbon neutrality [1,2,3]. Battery-swapping stations (BSSs) for electric heavy-duty trucks are more than just energy suppliers for vehicles. They are essential in achieving power-grid load balancing and play a vital role in working towards carbon-neutrality goals. Electric heavy-duty trucks are significant contributors to carbon emissions. By enabling the use of electric heavy-duty trucks through efficient battery-swapping, these stations directly reduce greenhouse gas emissions. In [4], Mueller et al. employed a multi-level, multi-dimensional analysis to assess the role of battery-electric and fuel-cell heavy-duty trucks in achieving carbon neutrality. Their study integrated policy analysis, market forecasting, and technological trends to evaluate their decarbonization potential. Key factors include declining battery costs, charging infrastructure development, and carbon-trading policies. Additionally, a life-cycle assessment quantifies the carbon-reduction potential under different energy structures, highlighting grid decarbonization as a crucial element in low-carbon transportation. In [5], Gunawan et al. proposed the Techno-Econo-Environmenta framework. This study compared zero- and low-emissions heavy-duty trucks for their potential to contribute to achieving carbon neutrality from technological, economic, and environmental perspectives. In [6], Borlaug et al. analyzed the impact of electric heavy-duty trucks on electricity-distribution systems, highlighting how optimized depot charging can mitigate grid stress. In [7], Liu et al. proposed an optimized scheduling model for BSSs, demonstrating how coordinated energy dispatch enhances grid stability and reliability. To further expand the market presence of electric heavy-duty trucks, the government and local power grids have introduced various policies to promote the development and management of BSSs. Local power grids often employ time-of-use pricing to guide the concentrated and orderly management of charging for electric heavy-duty trucks, enabling their involvement in peak-shaving and valley-filling adjustments [8].

However, electric heavy-duty trucks are privately owned assets, and their battery-swapping behavior is characterized by high randomness and abruptness, with weak temporal allocation patterns, making it difficult to model. This complicates demand forecasting for battery swapping, affecting the precision and reliability of related operational strategies. In addition, complex cooperative and competitive relationships exist among BSSs, imposing a significant challenge in ensuring mutual benefits among multiple stakeholders, including the distribution network and BSSs. Therefore, to achieve optimal revenue for electric heavy-duty truck BSSs and to support peak shaving and valley filling for the power grid, it is essential to conduct research on optimizing the economic-operation strategy of these BSSs under time-of-use pricing.

Regarding the optimization of economic operations for electric heavy-duty truck BSSs, Li et al. [9] proposed directing electric heavy-duty trucks to stations based on variance in electricity prices, thereby optimizing the overall charging load curve to reduce both power costs and battery degradation while effectively and economically meeting users’ driving needs. In [10], Wu et al. focused on the participation of BSSs in frequency-scheduling ancillary services, investigated aspects such as clustering, automatic generation control, and power allocation, and proposed corresponding models and control strategies to enhance economic efficiency. In [11], Yuan et al. presented an optimal-operation model for microgrids that integrated charging, swapping, and storage of electric heavy-duty trucks and aimed at reducing grid peak-valley differences and lowering the daily total operation costs of the microgrid. In [12], Wu et al. introduced an optimization model for BSSs, considering the generation costs, degradation costs from fast charging, and quantity of reserve batteries deployed. In [13], Esmaeili et al. proposed an optimized scheduling method for microgrids that comprehensively considered BSSs. The method aimed to improve overall microgrid efficiency by coordinating battery-swapping and charging demand. As a result, the reliability and economic efficiency of grid operations were enhanced, while the peak loads were reduced. In [14], Bichler et al. discussed the applications of flexible pricing in business-to-business electronic commerce, an approach that provides theoretical support for adopting dynamic pricing strategies for BSSs participating in the electricity market. However, the above studies consider time-of-use pricing or government subsidies only as incentives for charging and discharging, without analyzing the specific demand for battery-swapping for electric heavy-duty trucks or their impacts on demand-response optimizations. Consequently, the scheduling perspective remains overly broad, limiting its ability to effectively assess the participation potential of electric heavy-duty truck BSSs in actual operations.

In the area of demand forecasting for battery swapping for battery BSSs, in [15], Li et al. utilized attention mechanisms, bidirectional long short-term memory (BiLSTM), and a convolutional neural network (CNN) to design a precise deep learning-based model for demand forecasting for battery swapping at these stations. In [16], Kim et al. proposed a new parallel architecture that integrated spatial and temporal mutual residual graph convolution with dual long short-term memory to forecast the charging demand at electric heavy-duty truck BSSs. Experiments confirmed that this model achieved high forecasting accuracy and holds potential for profitable applications in the energy market. In [17], Hu et al. employed a framework based in machine-psychology theory to analyze users’ past charging behaviors and the variance in charging demand, proposing a short-term probabilistic model to forecast the quantiles of future demand at a station 15 min ahead. In [18], Li et al. studied the capacity expansion and planning of urban EV-charging stations, integrating user-side guidance on active charging, which aligns with the optimization and forecasting of BSS demand. However, the above studies do not account for multiple factors, such as the actual geographical environment, traffic conditions, and characteristics of electric heavy-duty trucks, and therefore do not realistically simulate battery-swapping behavior, resulting in less precise forecasting of battery-swapping demand at the stations.

Numerous studies have been conducted on demand-response models for BSSs. Zou et al. constructed an optimization model aimed at maximizing the aggregated comprehensive revenue of battery energy-storage systems [19]. This model obtains optimal day-ahead charging schedules for the battery energy-storage system and reports the scheduling capacity to the power grid, creating an incentive mechanism for participation in demand-response resources. In [20], Sun et al. introduced a pricing strategy grounded in a closed-loop reverse Stackelberg game to enhance demand-response scheduling. In [21], Wen et al. formulated a demand-response model utilizing dynamic pricing to manage demand on the supply side in smart grids. This model effectively shifts the peak electricity demand, thereby enhancing the stability and reliability of the power system. In [22], Jin et al. considered using a dual-incentive policy to guide electric heavy-duty trucks to participate in the day-ahead demand response for the power grid, thereby increasing their capacity to provide backup services. In [23], Sadeghianpourhamami et al. proposed a model-free reinforcement-learning method for optimizing electric heavy-duty truck battery-swapping coordination, with a particular focus on demand response and grid load management. By dynamically adjusting the battery-swapping strategies, this approach eliminates the need for a detailed grid model, effectively improving the battery-swapping efficiency and reducing load variance. However, it does not account for the complex interactions of interests between the distribution network and multiple BSSs, an omission that affects the fairness of the revenue allocation.

The Shapley value method, as a technique in cooperative games, is used to allocate revenue to members of a coalition. It allocates revenue based on each member’s contribution to the coalition’s overall objectives [24]. This method reflects the strategic interactions among members, considering the marginal contribution of each to the coalition. In [25], Liu et al. employed the Shapley value to fairly distribute earnings in cooperative games, effectively addressing cooperation issues and ensuring fairness among participants. Under these conditions, the system’s efficiency and stability were improved. In [26], Zhang et al. proposed a Shapley value-based game-theory approach for energy management in microgrids, presenting an optimization strategy that ensured fair resource allocation while enhancing the overall performance and reliability of the microgrid. In [27], Yang et al. proposed a Shapley value-based optimization algorithm to ensure fair resource allocation in cloud computing. This method not only considered resource-utilization efficiency, but also accounted for participants’ contribution levels, thereby ensuring fairness and rationality in resource allocation. In [28], Kim et al. analyzed network performance metrics and provided an optimized resource-allocation strategy aimed at balancing the interests of all parties, effectively addressing fairness issues in network resource allocation while enhancing overall network performance and user satisfaction. In [29], Zhang et al. applied the Shapley value method to multi-criteria decision-making in smart grids, exploring the question of how to utilize the Shapley value for resource allocation to meet multiple demands and constraints in smart grids. This approach increased the scientific and rational nature of decision-making. However, the above methods consider only the marginal contributions of participants in the pursuit of absolute fairness, neglecting individual differences in contributions; this omission may affect the willingness of BSSs to participate in the coalition and may not align with reality.

Despite the progress made in these studies, several challenges remain. Most existing demand-response models either focus solely on time-of-use pricing or rely on government subsidies, lacking a comprehensive approach that integrates dynamic pricing with cooperative economic strategies. These models often fail to accurately capture the participation capacity of electric heavy-duty truck BSSs, leading to suboptimal decision-making. Additionally, prior studies have not fully considered the multi-dimensional nature of battery-swapping demand, which includes influences from geographical distribution, traffic conditions, and vehicle-specific attributes.

To address these limitations, our study introduces an adaptive Shapley value-based economic-optimization framework that enhances the fairness of revenue allocation among BSSs. Unlike conventional Shapley value methods that assume equal weight for all participants, our approach incorporates revenue-allocation bias weights, ensuring that contributions are evaluated based on both market importance and operational characteristics. Furthermore, we develop a multi-dimensional demand-forecasting model, integrating spatial, temporal, and vehicle-specific factors to improve accuracy. In contrast to previous studies that separately optimize either profit maximization or grid load balancing, our approach achieves joint optimization to enhance peak shaving, valley filling, and financial returns. This novel framework not only improves the operational efficiency of battery swapping stations but also supports more stable and fair participation in the cooperative coalition, ultimately benefiting both energy providers and operators of electric trucks. The proposed algorithm was compared with state-of-the-art studies through five perspectives, as shown in

Table 1. Comprehensive comparison of the proposed work with state-of-the-art studies.

	Role in Balancing Grid Load	Role in Carbon Neutrality	Multidimensional Load Forecasting	Improvement of Shapley Value	Comprehensive Revenue Optimization
					Peak Shaving and Valley Filling	Revenue Maximization
[4]	✗	✓	✗	✗	✗	✓
[5]	✗	✓	✗	✓	✗	✓
[6]	✓	✗	✗	✗	✓	✗
[7]	✓	✗	✓	✓	✓	✗
Baseline 1 [14]	✗	✗	✗	✓	✗	✓
Baseline 2 [18]	✓	✗	✓	✗	✓	✗
Proposed	✓	✓	✓	✓	✓	✓

. References [4,5,6,7,14,18] ignore the key roles of electric heavy-duty trucks in either balancing power grid loads or achieving carbon neutrality. Although references [7,18] investigate multi-dimensional load forecasting, they lack comprehensive revenue optimization that considers peak shaving and valley filling, which play important roles in maintaining grid stability. References [4,6,18] did not explore the improvement of the Shapley value, resulting in inadequate exploitation of preference heterogeneity and inaccurate evaluation of member contributions.

The main contributions of this paper are as follows.

Adaptive Shapley Value-Based Economic Optimization: Unlike traditional cooperative game models that assume equal contribution among coalition members, our approach introduces revenue-allocation bias weights to ensure a fair and rational revenue distribution based on each station’s market importance and operational characteristics.

Multi-Dimensional Demand Forecasting: In contrast to previous methods, our model incorporates geographical environment, traffic conditions, and vehicle characteristics to enhance the accuracy of demand forecasting.

Comprehensive Revenue Optimization: While prior studies focused on either profit maximization or grid load balancing, our optimization model simultaneously achieves peak shaving, valley filling, and revenue maximization, providing a comprehensive solution.

2. System Model

Assuming that there are a total of $I$ BSSs, represented by the set $\mathcal{S}=\left\{s_1,\dots ,s_i,\dots ,s_I\right\}$, the 24 h of one day are divided into $T$ time slots, represented by the set $\mathcal{T}=\left\{1,\dots ,t,\dots ,T\right\}$. The time-slot-division step size (in minutes) is denoted as $t_{\mathrm{p}}$, that is,

$$t_{\mathrm{p}}={\displaystyle \frac{W_{\mathrm{B}}}{P_{\mathrm{ce}}}}\times 60$$

(1)

where $W_{\mathrm{B}}$ represents the battery rated capacity. $P_{\mathrm{ce}}$ represents the rated charging power of the battery.

2.1. Demand-Forecasting Model for Battery Swapping Considering Multi-Dimensional Factors

Due to the high randomness and suddenness in the battery-swapping behavior of electric heavy-duty trucks, accurately forecasting the battery-swapping demand of BSSs is extremely challenging, a problem that affects the precision and reliability of the related operational strategies [30]. Therefore, we propose a demand-forecasting model for battery swapping that considers multi-dimensional factors. This model considers various factors, such as the mass, velocity, slope, and operational characteristics of electric heavy-duty trucks to construct a mechanical power model for driving. This further enables the derivation of power consumption, which is then combined with historical battery-swapping data from stations to predict the battery-swapping demand, thereby improving prediction accuracy. This model integrates multiple factors, including vehicle mass, velocity, slope, and operational characteristics of electric heavy-duty trucks to construct a mechanical power model for driving. The power consumption is then derived and combined with historical battery-swapping data to enhance forecasting accuracy.

To justify the rationality of this model, we provide the following considerations:

Physical Consistency: To ensure physical consistency and enhance real-world applicability, the power-consumption model was formulated using longitudinal vehicle-dynamics equations that explicitly account for the effects of rolling resistance, aerodynamic drag, and gravitational force.

Empirical Validation: The key parameters of the model, including the rolling resistance coefficient, aerodynamic drag coefficient, and battery efficiency, were derived from experimental data and industry standards. This ensures that the model reflects real-world energy consumption behavior.

Comparative Analysis: Unlike traditional models of battery-swapping demand that primarily rely on statistical regression or time-series forecasting, our approach incorporates spatiotemporal traffic conditions and vehicle-specific characteristics. This allows for a more refined estimation of power consumption based on real-time driving environments.

By integrating these enhancements, our model provides a more robust and interpretable framework for forecasting battery-swapping demand, thereby improving both operational decision-making and load balancing in power systems.

First, we calculate the mechanical power of a driving electric heavy-duty truck by considering factors such as its mass, velocity, slope, and physical environment (road surface, vehicle dimensions, and engine performance). Based on the longitudinal dynamics, a force analysis of electric heavy-duty trucks is conducted to obtain the following equation:

$$F=ma+(F_{\mathrm{r}}+F_{\mathrm{a}}+F_{\mathrm{g}})$$

(2)

where $a$ represents the acceleration. $F_{\mathrm{r}}$, $F_{\mathrm{a}}$, and $F_{\mathrm{g}}$ represent the rolling resistance, aerodynamic resistance, and gravity, respectively, which are expressed as follows:

$$F_{\mathrm{r}}=mg{C}_{\mathrm{r}}\cos (\theta )$$

(3)

$$F_{\mathrm{a}}={\displaystyle \frac{1}{2}}\mathrm{A}\rho C_{\mathrm{d}}{\nu }^2$$

(4)

$$F_{\mathrm{g}}=mg\sin (\theta )$$

(5)

where $m$ represents the total weight of an electric heavy-duty truck. $g$ represents the gravitational constant. $C_{\mathrm{r}}$ is the rolling resistance coefficient. $\theta$ denotes the road gradient. $\mathrm{A}$ represents the frontal surface area of the electric heavy-duty truck. $\rho$ is the air density. $C_{\mathrm{d}}$ denotes the aerodynamic drag coefficient. $\nu$ represents the instantaneous velocity of an electric heavy-duty truck.

The mechanical power of the electric heavy-duty truck can then be expressed as follows:

$$\begin{array}{l}{P}_{\mathrm{M}}\left(\nu \right)=[ma+mg{C}_{\mathrm{r}}\cos \left(\theta \right)+{\displaystyle \frac{1}{2}}\mathrm{A}\rho C_{\mathrm{d}}{\nu }^2+\\ \mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}m}g\sin (\theta )]\nu /1000\end{array}$$

(6)

Since the changes in mechanical energy during acceleration/deceleration of a heavy truck are negligible compared to steady-state motion, we simplify the analysis by assuming zero acceleration, focusing primarily on energy consumption related to rolling resistance and aerodynamic drag. It is noted that zero acceleration is used only for calculating mechanical energy. In the speed-flow utility model, the acceleration is not zero.

Second, the mechanical power is converted into the electrical power required to drive an electric heavy-duty truck. Owing to the energy losses during the conversion process, the torque and rotational velocity must be converted into mechanical power through the engine-efficiency value at the given torque and rotational velocity. The electrical power is expressed as follows:

$$P_{\mathrm{E}}\left(\nu \right)=\left\{\begin{array}{c}{\varphi }^{\mathrm{d}}{P}_{\mathrm{M}},P_{\mathrm{M}}\ge 0\\ {\varphi }^{\mathrm{r}}{P}_{\mathrm{M}},P_{\mathrm{M}}<0\end{array}\right.$$

(7)

where ${\varphi }^d$ and ${\varphi }^r$ are dimensionless regression coefficients representing the motor system efficiency during the driving and regenerative braking processes, respectively. These coefficients are determined by the motor’s inherent characteristics and reflect its performance.

Finally, based on the battery efficiency, the electrical power is converted into the required battery energy, which is expressed as follows:

$$P_{\mathrm{B}}\left(\nu \right)=\left\{\begin{array}{c}{\phi }^{\mathrm{d}}{P}_{\mathrm{M}},P_{\mathrm{M}}\ge 0\\ {\phi }^{\mathrm{r}}{P}_{\mathrm{M}},P_{\mathrm{M}}<0\end{array}\right.$$

(8)

where $\phi$ represents the battery efficiency.

Let $\eta =\varphi \phi$, $\eta$ represents the overall energy-conversion efficiency, $t=d/v$; then, we obtain the power consumption of the electric heavy-duty truck as follows:

$$\begin{array}{c}H\left(\nu \right)=[mg{C}_{\mathrm{r}}\cos \left(\theta \right)+{\displaystyle \frac{1}{2}}\mathrm{A}\rho C_{\mathrm{d}}{\nu }^2+\\ mg\sin (\theta )]d/1000\eta \end{array}$$

(9)

where $d$ is the distance travelled.

The velocity of the electric heavy-duty truck is determined based on the speed-flow utility model. For an electric heavy-duty truck travelling on road $\lambda$, the velocity is calculated as

$$\left\{\begin{array}{l}{V}_{\lambda }(t)={\displaystyle \frac{V_{\lambda -0}}{1+{\left(\frac{q_{\lambda }(t)}{Q_{\lambda }}\right)}^{\epsilon }}}\\ \epsilon =\mu +\sigma {({\displaystyle \frac{q_{\lambda }(t)}{Q_{\lambda }}})}^3\end{array}\right.$$

(10)

where $V_{\lambda -0}$ is the zero-flow velocity of the road $\lambda$, taking the maximum velocity limit under the road class. $q_{\lambda }(t)$ is the road flow of road $\lambda$ during slot $t$. $Q_{\lambda }$ is the maximum number of vehicles that can pass on road $\lambda$ within a given timeframe for a given road class. The ratio of $q_{\lambda }(t)$ to $Q_{\lambda }$ is the saturation level of road $\lambda$ during slot $t$. $\mu$ and $\mu$ are adaptive coefficients that depend on road class.

Data-availability challenges stem from the need for high-resolution traffic-flow data, state-of-charge distributions, and grid load profiles. Road flow rate $q_{\lambda }(t)$ can be measured using camera-based traffic-monitoring systems that detect and track vehicles through continuous image sequences, analyzing trajectories to calculate traffic volume and speed. Alternatively, radar provides precise distance and speed measurements for individual vehicles and is especially effective in low-visibility conditions. Camera-radar fusion systems combine visual classification with radar’s ranging accuracy, improving reliability in complex scenarios. Key limitations include cameras’ dependency on lighting conditions, radar’s inability to distinguish vehicle types, and both requiring calibration for accuracy in distance estimation.

The speed-flow utility model in (10) dynamically adjusts the speed of electric heavy-duty trucks on road $\lambda$ based on real-time road flow $q_{\lambda }(t)$ and saturation levels $q_{\lambda }(t)/Q_{\lambda }$, which are specific to each road class, rather than assuming a constant velocity. Furthermore, we have provided a sensitivity analysis on the impact of saturation levels $q_{\lambda }(t)/Q_{\lambda }$ on battery-swapping demand. Road saturation level reflects the degree of road congestion. A higher saturation level $q_{\lambda }(t)/Q_{\lambda }$ reduces vehicle speed, extends traveling time, and significantly increases battery-swapping demand.

To account for the actual production conditions faced by the BSS $s_i$, historical operational data within a reasonable date range are selected to count the battery swaps per slot per day. The modal and maximum values of the number of battery swaps in each slot are obtained and then used as the statistical predictions of the basic demand and extreme demand for battery-swapping. These values are denoted as $D_i^{\mathrm{f}}$ and $D_i^{\mathrm{m}}$, respectively.

In this section, the power consumption of electric heavy-duty trucks is predicted based on the historical data of the road class and traffic volume. The prediction process consists of four main steps:

Vehicle-Dynamics Modeling: The mechanical power required for an electric heavy-duty truck is calculated using longitudinal dynamics equations, considering factors such as vehicle mass, velocity, road slope, and aerodynamic resistance.

Electrical-Power Conversion: The required mechanical power is then converted into demand for electrical power, incorporating motor efficiency and battery characteristics to reflect real-world energy consumption.

Integration of Traffic Data: Historical data on road class and traffic volume are used to estimate the electric heavy-duty truck’s expected speed and travel distance on each road segment. Specifically:

The road class determines the zero-flow velocity, i.e., the maximum allowable speed for an electric heavy-duty truck under free-flow conditions. Traffic-volume data provide the saturation level, influencing real-time speed adjustments based on congestion conditions. By integrating these factors, we refine the estimation of energy consumption under varying traffic conditions. Monte Carlo Simulation: To account for stochastic variations in the behavior of electric heavy-duty trucks, we employ a Monte Carlo method to simulate multiple trip scenarios. These include variations in trip length, traffic congestion, vehicle loading, and battery state-of-charge, ensuring a robust and reliable prediction of energy demand. Monte Carlo simulation begins by defining probability distributions for key stochastic variables like trip distance, traffic congestion, and vehicle loading. For each iteration, random samples are drawn from these distributions to generate 10,000+ unique trip profiles. This approach captures nonlinear interactions between variables (e.g., heavy loads exacerbating traffic delays) while maintaining computational tractability through parallel batch processing.

It is determined that electric heavy-duty trucks with a ratio of remaining power to battery capacity less than a threshold value have battery-swapping demand, and it is assumed that there are a total of $q_{\lambda }(t)$ electric heavy-duty trucks on road $\lambda$ in slot $t$. By simulating the distance travelled by each electric heavy-duty truck using the Monte Carlo method, we calculated the power consumption of the $j$-th electric heavy-duty truck, $H_j\left(t\right)$. The predicted value of the basic battery-swapping demand of the BSS $s_i$ on road $\lambda$ in slot $t$ is given by the following equation:

$$D_i\left(t\right)={\displaystyle \sum _{j=1}^{q_{\lambda }(t)}\mathbb{I}\left[\left(1-H_j\left(t\right)/W_{\mathrm{B}}\right)\le h_{\mathrm{th}}\right]}+\lambda \left(D_i^{\mathrm{f}}+\theta D_i^{\mathrm{m}}\right)$$

(11)

where $h_{\mathrm{th}}$ is the battery-swapping energy threshold. $\lambda$ is a weighting factor that weighs the statistical forecasts. $\theta$ is the probability of an extreme demand based on historical data.

2.2. Time-of-Use Pricing

The prices for power purchased from the grid by the BSS in different time slots are given as follows:

$$C_{\mathrm{p}}\left(t\right)=\left\{\begin{array}{l}{\delta }_{\mathrm{p}},t\in \mathrm{peak} \mathrm{slot},\\ {\delta }_{\mathrm{o}},t\in \mathrm{normal} \mathrm{slot},\\ {\delta }_{\mathrm{v}},t\in \mathrm{valley} \mathrm{slot}.\end{array}\right.$$

(12)

2.3. Operational Model of a Battery-Swapping Station

Assume that the total number of commonly used batteries in the BSS $s_i$ is $N_i$. This value includes $N_i^{\mathrm{f}}\left(t\right)$ fully charged batteries, $N_i^{\mathrm{n}}\left(t\right)$ non-input rechargeable batteries, and $N_i^{\mathrm{c}}\left(t\right)$ rechargeable batteries in slot $t$, where the expression representing $N_i^{\mathrm{c}}\left(t\right)$ is as follows:

$$N_i^{\mathrm{c}}\left(t\right)=n_i^{\mathrm{c}}\left(t\right)+n_i^{\mathrm{w}}\left(t\right)$$

(13)

Here, $n_i^{\mathrm{c}}\left(t\right)$ is the number of batteries being charged and $n_i^{\mathrm{w}}\left(t\right)$ is the number of batteries identified as needing to be charged but for which charging has not yet started.

The number of fully charged batteries at the BSS $s_i$ in slot $t$ must satisfy

$$N_i^{\mathrm{f}}\left(t\right)\ge D_i\left(t\right)$$

(14)

The maximum capacity of the BSS $s_i$ that can participate in grid scheduling in slot $t$ is given by the following equation:

$$P_i^{\max }\left(t\right)={\displaystyle \sum _{j\in \mathcal{J}}{H}_j\left(t\right)}$$

(15)

where $\mathcal{J}$ is the set of electric heavy-duty trucks with battery-swapping demand, that is, satisfying $\left(1-H_j\left(t\right)/W_{\mathrm{B}}\right)\le h_{\mathrm{th}}$.

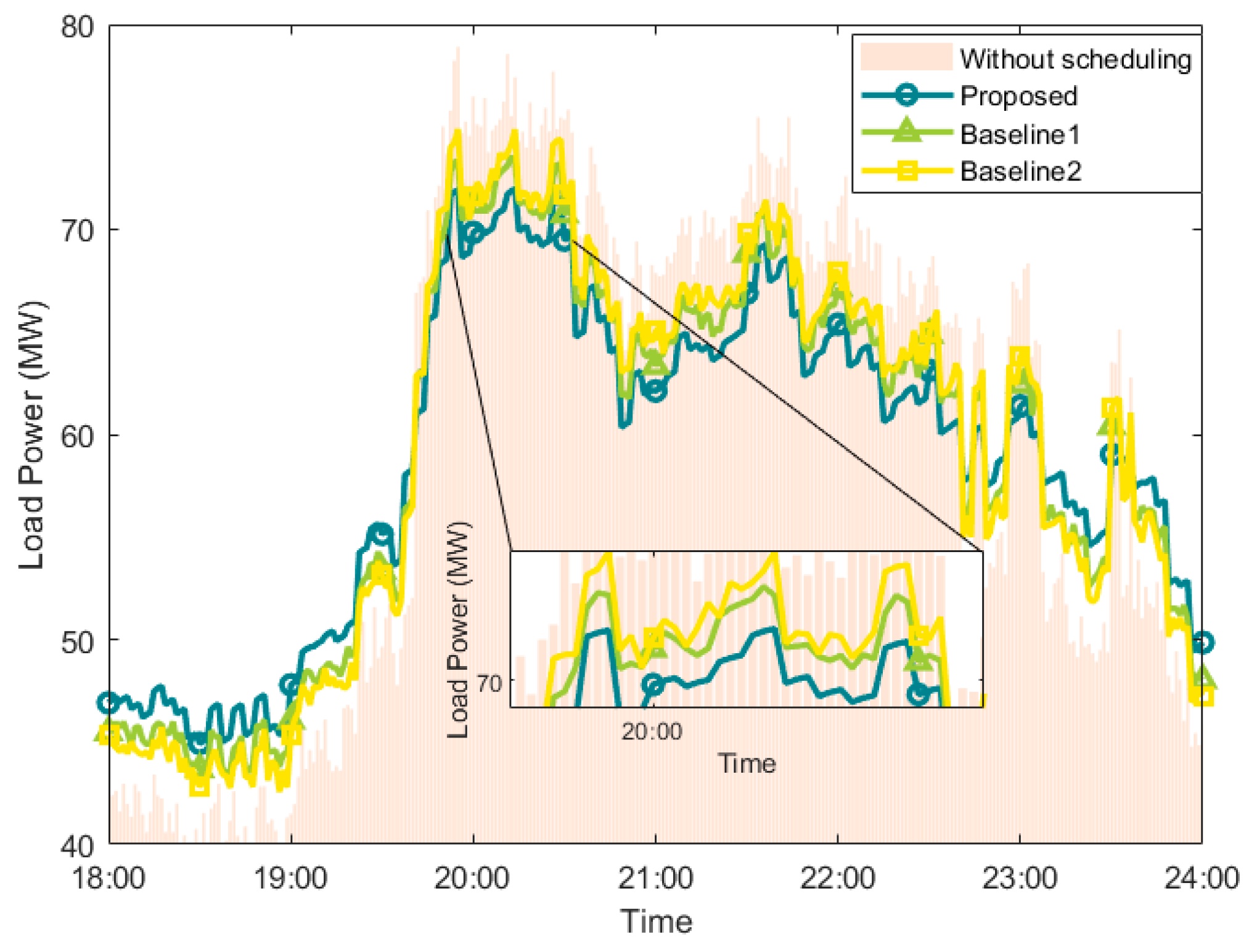
2.4. Peak-Shaving and Valley-Filling Effect Model

The effectiveness of peak shaving and valley filling is evaluated using the sum of the squared deviations of the load curve, which are expressed as follows:

$$y={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^I{\left(P_{\mathrm{L}}\left(t\right)+P_i^{\mathrm{cz}}\left(t\right)-P_{\mathrm{av}}\right)}^2}}$$

(16)

$$P_i^{\mathrm{cz}}\left(t\right)={\displaystyle \sum _{k=1}^{N_i^{\mathrm{c}}}{P}_i^{\mathrm{c}}\left(k\right)}$$

(17)

$$P_{\mathrm{av}}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^I\left(P_{\mathrm{L}}\left(t\right)+P_i^{\mathrm{cz}}\left(t\right)\right)}}$$

(18)

where $P_{\mathrm{L}}\left(t\right)$ is the background load value excluding the load of the BSS in slot $t$. $P_i^{\mathrm{cz}}\left(t\right)$ is the total charging power of the BSS $s_i$. $P_i^{\mathrm{c}}\left(k\right)$ is the charging power of the $k$-th battery. $P_{\mathrm{av}}$ is the average value of the background load of the BSS during the operation time slot.

2.5. Model of Economic Operations of a Battery-Swapping Station

2.5.1. Charging Revenue

The revenue achieved by the BSS $s_i$ from charging electric heavy-duty truck batteries in slot $t$ is given by the following equation:

$$w_i^{\mathrm{c}}=P_i^{\mathrm{cz}}\left(t\right)\times \left(C_{\mathrm{c}}\left(t\right)-\rho \right)\times t_{\mathrm{p}}$$

(19)

where $C_{\mathrm{c}}\left(t\right)$ is the charging price for electric heavy-duty trucks and $\rho$ is the charging loss cost of the BSS.

2.5.2. Cost of Time-of-Use Pricing

The cost of purchasing power from the grid during slot $t$ under time-of-use pricing for BSS $s_i$ is given by the following equation:

$$w_i^{\mathrm{p}}=P_i^{\mathrm{cz}}\left(t\right)\times C_{\mathrm{p}}\left(t\right)\times t_{\mathrm{p}}$$

(20)

2.5.3. Total Revenue

The total revenue for all $T$ time slots is given by the following equation:

$$w_{\mathrm{sum}}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^I\left(w_i^{\mathrm{c}}-w_i^{\mathrm{p}}+w_i^{\mathrm{tec}}+w_i^{\mathrm{EP}}\right)}}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^I\left(w_i^{\mathrm{sum}}\left(t\right)\right)}}$$

(21)

where $w_i^{\mathrm{tec}}$ is the technical revenue of the BSS and $w_i^{\mathrm{EP}}$ is the environmental revenue.

3. Optimization of Economic Operations for a Coalition of Battery-Swapping Stations Based on Adaptive Shapley Value

3.1. Optimization Problem Modeling

The optimization objective is to maximize the difference between the revenue of the electric heavy-duty truck BSS and the sum of the squared deviations of the load curve. The optimization problem presents several key challenges that must be addressed to ensure an optimal and computationally efficient solution.

High-Dimensional Complexity: The optimization involves multiple decision variables, including station revenue, battery availability, load-balancing constraints, and charging/discharging schedules. The interdependencies among these factors significantly increase the problem’s dimensionality, making traditional exhaustive search methods computationally infeasible.

Uncertainty in Demand Forecasting: The randomness of electric heavy-duty trucks’ arrival patterns and energy-consumption behavior, as well as that of fluctuating electricity prices, introduces uncertainty into the model. These variations impact battery-swapping demand and station profitability, requiring robust demand-prediction models to mitigate forecasting errors.

Non-Convexity of the Objective Function: The incorporation of battery-degradation costs, peak-shaving constraints, and cooperative revenue-allocation mechanisms results in a non-convex and highly nonlinear optimization problem. Traditional linear programming techniques are inadequate, necessitating the use of heuristic optimization algorithms or metaheuristic search methods to ensure efficient convergence to near-optimal solutions.

To tackle these challenges, we employ heuristic optimization techniques, i.e., non-sorting genetic algorithm III (NSGA-III) [31] and an adaptive Shapley value-based economic-allocation approach. The heuristic techniques enable efficient exploration of the high-dimensional solution space, while the adaptive Shapley value model ensures a fair revenue distribution among BSSs.

The objective of optimization problem P1 is to maximize the difference between the total revenue of the BSS coalition and the penalty for grid load fluctuations. The problem can be formulated as follows:

Objective Function:

$$\mathbf{P}\mathbf{1}:\underset{\left\{P_i^c\left(t\right)\right\}}{\max }f=w_{\mathrm{sum}}-\mu y$$

(22a)

where $w_{\mathrm{sum}}$ is the total revenue of the coalition, $y$ is the sum of squared deviations of the grid load, and $\mu$ is the weighting coefficient used to balance the revenue of the BSS and the sum of the squared deviations of the load curve, aligning their magnitudes.

The constraints are as follows:

$$C_1:P_i^{\min }⩽P_i^c\left(t\right)⩽P_i^{\max }\left(t\right),\forall s_i\in \mathcal{S},\forall t\in \mathcal{T}$$

(22b)

where $P_i^{\min }$ represents the minimum charging power. Constraint $C_1$ ensures that the charging power of each BSS remains between its technically permissible minimum and maximum power levels.

$$C_2:N_i^{\mathrm{f}}\left(t\right)\ge D_i\left(t\right),\forall s_i\in \mathcal{S},\forall t\in \mathcal{T}$$

(22c)

Constraint $C_2$ requires that the number of fully charged batteries at each station at any given time must be sufficient to meet the predicted swapping demand for that time, thereby guaranteeing service quality.

3.2. An Improved Shapley Value Model for the Economic Operation of Electric Heavy-Duty Truck Battery-Swapping Stations

A cooperative game coalition is constructed based on the set of BSSs, $\mathcal{S}$, with the total number of coalition members equal to the number of stations, $I$. The joint coalition revenue in slot $t$ is called $f\left(t\right)={\displaystyle \sum _{t=1}^t{\displaystyle \sum _{i=1}^I\left(w_i^{\mathrm{sum}}\left(t\right)-{\left(P_{\mathrm{L}}\left(t\right)+P_i^{\mathrm{cz}}\left(t\right)-P_{\mathrm{av}}\right)}^2\right)}}$. The characteristic function is $V\left(S,t\right)=f\left(t\right)$ and denotes the coalition revenue of coalition $S$. $x_i\left(t\right)$ denotes the benefit to member $i$ from joint coalition revenue. To eliminate the impact of the entry order on the-allocation scheme, the expectation of $x_i\left(t\right)$ is obtained by averaging over all possible sequences, expressed as follows:

$$\begin{array}{l}{x}_i(t)=\\ {\displaystyle {\displaystyle \sum }_{S\subset S\backslash i}}{\displaystyle \frac{\left|S\right|!(|I|-|S|-1)!}{I!}}[V(S\cup \{i\},t)-V(S,t)]\end{array}$$

(23)

where $\left|S\right|$ is the number of coalition members. $S\backslash i$ is a smaller set of coalitions after removing the member $i$. $V(S\cup \{i\},t)$ is the revenue of the coalition after member $i$ joined the current coalition.

Within the Shapley value-allocation framework, traditional models assume equal weights among the coalition members [32]. However, they fail to adequately account for preference heterogeneity, influence differences, and the impact of market policies on members. Given the inherent differences in the operational characteristics and revenue-generating capacities of members in the economic operation of actual BSSs, we introduce necessary improvements to the Shapley value model. We incorporate a weighting adjustment mechanism to reflect each member’s relative importance within the coalition and its market dynamics, fully considering the horizontal and vertical data characteristics of each member. The revenue allocation bias weight $\Delta M_i\left(t\right)$ for member $i$ in coalition is defined as follows:

$$\Delta M_i\left(t\right)=k_i\left(t\right){\displaystyle \frac{(w_i^{\mathrm{sum}}\left(t\right)-w^{\mathrm{av}}\left(t\right))}{{\displaystyle \sum _{i=1}^I{w}_i^{\mathrm{sum}}\left(t\right)}}}$$

(24)

where $w^{\mathrm{av}}\left(t\right)$ is the average return of all BSSs. $k_i\left(t\right)$ is the desired impact factor, $k_i\left(t\right)=t{D}_i\left(t\right)/{\displaystyle \sum _{i=1}^t{D}_i\left(t\right)}$, and the higher baseline forecast value for the BSS in the current period indicates that the BSS is experiencing a peak battery-swapping demand, which results in a higher expected influence factor. Likewise, BSSs with higher revenue receive a greater revenue-allocation bias weight, granting them a larger share of the revenue allocation within the coalition.

The Shapley value $x_i^{\mathrm{sha}}\left(t\right)$ after coordinated optimization of BSSs is expressed as follows:

$$x_i^{\mathrm{sha}}\left(t\right)=x_i(t)+V\left(S,t\right)\Delta M_i\left(t\right)$$

(25)

The adaptive Shapley value based on the weighting adjustment mechanism not only considers each member’s marginal contribution to the total coalition revenue but also incorporates each member’s horizontal and vertical data characteristics, fully accounting for differences in contributions among members. This enables fair and reasonable reallocation of joint coalition revenue.

3.3. Improved Shapley Game Model Constraints

Owing to the super-additivity of cooperative games, we establish the basic constraint condition where the joint coalition revenue exceeds the revenue generated by members acting independently, expressed as follows:

$$V(S,t)>V(S\backslash n,t)$$

(26)

To form a stable coalition, we must select members with appropriately matched capacities to ensure that the additional constraint stably influences revenue allocation. In the process of forming a coalition, members with appropriately matched capacities should be selected to ensure the stable influence of the additional constraint on revenue allocation. If smaller-capacity members are included within the coalition, the value of $k_n\left(t\right)$ will increase rapidly to ensure that the Shapley algorithm operates normally. However, this increase significantly reduces the influence of these smaller members, thereby diminishing the applicability of the algorithm. Therefore, coalition-construction constraints must satisfy the following inequality:

$$Z{\left(n\right)}_{\min }>{\displaystyle \frac{Z(S)}{k_n\left(t\right)I}}$$

(27)

where $Z{\left(n\right)}_{\min }$ is the minimum capacity of member $n$.

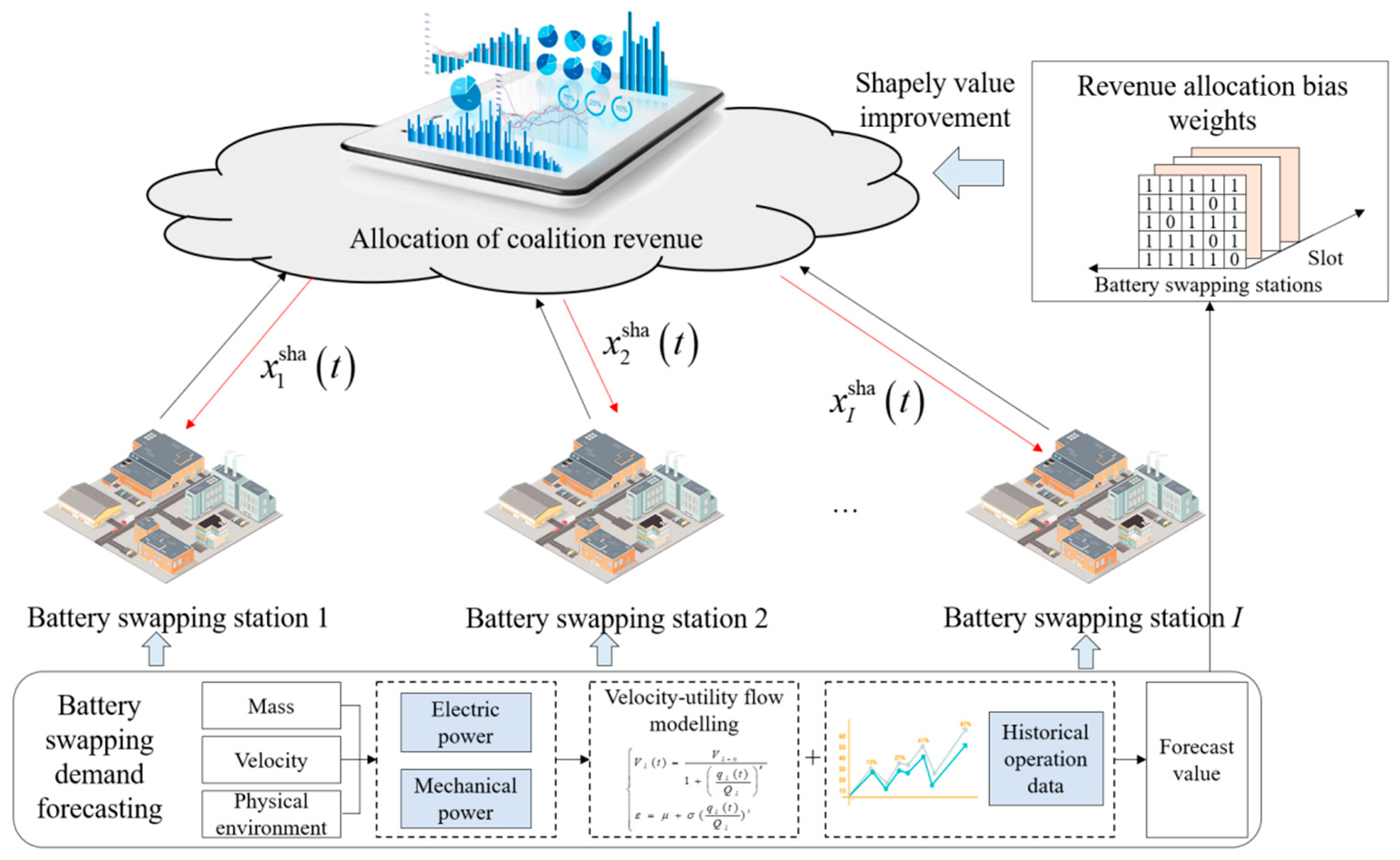
4. Process of Optimization of Economic Operations for a Coalition of Battery-Swapping Stations Based on the Adaptive Shapley Value

We first use the Monte Carlo algorithm to simulate the battery-swapping demand for electric heavy-duty truck BSSs. The specific process is as follows.

• Sample starting points and initial departure times of electric heavy-duty trucks.
• Sample the distance from the starting points to the BSSs.
• Determine the travel velocity on each road based on road grade and traffic flow.
• Determine the weight of the cargo based on order information.
• Calculate the energy consumption of the electric heavy-duty truck upon reaching the BSS.
• Assess whether the electric heavy-duty truck requires battery swapping.
• We sum the number of electric heavy-duty trucks requiring battery swapping and combine the resulting value with historical operational data to obtain the BSS demand.

Based on the demand-forecasting results, the economic operation of the BSS coalition is optimized. In the energy-transaction model within the coalition, each BSS acts as both a producer and a consumer. Multiple entities reach an agreement following a dynamic game with complete information in which the game order is predetermined. The solution to this dynamic game involves the following steps:

Game Formulation: The revenue allocation among BSSs is modeled as a cooperative game, where each station’s contribution to the coalition is assessed using the adaptive Shapley value method.

Stepwise Approach to a Solution:

• Each BSS submits its demand forecast and charging strategy based on time-of-use pricing.
• The marginal contribution of each station to the coalition is calculated using the characteristic function.
• The revenue-allocation bias weights are dynamically adjusted to ensure a fair distribution of coalition revenue.
• An iterative optimization process is conducted to refine the revenue allocation and charging strategy until an equilibrium state is reached.

Dynamic Adjustment Mechanism: Given the real-time fluctuations in electricity prices and demand, the revenue-allocation weights are updated dynamically. A feedback mechanism ensures that stations adapt to new conditions based on historical operational data, improving overall efficiency and fairness.

Through this iterative process, the dynamic game reaches a stable and fair equilibrium, optimizing revenue distribution and improving BSS cooperation.

First, each entity submits applications based on its demand forecast to determine its charging strategy. Then, the adaptive Shapley game algorithm is executed internally within the system, initially determining the charging strategy and revenue allocation for BSSs. This process iterates until the coalition revenue is maximized, thereby achieving the final optimal strategy for the optimization objective. The principle is illustrated in Figure 1, and the detailed process is as follows:

• The BSS enters its operational state.
• Each BSS submits applications based on its basic demand forecast.
• To maximize coalition revenue, the charging needs of each entity are evaluated against the constraints at the model runtime, as specified by (22), (26), and (27), to determine the charging scheme $Pla{n}_1$ for the BSSs.
• The marginal cost of the BSS operation is calculated, and the weights are optimized based on the basic demand forecast of the BSS and time-of-use pricing.
• The marginal cost in Step 4 and the charging strategy in Step 3 are brought into the characteristic function to realize the optimization of the economic operations of the BSSs based on the adaptive Shapley value and compute the subject’s optimal charging strategy $Pla{n}_2$ to obtain both the charging strategy and the revenue-allocation scheme.
• Adjust $Pla{n}_2$ according to the revenue-allocation scheme and compare the current revenue value with the previous value. If the deviation is below the threshold, the optimization ends; otherwise, take the current price into step 4, replace the marginal price cost, and continue the optimization.

The proposed method comprises parameter initialization, iterative solution-finding, and a convergence criterion, with the algorithmic process detailed in Algorithm 1.

Algorithm 1. Optimization of Economic Operations for a Swapping-Station Coalition based on Adaptive Shapley Value.
1	Initialization:
2	Initialize charging strategy $Pla{n}_0$ for all stations;
3	Set iteration counter $k=0$, max iterations $K_{max}$, and convergence threshold $ϵ$;
4	Iterative Optimization:
5	while $k<K_{max}$ and $\left|R^{(k)}-R^{(k+1)}\right|>\epsilon$
6	$k\leftarrow k+1$;
7	for each time slot $t\in \mathcal{T}$ do
8	Step 1: Demand Forecasting
9	for each station $s_i\in \mathcal{S}$ do
10	Calculate predicted demand $D_i(t)$ via Monte Carlo and Equation (11);
11	end for
12	Step 2: Run Adaptive Shapley Value Game
13	for each station $s_i\in \mathcal{S}$ do
14	Calculate marginal contributions $V(S\cup i,t)-V(S,t)$ for all $S\subset \mathcal{S}\backslash i$;
15	Calculate expected influence factor $k_i(t)$ and bias weight $\Delta M_i(t)$ via Equation (24);
16	end for
17	Calculate adaptive Shapley value $x_i^{sha}(t)$ for each station via Equations (23) and (25);
18	Step 3: Optimization and Policy Update
19	Solve optimization problem P1 (Equation (22)) to obtain optimal charging power $P_i^c(t)$;
20	end for
21	Update policy $Pla{n}_k\leftarrow P_i^c{(t)}_{\forall i,t}$ and total coalition revenue $R^{(k)}$;
22	end while
23	Output: optimized charging strategy $Pla{n}_k$ and profit-allocation scheme.

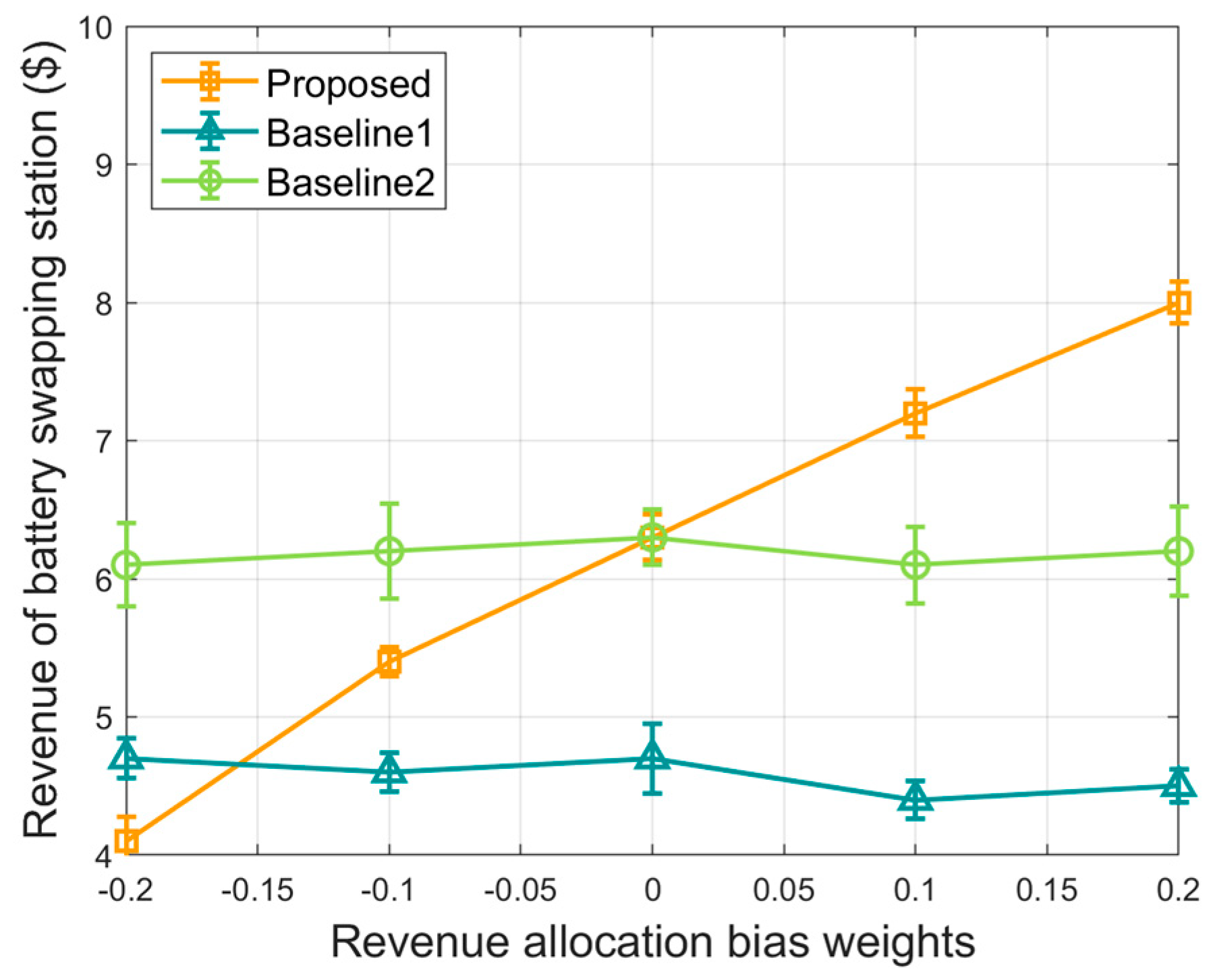
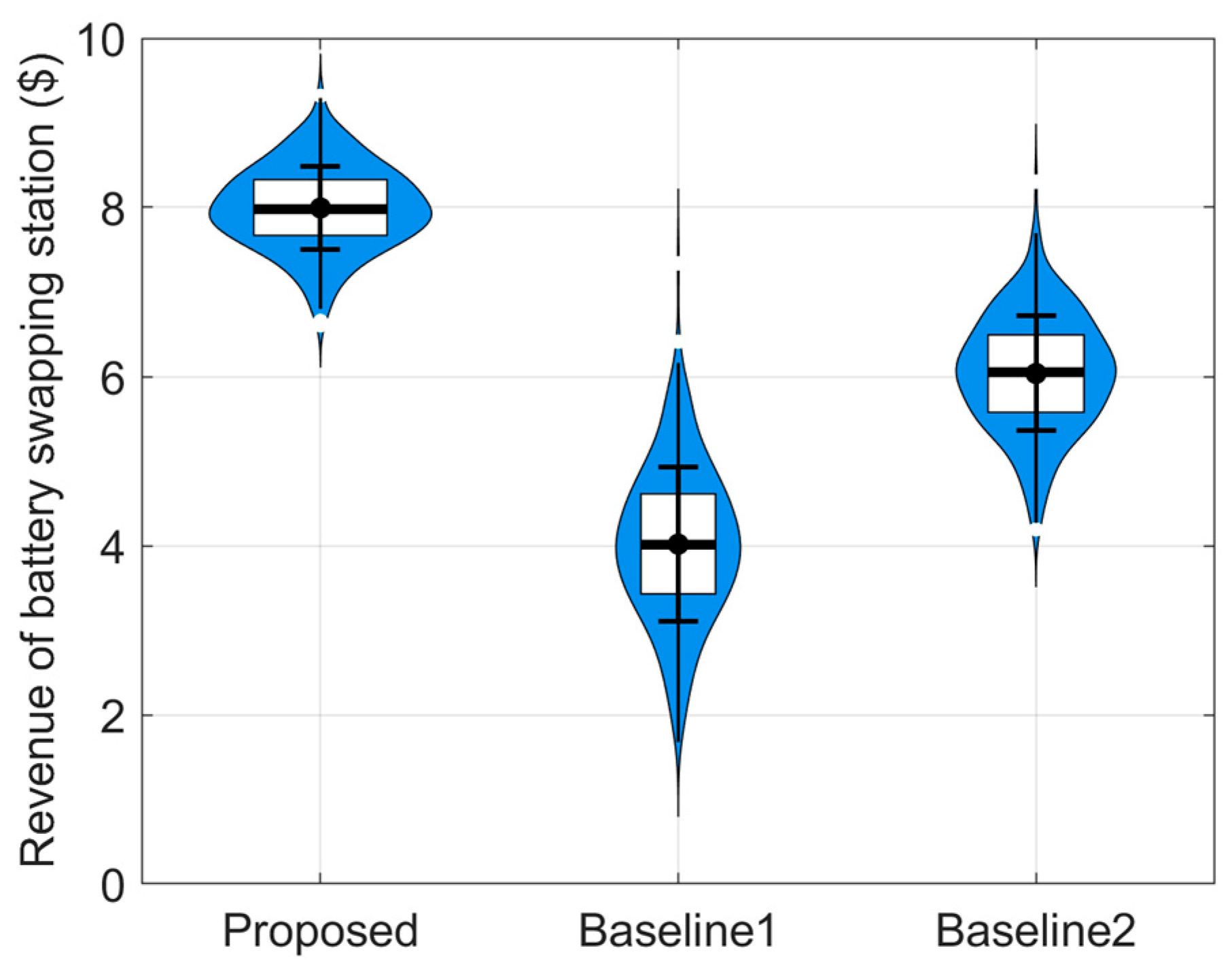
5. Simulation

In this study, a simulation model based on the IEEE 33-node test system was constructed to evaluate the effectiveness of the proposed algorithm, which is illustrated in Figure 2. The simulation topology mimics a typical medium-sized urban power grid with multiple key nodes distributed across the city center, urban edges, and major traffic arteries. Specifically, the BSSs ESS1 and ESS2 are located at nodes 4 and 13, respectively. These locations are in the city center, where there is high traffic flow and significant battery-swapping demand, simulating a high-demand scenario in the urban core area. The BSSs ESS3, ESS4, and ESS5 are situated at nodes 6, 22, and 26, respectively, near the urban edges and major traffic routes, representing the layout of BSSs in these areas. All BSSs are equipped with different scales of charging power (60 kW, 120 kW, and 240 kW) to meet the charging demands of electric heavy-duty trucks of various sizes. Additionally, the simulation considers variations in traffic flow and power demand across different time periods, especially during the peak hours from 18:00 to 24:00 when the battery-swapping demand surges. The simulation parameters are presented in

Table 2. Simulation parameters [33].

Parameter	Definition	Value
$I$	Number of BSSs	5
$T$	Total daily time slots (5 min step)	288
$\mu$	Speed-flow utility model shape coefficient	{1.72, 2.07, 2.39}
$\sigma$	Speed-flow utility model adjustment coefficient	{3.15, 2.87, 2.56}
${\delta }_p$	Peak electricity price	0.167 $/kWh
${\delta }_o$	Flat electricity price	0.127 $/kWh
${\delta }_v$	Valley electricity price	0.091 $/kWh
$\omega$	Weight of squared load deviations	[0.4, 1.6]

.

To validate the performance of the proposed algorithm, we considered two comparison algorithms. Baseline 1 [14] uses a quotation-bidding strategy to calculate node prices without considering the cooperative game relationship between BSSs. This lack of cooperative modeling results in inefficient load balancing and higher operational costs, as BSSs fail to coordinate charging schedules to stabilize the grid. Baseline 2 [18] optimizes the battery-swapping strategy for electric heavy-duty trucks based on a stochastic evolutionary game but ignores the differences in individual contributions among the BSSs. This oversight results in suboptimal battery scheduling, increasing grid instability and reducing overall efficiency due to uneven resource allocation across BSSs. Through comparative analysis, a comprehensive assessment of the proposed algorithm’s advantages in demand forecasting, revenue allocation, and grid stability can be achieved.

Simulations are conducted on a computer with an Intel Core i7-10700 CPU @ 3.80 GHz and 32 GB of RAM in the MATLAB R2022b environment. The maximum iteration number is set to 6000, and the crossover and mutation rates of NSGA-III are specified as 0.9 and 0.1, respectively. NAGA-III reaches convergence at around 2600 iterations [33]. For the proposed optimization algorithm based on the adaptive Shapley value, the total time to complete optimization for a full 24 h scheduling cycle is about 25 min. This computational efficiency indicates that the proposed algorithm has the potential for day-ahead and intra-day decision-making for scheduling in practical operations.

Figure 3 illustrates the relationship between the revenue of the BSS and the bias weight coefficient used for revenue allocation. Simulation results show that the revenue of the proposed algorithm increases significantly with the value of the revenue-allocation bias weight coefficient. Compared to Baseline 1 and Baseline 2, the revenue from the proposed algorithm is 35.91% and 28.54% higher, respectively. This improvement is mainly attributable to the adaptive Shapley value approach used in the proposed algorithm. Unlike traditional Shapley value methods that focus solely on marginal contributions, our approach introduces a bias weight coefficient for revenue allocation to evaluate the contribution and importance of each BSS within the coalition, leading to a more equitable and realistic revenue distribution. This not only encourages active participation but also enhances operational efficiency. In comparison, Baseline 1 lacks cooperation among BSSs, ignoring their synergistic resource sharing and coordinated scheduling, which results in inefficient resource allocation and higher revenue variance. Baseline 2, despite considering stochastic optimization, fails to account for individual contributions, leading to the generation of inflexible revenue-allocation bias weights. This causes suboptimal battery scheduling and load balancing, reducing overall efficiency and revenue. The proposed algorithm addresses these limitations by integrating both marginal contributions and individual characteristics, achieving superior performance in revenue enhancement and operational efficiency.

Figure 4 shows a box plot of the BSS revenue under different algorithms. The simulation results show that the revenue variance generated by the proposed algorithm is 68.29% and 12.09% lower, respectively, compared with Baseline 1 and Baseline 2. This is because the proposed algorithm constructs a demand-forecasting model for battery swapping that accurately simulates the battery-swapping behavior of electric heavy-duty trucks. This improves the accuracy of BSS demand forecasting, enabling more precise charging-strategy scheduling and power adjustment to meet actual needs, thus reducing resource wastage. Baseline 1 involves only competition, with no cooperation, and achieves low average revenue and the largest revenue variance.

Figure 5 illustrates the variation in load power across the distribution network versus time, considering the participation of BSSs in the demand response. The simulation results show that the variation in load power between 18:00 and 24:00 was reduced by 23.41% after the battery-swapping scheduling was applied according to the proposed algorithm. This is because the proposed algorithm can provide more accurate demand forecasting for BSSs to optimize the scheduling of the charging strategy. The adjustment of the charging power is allowed to adapt to the actual demand, effectively reducing the ineffective consumption of resources. To balance the load on the power grid and improve the stability and economy of the power system, power consumption is reduced during the time of peak power demand and power consumption is increased during the demand valley.

Figure 6 shows the variation of the distribution network’s load power, as optimized by different algorithms. Simulation results indicate that during the peak period of 18:00–24:00, the proposed algorithm significantly reduces the variance of load power; specifically, it reduces variance by 22.76% compared to Baseline 1 and by 26.11% compared to Baseline 2. This reduction is primarily due to the high accuracy of demand forecasting in the proposed algorithm, which simulates the battery-swapping behavior of electric heavy-duty trucks to achieve more precise load prediction. In addition, the algorithm calculates the revenue-allocation bias weights of coalition members based on their horizontal and vertical data characteristics, fully reflecting the differences in individual contributions and thus realizing an optimal battery-swapping scheme. In comparison, Baseline 1 employs a quotation-bidding strategy for BSS pricing, neglecting cooperative revenue-sharing mechanisms, which leads to uneven profit distribution and high revenue variance. Baseline 2, despite using stochastic optimization for swapping demand, fails to incorporate individual BSS characteristics, resulting in rigid revenue-allocation bias weights and reduced economic efficiency. The proposed algorithm effectively balances the load by increasing power consumption during off-peak hours and reducing it during peak hours, achieving more stable and efficient operation of the distribution network.

Figure 7 illustrates the variation in the revenue of the BSSs versus weights. When the weight increased from 0.4 to 1.6, the revenue of the BSS decreased by 18.18% and the load deviation decreased by 19.44%. This is because, with the increase in weight, the cooperation between the members of the coalition results in more attention being paid to the optimization of the load-deviation variance, rather than the revenue of the BSS. As a result, the BSS can enhance the priority of peak shaving and valley filling to reduce the variance in load power on the power grid.

6. Conclusions

This paper proposes an algorithm for optimization of economic operations for electric heavy-duty truck BSSs under time-of-use pricing with the aim of maximizing revenue and enhancing peak-shaving and valley-filling effects within the power grid. First, historical operational data from BSSs were analyzed, incorporating factors such as geographical environment, traffic conditions, and characteristics of electric heavy-duty trucks to realistically simulate battery-swapping behavior. Next, an economic operational model was developed for BSSs that aimed at maximizing the weighted difference between station revenue and squared load deviations. Finally, an optimization of economic operations for BSS coalitions was designed based on an adaptive Shapley value. This approach introduced revenue-allocation bias weights to evaluate each BSS’s contribution and importance within the coalition, establishing an allocation scheme that aligns with the interests of multiple stakeholders and with market dynamics. It ensures fair and reasonable revenue allocation among coalition members, thereby enhancing overall economic efficiency and grid stability. Compared to Baseline 1 and Baseline 2, the proposed algorithm improves average station revenue by 6.47% and 34.11%, reduces revenue variance by 68.29% and 12.09%, and reduces load-deviation variance by 22.76% and 26.11%, respectively.

The proposed algorithm faces scalability challenges when expanding from single region to multi-region coalition optimization. A distributed edge computing architecture could mitigate this by pre-processing forecasts of battery-swapping demand and regional decision making locally at each BSS before aggregating coalition-level inputs. Federated learning further enhances scalability by enabling inter-region collaborative model training across regions without raw data exchange, preserving privacy while reducing computational demands.

Regulatory constraints may arise from dynamic electricity-market rules, particularly in regions where time-of-use pricing mechanisms require pre-approval. Market adoption could be hindered if policy revisions are required to recognize BSS coalitions as qualified market participants and energy providers. Grid-interconnection standards may also require updates to accommodate bidirectional energy flows from aggregated batteries.

The feasibility of real-world implementation is demonstrated through the algorithm’s compatibility with existing BSS structures and electricity markets. Additionally, the total time to complete optimization for a full 24 h scheduling cycle is less than half an hour, demonstrating the feasibility of day-ahead and intra-day decision-making for scheduling in real-world implementations.

Future work will focus on how to address scalability issues in optimizations involving large-scale inter-region coalitions. A decentralized hierarchical optimization framework combining the advantages of edge computing and federated learning will be investigated. In particular, regional edge servers that collaboratively train shared optimization models under a federated learning architecture are preferred to enforce cross-region coordination. Other issues of model compression, convergence acceleration, and preservation of privacy will also be addressed.