Modeling Renewable Energy Feed-In Dynamics in a German Metropolitan Region
Abstract
1. Introduction
2. Methods
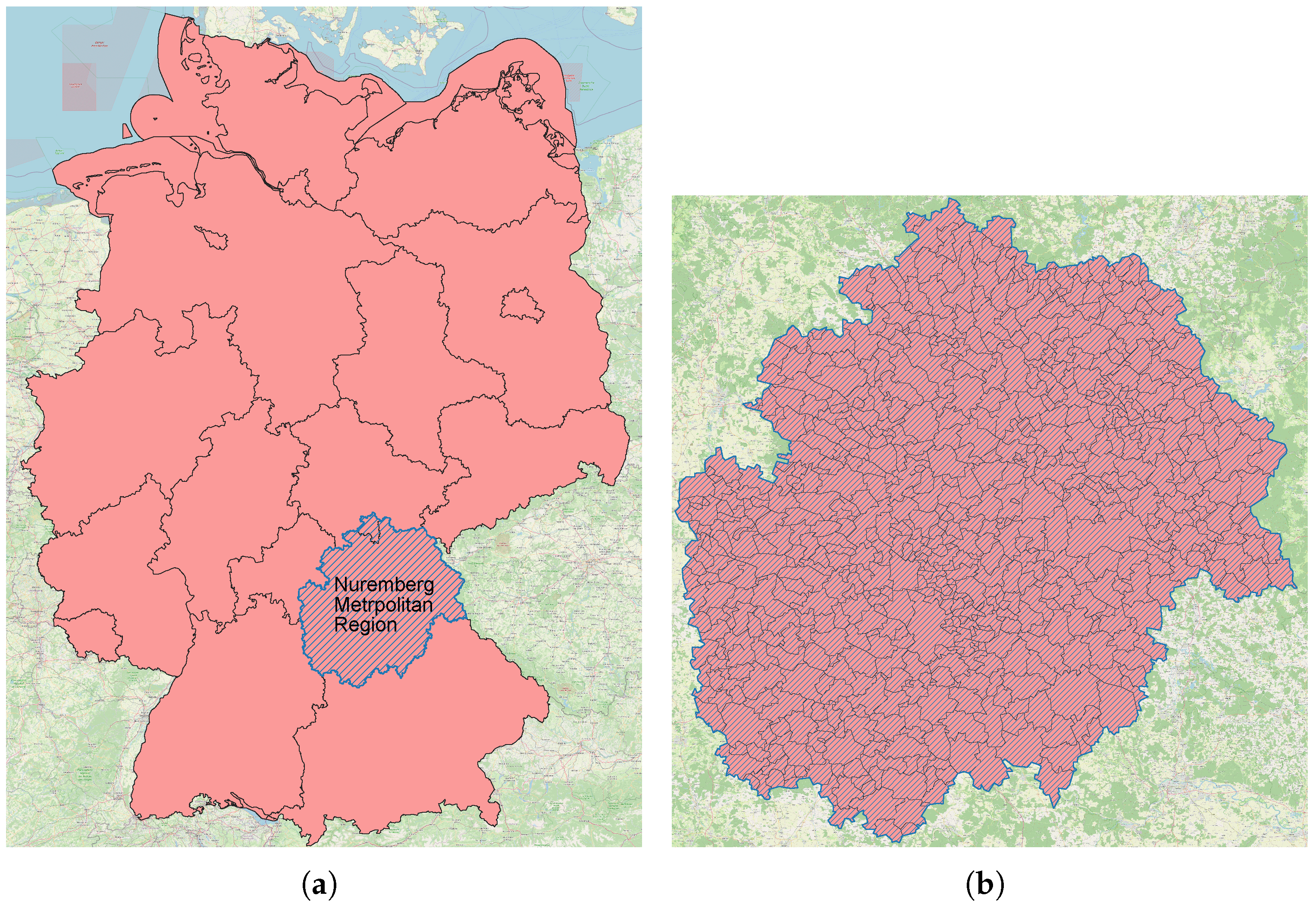
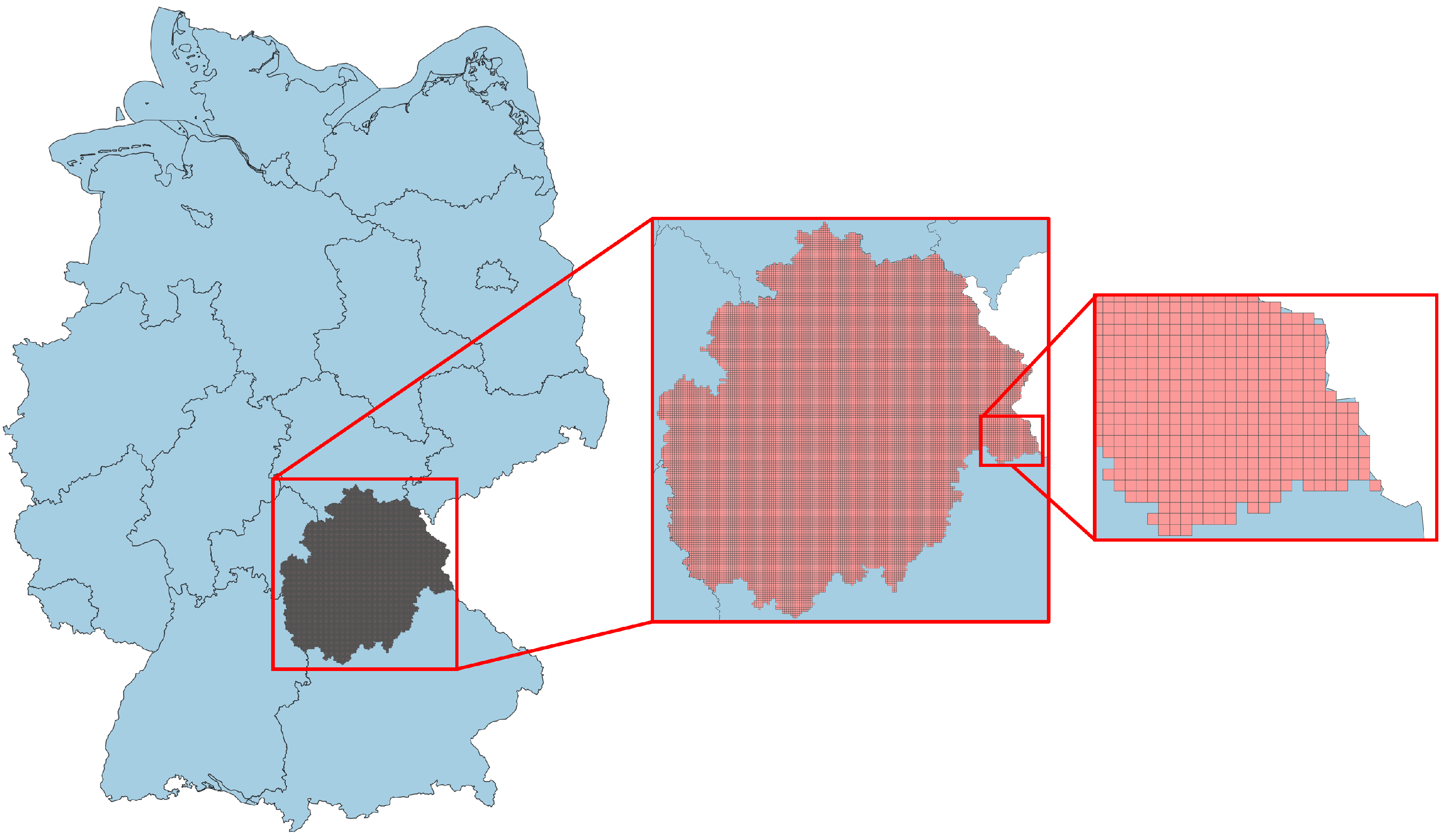
2.1. Visualization of the Model Region
2.2. PV Modeling Approach
2.3. Wind Modeling Approach
3. Results and Discussion
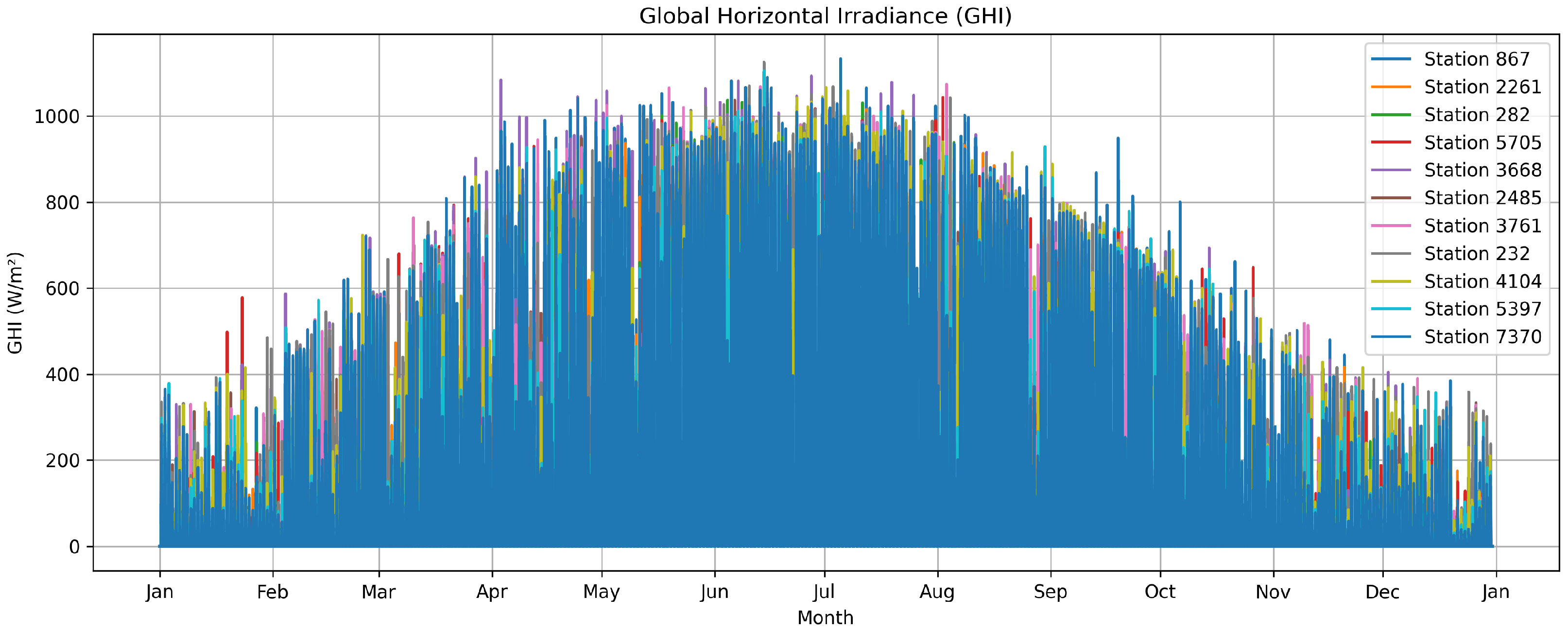
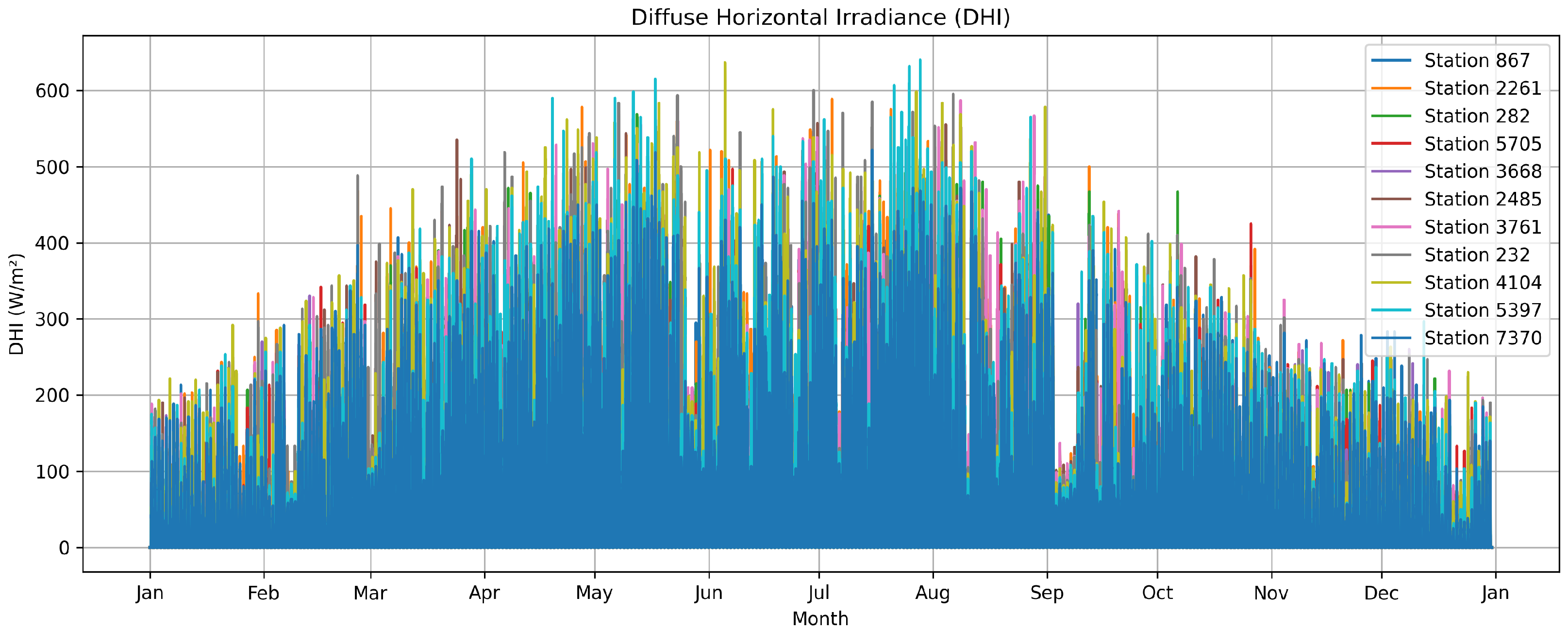
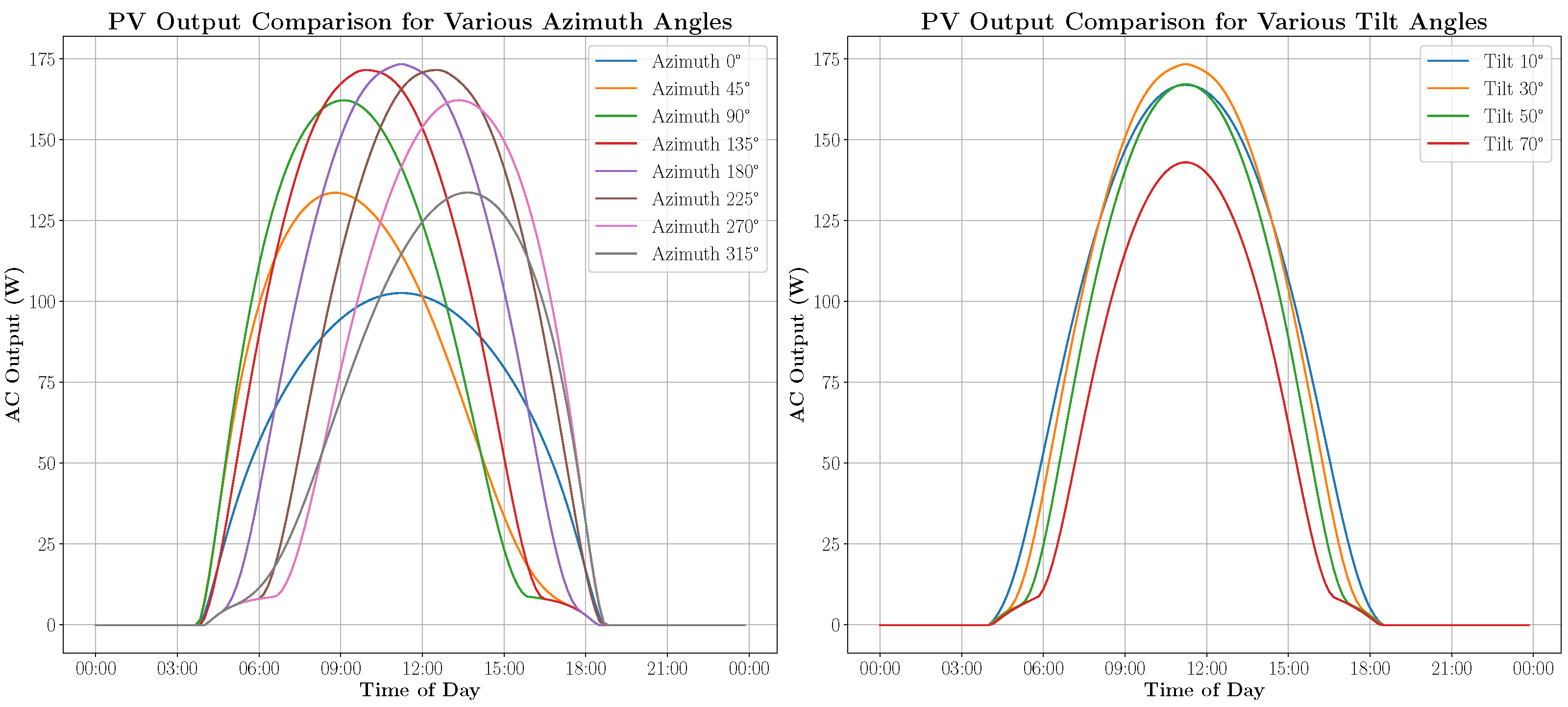
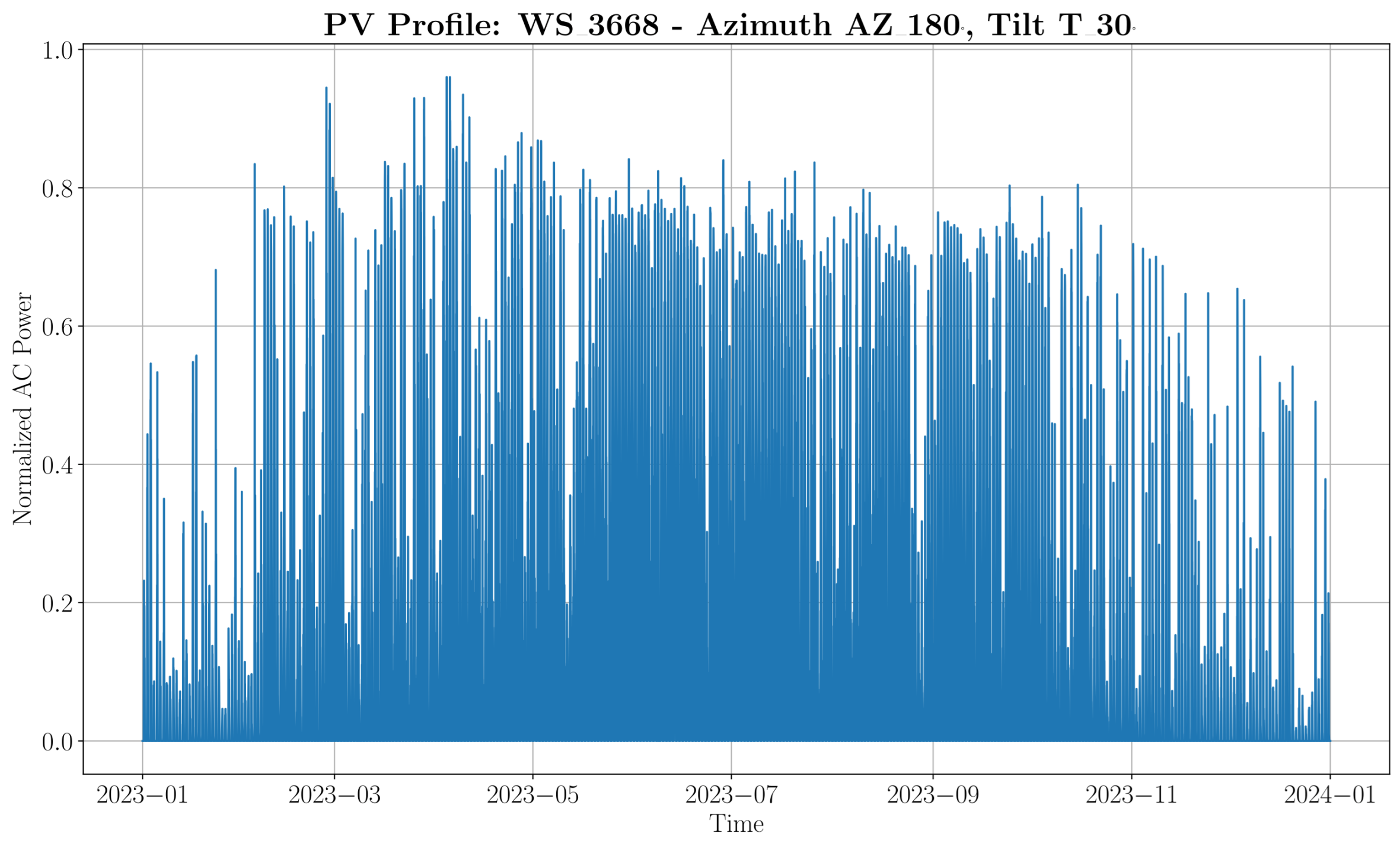
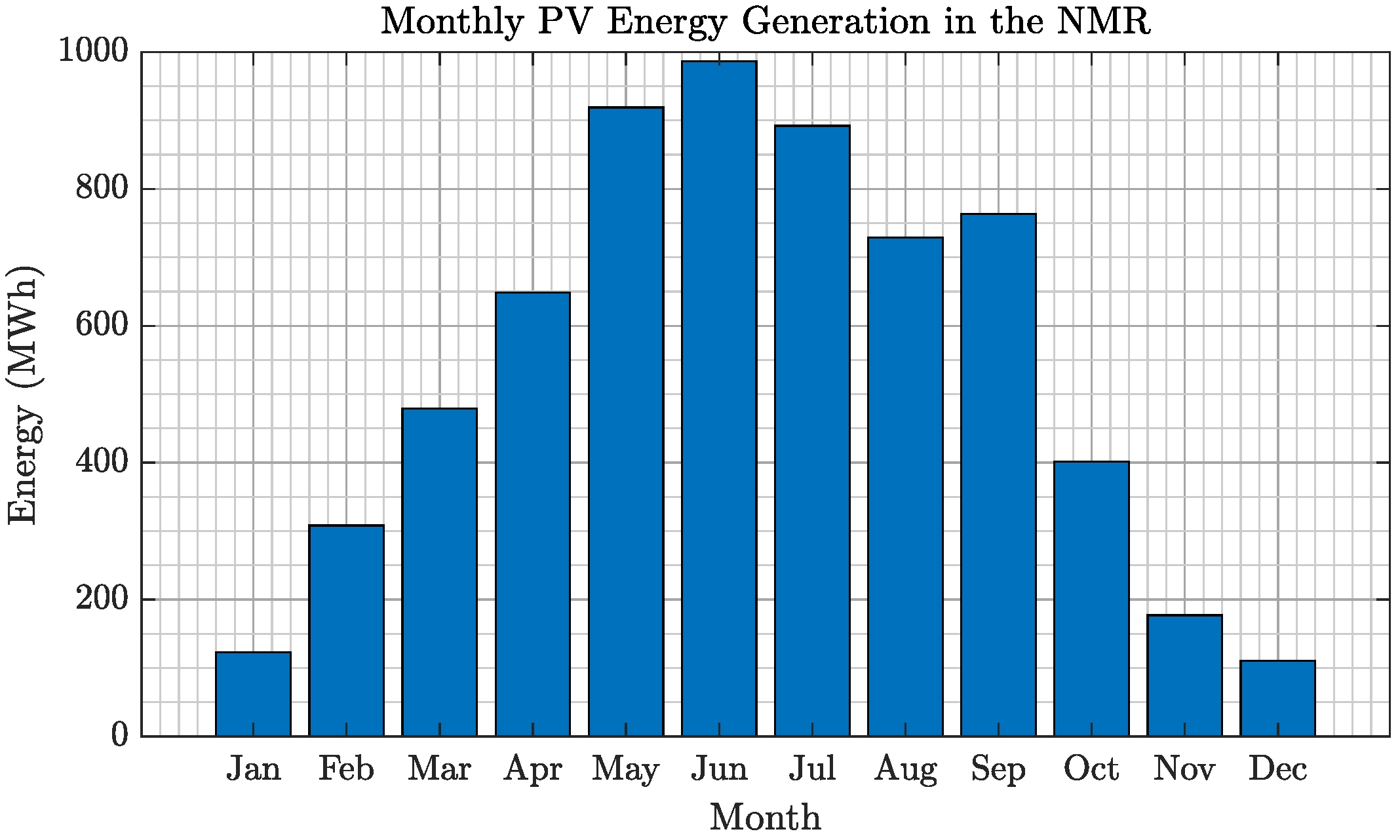
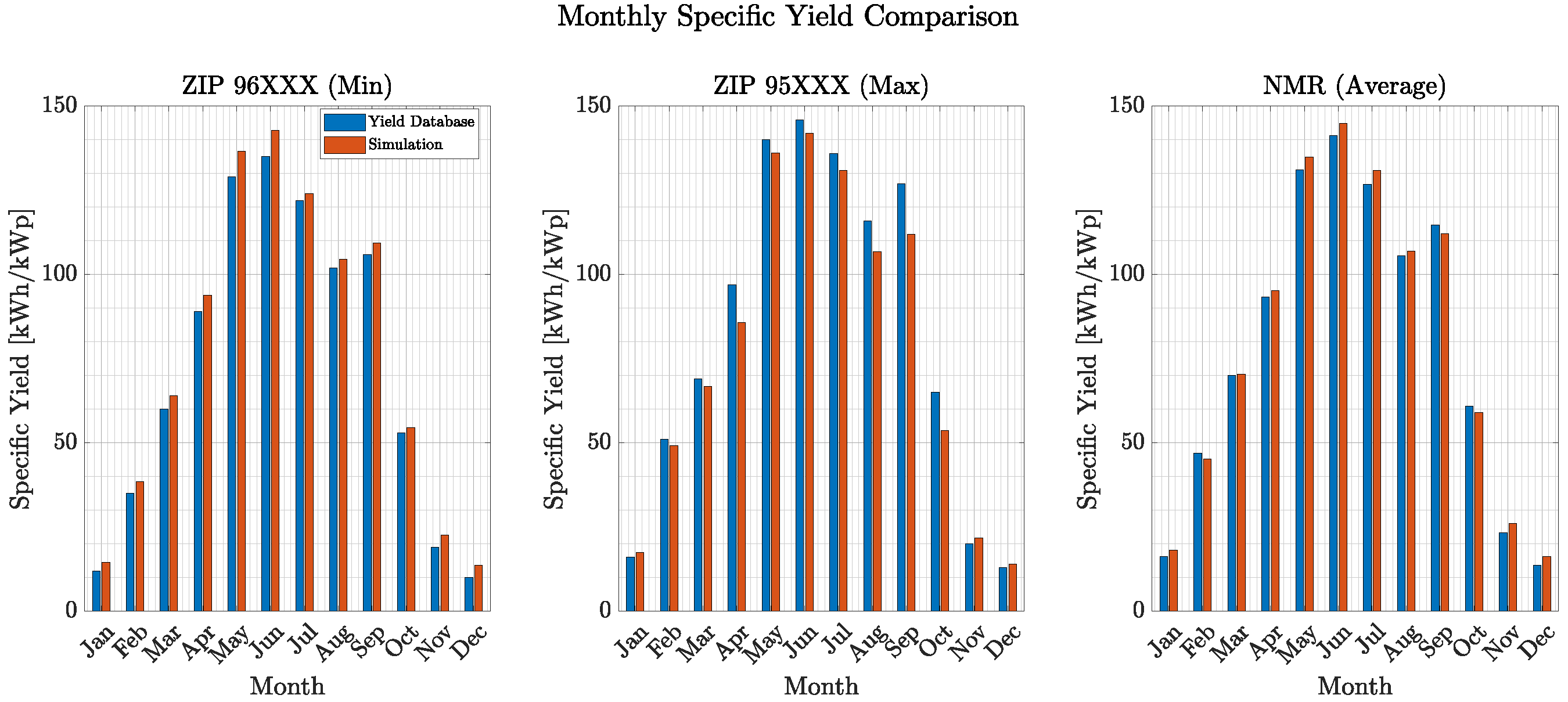
3.1. PV Simulation
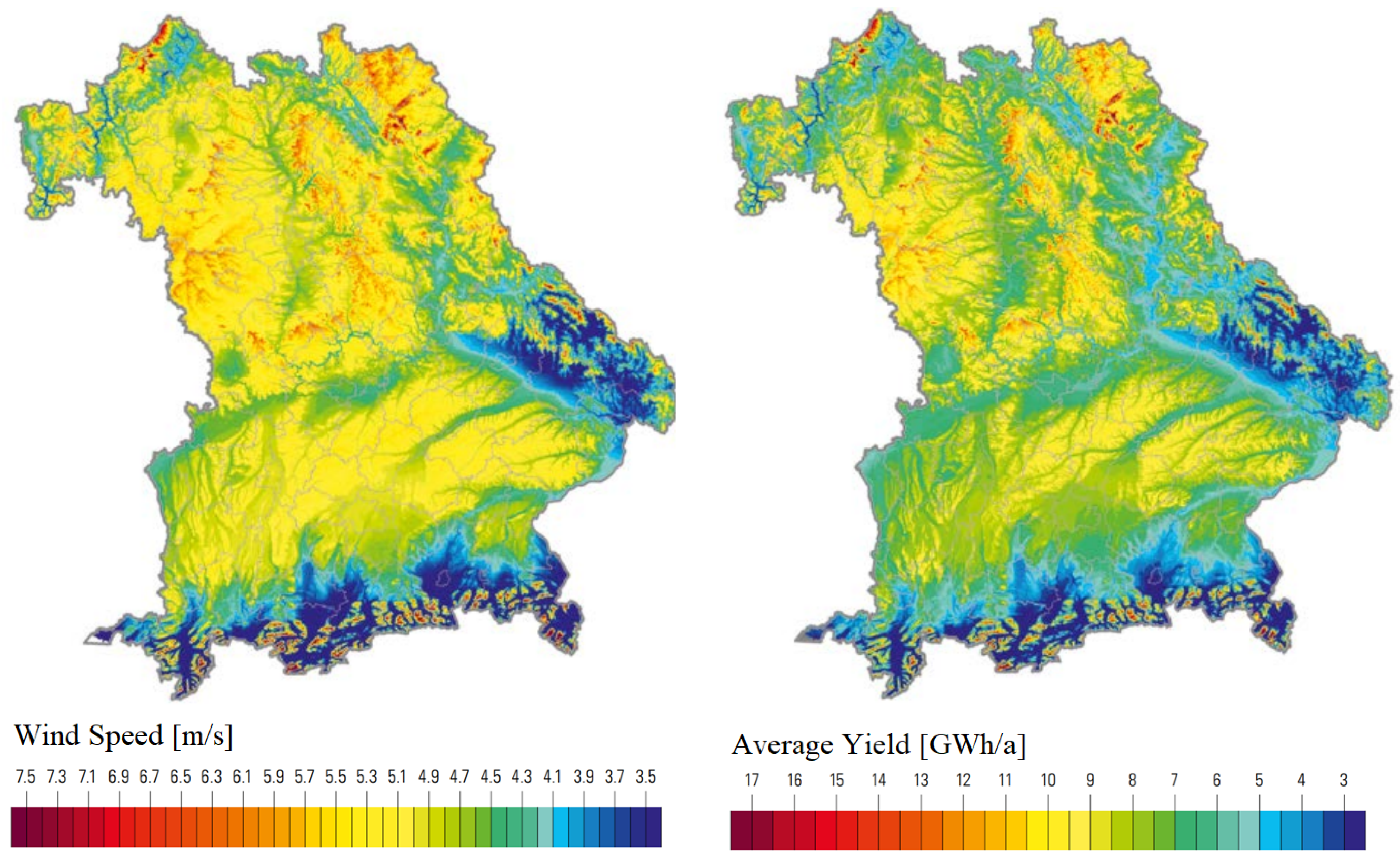
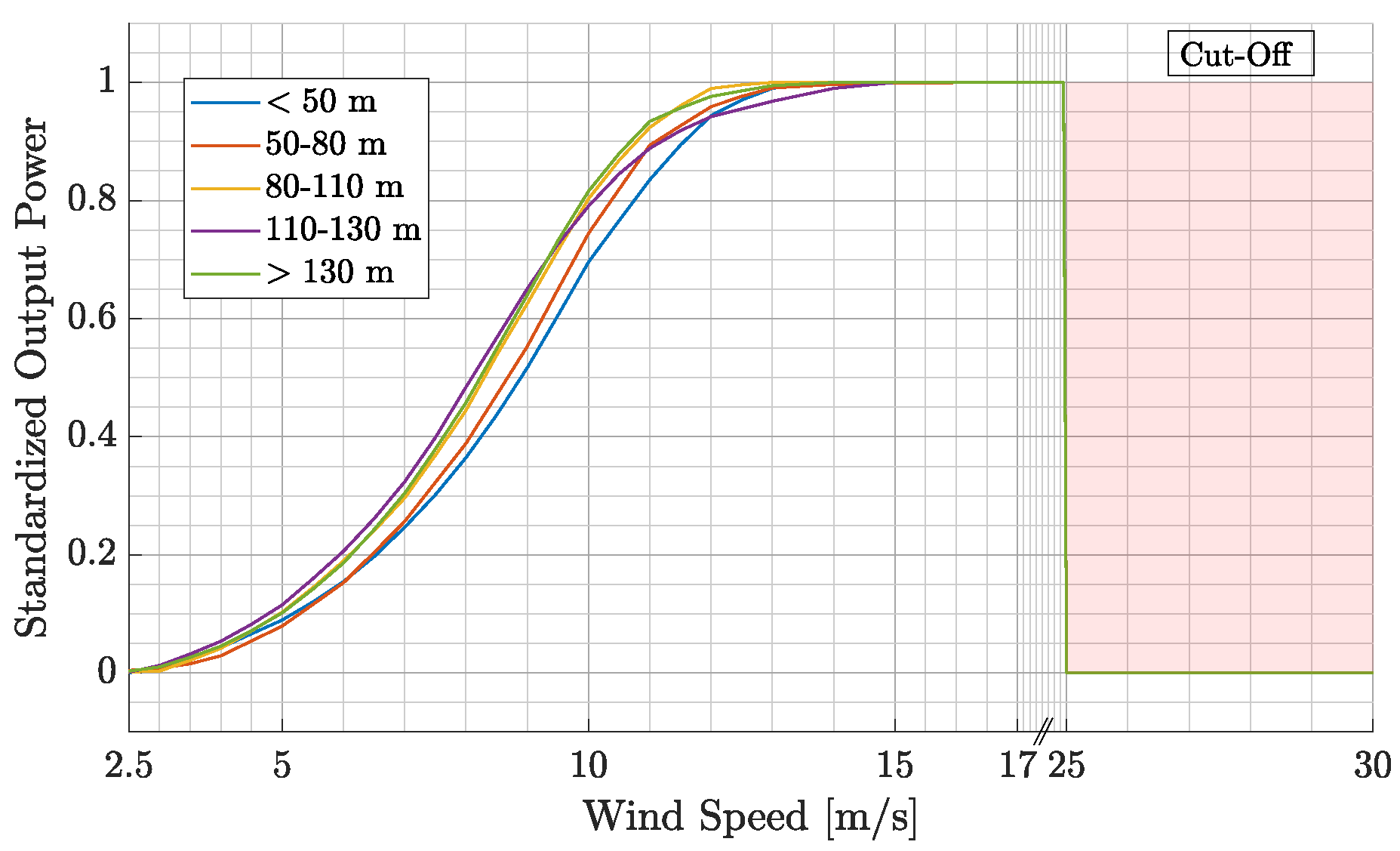
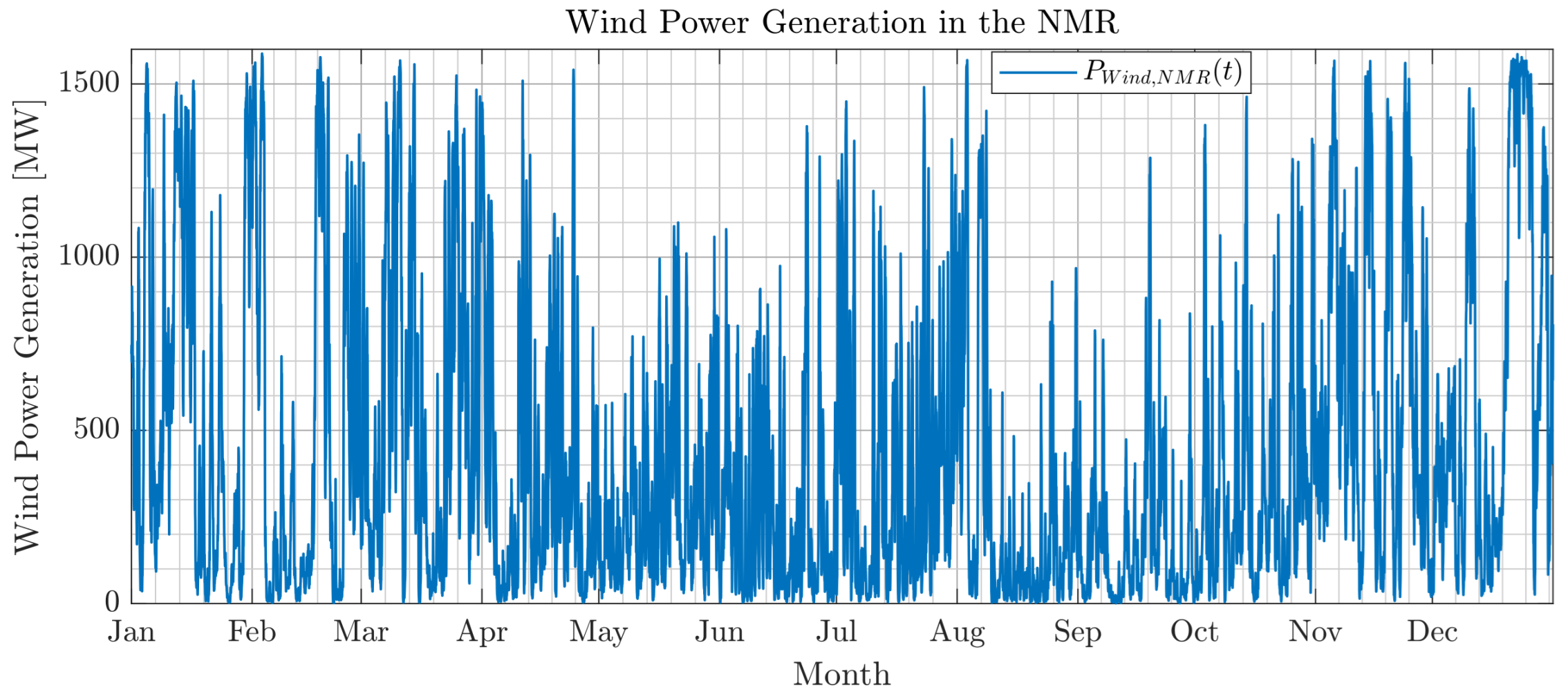
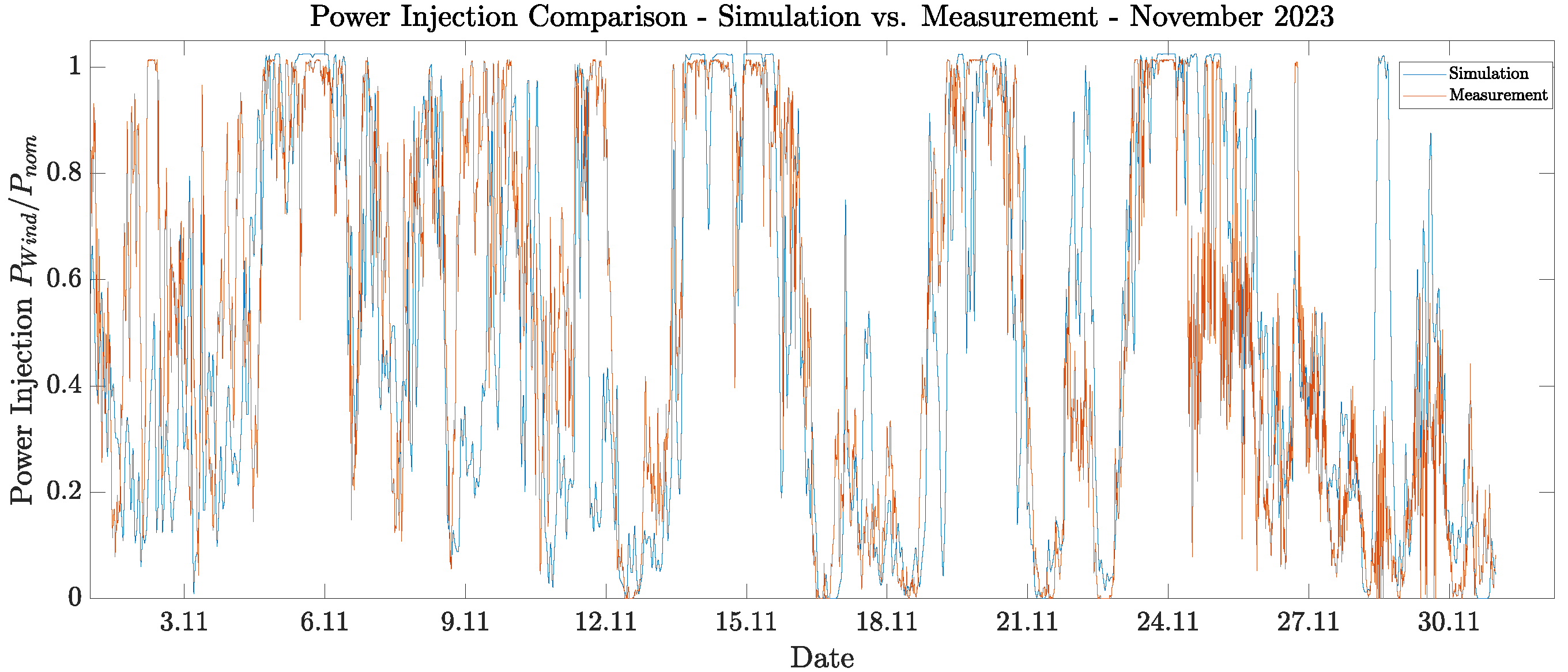
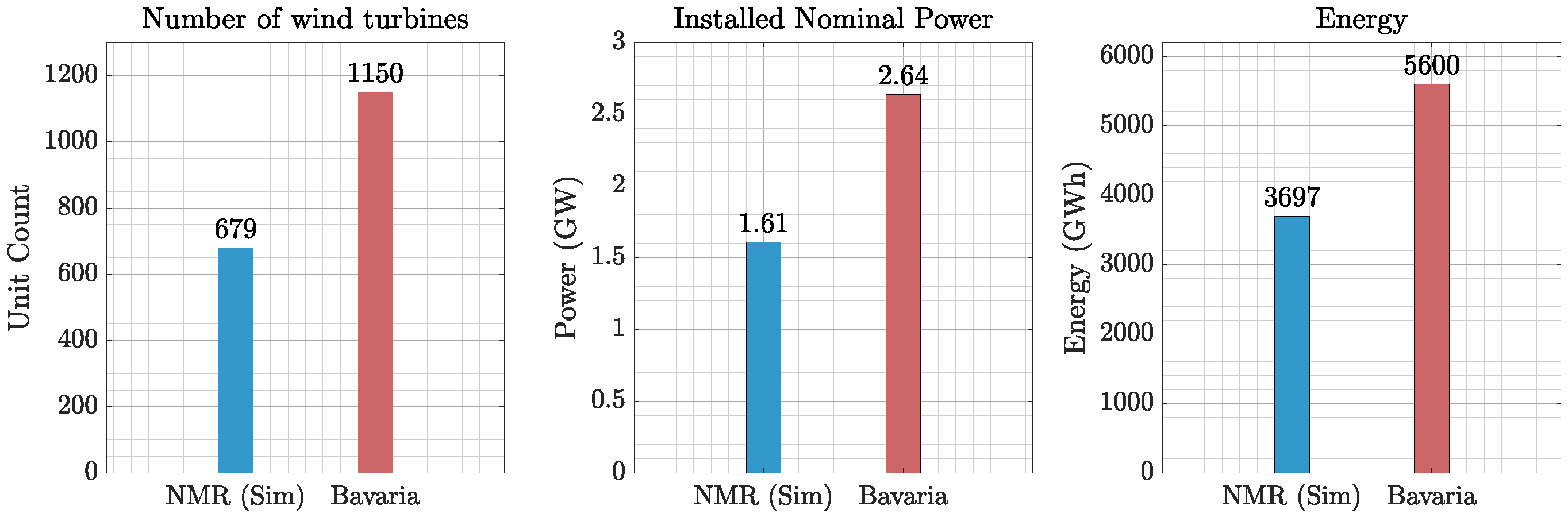
3.2. Wind Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value |
|---|---|
| Vac | 240 |
| Pso | 1.950539 |
| Paco | 300 |
| Pdco | 311.580872 |
| Vdco | 40 |
| C0 | −0.000034 |
| C1 | −0.000256 |
| C2 | 0.002453 |
| C3 | −0.028223 |
| Pnt | 0.09 |
| Vdcmax | 50 |
| Idcmax | 7.789522 |
| Mppt_low | 30 |
| Mppt_high | 50 |
| CEC_Date | — |
| CEC_Type | Utility Interactive |
| Parameter | Value |
|---|---|
| Vintage | 2013 |
| Area | 1.91 |
| Material | c-Si |
| Cells_in_Series | 72 |
| Parallel_Strings | 1 |
| Isco | 8.6388 |
| Voco | 43.5918 |
| Impo | 8.1359 |
| Vmpo | 34.9531 |
| Aisc | 0.0005 |
| Aimp | −0.0001 |
| C0 | 1.0121 |
| C1 | −0.0121 |
| Bvoco | −0.1532 |
| Mbvoc | 0 |
| Bvmpo | −0.1634 |
| Mbvmp | 0 |
| N | 1.0025 |
| C2 | −0.171 |
| C3 | −9.397451 |
| A0 | 0.9371 |
| A1 | 0.06262 |
| A2 | −0.01667 |
| A3 | 0.002168 |
| A4 | −0.0001087 |
| B0 | 1 |
| B1 | −0.00789 |
| B2 | 0.0008656 |
| B3 | −0.00003298 |
| B4 | |
| B5 | − |
| DTC | 3.2 |
| FD | 1 |
| A | −3.6024 |
| B | −0.2106 |
| C4 | — |
| C5 | — |
| IXO | — |
| IXXO | — |
| C6 | — |
| C7 | — |
References
- Iweh, C.D.; Gyamfi, S.; Tanyi, E.; Effah-Donyina, E. Distributed Generation and Renewable Energy Integration into the Grid: Prerequisites, Push Factors, Practical Options, Issues and Merits. Energies 2021, 14, 5375. [Google Scholar] [CrossRef]
- Oyekale, J.; Petrollese, M.; Tola, V.; Cau, G. Impacts of Renewable Energy Resources on Effectiveness of Grid-Integrated Systems: Succinct Review of Current Challenges and Potential Solution Strategies. Energies 2020, 13, 4856. [Google Scholar] [CrossRef]
- Müller, S.; Möst, D.; Fichtner, W. A Spatially Resolved Model of the German Electricity Sector to Evaluate Energy Transition Pathways. Electr. Power Syst. Res. 2018, 164, 177–190. [Google Scholar] [CrossRef]
- Sossan, F.; Bindner, H.; Marinopoulos, A.; Paolone, M. Probabilistic Characterization of Power Flows in Distribution Networks with High Penetration of Renewable Energy Sources. IEEE Trans. Power Syst. 2017, 32, 3464–3474. [Google Scholar]
- Eckardt, T.; Lutz, M.; Schierhorn, P.; Müller, U.P. Impacts of Decentralized Generation on Medium Voltage Grid Planning—A Meso-Scale GIS-Based Assessment. Appl. Energy 2021, 282, 116098. [Google Scholar] [CrossRef]
- Saha, T.K.; Nouri, H.; Pal, B.C. Impact of High Penetration of Renewable Energy Sources on Grid Frequency Behaviour: An Eigenvalue-Based Study. Int. J. Electr. Power Energy Syst. 2022, 141, 108701. [Google Scholar] [CrossRef]
- Metropolregion Nuernberg: Klimapakt2030plus, Simulationsmodell. Available online: https://www.klimapakt2030plus.de/forschung/emn-sim (accessed on 9 January 2025).
- Bundesamt für Kartographie und Geodäsie, Verwaltungsgebiete 1:5,000,000 (VG5000 01.01.), January 2024. Available online: https://gdz.bkg.bund.de/index.php/default/verwaltungsgebiete-1-5-000-000-stand-01-01-vg5000-01-01.html (accessed on 9 January 2025).
- Bundesnetzagentur, Markstammdatenregister. Available online: https://www.marktstammdatenregister.de/MaStR/Datendownload (accessed on 9 January 2025).
- Deutscher Wetterdienst, Solar Observations in Germany. Available online: https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/10_minutes/solar/historical/ (accessed on 9 January 2025).
- Anderson, K.; Hansen, C.; Holmgren, W.; Jensen, A.; Mikofski, M.; Driesse, A. Pvlib python: 2023 project update. J. Open Source Softw. 2023, 8, 5994. [Google Scholar] [CrossRef]
- Jordan, D.; Kurtz, S. Photovoltaic Degradation Rates—An Analytical Review. Prog. Photovoltaics: Res. Appl. 2013, 21, 12–29. [Google Scholar] [CrossRef]
- Deutscher Wetterdienst, Stationskarte. Available online: https://www.dwd.de/DE/fachnutzer/landwirtschaft/appl/stationskarte/_node.html (accessed on 13 January 2025).
- Bayerisches Staatsministerium für Wirtschaft, Landesentwicklung un Energie, Bayerischer Windatlas Potenzial der Windenergie in Bayern, February 2024. Available online: https://www.stmwi.bayern.de/fileadmin/user_upload/stmwi/publikationen/pdf/2024-02-01_Bayerischer_Windatlas_aktualisiert-2024.pdf (accessed on 13 January 2025).
- Deutscher Wetterdienst, Climate Data Center—HOSTRADA Hourly Windspeeds. Available online: https://opendata.dwd.de/climate_environment/CDC/grids_germany/hourly/hostrada/wind_speed/ (accessed on 13 January 2025).
- Deutscher Wetterdiesnst, HOSTRADA. Available online: https://www.dwd.de/DE/leistungen/uhi/info_methodic/01_hostrada.html (accessed on 13 January 2025).
- Quaschning, V. Regenerative Energiesysteme: Technologie-Berechnung-Klimaschutz; Carl Hanser Verlag: München, Germany, 2013; p. 480. ISBN 978-3-446-47777-3. [Google Scholar]
- Christoffer, J.; Ulbricht-Eissing, M. Die Bodennahen Windverhältnisse in der; Deutscher Wetterdienst: Offenbach, Germany, 1989. [Google Scholar]
- Bundesamt für Kartographie und Geodäsie, CORINE Land Cober 5ha (CLC5-2018). Available online: https://gdz.bkg.bund.de/index.php/default/open-data/corine-land-cover-5-ha-stand-2018-clc5-2018.html (accessed on 13 January 2025).
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2n ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wind-Turbine-Models, Windkraftanlagen Datenbank. Available online: https://www.wind-turbine-models.com/turbines (accessed on 13 January 2025).
- The Wind Power—Wind Energy Market Intelligence, E40/600. Available online: https://www.thewindpower.net/turbine_de_173_enercon_e40-600.php (accessed on 13 January 2025).
- Energieagentur Nordbayern, Energienutzungsplan Europäische Metropolregion Nürnberg, August 2019. Available online: https://klimaschutz.metropolregionnuernberg.de/fileadmin/media/mediathek-klimaschutz/downloads/studien/2019-10-Energienutzungsplan.pdf (accessed on 13 January 2025).
- Solarenergie-Förderverein, Ertragsdatenbank für Solarstrom. Available online: https://ertragsdatenbank.de/auswertung/region.html?j=2023&r=9&a=kurz (accessed on 13 January 2025).
- Heesen, H. Photovoltaik-Ertragsstudie 2020: Regionale Erträge und Performance von PV-Anlagen in Deutschland; Umwelt-Campus Birkenfeld: Hoppstädten-Weiersbach, Germany, 2020; Available online: https://www.umwelt-campus.de/fileadmin/Umwelt-Campus/User/HteHeesen/research/pv/Ertragsstudie_2020.pdf (accessed on 15 June 2025).
- Deutsche WindGuard, Anzahl der Windenergieanlagen in Bayern in den Jahren 2000 bis 2023, January 2024. Available online: https://de.statista.com/statistik/daten/studie/28315/umfrage/anzahl-der-windenergieanlagen-in-bayern-seit-1989/ (accessed on 14 January 2025).
- Deutsche WindGuard, Kumulierte Nennleistung der Windenergieanlagen in Bayern in den Jahren 2000 bis 2023 (in Megawatt), January 2024. Available online: https://de.statista.com/statistik/daten/studie/28176/umfrage/installierte-leistung-durch-windenergie-in-bayern-seit-1989/ (accessed on 14 January 2025).
- Bayerisches Staatsministerium für Wirtschaft, Landesentwicklung und Energie, Windenergie in Bayern. Available online: https://www.stmwi.bayern.de/energie/erneuerbare-energien/windenergie/#:~:text=Windenergieanlagen%20haben%20einen%20geringen%20Fl%C3%A4chenbedarf,2023%20betrug%205%2C6%20TWh%20 (accessed on 15 January 2025).
- Bundesnetzagentur SMARD, Energiemarkt Aktuell–Netzengpassmangement im Jahr 2023, May 2024. Available online: https://www.smard.de/page/home/topic-article/444/213590 (accessed on 15 January 2025).
- Bundesnetzagentur, Bundesnetzagentur Veröffentlicht Daten zum Strommarkt 2023, January 2024. Available online: https://www.bundesnetzagentur.de/SharedDocs/Pressemitteilungen/DE/2024/20240103_SMARD.html#:~:text=Insgesamt%20lag%20in%202023%20die,(100%2C6%20TWh%20) (accessed on 15 January 2025).
- Bundesverband WindEnergie e.V. (BWE). Flächenpotenziale für die Windenergie an Land: Analyse und Ausblick; Bundesverband WindEnergie e.V. (BWE): Berlin, Germany, 2022; Available online: https://www.wind-energie.de/fileadmin/redaktion/dokumente/publikationen-oeffentlich/themen/01-mensch-und-umwelt/02-planung/20220920_BWE_Flaechenpotentiale_Windenergie_an_Land.pdf (accessed on 15 June 2025).





| CLC ID | CLC-Class Name | Class | |
|---|---|---|---|
| 112 | Discontinuous urban fabric | Regularly covered with obstacles (forests, villages, suburbs) | 1 |
| 121 | Industrial or commercial units and public facilities | Regularly covered with obstacles (forests, villages, suburbs) | 1 |
| 211 | Non-irrigated arable land | Agricultural areas with low vegetation cover | 0.1 |
| 231 | Pastures, meadows and other permanent grasslands under agricultural use | Open flat terrain, grasslands | 0.03 |
| 311 | Broad-leaved forest | Regularly covered with obstacles (forests, villages, suburbs) | 1 |
| 312 | Coniferous forest | Regularly covered with obstacles (forests, villages, suburbs) | 1 |
| 313 | Mixed forest | Regularly covered with obstacles (forests, villages, suburbs) | 1 |
| 324 | Transitional woodland/shrub | Park landscapes with bushes and trees | 0.5 |
| Height [m] | Turbine Types |
|---|---|
| <50 | E40, LW52/750 |
| 50–80 | E40, D4, E53, V47 |
| 80–110 | E82, V90, MD77, NM82 |
| 110–130 | E70, V90, N117 |
| <130 | E82, N117, V112, E101 |
| Zip/Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Annual | Note |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 90XXX | 17 | 52 | 73 | 93 | 130 | 143 | 124 | 101 | 115 | 62 | 26 | 16 | 953 | |
| 91XXX | 17 | 52 | 73 | 93 | 130 | 143 | 124 | 101 | 115 | 62 | 26 | 16 | 953 | |
| 92XXX | 19 | 46 | 70 | 89 | 128 | 137 | 129 | 108 | 114 | 66 | 27 | 13 | 947 | |
| 95XXX | 16 | 51 | 69 | 97 | 140 | 146 | 136 | 116 | 127 | 65 | 20 | 13 | 996 | Max |
| 96XXX | 12 | 35 | 60 | 89 | 129 | 135 | 122 | 102 | 106 | 53 | 19 | 10 | 870 | Min |
| 97XXX | 16 | 46 | 75 | 99 | 130 | 144 | 126 | 106 | 111 | 57 | 22 | 14 | 945 | |
| Zip Mean: | 16.2 | 47.0 | 70.0 | 93.3 | 131.2 | 141.3 | 126.8 | 105.7 | 114.7 | 60.8 | 23.3 | 13.7 | 944.0 | |
| Simulation | 18.1 | 45.3 | 70.3 | 95.2 | 134.9 | 144.9 | 131.0 | 107.0 | 112.1 | 58.9 | 26.0 | 16.2 | 960.0 | Average |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bottler, S.; Weindl, C. Modeling Renewable Energy Feed-In Dynamics in a German Metropolitan Region. Processes 2025, 13, 2270. https://doi.org/10.3390/pr13072270
Bottler S, Weindl C. Modeling Renewable Energy Feed-In Dynamics in a German Metropolitan Region. Processes. 2025; 13(7):2270. https://doi.org/10.3390/pr13072270
Chicago/Turabian StyleBottler, Sebastian, and Christian Weindl. 2025. "Modeling Renewable Energy Feed-In Dynamics in a German Metropolitan Region" Processes 13, no. 7: 2270. https://doi.org/10.3390/pr13072270
APA StyleBottler, S., & Weindl, C. (2025). Modeling Renewable Energy Feed-In Dynamics in a German Metropolitan Region. Processes, 13(7), 2270. https://doi.org/10.3390/pr13072270





