Optimizing Perforated Duct Systems for Energy-Efficient Ventilation in Semi-Closed Greenhouses Through Process Regulation
Abstract
1. Introduction
2. Materials and Methods
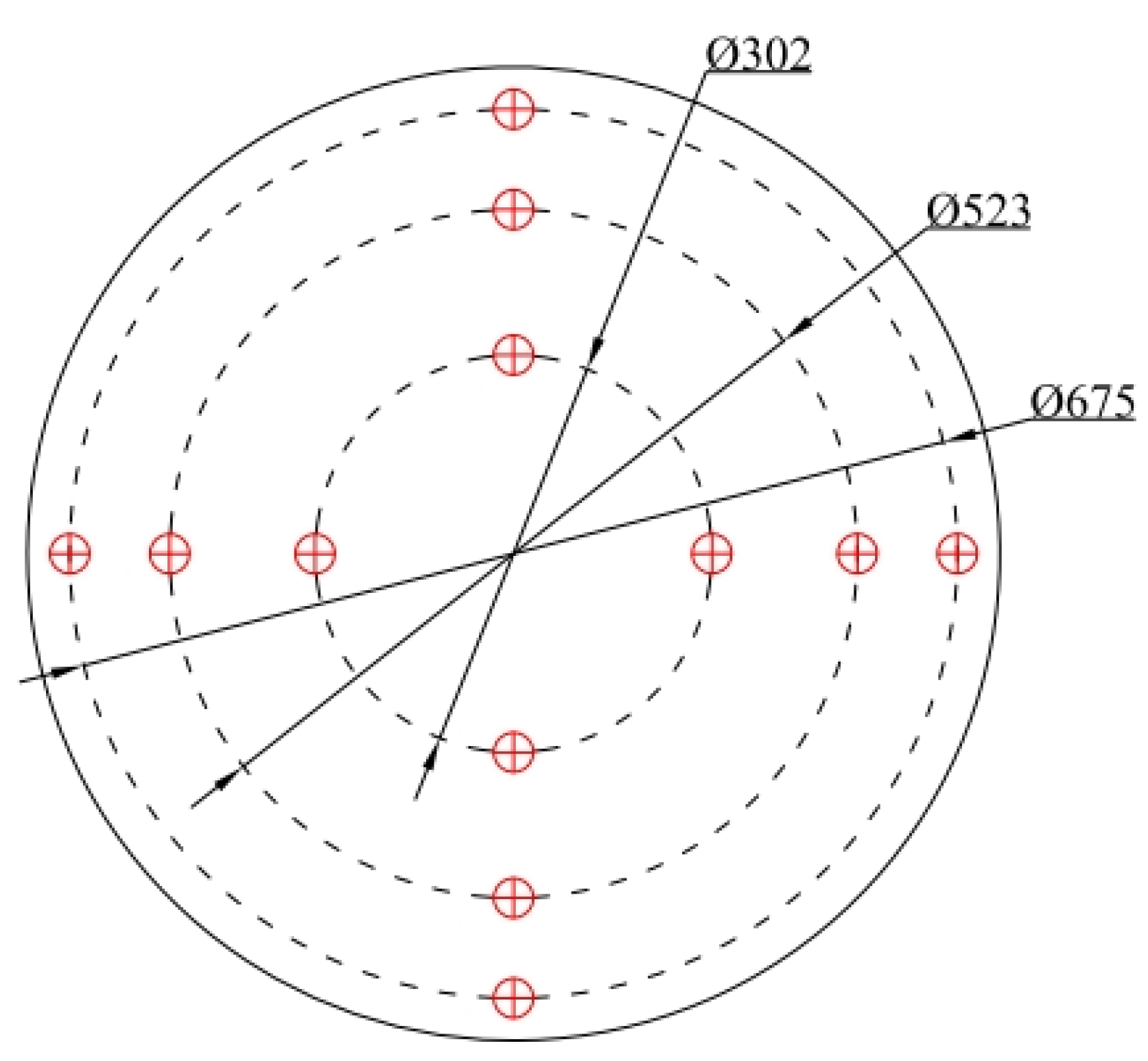
2.1. Physical Model Construction
2.2. CFD Model Construction
2.2.1. Mathematical Model
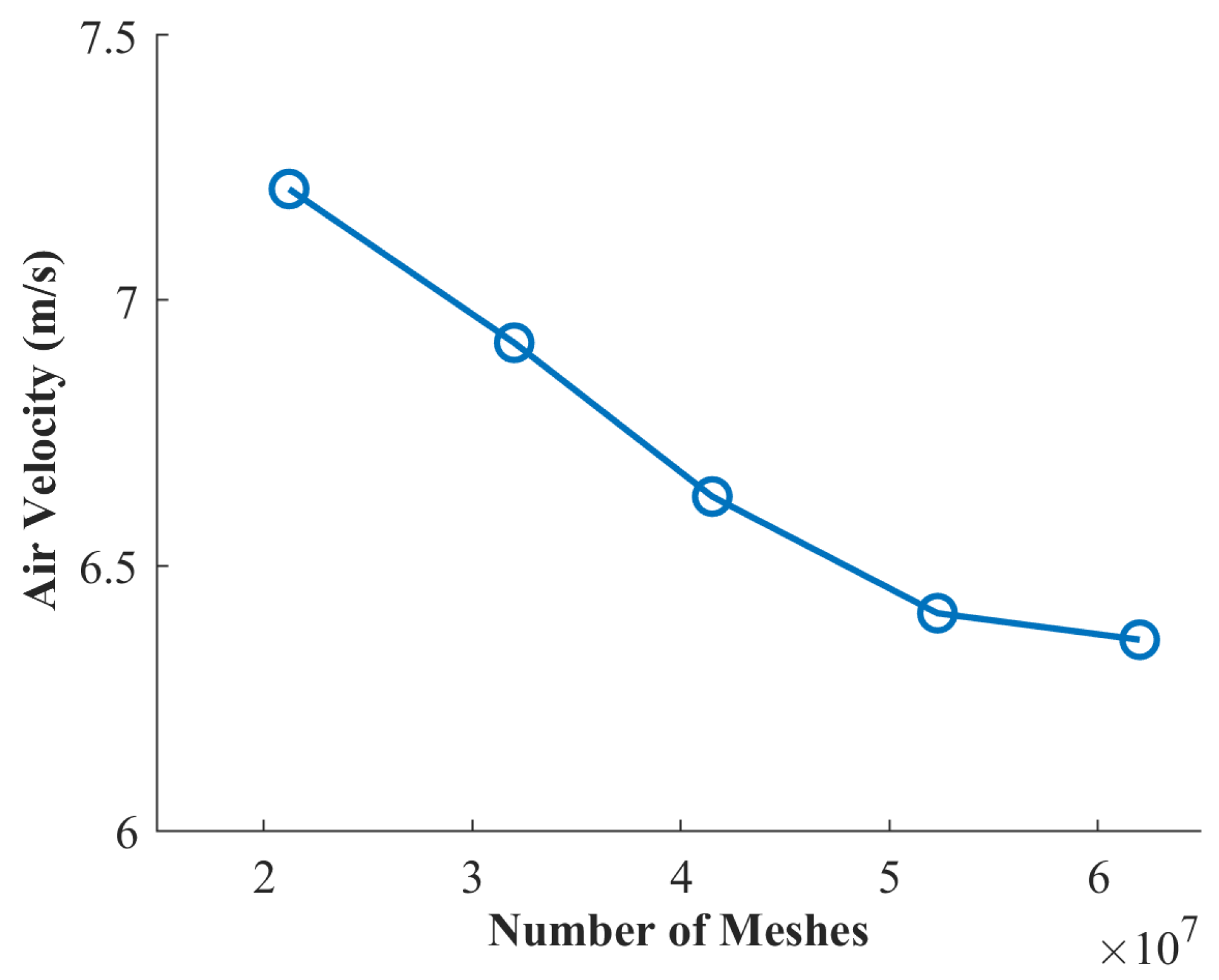
2.2.2. Mesh Generation and Independence Verification
2.2.3. Boundary Conditions and Solver Settings
2.3. Parameter Design
2.3.1. Velocity Design
2.3.2. Duct Parameter Design
2.3.3. Power Consumption Calculation
2.4. Response Surface Analysis
2.5. Multi-Objective Optimization
2.5.1. NSGA-II
2.5.2. Decision-Making Via Entropy-Weighted TOPSIS
2.6. Data Acquisition
2.6.1. Test Conditions
2.6.2. Test Method
3. Results and Discussion
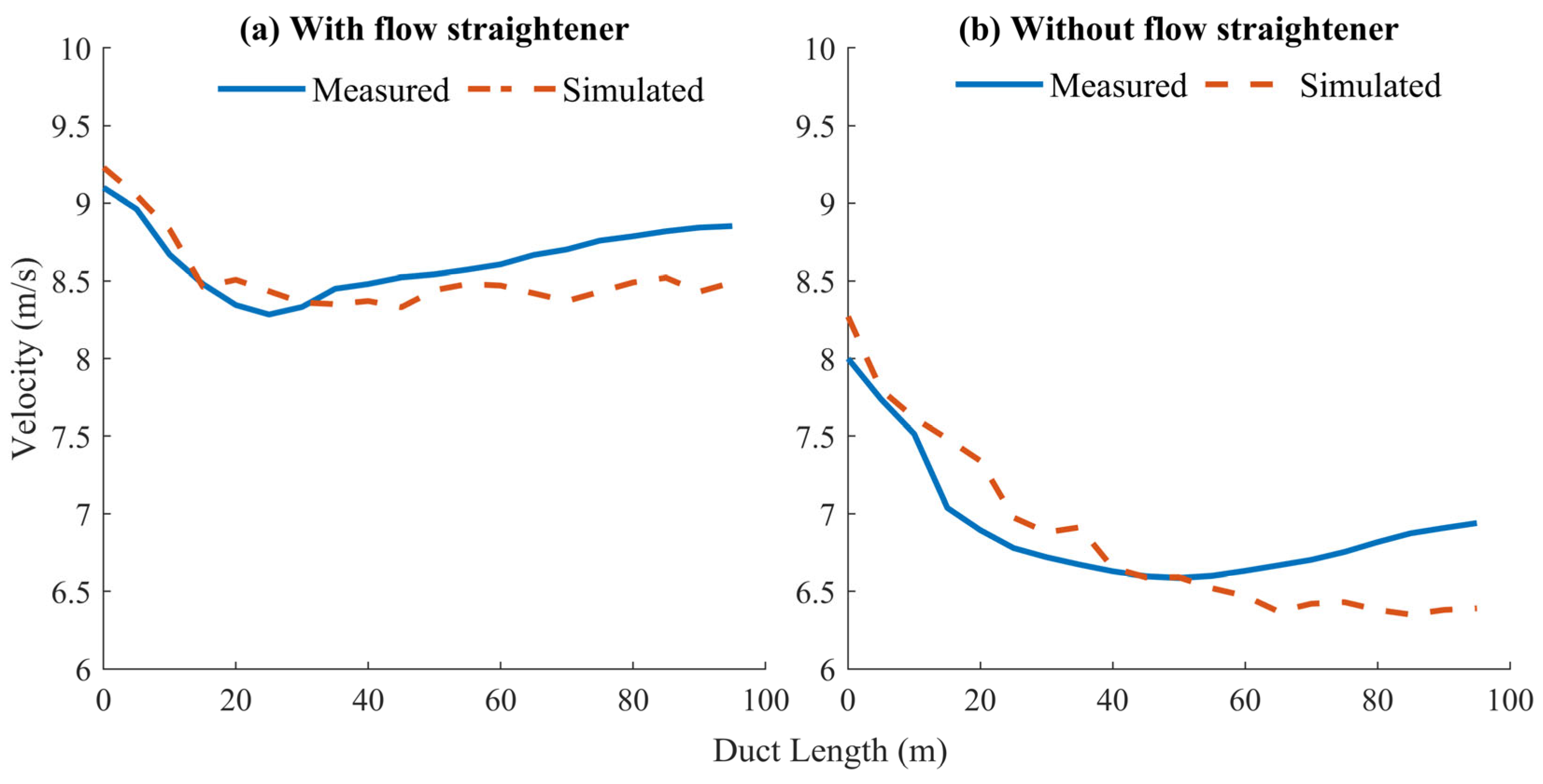
3.1. Model Validation
3.2. Single-Factor Analysis
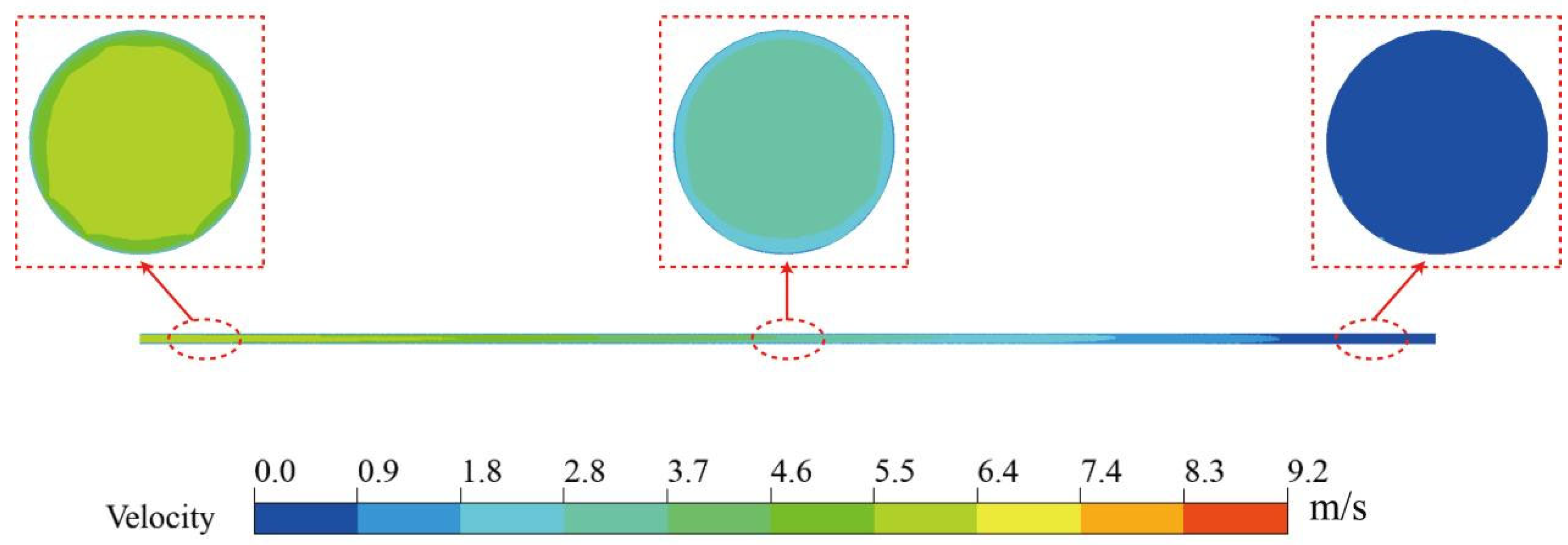
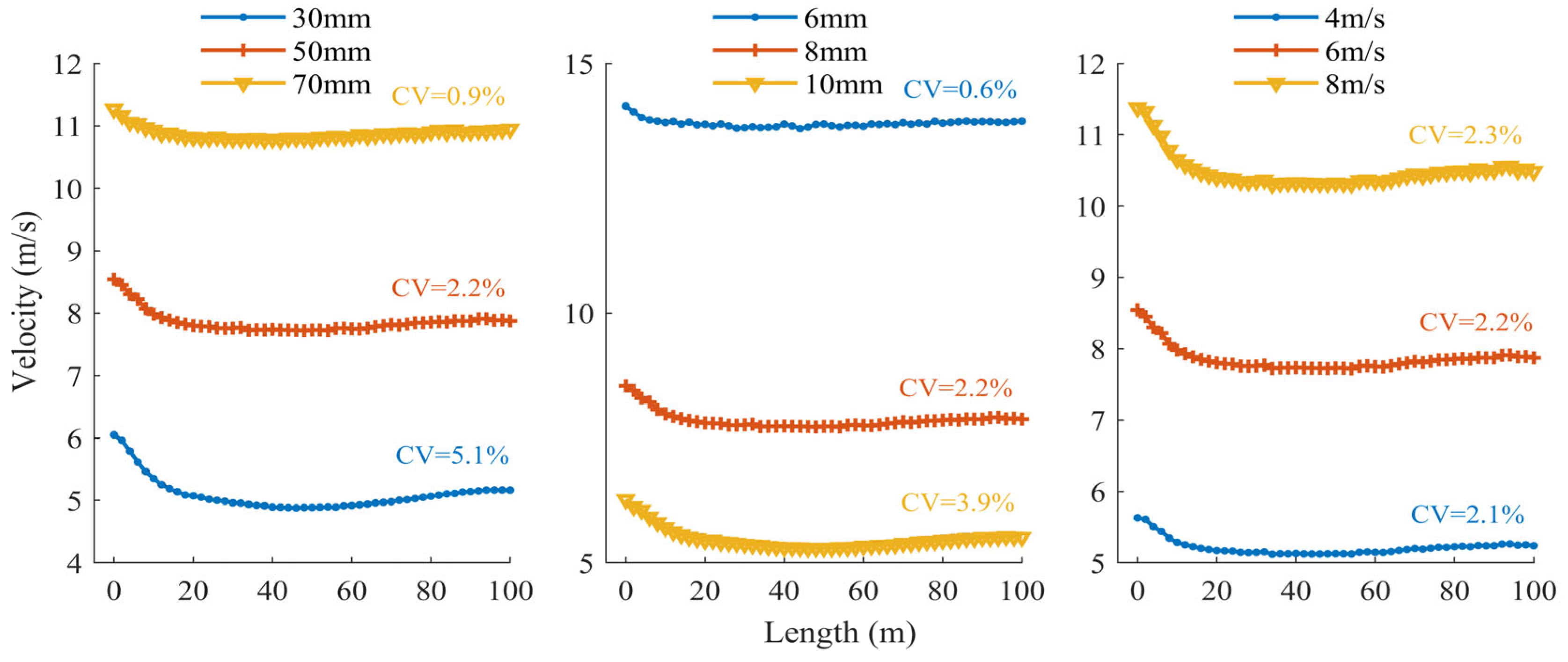
3.2.1. Velocity Field
3.2.2. Pressure Field
3.2.3. Temperature Field
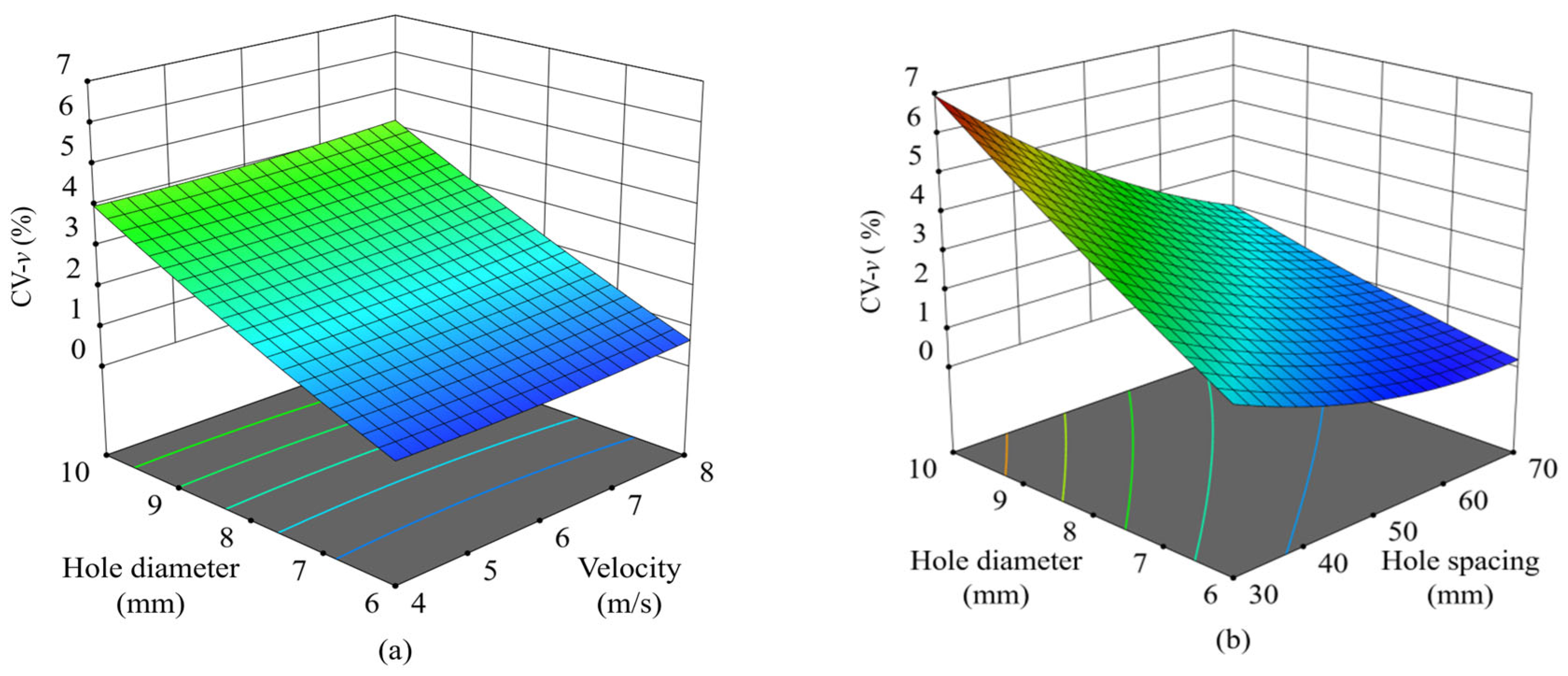
3.3. Response Surface
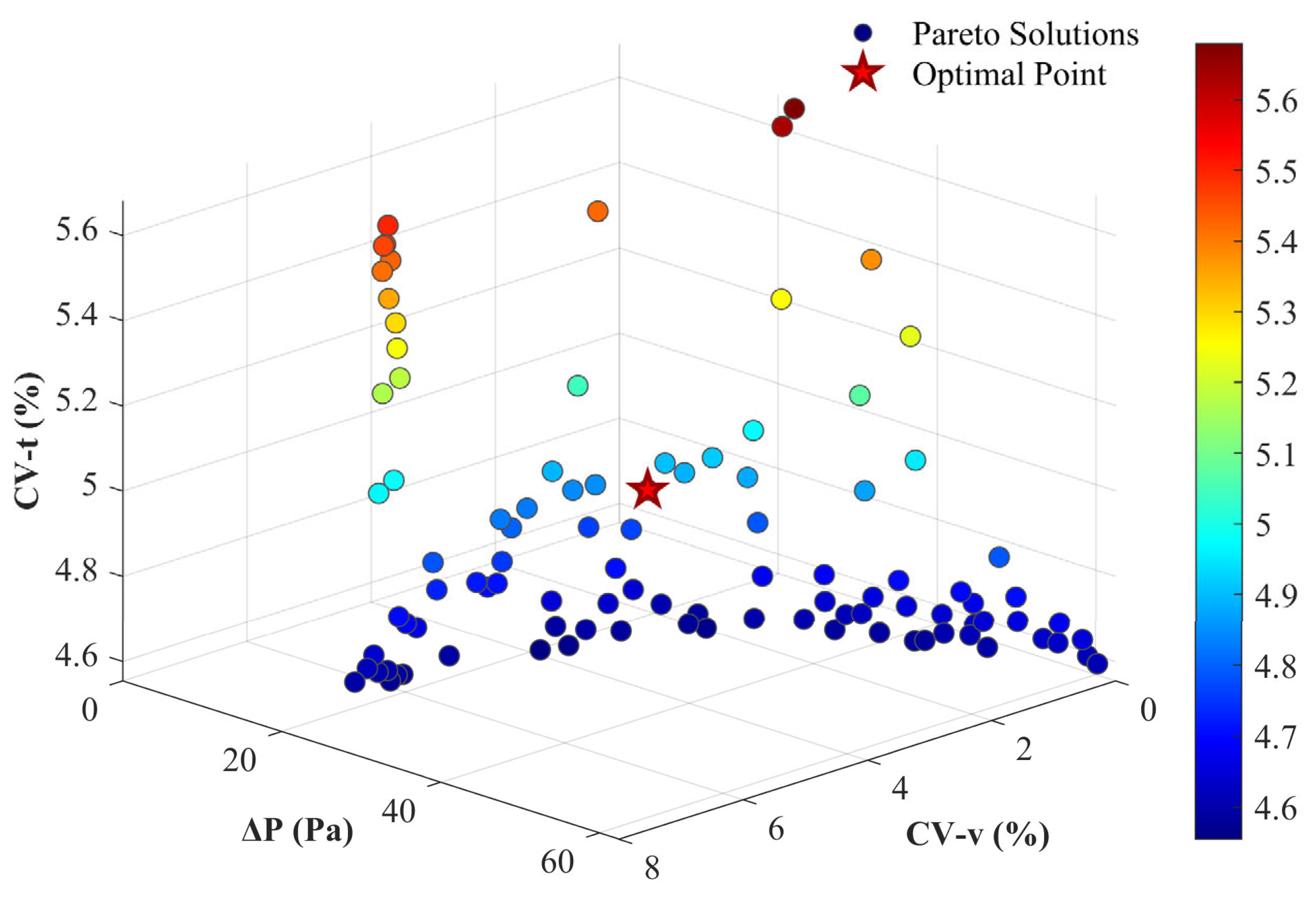
3.4. Parameter Optimization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Uncertainty Assessment
Appendix A.1.1. Type A Uncertainty
Appendix A.1.2. Type B Uncertainty
- Instrument Calibration Error
| Parameter | Error Limit °C | |
|---|---|---|
| Wind Speed Sensor | 0.5% FS | 0.19 m/s |
| Pressure Sensor | 0.5% FS | 0.46 Pa |
| Temperature Sensor | 0.2 °C | 0.12 °C |
- Probe Positioning Error
- Combined Type B Uncertainty
Appendix A.1.3. Combined Standard Uncertainty
Appendix A.1.4. Expanded Uncertainty
Appendix B
Appendix B.1. Materials and Methods
Appendix B.1.1. Experimental Setup

Appendix B.1.2. CFD Model
Appendix B.2. Model Validation
References
- Dijk, M.V.; Morley, T.; Rau, M.L.; Saghai, Y. A meta-analysis of projected global food demand and population at risk of hunger for the period 2010–2050. Nat. Food 2021, 2, 494–501. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Wei, R.; Xu, L. Energy consumption prediction of a greenhouse and optimization of daily average temperature. Energies 2018, 11, 65. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Wang, C.D.; Zheng, G.; Zhang, T.Z. Design and experiment of the positive pressure ventilation cooling system in glass multi-span greenhouse. J. Chin. Agric. Univ. 2020, 25, 152–162. [Google Scholar] [CrossRef]
- Sapounas, A.; Katsoulas, N.; Slager, B.; Bezemer, R.; Lelieveld, C. Design, control, and performance aspects of semi-closed greenhouses. Agronomy 2020, 10, 1739. [Google Scholar] [CrossRef]
- Park, M.-L.; Jeong, J.-W. Review of semi-closed greenhouse previous studies and required technology analysis for improving energy efficiency. KIEAE J. 2022, 22, 21–27. [Google Scholar] [CrossRef]
- Sannan, S.; Jerca, I.O.; Badulescu, L.A. A CFD study of the fluid flow through air distribution hoses in a greenhouse. Chem. Eng. Trans. 2023, 100, 385–390. [Google Scholar] [CrossRef]
- Tadj, N.; Nahal, M.A.; Constantinos, K.; Draoui, B. CFD simulation of heating greenhouse using a perforated polyethylene ducts. Int. J. Eng. Syst. Model. Simul. 2017, 9, 3–11. [Google Scholar] [CrossRef]
- Pardo-Pina, S.; Ferrández-Pastor, J.; Rodríguez, F.; Cámara-Zapata, J. Analysis of an evaporative cooling pad connected to an air distribution system of perforated polyethylene tubes in a greenhouse. Agronomy 2024, 14, 1187. [Google Scholar] [CrossRef]
- Lu, X.Y.; Yu, C.J. Simulation and experimental study of the air distribution characteristics of large-span film air duct in greenhouses. Trans. Chin. Soc. Agric. Eng. 2024, 40, 204–211. [Google Scholar] [CrossRef]
- Coomans, M.; Allaerts, K.; Wittemans, L.; Pinxteren, D. Monitoring and energetic performance of two similar semi-closed greenhouse ventilation systems. Energy Convers. Manag. 2013, 76, 128–136. [Google Scholar] [CrossRef]
- Mahmood, F.; Govindan, R.; Bermak, A.; Yang, D.; Khadra, C.; Al-Ansari, T. Energy utilization assessment of a semi-closed greenhouse using data-driven model predictive control. J. Clean. Prod. 2021, 324, 129172. [Google Scholar] [CrossRef]
- Moueddeb, K.E.; Barrington, S.; Barthakur, N. Perforated ventilation ducts: Part 1, a model for air flow distribution. J. Agric. Eng. Res. 1997, 68, 21–27. [Google Scholar] [CrossRef]
- Saunders, D.D.; Albright, L.D. Airflow from perforated polyethylene tubes. Trans. ASABE 1984, 27, 1144–1149. [Google Scholar] [CrossRef]
- Wells, C.M.; Amos, N.D. Design of air distribution systems for closed greenhouses. Acta Hortic. 1994, 361, 93–104. [Google Scholar] [CrossRef]
- El Moueddeb, K.; Barrington, S.; Barthakur, N. Perforated ventilation ducts: Part 2, Validation of an air distribution model. J. Agric. Eng. Res. 1997, 68, 29–37. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, Y.; Jiao, P.; Ling, Z. Study on Pressure Loss for a Muffler Based on CFD and Experiment. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 11–12 April 2009. [Google Scholar]
- Hu, X.Z.; Cheng, S.M.; Liu, S.J. Research on pressure loss of bypass perforated tube muffler. Mach. Tool. Hydraul. 2016, 44, 59–63. [Google Scholar] [CrossRef]
- Ibuki, R.; Behnia, M. Optimization of air flow circulation with branching perforating duct and fan system. Acta Hortic. 2013, 1008, 241–247. [Google Scholar] [CrossRef]
- MacKinnon, I.R. Air Distribution from Ventilation Ducts; McGill University: Montreal, QC, Canada, 1990. [Google Scholar]
- Gu, H.; Qian, J.; Li, S.; Jiang, Z.; Wang, X.; Li, J.; Yang, X. Design and optimization of air inlet in cuttings incubator. Agronomy 2024, 14, 871. [Google Scholar] [CrossRef]
- Safikhani, H. Modeling and multi-objective Pareto optimization of new cyclone separators using CFD, ANNs and NSGA II algorithm. Adv. Powder Technol. 2016, 27, 2277–2284. [Google Scholar] [CrossRef]
- Immonen, E. Shape optimization of annular S-ducts by CFD and high-order polynomial response surfaces. Eng. Comput. 2018, 35, 932–954. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Yin, S.; Jin, D.; Gui, X.; Zhu, F. Application and comparison of SST model in numerical simulation of the axial compressors. J. Therm. Sci. 2010, 19, 300–309. [Google Scholar] [CrossRef]
- ANSI/ASAE EP406.4; Heating, Ventilating and Cooling Greenhouses; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2008.
- Brown, G.O. The history of the darcy-weisbach equation for pipe flow resistance. In Proceedings of the ASCE Civil Engineering Conference and Exposition 2002, Washington, DC, USA, 3 November 2012. [Google Scholar] [CrossRef]
- Fatnassi, H.; Leyronas, C.; Boulard, T.; Bardin, M.; Nicot, P. Dependence of greenhouse tunnel ventilation on wind direction and crop height. Biosyst. Eng. 2009, 103, 338–343. [Google Scholar] [CrossRef]
- Liu, T.S.; Liu, J.; Wang, M.Z.; Jin, W.; Chen, Z.H.; Yang, S.T. Design and cooling effect of cooling fan-duct displacement ventilation system with up-fixing diffusers in beef cattle barn. Trans. CSAE 2014, 30, 240–249. [Google Scholar] [CrossRef]
- Zhang, Y.; Kacira, M. Air distribution and its uniformity. In Smart Plant Factory; Kozai, T., Ed.; Springer: Singapore, 2018; pp. 153–166. [Google Scholar] [CrossRef]
- Harel, D.; Fadida, H.; Slepoy, A.; Gantz, S.; Shilo, K. The effect of mean daily temperature and relative humidity on pollen, fruit set and yield of tomato grown in commercial protected cultivation. Agronomy 2014, 4, 167–177. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Riquelme, N.; Von Lücken, C.; Baran, B. Performance metrics in multi-objective optimization. In Proceedings of the 2015 Latin American Computing Conference (CLEI), Arequipa, Peru, 19–23 October 2015; pp. 1–11. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 2002, 3, 257–271. [Google Scholar] [CrossRef]
- Liu, J.; Lin, Z. Optimization of configurative parameters of stratum ventilated heating for a sleeping environment. J. Build. Eng. 2021, 38, 102167. [Google Scholar] [CrossRef]
- Suhardiyanto, H.; Matsuoka, T. Uniformity of cool air discharge along a perforated tube for zone cooling in a greenhouse. Environ. Control Biol. 1994, 32, 9–16. [Google Scholar] [CrossRef]
- El Moueddeb, K.; Barrington, S.; Barthakur, N.N. Modeling Fan and perforated ventilation ducts for airflow balance point. Trans. ASAE 1998, 41, 1131–1137. [Google Scholar] [CrossRef]
- Lee, S.; Moon, N.; Lee, J. Experimental research on the uniformity of air supply in long permeation-ejection fabric air dispersion system. J. Mech. Sci. Technol. 2012, 26, 2751–2758. [Google Scholar] [CrossRef]
- Wang, X.S.; Wu, L.Y.; Liu, D. A study on the exit flow characteristics determined by the orifice configuration of multi-perforated tubes. Build. Energy Environ. 2021, 40, 68–72. [Google Scholar] [CrossRef]












| governing equation | S | ||
| mass conservation | 1 | 0 | 0 |
| momentum equation | |||
| energy equation | T |
| Hole diameter (mm) | 6 | 8 | 10 |
| Theoretical spacing (mm) | 13.3~66.7 | 17.8~88.9 | 22.2~111.0 |
| −1 | 0 | 1 | |
|---|---|---|---|
| A: Velocity (m/s) | 4 | 6 | 8 |
| B: Hole space (mm) | 30 | 50 | 70 |
| C: Hole diameter (mm) | 6 | 8 | 10 |
| Y1 (CV-v) | Y2 (ΔP) | Y3 (CV-t) | ||||
|---|---|---|---|---|---|---|
| F-Value | F-Value | F-Value | p-Value | F-Value | p-Value | |
| Model | 88.25 | 74.93 | 50.5 | <0.0001 | 74.93 | <0.0001 |
| A | 0.5662 | 659.84 | 200.05 | <0.0001 | 659.84 | <0.0001 |
| B | 344.33 | 1.52 | 55.67 | <0.0001 | 1.52 | 0.2576 |
| C | 390.57 | 4.04 | 112.14 | <0.0001 | 4.04 | 0.0843 |
| AB | 0.0016 | 1.02 | 8.06 | 0.0001 | 1.02 | 0.3465 |
| AC | 0.0681 | 0.4124 | 15.15 | <0.0001 | 0.4124 | 0.5412 |
| BC | 41.02 | 0.0337 | 52.65 | <0.0001 | 0.0337 | 0.8596 |
| A2 | 0.4131 | 6.08 | 0.0946 | 0.0039 | 6.08 | 0.0431 |
| B2 | 15.51 | 0.7498 | 0.8115 | 0.1244 | 0.7498 | 0.4152 |
| C2 | 0.9058 | 0.2395 | 9.6 | 0.0279 | 0.2395 | 0.6395 |
| Lack of Fit | 2.39 | 0.2675 | 3.0 | 0.1582 | 0.2675 | 0.8463 |
| Indicator | Pre-Optimization | Post-Optimization | Rate of Change |
|---|---|---|---|
| CV-v (%) | 4.64 | 1.91 | −58.83% |
| ΔP (Pa) | 23.7 | 21.15 | −10.76% |
| CV-t (%) | 4.57 | 4.82 | +5.18% |
| 7.74 | 6.39 | −17.44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Fu, J.; Zhang, Q.; Sheng, B.; He, F.; Zhang, G.; Ding, X.; Cao, N. Optimizing Perforated Duct Systems for Energy-Efficient Ventilation in Semi-Closed Greenhouses Through Process Regulation. Processes 2025, 13, 2253. https://doi.org/10.3390/pr13072253
Wang C, Fu J, Zhang Q, Sheng B, He F, Zhang G, Ding X, Cao N. Optimizing Perforated Duct Systems for Energy-Efficient Ventilation in Semi-Closed Greenhouses Through Process Regulation. Processes. 2025; 13(7):2253. https://doi.org/10.3390/pr13072253
Chicago/Turabian StyleWang, Chuanqing, Jianlu Fu, Qiusheng Zhang, Baoyong Sheng, Fen He, Guanshan Zhang, Xiaoming Ding, and Nan Cao. 2025. "Optimizing Perforated Duct Systems for Energy-Efficient Ventilation in Semi-Closed Greenhouses Through Process Regulation" Processes 13, no. 7: 2253. https://doi.org/10.3390/pr13072253
APA StyleWang, C., Fu, J., Zhang, Q., Sheng, B., He, F., Zhang, G., Ding, X., & Cao, N. (2025). Optimizing Perforated Duct Systems for Energy-Efficient Ventilation in Semi-Closed Greenhouses Through Process Regulation. Processes, 13(7), 2253. https://doi.org/10.3390/pr13072253






