Hybrid Cloud-Based Information and Control System Using LSTM-DNN Neural Networks for Optimization of Metallurgical Production
Abstract
1. Introduction
2. Proposed Method
2.1. Mathematical Foundations for Error Detection and Correction
2.2. Algorithm for Processing Redundant Measurements
2.3. Integration of Hybrid Neural Network LSTM-DNN
- Hybrid neural networks can be used as a tool for the detection and correction of systematic errors. LSTM-DNN can analyze the time series of measurements and identify patterns that are not visible in traditional data processing [30]. This allows for the detection of systematic deviations in parameters arising from sensory drift, sensor degradation, and calibration errors. Deep neural networks (DNNs) are good at analyzing complex nonlinear relationships, which makes it possible to identify the hidden dependencies between technological parameters and their measurement errors [31,32].
- Automatic error correction. Hybrid models can predict true parameter values based on historical data, compensating for errors in measurements [33]. Unlike the traditional statistical analysis methods (e.g., noise filtering using Kalman methods), LSTM-DNN is trained on real data and can adapt to changing process conditions.
- “-”—limited applicability or a lack of the property;
- “+”—the presence of the property in the base form;
- “++”—a pronounced advantage of the model for the relevant criterion.
- Temperature in the heat treatment zone (T_furnace);
- Vibration level at the mill (Vibration_level_mill);
- Oxygen content (O2_content);
- Pulp acidity (pH);
- Reagent and fuel consumption.
2.4. Cloud Infrastructure and Model Deployment
3. Experimental Results
Practical Application in Metallurgy
- The data acquisition and pre-processing module.
- The Cloud Management Layer module (Cloud Management Layer).
- The data storage and management module (Data Lake/Data Warehouse).
- The information assurance module (Error Detection and Correction).
- The Artificial Intelligence Module (AI Engine).
- The business logic and decision-making module.
- The visualization and report generation module.
- The security and access control module.
- The integration module with external systems.
- The Operational Services and Administration Module.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gulyamov, S.M.; Temerbekova, B.M.; Mamanazarov, U.B. Noise Immunity Criterion for the Development of a Complex Automated Technological Process. E3S Web Conf. 2023, 452, 03014. [Google Scholar] [CrossRef]
- Nikulin, S.N. Control Systems and Data Reliability; Nikulin, S.N., Ovchinnikov, I.A., Eds.; UrFU: Ekaterinburg, Russia, 2020; 240p. [Google Scholar]
- Sevinov, J.U.; Boborayimov, O.K.; Bobomurodov, N.H. Algorithms for Synthesis of Adaptive Neural Network Control Systems Based on the Velocity Gradient Method. In Lecture Notes in Networks and Systems, Proceedings of the 16th International Conference on Applications of Fuzzy Systems, Soft Computing and Artificial Intelligence Tools-ICAFS-2023—ICAFS 2023, Antalya, Turkey, 14–15 September 2023; Aliev, R.A., Kacprzyk, J., Pedrycz, W., Jamshidi, M., Babanli, M., Sadikoglu, F.M., Eds.; Springer: Cham, Switzerland, 2024; Volume 1141. [Google Scholar] [CrossRef]
- Abdusalomov, A.; Umirzakova, S.; Boymatov, E.; Zaripova, D.; Kamalov, S.; Temirov, Z.; Jeong, W.; Choi, H.; Whangbo, T.K. A Human-Centric, Uncertainty-Aware Event-Fused AI Network for Robust Face Recognition in Adverse Conditions. Appl. Sci. 2025, 15, 7381. [Google Scholar] [CrossRef]
- Temerbekova, B.M.; Mamanazarov, U.B.; Bekimbetov, B.M.; Ibragimov, Z.M. Development of integrated digital twins of control systems for ensuring the reliability of information and measurement signals based on cloud technologies and artificial intelligence. Chernye Met. 2023, 2023. [Google Scholar] [CrossRef]
- Golubev, P.N. Forecasting in Information and Control Systems; Golubev, P.N., Smirnova, E.A., Eds.; Nauka: Novosibirsk, Russia, 2019; 256p. [Google Scholar]
- Bakhtin, V.I.; Ivanishko, I.A.; Lebedev, A.V.; Pindrik, O.I. (Eds.) The Method of Lagrange Multipliers: Methodical Manual for Students of Specialty 1-31 03 01-03 “Mathematics (Economic Activity)”; BSUL: Minsk, Belarus, 2012; 40p. [Google Scholar]
- Zhukov, A.L. Information and Management Systems Based on Cloud Technologies; Zhukov, A.L., Kuznetsova, N.V., Eds.; UrFU: Ekaterinburg, Russia, 2020; 290p. [Google Scholar]
- Zaitsev, D.A. (Ed.) Prediction Methods in Cloud Computing; TPU: Tomsk, Russia, 2018; 240p. [Google Scholar]
- Ivanov, R.N. Machine Learning and Forecasting in Control Systems; Ivanov, R.N., Lebedeva, O.S., Eds.; Fizmatlit: Moscow, Russia, 2019; 280p. [Google Scholar]
- Kozlov, E.V. (Ed.) Cloud Services for Analytics and Forecasting; BHV-Peterburg: St Petersburg, Russia, 2021; 260p. [Google Scholar]
- Lazarev, P.K. Integration of Machine Learning Methods in Cloud Platforms; Lazarev, P.K., Mikhailova, I.V., Eds.; DMK Press: Moscow, Russia, 2022; 300p. [Google Scholar]
- Medvedev, S.Y. (Ed.) Predictive Models in Cloud Information Systems; PGNIU: Perm, Russia, 2020; 230p. [Google Scholar]
- Nikolaev, A.P. (Ed.) Cloud Technologies in Management: Methods and Algorithms; YFU: Rostov-on-Don, Russia, 2019; 310p. [Google Scholar]
- Orlov, V.G. Machine Learning for Forecasting in Cloud Environments; Orlov, V.G., Pavlova, T.S., Eds.; Infra-M: Moscow, Russia, 2021; 280p. [Google Scholar]
- Temerbekova, B.M. Application of a Method for Detecting Systematic Error in Integral Measurements of Technological Parameters in Complex Technological Processes and Productions. Non-Ferr. Met. 2022, 79–86. [Google Scholar]
- Petrov, I.S. (Ed.) Information and Control Systems with Elements of Artificial Intelligence; Samara University: Samara, Russia, 2022; 320p. [Google Scholar]
- Romanov, D.V. (Ed.) Cloud Computing and Machine Learning in Enterprise Management; FEFU: Vladivostok, Russia, 2020; 290p. [Google Scholar]
- Sidorov, M.A. Forecasting Based on Machine Learning in Cloud Systems; Sidorov, M.A., Tikhomirova, L.V., Eds.; Bauman Moscow State Technical University: Moscow, Russia, 2018; 270p. [Google Scholar]
- Timofeev, Y.N. (Ed.) Integration of Cloud Services and AI Methods in Management; ITMO: St Petersburg, Russia, 2021; 250p. [Google Scholar]
- Singh, D.P. Cloud-Based Machine Learning: Opportunities and Challenges. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2024, 10, 264–270. [Google Scholar] [CrossRef]
- Andreev, A.V. Cloud Computing in Control Systems: Theory and Practice; Andreev, A.V., Petrov, I.S., Eds.; Bauman Moscow State Technical University Publishing House: Moscow, Russia, 2021; 320p. [Google Scholar]
- Fedorov, A.E. Cloud Technologies and Forecasting in Control Systems; Fedorov, A.E., Shestakova, M.V., Eds.; Logos: Moscow, Russia, 2022; 280p. [Google Scholar]
- Dyakonov, V.P. (Ed.) Integration of Cloud Technologies and Artificial Intelligence in Management; Goryachaya Liniya—Telecom: Moscow, Russia, 2022; 310p. [Google Scholar]
- Ulyanov, D.M. (Ed.) Cloud Computing for Developers; DMK Press: Moscow, Russia, 2020; 330p. [Google Scholar]
- Ivanov, P.A. Information and Control Systems of Metallurgical Production; Ivanov, P.A., Sidorov, N.V., Eds.; Metallurgy: Moscow, Russia, 2019; 320p. [Google Scholar]
- Petrov, I.S. Hybrid Cloud Technologies in Industry; Petrov, I.S., Kuznetsova, E.A., Eds.; Polytechnic: St Petersburg, Russia, 2020; 280p. [Google Scholar]
- Smirnov, D.V. (Ed.) Neural Networks in Control Systems: Theory and Practice; Nauka: Novosibirsk, Russia, 2021; 350p. [Google Scholar]
- Kuzmin, A.L. Deep Neural Networks for Forecasting Time Series; Kuzmin, A.L., Romanova, M.S., Eds.; Fizmatlit: Moscow, Russia, 2022; 290p. [Google Scholar]
- Borisov, V.N. (Ed.) Integration of Cloud Technologies and Neural Network Models in Industry; UrFU: Ekaterinburg, Russia, 2020; 310p. [Google Scholar]
- Zakharov, K.P. Architecture of Information-Management Systems Based on Hybrid Clouds; Zakharov, K.P., Mikhailova, L.V., Eds.; Kazan University: Kazan, Russia, 2021; 270p. [Google Scholar]
- Fedorov, A.E. (Ed.) Application of LSTM and DNN in the Forecasting of Technological Processes; TPU: Tomsk, Russia, 2019; 260p. [Google Scholar]
- Goncharov, S.I. Hybrid Neural Network Models in Production Management; Goncharov, S.I., Lebedeva, O.N., Eds.; Goryachaya Liniya—Telecom: Moscow, Russia, 2022; 300p. [Google Scholar]
- Medvedev, Y.K. (Ed.) Cloud Computing in Metallurgy: Approaches and Solutions; BHV-Peterburg: St Petersburg, Russia, 2021; 280p. [Google Scholar]
- Selvarajan, S.; Srivastava, G.; Khadidos, A.O.; Khadidos, A.O.; Baza, M.; Alshehri, A.; Lin, J.C.W. An artificial intelligence lightweight blockchain security model for security and privacy in IIoT systems. J. Cloud Comput. 2023, 12, 38. [Google Scholar] [CrossRef] [PubMed]
- San-Payo, G.; Ferreira, J.C.; Santos, P.; Martins, A.L. Machine learning for quality control system. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 4491–4500. [Google Scholar] [CrossRef]
- Su, W.; Xu, G.; He, Z.; Machica, I.K.; Quimno, V.; Du, Y.; Kong, Y. Cloud-Edge Computing-Based ICICOS Framework for Industrial Automation and Artificial Intelligence: A Survey. J. Circuits Syst. Comput. 2023, 32, 2350168. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Wang, H.; Chen, J. Application of Neural Network in Steelmaking and Continuous Casting. J. Iron Steel Res. Int. 2024, 31, 1023–1032. [Google Scholar]
- Turgunboev, A.Y.; Temerbekova, B.M.; Usmanova, K.A.; Mamanazarov, U.B. Application of the microwave method for measuring the moisture content of bulk materials in complex metallurgical processes. Chernye Met. 2023, 2023. [Google Scholar] [CrossRef]
- Yusupbekov, A.N.; Sevinov, J.U.; Mamirov, U.F.; Botirov, T.V. Synthesis Algorithms for Neural Network Regulator of Dynamic System Control. In Advances in Intelligent Systems and Computing, Proceedings of the 14th International Conference on Theory and Application of Fuzzy Systems and Soft Computing-ICAFS-2020—ICAFS 2020, Budva, Montenegro, 27–28 August 2021; Aliev, R.A., Kacprzyk, J., Pedrycz, W., Jamshidi, M., Babanli, M., Sadikoglu, F.M., Eds.; Springer: Cham, Switzerland, 2021; Volume 1306. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Abdusalomov, A.; Umirzakova, S.; Tashev, K.; Sevinov, J.; Temirov, Z.; Muminov, B.; Buriboev, A.; Safarova Ulmasovna, L.; Lee, C. AI-Driven Boost in Detection Accuracy for Agricultural Fire Monitoring. Fire 2025, 8, 205. [Google Scholar] [CrossRef]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A transformer-based framework for multivariate time series representation learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 2114–2124. [Google Scholar] [CrossRef]
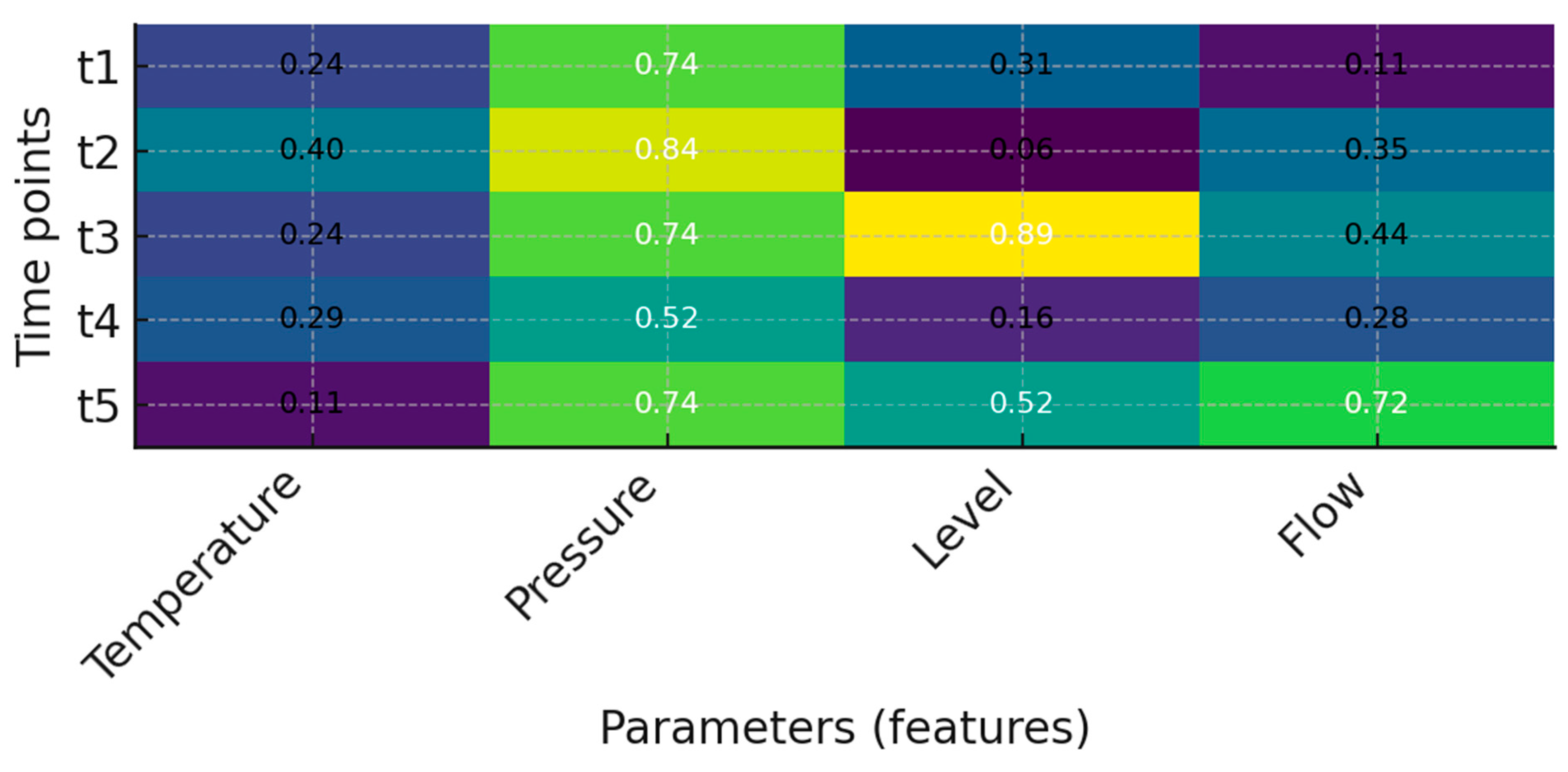


| № | Step # | Description |
|---|---|---|
| 1 | Input vector formation | Each parameter (for example, temperature, pressure, level, flow rate) is formed into a feature vector at time t: xt = [xt1, xt2, xt3, xt4] |
| 2 | Construction of a time matrix | A sequence of such vectors forms a matrix of dimension T × 4, where T is the length of the time series |
| 3 | Processing in LSTM | LSTM processes each xt in time order, forming hidden states ht |
| 4 | Collecting the hidden state | The hidden state h_T at the last step reflects generalized information about the entire sequence |
| 5 | Transmission to DNN | The Vector h_T is transmitted at the input пoлнocвязнoй of a fully connected neural network (DNN) for interpreting and making a decision |
| 6 | Getting a forecast | At the output of DNN, the final prediction is obtained—the parameter value or control action |
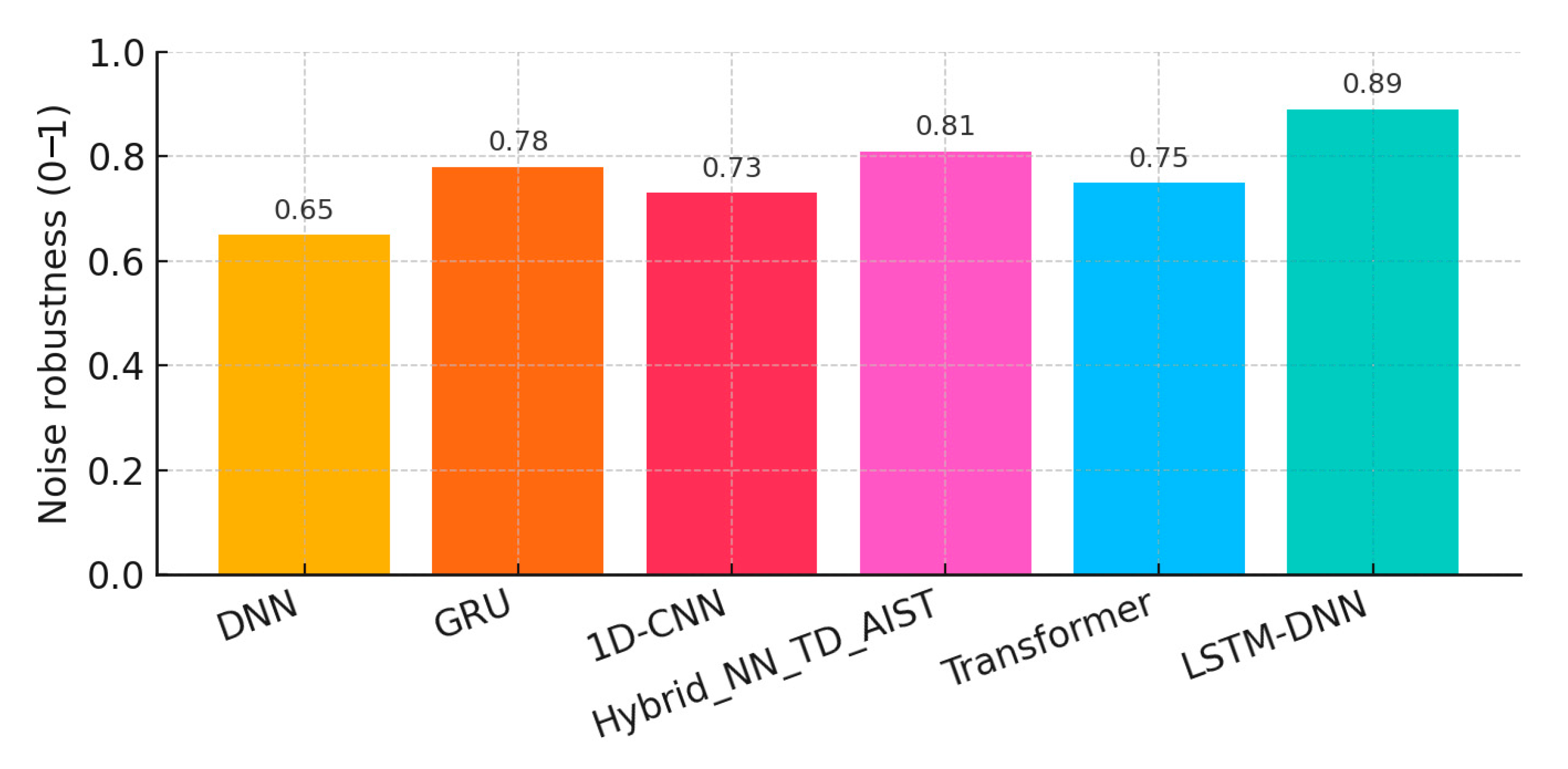
| Model | Accuracy (Val%) | RMSE (Test) | Noise Resistance (0–1) |
|---|---|---|---|
| DNN | 78.2 | 0.164 | 0.65 |
| GRU | 87.4 | 0.102 | 0.78 |
| 1D-CNN | 82.9 | 0.139 | 0.73 |
| Hybrid_NN_TD_AIST | 91.8 | 0.086 | 0.81 |
| LSTM-DNN (proposed) | 92.4 | 0.079 | 0.89 |
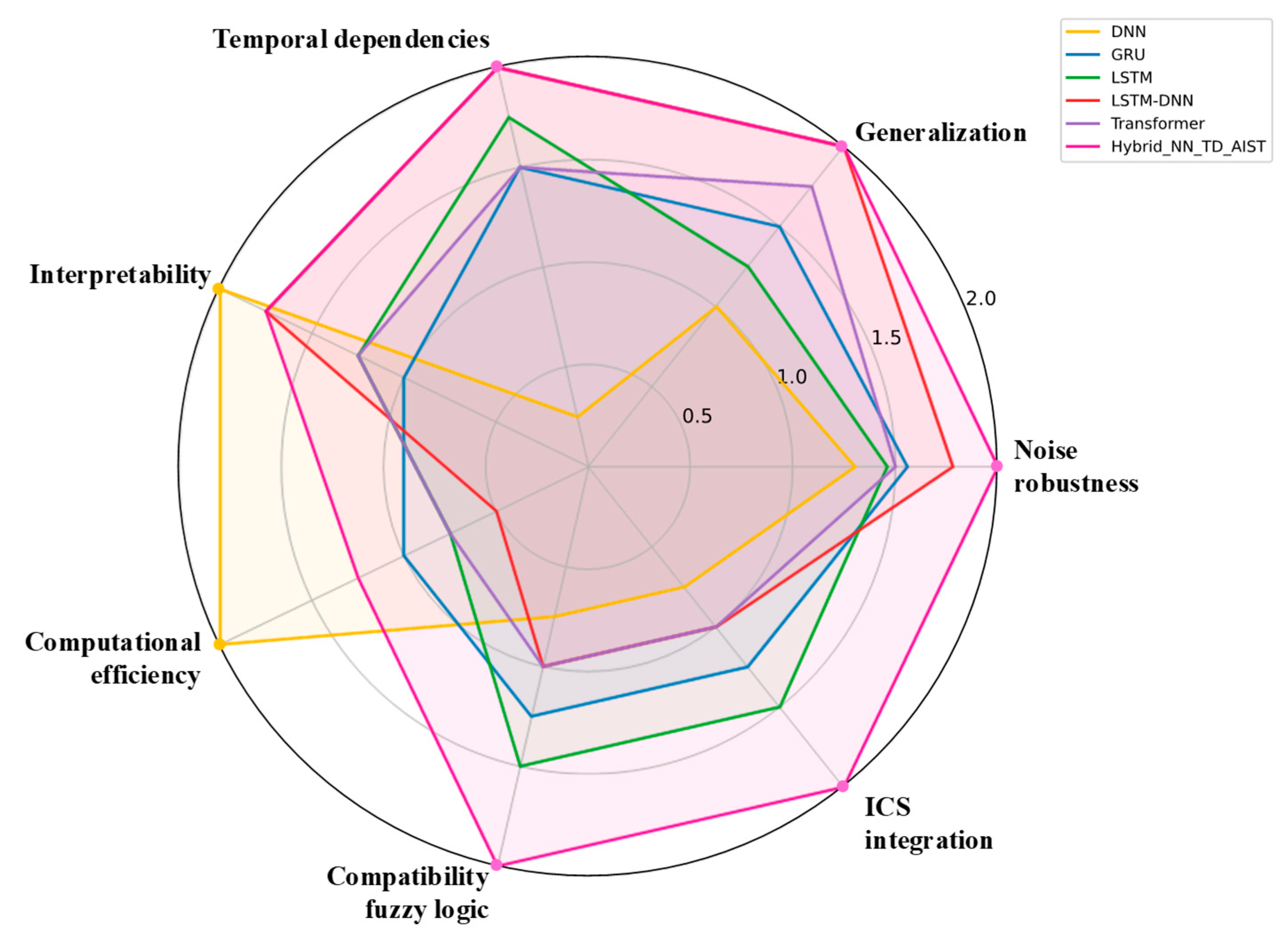
| Criterion | DNN | GRU | LSTM | LSTM-DNN | Transformer | Hybrid_NN_TD_AIST |
|---|---|---|---|---|---|---|
| Time dependencies | - | + | ++ | ++ | ++ | ++ |
| Generalizability | + | + | + | ++ | ++ | ++ |
| Noise resistance | - | + | + | ++ | + | + |
| Integration into the ISMS | + | + | + | ++ | - | - |
| Compatibility with fuzzy logic | + | + | + | ++ | - | - |
| Computational efficiency | ++ | + | + | + | - | - |
| Interpretability | ++ | + | + | ++ | - | - |
| Category | Variable | Description | Units of Measurement |
|---|---|---|---|
| Raw material and ore preparation parameters | F_ore | Ore consumption | t/h |
| d_particle | particle size | μm/mm | |
| Mineral_composition | mineralogical composition | % | |
| Hardness_index | strength index | scale | |
| Moisture_ore | ore moisture and temperature | % | |
| T_ore | °C | ||
| Crushing and grinding unit parameters | Power_mill | Mill capacity | kW |
| Mill_load | download | % | |
| Feed_rate | feed rate | t/h | |
| T_mill | temperature | °C | |
| Vibration_level_mill | vibrations | mm/s | |
| d_product | target product size | μm | |
| Parameters of flotation process (slurry) | pH | pH | - |
| Solids_content | solid content | % | |
| Density_pulp | pulp density | g/cm3 | |
| Temp_pulp | pulp temperature | °C | |
| Cake_thickness | cm | ||
| Heat treatment parameters (melting) | T_furnace | Furnace temperature | °C |
| O2_content | oxygen content | % | |
| F_fuel | fuel consumption | m3/h/kg/h | |
| Residence_time | dwell time | min | |
| Slag_volume | slag volume | t/h | |
| Metal_flow | metal consumption | t/h | |
| Parameters of economic efficiency | Cost_reagents | Cost of reagents | USD/t |
| Cost_energy | energies | USD/day | |
| Cost_water | waters | USD/day | |
| Labor_cost | labor force | USD/day | |
| Revenue_Cu | copper and molybdenum revenue | USD/day | |
| Revenue_Mo | performance | USD/day | |
| Throughput | profit | tpd | |
| Profit_margin | ROI | % | |
| ROI | - | ||
| Validity management parameters | P_R(k) | Probabilities of misrepresentation and credibility | - |
| P_E(k) | checksums | - | |
| ΔP | status and confidence in sensors | - | |
| CRC_check | true/false | ||
| Sensor_status | status | ||
| Confidence_level | 0-1 | ||
| Equipment monitoring parameters | Vibration_level | Vibration level | mm/s |
| Bearing_temperature | bearing temperature | °C | |
| Motor_current | motor current | A | |
| Lubrication_pressure | lubrication pressure | bar | |
| Equipment_downtime | downtime | ч | |
| Next_maintenance_date | date of service | date | |
| Integration and security settings | User_ID/Role | User ID | - |
| Session_timeout | session time | min | |
| Encryption_key_ID | encryption key | ID | |
| Access_log | call log | - | |
| External_API_calls | API calls | quantity |
| Parameter | Prior to the Introduction of LSTM-DNN and Cloud Computing | After Implementation |
|---|---|---|
| Parameter prediction accuracy | Medium (up to 75%) | High (up to 95%) |
| Reduced energy consumption | Suboptimal utilization of resources | −10% due to predictive management |
| Copper losses in waste | Significant losses due to inefficient flotation | −15–20% due to reagent optimization |
| Equipment downtime | High due to unexpected rejections | −30% due to failure prediction |
| Management flexibility | Depends on the human factor | Automatic parameter adaptation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avazov, K.; Sevinov, J.; Temerbekova, B.; Bekimbetova, G.; Mamanazarov, U.; Abdusalomov, A.; Cho, Y.I. Hybrid Cloud-Based Information and Control System Using LSTM-DNN Neural Networks for Optimization of Metallurgical Production. Processes 2025, 13, 2237. https://doi.org/10.3390/pr13072237
Avazov K, Sevinov J, Temerbekova B, Bekimbetova G, Mamanazarov U, Abdusalomov A, Cho YI. Hybrid Cloud-Based Information and Control System Using LSTM-DNN Neural Networks for Optimization of Metallurgical Production. Processes. 2025; 13(7):2237. https://doi.org/10.3390/pr13072237
Chicago/Turabian StyleAvazov, Kuldashbay, Jasur Sevinov, Barnokhon Temerbekova, Gulnora Bekimbetova, Ulugbek Mamanazarov, Akmalbek Abdusalomov, and Young Im Cho. 2025. "Hybrid Cloud-Based Information and Control System Using LSTM-DNN Neural Networks for Optimization of Metallurgical Production" Processes 13, no. 7: 2237. https://doi.org/10.3390/pr13072237
APA StyleAvazov, K., Sevinov, J., Temerbekova, B., Bekimbetova, G., Mamanazarov, U., Abdusalomov, A., & Cho, Y. I. (2025). Hybrid Cloud-Based Information and Control System Using LSTM-DNN Neural Networks for Optimization of Metallurgical Production. Processes, 13(7), 2237. https://doi.org/10.3390/pr13072237









