Abstract
This paper aims to enhance operational efficiency in the labor-intensive production of composite wind turbine blades, which are critical components of renewable energy systems. The study was conducted at a wind energy facility in Türkiye, integrating the Single-Minute Exchange of Die (SMED) methodology with a Multi-Mode Resource-Constrained Project Scheduling Problem (MRCPSP) model to reduce production cycle time and optimize labor utilization. An operational time analysis was used to identify and classify non-value-adding activities. SMED principles were then adapted to the fixed-position manufacturing environment, enabling the conversion of internal setup activities into external ones and facilitating task parallelization. These improvements significantly increased productivity and labor efficiency. Subsequently, a scheduling model was developed to optimize the sequence of operations while accounting for activity precedence and resource constraints. As a result, the proposed approach reduced cycle time by 28.6% and increased average labor utilization from 68% to 87%. Scenario analyses confirmed the robustness of the model under varying levels of workforce availability. The findings demonstrate that integrating lean manufacturing techniques with optimization-based scheduling can yield substantial efficiency gains without requiring major capital investment. Moreover, the proposed approach offers practical insights into workforce planning and production scheduling in renewable energy manufacturing environments.
1. Introduction
In today’s highly competitive and rapidly evolving global manufacturing landscape, industries face increasing pressure to enhance operational efficiency, reduce production lead times, and meet growing demands for customization and sustainability. These challenges are particularly significant in the renewable energy sector, where large-scale composite components such as wind turbine blades are essential for accelerating the global energy transition. However, the production of these components remains highly labor-intensive, relying on fixed-position layouts, manual operations, and extended cycle times. Such constraints create a compelling need for hybrid strategies that integrate lean manufacturing tools with formal scheduling models, especially in labor-intensive settings where full automation may not be economically viable [1].
Lean manufacturing principles have been widely implemented to reduce waste and enhance value across various industries [2]. Stump and Badurdeen [3] highlighted the critical role of lean strategies in enabling mass customization within complex production systems. Jebbor et al. [4] applied lean techniques to improve cycle times and reduce variability in traditional shipyard production. Maware and Parsley [5] examined the challenges of lean transformation and reported significant productivity gains in manufacturing environments implementing lean frameworks. Sarwar et al. [6] investigated the impact of stakeholder engagement on Lean Six Sigma projects in air-conditioner manufacturing, emphasizing the organizational factors influencing lean project costs and outcomes. Gavriluță et al. [7] proposed an algorithmic framework to support the systematic selection and implementation of lean manufacturing methods, aiming to improve production system performance through structured analysis and process optimization.
Among the various lean manufacturing tools, the Single-Minute Exchange of Die (SMED) methodology, originally developed by Shigeo Shingo [8], has become prominent for its effectiveness in minimizing setup times and increasing production flexibility [9]. Ribeiro et al. [10], through action research, demonstrated SMED’s effectiveness in agro-industrial settings, emphasizing its impact on systematic changeover improvements. Kumar and Abuthakeer [11] reported notable efficiency gains from SMED in the automotive industry. Almomani et al. [12] proposed an enhanced SMED implementation framework that incorporates multiple criteria decision-making techniques—such as AHP and TOPSIS—to systematically evaluate and prioritize setup improvement alternatives. Their integrated approach provides a structured decision support mechanism that considers not only setup time but also cost, safety, energy, and facility layout, thereby extending SMED’s applicability in complex manufacturing environments. Garcia-Garcia et al. [13] illustrated how SMED can be effectively applied even in highly constrained environments such as ready-meal food production, achieving a 30% reduction in setup time and 10% decrease in labor costs while improving overall equipment effectiveness. Huang et al. [14] showed that SMED enhances operational responsiveness in small-and-medium-sized enterprises. Santos et al. [15] demonstrated similar SMED benefits in the automotive industry, achieving a 31% reduction in calibration time for tire production equipment. More recently, Rahardjo et al. [16] introduced a smart lean framework combining IoT-based monitoring with SMED to enable dynamic setup time reduction. This approach aligns with the perspective of embedding traditional lean tools into semi-automated digital workflows, further reinforcing SMED’s relevance in contemporary industrial contexts.
Nevertheless, while SMED simplifies task flows and reduces changeover times, it may be insufficient in situations where resource constraints, particularly workforce limitations, are critical. In such cases, advanced project scheduling models such as the Multi-Mode Resource-Constrained Project Scheduling Problem (MRCPSP) offer structured approaches for optimizing task sequencing under limited resource conditions [17]. Sprecher et al. [18] presented a mathematical formulation and an exact branch-and-bound solution method for the MRCPSP, addressing multiple execution modes per activity. Kolisch and Padman [19] provided a comprehensive review of deterministic project scheduling models, including the MRCPSP, while Herroelen and Leus [20] further explored its application under uncertainty. Ramos et al. [21] introduced a stochastic variant of the MRCPSP, enabling flexible scheduling under fluctuating workforce capacity. Sabzehparvar and Seyed-Hosseini [22] incorporated time lags between tasks, improving the realism of project timelines.
Additionally, the growing complexity of scheduling problems in the renewable energy sector has driven the development of hybrid approaches that integrate optimization and forecasting techniques. For example, Cao et al. [23] proposed a coordinated scheduling framework for virtual power plants that addresses wind–solar uncertainty through source-load coordination. Gomes et al. [24] conducted a benchmark study comparing metaheuristic optimization methods for energy community scheduling. Furthermore, Aguilar et al. [25] introduced a robust multi-objective scheduling model enhanced by machine-learning-based probabilistic forecasting. Similarly, Bhadoria and Marwaha [26] developed a hybrid metaheuristic approach for optimizing generation scheduling under renewable integration constraints. Chen et al. [27] formulated a dual-energy hybrid project scheduling model for engineer-to-order assembly processes that integrates solar and grid energy sources to minimize delay, energy, and carbon emission costs. Their approach, which combines an integer programming model with a two-stage heuristic algorithm, demonstrates how renewable energy utilization can be systematically embedded into scheduling decisions under real-world constraints. Moreover, Li et al. [28] introduced a multi-temporal cooperative game-based scheduling strategy to manage resource allocation across distributed networks. While these studies focus primarily on energy systems rather than manufacturing, they highlight the relevance of robust scheduling strategies in resource- and constraint-sensitive environments.
To address the gap in integrating lean techniques with formal scheduling in labor-driven renewable energy manufacturing, the present study proposes a hybrid framework that combines SMED-based process improvements with MRCPSP-based scheduling optimization. Conducted at a wind turbine blade production facility in Türkiye, this study employs time-and-motion analysis to identify inefficiencies and applies mathematical modeling to minimize cycle time and maximize labor utilization. The resulting approach offers a scalable and cost-effective strategy for enhancing operational efficiency in labor-intensive renewable energy manufacturing environments.
The remainder of this paper is structured as follows: Section 2 introduces the SMED methodology, details the data collection through operational time analysis, and presents the MRCPSP mathematical model. Section 3 provides the optimization results based on the developed model and highlights the observed improvements. Section 4 discusses the implications of the findings, and Section 5 concludes with suggestions for future research.
2. Materials and Methods
This study adopts a case study methodology focused on a wind turbine blade manufacturing facility in Türkiye. Owing to the large dimensions and weight of composite blades, the production process follows a fixed-position layout. The facility relies heavily on manual labor, with the majority of operations carried out by human operators and minimal reliance on automation. Within this context, the study aims to optimize workforce allocation and reduce overall production cycle time by integrating the SMED methodology with an MRCPSP model.
In the mold preparation phase, the molds are thoroughly cleaned and treated with appropriate chemical agents to ensure optimal surface conditions for subsequent production steps. Controlled surface roughness on the bonding interfaces is achieved without mechanical abrasion by sequentially applying gelcoat, peel ply (also referred to as zero fabric), and aluminum mesh. Following surface preparation, the laminate construction begins with the sequential layup of outer skin fabrics, core materials, spar caps, and inner skin fabrics. Once the layup process is complete, a structural adhesive film is applied to the bonding areas. A vacuum infusion strategy is then developed, which involves sealing the edges of vacuum channels using tacky tape and attaching spiral tubing to ensure efficient air evacuation and resin distribution.
Subsequently, a vacuum bag is placed over the entire mold surface to isolate the part from the external environment and ensure airtightness during vacuum application. The integrity of the vacuum seal is verified through a drop test. Upon successful validation, the resin infusion process is initiated to impregnate the laminate under vacuum conditions.
After the infusion is complete, the mold’s integrated heating system is activated to initiate the curing cycle. Once the composite surface reaches the desired degree of cure and the temperature has sufficiently decreased, the debagging process is performed by removing all consumables used during infusion, such as peel plies and flow distribution media. The next stage involves the installation of the lightning protection system, during which cable routing points are precisely marked and positioned on the blade surface. In the subsequent dry-fit process, the adhesive bond gap between the two blade shells is measured and inspected to verify proper alignment and ensure the absence of interference. Additionally, the contact points between the spar cap and the root inserts are identified and marked.
Once alignment is verified, adhesive paste is applied to the designated bonding areas, and the blade halves are joined. The assembled structure is then subjected to a controlled elevated-temperature environment for an extended duration to complete the final curing process. Thermal imaging techniques are employed throughout to monitor temperature uniformity across the blade. Upon completion of the curing cycle, the blade is demolded. Finally, the blade is transferred to the finishing area, where post-processing operations such as surface sanding, coating, and painting are carried out to meet final quality and aerodynamic specifications. The blade molds used throughout this process are illustrated in Figure 1.

Figure 1.
Molds used in the manufacturing of composite wind turbine blades.
2.1. Data Collection and Operational Time Analysis
To gain a deeper understanding of production dynamics and obtain precise processing times, an extensive time-and-motion study was conducted over a one-month observation period. Each stage of the manufacturing process was video-recorded and collaboratively analyzed with two experienced production operators. The primary objectives were to generate realistic time estimates, standardize procedures, and identify sources of operational inefficiency.
Two primary mold types were analyzed in the study: the suction side (SS) and the pressure side (PS) molds, each comprising a sequence of specialized operations. The entire blade manufacturing process was divided into six main phases: mold preparation, lower core layup, core layup, upper core layup, infusion preparation, and debagging. A total of 61 distinct operations were recorded for the SS mold and 82 for the PS mold. For each operation, the minimum and maximum feasible workforce allocations were determined based on ergonomic considerations and occupational safety standards. The time study was conducted using a 100% performance rating as the baseline, with an additional 13% allowance applied for fatigue to ensure realistic and standardized time measurements.
2.2. Application of the SMED Methodology
Given the fixed-position layout and labor-intensive nature of the process, conventional die or mold changeover techniques were not feasible. However, the core principles of the SMED methodology were strategically adapted to suit this production environment. In this context, SMED was employed to identify (i) the distinction between value-adding and non-value-adding activities, (ii) the separation of internal operations—which require production stoppage—from external operations that can be executed concurrently, and (iii) the identification of opportunities for parallel task execution to enhance efficiency.
By converting internal setup operations into external ones and eliminating unnecessary movements, the production process was restructured to enable synchronized task execution comparable to the rapid workflows observed in high-performance assembly systems. Operator motion paths were mapped to identify inefficiencies, and setup sequences were systematically analyzed to inform workflow redesign efforts.
The precedence relationships used for scheduling operations and assigning workforce within the resource-constrained project scheduling framework were guided by the identification of parallelizable tasks through the SMED approach. Operations were classified as either internal or external. Internal tasks are performed within the mold and directly delay subsequent in-mold operations. In contrast, external tasks take place on the mold’s surface or in the blade’s root section and do not interfere with internal activities. These external operations can be carried out in parallel with internal ones, and this potential for concurrency was explicitly incorporated into the formulation of precedence constraints.
Preparatory activities such as material placement, tool readiness, and surface cleaning were critically reviewed and, where applicable, reclassified as external operations to be completed prior to the initiation of core production tasks. This reallocation allowed internal activities to proceed without interruption, thereby improving overall process efficiency. The reassignment aligns with lean manufacturing principles, particularly the distinction between value-added and non-value-added work. These refinements contributed to a more streamlined and predictable production flow, resulting in shorter cycle times and improved operational discipline.
Table 1 presents a detailed classification of the operations involved in the composite blade manufacturing process, distinguishing between internal and external tasks based on their influence on mold occupancy and production continuity.

Table 1.
Classification of internal and external operations in composite blade molding.
To further streamline the preparation phases and reduce production delays, operation-specific kits were introduced. These kits were designed not only to ensure that the right materials and tools are available at the right time but also to support standardized work procedures. For instance, toolkits and material kits were systematically organized based on specific operational stages, enabling workers to access required items immediately without disrupting the workflow. This practice significantly minimized time losses caused by searching for tools or retrieving missing or insufficient materials.
2.3. MRCPSP-Based Mathematical Modeling of PS Core Layup Operations
In resource-constrained project scheduling problems, activities are represented as nodes, and precedence relationships are modeled as directed arcs. Each activity can commence only after the completion of all its predecessor activities. Furthermore, the feasibility of execution is determined by the availability of required resources in each time period.
In MRCPSPs, each activity can be executed in different modes, where each mode corresponds to a unique combination of resource requirements and associated processing time. Following the SMED-based restructuring, the production process was modeled as an MRCPSP. Each activity could be performed in one of several modes, where each mode represents a distinct combination of workforce allocation and the corresponding task duration. The objective was to determine the optimal schedule and workforce allocation that would minimize the total cycle time, subject to precedence constraints and labor availability.
The mathematical model was constructed by incorporating precedence constraints and enforcing non-preemptive task execution. Additional constraints were introduced for each major production stage to accurately reflect practical limitations in the manufacturing process.
The formulation is based on the following assumptions:
- The project comprises both parallel and precedence-constrained activities, all of which are non-preemptive.
- If a successor activity is permitted to start before the completion of its predecessor, the two activities are treated as parallel.
- The precedence relationships among all activities are known.
- All workers are capable of performing each activity within the same timeframe.
- The durations of activities are assumed to be deterministic.
- Each activity has a defined minimum and maximum number of allowable assigned workers.
- For certain activities, the duration is inversely proportional to the number of assigned workers.
- For specific activities, both the assigned workforce and processing time are fixed.
- The primary objective is to minimize the project’s cycle time under a fixed workforce availability.
Scheduling formulations were created for the following activities in both PS and SS mold processes: mold preparation (modeled in two distinct parts), bottom core fabric placement, core placement, top core fabric placement, infusion preparation, and debagging. Additionally, a separate model was developed for the closure preparation stage, which is specific to the PS mold.
In cases where a successor activity is allowed to begin before its predecessor has fully completed, such pairs are treated as parallel operations. To ensure the model accurately captures real-world constraints, additional restrictions were incorporated to prevent the concurrent execution of operations that are not genuinely parallel. These constraints are explicitly embedded within the corresponding mathematical model formulations.
The mathematical formulation of the MRCPSP adopted in this study builds upon established models from the literature, notably those developed by Kyriakidis et al. [17], Kolisch and Padman [19], Hartmann and Drexl [29], and Cheng et al. [30]. The formulation includes standard constructs such as mode assignment, non-preemptive activity execution, renewable resource limitations, and precedence relationships. These components are formalized below.
| Sets | |
| N | Set of activities in the project, i.e., N = {0, 1, …, n}, where 0 and n + 1 denote the dummy start and end activities, respectively. |
| Modj | Set of feasible execution modes for activity j. |
| T | Set of discrete time periods, i.e., T = {1, 2, …, t}. |
| Indices | |
| j | Activity index (identifies each activity in the project). |
| t | Time period index (used to denote discrete scheduling time units). |
| m | Mode index, representing an execution alternative for activity j (i.e., a specific combination of resource usage and processing time). |
| Parameters | |
| Processing time (i.e., duration) of activity j when executed in mode m. | |
| Number of workers required to execute activity j in mode m. | |
| Total number of available workers in the system (i.e., the capacity of the renewable resource). | |
| Decision Variables | |
| . | |
| . | |
| Start time of activity j (i.e., the time period at which activity j begins execution). | |
| Completion time of activity j; denotes the total project duration (makespan) as the completion time of the final dummy activity. | |
The project considers a single type of renewable resource: a shared pool of workers, with an availability of up to 18 units in each discrete time period t. Each activity j ∈ N can be executed in a set of feasible modes m ∈ Modj, where each mode specifies a required number of workers and an associated processing time . Some activities exhibit flexible processing times that decrease linearly with the number of assigned workers, while others maintain fixed durations regardless of workforce allocation. This structure captures both flexible and inflexible task types. All time-related parameters are expressed in minutes to ensure consistency and precision in scheduling.
Objective Function
minimum C|n+1|
The objective is to minimize the completion time of the final dummy activity, denoted as C|n+1|, which denotes the project makespan [19,30].
Mode Selection Constraint
Activity Duration Constraint
Precedence Relationship Constraints
Workforce Capacity Constraint
Non-Preemption Constraint
Binary and Non-Negativity Constraints
Constraint (2) ensures that each activity is assigned to exactly one execution mode [29,30]. Constraint (3) guarantees that if mode m is selected for activity j, the corresponding processing time equals the activity duration defined for that mode [30]. Constraints (4) through (6) represent the precedence relationships among activities. Here, M denotes a sufficiently large constant used to enforce logical sequencing via the big-M method [17,19]. The “−1” term in Constraint (4) is used to ensure strict sequencing under integer-based time representation. Since activities can only start at discrete time units (e.g., 1, 2, 3, …), the condition ensures that activity j begins only after the completion of activity i. For instance, if activity j starts at time unit 5, activity i must be completed by time unit 4 at the latest. Constraint (7) enforces the workforce availability limit for each time period [19,30], while Constraint (8) ensures that activities are non-preemptive—that is, once started, they cannot be interrupted [29,30]. Constraints (9) and (10) specify that the associated decision variables are binary, and Constraints (11) and (12) ensure their non-negativity.
To account for practical execution constraints, the start and finish times of certain non-parallel operations were revised. Accordingly, additional constraints were incorporated into the mathematical models for both the PS and SS mold processes. Specifically, the following constraints were formulated for the PS core layup model, with analogous conditions applied to corresponding operations in both mold types.
Additional Temporal Execution Constraints
Constraints (13) through (16) define temporal dependencies that allow for either sequential or concurrent execution of specific operations. Constraint (13) ensures that Operation 3 starts no earlier than Operation 1, permitting simultaneous initiation if feasible. Similarly, Constraint (14) enforces that Operation 7 may begin only after or concurrently with Operation 6. Constraint (15) stipulates that Operation 13 can commence either after or concurrently with Operation 12. Lastly, Constraint (16) requires that Operation 14 starts no earlier than Operation 12, thereby allowing parallel execution where applicable.
3. Results
The mathematical optimization model, grounded in MRCPSP principles, was successfully implemented using LINGO 19.0 and applied to the wind turbine blade manufacturing process. LINGO was selected for its user-friendly modeling interface and suitability for mid-scale scheduling problems frequently encountered in industrial settings. The platform enabled efficient formulation of precedence constraints, multi-mode activity structures, and resource limitations. The model produced an optimal schedule for all operations in both the SS and PS molds, yielding reduced cycle times and optimal workforce allocation while satisfying all precedence and resource constraints.
Given the broad scope of the manufacturing process, this study focuses on the PS core layup operations as a representative case to demonstrate the model’s applicability. Table 2 presents detailed processing times and workforce requirements for this phase, which includes a mix of sequential and parallelizable tasks—each with specific resource needs and precedence constraints. The corresponding precedence network diagram is shown in Figure 2, illustrating the operational sequence and dependencies explicitly incorporated into the scheduling formulation. Each node represents an operation number as defined in Table 2.

Table 2.
Processing times and workforce requirements for PS core layup activities.
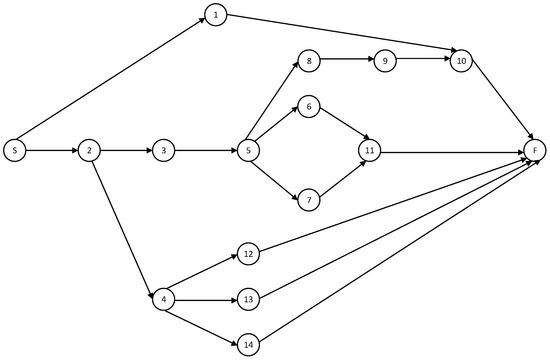
Figure 2.
Precedence diagram of PS core layup activities. The numbers inside the nodes (1–14) correspond to the operation numbers listed in Table 2. ‘S’ denotes the dummy start node, representing the beginning of the project without consuming any time or resources, while ‘F’ denotes the dummy finish node, representing the completion of the PS core layup activities.
The activity–mode matrix defines the processing time of each activity under various execution modes. For some activities, the processing time decreases linearly as more workers are assigned. Since each activity has predefined worker limits, a large constant value (1000, denoted as M) is assigned to mode configurations that fall outside the feasible range. Because feasible processing times are significantly smaller than M, these infeasible modes are effectively excluded during optimization. Table 3 presents the mode-dependent processing times for the main PS core layup activities.

Table 3.
Processing times per execution mode for PS core layup activities.
Following the execution of the scheduling optimization model, the selected execution modes and the corresponding number of workers for each operation were determined. These results are presented in Table 4, which summarizes the optimized start and end times, mode-specific activity durations, and resource assignments.

Table 4.
Assigned workers, activity durations, and scheduled times for PS core layup activities.
3.1. Cycle Time Reduction
The implementation of SMED and resource-constrained project scheduling resulted in significant reductions in the processing times of core production operations for both SS and PS molds. Table 5 and Figure 3 provide a comparative overview of selected molding phases before and after optimization, clearly demonstrating measurable gains at each stage. Specifically, the total processing time for core molding operations decreased from 28.83 h to 21.17 h, reflecting a 26.6% improvement across both mold types. These efficiency gains were primarily driven by the identification of parallelizable tasks, the transformation of internal setups into external ones, and improved synchronization between operations.

Table 5.
Optimized operation scheduling results for molding operations.

Figure 3.
Comparative analysis of processing times for SS and PS molding operations.
In addition to the reductions achieved in core fabrication processes, auxiliary time-dependent operations such as blade closure, thermal curing, and downstream post-processing also exhibited significant efficiency improvements. Specifically, the total processing time of these auxiliary stages decreased from 10.17 h to 6.70 h. This improvement was enabled by the strategic alignment of non-critical and flexible tasks, such as root-side surface preparation and internal cleaning, with fixed-duration phases like thermal curing. Although these activities were excluded from the formal scheduling model due to their temporal flexibility, their efficient overlap with critical operations contributed to enhanced resource utilization and minimized idle periods across the production line. As a result, the total production cycle time for a single blade decreased from 39 h to 27.87 h, reflecting a 28.6% improvement in overall efficiency.
3.2. Worker Allocation Efficiency
The model also enhanced the efficiency of labor utilization. Previously, sequential task dependencies and poor synchronization led to idle periods for some workers. The optimized schedule aligned task timings, reduced idle time, and enabled parallel task execution where feasible. Figure 4 illustrates a sample Gantt chart for operations in the PS core layup, highlighting how overlapping tasks were scheduled without violating precedence constraints or exceeding labor availability.
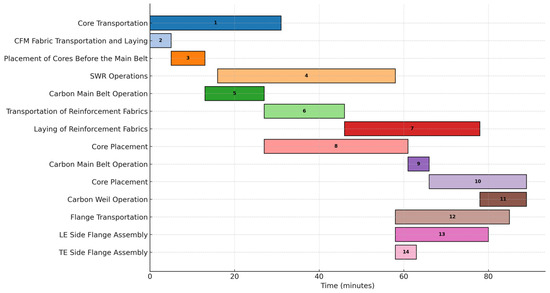
Figure 4.
Gantt chart for PS core layup activities.
Labor utilization metrics showed an increase from an average of 68% to 87%, demonstrating more effective workforce planning and balanced task distribution across the production timeline.
3.3. Precedence and Scheduling Integrity
All precedence relationships, which are critical in large-scale and complex manufacturing processes, were strictly preserved during optimization. Key operations such as composite layering, infusion, and debagging were sequenced in accordance with technical process requirements. The model ensured that no task started before the completion of its predecessors, thereby reducing quality and safety risks. Moreover, the use of flexible execution modes, such as varying workforce allocations, has improved adaptability to real-world shop floor conditions.
3.4. Scenario Analysis and Robustness
The robustness of the scheduling solution was evaluated through sensitivity analyses conducted under three labor availability scenarios. Scenario A represents the standard labor capacity and serves as the baseline. Scenario B models a 10% reduction in available workers, while Scenario C assumes a 20% increase in labor capacity—such as through shift expansion.
The analysis revealed distinct impacts across scenarios. Scenario A resulted in the most balanced performance in terms of both cycle time and labor utilization. Scenario B led to a 12% increase in cycle time due to workforce shortages. In Scenario C, although a slight reduction in cycle time was observed, labor utilization efficiency declined, indicating diminishing returns from overstaffing.
These findings emphasize the importance of strategic labor planning over indiscriminate workforce expansion. Additional scenario-based evaluations further suggest that moderate adjustments in labor capacity can meaningfully influence labor utilization, with minimal impact on overall cycle time.
4. Discussion
The results of this study confirm that integrating SMED techniques with MRCPSP can significantly improve the efficiency of labor-intensive manufacturing systems. In particular, the observed 28.6% reduction in total cycle time demonstrates how lean methodologies and mathematical scheduling models can be effectively combined to address real-world production challenges.
4.1. Theoretical Implications
From a theoretical perspective, this study contributes to the growing literature on hybrid models that combine lean manufacturing tools with quantitative optimization techniques. While SMED has traditionally been employed as a qualitative process improvement method, its integration with resource-constrained scheduling models remains relatively underexplored—particularly in large-scale, manual manufacturing environments.
The findings reinforce earlier work by Kolisch and Padman [19] and Herroelen and Leus [20], who emphasized the utility of constrained scheduling in complex project settings. Unlike prior research, which primarily focuses on automated production systems, this study demonstrates the applicability of such models in manual, fixed-position layouts such as wind turbine blade manufacturing.
4.2. Practical Implications
On a practical level, this research offers actionable insights for manufacturers in the renewable energy sector and similar industries. The case study highlights that the following:
- Significant reductions in setup and changeover times can be achieved without capital-intensive investments, through workflow reorganization and task standardization using SMED principles.
- Workforce allocation optimization, when guided by data-driven scheduling models, leads to higher labor utilization and reduced idle time.
- The use of visual management tools enhances operational transparency and facilitates cross-functional coordination.
- These improvements are particularly relevant for production environments characterized by variability, operator fatigue, and extended cycle times.
To support practical implementation, this study clearly presents the modeling assumptions, operational parameters, and constraint structures that underpin the proposed optimization framework. All task definitions, workforce capacities, and precedence relationships were derived from empirical data gathered during a lean transformation initiative that included SMED-based workflow restructuring and internal process documentation. These methodological components not only clarify the proposed framework but also enable practitioners to replicate it across similar fixed-position manufacturing contexts.
4.3. Comparison with Existing Studies
Compared to previous studies primarily focusing on isolated applications of SMED [11,31], this study integrates a formal scheduling framework that not only reduces processing time but also ensures resource feasibility. Furthermore, the scenario analyses validate the model’s robustness under varying conditions, aligning with the findings of Hartmann and Drexl [29] and Talbot [32], who emphasized the sensitivity of the MRCPSP to fluctuations in resource availability.
The combined use of SMED and MRCPSP offers a more comprehensive framework than either method alone. It balances operational simplification with optimized decision-making, providing a scalable methodology that can be adapted across various production contexts.
5. Conclusions
This study introduces a hybrid approach to enhance production efficiency in labor-intensive wind turbine blade manufacturing by combining SMED principles with the MRCPSP model. Integrating the results of process analysis with lean restructuring and mathematical optimization led to a 28.6% reduction in total cycle time, accompanied by significant improvements in labor utilization and workflow synchronization. These findings underscore the potential of combining lean methodologies with quantitative scheduling models to address operational challenges—particularly in renewable energy sectors characterized by large product sizes, fixed-position layouts, and manual labor.
SMED enabled the identification and transformation of internal setup operations into parallelizable tasks, while MRCPSP facilitated optimal workforce allocation under precedence and resource constraints. The proposed framework offers a scalable and cost-effective solution for manufacturers aiming to reduce lead times without requiring significant capital investment. It is particularly well suited to high-mix, low-volume production environments where flexibility and responsiveness are essential.
Future research may explore the following:
- Modeling uncertainty within scheduling parameters;
- Implementing real-time adaptive optimization via IoT and machine learning;
- Assessing the long-term impact of lean interventions on workforce productivity and morale.
Ultimately, the methodology presented in this study provides a practical and adaptable blueprint for industries seeking to merge process simplification with scheduling precision in pursuit of operational excellence.
Author Contributions
Conceptualization, G.T.; Methodology, G.T., G.Y., N.A. and G.K.; Software, G.T., N.A. and G.K.; Validation, G.T. and G.Y.; Formal analysis, G.T. and G.Y.; Investigation, N.A. and G.K.; Resources, G.T., N.A. and G.K.; Data curation, N.A. and G.K.; Writing—original draft, G.T., N.A. and G.K.; Writing—review & editing, G.T.; Visualization, G.T., G.Y., N.A. and G.K.; Supervision, G.T. and G.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author. The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tripathi, V.; Chattopadhyaya, S.; Mukhopadhyay, A.K.; Sharma, S.; Li, C.; Singh, S.; Saleem, W.; Salah, B.; Mohamed, A. Recent Progression Developments on Process Optimization Approach for Inherent Issues in Production Shop Floor Management for Industry 4.0. Processes 2022, 10, 1587. [Google Scholar] [CrossRef]
- Gil-Vilda, F.; Yagüe-Fabra, J.A.; Sunyer, A. From Lean Production to Lean 4.0: A Systematic Literature Review with a Historical Perspective. Appl. Sci. 2021, 11, 10318. [Google Scholar] [CrossRef]
- Stump, B.; Badurdeen, F. Integrating lean and other strategies for mass customization manufacturing: A case study. J. Intell. Manuf. 2012, 23, 109–124. [Google Scholar] [CrossRef]
- Jebbor, I.; Benmamoun, Z.; Hachimi, H. Optimizing Manufacturing Cycles to Improve Production: Application in the Traditional Shipyard Industry. Processes 2023, 11, 3136. [Google Scholar] [CrossRef]
- Maware, C.; Parsley, D.M., II. The Challenges of Lean Transformation and Implementation in the Manufacturing Sector. Sustainability 2022, 14, 6287. [Google Scholar] [CrossRef]
- Sarwar, J.; Khan, A.A.; Khan, A.; Hasnain, A.; Arafat, S.M.; Ali, H.U.; Uddin, G.M.; Sosnowski, M.; Krzywanski, J. Impact of Stakeholders on Lean Six Sigma Project Costs and Outcomes during Implementation in an Air-Conditioner Manufacturing Industry. Processes 2022, 10, 2591. [Google Scholar] [CrossRef]
- Gavriluţă, A.C.; Niţu, E.L.; Gavriluţă, C.A. Algorithm to Use Some Specific Lean Manufacturing Methods: Application in an Industrial Production Process. Processes 2021, 9, 641. [Google Scholar] [CrossRef]
- Shingo, S. A Revolution in Manufacturing: The SMED System, 1st ed.; Productivity Press: New York, NY, USA, 1985. [Google Scholar] [CrossRef]
- McIntosh, R.I.; Culley, S.J.; Mileham, A.R.; Owen, G.W. A critical evaluation of Shingo’s “SMED” (Single Minute Exchange of Die) methodology. Int. J. Prod. Res. 2000, 38, 2377–2395. [Google Scholar] [CrossRef]
- Ribeiro, M.A.S.; Santos, A.C.O.; de Amorim, G.d.F.; de Oliveira, C.H.; da Silva Braga, R.A.; Netto, R.S. Analysis of the Implementation of the Single Minute Exchange of Die Methodology in an Agroindustry through Action Research. Machines 2022, 10, 287. [Google Scholar] [CrossRef]
- Kumar, B.S.; Abuthakeer, S.S. Implementation of lean tools and techniques in an automotive industry. J. Appl. Sci. 2012, 12, 1032–1037. [Google Scholar] [CrossRef]
- Almomani, M.A.; Aladeemy, M.; Abdelhadi, A.; Mumani, A. A proposed approach for setup time reduction through integrating conventional SMED method with multiple criteria decision-making techniques. Comput. Ind. Eng. 2013, 68, 461–469. [Google Scholar] [CrossRef]
- Garcia-Garcia, G.; Singh, Y.; Jagtap, S. Optimising Changeover through Lean-Manufacturing Principles: A Case Study in a Food Factory. Sustainability 2022, 14, 8279. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Lee, D.; Chen, S.-C.; Tang, W. A Lean Manufacturing Progress Model and Implementation for SMEs in the Metal Products Industry. Processes 2022, 10, 835. [Google Scholar] [CrossRef]
- Santos, V.; Sousa, V.F.C.; Silva, F.J.G.; Matias, J.C.O.; Costa, R.D.; Pinto, A.G.; Campilho, R.D.S.G. Applying the SMED Methodology to Tire Calibration Procedures. Systems 2022, 10, 239. [Google Scholar] [CrossRef]
- Rahardjo, B.; Wang, F.-K.; Yeh, R.-H.; Chen, Y.-P. Lean Manufacturing in Industry 4.0: A Smart and Sustainable Manufacturing System. Machines 2023, 11, 72. [Google Scholar] [CrossRef]
- Kyriakidis, T.S.; Kopanos, G.M.; Georgiadis, M.C. MILP formulations for single- and multi-mode resource-constrained Project scheduling problems. Comput. Chem. Eng. 2012, 36, 369–385. [Google Scholar] [CrossRef]
- Sprecher, A.; Hartmann, S.; Drexl, A. An exact algorithm for project scheduling with multiple modes. Oper. Res. Spektrum 1997, 19, 195–203. [Google Scholar] [CrossRef]
- Kolisch, R.; Padman, R. An integrated survey of deterministic project scheduling. Omega 2001, 29, 249–272. [Google Scholar] [CrossRef]
- Herroelen, W.; Leus, R. Project scheduling under uncertainty: Survey and research potentials. Eur. J. Oper. Res. 2005, 165, 289–306. [Google Scholar] [CrossRef]
- Ramos, A.S.; Miranda-Gonzalez, P.A.; Nucamendi-Guillén, S.; Olivares-Benitez, E. A Formulation for the Stochastic Multi-Mode Resource-Constrained Project Scheduling Problem Solved with a Multi-Start Iterated Local Search Metaheuristic. Mathematics 2023, 11, 337. [Google Scholar] [CrossRef]
- Sabzehparvar, M.; Seyed-Hosseini, S.M. A mathematical model for the multi-mode resource-constrained project scheduling problem with mode dependent timelags. J. Supercomput. 2008, 44, 257–273. [Google Scholar] [CrossRef]
- Cao, W.; Yu, J.; Xu, M. Optimization Scheduling of Virtual Power Plants Considering Source-Load Coordinated Operation and Wind–Solar Uncertainty. Processes 2024, 12, 11. [Google Scholar] [CrossRef]
- Gomes, E.; Pereira, L.; Esteves, A.; Morais, H. Metaheuristic Optimization Methods in Energy Community Scheduling: A Benchmark Study. Energies 2024, 17, 2968. [Google Scholar] [CrossRef]
- Aguilar, D.; Quinones, J.J.; Pineda, L.R.; Ostanek, J.; Castillo, L. Optimal scheduling of renewable energy microgrids: A robust multi-objective approach with machine learning-based probabilistic forecasting. Appl. Energy 2024, 369, 123548. [Google Scholar] [CrossRef]
- Bhadoria, A.; Marwaha, S. An optimum generation scheduling of electrical power system considering the effect of renewable energy sources by using a hybrid metaheuristic search algorithm. OPSEARCH 2024, 61, 1301–1382. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, J.; Demeulemeester, E.; Chen, Z. Project scheduling for engineer-to-order assembly process with renewable energy. Expert Syst. Appl. 2025, 270, 126412. [Google Scholar] [CrossRef]
- Li, G.; Li, J.; Yan, K.; Bian, J. Centralized Distributed Scheduling Strategy of Distribution Network Based on Multi Temporal Hierarchical Cooperative Game. Energy Eng. 2025, 122, 1113–1136. [Google Scholar] [CrossRef]
- Hartmann, S.; Drexl, A. Project scheduling with multiple modes: A comparison of exact algorithms. Networks 1998, 32, 283–297. [Google Scholar] [CrossRef]
- Cheng, J.; Fowler, J.; Kempf, K.; Mason, S. Multi-mode resource-constrained project scheduling problems with non-preemptive activity splitting. Comput. Oper. Res. 2015, 53, 275–287. [Google Scholar] [CrossRef]
- McIntosh, R.; Owen, G.; Culley, S.; Mileham, T. Changeover improvement: Reinterpreting Shingo’s “SMED” methodology. IEEE Trans. Eng. Manag. 2007, 54, 98–111. [Google Scholar] [CrossRef]
- Talbot, F.B. Resource-Constrained Project Scheduling with Time-Resource Tradeoffs: The Nonpreemptive Case. Manag. Sci. 1982, 28, 1197–1210. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).