Key Parameter Optimization Study of Composite Rod Drill in Gas Extraction Borehole Drilling in Soft, Medium, and Hard Coal Seams
Abstract
1. Introduction
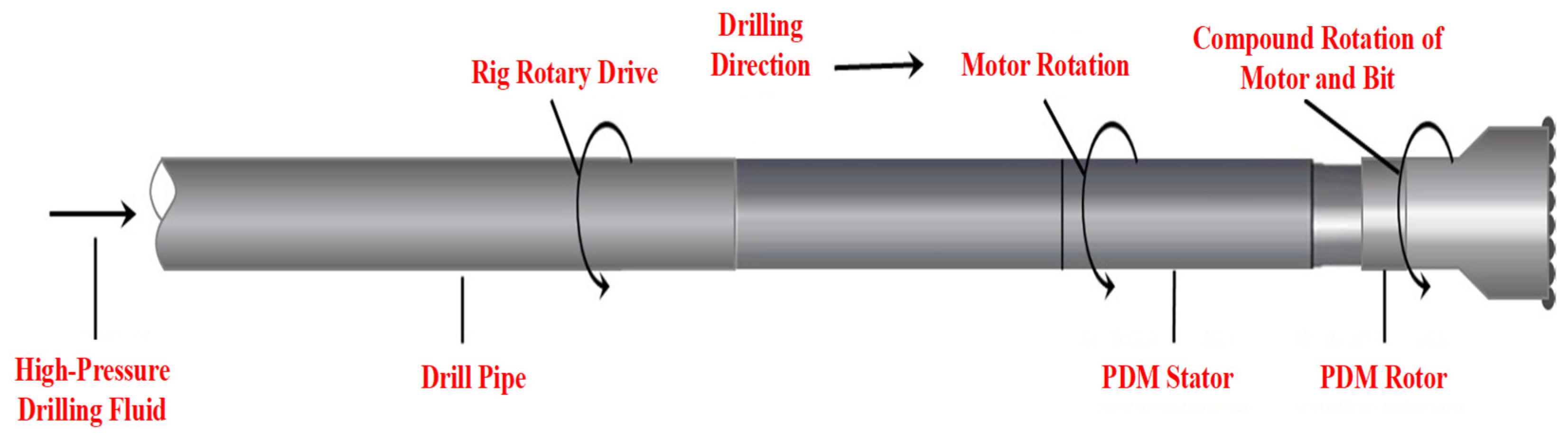
2. Composite Screw Drill-Bit Technology
2.1. Structure Principle of the Screw Drill Bit
2.2. Principle of Composite Screw Drill-Bit Drilling Technology
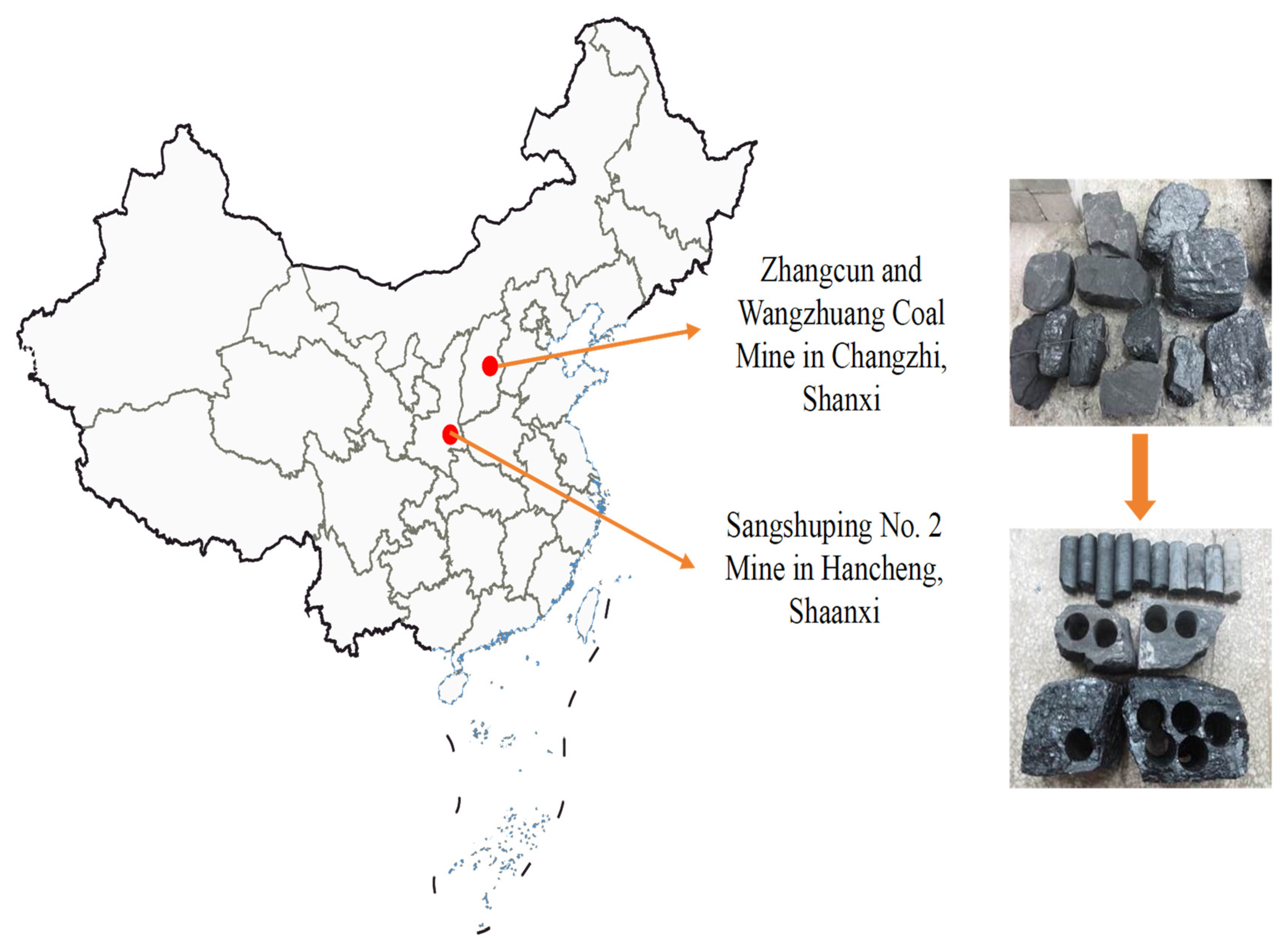
3. Measurement of Coal Seam Mechanical Parameters and Hardness Classification
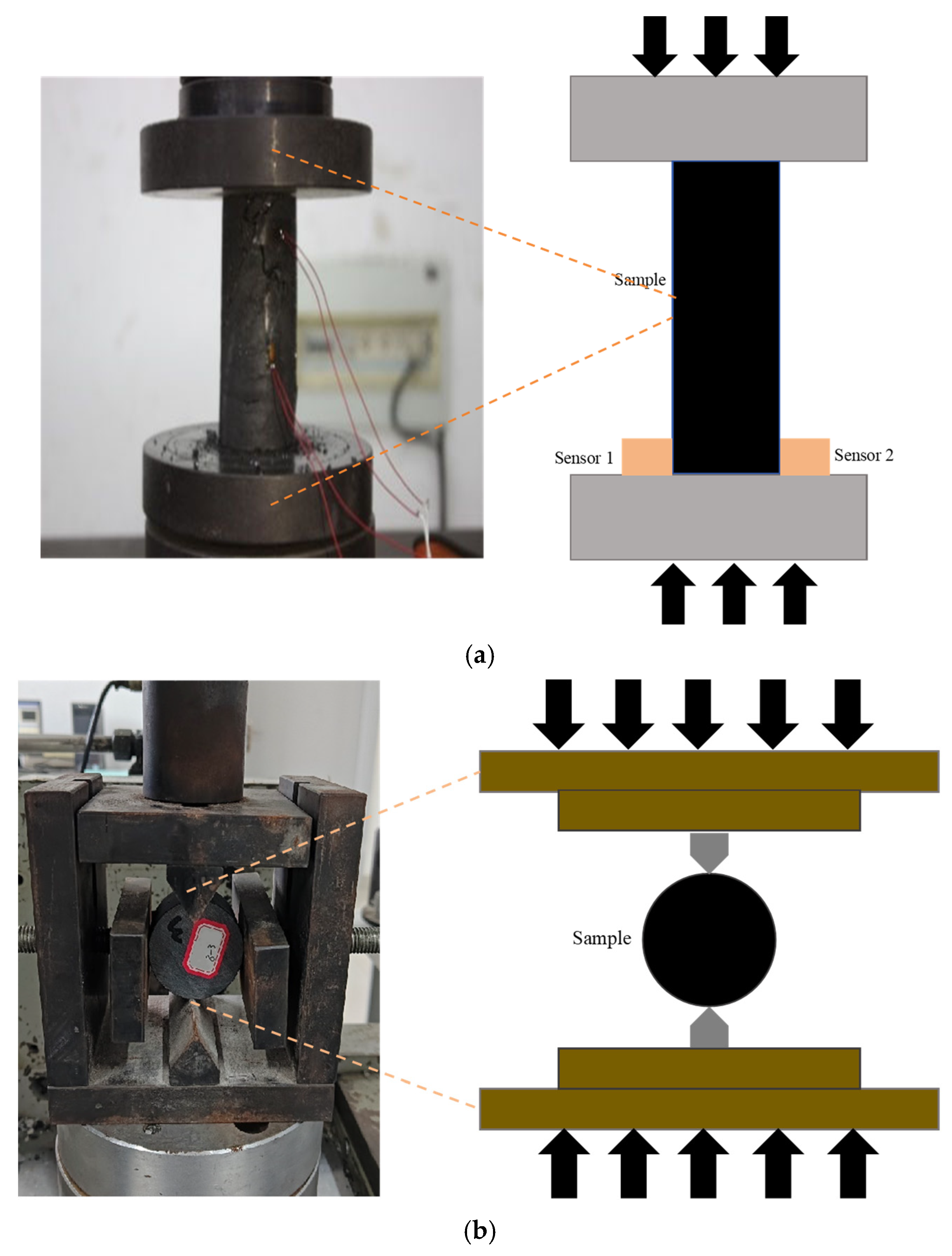
3.1. Measurement of Mechanical Parameters of Coal Samples
3.2. Calculation of the Pomeroy Hardness Coefficient
- ①
- Isotropy and Homogeneity: Equation (1) assumes that the material is isotropic and homogeneous. Although coal samples may not be perfectly isotropic and homogeneous due to their natural formation processes, those used in this study were carefully selected and prepared to minimize the effects of anisotropy and heterogeneity.
- ②
- Linear Elastic Behavior: The equation assumes linear elastic behavior up to failure. While coal may exhibit some nonlinear behavior under certain conditions, the uniaxial compressive strength used in the equation is typically determined under conditions where linear elastic behavior is predominant.
- ③
- Failure Mode: Equation (1) is based on the failure mode of rocks under uniaxial compression. For coal, it is assumed that the failure mode is similar under similar loading conditions. The uniaxial compressive strength test results (see Table 3, Table 4 and Table 5) provide a reasonable basis for estimating the Pomeroy hardness coefficient for coal.
- ④
- Scale Effects: The equation is applicable to a specific scale of rock samples. The coal samples in this study were prepared with dimensions typical for such tests, minimizing scale effects and ensuring comparability with rock results.
- ⑤
- Material Properties: The equation assumes consistent material properties across different types of rocks. While coal and rock have distinct material properties, the Pomeroy hardness coefficient offers a relative hardness measure that can be used to compare different coal samples.
4. Experimental Design and Methods for Drilling Parameter Optimization
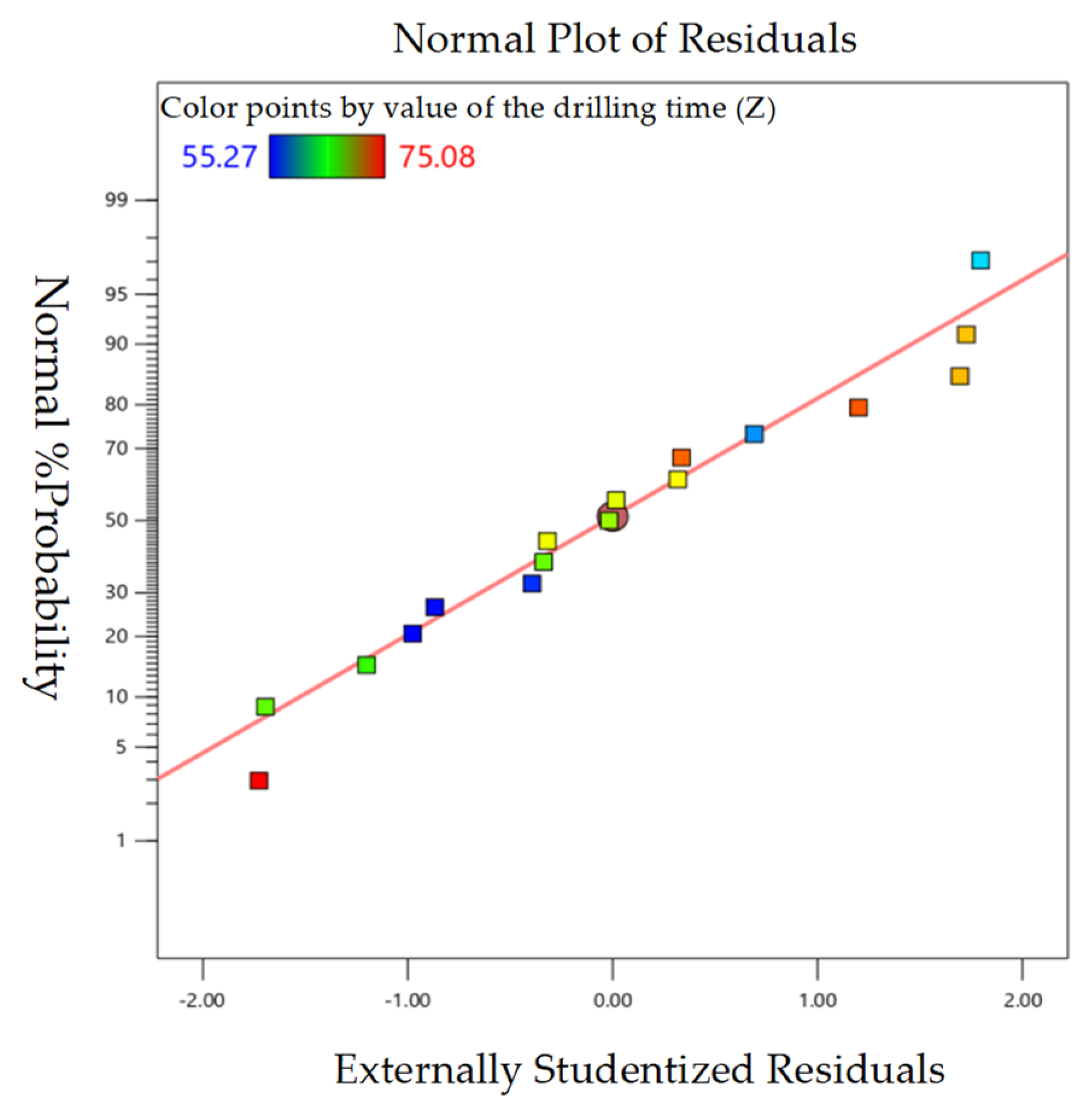
5. Results Analysis
5.1. Validation of Soft Coal Seam Adaptability
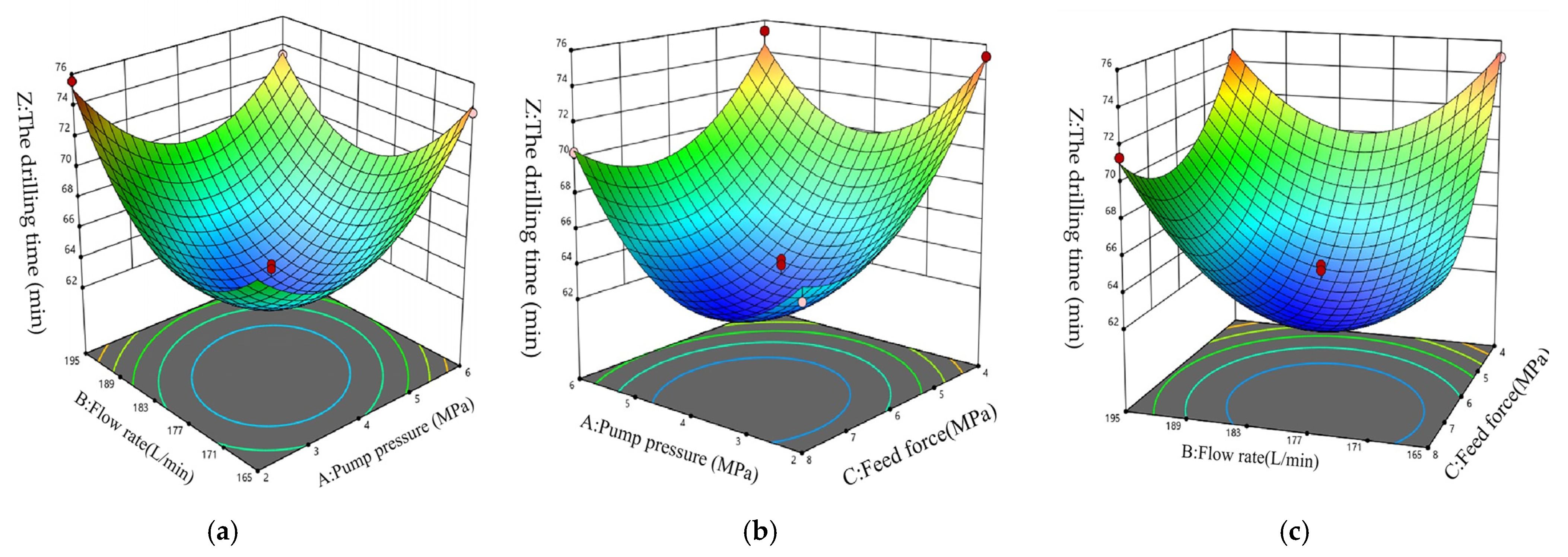
5.2. Optimal Drilling Parameters for Medium–Hard Coal Seams
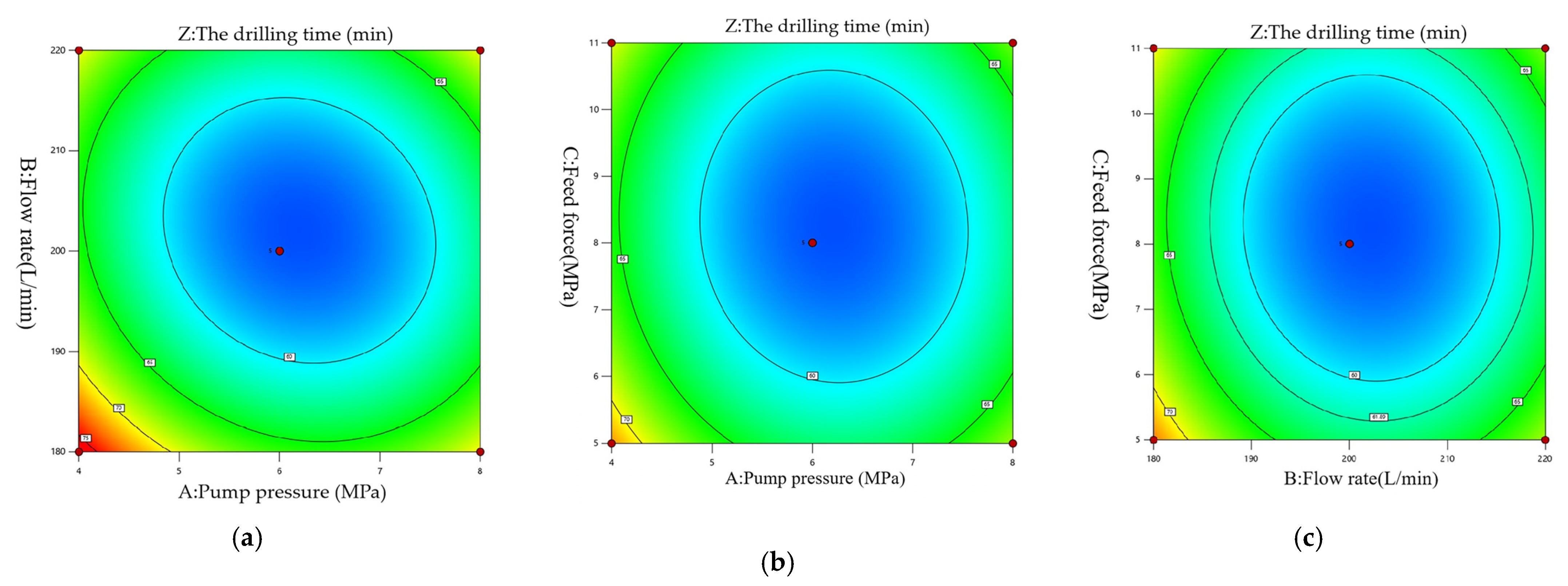
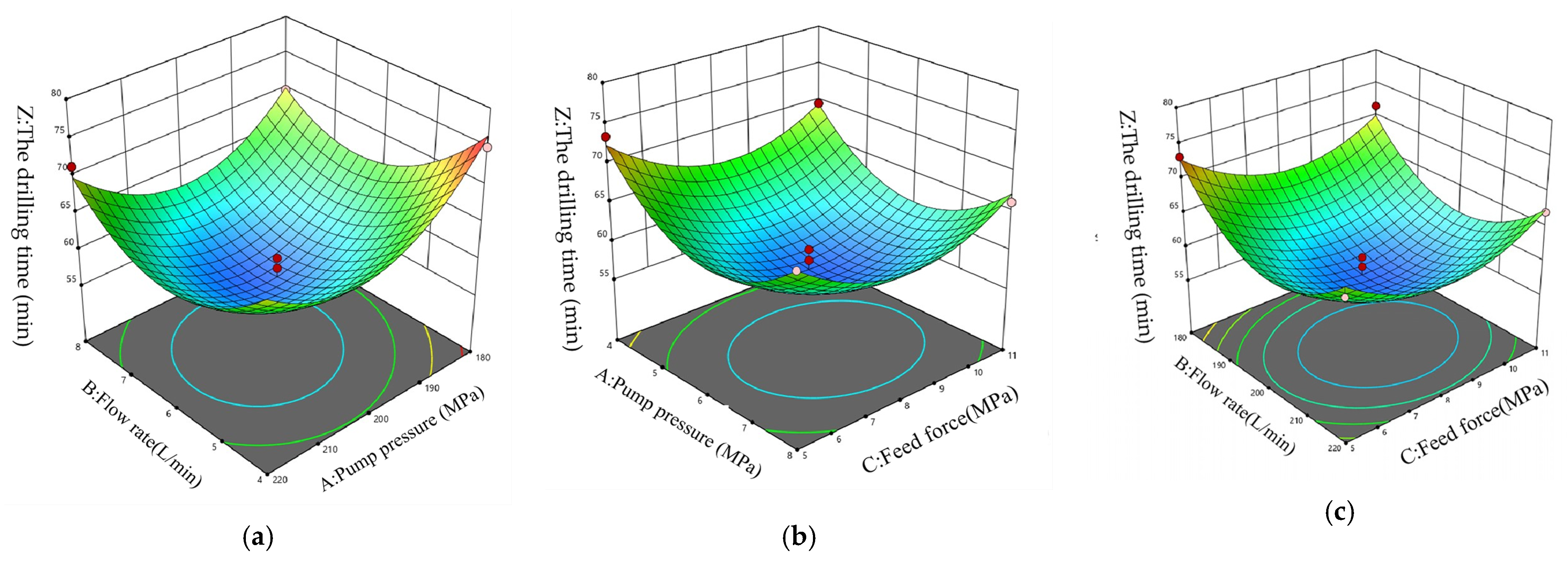
5.3. Optimal Drilling Parameters for Hard Coal Seams
6. Conclusions
- (1)
- The compressive strength of the coal seam in the north boundary tunnel of the No. 2 shaft at Sangshu Ping is 8.74 MPa, the tensile strength is 0.85 MPa, and the hardness coefficient is 0.87, which belongs to a soft coal seam. The compressive strength of the 2606 transport tunnel at Zhangcun Coal Mine is 21.6 MPa, the tensile strength is 1.63 MPa, and the hardness coefficient is 2.16, which belongs to a medium–hard coal seam. The compressive strength of the 91–105 dedicated return air tunnel at Wangzhuang Coal Mine is 34.7 MPa, the tensile strength is 2.42 MPa, and the hardness coefficient is 3.47, which belongs to a soft coal seam.
- (2)
- Using response surface methodology (RSM), it was concluded that the composite screw drill-bit technology is not suitable for soft coal seams but can be used in medium–hard and hard coal seams. The ranking of the impact degree of each key parameter on drilling time in medium–hard coal seams is feed force > flow rate > pump pressure; in hard coal seams, the ranking is flow rate > feed force > pump pressure.
- (3)
- According to the Design Expert software, under medium–hard coal seam conditions, the optimal drilling parameters for the composite screw drill-bit technology are a pump pressure of 4 MPa, a flow rate of 180 L/min, and a feed force of 6 MPa. Under these drilling parameters, the theoretical time to drill 100 m is 62 min and 33 s. Under hard coal seam conditions, the optimal drilling parameters are a pump pressure of 6 MPa, a flow rate of 200 L/min, and a feed force of 8 MPa. Under these parameters, the theoretical time to drill 100 m is 55 min and 27 s.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, J.H.; Cheng, Y.P. Current situation and prevention countermeasures of coal and gas outburst in Chinese coal mines. J. Min. Saf. Eng. 2007, 24, 7. [Google Scholar] [CrossRef]
- Cheng, J.; Ran, D.; Ju, Y. Plugging effects by GPM based two-phase flow in gas drainage fracture: A simulation study. Int. J. Rock Mech. Min. Sci. 2024, 174, 105639. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Zhang, Q.H.; Liu, J. Research progress and prospect of early warning systems for coal and gas outburst and compound dynamic disasters in China. J. China Coal Soc. 2025, 49, 911–923. [Google Scholar] [CrossRef]
- Yuan, A.Y.; Yang, X.L.; Hou, J.L. Comprehensive characterization of pore structure of coal seams with abnormal gas emission in deep close-distance coal seam groups. Coal Sci. Technol. 2024, 52, 116–126. [Google Scholar] [CrossRef]
- Cao, K.; Li, Z.H.; Yu, D.S. Study on the Predecessor Characteristics and Comprehensive Early Warning of Coal and Gas Outburst in Excavation Face. Coal Sci. Technol. 2020, 48, 147–152. [Google Scholar] [CrossRef]
- Zhao, H.C.; Wang, Q.S. Research on gas control in the un-protected layer area of high-outburst mines. Min. Saf. Environ. Prot. 2024, 51, 56–64. [Google Scholar] [CrossRef]
- Liang, Y.P.; Li, Z.Y.; Zhu, S.C. Research Status and Emission Reduction Countermeasures of Methane Emissions from Closed/Abandoned Coal Mines. J. China Coal Soc. 2023, 48, 1645–1660. [Google Scholar] [CrossRef]
- Cheng, J.; Ran, D.; Fu, Q. Solid–liquid particle flow sealing mucus (PFSM) in enhancing coalbed methane (CBM) recovery: Multiple-perspectives analysis and mechanism insights. Constr. Build. Mater. 2024, 435, 136670. [Google Scholar] [CrossRef]
- Ran, D.; Cheng, J.; Sheng, S. A two-phase particle flow method based on SCLB for enhancing CBM recovery: Experimental testing and engineering applications. Powder Technol. 2024, 440, 119754. [Google Scholar] [CrossRef]
- Ran, D.; Cheng, J.; Liu, Y. Experimental validation and mechanistic elucidation of crack division and two-phase flow-mediated sealing in coalbed methane extraction boreholes. Int. J. Rock Mech. Min. Sci. 2025, 186, 106021. [Google Scholar] [CrossRef]
- Zhao, Y.Z. Research on the Controlled Mechanism of Screw Drill Tool Drilling in Near-Horizontal Directional Holes in Coal Mines. Ph.D. Thesis, China Coal Research Institute, Beijing, China, 2008. [Google Scholar]
- Peng, X. Research on the High-Efficiency Rock-Breaking Mechanism of Composite Impact Screw Drill Tools in Coal Mines. Ph.D. Thesis, China Coal Research Institute, Beijing, China, 2021. [Google Scholar] [CrossRef]
- Shi, Z.J.; Xu, C.; Li, Q.X. Key technologies for efficient hole formation of 2570 m in-seam ultra-deep directional holes in coal mines. Coal Sci. Technol. 2020, 48, 196–201. [Google Scholar] [CrossRef]
- Bai, B.Z. Research on Drilling Acceleration Technology in the Paleozoic Formation of Shunbei Oilfield. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2023. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Xu, S.J.; Jiang, Z.X. Mechanical specific energy analysis and drilling parameter optimization for deep wells in the southern margin of Junggar Basin. J. Southwest Pet. Univ. 2021, 43, 51–61. [Google Scholar] [CrossRef]
- Wang, G.; Xu, B.Y. A method for predicting the drilling speed of PDC bits by integrating theoretical models and machine learning. Pet. Drill. Tech. 2024, 52, 117. [Google Scholar] [CrossRef]
- Zhang, X.; Qiao, D.Y.; Wang, X. Development and application of rotary impact drilling speed-up device. Drill. Prod. Technol. 2022, 45, 106–111. [Google Scholar] [CrossRef]
- Kang, Y.G.; Zhang, B.; Zhang, M. Key technologies and applications of the surface life-support hole project test in Meihuajing Mine. Saf. Coal Mines 2022, 6, 53. [Google Scholar] [CrossRef]
- Zhang, C. Application status and future development suggestions of screw drill tools. China Pet. Chem. Stand. Qual. 2016, 7, 2. [Google Scholar] [CrossRef]
- Qiang, Z.; Zhi, C.; Pengfei, Z. Hydraulic Circulation Test of Bypass Valve of Positive Displacement Motor with Uniform Wall Thickness. China Pet. Mach. 2015, 43, 13–16. [Google Scholar] [CrossRef]
- Shi, C.S.; Li, J.P.; Deng, J. Study on multi-roller rotary feed forming mechanism of spiral tube with uniform wall thickness. Int. J. Adv. Manuf. Technol. 2020, 106, 18. [Google Scholar] [CrossRef]
- Li, Q.X. Research and Application of Composite Directional Drilling Technology in Broken Soft Coal Seams. Coal Sci. Technol. 2018, 46, 101–106. [Google Scholar] [CrossRef]
- Luo, X. Research on the safety thickness of layered roof based on the improved Prandtl’s equilibrium arch theory. Coal Sci. Technol. 2021, 49, 8. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]


| Number | Mass (g) | Diameter (mm) | Height (mm) | Number | Mass (g) | Diameter (mm) | Height (mm) | Number | Mass (g) | Diameter (mm) | Height (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| U1-1 | 271.1 | 49.42 | 100.35 | U2-1 | 268.3 | 49.49 | 100.24 | U3-1 | 254.3 | 49.49 | 100.10 |
| U1-2 | 272.4 | 49.48 | 100.27 | U2-2 | 266.6 | 49.44 | 100.50 | U3-2 | 258.7 | 49.44 | 99.15 |
| U1-3 | 261.5 | 49.44 | 100.11 | U2-3 | 274.1 | 49.46 | 100.81 | U3-3 | 252.3 | 49.49 | 100.06 |
| U1-4 | 266.8 | 49.43 | 100.01 | U2-4 | 262.3 | 49.49 | 100.11 | U3-4 | 260.1 | 49.46 | 101.08 |
| U1-5 | 259.4 | 49.47 | 99.95 | U2-5 | 265.0 | 49.42 | 100.13 | U3-5 | 254.4 | 49.50 | 100.22 |
| U1-6 | 268.8 | 49.45 | 101.02 | U2-6 | 266.4 | 49.44 | 100.15 | U3-6 | 255.8 | 49.45 | 100.41 |
| U1-7 | 267.1 | 49.47 | 100.82 | U2-7 | 258.7 | 49.45 | 100.48 | U3-7 | 244.4 | 49.50 | 100.19 |
| U1-8 | 266.2 | 49.48 | 100.27 | U2-8 | 252.9 | 49.49 | 100.37 | U3-8 | 247.8 | 49.44 | 100.76 |
| U1-9 | 265.4 | 49.46 | 100.34 | U2-9 | 253.1 | 49.50 | 100.06 | U3-9 | 249.9 | 49.45 | 100.44 |
| U1-10 | 265.5 | 49.44 | 100.43 | U2-10 | 255.8 | 49.46 | 100.48 | U3-10 | 248.8 | 49.47 | 100.85 |
| Number | Mass (g) | Diameter (mm) | Height (mm) | Number | Mass (g) | Diameter (mm) | Height (mm) | Number | Mass (g) | Diameter (mm) | Height (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| B1-1 | 128.6 | 49.64 | 50.18 | B2-1 | 129.2 | 49.66 | 50.27 | B3-1 | 127.2 | 49.59 | 50.15 |
| B1-2 | 130.7 | 49.84 | 50.14 | B2-2 | 131.3 | 49.73 | 50.71 | B3-2 | 128.4 | 49.43 | 50.44 |
| B1-3 | 129.8 | 49.48 | 50.16 | B2-3 | 127.1 | 49.84 | 50.68 | B3-3 | 126.2 | 49.46 | 50.38 |
| B1-4 | 132.4 | 49.77 | 50.01 | B2-4 | 124.2 | 49.88 | 50.44 | B3-4 | 130.1 | 49.48 | 50.14 |
| B1-5 | 128.7 | 49.26 | 49.98 | B2-5 | 130.5 | 49.90 | 50.35 | B3-5 | 127.2 | 49.66 | 50.26 |
| B1-6 | 133.4 | 49.59 | 50.50 | B2-6 | 129.2 | 49.79 | 50.14 | B3-6 | 127.9 | 49.63 | 50.04 |
| B1-7 | 132.6 | 49.81 | 50.47 | B2-7 | 129.4 | 49.75 | 50.50 | B3-7 | 122.2 | 49.57 | 50.49 |
| B1-8 | 132.1 | 49.92 | 50.14 | B2-8 | 126.5 | 49.48 | 50.59 | B3-8 | 123.9 | 49.55 | 50.69 |
| B1-9 | 131.7 | 49.94 | 50.17 | B2-9 | 124.4 | 49.69 | 50.41 | B3-9 | 125.0 | 49.64 | 50.41 |
| B1-10 | 130.8 | 49.66 | 50.22 | B2-10 | 127.9 | 49.81 | 50.44 | B3-10 | 124.4 | 49.58 | 50.34 |
| No. | Elastic Modulus (GPa) | Uniaxial Compressive Strength (MPa) | No. | Tensile Strength (MPa) |
|---|---|---|---|---|
| U1-1 | 1.36 | 7.38 | B1-1 | 0.89 |
| U1-2 | 1.49 | 9.14 | B1-2 | 0.76 |
| U1-3 | 1.26 | 8.29 | B1-3 | 0.79 |
| U1-4 | 1.38 | 9.48 | B1-4 | 0.84 |
| U1-5 | 1.48 | 10.21 | B1-5 | 0.81 |
| U1-6 | 1.44 | 8.99 | B1-6 | 0.84 |
| U1-7 | 1.38 | 8.61 | B1-7 | 0.94 |
| U1-8 | 1.50 | 9.49 | B1-8 | 0.99 |
| U1-9 | 1.48 | 7.29 | B1-9 | 0.82 |
| U1-10 | 1.39 | 8.55 | B1-10 | 0.81 |
| No. | Elastic Modulus (GPa) | Uniaxial Compressive Strength (MPa) | No. | Tensile Strength (MPa) |
|---|---|---|---|---|
| U2-1 | 2.64 | 20.36 | B2-1 | 1.54 |
| U2-2 | 2.39 | 22.31 | B2-1 | 1.78 |
| U2-3 | 2.52 | 21.68 | B2-1 | 1.66 |
| U2-4 | 2.24 | 19.87 | B2-1 | 1.49 |
| U2-5 | 2.48 | 24.44 | B2-1 | 1.61 |
| U2-6 | 2.15 | 21.48 | B2-1 | 1.58 |
| U2-7 | 2.44 | 22.29 | B2-1 | 1.69 |
| U2-8 | 2.81 | 22.59 | B2-1 | 1.74 |
| U2-9 | 2.45 | 20.54 | B2-1 | 1.62 |
| U2-10 | 2.38 | 19.94 | B2-10 | 1.57 |
| No. | Elastic Modulus (GPa) | Uniaxial Compressive Strength (MPa) | No. | Tensile Strength (MPa) |
|---|---|---|---|---|
| U3-1 | 3.46 | 31.4 | B3-1 | 2.55 |
| U3-2 | 3.44 | 39.8 | B3-1 | 2.42 |
| U3-3 | 3.49 | 37.4 | B3-1 | 2.38 |
| U3-4 | 3.43 | 32.6 | B3-1 | 2.61 |
| U3-5 | 3.40 | 39.2 | B3-1 | 2.14 |
| U3-6 | 3.49 | 29.9 | B3-1 | 2.48 |
| U3-7 | 3.43 | 36.6 | B3-1 | 2.41 |
| U3-8 | 3.48 | 35.4 | B3-1 | 2.94 |
| U3-9 | 3.40 | 30.1 | B3-1 | 2.18 |
| U3-10 | 3.44 | 34.3 | B3-10 | 2.11 |
| Sampling Location | Elastic Modulus (GPa) | Uniaxial Compressive Strength (MPa) | Poisson’s Ratio (v) | Tensile Strength (MPa) |
|---|---|---|---|---|
| North Boundary Tunnel | 1.42 ± 0.07 | 8.74 ± 0.93 | 0.23 | 0.85 ± 0.07 |
| 2606 Transport Tunnel | 2.45 ± 0.18 | 21.6 ± 1.43 | 0.16 | 1.63 ± 0.09 |
| 91–105 Dedicated Return Air Tunnel | 3.45 ± 0.03 | 34.7 ± 3.61 | 0.13 | 2.42 ± 0.24 |
| No. | Coal Mine | Sampling Location | Classification | |
|---|---|---|---|---|
| 1 | Sangshuping No. 2 Shaft | North Boundary Tunnel | 0.87 | Soft Coal |
| 2 | Zhangcun Coal Mine | 2606 Transport Tunnel | 2.16 | Medium Hard Coal |
| 3 | Wangzhuang Coal Mine | 91–105 Dedicated Return Air Tunnel | 3.47 | Hard Coal |
| Factor | Unit | Level | ||
|---|---|---|---|---|
| Pump Pressure | MPa | 2 | 3 | 4 |
| Flow Rate | L/min | 150 | 160 | 170 |
| Feed Pressure | MPa | 1.5 | 2 | 2.5 |
| Number of Groups | A | B | C | Z |
|---|---|---|---|---|
| 1 | 4 | 160 | 1.5 | / |
| 2 | 2 | 160 | 2.5 | / |
| 3 | 3 | 160 | 2 | / |
| 4 | 3 | 170 | 2.5 | 83 min 16 s |
| 5 | 3 | 160 | 2 | 89 min 34 s |
| 6 | 4 | 160 | 2.5 | / |
| 7 | 3 | 160 | 2 | / |
| 8 | 3 | 150 | 2.5 | / |
| 9 | 4 | 170 | 2 | 83 min 51 s |
| 10 | 2 | 150 | 2 | / |
| 11 | 3 | 160 | 2 | / |
| 12 | 3 | 150 | 1.5 | 79 min 52 s |
| 13 | 3 | 170 | 1.5 | / |
| 14 | 4 | 150 | 2 | / |
| 15 | 2 | 170 | 2 | / |
| 16 | 3 | 160 | 2 | 86 min 01 s |
| 17 | 2 | 160 | 1.5 | / |
| Factor | Unit | Level | ||
|---|---|---|---|---|
| Pump Pressure | MPa | 2 | 4 | 6 |
| Flow Rate | L/min | 165 | 180 | 195 |
| Feed Pressure | MPa | 4 | 6 | 8 |
| Number of Groups | A | B | C | Z |
|---|---|---|---|---|
| 1 | 2 | 180 | 8 | 65 min 15 s |
| 2 | 4 | 180 | 6 | 64 min 37 s |
| 3 | 2 | 195 | 6 | 75 min 18 s |
| 4 | 6 | 180 | 8 | 70 min 33 s |
| 5 | 4 | 180 | 6 | 63 min 03 s |
| 6 | 2 | 180 | 4 | 75 min 47 s |
| 7 | 6 | 165 | 6 | 74 min 15 s |
| 8 | 4 | 180 | 6 | 62 min 66 s |
| 9 | 4 | 165 | 4 | 75 min 02 s |
| 10 | 4 | 195 | 4 | 74 min 18 s |
| 11 | 6 | 180 | 4 | 75 min 03 s |
| 12 | 6 | 195 | 6 | 73 min 53 s |
| 13 | 2 | 165 | 6 | 69 min 37 s |
| 14 | 4 | 165 | 8 | 66 min 18 s |
| 15 | 4 | 195 | 8 | 71 min 20 s |
| 16 | 4 | 180 | 6 | 62 min 19 s |
| 17 | 4 | 180 | 6 | 63 min 18 s |
| Source | Sequential p-Value | Lack of Fit p-Value | Adjusted R2 | |
|---|---|---|---|---|
| Linear | 0.2723 | 0.0787 | −0.1132 | |
| 2FI | 0.8159 | −0.0950 | −0.6298 | |
| Quadratic | <0.0001 | 0.9758 | 0.8945 | Suggested |
| Cubic Model | 0.2788 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 426.62 | 9 | 47.40 | 72.58 | <0.0001 |
| A | 7.57 | 1 | 7.57 | 11.58 | 0.0114 |
| B | 11.47 | 1 | 11.47 | 17.57 | 0.0041 |
| C | 89.38 | 1 | 89.38 | 136.85 | <0.0001 |
| AB | 12.39 | 1 | 12.39 | 18.97 | 0.0033 |
| AC | 6.71 | 1 | 6.71 | 10.27 | 0.0150 |
| BC | 8.58 | 1 | 8.58 | 13.14 | 0.0084 |
| A2 | 100.79 | 1 | 100.79 | 154.32 | <0.0001 |
| B2 | 108.12 | 1 | 108.12 | 165.55 | <0.0001 |
| C2 | 51.95 | 1 | 51.95 | 79.54 | <0.0001 |
| Residual | 4.57 | 7 | 0.6531 | ||
| Lack of Fit | 2.66 | 3 | 0.8854 | 1.85 | |
| Pure Error | 1.92 | 4 | 0.4789 | ||
| Total Deviation | 431.19 | 16 |
| Factor | Unit | Level | ||
|---|---|---|---|---|
| Pump Pressure | MPa | 4 | 6 | 8 |
| Flow Rate | L/min | 180 | 200 | 220 |
| Feed Pressure | MPa | 6 | 8 | 10 |
| Number of Groups | A | B | C | Z |
|---|---|---|---|---|
| 1 | 6 | 220 | 5 | 67 min 04 s |
| 2 | 4 | 200 | 5 | 73 min 41 s |
| 3 | 6 | 180 | 11 | 71 min 48 s |
| 4 | 8 | 200 | 5 | 68 min 19 s |
| 5 | 6 | 180 | 5 | 73 min 14 s |
| 6 | 6 | 220 | 11 | 67 min 18 s |
| 7 | 8 | 180 | 8 | 69 min 84 s |
| 8 | 8 | 220 | 8 | 71 min 31 s |
| 9 | 4 | 220 | 8 | 70 min 21 s |
| 10 | 8 | 200 | 11 | 66 min 21 s |
| 11 | 6 | 200 | 8 | 55 min 43 s |
| 12 | 6 | 200 | 8 | 58 min 12 s |
| 13 | 4 | 180 | 8 | 75 min 08 s |
| 14 | 6 | 200 | 8 | 59 min 54 s |
| 15 | 4 | 200 | 11 | 69 min 57 s |
| 16 | 6 | 200 | 8 | 56 min 21 s |
| 17 | 6 | 200 | 8 | 55 min 27 s |
| Source | Sequential p-Value | Lack of Fit p-Value | Adjusted R2 | |
|---|---|---|---|---|
| Linear | 0.8061 | −0.1445 | −0.3405 | |
| 2FI | 0.9801 | −0.4619 | −1.1752 | |
| Quadratic | <0.0001 | 0.9222 | 0.7294 | Suggested |
| Cubic Model | 0.4599 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 699.36 | 9 | 77.71 | 22.07 | 0.0002 |
| A | 20.22 | 1 | 20.22 | 5.74 | 0.0477 |
| B | 23.80 | 1 | 23.80 | 6.76 | 0.0054 |
| C | 6.73 | 1 | 6.73 | 1.91 | 0.0092 |
| AB | 10.05 | 1 | 10.05 | 2.85 | 0.0350 |
| AC | 0.8649 | 1 | 0.8649 | 0.2456 | 0.6354 |
| BC | 0.8100 | 1 | 0.8100 | 0.2300 | 0.6461 |
| A2 | 216.19 | 1 | 216.19 | 61.39 | 0.0001 |
| B2 | 238.77 | 1 | 238.77 | 67.80 | <0.0001 |
| C2 | 116.74 | 1 | 116.74 | 33.15 | 0.0007 |
| Residual | 24.65 | 7 | 3.52 | ||
| Lack of Fit | 10.90 | 3 | 3.63 | ||
| Pure Error | 13.75 | 4 | 3.44 | 1.06 | |
| Total Deviation | 724.01 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Gong, X.; Fan, X.; Zeng, X.; Ma, X. Key Parameter Optimization Study of Composite Rod Drill in Gas Extraction Borehole Drilling in Soft, Medium, and Hard Coal Seams. Processes 2025, 13, 2195. https://doi.org/10.3390/pr13072195
Sun B, Gong X, Fan X, Zeng X, Ma X. Key Parameter Optimization Study of Composite Rod Drill in Gas Extraction Borehole Drilling in Soft, Medium, and Hard Coal Seams. Processes. 2025; 13(7):2195. https://doi.org/10.3390/pr13072195
Chicago/Turabian StyleSun, Baoqiang, Xuanping Gong, Xiaogang Fan, Xiangzhen Zeng, and Xingying Ma. 2025. "Key Parameter Optimization Study of Composite Rod Drill in Gas Extraction Borehole Drilling in Soft, Medium, and Hard Coal Seams" Processes 13, no. 7: 2195. https://doi.org/10.3390/pr13072195
APA StyleSun, B., Gong, X., Fan, X., Zeng, X., & Ma, X. (2025). Key Parameter Optimization Study of Composite Rod Drill in Gas Extraction Borehole Drilling in Soft, Medium, and Hard Coal Seams. Processes, 13(7), 2195. https://doi.org/10.3390/pr13072195






