Three-Dimensional Modeling of Condensing and Superimposing Deltamethrin Droplets on Strawberry Leaf Surface from Dynamic Wetting Process Monitoring Data
Abstract
1. Introduction
2. Experiments and Methods
2.1. Materials and Instruments
2.1.1. Experimental Material
2.1.2. Measuring Instruments
2.2. Experimental Method
2.3. Measurement Methods
2.3.1. Microanalysis System Data Measurement
2.3.2. Surface Tension Measurement by the Suspended Drop Method
2.3.3. Spreading Diameter Measurement by the Laying Drop Method
2.4. Modeling Method
2.4.1. Three-Dimensional Dynamic Trend Surface Modeling Methodology
2.4.2. Significance Tests for Three-Dimensional Trend Surface Modeling
3. Results and Discussion
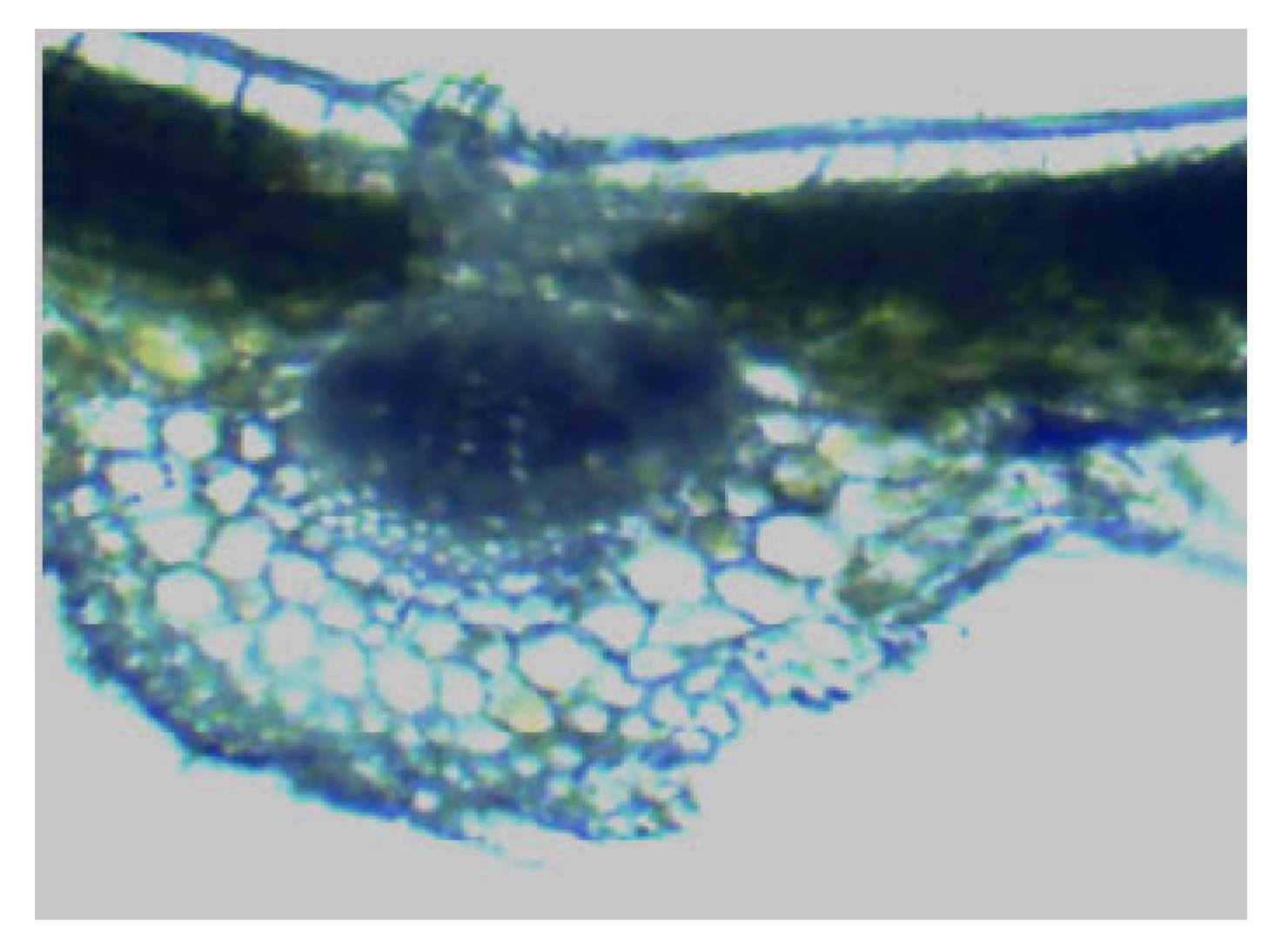
3.1. Characteristic Parameters of Leaf Blade Anatomical Structure
3.2. Surface Tension of Deltamethrin Reagent
3.3. Observation of Droplet Superposition and Condensation Behavior
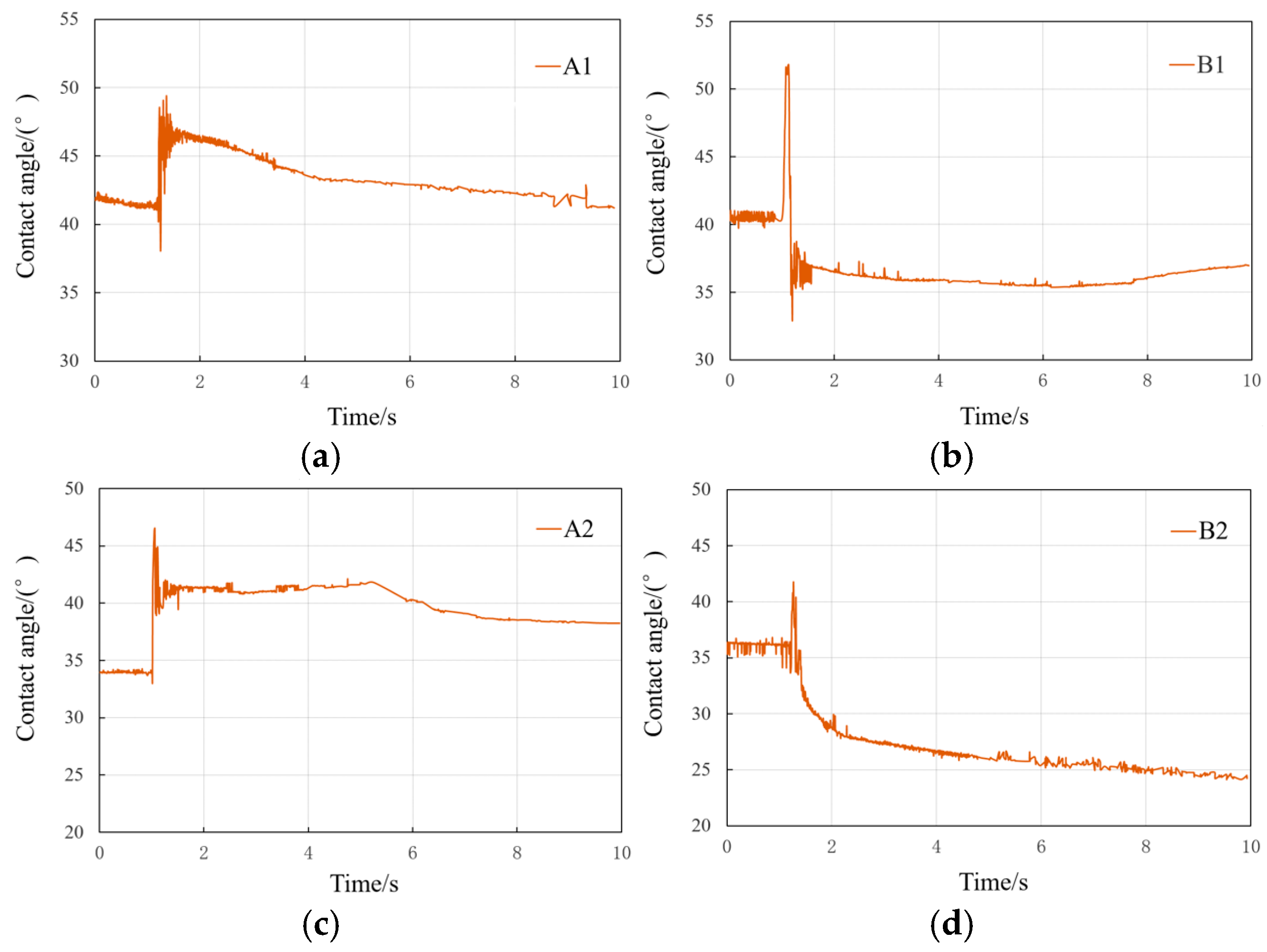
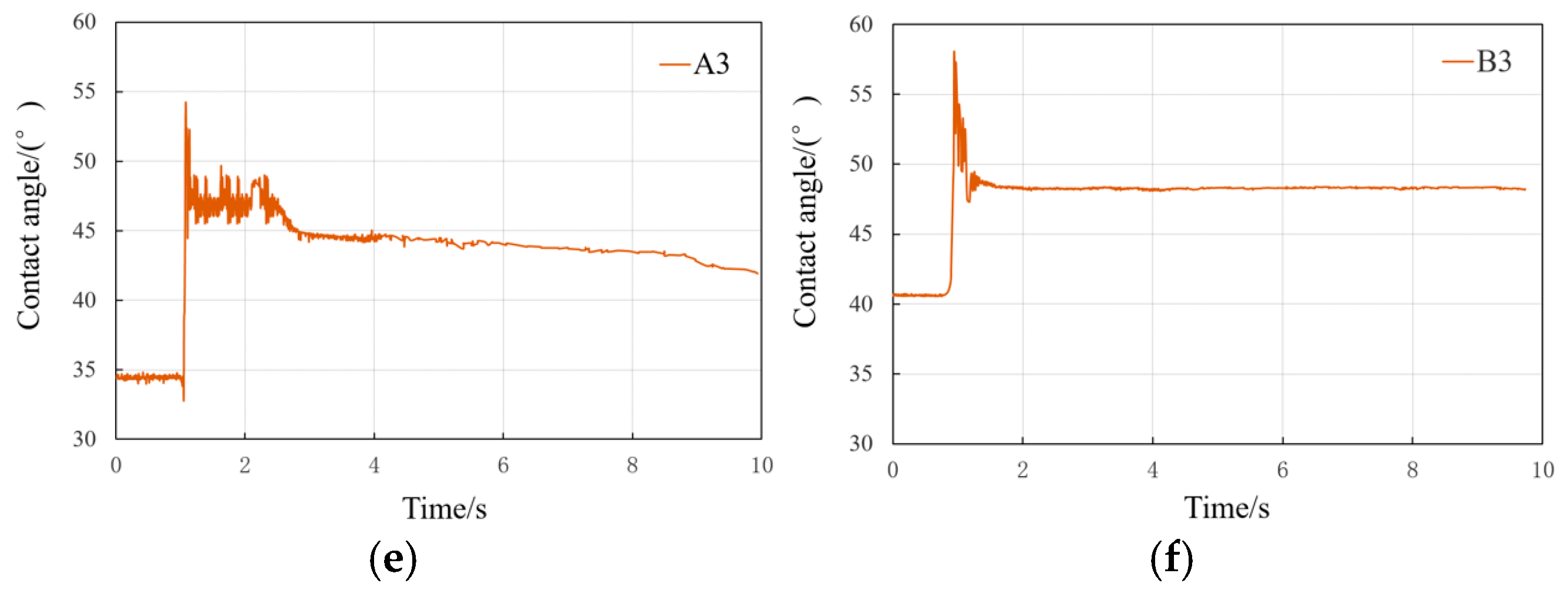
3.4. Contact Angle Analysis of Stacked Condensation Processes
3.5. Volume Changes During Superimposed Condensation
3.6. Variation of Spreading Diameter During Superposition Condensation
3.7. Stacked Condensation and Contact Angle Trend Surface Modeling
3.8. Superimposed Condensation and Contact Angle Trend Surface Modeling Test
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Nestler, B. Wetting and contact-angle hysteresis: Density asymmetry and van der waals force. Phys. Rev. Lett. 2024, 132, 126202. [Google Scholar]
- Zhang, H.; Lu, J.; Wei, D.; Hu, Y. Wetting state and dynamic spreading behavior of alkyl polyglycoside drop on cucumber leaf surface. Trans. Chin. Soc. Agric. Eng. 2002, 18, 203–206. [Google Scholar]
- Yang, X.; Dai, M.; Song, J.; Zhao, J.; He, X. Effect of droplet size, leaf characteristics and angle on pesticide deposition. Trans. Chin. Soc. Agric. Eng. 2012, 28, 70–73. [Google Scholar]
- Xu, G.; Gu, Z.; Xu, D.; Xu, X. Characteristics of rice leaf surface and droplets deposition behavior on rice leaf surface with different inclination angles. Sci. Agric. Sin. 2014, 47, 4280–4290. [Google Scholar]
- Nairn, J.J.; Forster, W.A. Due diligence required to quantify and visualize agrichemical spray deposits using dye tracers. Crop Prot. 2019, 115, 92–98. [Google Scholar]
- Wang, S.; Zhang, W.; He, H.; Wang, W.; Hu, X. Effection of typical plants leaves on pesticide wetting speciality and retentivity. J. Jilin Univ. (Eng. Technol. Ed.) 2013, 43, 564–568. [Google Scholar]
- Lu, J.; Zhang, H.; Wei, D.; Hu, Y. Dynamic contact angle forecasting and modeling method for drop-leaf interface base on time series analysis. Trans. Chin. Soc. Agric. Mach. 2013, 44, 80–86. [Google Scholar]
- Jensen, P.K.; Lund, I.; Nuyttens, D. Spray liquid distribution and biological efficacy of commercially available nozzles used for precision weed control. Biosyst. Eng. 2013, 116, 316–325. [Google Scholar]
- Martin, D.E.; Latheef, M.A. Aerial electrostatic spray deposition and canopy penetration in cotton. J. Electrost. 2017, 90, 38–44. [Google Scholar]
- Ferguson, J.C.; Chechetto, R.G.; Adkins, S.W.; Hewitt, A.J.; Chauhan, B.S.; Kruger, G.R.; O’Donnell, C.C. Effect of spray droplet size on herbicide efficacy on four winter annual grasses. Crop Prot. 2018, 112, 118–124. [Google Scholar]
- Kovalchuk, N.M.; Trybala, A.; Arjmandi-Tash, O.; Starov, V. Surfactant-enhanced spreading: Experimental achievements and possible mechanisms. Adv. Colloid Interface Sci. 2016, 233, 155–160. [Google Scholar] [PubMed]
- Kumar, K.; Nikolov, A.D.; Wasan, D.T. Effect of Film Curvature on Drainage of Thin Liquid Films. J. Colloid Interface Sci. 2002, 256, 194–200. [Google Scholar]
- Zhang, S.; Wu, X.; You, Z.; Zhang, L. Leaf image based cucumber disease recognition using sparse representation classification. Comput. Electron. Agric. 2017, 134, 135–141. [Google Scholar]
- Kira, O.; Dubowski, Y.; Linker, R. In-situ open path FTIR measurements of the vertical profile of spray drift from air-assisted sprayers. Biosyst. Eng. 2018, 139, 32–41. [Google Scholar]
- Bueno, M.R.; Cunha, J.P.A.R.D.; Santana, D.G.D. Assessment of spray drift from pesticide applications in soybean crops. Biosyst. Eng. 2017, 154, 35–45. [Google Scholar]
- Jia, W.; Zhu, H.; Dong, X.; Xue, F. Impact of spray droplet on soybean leaf surface. Trans. Chin. Soc. Agric. Mach. 2013, 44, 87–93. [Google Scholar]
- Yu, S.; Cui, L.; Cui, H.; Liu, X.; Liu, J.; Xin, Z.; Yuan, J.; Wang, D. Spray performance of flexible shield canopy opener and rotor wind integrated boom-sprayer application in soybean: Effects on droplet deposition distribution. Pest. Manag. Sci. 2024, 80, 3334–3348. [Google Scholar]
- Zhang, J.T.; Huang, L.S.; Liu, G.B.; Lan, Y.B.; Wen, S. The dynamic wetting and spreading behavior of pesticide droplet on rice leaf surface. Sci. Agric. Sin. 2024, 57, 2583–2598. [Google Scholar]
- Gatne, K.P.; Jog, M.A.; Manglik, R.M. Surfactant-induced modification of low weber number droplet impact dynamics. Langmuir Acs J. Surf. Colloids 2009, 25, 8122–8130. [Google Scholar]
- Vittal, L.V.M.; Rookes, J.; Boyd, B.; Cahill, D. Analysis of plant cuticles and their interactions with agrochemical surfactants using a 3d printed diffusion chamber. Plant Methods 2023, 19, 37–50. [Google Scholar]
- Ding, W.; Jin, M.; Luo, L.; Wu, F.; Xu, L.; Ji, G.; Zhu, D. Behavior analysis of spray droplet interacting with plant leaves based on virtual model. Trans. Chin. Soc. Agric. Eng. 2017, 33, 40–48. [Google Scholar]
- Zhao, J.; Du, Y.; Zhang, J.; Li, J.; Xu, G. Effect of physical properties of pesticides on the size distribution and collision behavior of droplets: Regulation strategy in agricultural spraying. Comput. Electron. Agric. 2021, 182, 105999. [Google Scholar]
- Li, L.; Zhang, S.; Wang, B. Plant disease detection and classification by deep learning—A review. IEEE Access 2021, 9, 56683–56698. [Google Scholar]
- Zhang, Y.; Zhang, N.; Zhu, J.; Sun, T.; Chai, X.; Dong, W. Efficient triple attention and attentionMix: A novel network for fine-grained crop disease classification. Agriculture 2024, 15, 313–329. [Google Scholar]
- Lu, J.; Jin, T.; Zhang, H. Deltamethrin emulsifiable concentrates droplets superposition and coagulation behavior on water spinach leaf surface. Chin. J. Pestic. Sci. 2019, 21, 514–522. [Google Scholar]
- Li, G.; Dai, W.; Zeng, F.; Liu, B. Application of three -dimensional dynamic trend surface fitting model on land subsidence. J. Geod. Geodyn. 2016, 36, 508–512. [Google Scholar]
- Jiang, S.; Hu, Y.; Zheng, S.; Li, J.; Zhao, N.; Gao, Y.; Gu, S. Morphologic effects of different light intensities and light qualities on the leaf of ‘Darselect’ strawberry (Fragaria ananassa Duch). J. Chin. Electron Microsc. Soc. 2009, 28, 453–461. [Google Scholar]
- Liu, Q.; Qiu, A.; Xie, X.; Liu, R.; Wang, W.; Wu, C. Relationships between blade anatomical structure and drought resistances of five strawberry varieties. Tianjin Agric. Sci. 2019, 25, 18–22. [Google Scholar]
- Lu, J.; Sheng, K.; Chen, J.; Ding, X.; Wen, Z.; Li, S. Influence of particle size and hot-pressing parameters on mechanical properties of bamboo-based composite materials. Biomimetics 2025, 10, 156. [Google Scholar]
- Vezakis, A.; Vezakis, I.; Petropoulou, O.; Miloulis, S.T.; Anastasiou, A.; Kakkos, I.; Matsopoulos, G.K. Comparative analysis of deep neural networks for automated ulcerative colitis severity assessment. Bioengineering 2025, 12, 413. [Google Scholar] [CrossRef]
- McCarthy, M.E.; Reiterdank, I.F.V.; Pallandt, O.H.P.V.; Taggart, M.S.; Charlès, L.; Uygun, K.; Lellouch, A.G.; Ce-trulo, C.L., Jr.; Uygun, B.E. Decellularization of human digits: A step towards off-the-shelf composite allograft transplantation. Bioengineering 2025, 12, 383. [Google Scholar] [CrossRef] [PubMed]
- Horr, A.M.; Drexler, H. Real-time models for manufacturing processes: How to build predictive reduced models. Processes 2025, 13, 252. [Google Scholar] [CrossRef]
- Wang, X.; Liu, F. Molecular dynamics simulation on the wetting characteristics of CO2 droplets on stainless steel surfaces. Appl. Surf. Sci. 2025, 682, 161618. [Google Scholar]
- Martí-Coll, A.; Rodríguez-Ramo, A.; Llanes-Santiago, O. An optimization approach to select koopman observables for data-based modeling using dynamic mode decomposition with control. Processes 2025, 13, 284. [Google Scholar] [CrossRef]
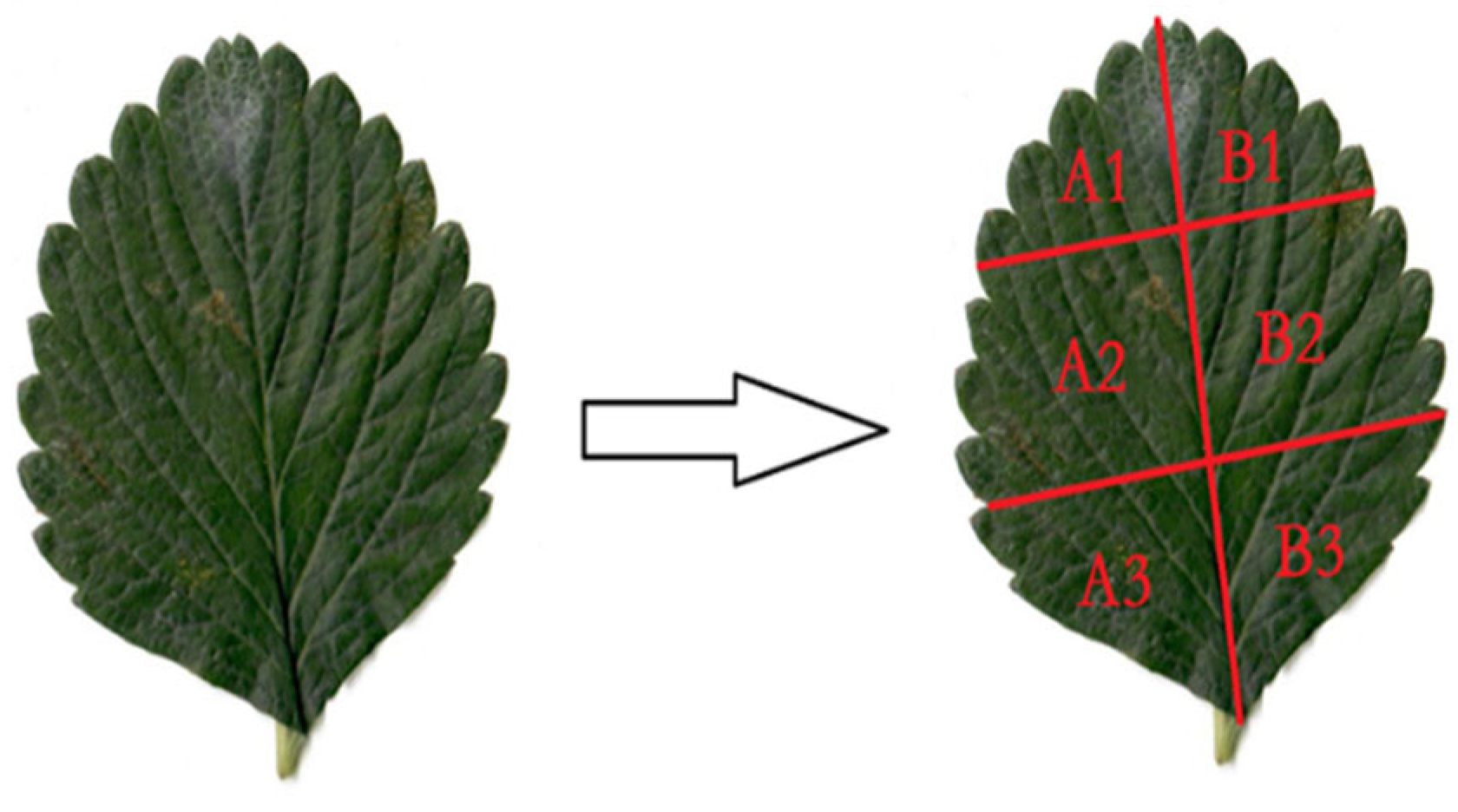





| Main Parameters | Technical Specifications |
|---|---|
| Image resolution/pixel | 1280 × 1024 |
| Maximum image acquisition speed/(ms·frame−1) | 203 |
| diagonal/(mm) | 3.5 to 7.5 |
| Light source | LED background |
| LED light source voltage/V | 12 |
| Contact angle measurement range/(°) | 0 to 180 |
| Contact angle measurement accuracy/(°) | ±0.01 |
| Surface tension measurement range/(mN·m−1) | 0.01 to 1000 |
| Surface tension measurement accuracy/(mN·m−1) | ±0.01 |
| Blade Structure Parameters | A1 | B1 | A2 | B2 | A3 | B3 |
|---|---|---|---|---|---|---|
| Blade thickness/μm | 118.43 | 119.27 | 131.49 | 127.31 | 135.46 | 136.35 |
| Upper epidermal thickness/μm | 18.25 | 19.01 | 21.18 | 20.54 | 24.42 | 23.18 |
| Lower epidermal thickness/μm | 6.96 | 7.15 | 8.37 | 8.10 | 9.13 | 8.98 |
| Thickness of cuticular membrane/μm | 5.87 | 6.04 | 6.23 | 6.05 | 7.25 | 6.87 |
| Vein thickness/μm | 265.44 | 263.19 | 289.52 | 293.83 | 301.74 | 299.96 |
| Fenestrated tissue thickness/μm | 55.36 | 54.67 | 63.65 | 61.72 | 70.04 | 69.81 |
| Spongy tissue thickness/μm | 41.50 | 43.48 | 48.74 | 47.43 | 51.20 | 50.13 |
| Leaf structure compactness/% | 46.74 | 45.84 | 48.41 | 48.48 | 51.71 | 51.20 |
| Leaf structure laxity/% | 35.04 | 36.46 | 37.07 | 37.26 | 37.80 | 36.77 |
| Stomatal size/μm2 | 37.56 | 36.98 | 40.43 | 39.44 | 44.51 | 45.80 |
| Stomatal density/(pcs/mm2) | 579.84 | 583.22 | 598.26 | 592.46 | 610.25 | 608.43 |
| Strawberry Leaf Segmented Parts | Trend Surface Modeling | Correspondence Figure |
|---|---|---|
| A1 | Figure 7a | |
| B1 | Figure 7b | |
| A2 | Figure 7c | |
| B2 | Figure 7d | |
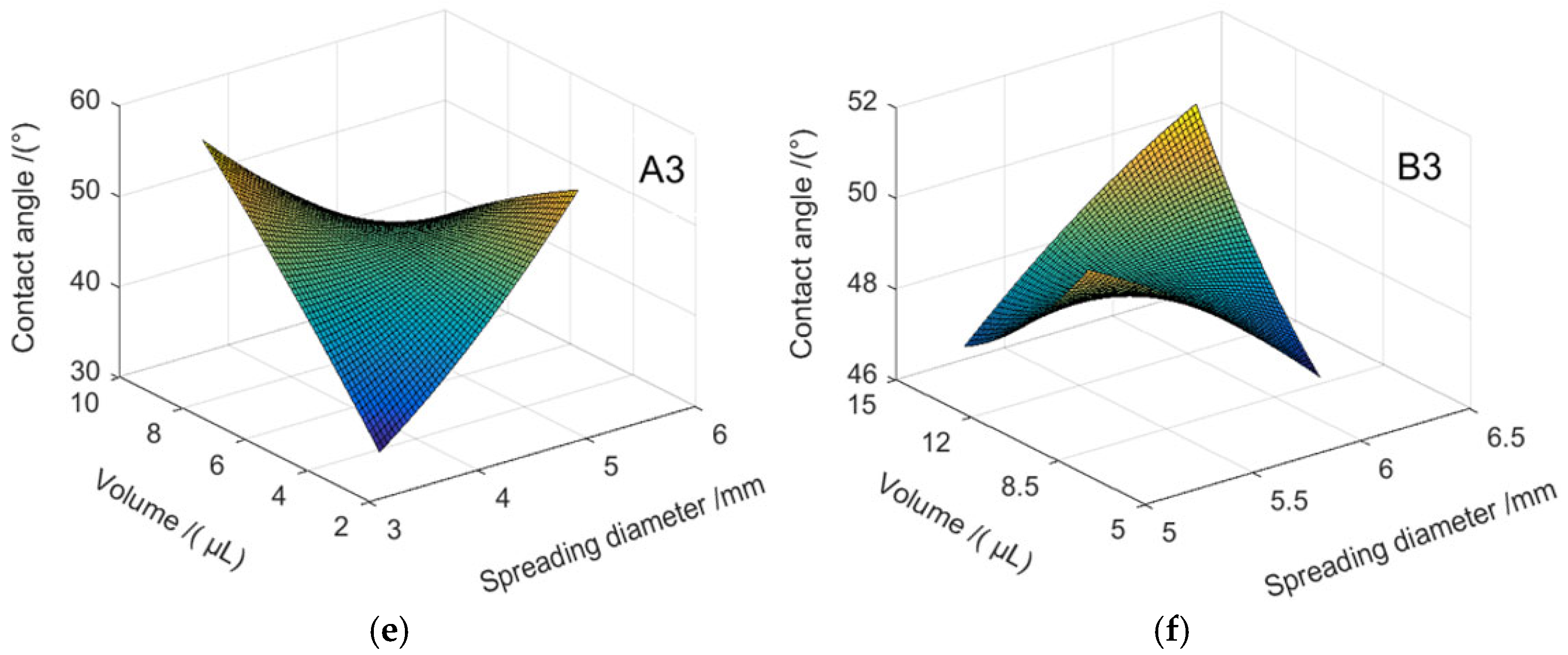
| A3 | Figure 7e | |
| B3 | Figure 7f |
| Trend Surface | Sample Size | Mean Value of Residuals | Standard Deviation of Residuals | F | p | T | R2 | Er |
|---|---|---|---|---|---|---|---|---|
| A1 | 157 | −0.0017 | 1.7894 | 36.4556 | 0.0001 | 8.4231 | 0.5621 | 5.54% |
| A2 | 161 | −0.0023 | 2.5498 | 6.3072 | 0.0001 | 12.5213 | 0.1817 | 8.47% |
| A3 | 152 | −0.0088 | 1.7401 | 105.8041 | 0.0001 | 3.7642 | 0.7884 | 3.89% |
| B1 | 124 | −0.0072 | 3.3734 | 14.3248 | 0.0001 | 9.8604 | 0.4010 | 6.18% |
| B2 | 156 | −0.0029 | 2.8848 | 12.3740 | 0.0001 | 12.8649 | 0.3035 | 7.95% |
| B3 | 157 | −0.0013 | 1.5165 | 1.2746 | 0.2828 | 17.9727 | 0.0430 | 9.02% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wen, Z.; Wang, X.; Ding, X. Three-Dimensional Modeling of Condensing and Superimposing Deltamethrin Droplets on Strawberry Leaf Surface from Dynamic Wetting Process Monitoring Data. Processes 2025, 13, 2181. https://doi.org/10.3390/pr13072181
Lu J, Wen Z, Wang X, Ding X. Three-Dimensional Modeling of Condensing and Superimposing Deltamethrin Droplets on Strawberry Leaf Surface from Dynamic Wetting Process Monitoring Data. Processes. 2025; 13(7):2181. https://doi.org/10.3390/pr13072181
Chicago/Turabian StyleLu, Jun, Zichao Wen, Xueying Wang, and Xumin Ding. 2025. "Three-Dimensional Modeling of Condensing and Superimposing Deltamethrin Droplets on Strawberry Leaf Surface from Dynamic Wetting Process Monitoring Data" Processes 13, no. 7: 2181. https://doi.org/10.3390/pr13072181
APA StyleLu, J., Wen, Z., Wang, X., & Ding, X. (2025). Three-Dimensional Modeling of Condensing and Superimposing Deltamethrin Droplets on Strawberry Leaf Surface from Dynamic Wetting Process Monitoring Data. Processes, 13(7), 2181. https://doi.org/10.3390/pr13072181






