Abstract
Creep and stress sensitivity can lead to the long-term conductivity degradation of fractures, and this influences the accuracy of long-term productivity predictions in ultra-deep carbonate reservoirs (UDCRs). However, the current models do not consider these two factors. For the long-term conductivity degradation of acid-etched symmetry fractures in UDCRs, a new fracture permeability evolution model incorporating creep and stress sensitivity effects was established. Building upon this, a numerical simulation model for UDCRs was developed for the first time to quantitatively analyze the impacts of creep, stress sensitivity, and production strategies on well productivity. The research revealed that the creep and stress sensitivity characteristics of acid-etched fractures had a significant impact on the well productivity for UDCRs. The larger the creep coefficient and stress sensitivity coefficient, the lower the oil well productivity. The larger the initial reservoir pressure and drawdown pressure, the higher the daily production and cumulative production of the oil well, but the cumulative production growth rate decreased. The cumulative production in the early stage of the released-pressure production was significantly higher than that of the pressure-controlled production, but with the increase in the pressure-controlled time, the cumulative production reversed. When the pressure was controlled for three years, the cumulative production increased by 5952 m3 (38.8%); as the creep coefficient increased, the cumulative production increased by greater than the pressure-released production. This shows that the larger the creep coefficient, the better the effect of controlling pressure production. The research results can provide a theoretical basis and technical support for the efficient development of UDCRs.
1. Introduction
As global oil and gas exploration and development advance towards deep strata, the development of UDCRs is increasingly attracting research interest. UDCRs have characteristics of high temperature, high pressure, and complex rock mechanical properties [1,2], and their development faces many challenges, among which the creep and stress sensitivity problems are particularly prominent. During the production process of UDCR oil wells, carbonate rocks exhibit significant time-dependent deformation characteristics under high-temperature and high-pressure environments, and artificial fractures will creep, resulting in the fractures gradually closing (Figure 1). After carbonate rock acid-etching, the mechanical properties of the rock will change significantly. Under the action of high closure pressure, the creep rate of acid-etching fractures is significantly increased, and the fractures are more likely to undergo closure, resulting in a decrease in the conductivity or even loss [3,4]. At the same time, pore pressure decreases in the production process, resulting in overlay pressure increase, and the conductivity decreases (as known for stress sensitivity effects) [5,6,7], further aggravating the fracture closure and the decrease in permeability. These factors lead to a rapid decrease in carbonate oil well production and a decrease in final recovery (EUR).
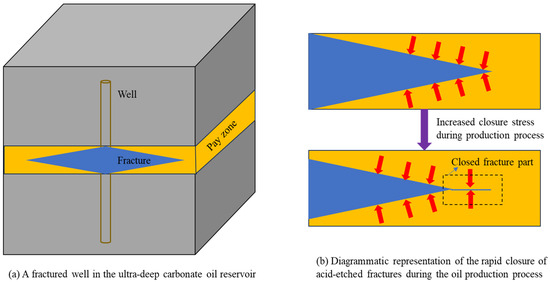
Figure 1.
A physical model of oil well with symmetry fracture in UDCRs.
In recent years, scholars have conducted extensive research on the creep and stress sensitivity of oil and gas reservoirs. An et al. [8] proposed an improved stress-dependent permeability model that considers the effect of time-dependent compaction behavior on permeability measurements by incorporating the stress creep mechanism. Qi et al. [3] carried out a triaxial creep experiment on acid-etched limestone and found that the creep of acid-etched limestone cracks exhibits hysteresis elasticity. Zhou et al. [9] found that when the Young’s modulus of carbonate reservoirs in the Middle East is less than 20 GPa, the fracture conductivity is very sensitive to closure stress. Li et al. [10] also studied the relationship between elastic modulus and permeability stress sensitivity. Zhou et al. [11] conducted a stress sensitivity analysis of the long-term flow diversion capacity of acid-etching fractures. Teng et al. [12,13] proposed a new fracture permeability model to account for the influences of proppant-pack permeability, proppant-pack porosity, and fracture width on fracture permeability. Pang et al. [14] developed correlations of effective porosity and permeability by considering the combined effects of gas adsorption and stress for shale. Ankit Mirani et al. [15] developed a model that mimics the effect of depletion-induced in situ stress variations on short-term and long-term productivity by taking into account several phenomena, such as stress-dependent matrix and natural-fracture permeability, as well as reduction in hydraulic-fracture conductivity caused by proppant crushing, deformation, embedment, and fracture-face creep. Zhang et al. [16] developed a transient source-function-based embedded discrete fracture model for CBM that mimics the effect of matrix deformation with creep and deformation caused by adsorption-induced expansion. Zhou et al. [17,18] developed a permeability evolution model considering the effects of matrix–fracture interaction and creep deformation on the permeability evolution of deep coal. Cui et al. [19] employed a combination of water seepage experiment data from clayey-silt cores and numerical simulation methods to study the development of hydrate reservoirs through depressurization-induced vertical wells. The simulation results show that creep effects reduce the effective reservoir porosity and permeability. Chen [20] revealed the temporal behavior and permeability variation law under the stress–seepage coupling of complex fractured limestone. Du et al. [21] proposed a characterization method for fracture dynamic closure considering the influence of stress state in three-dimensional space based on an embedded discrete fracture model and found that dynamic fracture closure leads to partial production loss. Tang et al. [22] conducted an experimental study of creep characteristics in layered water-bearing shale. Feng et al. [23] established the relationship between stress–strain and fracture aperture of rock based on experimental results and mathematical derivation. Zhao [24] developed a model for simulating the long-term conductivity of fractures to study the influence of creep on fracture width. Liu [25] constructed a model and carried out laboratory tests to study the permeability evolution law of intact sandstone, single-fracture sandstone, and multi-fracture sandstone. Rang [26] established typical numerical models for single-well and multi-well production scenarios, analyzed the development characteristics considering fracture deformation, and formed a set of numerical simulation methods for shale oil reservoir production dynamics.
However, in the above studies, the permeability evolution mechanism of UDCR has mainly been studied experimentally, and the impact on the well productivity of UDCR under the synergistic effect of creep and stress sensitivity has rarely been studied. At the same time, the study of the permeability evolution mechanism has the following limitations: traditional permeability models often consider elastic deformation but ignore the time-dependent creep closure process; stress sensitivity coefficients mostly use static experimental values, which do not reflect the effective stress changes during dynamic production. Traditional UDCR oil well production simulation methods often ignore the combined effect of these factors, resulting in inaccurate predictions of UDCR oil well production. Therefore, it is of great theoretical and practical significance to conduct numerical simulation research on UDCR oil wells that consider creep and stress sensitivity.
Based on a physical model of an oil well with symmetric fractures in UDCRs (Figure 1), this paper establishes a numerical model of a permeability–stress-coupled ultra-deep carbonate reservoir, quantifies the influence of the coupling effect between creep and stress sensitivity on the productivity of UDCR oil wells, and provides theoretical guidance for optimizing development plans.
2. The Model of Matrix–Fracture Coupling Seepage
2.1. Basic Assumptions
- (1)
- The ultra-deep carbonate reservoir is an isothermal seepage system, and the temperature remains constant during the oil well production process;
- (2)
- The seepage of the reservoir is a single-phase micro-compressible fluid, and the seepage in the reservoir follows Darcy’s law;
- (3)
- The reservoir is a cracked carbonate rock, and the creep and stress sensitivity of the matrix and natural fractures are not considered;
- (4)
- Both the matrix and the fracture are continuous medium and are isotropic;
- (5)
- This is a two-dimensional seepage model, and the influence of gravity is not considered.
2.2. Mathematical Model
- (1)
- Acid-etched Fracture conductivity reduction Model
In the production process of UDCR oil wells, acid-etched fractures are affected by the increasing effective closure stress. Acid-etched fracture width and permeability decrease due to the increasing effective closure stress and creep effect. The attenuation of acid-etched fracture conductivity (FCD) with consideration of stress sensitivity in UDCR can be expressed as follows [7]:
where Kfi is the initial acid-etched fracture permeability (D); Wfi is the initial acid-etched fracture width in meters (m); FCD is the acid-etched fracture conductivity considering stress variation (D·m); df is the acid-etched fracture stress sensitivity coefficient (Pa−1); and Δσeff is the change in effective stress (Pa). During production, the relationship between the change in effective stress and the change in pore pressure is calculated as follows [27]:
By substituting Equation (2) into Equation (1), we obtain the following:
where γf is the acid-etched fracture pressure sensitivity coefficient, defined as follows:
where δ is the effective stress coefficient (dimensionless); ν is the Poisson ratio (dimensionless); and Δp is the pore pressure variation (Pa).
- (2)
- Acid-etched Fracture deformation Model
The creep deformation of acid-etched fracture increases with time and effective stress, which leads to a decrease in fracture conductivity. The relationship between fracture width and creep is
where Wfc is the crack width considering the influence of creep (m); ε is the creep strain (dimensionless). Relevant experimental studies have shown that the relationship between creep strain, time, and effective stress difference can be expressed as follows [3,27]:
where t is the time (d); A is the creep parameter based on experimental fitting (Pa−1); λc is the experimental regression coefficient for the creep effect (dimensionless); and Δσ is stress difference (Pa).
The conductivity of acid-etched fracture affected by stress sensitivity and creep is expressed as
where FCDSC is the conductivity of acid-etched fracture considering creep and stress variation (D·m).
The creep deformation and stress sensitivity coefficient are not constants, but functions of the rate of change in effective confining pressure; that is, the faster the pressure drop rate, the greater the values of both parameters.
- (3)
- Matrix Seepage Equation
Dual Porosity Dual Permeability (DPDK) was used to describe flow in the matrix and in natural fractures, respectively. The matrix system seepage equation can be expressed as follows [28,29]:
where ϕm is the matrix porosity (dimensionless); ctm is the total matrix compression coefficient (Pa−1); μo is the oil viscosity (Pa·s) ρo is the oil density (kg/m3); km is the matrix permeability (D); pm is the matrix pressure (Pa); α is the shape factor (1/m2); and pf is the natural-fracture system pressure (Pa).
- (4)
- Natural-Fracture Seepage Equation
- (5)
- Acid-etched fracture Seepage Equation
Considering the acid-etched fracture as a finite flow vertical fracture, its internal flow equation can be expressed as follows:
where pF is the acid-etched fracture pressure (Pa); ϕF is the acid-etched fracture porosity (dimensionless); kF is the acid-etched fracture permeability (D); and qwell is the mass flow rate into the wellbore from the acid-etched fracture (kg/m3/s).
- (6)
- Boundary and Initial Conditions
Assuming that the outer boundary of the model is closed and the flow pressure is determined by the inner boundary, the following is obtained:
where pwf is the bottom-hole flowing pressure (Pa); pi is the initial pressure (Pa); xw and yw are the coordinate positions of the well in the reservoir (m); and xmax and ymax are the length and width of the reservoir, respectively (m).
2.3. Model Solution
The finite difference method is used to obtain the discrete matrix seepage differential equation for the numerical calculation model. The discrete form of matrix seepage equation (Equation (8)) is
The finite difference equation (Equation (12)) can be summarized as follows:
The discrete form of the natural-fracture seepage equation (Equation (9)) is
The finite difference equation (Equation (14)) can be summarized as follows:
The discrete form of the acid-etched fracture seepage equation (Equation (10)) is as follows:
Assuming that the outer boundary of the model is closed and the flow pressure or constant production is determined by the inner boundary, the above mathematical models of the matrix, natural fractures, and acid-etched fractures are spatially and temporally discretized, converting the partial differential equations into algebraic equations. Given the attribute parameters, the pressure distribution of reservoirs at different moments is obtained through coupled iterative solutions. The fracture permeability is updated according to the pressure distribution, and the well production is calculated at each time step until the set time is reached, thereby obtaining the oil well production curve of UDCR.
2.4. Model Validation
To validate the accuracy of the proposed model, comparative validations were conducted with the real historical production data and the predicted data of our model. The parameters from the reservoir and fracture parameters of an UDCR oil well A in the Tarim Basin used for simulation are listed in Table 1. As we can see in Figure 2, the data predicted by the model can match the real-life data for well A.

Table 1.
Reservoir and fracturing parameters of a UDCR oil well.
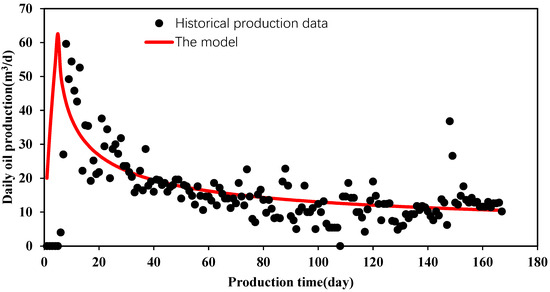
Figure 2.
Comparison results of daily oil production between real-life data and the model.
3. Sensitivity Analysis of Influence Factors
As can be seen from Figure 3, stress sensitivity and creep have significant impacts on daily and cumulative production. Ignoring stress sensitivity and creep overestimates productivity, with the initial daily production being 4.9% higher and cumulative production being 32.6% higher. Considering only stress sensitivity, the initial daily production is 2.4% higher and cumulative production is 18.8% higher; considering only creep, the initial daily production is 2.7% higher and cumulative production is 4.4% higher.
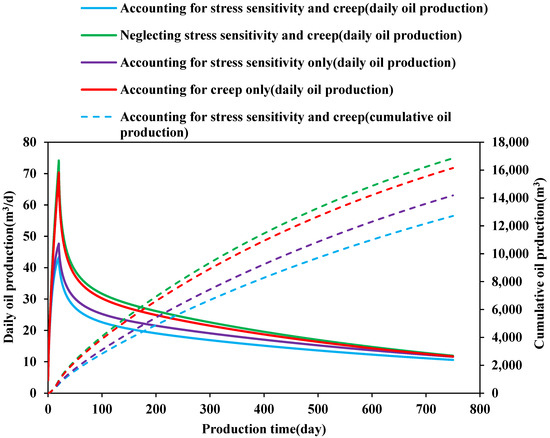
Figure 3.
Effect of stress sensitivity and creep on the daily production and cumulative production of UDCR oil wells.
3.1. Effect of Stress Sensitivity on Well Productivity
Figure 4 shows the impact of the stress sensitivity coefficient on production. It can be seen from the figure that after considering the influence of stress sensitivity, daily production gradually increases and then decreases rapidly in the early stage. With the increase in the stress sensitivity coefficient, the initial increase in daily production is smaller and lasts shorter, and cumulative production also decreases accordingly. When the stress sensitivity coefficient increases from 0.02 MPa−1 to 0.04 MPa−1, cumulative production decreases by 10.2%; when it increases from 0.04 MPa−1 to 0.06 MPa−1, cumulative production decreases by 12.7%; and when it increases from 0.06 MPa−1 to 0.08 MPa−1, cumulative production decreases by 13.5%. As the stress sensitivity coefficient increases, cumulative production decreases gradually. When the stress sensitivity coefficient increases from 0.02 MPa−1 to 0.08 MPa−1, cumulative production results in a total loss of 5080 m3. Increasing the stress sensitivity coefficient indicates that permeability is more sensitive to stress changes. During oil well production, as the bottom pressure drops, effective stress increases and permeability decreases, resulting in a decrease in oil well production and EUR. Especially in cases of high stress sensitivity coefficients, oil well production may decrease significantly in a short period of time, or even enter the low-yield stage prematurely.
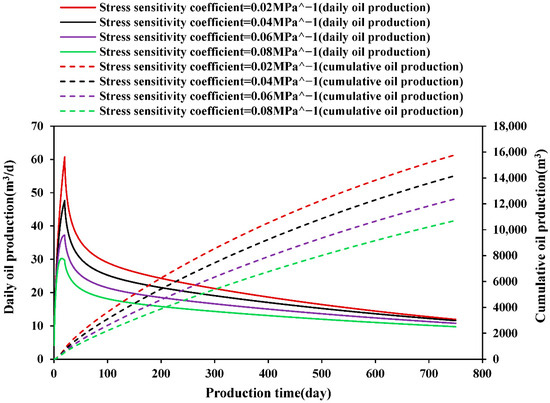
Figure 4.
Effect of stress sensitivity coefficient on the daily production and cumulative production of UDCR oil wells.
3.2. Effect of Creep on Well Productivity
Figure 5 shows the impact of creep coefficient on well production. As can be seen from the figure, the impact of fracture creep on initial production is relatively small. As the creep coefficient increases, the long-term effects of creep begin to manifest, and cumulative production decreases accordingly. When the creep coefficient increases from 0.1 to 0.2, cumulative production decreases by 5.8%; when it increases from 0.2 to 0.3, cumulative production decreases by 6.3%; and when it increases from 0.3 to 0.4, cumulative production decreases by 7.1%. As the creep coefficient increases, cumulative production gradually decreases. When the creep coefficient increases from 0.1 to 0.4, cumulative production results in a total loss of 3020 m3.
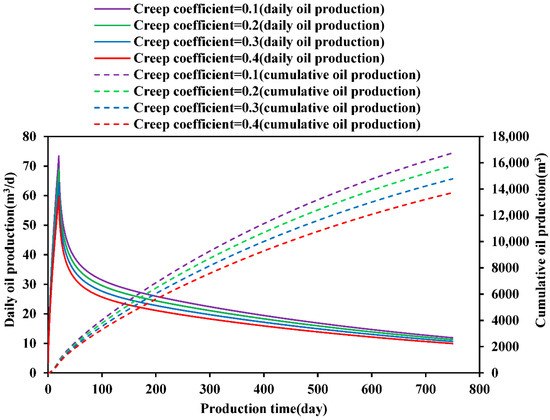
Figure 5.
Effect of creep coefficient on the daily production and cumulative production of UDCR oil wells.
3.3. Effect of Other Factors on Well Productivity
- (1)
- Effect of Initial Pressure
As can be seen from Figure 6, as the initial reservoir pressure increases, the previous daily production increases less and has a shorter duration. When the initial reservoir pressure increases from 90 MPa to 100 MPa, cumulative production increases by 7.9%; when it increases from 100 MPa to 110 MPa, cumulative production increases by 6.6%; and when it increases from 110 MPa to 120 MPa, cumulative production increases by 5.6%, indicating that the increase diminishes gradually. Different initial effective stress levels can also affect creep’s impact on productivity. In reservoirs with higher initial effective stress, the same pressure drop causes greater effective stress changes, leading to a greater reduction in permeability, which has a more significant impact on oil well productivity.
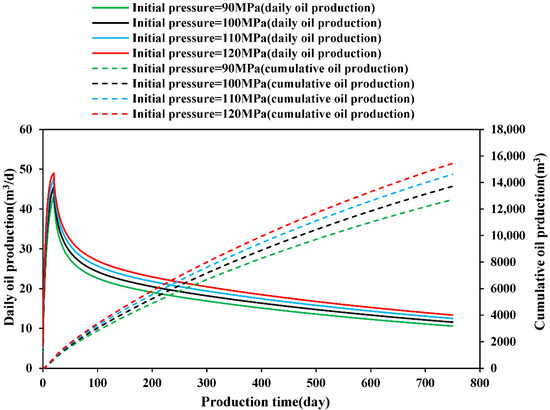
Figure 6.
Effect of initial pressure on the daily production and cumulative production of UDCR oil wells.
- (2)
- Effect of Drawdown Pressure
As can be seen from Figure 7, with the increase in drawdown pressure, the increase in daily production in the early stage becomes larger, but the duration is shorter. This is because the drawdown pressure plays a leading role, and differential pressure drive is the key production mechanism. Compared with other sensitivity analysis results, it can be seen that under the same conditions, the drawdown pressure has the greatest impact on productivity. When the drawdown pressure increases from 30 MPa to 60 MPa, the cumulative production growth rate decreases by 13.4%. Drawdown pressure is a key control parameter for oil well production. Larger drawdown pressure enhances stress sensitivity and creep, resulting in a reduction in permeability and oil well production (in this case, the negative impact of creep and stress sensitivity on output has not exceeded the positive impact of the drawdown pressure on productivity).
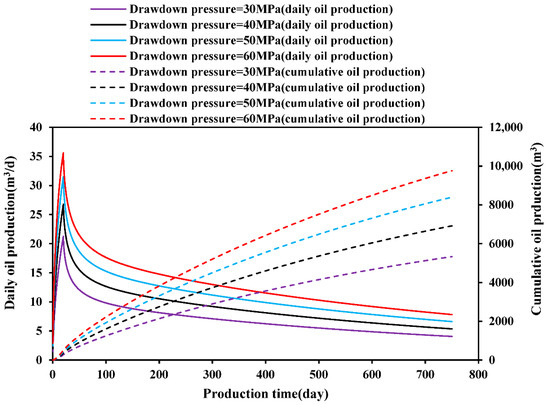
Figure 7.
Effect of drawdown pressure on the daily production and cumulative production of UDCR oil wells.
- (3)
- Effect of Production System
As can be seen from Figure 8, in the early production stage, the cumulative oil production for the three creep coefficients is higher than that under controlled-pressure production. However, as production progresses, a production reversal occurs. This is because the pressure difference in the early stage plays a leading role, and the pressure difference in pressure-release mode is greater than that of pressure-controlled production, so the oil production is higher. However, as production time increases, the negative impact of creep and stress sensitivity on productivity in the pressure-release production mode is more significant, exceeding the positive impact of the pressure difference on productivity, resulting in a reversal of the controlled-pressure production. The creep coefficients are 0.1, 0.2, and 0.3. Compared to the released-pressure model, the increase in cumulative production for the pressure-controlled model is 3.1%, 11.2%, and 23.1%, respectively. This indicates that the larger the creep coefficient, the more pronounced the effect of pressure-controlled production. In other words, the higher the creep coefficient, the more beneficial it is to employ pressure-controlled production.
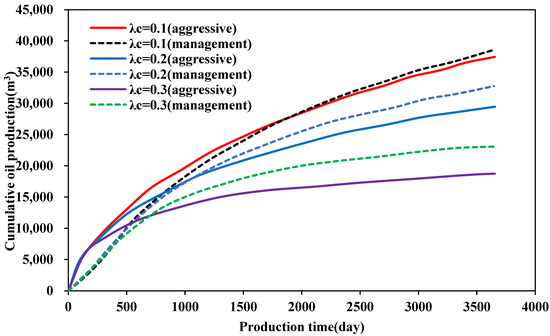
Figure 8.
Effect of creep coefficient on the daily production and cumulative production of UDCR oil wells for aggressive and management drawdown.
- (4)
- Effect of Management Time
As shown in Figure 9, the cumulative production in the early stage of pressure-released production is significantly higher than that in pressure-controlled production. However, as the pressure-controlled time increases, production reversal occurs. The one-year pressure-control period shows the largest production increase at 25.1%. The two-year pressure-control period has a significantly lower cumulative production increase rate compared to the one-year period, with a growth of 8.4%. The three-year pressure-control period shows a smaller increase in cumulative production compared to the two-year period, with a small growth of 2.3%. So, in this case, an optimal pressure-control duration of about three years is recommended to maximize oil production. It can be seen that production increases by more than one year of pressure control are very small. As the pressure-control time increases, the early-stage daily production becomes smaller, but the late-stage cumulative production gradually increases. When the pressure-control duration reaches three years, cumulative production increases by 5952 m3 (38.8%), indicating that pressure-controlled production can significantly enhance the productivity of UDCR oil wells.
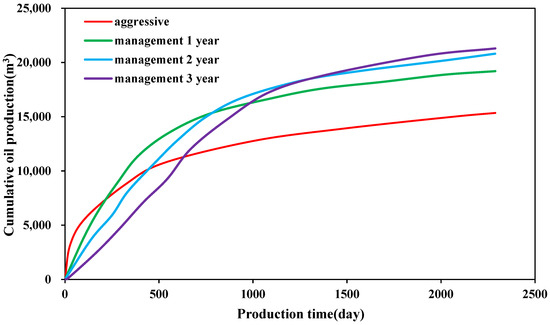
Figure 9.
Effect of management time on the daily production and cumulative production of UDCR oil wells.
4. Conclusions
- This study successfully constructed a numerical model of a UDCR oil well that considers creep and stress sensitivity. This model can more accurately describe the coupling mechanism between rock mechanical characteristics and seepage characteristics during oil well production. When traditional models ignore the coupling effect between the two, the oil well productivity is overestimated.
- The creep and stress sensitivity characteristics of rocks have a significant impact on the production capacity of UDCR oil wells. The greater the creep coefficient and stress-sensitive coefficient, the lower the oil well productivity. The greater the initial reservoir pressure and drawdown pressure, the higher the daily production and cumulative production of the oil wells. However, at the same time, the greater initial reservoir pressure and drawdown pressure will enhance stress sensitivity and creep, resulting in a decrease in permeability, thereby reducing the cumulative production growth.
- The cumulative production in the early stage of pressure-release production is significantly higher than that in pressure-controlled production. However, as the pressure-control time increases, production reversal occurs. When the pressure-control duration reaches three years, the cumulative production increases by 5952 m3 (38.8%). As the creep coefficient increases, the increase in cumulative production for pressure-controlled production compared to pressure-release production becomes more significant. This indicates that the larger the creep coefficient, the better the effect of pressure-control production. In other words, the larger the creep coefficient, the more beneficial pressure-control production becomes.
- During the development of UDCR, the effects of creep and stress sensitivity should be fully considered. The production system should be optimized, and the production pressure should be reasonably controlled to enhance the EUR of UDCR oil wells and improve the overall development efficiency of the reservoir.
Author Contributions
Z.L.: Methodology, writing—original draft, writing—review; L.S.: Methodology, computational analysis, funding acquisition; B.H.: Data processing, format adjustment; S.L.: Data processing, format adjustment. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Science and Technology Research Program of CNPC (2021DJ1002), the Science and Technology Research Program of CNPC (2024-KFKT-21), and the Science and Technology Research Program of Chongqing Municipal Education Commission (KJQN202201519), which are gratefully acknowledged.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Linghui Sun is employed by the company of Research Institute of Petroleum Exploration & Development of China National Petroleum Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Yi, H.Y.; Zhang, B.J.; Gu, M.F.; Ma, H.L.; Zhang, X.H.; Chen, X.; Xie, C.; Gao, Z.L.; Shan, S.J.; Zhu, K.D. Discovery of isolated shoals in the Permian Maokou Formation of eastern Sichuan Basin and their natural gas exploration potential. Nat. Gas Ind. 2024, 44, 1–11. [Google Scholar]
- Qu, Z.; Lin, Q.; Guo, T. Experimental study on acid fracture conductivity of carbonate rock in Shunbei Oilfield. Fault-Block Oil Gas Field 2019, 26, 533–536. [Google Scholar]
- Qi, N.; Ma, T.; Zhang, Z.; Liu, X.; Liu, L. Creep closure mechanism of acid-etched fractures in limestone. Nat. Gas Ind. 2024, 44, 73–82. [Google Scholar]
- Han, X. Study on Mechanical Characteristics and Conductivity of Acid Etch Soften Layer in Limestone. Ph.D. Thesis, Chengdu University of Technology, Chengdu, China, 2018. [Google Scholar]
- Xiao, Y.; Wang, H.; Mi, Z.; Cheng, Y.; Cao, X.; Qu, J.; Guo, J. Laboratory measurements of acid-etched fracture conductivity for medium-high porosity and low permeability limestone reservoirs in EE oil field. In Proceedings of the 54th U.S. Rock Mechanics/Geomechanics Symposium, Golden, CO, USA, 28 June–1 July 2020; p. ARMA-2020-1394. [Google Scholar]
- Yao, S.; Wang, X.; Yuan, Q.; Zeng, F. Transient-Rate Analysis of Stress-Sensitive Hydraulic Fractures: Considering the Geomechanical Effect in Anisotropic Shale. SPE Reserv. Eval. Eng. 2018, 21, 863–888. [Google Scholar] [CrossRef]
- Wang, J.; Luo, W.; Chen, Z. An integrated approach to optimize bottomhole-pressure-drawdown management for a hydraulically fractured well using a transient inflow performance relationship. SPE Reserv. Eval. Eng. 2020, 23, 95–111. [Google Scholar] [CrossRef]
- An, C.; Killough, J.; Xia, X. Investigating the effects of stress creep and effective stress coefficient on stress-dependent permeability measurements of shale rock. J. Pet. Sci. Eng. 2020, 198, 108155. [Google Scholar] [CrossRef]
- Zhou, J. Study on the Conductivity of Acid Etching Fractures in Low Young’s Modulus Carbonate Rocks. Master’s Thesis, Institute of Porous Flow & Fluid Mechanics, China National Petroleum Corporation & Chinese Academy of Science, Langfang, China, 2021. [Google Scholar]
- Li, D.; Li, H.; Zhu, S. Study of permeability stress sensitivity of large-scale discrete fracture: A case study of Shunbei Oil Field. Fault-Block Oil Gas Field 2024, 31, 147–153. [Google Scholar]
- Zhou, B. Study on Stress Sensitivity of Long-Term Acid Fracture Conductivity in Carbonate Reservoirs. Master’s Thesis, China University of Petroleum (Beijing), Beijing, China, 2019. [Google Scholar]
- Teng, B.; Li, H.; Yu, H. A Novel Analytical Fracture-Permeability Model Dependent on Both Fracture Width and Proppant-Pack Properties. SPE J. 2020, 25, 3031–3050. [Google Scholar] [CrossRef]
- Teng, B.; Luo, W.; Chen, Z.; Kang, B.; Chen, L.; Wang, T. A comprehensive study of the effect of Brinkman flow on the performance of hydraulically fractured wells. J. Pet. Sci. Eng. 2022, 213, 110355. [Google Scholar] [CrossRef]
- Pang, Y.; Soliman, M.Y.; Deng, H.; Emadi, H. Analysis of Effective Porosity and Effective Permeability in Shale-Gas Reservoirs with Consideration of Gas Adsorption and Stress Effects. SPE J. 2017, 22, 1739–1759. [Google Scholar] [CrossRef]
- Mirani, A.; Marongiu-Porcu, M.; Wang, H.; Enkababian, P. Production-Pressure-Drawdown Management for Fractured Horizontal Wells in Shale-Gas Formations. SPE Reserv. Eval. Eng. 2018, 21, 550–565. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, J.; Zeng, J.; Zhang, H.; Zhao, Z.; Zeng, F.; Wang, W. A transient source-function-based embedded discrete fracture model for simulation of multiscale-fractured reservoir: Application in coalbed methane extraction. Gas Sci. Eng. 2025, 133, 205500. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, L.J.; Rong, T.L.; Zhang, L.; Ren, W.G.; Su, T. Creep-based permeability evolution in deep coal under unloading confining pressure. J. Nat. Gas Sci. Eng. 2019, 65, 185–196. [Google Scholar] [CrossRef]
- Zhou, H.W.; Zhang, L.; Wang, X.Y.; Rong, T.L.; Wang, L.J. Effects of matrix fracture interaction and creep deformation on permeability evolution of deep coal. Int. J. Rock Mech. Min. Sci. 2020, 127, 104236. [Google Scholar] [CrossRef]
- Cui, Y.; Lu, C.; Guan, Z.; Luo, W.; Teng, B.; Meng, F.; Peng, Y. Effects of creep on depressurization-induced gas well productivity in South China Sea natural gas hydrate reservoirs. Pet. Reserv. Eval. Dev. 2023, 13, 809–818. [Google Scholar]
- Chen, H. Study on Creep Mechanical Behavior and Creep Model of Fractured Rock Under Stress-Seepage Coupling Conditions. Master’s Thesis, Xihua University, Chengdu, China, 2023. [Google Scholar]
- Du, X.; Cheng, L.; Niu, L.; Chen, Y.; Cao, R.; Xie, Y. Numerical Simulation of 3D Discrete Fracture Networks Considering Dynamic Closure of Hydraulic Fractures and Natural Fractures. Chin. J. Comput. Phys. 2022, 39, 453–464. [Google Scholar]
- Tang, J.; Teng, J.; Zhang, C.; Liu, S. Experimental study of creep characteristics of layered water bearing shale. Rock Soil Mech. 2018, 39 (Suppl. S1), 33–41. [Google Scholar]
- Feng, J.; Sun, Z.; Wang, Y.; She, J. Study on Stress Sensitivity of or dovician Fractures in Hetianhe Gas Field, Tarim Basin. Geol. J. China Univ. 2019, 25, 276–286. [Google Scholar]
- Zhao, J. Study on Pore-Elastic Viscoplasticity Mechanical Properties of Shale and Its Influence on Conductivity of Artificial Fracture. Master’s Thesis, China University of Petroleum (Beijing), Beijing, China, 2023. [Google Scholar]
- Liu, W. Stress and Time Effects of Fractured Sandstone Permeability. Master’s Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2022. [Google Scholar]
- Rang, T. Research on Fracture Deformation Mechanism and Numerical Simulation Methods of Shale Oil Reservoir. Master’s Thesis, China University of Petroleum (Beijing), Beijing, China, 2023. [Google Scholar]
- Guo, W.; Liu, J.; Zhang, X.; Teng, B.; Kang, L.; Gao, J.; Liu, Y.; Luo, W. Study on the mechanism ofdrawdown management of shale gas horizontal well considering creep effect. Chin. J. Theor. Appl. Mech. 2023, 55, 630–642. [Google Scholar]
- Warren, J.E.; Root, P.J. The behavior of naturally fracture reservoirs. Soc. Pet. Eng. J. 1963, 228, 245–255. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of a coupled dual continuum and discrete fracture model for the simulation of unconventional reservoirs. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 February 2013; p. SPE-163647-MS. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).