Intelligent Kick Warning Model Based on Machine Learning
Abstract
1. Introduction
2. Analysis of Kick Characterization Parameters
2.1. Kick Mechanism
2.2. Characteristic Parameters of Kick
- (1)
- Direct Symptom Parameters:
- (2)
- Indirect Symptom Parameters:
2.3. Parameter Selection
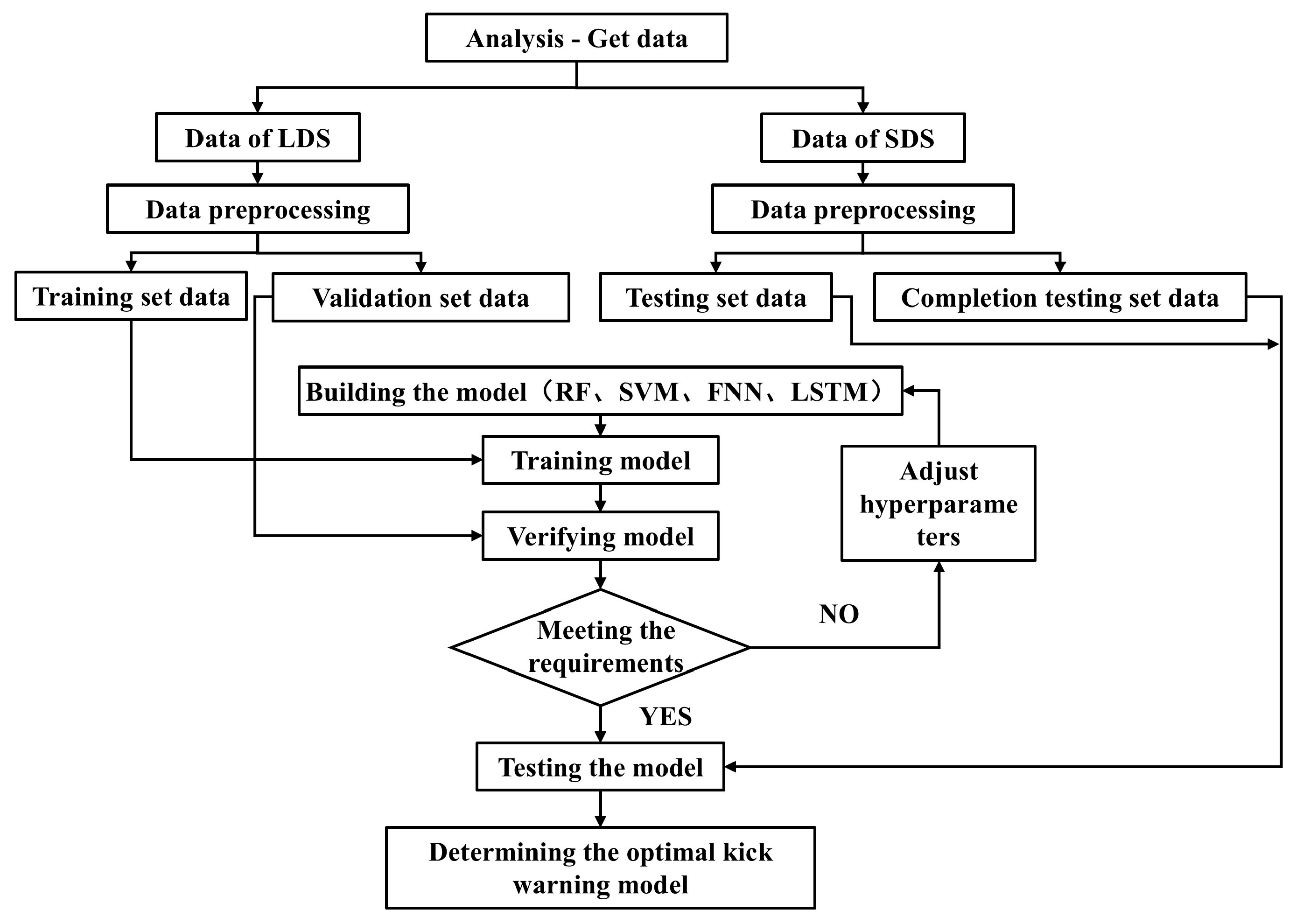
3. Data Acquisition and Preprocessing
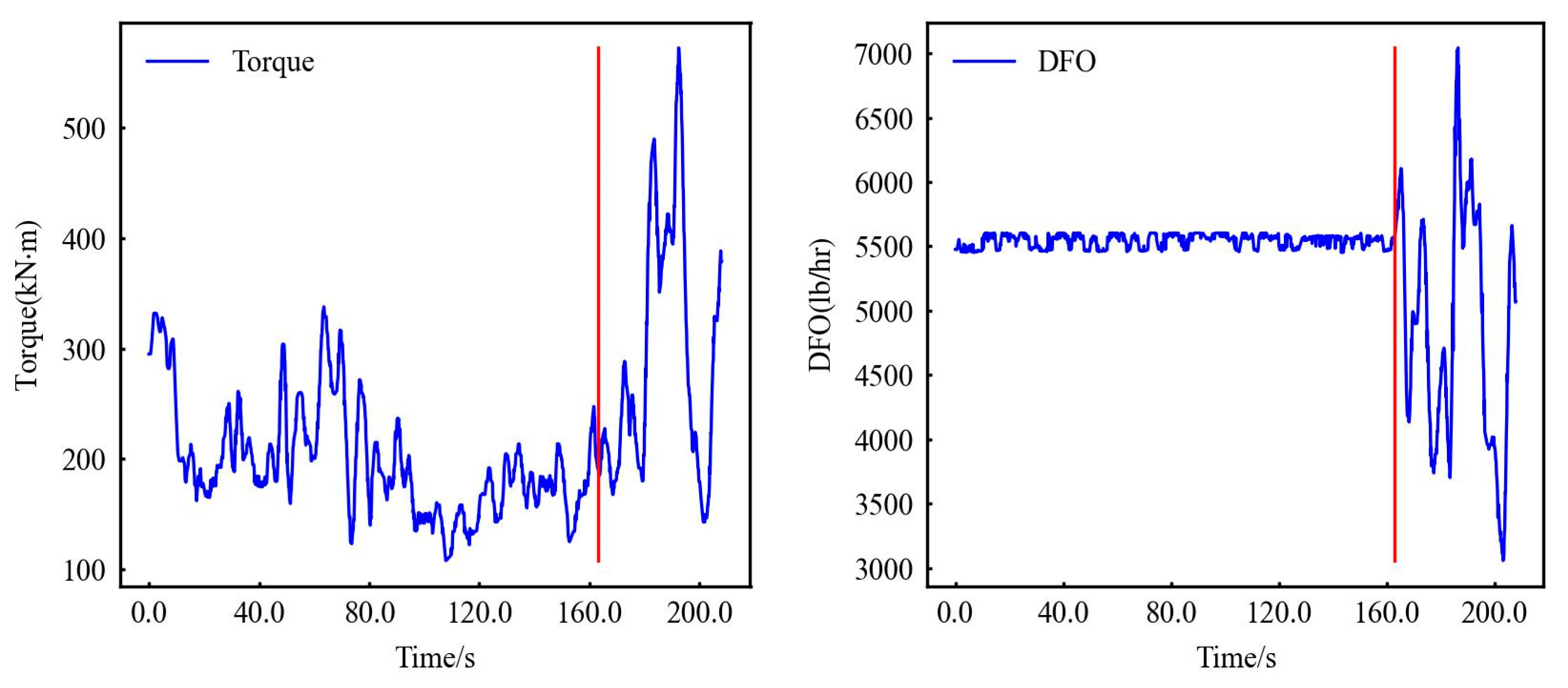
3.1. Data Acquisition
3.2. Data Preprocessing
3.2.1. Data Label
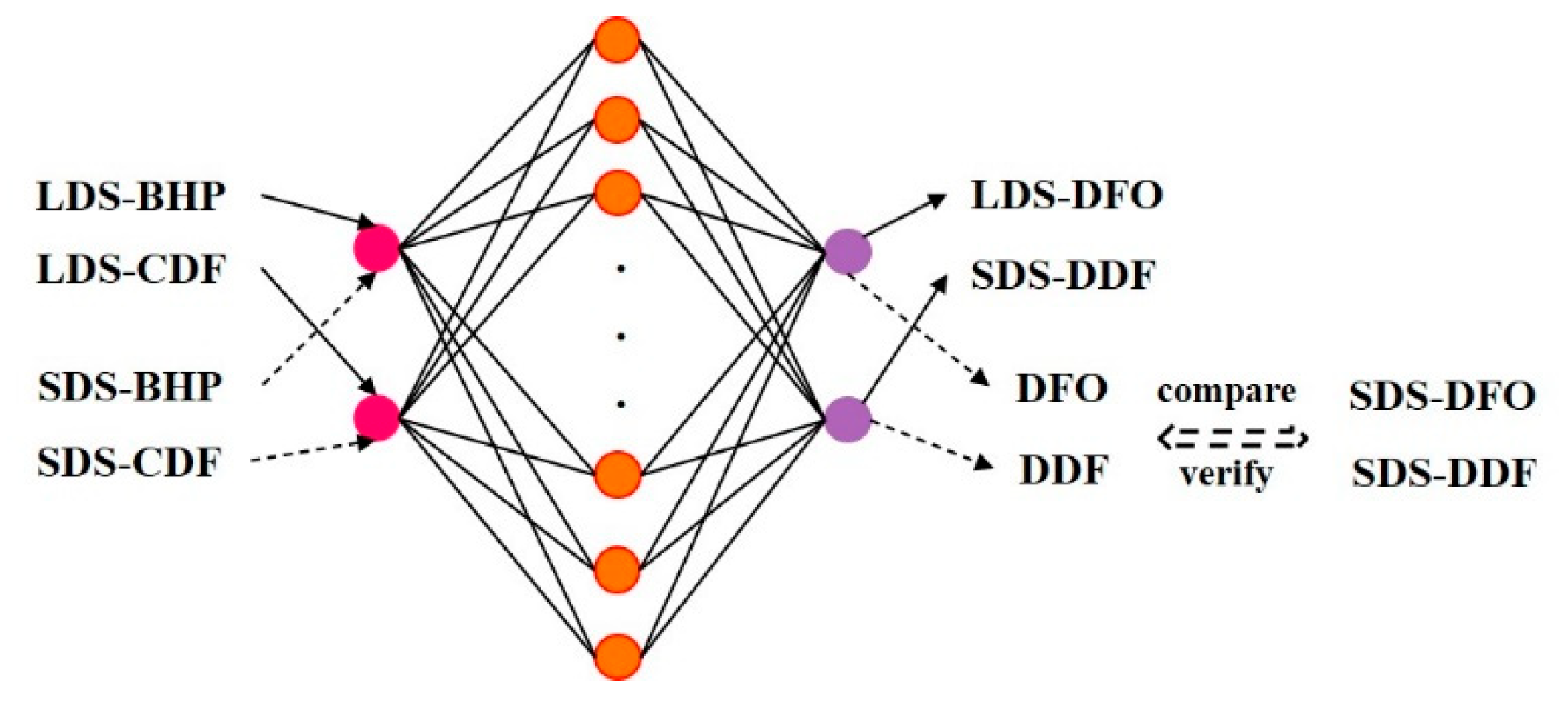
3.2.2. Data Completion
3.2.3. Split Data Set
4. Model Building and Results
4.1. Results Evaluation Indicators
4.2. Algorithm Implementation and Model Optimization
4.2.1. Train and Validate the Model
4.2.2. Test the Model
- (1)
- The results of the APRFM are as follows Table 9.
- (2)
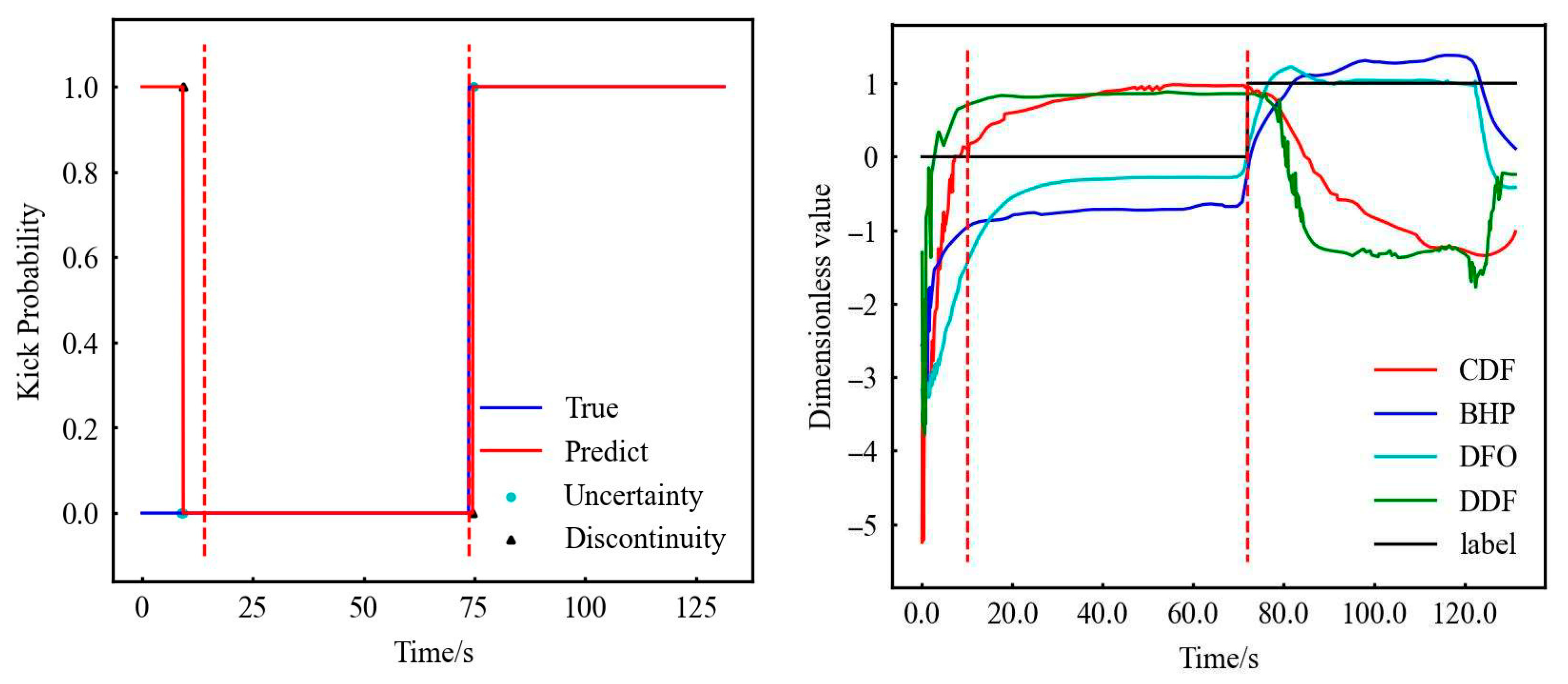
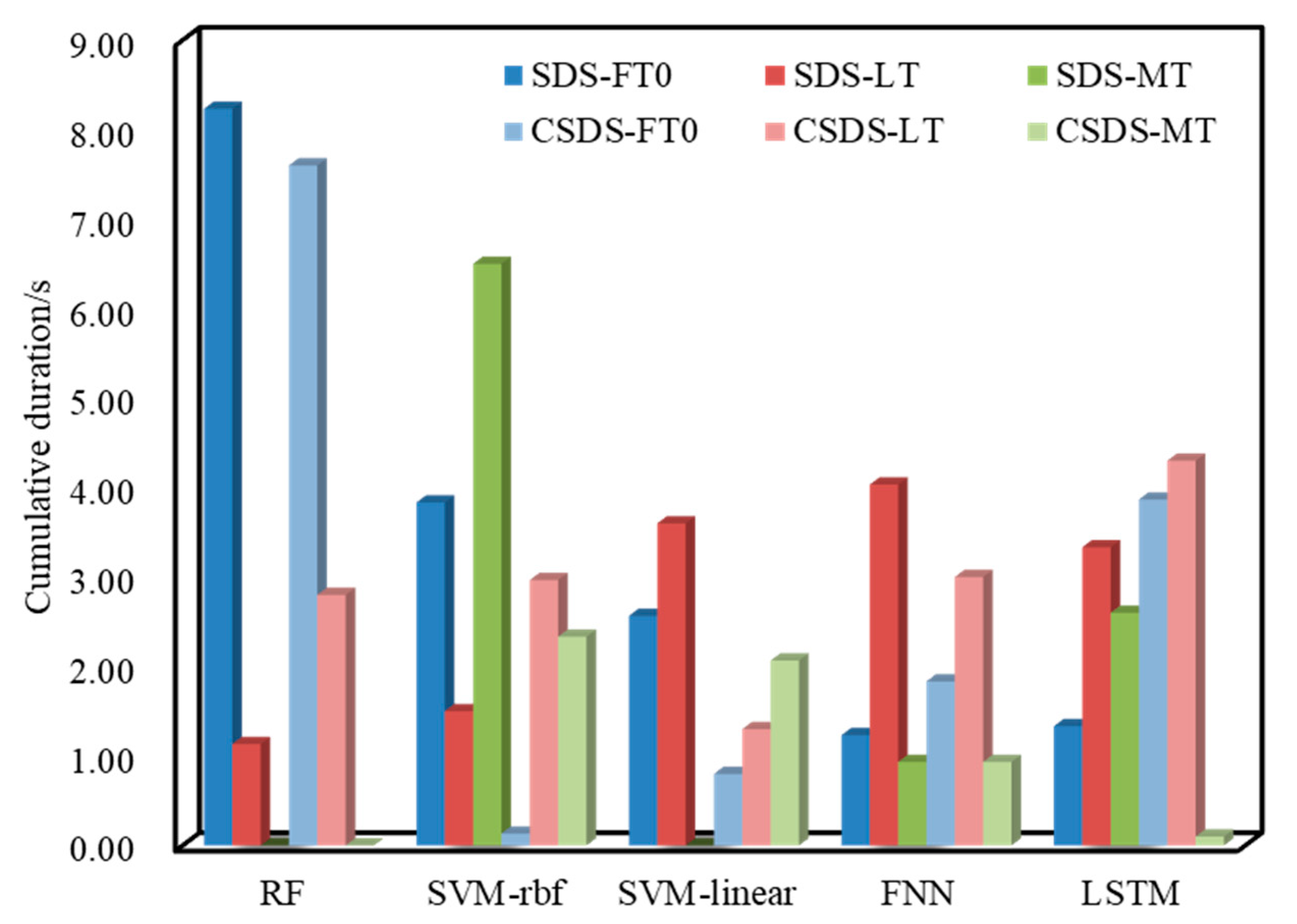
- Warning time analysis
5. Analysis and Discussion
6. Conclusions
- Although from theoretical analysis, parameters such as DOF, torque, and DDF contribute to the improvement of the model, the effect of actual data indicates that its effect may not be obvious during application.
- Use experimental data to test RF, the SVM, FNN, and LSTM to train, verify, and test models. The results show that the above models are evaluated by APRMF and CET. Among them, the SVM-linear model can achieve the highest accuracy rate of 0.968 and only has the M of 0.06 and the F of 0.11. The LT is 1.3 s, and the CET is 23.13. The effect of the SVM-linear model is the best. However, when using complex data, the effect of the slightly worse SVM-rbf model may exceed the SVM-linear model. The FNN and LSTM models are slightly inferior to the SVM model, but they also have an accuracy of about 0.950 and the two models are more stable for different data, and the ensemble model effect may be better than the SVM model. The RF model has an accuracy of only about 0.900, which is the worst overall.
- This article analyzes the reason for the different performance of the four models after adding features: RF reduces the original high-weight features and assigns new feature weights to increase the available information of the model. The result tends to balance the M and F; the SVM model improves the model effect by changing the number of kick and non-kick vectors, especially focusing on the vectors near the special points; the neural network extracts new feature information to balance false alarms and missed alarm, on the one hand, and keep the model stable on the other hand.
- In the comparison of the four models, the SVM model has the best effect (accuracy rate of 0.968), but it has the hidden danger of reduced effect due to complex training data. The ensemble FNN model is slightly inferior or slightly better than the SVM (accuracy rate is about 0.950) model, but it has good stability.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Accuracy |
| BHP | Bottom Hole Pressure |
| CDF | Conductivity of Drilling Fluid |
| DDF | Density of Drilling Fluid |
| DF | Differential Flow |
| F | Missed Alarm Rate |
| FNN | Fully Connected Neural Network |
| GP | Gas Pressure |
| LDS | Large-scale Drilling Simulator |
| LSTM | Long Short-term Memory Neural Network |
| M | False Alarm Rate |
| P | Precision |
| R | Recall Rate |
| RF | Random Forest |
| ROP | Rate Of Penetration |
| RPM | Rate Per Minute |
| SDS | Small-scale Drilling Simulator |
| SPP | Standpipe Pressure |
| SVM | Support Vector Machine |
| SVM-linear | SVM using Linear Kernel Function |
| SVM-rbf | SVM using RBF Kernel Function |
| WOB | Weight On Bit |
| WOH | Weight On Hook |
| Parameter Timeliness Score | |
| Parameter Credibility Score | |
| Parameter Total Score |
Appendix A
| Model | Experiment | Indicators | SDS Data | CSDS Data | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | P | R | M | F | A | P | R | M | F | |||
| RF | First | max | 0.942 | 0.982 | 0.894 | 0.137 | 0.021 | 0.932 | 0.982 | 0.876 | 0.124 | 0.015 |
| min | 0.922 | 0.975 | 0.863 | 0.106 | 0.015 | 0.932 | 0.982 | 0.876 | 0.124 | 0.015 | ||
| max-min | 0.020 | 0.007 | 0.031 | 0.031 | 0.006 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| error | 0.021 | 0.007 | 0.035 | 0.228 | 0.304 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| std | 0.009 | 0.002 | 0.015 | 0.015 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| cv | 0.009 | 0.003 | 0.017 | 0.125 | 0.112 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Second | max | 0.941 | 0.976 | 0.900 | 0.103 | 0.024 | 0.925 | 0.933 | 0.904 | 0.107 | 0.058 | |
| min | 0.938 | 0.973 | 0.897 | 0.100 | 0.021 | 0.919 | 0.933 | 0.893 | 0.096 | 0.057 | ||
| max-min | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.005 | 0.000 | 0.010 | 0.010 | 0.001 | ||
| error | 0.003 | 0.003 | 0.003 | 0.030 | 0.125 | 0.006 | 0.000 | 0.011 | 0.096 | 0.010 | ||
| std | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.002 | 0.000 | 0.004 | 0.004 | 0.000 | ||
| cv | 0.001 | 0.001 | 0.001 | 0.008 | 0.041 | 0.002 | 0.000 | 0.005 | 0.042 | 0.004 | ||
| Third | max | 0.926 | 0.984 | 0.866 | 0.141 | 0.018 | 0.920 | 0.936 | 0.888 | 0.140 | 0.054 | |
| min | 0.922 | 0.979 | 0.859 | 0.134 | 0.014 | 0.905 | 0.936 | 0.860 | 0.112 | 0.052 | ||
| max-min | 0.004 | 0.005 | 0.007 | 0.007 | 0.004 | 0.015 | 0.000 | 0.028 | 0.028 | 0.002 | ||
| error | 0.004 | 0.005 | 0.008 | 0.047 | 0.247 | 0.017 | 0.000 | 0.032 | 0.202 | 0.028 | ||
| std | 0.002 | 0.002 | 0.003 | 0.003 | 0.001 | 0.007 | 0.000 | 0.014 | 0.014 | 0.001 | ||
| cv | 0.002 | 0.002 | 0.003 | 0.022 | 0.094 | 0.008 | 0.000 | 0.016 | 0.106 | 0.014 | ||
| SVM | First | max | 0.949 | 0.968 | 0.918 | 0.082 | 0.025 | 0.958 | 0.942 | 0.961 | 0.039 | 0.044 |
| min | 0.949 | 0.968 | 0.918 | 0.082 | 0.025 | 0.958 | 0.942 | 0.961 | 0.039 | 0.044 | ||
| max-min | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| error | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| std | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| cv | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Second | max | 0.957 | 0.921 | 0.984 | 0.016 | 0.062 | 0.957 | 0.907 | 0.996 | 0.004 | 0.071 | |
| min | 0.957 | 0.921 | 0.984 | 0.016 | 0.062 | 0.957 | 0.907 | 0.996 | 0.004 | 0.071 | ||
| max-min | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| error | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| std | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| cv | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Third | max | 0.951 | 0.920 | 0.965 | 0.035 | 0.060 | 0.988 | 0.972 | 1.000 | 0.000 | 0.021 | |
| min | 0.951 | 0.920 | 0.965 | 0.035 | 0.060 | 0.988 | 0.972 | 1.000 | 0.000 | 0.021 | ||
| max-min | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| error | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| std | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| cv | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| FNN | First | max | 0.954 | 0.938 | 0.990 | 0.046 | 0.114 | 0.968 | 0.986 | 0.950 | 0.085 | 0.064 |
| min | 0.920 | 0.833 | 0.954 | 0.010 | 0.046 | 0.941 | 0.914 | 0.915 | 0.050 | 0.011 | ||
| max-min | 0.033 | 0.105 | 0.036 | 0.036 | 0.067 | 0.027 | 0.072 | 0.035 | 0.035 | 0.053 | ||
| error | 0.035 | 0.112 | 0.036 | 0.775 | 0.592 | 0.028 | 0.073 | 0.037 | 0.410 | 0.824 | ||
| std | 0.009 | 0.031 | 0.010 | 0.010 | 0.020 | 0.008 | 0.024 | 0.011 | 0.011 | 0.018 | ||
| cv | 0.010 | 0.036 | 0.010 | 0.429 | 0.195 | 0.008 | 0.025 | 0.012 | 0.171 | 0.777 | ||
| Second | max | 0.973 | 0.939 | 1.000 | 0.013 | 0.086 | 0.969 | 0.944 | 0.986 | 0.031 | 0.078 | |
| min | 0.944 | 0.887 | 0.987 | 0.000 | 0.048 | 0.942 | 0.899 | 0.969 | 0.014 | 0.044 | ||
| max-min | 0.029 | 0.052 | 0.013 | 0.013 | 0.038 | 0.027 | 0.046 | 0.017 | 0.017 | 0.034 | ||
| error | 0.030 | 0.056 | 0.013 | 1.000 | 0.446 | 0.027 | 0.048 | 0.017 | 0.543 | 0.435 | ||
| std | 0.007 | 0.013 | 0.004 | 0.004 | 0.009 | 0.008 | 0.015 | 0.006 | 0.006 | 0.011 | ||
| cv | 0.007 | 0.014 | 0.004 | 1.789 | 0.144 | 0.009 | 0.016 | 0.006 | 0.275 | 0.172 | ||
| Third | max | 0.976 | 0.944 | 1.000 | 0.008 | 0.064 | 0.966 | 0.948 | 0.973 | 0.055 | 0.061 | |
| min | 0.959 | 0.913 | 0.992 | 0.000 | 0.042 | 0.941 | 0.920 | 0.945 | 0.027 | 0.040 | ||
| max-min | 0.017 | 0.031 | 0.008 | 0.008 | 0.022 | 0.024 | 0.028 | 0.029 | 0.029 | 0.021 | ||
| error | 0.017 | 0.033 | 0.008 | 1.000 | 0.348 | 0.025 | 0.029 | 0.029 | 0.516 | 0.348 | ||
| std | 0.004 | 0.008 | 0.002 | 0.002 | 0.006 | 0.007 | 0.010 | 0.010 | 0.010 | 0.007 | ||
| cv | 0.004 | 0.009 | 0.002 | 2.409 | 0.100 | 0.008 | 0.011 | 0.010 | 0.239 | 0.130 | ||
| LSTM | First | max | 0.921 | 0.859 | 0.964 | 0.047 | 0.113 | 0.966 | 0.984 | 0.945 | 0.082 | 0.045 |
| min | 0.915 | 0.837 | 0.953 | 0.036 | 0.100 | 0.951 | 0.940 | 0.918 | 0.055 | 0.013 | ||
| max-min | 0.006 | 0.023 | 0.011 | 0.011 | 0.014 | 0.015 | 0.044 | 0.027 | 0.027 | 0.033 | ||
| error | 0.007 | 0.027 | 0.011 | 0.233 | 0.119 | 0.016 | 0.045 | 0.029 | 0.333 | 0.724 | ||
| std | 0.002 | 0.006 | 0.004 | 0.004 | 0.004 | 0.004 | 0.013 | 0.009 | 0.009 | 0.010 | ||
| cv | 0.002 | 0.007 | 0.004 | 0.085 | 0.034 | 0.005 | 0.013 | 0.009 | 0.123 | 0.580 | ||
| Second | max | 0.963 | 0.931 | 0.991 | 0.018 | 0.067 | 0.947 | 0.927 | 0.978 | 0.051 | 0.098 | |
| min | 0.955 | 0.914 | 0.982 | 0.009 | 0.055 | 0.922 | 0.874 | 0.949 | 0.022 | 0.058 | ||
| max-min | 0.008 | 0.017 | 0.009 | 0.009 | 0.012 | 0.024 | 0.054 | 0.028 | 0.028 | 0.039 | ||
| error | 0.008 | 0.018 | 0.009 | 0.486 | 0.183 | 0.026 | 0.058 | 0.029 | 0.560 | 0.402 | ||
| std | 0.003 | 0.006 | 0.002 | 0.002 | 0.004 | 0.008 | 0.016 | 0.009 | 0.009 | 0.012 | ||
| cv | 0.003 | 0.007 | 0.002 | 0.178 | 0.075 | 0.008 | 0.018 | 0.009 | 0.216 | 0.136 | ||
| Third | max | 0.963 | 0.932 | 0.991 | 0.034 | 0.060 | 0.945 | 0.931 | 0.955 | 0.069 | 0.067 | |
| min | 0.951 | 0.920 | 0.966 | 0.009 | 0.051 | 0.932 | 0.913 | 0.931 | 0.045 | 0.054 | ||
| max-min | 0.012 | 0.012 | 0.025 | 0.025 | 0.009 | 0.013 | 0.017 | 0.024 | 0.024 | 0.013 | ||
| error | 0.013 | 0.013 | 0.025 | 0.728 | 0.143 | 0.014 | 0.019 | 0.025 | 0.346 | 0.192 | ||
| std | 0.004 | 0.005 | 0.009 | 0.009 | 0.003 | 0.004 | 0.005 | 0.007 | 0.007 | 0.003 | ||
| cv | 0.004 | 0.005 | 0.009 | 0.460 | 0.056 | 0.004 | 0.005 | 0.007 | 0.111 | 0.053 | ||
| Experiment | Model | Kick Time Point | SDS Data | CSDS Data | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kick | LT | FT0 | MT | Kick | LT | FT0 | MT | |||
| First | RF | 74.5 | 75.80 | 1.30 | 0.00 | 7.10 | 75.40 | 0.90 | 7.80 | 0.00 |
| SVM | 76.30 | 1.80 | 3.40 | 1.10 | 75.40 | 0.90 | 1.60 | 4.80 | ||
| LSTM | 75.50 | 1.00 | 1.10 | 7.20 | 75.30 | 0.80 | 3.30 | 0.00 | ||
| BP | 75.40 | 0.90 | 2.00 | 5.20 | 75.30 | 0.80 | 3.30 | 0.50 | ||
| Second | RF | 72.1 | 73.60 | 1.50 | 0.00 | 0.00 | 76.60 | 4.50 | 4.70 | 0.00 |
| SVM | 78.10 | 6.00 | 0.80 | 0.20 | 74.50 | 2.40 | 0.10 | 3.20 | ||
| LSTM | 77.30 | 5.20 | 0.00 | 0.00 | 76.20 | 4.10 | 1.10 | 0.00 | ||
| BP | 75.40 | 3.30 | 0.70 | 0.00 | 73.80 | 1.70 | 1.10 | 0.00 | ||
| Third | RF | 73.8 | 74.90 | 1.10 | 0.00 | 0.00 | 77.40 | 3.60 | 6.70 | 0.00 |
| SVM | 78.30 | 4.50 | 1.90 | 0.20 | 76.10 | 2.30 | 0.00 | 0.00 | ||
| LSTM | 78.30 | 4.50 | 0.00 | 0.00 | 77.20 | 3.40 | 2.10 | 0.00 | ||
| BP | 76.90 | 3.10 | 1.20 | 0.00 | 75.10 | 1.30 | 2.40 | 0.00 | ||
References
- Burton, Z.F.M.; Kroeger, K.F.; Hosford Scheirer, A.; Seol, Y.; Burgreen-Chan, B.; Graham, S.A. Tectonic uplift destabilizes subsea gas hydrate: A model example from Hikurangi margin, New Zealand. Geophys. Res. Lett. 2020, 47, e2020GL087150. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, J.; Wang, Z.; He, Z.; Song, C.; Liu, X.; Zhang, N.; Ji, T. Analysis of the world deepwater oil and gas exploration situation. Pet. Explor. Dev. 2023, 50, 1060–1076. [Google Scholar]
- Randolph, M.F.; Gaudin, C.; Gourvenec, S.M.; White, D.J.; Boylan, N.; Cassidy, M.J. Recent advances in offshore geotechnics for deep water oil and gas developments. Ocean Eng. 2011, 38, 818–834. [Google Scholar] [CrossRef]
- Burton, Z.F.M.; Moldowan, J.M.; Magoon, L.B.; Sykes, R.; Graham, S.A. Interpretation of source rock depositional environment and age from seep oil, east coast of New Zealand. Int. J. Earth Sci. 2019, 108, 1079–1091. [Google Scholar] [CrossRef]
- Burton, Z.F.M.; Dafov, L.N. Testing the sediment organic contents required for biogenic gas hydrate formation: Insights from synthetic 3-D basin and hydrocarbon system modelling. Fuels 2022, 3, 555–562. [Google Scholar] [CrossRef]
- Burton, Z.F.M.; Dafov, L.N. Salt Diapir-Driven Recycling of Gas Hydrate. Geochem. Geophys. Geosyst. 2023, 24, e2022GC010704. [Google Scholar] [CrossRef]
- Dafov, L.N.; Burton, Z.F.M.; Haines, S.S.; Hosford Scheirer, A.; Masurek, N.; Boswell, R.; Frye, M.; Seol, Y.; Graham, S.A. Terrebonne Basin, Gulf of Mexico gas hydrate resource evaluation and 3-D modeling of basin-scale sedimentation, salt tectonics, and hydrate system evolution since the early Miocene. Mar. Pet. Geol. 2025, 176, 107330. [Google Scholar] [CrossRef]
- Wang, H.; Huang, H.; Bi, W.; Ji, G.; Zhou, B.; Zhuo, L. Deep and ultra-deep oil and gas well drilling technologies: Progress and prospect. Nat. Gas Ind. B 2022, 9, 141–157. [Google Scholar] [CrossRef]
- Onita, F.B.; Ochulor, O.J. Geosteering in deep water wells: A theoretical review of challenges and solutions. World J. Eng. Technol. Res. 2024, 3, 46–54. [Google Scholar]
- Muehlenbachs, L.; Cohen, M.A.; Gerarden, T. The impact of water depth on safety and environmental performance in offshore oil and gas production. Energy Policy 2013, 55, 699–705. [Google Scholar] [CrossRef]
- Si, M. Research on Real-Time Early Warning Methods of Drilling Kick. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2016. [Google Scholar]
- Han, J.; Yang, H.; Zhang, J. Accurate discovery of kick research and field application in the northwest industrial area. Logging Eng. 2017, 28, 69–74. [Google Scholar] [CrossRef]
- Joye, S.B. Deepwater Horizon, 5 years on. Science 2015, 349, 592–593. [Google Scholar] [CrossRef]
- Reader, T.W.; O’Connor, P. The Deepwater Horizon explosion: Non-technical skills, safety culture, and system complexity. J. Risk Res. 2014, 17, 405–424. [Google Scholar] [CrossRef]
- McNutt, M.K.; Camilli, R.; Crone, T.J.; Guthrie, G.D.; Hsieh, P.A.; Ryerson, T.B.; Savas, O.; Shaffer, F. Review of flow rate estimates of the Deepwater Horizon oil spill. Proc. Natl. Acad. Sci. USA 2012, 109, 20260–20267. [Google Scholar] [CrossRef]
- Skogdalen, J.E.; Vinnem, J.E. Quantitative risk analysis of oil and gas drilling, using Deepwater Horizon as case study. Reliab. Eng. Syst. Saf. 2012, 100, 58–66. [Google Scholar] [CrossRef]
- Aldred, W.; Plumb, D.; Bradford, I.; Cook, J.; Gholkar, V.; Cousins, L.; Minton, R.; Fuller, J.; Goraya, S.; Tucker, D. Managing Drilling Risk. Oilf. Rev. 1999, 11, 2–19. [Google Scholar]
- Griffin, P. Early Kick Detection Holds Kill Pressure Lower. In Proceedings of the SPE Mechanical Engineering Aspects of Drilling and Production Symposium, Fort Worth, TX, USA, 5–7 March 1967; p. SPE-1755-MS. [Google Scholar] [CrossRef]
- Zhou, J.; Gravdal, J.E.; Strand, P.; Hovland, S. Automated kick control procedure for an influx in managed pressure drilling operations. MIC J. 2016, 37, 31–40. [Google Scholar] [CrossRef]
- Fraser, D.; Lindley, R.; Moore, D.; Vander Staak, M.; Corp, H. Early Kick Detection Methods and Technologies Introduction : The Significance of Early Kick Detection Proposed Performance Indicators for Analyzing Kick Detection and Kick. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- Johnson, A.; Leuchtenberg, C.; Petrie, S.; Cunningham, D. Advancing deepwater kick detection. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Fort Worth, TX, USA, 4–6 March 2014; p. SPE-167990. [Google Scholar]
- Sun, H.; Li, D.; Huang, H.; Li, Y.; Tao, Q.; Fu, X.; Guo, S. Application of outlet flow monitoring technology in kick warning. Logging Eng. 2015, 25, 59–62. [Google Scholar]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, H.; Zhang, J.; Mi, L. Research on the Application of BP Neural Network in Intelligent Early Warning of Drilling Overflow in Development Wells. Inf. Commun. 2014, 2014, 3–4. [Google Scholar]
- Gurina, E.; Klyuchnikov, N.; Zaytsev, A.; Romanenkova, E.; Antipova, K.; Simon, I.; Makarov, V.; Koroteev, D. Application of machine learning to accidents detection at directional drilling. J. Pet. Sci. Eng. 2019, 184, 106519. [Google Scholar] [CrossRef]
- Haibo, L.; Zhi, W. Application of an intelligent early-warning method based on DBSCAN clustering for drilling overflow accident. Clust. Comput. 2018, 22, 2599–12608. [Google Scholar] [CrossRef]
- Liang, H.; Zou, J.; Liang, W. An early intelligent diagnosis model for drilling overflow based on GA–BP algorithm. Clust. Comput. 2019, 22, 10649–10668. [Google Scholar] [CrossRef]
- Liang, H.; Li, G.; Liang, W. Intelligent early warning model of early-stage overflow based on dynamic clustering. Clust. Comput. 2019, 22, 481–492. [Google Scholar] [CrossRef]
- Liang, H.; Liu, G.; Gao, J.; Khan, M.J. Overflow remote warning using improved fuzzy c-means clustering in IoT monitoring system based on multi-access edge computing. Neural Comput. Appl. 2019, 32, 15399–15410. [Google Scholar] [CrossRef]
- Muojeke, S.; Venkatesan, R.; Khan, F. Supervised data-driven approach to early kick detection during drilling operation. J. Pet. Sci. Eng. 2020, 192, 107324. [Google Scholar] [CrossRef]
- Osarogiagbon, A.; Muojeke, S.; Venkatesan, R.; Khan, F.; Gillard, P. A new methodology for kick detection during petroleum drilling using long short-term memory recurrent neural network. Process Saf. Environ. Prot. 2020, 142, 126–137. [Google Scholar] [CrossRef]
- Nhat, D.M.; Venkatesan, R.; Khan, F. Data-driven Bayesian network model for early kick detection in industrial drilling process. Process Saf. Environ. Prot. 2020, 138, 130–138. [Google Scholar] [CrossRef]
- Yin, Q.; Yang, J.; Tyagi, M.; Zhou, X.; Hou, X.; Cao, B. Field data analysis and risk assessment of gas kick during industrial deepwater drilling process based on supervised learning algorithm. Process Saf. Environ. Prot. 2021, 146, 312–328. [Google Scholar] [CrossRef]
- Yin, Q.; Zhu, Q.; Song, Z.; Guo, Y.; Yang, J.; Xu, Z.; Chen, K.; Sun, L.; Tyagi, M. Deep Learning based early warning methodology for gas kick of deepwater drilling using Pilot-Scale Rig Data. Process Saf. Environ. Prot. 2025, 196, 106844. [Google Scholar] [CrossRef]
- Fjetland, A.K.; Zhou, J.; Abeyrathna, D.; Gravdal, J.E. Kick detection and influx size estimation during offshore drilling operations using deep learning. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 2321–2326. [Google Scholar]
- Sha, Q.; Ding, Y.; Cui, M.; Cui, Y.; Gao, R.; Zhao, F.; Xing, S.; Lyu, C. Automatic Kick Detection Using Artificial Intelligence. In Proceedings of the International Petroleum Technology Conference IPTC, Dhahran, Saudi Arabia, 12 February 2024. [Google Scholar] [CrossRef]
- Bao, K. Research on the Kick Mechanism of High-Pressure Gas Wells in Northeastern Sichuan. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2006. [Google Scholar]
- Ma, C.; Zhang, Y.; Wan, X.; Huang, L.; Zhu, J. Research on the Downhole Data Transmission Method of the Measurement While Drilling System. West. Explor. Eng. 2014, 26, 58–61. [Google Scholar]
- Islam, R.; Khan, F.; Venkatesan, R. Real time risk analysis of kick detection: Testing and validation. Reliab. Eng. Syst. Saf. 2017, 161, 25–37. [Google Scholar] [CrossRef]
- Duan, S.; Song, X.; Cui, Y.; Xu, Z.; Liu, W.; Fu, J.; Zhu, Z.; Li, D. Intelligent kick warning based on drilling activity classification. Geoenergy Sci. Eng. 2023, 222, 211408. [Google Scholar] [CrossRef]






| Risk | Torque | WOH | SSP | DF | ROP |
|---|---|---|---|---|---|
| Kick | D | I/D | D | I | I |
| Lost circulation | /I | D | D | I | |
| Mud pack | I/F | I | I | D | |
| Mild well collapse | I/F | I/D | I | D | |
| Sand bridge stuck | I | I/D | I | D | |
| Reduced drill stuck | I/F | I/D | /I | ||
| Keyway stuck | I | ||||
| Drill string washout | I | D | D | ||
| Nozzle puncture | D | D | |||
| Nozzle dropped | D | D | |||
| Nozzle blocked | I/F | D | |||
| broken drill tool | D | D | D | D | |
| Stuck pipe | D | I/D | D | ||
| Severe well collapse | I | I/D | I | D | D |
| Blowout | D | I | I | ||
| Drill bit falling | D | D | D | ||
| Falling objects | I/F | I | D | ||
| Statistics | 7 | 11 | 5 | 1 | 1 |
| Rank | Parameter | Timeliness | Credibility | Total Score | Note |
|---|---|---|---|---|---|
| 1 | DFO | 10 | 9 | 19 | A |
| 2 | ROP | 10 | 9 | 19 | B |
| 3 | Torque | 10 | 5 | 15 | B |
| 4 | SSP | 10 | 5 | 15 | |
| 5 | Casing pressure | 10 | 5 | 15 | |
| 6 | DDF | 5 | 10 | 15 | C |
| 7 | CDF | 5 | 10 | 15 | C |
| 8 | Annulus pressure | 5 | 10 | 15 | C |
| 9 | Bottom hole temperature | 5 | 10 | 15 | C |
| 10 | Gas composition | 5 | 10 | 15 | C |
| 11 | WOH | 10 | 0 | 10 |
| SDS Data | LDS Data | ||||
|---|---|---|---|---|---|
| DF (lb/hr) | 3753.18 | DF (lb/hr) | 5400.78 | Torque (kN·m) | 218.49 |
| BHP (psig) | 14.83 | BHP (psig) | 14.96 | RPM | 59.42 |
| CDF (uS/cm) | 91.19 | CDF (uS/cm) | 366.8 | WOB (kN) | 0.75 |
| DDF (lb/ft3) | 58.5 | DDF (lb/ft3) | 52.1 | GP (psig) | 85.21 |
| Data Preprocessing Method | Number of Neurons | Activation Function |
|---|---|---|
| Standardization | 200 500 | Tanh Sigmoid Relu |
| Normalized | ||
| Original value reduced | ||
| Original value |
| Number of Neurons | Activation Function | The Maximum Value of R | |||
|---|---|---|---|---|---|
| Standardization | Normalized | Original Value Reduced | Original Value | ||
| 200 | sigmoid | 0.31 | −3.54 | −18.54 | −86.33 |
| tanh | 0.41 | −5.93 | −31.13 | −82 | |
| relu | 0.26 | −6.59 | −54.09 | −136.59 | |
| 500 | sigmoid | 0.3 | −6.28 | −16.15 | −66.23 |
| tanh | 0.42 | −5.99 | −25.07 | −59.66 | |
| relu | 0.32 | −7.37 | −21.61 | −133.67 | |
| Data Set | Total Number of Data | Number of Kick Data | Percentage |
|---|---|---|---|
| LDS-Train | 1387 | 300 | 21.63% |
| LDS-Validation | 694 | 150 | 21.63% |
| SDS1 | 1314 | 551 | 41.93% |
| CSDS1 | 1314 | 551 | 41.93% |
| SDS2 | 1314 | 593 | 45.13% |
| CSDS2 | 1314 | 593 | 45.13% |
| SDS3 | 1314 | 593 | 45.13% |
| CSDS3 | 1314 | 593 | 45.13% |
| Algorithm | RF | SVM | FNN | LSTM |
|---|---|---|---|---|
| Adjustment parameters | Number of trees | Kernel function | Number of neurons | Number of neurons |
| Minimum sample number of leaf nodes | C value | Activation function | Weight of class in loss function | |
| Weight of class in loss function | Weight of class in loss function | Weight of class in loss function |
| Data | Algorithm Model | A | P | R | M | F |
|---|---|---|---|---|---|---|
| FLDS | RF | 0.999 | 1.000 | 0.993 | 0.007 | 0.000 |
| SVM-linear | 0.999 | 1.000 | 0.993 | 0.007 | 0.000 | |
| SVM-rbf | 0.999 | 1.000 | 0.993 | 0.007 | 0.000 | |
| FNN | 0.999 | 1.000 | 0.993 | 0.007 | 0.000 | |
| LSTM | 0.999 | 1.000 | 0.993 | 0.007 | 0.000 | |
| ELDS | RF | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 |
| SVM-linear | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | |
| SVM-rbf | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | |
| FNN | 0.999 | 1.000 | 0.993 | 0.007 | 0.000 | |
| LSTM | 0.999 | 1.000 | 0.993 | 0.007 | 0.000 |
| Data | Model | A | P | R | M | F |
|---|---|---|---|---|---|---|
| SDS data | RF | 0.932 | 0.880 | 0.979 | 0.021 | 0.106 |
| SVM-rbf | 0.909 | 0.929 | 0.860 | 0.140 | 0.052 | |
| SVM-linear | 0.952 | 0.956 | 0.936 | 0.064 | 0.035 | |
| FNN | 0.952 | 0.991 | 0.898 | 0.102 | 0.006 | |
| LSTM | 0.945 | 0.975 | 0.898 | 0.102 | 0.018 | |
| CSDS data | RF | 0.922 | 0.882 | 0.950 | 0.050 | 0.100 |
| SVM-rbf | 0.958 | 0.997 | 0.907 | 0.093 | 0.002 | |
| SVM-linear | 0.968 | 0.986 | 0.940 | 0.060 | 0.011 | |
| FNN | 0.954 | 0.958 | 0.938 | 0.062 | 0.033 | |
| LSTM | 0.943 | 0.943 | 0.929 | 0.071 | 0.045 |
| Model | Comparison Index | A | P | R | M | F |
|---|---|---|---|---|---|---|
| RF | diff | −0.010 | 0.002 | −0.029 | 0.029 | −0.005 |
| ratio | −1.06% | 0.23% | −2.92% | 135.19% | −4.87% | |
| SVM-rbf | diff | 0.049 | 0.068 | 0.047 | −0.047 | −0.050 |
| ratio | 5.36% | 7.34% | 5.50% | −33.74% | −96.57% | |
| SVM-linear | diff | 0.015 | 0.030 | 0.004 | −0.004 | −0.024 |
| ratio | 1.60% | 3.12% | 0.44% | −6.41% | −68.94% | |
| FNN | diff | 0.003 | −0.033 | 0.041 | −0.041 | 0.027 |
| ratio | 0.27% | −3.38% | 4.54% | −39.74% | 450.00% | |
| LSTM | diff | −0.002 | −0.032 | 0.032 | −0.032 | 0.027 |
| ratio | −0.17% | −3.28% | 3.52% | −30.80% | 150.96% |
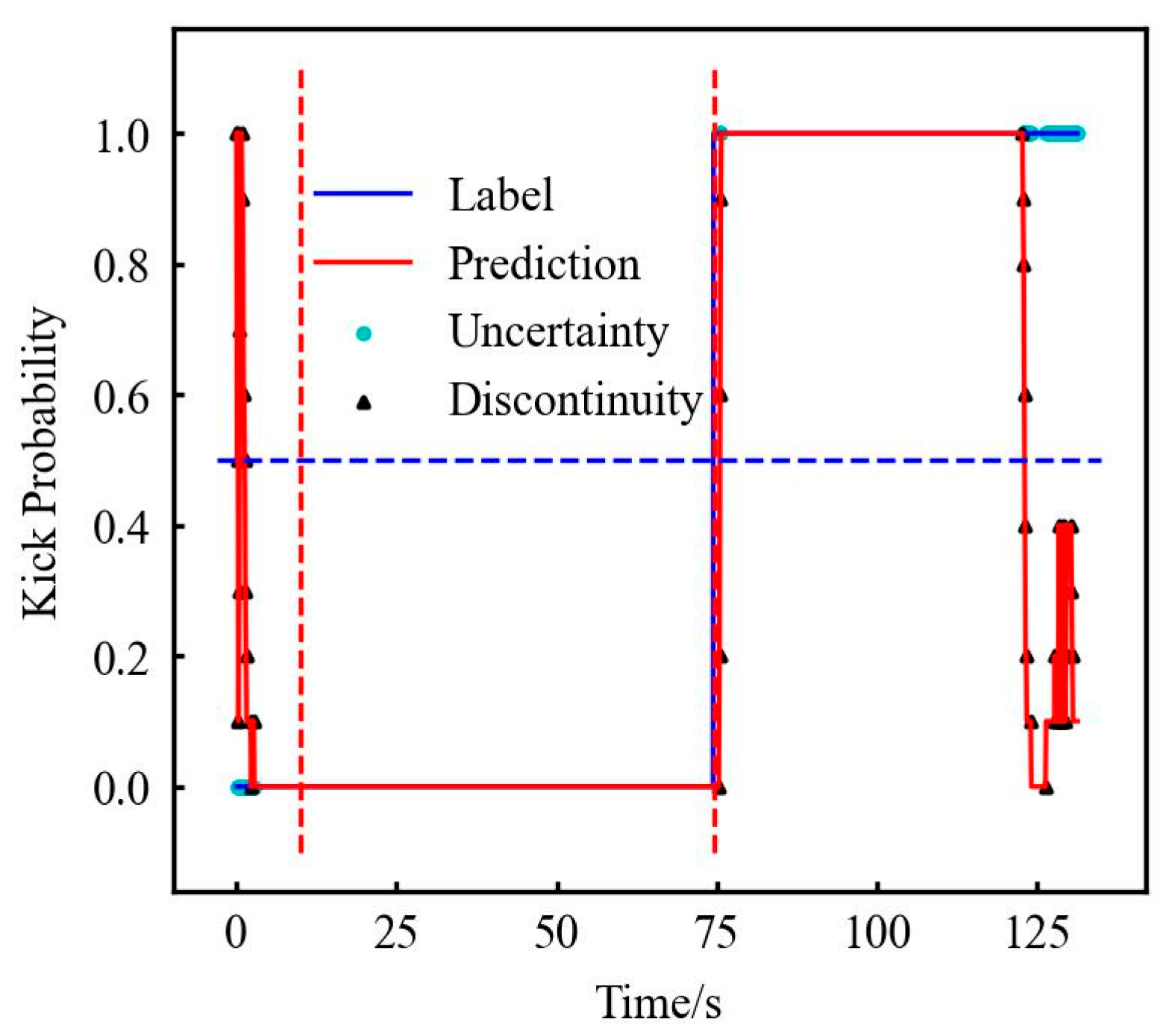
| Data | Begin Normal Drilling Time Point/s | Kick Time Point/s |
|---|---|---|
| Experiment 1 | 10.00 | 74.50 |
| Experiment 2 | 12.00 | 72.10 |
| Experiment 3 | 14.00 | 73.80 |
| Data | Algorithm | FT0 | FT1 | Alarm Time Point | LT | MT | CET |
|---|---|---|---|---|---|---|---|
| SDS | RF | 8.23 | 0.00 | 74.60 | 1.13 | 0.00 | 22.13 |
| SVM-rbf | 3.83 | 0.00 | 74.97 | 1.50 | 6.50 | 34.67 | |
| SVM-linear | 2.57 | 0.00 | 77.07 | 3.60 | 0.00 | 23.13 | |
| FNN | 1.23 | 0.00 | 77.50 | 4.03 | 0.93 | 25.43 | |
| LSTM | 1.33 | 0.00 | 76.80 | 3.33 | 2.60 | 27.13 | |
| CSDS | RF | 7.60 | 0.00 | 76.27 | 2.80 | 0.00 | 29.20 |
| SVM-rbf | 0.13 | 0.00 | 76.43 | 2.97 | 2.33 | 22.10 | |
| SVM-linear | 0.80 | 0.00 | 74.77 | 1.30 | 2.07 | 14.30 | |
| FNN | 1.83 | 0.00 | 76.47 | 3.00 | 0.93 | 21.47 | |
| LSTM | 3.87 | 0.00 | 77.77 | 4.30 | 0.10 | 29.53 |
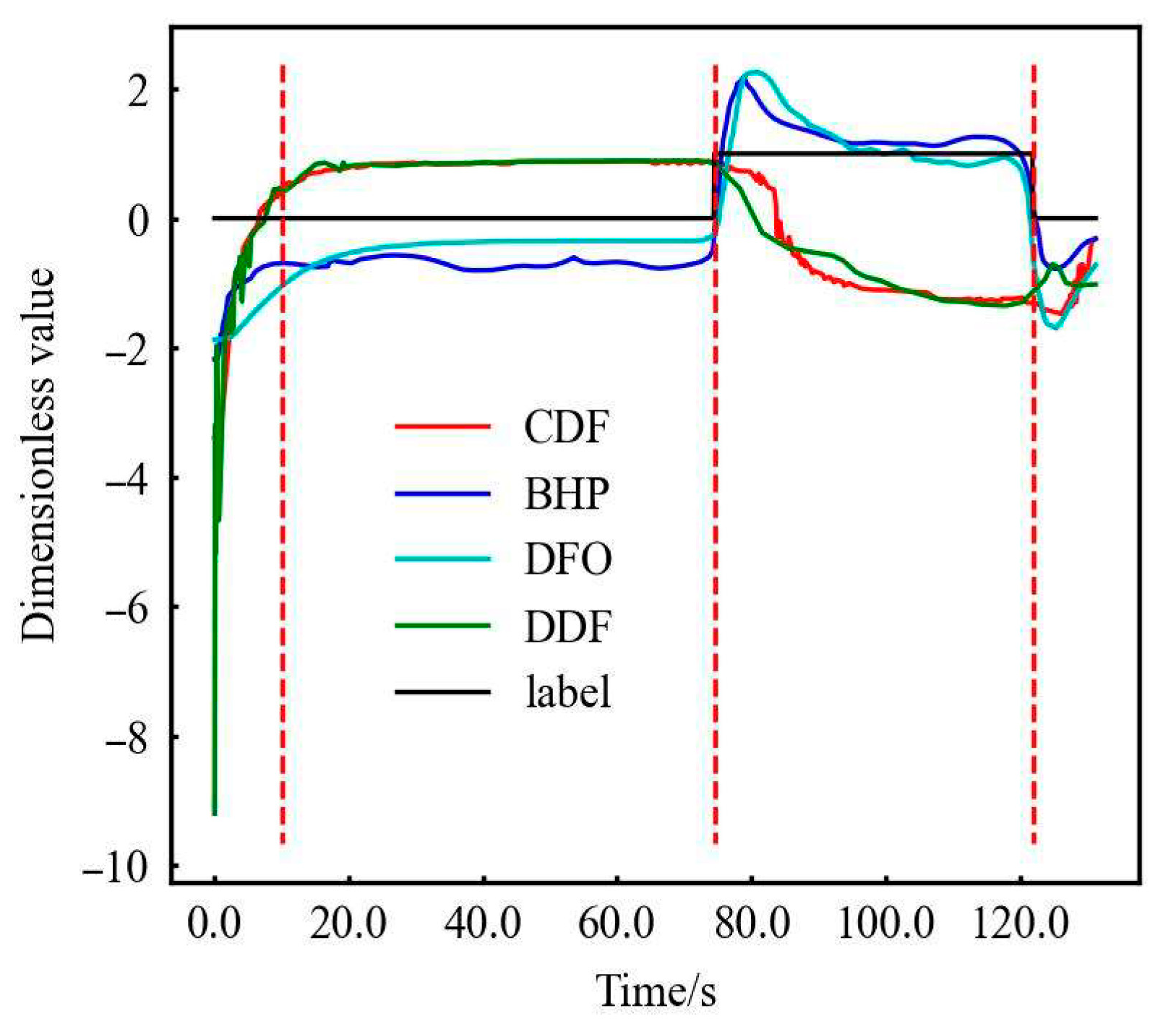
| RF SDS data parameter weight | CDF | BHP | DF | DDF |
| 0.122 | 0.402 | 0.025 | 0.451 | |
| RF completion data parameter weight | CDF | BHP | DF | DDF |
| 0.152 | 0.218 | 0.080 | 0.225 | |
| Torque | RPM | WOB | GP | |
| 0.023 | 0.005 | 0.000 | 0.297 |
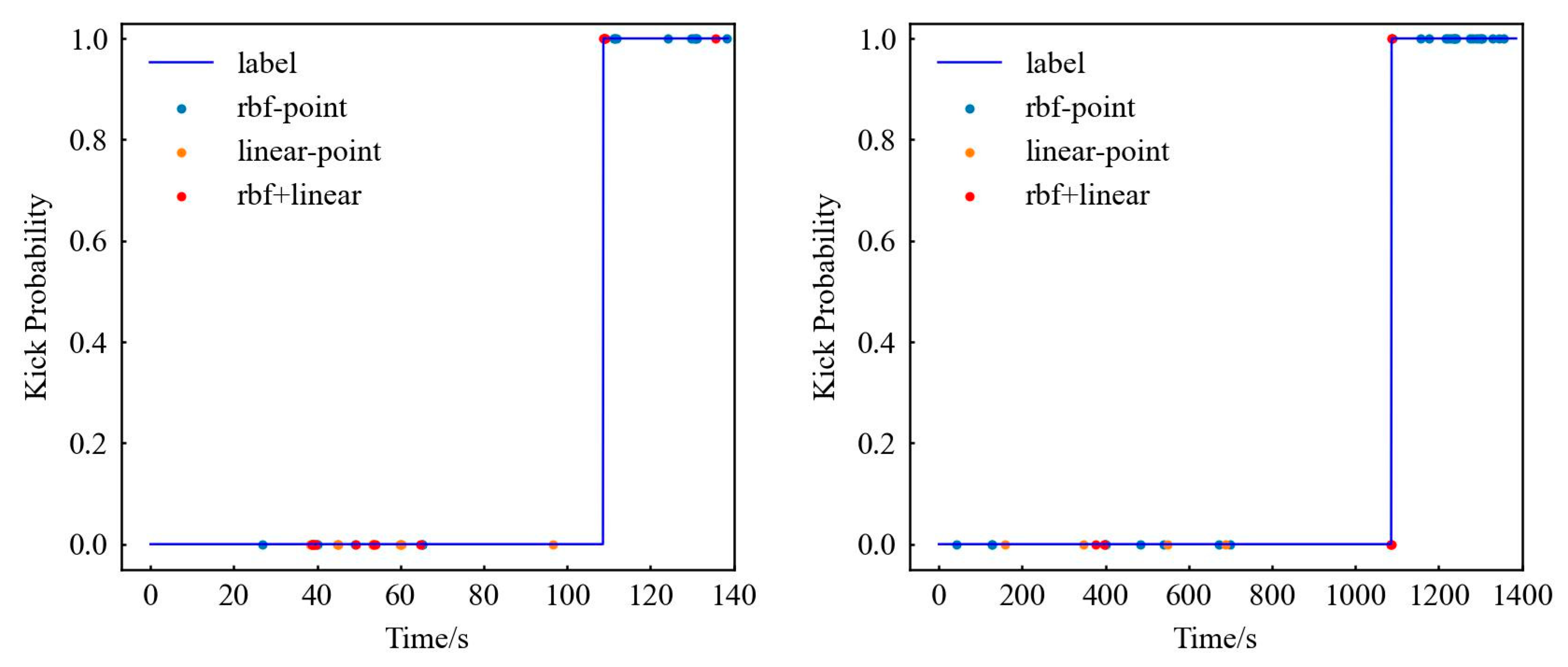
| Data | Algorithm | Total Support Vector | Non-Kick Vector | Kick Vector |
|---|---|---|---|---|
| SDS data | SVM-RBF | 34 | 19 | 15 |
| SVM-linear | 30 | 22 | 8 | |
| Same vector | 15 | 9 | 6 | |
| CSDS data | SVM-RBF | 36 | 12 | 24 |
| SVM-linear | 11 | 6 | 5 | |
| Same vector | 7 | 2 | 5 | |
| The same vector of the SDS data and the CSDS data | SVM-RBF | 11 | 5 | 6 |
| SVM-linear | 3 | 1 | 2 | |
| Same vector | 3 | 1 | 2 |
| Data | Model | A | P | R | M | F |
|---|---|---|---|---|---|---|
| SDS data | RF | 0.882 | 0.777 | 0.975 | 0.025 | 0.178 |
| SVM-rbf | 0.954 | 0.922 | 0.966 | 0.034 | 0.054 | |
| SVM-linear | 0.901 | 0.837 | 0.929 | 0.071 | 0.115 | |
| FNN | 0.938 | 0.912 | 0.932 | 0.068 | 0.058 | |
| LSTM | 0.933 | 0.899 | 0.936 | 0.064 | 0.068 | |
| CSDS data | RF | 0.870 | 0.774 | 0.945 | 0.055 | 0.176 |
| SVM-rbf | 0.942 | 0.913 | 0.941 | 0.059 | 0.057 | |
| SVM-linear | 0.947 | 0.900 | 0.973 | 0.027 | 0.068 | |
| FNN | 0.905 | 0.840 | 0.937 | 0.063 | 0.114 | |
| LSTM | 0.891 | 0.823 | 0.923 | 0.077 | 0.127 |
| Model | Comparison Index | A | P | R | M | F |
|---|---|---|---|---|---|---|
| RF | diff | −0.011 | −0.003 | −0.030 | 0.030 | −0.002 |
| ratio | −1.29% | −0.43% | −3.11% | 120.70% | −0.98% | |
| SVM-rbf | diff | −0.013 | −0.009 | −0.025 | 0.025 | 0.003 |
| ratio | −1.33% | −0.96% | −2.56% | 72.58% | 6.12% | |
| SVM-linear | diff | 0.047 | 0.063 | 0.044 | −0.044 | −0.047 |
| ratio | 5.18% | 7.55% | 4.75% | −61.94% | −41.12% | |
| FNN | diff | −0.033 | −0.072 | 0.005 | −0.005 | 0.055 |
| ratio | −3.51% | −7.90% | 0.51% | −7.00% | 95.06% | |
| LSTM | diff | −0.042 | −0.077 | −0.013 | 0.013 | 0.059 |
| ratio | −4.51% | −8.51% | −1.42% | 20.84% | 85.76% |
| Data | Threshold | A | P | R | M | F |
|---|---|---|---|---|---|---|
| SDS data | 3 | 0.928 | 0.972 | 0.858 | 0.142 | 0.019 |
| 0.964 | 0.998 | 0.922 | 0.078 | 0.001 | ||
| 0.968 | 1.000 | 0.927 | 0.073 | 0.000 | ||
| Average | 0.953 | 0.990 | 0.902 | 0.098 | 0.007 | |
| 5 | 0.920 | 0.975 | 0.837 | 0.163 | 0.016 | |
| 0.963 | 1.000 | 0.917 | 0.083 | 0.000 | ||
| 0.966 | 1.000 | 0.922 | 0.078 | 0.000 | ||
| Average | 0.950 | 0.992 | 0.892 | 0.108 | 0.005 | |
| 7 | 0.922 | 0.983 | 0.833 | 0.167 | 0.011 | |
| 0.961 | 1.000 | 0.914 | 0.086 | 0.000 | ||
| 0.965 | 1.000 | 0.920 | 0.080 | 0.000 | ||
| Average | 0.949 | 0.994 | 0.889 | 0.111 | 0.004 | |
| CSDS data | 3 | 0.960 | 0.927 | 0.984 | 0.016 | 0.059 |
| 0.957 | 0.975 | 0.929 | 0.071 | 0.019 | ||
| 0.947 | 0.950 | 0.929 | 0.071 | 0.038 | ||
| Average | 0.955 | 0.951 | 0.947 | 0.053 | 0.039 | |
| 5 | 0.961 | 0.930 | 0.984 | 0.016 | 0.056 | |
| 0.955 | 0.980 | 0.919 | 0.081 | 0.015 | ||
| 0.949 | 0.960 | 0.922 | 0.078 | 0.030 | ||
| Average | 0.955 | 0.957 | 0.942 | 0.058 | 0.034 | |
| 7 | 0.967 | 0.941 | 0.984 | 0.016 | 0.047 | |
| 0.953 | 0.982 | 0.912 | 0.088 | 0.014 | ||
| 0.950 | 0.964 | 0.920 | 0.080 | 0.027 | ||
| Average | 0.956 | 0.962 | 0.939 | 0.061 | 0.029 |
| Data | Threshold | FT0 | FT1 | Alarm Time | LT | MT | Weighted |
|---|---|---|---|---|---|---|---|
| SDS Data Time Result | 3 | 1.4 | 0 | 75.4 | 0.9 | 7.1 | 30.7 |
| 0.1 | 0 | 76.6 | 4.5 | 0 | |||
| 0 | 0 | 77.9 | 4.1 | 0 | |||
| 5 | 1.2 | 0 | 75.4 | 0.9 | 8.3 | 23.9 | |
| 0 | 0 | 76.9 | 4.8 | 0 | |||
| 0 | 0 | 78.2 | 4.4 | 0 | |||
| 7 | 0.8 | 0 | 75.5 | 1 | 8.4 | 21.7 | |
| 0 | 0 | 77.1 | 5 | 0 | |||
| 0 | 0 | 78.3 | 4.5 | 0 | |||
| CSDS Data Time Result | 3 | 4.4 | 0 | 75.3 | 0.8 | 0 | 12.1 |
| 1.4 | 0 | 76.2 | 4.1 | 0 | |||
| 2.8 | 0 | 77.8 | 4 | 0 | |||
| 5 | 4.2 | 0 | 75.3 | 0.8 | 0 | 25.4 | |
| 1.1 | 0 | 76.8 | 4.7 | 0 | |||
| 2.2 | 0 | 78.2 | 4.4 | 0 | |||
| 7 | 3.5 | 0 | 75.3 | 0.8 | 0 | 26.2 | |
| 1 | 0 | 77.1 | 5 | 0.1 | |||
| 2 | 0 | 78.3 | 4.5 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhu, Z.; Cui, Y.; Wang, H.; Xu, Z.; Duan, S.; Zhou, M. Intelligent Kick Warning Model Based on Machine Learning. Processes 2025, 13, 2162. https://doi.org/10.3390/pr13072162
Li C, Zhu Z, Cui Y, Wang H, Xu Z, Duan S, Zhou M. Intelligent Kick Warning Model Based on Machine Learning. Processes. 2025; 13(7):2162. https://doi.org/10.3390/pr13072162
Chicago/Turabian StyleLi, Changsheng, Zhaopeng Zhu, Yueqi Cui, Haobo Wang, Zhengming Xu, Shiming Duan, and Mengmeng Zhou. 2025. "Intelligent Kick Warning Model Based on Machine Learning" Processes 13, no. 7: 2162. https://doi.org/10.3390/pr13072162
APA StyleLi, C., Zhu, Z., Cui, Y., Wang, H., Xu, Z., Duan, S., & Zhou, M. (2025). Intelligent Kick Warning Model Based on Machine Learning. Processes, 13(7), 2162. https://doi.org/10.3390/pr13072162








