A Multi-Objective Optimization Framework for Robust and Accurate Photovoltaic Model Parameter Identification Using a Novel Parameterless Algorithm

Abstract

Photovoltaic (PV) models are hard to optimize due to their intrinsic complexity and changing operation conditions. Root mean square error (RMSE) is often given precedence in classic single-objective optimization methods, limiting them to address the intricate nature of PV model calibration. To bypass these limitations, this research proposes a novel multi-objective optimization framework balancing accuracy and robustness by considering both maximum error and the L2 norm as significant objective functions. Along with that, we introduce the Random Search Around Bests (RSAB) algorithm, which is a parameterless metaheuristic designed to be effective at exploring the solution space. The primary contributions of this work are as follows: (1) an extensive performance evaluation of the proposed framework; (2) an adaptable function to adjust dynamically the trade-off between robustness and error minimization; and (3) the elimination of manual tuning of the RSAB parameters. Rigorous testing across three PV models demonstrates RSAB’s superiority over 17 state-of-the-art algorithms. By overcoming significant issues such as premature convergence and local minima entrapment, the proposed procedure provides practitioners with a reliable tool to optimize PV systems. Hence, this research supports the overarching goals of sustainable energy technology advancements by offering an organized and flexible solution enhancing the accuracy and efficiency of PV modeling, furthering research in renewable energy.

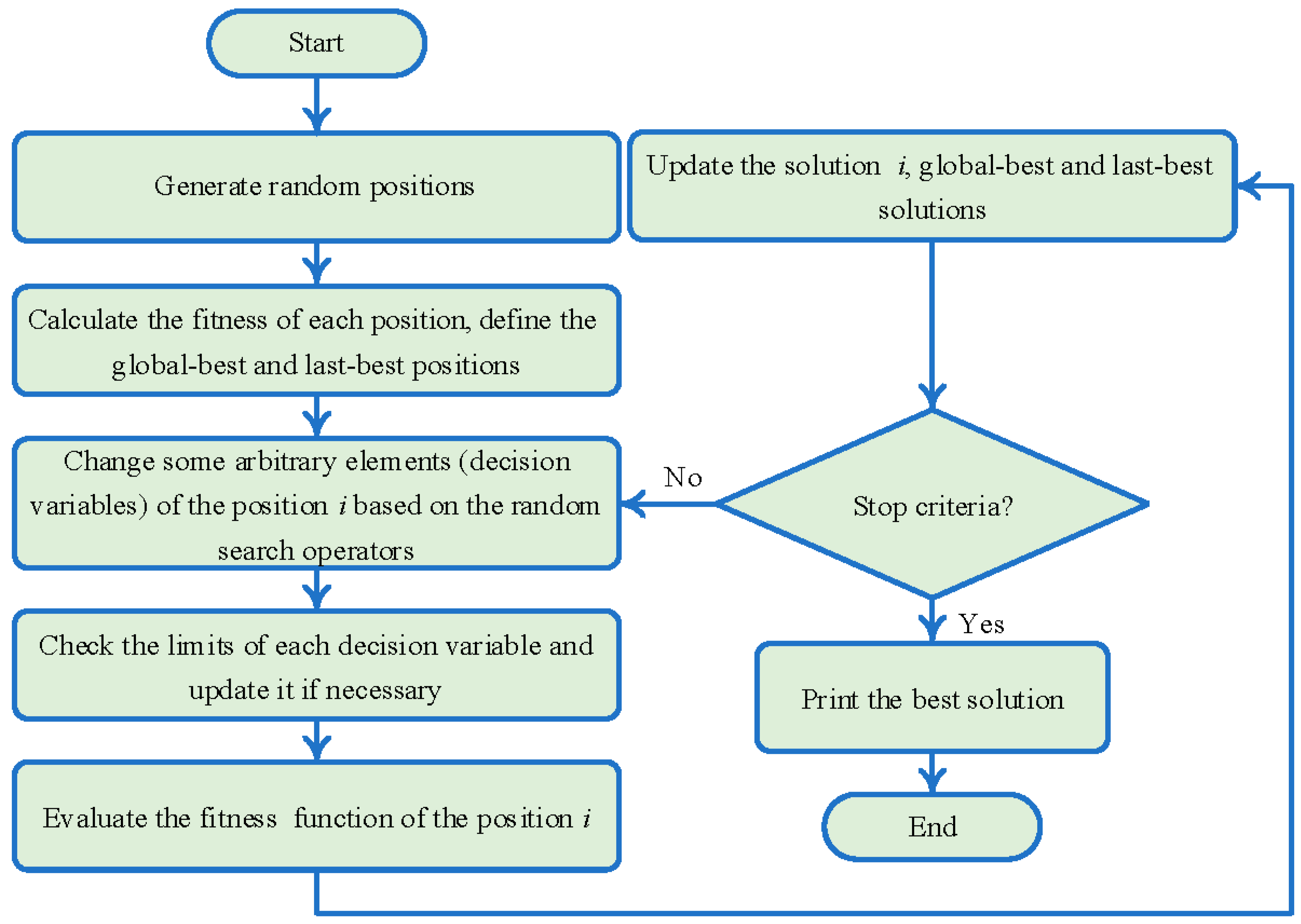
1. Introduction

Solar power systems play an imperative role in achieving sustainable and renewable sources of energy around the globe. Photovoltaic (PV) modules and cells are integral parts of solar power systems, highlighting the vital requirement of precise parameter estimation to maximize their efficiency and dependability [1]. With this, improving solar energy efficiency and affordability has generated significant interest in PV optimization [2].

The PV parameters need to be accurately determined to create reliable models that reflect solar cell behavior in different situations. Optimization algorithms do this by making discrepancies between calculated and experimentally obtained current-voltage (I-V) plots minimally. Classical optimization techniques used in PV parameter extraction often do not find it possible to achieve both accuracy and robustness at the same time. Solving these issues is an arduous optimization process needing precise predictions over the complete dataset as well as resistance to outliers. Our goal is to overcome these difficulties and ensure an overall solution that guarantees precise parameter estimation and resilient model performance.

The existing research in PV parameter extraction, optimization algorithms, and challenges of extracting accurate solar cell models are extensively reviewed in this literature. This review provides the foundation by establishing the framework of the proposed multi-objective optimization framework and presenting the RSAB algorithm.

Among the numerous PV parameter extraction methods discussed, analytical methods such as Lambert W function-based methods [3], and numerical optimization algorithms such as Differential Evolution (DE) [4], Genetic Algorithms (GA) [5], and Particle Swarm Optimization (PSO) [6] are presented. Analytical methods are unlikely to be accurate when there are non-idealities even though they provide closed-form solutions. Due to applicability to complicated optimization landscapes, numerical methods increasingly find favor. Optimization algorithm applications are crucial to PV modeling. With varying degrees of achievements, conventional methods like GA and PSO have widely been employed. Their sensitivity to parameter tuning and patchy convergence plots remind us of the need to find more reliable and convenient optimization tools by making them highly desirable.

The review offers an extensive analysis of the different optimization algorithms used by scholars, providing useful information about their merits, limitations, and advantages. Scholars have made use of numerous algorithms, and each of them has its own unique set of features. Sheng et al.’s development of the Moth–Flame Optimization (MFO) algorithm [1] proves to have a high rate of convergence. However, computation time issues and testing of commercial modules require consideration at length. Ishaque and Salam proved that DE [4] is effective in achieving accuracy for the SM55 Module, while limitations include limited exploitation scope and tuning of parameters. The use of PSO by Khanna et al. [6] proves to be of outstanding accuracy, acknowledging its simplicity and robustness. Still, local minimum and convergence issues are reported. The Bacterial Foraging Algorithm (BFA), as applied by Krishnakumar et al. [7], yields good results at low computation cost. Convergence rate issues, however, bring forth considerations to certain applications. The Artificial Bee Colony (ABC) algorithm [8], with superior accuracy and robustness, was used by Jamadi et al. Nonetheless, computation time, frequent tuning, and convergence issues in early time periods require consideration in time-sensitive applications. The GA [9], designed by Kumari and Geethanjali, is of fair accuracy in complex landscapes with limitations in local minimum and local searching ability. Yu et al.’s JAYA algorithm and IJAYA algorithm [10] offer computational cost and respect to local minimum and accuracy in solution, especially in cases with limited resources. Oliva et al.’s use of the Whale Optimization Algorithm (WOA) [11] proves low computational cost and simplicity of application. Convergence issues and issues of exploration are, however, brought to light by its application considerations. The Salp Swarm Algorithm (SSA) algorithm, with its high convergence rate and good tradeoff between exploration and exploitation, was used by Abbassi et al. [12]. The advantages and limitations of further clarification are recommended. Fair accuracy and simplicity of use are reported in Montoya et al.’s Sine Cosine Algorithm (SCA) implementation [13]. Limitation lies in possible entrapment by local minima and testing solely particular modules. The Teaching–Learning-based Optimization (TLBO) algorithm, known to be simple and of rapid convergence rate, is used in [14]. Computation cost issues and accuracy of the solution, however, require cautious consideration. As an innovative prospect introduced as an alternative, the War Strategy Optimization (WSO) algorithm [15] is an effective solution to numerous types of PV and models. Although it has minimal CPU time exhibits, issues of robustness highlight the call for additional research to address uncertainties and variations. Some recent studies involved optimization of the RMSE metric in order to further analyze PV parameter extraction. One notable example is the Northern Goshawk Optimization (NGO) algorithm [16], which places topmost emphasis on accuracy and robustness for PV module optimization, Double-Diode Model (DDM), and Single-Diode Model (SDM). The Modified Bald Eagle Search (mBES) [17] proves effective in Triple-Diode Model (TDM) optimization by providing low optimal fitness values. The Tree Seed Algorithm (TSA) [18] proves to be of rapid convergence and low fitness values in PV module parameter extraction. Order by Fraction Harris Hawks Optimization (FCHHHO) [19], enhances SDM, DDM, and TDM optimization’s performance, accuracy, and robustness. The modified Salp Swarm Optimization (MSSA) [20] enhances performance and prevents local optima in SDM, DDM, and PV module optimization. The Differential Evolution Algorithm by Elite and Obsolete Dynamic Learning (DOLADE) [21] rivals accuracy, reliability, and computational cost in SDM, DDM, and PV module optimization. Improved Teaching–Learning-Based Optimization (ITSA) provides improved stability and higher convergence accuracy for SDM, DDM, and PV module optimization [22]. RMSE optimization of SDM, DDM, TDM, and PV module models stands strong with Sine Cosine Differential Gradient-Based Optimizer (SDGBO) [23].

Recent advancements in metaheuristic algorithms have significantly improved the accuracy and efficiency of PV model parameter estimation. A hybrid Kepler optimization algorithm (HKOA) was proposed to enhance exploration–exploitation balance, outperforming conventional methods in identifying PV module parameters [24]. Similarly, the Adapted Human Evolutionary Optimizer (AHEO) algorithm demonstrated robust performance in optimizing PV system parameters, offering high precision for renewable energy applications [25]. Parameterless artificial optimization (APLO) techniques have also gained traction, leveraging randomized step lengths to achieve reliable results without manual tuning [26]. The Pelican Optimization Algorithm (POA) further advanced single-diode model accuracy by minimizing current prediction errors [27], while an improved Light Spectrum Optimizer (ILSO) achieved superior fitness values for triple-diode models [28]. Modified social group optimization (MSGO) and the Flood Algorithm (FLA) were introduced to address convergence speed and global search capabilities, with FLA notably surpassing nine competing metaheuristics [29,30]. Comprehensive surveys highlight the strengths of genetic algorithms and Particle Swarm Optimization (PSO) for PV parameter identification, though newer methods like the Fully Informed Search Algorithm (FISA) now offer faster convergence and stability [31,32]. These developments are systematically reviewed in [33], which identifies optimal metaheuristics for PV, battery, and fuel cell models, underscoring their transformative potential in sustainable energy systems. In [34], an Improved Whale Optimization Algorithm (IWOA) has been proposed, demonstrating enhanced accuracy in PV parameter estimation. The work in [35] applied biogeography-based optimization named CMM-DE/BBO with a covariance matrix migration strategy, improving convergence behavior. A repaired adaptive differential evolution called Rcr-JADE approach has been presented in [36], offering robust parameter extraction for solar cell models. A hybrid algorithm combining rat swarm optimization and pattern search (hARS-PS) has been proposed in [37], achieving high precision in PV model identification. In [38], an improved teaching–learning-based optimization with an elite strategy (STLBO) has been introduced, effectively identifying parameters for both fuel cell and solar cell models. Lastly, [39] presented a Quantum Multiverse Optimization (QMVO) algorithm, showcasing its applicability in solving complex optimization problems, including PV parameter estimation.

The reviews of these optimization algorithms outline the distinguishing features, benefits, and flaws of every optimization algorithm. The specific limitations and requirements of the PV parameter extraction task at issue need to be seriously considered when deciding on an algorithm. The algorithm presented here is a novel parameterless optimization option that reduces the complexity of optimization and improves the algorithm’s usability to suit a variety of optimization problems.

Despite increasing emphasis to optimize PV models, there remains an extensive research gap in overcoming complexity due to diverging PV models and varying operating conditions. Most of the available models concentrate on single-objective optimization, typically targeting the root mean square error. This work remarkably improves this area by proposing a novel multi-objective optimization framework. This advanced framework strives to bridge the gap between precise prediction and outlier robustness by considering the L2 norm and maximum error as objective functions. This offers a deeper treatment of PV model optimization. This move away from a conventional focus on single-objective optimization brings forth new avenues of precise, effective, and flexible solutions that are compatible with real PV systems. Furthermore, all algorithms face issues such as early convergence, local minima trapping, and high computation time. Developing algorithms that can negotiate complex solution space, overcome premature convergence, and are less sensitive to tuning parameters must be the primary concern of the developments. This strategy aims to promote and overcome existing challenges in PV model optimization. Although recent hybrid algorithms such as IWOA [5] and MSSA [6] enhance the estimation of PV parameters, most of them depend on problem-oriented tuning or sophisticated hybridization, which constrains scalability. In contrast, the proposed contribution is as follows: (1) a new parameterless metaheuristic (RSAB), which continually adapts to the PV models automatically, and (2) a multi-objective trade-off between the L2 norm and the maximum error—a trade-off not examined in previous papers. The proposed methodology is free from the accuracy vs. robustness trade-off, as shown against 16 algorithms in Section 4.

This paper introduces the following key innovations, which distinguish it from prior studies:

• A novel multi-objective optimization framework that simultaneously minimizes both global error (L2 norm) and maximum local deviations, overcoming the limitations of conventional single-objective approaches that typically prioritize only RMSE minimization.
• A novel parameterless metaheuristic algorithm (RSAB) specifically designed for PV systems, eliminating the need for manual parameter tuning while maintaining robust performance across different solar cell models and operating conditions.
• A dynamic exploration–exploitation mechanism that automatically balances global search and local refinement without user intervention, preventing premature convergence common in existing algorithms like PSO and GA.
• Comprehensive validation demonstrating superior accuracy and stability compared to both classical methods and state-of-the-art hybrid algorithms, particularly for complex double-diode and PV module models.
• A practical, ready-to-implement solution that addresses real-world challenges in PV system design by providing reliable parameter estimates with minimal computational overhead.

The remainder of this paper is organized as follows: multi-objective optimization for PV parameter extraction is examined in the paper’s later sections (Section 2). The RSAB algorithm is represented in Section 3, which is a parameterless optimization technique created especially for PV parameter extraction. A thorough summary of the simulation results, along with a case study comparison with alternative optimization algorithms, is provided in Section 4. The paper’s main contributions are briefly outlined in the conclusion of Section 5, which also offers suggestions for possible future research directions.

2. Multi-Objective Optimization for PV Parameter Extraction

Optimizing solar energy system performance and reliability needs to be done with precise estimation of parameters governing PV cell and module behavior. This precision can be ensured by achieving the optimization objectives presented in this article. The prime objective is to find unknown PV cell and module parameters with precision. An optimization algorithm is employed to bring discrepancies between estimated and experiment I-V values of PV systems to minimal values. This requires minimizing both the maximum error and the L2 norm as objective functions. Minimizing the L2 norm ensures good fit of the proposed PV models to measurements and captures total differences as well as giving an overall assessment of prediction accuracy. Concurrently, enhancing robustness of the parameter estimation process necessitates minimizing maximum error. To reduce abnormally large errors and provide reliable and robust estimates, this step tries to minimize outlier influence.

2.1. Optimization Problem Formulation

The optimization problem is formulated as follows:

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} {OF}_1:\mathrm{L}2 \mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}$$

$${OF}_1=\sqrt{{\sum }_{s=1}^S\mathrm{ }(I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}-I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{x}\mathrm{p}}{)}^2}$$

(1)

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} {OF}_2:\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} \mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m} \mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}$$

$${OF}_2=\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} \underset{s}{\mathrm{m}\mathrm{a}\mathrm{x}}|I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}-I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{x}\mathrm{p}}|$$

(2)

$$\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t} \mathrm{t}\mathrm{o}: x_{i,\mathrm{m}\mathrm{i}\mathrm{n}}\le x_i\le x_{i,\mathrm{m}\mathrm{a}\mathrm{x}}$$

(3)

In this context, the L2 norm signifies the square root of the sum of the squares of the elements, where S represents the number of paired experimental sample data. The variables $I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}$ and $I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{x}\mathrm{p}}$ refer to the estimated and measured values of PV output current for the s-th sample, with the corresponding parameter values derived from the optimization variables. The decision variables (x) represent the parameters subject to optimization. For the SDM depicted in Figure 1a and the PVMM shown in Figure 1c, these decision variables are denoted as follows:

$$x=[I_p,I_d,R_{sh},R_s,u]$$

(4)

Here,

• $I_p$ is the photogenerated current;
• $I_d$ is a diode current-related parameter;
• $R_{sh}$ is the shunt resistance;
• $R_s$ is the series resistance;
• $u$ is the diode ideality factor.

For the DDM (Figure 1b), seven decision variables are considered using an optimization technique:

$$x=[I_p,I_{d1},I_{d2},R_{sh},R_s,u_1,u_2]$$

(5)

Here,

• $I_p$ is the photogenerated current;
• $I_{\mathrm{d}1}$ and $I_{\mathrm{d}2}$ are current-related parameters for the two diodes;
• $R_{sh}$ is the shunt resistance;
• $R_s$ is the series resistance;
• $u_1$ and $u_2$ are the ideality factors for the two diodes.

In order to reduce the discrepancies between the estimated and experimental I-V data, the optimization algorithm aims to modify these decision variables. Equations (6), (7), and (8), respectively, are simplified formulas based on SDM, DDM, and PVMM that express the computed PV output current ($I_{\mathrm{o},\mathrm{s}}$) for each sample s.

$$\mathrm{S}\mathrm{D}\mathrm{M}: I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}=I_p-{\displaystyle \frac{V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}+R_s{I}_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}}{R_{sh}}}-I_d\left[\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}+R_s{I}_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}}{uv}}\right)-1\right]$$

(6)

$$\mathrm{D}\mathrm{D}\mathrm{M}: I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}=I_p-{\displaystyle \frac{V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}+R_s{I}_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}}{R_{sh}}}-I_{d2}\left[\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}+R_s{I}_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}}{u_{2}v}}\right)-1\right]-I_{d1}\left[\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}+R_s{I}_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}}{u_{1}v}}\right)-1\right]$$

(7)

$$\mathrm{P}\mathrm{V}\mathrm{M}\mathrm{M}: I_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}=M{I}_p-{\displaystyle \frac{V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}+R_s{I}_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}\frac{N}{M}}{R_{sh}\frac{N}{M}}}-M{I}_d\left[\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}+R_s{I}_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}\frac{N}{M}}{uv}}\right)-1\right]$$

(8)

where $V_{\mathrm{o},\mathrm{s}}^{\mathrm{e}\mathrm{s}\mathrm{t}}$ is the estimated cell/module output voltage for the $s$-th sample, $x$ represents the unknown parameters, and $v$ is the junction thermal voltage. $M$ and $N$ represent the number of solar cells in parallel and series, respectively.

2.2. Combined Multi-Objective Function

The combined multi-objective function, CMOF, is a weighted sum of the following objectives:

$$\mathrm{C}\mathrm{M}\mathrm{O}\mathrm{F}=w_1\times {OF}_1+w_2\times {OF}_2$$

(9)

Weighting factors $w_1$ and $w_2$ are important in this case because they provide a fair trade-off between minimizing the maximum error and minimizing the overall error. The L2 norm (OF₁) ensures global accuracy by minimizing cumulative deviations, while maximum error (OF₂) targets outlier resilience. Weighting factors balance these objectives, e.g., w₁ = w₂ = 0.5 optimizes both metrics. This dual approach avoids overfitting average errors, common in RMSE-only methods. In order to guarantee accurate predictions throughout the entire dataset and robustness against abnormally large errors, this formulation is intended to find the ideal parameter values that achieve a harmonious balance. The deliberate attempt to strike a balance between the maximum error and the L2 norm is crucial. It guarantees that the optimization procedure yields parameter values that minimize the likelihood of abnormally large errors while also accurately representing the PV system throughout the whole dataset. The suggested models’ predictive power is greatly increased by this improvement, making them useful instruments for accurate system analysis and design.

In conclusion, the optimization objectives described in this work go beyond simple parameter estimation and aid in the creation of precise, dependable, and resilient PV models. These models highlight the wider impact of this research and are essential to the advancement of solar energy research and applications.

3. RSAB Algorithm

One parameterless metaheuristic optimization technique that is specifically tailored for the effective exploration of solution spaces is the RSAB algorithm. This section explores the RSAB algorithm’s intricate formulation, emphasizing its special characteristics, such as the updating operators. The parameterless nature of RSAB, which eliminates the need for manual parameter tuning, is one of its distinguishing features. This intrinsic feature makes it easier to apply RSAB to a variety of optimization tasks and provides a user-friendly interface. The algorithm’s ability to function well without requiring parameter changes not only increases its adaptability but also makes it a desirable option for optimization problems in a variety of fields.

3.1. Initialization

By defining the initial population and determining the global-best and last-best solutions, the initialization phase lays the groundwork for the RSAB algorithm. The initialization of each element $X_{i,j}\left(t\right)$ at iteration t can be expressed mathematically as follows:

$$X_{i,j}\left(t\right)=x_{\mathrm{m}\mathrm{i}\mathrm{n},j}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\cdot (x_{\mathrm{m}\mathrm{a}\mathrm{x},j}-x_{\mathrm{m}\mathrm{i}\mathrm{n},j}); \forall t=1,\forall i=\mathrm{1,2},\dots ,npop,\forall j=\mathrm{1,2},\dots ,D$$

(10)

This equation denotes the random selection of initial positions within the problem’s decision space.

3.2. Updating Operators

3.2.1. Search Around the Global Best

Suppose ${\rm Y}$ denotes the decision vector. The random search operator around the global best is given by:

$$Y_{i,j}\left(t\right)=X_{B,j}\left(t\right)+{\alpha }_1\cdot \left(X_{LB,j}\right(t)-X_{i,j}(t\left)\right); \forall i=\mathrm{1,2},\dots ,npop, j\in {\mathsf{{\rm Y}}}_i$$

(11)

Here, $X_{B,j}\left(t\right)$ is the global-best solution, $X_{LB,j}\left(t\right)$ is the last-best solution, and ${\alpha }_1=rand/randn$ is the scaling factor.

3.2.2. Search Around the Last-Best

For remaining elements, the search is performed around the last-best solution:

$$Y_{i,k}\left(t\right)=X_{L,j}\left(t\right)+{\alpha }_2\cdot \left(X_{LB,j}\right(t)-X_{i,k}(t\left)\right); \forall i=\mathrm{1,2},\dots ,npop, k\in \mathsf{{\rm Y}}\backslash {\mathsf{{\rm Y}}}_i$$

(12)

Here, ${\alpha }_2=rand/randn$.

3.2.3. Bounds Checking

To ensure that each element stays within bounds, any violation is corrected:

$$Y_{i,j}(t)=\left\{\begin{array}{ll}{x}_{\mathrm{m}\mathrm{i}\mathrm{n},j}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\cdot (x_{\mathrm{m}\mathrm{a}\mathrm{x},j}-x_{\mathrm{m}\mathrm{i}\mathrm{n},j}),& \mathrm{i}\mathrm{f}{ Y}_{i,j}\left(t\right)<x_{\mathrm{m}\mathrm{i}\mathrm{n},j} \mathrm{o}\mathrm{r} Y_{i,j}\left(t\right)>x_{\mathrm{m}\mathrm{a}\mathrm{x},j}\\ Y_{i,j}\left(t\right),& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(13)

Bounds are enforced via reinitialization; if $Y_{i,j}\left(t\right)$ exceeds [$x_{\mathrm{m}\mathrm{i}\mathrm{n},j}$, $x_{\mathrm{m}\mathrm{a}\mathrm{x},j}$], it is reset to a random value within bounds. This ‘clipping’ strategy maintains feasibility without distorting the search distribution.

3.2.4. Solution Update

The final updating operator is as follows:

$$X_i(t+1)=\left\{\begin{array}{ll}{Y}_i\left(t\right),& \mathrm{i}\mathrm{f} f\left(Y_i\right(t\left)\right)<f\left(X_i\right(t\left)\right)\\ X_i\left(t\right),& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.$$

(14)

Here, $f(\cdot )$ represents the fitness function.

Figure 2 provides a graphical representation of the exploration-–exploitation strategy using vectors to provide a visual representation of the search procedure. The RSAB algorithm’s skillfully designed initialization and updating operators are the foundation of its effectiveness in navigating complex solution spaces. The underlying principles of the algorithm’s exploration–exploitation approach are captured in the given equations. RSAB searches across both the global-best (X_B) and the last-best (X_LB) solutions (Equations (13) and (14)). The population is also randomized initially (Equation (12)), providing varied starting points. The two-pronged approach averts sole dependence on one solution, which ensures robustness. The step size in RSAB is adaptively controlled by scaling factors α₁ and α₂. The latter ensures dynamic adaptation with wider steps during the early iterations and finer movements towards the end. In contrast to stepwise schemes, there is no need for manual tuning of the parameters.

The mathematical equations of RSAB are new contributions of this research. Although motivated by the principles of metaheuristics (e.g., population-based search), the parameterless structure and double search approach (global-best + last-best) are specific to RSAB. The pre-existing algorithms such as PSO and DE are based on tuned parameters, while the same is avoided by RSAB through the usage of scaling factors. Algorithm 1 presents the pseudocode for the suggested RSAB, which is supplemented by a thorough flowchart shown in Figure 3 to give a thorough understanding.

Algorithm 1: Random Search Around Bests (RSAB)
	Initialization:
1:	Initialize population randomly
2:	Evaluate fitness of each solution
3:	Set global-best solution as the current best and set last-best solution as the current best
	Main Loop:
4:	$t\leftarrow 1$
5:	While $t\le Itmax$
6:		For each solution $i$ in the population do
	Updating Operators:
7:			For each arbitrary element $j$ in the decision vector ${\rm Y}$ do
8:				Random search operator around global best (Equation (2))
9:			End for
10:			For each remaining element $k$ in the decision vector ${\rm Y}\backslash {{\rm Y}}_i$ do
11:				Search around the last-best solution (Equation (3))
12:			End for
	Bounds Checking:
13:			Check and correct bounds if necessary (Equation (4))
14:			Evaluate fitness of the solution
	Solution Update:
15:			Update solutions based on fitness (Equation (5))
16:			$t\leftarrow t+1$
17:		End while
18:		Return the global-best solution

4. Simulation Results

This section assesses the performance of the suggested RSAB algorithm in parameter estimation for three different PV models: the PVMM, the SDM, and the DDM. The main objective is to use current-voltage data from experimental setups to identify the unknown parameters of these models. To guarantee robustness and dependability in evaluating optimization performance, a constant maximum of 50,000 function evaluations was used throughout the experiments, and each algorithm was run 30 times independently. We used current-voltage data from silicon solar cells with a diameter of 57 mm (R.T.C. Suresne, France) for the standard experiments on SDM and DDM [40]. The following are the features of the silicon solar cell:

• Top of Form
• $V_{oc}$ (Open-Circuit Voltage): 0.5728 V
• $I_{sc}$ (Short-Circuit Current): 0.7603 A
• $V_m$ (Voltage at Maximum Power): 0.4507 V
• $I_m$ (Current at Maximum Power): 0.6894 A

Additionally, a PV module (Photo Watt-PWP 201, Bourgoin-Jallieu, France) with 36 polycrystalline PV cells was used under 1000 W/m² irradiance [40]. The characteristics of the PV module are as follows:

• $V_{oc}$: 16.778 V
• $I_{sc}$: 1.030 A
• $V_m$: 12.649 V
• $I_m$: 0.912 A

We carefully take into account the parameter ranges unique to the PV models when constructing the optimization problem, as given in

Table 1. Parameter bound for SDM, DDM, and PVMM.

Parameter	SDM Range	DDM Range	PVMM Range
Photocurrent ($I_{ph}$)	0–1 A	0–1 A	0–2 A
Diode Current ($I_{sd}$)	0–1 μA	0–1 μA	0–50 μA
Shunt Resistance ($R_{sh}$)	0–100 Ω	0–100 Ω	0–2000 Ω
Series Resistance ($R_s$)	0–1 Ω	0–1 Ω	0–50 Ω
Ideality Factor (u)	1–2	1–2 (u1, u2)	1–50

. The optimization problem’s parameter space is established by these specified bounds, which direct the search for each PV model’s ideal parameter values.

4.1. Population Size Analysis

The main goal in this thorough analysis is to investigate how population size (npop) affects the RSAB algorithm’s performance when estimating parameters for PV cell/module models. The comprehensive findings in

Table 2. Performance metrics of RSAB with different population sizes for solving the multiobjective optimization problem ($w_1=w_2=0.5$).

Model	Metric	$\mathit{n}\mathit{p}\mathit{o}\mathit{p}$
		10	20	40	50	80	100
PVMM	Min	0.0081893	0.0081814	0.0081812	0.0081812	0.0081812	0.0081816
	Mean	0.0100591	0.0082061	0.0081866	0.0081870	0.0081869	0.0081901
	Max	0.0295264	0.0082907	0.0082100	0.0082191	0.0082159	0.0082196
	SD	0.0052702	0.0000304	0.0000066	0.0000097	0.0000073	0.0000102
	Mean Rank in Friedman	5.8	3.96667	2.76667	3	2.63333	2.83333
	Time (s)	66.2892017	66.409795	64.2251201	64.3869331	65.0795774	64.5667326
DDM	Min	0.0036090	0.0035878	0.0035686	0.0035957	0.0035680	0.0035928
	Mean	0.0123856	0.0068335	0.0076583	0.0043080	0.0064458	0.0073576
	Max	0.0322132	0.0310228	0.0310828	0.0060330	0.0285776	0.0241648
	SD	0.0116808	0.0079195	0.0084400	0.0006380	0.0065660	0.0059838
	Mean Rank in Friedman	4.56667	3.26667	3.5	2.9	2.9	3.86667
	Time (s)	70.36015	67.57589	66.7606	66.68019	66.46328	67.97729
SDM	Min	0.0038196	0.0036174	0.0035866	0.0035754	0.0035763	0.0036146
	Mean	0.0177240	0.0066485	0.0055802	0.0046390	0.0039343	0.0047935
	Max	0.0352545	0.0318697	0.0323016	0.0314178	0.0096278	0.0315137
	SD	0.0129999	0.0082927	0.0066823	0.0050603	0.0010982	0.0050545
	Mean Rank in Friedman	5.7	4.13333	2.83333	2.4	2.5	3.43333
	Time (s)	67.25048	67.54377	66.08529	64.79251	64.32273	64.27668

cover the main statistical measures of the Combined Multi-Objective Function (CMOF) for different population sizes, including minimum (Min), mean, maximum (Max), and standard deviation (SD). We used the Friedman test, which looks at mean ranks for each population size across various models, to thoroughly evaluate the significance of population size differences.

In-depth analysis has revealed some clear findings and suggestions:

• Consistent patterns show up in all models, including PVMM, DDM, and SDM. Standard deviation falls as population sizes increase, suggesting more dependable convergence, while minimum and mean values tend to stabilize and improve. The Friedman test consistently produces better results in terms of both performance metrics and statistical significance for larger population sizes, namely npop = 80 or npop = 100.
• A population size of npop = 50 seems to be adequate for the PVMM, yielding steady and reliable results without a noticeable rise in processing requirements. On the other hand, larger population sizes—specifically, npop = 80 or npop = 100—are advised for the more complex DDM and SDM, as they demonstrate better performance and enhanced convergence. The suggestions emphasize the necessity of a sophisticated strategy.
• The Friedman test’s statistical significance, solution quality, and computational efficiency should all be taken into consideration when choosing a population size. Furthermore, the stability of the RSAB algorithm across various population sizes is reinforced by the consistency of CPU time across models.
• The population size (npop) was determined empirically by evaluating convergence behavior across different sizes (10, 20, 40, 50, 80, 100). Larger population sizes (e.g., npop = 80 or 100) demonstrated improved stability and lower standard deviation (SD) in CMOF values, particularly for complex models like DDM and SDM. This suggests that a higher population size enhances exploration, reducing premature convergence. The Friedman test further validated that npop = 50 was sufficient for PVMM, while npop = 80–100 was optimal for SDM and DDM.

4.2. Impact of Weighting Factors on Multi-Objective Optimization

Finding a balance between minimizing the L2 norm (${OF}_1$) and minimizing the maximum error (${OF}_2$) is largely dependent on the weighting factors ($w_1$ and $w_2$) in the combined multi-objective function. This subsection explores how different weighting factors affect how well the optimization algorithm estimates parameters for various PV models.

The optimization results for the SDM under various combinations of weighting factors are shown in

Table 3. The results of the optimization process for the PV models with different combinations of weighting factors.

Model	SDM		DDM		PVMM
(${\mathit{w}}_1$$, {\mathit{w}}_2$)	${\mathit{O}\mathit{F}}_1$	${\mathit{O}\mathit{F}}_2$	${\mathit{O}\mathit{F}}_1$	${\mathit{O}\mathit{F}}_2$	${\mathit{O}\mathit{F}}_1$	${\mathit{O}\mathit{F}}_2$
(1, 0)	0.00503	0.00251	0.00501	0.00255	0.01213	0.00483
(0.9, 0.1)	0.00504	0.00234	0.00502	0.00237	0.01214	0.00456
(0.8, 0.2)	0.00508	0.00213	0.00507	0.00214	0.01217	0.00440
(0.7, 0.3)	0.00510	0.00206	0.00509	0.00207	0.01221	0.00426
(0.6, 0.4)	0.00515	0.00199	0.00511	0.00205	0.01232	0.00407
(0.5, 0.5)	0.00524	0.00192	0.00515	0.00199	0.01241	0.00395
(0.4, 0.6)	0.00547	0.00191	0.00522	0.00193	0.01251	0.00387
(0.3, 0.7)	0.00536	0.00191	0.00542	0.00199	0.01274	0.00375
(0.2, 0.8)	0.00812	0.00266	0.00590	0.00212	0.01289	0.00369
(0.1, 0.9)	0.00545	0.00190	0.00671	0.00205	0.01304	0.00366
(0, 1)	0.02087	0.00520	0.00701	0.00223	0.01543	0.00464

. Both goals are impacted by modifications to the weighting factors. The algorithm gives priority to a thorough fit across the whole dataset when $w_1=1$ (just minimizing the L2 norm). On the other hand, the emphasis switches to lessening the influence of outliers or abnormally large errors when $w_2=1$ (just minimizing the maximum error). When using a balanced combination of weighting factors (e.g., $w_1=0.5$ and $w_2=0.5$), the trade-off becomes clear and both robustness against outliers and accurate predictions are achieved. Competitive values for both objectives are obtained for the SDM when $w_1=0.5$ and $w_2=0.5$ are balanced. Similar findings apply to the DDM, as shown in Table 3. The trade-off between accurately fitting the entire dataset and reducing the impact of large errors is influenced by the weighting factors. Once more, both goals are successfully attained with a balanced combination ($w_1=0.5$ and $w_2=0.5$). Table 3’s PVMM results demonstrate how weighting factors affect the optimization procedure. Robustness against outliers and accurate predictions are successfully balanced by a well-balanced combination of weighting factors ($w_1=0.5$ and $w_2=0.5$). A balanced combination of weighting factors, like $w_1=0.5$ and $w_2=0.5$, frequently produces a well-rounded optimization result, according to analysis across various PV models.

This method maintains robustness against significant errors while guaranteeing accurate parameter estimation throughout the entire dataset. Finding the ideal combination, however, may differ based on particular PV system characteristics, necessitating additional testing for fine-tuning in particular applications. The choice of weighting factors is an essential part of the multi-objective optimization process, highlighting the significance of striking a balance between minimizing the maximum error and minimizing the L2 norm for reliable and accurate parameter estimates in different PV models.

4.3. Algorithmic Parameter Optimization for PV Models

In this case study, we examine the performance of various optimization algorithms applied to the task of identifying optimal parameters for three PV models: SDM, DDM, and PVMM. The algorithms include PSO [6], DE [4], GA [9], Jaya [10], SSA [12], TLBO [14], WSO [15], Grey Wolf Optimizer (GWO) [41], and RSAB.

Table 4. Optimal results for parameter identification using different applied algorithms.

PV Model	Algorithm	Min	Mean	Max	SD	Mean Rank (Friedman)	Time (s)	Max Current Abs. Error	Max Power Abs. Error
SDM	SSA	0.6567	0.7073	0.8095	0.0269	7.23	53.6	0.3215	0.1360
	GWO	0.0400	0.7593	0.8096	0.1913	8.20	52.3	0.0183	0.0102
	WSO	0.0036	0.3227	1.1294	0.4518	4.90	53.2	0.0020	0.0012
	JAYA	0.0144	0.0229	0.0396	0.0061	3.90	52.2	0.0090	0.0053
	TLBO	0.0037	0.0337	0.0750	0.0249	4.57	65.3	0.0020	0.0012
	GA	0.0174	0.4908	1.1056	0.4300	6.80	88.8	0.0090	0.0048
	PSO	0.0038	0.0156	0.0314	0.0087	3.17	80.5	0.0020	0.0012
	DE	0.0221	0.0276	0.0319	0.0028	5.00	79.1	0.0109	0.0059
	RSAB	0.0036	0.0037	0.0040	0.0001	1.23	67.1	0.0019	0.0011
DDM	SSA	0.0973	0.1688	0.2065	0.0216	8.97	55.30	0.0554	0.0179
	GWO	0.0042	0.0418	0.2433	0.0563	7.40	53.77	0.0028	0.0017
	WSO	0.0036	0.0039	0.0088	0.0010	2.00	54.69	0.0020	0.0012
	JAYA	0.0068	0.0152	0.0540	0.0086	7.07	53.31	0.0035	0.0018
	TLBO	0.0036	0.0047	0.0068	0.0007	3.47	67.81	0.0020	0.0012
	GA	0.0063	0.0097	0.0150	0.0020	6.37	130.24	0.0035	0.0019
	PSO	0.0036	0.0054	0.0069	0.0009	4.37	82.35	0.0020	0.0012
	DE	0.0040	0.0051	0.0063	0.0006	4.00	80.75	0.0025	0.0014
	RSAB	0.0036	0.0037	0.0044	0.0002	1.37	69.55	0.0020	0.0012
PVMM	SSA	0.0547	0.2004	0.9265	0.2482	6.77	55.86	0.0327	0.2679
	GWO	0.0121	0.1724	0.9267	0.2728	5.40	53.01	0.0064	0.0682
	WSO	0.0082	0.3211	1.5589	0.4930	4.47	54.69	0.0039	0.0652
	JAYA	0.0270	0.2234	0.5610	0.1358	7.13	52.97	0.0136	0.2284
	TLBO	0.0126	0.0221	0.0334	0.0054	3.27	65.70	0.0065	0.0797
	GA	0.0260	0.5363	1.0817	0.4366	7.73	88.69	0.0122	0.2034
	PSO	0.0114	0.0619	0.1722	0.0627	4.73	81.03	0.0065	0.0563
	DE	0.0217	0.0289	0.0323	0.0029	4.27	80.23	0.0106	0.1329
	RSAB	0.0082	0.0082	0.0082	0.0000	1.23	67.27	0.0039	0.0652

provides a summary of the Min, Mean, Max, SD, mean rank in the Friedman test, computational time (in seconds), and the maximum absolute errors in current and power.

A thorough analysis of the effectiveness of various optimization algorithms in the parameter identification of various PV models is provided by the results shown in Table 4.

A thorough analysis of the findings is summarized as follows:

• With a mean CMOF value of 0.0037, RSAB is the most notable algorithm for the SDM model, outperforming SSA (0.7073), GWO (0.7593), and PSO (0.0156). The computational time of RSAB (67.1 s) is significantly less than that of TLBO (65.3 s) and GA (88.8 s). Furthermore, RSAB shows low maximum absolute errors in power (0.0011) and current (0.0019), indicating accurate parameter identification. With a mean rank of 1.23, the Friedman test consistently rates RSAB favorably, demonstrating its statistical significance in outperforming other algorithms.

  Table 5. Optimal parameters of the SDM extracted by various optimization algorithms.

  Algorithm	${\mathit{I}}_{\mathit{p}\mathit{h}}$ (A)	${\mathit{I}}_{\mathit{s}\mathit{d}}$ (μA)	${\mathit{R}}_{\mathit{s}\mathit{h}}$ (Ω)	${\mathit{R}}_{\mathit{s}}$ (Ω)	$\mathit{m}$	CMOF
  SSA	0.87357943	7.84 × 10−7	0.96768859	0.00080722	1.7205111	0.65674362
  GWO	0.77339552	1.37 × 10−6	27.0801642	0.01193027	1.99189252	0.04004268
  WSO	0.7607613	3.39 × 10−7	54.7808663	0.03619266	1.48626645	0.0035679
  JAYA	0.76216184	1.69 × 10−6	97.537487	0.02793098	1.66912122	0.01438228
  TLBO	0.76111254	3.39 × 10−7	51.3681934	0.03619902	1.48604988	0.00365331
  GA	0.76359445	2.51 × 10−6	70.2348639	0.02533783	1.72238211	0.01737739
  PSO	0.76069605	4.07 × 10−7	62.0527057	0.03553692	1.50471695	0.00380059
  DE	0.76591306	4.49 × 10−6	93.5186243	0.02253627	1.80529033	0.02213357
  RSAB	0.76073295	3.55 × 10−7	56.2315572	0.03602224	1.49070616	0.00357827

  lists the performance metrics and settings of the different optimization algorithms used in the parameter extraction process for the SDM. Insights into the algorithms’ effectiveness in optimizing the SDM for precise modeling of photovoltaic cells and modules can be gained from this table, which provides a thorough summary of the ideal parameters attained by the algorithms.
• With a mean CMOF value of 0.0037, RSAB performs competitively in the DDM case, as indicated in Table 4, and is on par with GA (0.0097) and GWO (0.0418). In comparison to GA (130.24 s), RSAB’s computation time (69.55 s) is moderate. The stability and effectiveness of RSAB are highlighted by its low maximum absolute errors in power (0.0012) and current (0.0020). With a mean rank of 1.37, the Friedman test consistently rates RSAB, confirming its statistical significance. The applied algorithms were thoroughly evaluated in the field of optimizing the DDM for accurate photovoltaic parameter extraction, and

  Table 6. Optimal parameters of the DDM extracted by various optimization algorithms.

  Algorithm	${\mathit{I}}_{\mathit{p}\mathit{h}}$ (A)	${\mathit{I}}_{\mathit{s}\mathit{d},1}$ (μA)	${\mathit{I}}_{\mathit{s}\mathit{d},2}$ (μA)	${\mathit{R}}_{\mathit{s}}$ (Ω)	${\mathit{R}}_{\mathit{s}\mathit{h}}$ (Ω)	${\mathit{m}}_1$	${\mathit{m}}_2$	CMOF
  SSA	0.785202	0	0.000001	0.0195	5.577	1.959	1.619	0.097258
  GWO	0.760545	2.8 × 10−7	3 × 10−8	0.036841	53.029	1.477	1.457	0.004204
  WSO	0.760763	3.4 × 10−7	0	0.036203	54.696	1.486	1.000	0.003568
  JAYA	0.759223	2.9 × 10−7	1 × 10−8	0.036742	92.889	1.470	2.000	0.006842
  TLBO	0.7606	1.7 × 10−7	3.3 × 10−7	0.036146	58.205	1.997	1.484	0.003608
  GA	0.761688	2.6 × 10−7	3.9 × 10−7	0.033535	63.374	1.605	1.531	0.006254
  PSO	0.760736	1.2 × 10−7	2.9 × 10−7	0.036271	55.554	1.728	1.475	0.003573
  DE	0.761196	1.5 × 10−7	2.8 × 10−7	0.036167	57.282	1.446	1.577	0.003984
  RSAB	0.760756	3.2 × 10−7	2 × 10−8	0.036188	54.836	1.484	1.524	0.003568

  provides a concise summary of the findings. This table lists the ideal parameters that the algorithms were able to attain, offering a detailed comparison of how well each of them improved the DDM’s precision and dependability for modeling solar cells and modules.
• With a mean value of 0.0082 in the PVMM, as shown in Table 4, RSAB performs competitively with GA (0.5363) and TLBO (0.0221). When compared to GA (88.69 s), RSAB’s computational time (67.27 s) is more efficient. RSAB’s ability to accurately identify parameters is demonstrated by its low maximum absolute errors in both current (0.0039) and power (0.0652). RSAB’s statistical significance is further supported by the Friedman test results, which show a mean rank of 1.23.

Examining the PVMM’s complexities and parameter optimization, a thorough summary of the ideal values for the five unknown parameters attained by using different algorithms is provided in

Table 7. Optimal parameters of the PVMM extracted by various optimization algorithms.

Algorithm	${\mathit{I}}_{\mathit{p}\mathit{h}}$ (A)	${\mathit{I}}_{\mathit{s}\mathit{d}}$ (μA)	${\mathit{R}}_{\mathit{s}\mathit{h}}$ (Ω)	${\mathit{R}}_{\mathit{s}}$ (Ω)	$\mathit{m}$	CMOF
SSA	1.068685286	1.84 × 10−5	6.925071132	0.026709513	1.560343662	0.054738812
GWO	1.025444687	8.39 × 10−6	321.0845974	0.030454325	1.451748352	0.012063065
WSO	1.030153421	3.52 × 10−6	26.88533784	0.033236188	1.352626891	0.008181191
JAYA	1.027400616	2.13 × 10−5	670.2794259	0.026334392	1.578442004	0.026978327
TLBO	1.025000680	8.69 × 10−6	2000.000000	0.030698019	1.456000388	0.012615985
GA	1.032573193	2.98 × 10−5	1662.963082	0.024855431	1.627514518	0.026019809
PSO	1.025181092	7.50 × 10−6	461.2267452	0.031015498	1.437960389	0.01138384
DE	1.030124935	2.11 × 10−5	1968.886457	0.026651259	1.575702557	0.021688211
RSAB	1.030142268	3.53 × 10−6	26.92251642	0.033234189	1.352721034	0.0081812

. This table is a useful resource for understanding how well these algorithms work to improve PVMM’s accuracy for modeling solar cells and modules.

Comparison Across Models

RSAB consistently exhibits competitive mean values, shorter computation times, and accurate parameter identification when compared to other PV models. The Friedman test results provide additional support for the statistical significance of RSAB’s superiority over the SDM, DDM, and PVMM models. RSAB is a viable option for determining the ideal parameters in SDM, DDM, and PVMM models when taking into account the overall performance metrics, which include mean values, CPU time, Friedman test results, and maximum absolute errors. Other algorithms might perform better in particular situations, but RSAB is a strong contender for PV model parameter identification due to its reliable performance across a range of models and computational time efficiency.

The cross-model comparison reveals several critical insights into RSAB’s performance:

• For the SDM, RSAB achieves superior accuracy with a mean CMOF of 0.0037, outperforming all compared algorithms including PSO (0.0156) and DE (0.0276). This represents a 76% improvement in solution quality while maintaining competitive computation time (67.1 s vs. PSO’s 80.5 s).
• In DDM optimization, RSAB matches the accuracy of WSO (both at 0.0036 CMOF) but demonstrates better consistency, as evidenced by its lower standard deviation (0.0002 vs WSO’s 0.0010). This highlights RSAB’s robustness in handling more complex parameter spaces.
• For PVMM, RSAB shows exceptional stability with zero standard deviation across 30 runs, while delivering the lowest maximum absolute current error (0.0039 A) among all algorithms. This combination of precision and reliability makes RSAB particularly suitable for real-world PV system applications.
• These results demonstrate that RSAB maintains consistently high performance across different PV model complexities, combining the accuracy of specialized single-model optimizers with the versatility needed for practical engineering applications.

4.4. Convergence Behavior of Optimization Algorithms for PV Models

The convergence behavior of different optimization algorithms applied to SDM, DDM, and PVMM for PV systems is thoroughly examined in this section. Figure 4, Figure 5 and Figure 6 provide a visual representation of the convergence data for each algorithm.

The 50,000 function evaluations (iterations) number was deliberately chosen to facilitate a comparative analysis of the algorithms in a reasonable and fair manner and also to ensure strong convergence for all the photovoltaic models (SDM, DDM, PVMM). Our convergence analysis indicated that stable solutions are achieved by the RSAB algorithm at 5000 iterations for SDM/DDM and 15,000 iterations for the PVMM model from the CMOF plateau (Figure 4, Figure 5 and Figure 6). However, we used a slightly higher uniform iteration to ensure late-converging algorithms are included in our comparative evaluation and to compensate for the different complexity of the various models (five to seven parameters). The right maximum iteration number is essentially a problem of problem geometry and search space complexity and thus requires a balance between solution quality and computational expense. Based on our observations from the experiments, we suggest an adaptive termination condition under which the iterations stop when CMOF improvement is less than 10^–6 for 5000 iterations—this will essentially identify the convergence point and avoid unnecessary computations. The proposed mechanism is specifically well-suited for the problems of PV parameter estimation since it automatically learns the different character of each model without the need for iteration tuning. Our experiments also verified that the chosen threshold consistently marks true convergence without impairing the algorithm’s capability to escape from the presence of the early occurrence of local optima during the early iterations. The 50,000-iteration limit was eventually used conservatively so that all the compared algorithms had an adequate amount of time to exhibit their best in our benchmarking exercise.

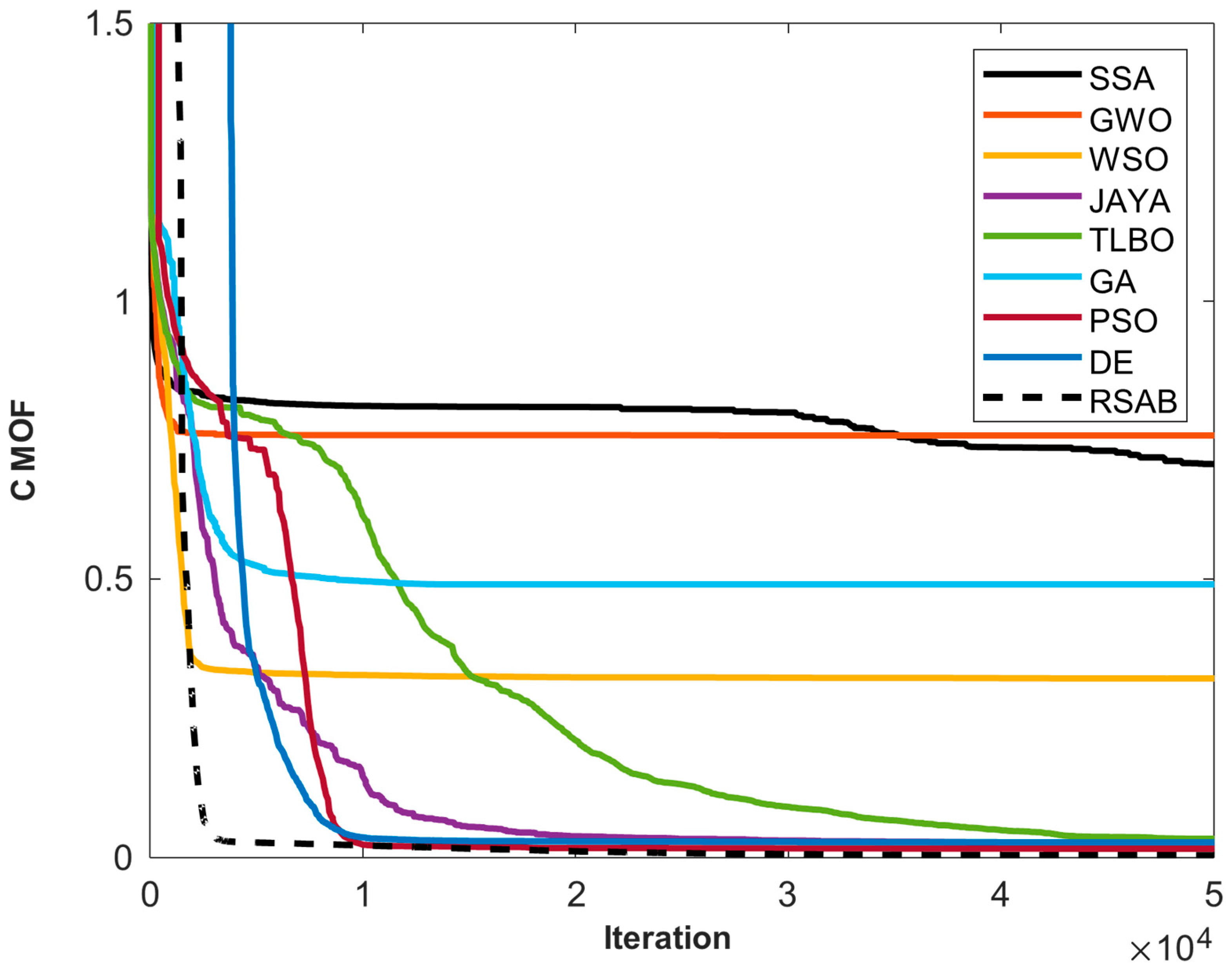
4.4.1. Convergence Behavior Analysis for SDM

Convergence curves showing the optimization performance of applied algorithms in determining SDM parameters are shown in Figure 4. The graph focuses on the CMOF as the main metric for assessing optimization success, highlighting each algorithm’s best runs over its iterations. Important findings include the following:

• Early Convergence: algorithms such as SSA, GWO, WSO, JAYA, and RSAB exhibit rapid convergence, achieving lower objective function values in the first iterations. In particular, RSAB exhibits effective early convergence, suggesting that it is a useful tool for exploring the solution space.
• Intermediate Convergence: with higher objective function values in the initial iterations, TLBO, GA, and PSO show slower convergence in comparison to the previously mentioned algorithms. During this stage, RSAB maintains competitive convergence, possibly outperforming some conventional optimization techniques.
• Divergence and Stagnation: early iterations of GA show a sharp rise in the objective function value, which may indicate problems with convergence or inadequate exploration. RSAB may lessen the early convergence seen in some algorithms while preserving competitive convergence.
• Stability and Smoothness: RSAB is notable for its consistent convergence over iterations, eschewing the abrupt spikes or fluctuations seen in other algorithms.

Figure 4. Convergence curves of applied algorithms for SDM parameter identification, highlighting best runs and CMOF progress.

Figure 4. Convergence curves of applied algorithms for SDM parameter identification, highlighting best runs and CMOF progress.

4.4.2. Convergence Behavior Analysis for DDM

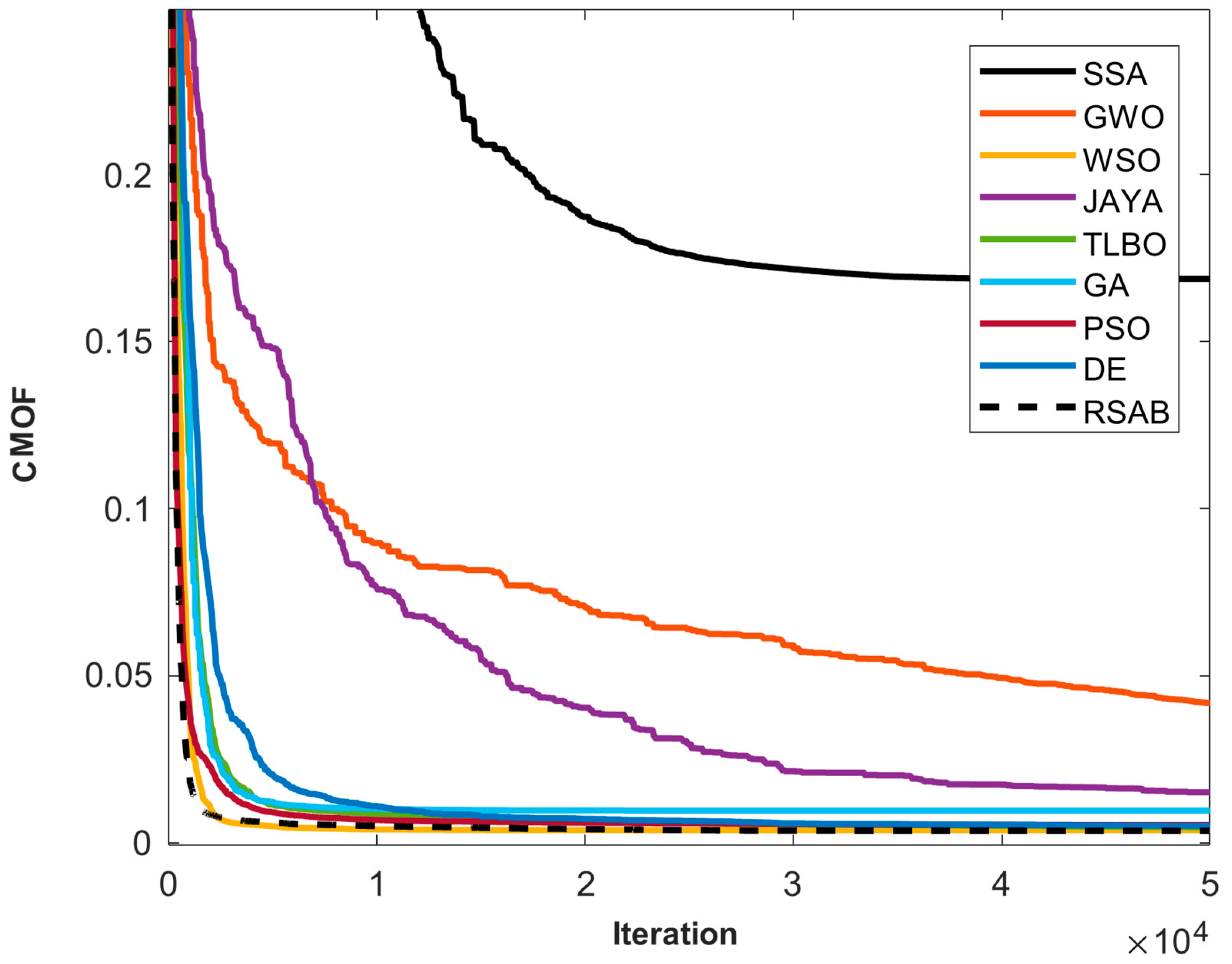
A thorough depiction of the convergence behavior of the algorithms used to determine the DDM’s parameters can be found in Figure 5. With a primary focus on assessing optimization success using the CMOF metric, the graph displays each algorithm’s most successful runs across iterations. Among the important conclusions drawn from this analysis are the following:

• Early Convergence: for the double-diode model, SSA, GWO, WSO, and JAYA show quick convergence in the first iterations, just like the single-diode model. RSAB’s ability to explore the solution space effectively is demonstrated by its competitive early convergence.
• Intermediate Convergence: in the early iterations, TLBO, GA, and PSO show slower convergence, suggesting a longer exploration phase. RSAB remains effective throughout this time, highlighting its capacity to strike a balance between exploration and exploitation.
• Exploration and Exploitation Trade-off: RSAB continuously exhibits a balance between exploration and exploitation, which may prevent premature convergence and encourage solution diversity. Additionally, DE demonstrates a good balance between exploration and exploitation, effectively adjusting to the intricacy of the optimization environment.
• Divergence and Stagnation: early on, GA shows a sharp rise in the objective function value, which may indicate problems with convergence or insufficient exploration. Because of its randomized methodology, RSAB performs robustly by avoiding premature convergence and maintaining stability.
• Stability and Smoothness: RSAB’s ability to find optimal or nearly optimal solutions is improved by its stable convergence, which is free of abrupt spikes or fluctuations.

Figure 5. Convergence curves of applied algorithms for DDM parameter identification, highlighting best runs and CMOF progress.

Figure 5. Convergence curves of applied algorithms for DDM parameter identification, highlighting best runs and CMOF progress.

4.4.3. Convergence Behavior Analysis for PVMM

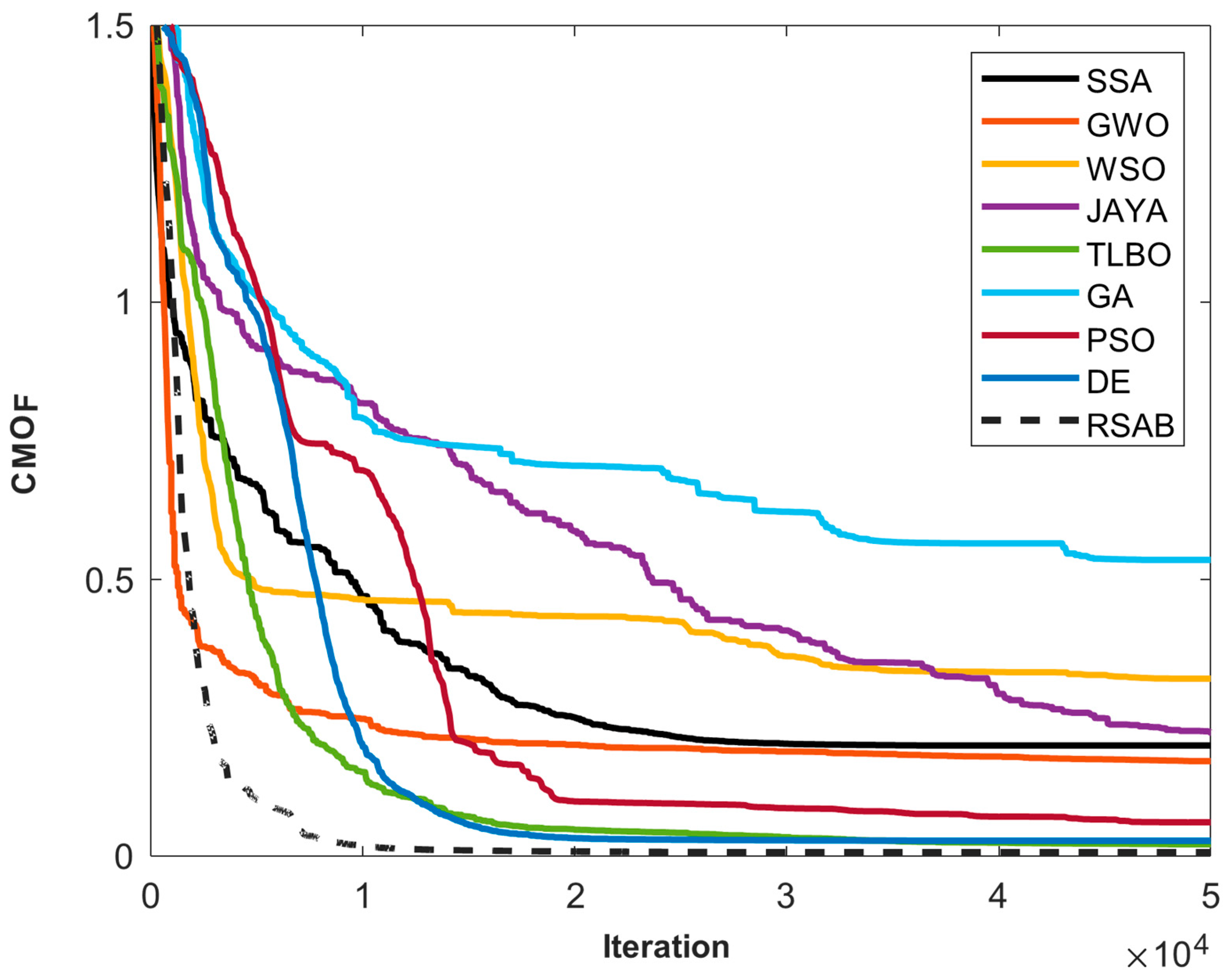
The convergence behavior of the algorithms used to identify parameters in the PVMM is shown graphically in Figure 6. With an emphasis on assessing the critical optimization success metric, CMOF, the graph displays each algorithm’s optimal runs over iterations. The following important findings from this analysis provide insight into the dynamics of performance:

• Early Convergence: interestingly, in the first iterations of the PV module model, SSA, GWO, WSO, JAYA, TLBO, and GA show quick convergence. Competitive early convergence is also demonstrated by the RSAB algorithm, suggesting that it may be useful for finding optimal or nearly optimal solutions.
• Intermediate Convergence: in the early iterations, PSO and DE exhibit a somewhat slower convergence, suggesting a longer exploration phase. RSAB remains effective throughout this time, highlighting its ability to successfully strike a balance between exploration and exploitation.
• Exploration and Exploitation Trade-off: RSAB continuously demonstrates a fair trade-off between exploration and exploitation, avoiding untimely convergence and encouraging a variety of solutions. Despite showing a slow convergence, PSO and DE highlight their superior exploration capabilities.
• Divergence and Stagnation: GA’s objective function value fluctuates, which may indicate problems with convergence or insufficient exploration. Because of its randomized methodology, RSAB exhibits stability, preventing premature convergence and adding to its strong performance.
• Stability and Smoothness: RSAB’s convergence is characterized by stability, free of abrupt spikes or fluctuations, enhancing its dependability in locating ideal or nearly ideal solutions for the PVMM.

With its effectiveness and stability in a range of optimization scenarios, the convergence behavior analysis highlights RSAB as a promising algorithm for parameter identification across different photovoltaic models.

Figure 6. Convergence curves of applied algorithms for PVMM parameter identification, highlighting best runs and CMOF progress.

Figure 6. Convergence curves of applied algorithms for PVMM parameter identification, highlighting best runs and CMOF progress.

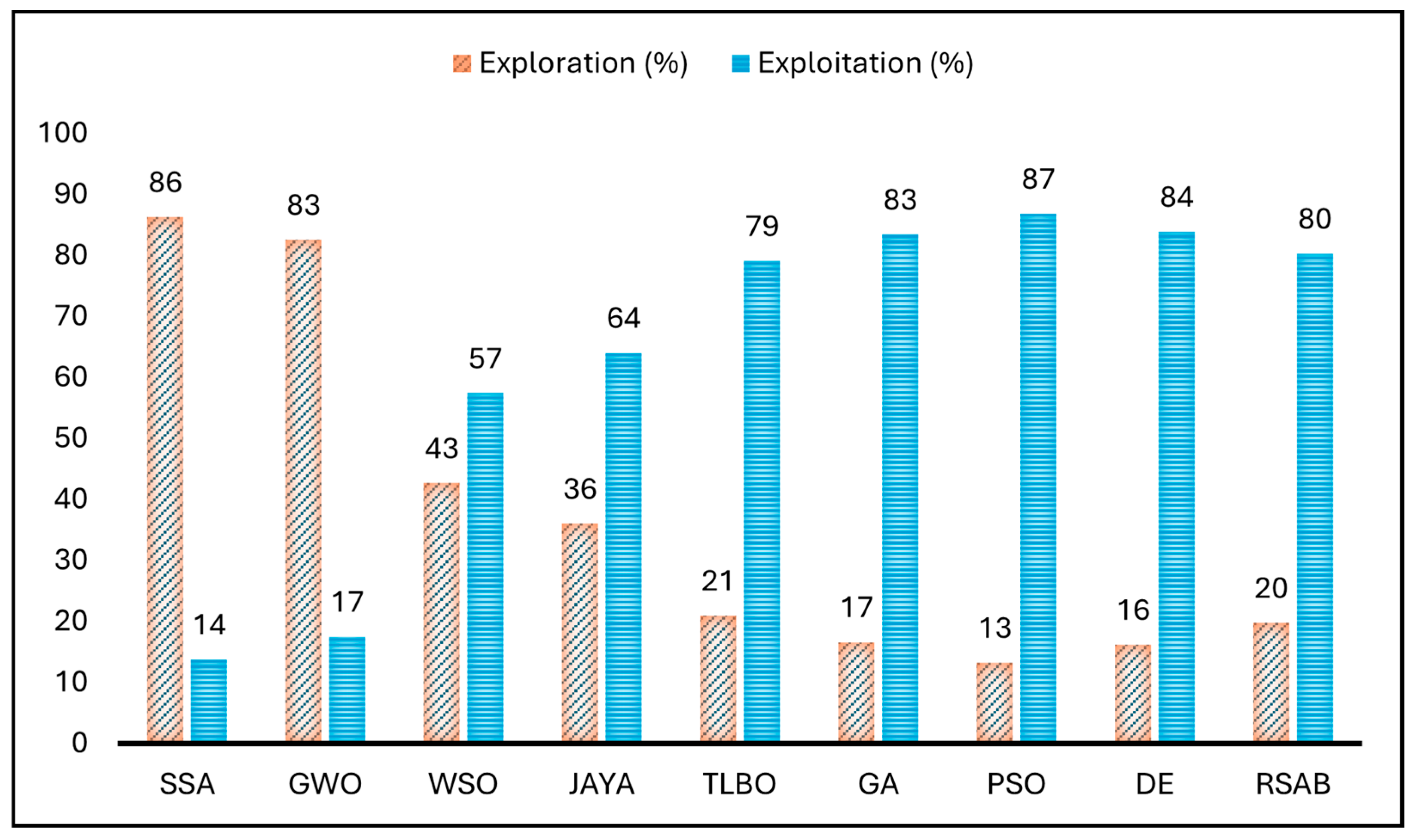
4.5. Differences in Exploration and Exploitation

When applied to the Single-Diode Model (SDM), the percentages shown in Figure 7 reveal subtle tactics used by different optimization algorithms. With 20% devoted to exploration and 80% to exploitation, RSAB achieves a well-balanced exploration–exploitation trade-off. This balance enables RSAB to effectively traverse complex optimization environments, utilizing the advantages of both exploration and exploitation. The DE algorithm employs a more mixed approach, allocating 84% of its resources to exploitation and 16% to exploration. This flexibility enables DE to successfully traverse a variety of terrains, demonstrating a flexible strategy that deftly strikes a balance between exploration and exploitation.

Different algorithms exhibit different tendencies when compared. Higher percentages in this dimension are emphasized by exploration-leaning algorithms such as SSA and GWO. However, algorithms like WSO and JAYA successfully balance exploitation and exploration. Higher percentages in this area, however, indicate a preference for exploitation by TLBO, GA, PSO, DE, and RSAB.

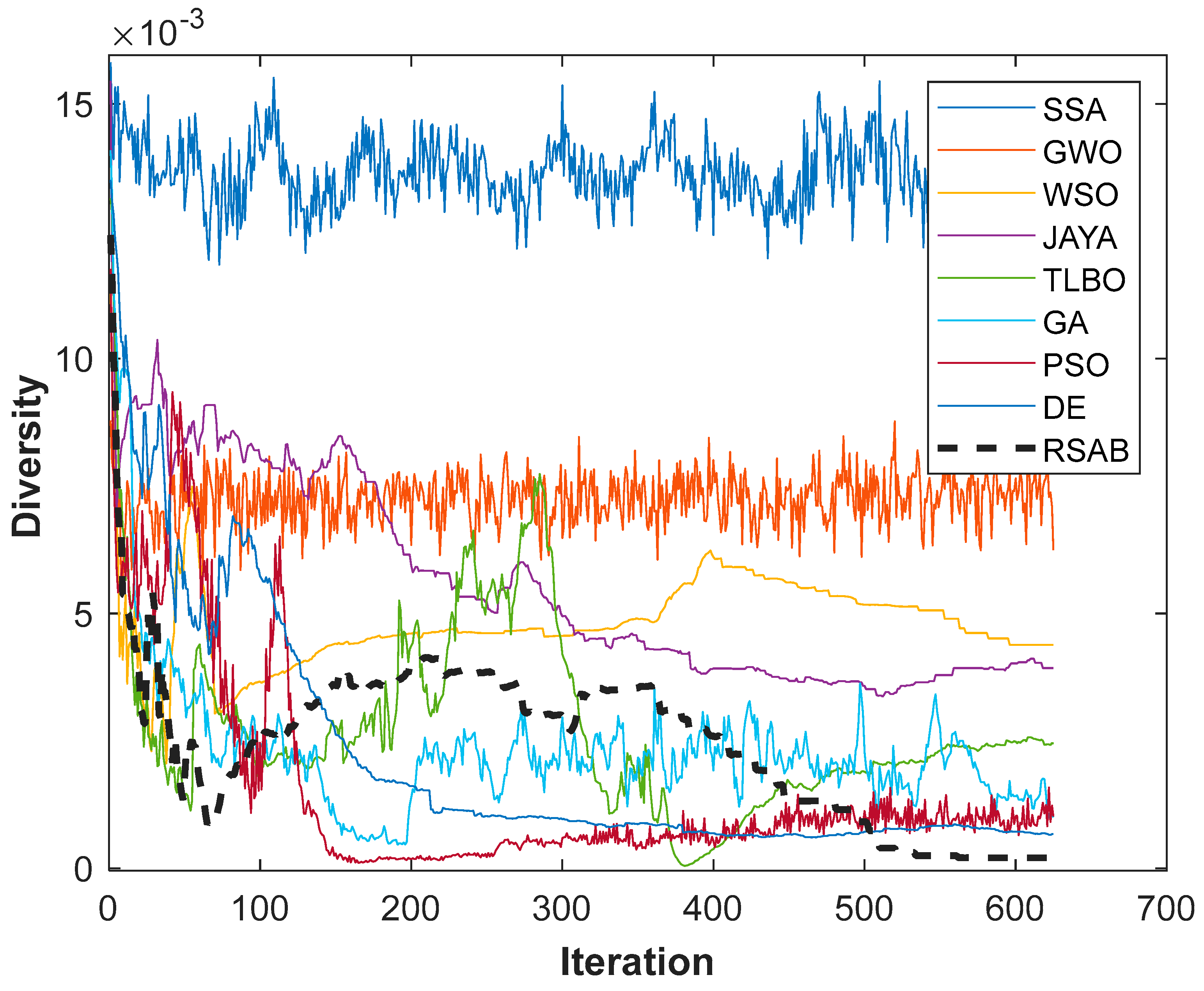
4.6. Diversity Analysis

As shown in Figure 8, the diversity metric results provide important information about the exploration–exploitation traits displayed by various algorithms applied to the SDM. By calculating the average distance between people in the population, this metric acts as a crucial indicator. We can learn a lot about how much each algorithm explores and uses the solution space during the iteration process by using this metric [42].

In the first iterations, the SSA algorithm starts with a diversity value of 0.0150, indicating a high exploration phase (Figure 8). By the tenth iteration, this value steadily decreased to 0.0129. A moderate exploration phase is suggested by GWO’s initial diversity value of 0.0064, which stabilizes at 0.0074 in the early iterations. WSO shows a steady decrease in diversity over these early iterations, starting with a diversity value of 0.0049. By the tenth iteration, JAYA’s diversity value has progressively dropped from its initial value of 0.0084 to 0.0077. Moderate exploration is indicated by TLBO, which starts with a diversity value of 0.0064 and gradually drops to 0.0044. Beginning with a diversity value of 0.0098, GA gradually decreases over the course of the first few iterations before stabilizing at 0.0027. The diversity value of PSO begins at 0.0060, shows a downward trend, and reaches 0.0029 by the tenth iteration. In the early iterations, DE drops to 0.0054 from its initial diversity value of 0.0096, which indicates high exploration. By iteration 10, the diversity value of RSAB has decreased from its initial value of 0.0054 to 0.0032.

A shift towards exploitation is indicated by SSA’s continued downward trend into the mid-iterations, which reaches 0.0131 by iteration 30. A balanced exploration–exploitation approach is suggested by GWO’s steady diversity, which hovers around 0.0074. WSO keeps dropping, hitting 0.0039, highlighting the mid-iterations’ exploitative nature. Around 0.0080, JAYA exhibits steady diversity, preserving equilibrium between exploration and exploitation. TLBO gradually drops to 0.0014, suggesting that exploitation is heavily prioritized in the middle iterations. Around 0.0020, GA maintains low diversity, indicating an emphasis on exploitation in the middle iterations. PSO keeps declining, hitting 0.0011, highlighting an exploitative approach in the middle iterations. In the middle iterations, DE exhibits a trend toward exploitation as it declines to 0.0047. A focus on exploitation in the middle iterations is indicated by the RSAB’s continued decline to 0.0013.

By iteration 40, as we approach the final iterations, SSA has stabilized at about 0.0124, suggesting a persistent exploitative approach. A balanced exploration–exploitation approach is suggested by GWO’s stability in diversity, which hovers around 0.0074. With a diversity value of 0.0039 at the end, WSO highlights its exploitative nature. In the final iterations, JAYA maintains a balance between exploration and exploitation by stabilizing at about 0.0078. With a diversity value of 0.0011 at the end, TLBO places a significant focus on exploitation. Around 0.0019, GA maintains a low diversity, indicating an emphasis on exploitation in the final iterations. With a diversity value of 0.0007 at the end, PSO highlights an exploitative approach in the final iterations. In the final iterations, DE stabilizes at about 0.0022, suggesting a balanced exploration–exploitation approach. The diversity value of 0.0002 at the end of RSAB indicates a heavy focus on exploitation.

A thorough understanding of how each algorithm handles exploration and exploitation during the optimization process is given by this overall comparison. It is crucial to remember that an algorithm’s efficacy is contingent upon the issue at hand and the equilibrium it strikes between exploitation and exploration.

4.7. Statistical Performance Comparison of RSAB with State-of-the-Art Algorithms

Table 8. Statistical performance comparison of RSAB with state-of-the-art optimization algorithms for PV parameter estimation (RMSE minimization objective).

Model	Metric	IWOA	MSSA	CMM-DE/BBO	APLO	Rcr-JADE	hARS-PS	STLBO	QMVO	RSAB
SDM	SD	1.13 × 10−5	3.01 × 10−7	8.17 × 10−5	1.60 × 10−16	5.12 × 10−16	3.01 × 10−7	1.86 × 10−5	1.94 × 10−4	2.95 × 10−17
	Mean	1.03 × 10−3	9.86 × 10−4	1.05 × 10−3	9.86 × 10−4	9.86 × 10−4	9.85 × 10−4	9.86 × 10−4	1.14 × 10−3	9.86 × 10−4
	Max	9.95 × 10−4	9.87 × 10−4	1.35 × 10−3	9.86 × 10−4	9.86 × 10−4	9.87 × 10−4	9.86 × 10−4	1.03 × 10−3	9.86 × 10−4
	Min	9.86 × 10−4	9.86 × 10−4	9.86 × 10−4	9.86 × 10−4	9.86 × 10−4	9.84 × 10−4	9.86 × 10−4	9.88 × 10−4	9.86 × 10−4
DDM	SD	1.93 × 10−5	1.49 × 10−6	2.94 × 10−4	7.80 × 10−5	9.86 × 10−5	1.45 × 10−7	2.90 × 10−4	4.02 × 10−4	3.05 × 10−7
	Mean	1.09 × 10−3	9.94 × 10−4	1.55 × 10−3	1.02 × 10−3	9.86 × 10−4	9.84 × 10−4	1.06 × 10−3	1.37 × 10−3	9.84 × 10−4
	Max	9.97 × 10−4	9.99 × 10−4	2.06 × 10−3	1.34 × 10−3	9.83 × 10−4	9.87 × 10−4	2.45 × 10−3	1.04 × 10−3	9.88 × 10−4
	Min	9.83 × 10−4	9.83 × 10−4	1.01 × 10−3	9.83 × 10−4	9.82 × 10−4	9.82 × 10−4	9.83 × 10−4	9.83 × 10−4	9.82 × 10−4
PVMM	SD	2.24 × 10−6	1.75 × 10−5	3.55 × 10−7	5.96 × 10−17	2.90 × 10−17	1.38 × 10−5	6.90 × 10−2	1.58 × 10−4	2.12 × 10−17
	Mean	2.43 × 10−3	2.54 × 10−3	2.43 × 10−3	2.43 × 10−3	2.43 × 10−3	2.43 × 10−3	2.06 × 10−2	2.54 × 10−3	2.42 × 10−3
	Max	2.43 × 10−3	2.78 × 10−3	2.43 × 10−3	2.43 × 10−3	2.43 × 10−3	2.50 × 10−3	2.74 × 10−1	2.46 × 10−3	2.43 × 10−3
	Min	2.43 × 10−3	2.42 × 10−3	2.43 × 10−3	2.43 × 10−3	2.43 × 10−3	2.42 × 10−3	2.43 × 10−3	2.43 × 10−3	2.42 × 10−3

shows a detailed statistical comparison of the suggested RSAB algorithm with a number of state-of-the-art optimization methodologies—MSSA [20], hARS-PS [37], APLO [26], IWOA [34], CMM-DE/BBO [35], Rcr-JADE [36], STLBO [38], and QMVO [39] applied to the estimation of the parameters of the PV under the objective of minimizing the RMSE. As seen from Table 8, for the SDM, RSAB achieves the lowest SD (2.95 × 10⁻¹⁷), indicating superior stability compared to other algorithms, with IWOA (1.13 × 10⁻⁵), CMM-DE/BBO (8.17 × 10⁻⁵), and QMVO (1.94 × 10⁻⁴) exhibiting higher variability. The mean RMSE (9.86 × 10⁻⁴) of RSAB matches the best-performing algorithms, including MSSA, APLO, Rcr-JADE, and STLBO, while significantly outperforming IWOA (1.03 × 10⁻³) and QMVO (1.14 × 10⁻³). In the DDM case, RSAB again demonstrates exceptional consistency, recording the second-lowest SD (3.05 × 10⁻⁷), only slightly higher than hARS-PS (1.45 × 10⁻⁷). The mean RMSE (9.84 × 10⁻⁴) is the lowest among all competitors, with CMM-DE/BBO (1.55 × 10⁻³), APLO (1.02 × 10⁻³), and QMVO (1.37 × 10⁻³) showing significantly higher errors. For PVMM, RSAB maintains superior precision, achieving the lowest SD (2.12 × 10⁻¹⁷) and mean RMSE (2.42 × 10⁻³), outperforming MSSA (2.54 × 10⁻³) and QMVO (2.54 × 10⁻³). Notably, STLBO (6.90 × 10⁻² SD, 2.06 × 10⁻² mean) exhibits poor convergence, likely due to premature stagnation.

From the comparative outcomes, the presented RSAB possesses a number of advantages. (1) RSAB returns the smallest or near smallest SD values, illustrating enhanced robustness in the estimation of parameters; (2) the averaged RMSE of RSAB is the best or very competitive, validating its enhanced accuracy; (3) relative to metaheuristic hybrids (e.g., hARS-PS, Rcr-JADE), the proposed RSAB possesses enhanced stability with minimal deviation in runs; and (4) QMVO and CMM-DE/BBO are more variable, which implies sensitivity to initialization or local optima. The statistical analysis confirms that RSAB outperforms existing algorithms in both accuracy and reliability for PV parameter extraction, making it a highly effective solution for solar cell modeling.

4.8. Recommendations for Further Analysis

RSAB’s parameterless design eliminates manual tuning, making it scalable for real-world PV systems with varying conditions. Its adaptive search (Section 3.1) ensures consistent performance across different PV models without recalibration. Even though the preliminary findings are encouraging, more research can greatly improve our understanding of RSAB’s robustness and generalizability. This includes statistical comparisons and sensitivity studies. Our assessment of the RSAB’s overall performance can be strengthened by conducting comparative analyses across different runs or datasets. These thorough evaluations are essential for enabling researchers to select an optimization algorithm that is suited to PV models with knowledge.

5. Conclusions

This paper offered a new multi-objective optimization approach for PV parameter extraction with the RSAB algorithm to overcome the twin problems of accuracy and robustness in the modeling of a PV. The RSAB algorithm innovates within PV parameter identification by (1) avoiding manual tuning, (2) outperforming 16 state-of-the-art algorithms in both accuracy and stability (Table 4, Table 5, Table 6, Table 7 and Table 8), and (3) presenting a multi-objective framework that optimizes together the L2 norm and the maximum error—a paradigm shift from single-objective approaches. The main contributions and findings directly supported by the results in Section 3 and Section 4 are outlined as follows:

• The suggested combined multi-objective function (CMOF)—a balance between the L2 norm (overall accuracy) and maximum error (resilience to outliers)—showed robust improvements over single-objective strategies. As shown from Table 3, an optimal balance is achieved by w₁ = w₂ = 0.5.
• RSAB’s parameterless architecture eliminated the need for tuning by hand and outperformed nine state-of-art algorithms (Table 4, Table 5, Table 6 and Table 7). For SDM, the lowest mean RMSE (9.86 × 10⁻⁴) and standard deviation (2.95 × 10⁻¹⁷) by RSAB evidenced its stability (Table 8). Its adaptive balance of exploration–exploitation (Section 4.5, Figure 7) precluded premature convergence, which is well-known.
• RSAB achieved competitive performances in SDM, DDM, and PVMM with reasonable results compared to the state-of-the-art hybrid algorithms (Table 8), and faster convergence than most of the applied algorithms (Figure 4, Figure 5 and Figure 6). The algorithm’s scalability was also supported by its population size insensitivity (Table 2), for which npop = 80–100 worked best for complex models.
• Statistical significance of the results of RSAB (Friedman test ranks: 1.23 for SDM, 1.37 for DDM) and low computational duration (67.1 s average) (Table 4) qualify it for practical application in real-time PV systems. Case studies attested to its capability to reduce errors in current/power (e.g., 0.0019 a max. error in current for SDM), essential for grid integration.

Future research will aim at extending RSAB to multi-objective Pareto optimization, monitoring parameters in real-time under different environmental conditions, and application to solve real-world optimization problems. The flexibility of the framework further suggests possibilities for applications in fuel cell and battery modeling.