Spatial Risk Prediction of Coal Seam Gas Using Kriging Under Complex Geological Conditions
Abstract
1. Introduction
2. Engineering Geological Overview
3. Coal Seam Parameter Determination
3.1. Gas Properties
3.2. Gas Pressure
3.3. Gas Content
3.4. Gas Flow Decay Coefficient in Boreholes
3.5. Determination of the Coal Seam Permeability Coefficient
3.6. Determination of Other Parameters of Coal Seam
4. Application of the Kriging Algorithm for Advanced Identification Prediction
4.1. Exploratory Spatial Data Analysis
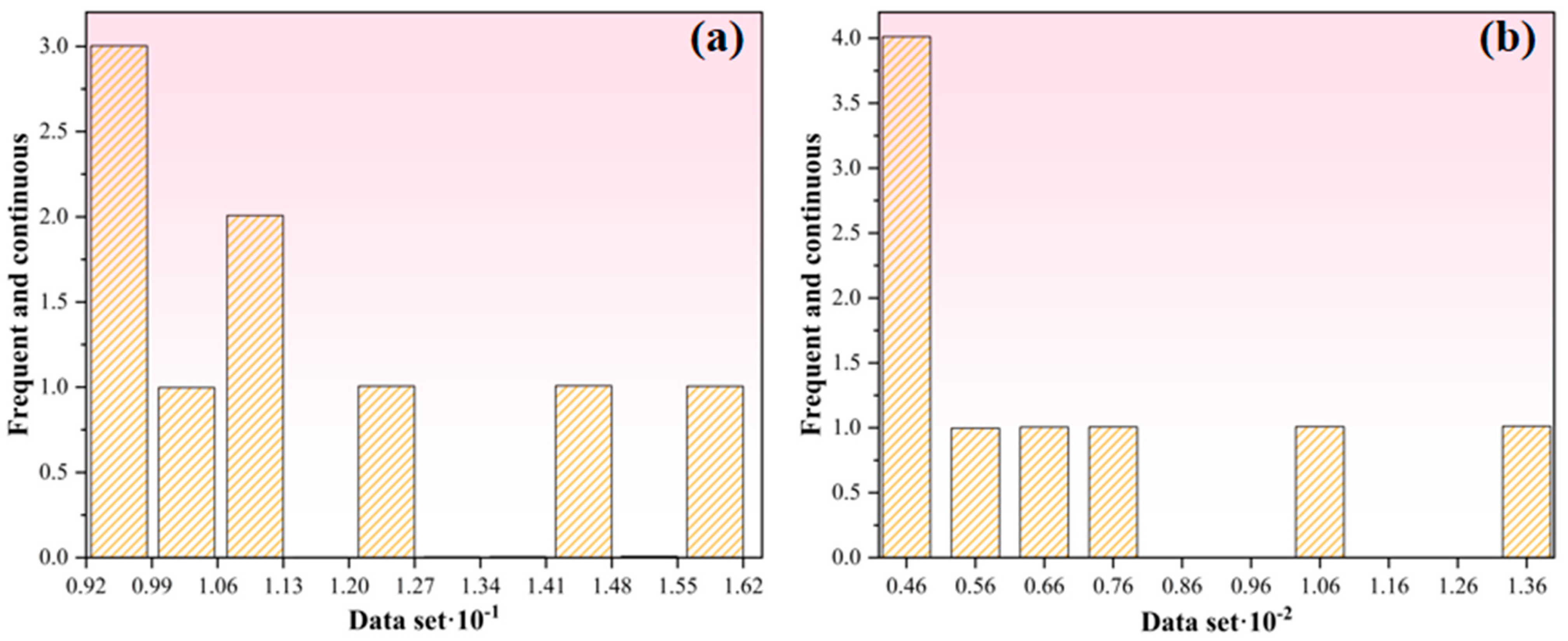
4.1.1. Frequency Analysis
4.1.2. Outlier Analysis
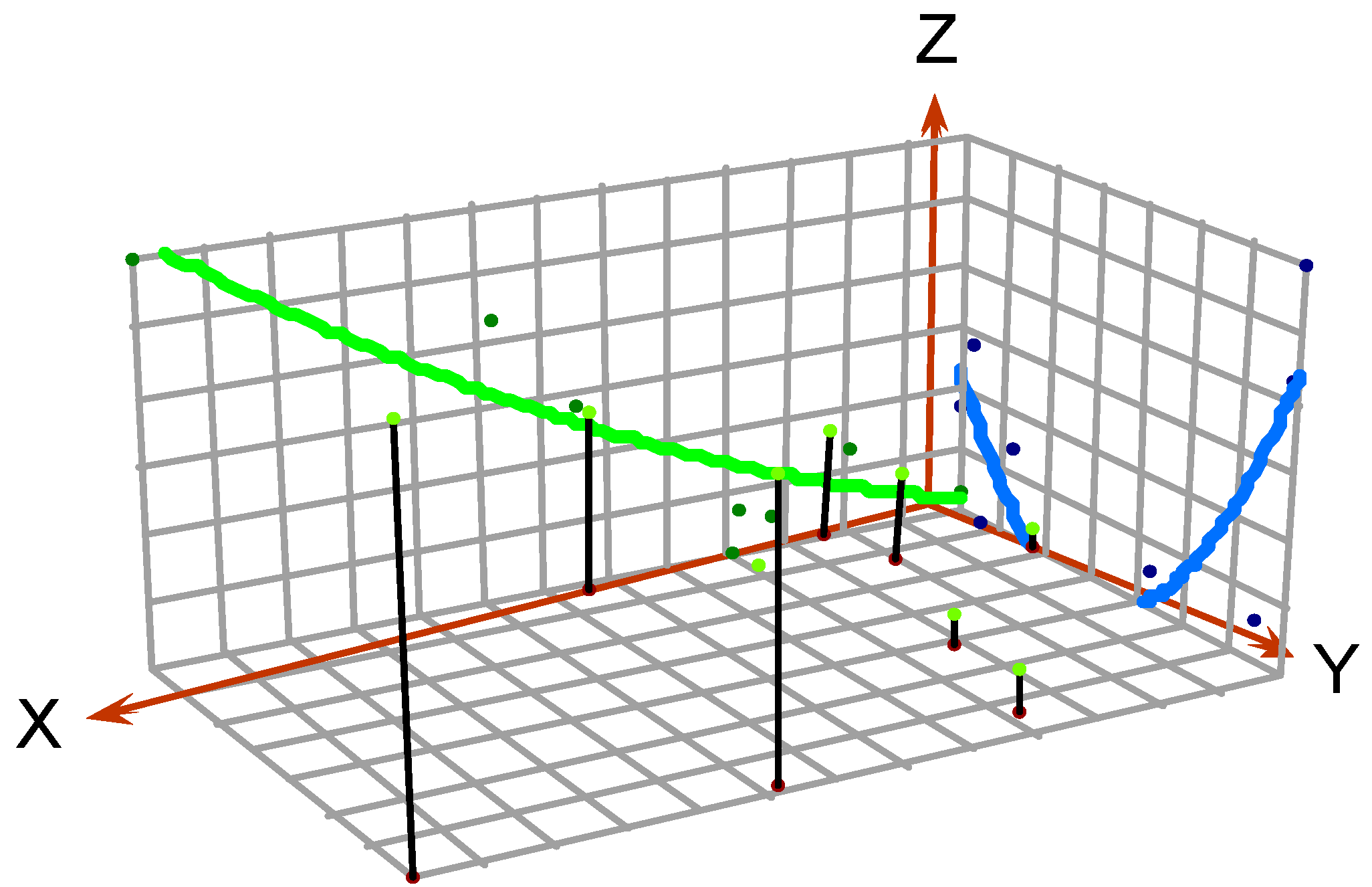
4.1.3. Global Trends
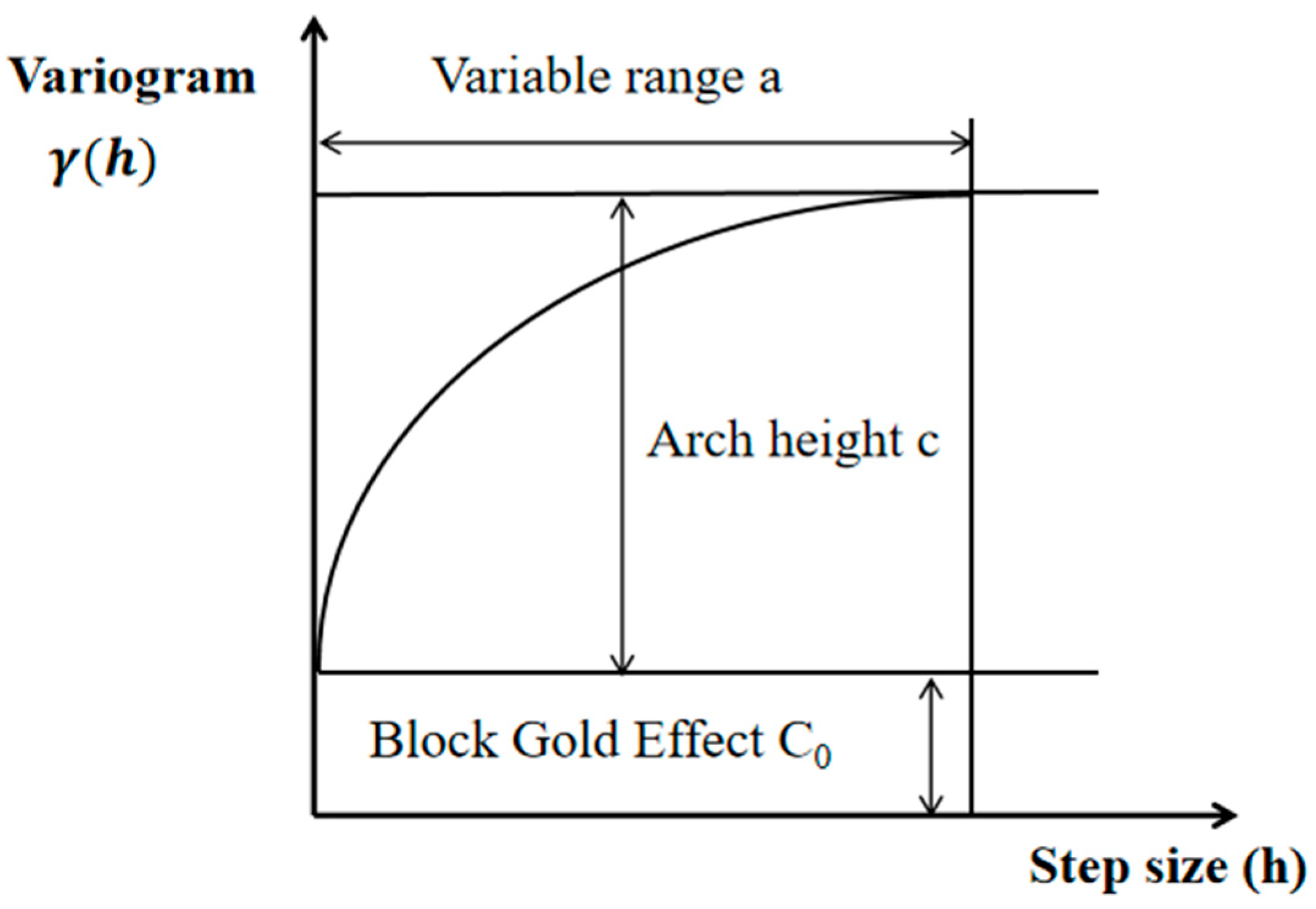
4.2. Variation Function
4.2.1. Theoretical Model Selection
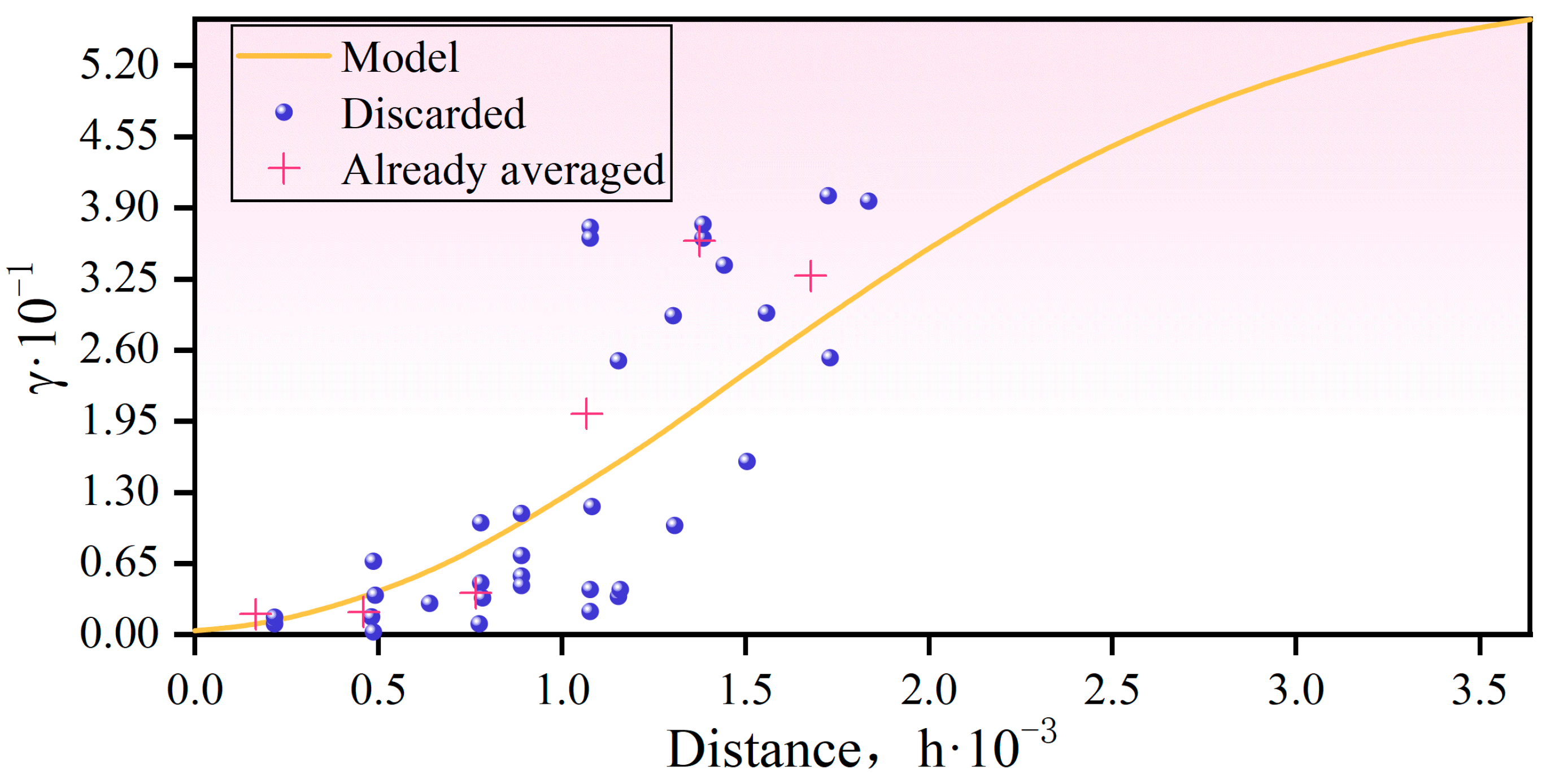
4.2.2. Variogram Model
4.3. Forecast Algorithm
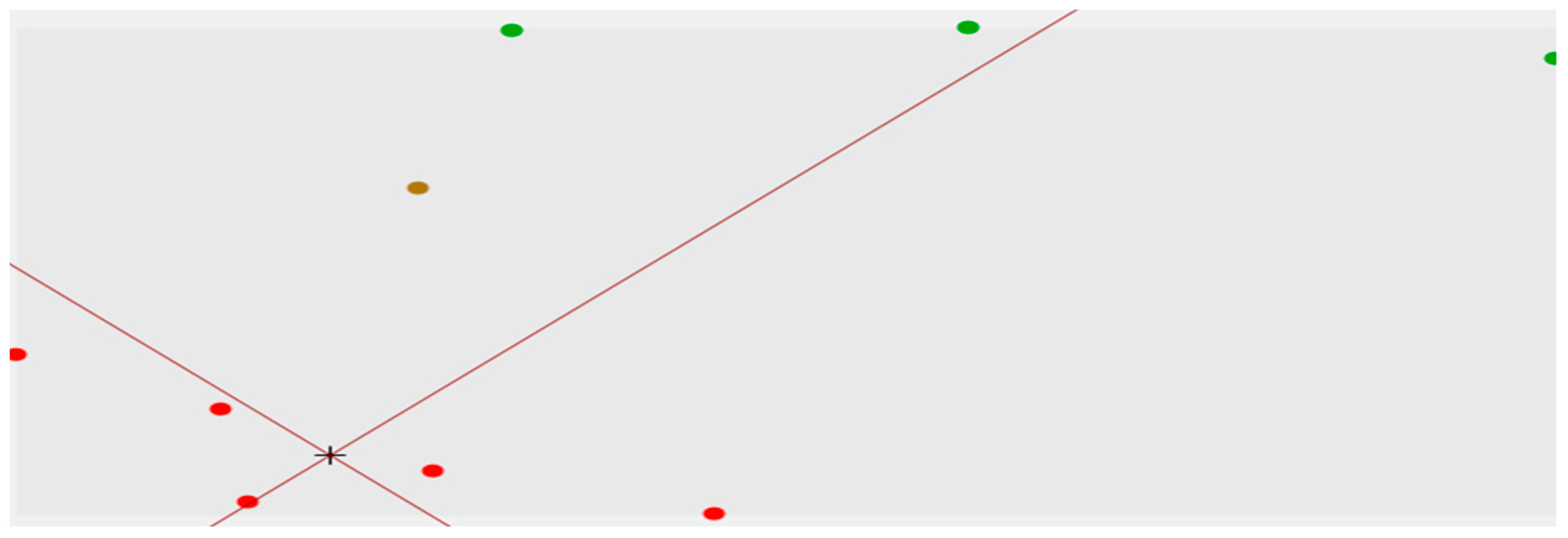
4.3.1. Search Field
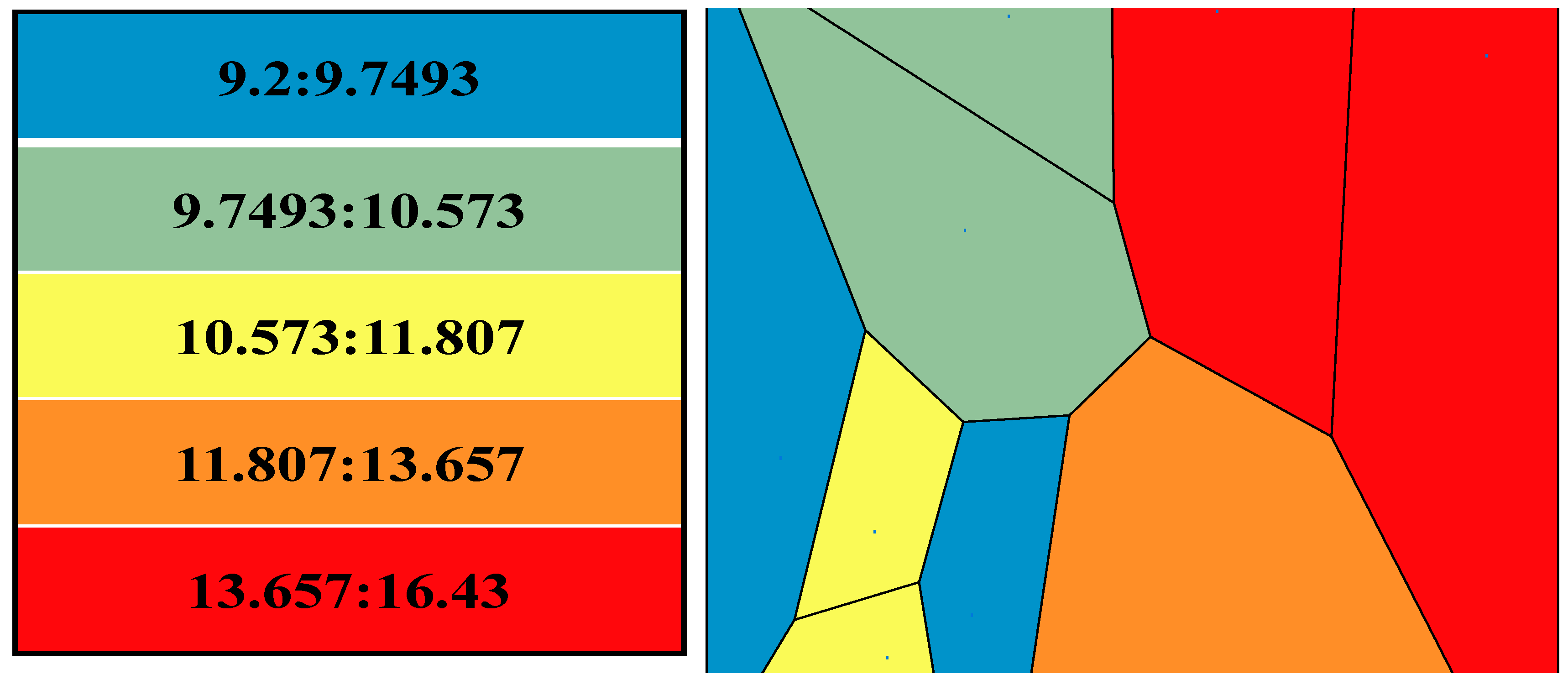
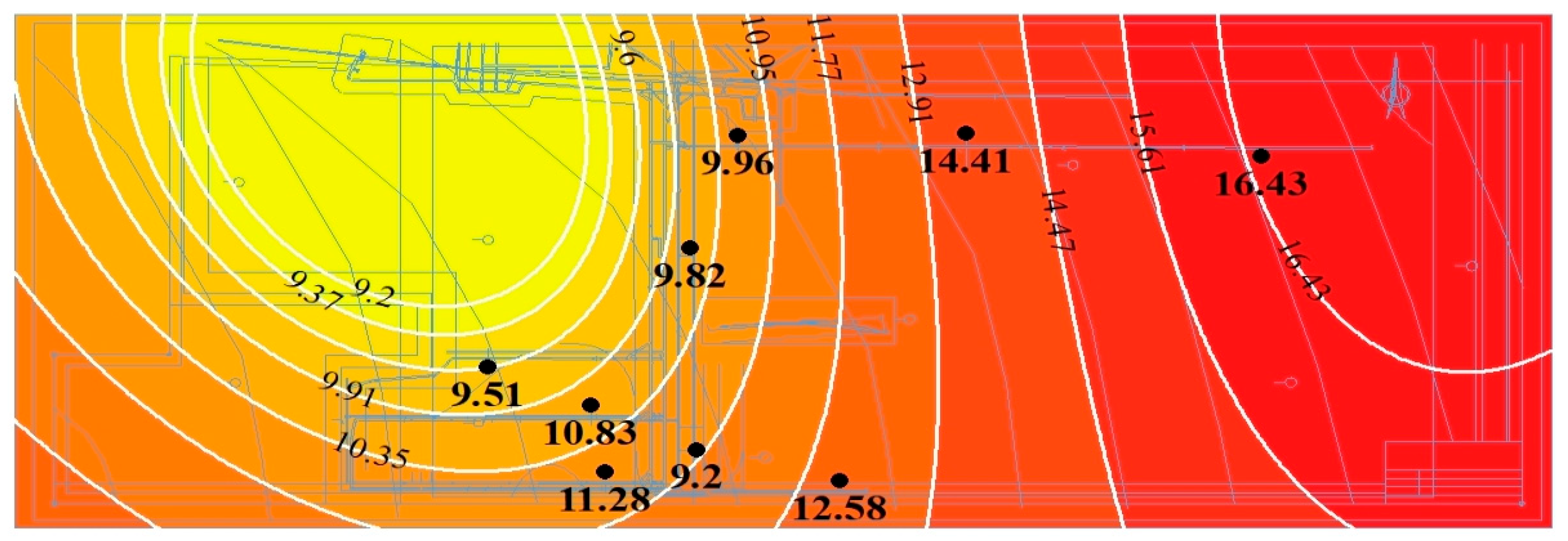
4.3.2. Ordinary Kriging Prediction
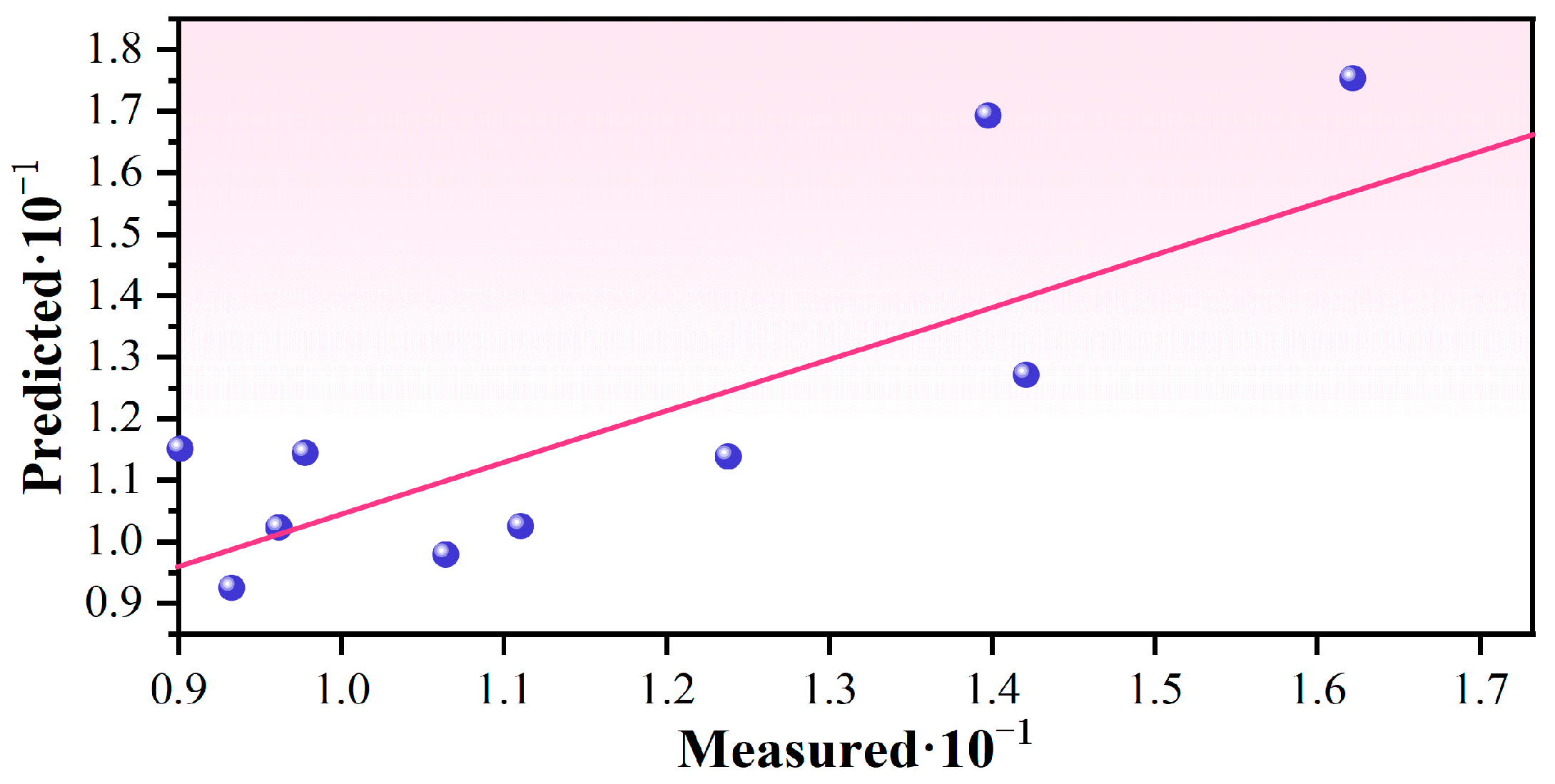
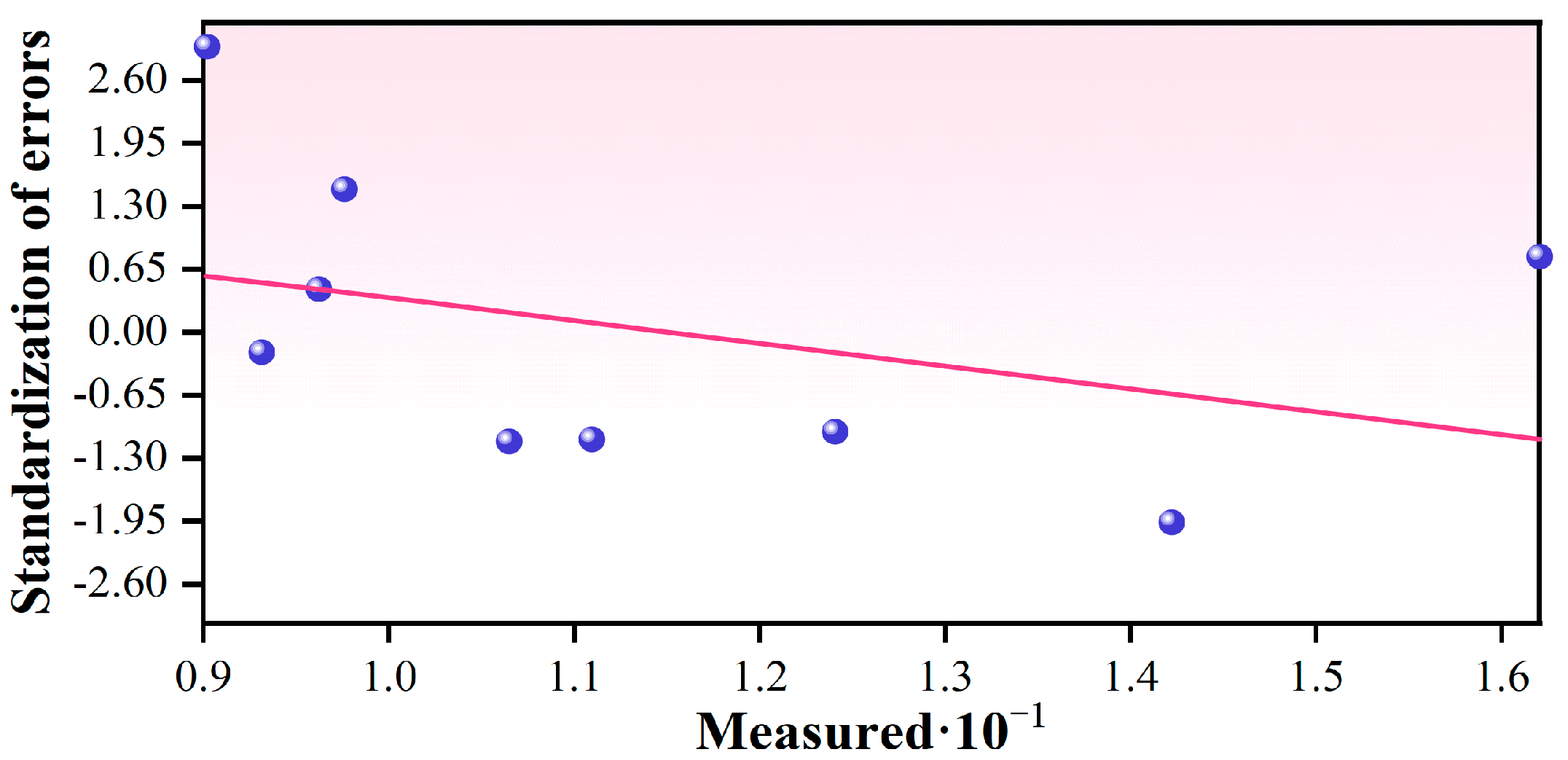
4.3.3. Cross-Validation Comparison
4.4. Discussion
5. Conclusions
- (1)
- Based on the relationships among the gas content, elevation, and buried depth measured in the No. 9 coal seam of Longfeng Coal Mine, the gas content as a function of the elevation conforms to the following formula: y = −0.0406x + 54.845, R2 = 0.9202. The relationship between the gas content and the buried depth follows the following relation: y = 0.0269x + 5.1801, R2 = 0.8925.
- (2)
- According to the relationship between the buried depth (or height) and the parameters, the outburst danger area can be divided according to the buried depth (or elevation). The gas content of the No. 9 coal seam reaches a critical value of 8 m3/t at a buried depth of 105 m, so the area below 105 m is defined as the outburst danger area.
- (3)
- Based on the Kriging algorithm, the spatial position of the prediction points or prediction surface is considered. Through the analysis of the measured samples, the prediction function of the gas content of the No. 9 coal seam could be represented by Y = 0.84X + 1.840, where X and Y are the measured value and the predicted value, respectively, while the average prediction rate was obtained as 90.44%.
- (4)
- Deep coal seams have more complex geological and gas conditions. The sustainable exploitation of deep coal seam resources requires new technologies for safe mining, with further research needed on deep coal seam geology. Our study integrates complex deep geological conditions with gas prediction. The results are directly applicable in production, offering a reusable technical framework for similar geological coal mines. This shifts gas disaster prevention from “passive response” to “active prediction”, aiding deep resource development.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol or Abbreviation | Description | Unit or Parameter |
| PF9-1 to PF9-6 | Different borehole location numbers for measuring coal seam gas pressure | - |
| Azimuth | Borehole azimuth | - |
| Dip angle | Borehole dip angle | - |
| Predicted coal seam length | Predicted coal seam length | m |
| Seal hole length | Seal hole length | m |
| X | Coal seam gas content | m3/t |
| y | Dependent variable in the formula for the relationship between gas content and elevation or burial depth | - |
| x | Independent variable in the formula for the relationship between gas content and elevation or burial depth | - |
| R2 | Coefficient of determination in the relationship formula | - |
| q0 | Initial gas flow rate | m3/min |
| α | Gas flow decay coefficient | d−1 |
| qt | Gas flow rate at time t | m3/min |
| t | Gas flow decay time | d |
| Qt | Total gas flow at any time t | m3 |
| QJ | Maximum total gas flow | m3 |
| λ | Coal seam permeability coefficient | m2/(MPa2·d) |
| P0 | Original gas pressure of the coal seam | MPa |
| P1 | Gas pressure in the borehole | MPa |
| r1 | Borehole radius | m |
| q | Gas flow rate per unit area of borehole coal wall at gas drainage time t | m3/(m2·d) |
| Q | Borehole gas flow rate at time t | m3/d |
| L | Borehole length, generally taken as coal seam thickness | m |
| X | Coal seam gas volume content | m3/m3 |
| A and B | Constants in the formula | - |
| Y | Flow number | - |
| F0 | Time criterion | - |
| a and b | Coefficients in the formula | - |
| h | Modulus of vector h, indicating the distance between two regionalized variable values Z(X) and Z(X + h) | - |
| α | Range value of the variogram | - |
| C0 | Nugget effect, reflecting the size of randomness within the regionalized vector | - |
| c | Sill, representing the part of the variable where the variable structure has changed | - |
| Numbering | Data point numbering | - |
| X and Y | Coordinates of data points | m |
| Gas content | Coal seam gas content | m3/t |
| m | Mathematical expectation, unknown constant | - |
| λ | Lagrange multipliers | - |
References
- Lyu, P.; He, L.; He, Z.; Liu, Y.; Deng, H.; Qu, R.; Wang, J.; Zhao, Y.; Wei, Y. Research on remote sensing prospecting technology based on multi-source data fusion in deep-cutting areas. Ore Geol. Rev. 2021, 138, 104359. [Google Scholar] [CrossRef]
- Kang, H.P. Temporal scale analysis on coal mining and strata control technologies. J. Min. Strat. Control Eng. 2021, 3, 5–27. [Google Scholar]
- Li, J.; Wang, Y.; Nguyen, X.; Zhuang, X.; Li, J.; Querol, X.; Li, B.; Moreno, N.; Hoang, V.; Cordoba, P.; et al. First insights into mineralogy, geochemistry, and isotopic signatures of the Upper Triassic high-sulfur coals from the Thai Nguyen Coal field, NE Vietnam. Int. J. Coal Geol. 2022, 261, 104097. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yuan, L.; Xue, J.H.; Tian, Z.C.; Duan, C.R.; Chen, B.L. Research status and development trend of mechanism and simulation test of coal and gas outburst. Ind. Mine Autom. 2018, 44, 43–50. [Google Scholar]
- Sun, J.; Cheng, J. Study on the perception and alarm method of coal mine rock burst and coal and gas outburst. Ind. Mine Autom. 2022, 48, 2236–2248. [Google Scholar]
- Yuan, L. Research progress of mining response and disaster prevention and control in deep coal mines. J. China Coal Soc. 2021, 46, 716–725. [Google Scholar]
- Tarkowski, R.; Uliasz-Misiak, B.; Tarkowski, P. Storage of hydrogen, natural gas, and carbon dioxide–Geological and legal conditions. Int. J. Hydrogen Energy 2021, 46, 20010–20022. [Google Scholar] [CrossRef]
- Yuan, L. Risk identification, monitoring and early warning of typical coal mine dynamic disasters during the 13th Five-Year Plan period. J. Min. Sci. Technol. 2021, 6, 1–8. [Google Scholar]
- Yang, Y.Z.; Wu, L.Y.; He, J. Theory and Application of Major Disaster Warning in Coal Mine Gas; Beijing Normal University Press: Beijing, China, 2010. [Google Scholar]
- He, X.; Wang, A.; Dou, L.; Song, D.; Zu, Z.; Li, Z. Technology of microseismic dynamic monitoring on coal and gas outburst-prone zone. J. China Coal Soc. 2018, 43, 3122–3129. [Google Scholar]
- Li, B.; Wang, E.; Shang, Z.; Liu, X.; Li, Z.; Dong, J. Deep learning and heterogeneous signal fusion approach to precursor feature recognition and early warning of coal and gas outburst. Process Saf. Environ. Prot. 2023, 178, 995–1008. [Google Scholar] [CrossRef]
- Shu, L.; Liu, Z.; Wang, K.; Zhu, N.; Yang, J. Characteristics and classification of microseismic signals in heading face of coal mine: Implication for coal and gas outburst warning. Rock Mech. Rock Eng. 2022, 55, 6905–6919. [Google Scholar] [CrossRef]
- Li, B.; Wang, E.; Shang, Z.; Liu, X.; Li, Z.; Li, B.; Wang, H.; Niu, Y.; Song, Y. Optimize the early warning time of coal and gas outburst by multi-source information fusion method during the tunneling process. Process Saf. Environ. Prot. 2021, 149, 839–849. [Google Scholar] [CrossRef]
- Dou, L.; Feng, L.; Cai, W.; Wang, H.; He, H.; Jiao, B.; Zhang, M. Seismo-acoustic precursor identification and comprehensive warning model for the catastrophic failure process of coal and rock. J. Min. Saf. Eng. 2020, 37, 960–976. [Google Scholar]
- Dou, L.; Zhou, K.; Song, S.; Cao, A.; Cui, H.; Gong, S.; Ma, X. Occurrence mechanism, monitoring and prevention technology of rockburst in coal mines. J. Eng. Geol. 2021, 29, 917–932. [Google Scholar]
- Huang, X.; Sun, D. Coal and gas outburst status and early warning technology in China coal mine. Coal Sci. Technol. 2011, 39, 61–69. [Google Scholar]
- Wang, E.; Li, Z.; Li, B.; Qin, B.; Xu, J.; Li, N.; Xia, H.; Zhang, G.; Li, Y.; Feng, X.; et al. Big data monitoring and early warning cloud platform for coal mine gas disaster risk and potential danger and its application. Coal Sci. Technol. 2022, 50, 142–150. [Google Scholar]
- Montero, J.M.; Fernández-Avilés, G. Functional kriging prediction of atmospheric particulate matter concentrations in Madrid, Spain: Is the new monitoring system masking potential public health problems? J. Clean. Prod. 2018, 175, 283–293. [Google Scholar] [CrossRef]
- Kemala, P.N.; Hakam, D.F. Optimizing final investment decision with real options valuation: A case study of offshore natural gas development project in Indonesia. Energy 2025, 316, 134363. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Zhang, Q.H.; Liu, J. Research progress and prospects of coal and gas outburst and composite dynamic disaster warning systems in China. J. China Coal Soc. 2024, 49, 1–13. [Google Scholar]
- Zyrianova, M.; Collett, T.; Boswell, R. Characterization of the Structural–Stratigraphic and Reservoir Controls on the Occurrence of Gas Hydrates in the Eileen Gas Hydrate Trend, Alaska North Slope. J. Mar. Sci. Eng. 2024, 12, 472. [Google Scholar] [CrossRef]
- Xue, S.; Zheng, X.; Yuan, L.; Lai, W.; Zhang, Y. A review on coal and gas outburst prediction based on machine learning. J. China Coal Soc. 2024, 49, 664–694. [Google Scholar]
- Bashir, T.A.; Zubairu, A.A.; Dadet, W.P.; Eletta, O.A.A. Parametric analysis of operating conditions on compressed natural gas production in Nigeria. J. Eng. Appl. Sci. 2025, 72, 1–18. [Google Scholar] [CrossRef]
- Krasnovyd, S.; Konchits, A.; Shanina, B.; Valakh, M.; Yukhymchuk, V.; Skoryk, M.; Molchanov, O.; Kamchatny, O. Coal from the outburst hazardous mine seams: Spectroscopic study. Min. Miner. Depos. 2023, 17, 93–100. [Google Scholar] [CrossRef]
- Tamaki, M.; Fujimoto, A.; Boswell, R.; Collett, T.S. Geological reservoir characterization of a gas hydrate prospect associated with the Hydrate-01 stratigraphic test well, Alaska North Slope. Energy Fuels 2022, 36, 8128–8149. [Google Scholar] [CrossRef]
- AQ/T1047-2007; Direct Measurement Method of Coal Seam Gas Pressure in Coal Mine. State Administration of Work Safety: Chongqing, China, 2007.
- Liu, G.; Li, B.; Zhang, Z.; Liu, H.; Guan, W.; Si, N. Gas expansion energy of coals with different metamorphic degrees: Evolutionary characteristics and their implications for the outburst prediction. Coal Geol. Explor. 2023, 51, 1–8. [Google Scholar]
- Zhao, X.; Hu, B.; Nie, B.; Liu, X.; Zhao, D.; Li, H.; Deng, C.; Duan, Z. Experimental study and field application of hydraulic flushing technology in soft coal seam. Sci. Rep. 2025, 15, 3304. [Google Scholar] [CrossRef]
- Liang, Y.; Zheng, M.; Li, Q.; Mao, S.; Li, X.; Li, J.; Zhou, J. A review on prediction and early warning methods of coal and gas outburst. J. China Coal Soc. 2023, 48, 2976–2994. [Google Scholar]
- Qiu, L.; Dang, J.; Zhang, J.; Wang, M.; Liu, Q.; Si, L.; Jiang, Z.; Khan, M. Investigating nonlinear resistivity characteristics and mechanisms of coal during various loading stages. J. Appl. Geophys. 2025, 238, 105705. [Google Scholar] [CrossRef]
- Fan, C.; Li, S.; Luo, M.; Du, W.; Yang, Z. Coal and gas outburst dynamic system. Int. J. Min. Sci. Technol. 2017, 27, 49–55. [Google Scholar] [CrossRef]
- Fan, C.; Xu, L.; Elsworth, D.; Luo, M.; Liu, T.; Li, S.; Zhou, L.; Su, W. Spatial–temporal evolution and countermeasures for coal and gas outbursts represented as a dynamic system. Rock Mech. Rock Eng. 2023, 56, 6855–6877. [Google Scholar] [CrossRef]
- Ren, Z.; Yu, Q. Gas concentration pre-warning system based on fuzzy structured element. J. Coal Sci. Eng. 2008, 14, 581–584. [Google Scholar] [CrossRef]
- Dazhao, S.; Qiang, L.; Liming, Q.; Jianguo, Z.; Khan, M.; Yujie, P.; Yingjie, Z.; Man, W.; Minggong, G.; Taotao, H. Experimental study on resistivity evolution law and precursory signals in the damage process of gas-bearing coal. Fuel 2024, 362, 130798. [Google Scholar] [CrossRef]

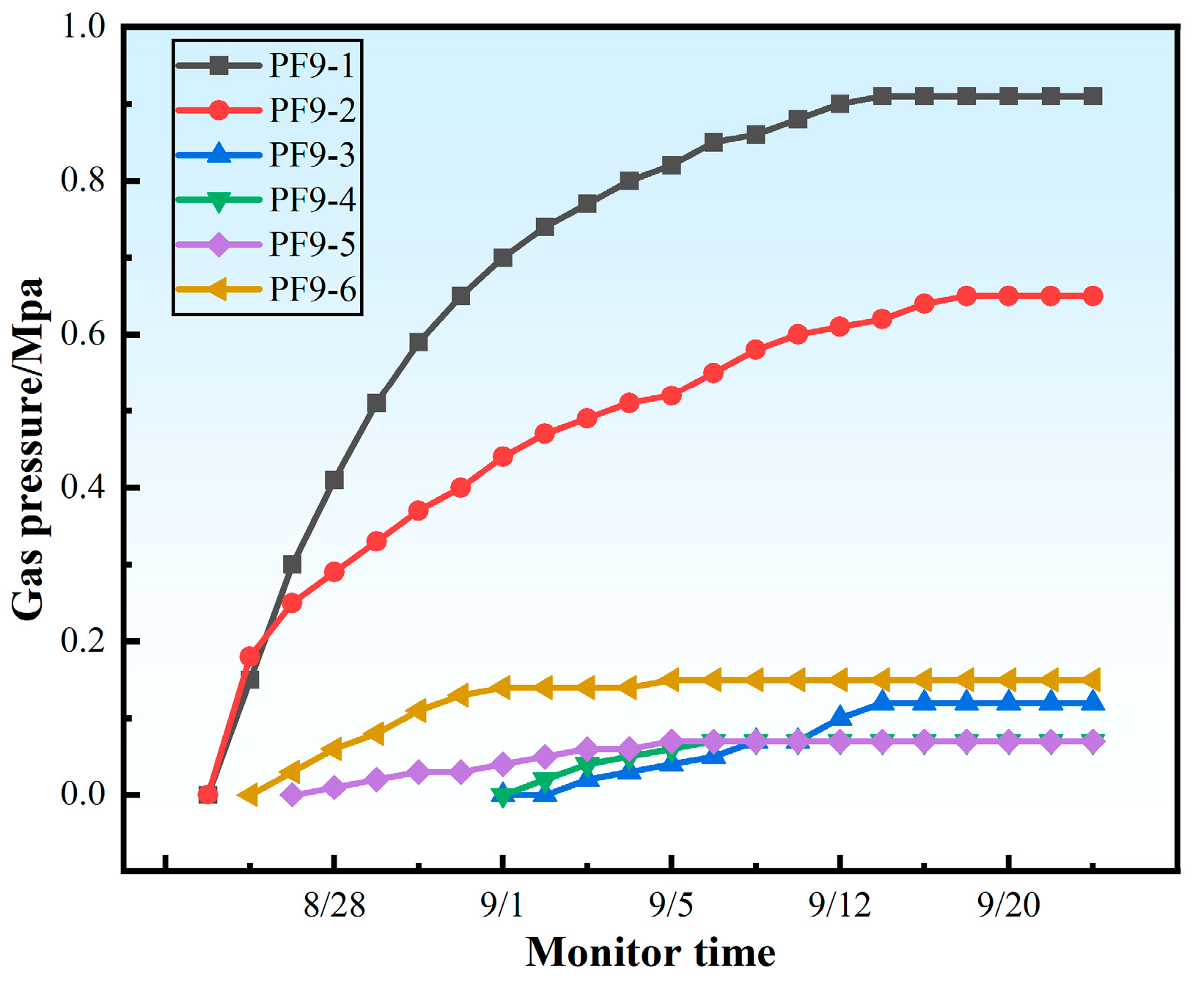


| Coal Seam | Drilling Location ID | Testing Location | Azimuth (°) | Dip Angle (°) | Predicted Coal Seam Length (m) | Seal Hole Length (m) | Remark (s) |
|---|---|---|---|---|---|---|---|
| No. 9 | PF9-1 | 59210 Bottom pumping roadway of wind roadway | 0 | 20 | 35 | 20 | Pressure measurement |
| PF9-2 | 180 | 20 | 40 | 20 | Pressure measurement content | ||
| PF9-3 | The second mining area belt up the mountain | 90 | 20 | 55 | 20 | Pressure measurement | |
| PF9-4 | 90 | 20 | 40 | 20 | Pressure measurement content | ||
| PF9-5 | 5923 Transportation roadway bottom pumping roadway | 0 | 20 | 28 | 20 | Pressure measurement | |
| PF9-6 | 180 | 20 | 28 | 20 | Pressure measurement content |
| Drilling Location ID | Testing Location | Initial Gas Flow Rate from the Borehole (q0) | Drilling Natural Gas Flow Attenuation Coefficient (α) |
|---|---|---|---|
| P9-1 | 59210 Bottom pumping roadway of wind roadway | 9.482 | 0.068 |
| P9-2 | 59210 Bottom pumping roadway of wind roadway | 4.709 | 0.084 |
| P9-3 | The second mining area belt up the mountain | 0.349 | 0.124 |
| P9-4 | The second mining area belt up the mountain | 0.792 | 0.097 |
| P9-5 | 5921 Transportation roadway bottom pumping roadway | 1.187 | 0.084 |
| P9-6 | 5921 Transportation roadway bottom pumping roadway | 0.892 | 0.045 |
|
Flow Number (Y) |
Time Criterion (F0 = Bλ) | Coefficient (a) |
Coefficient (b) |
Coal Seam Permeability Coefficient (λ) |
Constant (A) |
Constant (B) |
|---|---|---|---|---|---|---|
| Y = A/λ = aF0b | 10−2~1 | 1 | −0.38 | λ = A1.61B1/1.64 | ||
| 1~10 | 1 | −0.28 | λ = A1.39B1/2.56 | |||
| 10~102 | 0.93 | −0.20 | λ = 1.1A1.25B0.25 | |||
| 102~103 | 0.588 | −0.12 | λ = 1.83A1.14B1/7.3 | |||
| 103~105 | 0.512 | −0.10 | λ = 2.1A1.11B1/9 | |||
| 105~107 | 0.344 | −0.065 | λ = 3.14A1.07B1/14.4 |
| Drilling Location ID | Coal Seam Gas Volume Content X (m3/t) | Absolute Gas Pressure P0 (MPa) | Coal Seam Gas Content Coefficient α (m3/m3.MPa0.5) | Borehole Length L (m) | Radius of Drill Hole r1 (m) | Drilling Pressure Relief Time t (d) | Gas Flow in the Borehole Q (m3/d) | Gas Pressure When Drilling Pressure Relief P1 (MPa) | Gas Permeability Coefficient λ m2/(MPa2·d) |
|---|---|---|---|---|---|---|---|---|---|
| P9-1 | 14.64 | 0.36 | 24.4 | 13.5 | 0.0375 | 9 | 0.800 | 0.1 | 0.178 |
| P9-2 | 7.95 | 0.51 | 13.82 | 11.25 | 0.0375 | 9 | 3.200 | 0.1 | 0.636 |
| P9-3 | 10.71 | 0.59 | 13.94 | 3.0 | 0.0375 | 9 | 0.478 | 0.1 | 0.358 |
| P9-4 | 9.98 | 0.52 | 13.84 | 3.0 | 0.0375 | 9 | 0.189 | 0.1 | 0.155 |
| P9-5 | 15.92 | 0.64 | 26.53 | 6.75 | 0.0375 | 9 | 0.873 | 0.1 | 0.193 |
| P9-6 | 12.36 | 0.78 | 13.99 | 6.75 | 0.0375 | 9 | 0.873 | 0.1 | 0.140 |
| Coal Seam | M9 | |
|---|---|---|
| Bulk density of coal | True density TRD (t/m3) | 1.55 |
| Apparent density TRD (t/m3) | 1.47 | |
| Average of the firmness coefficient (f) | 1.71 | |
| Type of damage | Class II (fractured coal) | |
| Initial velocity of gas diffusion Δp (mmHg) | 21 | |
| Adsorption constants | A (m3/t.r) | 35.619 |
| B (MPa−1) | 1.493 | |
| Industrial analysis | Ad (%) | 11.27 |
| Mab (%) | 3.27 | |
| Vdaf (%) | 7.54 | |
| Porosity (%) | 5.16 | |
| Total | Minimum | Maximum | Average | Standard Deviation | Bias Angle | Kurtosis | 1/4 Digits | 3/4 Digits | Median | |
|---|---|---|---|---|---|---|---|---|---|---|
| Unconverted | 9 | 9.2 | 16.43 | 11.56 | 2.47 | 0.95 | 2.62 | 9.74 | 13.04 | 10.83 |
| Log converts | 9 | 2.22 | 2.80 | 2.43 | 0.2 | 0.75 | 2.27 | 2.28 | 2.57 | 2.38 |
| 9 | 0.49 | 0.5 | 0.5 | 0.001 | 0.37 | 1.81 | 0.49 | 0.50 | 0.50 | |
| 9 | 0.89 | 0.94 | 0.91 | 0.017 | 0.56 | 1.99 | 0.90 | 0.92 | 0.91 | |
| 9 | 8.2 | 15.43 | 10.56 | 2.47 | 0.95 | 2.62 | 8.74 | 12.04 | 9.83 | |
| 9 | 41.82 | 134.47 | 69 | 31.40 | 1.14 | 3.04 | 46.96 | 84.80 | 58.14 | |
| 9 | 259.23 | 1478.1 | 581.6 | 409.9 | 1.33 | 3.51 | 308.1 | 746.7 | 423.1 |
| Model | Number of Steps | Maximum Step Size | Range Value | Nugget | Arch Rise |
|---|---|---|---|---|---|
| Stable form | 12 | 303 | 3318.7 | Nil | 17.87 |
| Spherical model | 12 | 303 | 3635.6 | 0 | 17.28 |
| Exponential model | 12 | 303 | 3635.6 | 0 | 11.94 |
| Gaussian model | 12 | 303 | 2411.8 | 0 | 22.34 |
| 12 | 303 | 3635.6 | 0.82 | 33.99 |
| Data Type | Global Trend | Theoretical Model | Range Value | Nugget | Arch Rise |
|---|---|---|---|---|---|
| Monotony | Not eliminated | Gaussian model | 3635.6 | 0.82 | 33.99 |
| Box–Cox transformation | Not eliminated | Gaussian model | 3635.6 | 59.85 | 5885 |
| Numbering | X | Y | Gas Content (m3/t) |
|---|---|---|---|
| 0 | 17,676.14 | 29,518.6 | - |
| 1 | 17,619.091 | 29,430.268 | 9.51 |
| 2 | 17,808.538 | 29,481.565 | 10.83 |
| 3 | 17,591.725 | 29,590.763 | 11.28 |
| 4 | 17,380.450 | 29,681.762 | 9.2 |
| 5 | 18,098.941 | 29,408.767 | 12.58 |
| Measured Value | Predicted Value | Differentials | Standard Error | Standardized Error | Standard Value | Prediction Ratios (%) |
|---|---|---|---|---|---|---|
| 9.2 | 11.53 | 2.33 | 0.78 | 2.97 | 1.59 | 79.83 |
| 12.58 | 11.38 | −1.20 | 1.17 | −1.02 | −0.28 | 90.45 |
| 11.28 | 10.24 | −1.04 | 0.96 | −1.08 | −0.59 | 90.81 |
| 10.83 | 9.83 | −1.00 | 0.90 | −1.12 | −0.97 | 90.74 |
| 9.82 | 10.25 | 0.43 | 0.93 | 0.46 | 0.28 | 95.84 |
| 9.96 | 11.46 | 1.50 | 1.01 | 1.49 | 0.97 | 86.94 |
| 14.41 | 12.73 | −1.68 | 0.87 | −1.93 | −1.59 | 88.35 |
| 9.51 | 9.26 | −0.25 | 1.26 | −0.20 | 0.00 | 97.32 |
| 16.43 | 17.54 | 1.11 | 1.40 | 0.79 | 0.59 | 93.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wei, Y.; Luo, W.; Zhao, X.; Li, H.; Duan, Z. Spatial Risk Prediction of Coal Seam Gas Using Kriging Under Complex Geological Conditions. Processes 2025, 13, 2110. https://doi.org/10.3390/pr13072110
Li Q, Wei Y, Luo W, Zhao X, Li H, Duan Z. Spatial Risk Prediction of Coal Seam Gas Using Kriging Under Complex Geological Conditions. Processes. 2025; 13(7):2110. https://doi.org/10.3390/pr13072110
Chicago/Turabian StyleLi, Qingsong, Yanjun Wei, Weidong Luo, Xun Zhao, Hongsheng Li, and Zhengpeng Duan. 2025. "Spatial Risk Prediction of Coal Seam Gas Using Kriging Under Complex Geological Conditions" Processes 13, no. 7: 2110. https://doi.org/10.3390/pr13072110
APA StyleLi, Q., Wei, Y., Luo, W., Zhao, X., Li, H., & Duan, Z. (2025). Spatial Risk Prediction of Coal Seam Gas Using Kriging Under Complex Geological Conditions. Processes, 13(7), 2110. https://doi.org/10.3390/pr13072110






