The Flow Field Characteristics and Separation Performance of the Compact Series Gas–Liquid Separator
Abstract
1. Introduction
2. Structure and Working Principle
3. Methods
3.1. Numerical Methods
3.1.1. Numerical Models
- Continuity equation:
- The momentum equation is as follows:
3.1.2. Turbulence Models
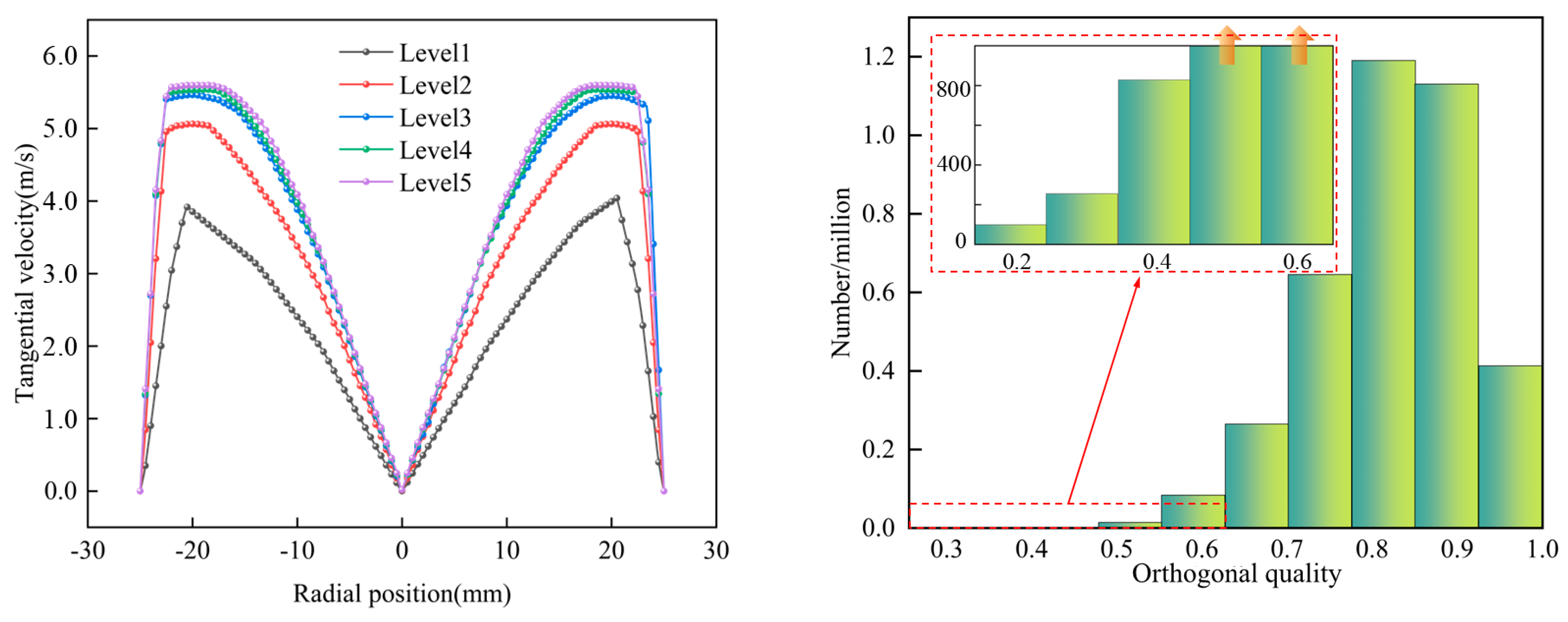
3.2. Grid Generation and Grid Independence Verification
3.3. Boundary Conditions and Performance Indicators
3.4. Laboratory Experimental and Numerical Simulation Reliability Verification
3.4.1. Laboratory Experimental
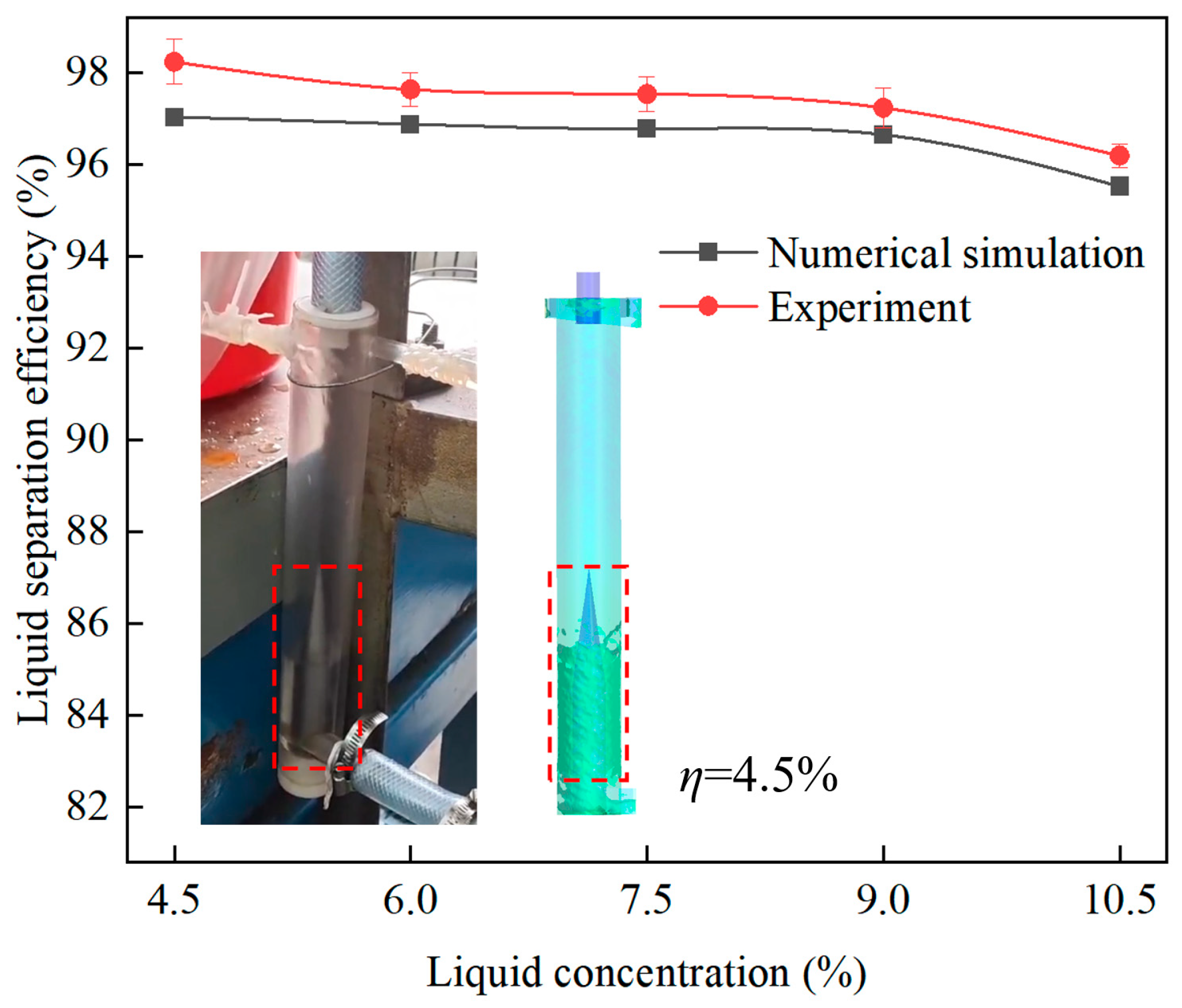
3.4.2. Numerical Simulation Reliability Verification
4. Results
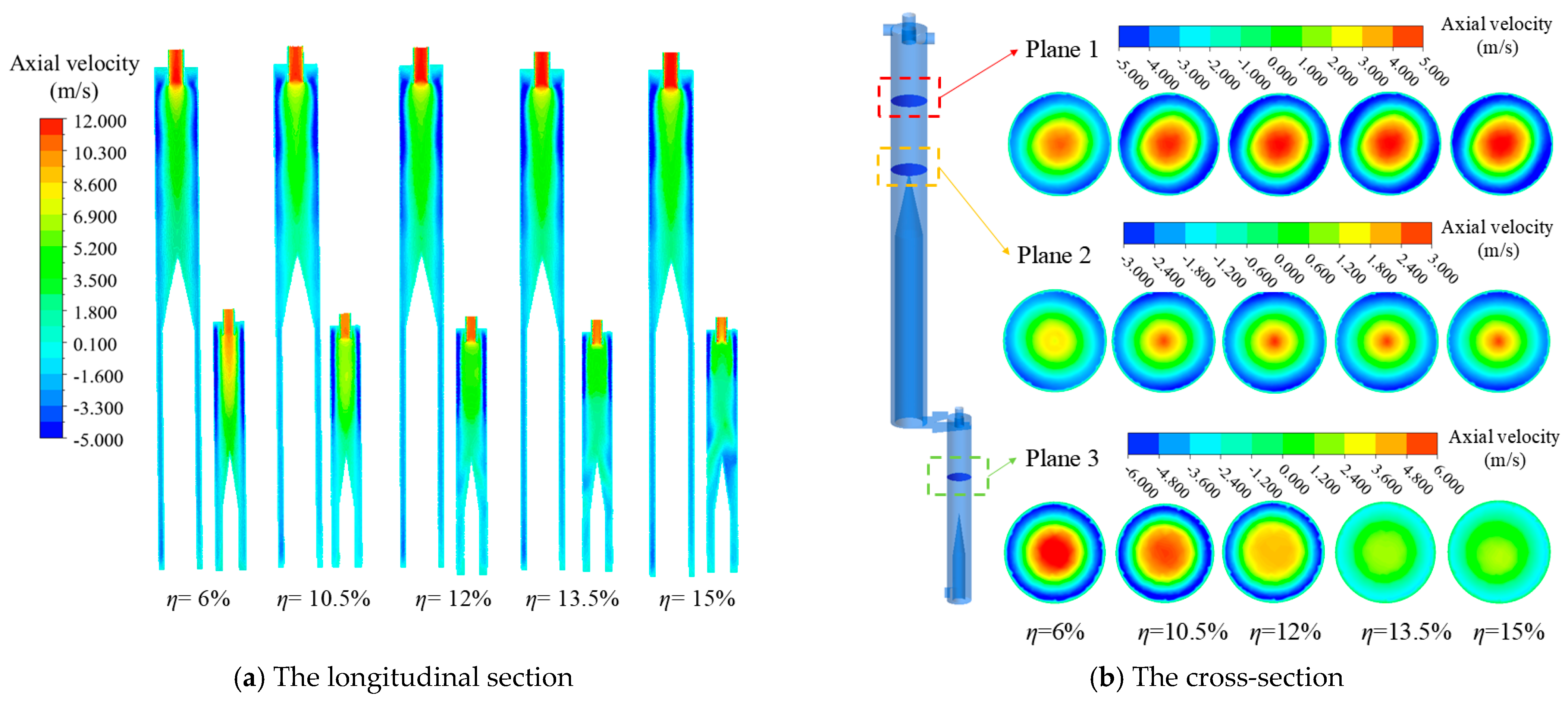
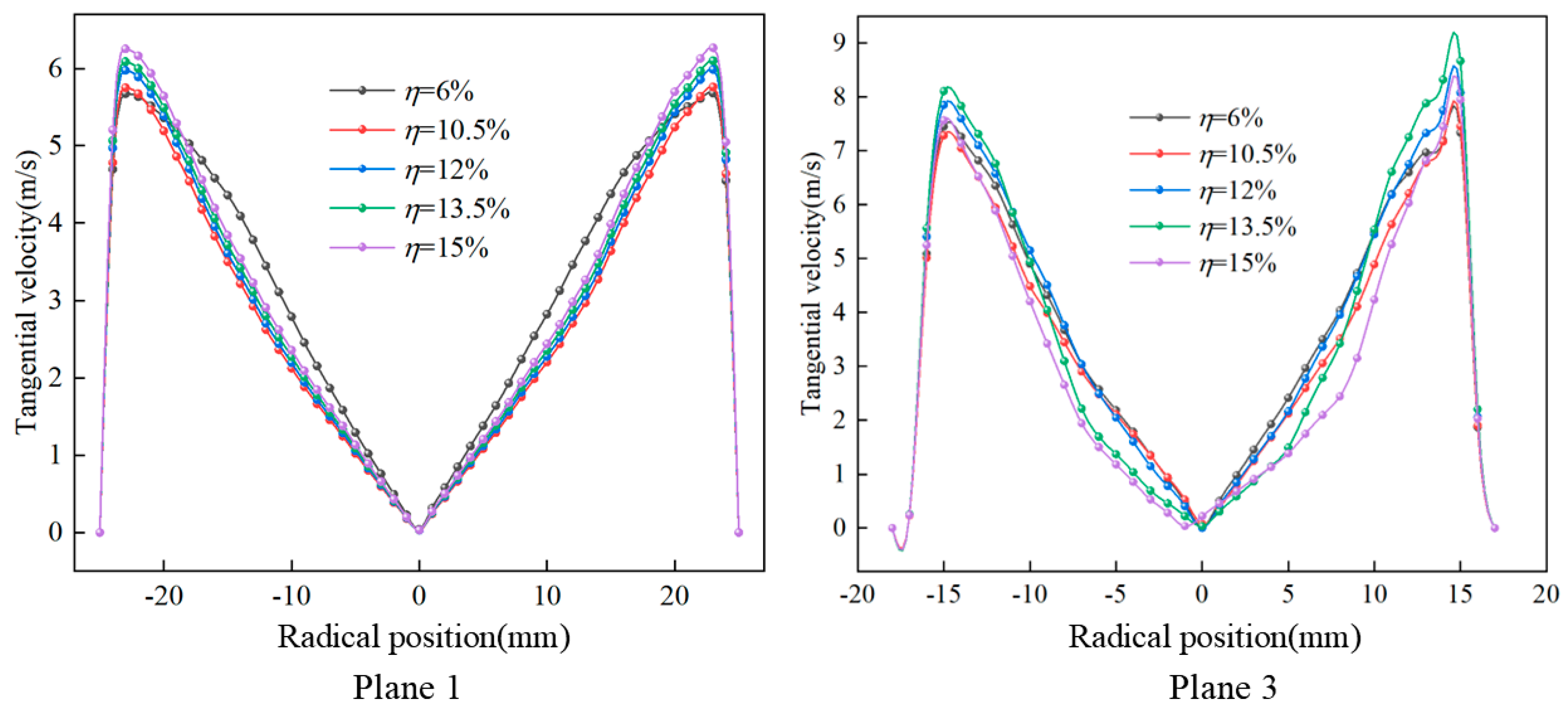
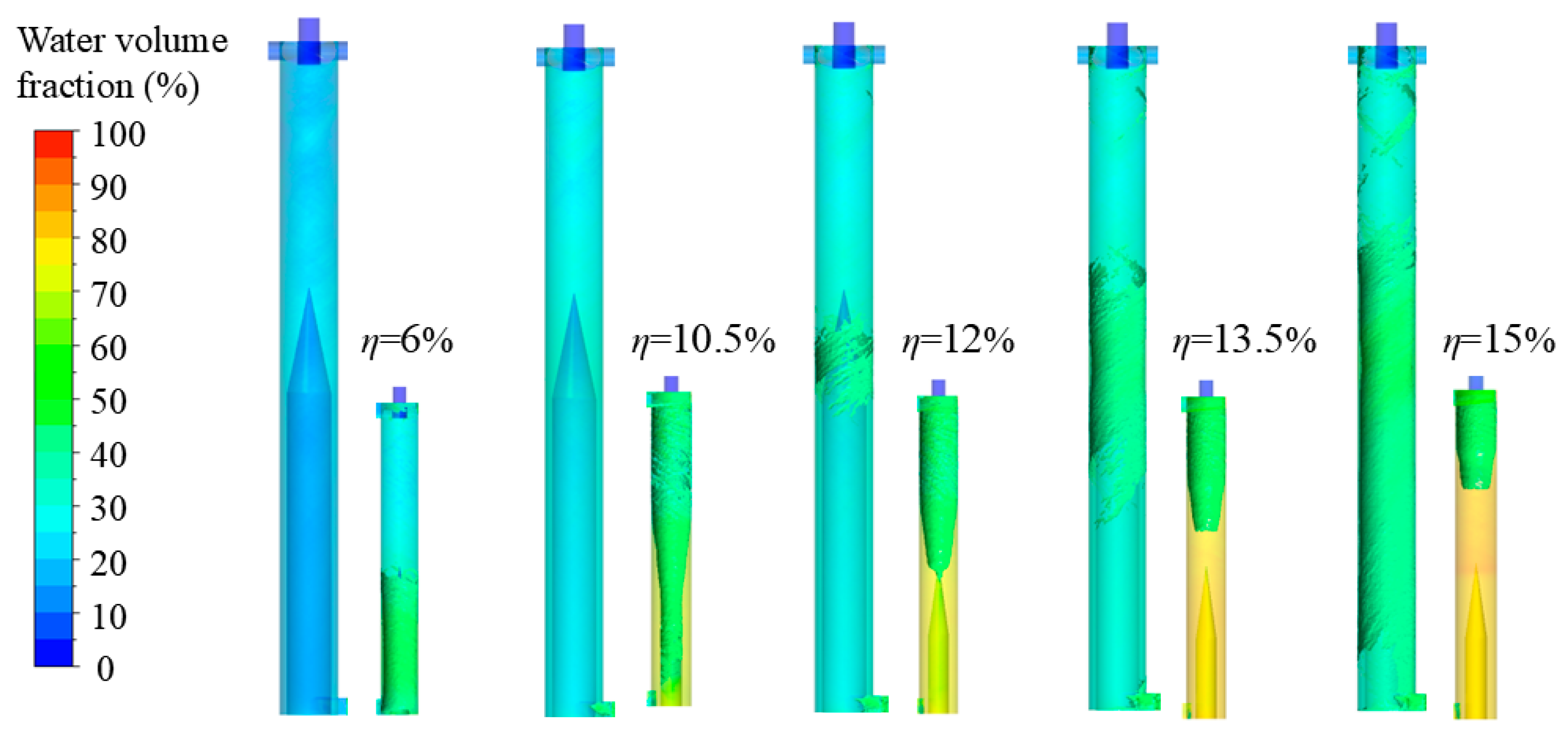
4.1. Effect of Liquid Concentration on Flow Field Characteristics
4.1.1. Velocity Field Analysis at Different Liquid Concentrations
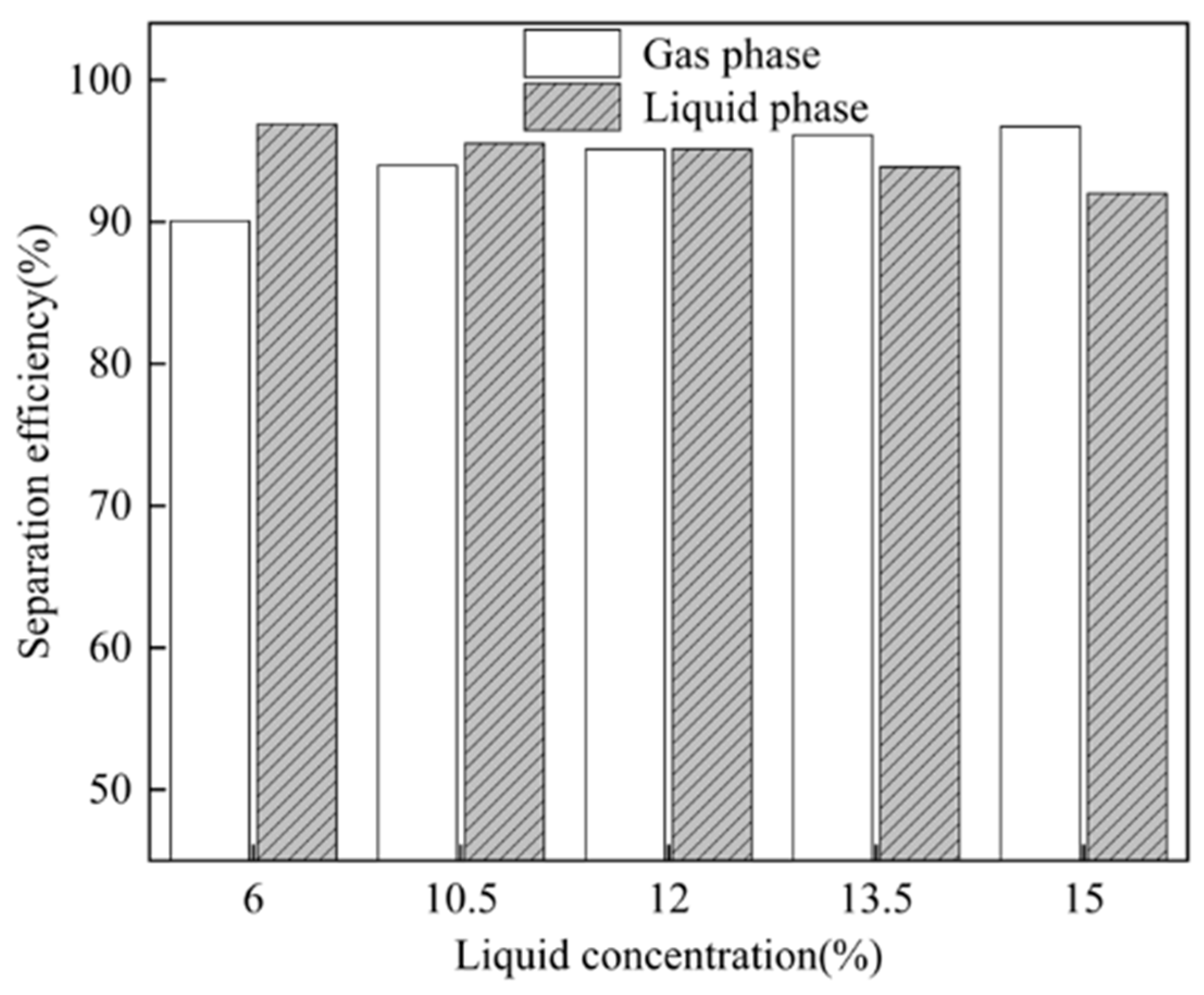
4.1.2. Separation Performance Analysis Under Different Liquid Concentrations
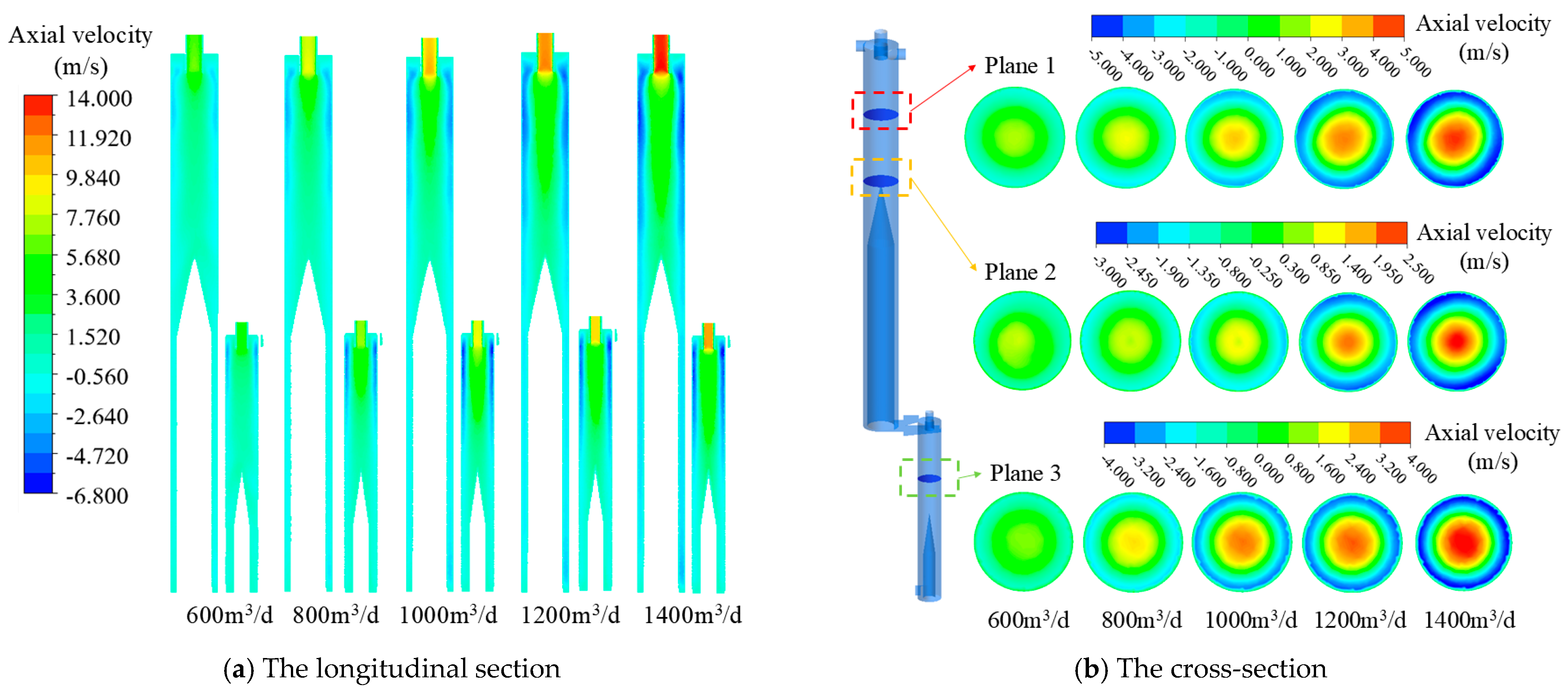
4.2. Effect of Inlet Flow Rate on Flow Field Characteristics
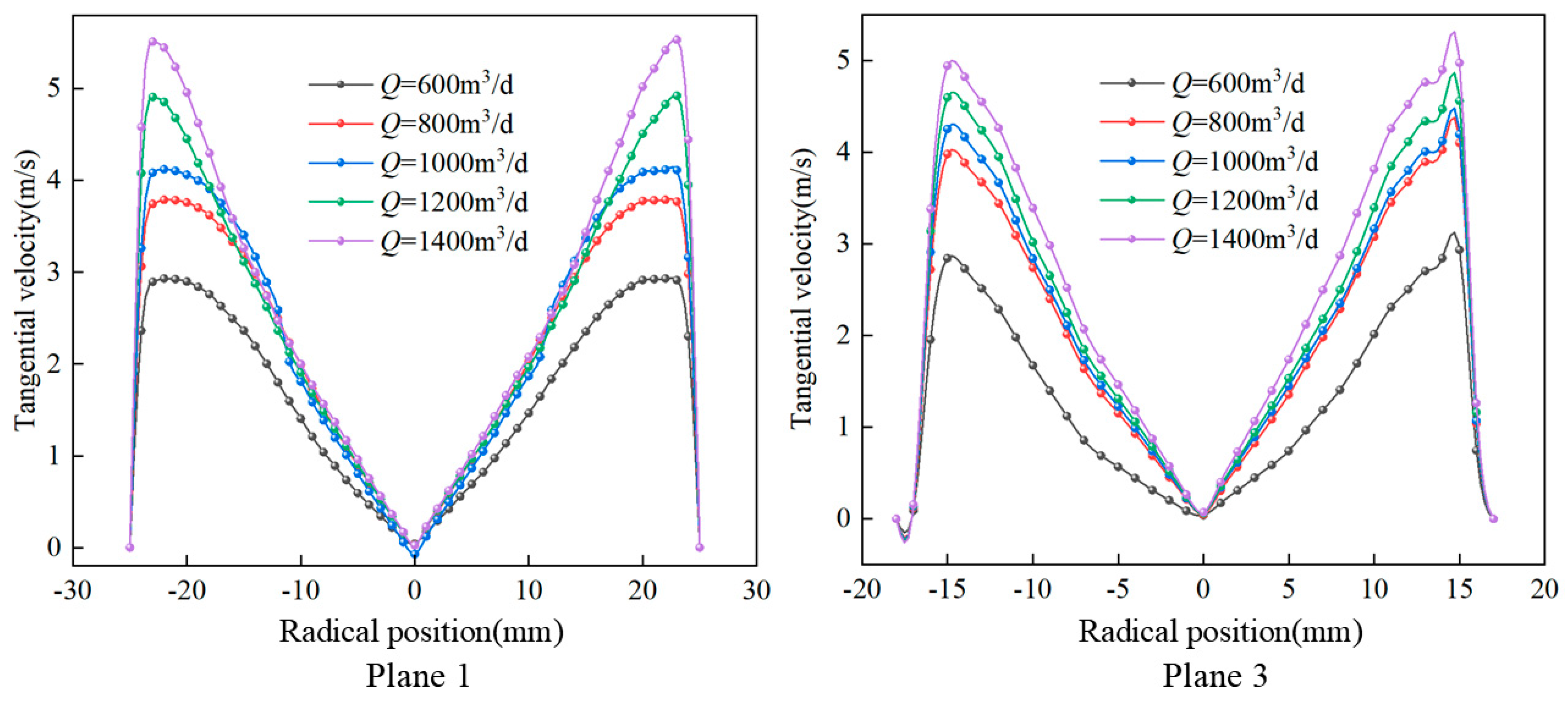
4.2.1. Velocity Field Analysis at Different Inlet Flow Rates
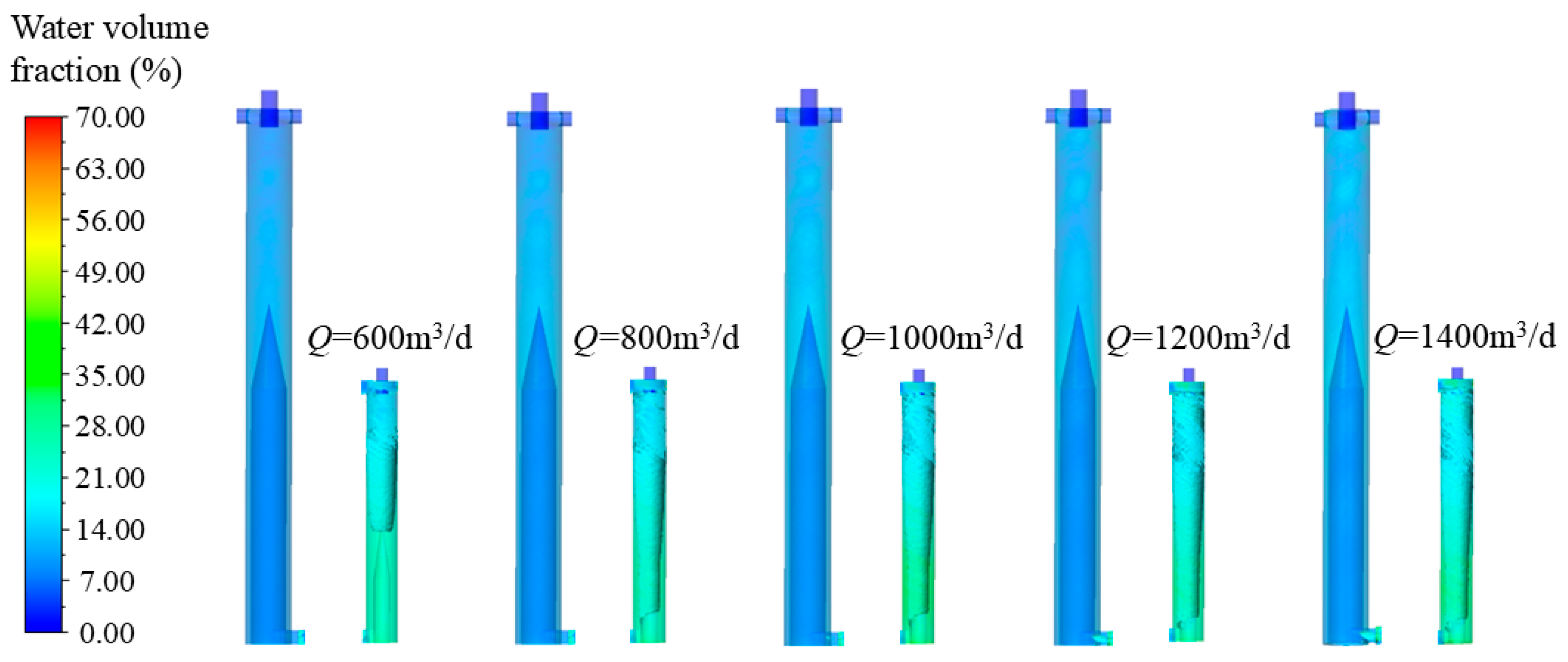
4.2.2. Separation Performance Analysis Under Different Inlet Flow Rates
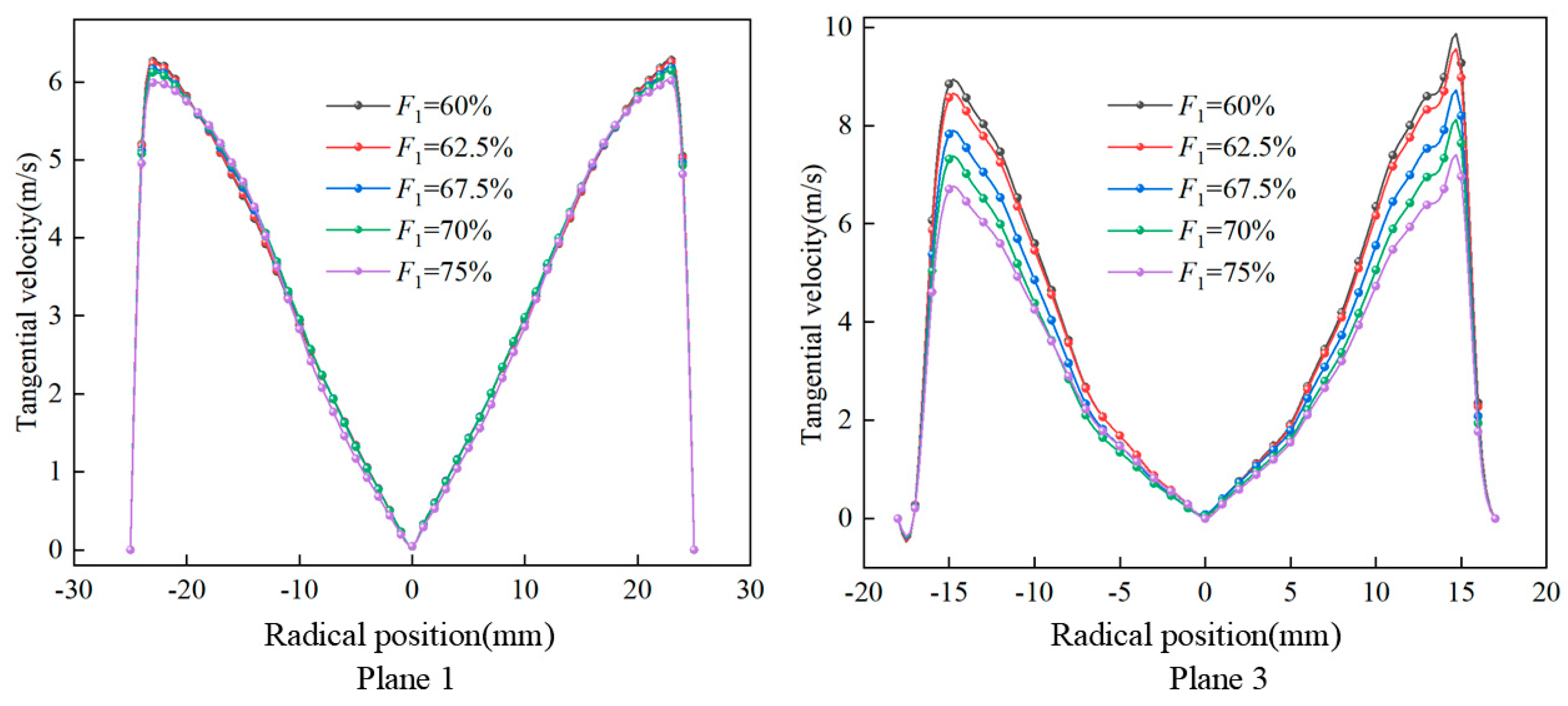
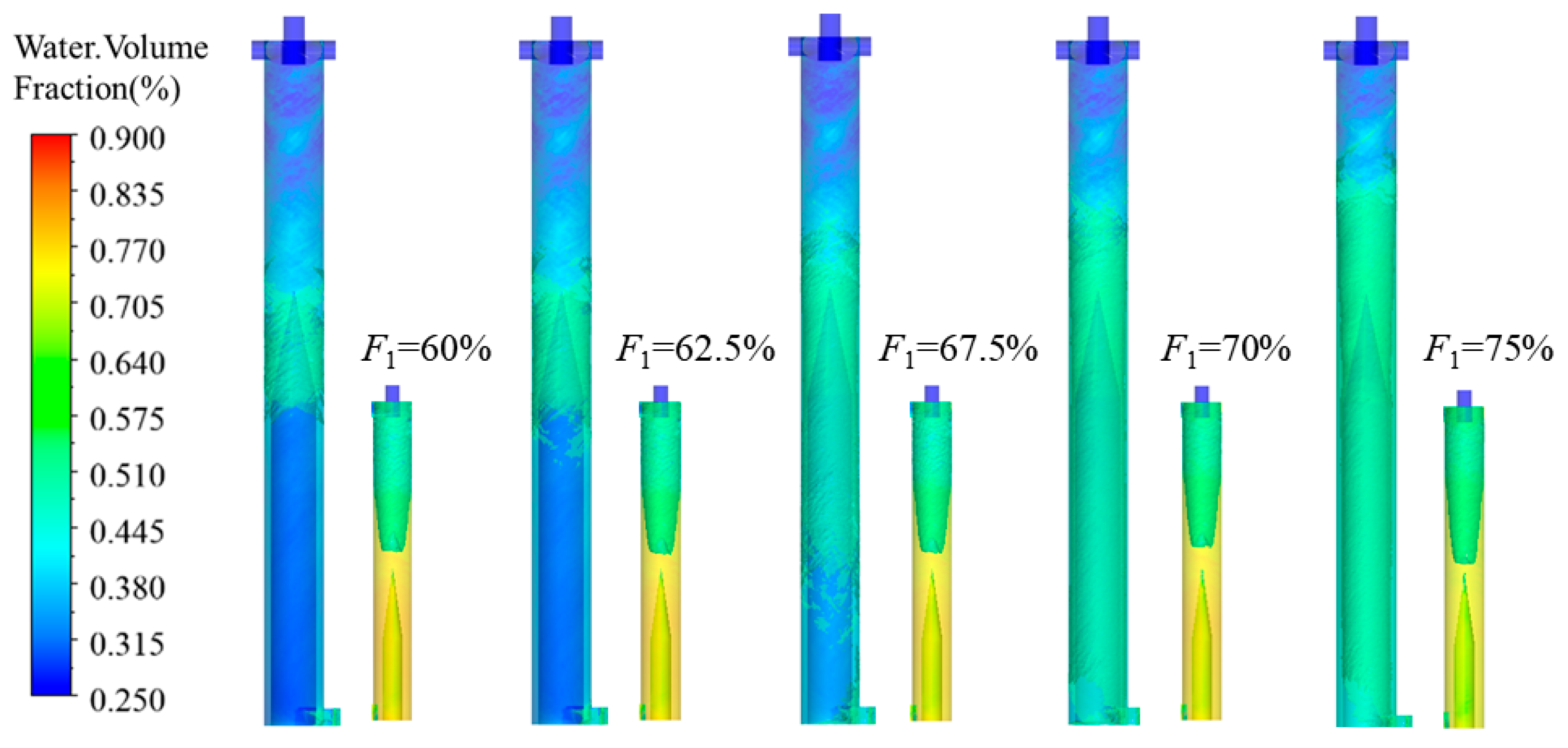
4.3. Effect of Split Ratio on Flow Field Characteristics
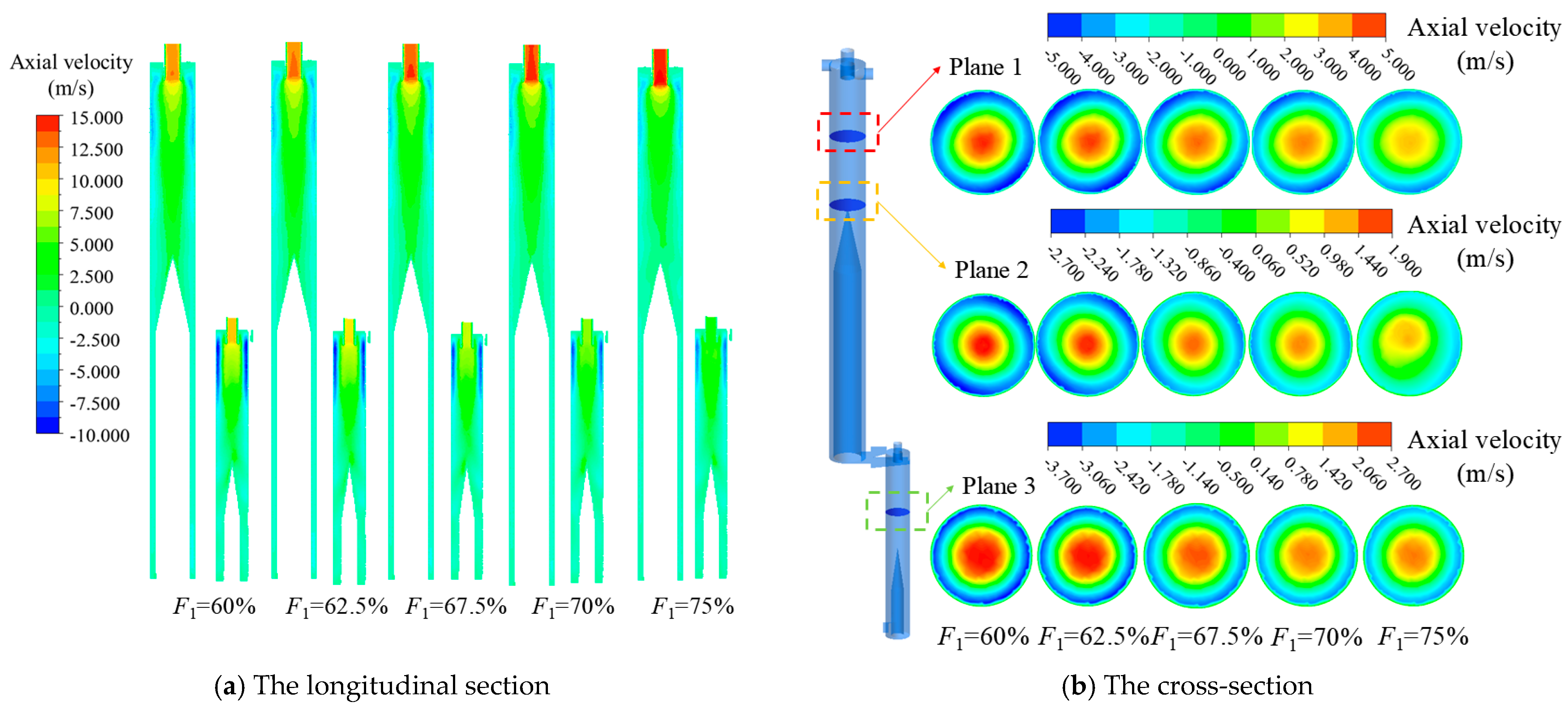
4.3.1. Velocity Field Analysis at Different Primary Overflow Split Ratios
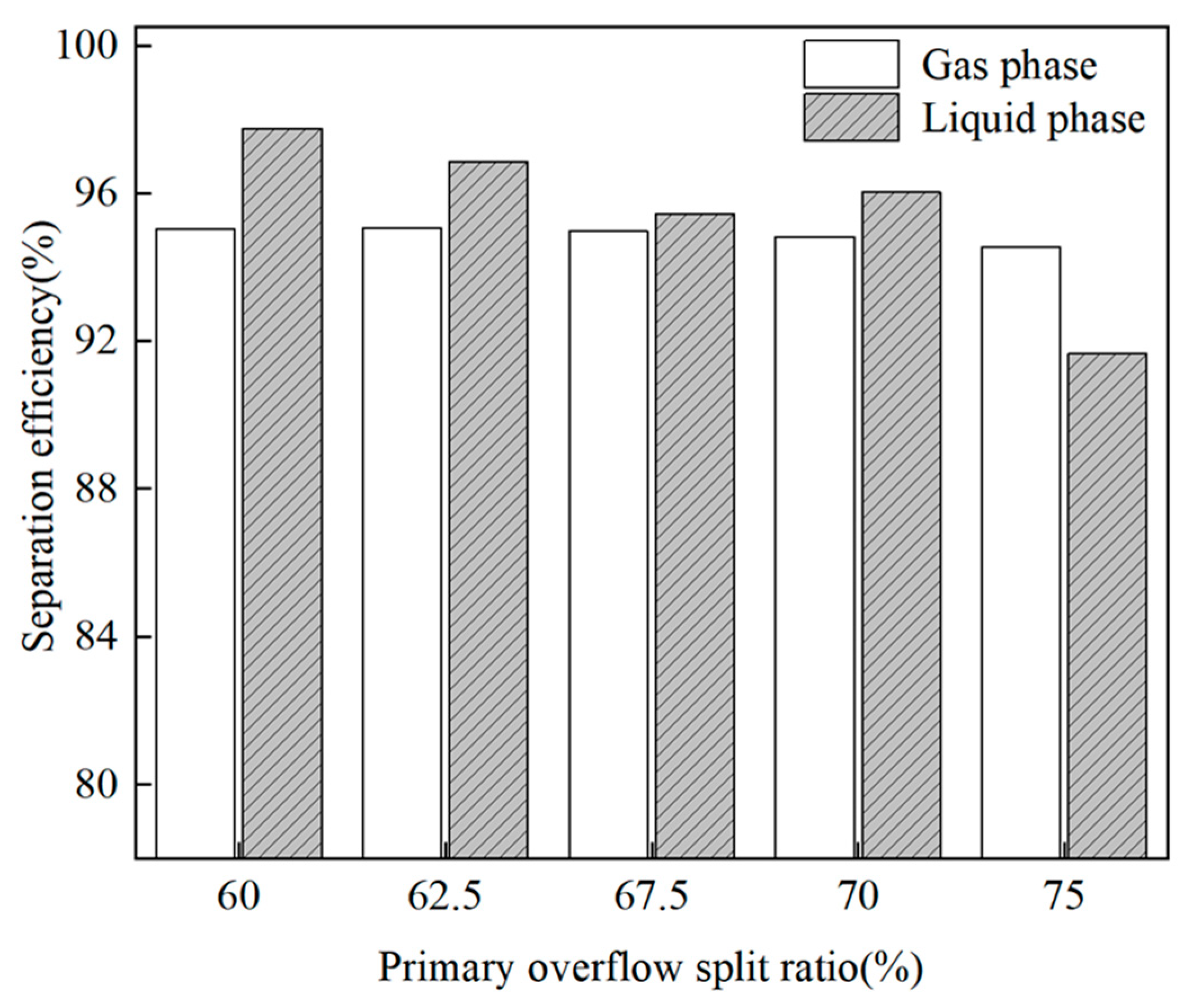
4.3.2. Separation Performance Analysis Under Different Primary Overflow Split Ratios
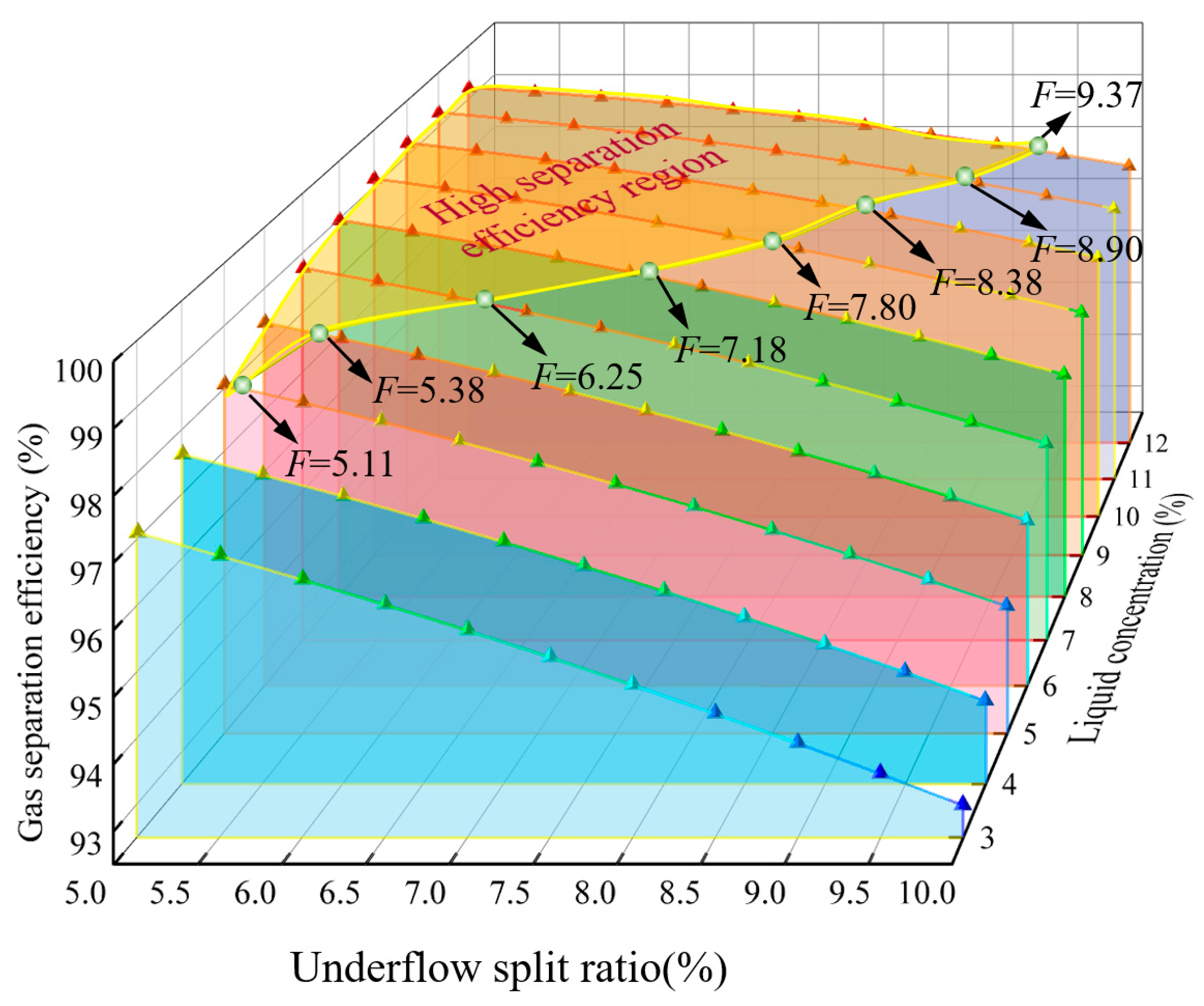
4.4. Operating Parameter Optimization Based on Response Surface Method
4.4.1. Optimization Design Based on Box–Behnken Response Surface Method
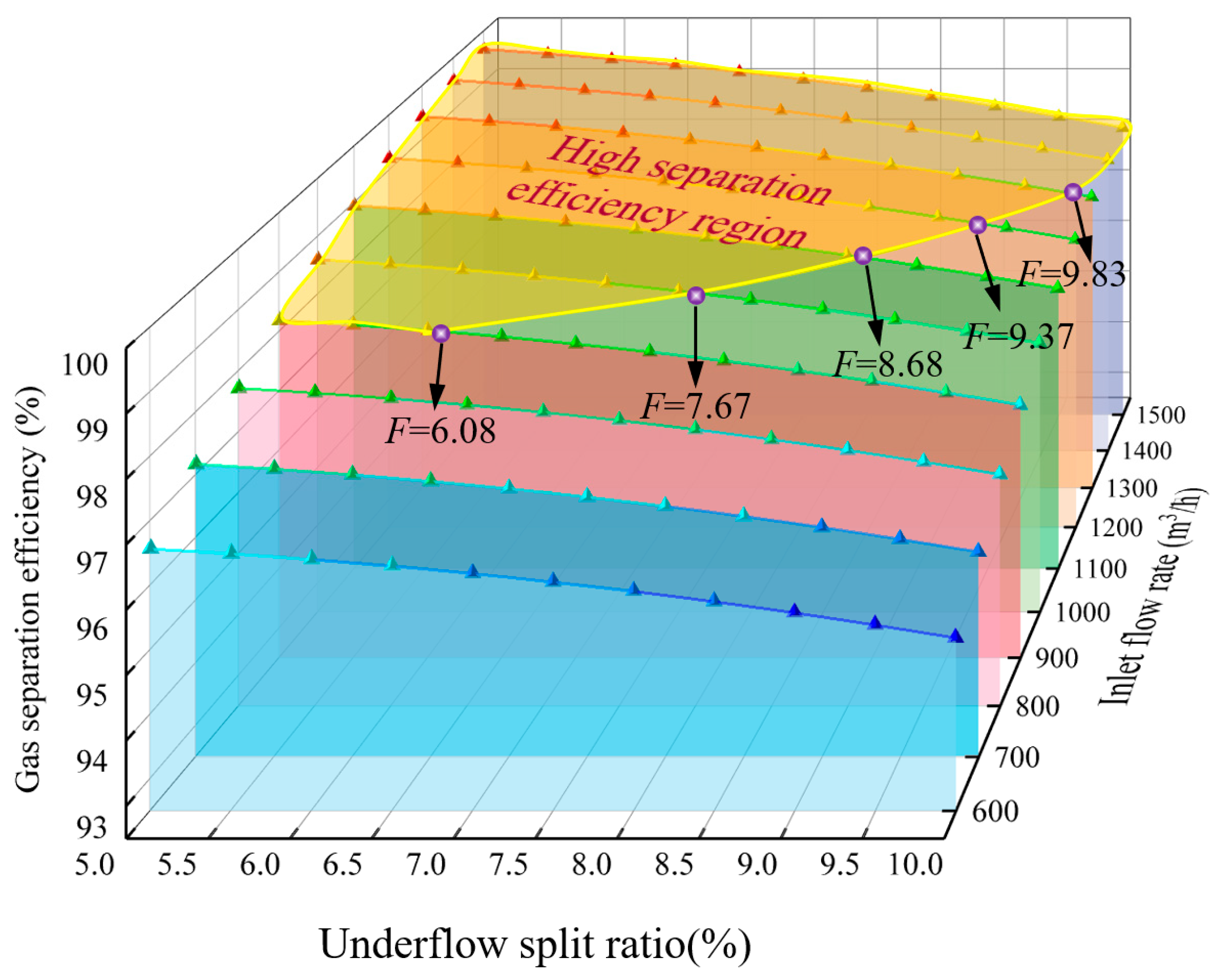
4.4.2. The Regulation Law Analysis of the Underflow Under Different Operating Parameters
5. Conclusions
- (1)
- Taking the axial velocity and liquid concentration as indicators for analyzing flow field characteristics, the flow field characteristics of the CTGLS were analyzed using the single-factor method under various operating parameters. The increase in liquid concentration has no significant impact on the axial velocity of the gas–liquid separator as a whole, with localized fluctuations only in the underflow region of the secondary separator. With the increase in the inlet flow rate and the primary overflow split ratio, the axial velocity at the overflow gradually increases, the velocity gradient gradually increases, and the morphology of the gas–liquid interface changes significantly with the increase in the liquid concentration and the inlet flow rate.
- (2)
- Using mass separation efficiency as the evaluation index for separation performance, the separation performance analysis of the CTGLS under different operating parameters was conducted. As the liquid concentration, inlet flow rate, and primary overflow split ratio increased, the liquid separation efficiency exhibited a consistently decreasing trend. Among them, the liquid separation efficiency shows the maximum decline of 16.41% within the liquid concentration range of 4.5% to 15%. The gas separation efficiency only shows a significant upward trend with the increase in the liquid concentration, peaking at 96.71% when the liquid concentration reaches 15%.
- (3)
- Using the response surface methodology, a quadratic polynomial regression model was obtained to describe the relationship between the liquid concentration of 3~12%, the inlet flow rate of 600~1500 m3/d, the underflow split ratio of 5~15%, and the gas separation efficiency. Furthermore, the numerical simulation method was employed to construct an optimal split ratio regulatory scheme under different inlet flow rates and liquid concentration conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, S.H. Measurements in Oilfields. Meas. Control 2010, 43, 175. [Google Scholar] [CrossRef]
- Choi, H.O.; Park, H. “Oil is the New Data”: Energy Technology Innovation in Digital Oil Fields. Energies 2020, 13, 5547. [Google Scholar] [CrossRef]
- Soomro, A.A.; Mokhtar, A.A.; Kurnia, J.C.; Lashari, N.; Lu, H.; Sambo, C. Integrity assessment of corroded oil and gas pipelines using machine learning: A systematic review. Eng. Fail. Anal. 2022, 131, 105810. [Google Scholar] [CrossRef]
- Zhang, K.P.; Ku, H.C.; He, X.G.; Lu, H.L.; Zhang, M.; Guo, C.B. Measurement of gas and liquid flow rates in two-phase pipe flows with distributed acoustic sensing. Measurement 2025, 250, 117137. [Google Scholar] [CrossRef]
- Knobelspies, S.; Bierer, B.; Perez, A.O.; Wöllenstein, J.; Kneer, J.; Palzer, S. Low-cost gas sensing system for the reliable and precise measurement of methane, carbon dioxide and hydrogen sulfide in natural gas and biomethane. Sens. Actuators B Chem. 2016, 236, 885–892. [Google Scholar] [CrossRef]
- Stewart, M.; Arnold, K. Gas-Liquid and Liquid-Liquid Separators; Gulf Professional Publishing: Houston, TX, USA, 2008. [Google Scholar]
- Wang, J.Z.; Wang, Y.C.; Han, J.Z.; Xu, Q.; Xie, X.; Pan, Y.; Guo, L. Experimental investigation on separation characteristics of axial cyclone separator. Sci. China Technol. Sci. 2023, 66, 3231–3244. [Google Scholar] [CrossRef]
- Erdal, F.M.; Shirazi, S.A. Effect of the Inlet Geometry on the Flow in a Cylindrical Cyclone Separator. J. Energy Resour. Technol. 2006, 128, 62–69. [Google Scholar] [CrossRef]
- Rui, Y.; Lei, Z.; Chao, L.; Zhu, B. The structure design and the flow field analysis of the gas-liquid separation cyclone. IOP Conf. Ser. Earth Environ. Sci. 2021, 657, 012080. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Li, K.; Hao, S. Research on separation performance of gas-liquid cylindrical cyclone under the condition of high gas liquid ratio. Fluid Mach. 2018, 46, 32–35+19. [Google Scholar]
- Gupta, R.; Kaulaskar, M.D.; Kumar, V.; Sripriya, R.; Meikap, B.C.; Chakraborty, S. Studies on the understanding mechanism of air core and vortex formation in a hydrocyclone. Chem. Eng. J. 2008, 144, 153–166. [Google Scholar] [CrossRef]
- Meng, F.; Shi, S.; Ma, N. Study of the performance of a new kind of downhole gas-liquid separation with high gas content. J. Energy Nat. Resour. 2019, 8, 45. [Google Scholar] [CrossRef]
- Miao, C.; Xing, L.; Li, F.; Jiang, M.; Li, X. Significance analysis of structural parameters of the compact gas-liquid hydrocyclone. China Pet. Mach. 2023, 51, 86–93. [Google Scholar]
- Li, T.; Sun, Z.; Geng, K.; Sun, M.; Wang, Z. Numerical analysis of a novel cascading gas–liquid cyclone separator. Chem. Eng. Sci. 2023, 270, 118518. [Google Scholar] [CrossRef]
- Zheng, C.; Yang, W.; Meng, X.; Li, A.; Shen, Q.; Zhao, J.; Xuan, D. Design and performance evaluation of a novel downhole gas-liquid separator for offshore high gas bearing wells. China Offshore Oil Gas 2020, 32, 128–135. [Google Scholar]
- Wang, S.; Luis, G.E.; Ram, M.S.; Petroleum, O.S. Gas-liquid cylindrical cyclone (GLCC) compact separators for wet gas applications. J. Energy Resour. Technol. 2003, 125, 43–50. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Yang, Y.; Han, M.; Zhou, Y.; Ye, S.; Yan, C.; Yue, T. Experimental and numerical performance study of a downward dual-inlet gas-liquid cylindrical cyclone (GLCC). Chem. Eng. Sci. 2021, 238, 116595. [Google Scholar] [CrossRef]
- Fu, P.; Zhu, J.; Li, Q.; Cheng, T.; Zhang, F.; Huang, Y.; Ma, L.; Xiu, G.; Wang, H. DPM simulation of particle revolution and high-speed self-rotation in different pre-self-rotation cyclones. Powder Technol. 2021, 394, 290–299. [Google Scholar] [CrossRef]
- Lan, W.; Wang, H.; Li, Y.; Feng, K.; Zhang, X.; Liu, Y.; Zhu, X.; Chen, S. Numerical and experimental investigation on a downhole gas-liquid separator for natural gas hydrate exploitation. J. Pet. Sci. Eng. 2022, 208, 109743. [Google Scholar] [CrossRef]
- Chen, G.; Fan, J.; Zhang, P.; Wang, W. Experimental and CFD investigation on effects of internals on the flow pattern and performance of a divergent cyclone separator. J. Taiwan Inst. Chem. Eng. 2020, 115, 160–168. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhao, M.; Ge, T.; Wang, C. The numerical simulation of sediment scour based on a Eulerian model. J. Harbin Eng. Univ. 2019, 40, 47–53. [Google Scholar]
- Nguyen, X.; Ma, K.; Lai, H. Numerical study of internal flow field of a centrifugal pump impeller using different turbulence models. J. East China Univ. Sci. Technol. 2014, 40, 798–803. [Google Scholar]
- Zeng, X.; Xu, Y.; Zhao, L.; Fan, G.; Yan, C. Numerical investigation on axial liquid-liquid separators with different swirl chambers. Chem. Eng. Process. Process Intensif. 2021, 161, 108324. [Google Scholar] [CrossRef]
- Xing, L.; Guan, S.; Jiang, M.; Zhao, L.; Cai, M.; Liu, H.; Chen, D. Study on structure optimization and performance of downhole gas-liquid hydrocyclone under high gas-liquid ratio. CIESC J. 2024, 75, 900–913. [Google Scholar]
- Zhang, M.; Sun, H.; Wang, Q.; Chen, J.; Shang, C.; Li, X.; Wang, C.; Kong, L. Study of flow field characteristics and separation performance of inline cyclone gas-liquid separator. Chin. J. Process Eng. 2024, 24, 772–782. [Google Scholar]
- Fang, X.; Chen, J.; Liu, M.; Ji, Y. Numerical simulation research of bubble enhanced hydrocyclone. J. Petrochem. Univ. 2016, 29, 82–88. [Google Scholar]
- Zhao, Q. Study on Hydrocyclone Separation Process Based on the Characteristics of Axial Velocity Wave Zone. PhD Thesis, Northeast University, Boston, MA, USA, 2022. [Google Scholar]
- Zhou, Y.; Chen, J.; Wang, Y.; Zhang, D.; Ma, H.; Li, Z. Experimental and numerical study on the performance of a new dual-inlet gas–liquid cylindrical cyclone (GLCC) based on flow pattern conditioning. Chem. Eng. J. 2023, 453, 139778. [Google Scholar] [CrossRef]
- Zeng, X.; Zheng, C.; Li, A.; Fan, G.; Xiao, Y.; Yan, C. Numerical study on a new separator for downhole gas-liquid separation. Chem. Eng. Res. Des. 2025, 214, 317–326. [Google Scholar] [CrossRef]
- Chen, T.; Pan, Z.; Chen, Y.; Liu, M.; Chen, T.; Zhong, Y. Effect of hydrocyclone split ratio on carbon release performance of excess sludge. CIESC J. 2021, 72, 5761–5769. [Google Scholar]
- Kumar, V.; Jha, K. Multi-objective shape optimization of vortex finders in cyclone separators using response surface methodology and genetic algorithms. Sep. Purif. Technol. 2019, 215, 25–31. [Google Scholar] [CrossRef]
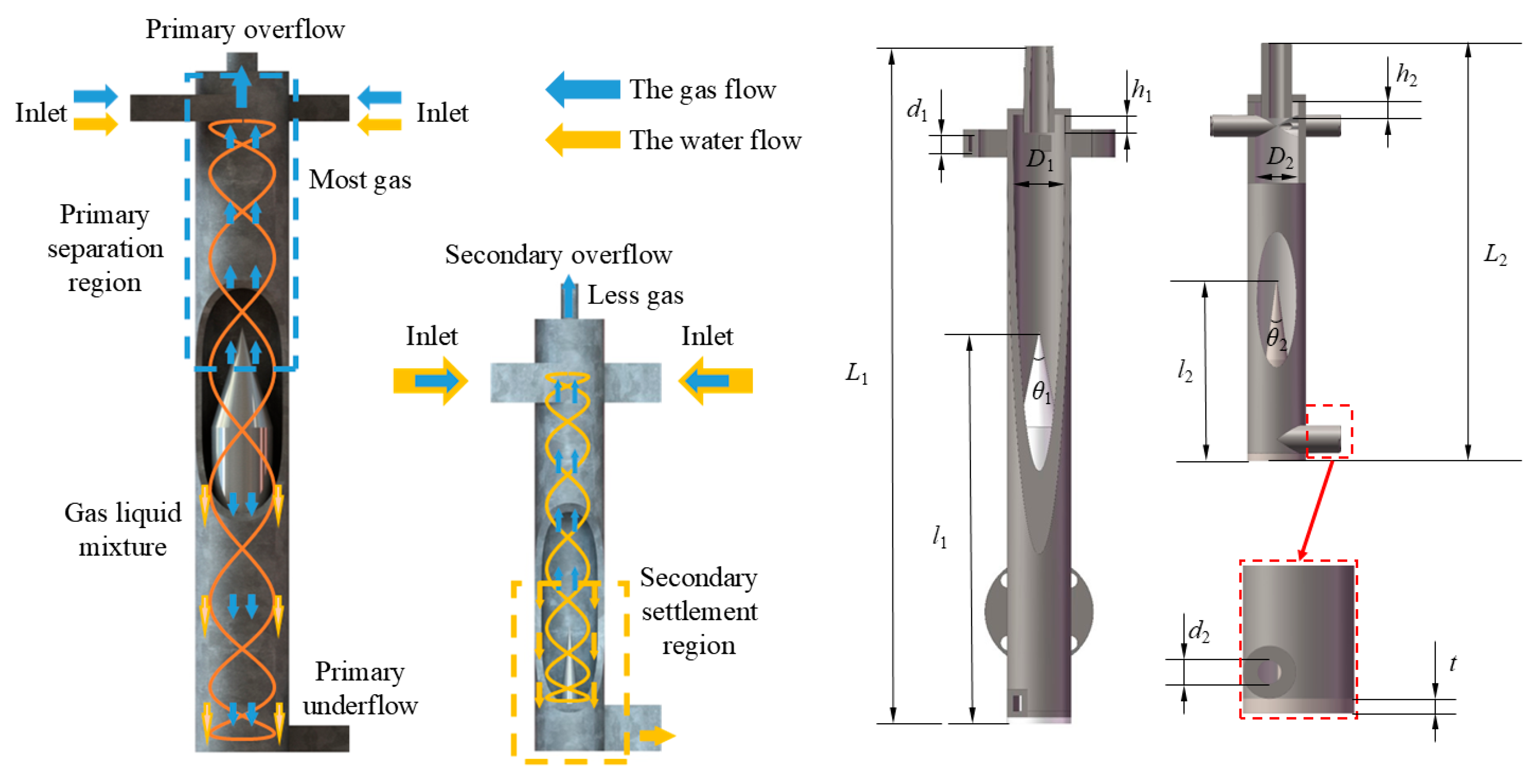
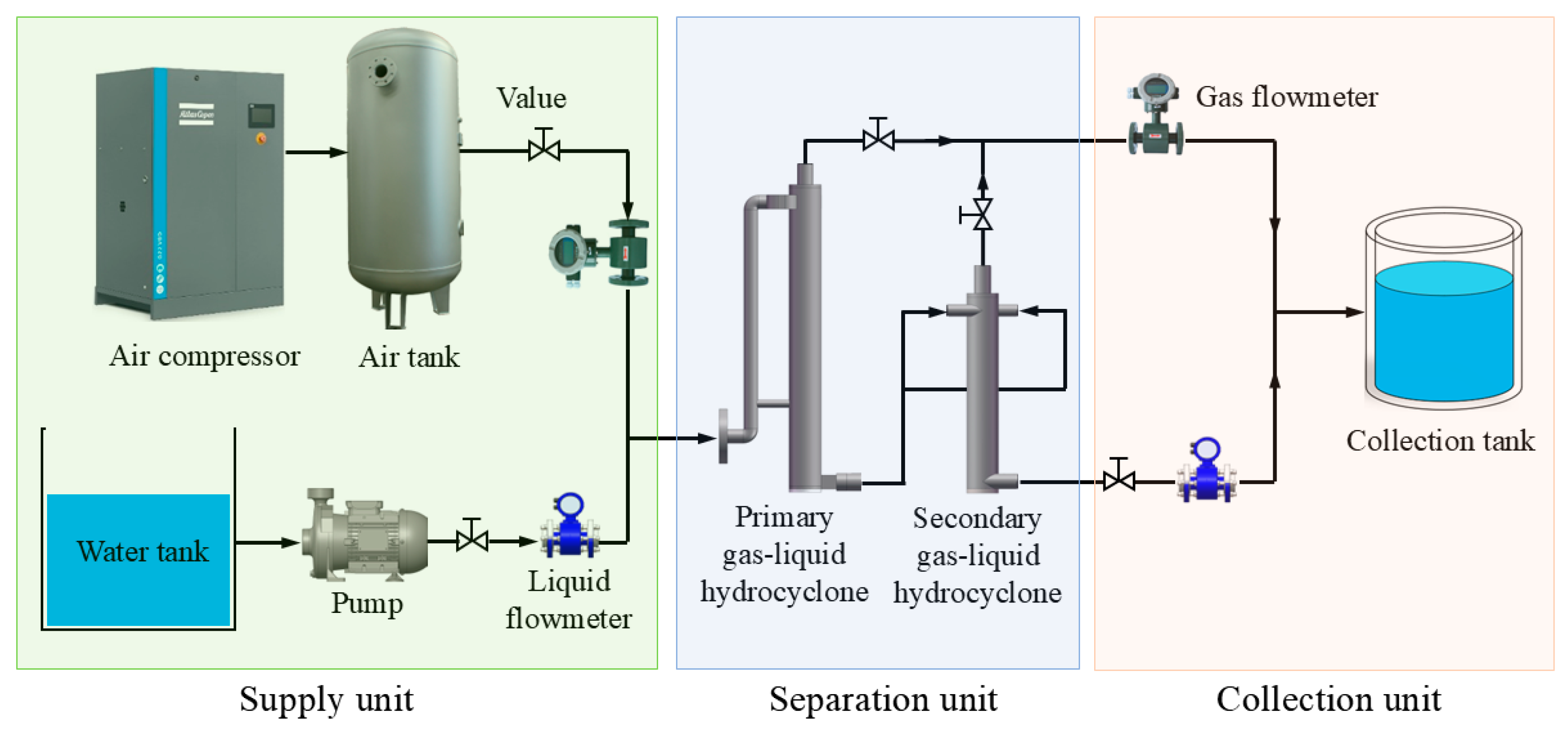

| Main Structure | Dimension |
|---|---|
| Diameter of the inlet pipe (d1) | 5 mm |
| Diameter of the outlet pipe (d2) | 9.6 mm |
| Length of primary cyclone (L1) | 640 mm |
| Length of secondary cyclone (L2) | 320 mm |
| Angle of primary reversed cone (θ1) | 12° |
| Angle of secondary reversed cone (θ2) | 6° |
| Insertion depth of primary overflow pipe (h1) | 15 mm |
| Primary body diameter (D1) | 60 mm |
| Length of primary reverse cone (l1) | 300 mm |
| Insertion depth of secondary overflow pipe (h2) | 12 mm |
| Secondary body diameter (D2) | 40 mm |
| Length of secondary reverse cone (l2) | 120 mm |
| Thickness of the base plate (t) | 12 mm |
| Factor | Level | ||
|---|---|---|---|
| Low (−1) | Central (0) | High (+1) | |
| Inlet flow rate x1/m3 | 600 | 1050 | 1500 |
| Split ratio of underflow x2/% | 5 | 10 | 15 |
| Liquid concentration x3/% | 3 | 7.5 | 12 |
| Number | Factors | y (%) | ||
|---|---|---|---|---|
| x1 | x2 | x3 | ||
| 1 | 1050 | 10 | 7.5 | 95.65 |
| 2 | 1050 | 10 | 7.5 | 95.65 |
| 3 | 1050 | 5 | 3 | 96.90 |
| 4 | 600 | 10 | 3 | 92.01 |
| 5 | 1050 | 15 | 3 | 87.48 |
| 6 | 600 | 15 | 7.5 | 90.15 |
| 7 | 1050 | 10 | 7.5 | 95.65 |
| 8 | 1050 | 10 | 7.5 | 95.65 |
| 9 | 1050 | 10 | 7.5 | 95.65 |
| 10 | 600 | 5 | 7.5 | 97.20 |
| 11 | 1500 | 10 | 12 | 98.12 |
| 12 | 600 | 10 | 12 | 95.04 |
| 13 | 1500 | 5 | 7.5 | 98.92 |
| 14 | 1500 | 15 | 7.5 | 91.57 |
| 15 | 1050 | 15 | 12 | 94.58 |
| 16 | 1500 | 10 | 3 | 92.68 |
| 17 | 1050 | 5 | 12 | 98.87 |
| Source | Sum of Squares | Mean Squares | F Value | p-Value |
|---|---|---|---|---|
| model | 156.85 | 17.43 | 127.07 | <0.0001 |
| x1 | 5.93 | 5.93 | 43.27 | 0.0003 |
| x2 | 97.72 | 97.72 | 712.52 | <0.0001 |
| x3 | 37.80 | 37.80 | 275.63 | <0.0001 |
| x1x2 | 0.0225 | 0.0225 | 0.1641 | 0.6975 |
| x1x3 | 1.45 | 1.45 | 10.59 | 0.0140 |
| x2x3 | 6.97 | 6.97 | 50.82 | 0.0002 |
| x12 | 1.91 | 1.91 | 13.94 | 0.0073 |
| x22 | 2.16 | 2.16 | 15.75 | 0.0054 |
| x32 | 2.15 | 2.15 | 15.64 | 0.0055 |
| Residual | 0.9600 | 0.1371 | - | - |
| Lack of fit | 0.1600 | 0.0533 | 0.2667 | 0.8469 |
| Cor Total | 157.81 | - | - | - |
| Std. Dev. | 0.3703 | R-Squared | 0.9939 |
| Mean | 94.86 | Adj. R-Squared | 0.9861 |
| C.V. % | 0.3904 | Pred. R-Squared | 0.9759 |
| - | - | Adep. Precision | 40.3475 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Liu, Y.; Xing, L.; Wang, J.; Gao, S. The Flow Field Characteristics and Separation Performance of the Compact Series Gas–Liquid Separator. Processes 2025, 13, 2063. https://doi.org/10.3390/pr13072063
Zhang R, Liu Y, Xing L, Wang J, Gao S. The Flow Field Characteristics and Separation Performance of the Compact Series Gas–Liquid Separator. Processes. 2025; 13(7):2063. https://doi.org/10.3390/pr13072063
Chicago/Turabian StyleZhang, Ruijie, Yueyao Liu, Lei Xing, Jingfu Wang, and Sheng Gao. 2025. "The Flow Field Characteristics and Separation Performance of the Compact Series Gas–Liquid Separator" Processes 13, no. 7: 2063. https://doi.org/10.3390/pr13072063
APA StyleZhang, R., Liu, Y., Xing, L., Wang, J., & Gao, S. (2025). The Flow Field Characteristics and Separation Performance of the Compact Series Gas–Liquid Separator. Processes, 13(7), 2063. https://doi.org/10.3390/pr13072063





