Data-Driven Fault Detection for HVAC Control Systems in Pharmaceutical Manufacturing Workshops
Abstract
1. Introduction and Literature Review
1.1. Introduction
1.2. Literature Review
2. Materials and Methods
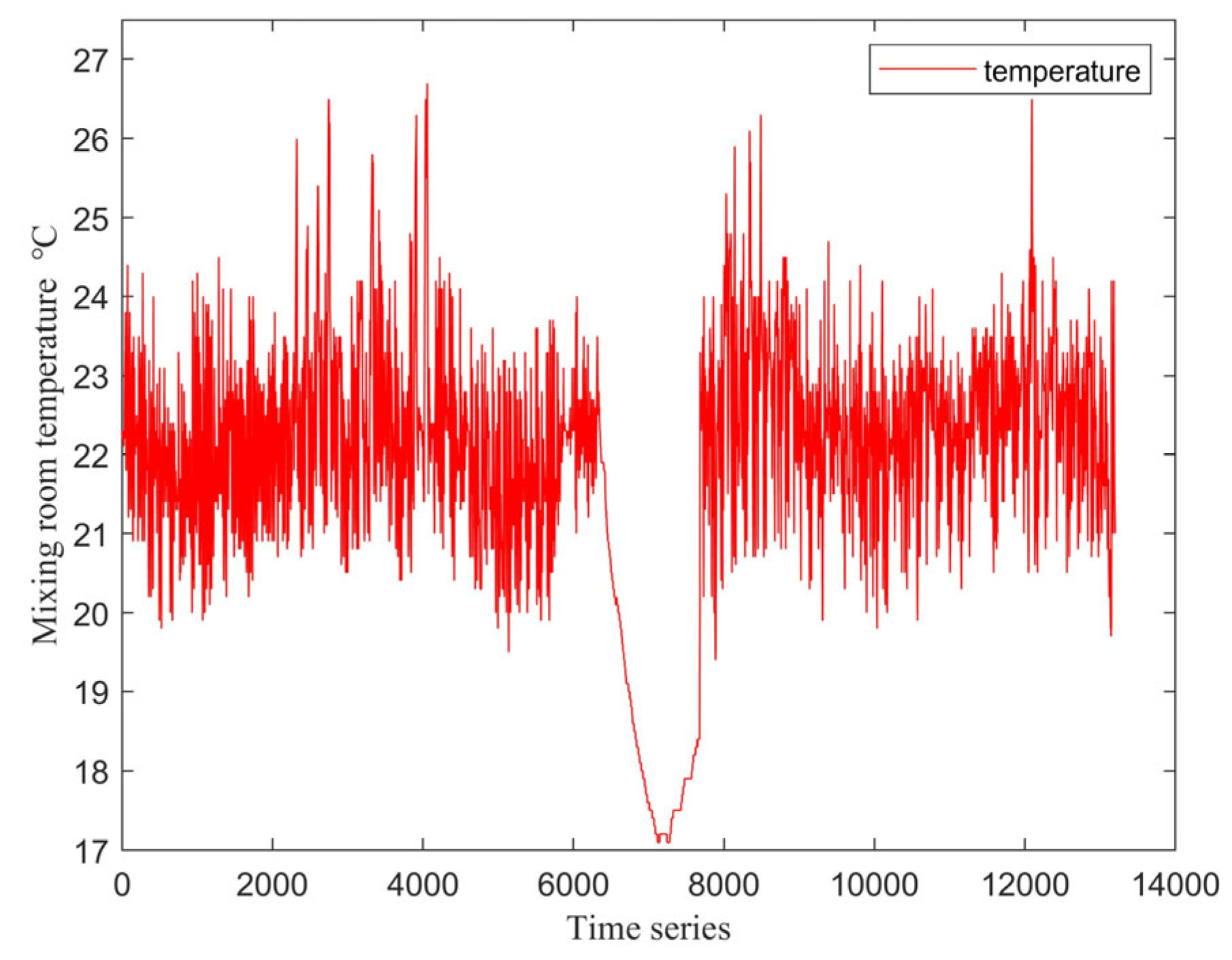
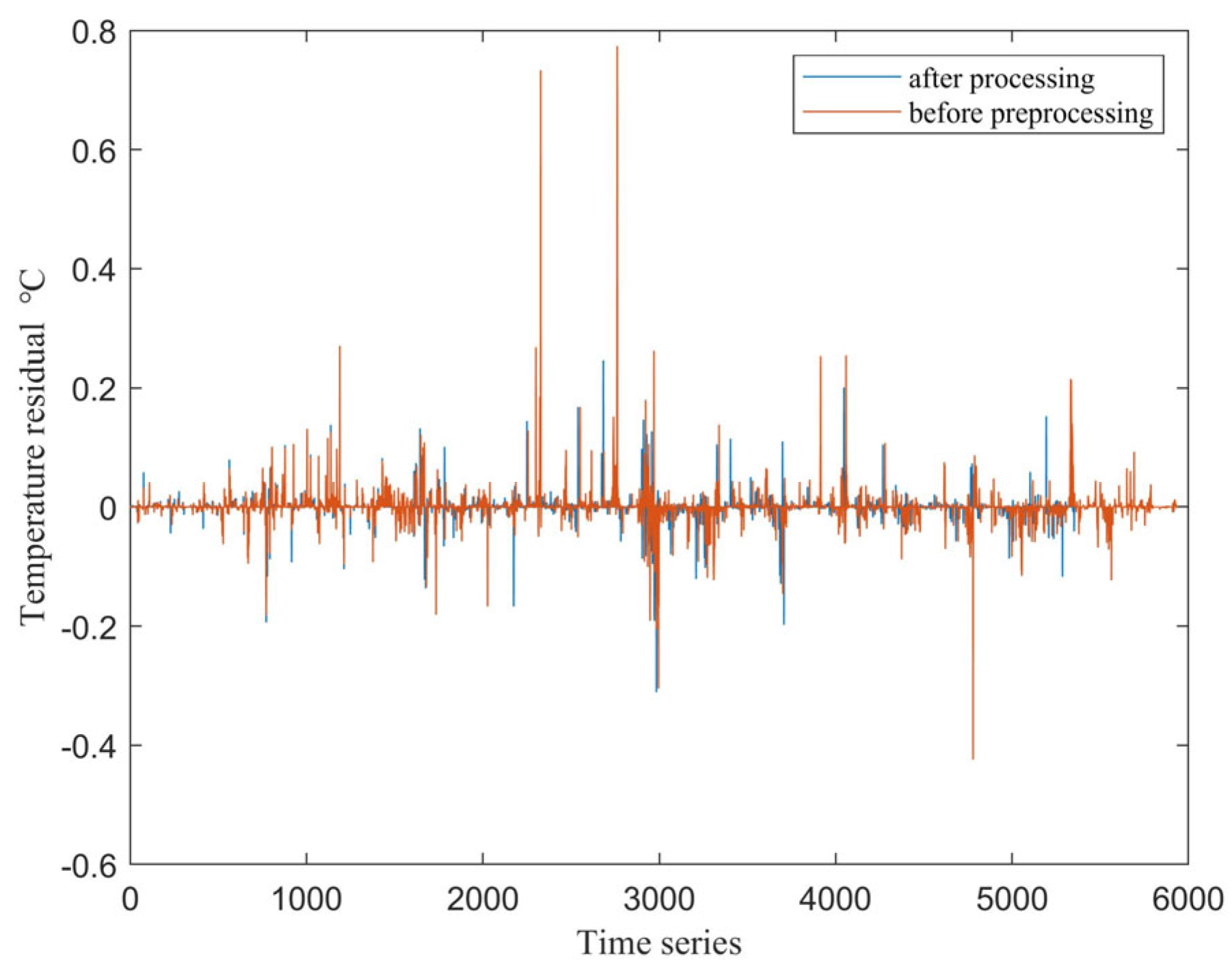
2.1. Data Preprocessing
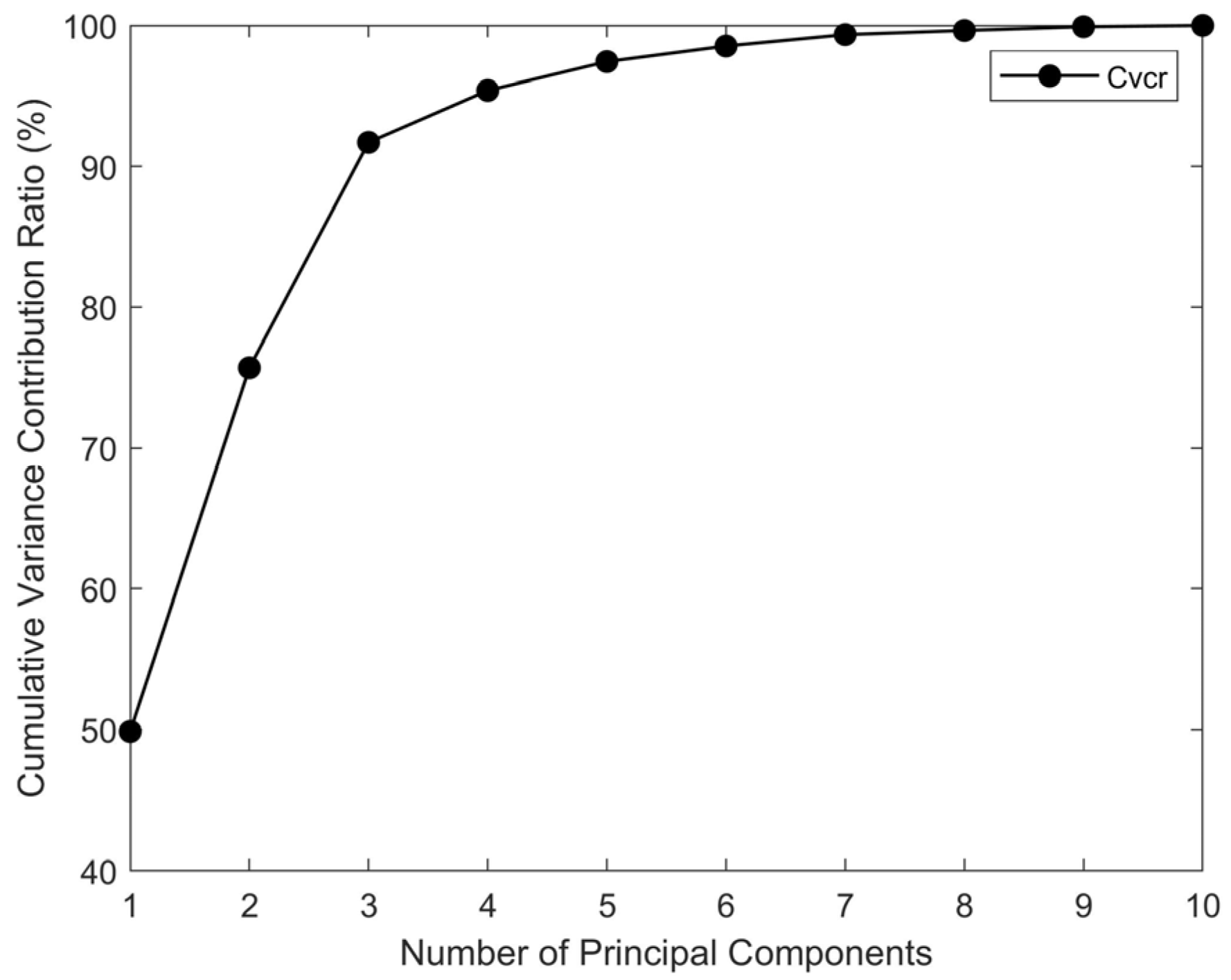
2.2. Feature Selection and Principal Component Analysis
- Data preprocessing. Prepare the raw data for analysis, typically involving normalization or standardization.
- Calculation of correlation coefficients. Compute the pairwise correlation coefficients among all variables to obtain the correlation coefficient matrix .
- Eigenvalue and eigenvector computation. Calculate the eigenvalues and corresponding eigenvectors of the correlation coefficient matrix . The eigenvectors represent the directions of the principal components.
- Calculation of variance contribution rates. Determine the variance contribution rate of each principal component, as well as the cumulative variance contribution rate of the first principal components.
2.3. Nonlinear State Estimation Modeling
3. Results and Discussion
3.1. Data Preprocessing Effects
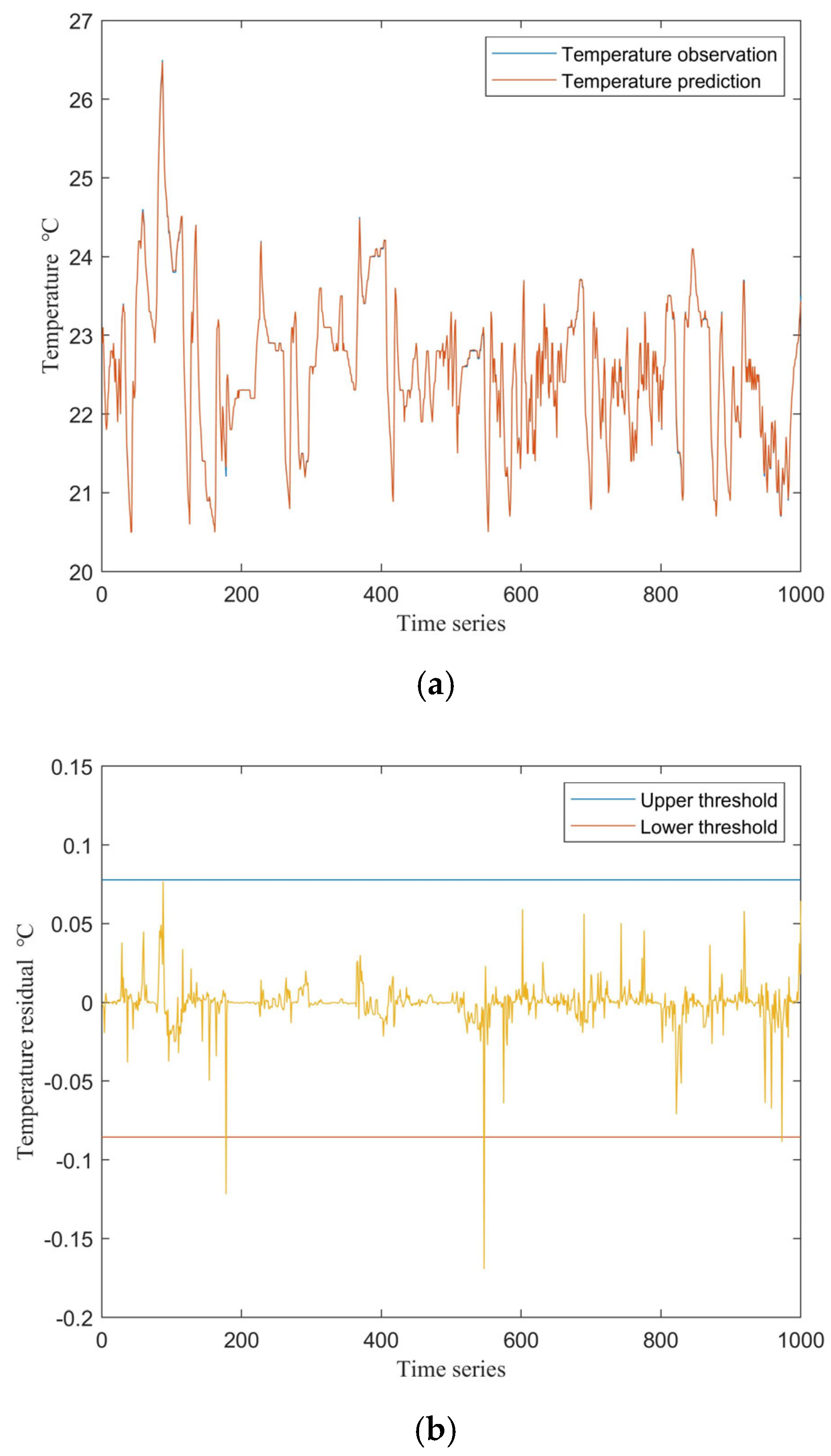
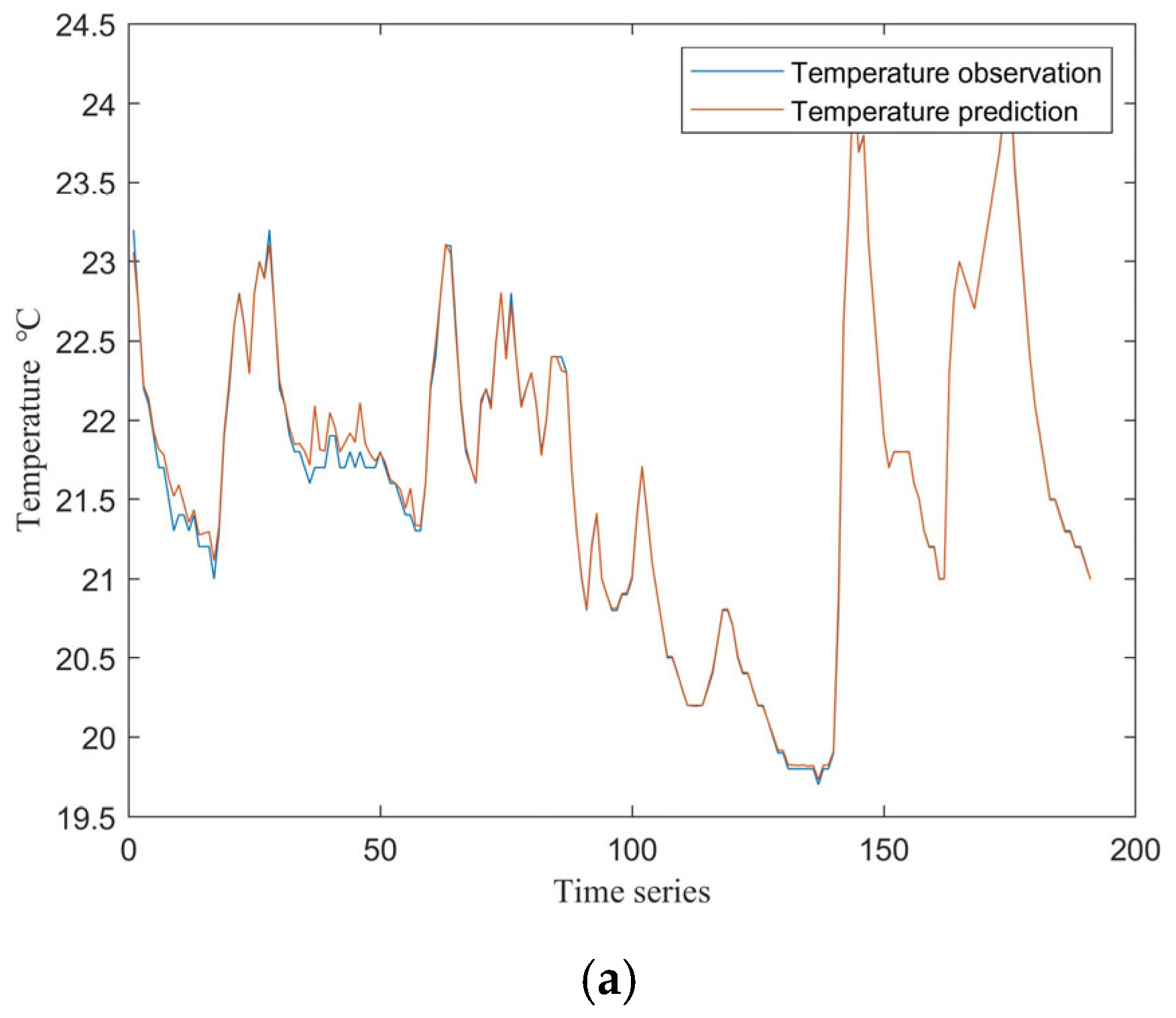
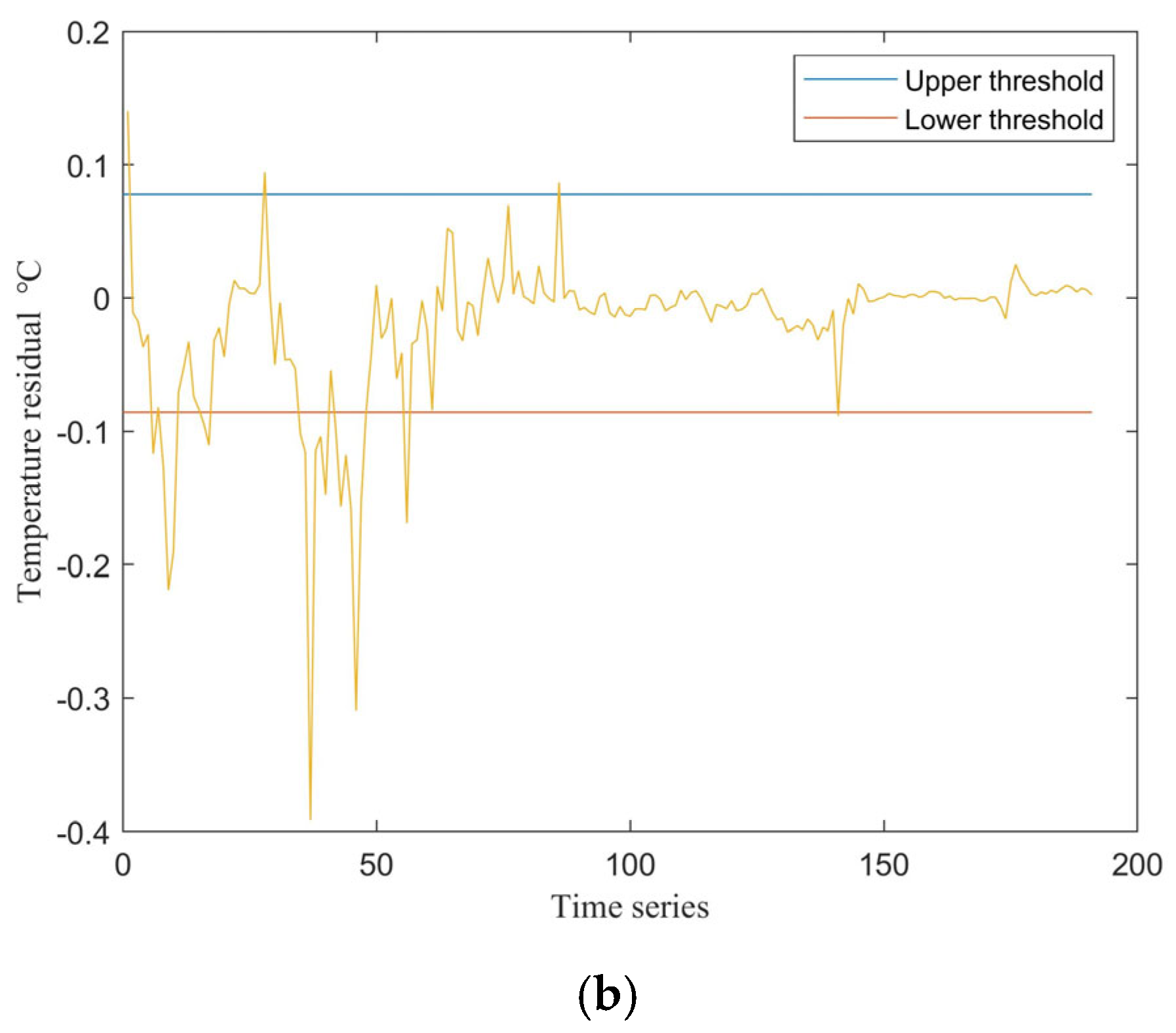
3.2. Model Comparison and Fault Detection Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, J.; Li, D.; Wei, Y.; Peng, K. A Novel Process Monitoring and Root Cause Diagnosis Strategy Based on Knowledge-Data-Integrated Causal Digraph for Complex Industrial Processes. IEEE Trans. Instrum. Meas. 2025, 74, 1–12. [Google Scholar] [CrossRef]
- Luo, L.; Xie, L.; Su, H. Deep Learning with Tensor Factorization Layers for Sequential Fault Diagnosis and Industrial Process Monitoring. IEEE Access 2020, 8, 105494–105506. [Google Scholar] [CrossRef]
- Simani, S.; Patton, R.J. Fault diagnosis of an industrial gas turbine prototype using a system identification approach. Control Eng. Pract. 2008, 16, 796–808. [Google Scholar] [CrossRef]
- Uidhir, T.M.; Rogan, F.; Collins, M.; Curtis, J.; Gallachóir, B.P.Ó. Improving energy savings from a residential retrofit policy: A new model to inform better retrofit decisions. Energy Build. 2020, 209, 109656. [Google Scholar] [CrossRef]
- Babayigit, B.; Abubaker, M. Industrial Internet of Things: A Review of Improvements Over Traditional SCADA Systems for Industrial Automation. IEEE Syst. J. 2024, 18, 120–133. [Google Scholar] [CrossRef]
- West, S.R.; Ward, J.K.; Wall, J. Trial results from a model predictive control and optimisation system for commercial building HVAC. Energy Build. 2014, 72, 271–279. [Google Scholar] [CrossRef]
- Es-sakali, N.; Zoubir, Z.; Idrissi Kaitouni, S.; Mghazli, M.O.; Cherkaoui, M.; Pfafferott, J. Advanced predictive maintenance and fault diagnosis strategy for enhanced HVAC efficiency in buildings. Appl. Therm. Eng. 2024, 254, 123910. [Google Scholar] [CrossRef]
- Tun, W.; Wong, J.K.; Ling, S. Hybrid Random Forest and Support Vector Machine Modeling for HVAC Fault Detection and Diagnosis. Sensors 2021, 21, 8163. [Google Scholar] [CrossRef]
- Taqvi, S.A.A.; Zabiri, H.; Tufa, L.D.; Uddin, F.; Fatima, S.A.; Maulud, A.S. A Review on Data-Driven Learning Approaches for Fault Detection and Diagnosis in Chemical Processes. ChemBioEng Rev. 2021, 8, 239–259. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Yin, K.; Kavuri, S.N. A review of process fault detection and diagnosis: Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 27, 293–311. [Google Scholar] [CrossRef]
- Liu, L.; Huang, Y. HVAC Design Optimization for Pharmaceutical Facilities with BIM and CFD. Buildings 2024, 14, 1627. [Google Scholar] [CrossRef]
- Smalls-Mantey, L.; Montalto, F. The seasonal microclimate trends of a large scale extensive green roof. Build. Environ. 2021, 197, 107792. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Wang, P.; Tian, Y. Failure warning of gearbox for wind turbine based on 3σ-median criterion and NSET. Energy Rep. 2021, 7, 1182–1197. [Google Scholar] [CrossRef]
- Aghili, S.A.; Khanzadi, M.; Haji Mohammad Rezaei, A.; Rahbar, M. Data-driven approach to fault detection for hospital HVAC system, Smart Sustain. Built Environ. 2024. ahead-of-print. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, Y.; Hu, S.; Tahir, M.; Yuan, W.; Yang, J. A three-stage adjustable robust optimization framework for energy base leveraging transfer learning. Energy 2025, 319, 135037. [Google Scholar] [CrossRef]
- Mirnaghi, M.S.; Haghighat, F. Fault detection and diagnosis of large-scale HVAC systems in buildings using data-driven methods: A comprehensive review. Energy Build. 2020, 229, 110492. [Google Scholar] [CrossRef]
- Dey, M.; Rana, S.P.; Dudley, S. Smart building creation in large scale HVAC environments through automated fault detection and diagnosis. Future Gener. Comput. Syst. 2020, 108, 950–966. [Google Scholar] [CrossRef]
- Qin, S.J. Statistical process monitoring: Basics and beyond. J. Chemom. 2003, 17, 480–502. [Google Scholar] [CrossRef]
- Martínez, S.; Eguía, P.; Granada, E.; Moazami, A.; Hamdy, M. A performance comparison of multi-objective optimization-based approaches for calibrating white-box building energy models. Energy Build. 2020, 216, 109942. [Google Scholar] [CrossRef]
- Somu, N.; Raman, G.M.R.; Ramamritham, K. A deep learning framework for building energy consumption forecast. Renew. Sustain. Energy Rev. 2021, 137, 110591. [Google Scholar] [CrossRef]
- Kaib, M.T.H.; Kouadri, A.; Harkat, M.; Bensmail, A.; Mansouri, M. Improvement of Kernel Principal Component Analysis-Based Approach for Nonlinear Process Monitoring by Data Set Size Reduction Using Class Interval. IEEE Access 2024, 12, 11470–11480. [Google Scholar] [CrossRef]
- Shittu, E.; Stojceska, V.; Gratton, P.; Kolokotroni, M. Environmental impact of cool roof paint: Case-study of house retrofit in two hot islands. Energy Build. 2020, 219, 110007. [Google Scholar] [CrossRef]
- Afroz, Z.; Higgins, G.; Shafiullah, G.M.; Urmee, T. Evaluation of real-life demand-controlled ventilation from the perception of indoor air quality with probable implications. Energy Build. 2020, 219, 110018. [Google Scholar] [CrossRef]
- Yuan, X.; Ma, C.; Chen, S. Research on Equipment Parameter Early Warning Based on GMM and NSET Optimization Algorithm. Kongzhi Gongcheng = Control Eng. China 2022, 29, 1058–1064. [Google Scholar] [CrossRef]
- Bonvini, M.; Sohn, M.D.; Granderson, J.; Wetter, M.; Piette, M.A. Robust on-line fault detection diagnosis for HVAC components based on nonlinear state estimation techniques. Appl. Energy 2014, 124, 156–166. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.; Do, S.; Mago, P.J.; Lee, K.H.; Cho, H. Energy Modeling and Model Predictive Control for HVAC in Buildings: A Review of Current Research Trends. Energies 2022, 15, 7231. [Google Scholar] [CrossRef]
- Kazemi, H.; Yazdizadeh, A. Optimal state estimation and fault diagnosis for a class of nonlinear systems. IEEE/CAA J. Autom. Sin. 2020, 7, 517–526. [Google Scholar] [CrossRef]
- Matetić, I.; Štajduhar, I.; Wolf, I.; Ljubic, S. A review of data-driven approaches and techniques for fault detection and diagnosis in HVAC systems. Sensors 2022, 23, 1. [Google Scholar] [CrossRef]
- Ma, Y.; Borrelli, F.; Hencey, B.; Coffey, B.; Bengea, S.; Haves, P. Model predictive control for the operation of building cooling systems. IEEE Trans. Control Syst. Technol. 2012, 20, 796–803. [Google Scholar] [CrossRef]
- Li, D.; Hu, G.; Spanos, C.J. A data-driven strategy for detection and diagnosis of building chiller faults using linear discriminant analysis. Energy Build. 2016, 128, 519–529. [Google Scholar] [CrossRef]
- Na, W.; Zan, Q.; Gao, Y.; Guo, S.; Wang, Z. Real-time diagnosis and fault-tolerant control of a sensor single fault based on a data-driven feedforward-feedback control system. Processes 2022, 10, 1237. [Google Scholar] [CrossRef]
- Toumi, R.; Kourd, Y.; Lefebvre, D. A novel fault detection approach based on multilinear sparse PCA: Application on the semiconductor manufacturing processes. Elektr. Turk. J. Electr. Eng. Comput. Sci. 2022, 30, 1586–1599. [Google Scholar] [CrossRef]
- Windmann, S. Data-driven fault detection in industrial batch processes based on a stochastic hybrid process model. IEEE Trans. Autom. Sci. Eng. 2022, 19, 3888–3902. [Google Scholar] [CrossRef]
- Tao, Y.; Shi, H.; Song, B.; Tan, S. A novel dynamic weight principal component analysis method and hierarchical monitoring strategy for process fault detection and diagnosis. IEEE Trans. Ind. Electron. 2020, 67, 7994–8004. [Google Scholar] [CrossRef]
- Hamza, M.; Bafail, O.; Alidrisi, H. HVAC Systems Evaluation and Selection for Sustainable Office Buildings: An Integrated MCDM Approach. Buildings 2023, 13, 1847. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N. A review of process fault detection and diagnosis: Part II: Qualitative models and search strategies. Comput. Chem. Eng. 2003, 27, 313–326. [Google Scholar] [CrossRef]
- Lu, L.; Gao, X.; Shahnam, M.; Rogers, W.A. Open source implementation of glued sphere discrete element method and nonspherical biomass fast pyrolysis simulation. AIChE J. 2021, 67, e17211. [Google Scholar] [CrossRef]
- Ali, U.; Shamsi, M.H.; Hoare, C.; Mangina, E.; O’Donnell, J. Review of urban building energy modeling (UBEM) approaches, methods and tools using qualitative and quantitative analysis. Energy Build. 2021, 246, 111073. [Google Scholar] [CrossRef]
- Alghanmi, A.; Yunusa-Kaltungo, A. A whole-building data-driven fault detection and diagnosis approach for public buildings in hot climate regions. Energy Built Environ. 2024, 5, 911–932. [Google Scholar] [CrossRef]
- Yun, W.; Hong, W.; Seo, H. A data-driven fault detection and diagnosis scheme for air handling units in building HVAC systems considering undefined states. J. Build. Eng. 2021, 35, 102111. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Y.; Zhang, C.; Luo, J.; Zhang, X. A knowledge-guided and data-driven method for building HVAC systems fault diagnosis. Build. Environ. 2021, 198, 107850. [Google Scholar] [CrossRef]
- Ajagekar, A.; You, F. Quantum computing assisted deep learning for fault detection and diagnosis in industrial process systems. Comput. Chem. Eng. 2020, 143, 107119. [Google Scholar] [CrossRef]


| Parameter | Operating Range | Pearson Correlation Coefficient |
|---|---|---|
| Supply air duct humidity | [13.4, 73.2] | −0.280 |
| Supply air duct flow rate | [4912, 11,687] | −0.167 |
| Fan frequency | [34.8, 50] | −0.181 |
| Workshop air flow rate | [57.5, 22,268] | −0.146 |
| Mixing room temperature | [18.8, 26.7] | 1 |
| Mixing room humidity | [21, 68.1] | −0.191 |
| Weighing room temperature | [18.8, 25.7] | 0.831 |
| Weighing room humidity | [22.1, 71.9] | −0.108 |
| Preprocessing room temperature | [19, 26.4] | 0.900 |
| Preprocessing room humidity | [21.8, 70.6] | −0.280 |
| Operating Parameter | Variance Contribution Rate | Cumulative Contribution Rate |
|---|---|---|
| Mixing room temperature | 0.4986 | 0.4986 |
| Preprocessing room temperature | 0.2584 | 0.757 |
| Weighing room temperature | 0.1601 | 0.9171 |
| Supply air duct humidity | 0.0368 | 0.9536 |
| Mixing room humidity | 0.0204 | 0.974 |
| Fan frequency | 0.0110 | 0.984 |
| Supply air duct flow rate | 0.0081 | 0.9921 |
| Preprocessing room humidity | 0.0029 | 0.995 |
| Workshop air flow rate | 0.0030 | 0.998 |
| Weighing room humidity | 0.0020 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Yan, W. Data-Driven Fault Detection for HVAC Control Systems in Pharmaceutical Manufacturing Workshops. Processes 2025, 13, 2015. https://doi.org/10.3390/pr13072015
Huang D, Yan W. Data-Driven Fault Detection for HVAC Control Systems in Pharmaceutical Manufacturing Workshops. Processes. 2025; 13(7):2015. https://doi.org/10.3390/pr13072015
Chicago/Turabian StyleHuang, Daiyuan, and Wenjun Yan. 2025. "Data-Driven Fault Detection for HVAC Control Systems in Pharmaceutical Manufacturing Workshops" Processes 13, no. 7: 2015. https://doi.org/10.3390/pr13072015
APA StyleHuang, D., & Yan, W. (2025). Data-Driven Fault Detection for HVAC Control Systems in Pharmaceutical Manufacturing Workshops. Processes, 13(7), 2015. https://doi.org/10.3390/pr13072015





