Residual Inertia Estimation Method for KEPCO Power Systems Using PMU and EMS-Based Frequency Response Analysis
Abstract
1. Introduction
Contributions
- Development of a novel framework for estimating both synchronous and residual inertia, offering a more comprehensive and accurate analysis of system stability;
- Application of the proposed method using limited PMU coverage, making it applicable to systems where full PMU deployment is impractical, such as large-scale power systems;
- Validation of the method using real PMU and EMS data from the KEPCO system, showcasing its practical effectiveness in evaluating frequency stability under varying load and generation conditions;
- The proposed method allows for more informed operational decision-making by accounting for both synchronous and non-synchronous inertia, crucial for optimizing reserve allocation and improving system resilience, particularly in grids with high renewable energy penetration.
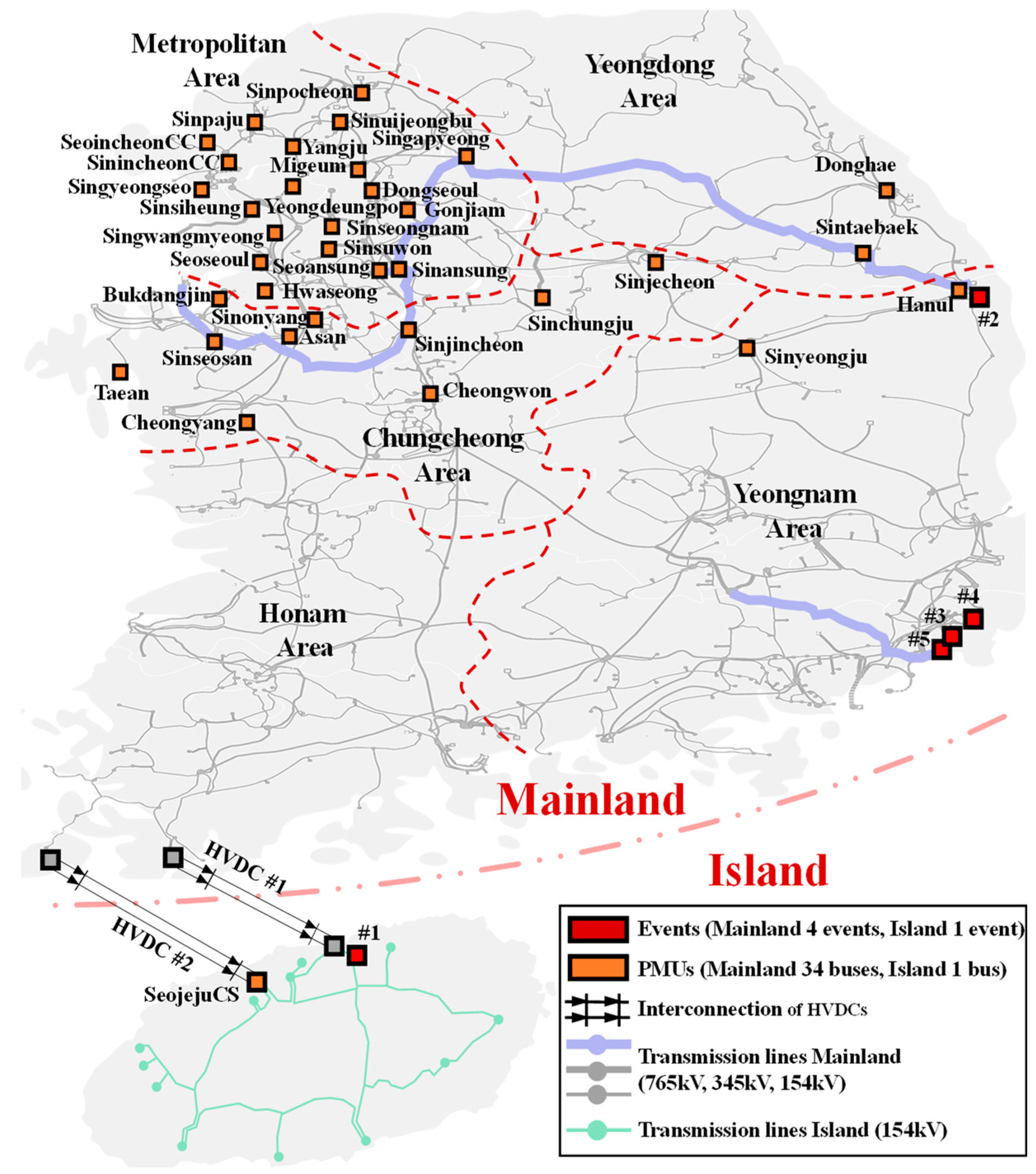
2. KEPCO Wide Monitoring Systems
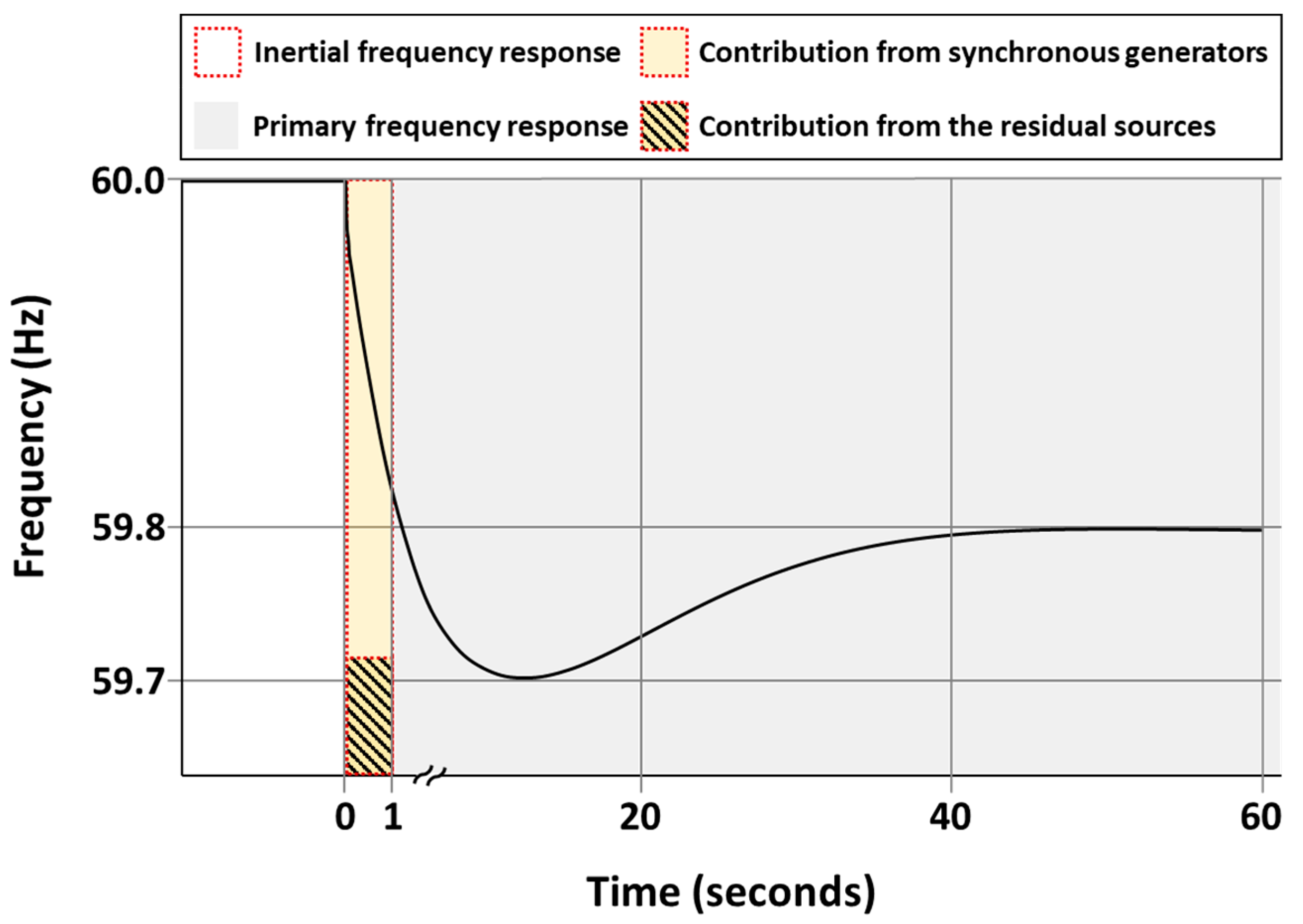
3. Residual Inertia Estimation
3.1. Theoretical Background
3.2. Residual Inertia Estimation of Power Systems
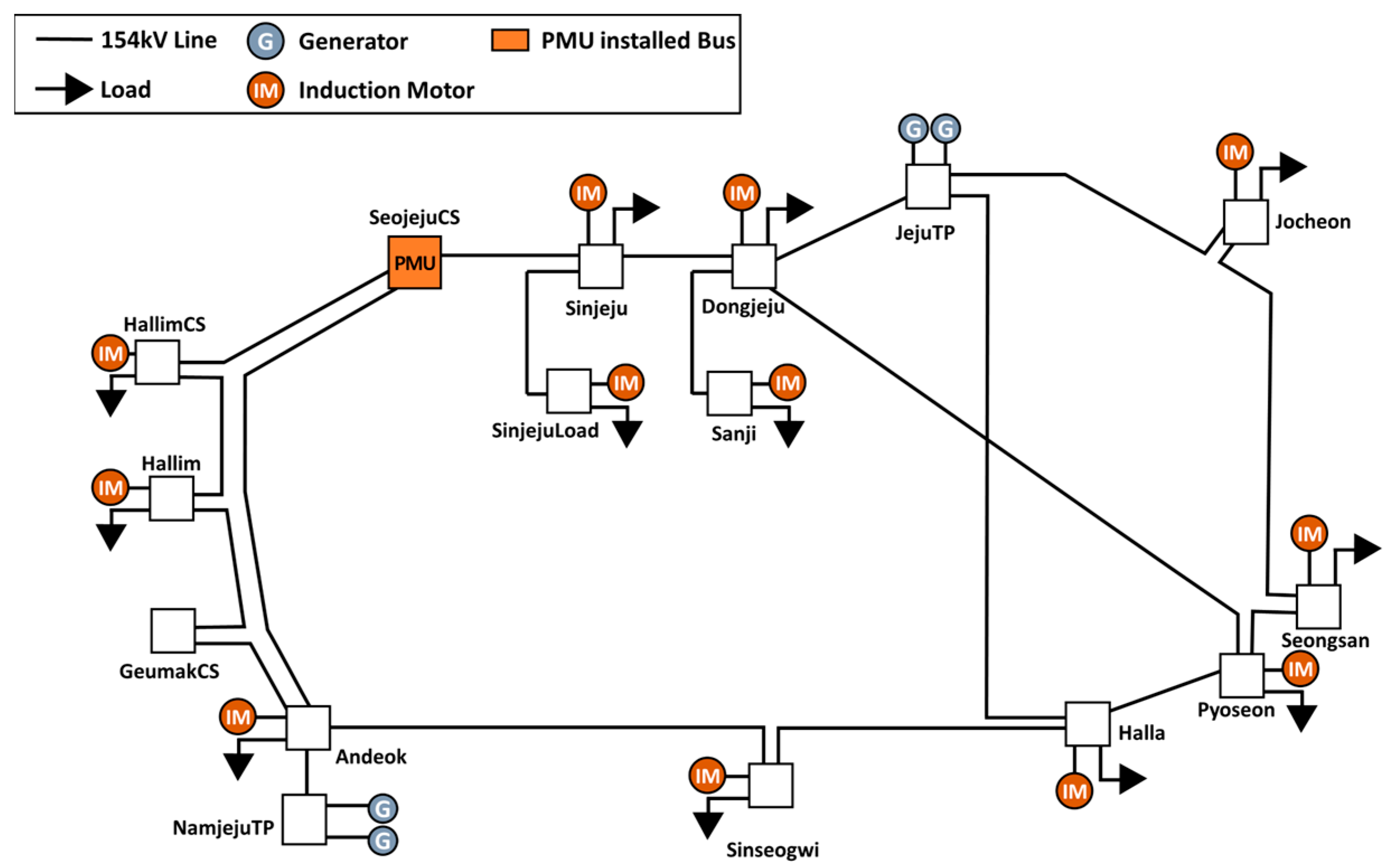
4. Example of the Modeled KEPCO Island System
4.1. Simulation Scenarios and Models
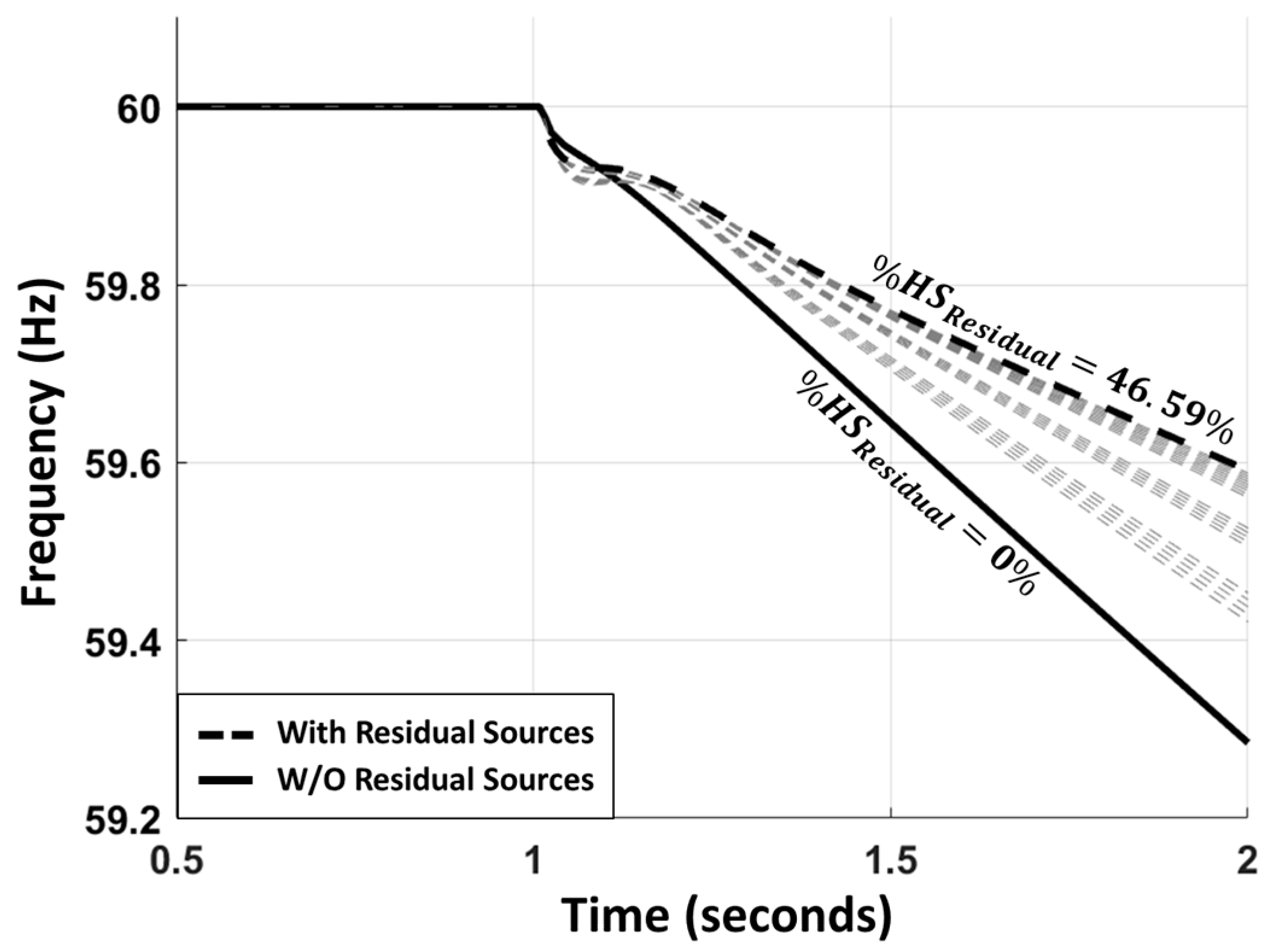
4.2. Simulation Results
5. Residual Inertia of KEPCO Systems
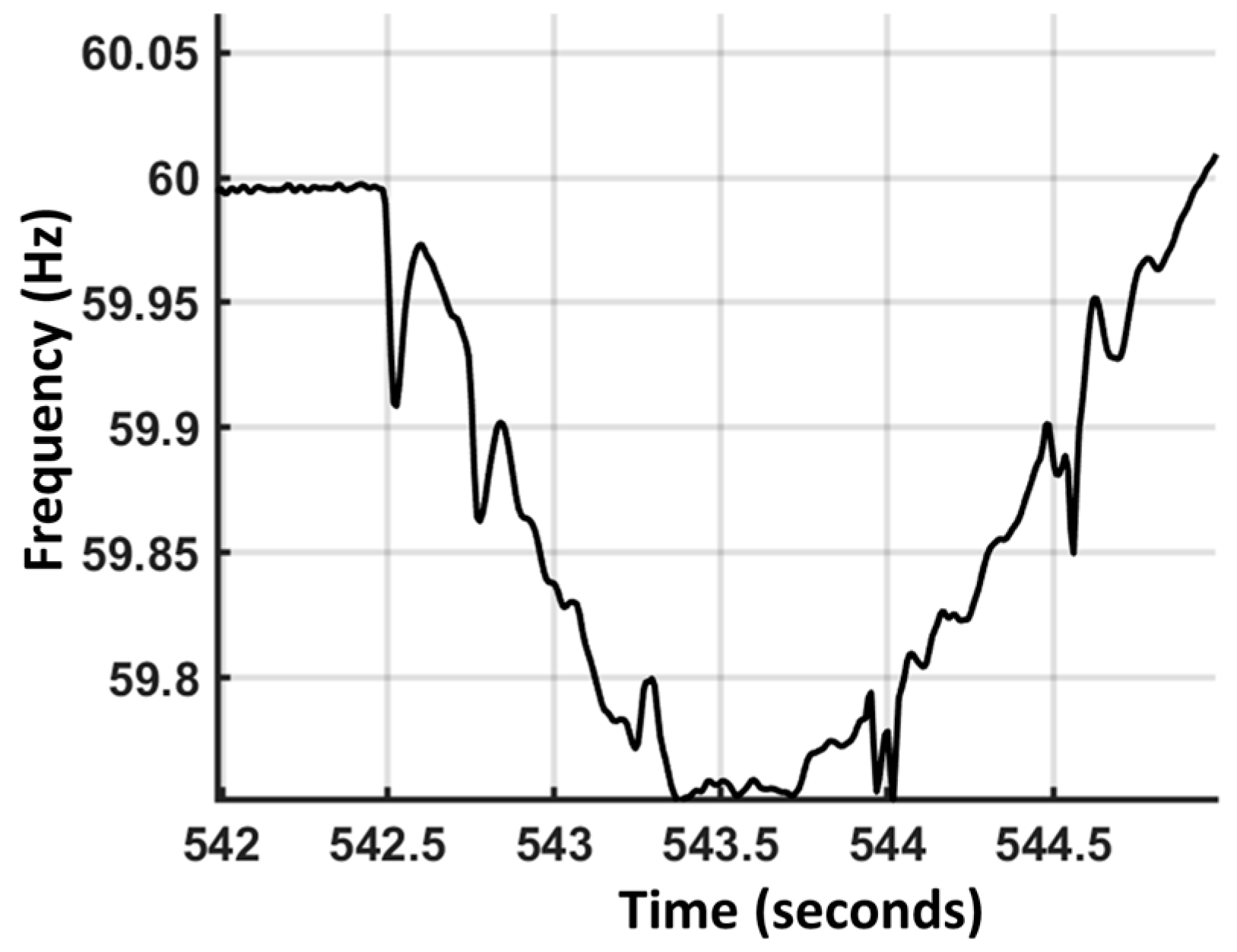
5.1. Residual Inertia Result from an Island System Event
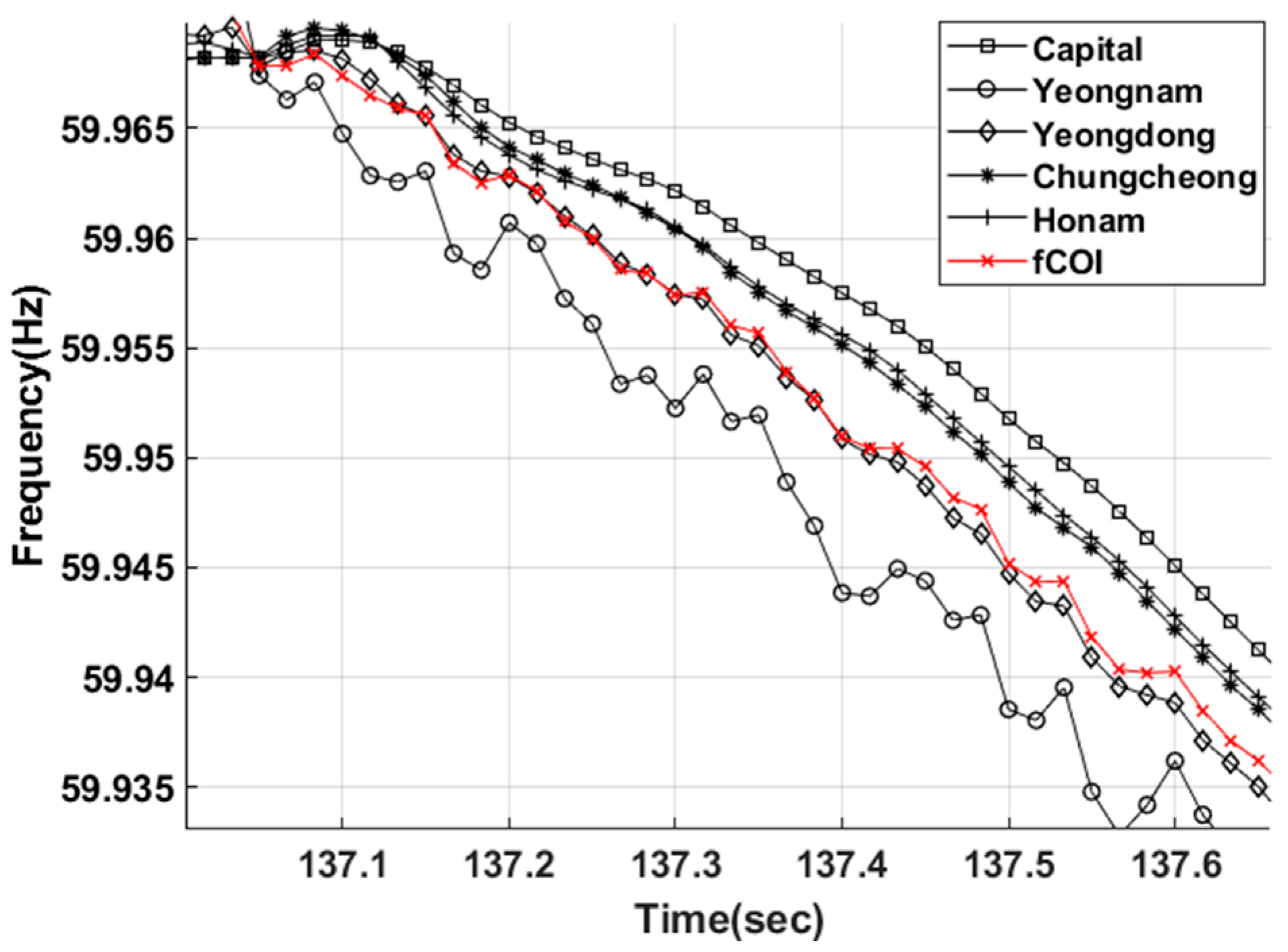
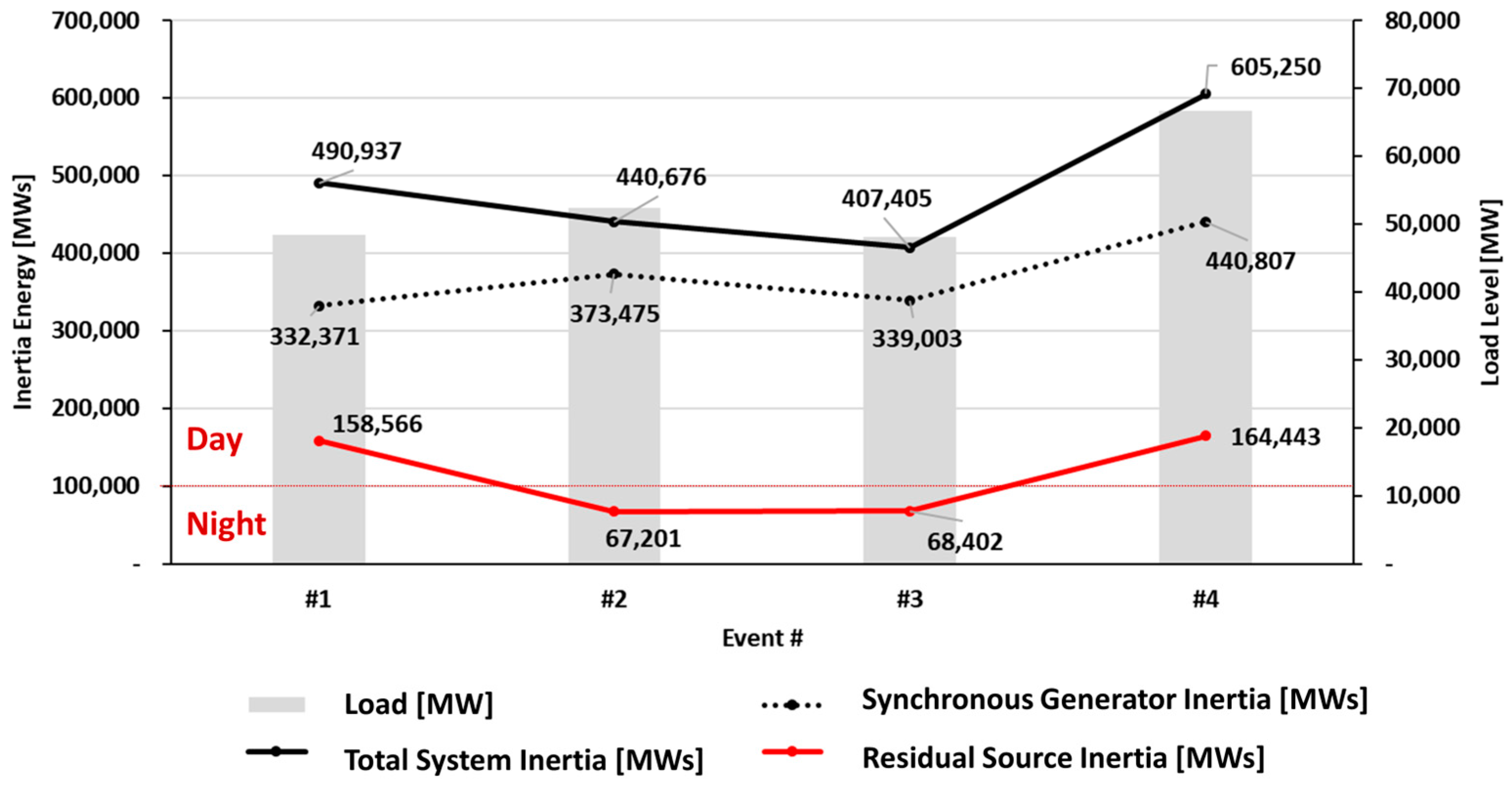
5.2. Residual Inertia Results from Mainland System Events
6. Discussion
6.1. Methodological Limitations and Sensitivity Considerations
6.2. Operational Implications
6.3. Applicability to Other Power Systems
6.4. Future Works
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMU | Phasor Measurement Unit |
| EMS | Energy Management System |
| SE | State Estimation |
| SCADA | Supervisory Control and Data Acquisition |
| fCOI | Center of Inertia Frequency |
| RES | Renewable Energy Source |
| HVDC | High Voltage Direct Current |
| FACTS | Flexible AC Transmission Systems |
| KEPCO | Korea Electric Power Corporation |
| K-WAMS | Korea Wide Area Monitoring System |
| RoCoF | Rate of Change of Frequency |
| PSSE | Power System Simulator for Engineering |
References
- The Government of the Republic of Korea. 2050 Carbon Neutral Strategy of the Republic of Korea. Republic of Korea, 2020. Available online: https://www.korea.kr/archive/expDocView.do?docId=39241 (accessed on 11 May 2024).
- Kwon, P.S. Transforming the Energy Sector to Reach Net-Zero. Republic of Korea, 2021. Available online: https://news.skecoplant.com/plant-tomorrow/1695 (accessed on 17 July 2024).
- Ministry of Trade, Industry and Energy of the Republic of Korea. The 10th Basic Plan for Long-Term Electricity Supply and Demand. Republic of Korea. 2023. Available online: https://www.motie.go.kr/kor/article/ATCLc01b2801b/68162/view (accessed on 11 July 2024).
- Castro Martínez, J.; Arnaltes, S.; Alonso Martínez, J.; Rodríguez Amenedo, J.L. Contribution of Wind Farms to the Stability of Power Systems with High Penetration of Renewables. Energies 2021, 14, 2207. [Google Scholar] [CrossRef]
- National Grid. Normal Infeed Loss Risk, GSR015. National Grid. 2014. Available online: https://www.neso.energy/industry-information/codes/sqss/modifications/gsr015-normal-infeed-loss-risk (accessed on 15 May 2024).
- Fingrid. TSO Report on Balancing in Accordance with Article 60 of Commission Regulation (EU) 2017/2195 of 23 November 2017 Establishing a Guideline on Electricity Balancing. Fingrid. February 2022. Available online: https://www.fingrid.fi/globalassets/dokumentit/fi/sahkomarkkinat/reservit/ebgl60-tso-report-on-balancing-2022.pdf (accessed on 13 May 2024).
- ENTSO-E. Future System Inertia 2. ENTSO-E. 2017. Available online: https://www.statnett.no/globalassets/for-aktorer-i-kraftsystemet/utvikling-av-kraftsystemet/nordisk-frekvensstabilitet/future-system-inertia-phase-2.pdf (accessed on 11 July 2024).
- Shao, H.; Cai, X.; Zhou, D.; Li, Z.; Zheng, D.; Cao, Y.; Wang, Y.; Rao, F. Equivalent Modeling and Comprehensive Evaluation of Inertia Emulation Control Strategy for DFIG Wind Turbine Generator. IEEE Access 2019, 7, 64798–64811. [Google Scholar] [CrossRef]
- Arani, A.N.; El-Saadany, E. Implementing Virtual Inertia in DFIG-Based Wind Power Generation. IEEE Trans. Power Syst. 2013, 28, 1373–1384. [Google Scholar] [CrossRef]
- Ashton, P.M.; Saunders, C.S.; Taylor, G.A.; Carter, A.M.; Bradley, M.E. Inertia Estimation of the GB Power System Using Synchrophasor Measurements. IEEE Trans. Power Syst. 2015, 30, 701–709. [Google Scholar] [CrossRef]
- Ashton, P.M.; Taylor, G.A.; Carter, A.M.; Bradley, M.E.; Hung, W. Application of Phasor Measurement Units to Estimate Power System Inertial Frequency Response. In Proceedings of the IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Shiroei, M.; Mohammadi-Ivatloo, B.; Parniani, M. Low-Order Dynamic Equivalent Estimation of Power Systems Using Data of Phasor Measurement Units. Int. J. Electr. Power Energy Syst. 2016, 74, 134–141. [Google Scholar] [CrossRef]
- Duong, D.T.; Uhlen, K.; Jansson, E.A. Estimation of Hydro Turbine–Governor System’s Transfer Function from PMU Measurements. In Proceedings of the IEEE Power & Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Lara-Jimenez, J.D.; Ramírez, J.M.; Mancilla-David, F. Allocation of PMUs for Power-System-Wide Inertial Frequency Response Estimation. IET Gen. Transm. Distrib. 2017, 11, 2902–2911. [Google Scholar] [CrossRef]
- IEEE C37.118.2-2011; IEEE Standard for Synchrophasor Data Transfer for Power Systems. IEEE: New York, NY, USA, 2011.
- Kundur, P. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994; pp. 109–115. [Google Scholar]
- Anderson, P.M.; Mirheydar, M. A Low-Order System Frequency Response Model. IEEE Trans. Power Syst. 1990, 5, 720–729. [Google Scholar] [CrossRef]
- El Aeraj, O.; Leghris, C. Intrusion Detection System Based on an Intelligent Multilayer Model Using Machine Learning. J. Artif. Intell. Technology. 2024, 4, 332–341. [Google Scholar]
- Shadi, M.R.; Ameli, M.T.; Azad, S. A real-time hierarchical framework for fault detection, classification, and location in power systems using PMUs data and deep learning. Int. J. Electr. Power Energy Syst. 2022, 134, 107399. [Google Scholar] [CrossRef]
- Touil, M.; Bahatti, L.; Elmagri, A. Automatic sleep quality analysis using an artificial intelligence algorithm and EEG signal processing. J. Artif. Intell. Technol. 2024, 4, 153–159. [Google Scholar] [CrossRef]
- Fang, T.; Hui, Z.; Rey, W.P.; Yang, A.; Liu, B.; Xie, Z. Digital Restoration of Historical Buildings by Integrating 3D PC Reconstruction and GAN Algorithm. J. Artif. Intell. Technol. 2024, 4, 179–187. [Google Scholar] [CrossRef]
| Method | Measurement Requirements | Residual Inertia Estimation | PMU Coverage | Applicability |
|---|---|---|---|---|
| Great Britain PMU-based method [10,11] | PMU frequency at multiple regional buses | Included | Moderate PMU coverage | Event-based regional inertia estimation |
| Online RoCoF-based generator estimation [12,13,14] | PMU frequency and active power at generator buses | Not included | PMU at each generator | Real-time synchronous inertia estimation |
| Proposed method | PMU frequency at system bus and EMS data | Included | Minimal PMU coverage | Event-based total system inertia estimation |
| Case | Ratio [%] | [MWs] | [MWs] | Difference [%] | |
|---|---|---|---|---|---|
| Basecase | 0 | 1.00 | 0 | 0 | - |
| 1 | 15.75 | 1.19 | 342.19 | 336.47 | −1.70 |
| 2 | 17.20 | 1.21 | 376.94 | 373.85 | −0.83 |
| 3 | 18.60 | 1.23 | 410.97 | 411.24 | 0.07 |
| 4 | 19.95 | 1.25 | 444.39 | 448.62 | 0.94 |
| 5 | 21.26 | 1.27 | 477.32 | 486.01 | 1.79 |
| 6 | 30.37 | 1.45 | 801.39 | 785.09 | −2.08 |
| 7 | 31.36 | 1.46 | 830.10 | 822.47 | −0.93 |
| 8 | 32.33 | 1.48 | 858.29 | 859.86 | 0.18 |
| 9 | 33.27 | 1.49 | 885.98 | 897.24 | 1.26 |
| 10 | 34.18 | 1.51 | 913.18 | 934.63 | 2.30 |
| 11 | 40.67 | 1.70 | 1259.62 | 1233.71 | −2.10 |
| 12 | 41.39 | 1.71 | 1275.27 | 1271.09 | −0.33 |
| 13 | 42.10 | 1.72 | 1302.62 | 1308.48 | 0.45 |
| 14 | 42.78 | 1.73 | 1321.62 | 1345.86 | 1.80 |
| 15 | 43.46 | 1.79 | 1418.69 | 1383.25 | −2.56 |
| 16 | 44.11 | 1.80 | 1432.78 | 1420.63 | −0.85 |
| 17 | 44.75 | 1.80 | 1446.58 | 1458.02 | 0.78 |
| 18 | 45.38 | 1.83 | 1496.32 | 1495.41 | −0.06 |
| 19 | 45.99 | 1.84 | 1514.03 | 1532.79 | 1.22 |
| 20 | 46.59 | 1.85 | 1531.35 | 1570.18 | 2.47 |
| Event Date/Time | [Hz/s] | [Hz/s] | [MWs] | [MWs] |
|---|---|---|---|---|
| 14 August 2020 (Fri)/14:19:02 | 0.5426 | 0.3230 | 4393.46 | 2987.01 |
| Event | #1 | #2 | #3 | #4 |
|---|---|---|---|---|
| Event Date/Time | 2020-07-19 (Sun) 12:03 | 2020-09-03 (Thurs) 00:46 | 2020-09-03 (Thurs) 03:03 | 2022-04-26 (Tues) 13:27 |
| 1000 | 977 | 978 | 1422 | |
| [Hz/s] | 0.0903 | 0.0785 | 0.0865 | 0.0968 |
| [Hz/s] | 0.0611 | 0.0665 | 0.0720 | 0.0705 |
| [MWs] | 332,371 | 373,475 | 339,003 | 440,807 |
| 158,566 | 67,201 | 68,402 | 164,443 | |
| % Resid | 32.30% | 15.25% | 16.79% | 27.17% |
| % Gen | 67.70% | 84.75% | 83.21% | 72.83% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, N.; Nam, S. Residual Inertia Estimation Method for KEPCO Power Systems Using PMU and EMS-Based Frequency Response Analysis. Processes 2025, 13, 2012. https://doi.org/10.3390/pr13072012
Choi N, Nam S. Residual Inertia Estimation Method for KEPCO Power Systems Using PMU and EMS-Based Frequency Response Analysis. Processes. 2025; 13(7):2012. https://doi.org/10.3390/pr13072012
Chicago/Turabian StyleChoi, Namki, and Suchul Nam. 2025. "Residual Inertia Estimation Method for KEPCO Power Systems Using PMU and EMS-Based Frequency Response Analysis" Processes 13, no. 7: 2012. https://doi.org/10.3390/pr13072012
APA StyleChoi, N., & Nam, S. (2025). Residual Inertia Estimation Method for KEPCO Power Systems Using PMU and EMS-Based Frequency Response Analysis. Processes, 13(7), 2012. https://doi.org/10.3390/pr13072012







