(1) Parameter importance evaluation method based on correlation analysis: By quantitatively calculating the correlation between each process parameter and the quality index, the influence of each parameter on the quality index is systematically evaluated, and its importance is sorted. This method provides a scientific basis and decision support for the subsequent parameter stratification and optimization, thereby improving the stability of the process and product quality.
(2) Hierarchical model of process parameters based on importance evaluation: Based on the importance ranking results, the random forest regression model is used to stratify the process parameters. By analyzing the comprehensive evaluation index of the stability of the model, the process parameters are divided into different levels to reduce the impact of the complexity of the parameter dimension and improve the optimization efficiency.
(3) Multi-level progressive optimization model based on improved particle swarm optimization algorithm: The multi-level progressive modeling strategy is adopted to establish the mapping model of each layer of process parameters and quality indicators layer by layer, and the improved particle swarm optimization is used to search for the optimal combination of process parameters. In the process of constructing the prediction model, the optimal parameter combination of each layer is transmitted to the next layer as a fixed input so as to realize the multi-level progressive optimization of process parameters.
2.1. Hierarchical Model of Process Parameters Based on Importance Evaluation
2.1.1. Process Parameter Importance Evaluation Method Based on Correlation Analysis
Due to the significant difference in the influence of process parameters on quality indicators, it is very important to reasonably evaluate the importance of each process parameter to achieve effective quality control and process optimization. Therefore, this paper adopts the importance evaluation method of process parameters based on correlation analysis. This method systematically evaluates the influence of each parameter on the quality index by calculating the correlation between the process parameters and the quality index. Since the Pearson correlation coefficient can effectively reveal the correlation between the two [
24], this study uses this coefficient to quantitatively analyze the correlation between process parameters and quality indicators. The Pearson correlation coefficient expression is as follows:
In the formula, and represent process parameters and quality indicators, respectively; and represent the mean value of process parameters and quality indicators respectively; and represents the correlation between them. The calculated correlation coefficient, reflects the correlation strength between the two, and its value range is . The closer the value is to 1 or −1, the stronger the correlation is.
On the basis of calculating the correlation of each process parameter to the quality index, all the process parameters are sorted in descending order according to the correlation. The sorting process is as follows:
In the formula, represents the process parameter with the strongest correlation with the quality index , and is the process parameter with the weakest correlation.
The sorted set of process parameters can lay the foundation for the subsequent hierarchical operation of process parameters according to its correlation with quality indicators.
2.1.2. Hierarchical Model of Process Parameters for High-Dimensional Processes
Since the dimension of process parameters is often high, the direct use of all sorted parameters for modeling or optimization will face significant computational complexity problems [
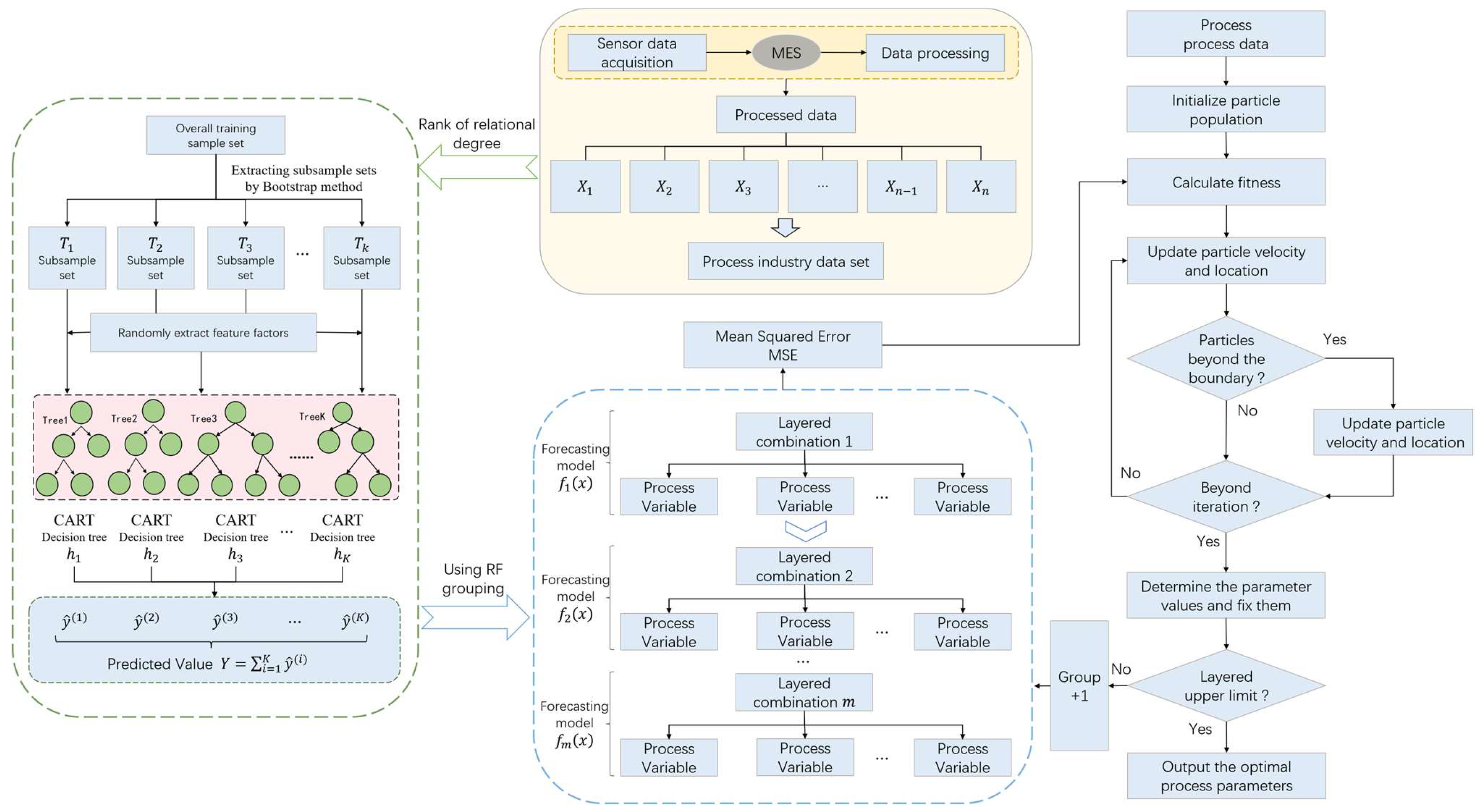
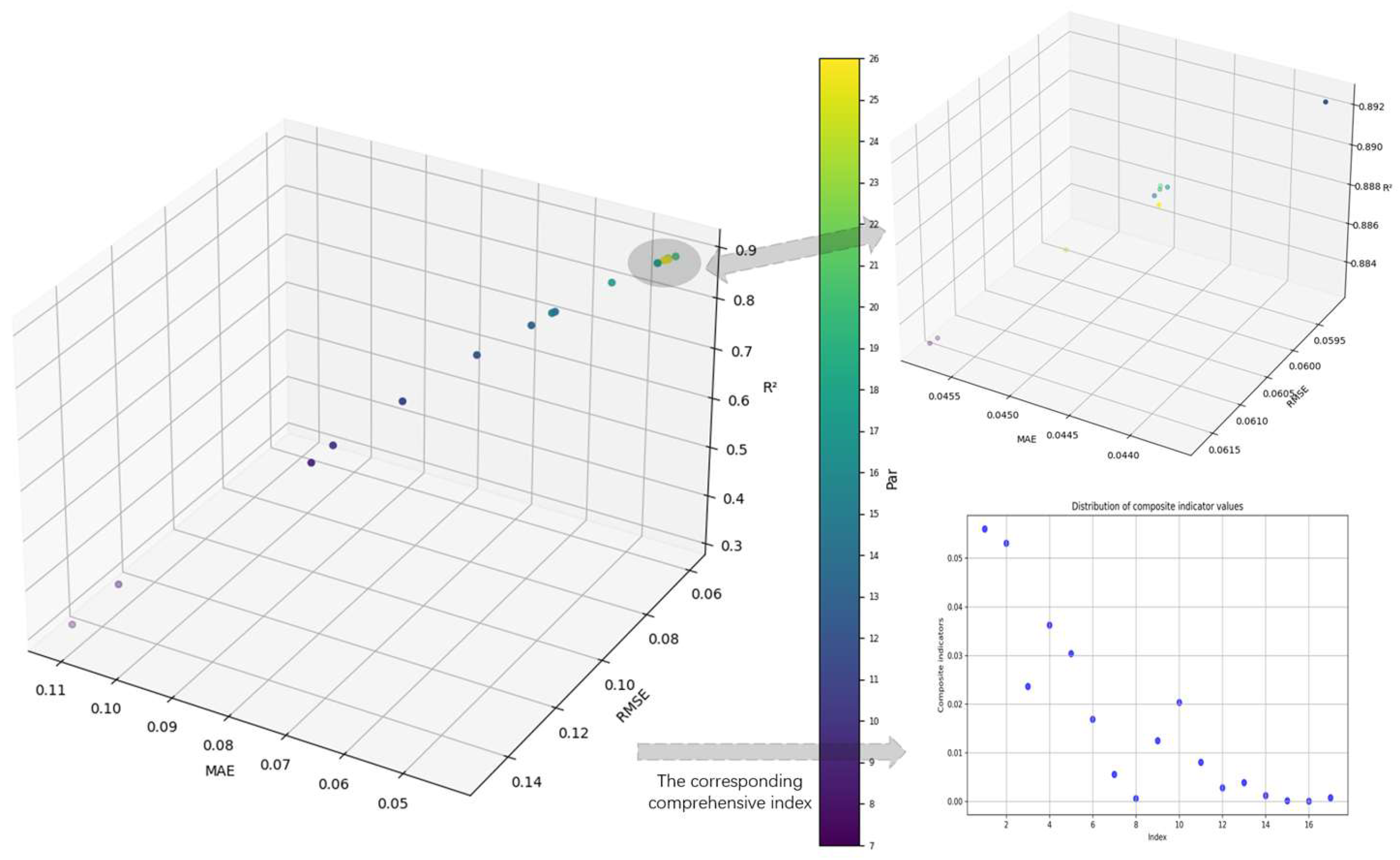
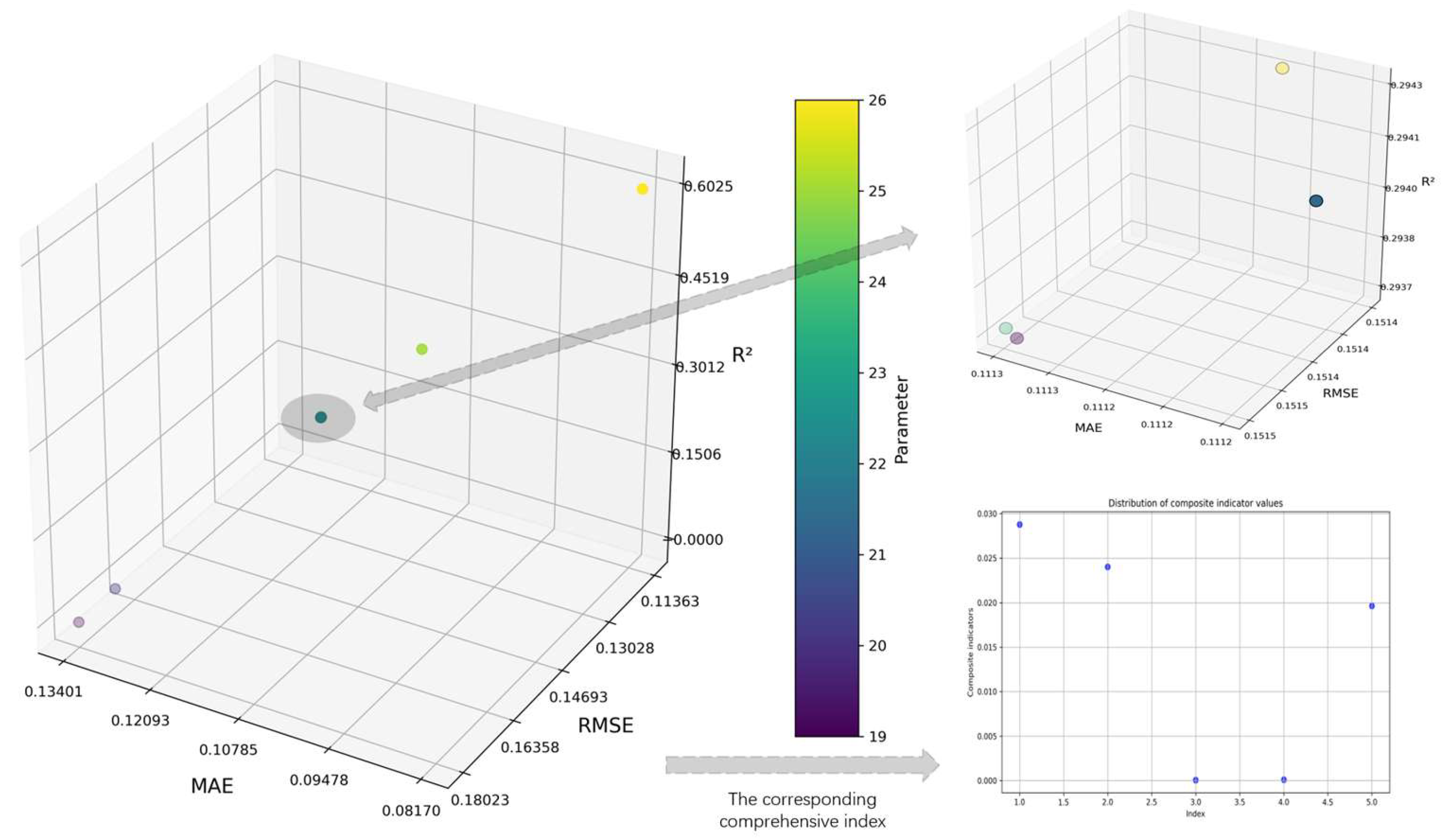
25]. In order to effectively reduce the complexity of the model and improve the computational efficiency, a hierarchical model of process parameters based on importance evaluation is constructed. Firstly, the correlation degree between each process parameter and quality index is calculated by correlation degree analysis, and the process parameters are sorted according to the degree of correlation. Subsequently, the random forest regression model was used to hierarchically process the sorted process parameters. Among them, the process parameter stratification method is shown in
Figure 2.
The specific processes are as follows:
(1) Data input: The process data set is composed of process parameters and quality index , which can be expressed as , where represents the process parameters, represents the quality index, represents the number of process parameters, and represents the number of samples in the process data set. On the basis of preprocessing the original data, and are used as the input of the hierarchical model of process parameters.
(2) Parameter importance assessment: The correlation degree between process parameters and quality index is calculated so as to realize the sorting of process parameters according to the correlation degree. Its calculation is publicized as follows:
(3) Determine the initial process parameters: The process parameters with the largest correlation degree are selected as the initial process parameters, and the selected process parameters are temporarily divided into one layer.
(4) Model selection: Random forests can effectively capture complex nonlinear relationships and have excellent stability and robustness [
26]. Therefore, this paper uses the random forest regression model to stratify the process parameters. Among them, the expression of the random forest objective function is
In the formula,
represents the total number of samples,
represents the true value,
represents the model prediction value,
represents the loss function,
represents the
-th tree,
represents the regular term, the loss function, and the regular term are expressed as follows:
In the formula,
and
are penalty coefficients,
is the number of leaf nodes, and
is the weight of leaf nodes. Among them, the sum of the prediction results of the
-th decision tree is the prediction results of the random forest model. The calculation of the model prediction results is publicized according to Formula (5):
In the formula, represents the -th sample, represents the number of iterations, and represents the weight of the -th sample at the leaf nodes of the -th decision tree.
(5) The calculation of goodness of fit (
):
is used to measure the fitting ability of the model to the data [
27]. The value of
is between 0 and 1, and the closer to 1, the stronger the explanatory ability of the process parameters to the quality index.
(6) Stability evaluation: In the process of model training, when adding a process parameter, it is necessary to directly observe the influence of the process parameters on the accuracy of the model. By analyzing the changes in the model accuracy under different parameter settings, it can be judged whether the model accuracy reaches a stable state within a certain range during the process of parameter increase. If not stabilized, then continue to increase the process parameters, and then repeat steps (3)~(6). If it has stabilized, the current process parameter combination is determined as a layer. Among them, in the stability judgment, the slope change rate is used as the main index to evaluate the change range of the model accuracy under the setting of adjacent parameters. When the number of process parameters is greater than 4, the calculation formula is as follows:
Here,
represents the value of the accuracy of the i-th model, that is, the
value representing the
-th. However, due to the possible correlation between some parameters during the model training process, the model accuracy fluctuates, which can be understood as a sudden change. In order to more effectively identify the stability of the trend, this paper introduces the mutation rate as an auxiliary index to measure the degree of mutation under different parameter levels. Its calculation formula is
Therefore, based on the above two indicators, the stability comprehensive index is introduced, and the overall stability of the model is quantitatively evaluated by the product of the slope change rate and the mutation rate. The calculation formula is as follows:
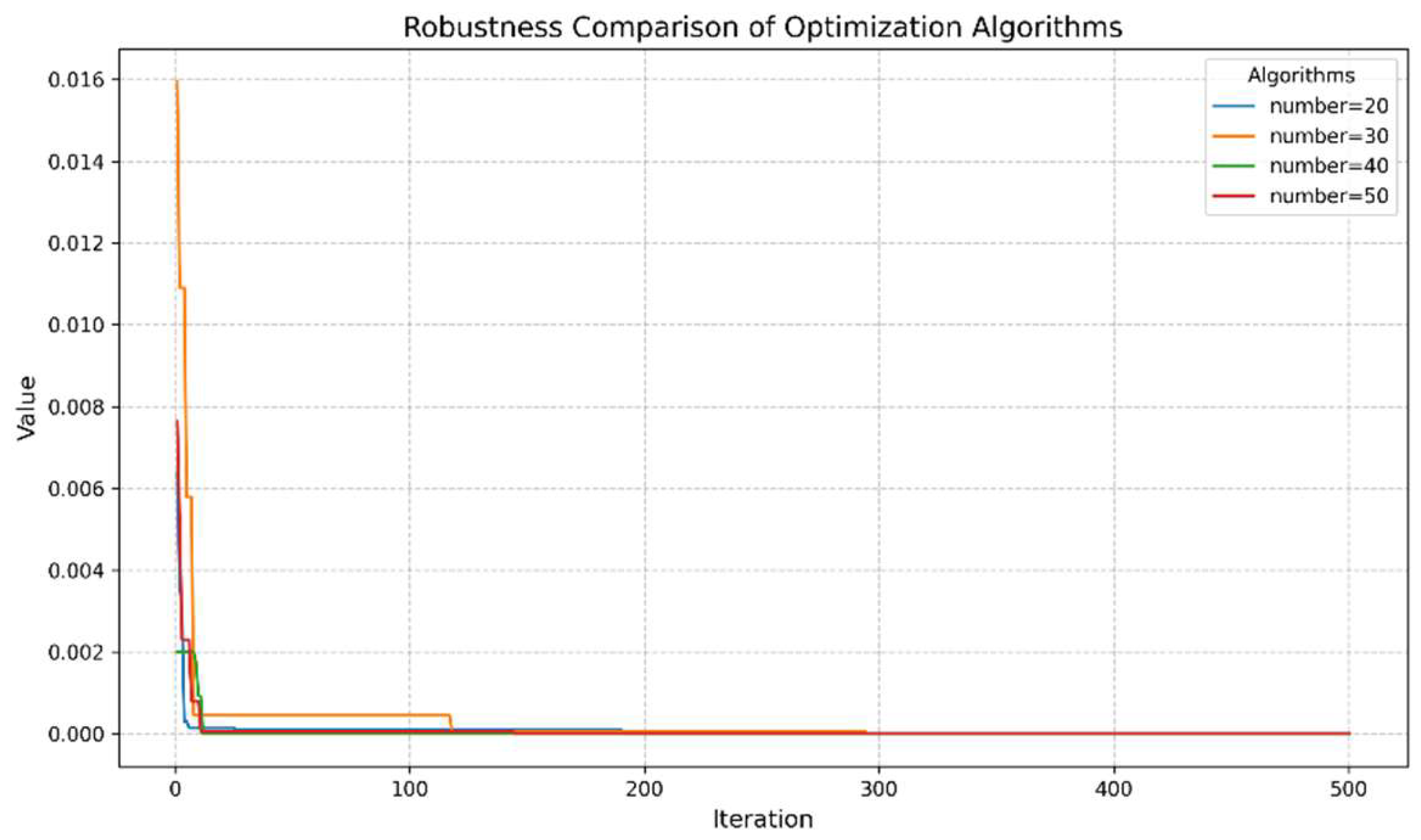
The stability of the model is judged by observing that the comprehensive index is less than 0.003 for the first time, and all subsequent values are always kept within 0.003. When this condition is satisfied, the model is considered to have reached a stable state. If the comprehensive index fails to remain below 0.003, skip this point and continue to observe the next point less than 0.003, and only when all the indicators remain within 0.003 after this point is the model judged to be stable. The selection of 0.003 as the threshold is based on in-depth analysis of experimental data and multiple experimental observations.
(7) Terminate condition checking: Determine whether the given termination condition is satisfied and determine the stratification result. If it is not satisfied, the process parameters that have completed the layering are deleted, and (3)~(7) is repeated.
2.2. Multi-Level Progressive Optimization Model of Process Parameters Based on Improved Particle Swarm Optimization Algorithm
Because the complex relationship between process parameters and quality indicators of each layer is still difficult to directly judge [
28], it is impossible to directly construct the functional relationship model between them [
29], so it is impossible to directly solve the optimal process parameter combination of each layer. In addition, considering the huge amount of process data in the process industry, it is impractical to use the exhaustive method to optimize the calculation.
Suppose that the process parameters are recorded as
, the number of process parameters is
, and the amount of data for each process parameter is
, that is:
It is assumed that the exhaustive method is used to optimize the whole process parameters directly. If the optimization combination is
and the number of combinations is
, the combination and quantity formulas are as follows:
It can be seen from the above publicity that even if the values of
and
are extremely small, the calculation amount of process parameter optimization is also extremely large. Therefore, this paper introduces a hierarchical optimization strategy to reduce the computational burden. Assuming that the grouping is
, the process parameters are optimized hierarchically. The formula is as follows:
Among them,
represent the process parameter group,
represents the number of groups,
,
,
represent the number of process parameters contained in different levels. The corresponding combination
and number
formulas are as follows:
Through the above analysis, the number of combinations is changed from the original multiplication to the accumulation of layers, so that the combination value is significantly reduced compared with . This shows that the hierarchical optimization strategy can effectively reduce the complexity of optimization calculation and further proves the necessity of this method.
Although
has been significantly reduced compared to
, it still has a huge amount of calculation, and direct use of exhaustive optimization will consume a lot of time and resources. Therefore, this paper introduces the particle swarm optimization algorithm [
30] to search for the optimal parameter combination of each layer and accelerate the optimization process. In addition, in order to solve the problem that the optimization algorithm is difficult to take the accuracy of the algorithm into account while pursuing the convergence speed [
31], the particle swarm optimization algorithm is improved as follows:
(1) The linear decreasing strategy of inertia weight is introduced to improve the convergence efficiency of the particle swarm optimization algorithm.
In the particle swarm optimization algorithm, the inertia weight
s usually a fixed constant, which is used to control the search range of the particles. The larger inertia weight enables the particles to carry out extensive exploration in the search space, while the smaller inertia weight enhances the dependence of the particles on the historical optimal solution, thereby improving the local search accuracy. However, fixed inertia weight may lead to too scattered a search in the early stage and too concentrated a search in the later stage, which ultimately affects convergence efficiency. To this end, a linear decreasing strategy of inertia weight is introduced. The inertia weight
is defined as
In the formula, represents the maximum inertia weight; represents the minimum inertia weight; is the maximum number of iterations; is the current number of iterations. As the iteration progresses, the inertia weight gradually decreases, thereby enhancing the global search ability of the particles in the early stage of the algorithm and enhancing the local search ability in the later stage to avoid premature convergence.
(2) Adaptively adjust the acceleration factor to improve the global and local search balance of the particle swarm optimization algorithm.
In the particle swarm optimization algorithm, the acceleration factors
and
control the dependence of the particles on the individual optimal solution and the global optimal solution. Although a larger acceleration factor can accelerate the particles to move closer to the optimal solution, an excessively high acceleration factor may lead to excessive concentration of the search process, thus lacking sufficient diversity. Therefore, the dynamic adjustment of the acceleration factor is an important method to optimize the search process so that it can be dynamically adjusted with the increase in the number of iterations. The changes of
and
in each iteration should follow:
In the formula, and represent the corresponding maximum acceleration factor, and represent the corresponding minimum acceleration factor. Specifically, in the early stage of the search, the value is small, which helps the particles to perform global search, thereby avoiding premature convergence. As the iteration progresses, the value gradually increases, which enhances the dependence of the particles on the best position of the individual, thereby promoting the refinement of the local search. In contrast, in the early stage of the search, the value is larger, which promotes the particle to move closer to the global optimal position; as the iteration progresses, the value gradually decreases, reducing the dependence of the particles on the global optimal position and promoting a more concentrated local search. Through dynamic adjustment, a good balance between global search and local search is found so as to improve the search efficiency of the algorithm.
(3) The search position of particles is limited to ensure that the particle swarm optimization algorithm searches in the feasible solution space.
In the problem of high-dimensional parameter optimization, particles may move to infeasible regions. In order to ensure that the particles are always in the feasible solution space, the position of the particles is constrained so that the position of the particles is always kept within a reasonable range. The constraint expression is as follows:
In the formula,
represents the particle position,
represents the lower limit of particle search, and
represents the upper limit of particle search. In this way, the position of the particles will always be limited to the range of
, preventing the particles from jumping out of the effective search area, thus ensuring the stability and effectiveness of the search process.
Through the above description, it can be seen that the search process of particles is dynamically optimized through the linear decrease in inertia weight, the adaptive adjustment of acceleration factor, and the restriction of particle search position, thus forming an improved particle swarm optimization algorithm. In the early stage of the algorithm, the population can enhance the global search ability and expand the search range, while in the later stage, the local search ability is enhanced and the convergence speed is accelerated, which helps to find the optimal solution more effectively.
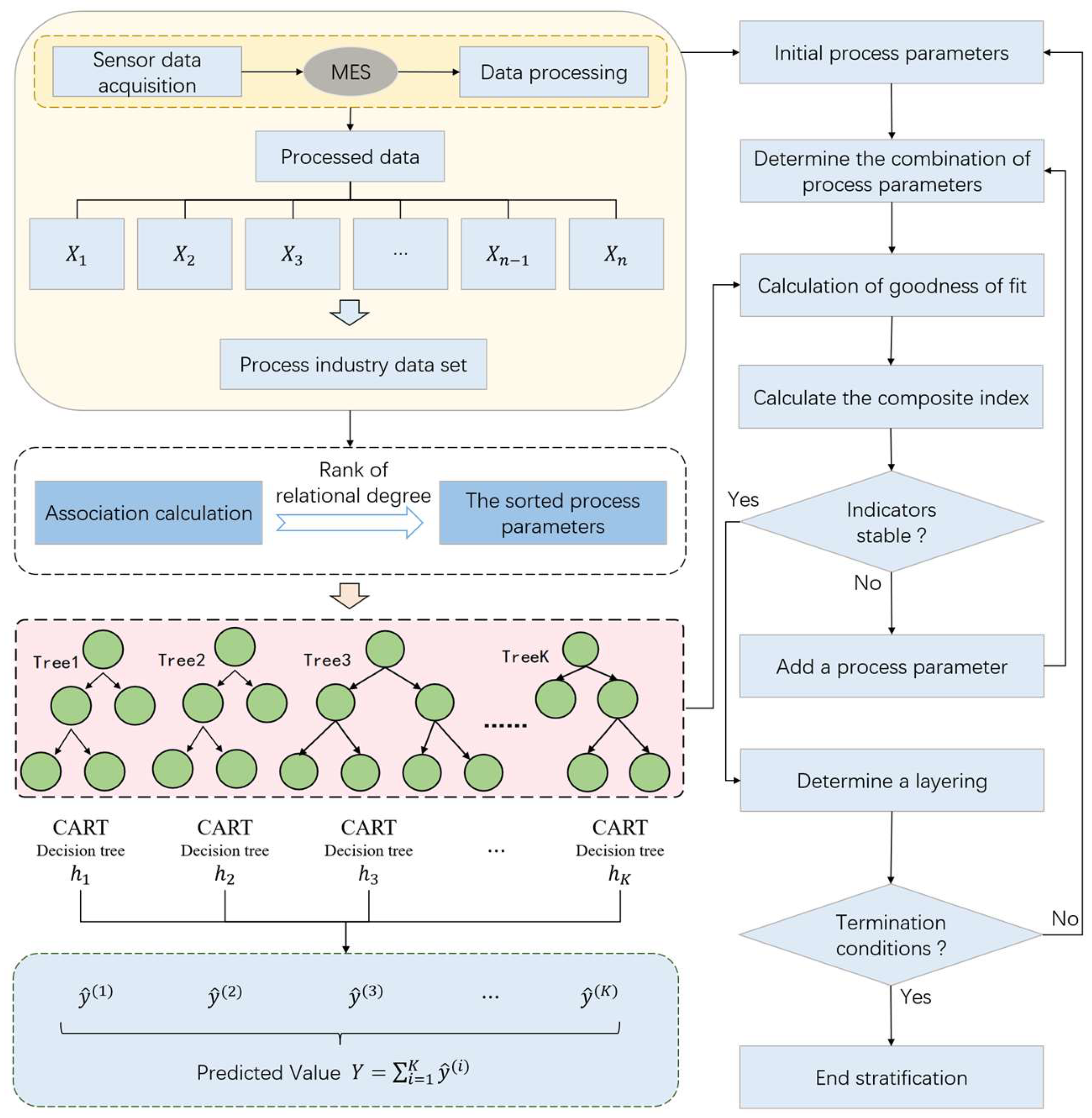
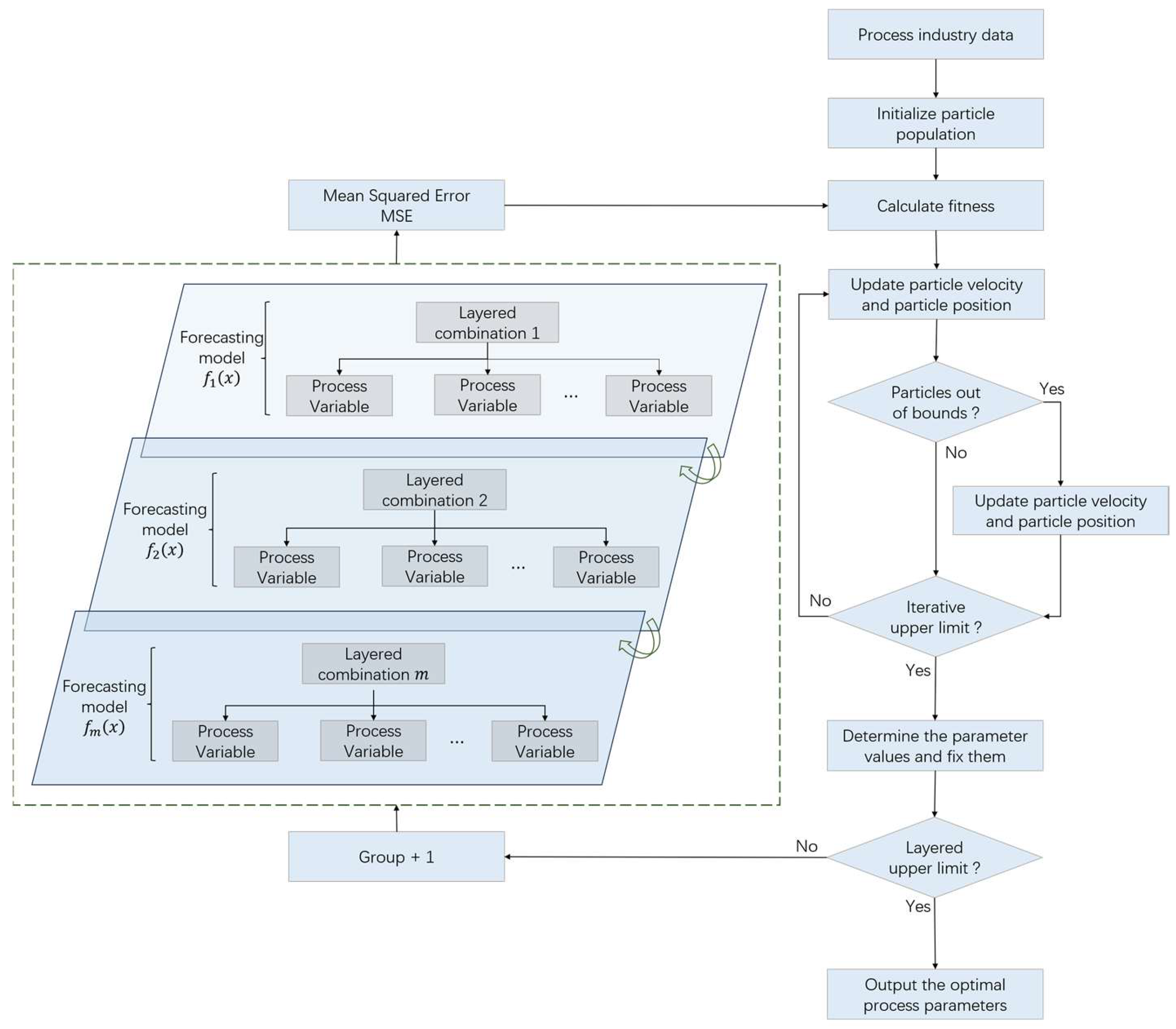
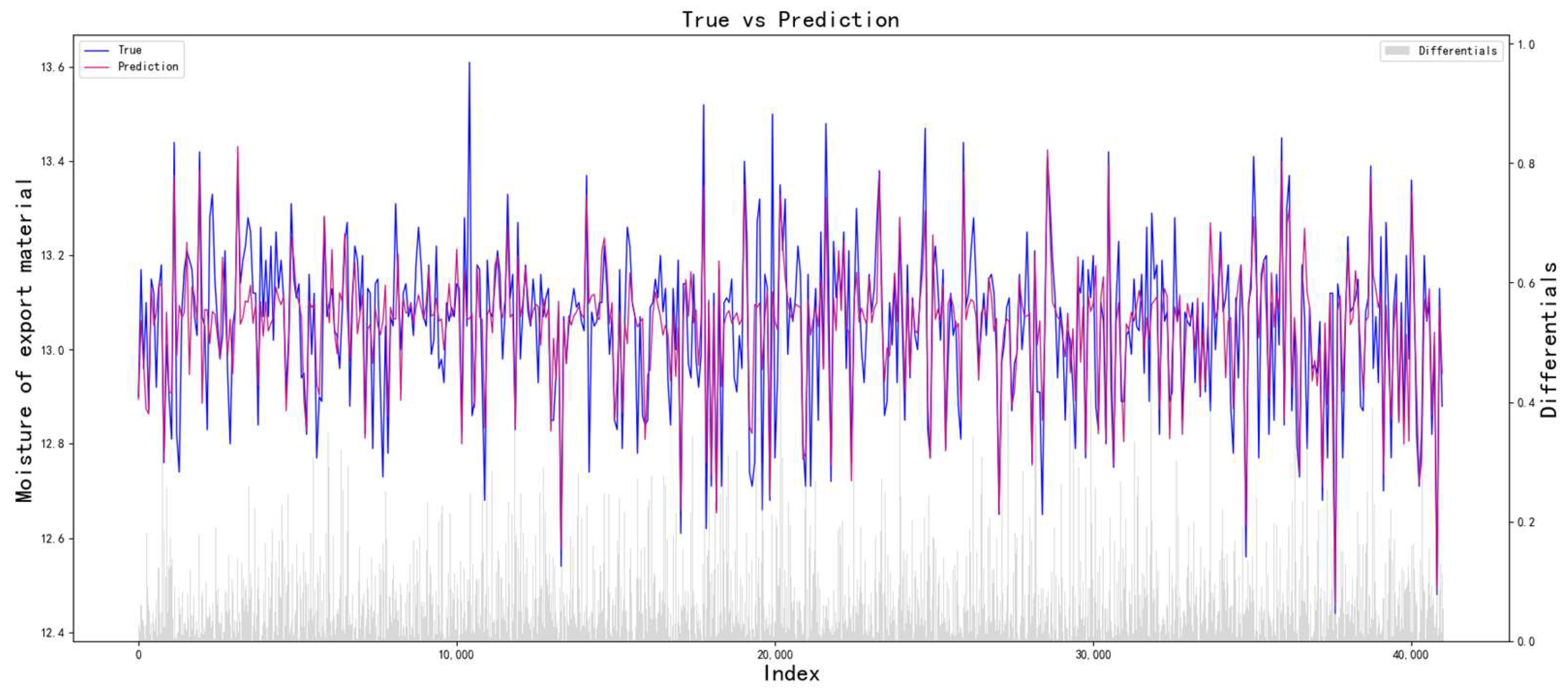
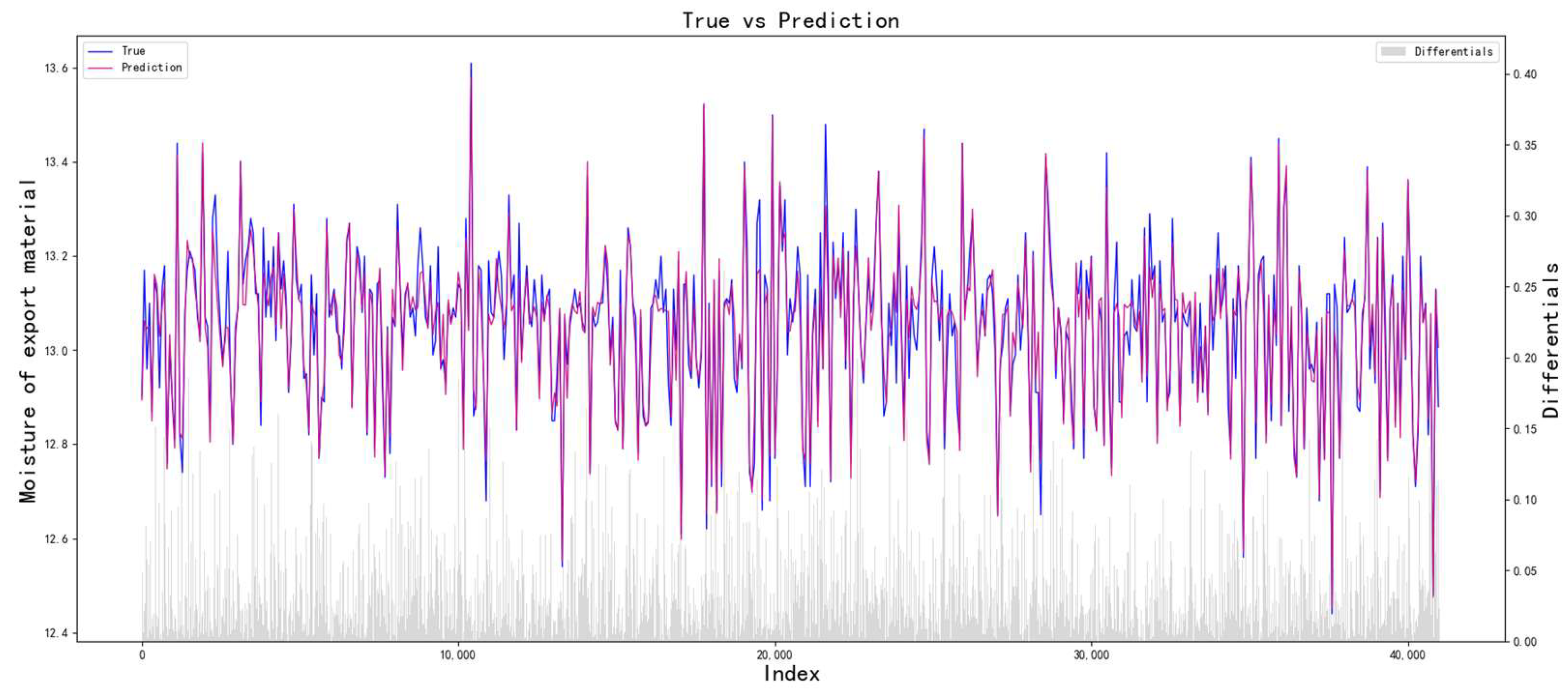
Therefore, according to the above analysis of process parameter optimization and particle swarm optimization algorithm, this paper constructs a multi-level progressive optimization model of process parameters based on an improved particle swarm optimization algorithm. The process of the multi-level progressive optimization model is shown in
Figure 3. The model uses a multi-level progressive modeling strategy to establish a nonlinear mapping relationship between process parameters and quality indicators layer by layer and uses the improved particle swarm optimization to search for the optimal combination of process parameters. When constructing the prediction model, the optimal parameter combination of each layer is transmitted to the next layer as a constant input to achieve multi-level progressive optimization of process parameters.
The parameters involved in the algorithm are shown in
Table 1.
The process of the multi-level progressive optimization model is as follows:
(1) Randomly initialize the particle swarm.
(2) Calculate the fitness of each particle.
(3) Update pbest and gbest. Each particle searches for the position with the best fitness value as its individual optimal position (pbest), while the position of the particle with the best fitness value across the entire swarm is designated as the global optimal position (gbest).
(4) Update the inertia weight according to Formula (20), and update the acceleration factors and according to Formulas (21) and (22).
(5) Update the particle velocity
and position
according to the formulas.
(6) Limit the particle position. According to Formula (23), if any particles are beyond the range, then put them back into the search range.
(7) Determine whether the maximum number of iterations is reached. If the maximum number of iterations is reached, the optimal process parameters of the layer are recorded. If the maximum number of iterations is not reached, steps (2) to (7) are repeated.
(8) Determine whether the upper limit of the number of groups is reached. If the upper limit of the number is reached, the overall optimal process parameters are output. If the upper limit of the number is not reached, another hierarchical group is added. Based on the optimization of the process parameters of all the previous layers, the prediction model is constructed for the layer, and then steps (2) to (8) are repeated.
Through the above optimization process, the optimal process parameters can be obtained layer by layer, and the optimal process parameters of each layer are based on the optimization of the previous layers. Specifically, this process fully considers the influence of parameters on quality indicators and also greatly weakens the errors caused by non-critical parameters.