Understanding Steel Corrosion: Surface Chemistry and Defects Explored Through DFT Modelling—A Review
Abstract
1. Introduction
| Method | Key Strengths | Primary Limitations | Main Outputs | Recent Applications | Refs. |
|---|---|---|---|---|---|
| Density Functional Theory (DFT) | •Provide a good balance between accuracy and computational cost •Excellent for surface adsorption and reaction energetics, and electronic structures •Reliable prediction of thermodynamic properties | •Fail to capture long-range dispersion forces accurately • Less feasible for large systems •Restricted to short simulation durations | Adsorption energies, defect formation energies, and interlayer relaxation Electronic Properties: Work functions, density of state, Mulliken population, and Bader charge analysis Magnetic Properties | Adsorption and passivation mechanisms, identifying reactive sites and surface stability, and inhibitor design | [23,35,36] |
| Ab Initio Molecular Dynamics (AIMD) | •Forces on atoms are derived from quantum calculations, yielding highly accurate structures and bonding •Provide kinetic and thermodynamic insights •Ideal for understanding reaction pathways and electronic interactions. •Highly transferable across different surface types, adsorbates, and environmental conditions | •Computationally expensive, limiting its application to large systems and long simulation times •Convergence issues for complex systems | Diffusion coefficients and reaction rates (short-time scale) Reaction pathways and barriers Dissolution energies, chemical binding, and charge transfer | Water–metal interfaces, oxide nucleation, and dissolution corrosion | [34,37] |
| Reactive Force Fields (ReaxFF) | •Enable the study of chemical reactions with bond formation/breaking • Capability to model the effects of temperature, pH, and aggressive ions on corrosion rate and mechanism • Enables modelling of complex reactive systems over a long time | • Depends on empirical parameters, limiting its accuracy and transferability across different systems • Needs reparameterization when applied to a new chemical environment (e.g., introducing new alloy elements, different pH, or complex oxidizers) | Diffusion coefficient and reaction rates Oxide layer thickness | Growth of oxide layers, pit formation studies, and stress corrosion | [34,38] |
| Monte-Carlo and Kinetic Modelling | • Computationally efficient for large systems and high-dimensional phase spaces. • Effectively samples equilibrium configurations and capable of simulating short-range order in high-entropy or multi-element alloy surfaces exposed to corrosive environments • Successfully simulate the kinetics of corrosion processes at different scales | • Relies on empirical or fitted potential energy models, which limits its transferability and accuracy for systems with complex chemistries | Phase diagrams Order–disorder transitions in surface adsorbates or alloy atoms Corrosion mass gain and corrosion rates Equilibrium surface coverage and segregation profiles | Kinetics of passive film formation, alloy segregation behaviour, and modelling of corrosion inhibitors | [39,40] |
| Finite Element method | • Provide macroscale structural analysis • Capability to handle complex geometries, and multi-field coupling | • Lacks the capability to capture atomistic-scale phenomena •Depends on precise material properties and constitutive models to generate reliable results | Stress distributions Mechanical strength and structural integrity Life span of materials | Pipeline corrosion assessment, coating failure analysis, and galvanic corrosion modelling | [23,41] |
| Machine learning and AI modelling | • Can integrate experimental and simulation data to predict the severity of corrosion • Can be tailored to different data characteristics, balancing between accuracy, computational cost, and robustness to noise/outliers • Can handle and analyse very large volumes of data efficiently | • The effectiveness of the outcome relies on having ample, reliable, and varied data to learn from. | Corrosion rate Corrosion-fatigue crack growth Corrosion defect growth | Automated corrosion detection by image processing, corrosion severity prediction, and defect depth estimation in infrastructure | [23,42,43] |
| Multiscale Modelling | • Bridges multiple length/time scales • Provide a comprehensive modelling approach • Provide synergistic accuracy enhancement • Reduces computational cost vs. full quantum | • Complex implementation and validation • Error propagation between scales • High computational demands • Interface definition challenges | Hierarchical predictions Validated mechanisms Corrosion inhibitors and alloy design guidelines | Design of corrosion-resistant alloys, modelling corrosion at grain boundaries and interfaces | [19,44] |
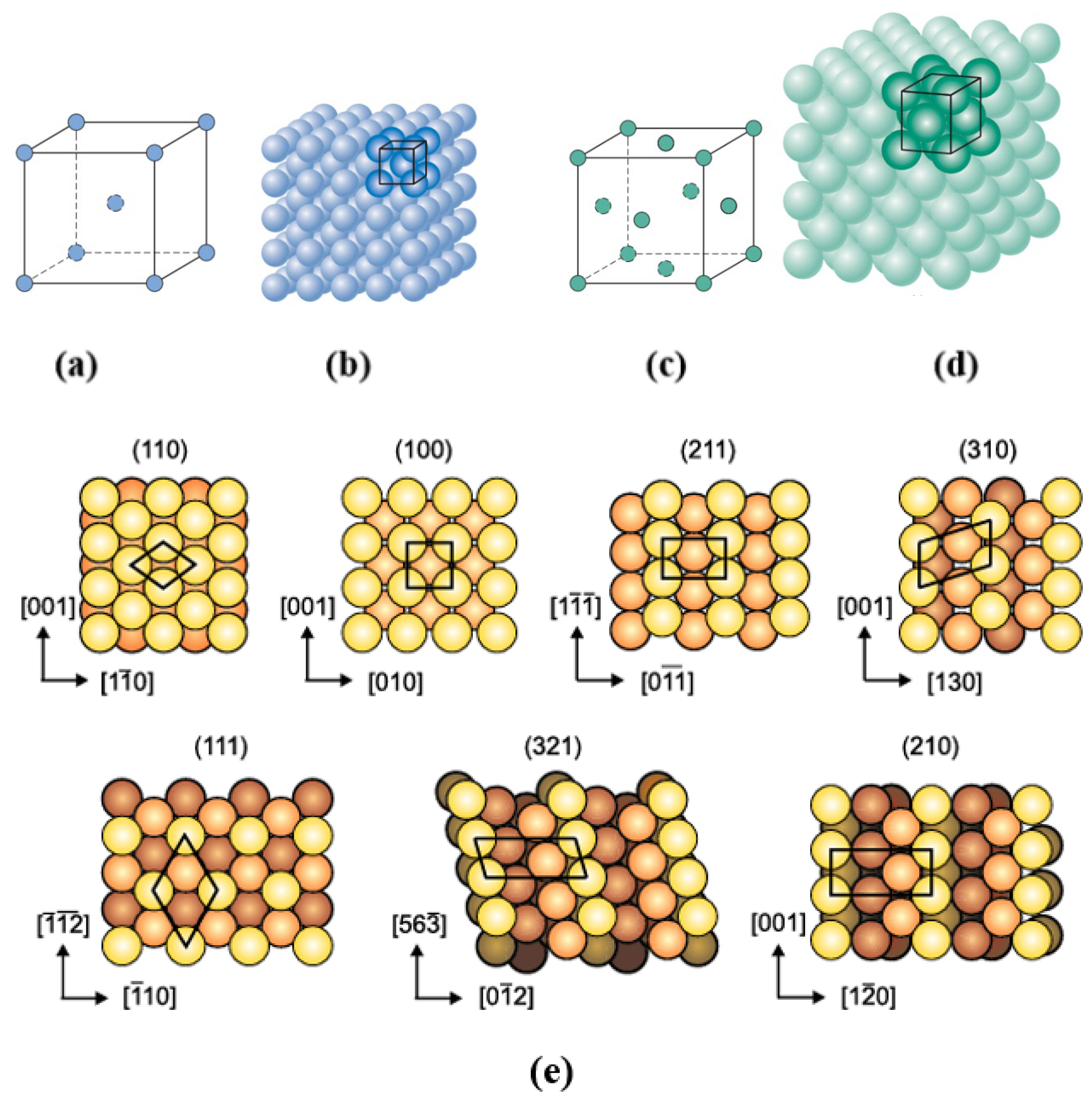
2. Surface Slab Setup for Simulation
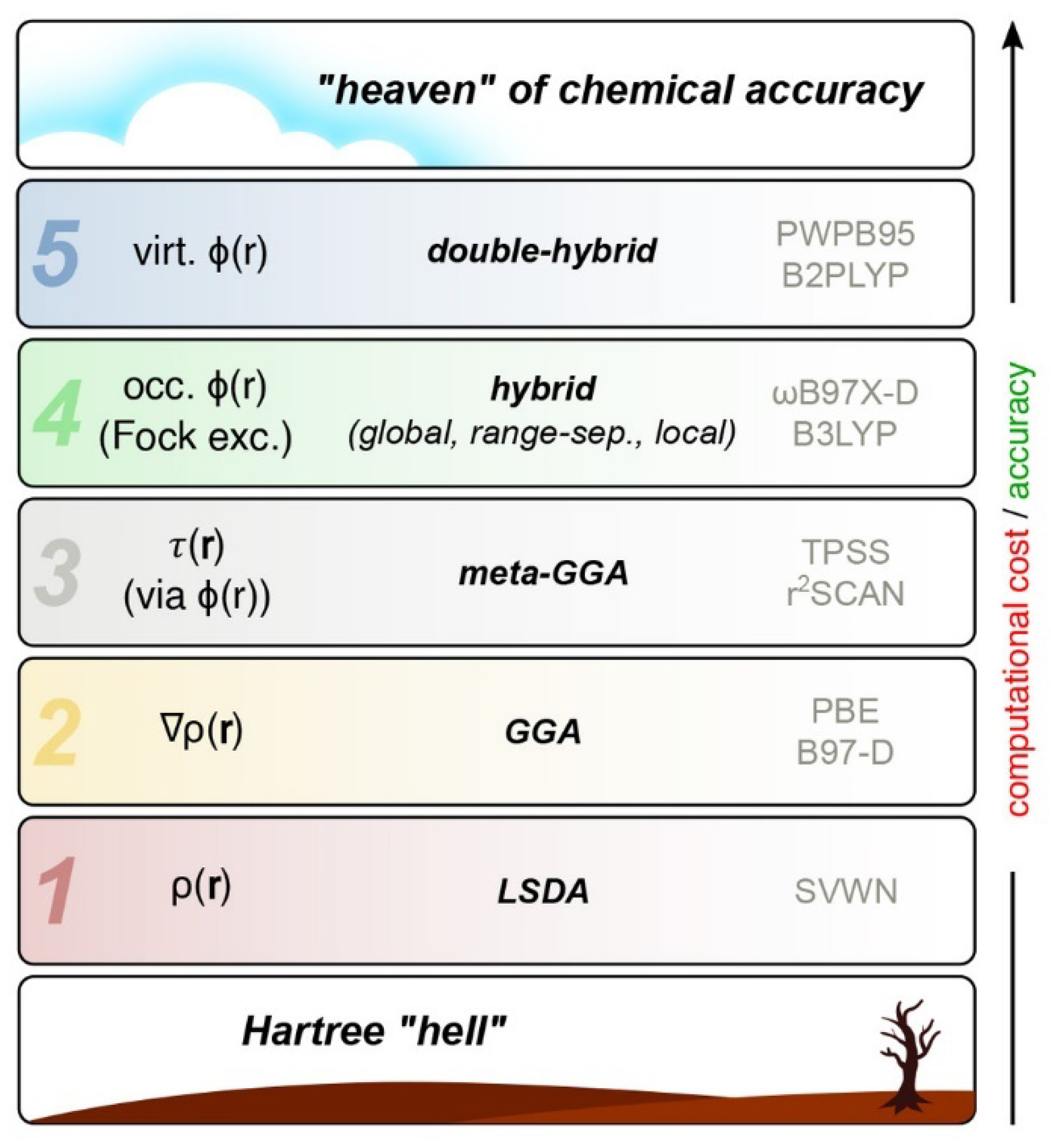
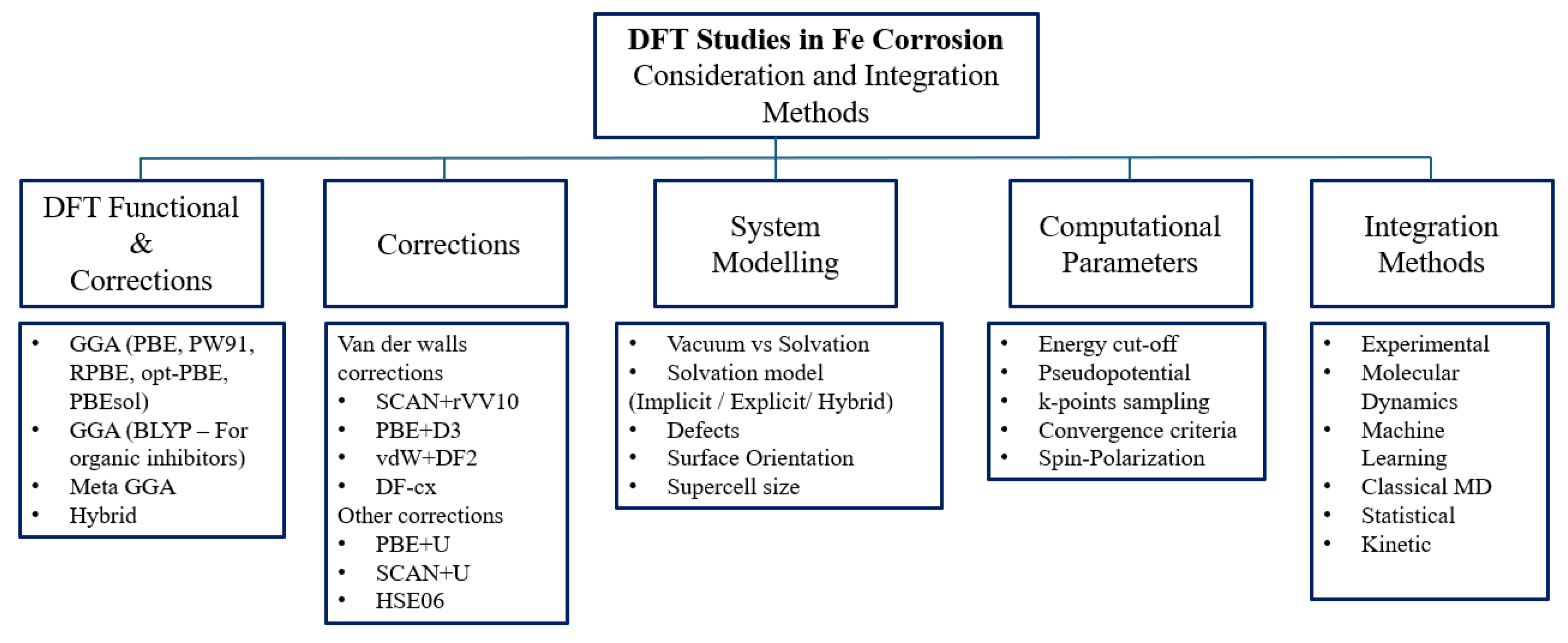
3. DFT Based Approaches in Corrosion Studies
| Software | Basis Set | Computational Demand | Licensing | Recent Applications in Corrosion |
|---|---|---|---|---|
| VASP | Plane-wave | High | Commercial | [2,5,70,71] |
| CASTEP | Plane-wave | Moderate | Open source | [10,72] |
| Quantum ESPRESSO | Plane-wave | Moderate | Open source | [73,74] |
| WIEN2k | Full-potential LAPW | High | Commercial | [75,76] |
| Gaussian | Localised/flexible | Flexible | Commercial | [77] |
| ABINIT | Plane-wave | Moderate | Open source | [78] |
| CP2K | Hybrid (Gaussian + PW) | Lower | Open source | [52] |
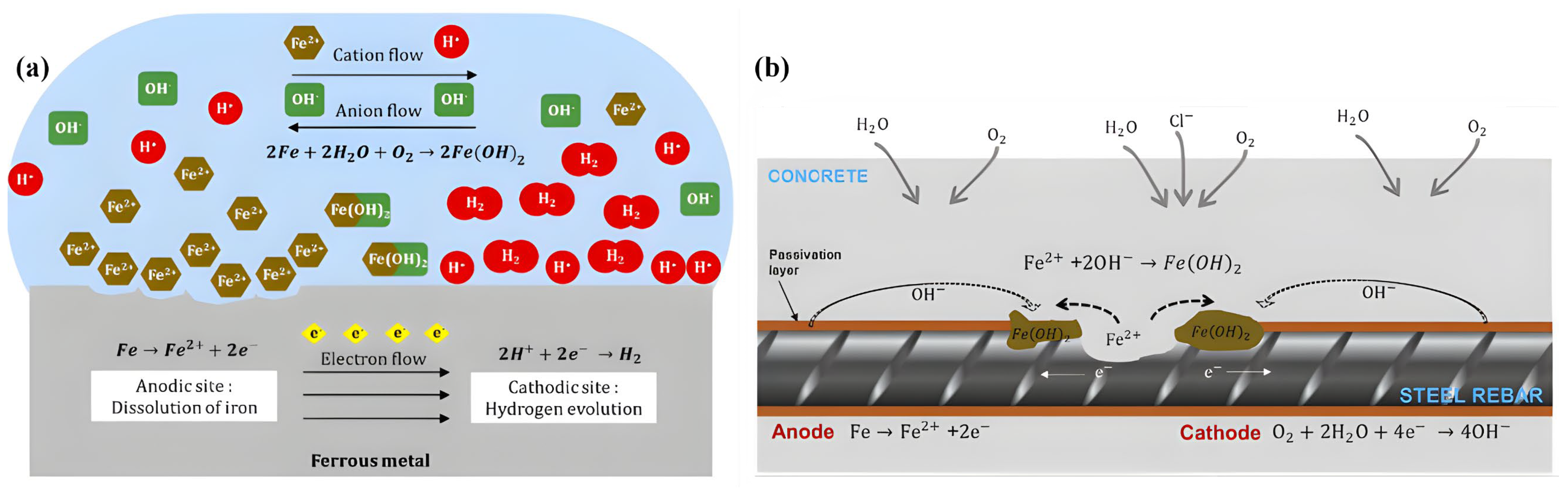
4. Corrosive Agents and Their Chemistry
4.1. Chemistry of Oxidation with Oxygen
4.2. Other Oxidation Agent
4.3. The Role of Water in Corrosion Processes
4.4. Hydrogen Embrittlement
5. Modelling Defects on the Iron Surface
5.1. Modelling the Effects of Point Defects
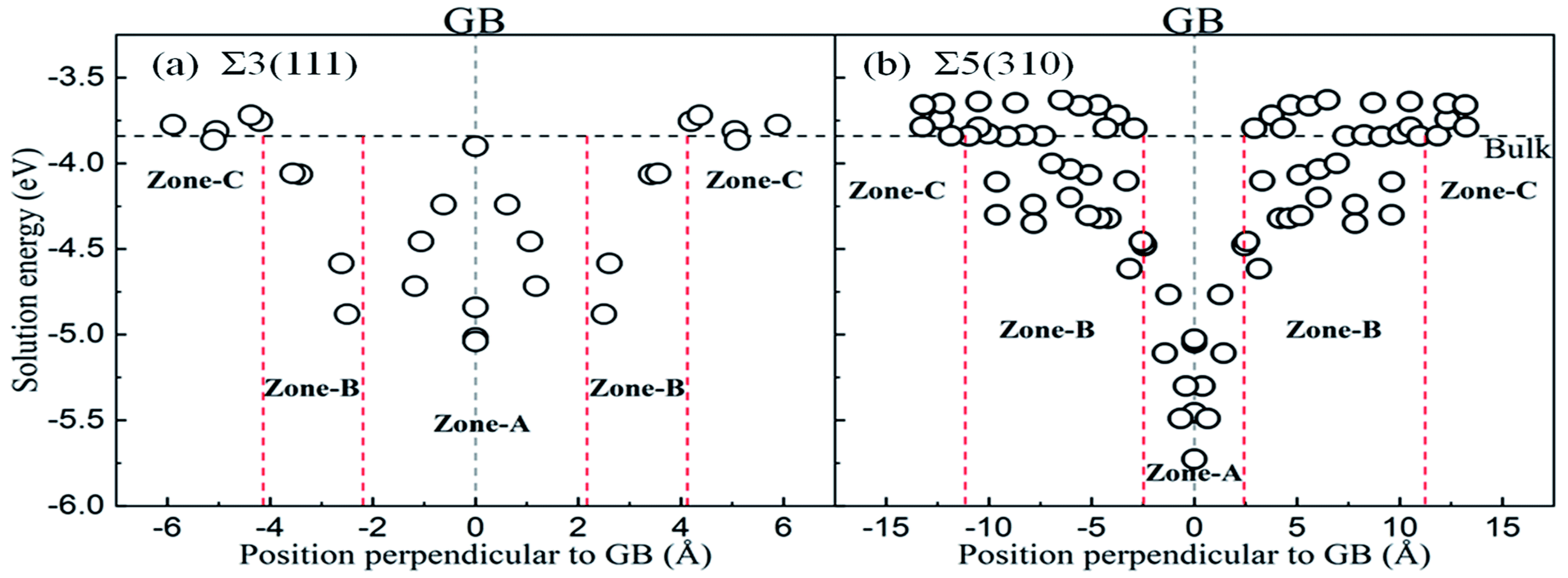
5.2. Planar Defects and Their Modelling
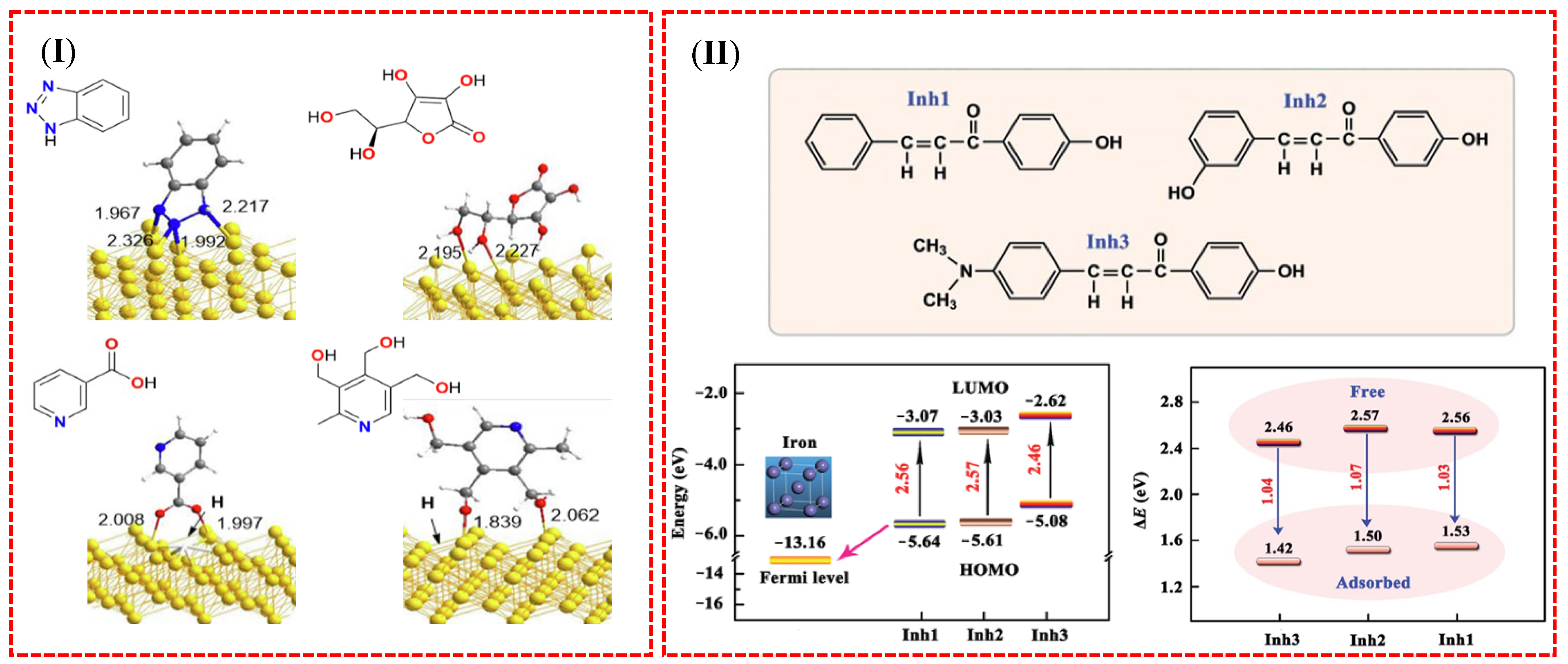
6. Corrosion Prevention Strategies: Organic Corrosion Inhibitors
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ibrahimi, B.E.; Nardeli, J.V.; Guo, L. An overview of corrosion. In Sustainable Corrosion Inhibitors I: Fundamentals, Methodologies, and Industrial Applications; American Chemical Society: Washington, DC, USA, 2021; pp. 1–19. [Google Scholar]
- Jin, H.; Blackwood, D.J.; Wang, Y.; Ng, M.-F.; Tan, T.L. First-principles study of surface orientation dependent corrosion of BCC iron. Corros. Sci. 2022, 196, 110029. [Google Scholar] [CrossRef]
- Almusallam, A.A. Effect of degree of corrosion on the properties of reinforcing steel bars. Constr. Build. Mater. 2001, 15, 361–368. [Google Scholar] [CrossRef]
- NACE International. 2016. Available online: https://impact.nace.org/ (accessed on 17 January 2025).
- Li, Y.; Zhou, R.; Gao, T.; Chen, C. First-principles explain the anodic dissolution corrosion of stainless steel surface. Comput. Mater. Sci. 2023, 229, 112392. [Google Scholar] [CrossRef]
- Omer, R.A.; Azeez, Y.H.; Kareem, R.O.; Ahmed, L.O.; Safin, D.A. Combined DFT and Monte Carlo simulation studies of potential corrosion inhibition properties of coumarin derivatives. J. Mol. Model. 2024, 30, 288. [Google Scholar] [CrossRef]
- Schlegel, J. The World of Steel; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Kisku, N. Strengthening of High-Alloy Steel through Innovative Heat Treatment Routes. In Welding-Modern Topics; IntechOpen: London, UK, 2020. [Google Scholar]
- Dutta, S. Different types and new applications of stainless steel. Stainl. Steel 2018, 62, 86–91. [Google Scholar]
- Chen, Z.; Nong, Y.; Chen, J.; Chen, Y.; Yu, B. A DFT study on corrosion mechanism of steel bar under water-oxygen interaction. Comput. Mater. Sci. 2020, 171, 109265. [Google Scholar] [CrossRef]
- Vakili, M.; Koutnik, P.; Kohout, J. Corrosion by Polythionic Acid in the Oil and Gas Sector: A Brief Overview. Materials 2023, 16, 7043. [Google Scholar] [CrossRef]
- Katona, R.M.; Taylor, J.M.; McCready, T.A.; Bryan, C.R.; Schaller, R.F. Towards understanding stress corrosion cracking of austenitic stainless steels exposed to realistic sea salt brines. Corros. Sci. 2024, 232, 111992. [Google Scholar] [CrossRef]
- Sulaiman, K.O.; Onawole, A.T.; Faye, O.; Shuaib, D.T. Understanding the corrosion inhibition of mild steel by selected green compounds using chemical quantum based assessments and molecular dynamics simulations. J. Mol. Liq. 2019, 279, 342–350. [Google Scholar] [CrossRef]
- Minagalavar, R.L.; Rajappa, S.K.; Rathod, M.R.; Sajjan, A.M. Investigation of corrosion inhibition performance of expired fluconazole drug on mild steel in 0.5M H2SO4 medium. J. Mol. Liq. 2023, 391, 123291. [Google Scholar] [CrossRef]
- Bahraq, A.A.; Obot, I.B.; Al-Osta, M.A.; Ibrahim, M. Molecular simulations of anticorrosion behavior of inhibitors for steel in concrete: A review on recent advances and progress. Constr. Build. Mater. 2024, 412, 134808. [Google Scholar] [CrossRef]
- Hu, J.Y.; Zhang, S.S.; Chen, E.; Li, W.G. A review on corrosion detection and protection of existing reinforced concrete (RC) structures. Constr. Build. Mater. 2022, 325, 126718. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, Z.; Feng, Q.; Huang, Z.; Zhu, X.; Xiao, L.; He, J.; Wang, N.; Xu, Y. First Principles Study of Atomic Oxygen Adsorption on Austenitic Stainless Steels Surfaces: A Theoretical Study. Coatings 2023, 13, 455. [Google Scholar] [CrossRef]
- Waseda, Y.; Suzuki, S.; Waseda, Y. Characterization of Corrosion Products on Steel Surfaces; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Wenga, T.; Macdonald, D.D.; Ma, W. Multi-scale computational study of high-temperature corrosion and the design of corrosion-resistant alloys. Prog. Mater. Sci. 2024, 148, 101359. [Google Scholar] [CrossRef]
- Haris, N.I.N.; Sobri, S.; Yusof, Y.A.; Kassim, N.K. An overview of molecular dynamic simulation for corrosion inhibition of ferrous metals. Metals 2020, 11, 46. [Google Scholar] [CrossRef]
- Huet, B.; L’hostis, V.; Santarini, G.; Feron, D.; Idrissi, H. Steel corrosion in concrete: Determinist modeling of cathodic reaction as a function of water saturation degree. Corros. Sci. 2007, 49, 1918–1932. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, Z.; Chen, Y.; Nong, Y.; Yi, C. Molecular insight into iron corrosion induced by chloride and sulphate. Comput. Mater. Sci. 2022, 209, 111429. [Google Scholar] [CrossRef]
- Li, S.; Li, C.; Wang, F. Computational experiments of metal corrosion studies: A review. Mater. Today Chem. 2024, 37, 101986. [Google Scholar] [CrossRef]
- Wei, J.; Fu, Q.; Chen, D.; Wang, X.; Cao, W.; Xu, D.; Zheng, H. Multi-scale investigation of stainless-steel passivation in seawater concrete pore solution. Case Stud. Constr. Mater. 2024, 21, e04078. [Google Scholar] [CrossRef]
- Xue, S.; Su, T.; Zhao, X.; Zong, Z. Multi-scale analysis of corrosion-induced fracture failure mechanisms of high-strength steel wire. Appl. Eng. Sci. 2024, 17, 100172. [Google Scholar] [CrossRef]
- Elaraby, A.; Qasim, K.F.; Mohamed, S.K.; El-Sharkawy, E.; Abdelhamed, S. Multi-scale quantum (DFT, MCs and MDs) insights and electrochemical validation of di-imine Schiff base inhibitor for carbon steel corrosion control in 1 M HCl solution. Appl. Mater. Today 2025, 42, 102615. [Google Scholar] [CrossRef]
- Ser, C.T.; Žuvela, P.; Wong, M.W. Prediction of corrosion inhibition efficiency of pyridines and quinolines on an iron surface using machine learning-powered quantitative structure-property relationships. Appl. Surf. Sci. 2020, 512, 145612. [Google Scholar] [CrossRef]
- Guo, Z.; Qin, L.; Zhao, S.; Wang, D.; Lv, X.; Qiang, Y.; Guo, W.; Shu, Q.; Yao, Y. Unveiling the corrosion mechanism of 3-nitro-1, 2, 4-triazol-5-one (NTO) toward mild steel from ab initio molecular dynamics: How the “nitro-to-amino” reaction matters. J. Mater. Chem. A 2023, 11, 16049–16058. [Google Scholar] [CrossRef]
- Sundar, A.; Chen, G.; Qi, L. Substitutional adsorptions of chloride at grain boundary sites on hydroxylated alumina surfaces initialize localized corrosion. NPJ Mater. Degrad. 2021, 5, 18. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Ma, L.; Li, Y.; Le, J.; Fu, Z.; Lu, L.; Zhang, D. Understanding the adsorption of imidazole corrosion inhibitor at the copper/water interface by ab initio molecular dynamics. Corros. Sci. 2024, 236, 112237. [Google Scholar] [CrossRef]
- Chen, D.; Zhou, W.; Ji, Y.; Dong, C. Applications of density functional theory to corrosion and corrosion prevention of metals: A review. Mater. Genome Eng. Adv. 2025, 3, e83. [Google Scholar] [CrossRef]
- Devi, A.A.S.; Javaheri, V.; Pallaspuro, S.; Komi, J. The role of density functional theory in decoding the complexities of hydrogen embrittlement in steels. Phys. Chem. Chem. Phys. 2024, 26, 26222–26237. [Google Scholar] [CrossRef]
- Parangusan, H.; Bhadra, J.; Al-Thani, N. A review of passivity breakdown on metal surfaces: Influence of chloride-and sulfide-ion concentrations, temperature, and pH. Emergent Mater. 2021, 4, 1187–1203. [Google Scholar] [CrossRef]
- Arachchige, L.J.; Li, C.; Wang, F. Recent advances in understanding iron/steel corrosion: Mechanistic insights from molecular simulations. Curr. Opin. Solid State Mater. Sci. 2025, 35, 101216. [Google Scholar] [CrossRef]
- Hasnip, P.J.; Refson, K.; Probert, M.I.; Yates, J.R.; Clark, S.J.; Pickard, C.J. Density functional theory in the solid state. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130270. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, J.; Liu, Y.; Xi, J.; Li, Q.; Xiang, H.; Zhou, Y. Application of high-throughput first-principles calculations in ceramic innovation. J. Mater. Sci. Technol. 2021, 88, 143–157. [Google Scholar] [CrossRef]
- Jiang, L.; Qiu, J.; Lin, S.; Yin, H.; Wu, X.; Shen, C.; Zhang, B.; Liu, W. Chemical states of corrosion products in liquid lead from ab initio molecular dynamics. J. Nucl. Mater. 2024, 599, 155237. [Google Scholar] [CrossRef]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M. The ReaxFF reactive force-field: Development, applications and future directions. NPJ Comput. Mater. 2016, 2, 15011. [Google Scholar] [CrossRef]
- Zhang, Z.; Niu, G.; Yang, X.; Chen, H.; Anijdan, S.M.; Zhang, P.; Yu, X.; Gong, N.; Liu, H.; Mao, X. Corrosion resistance behavior of enhanced passivation Cr-modified rebars and their service life prediction based on Monte Carlo simulation. Constr. Build. Mater. 2024, 438, 137130. [Google Scholar] [CrossRef]
- Martin-Bragado, I.; Borges, R.; Balbuena, J.P.; Jaraiz, M. Kinetic Monte Carlo simulation for semiconductor processing: A review. Prog. Mater. Sci. 2018, 92, 1–32. [Google Scholar] [CrossRef]
- Alaneme, K.K.; Kareem, S.A.; Ozah, B.N.; Alshahrani, H.A.; Ajibuwa, O.A. Application of finite element analysis for optimizing selection and design of Ti-based biometallic alloys for fractures and tissues rehabilitation: A review. J. Mater. Res. Technol. 2022, 19, 121–139. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Yang, L.; Zhou, Y.C. A multiscale model integrating artificial neural networks for failure prediction in turbine blade coatings. Surf. Coat. Technol. 2023, 457, 129218. [Google Scholar] [CrossRef]
- Jiang, D.; Xie, L.; Wang, L. Current application status of multi-scale simulation and machine learning in research on high-entropy alloys. J. Mater. Res. Technol. 2023, 26, 1341–1374. [Google Scholar] [CrossRef]
- Callister Jr, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Chen, Q.; Sundman, B. Modeling of thermodynamic properties for Bcc, Fcc, liquid, and amorphous iron. J. Phase Equilibria 2001, 22, 631–644. [Google Scholar] [CrossRef]
- Körmann, F.; Breidi, A.A.H.; Dudarev, S.L.; Dupin, N.; Ghosh, G.; Hickel, T.; Korzhavyi, P.; Muñoz, J.A.; Ohnuma, I. Lambda transitions in materials science: Recent advances in CALPHAD and first-principles modelling. Phys. Status Solidi (b) 2014, 251, 53–80. [Google Scholar] [CrossRef]
- Ehteshami, H.; Korzhavyi, P.A. Thermophysical properties of paramagnetic Fe from first principles. Phys. Rev. B 2017, 96, 224406. [Google Scholar] [CrossRef]
- Błoński, P.; Kiejna, A. Structural, electronic, and magnetic properties of bcc iron surfaces. Surf. Sci. 2007, 601, 123–133. [Google Scholar] [CrossRef]
- Ameh, E.S. A review of basic crystallography and x-ray diffraction applications. Int. J. Adv. Manuf. Technol. 2019, 105, 3289–3302. [Google Scholar] [CrossRef]
- Yin, X.; Wang, H.; Han, E.-H. Effects of solvation and applied potential on the adsorption behaviors of H, O, OH and H2O on Fe(110) surface. Surf. Sci. 2020, 691, 121504. [Google Scholar] [CrossRef]
- Glezakou, V.-A.; Dang, L.X.; McGrail, B.P. Spontaneous activation of CO2 and possible corrosion pathways on the low-index iron surface Fe (100). J. Phys. Chem. C 2009, 113, 3691–3696. [Google Scholar] [CrossRef]
- Freindl, K.; Ossowski, T.; Zając, M.; Spiridis, N.; Wilgocka-Ślęzak, D.; Madej, E.; Giela, T.; Kiejna, A.; Korecki, J. Oxygen Adsorption on the Fe(110) Surface: The Old System—New Structures. J. Phys. Chem. C 2016, 120, 3807–3813. [Google Scholar] [CrossRef]
- Ossowski, T.; Da Silva, J.L.; Kiejna, A. Water adsorption on the stoichiometric and defected Fe (110) surfaces. Surf. Sci. 2018, 668, 144–149. [Google Scholar] [CrossRef]
- Guo, L.; Obot, I.B.; Zheng, X.; Shen, X.; Qiang, Y.; Kaya, S.; Kaya, C. Theoretical insight into an empirical rule about organic corrosion inhibitors containing nitrogen, oxygen, and sulfur atoms. Appl. Surf. Sci. 2017, 406, 301–306. [Google Scholar] [CrossRef]
- Xu, L.; Kirvassilis, D.; Bai, Y.; Mavrikakis, M. Atomic and molecular adsorption on Fe(110). Surf. Sci. 2018, 667, 54–65. [Google Scholar] [CrossRef]
- Yu, J.; Lin, X.; Wang, J.; Chen, J.; Huang, W. First-principles study of the relaxation and energy of bcc-Fe, fcc-Fe and AISI-304 stainless steel surfaces. Appl. Surf. Sci. 2009, 255, 9032–9039. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.; Joannopoulos, A.J. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A modular and open-source software project for quantumsimulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.; Marks, L.D. WIEN2k: An APW+ lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Gonze, X. A brief introduction to the ABINIT software package. Z. Für Krist.-Cryst. Mater. 2005, 220, 558–562. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Hafner, J.; Kresse, G. The vienna ab-initio simulation program VASP: An efficient and versatile tool for studying the structural, dynamic, and electronic properties of materials. In Properties of Complex Inorganic Solids; Springer: Berlin/Heidelberg, Germany, 1997; pp. 69–82. [Google Scholar]
- Hafner, J. Materials simulations using VASP—A quantum perspective to materials science. Comput. Phys. Commun. 2007, 177, 6–13. [Google Scholar] [CrossRef]
- Kitchin, J. Modeling Materials Using Density Functional Theory; Free Software Foundation: Boston, MA, USA, 2008. [Google Scholar]
- Ossowski, T.; Kiejna, A. Structure and energetics of FeO/Fe(001) interfaces. J. Phys. Condens. Matter 2023, 35, 465001. [Google Scholar] [CrossRef] [PubMed]
- Versteylen, C.D.; van Dijk, N.H.; Sluiter, M.H.F. First-principles analysis of solute diffusion in dilute bcc Fe-X alloys. Phys. Rev. B 2017, 96, 094105. [Google Scholar] [CrossRef]
- Gong, L.; Fu, H.; Zhi, X. First-principles study on corrosion resistance of copper-bearing hypereutectic high chromium cast iron. Mater. Today Commun. 2022, 33, 104345. [Google Scholar] [CrossRef]
- Huang, X.; Ramadugu, S.K.; Mason, S.E. Surface-specific DFT+ U approach applied to α-Fe2O3 (0001). J. Phys. Chem. C 2016, 120, 4919–4930. [Google Scholar] [CrossRef]
- Fatti, G.; Restuccia, P.; Calandra, C.; Righi, M.C. Phosphorus Adsorption on Fe(110): An ab Initio Comparative Study of Iron Passivation by Different Adsorbates. J. Phys. Chem. C 2018, 122, 28105–28112. [Google Scholar] [CrossRef]
- Mouatassime, M.; Selmani, Y.; Idrissi, S.; Bahmad, L.; Goumrhar, F.; Labrim, H.; Benyoussef, A. Magnetic properties and half metallic behavior of the Full-Heusler Co2FeGe alloy: DFT and Monte Carlo studies. J. Solid State Chem. 2021, 304, 122534. [Google Scholar] [CrossRef]
- Yu, X.-x.; Gulec, A.; Cwalina, K.L.; Scully, J.R.; Marks, L.D. New insights on the role of chloride during the onset of local corrosion: TEM, APT, surface energy, and morphological instability. Corrosion 2019, 75, 616–627. [Google Scholar] [CrossRef]
- Azeez, Y.H.; Kareem, R.O.; Qader, A.F.; Omer, R.A.; Ahmed, L.O. Spectroscopic characteristics, stability, reactivity, and corrosion inhibition of AHPE-dop compounds incorporating (B, Fe, Ga, Ti): A DFT investigation. Next Mater. 2024, 3, 100184. [Google Scholar] [CrossRef]
- Torrent, M.; Jollet, F.; Bottin, F.; Zérah, G.; Gonze, X. Implementation of the projector augmented-wave method in the ABINIT code: Application to the study of iron under pressure. Comput. Mater. Sci. 2008, 42, 337–351. [Google Scholar] [CrossRef]
- Makkar, P.; Ghosh, N.N. A review on the use of DFT for the prediction of the properties of nanomaterials. RSC Adv. 2021, 11, 27897–27924. [Google Scholar] [CrossRef] [PubMed]
- Kiely, E.; Zwane, R.; Fox, R.; Reilly, A.M.; Guerin, S. Density functional theory predictions of the mechanical properties of crystalline materials. CrystEngComm 2021, 23, 5697–5710. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413. [Google Scholar] [CrossRef]
- Janthon, P.; Kozlov, S.M.; Vines, F.; Limtrakul, J.; Illas, F. Establishing the accuracy of broadly used density functionals in describing bulk properties of transition metals. J. Chem. Theory Comput. 2013, 9, 1631–1640. [Google Scholar] [CrossRef]
- Bursch, M.; Mewes, J.M.; Hansen, A.; Grimme, S. Best-practice DFT protocols for basic molecular computational chemistry. Angew. Chem. 2022, 134, e202205735. [Google Scholar] [CrossRef]
- Grubova, I.Y.; Surmeneva, M.A.; Surmenev, R.A.; Neyts, E.C. Effect of van der Waals interactions on the adhesion strength at the interface of the hydroxyapatite-titanium biocomposite: A first-principles study. RSC Adv. 2020, 10, 37800–37805. [Google Scholar] [CrossRef]
- Reilly, A.M.; Tkatchenko, A. van der Waals dispersion interactions in molecular materials: Beyond pairwise additivity. Chem. Sci. 2015, 6, 3289–3301. [Google Scholar] [CrossRef]
- Patra, A.; Bates, J.E.; Sun, J.; Perdew, J.P. Properties of real metallic surfaces: Effects of density functional semilocality and van der Waals nonlocality. Proc. Natl. Acad. Sci. USA 2017, 114, E9188–E9196. [Google Scholar] [CrossRef]
- Park, J.; Yu, B.D.; Hong, S. Van der Waals density functional theory study for bulk solids with BCC, FCC, and diamond structures. Curr. Appl. Phys. 2015, 15, 885–891. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Comparative DFT study of van der Waals complexes: Rare-gas dimers, alkaline-earth dimers, zinc dimer, and zinc-rare-gas dimers. J. Phys. Chem. A 2006, 110, 5121–5129. [Google Scholar] [CrossRef] [PubMed]
- Vlaisavljevich, B.; Huck, J.; Hulvey, Z.; Lee, K.; Mason, J.A.; Neaton, J.B.; Long, J.R.; Brown, C.M.; Alfe, D.; Michaelides, A.; et al. Performance of van der Waals Corrected Functionals for Guest Adsorption in the M(2)(dobdc) Metal-Organic Frameworks. J. Phys. Chem. A 2017, 121, 4139–4151. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Li, J.; Su, G.; Ferri, N.; Liu, W.; Tkatchenko, A. Tuning the work function of stepped metal surfaces by adsorption of organic molecules. J. Phys. Condens. Matter 2017, 29, 204001. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, W.; Li, S.; Zhang, D.; Zhao, Y.; Lavernia, E.J.; Zhu, Y. Contribution of van der Waals forces to the plasticity of magnesium. Acta Mater. 2016, 107, 127–132. [Google Scholar] [CrossRef]
- White, J.J.; Liu, J.; Hinsch, J.J.; Wang, Y. Theoretical understanding of the properties of stepped iron surfaces with van der Waals interaction corrections. Phys. Chem. Chem. Phys. 2021, 23, 2649–2657. [Google Scholar] [CrossRef]
- Berland, K.; Hyldgaard, P. Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional. Phys. Rev. B 2014, 89, 1–6. [Google Scholar] [CrossRef]
- White, J.J.; Hinsch, J.J.; Bennett, W.W.; Wang, Y. Theoretical understanding of water adsorption on stepped iron surfaces. Appl. Surf. Sci. 2022, 605, 154650. [Google Scholar] [CrossRef]
- Fu, Y.; Singh, D.J. Applicability of the Strongly Constrained and Appropriately Normed Density Functional to Transition-Metal Magnetism. Phys. Rev. Lett. 2018, 121, 207201. [Google Scholar] [CrossRef]
- Dannenberg, A.; Gruner, M.E.; Hucht, A.; Entel, P. Surface energies of stoichiometric FePt and CoPt alloys and their implications for nanoparticle morphologies. Phys. Rev. B—Condens. Matter Mater. Phys. 2009, 80, 245438. [Google Scholar] [CrossRef]
- Błoński, P.; Kiejna, A. Calculation of surface properties of bcc iron. Vacuum 2004, 74, 179–183. [Google Scholar] [CrossRef]
- Ye, Z.; Lei, Y.; Zhang, J.; Zhang, Y.; Li, X.; Xu, Y.; Wu, X.; Liu, C.S.; Hao, T.; Wang, Z. Effects of oxygen concentration and irradiation defects on the oxidation corrosion of body-centered-cubic iron surfaces: A first-principles study. Chin. Phys. B 2022, 31, 086802. [Google Scholar] [CrossRef]
- Tyson, W.R.; Miller, W.A. Surface free energies of solid metals: Estimation from liquid surface tension measurements. Surf. Sci. 1977, 62, 267–276. [Google Scholar] [CrossRef]
- Kołaczkiewicz, J.; Bauer, E. V and Fe on the W(110) face. Surf. Sci. 2000, 450, 106–116. [Google Scholar] [CrossRef]
- Albrecht, M.; Gradmann, U.; Furubayashi, T.; Harrison, W. Magnetic moments in rough Fe surfaces. Europhys. Lett. 1992, 20, 65. [Google Scholar] [CrossRef]
- Mohapatra, J.; Liu, X.; Joshi, P.; Liu, J.P. Hard and semi-hard Fe-based magnetic materials. J. Alloys Compd. 2023, 955, 170258. [Google Scholar] [CrossRef]
- Li, X.; Ma, Y.; Zhou, W.; Liu, Z. Spin-polarized DFT calculations of elemental effects on hydrogen atom adsorption on FeCrAl (1 1 0) surface. Appl. Surf. Sci. 2022, 581, 152273. [Google Scholar] [CrossRef]
- Jiang, D.; Carter, E.A. Carbon atom adsorption on and diffusion into Fe (110) and Fe (100) from first principles. Phys. Rev. B—Condens. Matter Mater. Phys. 2005, 71, 045402. [Google Scholar] [CrossRef]
- Johnson, D.F.; Jiang, D.; Carter, E.A. Structure, magnetism, and adhesion at Cr/Fe interfaces from density functional theory. Surf. Sci. 2007, 601, 699–705. [Google Scholar] [CrossRef]
- Banerjee, A.; Kohnert, A.A.; Holby, E.F.; Uberuaga, B.P. Critical assessment of the thermodynamics of vacancy formation in Fe2O3 using hybrid density functional theory. J. Phys. Chem. C 2020, 124, 23988–24000. [Google Scholar] [CrossRef]
- Soulairol, R.; Fu, C.-C.; Barreteau, C. Structure and magnetism of bulk Fe and Cr: From plane waves to LCAO methods. J. Phys. Condens. Matter 2010, 22, 295502. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Ceder, G. Efficient creation and convergence of surface slabs. Surf. Sci. 2013, 617, 53–59. [Google Scholar] [CrossRef]
- Forti, M.; Alonso, P.R.; Gargano, P.H.; Balbuena, P.B.; Rubiolo, G.H. A DFT study of atomic structure and adhesion at the Fe (BCC)/Fe3O4 interfaces. Surf. Sci. 2016, 647, 55–65. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.-W.; Wang, J.; Jiao, H. Reaction of CO, H2O, H2 and CO2 on the clean as well as O, OH and H precovered Fe(100) and Fe(111) surfaces. Catal. Sci. Technol. 2017, 7, 427–440. [Google Scholar] [CrossRef]
- Ming, X.; Cai, Y.; Li, Z. Atomic scale insight into the mechanisms of chloride induced steel corrosion in concrete. Constr. Build. Mater. 2022, 351, 128811. [Google Scholar] [CrossRef]
- Chen, M.-F.; Chen, Y.; Lim, Z.J.; Wong, M.W. Adsorption of imidazolium-based ionic liquids on the Fe (1 0 0) surface for corrosion inhibition: Physisorption or chemisorption? J. Mol. Liq. 2022, 367, 120489. [Google Scholar] [CrossRef]
- Yin, X.; Wang, H.; Han, E.-H. Cl-induced passivity breakdown in α-Fe2O3 (0001), α-Cr2O3 (0001), and their interface: A DFT study. J. Mater. Sci. Technol. 2022, 129, 70–78. [Google Scholar] [CrossRef]
- Liu, G.; Li, J.; Zhang, Y. Corrosion of carbon steels subjected to chloride and sulfate in simulated concrete pore solutions with different pH. Constr. Build. Mater. 2024, 440, 137445. [Google Scholar] [CrossRef]
- Yang, S.; Liang, G.; Huang, Y.; Hao, X.; Zhao, J.; Lv, M. Adsorption structure and properties of Ni/Fe electrodeposition interface: A DFT study. Model. Simul. Mater. Sci. Eng. 2024, 32, 055024. [Google Scholar] [CrossRef]
- Błoński, P.; Kiejna, A.; Hafner, J. Theoretical study of oxygen adsorption at the Fe (1 1 0) and (1 0 0) surfaces. Surf. Sci. 2005, 590, 88–100. [Google Scholar] [CrossRef]
- Ossowski, T.; Kiejna, A. Oxygen adsorption on Fe(110) surface revisited. Surf. Sci. 2015, 637–638, 35–41. [Google Scholar] [CrossRef]
- Chohan, U.K.; Koehler, S.P.K.; Jimenez-Melero, E. Incipient FeO(1 1 1) monolayer formation during O-adsorption on Fe(1 1 0) surface. Comput. Mater. Sci. 2017, 134, 109–115. [Google Scholar] [CrossRef][Green Version]
- Yin, X.; Wang, H.; Sun, S.; Han, E.-H. Comparative study on the adsorption behaviors of O and Cl on Fe(110) surfaces with different Cr content. Mater. Today Commun. 2020, 24, 101122. [Google Scholar] [CrossRef]
- Lu, J.P.; Albert, M.R.; Bernasek, S.L.; Dwyer, D.J. The adsorption of oxygen on the Fe(100) surface. Surf. Sci. 1989, 215, 348–362. [Google Scholar] [CrossRef]
- Barouh, C.; Schuler, T.; Fu, C.-C.; Nastar, M. Interaction between vacancies and interstitial solutes (C, N, and O) inα−Fe: From electronic structure to thermodynamics. Phys. Rev. B 2014, 90, 054112. [Google Scholar] [CrossRef]
- You, Y.; Yan, M.-F.; Yan, J.-H.; Sun, G.; Wang, C. First principles study of interactions of oxygen–carbon–vacancy in bcc Fe*. Chin. Phys. B 2019, 28, 106102. [Google Scholar] [CrossRef]
- Shang, S.L.; Fang, H.Z.; Wang, J.; Guo, C.P.; Wang, Y.; Jablonski, P.D.; Du, Y.; Liu, Z.K. Vacancy mechanism of oxygen diffusivity in bcc Fe: A first-principles study. Corros. Sci. 2014, 83, 94–102. [Google Scholar] [CrossRef]
- Wang, X.; Posselt, M.; Faßbender, J. Influence of substitutional atoms on the diffusion of oxygen in dilute iron alloys. Phys. Rev. B 2018, 98, 064103. [Google Scholar] [CrossRef]
- Claisse, A.; Olsson, P. First-principles calculations of (Y, Ti, O) cluster formation in body centred cubic iron-chromium. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2013, 303, 18–22. [Google Scholar] [CrossRef]
- Das, N.K.; Suzuki, K.; Takeda, Y.; Ogawa, K.; Shoji, T. Quantum chemical molecular dynamics study of stress corrosion cracking behavior for fcc Fe and Fe–Cr surfaces. Corros. Sci. 2008, 50, 1701–1706. [Google Scholar] [CrossRef]
- Das, N.K.; Suzuki, K.; Ogawa, K.; Shoji, T. Early stage SCC initiation analysis of fcc Fe–Cr–Ni ternary alloy at 288 °C: A quantum chemical molecular dynamics approach. Corros. Sci. 2009, 51, 908–913. [Google Scholar] [CrossRef]
- Wagner, C. The distribution of cations in metal oxide and metal sulphide solid solutions formed during the oxidation of alloys. Corros. Sci. 1969, 9, 91–109. [Google Scholar] [CrossRef]
- Frazer, D.; Qvist, S.; Parker, S.; Krumwiede, D.L.; Caro, M.; Tesmer, J.; Maloy, S.A.; Wang, Y.Q.; Hosemann, P. Degradation of HT9 under simultaneous ion beam irradiation and liquid metal corrosion. J. Nucl. Mater. 2016, 479, 382–389. [Google Scholar] [CrossRef]
- Yao, C.; Wang, Z.; Zhang, H.; Chang, H.; Sheng, Y.; Shen, T.; Zhu, Y.; Pang, L.; Cui, M.; Wei, K.; et al. HLMIF, a facility for investigating the synergistic effect of ion-irradiation and LBE corrosion. J. Nucl. Mater. 2019, 523, 260–267. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Z.; Zhang, D.; Peng, L.; Lai, X. Corrosion behavior of passivation layer Cr2O3 of uncoated stainless steel under the anodic and cathodic conditions: A first-principles study. Chem. Eng. J. 2024, 493, 152658. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, C.; Wang, S.; Xue, C.; Tian, G.; Su, H.; Yan, C.; Yan, Z.; Liu, X.; Wang, J. Towards quantum corrosion chemistry: Screening perfect Cr, Ni sites and stoichiometry on top of an Fe (110) surface using DFT. RSC Adv. 2023, 13, 9945–9953. [Google Scholar] [CrossRef]
- Cui, P.; Bao, Z.; Liu, Y.; Zhou, F.; Lai, Z.; Zhou, Y.; Zhu, J. Corrosion behavior and mechanism of dual phase Fe1. 125Ni1. 06CrAl high entropy alloy. Corros. Sci. 2022, 201, 110276. [Google Scholar] [CrossRef]
- McCafferty, E. Sequence of steps in the pitting of aluminum by chloride ions. Corros. Sci. 2003, 45, 1421–1438. [Google Scholar] [CrossRef]
- Arachchige, L.J.; Li, C.; Wang, F. Mechanistic insights into early stages of iron corrosion under electrochemical conditions: A DFT study. Comput. Mater. Sci. 2025, 257, 114004. [Google Scholar] [CrossRef]
- Liu, S.; Tian, X.; Wang, T.; Wen, X.; Li, Y.W.; Wang, J.; Jiao, H. Coverage dependent water dissociative adsorption on Fe(110) from DFT computation. Phys. Chem. Chem. Phys. 2015, 17, 8811–8821. [Google Scholar] [CrossRef]
- Liu, W.; Sun, J.; Ye, C. The influence of tensile strain on water adsorbed on Fe (100) surface: Surface chemistry aspect of stress corrosion cracking. Appl. Surf. Sci. 2019, 481, 192–199. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.-W.; Wang, J.; Jiao, H. Reactions of CO, H2O, CO2, and H2 on the Clean and Precovered Fe(110) Surfaces—A DFT Investigation. J. Phys. Chem. C 2015, 119, 28377–28388. [Google Scholar] [CrossRef]
- Eder, M.; Terakura, K.; Hafner, J. Initial stages of oxidation of (100) and (110) surfaces of iron caused by water. Phys. Rev. B 2001, 64, 115426. [Google Scholar] [CrossRef]
- Yang, B.; Shi, K.; Li, H.; Jiang, L.; Zhang, C.-H. Water dissociative adsorption on the precovered Fe (100) surface from DFT computation. Indian J. Phys. 2019, 93, 1019–1029. [Google Scholar] [CrossRef]
- Zhang, C.H.; Chen, B.; Sun, D.B. A DFT study of H2O dissociation on metal-precovered Fe (100) surface. Surf. Interface Anal. 2018, 50, 420–429. [Google Scholar] [CrossRef]
- Chew, K.H.; Kuwahara, R.; Ohno, K. First-principles study on the atomistic corrosion processes of iron. Phys. Chem. Chem. Phys. 2018, 20, 1653–1663. [Google Scholar] [CrossRef]
- Taylor, C.D.; Ke, H. Investigations of the intrinsic corrosion and hydrogen susceptibility of metals and alloys using density functional theory. Corros. Rev. 2021, 39, 177–209. [Google Scholar] [CrossRef]
- Tobón, L.L.A.; Branda, M.M. Explicit solvation effects on low-index Fe surfaces and small particles as adsorbents of Arsenic species: A DFT study. Theor. Chem. Acc. 2021, 140, 67. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, Y.; Ding, X. An in-depth understanding of the solvation effect of methanol on the anisotropy of electrochemical corrosion of Ta. Electrochim. Acta 2022, 435, 141359. [Google Scholar] [CrossRef]
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.A.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef]
- Liu, M.; Jin, Y.; Pan, J. Relevance of implicit and explicit solvent in density-functional theory study of adsorption at electrochemical NaCl/Al interface. Mater. Today Commun. 2022, 31, 103425. [Google Scholar] [CrossRef]
- Aziz, A.; Carrasco, J. Modeling magnesium surfaces and their dissolution in an aqueous environment using an implicit solvent model. J. Chem. Phys. 2022, 156, 174702. [Google Scholar] [CrossRef] [PubMed]
- Delley, B. The conductor-like screening model for polymers and surfaces. Mol. Simul. 2006, 32, 117–123. [Google Scholar] [CrossRef]
- Yoo, S.H.; Todorova, M.; Neugebauer, J. Selective Solvent-Induced Stabilization of Polar Oxide Surfaces in an Electrochemical Environment. Phys. Rev. Lett. 2018, 120, 066101. [Google Scholar] [CrossRef]
- Dogan, O.; Kapci, M.F.; Esat, V.; Bal, B. Experimental and molecular dynamics simulation-based investigations on hydrogen embrittlement behavior of chromium electroplated 4340 steel. J. Eng. Mater. Technol. 2021, 143, 041010. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M. Hydrogen embrittlement in different materials: A review. Int. J. Hydrogen Energy 2018, 43, 21603–21616. [Google Scholar] [CrossRef]
- Xing, B.; Gao, R.; Wu, M.; Wei, H.; Chi, S.; Hua, Z. Differentiation on crystallographic orientation dependence of hydrogen diffusion in α-Fe and γ-Fe: DFT calculation combined with SKPFM analysis. Appl. Surf. Sci. 2023, 615, 156395. [Google Scholar] [CrossRef]
- Chohan, U.K.; Koehler, S.P.K.; Jimenez-Melero, E. Diffusion of hydrogen into and through γ-iron by density functional theory. Surf. Sci. 2018, 672–673, 56–61. [Google Scholar] [CrossRef]
- Jiang, D.E.; Carter, E.A. Diffusion of interstitial hydrogen into and through bcc Fe from first principles. Phys. Rev. B 2004, 70, 064102. [Google Scholar] [CrossRef]
- Boda, A.; Ali, S.M. First principles DFT analysis on the diffusion kinetics of hydrogen isotopes through bcc iron (Fe): Role of temperature and surface coverage. Int. J. Hydrogen Energy 2022, 47, 31481–31498. [Google Scholar] [CrossRef]
- Hasan, M.A.A.; Wang, J.; Lim, Y.C.; Hu, A.; Shin, S. Concentration dependence of hydrogen diffusion in α-iron from atomistic perspectives. Int. J. Hydrogen Energy 2019, 44, 27876–27884. [Google Scholar] [CrossRef]
- Wu, G.; Su, Y.; Qiao, L.; Gao, L. Effects of strain and Cr doping on hydrogen adsorption behaviors of α-Fe2O3 oxide film: A density functional theory study. Comput. Mater. Sci. 2025, 246, 113499. [Google Scholar] [CrossRef]
- Álvarez, G.; Sánchez, J.; Segurado, J.; de Andres, P.L.; Ridruejo, Á. Hydrogen diffusion in BCC-Fe: DFT study of tensorial stress effects and interactions with point defects. Results Phys. 2024, 59, 107590. [Google Scholar] [CrossRef]
- Chen, L.; Shi, C.; Li, X.; Mi, Z.; Wang, D.; Liu, H.; Qiao, L. Strain effect on electronic structure and work function in α-Fe2O3 films. Materials 2017, 10, 273. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Bouhali, O.; Mousseau, N.; Becquart, C.S.; El-Mellouhi, F. Influence of surface vacancy defects on the carburisation of Fe 110 surface by carbon monoxide. J. Chem. Phys. 2016, 145, 044710. [Google Scholar] [CrossRef]
- Barouh, C.; Schuler, T.; Fu, C.-C.; Jourdan, T. Predicting vacancy-mediated diffusion of interstitial solutes inα-Fe. Phys. Rev. B 2015, 92, 104102. [Google Scholar] [CrossRef]
- Restrepo, O.A.; Mousseau, N.; Trochet, M.; El-Mellouhi, F.; Bouhali, O.; Becquart, C.S. Carbon diffusion paths and segregation at high-angle tilt grain boundaries inα-Fe studied by using a kinetic activation-relation technique. Phys. Rev. B 2018, 97, 054309. [Google Scholar] [CrossRef]
- Li, G.; Blake, G.R.; Palstra, T.T. Vacancies in functional materials for clean energy storage and harvesting: The perfect imperfection. Chem. Soc. Rev. 2017, 46, 1693–1706. [Google Scholar] [CrossRef]
- Kopeliovich, D.; Imperfections of Crystal Structure. SubsTech. 2023. Available online: https://www.substech.com/dokuwiki/doku.php#google_vignette (accessed on 4 March 2025).
- Zhang, Y.; Manzoor, A.; Jiang, C.; Aidhy, D.; Schwen, D. A statistical approach for atomistic calculations of vacancy formation energy and chemical potentials in concentrated solid-solution alloys. Comput. Mater. Sci. 2021, 190, 110308. [Google Scholar] [CrossRef]
- Mattsson, T.R.; Mattsson, A.E. Calculating the vacancy formation energy in metals: Pt, Pd, and Mo. Phys. Rev. B 2002, 66, 214110. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Bentria, E.T.; Omotayo, S.A.; Bouhali, O.; Mousseau, N.; Becquart, C.S.; El Mellouhi, F. Elucidating the role of extended surface defects at Fe surfaces on CO adsorption and dissociation. Appl. Surf. Sci. 2019, 491, 792–798. [Google Scholar] [CrossRef]
- Ahlawat, S.; Srinivasu, K.; Biswas, A.; Choudhury, N. First-principle investigation of electronic structures and interactions of foreign interstitial atoms (C, N, B, O) and intrinsic point defects in body-and face-centered cubic iron lattice: A comparative analysis. Comput. Mater. Sci. 2019, 170, 109167. [Google Scholar] [CrossRef]
- Wen, X.; Bai, P.; Han, Z.; Zheng, S.; Luo, B.; Fang, T.; Song, W. Effect of vacancy on adsorption/dissociation and diffusion of H2S on Fe (1 0 0) surfaces: A density functional theory study. Appl. Surf. Sci. 2019, 465, 833–845. [Google Scholar] [CrossRef]
- Domain, C.; Becquart, C.S.; Foct, J. Ab initiostudy of foreign interstitial atom (C, N) interactions with intrinsic point defects inα-Fe. Phys. Rev. B 2004, 69, 144112. [Google Scholar] [CrossRef]
- Fu, C.L.; Krcmar, M.; Painter, G.S.; Chen, X.Q. Vacancy mechanism of high oxygen solubility and nucleation of stable oxygen-enriched clusters in Fe. Phys. Rev. Lett. 2007, 99, 225502. [Google Scholar] [CrossRef]
- Wang, X.; Faßbender, J.; Posselt, M. Mutual dependence of oxygen and vacancy diffusion in bcc Fe and dilute iron alloys. Phys. Rev. B 2020, 101, 174107. [Google Scholar] [CrossRef]
- Pang, Q.; DorMohammadi, H.; Isgor, O.B.; Árnadóttir, L. The effect of surface defects on chloride-induced depassivation of iron—A density functional theory study. Corrosion 2020, 76, 690–697. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Nong, Y.; Wei, Z.; Chen, Y. Mechanism of rebar depassivation in concrete containing sulphate: A vicious cycle between sulphate adsorption and surface vacancy formation. Corros. Sci. 2024, 234, 112126. [Google Scholar] [CrossRef]
- Li, H.-X.; Li, D.-P.; Zhang, L.; Wang, Y.-W.; Wang, X.-Y.; Lu, M.-X. Passivity breakdown of 13Cr stainless steel under high chloride and CO2 environment. Int. J. Miner. Metall. Mater. 2019, 26, 329–336. [Google Scholar] [CrossRef]
- Pang, Q.; DorMohammadi, H.; Isgor, O.B.; Árnadóttir, L. The effect of surface vacancies on the interactions of Cl with a α-Fe2O3 (0001) surface and the role of Cl in depassivation. Corros. Sci. 2019, 154, 61–69. [Google Scholar] [CrossRef]
- Guo, Q.; Nong, J.; Wu, Y.; Liang, F.; Ren, L.; Xu, J.; Shoji, T. Effects of in-situ hydrogen charging on the oxide film of iron in high-temperature water: Experiments and DFT calculations. Scr. Mater. 2022, 221, 114990. [Google Scholar] [CrossRef]
- Sarfo, K.O.; Isgor, O.B.; Santala, M.K.; Tucker, J.D.; Árnadóttir, L. Bulk diffusion of Cl through O vacancies in α-Cr2O3: A density functional theory study. J. Electrochem. Soc. 2021, 168, 071503. [Google Scholar] [CrossRef]
- Peng, Y.; Lin, Y.; Xia, R.; Dai, Z.; Zhang, W.; Liu, W. Electrochemical Investigation of Chloride Ion-Induced Breakdown of Passive Film on P110 Casing Steel Surface in Simulated Pore Solution: Behavior and Critical Value Determination. Metals 2024, 14, 93. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, J.; Shao, Y.; Zhang, G.; Yan, D.; Liu, Y.; Ji, H.; Jin, N.; Jin, X.; Zhou, Z. Dynamic analysis of chloride-induced passive film breakdown mechanisms in carbon steel within simulated concrete pore solution. Case Stud. Constr. Mater. 2025, 22, e04409. [Google Scholar] [CrossRef]
- Chen, T.; Li, C.; Cai, X.; Wu, F.; Wang, Z.; Cheng, X.; Li, X.; Yang, S.; Liu, C. Deterioration mechanism of passivation behavior of ductile iron induced by shrinkage defects in simulated concrete pore solution. J. Mater. Sci. Technol. 2025, 236, 136–149. [Google Scholar] [CrossRef]
- Huang, C.; Song, K.; Zhou, S.; Su, Y.; Qiao, L.; Gao, L. Hydrogen atom solution and diffusion behaviors at Σ3 and Σ5 grain boundaries of Fe, Ni, Cu and Al: A first-principles study. Mater. Today Commun. 2023, 37, 107222. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Li, X.; Xu, Y.; Wu, X.; Liu, C.; Kong, X.; Yao, C.; Wang, Z. Investigation of the dissolution and diffusion properties of interstitial oxygen at grain boundaries in body-centered-cubic iron by the first-principles study. RSC Adv. 2021, 11, 8643–8653. [Google Scholar] [CrossRef]
- Yuan, R.; Xie, Y.-P.; Li, T.; Xu, C.-H.; Yao, M.-Y.; Xu, J.-X.; Guo, H.-B.; Zhou, B.-X. An origin of corrosion resistance changes of Zr alloys: Effects of Sn and Nb on grain boundary strength of surface oxide. Acta Mater. 2021, 209, 116804. [Google Scholar] [CrossRef]
- Wei, Q.; Kecskes, L.; Jiao, T.; Hartwig, K.T.; Ramesh, K.T.; Ma, E. Adiabatic shear banding in ultrafine-grained Fe processed by severe plastic deformation. Acta Mater. 2004, 52, 1859–1869. [Google Scholar] [CrossRef]
- Hou, T.; Zhang, Y.; Fan, Z.; Tian, B.; Liu, Z.; Zhang, Z. First-Principles Study of Sulfur Corrosion Mechanism at Carbon Steel Grain Boundaries. J. Mater. Eng. Perform. 2024, 1–13. [Google Scholar] [CrossRef]
- Fan, X.; Mi, Z.; Yang, L.; Su, H. Application of DFT Simulation to the Investigation of Hydrogen Embrittlement Mechanism and Design of High Strength Low Alloy Steel. Materials 2022, 16, 152. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Xiong, K.; Wang, M.; Liu, Z.; Shen, K.; Mao, Y.; Chen, H. Grain boundary alloying segregation to resist hydrogen embrittlement in BCC-Fe steels: Atomistic insights into solute-hydrogen interactions. Scr. Mater. 2024, 238, 115757. [Google Scholar] [CrossRef]
- Bauer, K.-D.; Todorova, M.; Hingerl, K.; Neugebauer, J. A first principles investigation of zinc induced embrittlement at grain boundaries in bcc iron. Acta Mater. 2015, 90, 69–76. [Google Scholar] [CrossRef]
- Teus, S.; Mazanko, V.; Olive, J.-M.; Gavriljuk, V. Grain boundary migration of substitutional and interstitial atoms in α-iron. Acta Mater. 2014, 69, 105–113. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yin, H.; He, X.; Liu, M.; Qiu, J.; Liu, W. First-principles study on the corrosion resistance of iron oxide surface and grain boundary in austenitic steel to lead–bismuth eutectic. Appl. Surf. Sci. 2023, 640, 158409. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Amin, S.; Mohamed, A.A. Current and emerging trends of inorganic, organic and eco-friendly corrosion inhibitors. RSC Adv. 2024, 14, 31877–31920. [Google Scholar] [CrossRef]
- Zehra, S.; Mobin, M.; Aslam, J. Chapter 13—Chromates as corrosion inhibitors. In Inorganic Anticorrosive Materials; Verma, C., Aslam, J., Hussain, C.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 251–268. [Google Scholar]
- Raja, P.B.; Sethuraman, M.G. Natural products as corrosion inhibitor for metals in corrosive media—A review. Mater. Lett. 2008, 62, 113–116. [Google Scholar] [CrossRef]
- Guo, L.; Qi, C.; Zheng, X.; Zhang, R.; Shen, X.; Kaya, S. Toward understanding the adsorption mechanism of large size organic corrosion inhibitors on an Fe (110) surface using the DFTB method. RSC Adv. 2017, 7, 29042–29050. [Google Scholar] [CrossRef]
- El-Hendawy, M.M.; Kamel, A.M.; Mohamed, M.M. The anti-corrosive behavior of benzo-fused N-heterocycles: An in silico study toward developing organic corrosion inhibitors. Phys. Chem. Chem. Phys. 2022, 24, 743–756. [Google Scholar] [CrossRef]
- Id El Mouden, O.; Al-Moubaraki, A.H.; Chafiq, M.; Bakhouch, M.; Batah, A.; Bammou, L.; Belkhaouda, M.H.; Chaouiki, A.; Ko, Y.G. BMPD-assisted enhancement of corrosion resistance of carbon steel: Experimental and first-principle DFTB insights. Metals 2024, 14, 69. [Google Scholar] [CrossRef]
- Liu, P.; Xu, Q.; Zhang, Q.; Huang, Y.; Liu, Y.; Li, H.; Zhang, R.; Lei, G. A new insight into corrosion inhibition mechanism of the corrosion inhibitors: Review on DFT and MD simulation. J. Adhes. Sci. Technol. 2024, 38, 1563–1584. [Google Scholar] [CrossRef]
- Hamidi, H.; Shojaei, F.; Pourfath, M.; Vaez-Zadeh, M. Adsorption behavior of some green corrosion inhibitors on Fe (110) surface: The critical role of d-π interactions in binding strength. Appl. Surf. Sci. 2024, 655, 159425. [Google Scholar] [CrossRef]
- Liu, Z.-Y.; Wang, D.; Li, D.-T.; Wang, H.-Q. The inhibition efficiencies of some organic corrosion inhibitors of iron: An insight from density functional theory study. Comput. Theor. Chem. 2022, 1214, 113759. [Google Scholar] [CrossRef]


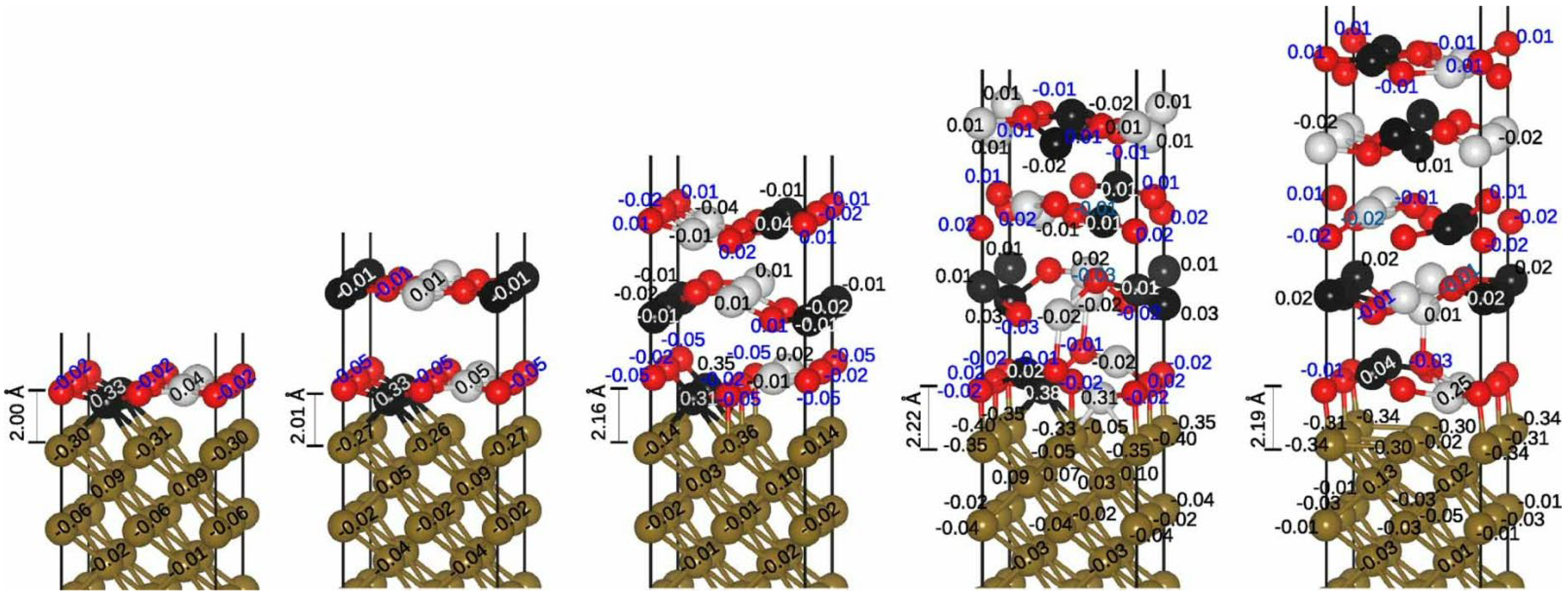
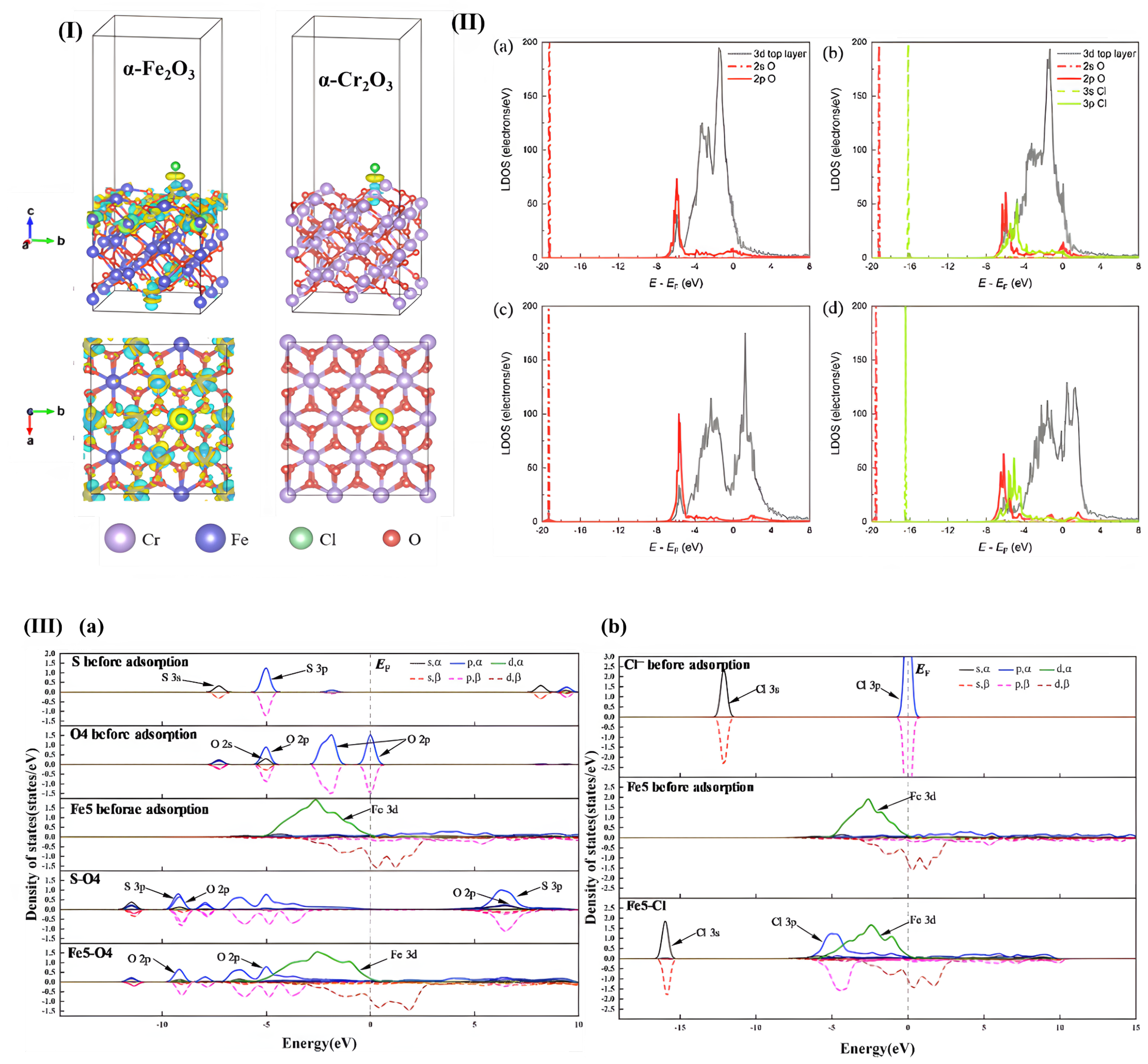

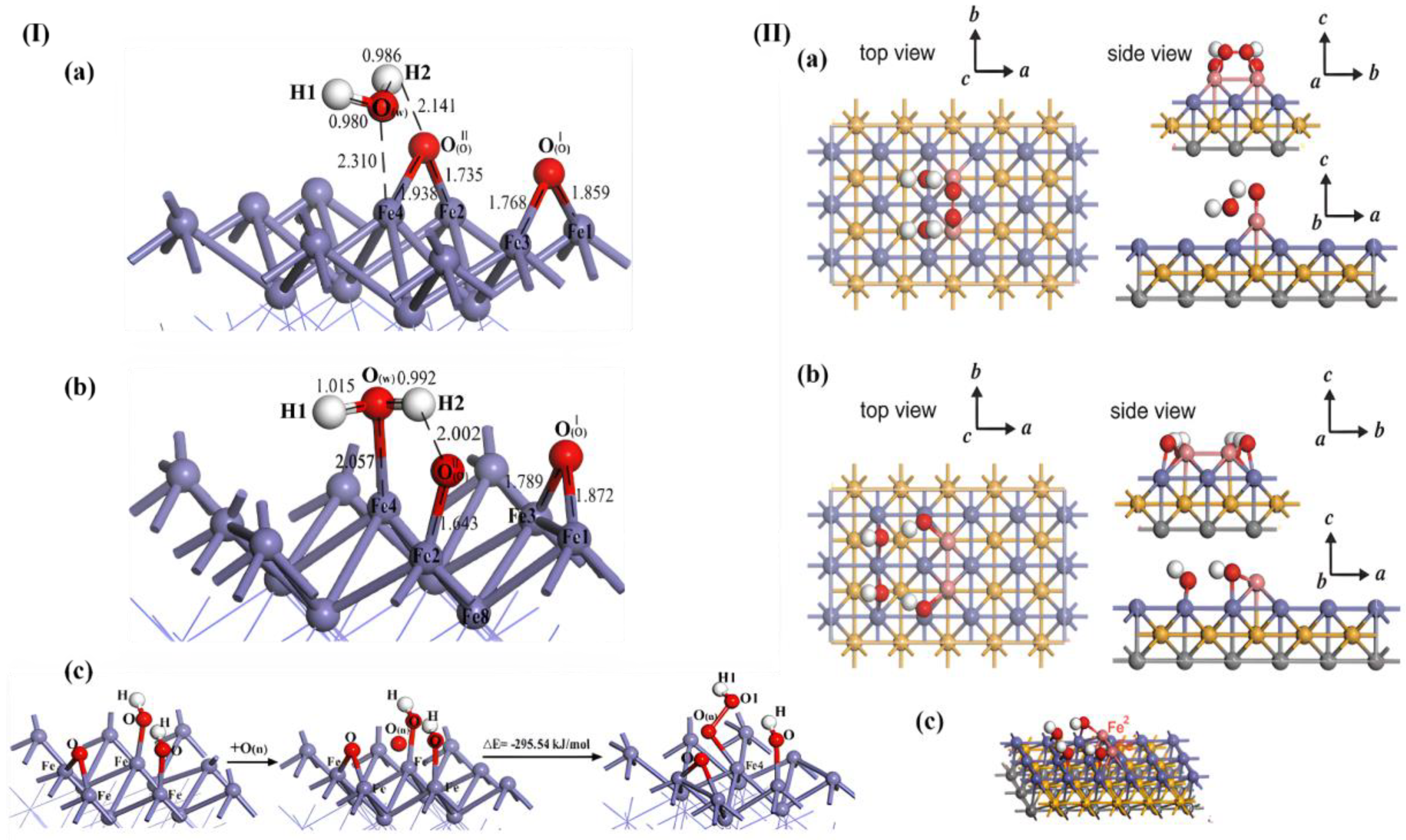
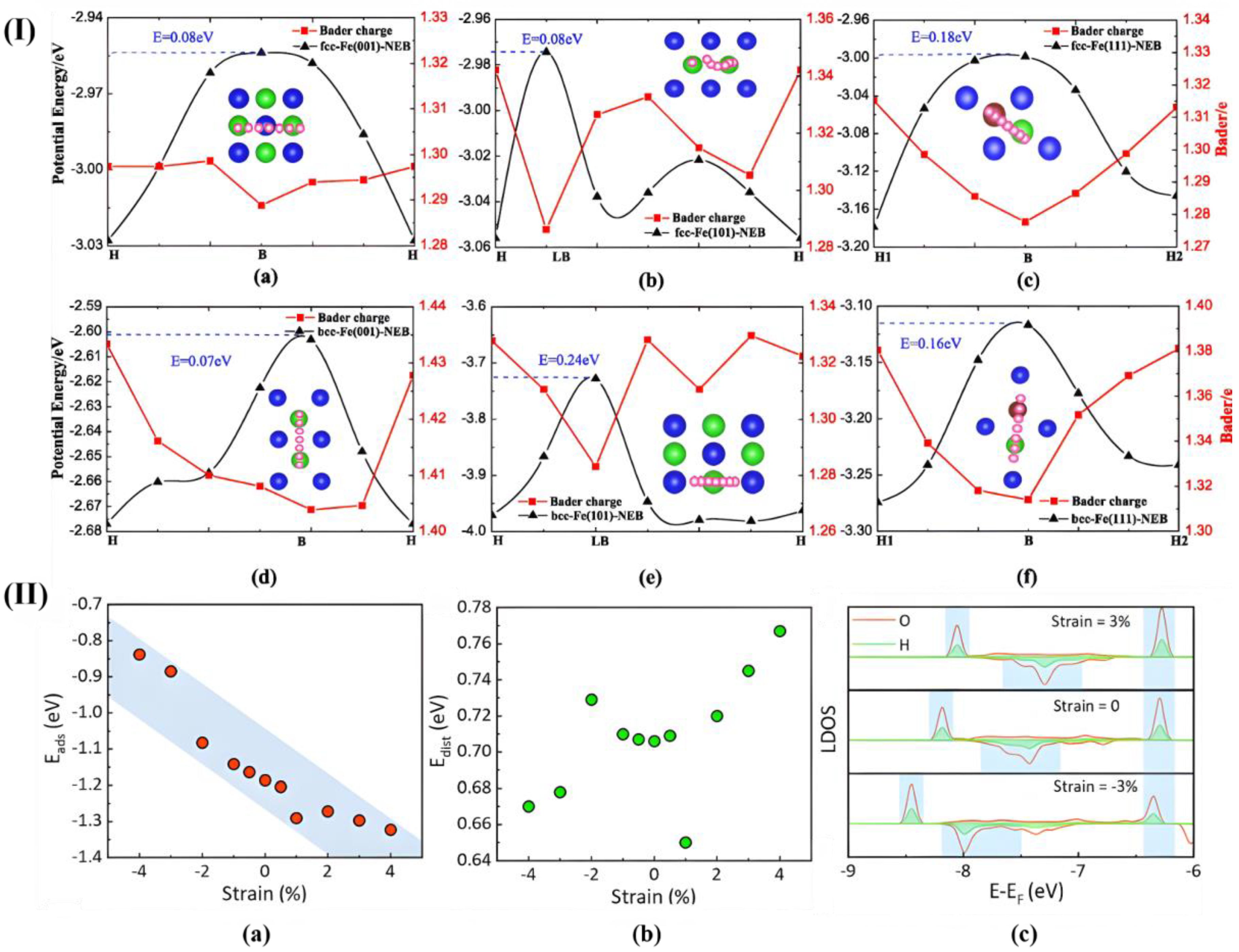
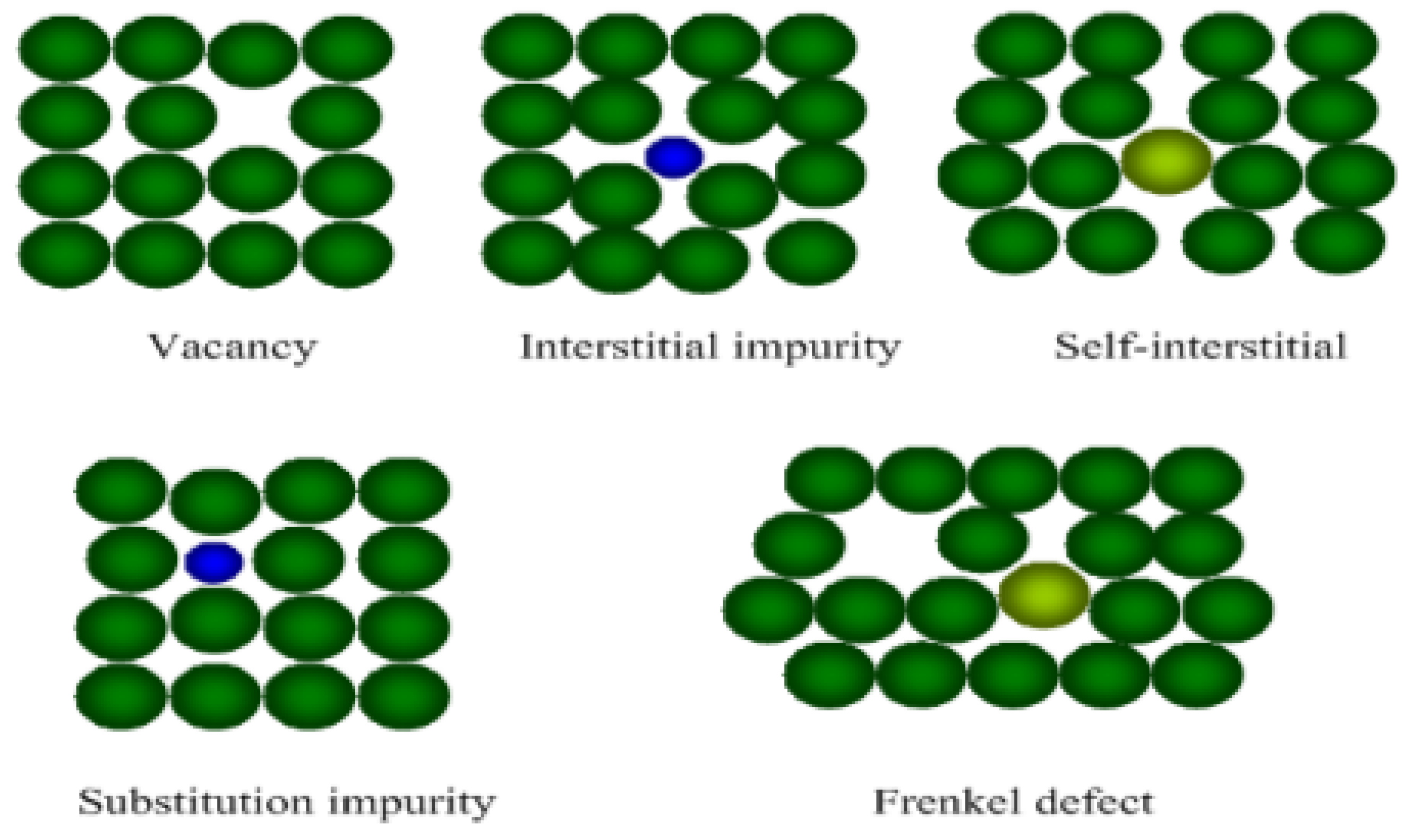


| Method | Orientation | Surface Energy (J/m2) | Magnetic Moment (µB) | Work Function (eV) | Refs. |
|---|---|---|---|---|---|
| PBE | Fe(100) | 2.59 | 2.97 | 3.92 | [2] |
| Expt | Fe(100) | 2.36 a | - | 4.67 b | a—[97], b—[98] |
| PBE | Fe(110) | 2.41 | 2.60 | 4.75 | [99] |
| PBE DF CX | Fe(110) | 2.46 | 2.13 | 5.06 | [93] |
| Expt | Fe(110) | 2.41 c | 2.90–3.10 d | 4.80 e | c—[100], d—[101], e—[102] |
| PBE | Fe(111) | 2.76 | 2.87 | 3.87 | [2] |
| Study | Surface | DFT Vxc | Software | Details * | Basic Set # | Ref. |
|---|---|---|---|---|---|---|
| Impact of oxygen coverage, diffusion, and defects on oxidation | Fe(100), (110) | PBE | VASP | 3 × 3 9 a 15 Å | 500, 551 −0.01 | [99] |
| Dissociative adsorption of O2 and co-adsorption of H2O and O2 | Fe(100) | PW91 | CASTEP | 2 × 2 5 a 15 Å | 340, 441 −0.03 | [10] |
| Properties of the oxide/metal interface | Fe(001) | PBE + U | VASP | 2 × 2 9 a 27 Å b | 500, 441 d −0.01 | [70] |
| Adsorption of O on stepped iron surfaces | Fe(110), (210), (211) | PBE DF-CX | VASP | - 7(3), 13(5), 21(7) 15 Å | 520, 2π × 0.04 Å−1 −0.001 | [93] |
| Cl adsorption: α-Fe2O3 vs. α-Cr2O3 (0001) surfaces | α-Fe2O3 (0001), Cr2O3 (0001) | PBE + U | VASP | 2 × 1 18 c 15 Å | 500, 361 −0.02 | [115] |
| Cl induced depassivation (interactions with Cl, O, OH, and H2O) | Fe(100) | PBE + D3 | VASP | 2 × 2 5 a 15 Å | 400, 441 −0.01 | [113] |
| Sequential and simultaneous adsorption of chloride and sulphate | Fe(100) | PW91 | CASTEP | 4 × 4 5 a 15 Å | 340, 441 −0.03 | [22,116] |
| Properties of Ni/Fe interface | Fe(100) | PBE | CASTEP | 2 × 2 6 a 15 Å | 400, 551,−0.001 | [117] |
| Surface | DFT Vxc | Vacuum/Solvation | Eads (eV) | d(Fe-O) (Å) | Ref. |
|---|---|---|---|---|---|
| Fe(110) | PBE | Vacuum | −0.38 | 2.183 | [138] |
| PBE | Vacuum | −0.296 | 2.27 | [54] | |
| PBE + D3 | Vacuum | −0.50 | 2.25 | [54] | |
| opt-PBE | Vacuum | −0.43 | 2.24 | [95] | |
| PBE | Vacuum | −0.29 | 1.78 | [51] | |
| PBE | Implicit solvation (Linear PCM) | −0.21 | 2.11 | [51] | |
| Fe(100) | PW91 | Vacuum | −0.36 | 2.248 | [10] |
| PBE | Vacuum | −0.42 | 2.25 | [139] | |
| PBE a | Vacuum | −0.50 | 2.19 | [139] | |
| opt-PBE | Hybrid solvation (explicit-implicit) | −0.69 | 2.92 [d(Fe-H2O)] | [137] |
| Agents | Behaviour/Property | Fe(110) | Fe(100) |
|---|---|---|---|
| O/O2 | Preferred adsorption site | 3-fold hollow | 4-fold hollow |
| Coverage dependence | With increasing coverage, O–O repulsion makes adsorption less favourable, due to the high atomic density Low coverage—molecular adsorption is common High coverage—dissociative adsorption is favoured | Dissociative adsorption is favoured | |
| Diffusion | Surface to subsurface barrier: 2.74 eV Bulk diffusion: 0.57 eV | Surface to subsurface diffusion, easier than Fe(110) | |
| H2O | Adsorption | Stable adsorption with high mobility | Weak adsorption, enhanced with pre-adsorbed O |
| Coverage dependence | Low coverage: molecular adsorption is preferred High coverage: dissociative adsorption is preferred | Low coverage: molecular adsorption is preferred High coverage: dissociative adsorption is preferred |
| Type of Defects | Study | Lattice/Surface | DFT Functional | Key Findings | Ref. |
|---|---|---|---|---|---|
| Vacancy | Effect of vacancies on oxidation | Fe(100), Fe(110) * | PBE | Vacancies form more easily at surfaces, enhance O dissolution and diffusion, and create stable V–O pairs | [99] |
| Interactions of foreign interstitial atoms with vacancy defects | BCC, FCC | PBE | Vacancies trap foreign atoms much more strongly in BCC-Fe than in FCC-Fe | [171] | |
| Interactions of Cl with the α-Fe2O3 (0001) surface | α-Fe2O3 (0001) | DFT + U, PBE | Cl adsorption makes Fe vacancy formation more favourable; Fe vacancies are stable in the bulk, while O vacancies are stable on the surface | [179] | |
| Interaction of Cl− with hematite and chromia | α-Fe2O3 (0001), α-Cr2O3 (0001) | DFT + U, PBE | Cl insertion into an O vacancy is more favourable than into Fe vacancies or interstitials | [115] | |
| GB | Σ3 and Σ5 grain boundaries of Fe | * | PBE | Higher Σ GBs have higher energy and are more prone to degradation and adsorbate diffusion | [185] |
| Dissolution and diffusion properties of O at GBs | Σ3<110>(111), Σ5<001>(310) * | PBE | GBs enhance O dissolution and diffusion; oxygen segregation is greater at Σ3(111) than at Σ5(310) | [186] | |
| Segregation of elements on the GB | FCC Fe3O4, Fe(001) # | DFT + U | GB strength varies with segregating element; Sn weakens, and Nb strengthens GB cohesion | [187] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasooriya, H.; Li, C.; Wang, F. Understanding Steel Corrosion: Surface Chemistry and Defects Explored Through DFT Modelling—A Review. Processes 2025, 13, 1971. https://doi.org/10.3390/pr13071971
Balasooriya H, Li C, Wang F. Understanding Steel Corrosion: Surface Chemistry and Defects Explored Through DFT Modelling—A Review. Processes. 2025; 13(7):1971. https://doi.org/10.3390/pr13071971
Chicago/Turabian StyleBalasooriya, Heshani, Chunqing Li, and Feng Wang. 2025. "Understanding Steel Corrosion: Surface Chemistry and Defects Explored Through DFT Modelling—A Review" Processes 13, no. 7: 1971. https://doi.org/10.3390/pr13071971
APA StyleBalasooriya, H., Li, C., & Wang, F. (2025). Understanding Steel Corrosion: Surface Chemistry and Defects Explored Through DFT Modelling—A Review. Processes, 13(7), 1971. https://doi.org/10.3390/pr13071971








