An Energy Efficiency Evaluation Model for Oil–Gas Gathering and Transportation Systems Based on Combined Weighting and Grey Relational Analysis
Abstract
1. Introduction
1.1. Background
1.2. Related Works
1.3. Contribution
1.4. Organization
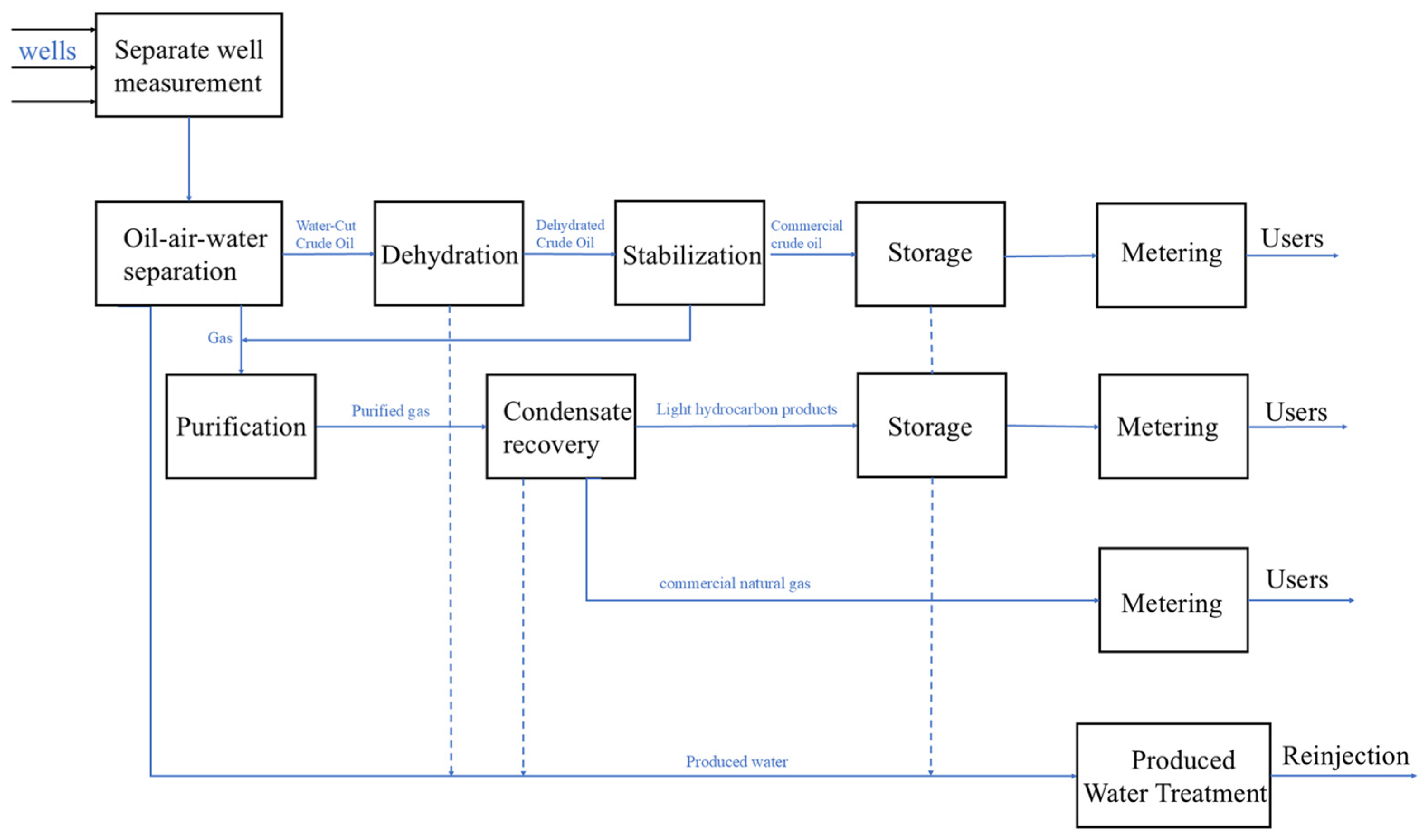
2. Problem Description
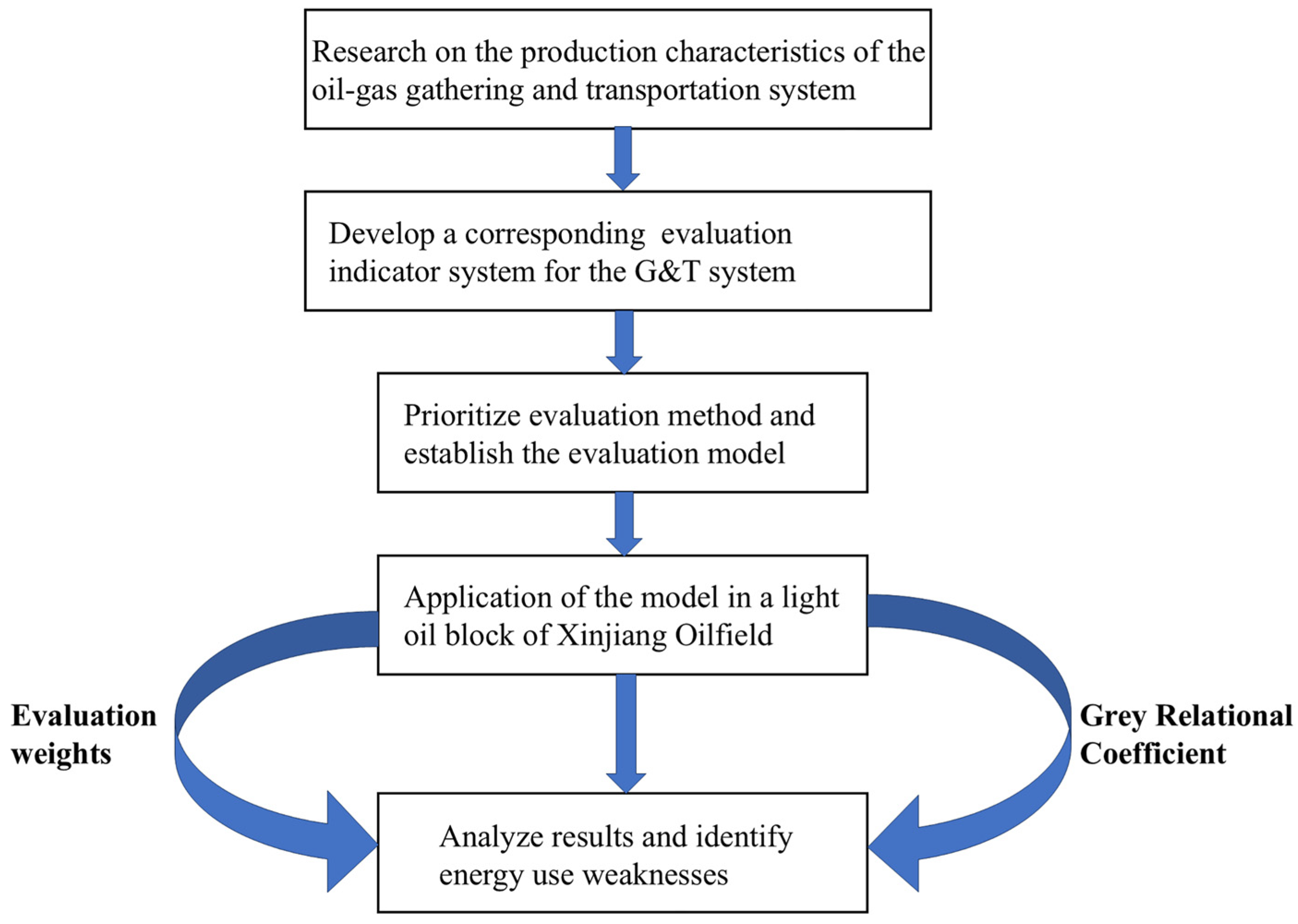
3. Method
3.1. Construction of Evaluation Indicator System
3.2. Indicator Weighting Calculation
3.2.1. AHP for Subjective Weight Determination
3.2.2. EWM for Objective Weight Determination
3.2.3. Integration of Subjective and Objective Weights
3.3. Comprehensive Evaluation Model Construction
- (1)
- Normalize individual sequences.
- (2)
- Calculate the absolute difference between the reference and comparative sequences.
- (3)
- Calculate the correlation degree :
- (4)
- Calculate the grey relational degree :
4. Case Study
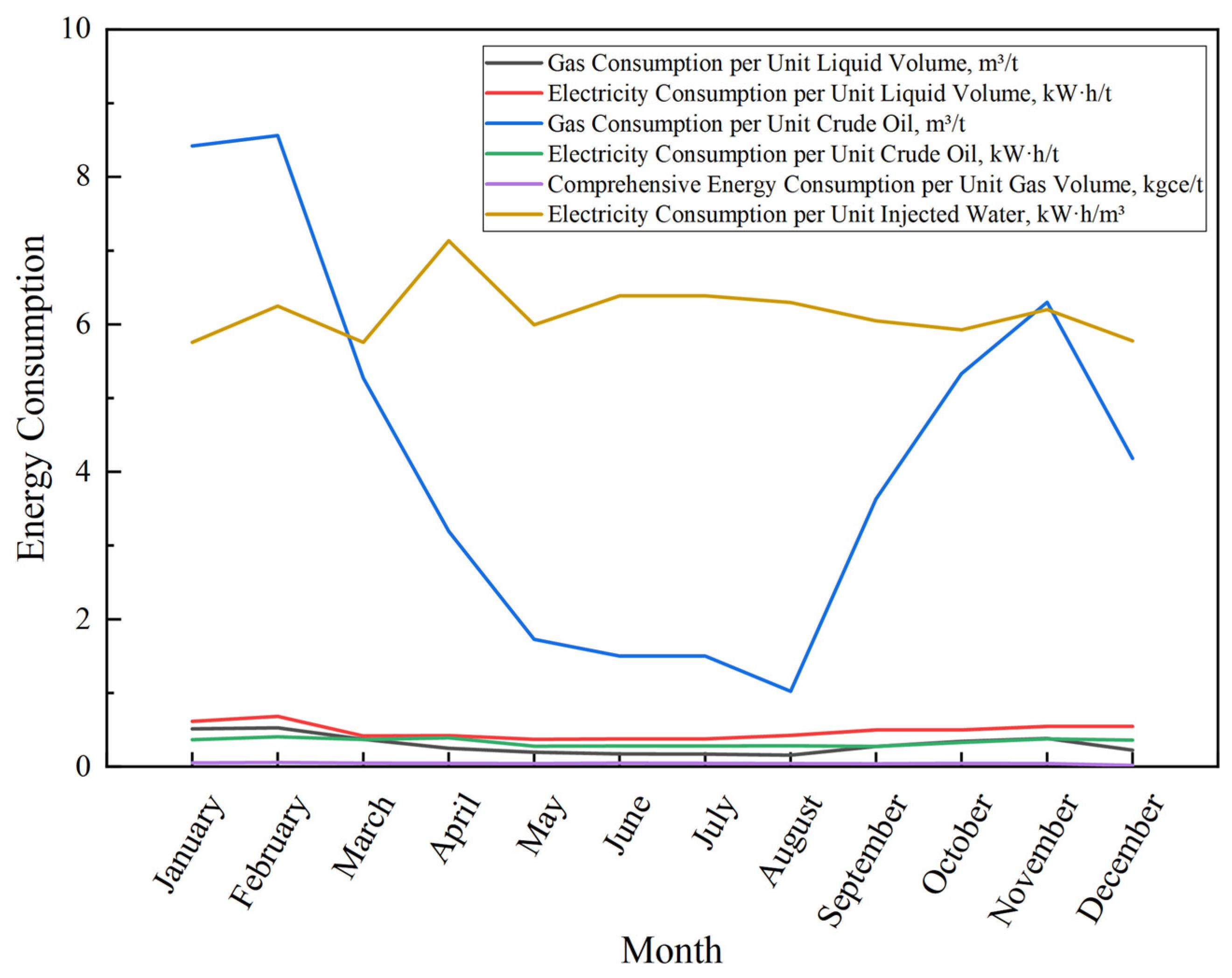
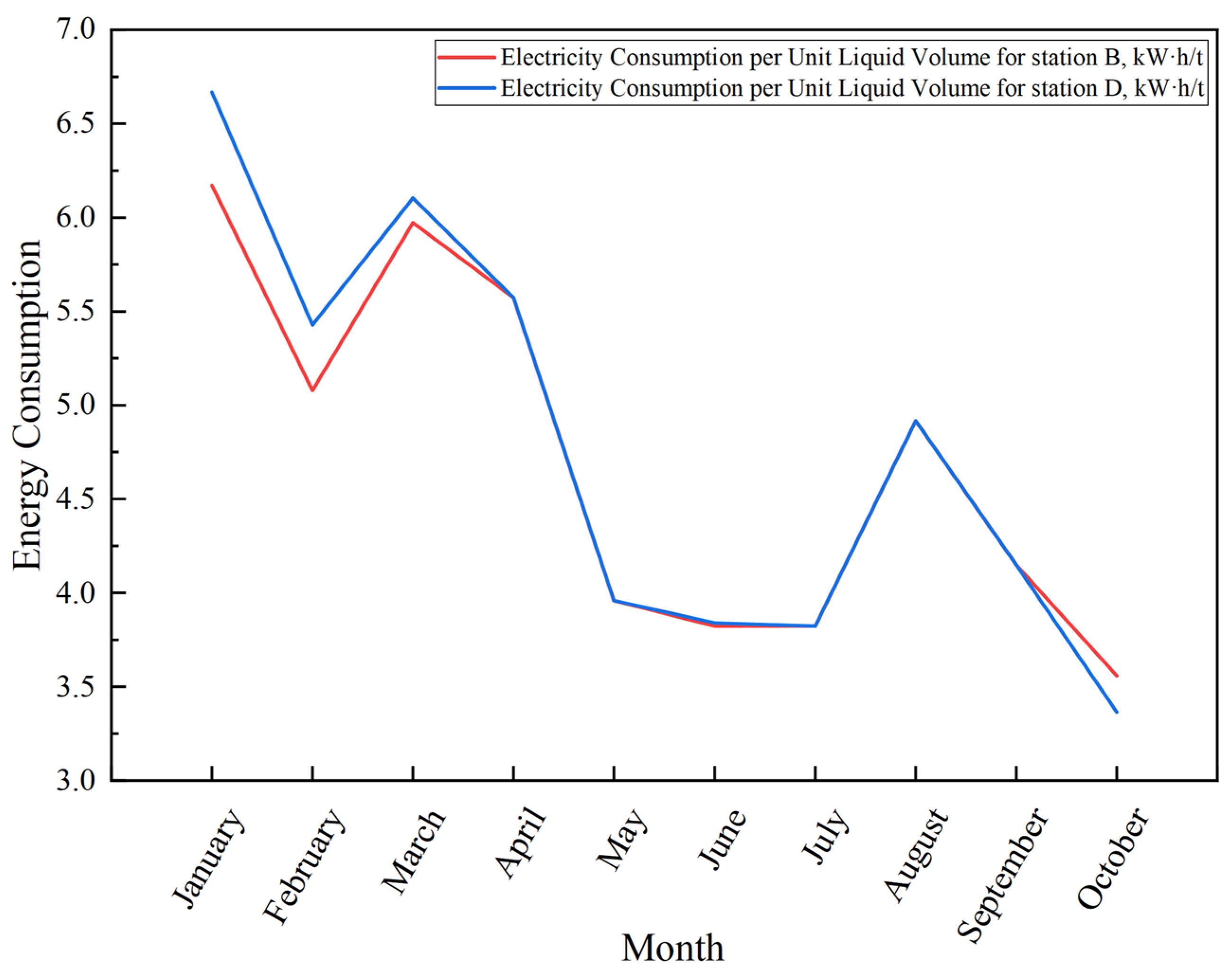
4.1. Basic Data
4.2. Calculation of Indicator Weights
4.3. Results and Discussion
5. Conclusions
6. Limitations and Future Outlook
- (1)
- The model in this paper was constructed based on the characteristics of light oil blocks, and their applicability to blocks with significantly different gathering and transportation modes needs to be further verified.
- (2)
- The current method is a static evaluation method, which can identify the main energy efficiency bottlenecks but may not be able to dynamically capture the changes in the system.
- (1)
- Based on the proposed model, we plan to introduce dynamic capture capabilities, explore the adaptive update of indicator weights, etc., to identify new emerging inefficiency points.
- (2)
- We plan to expand the dataset and apply the model to blocks with different characteristics to verify its universality; according to the differences in application scenarios, we will study the customized needs of the evaluation indicator system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. AHP Indicators Description
- (1)
- Electricity Consumption per Unit of Crude Oil (Me):
- (2)
- Gas Consumption per Unit of Crude Oil (Mgas):
- (3)
- Electricity Consumption per Unit of Liquid Volume (Mel):
- (4)
- Gas Consumption per Unit of Liquid Volume (Mgasl)
- (5)
- Energy Consumption per Unit of Gas Volume (Mg)
- (6)
- Electricity Consumption per Unit of Injected Water (Mi):
- (1)
- Pump Efficiency ():
- (2)
- Compressor Efficiency ():
- (3)
- Heater Efficiency ():
Appendix A.2. AHP Judgment Matrix
| Gas Consumption per Unit of Liquid Volume | Electricity Consumption per Unit of Liquid Volume | Multiphase Pump Efficiency | Heater Efficiency | Chemical Dosing Costs | Equipment Cleaning & Maintenance Costs | |
|---|---|---|---|---|---|---|
| Gas Consumption per Unit of Liquid Volume | 1 | 4/5 | 3/4 | 5/4 | 4 | 5/2 |
| Electricity Consumption per Unit of Liquid Volume | 5/4 | 1 | 4/5 | 3/2 | 5 | 3 |
| Multiphase Pump Efficiency | 4/3 | 5/4 | 1 | 3/2 | 4 | 4 |
| Heater Efficiency | 4/5 | 2/3 | 2/3 | 1 | 4 | 2 |
| Chemical Dosing Costs | 1/4 | 1/5 | 1/4 | 1/4 | 1 | 1/2 |
| Equipment Cleaning and Maintenance Costs | 2/5 | 1/3 | 1/4 | 1/2 | 2 | 1 |
| Gas Consumption per Unit of Liquid Volume | Electricity Consumption per Unit of Liquid Volume | Multiphase Pump Efficiency | Dosing Pump Efficiency | Injection Water Pump Efficiency | Chemical Dosing Costs | Equipment Cleaning & Maintenance Costs | |
|---|---|---|---|---|---|---|---|
| Gas Consumption per Unit of Liquid Volume | 1 | 1/3 | 5/4 | 5/3 | 1 | 3/2 | 5/4 |
| Electricity Consumption per Unit of Liquid Volume | 3 | 1 | 4 | 5 | 3 | 5 | 4 |
| Multiphase Pump Efficiency | 4/5 | 1/4 | 1 | 3/2 | 4/5 | 4/3 | 5/4 |
| Dosing Pump Efficiency | 3/5 | 1/5 | 2/3 | 1 | 3/5 | 4/5 | 2/3 |
| Injection Water Pump Efficiency | 1 | 1/3 | 5/4 | 5/3 | 1 | 3/2 | 5/4 |
| Chemical Dosing Costs | 2/3 | 1/5 | 3/4 | 5/4 | 2/3 | 1 | 4/5 |
| Equipment Cleaning and Maintenance Costs | 4/5 | 1/4 | 4/5 | 3/2 | 4/5 | 5/4 | 1 |
| Gas Consumption per Unit of Liquid Volume | Electricity Consumption per Unit of Liquid Volume | Multiphase Pump Efficiency | Heater Efficiency | Chemical Dosing Costs | Equipment Cleaning & Maintenance Costs | |
|---|---|---|---|---|---|---|
| Gas Consumption per Unit of Liquid Volume | 1 | 4/5 | 3/4 | 5/4 | 4 | 5/2 |
| Electricity Consumption per Unit of Liquid Volume | 5/4 | 1 | 4/5 | 3/2 | 5 | 3 |
| Multiphase Pump Efficiency | 4/3 | 5/4 | 1 | 3/2 | 4 | 4 |
| Heater Efficiency | 4/5 | 2/3 | 2/3 | 1 | 4 | 2 |
| Chemical Dosing Costs | 1/4 | 1/5 | 1/4 | 1/4 | 1 | 1/2 |
| Equipment Cleaning and Maintenance Costs | 2/5 | 1/3 | 1/4 | 1/2 | 2 | 1 |
References
- Li, Z.; Hao, J.; Lu, Y.; Hu, W.; Jiang, H.; Zhou, B.; Yang, H.; Kang, W.; Sarsenbekuly, B. Tunable macroscopic self-healing of supramolecular gel through host–guest inclusion. Phys. Fluids 2024, 36, 113–126. [Google Scholar] [CrossRef]
- Liang, T.; Yang, C.; Zhang, Y.; Li, P.; Qu, M.; Hou, J. Research and Application Progress of Nanofluid for Enhanced Oil Recovery. Xinjiang Oil Gas 2023, 19, 29–41. [Google Scholar] [CrossRef]
- Fan, Y.; Li, H.; Duan, S.; Gu, P.; Ren, N. Concentrated Solar Steam Generation Technology Enables Low Carbon Shallow SuperHeavy Oil Production. Xinjiang Oil Gas 2023, 19, 82–87. [Google Scholar] [CrossRef]
- Liu, W.; Ji, G.; Luo, Z.; Tian, Z. Energy analysis and evaluation method study of natural gas gathering and transportation system. Chem. Eng. Oil Gas 2016, 45, 109–116. [Google Scholar]
- Si, Z.; Duan, Z.; Qian, Q.; Chang, T.; Huang, Z. Research on Energy Efficiency Evaluation System of Oil Transfer Station System Based on Analytic Hierarchy Process. Oil-Gasfield Surf. Eng. 2019, 38, 5. [Google Scholar] [CrossRef]
- Cao, Y.; Song, M.; Zhao, W.; Xu, X.; Lin, G. Analysis on energy efficiency evaluation method of key energy system in oil and gas fields: Taking the Tarim oilfield as an example. Chem. Eng. Oil Gas 2020, 49, 106–114. [Google Scholar]
- Liu, S.; Shen, J. Improved Thermoeconomic Energy Efficiency Analysis for Integrated Energy Systems. Processes 2022, 10, 137. [Google Scholar] [CrossRef]
- Awow, C.D.; Muguthu, J.; Njoka, F. Energy efficiency potentials in oil & gas operations: A case study of South Sudan’s petroleum industry. Energy Rep. 2025, 13, 1673–1690. [Google Scholar]
- Abdulhaq, H.A.; Geiger, J.; Vass, I.; Tóth, T.M.; Medgyes, T.; Szanyi, J. Transforming Abandoned Hydrocarbon Fields into Heat Storage Solutions: A Hungarian Case Study Using Enhanced Multi-Criteria Decision Analysis–Analytic Hierarchy Process and Geostatistical Methods. Energies 2024, 17, 3954. [Google Scholar] [CrossRef]
- Li, Q.; Hao, Y.; Wang, P.; Wang, F.; Xu, M.; Bai, L.; Wang, X.; Zhang, Y. Research on Safety Evaluation of CO2 Enhanced Oil and Gas Recovery (CO2-EOR) Project: A Case Study of Dagang Oilfield. Processes 2024, 13, 28. [Google Scholar] [CrossRef]
- Majidi, A.G.; Ramos, V.; Rosa-Santos, P.; Akpınar, A.; das Neves, L.; Taveira-Pinto, F. Development of a multi-criteria decision-making tool for combined offshore wind and wave energy site selection. Appl. Energy 2025, 384, 125422. [Google Scholar] [CrossRef]
- Phani Raghav, L.; Seshu Kumar, R.; Koteswara Raju, D.; Singh, A.R. Analytic Hierarchy Process (AHP)—Swarm intelligence based flexible demand response management of grid-connected microgrid. Appl. Energy 2022, 306, 118058. [Google Scholar] [CrossRef]
- Chen, L.; Xiao, K.; Hu, F.; Li, Y. Performance evaluation and optimization design of integrated energy system based on thermodynamic, exergoeconomic, and exergoenvironmental analyses. Appl. Energy 2022, 326, 119987. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, C.; Liu, Z.; Li, P. Indentification for Leakage Risks of Crude Oil Tanks Based on Fault TreeAnalytic Hierarchy Process. Xinjiang Oil Gas 2023, 19, 80–85. [Google Scholar] [CrossRef]
- Zheng, M.; Teng, H.; Hu, J.; Zhao, Y.; Yu, L. Notable Problems of Grey Theory Used in Safety Evaluation of Oil and Gas Pipeline. Welded Pipe Tube 2013, 36, 20–22. [Google Scholar]
- Oluyemi, G.; Vilela, M.; Petrovski, A. A fuzzy inference system applied to value of information assessment for oil and gas industry. Decis. Mak. Appl. Manag. Eng. 2019, 2, 1–18. [Google Scholar]
- Tran, N.T.; Trinh, V.L.; Chung, C.K. An Integrated Approach of Fuzzy AHP-TOPSIS for Multi-Criteria Decision-Making in Industrial Robot Selection. Processes 2024, 12, 1723. [Google Scholar] [CrossRef]
- Zhao, D.; Zhang, J.; Wang, S.; Li, Z. Study on Energy Consumption Evaluation System of Oil Field Gathering Pump Unit Based on Correlation Coefficient Index Screening Method. Math. Pract. Theory 2021, 51, 137–144. [Google Scholar]
- Xiao, L.; Chen, W.; Cui, X.; Zhong, S.; Yu, C.; Yu, T.; Zhang, S. Application of Gray Analysis Method in Benefit Evaluation of Oil and Gas Exploration. Drill. Prod. Technol. 2007, 30, 67–69. [Google Scholar]
- Zhang, X.; Fan, J.; Chen, T.; Gu, Q. Integrative assessment of water flooding through fuzzy theory. Spec. Oil Gas Reserv. 2002, 9, 34–36+82. [Google Scholar]
- Xiong, Y.; Sun, L.; Sun, L.; Wu, Y. Fuzzy evaluation for developing high pour point oil with water drive in Shen 84 block. Spec. Oil Gas Reserv. 2001, 8, 49–52+114. [Google Scholar]
- Gao, Y. Evaluation of Oil and Gas Pipeline Emergency Management Capability based on Combination-weighted and Matter-element Extension Model. Welded Pipe Tube 2024, 47. [Google Scholar] [CrossRef]
- Wang, J.; Jiao, J.; Li, H.; Gong, J.; Li, X.; He, Z.; Sun, X. Smart Oil Depot Maturity Assessment Using the AHP-EWM Fuzzy Comprehensive Evaluation Model. Pet. New Energy 2024, 36, 41–47. [Google Scholar] [CrossRef]
- Yingming, Z.; Shuwei, W.; Dong, L.; Guozhong, W. Application of Grey Correlation Method in Energy Consumption Analysis of Crude Oil Gathering System. In Proceedings of the 2010 International Conference on Digital Manufacturing & Automation, Changsha, China, 18–20 December 2010. [Google Scholar]
- Tang, C.; Pang, Y.; Li, Z.; Zhang, X.; Sun, W. Study on Multi Level Energy Efficiency Evaluation System of Crude Oil Gathering and Transportation System. Math. Pract. Theory 2021, 51, 1–8. [Google Scholar]
- Li, Y.; Wu, X.; Han, F. Study on the Energy Consumption of the Gathering and Transportation System Based on the AHP Integrated Fuzzy Comprehensive Evaluation Method. Oil-Gas Field Surf. Eng. 2017, 36, 41–45. [Google Scholar] [CrossRef]
- Cheng, Q.; Chang, T.; Wang, Y.; Wang, S.; Wang, R.; Meng, F. Establishment and Analysis Method of Energy Efficiency Index System of Oil Field Gathering and Transportation System. J. Petrochem. Univ. 2020, 33, 67–73. [Google Scholar] [CrossRef]
- Peng, F. Research on comprehensive energy efficiency evaluation of gathering and transportation system based on combination model. Energy Conserv. Meas. Pet. Petrochem. Ind. 2024, 14, 67–72. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Q.; Sun, W.; Zhao, Y.; Li, Z. Research on a TOPSIS energy efficiency evaluation system for crude oil gathering and transportation systems based on a GA-BP neural network. Pet. Sci. 2024, 21, 621–640. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Y.; Ma, D.; Su, J.; Wu, D.; Li, X.; Lan, M. Energy Consumption Analysis of Closed Transfer Station Gathering and Transportation System in Ultra-Thick Oilfield Based on Grey Correlation-Fuzzy Comprehensive Evaluation. In Proceedings of the 2024 3rd International Conference on Energy and Electrical Power Systems (ICEEPS), Guangzhou, China, 14–16 July 2024; pp. 1–7. [Google Scholar]
- He, S.; Li, H.; Fan, J.; Qi, H.; Ji, Y.; Tang, K.; Du, M.; Yu, R. Evaluation of energy efficiency for the gas reservoir-wellbore-gathering and transmission pipeline network system in Dongsheng Gas Field. Oil Gas Storage Transp. 2025, 44, 220–229. [Google Scholar] [CrossRef]
- Shen, M.; Xue, X.; Zhang, X. Determination of Discrimination Coefficient in Grey Incidence Analysis. J. Air Force Eng. Univ. 2003, 4, 68–70. [Google Scholar]
- Guo, J.; Zhang, Z.; Sun, Q. Study and Applications of Analytic Hierarchy Process. China Saf. Sci. J. 2008, 169, 1–29. [Google Scholar]
- Qi, G.; Huang, R.; Zeng, Z.; Wan, J. An AHP based multi-factors weight method for route selection of oil and gas pipelines. Sci. Surv. Mapp. 2013, 38, 122–125. [Google Scholar]
- Liu, Z. Study on application of AHP in agricultural system. Guangdong Agric. Sci. 2013, 40, 228–232. [Google Scholar]
- Saaty, R.W. The Analytic Hierarchy Process: What and How It Is Used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Wu, J.; Li, P.; Qian, H.; Chen, J. On the sensitivity of entropy weight to sample statistics in assessing water quality: Statistical analysis based on large stochastic samples. Environ. Earth Sci. 2015, 74, 2185–2195. [Google Scholar] [CrossRef]
- Yan, F.; Qian, B.; Xiao, X.; Ma, L. Geo-accumulation vector model for evaluating the heavy metal pollution in the sediments of Western Dongting Lake. J. Hydrol. 2019, 573, 40–48. [Google Scholar]
- Yan, F.; Qiao, D.; Qian, B.; Ma, L.; Xing, X.; Zhang, Y.; Wang, X. Improvement of CCME WQI using grey relational method. J. Hydrol. 2016, 543, 316–323. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Arce, M.E.; Saavedra, N.; Míguez, J.L.; Granada, E. The use of grey-based methods in multi-criteria decision analysis for the evaluation of sustainable energy systems: A review. Renew. Sustain. Energy Rev. 2015, 47, 924–932. [Google Scholar] [CrossRef]
- Deng, J. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Wu, J. Characteristics and Application of Submerged Water Injection in Thin Oil Reservoirs. Chem. Eng. Des. Commun. 2019, 45, 55. [Google Scholar]
- Zhu, F.; Ren, Y.; Teng, H. Ground Gathering and Transportation Technology of Light Oil and Heavy Oil in Xinjiang Oilfiled. Contemp. Chem. Ind. 2016, 45, 1564–1567. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, X.; Cao, Y.; Xue, X.; Li, H.; Li, W. Study on the Energy Consumption Evaluation Index System for the Water Injection System in Xinjiang Oilfield. Oil-Gas Field Surf. Eng. 2018, 37, 19–23+27. [Google Scholar]
- Ruan, L.; Zhu, T.; Wang, Y. Research and Application of Heating and Energy-saving Technology of Thin Oil Gathering and Transporting System. Energy Conserv. Pet. Petrochem. Ind. 2021, 11, 10–13. [Google Scholar] [CrossRef]



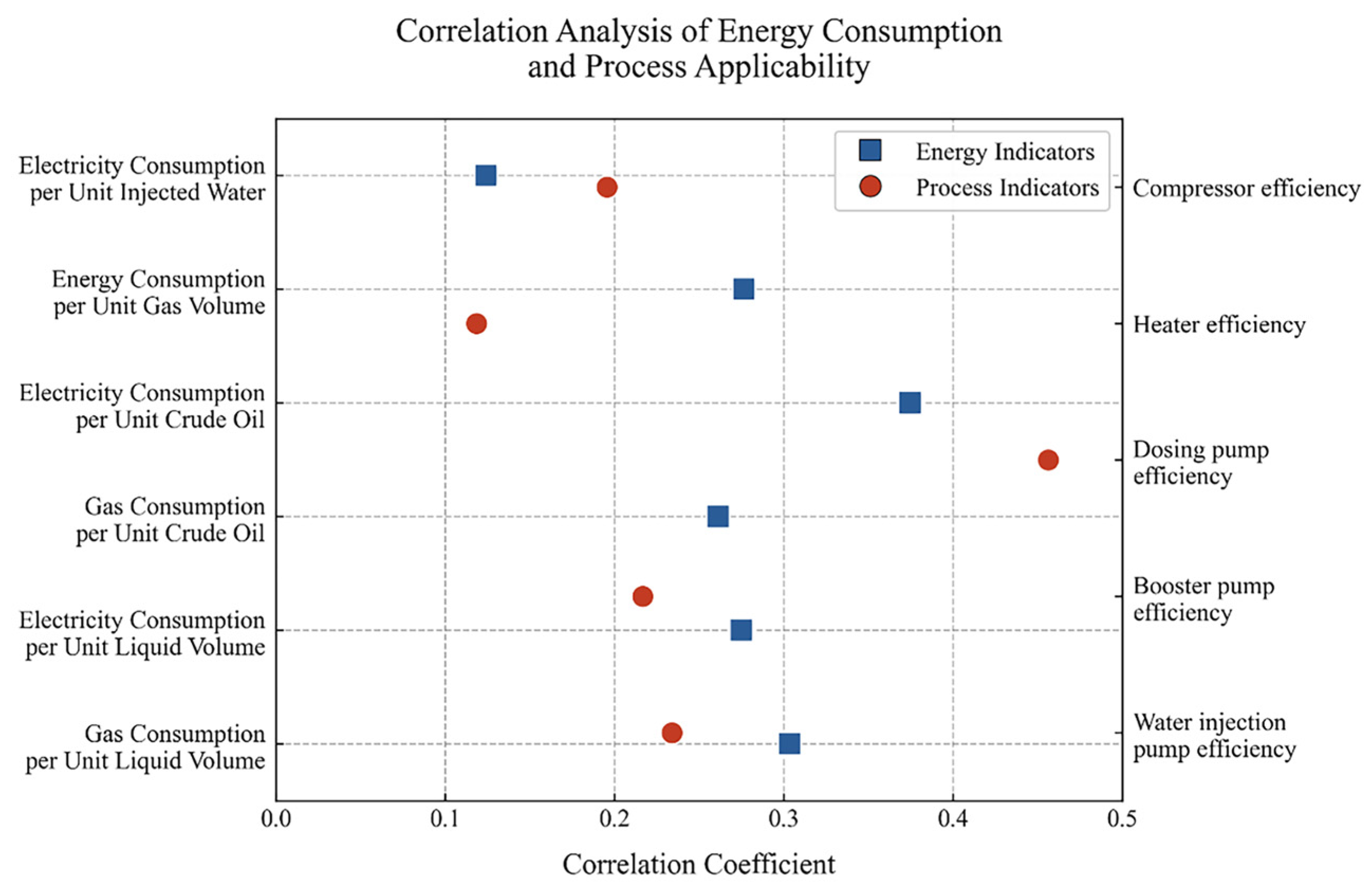
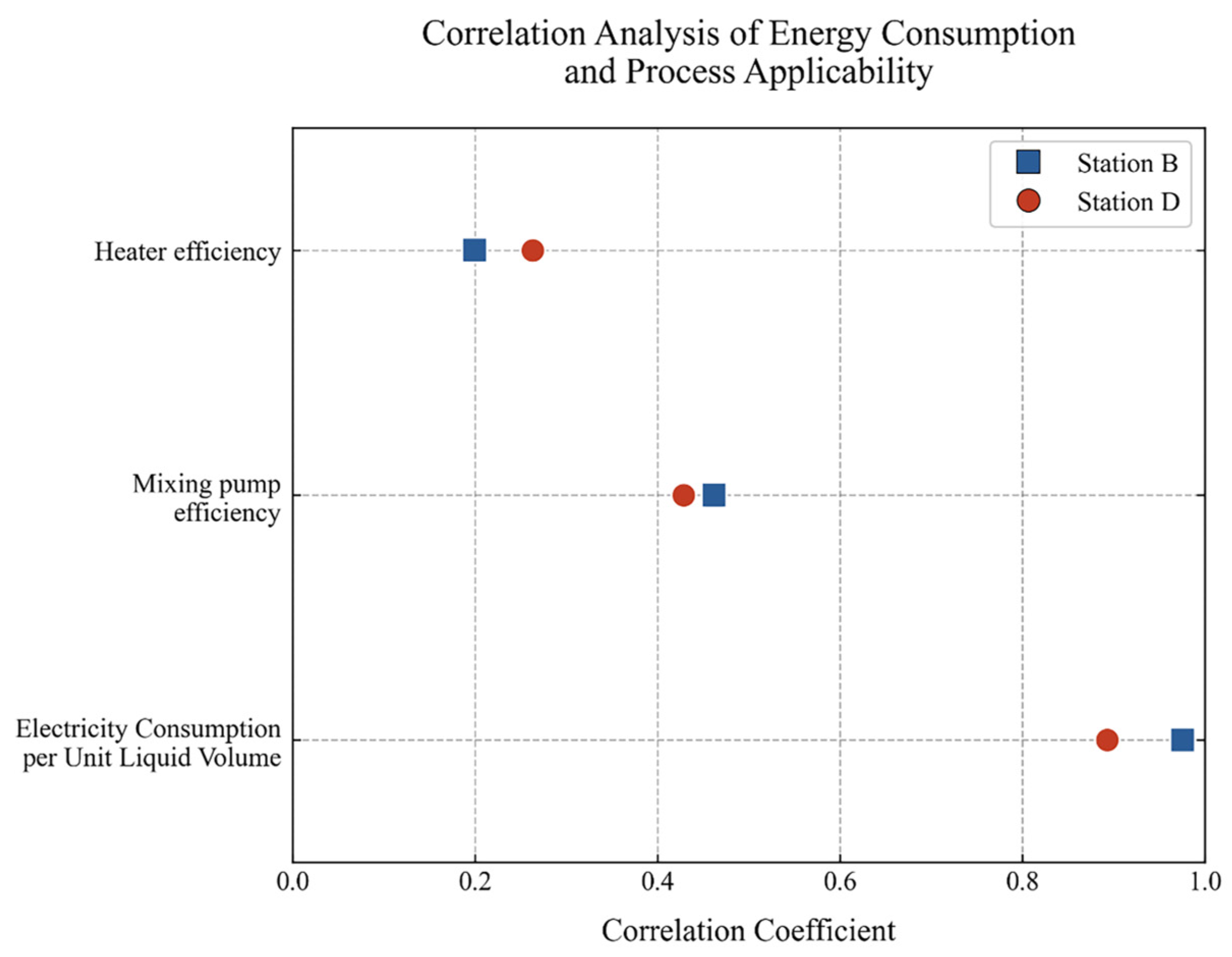
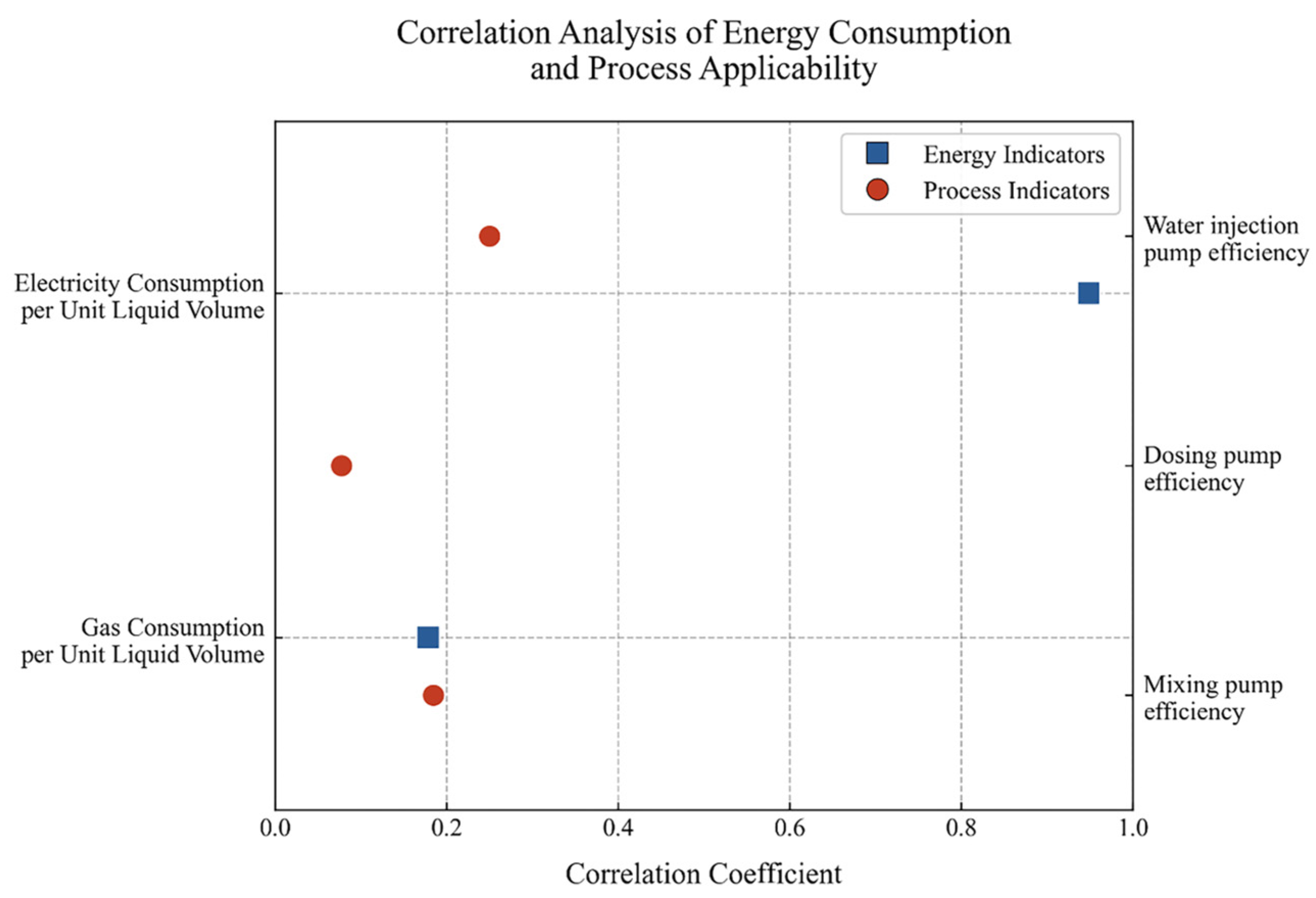
| Level 2 Indicators | Weights | |||
|---|---|---|---|---|
| A | B | C | D | |
| Energy consumption | 0.54 | 0.66 | 0.55 | 0.70 |
| Process applicability | 0.43 | 0.31 | 0.17 | 0.28 |
| Economic cost | 0.03 | 0.03 | 0.28 | 0.02 |
| Level 3 Indicators | weights | |||
| A | B | C | D | |
| Energy consumption per unit of liquid volume | 0.16 | 0.66 | 0.55 | 0.70 |
| Energy consumption per unit of crude oil | 0.19 | - | - | - |
| Energy consumption per unit of gas volume | 0.16 | - | - | - |
| Electricity consumption per unit of injected water | 0.03 | - | - | - |
| Pump efficiency | 0.34 | 0.21 | 0.17 | 0.19 |
| Heater efficiency | 0.04 | 0.10 | - | 0.09 |
| Equipment cleaning and maintenance costs | 0.02 | 0.03 | 0.05 | 0.02 |
| Chemical dosing costs | 0.01 | - | 0.23 | - |
| Level 4 indicators | weights | |||
| A | B | C | D | |
| Gas consumption per unit of liquid volume | 0.09 | 0.26 | 0.08 | 0.30 |
| Electricity consumption per unit of liquid volume | 0.07 | 0.40 | 0.47 | 0.40 |
| Gas consumption per unit of crude oil | 0.09 | - | - | - |
| Electricity consumption per unit of crude oil | 0.10 | - | - | - |
| Injection water pump efficiency | 0.09 | - | 0.07 | - |
| Booster pump efficiency | 0.08 | - | - | - |
| Chemical injection pump efficiency | 0.17 | - | 0.04 | - |
| Multiphase pump efficiency | - | 0.21 | 0.06 | 0.19 |
| Level 1 Indicator | Central Processing Station | Lu-22 Multiphase Pumping Station | Lu-12 Dehydration Station | Lu-15 Multiphase Pumping Station |
|---|---|---|---|---|
| weights | 0.44 | 0.25 | 0.04 | 0.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Sun, Y.; Zhang, Y.; Mahan, M.; Chen, Y.; Xu, M.; Wu, K.; Hong, B.; Song, S. An Energy Efficiency Evaluation Model for Oil–Gas Gathering and Transportation Systems Based on Combined Weighting and Grey Relational Analysis. Processes 2025, 13, 1967. https://doi.org/10.3390/pr13071967
Shi Y, Sun Y, Zhang Y, Mahan M, Chen Y, Xu M, Wu K, Hong B, Song S. An Energy Efficiency Evaluation Model for Oil–Gas Gathering and Transportation Systems Based on Combined Weighting and Grey Relational Analysis. Processes. 2025; 13(7):1967. https://doi.org/10.3390/pr13071967
Chicago/Turabian StyleShi, Yao, Yingting Sun, Yonghu Zhang, Maerpuha Mahan, Yingli Chen, Mingzhe Xu, Keyu Wu, Bingyuan Hong, and Shangfei Song. 2025. "An Energy Efficiency Evaluation Model for Oil–Gas Gathering and Transportation Systems Based on Combined Weighting and Grey Relational Analysis" Processes 13, no. 7: 1967. https://doi.org/10.3390/pr13071967
APA StyleShi, Y., Sun, Y., Zhang, Y., Mahan, M., Chen, Y., Xu, M., Wu, K., Hong, B., & Song, S. (2025). An Energy Efficiency Evaluation Model for Oil–Gas Gathering and Transportation Systems Based on Combined Weighting and Grey Relational Analysis. Processes, 13(7), 1967. https://doi.org/10.3390/pr13071967







