A New Method for Calculating Carbonate Mineral Content Based on the Fusion of Conventional and Special Logging Data—A Case Study of a Carbonate Reservoir in the M Oilfield in the Middle East
Abstract
1. Introduction
2. Geological Overview and Material Sources
2.1. Geological Overview
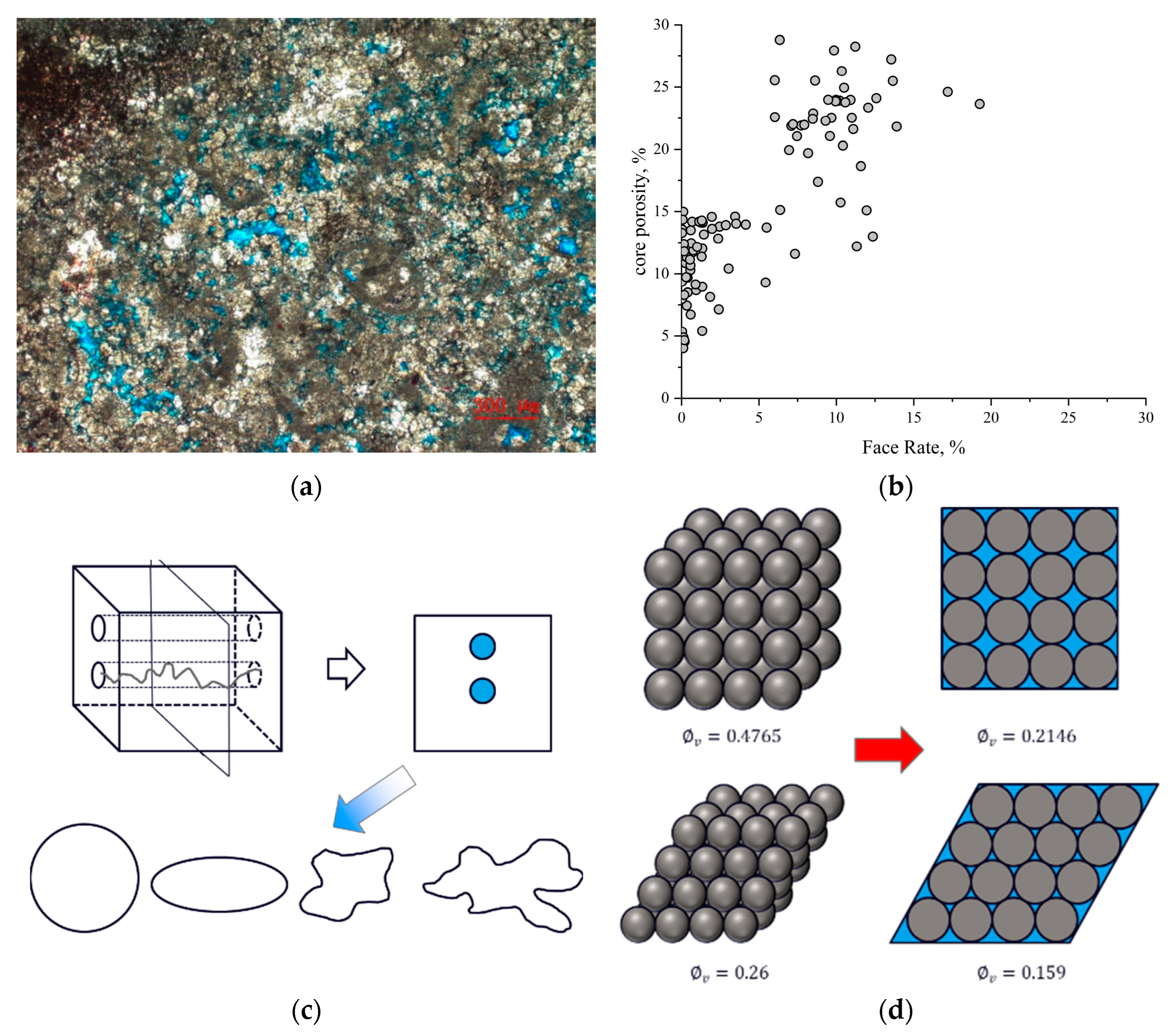
2.2. Material Source and Determination of Core Mineral Content
3. Methods and Principles
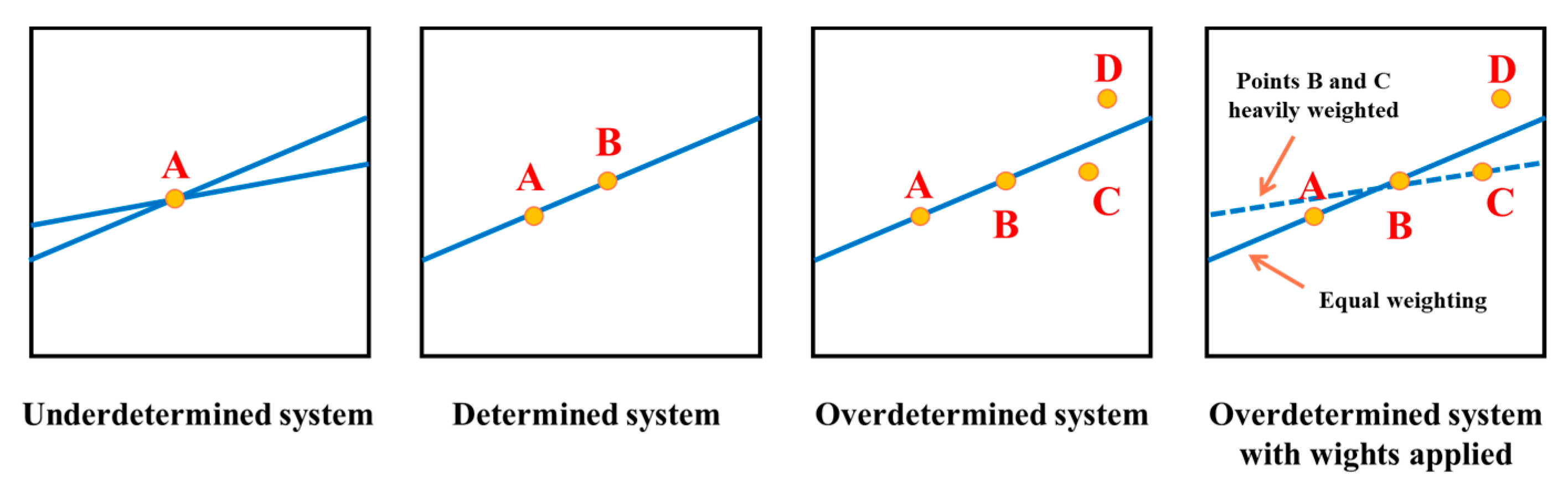
3.1. Construction of Linear Equations
3.2. The Objective Function Based on the Principle of Linear Weighted Least Squares
3.3. Improvement and Application of Sequential Quadratic Programming Method
3.3.1. Principle and Solving Steps of Sequential Quadratic Programming Method
- (1)
- Define the objective function: Initially, the objective function and constraints of the nonlinear constrained optimization problem are mathematically modeled. The objective function can be nonlinear, while the constraints typically consist of both equality and inequality conditions.
- (2)
- Select an initial point: An initial point is chosen to start the optimization process. This point must generally satisfy the constraint conditions to ensure that the optimization procedure proceeds smoothly.
- (3)
- Linearize the objective function and constraints: Based on the current point, the objective function and constraints are linearized to formulate a linear programming subproblem.
- (4)
- Solve the linear subproblem: Linear programming solving techniques, such as interior-point methods or gradient projection methods, are employed to solve the linear subproblem and obtain a new iteration point.
- (5)
- Determine the step size: The step size from the current point to the new iteration point is computed, typically by using a one-dimensional search method (e.g., Armijo’s rule), ensuring that each iteration makes sufficient progress.
- (6)
- Update the current point: The current point is updated to the new iteration point, where the step size is denoted as .
- (7)
- Check for convergence: Finally, the method checks whether the current point meets the convergence criteria, such as whether the change in the objective function is below a predefined threshold or the constraint conditions are satisfied. If the termination criteria are not met, the process returns to step 3 for further iterations until convergence is achieved.
3.3.2. Construction of SQP_AW Model
3.4. Method Steps
- (1)
- First, conventional logging curves, modulus curves, and nuclear magnetic porosity curves are imported. The mineral composition data from the core XRD experimental results are combined with the least squares method to determine the transformation coefficients (constants in the equations) and initialize the uncertainty matrix.
- (2)
- The mineral composition contents, equation weights, and Adam optimization algorithm parameters are initialized; then, the inversion system of equations is constructed.
- (3)
- The iterative optimization process, where the equations are solved by using the SQP method and the error gradient is calculated, is entered. The weights are updated with the Adam algorithm, which dynamically adjusts the optimization process.
- (4)
- The optimal inversion results are output, the mineral content in the new well is calculated, and these results are compared with the core XRD data.
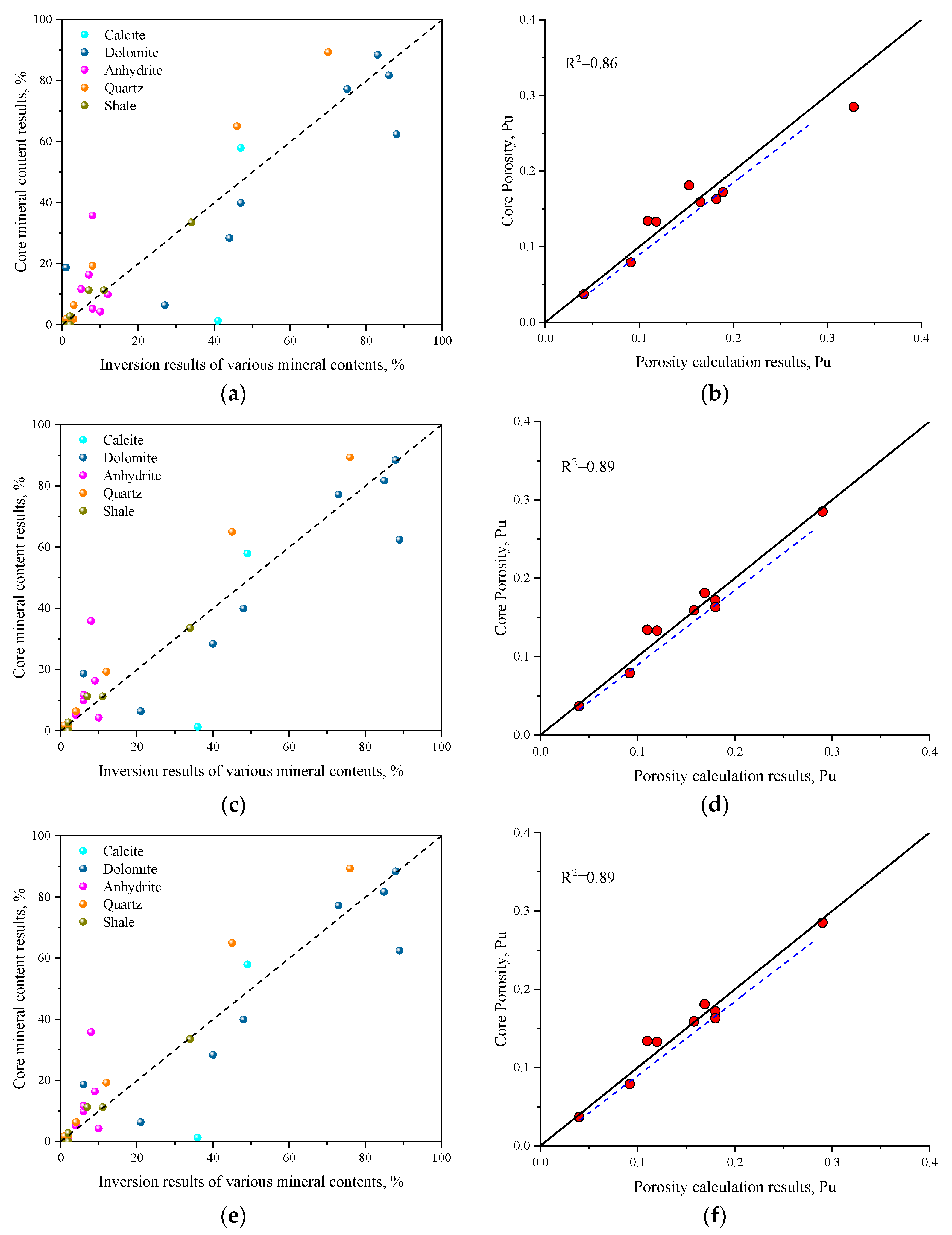
4. Results
4.1. The Results of Coefficient Calibration and Weight Calculation
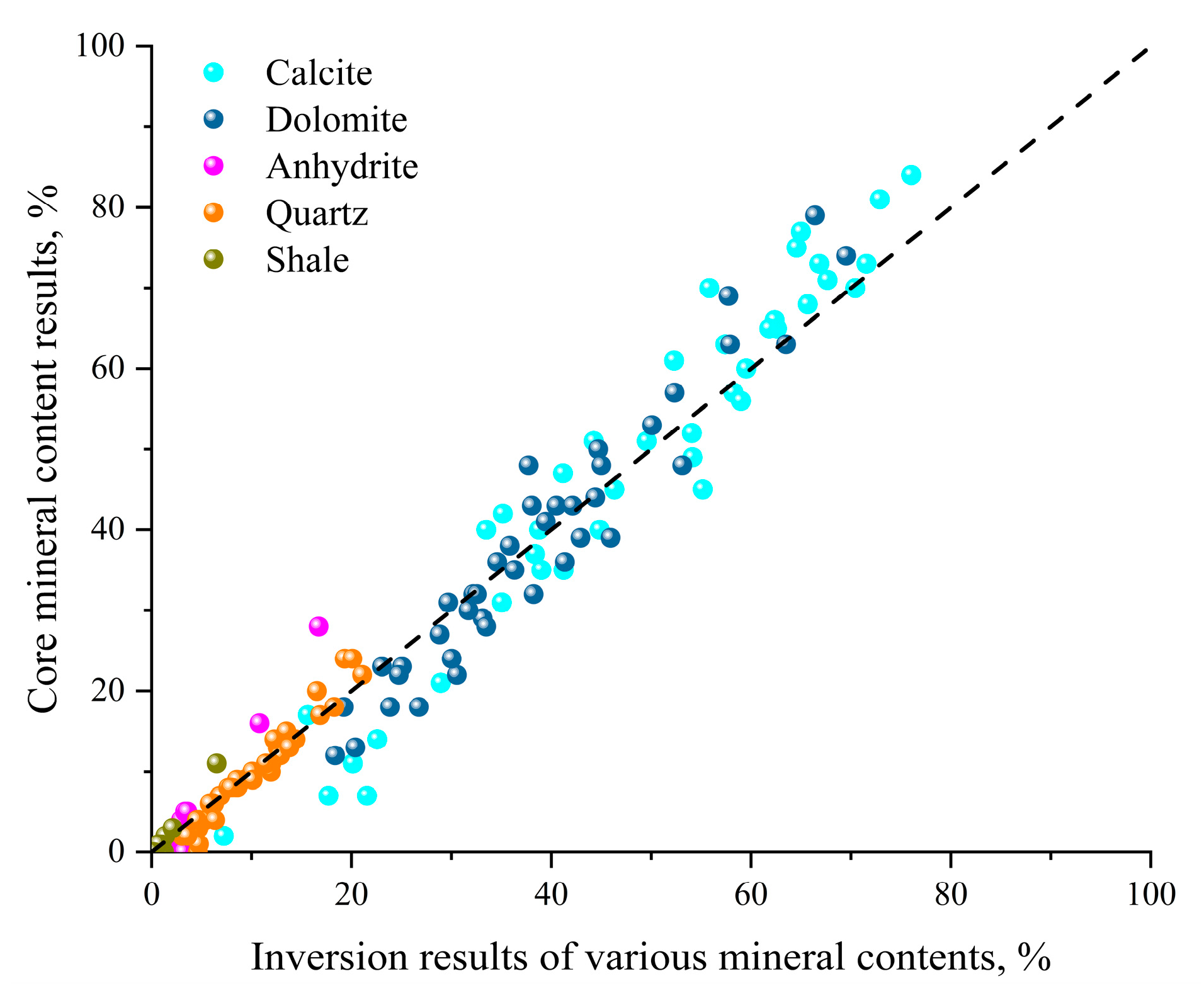
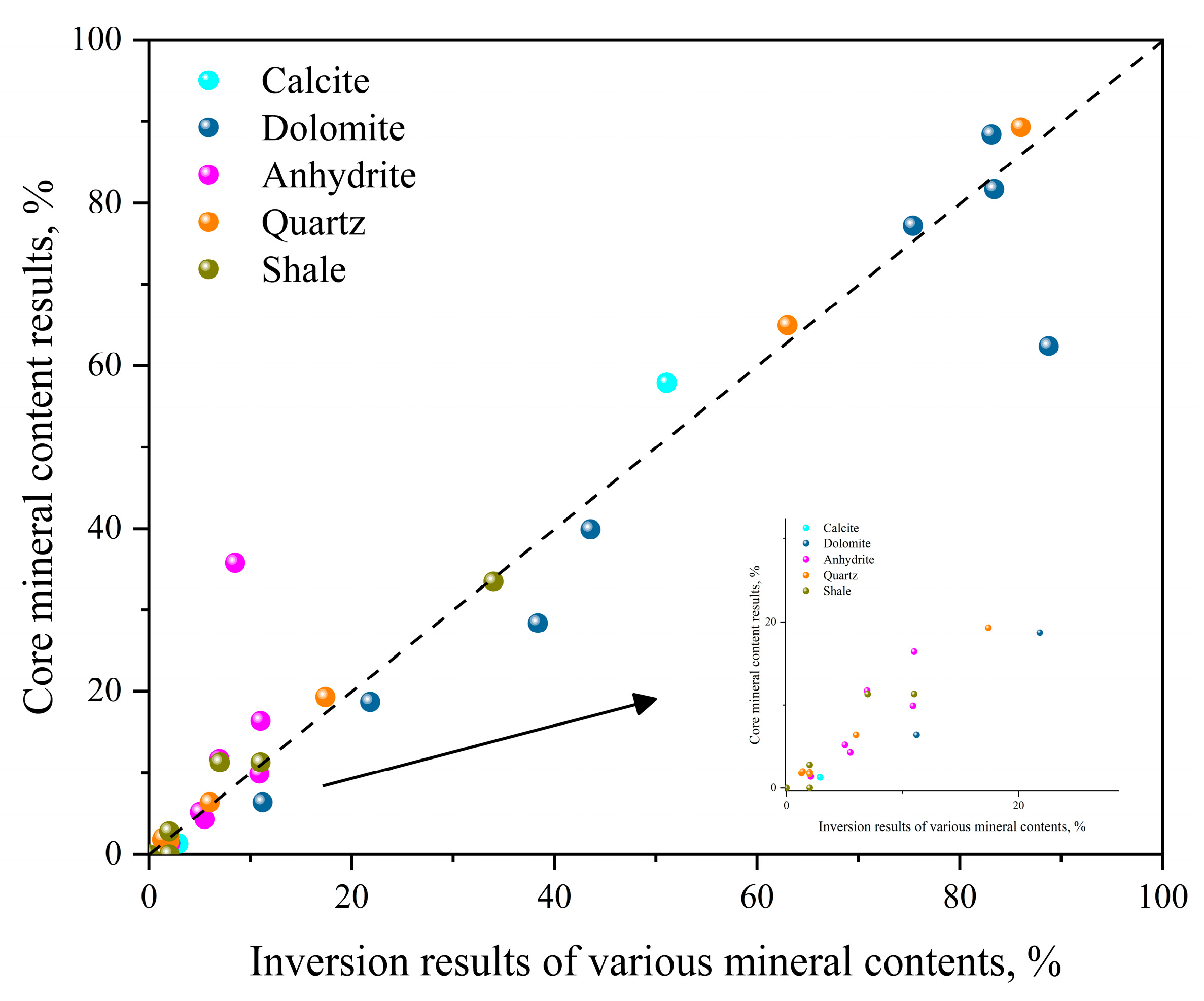
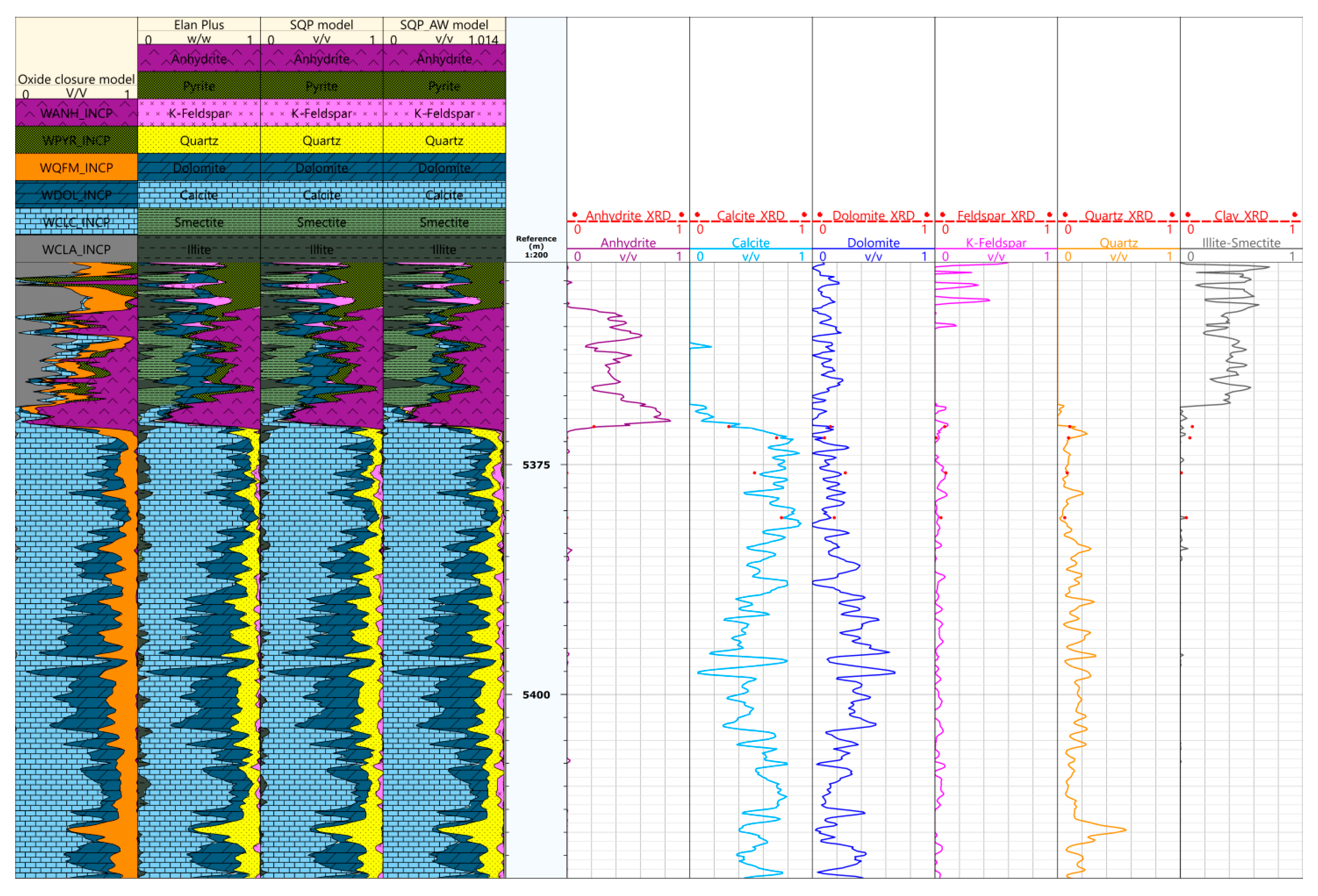
4.2. Mineral Content Inversion Results
5. Discussion
5.1. Advantages of the New Method
5.2. Extensibility of the New Method
5.3. Limitations of the New Method and Future Research Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SQP | Sequential Quadratic Programming |
| XRD | X-ray diffraction |
| ECS | Elemental capture spectroscopy |
| LD | Linear dichroism |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| DNN | Deep Neural Network |
| DCNN | Deep Convolutional Neural Network |
| STNN | Spatiotemporal Neural Network |
| Adam | Adaptive Moment Estimation |
| SVD | Singular value decomposition |
| SEM | Scanning Electron Microscopy |
| Q-F-M | Quartz–feldspar–mica |
References
- Feng, Z.; Li, X.; Wu, H.; Xia, S.; Liu, Y. Multimineral optimization processing method based on elemental capture spectroscopy logging. Appl. Geophys. 2014, 11, 41–49. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Z.; Zhang, C.; Zhao, Q.; Tang, X. Enhanced water saturation evaluation method using an improved electrical efficiency model: A case study of the Mishrif Formation, Iraq. J. Appl. Geophys. 2025, 236, 105656. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, W.; Yang, W.; Zhang, C.; Zhang, C. An improved method in petrophysical rock typing based on mercury-injection capillary pressure data. Energy Source Part A 2024, 46, 12647–12662. [Google Scholar] [CrossRef]
- Hollis, C.; Vahrenkamp, V.; Tull, S.; Mookerjee, A.; Taberner, C.; Huang, Y. Pore system characterisation in heterogeneous carbonates: An alternative approach to widely-used rock-typing methodologies. Mar. Petrol. Geol. 2010, 27, 772–793. [Google Scholar] [CrossRef]
- Hussein, H.S.; Mansurbeg, H.; Bábek, O. A new approach to predict carbonate lithology from well logs: A case study of the Kometan formation in northern Iraq. Heliyon 2024, 10, e25262. [Google Scholar] [CrossRef]
- Leisi, A.; Shad Manaman, N. Seismic and geomechanical characterization of Asmari formation using well logs and simultaneous inversion in an Iranian oil field. Sci. Rep. 2025, 15, 11276. [Google Scholar] [CrossRef]
- Stadtműller, M.; Jarzyna, J.A. Estimation of petrophysical parameters of carbonates based on well logs and laboratory measurements, a review. Energies 2023, 16, 4215. [Google Scholar] [CrossRef]
- Lai, J.; Fan, X.; Liu, B.; Pang, X.; Zhu, S.; Xie, W.; Wang, G. Qualitative and quantitative prediction of diagenetic facies via well logs. Mar. Petrol. Geol. 2020, 120, 104486. [Google Scholar] [CrossRef]
- Gavidia, J.C.R.; Chinelatto, G.F.; Basso, M.; Souza, J.P.; Soltanmohammadi, R.; Vidal, A.C.; Goldstein, R.H.; Mohammadizadeh, S.M. Utilizing integrated artificial intelligence for characterizing mineralogy and facies in a pre-salt carbonate reservoir, Santos Basin, Brazil, using cores, wireline logs, and multi-mineral petrophysical evaluation. Geoenergy Sci. Eng. 2023, 231, 212303. [Google Scholar] [CrossRef]
- Lee, H.; Lee, H.P. Formation lithology predictions based on measurement while drilling (MWD) using gradient boosting algorithms. Geoenergy Sci. Eng. 2023, 227, 211917. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, S.; Peng, H.; Ji, C. Improving Interpretation Accuracy of ECS Mineral Content with Core Analysis Data. Logging Technol. 2018, 42, 49–53. [Google Scholar]
- Li, D.; Li, X.; Liu, L.; He, W.; Li, Y.; Li, S.; Shi, H.; Fan, G. Prediction on rock strength by mineral composition from machine learning of ECS logs. Energy Geosci. 2025, 6, 100386. [Google Scholar] [CrossRef]
- Sun, J.; Jiang, D.; Yin, L. A method for determining mineral content by formation element logging. Nat. Gas Ind. 2014, 34, 42–47. [Google Scholar]
- Zhao, J.; Chen, H.; Yin, L.; Li, N. Mineral inversion for element capture spectroscopy logging based on optimization theory. J. Geophys. Eng. 2017, 14, 1430–1436. [Google Scholar] [CrossRef]
- Mohamed, A.; Ibrahim, E.; Sabry, A. Petrophysical characteristics of Wakar formation, Port Fouad marine field, north Nile delta, Egypt. Arab. J. Geosci. 2013, 6, 1485–1497. [Google Scholar] [CrossRef]
- Parra, J.; Emery, X. Geostatistics applied to cross-well reflection seismic for imaging carbonate aquifers. J. Appl. Geophys. 2013, 92, 68–75. [Google Scholar] [CrossRef]
- Gao, C. An Optimum Algorithm to Inverse Geochemical Logging Data to the Composition of Rock Materials. J. Petrol. Nat. Gas 1999, 21, 26–28. [Google Scholar]
- Amosu, A.; Sun, Y. MinInversion: A program for petrophysical composition analysis of geophysical well log data. Geosciences 2018, 8, 65. [Google Scholar] [CrossRef]
- Li, J.; Lu, S.; Wang, M.; Chen, G.; Tian, W.; Jiao, C. A novel approach to the quantitative evaluation of the mineral composition, porosity, and kerogen content of shale using conventional logs: A case study of the Damintun Sag in the Bohai Bay Basin, China. Interpretation 2019, 7, 83–95. [Google Scholar] [CrossRef]
- Pan, B.; Xue, L.; Huang, B.; Yan, G.; Zhang, L. Evaluation of volcanic reservoirs with the “QAPM mineral model” using a genetic algorithm. Appl. Geophys. 2008, 5, 1–8. [Google Scholar] [CrossRef]
- Boiger, R.; Churakov, S.V.; Ballester Llagaria, I.; Kosakowski, G.; Wüst, R.; Prasianakis, N.I. Direct mineral content prediction from drill core images via transfer learning. Swiss J. Geosci. 2024, 117, 8. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, W.; Song, X. Well Logs Reconstruction Based on Deep Learning Technology. IEEE Geosci. Remote Sens. 2024, 21, 7501205. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J.; You, J. Reconstruction of logging traces based on GRU neural network. Oil Geophys. Prospect. 2020, 55, 510–520. [Google Scholar] [CrossRef]
- Tariq, Z.; Gudala, M.; Yan, B.; Sun, S.; Mahmoud, M. A fast method to infer Nuclear Magnetic Resonance based effective porosity in carbonate rocks using machine learning techniques. Geoenergy Sci. Eng. 2023, 222, 211333. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, Z.; Hu, C.; Li, G.; He, W.; Ma, F. Research on evaluation method of rock mineral composition content by logging based on deep convolutional neural networks. Prog. Geophys. 2023, 38, 748–758. [Google Scholar]
- Wang, J.; Cao, J.; You, J.; Cheng, M.; Zhou, P. A method for well log data generation based on a spatio-temporal neural network. J. Geophys. Eng. 2021, 18, 700–711. [Google Scholar] [CrossRef]
- Zhai, X.; Gao, G.; Li, Y.; Chen, D.; Gui, Z.; Wang, Z. Reconstruction method of logging curves by 2D convolutional neural network integrating attention mechanism. Oil Geophys. Prospect. 2023, 58, 1031–1041. [Google Scholar]
- Guo, J.; Zhang, Z.; Xiao, H.; Zhang, C.; Zhu, L.; Wang, C. Quantitative interpretation of coal industrial components using a gray system and geophysical logging data: A case study from the Qinshui Basin, China. Front. Earth Sci. 2023, 10, 1031218. [Google Scholar] [CrossRef]
- Moradi, M.; Kadkhodaie, A.; Taheri, M.R.; Chenani, A. Estimation of porosity distribution from formation image logs and comparing the results with NMR log analysis: Implications for the heterogeneity analysis of carbonate reservoirs with an example from the Asmari reservoir, southwest Iran. J. Afr. Earth Sci. 2024, 218, 105366. [Google Scholar] [CrossRef]
- Taheri, K.; Alizadeh, H.; Askari, R.; Kadkhodaie, A.; Hosseini, S. Quantifying fracture density within the Asmari reservoir: An integrated analysis of borehole images, cores, and mud loss data to assess fracture-induced effects on oil production in the Southwestern Iranian Region. Carbonates Evaporites 2024, 39, 8. [Google Scholar] [CrossRef]
- Lv, H.; Guo, J.; Gu, B.; Liu, Y.; Wang, L.; Wang, L.; Zhu, Z.; Zhang, Z. High-Precision Permeability Evaluation of Complex Carbonate Reservoirs in Marine Environments: Integration of Gaussian Distribution and Thomeer Model Using NMR Logging Data. J. Mar. Sci. Eng. 2024, 12, 2135. [Google Scholar] [CrossRef]
- Lv, H.; Guo, J.; Gu, B.; Zhu, Z.; Zhang, Z. A fracture identification method using fractal dimension and singular spectrum entropy in array acoustic logging: Insights from the Asmari Formation in the M oilfield, Iraq. J. Appl. Geophys. 2025, 233, 105631. [Google Scholar] [CrossRef]
- Khazaie, E.; Noorian, Y.; Moussavi-Harami, R.; Mahboubi, A.; Kadkhodaie, A.; Omidpour, A. Electrofacies modeling as a powerful tool for evaluation of heterogeneities in carbonate reservoirs: A case from the Oligo-Miocene Asmari Formation (Dezful Embayment, southwest of Iran). J. Afr. Earth Sci. 2022, 195, 104676. [Google Scholar] [CrossRef]
- Ge, Y.; Wu, W.; Yang, C.; He, L.; Hu, G. Calculation of elemental logging yield and analysis of influencing factors. Prog. Geophys. 2020, 35, 950–954. [Google Scholar] [CrossRef]
- Kumar, V.; Sondergeld, C.; Rai, C.S. Effect of mineralogy and organic matter on mechanical properties of shale. Interpretation 2015, 3, 9–15. [Google Scholar] [CrossRef]
- Li, C.; Hu, F.; Yuan, C.; Li, X.; Li, C.; Liu, X. Determining multi-mineral compositions in tight reservoirs using a combination of NMR and conventional logging methods. J. Petrol. 2018, 39, 1019–1027. [Google Scholar] [CrossRef]
- Quirein, J. A coherent framework for developing and applying multiple formation models. In Proceedings of the Society of Professional Well Log Analysts 27th Annual Logging Symposium, Houston, TX, USA, 9–13 June 1986; pp. 1–17. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Yi, D.; Ahn, J.; Ji, S. An effective optimization method for machine learning based on ADAM. Appl. Sci. 2020, 10, 1073. [Google Scholar] [CrossRef]





| Quartz | Calcite | Dolomite | Anhydrite | Shale | |
|---|---|---|---|---|---|
| Bulk density (g/cm3) | 2.65 | 2.71 | 2.87 | 2.99 | 2.45 |
| Neutron porosity (%) | −0.03 | 0 | 0.03 | −0.03 | 0.4 |
| Longitudinal wave time difference (μs/ft) | 55.5 | 47.5 | 43.5 | 50 | 100 |
| 44 | 27.9 | 44.5 | 29.5 | 8.8 | |
| K | 37 | 68.2 | 94.2 | 57.4 | 24.8 |
| 0.18 | 0.05 | 0.09 | 0.006 | 0.01 |
| Curve Equation | Curve Weight |
|---|---|
| Bulk density | 2.03 |
| Neutron porosity | 1.92 |
| Longitudinal wave time difference | 1.84 |
| 1.92 | |
| K | 1.77 |
| 1.22 |
| Evaluating Index | Quartz | Calcite | Dolomite | Anhydrite | Shale |
|---|---|---|---|---|---|
| Mean Relative Error (%) | 5.5 | 9.4 | 10.2 | 24.6 | 11.7 |
| Mean Absolute Error (%) | 3.2 | 4.9 | 5.2 | 5.9 | 1.8 |
| R2 (Pu) | 0.92 | 0.84 | 0.82 | 0.61 | 0.73 |
| Element | Optimal Weighting | Average Error (%) |
|---|---|---|
| Al | 1.85 | 0.80 |
| Ca | 1.73 | 0.24 |
| Fe | 1.95 | 0.20 |
| K | 1.19 | 0.01 |
| Mg | 2.21 | 0.12 |
| Na | 0.69 | 0.01 |
| Si | 1.29 | 0.09 |
| S | 0.88 | 0.12 |
| Ti | 0.65 | 1.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, B.; Tong, K.; Wang, L.; Zhu, Z.; Lv, H.; Zhang, Z.; Guo, J. A New Method for Calculating Carbonate Mineral Content Based on the Fusion of Conventional and Special Logging Data—A Case Study of a Carbonate Reservoir in the M Oilfield in the Middle East. Processes 2025, 13, 1954. https://doi.org/10.3390/pr13071954
Gu B, Tong K, Wang L, Zhu Z, Lv H, Zhang Z, Guo J. A New Method for Calculating Carbonate Mineral Content Based on the Fusion of Conventional and Special Logging Data—A Case Study of a Carbonate Reservoir in the M Oilfield in the Middle East. Processes. 2025; 13(7):1954. https://doi.org/10.3390/pr13071954
Chicago/Turabian StyleGu, Baoxiang, Kaijun Tong, Li Wang, Zuomin Zhu, Hengyang Lv, Zhansong Zhang, and Jianhong Guo. 2025. "A New Method for Calculating Carbonate Mineral Content Based on the Fusion of Conventional and Special Logging Data—A Case Study of a Carbonate Reservoir in the M Oilfield in the Middle East" Processes 13, no. 7: 1954. https://doi.org/10.3390/pr13071954
APA StyleGu, B., Tong, K., Wang, L., Zhu, Z., Lv, H., Zhang, Z., & Guo, J. (2025). A New Method for Calculating Carbonate Mineral Content Based on the Fusion of Conventional and Special Logging Data—A Case Study of a Carbonate Reservoir in the M Oilfield in the Middle East. Processes, 13(7), 1954. https://doi.org/10.3390/pr13071954






