Thermal Management Design for the Be Target of an Accelerator-Based Boron Neutron Capture Therapy System Using Numerical Simulations with Boiling Heat Transfer Models

Abstract

Recently, studies on accelerator-based boron neutron capture therapy (AB-BNCT) systems for cancer treatment have attracted the attention of researchers around the world. A neutron source can be obtained through the impingement of high-intensity proton beams emitted from the accelerator onto the target. This process would deposit a large amount of heat within this target. A thermal management system design is needed for AB-BNCT systems to prevent the degradation of the target due to thermal/mechanical loading. However, there are few studies that investigate this topic. In this paper, a cooling channel with a boiling heat transfer mechanism is numerically designed for thermal management in order to remove heat deposited in the Be target of the AB-BNCT system of Heron Neutron Medical Corp. A three-dimensional (3D) CFD methodology with a two-fluid model and an RPI wall boiling model is developed to investigate its availability. Two subcooled boiling experiments from previous works are adopted to validate the present CFD boiling model. This validated model can be confidently applied to assist in thermal management design for the AB-BNCT system. Based on the simulation results under the typical operating conditions of the AB-BNCT system set by Heron Neutron Medical Corp., the present coolant channel employing the boiling heat transfer mechanism can efficiently remove the heat deposited in the Be target, as well as maintain its integrity during long-term operation. In addition, compared with the channel with the single-phase convection traditionally designed for an AB-BNCT system, the boiling heat transfer mechanism can result in a lower peak temperature in the Be target and its corresponding deformation.

1. Introduction

For decades, boron neutron capture therapy (BNCT) has been considered an innovative type of radiotherapy that uses neutron irradiation to destroy cancer cells [1]. However, traditional BNCT may not be adopted in hospitals since it should be installed at sites near the research reactor. Accelerator-based BNCT (AB-BNCT) systems have thus attracted much attention from researchers around the world [2], as it is feasible to install these systems in hospitals for the treatment of more patients. The main parts of an AB-BNCT system includes intense ion sources, accelerator tubes, transport systems for intense beams, beam diagnostics and control systems, the neutron source (i.e., neutron production reactions), the appropriate coolant channel or thermal management system, etc. Beryllium (Be) is usually adopted as the target material in an AB-BNCT system for producing a secondary neutron. Due to the thermal and mechanical loading from the impingement of high-intensity proton beams from the accelerator, the Be target should sustain its integrity during the long-term operation of an AB-BNCT system. Therefore, it is crucial to conduct investigations to determine the appropriate thermal management for the design of an AB-BNCT system. A thermal management design should reduce temperature increases in the Be target to prevent the material from melting and maintain uniform temperature distribution to prevent excess mechanical loading from thermal shock [3].

Our review of the literature reveals that little research has been conducted on thermal management for AB-BNCT systems. The University of Tsukuba developed an AB-BNCT facility [3] using Be as the neutron target material. This Be target system was designed using Monte Carlo estimation, and heat removal analysis was performed using ANSYS. Ammugan et al. [4] investigated the thermal shock response of various Be targets, which was induced by high-energy and high-intensity proton beams at CERN’s HiRadMat facility. Carpenter [5] discussed the motivation for using gallium to cool targets for compact accelerator-based neutron sources. Analytical calculations were performed to obtain the temperature of the target and the drops in pressure across the cooling channel. He also recommended that numerical thermal–hydraulic analysis be conducted when designing the coolant channel. Hu et al. [6] performed a CFD heat transfer simulation in a rotating target system with a Gaussian beam and a uniform beam. According to the simulation results, the equilibrium temperatures of the Li target with the Gaussian beam are 102, 144, and 142 °C. These values are lower than the melting point of Li. They also reported that the maximum temperature of the target and cyclic thermal stress could be reduced by increasing the rotating speed.

A single-phase convection mechanism is traditionally designed for heat removal for AB-BNCT systems. Refrigeration equipment and a high-capacity pump are needed to obtain cooling water at a lower inlet temperature and a higher flowrate, which can provide adequate heat removal in these systems. However, these additional sets of equipment would also increase construction and operation costs for AB-BNCT systems. With the advantage of greater heat removal, the boiling heat transfer mechanism may lower the peak temperature, as well as lead to more uniform distribution in the wall temperature, which reduces thermal degradation for the target for long-term operation. Therefore, we investigate the feasibility of applying boiling heat transfer to the thermal management for AB-BNCT systems in this work by way of CFD simulations. The simulation domain in the present work only consists of the coolant channel and Be target. The CFD boiling model has been assessed against the experimental data from previous works [7,8], which includes a two-fluid boiling model for the water and vapor phases with interfacial exchange models and a wall heat flux portioning model (RPI model) [9]. With the validated results, this CFD boiling model can be used with confidence to assist in designing thermal management for AB-BNCT systems.

2. Simulation Methodology

The simulation methodology presented in the current section includes the nucleate boiling models and the numerical treatment. The nucleate boiling models adopted in this work consist of the governing equations of the water and vapor phases, namely, the turbulence model for the continuous liquid phase, the wall heat flux partitioning model, interfacial transfer models, bubble dynamics models, and the appropriate boundary conditions. All of these models and their numerical treatment can be described as follows:

2.1. Nucleate Boiling Models

• Governingequations

Continuity equation

$$\nabla •\left({\alpha }_k{\rho }_k{\overrightarrow{U}}_k\right)={\Gamma }_k$$

(1)

where

• k = $\mathcal{l}$ for the continuous liquid phase;
• k = v for the dispersed vapor phase.

Momentum equation

$$\nabla •\left({\alpha }_k{\rho }_k{\overrightarrow{U}}_k{\overrightarrow{U}}_k\right)=-{\alpha }_k\nabla P+{\alpha }_k\overrightarrow{B}+\nabla •({\alpha }_k{\mu }_k\nabla {\overrightarrow{U}}_k)+{\overrightarrow{M}}_k+{\Gamma }_k{\overrightarrow{U}}_I$$

(2)

where

${\overrightarrow{M}}_k=$ the vector of the interfacial momentum transfer for phase k, which can be described as follows:

Energy equation

$$\nabla •\left({\alpha }_k{\rho }_k{\overrightarrow{U}}_k{h}_k\right)=\nabla •({\alpha }_k{\lambda }_k\nabla T_k)+{\Gamma }_k{h}_I$$

(3)

• Interfacial transfer models

Void fraction

$${\displaystyle \sum _k{\alpha }_k=1}$$

(4)

Interfacial mass transfer

$${\Gamma }_{\mathcal{l}}={\displaystyle \frac{Q_e}{H+C{p}_{\mathcal{l}}\Delta T_{sub}}}+\max \left[{\displaystyle \frac{h_{\mathcal{l}v}(T_{\mathcal{l}}-T_{sat})}{H}}, 0\right];\hspace{1em}{\Gamma }_v=-{\Gamma }_{\mathcal{l}}$$

(5)

$$Q_e={\displaystyle \frac{\pi }{6}}{D}_b{f}_b{n}_A{\rho }_{v}H$$

(6)

$$h_{\mathcal{l}v}={\displaystyle \frac{6{\lambda }_{\mathcal{l}}{\alpha }_{\mathcal{l}}{\alpha }_{v}Nu}{D_b^2}}$$

(7)

The Nu number can be estimated using the following equation [10]:

$$Nu=2.0+0.6{\mathrm{Re}}^{1/2}{\mathrm{Pr}}^{1/3}$$

(8)

Interfacial momentum transfer

$${\stackrel{\rightharpoonup }{M}}_k={\stackrel{\rightharpoonup }{M}}_k^D+{\stackrel{\rightharpoonup }{M}}_k^L+{\stackrel{\rightharpoonup }{M}}_k^W+{\stackrel{\rightharpoonup }{M}}_k^{VM}+{\stackrel{\rightharpoonup }{M}}_k^{TD}$$

(9)

${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^D$ is the interfacial drag force for the liquid phase

$${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^D={\displaystyle \frac{3}{4}}{\displaystyle \frac{C_D}{D_b}}{\alpha }_v{\rho }_{\mathcal{l}}({\overrightarrow{U}}_v-{\overrightarrow{U}}_{\mathcal{l}})\left|{\overrightarrow{U}}_v-{\overrightarrow{U}}_{\mathcal{l}}\right|=-{\stackrel{\rightharpoonup }{M}}_v^D$$

(10)

where

C_D is estimated using the Ishii model [11].

$$C_D=\min (C_{D_{vis}},C_{D_{dis}})$$

(11)

$$C_{D_{vis}}={\displaystyle \frac{24}{\mathrm{Re}}}(1+0.15{\mathrm{Re}}^{0.75})$$

(12)

$$C_{D_{dis}}={\displaystyle \frac{2}{3}}{\displaystyle \frac{D_b}{\sqrt{\frac{\sigma }{g\left|{\rho }_v-{\rho }_{\mathcal{l}}\right|}}}}$$

(13)

${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^L$ is interfacial lift force for the liquid phase, can be estimated using the following equation [12]

$${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^L=C_L{\alpha }_v{\rho }_{\mathcal{l}}({\overrightarrow{U}}_v-{\overrightarrow{U}}_{\mathcal{l}})\times \nabla \times {\overrightarrow{U}}_{\mathcal{l}}=-{\stackrel{\rightharpoonup }{M}}_v^L$$

(14)

where

$$C_L=\left\{\begin{array}{ll}0.076& \varphi \le 6000\\ -(0.12-0.2e^{-{\displaystyle \frac{\varphi }{3.6}}\times {10}^{-5}})e^{-{\displaystyle \frac{\varphi }{3}}\times {10}^{-7}}& 6000<\varphi <5\times {10}^7\\ -0.6353& \varphi \ge 5\times {10}^7\end{array}\right.$$

(15)

$$\varphi =\mathrm{Re}•{\mathrm{Re}}_{\omega }$$

(16)

$$\mathrm{Re}={\displaystyle \frac{{\rho }_{\mathcal{l}}\left|{\overrightarrow{U}}_v-{\overrightarrow{U}}_{\mathcal{l}}\right|D_b}{{\mu }_{\mathcal{l}}}}$$

(17)

$${\mathrm{Re}}_{\omega }={\displaystyle \frac{{\rho }_{\mathcal{l}}\left|\nabla \times {\overrightarrow{U}}_{\mathcal{l}}\right|D_b^2}{{\mu }_{\mathcal{l}}}}$$

(18)

${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^W$ is interfacial wall force for the liquid phase, can be estimated using the following equation [13]:

$${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^W=-C_W{\alpha }_v{\rho }_{\mathcal{l}}{\left|u_{\mathcal{l},W}-u_{v,W}\right|}^2{\overrightarrow{n}}_W=-{\stackrel{\rightharpoonup }{M}}_v^W$$

(19)

where

$$C_W=\max \left(0, {\displaystyle \frac{C_{W1}}{D_b}}+{\displaystyle \frac{C_{W2}}{y_W}}\right)$$

(20)

C_W1 = −0.01; C_W2 = 0.05

(21)

$u_{\mathcal{l},W}, u_{v,W}$ are the velocity components tangential to the wall surface of the liquid and vapor phase, respectively.

${\overrightarrow{n}}_W$ is the unit normal pointing away from the wall.

y_w is the distance to the nearest wall.

${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^{TD}$ is interfacial turbulent dispersion force for the liquid phase [14].

$${\stackrel{\rightharpoonup }{M}}_{\mathcal{l}}^{TD}=C_{TD}{\displaystyle \frac{{\mu }_{t,\mathcal{l}}}{{\rho }_{\mathcal{l}}{\sigma }_{\mathcal{l}}^{TD}}}({\displaystyle \frac{\nabla {\alpha }_v}{{\alpha }_v}}-{\displaystyle \frac{\nabla {\alpha }_{\mathcal{l}}}{{\alpha }_{\mathcal{l}}}})=-{\stackrel{\rightharpoonup }{M}}_v^{TD}$$

(22)

C_TD = 0.5

(23)

• Turbulence model

In this work, turbulent characteristics are only considered in the continuous liquid phase. The turbulence enhancement caused by bubble disturbance is then incorporated into the turbulence-induced viscosity of the liquid phase. Due to the simple layout of the coolant channel, the standard k-ε turbulence model (SKE) [15] is sufficient to capture the turbulent characteristics and is adopted in the present simulations. The standard SKE can be expressed as

Turbulent kinetic energy, k

$$\nabla •\left({\alpha }_{\mathcal{l}}{\rho }_{\mathcal{l}}{\overrightarrow{U}}_{\mathcal{l}}k\right)=\nabla •\left[{\alpha }_{\mathcal{l}}\left({\mu }_{\mathcal{l}}+{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right)\nabla k\right]+{\alpha }_{\mathcal{l}}{G}_k-{\rho }_{\mathcal{l}}{\alpha }_{\mathcal{l}}\epsilon$$

(24)

Turbulent dissipation rate, ε

$$\nabla •\left({\alpha }_{\mathcal{l}}{\rho }_{\mathcal{l}}{\overrightarrow{U}}_{\mathcal{l}}\epsilon \right)=\nabla •\left[{\alpha }_{\mathcal{l}}\left({\mu }_{\mathcal{l}}+{\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\right)\nabla \epsilon \right]+{\displaystyle \frac{{\alpha }_{\mathcal{l}}\epsilon }{k}}\left(C_{\epsilon 1}{G}_k-C_{\epsilon 2}\rho \epsilon \right)$$

(25)

where

$$G_k=\left({\mu }_{\mathcal{l}}+{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\right)\nabla {\overrightarrow{U}}_{\mathcal{l}}•\left[\nabla {\overrightarrow{U}}_{\mathcal{l}}+{(\nabla {\overrightarrow{U}}_{\mathcal{l}})}^T\right]$$

(26)

In the present work, Sato’s model [16] is used to simulate the enhancement of liquid phase induced by bubble disturbance. Then the turbulence-induced viscosity can be described as

$${\mu }_t=C_{\mu }{\displaystyle \frac{k^2}{\epsilon }}+C_{\mu ,v}{\alpha }_v{D}_b\left|{\overrightarrow{U}}_v-{\overrightarrow{U}}_{\mathcal{l}}\right|$$

(27)

C_μ, C_ε1, C_ε2, σ_k, σ_ε, and C_μ,v are empirical constants for turbulent models and are illustrated in

Table 1. Constant values in the turbulence model.

Cμ	Cε1	Cε2	σk	σε	Cμ,v
0.09	1.44	1.92	1.0	1.3	0.6

[15].

• Wall heat flux partitioning model

The wall heat flux partitioning model (RPI model) [9] is a well-known wall boiling model that is usually adopted in CFD simulations of nucleate boiling. This wall boiling model essentially considers three heat flux components, namely, evaporation heat flux (${q^{″}}_e$) caused by latent heat of bubble evaporation, quenching heat flux (${q^{″}}_q$) due to heat removal from bubble departure, and convection heat flux (${q^{″}}_c$) induced by convection heat transfer to the liquid phase. The total nucleate boiling heat flux (${q^{″}}_t$) is composed of three components of heat flux, i.e.,

$${q^{″}}_t={q^{″}}_c+{q^{″}}_e+{q^{″}}_q$$

(28)

where

$${q^{″}}_e={\displaystyle \frac{\pi }{6}}{D}_b^3{\rho }_v{h}_{fg}{f}_b{n}_A$$

(29)

$${q^{″}}_c=h_c(T_w-T_{\mathcal{l}})(1-A_b)$$

(30)

$${q^{″}}_q={\displaystyle \frac{2A_b{\lambda }_{\mathcal{l}}}{\sqrt{\pi {\sigma }_{\mathcal{l}}/f_b}}}(T_w-T_{\mathcal{l}})$$

(31)

$$A_b = \mathrm{bubble} \mathrm{influence} \mathrm{area} = K_b{\displaystyle \frac{n_A\pi D_b^2}{4}}$$

(32)

The correlations for the D_b [17], n_A[18], and f_b[19] can be described as

$$D_b = \mathrm{bubble} \mathrm{departure} \mathrm{diameter} = \min \left(0.0014, 0.0006e^{-\Delta T_{sub}/45}\right)$$

(33)

$$n_A = \mathrm{active} \mathrm{nucleate} \mathrm{site} \mathrm{density} = {210}^{1.805}{\left(T_w-T_{sat}\right)}^{1.805}$$

(34)

$$f = \mathrm{bubble} \mathrm{departure} \mathrm{frequency} = \sqrt{{\displaystyle \frac{4g\left({\rho }_{\mathcal{l}}-{\rho }_v\right)}{3{\rho }_{\mathcal{l}}{D}_b}}}$$

(35)

K_b can be set to 4 based on the suggestion of Han and Griffith [20].

$h_c$ convective heat transfer for a single phase, which can be estimated as

$$h_c={\displaystyle \frac{{(\rho Cp)}_{\mathcal{l}}{u}_{\tau }}{T^{+}}}$$

(36)

$$u_{\tau }=\sqrt{{\displaystyle \frac{{\tau }_w}{{\rho }_{\mathcal{l}}}}}$$

(37)

$$T^{+}=\mathrm{Pr}\cdot y^{+}{e}^{-\Psi }+[2.12\ln (y^{+})+\beta \cdot \mathrm{Pr}]e^{-{\Psi }^{-1}}$$

(38)

$$\Psi ={\displaystyle \frac{0.01{(\mathrm{Pr}\cdot y^{+})}^4}{(1+5y^{+}{\mathrm{Pr}}^3)}}$$

(39)

$$\beta ={(3.85{\mathrm{Pr}}^{1/3}-1.3)}^2+2.12\ln (\mathrm{Pr})$$

(40)

• $T_w$ = wall temperature
• $T_{\mathcal{l}}$ = near wall liquid temperature

2.2. Numerical Treatments

Equations for modeling nucleate boiling characteristics essentially belong to the class of non-linear partial differential equations (PDEs), which should be discretized into finite differencing forms for numerical calculations. The second-order upwind scheme is adopted to treat the convection terms in these PDEs. The gradient terms are discretized by the least-squares cell-based method. The phase-coupled SIMPLE scheme [21] is used to solve finite difference equations for velocities coupled with pressure for the water–vapor two-phase flow. The Algebraic MultiGrid (AMG) linear solver is adopted for all the finite differencing equations. All of the simulation works presented in this paper were performed using FLUENT code [21] on a PC with an Intel^® Core i7-4960X CPU. An approximate computing time of 18.3 min is needed to perform the typical calculation for an AB-BNCT boiling heat transfer simulation. The convergence criteria for all of the governing equations are set such that the summation of the relative residual in every control volume is less than ${10}^{-5}$. The decay trend in the residual plot for each equation is also considered as an alternative criterion. Both of these criteria should be met to ensure the convergence of the numerical simulations.

3. Results and Discussion

As described above, this study investigates the feasibility of thermal management through the boiling heat transfer mechanism for the Be target of an AB-BNCT system by way of CFD simulations. This CFD model includes the conservation equations of mass, momentum, and energy for both the water and vapor phases, the SKE turbulence model, the RPI wall boiling model, interfacial transfer models, and bubble dynamics models. A flow chart of the present simulation work is shown in Figure 1.

Two benchmark cases [7,8] are used to validate the CFD boiling model proposed in the present work. Figure 2 shows the simulation layouts for these two validated cases. The corresponding simulation conditions are indicated in

Table 2. Simulation conditions for validated cases.

	Pipe Height (m)	Pipe Diameter (m)	${\mathit{q}}_{\mathit{w}}^{″}$ (W/m2)	Tin (K)	Gin (kg/m2-s)	Pout (Mpa)
Case 1 [7]	2	0.0154	5.7 × 105	473.15	900	4.5
Case 2 [8]	1.5	0.012	1.1 × 106	426.74	1000	3

. The mass flux (G_in) and the temperature (T_in) are set as the inlet boundary conditions. The pressure (P_out) is set at the outlet of the pipe. The axisymmetric boundary condition is applied along the pipe axis so that the 2D plane can be used to simulate the 3D pipe. Constant heat flux is applied on the heating wall. Structured rectangular mesh models with dimensions of 14 × 200 and 14 × 150, respectively, are set for these two cases. 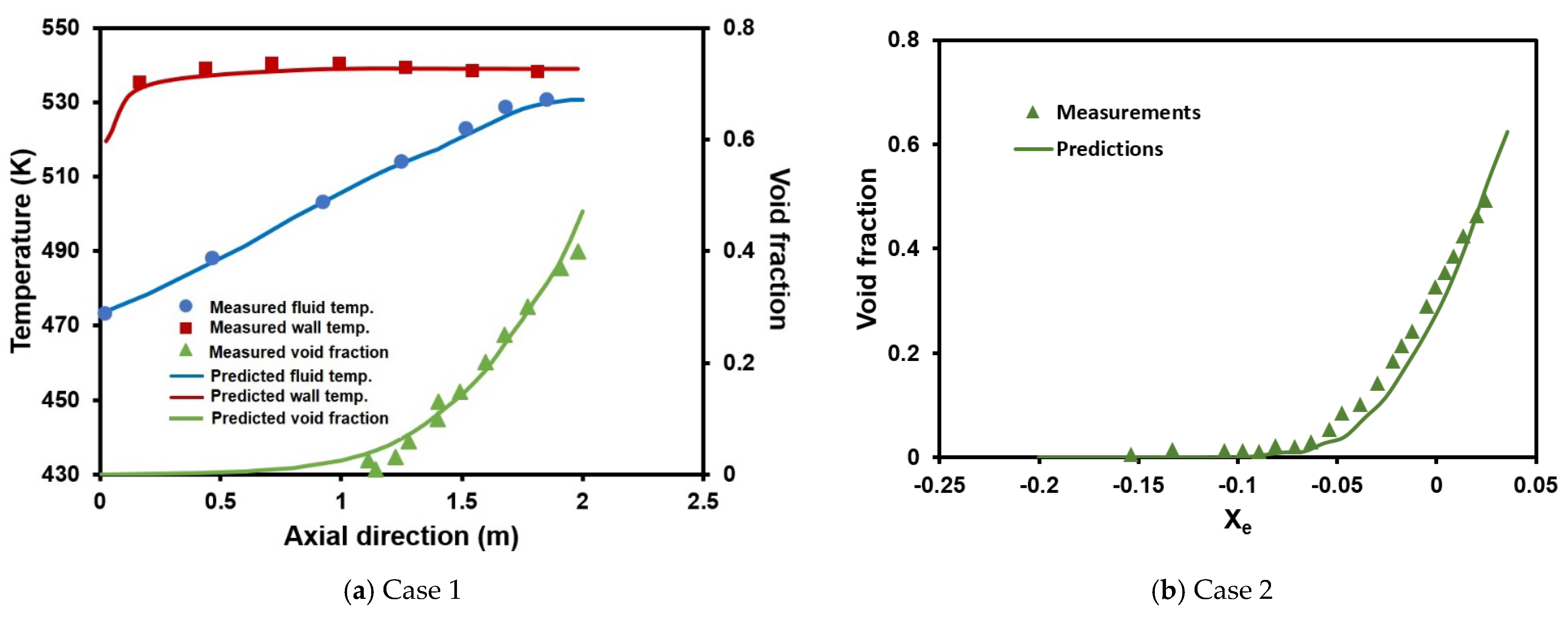Figure 3a displays a comparison of wall temperature, average fluid temperature, and average void fraction along the axial direction of the heat wall between the measurements (dots) [7] and predictions (lines). The good agreement shown in this comparison reveals that the CFD boiling model proposed in this paper can reproduce the wall/fluid temperature distributions from the experimental data [7]. A comparison of these results with those of Zhang et al. [8] are presented in Figure 3b, which shows the average void fraction (α) versus the thermal equilibrium quality (X_e). Observation of this figure shows that the relationship of α vs. X_e predicted from the present boiling model corresponds well with the measured data. These agreement results confirm that the present CFD boiling model can be confidently applied to simulations of boiling heat removal for the Be target of an AB-BNCT system.

For the AB-BNCT system designed by Heron Neutron Medical Corp, the high-energy and high-intensity protons emitted from the accelerator would impinge on the Be target. The ⁹Be (p, n) reaction is exothermic and can thus deposit more heat in the target. A thermal management system should be designed to efficiently remove this high energy generation so as to withstand the thermal and mechanical loadings for the Be target during long-term operation. In the present work, the simulation domain for the thermal management of the AB-BNCT system only includes the coolant channel and Be target. Figure 4a shows the solution domain for the AB-BNCT system simulated in the present work. The corresponding mesh models are also illustrated in plot (b). As shown in Figure 4a, a simple coolant channel with a rectangular cross-section of 8 cm (W) × 1 cm (H) and a length of 18 cm (L) is attached to the round Be target with a diameter of 7 cm and a thickness of 5.5 mm. The target heat source, created by the ⁹Be (p, n) reaction, is about 30 kW, as estimated by the staff of Heron Neutron Medical Corp. Based on this Be target with a cross-section of 3.847 × 10⁻³ m², the average heat flux would reach approximately 7.8 MW/m². The coolant channel employing the boiling heat transfer mechanism is designed in this work to remove this heat source. The inlet conditions of the cooling water are set as follows: an inlet velocity of 3.6 m/s (i.e., mass flowrate = 2.87 kg/s, corresponding Re = 5.15 × 10⁵), a pressure of 4 atm, and a temperature of 300 K (i.e., ΔT_sub ~117 K). These coolant conditions for the AB-BNCT system of Heron Corp. are set based on the CHF data [22]; the critical heat flux (CHF) is larger than 10 MW/m² under the present flow conditions. Therefore, CHF would not occur under the preset coolant conditions, implying that the present CFD boiling model can be applied in this nucleate boiling region.

Figure 4b displays the typical mesh distributions. The present mesh model is essentially composed of structured (hexahedral) grids. There are 476 and 1134 grids on the cross-sections (X-Z plane) of the Be target and coolant channel, respectively. Seven grids are applied across the Be target thickness (Y-direction). In addition, heat transfer occurs mainly in the radial direction (Y-direction), and the depth of the coolant channel is much less than its width and length. Sensitivity calculations are conducted using various grid numbers in the Y-direction. The numbers of grids normal to the wall (Y-direction) are 28, 42 (typical mesh shown in Figure 4b), and 56, respectively, since the y+ values for these three grids are located within the range of 30 to 80.

The mesh-independent calculation results are shown in Figure 5, which compares the predicted results for maximum target temperature, maximum target heat flux, and average outlet temperature under a variable number of radial grids (along the Y-direction in the coolant channel). These parameters are selected since these are what AB-BNCT system designers are typically concerned with. Detailed observation of this figure reveals that the maximum target temperature, the maximum target heat flux, and the average outlet temperature would reach saturated values as the grid number along the Y-direction in the coolant channel increases from 42 to 56. According to the mesh uncertainty estimation from the ASME V&V 20-2009 [23], the values of the fine Grid Convergence Index (GCI) for the maximum target temperature and the maximum target heat flux obtained from these three mesh models are 0.27% and 0.22%, respectively. The corresponding mesh errors of these two parameters from the fine mesh (56 grids in the Y-direction) are approximately 0.23% and 0.19%, which are estimated using a safety factor of 3 and an expansion factor of 1.15. The CFD-predicted results using the fine mesh are considered to be mesh-independent. Therefore, the results shown as follows are obtained using the fine mesh model. In addition, sensitivity calculations with different turbulence models, including the SKE and SST-Kω models, are also performed. The deviation for the peak temperature in the Be target obtained from these two turbulence models is less than 0.5%. Therefore, the SKE turbulence model is adopted in the following simulation works.

Figure 6 shows the calculated 2D contour of the void fraction on the cross-section taken vertically through the central axis of the coolant channel. The corresponding scales for this plot are indicated on the right side of this figure. It is clearly revealed in this figure that the higher void fraction (red) appears near the target wall, and the zero void fraction (blue) occupies most of the coolant channel. This result implies that the boiling characteristics in the coolant channel designed in this work correspond to subcooled nucleate boiling. Most of the bubbles are accumulated near the Be target surface, and the bubbles detaching from the wall condense in the subcooled liquid of the channel core. 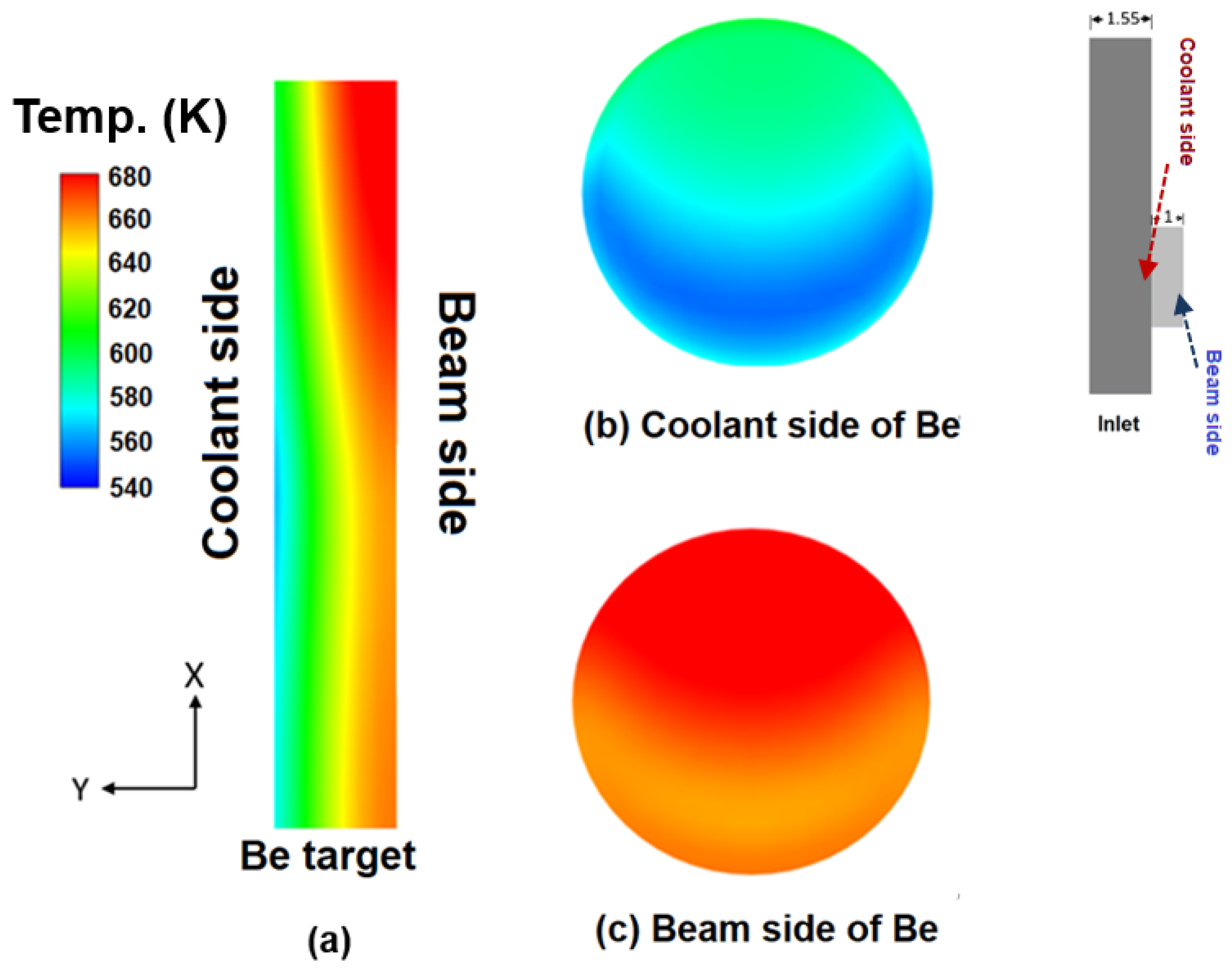Figure 7 shows the calculated temperature distribution characteristics for the Be target of the AB-BNCT system. Plot (a) displays the temperature contours on the 2D plane taken through the axial central plane of the Be target. The lower temperature distribution is shown near the left side, closer to the coolant. The right side faces the proton beam, resulting in higher temperatures. Figure 7b,c illustrate the 2D temperature contours on both sides of the Be target. The corresponding explanations for both sides of the Be target are presented in the right portion of this figure. A comparison of these two plots clearly shows that the temperature (ranging from 540 K to 580 K) at the cross-section near the coolant channel is clearly much lower than that (ranging 640 K to 680 K) at the surface facing the beam. In addition, a peak temperature of ~680 K occurs at the surface near to the beam side, and this value is much lower than the melting point (1560 K) [24] of the Be target. This result confirms that the present thermal management design, using the coolant channel employing the boiling heat transfer mechanism and the preset flow conditions, can efficiently remove the heat (30 kW suggested by Heron Neutron Medical Corp.) deposited in the Be target. The Be target cannot be melted or degraded under this rated heat loading.

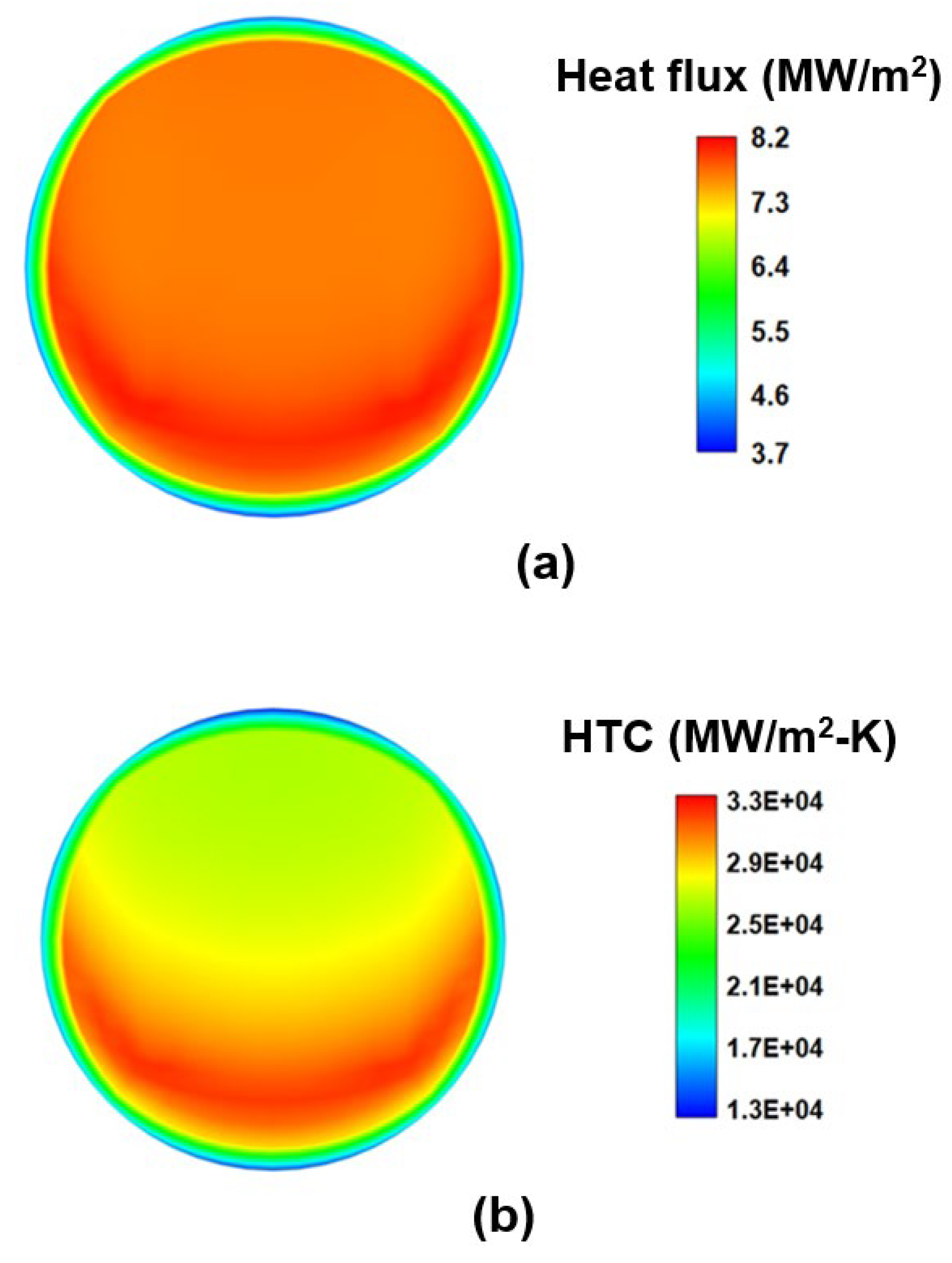
The contours of the calculated wall heat flux and the corresponding heat transfer coefficient (HTC) on the Be target surface facing the coolant are also shown in Figure 8a,b, respectively. It can be clearly seen in Figure 8a that the maximum heat flux is about 8.2 MW/m², which is much lower than the CHF value (>10 MW/m²). The HTC of boiling water in the present simulation conditions can reach 2.5~3.3 × 10⁴ W/m²-s. In addition to the higher HTC and lower temperature of the Be target, the boiling heat transfer mechanism can also result in a more uniform heat flux (7~8 MW/m²) on the target surface. These are the advantages of the boiling heat transfer mechanism applied to thermal management design for the AB-BNCT system.

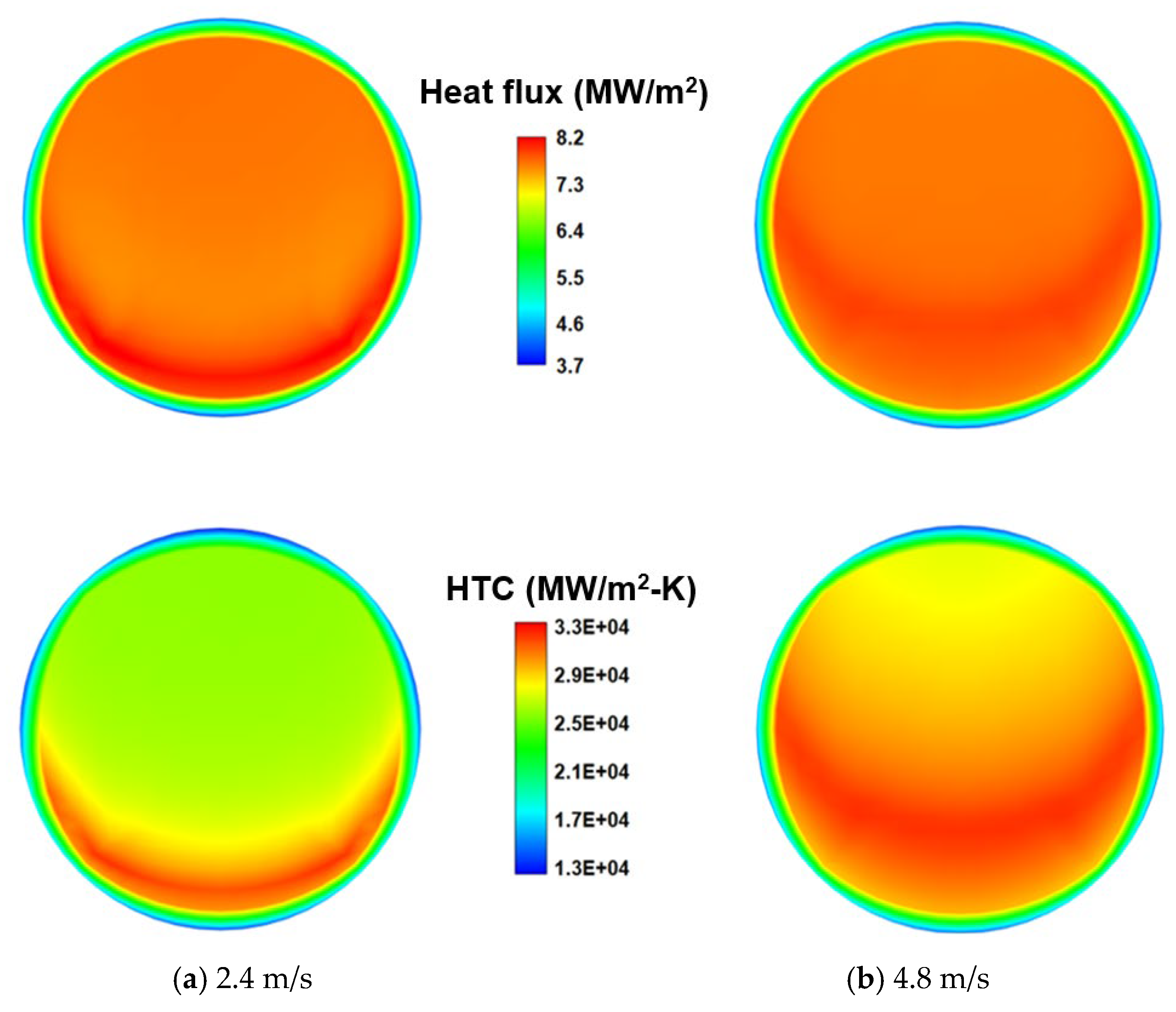
The effect of the inlet coolant mass flowrate on the thermal management design for the AB-BNCT system is also considered in the present simulation work. Figure 9 shows the calculated void fraction distributions on the cross-section taken through the central axis of the coolant channel under inlet coolant velocities of 2.4 m/s (Re = 3.43 × 10⁵) and 4.8 m/s (Re = 6.86 × 10⁵), respectively. The corresponding scales for both the plots can be referred to from the right portion of Figure 6. The bubbles generated from the target surface are removed more efficiently downward as the inlet coolant velocity increases. The region occupied by the vapor then decreases with the increasing inlet velocity, as revealed when comparing Figure 6 and Figure 9. The effect of inlet velocity on the surface temperature distributions of the Be target surface facing the coolant side is shown in Figure 10, and the corresponding effect on the HTC distributions is also indicated in Figure 11. Observation of temperature distributions in Figure 7b and the upper plots of Figure 10 reveals that the lower-temperature region (blue) on the target surface near the coolant increases with increasing inlet velocity due to higher heat transfer. The higher-temperature region (red) on the surface near the beam (Figure 7c and the lower plots of Figure 10) decrease with the increase in the coolant velocity. The higher heat transfer due to the higher inlet velocity is also confirmed in a comparison of HTC for various inlet velocities, as shown when contrasting Figure 8a with the lower plots in Figure 11. The HTC region (red) increases as the inlet coolant velocity increases from 2.4 m/s to 4.8 m/s. This higher HTC for the higher inlet velocity results in the lower target temperature, as well as the more uniform heat flux distribution on the target surface. A detailed comparison of Figure 8b and the upper plots in Figure 11 implies a more uniform distribution in surface heat flux for an inlet velocity of 4.8 m/s. However, more pumping power is needed to produce a larger flowrate of cooling water, which also increases the design and operational costs. These are the disadvantages of using a higher coolant flowrate for the thermal management of the AB-BNCT system. The temperature is usually higher in the central region of the Be target. 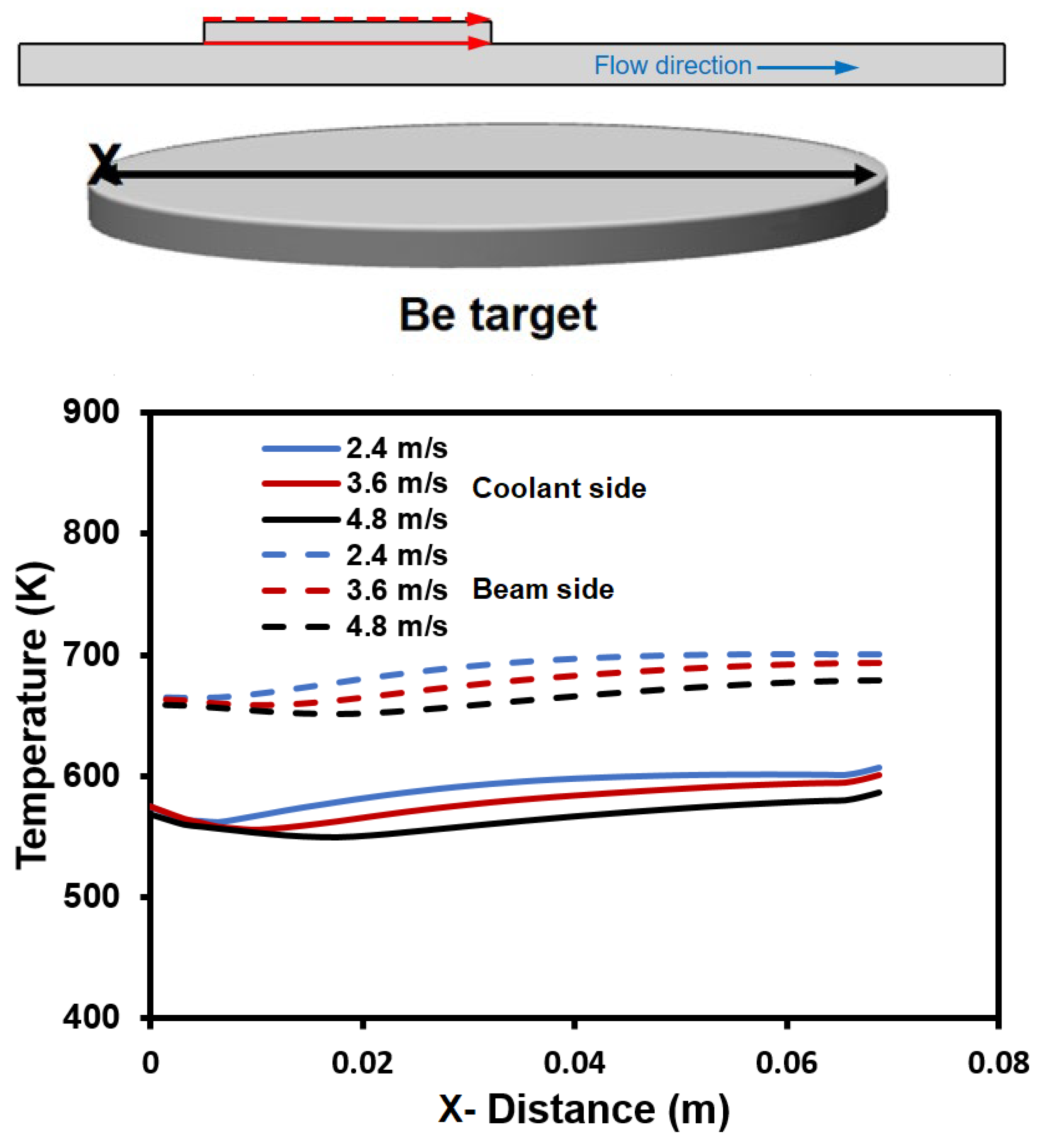Therefore, the temperature distributions along the central line on both sides of the target can be clearly demonstrated using the line curves (Figure 12). The abscissa is the distance (x) along this central line, which is schematically illustrated in the upper portion of this figure. The dashed lines represent the temperature distributions on the surface near the beam side, and the solid lines are those on the surface near the coolant side (as indicated in the upper portion). As clearly seen in this figure, the maximum temperature in the target is much lower than the melting point (1560 K) of the Be target under various inlet velocities (mass flowrate), confirming the integrity of the Be target and the capability of the present thermal management design.

However, the deformation of the Be target is another matter of concern for the long-term operation of the AB-BNCT system under the conditions of high proton intensity and high energy deposition. The Be target is generally confined using a circumferential ring in order to fix its position. The expansion of Be in the x–z-direction (as shown in Figure 3) due to thermal stress is prevented. Thus, the deformation of the Be target is limited to the y-direction (i.e., the vertical direction relative to the disk-shaped Be target). With the temperature distribution in the Be target obtained, its deformation can be evaluated using ANSYS [20]. 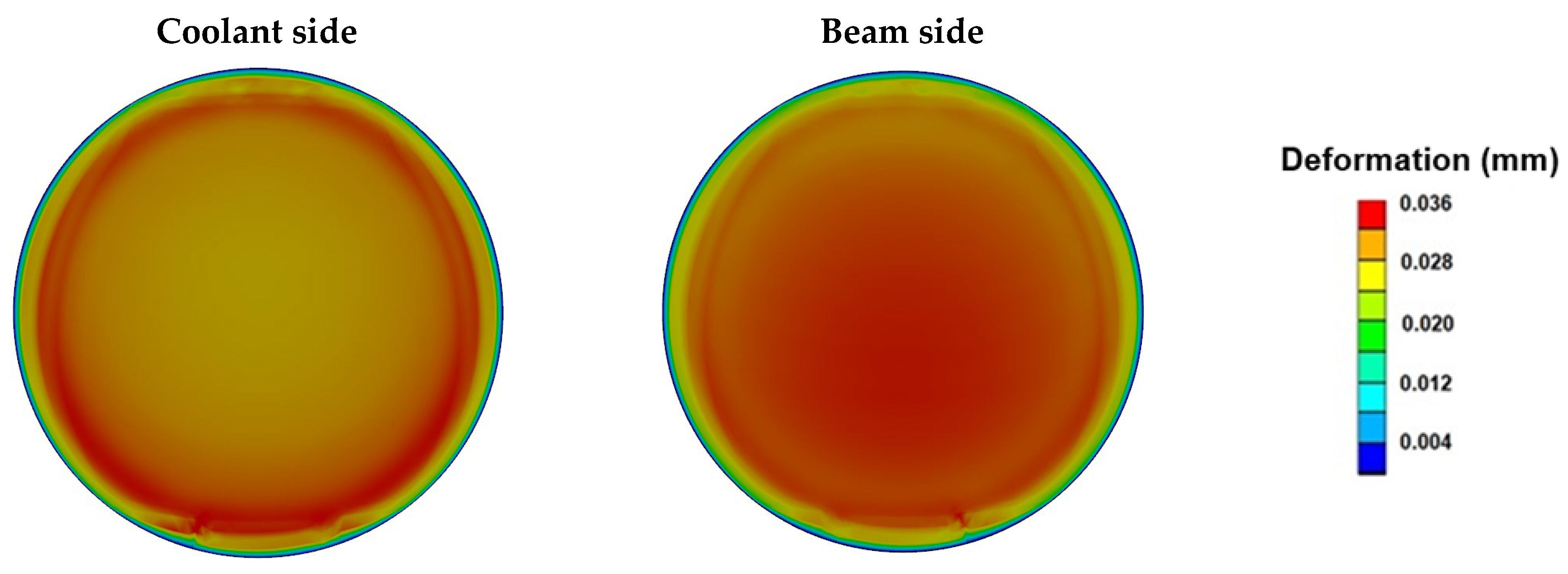Figure 13 shows the deformation of the Be target on both sides under various values of inlet coolant velocity. This comparison clearly reveals that the target deformation is less severe as the inlet velocity increases (i.e., the heat transfer capability increases). The maximum values of deformation on the beam side of the target are predicted to be 37.64 μm, 36.01 μm, and 34.40 μm for inlet velocities of 2.4 m/s, 3.6 m/s, and 4.8 m/s, respectively. The small amount of thermal deformation for the various inlet coolant velocities also confirms the Be target’s integrity for the AB-BNCT system (30 kW) and the present thermal management design. With increasing beam intensities from the accelerator facility, more heat would be deposited into the Be target of the AB-BNCT system. Therefore, we investigated the effect of the power deposited in the Be target on the peak temperature, and the predicted result is shown in Figure 14. It is clearly revealed in this figure that the peak temperature of the Be target increases with increasing power. The increasing trend is approximately linear. Through sensitivity calculations of power, the CFD boiling model proposed in this paper demonstrates that increasing neutron production efficiency (i.e., increasing amount of deposited power in the target) would not compromise the integrity of the Be target for reliable long-term operation of the AB-BNCT system. However, if the staff of Heron Neutron Medical Corp. want to obtain a much more powerful neutron source, system pressure must be elevated in order to increase the CHF and ensure that the deposited maximum heat flux is less than the CHF. In addition, under these near-CHF conditions, stable nucleate boiling cannot be maintained, making the present nucleate boiling model no longer applicable.

Thermal management through traditional single-phase convection is also simulated herein. An inlet velocity of 3.6 m/s and a pressure of 4 atm are set. However, a lower inlet temperature (283.15 K) is adopted in order to obtain higher convective heat transfer, resulting in the need for refrigeration equipment to obtain cooling water. Figure 15 compares the predicted temperature distributions along the central line on both sides of the target between these two cooling mechanisms. The abscissa in this figure also represents the distance (x) along the central line, which is schematically illustrated in the upper portion of Figure 12. It is clearly seen in this figure that the temperature distributions on both sides of the Be target when employing thermal management through boiling heat transfer are much lower than those using single-phase convection cooling. The corresponding deformation of the Be target under the single-phase cooling mechanism is presented in Figure 16. The maximum value of deformation is 53.7 μm for single-phase cooling with an inlet velocity of 3.6 m/s, which is much higher than that for boiling heat transfer cooling under the same inlet velocity. A comparison of Figure 13 and Figure 16 reveals that deformation of the target when employing thermal management through the boiling heat transfer is much smaller than that using single-phase cooling under the same inlet flowrate. This is one of the main advantages of boiling heat transfer applied in the thermal management of the AB-BNCT system. In order to clearly compare the simulation results of key parameter values under various operating conditions,

Table 3. Summary of key parameter values from simulations under various operating conditions.

Heat Removal Mechanism	Operating Conditions	Tmax (K)	Defmax (μm)
Boiling heat transfer mechanism	Vin = 2.4 m/s Power = 30 kW	699.8	37.64
	Vin = 3.6 m/s Power = 30 kW	689.9	36.01
	Vin = 4.8 m/s Power = 30 kW	673.7	34.40
	Vin = 3.6 m/s Power = 20 kW	586.7
	Vin = 3.6 m/s Power = 40 kW	800.9
Single-phase convection mechanism	Vin = 3.6 m/s Power = 30 kW	823.6	53.70

summarizes these sensitivity calculation results.

4. Conclusions

In this study, using CFD simulations, we investigated the feasibility of thermal management through the boiling heat transfer mechanism for an AB-BNCT system. Traditionally, single-phase convection has been used as the heat removal mechanism for an AB-BNCT system’s Be target; boiling heat transfer presents an alternative, which is one of the main contributions of the present work. This CFD boiling model has been assessed using the measured data of previous works [6,7]. The simulation results strongly reveal that the subcooled nucleate boiling mechanism can provide sufficient heat transfer capability and allows for stable thermal management for the Be target of the AB-BNCT system designed by Heron Neutron Medical Corp. under the rated operating conditions (i.e., power of 30 kW, system pressure of 4 atm, and inlet velocity of 3.6 m/s). Compared with the single-phase convection cooling channel usually adopted for AB-BNCT systems, the channel employing the boiling heat transfer mechanism offers the essential advantages of lower peak temperature and smaller deformation in the Be target. In addition, the temperature and deformation characteristics of the Be target can be fed back into neutronic simulations. This simulation approach, coupling neutronics, CFD, and stress analysis, will be investigated in future work.