Numerical Simulation of a Novel Secondary Separation Cyclone
Abstract
1. Introduction
2. Model and Methodology
2.1. Numerical Calculation Models
2.1.1. Gas Phase Solution Model
2.1.2. Discrete Phase Modeling Settings
2.2. Geometry Details of the Cyclone Separator
2.3. Numerical Schemes and Boundary Conditions
2.4. Grid Independency Study
3. Experiments
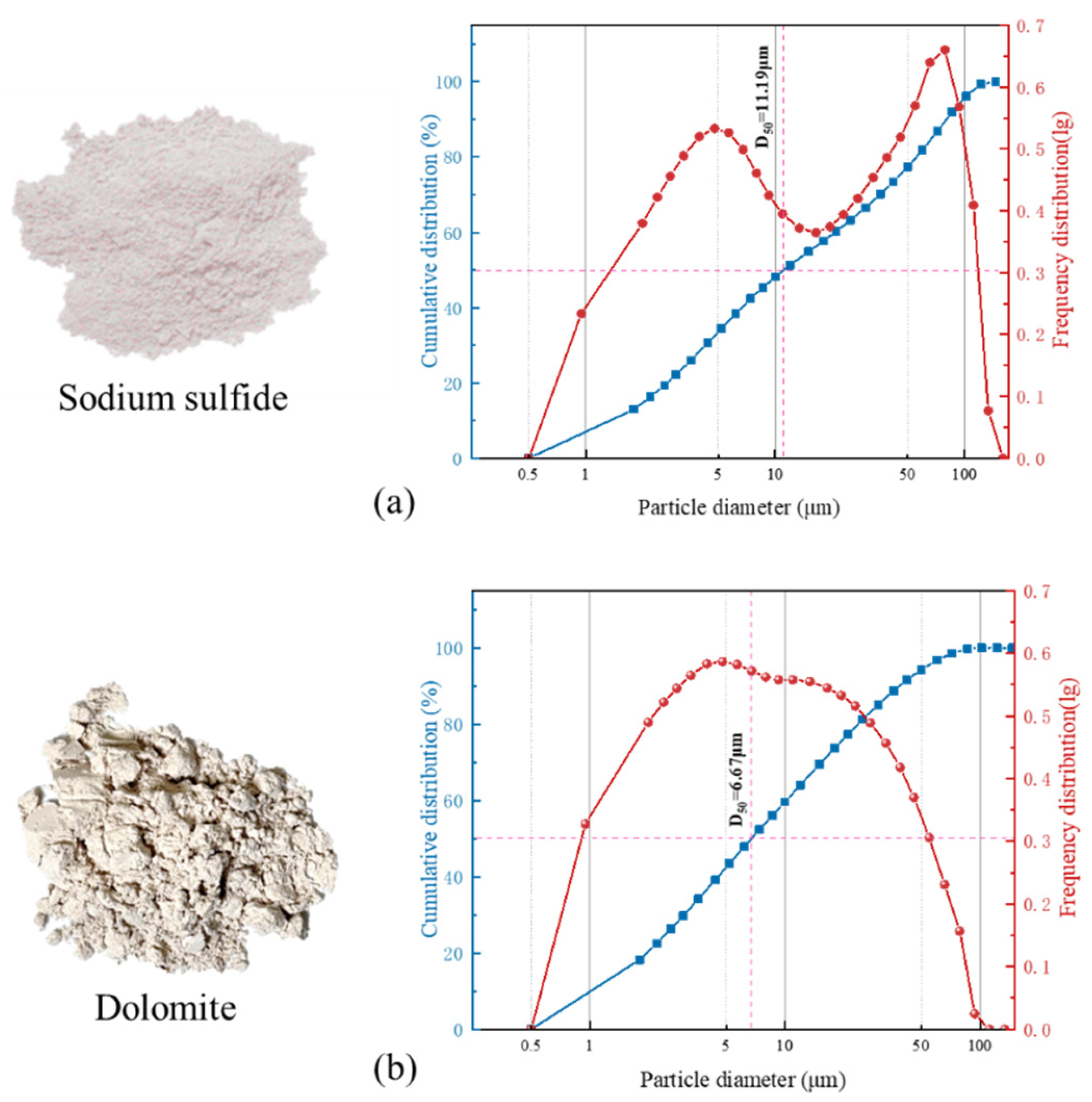
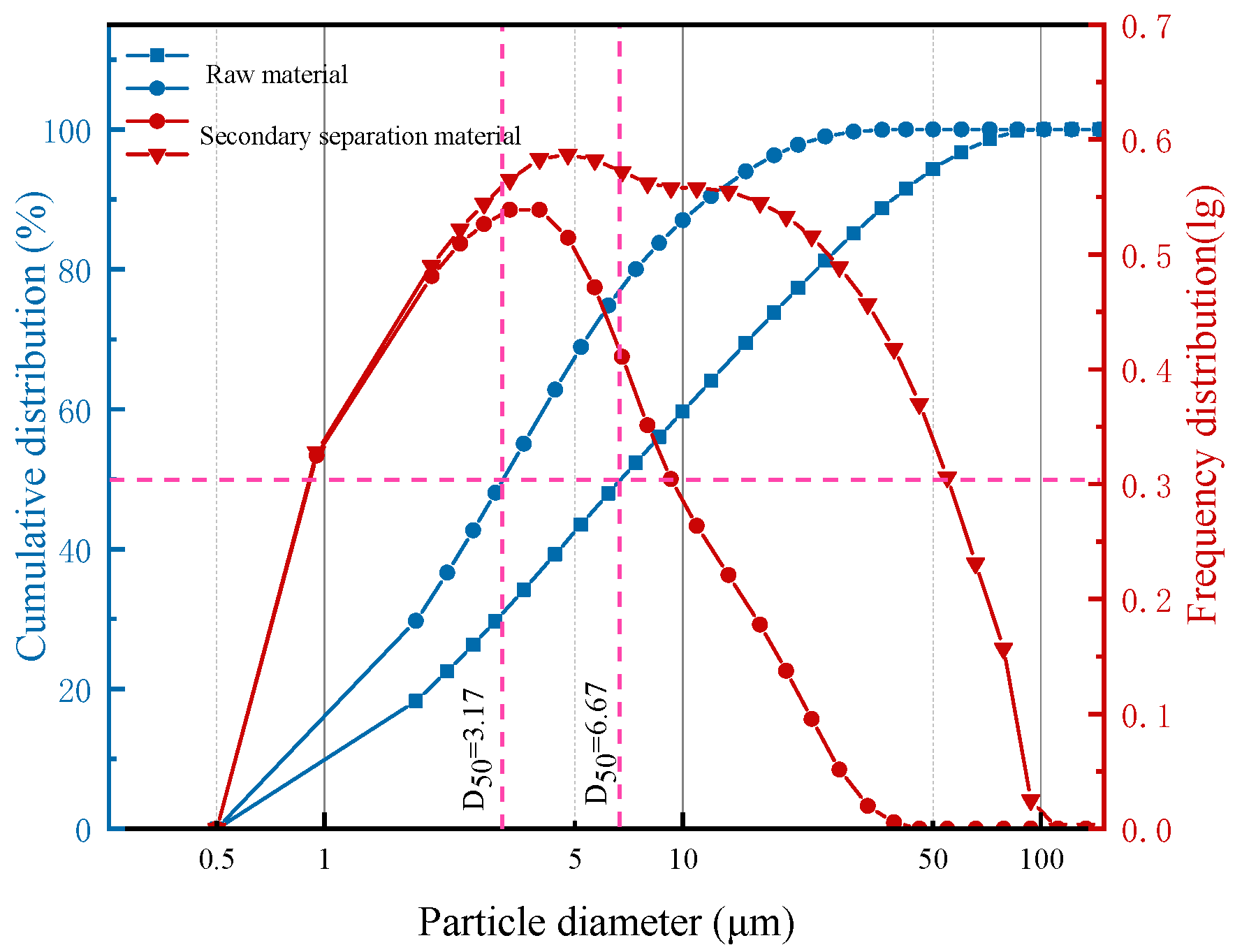
3.1. Materials
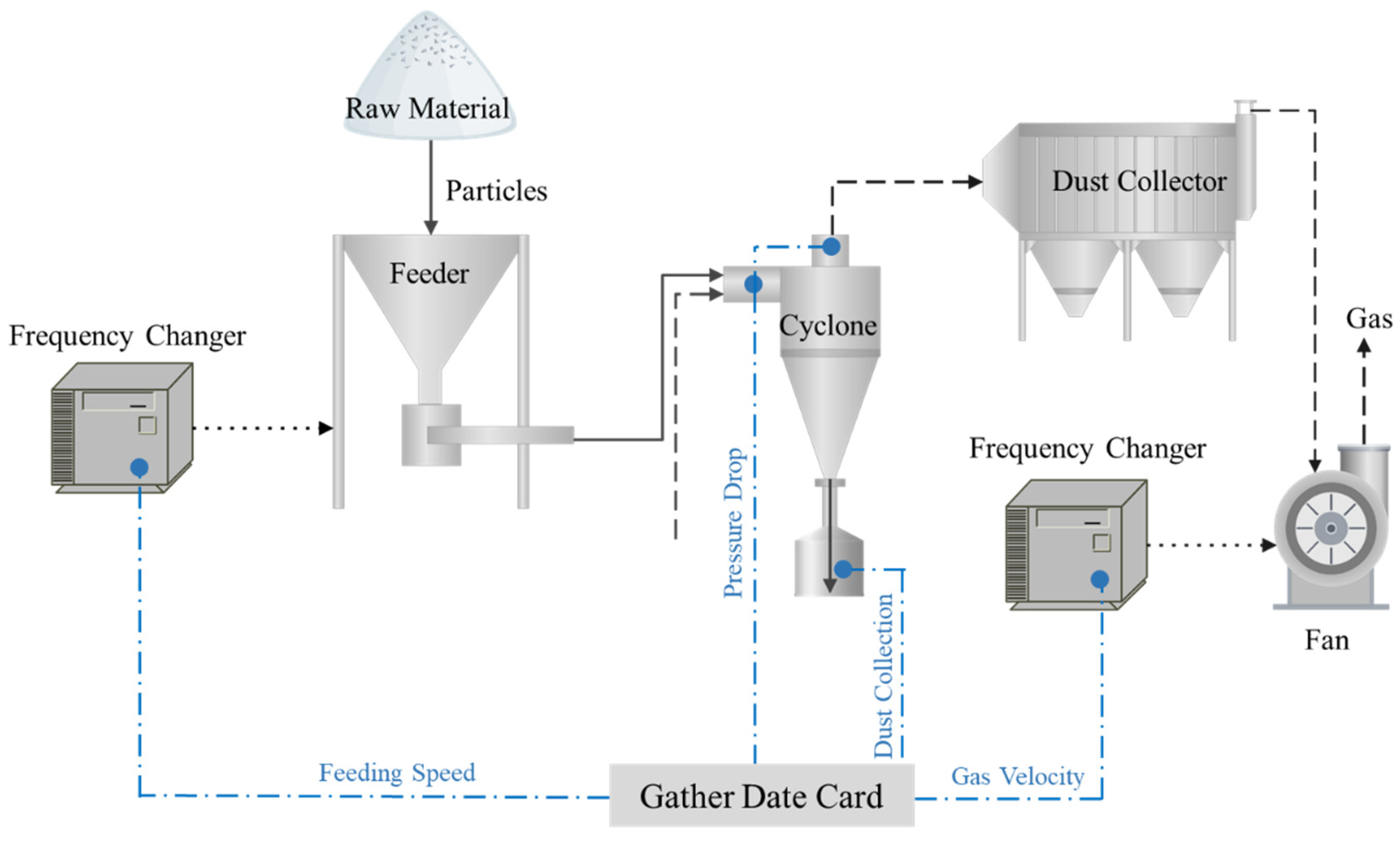
3.2. Test System and Model
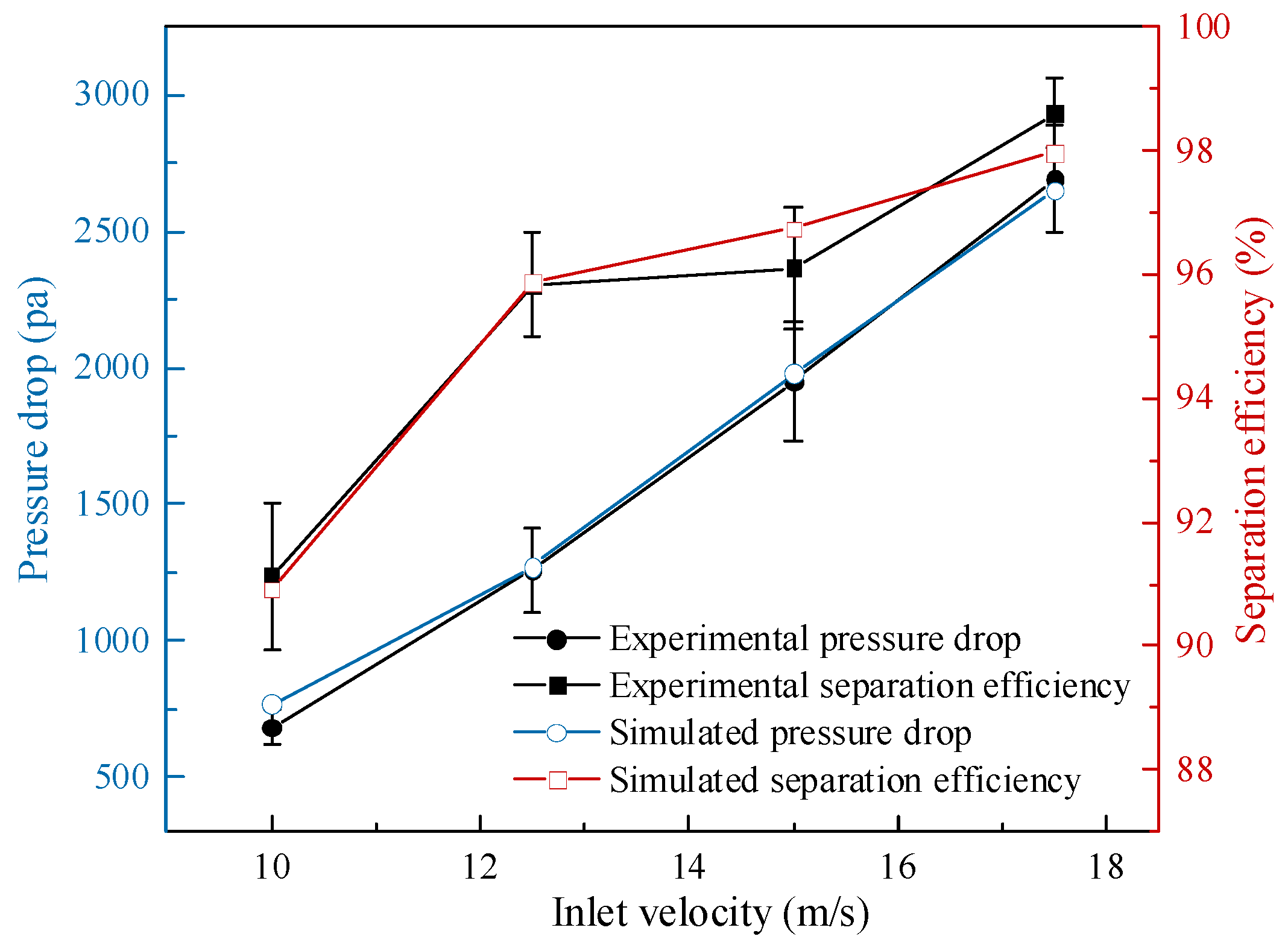
3.3. Validation of Numerical Simulation
4. Results and Discussion
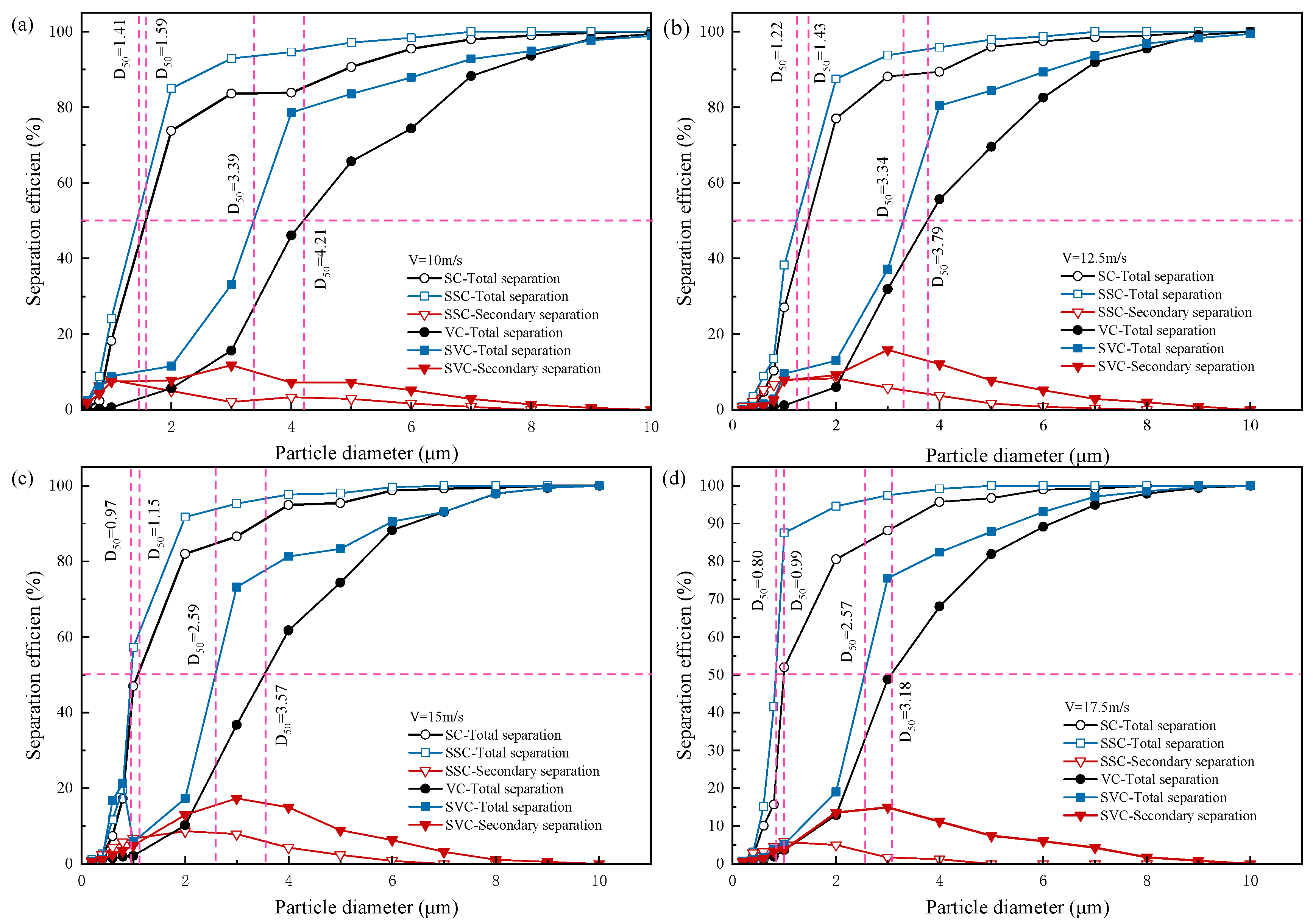
4.1. Particle Separation Efficiency
4.2. Velocity Distribution
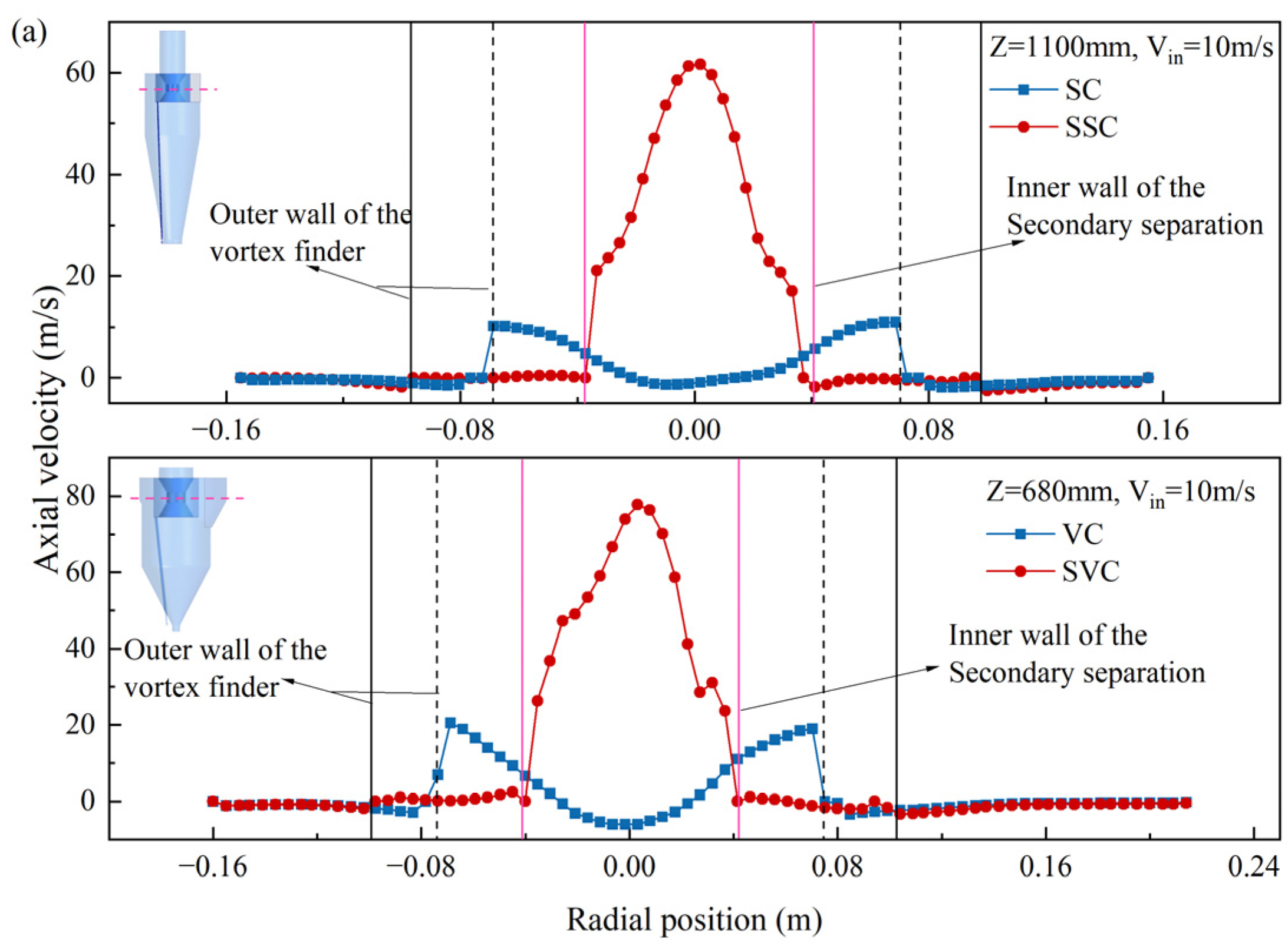
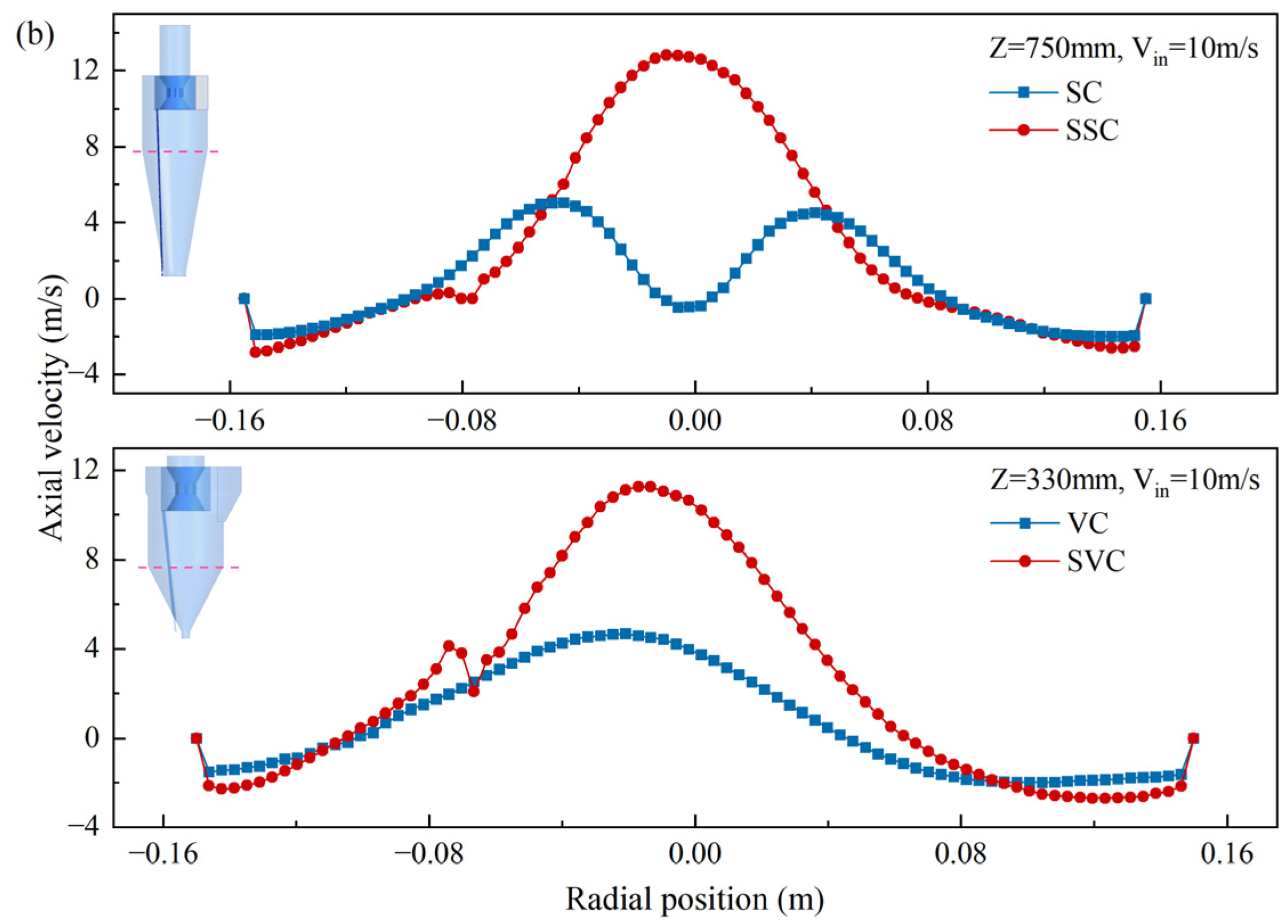
4.2.1. Axial Velocity
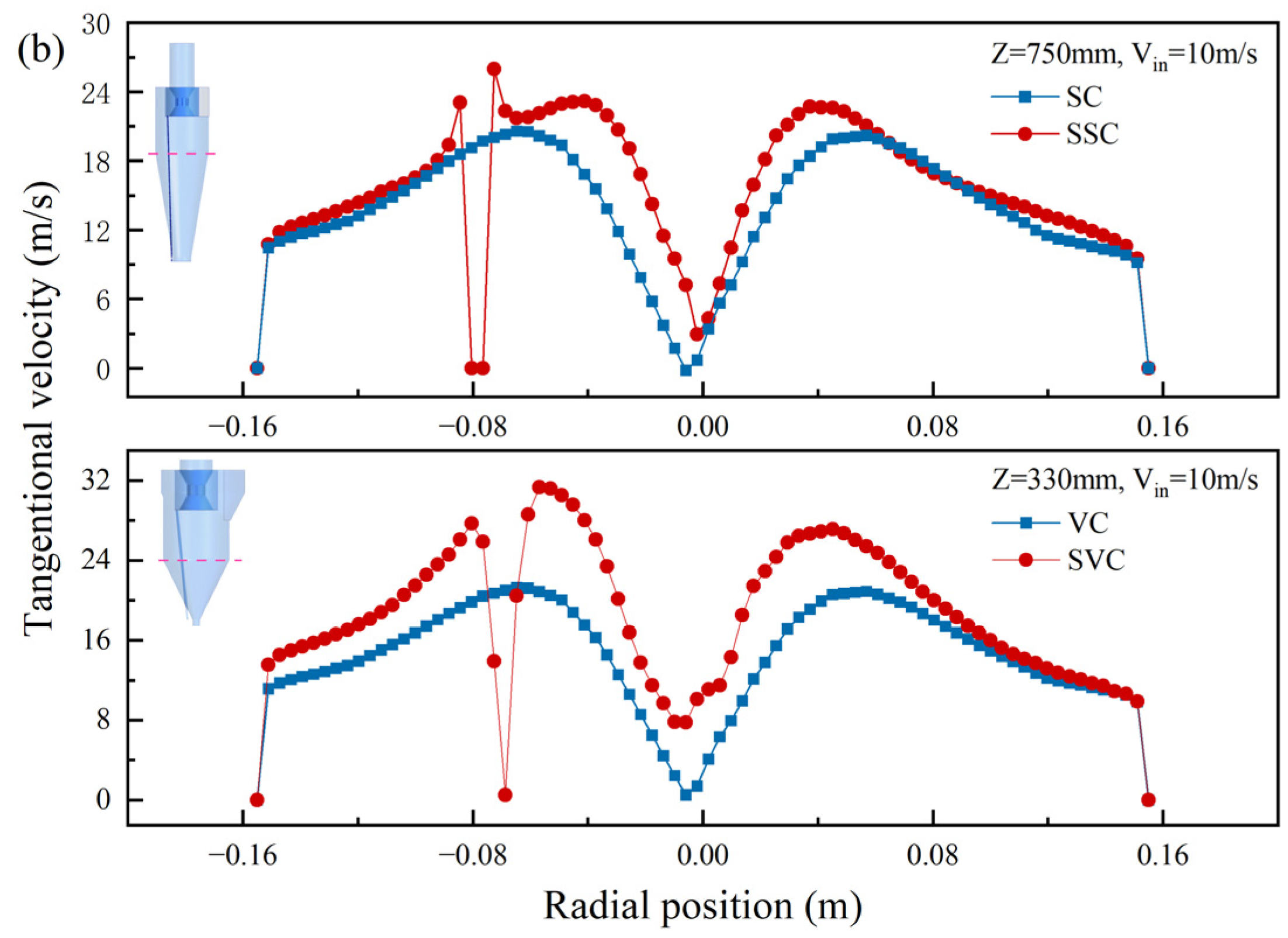
4.2.2. Tangential Velocity
4.3. Pressure Distribution
4.3.1. Static Pressure Distribution
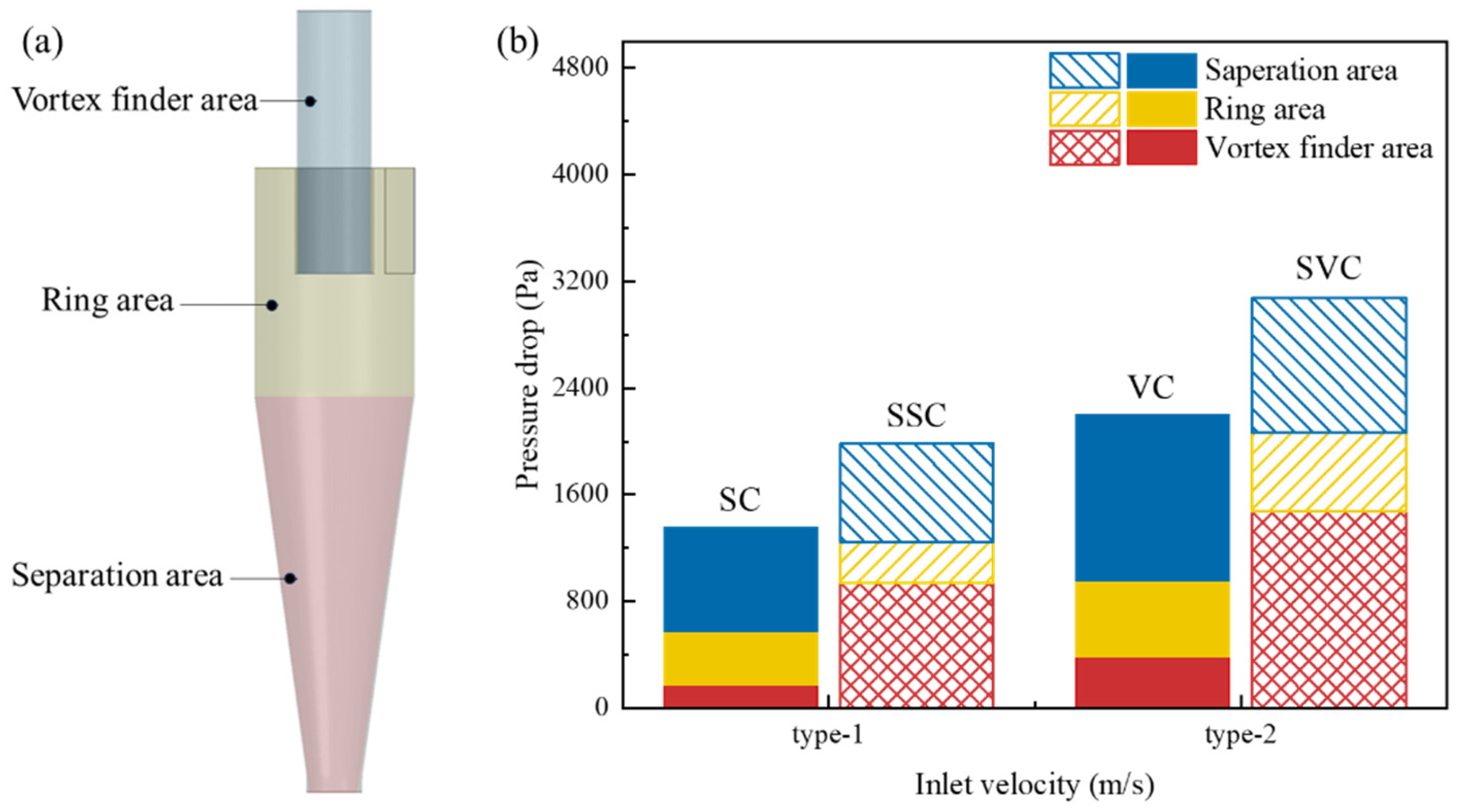
4.3.2. Regional Pressure Drop
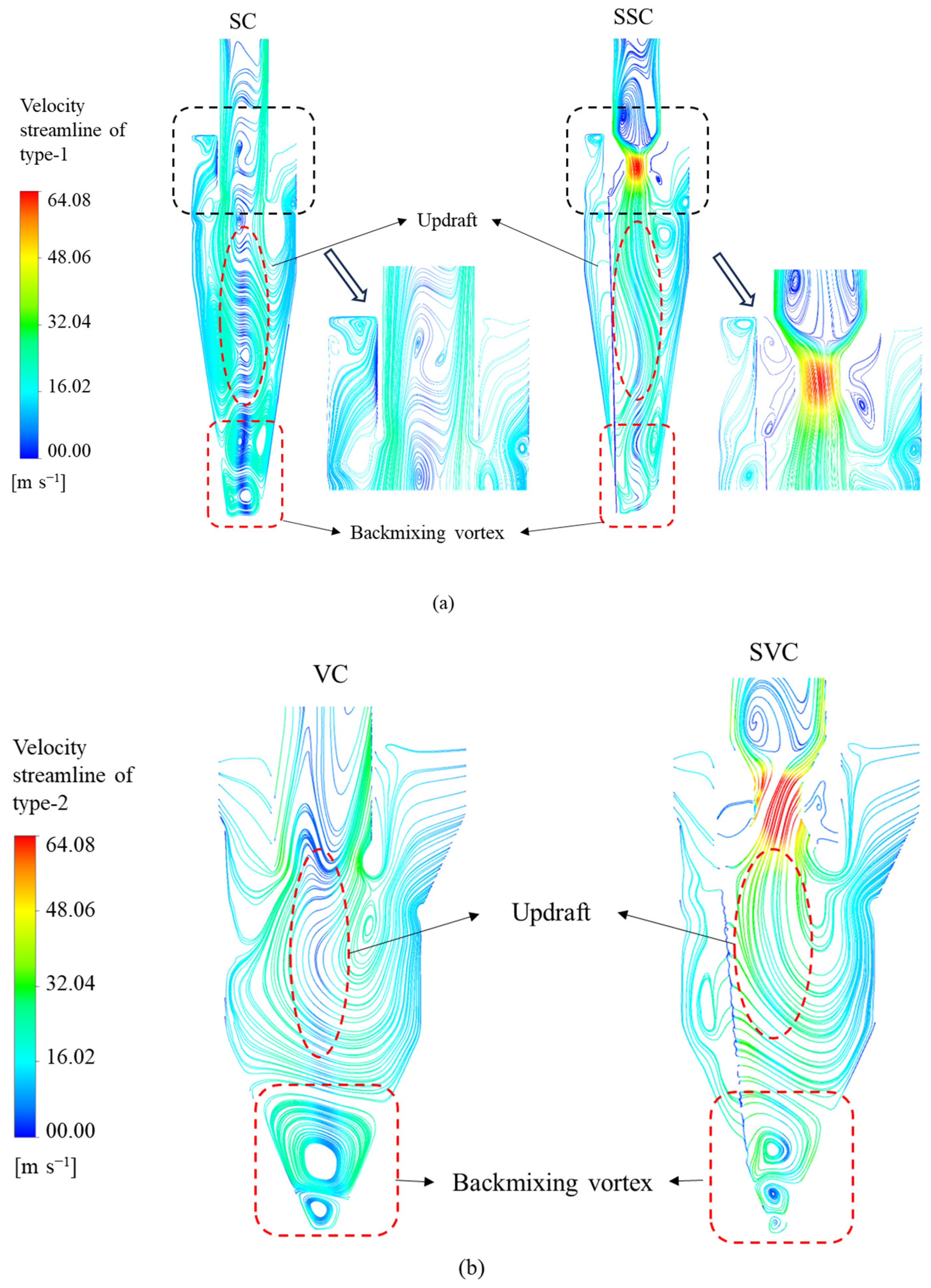
4.4. Vortex Distribution
4.4.1. Iso-Vortex Surfaces
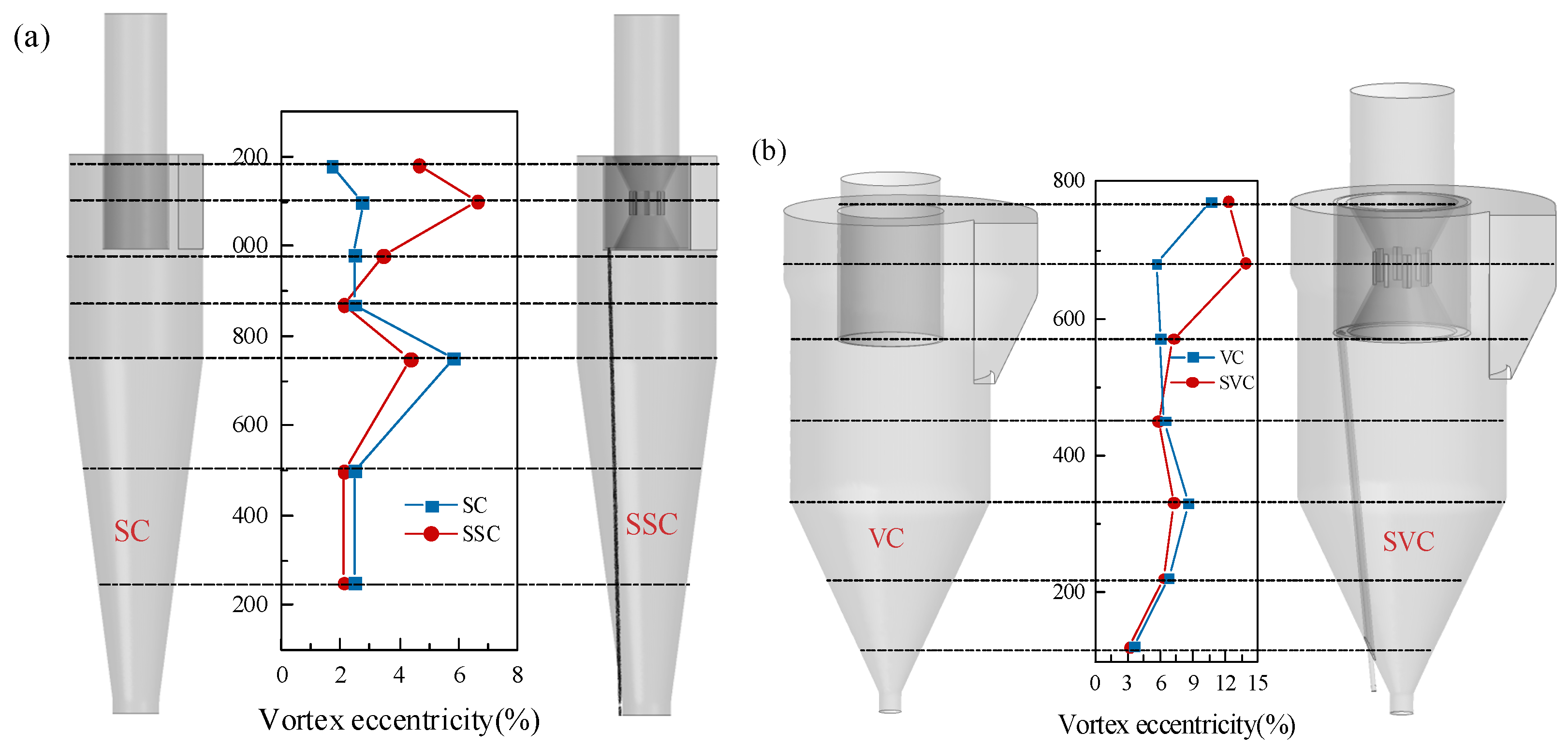
4.4.2. Eccentricity of the Vortex Core
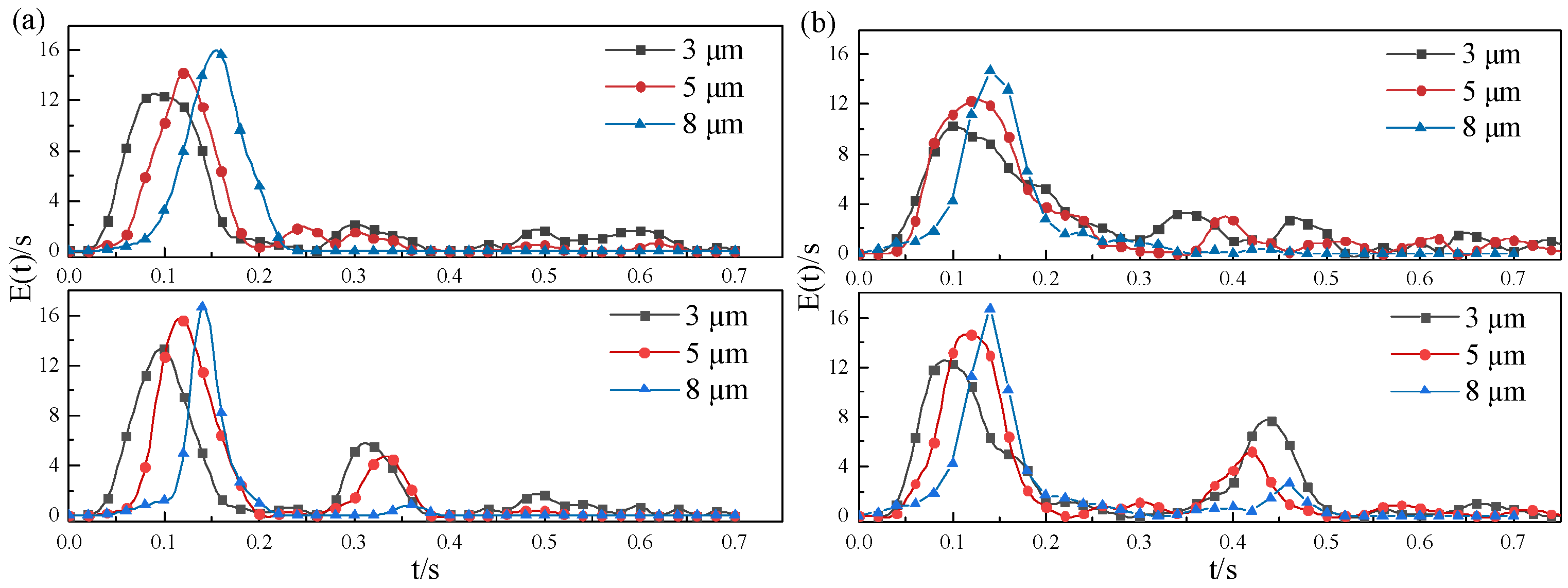
4.5. Particle Behavior
5. Conclusions
- (1)
- The simulation results exhibit a high degree of consistency with the experimental results. By ensuring the reliability of the findings, the study achieves its goal of reducing trial-and-error costs through numerical simulation.
- (2)
- The secondary separation structure proposed in this study effectively improves the separation efficiency of fine particles in two types of cyclone separators commonly used in the Na2S production process.
- (3)
- The secondary separation structure suppresses short-circuit flow and particle back-mixing, markedly reducing the cut size.
6. Future Work
- (1)
- Industrial Validation and Durability Testing: While acrylic models were employed for particle trajectory visualization in this study, future work must adopt industrially representative materials and rigorously evaluate localized erosion effects on component degradation.
- (2)
- Energy-Efficiency Optimization: Subsequent research should establish cost–benefit frameworks that balance enhanced fine-particle collection efficiency with associated energy consumption penalties to determine economic viability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, J.; Chen, Z.K.; Chen, J. The Application of Sodium Sulphide on Flotation of one Refraclory Tin-Copper Sulfide Ore. Yunnan Metall. 2017, 1, 28–32. [Google Scholar]
- Wan, H.M. The application of sodium sulfide to separation of Pb-Zn middings. Conserv. Util. Miner. Resour. 2000, 4, 2. [Google Scholar]
- Guo, M.; Yang, L.; Son, H.; Le, D.K.; Manickam, S.; Sun, X.; Yoon, J.Y. An overview of novel geometrical modifications and optimizations of gas-particle cyclone separators. Sep. Purif. Technol. 2024, 329, 125136. [Google Scholar] [CrossRef]
- Yang, L.; Chen, X.; Huang, C.; Liu, S.; Ning, B.; Wang, K. A review of gas-liquid separation technologies: Separation mechanism, application scope, research status, and development prospects. Chem. Eng. Res. Des. 2024, 201, 257–274. [Google Scholar] [CrossRef]
- Karagoz, I.; Avci, A.; Surmen, A.; Sendogan, O. Design and performance evaluation of a new cyclone separator. J. Aerosol Sci. 2013, 59, 57–64. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, M.; Ling, X. Experimental study on the separation performance of a novel gas–liquid separator. Adv. Powder Technol. 2022, 33, 103795. [Google Scholar] [CrossRef]
- Huang, L.; Deng, S.; Chen, Z.; Guan, J.; Chen, M. Numerical analysis of a novel gas-liquid pre-separation cyclone. Sep. Purif. Technol. 2018, 194, 470–479. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J. Investigation of velocity and magnetic field effects in an improved electrostatic cyclone precipitator for removal of submicron particles. Fuel 2025, 379, 133035. [Google Scholar] [CrossRef]
- Safikhani, H.; Allahdadi, S. The effect of magnetic field on the performance of new design cyclone separators. Adv. Powder Technol. 2020, 31, 2541–2554. [Google Scholar] [CrossRef]
- Zhang, C.-A.; Zhu, Z.-L.; Gao, G.-Y.; Fan, P.-P.; Fan, M.-Q. Effect of coaxial electromagnetic field on separation density of dense-medium cyclone. Miner. Eng. 2019, 138, 188–194. [Google Scholar] [CrossRef]
- Luckner, H.J.; Gradoń, L.; Ciach, T.; Podgórski, A.; Wertejuk, Z. Dust removal in cyclones with external electric field. J. Aerosol Sci. 1997, 28, S299–S300. [Google Scholar] [CrossRef]
- Lim, K.S.; Kim, H.S.; Lee, K.W. Comparative performances of conventional cyclones and a double cyclone with and without an electric field. J. Aerosol Sci. 2004, 35, 103–116. [Google Scholar] [CrossRef]
- Siadaty, M.; Kheradmand, S.; Ghadiri, F. Improvement of the cyclone separation efficiency with a magnetic field. J. Aerosol Sci. 2017, 114, 219–232. [Google Scholar] [CrossRef]
- Sun, X.; Kim, S.; Yang, S.D.; Kim, H.S.; Yoon, J.Y. Multi-objective optimization of a Stairmand cyclone separator using response surface methodology and computational fluid dynamics. Powder Technol. 2017, 320, 51–65. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, G.; Song, Z.; Yuan, S.; Qian, Z. Effect of inlet volute wrap angle on the flow field and performance of double inlet gas cyclones. Particuology 2023, 77, 29–36. [Google Scholar] [CrossRef]
- Guo, M.; Xue, H.; Pang, J.; Le, D.K.; Sun, X.; Yoon, J.Y. Numerical investigation on the swirling vortical characteristics of a Stairmand cyclone separator with slotted vortex finder. Powder Technol. 2023, 416, 118236. [Google Scholar] [CrossRef]
- Jang, K.; Lee, G.G.; Huh, K.Y. Evaluation of the turbulence models for gas flow and particle transport in URANS and LES of a cyclone separator. Comput. Fluids 2018, 172, 274–283. [Google Scholar] [CrossRef]
- Fu, S.; Zhou, F.; Sun, G.; Yuan, H.; Zhu, J. Performance evaluation of industrial large-scale cyclone separator with novel vortex finder. Adv. Powder Technol. 2021, 32, 931–939. [Google Scholar] [CrossRef]
- Zhou, F.; Sun, G.; Han, X.; Zhang, Y.; Bi, W. Experimental and CFD study on effects of spiral guide vanes on cyclone performance. Adv. Powder Technol. 2018, 29, 3394–3403. [Google Scholar] [CrossRef]
- Dong, S.; Wang, C.; Zhang, Z.; Cai, Q.; Dong, K.; Cheng, T.; Wang, B. Numerical study of short-circuiting flow and particles in a gas cyclone. Particuology 2023, 72, 81–93. [Google Scholar] [CrossRef]
- Dong, S.; Jiang, Y.; Jin, R.; Dong, K.; Wang, B. Numerical study of vortex eccentricity in a gas cyclone. Appl. Math. Model. 2020, 80, 683–701. [Google Scholar] [CrossRef]
- Kitamura, O.; Yamamoto, M.; Arakawa, C.; Kawata, Y. Computation of Turbulent Flow in a Cyclone Chamber with a Reynolds Stress Turbulence Model. Trans. Jpn. Soc. Mech. Eng. Ser. B 1993, 60, 580. [Google Scholar] [CrossRef]
- Abbass, N.A.; Elsayed, K.; Elnady, A.O.; Elshaer, Y.I. CFD Study of Novel Vortex Finder Pressure Drop Holes to Enhance Cyclone Separators Performance. J. Phys. Conf. Ser. 2024, 2811, 012006. [Google Scholar] [CrossRef]
- Haidiezul, A.H.M.; Dolah, M.S.; Khor, C.Y.; Faizal, W.M.; Hazwan, M.H.M.; Ahmad, M.; Nawi, M.A.M. A CFD Simulation Study on the Impact of Parametric Variations on Particle Dispersion During Sand Blasting. In Proceedings of the International Conference on Computational Heat and Mass Transfer, Düsseldorf, Germany, 4–8 September 2024; pp. 654–661. [Google Scholar]
- Elaswad, R.; Mohamad, A.; El-Sheimy, N. Trajectory dynamics of particles in accelerated toroidal pipe: A computational study using CFD-DPM simulations. J. Comput. Sci. 2024, 78, 102285. [Google Scholar] [CrossRef]
- Zhuwei, G.; Juan, W.; Jiangyun, W.; Liuhai, F.; Yu, M.; Yaodong, W. Simulation Analysis of Particle Concentration of Cyclone Separator Using the DPM Model. Acta Pet. Sin. (Pet. Process. Sect.) 2018, 34, 507–5147. [Google Scholar]
- Park, D.; Cha, J.; Kim, M.; Go, J.S. Multi-objective optimization and comparison of surrogate models for separation performances of cyclone separator based on CFD, RSM, GMDH-neural network, back propagation-ANN and genetic algorithm. Eng. Appl. Comput. Fluid Mech. 2020, 14, 180–201. [Google Scholar] [CrossRef]
- Misiulia, D.; Elsayed, K.; Andersson, A.G. Geometry optimization of a deswirler for cyclone separator in terms of pressure drop using CFD and artificial neural network. Sep. Purif. Technol. 2017, 185, 10–23. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, Z.; Sun, Z.; Yang, H.; Yang, G. Performance evaluation and prediction model for novel elliptical cyclone separators. Sep. Purif. Technol. 2025, 354, 128888. [Google Scholar] [CrossRef]
- He, F.; Chen, Y.; Zhao, B.; Chen, C.; Huang, S.; Peng, S. H2 Reduction of Na2SO4 to Na2S Based on Dilute-Phase Fluidization. Processes 2024, 12, 776. [Google Scholar] [CrossRef]
- Guo, M.; Le, D.; Sun, X.; Yoon, J. Multi-objective optimization of a novel vortex finder for performance improvement of cyclone separator. Powder Technol. 2022, 410, 117856. [Google Scholar] [CrossRef]
- Jeong, J.J.J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 332, 339–363. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. Stud. Turbul. Using Numer. Simul. Databases 1988, 2, 193–208. [Google Scholar]
- Liu, C.Q.; Wang, Y.Q.; Yang, Y.; Duan, Z.W. New omega vortex identification method. Sci. China 2016, 59, 684711. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Tian, S.; Dong, X. Rortex A New Vortex Vector Definition and Vorticity Tensor and Vector Decompositions. Phys. Fluids 2018, 30, 035103. [Google Scholar] [CrossRef]
- Liu, C. Letter: Galilean invariance of Rortex. Phys. Fluids 2018, 30, 111701. [Google Scholar] [CrossRef]
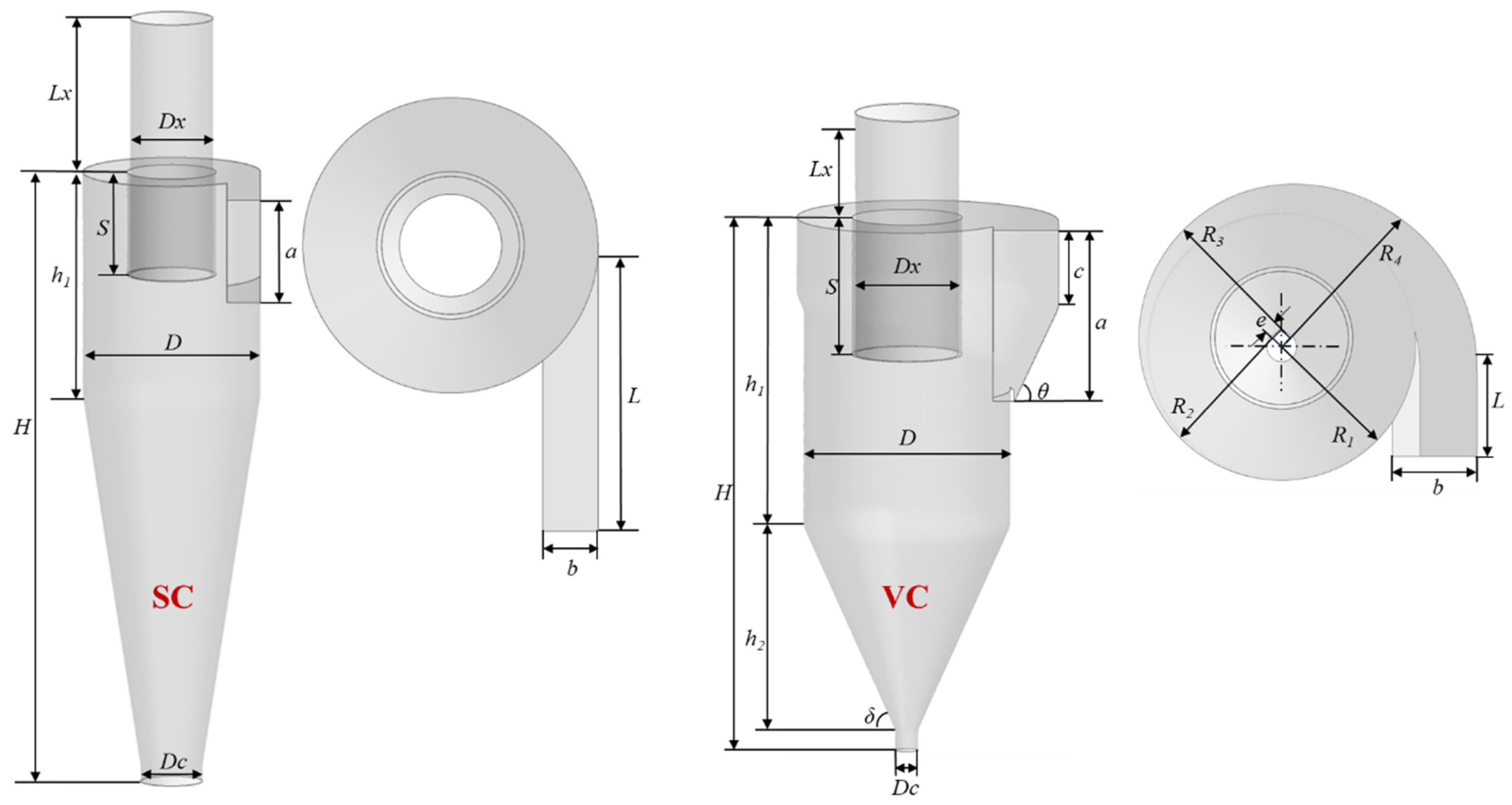
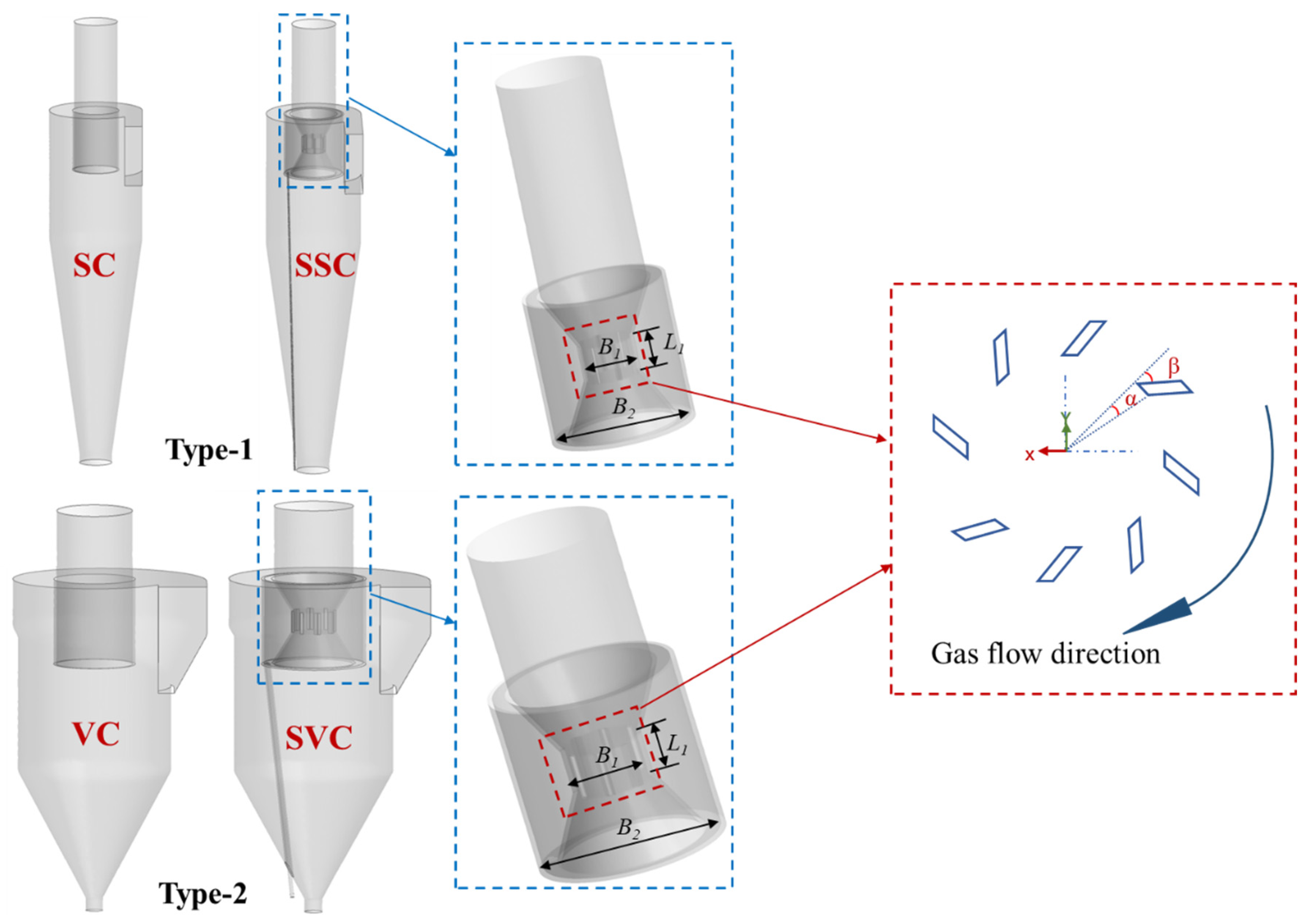





| Dimension | SC | VC |
|---|---|---|
| Inlet height, a/D | 0.64 | 0.83 |
| Inlet width, b/D | 0.19 | 0.32 |
| Inlet right height, c/D | --- | 0.38 |
| Inlet angle, θ/D | --- | 65° |
| Gas outlet diameter, Dx/D | 0.47 | 0.50 |
| Vortex finder length, S/D | 0.64 | 0.67 |
| Cone tip diameter, Dc/D | 0.35 | 0.11 |
| Barrel height, h1/D | 1.40 | 1.50 |
| Cone height, h2/D | --- | 1.00 |
| Cone Angle, δ | --- | 66° |
| Cyclone height, H/D | 3.84 | 2.60 |
| Outlet tube length, Lx/D | 0.97 | 0.33 |
| Eccentricity, e/D | --- | 0.08 |
| Volute radius, R1, R2, R3, R4/D | --- | 0.78, 0.89, 1.00, 1.02 |
| Item | Spatial Discretization |
|---|---|
| Gradient | Least Squares Cell Based |
| Pressure | PRESTO |
| Momentum | QUICK |
| Turbulent Kinetic Energy | Second Order Upwind |
| Turbulent Dissipation Rate | Second Order Upwind |
| Reynolds Stresses | Second Order Upwind |
| Boundary | Boundary Conditions of Gas Phase | Boundary Conditions of Solid Phase |
|---|---|---|
| Inlet | Velocity-inlet | Escape |
| Outlet of gas | Pressure-outlet | Escape |
| Outlet of particles | Wall | Trap |
| Secondary separation outlet of particles | Wall | Trap |
| Wall | Wall | Reflect |
| Model | Producer | |
|---|---|---|
| Induced draft fan | — | Weifang Zhengyuan powder equipment |
| Feeding machine | LG-VF-T38 | Wuxi Lingge |
| Manometer | Kimo MP210 | France KIMO company |
| Pressure transmitter | 2600T | Shanghai ABB Engineering limited company |
| Pitot tube | PTL-08-350 | Shanghai |
| Laser particle size analyzer | HELOS/BR/OM/RODOS/T4-R4 | Shanghai |
| Cyclone Separators | Total Separation Efficiency (%) | |||
|---|---|---|---|---|
| Inlet Gas Velocity (m/s) | 10 | 12.5 | 15 | 17.5 |
| SC | 85.25 | 86.11 | 87.89 | 89.29 |
| SSC | 90.92 | 95.88 | 96.74 | 97.96 |
| VC | 58.16 | 62.77 | 66.63 | 69.19 |
| VSC | 68.30 | 72.19 | 74.35 | 76.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Chen, Y.; Zhang, L.; Zhao, B.; Li, Y. Numerical Simulation of a Novel Secondary Separation Cyclone. Processes 2025, 13, 1874. https://doi.org/10.3390/pr13061874
Chen J, Chen Y, Zhang L, Zhao B, Li Y. Numerical Simulation of a Novel Secondary Separation Cyclone. Processes. 2025; 13(6):1874. https://doi.org/10.3390/pr13061874
Chicago/Turabian StyleChen, Jingyi, Yanxin Chen, Leilei Zhang, Bo Zhao, and Yongsheng Li. 2025. "Numerical Simulation of a Novel Secondary Separation Cyclone" Processes 13, no. 6: 1874. https://doi.org/10.3390/pr13061874
APA StyleChen, J., Chen, Y., Zhang, L., Zhao, B., & Li, Y. (2025). Numerical Simulation of a Novel Secondary Separation Cyclone. Processes, 13(6), 1874. https://doi.org/10.3390/pr13061874







