Data-Driven Prediction of Crystal Size Metrics Using LSTM Networks and In Situ Microscopy in Seeded Cooling Crystallization
Abstract
1. Introduction
2. Materials and Methods
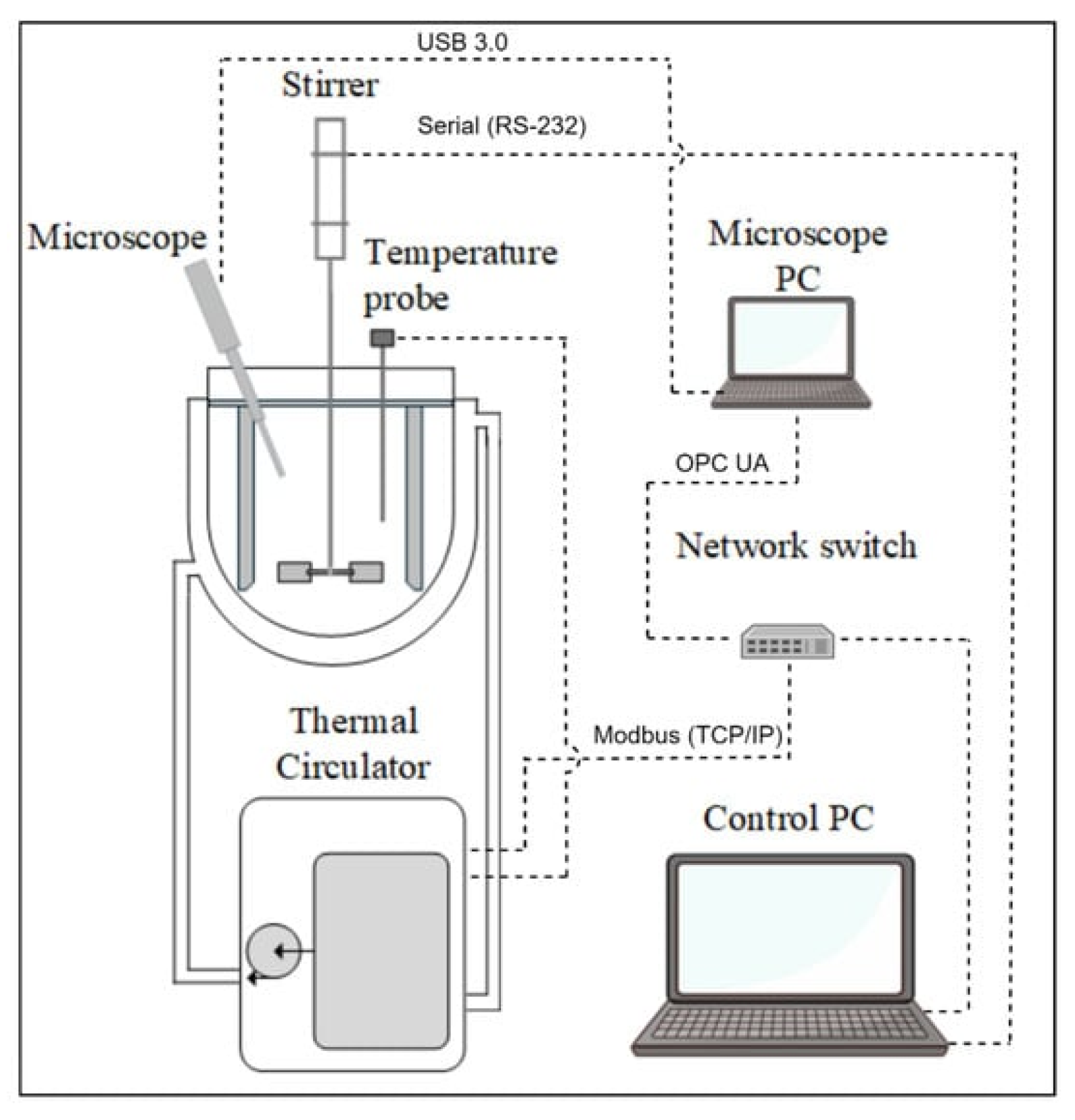
2.1. Experimental Material and Crystallizer Setup
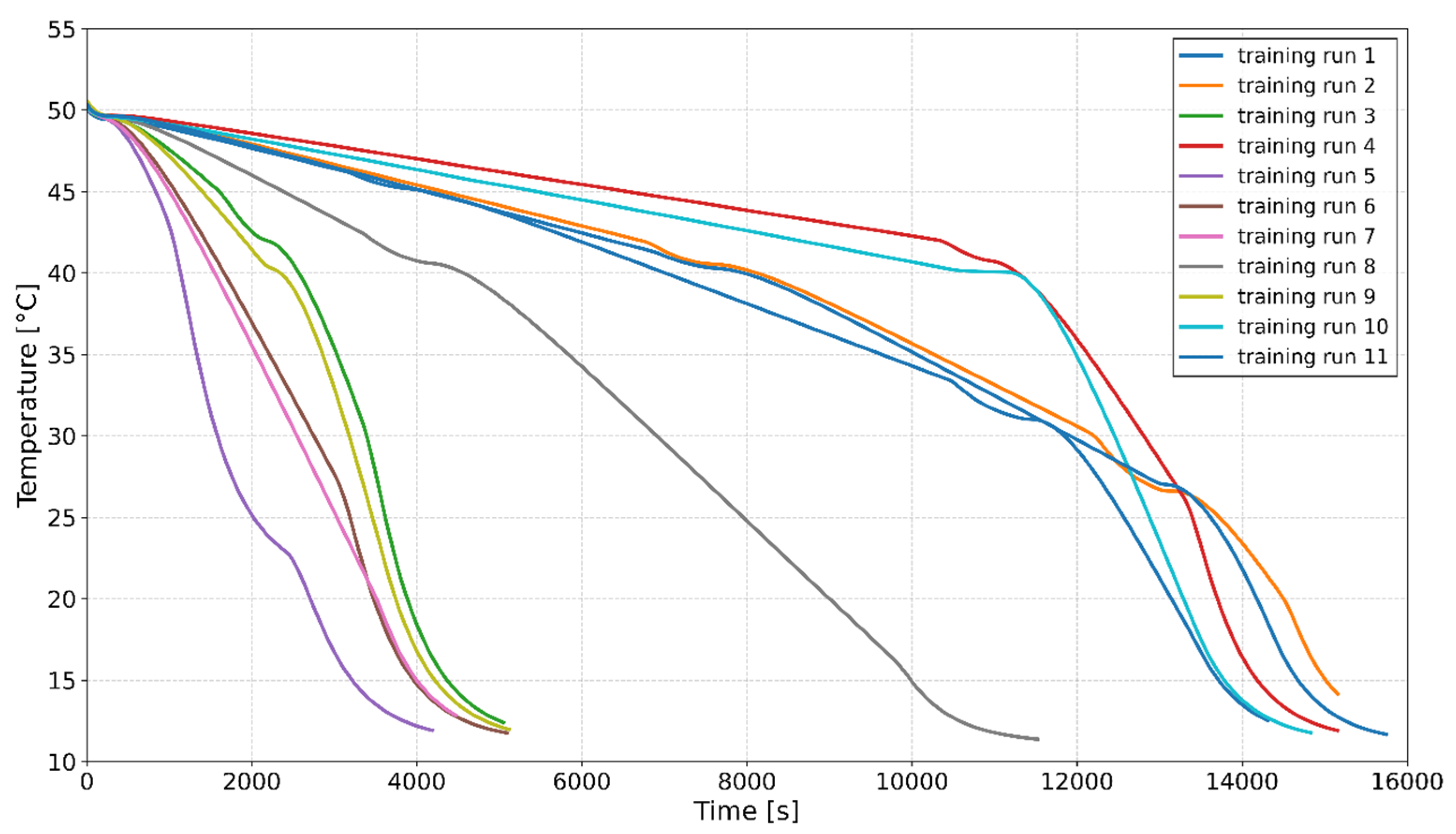
2.2. Crystallization Experiments for Model Training
- 0.5% Seed Loading: Training Runs 1, 3, 4, 6, 11
- 2% Seed Loading: Training Runs 2, 7, 8, 9, 10
- 3.5% Seed Loading: Training Run 5
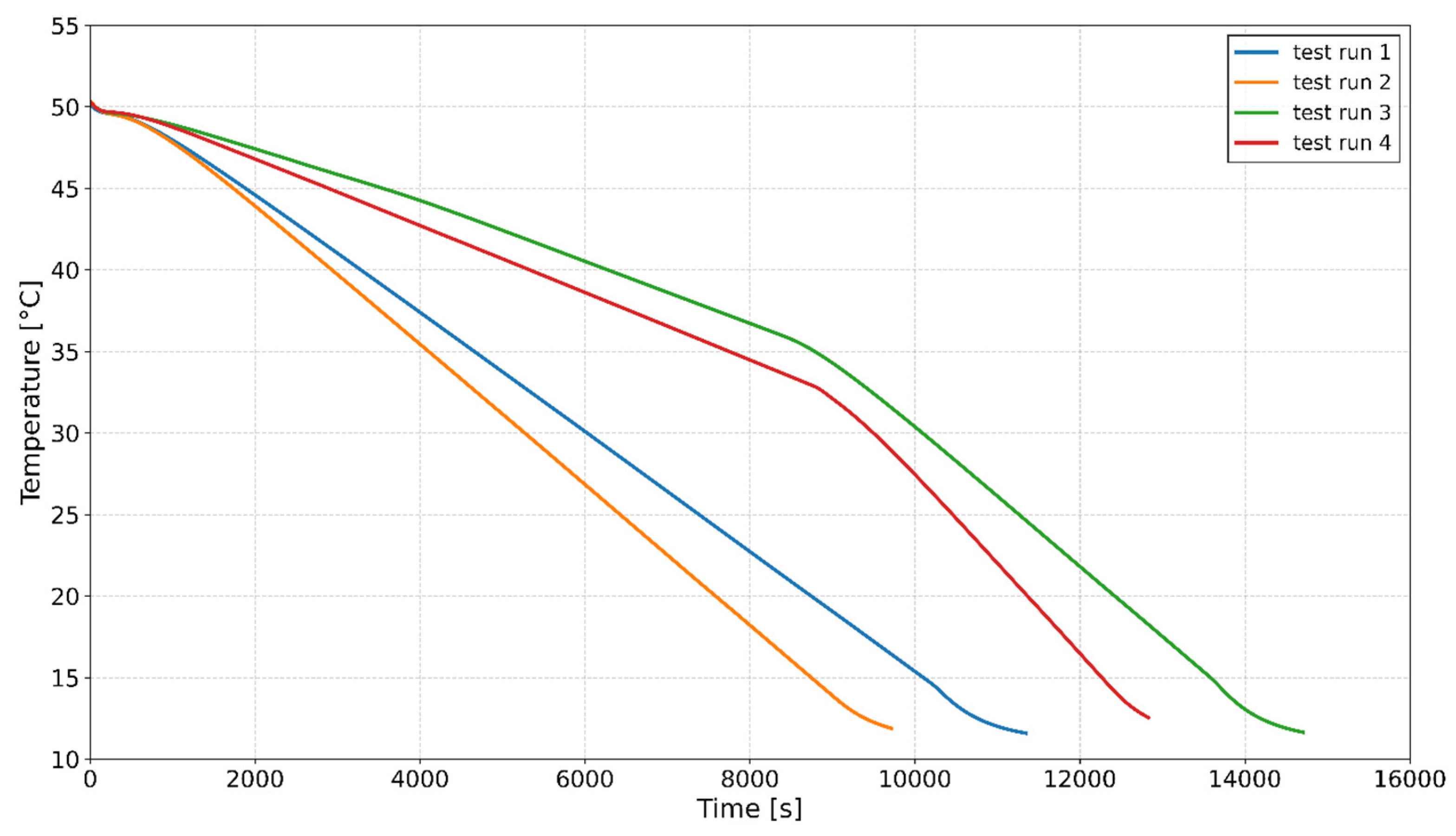
2.3. Crystallization Experiments for Model Testing
2.4. Model Building
2.4.1. Data Scaling
2.4.2. Feature Engineering from Temperature Profile
2.4.3. LSTM Model—Hyperparameter Optimization
- Hidden units: the number of hidden units in the LSTM layers (32, 64, 96).
- Number of layers: the number of stacked layers (2, 3).
- Lag: the number of the time steps included in the input sequence (24, 46, 60).
3. Results and Discussion
3.1. Variability in SW D10, D50, D90, and SW Counts Across Crystallization Training Runs
- Training runs 3 and 11 (0.5% seed loading) show the lowest SW counts, which is due to the limited nucleation sites.
- Training runs 8 and 10 (2% seed loading) show intermediate SW counts, which is due to an increase in nucleation events.
- Training run 5 (3.5% seed loading) achieves the highest SW counts, which is due to the fact that a larger seed load provides more nucleation sites and a high degree of supersaturation throughout the process due to the rapid cooling profile.
3.2. Evaluation of LSTM Hyperparameters for Feature-Engineered and Non-Feature-Engineered Models
3.3. Analysis of Model Performance Across Test Runs
3.3.1. Overview of Results
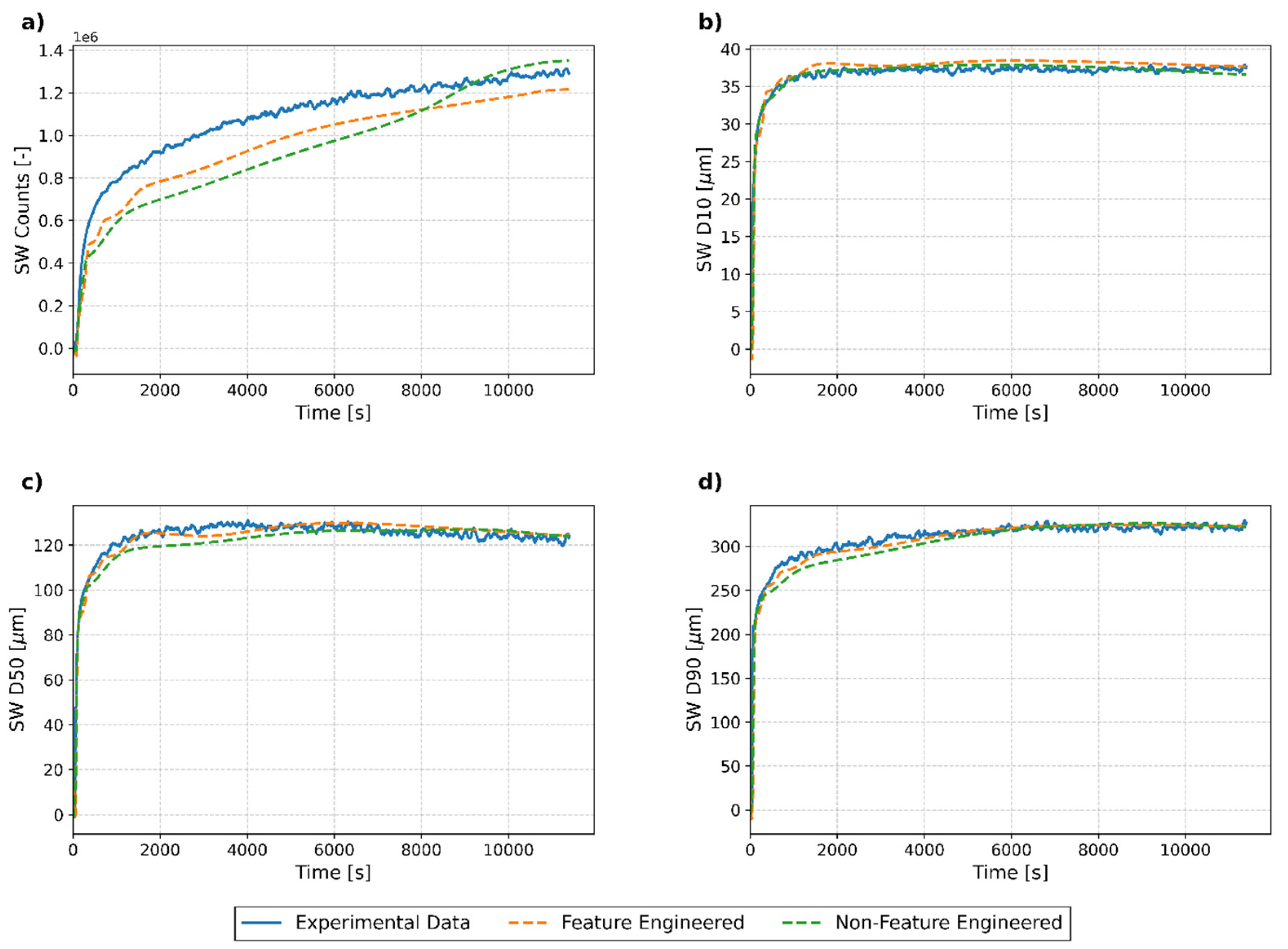
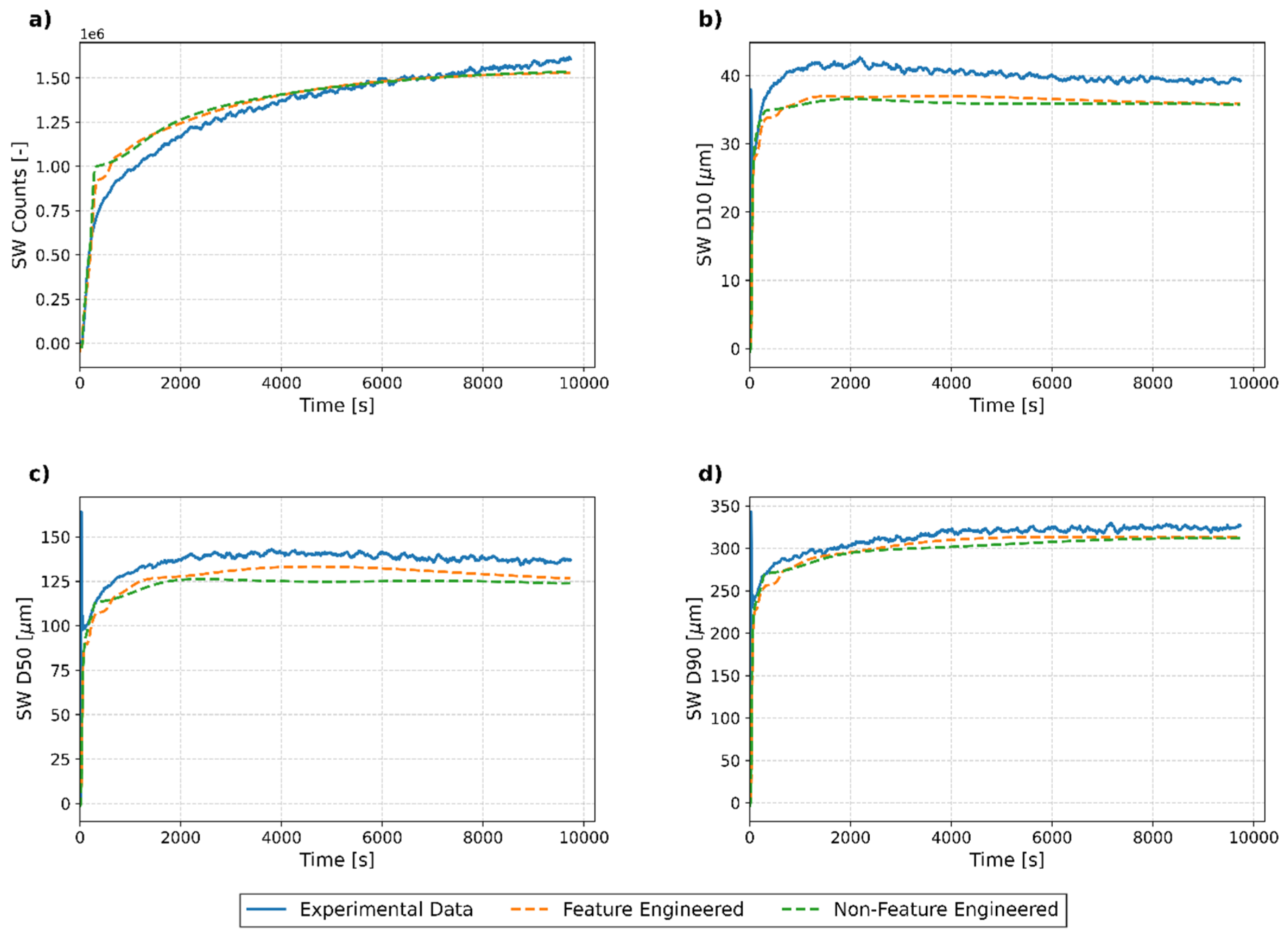
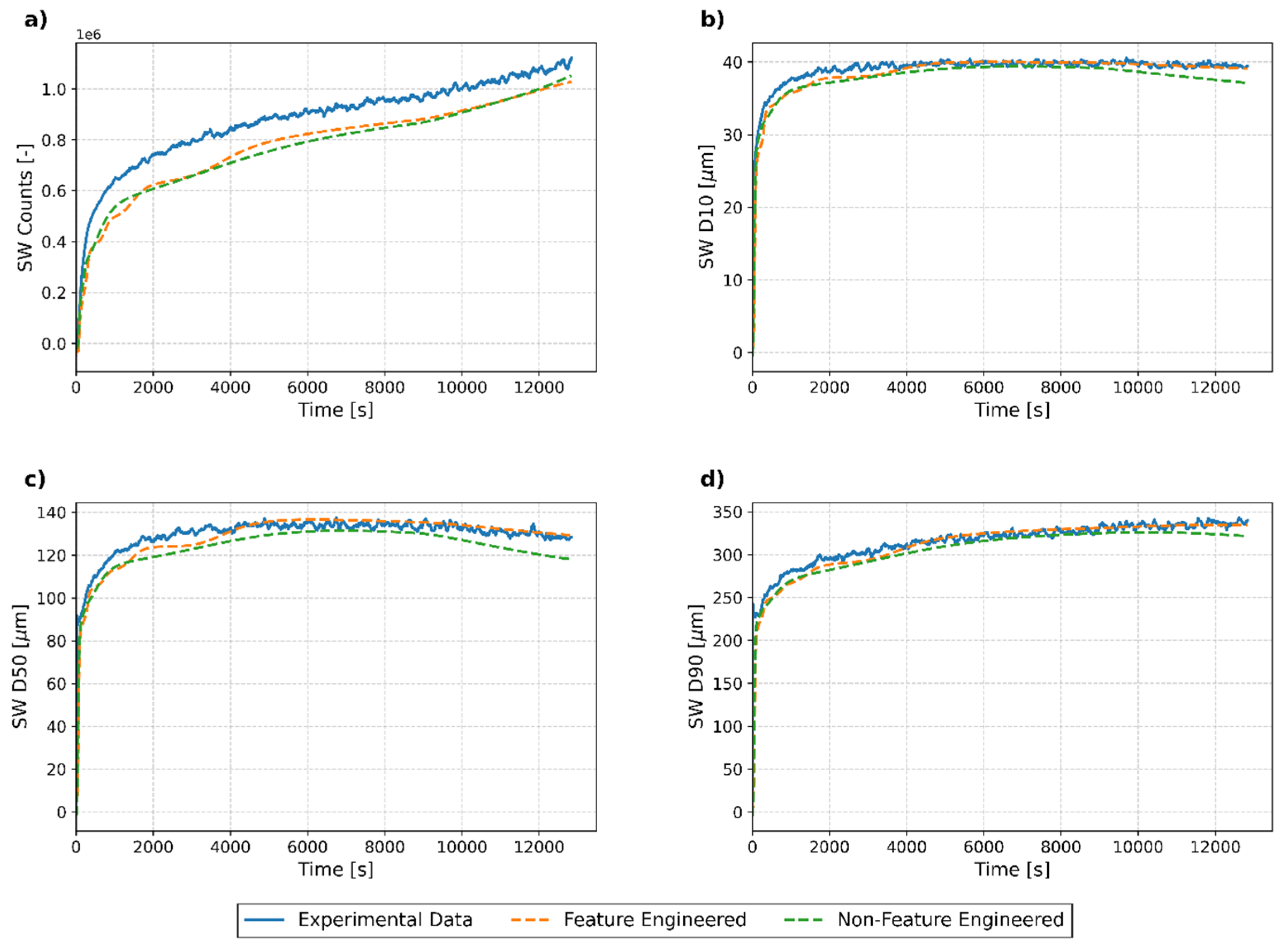
3.3.2. Individual Run Analysis
Test Run 1
Test Run 2
Test Run 3
Test Run 4
3.3.3. Key Findings
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zokić, I.; Kardum, J.P. Crystallization Behavior of Ceritinib: Characterization and Optimization Strategies. ChemEngineering 2023, 7, 84. [Google Scholar] [CrossRef]
- Garg, M.; Rathore, A.S. Process development in the QbD paradigm: Implementing design of experiments (DoE) in anti-solvent crystallization for production of pharmaceuticals. J. Cryst. Growth 2021, 571, 126263. [Google Scholar] [CrossRef]
- Chen, J.; Sarma, B.; Evans, J.M.B.; Myerson, A.S. Pharmaceutical crystallization. Cryst. Growth Des. 2011, 11, 887–895. [Google Scholar] [CrossRef]
- Lee, H.L.; Lin, H.Y.; Lee, T. The impact of reaction and crystallization of acetaminophen (Paracetamol) on filtration and drying through in-process controls. In Proceedings of the Particle Technology Forum 2014—Core Programming Area at the 2014 AIChE Annual Meeting, Atlanta, GA, USA, 16–21 November 2014; pp. 275–286. [Google Scholar]
- Wei, H.Y. Computer-aided design and scale-up of crystallization processes: Integrating approaches and case studies. Chem. Eng. Res. Des. 2010, 88, 1377–1380. [Google Scholar] [CrossRef]
- Woinaroschy, A.; Isopescu, R.; Filipescu, L. Crystallization process optimization using artificial neural networks. Chem. Eng. Technol. 1994, 17, 269–272. [Google Scholar] [CrossRef]
- Worlitschek, J.; Mazzotti, M. Model-based optimization of particle size distribution in batch-cooling crystallization of paracetamol. Cryst. Growth Des. 2004, 4, 891–903. [Google Scholar] [CrossRef]
- Mazzotti, M.; Vetter, T.; Ochsenbein, D.R. Crystallization Process Modeling. In Polymorphism in the Pharmaceutical Industry; Wiley-VCH Verlag GmbH & Co., KGaA: Weinheim, Germany, 2018; pp. 285–304. [Google Scholar] [CrossRef]
- Pickles, T.; Svoboda, V.; Marziano, I.; Brown, C.J.; Florence, A.J. Integration of a model-driven workflow into an industrial pharmaceutical facility: Supporting process development of API crystallisation. CrystEngComm 2024, 26, 4678–4689. [Google Scholar] [CrossRef]
- Fiordalis, A.; Georgakis, C. Data-driven, using design of dynamic experiments, versus model-driven optimization of batch crystallization processes. J. Process Control 2013, 23, 179–188. [Google Scholar] [CrossRef]
- Le Minh, T.; Thanh, T.P.; Hong, N.N.T.; Minh, V.P. A Simple Population Balance Model for Crystallization of L-Lactide in a Mixture of n-Hexane and Tetrahydrofuran. Crystals 2022, 12, 221. [Google Scholar] [CrossRef]
- Szilagyi, B.; Eren, A.; Quon, J.L.; Papageorgiou, C.D.; Nagy, Z.K. Application of Model-Free and Model-Based Quality-by-Control (QbC) for the Efficient Design of Pharmaceutical Crystallization Processes. Cryst. Growth Des. 2020, 20, 3979–3996. [Google Scholar] [CrossRef]
- Rosenbaum, T.; Tan, L.; Engstrom, J. Advantages of utilizing population balance modeling of crystallization processes for particle size distribution prediction of an active pharmaceutical ingredient. Processes 2019, 7, 355. [Google Scholar] [CrossRef]
- Jha, S.K.; Karthika, S.; Radhakrishnan, T.K. Modelling and control of crystallization process. Resour. Technol. 2017, 3, 94–100. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Braatz, R.D. Advances and new directions in crystallization control. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 55–75. [Google Scholar] [CrossRef]
- Ma, Y.; Li, W.; Yang, H.; Gong, J.; Nagy, Z.K. Digital Design of Cooling Crystallization Processes Using a Machine Learning-Based Strategy. Ind. Eng. Chem. Res. 2024, 63, 20236–20251. [Google Scholar] [CrossRef]
- Bosetti, L.; Mazzotti, M. Population Balance Modeling of Growth and Secondary Nucleation by Attrition and Ripening. Cryst. Growth Des. 2020, 20, 307–319. [Google Scholar] [CrossRef]
- Herceg, T.; Andrijić, Ž.U.; Gavran, M.; Sacher, J.; Vrban, I.; Bolf, N. Application of Neural Networks for Estimating the Concentration of Active Ingredients Solution using In-situ ATR-FTIR Spectroscopy. Kem. Ind. 2023, 72, 639–650. [Google Scholar] [CrossRef]
- Zhang, F.; Du, K.; Guo, L.; Xu, Q.; Shan, B. Comparative Study of Preprocessing on an ATR-FTIR Calibration Model for In Situ Monitoring of Solution Concentration in Cooling Crystallization. Chem. Eng. Technol. 2021, 44, 2279–2289. [Google Scholar] [CrossRef]
- Togkalidou, T.; Fujiwara, M.; Patel, S.; Braatz, R.D. Solute concentration prediction using chemometrics and ATR-FTIR spectroscopy. J. Cryst. Growth 2001, 231, 534–543. [Google Scholar] [CrossRef]
- Togkalidou, T.; Tung, H.H.; Sun, Y.; Andrews, A.; Braatz, R.D. Solution concentration prediction for pharmaceutical crystallization processes using robust chemometrics and ATR FTIR spectroscopy. Org. Process Res. Dev. 2002, 6, 317–322. [Google Scholar] [CrossRef]
- Lewiner, F.; Klein, J.P.; Puel, F.; Feh, G. On-line ATR FTIR measurement of supersaturation during solution crystallization processes. Calibration and applications on three solute/solvent systems. Chem. Eng. Sci. 2001, 56, 2069–2084. [Google Scholar] [CrossRef]
- Lin, M.; Wu, Y.; Rohani, S. Simultaneous Measurement of Solution Concentration and Slurry Density by Raman Spectroscopy with Artificial Neural Network. Cryst. Growth Des. 2020, 20, 1752–1759. [Google Scholar] [CrossRef]
- Gavran, M.; Andrijić, Ž.U.; Bolf, N.; Rimac, N.; Sacher, J.; Šahnić, D. Development of a Calibration Model for Real-Time Solute Concentration Monitoring during Crystallization of Ceritinib Using Raman Spectroscopy and In-Line Process Microscopy. Processes 2023, 11, 3439. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.; Zhang, D.; Li, K.; Qian, Y. On-line concentration measurement for anti-solvent crystallization of β-artemether using UVvis fiber spectroscopy. J. Cryst. Growth 2011, 314, 185–189. [Google Scholar] [CrossRef]
- Simone, E.; Saleemi, A.N.; Tonnon, N.; Nagy, Z.K. Active polymorphic feedback control of crystallization processes using a combined raman and ATR-UV/Vis spectroscopy approach. Cryst. Growth Des. 2014, 14, 1839–1850. [Google Scholar] [CrossRef]
- Saleemi, A.N.; Rielly, C.D.; Nagy, Z.K. Monitoring of the combined cooling and antisolvent crystallisation of mixtures of aminobenzoic acid isomers using ATR-UV/vis spectroscopy and FBRM. Chem. Eng. Sci. 2012, 77, 122–129. [Google Scholar] [CrossRef]
- Billot, P.; Couty, M.; Hosek, P. Application of ATR-UV spectroscopy for monitoring the crystallisation of UV absorbing and nonabsorbing molecules. Org. Process Res. Dev. 2010, 14, 511–523. [Google Scholar] [CrossRef]
- Vrban, I.; Šahnić, D.; Bolf, N. Artificial Neural Network Models for Solution Concentration Measurement during Cooling Crystallization of Ceritinib. Teh. Glas. 2024, 18, 354–362. [Google Scholar] [CrossRef]
- Qu, H.; Alatalo, H.; Hatakka, H.; Kohonen, J.; Kultanen, M.L.; Reinikainen, S.P.; Kallas, J. Raman and ATR FTIR spectroscopy in reactive crystallization: Simultaneous monitoring of solute concentration and polymorphic state of the crystals. J. Cryst. Growth 2009, 311, 3466–3475. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, X.; Wu, Z. Machine Learning Modeling and Predictive Control of the Batch Crystallization Process. Ind. Eng. Chem. Res. 2022, 61, 5578–5592. [Google Scholar] [CrossRef]
- Lu, M.; Rao, S.; Yue, H.; Han, J.; Wang, J. Recent Advances in the Application of Machine Learning to Crystal Behavior and Crystallization Process Control. Cryst. Growth Des. 2024, 24, 5374–5396. [Google Scholar] [CrossRef]
- Sitapure, N.; Kwon, J.S.I. Machine learning meets process control: Unveiling the potential of LSTMc. AIChE J. 2024, 70, 1–18. [Google Scholar] [CrossRef]
- Liu, Y.; Acevedo, D.; Yang, X.; Naimi, S.; Wu, W.; Pavurala, N.; Nagy, Z.; O’Connor, T. Population Balance Model Development Verification and Validation of Cooling Crystallization of Carbamazepine. Cryst. Growth Des. 2020, 20, 5235–5250. [Google Scholar] [CrossRef]
- Kumar, K.V.; Martins, P.; Rocha, F. Modelling of the batch sucrose crystallization kinetics using artificial neural networks: Comparison with conventional regression analysis. Ind. Eng. Chem. Res. 2008, 47, 4917–4923. [Google Scholar] [CrossRef]
- Nyande, B.W.; Nagy, Z.K.; Lakerveld, R. Data-driven identification of crystallization kinetics. AIChE J. 2024, 70, 1–11. [Google Scholar] [CrossRef]
- Lima, F.A.R.D.; de Miranda, G.F.M.; de Moraes, M.G.F.; Capron, B.D.O.; de Souza, M.B. A Recurrent Neural Networks-Based Approach for Modeling and Control of a Crystallization Process. Comput. Aided Chem. Eng. 2022, 51, 1423–1428. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A tutorial into Long Short-Term Memory Recurrent Neural Networks. arXiv 2019, arXiv:1909.09586. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Meyer, C.; Arora, A.; Scholl, S. A method for the rapid creation of AI driven crystallization process controllers. Comput. Chem. Eng. 2024, 186, 108680. [Google Scholar] [CrossRef]
- Omar, H.M.; Rohani, S. Crystal Population Balance Formulation and Solution Methods: A Review. Cryst. Growth Des. 2017, 17, 4028–4041. [Google Scholar] [CrossRef]
- Yang, X.; Muhammad, T.; Bakri, M.; Muhammad, I.; Yang, J.; Zhai, H.; Abdurahman, A.; Wu, H. Simple and fast spectrophotometric method based on chemometrics for the measurement of multicomponent adsorption kinetics. J. Chemom. 2020, 34, 1–13. [Google Scholar] [CrossRef]
- Sitapure, N.; Kwon, J.S.-I. CrystalGPT: Enhancing system-to-system transferability in crystallization prediction and control using time-series-transformers. Comput. Chem. Eng. 2023, 177, 108339. [Google Scholar] [CrossRef]
- Salami, H.; McDonald, M.A.; Bommarius, A.S.; Rousseau, R.W.; Grover, M.A. In Situ Imaging Combined with Deep Learning for Crystallization Process Monitoring: Application to Cephalexin Production. Org. Process Res. Dev. 2021, 25, 1670–1679. [Google Scholar] [CrossRef]
- Piskunova, N.N. Non-reversibility of crystal growth and Dissolution: Nanoscale direct observations and kinetics of transition through the saturation point. J. Cryst. Growth 2024, 631, 127614. [Google Scholar] [CrossRef]
- Mentges, J.; Bischoff, D.; Walla, B.; Weuster-Botz, D. In Situ Microscopy with Real-Time Image Analysis Enables Online Monitoring of Technical Protein Crystallization Kinetics in Stirred Crystallizers. Crystals 2024, 14, 1009. [Google Scholar] [CrossRef]
- Sacher, J.B.; Bolf, N.; Sejdić, M. Batch Cooling Crystallization of a Model System Using Direct Nucleation Control and High-Performance In Situ Microscopy. Crystals 2024, 14, 1079. [Google Scholar] [CrossRef]
- Antonio, J.; Candow, D.G.; Forbes, S.C.; Gualano, B.; Jagim, A.R.; Kreider, R.B.; Rawson, E.S.; Smith-Ryan, A.E.; VanDusseldorp, T.A.; Willoughby, D.S.; et al. Common questions and misconceptions about creatine supplementation: What does the scientific evidence really show? J. Int. Soc. Sport. Nutr. 2021, 18, 13. [Google Scholar] [CrossRef]
- Jäger, R.; Purpura, M.; Shao, A.; Inoue, T.; Kreider, R.B. Analysis of the efficacy, safety, and regulatory status of novel forms of creatine. Amino Acids 2011, 40, 1369–1383. [Google Scholar] [CrossRef]
- de Amorim, L.B.V.; Cavalcanti, G.D.C.; Cruz, R.M.O. The choice of scaling technique matters for classification performance. Appl. Soft Comput. 2023, 133, 109924. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Yu, H.; Hu, Y.; Shi, P. A Prediction Method of Peak Time Popularity Based on Twitter Hashtags. IEEE Access 2020, 8, 61453–61461. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]





| Reference | Authors | Problems Addressed | Solving Method |
|---|---|---|---|
| [34] | Y. Liu et al. | Model for cooling crystallization of carbamazepine | PBE |
| [11] | T. Le Minh et al. | Model for crystallization of L-Lactide in a mixture of n-Hexane and Tetrahydrofuran | PBE |
| [17] | L. Bosetti et al. | Model of crystal growth and secondary nucleation by attrition and ripening | PBE |
| [16] | Y. Ma et al. | predicting the final yield and particle size distribution (PSD) in cooling crystallization processes. | ANN |
| [35] | K. Vasanth Kumar et al. | Model for the crystal growth rate of sucrose | ANN |
| [36] | B. W. Nyande et al. | Model isothermal crystallization of lysozyme in a batch stirred tank and cooling crystallization of paracetamol | Sparse identification of nonlinear dynamics (SINDy) |
| [31] | Y. Zheng et al. | Machine-learning-based predictive control schemes for batch crystallization processes | RNN |
| [37] | F. A. R. D. Lima et al. | Predict the moments of particle-size distribution | Multilayer perceptron (MLP) network, echo state network (ESN), LSTM |
| Test Run | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Seed Loading (%) | 1.2 | 2.5 | 3 | 0.75 |
| Run | Variable | MedAE (FE) | MedAE (NFE) | RMSE (FE) | RMSE (NFE) |
|---|---|---|---|---|---|
| Test Run 1 | SW counts/105 | 1.17 | 1.86 | 1.23 | 1.73 |
| SW D10/µm | 0.87 | 0.40 | 1.33 | 0.83 | |
| SW D50/µm | 2.27 | 2.96 | 3.41 | 4.36 | |
| SW D90/µm | 3.13 | 5.15 | 9.61 | 10.86 | |
| Test Run 2 | SW counts/105 | 0.40 | 0.40 | 0.63 | 0.71 |
| SW D10/µm | 3.49 | 4.13 | 4.01 | 4.42 | |
| SW D50/µm | 8.31 | 13.11 | 10.94 | 14.91 | |
| SW D90/µm | 9.68 | 13.13 | 17.46 | 18.99 | |
| Test Run 3 | SW counts/105 | 0.20 | 0.45 | 0.45 | 0.61 |
| SW D10/µm | 0.34 | 2.35 | 1.56 | 2.72 | |
| SW D50/µm | 1.42 | 13.35 | 5.51 | 13.82 | |
| SW D90/µm | 4.17 | 18.15 | 10.72 | 20.06 | |
| Test Run 4 | SW counts/105 | 0.92 | 1.09 | 1.02 | 1.10 |
| SW D10/µm | 0.34 | 1.12 | 1.72 | 1.85 | |
| SW D50/µm | 2.23 | 5.78 | 6.28 | 7.95 | |
| SW D90/µm | 4.09 | 8.67 | 15.10 | 15.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrban, I.; Bolf, N.; Budimir Sacher, J. Data-Driven Prediction of Crystal Size Metrics Using LSTM Networks and In Situ Microscopy in Seeded Cooling Crystallization. Processes 2025, 13, 1860. https://doi.org/10.3390/pr13061860
Vrban I, Bolf N, Budimir Sacher J. Data-Driven Prediction of Crystal Size Metrics Using LSTM Networks and In Situ Microscopy in Seeded Cooling Crystallization. Processes. 2025; 13(6):1860. https://doi.org/10.3390/pr13061860
Chicago/Turabian StyleVrban, Ivan, Nenad Bolf, and Josip Budimir Sacher. 2025. "Data-Driven Prediction of Crystal Size Metrics Using LSTM Networks and In Situ Microscopy in Seeded Cooling Crystallization" Processes 13, no. 6: 1860. https://doi.org/10.3390/pr13061860
APA StyleVrban, I., Bolf, N., & Budimir Sacher, J. (2025). Data-Driven Prediction of Crystal Size Metrics Using LSTM Networks and In Situ Microscopy in Seeded Cooling Crystallization. Processes, 13(6), 1860. https://doi.org/10.3390/pr13061860









