Assessment of Reasons for Low Productivity in Ultra-Deep Fractured Tight Sandstone Reservoirs Using Data-Driven Analysis
Abstract
1. Introduction
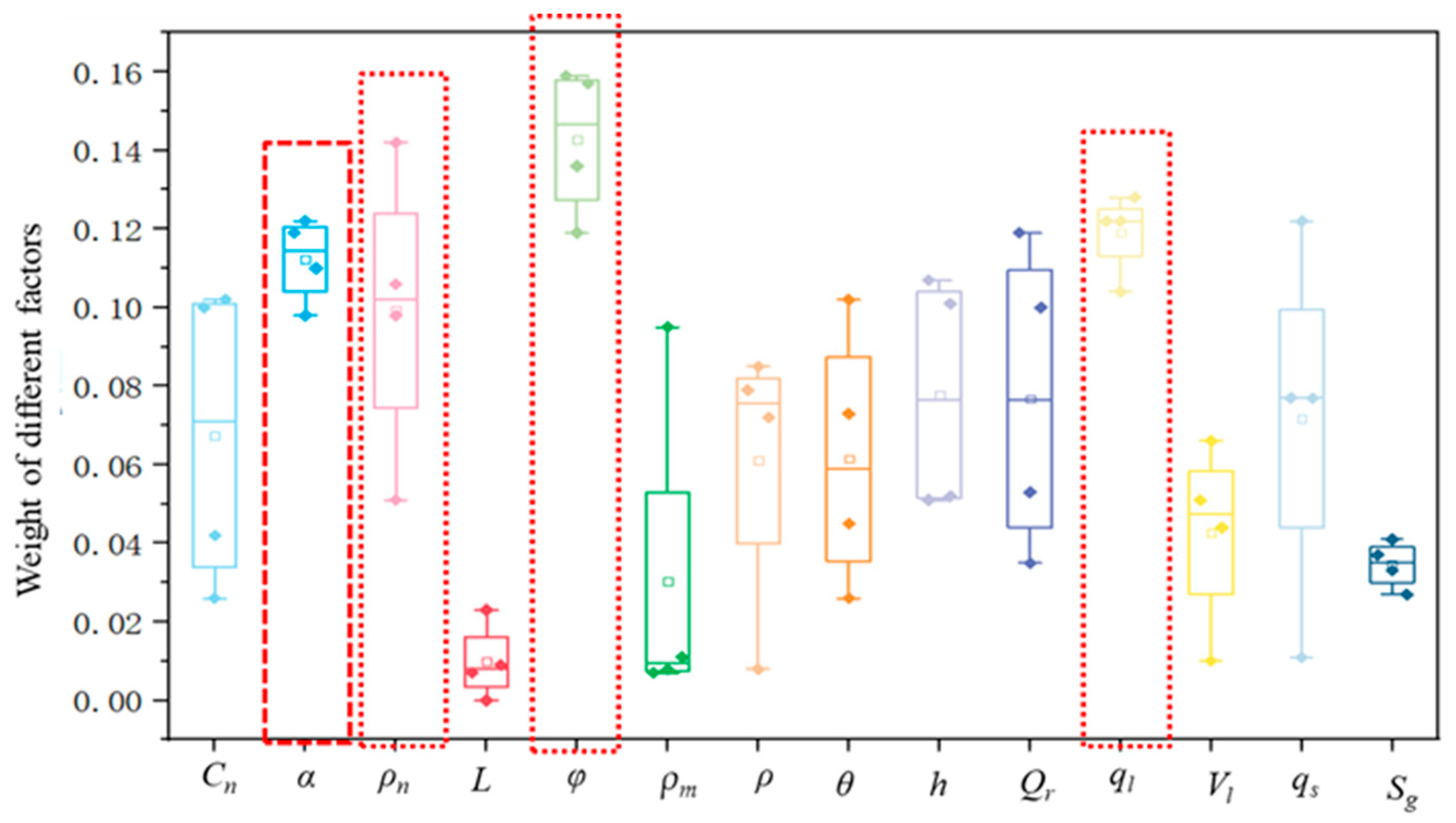
2. Analysis of Main Factors Controlling Productivity
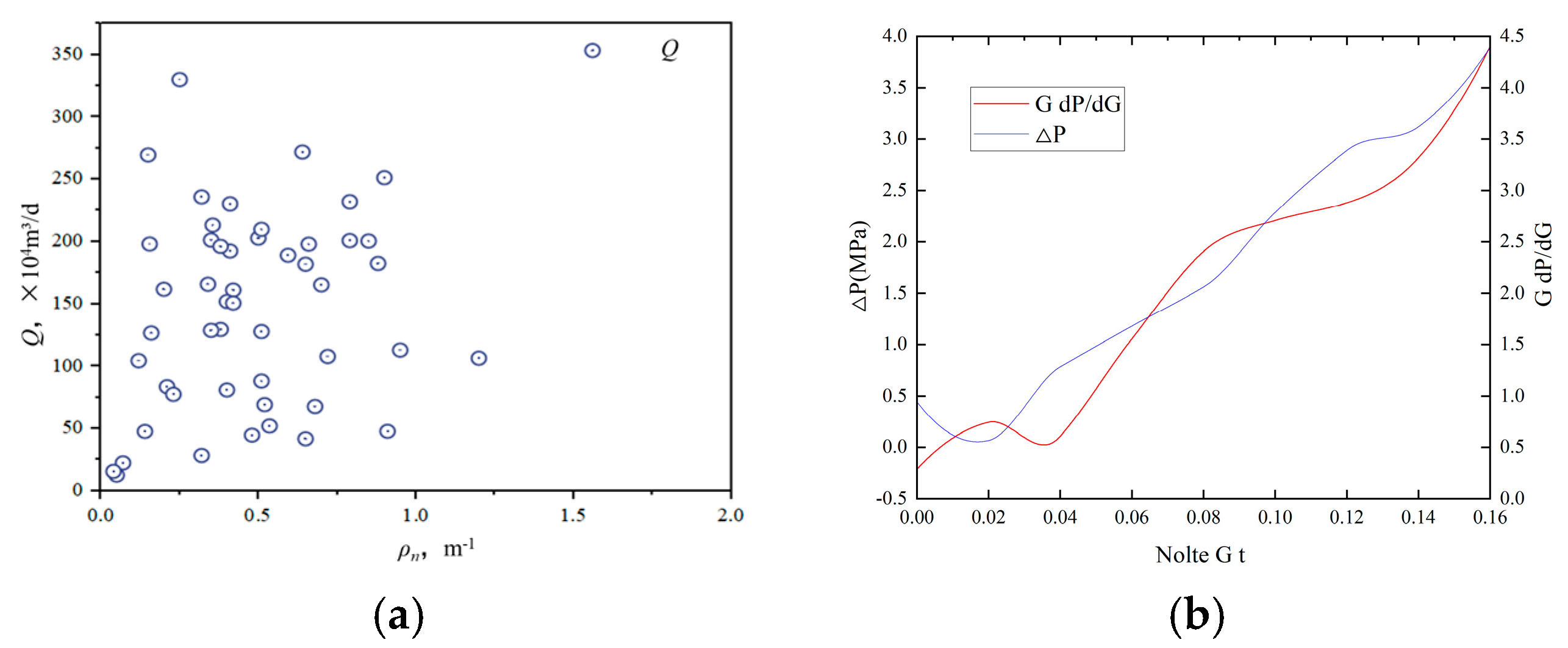
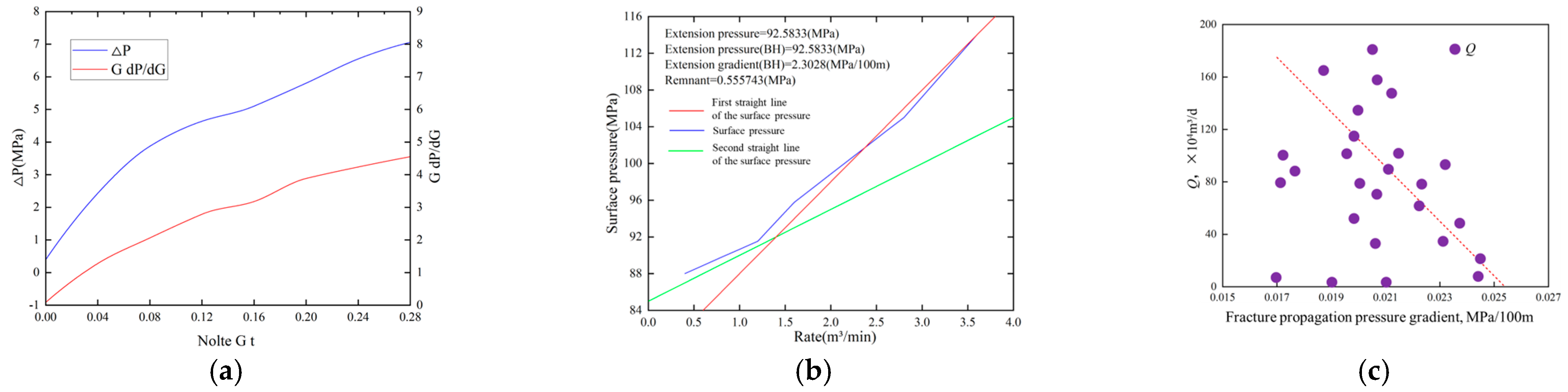
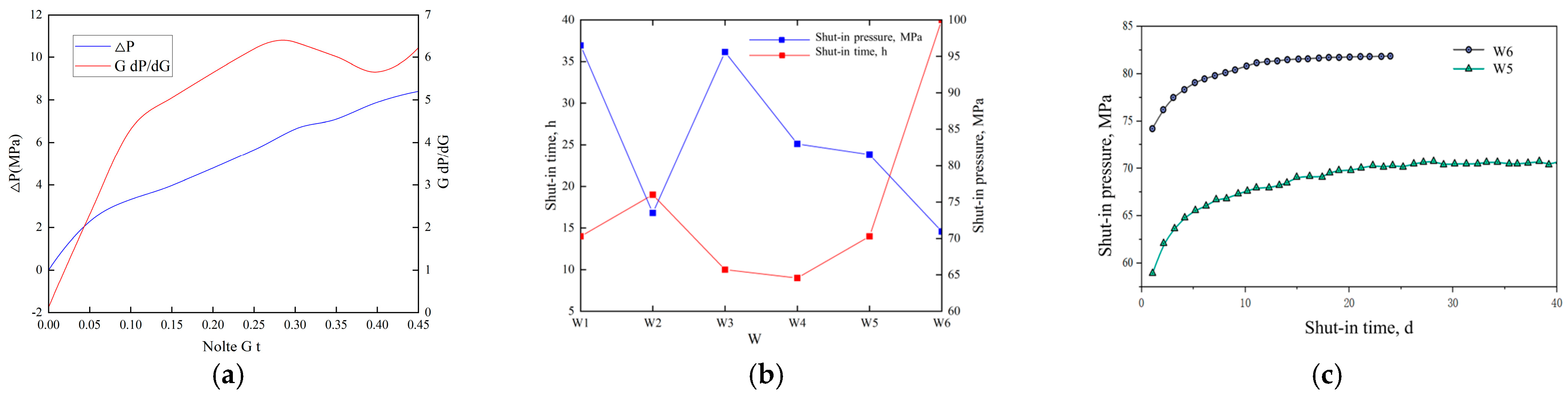
3. Deciphering Reasons for Low Productivity
4. Potential Technology for Low-Productivity Well
5. Conclusions
- (1)
- The key factors controlling productivity in the BD area include pressure coefficient, porosity, and natural fracture density.
- (2)
- The reasons for the low productivity of ultra-deep fractured tight sandstone in the BD area include the following: (1) difficulty in forming a complex fracture network due to a low natural fracture density; (2) a limited stimulation scope due to a high fracture propagation pressure; (3) a low formation pressure coefficient; and (4) the poor physical properties at far-well positions.
- (3)
- The development degree of natural fractures is still a key factor affecting the performance of composite stimulation.
- (4)
- For reservoirs with a low natural fracture density, hydraulic fracturing should be the main method used for enhancing the fractures, and small-scale acidification could be implemented for activating the fractures; for reservoirs with a high natural fracture density, composite stimulation shows great potential to increase productivity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Wang, C.; Xu, K.; Zhang, H.; Chen, N.; Deng, H.; Hu, X.; Yang, Y.; Feng, X.; Du, Y.; et al. Characteristics and Control Factors of Tectonic Fractures of Ultra-deep Tight Sandstone: Case Study of the Lower Cretaceous reservoir in Bozi-Dabei area, Kuqa Depression, Tarim Basin, China. J. Nat. Gas Geosci. 2023, 8, 439–453. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Chen, D.; Chen, B.; Liu, L.; Luo, M. Porosity Structure Characteristics and Influencing Factors Analysis of Basijiqike Tight Sandstone Reservoir in Keshen Gasfield. Bull. Geol. Sci. Technol. 2018, 37, 70–77. (In Chinese) [Google Scholar]
- Mahmoud, D.; Zeeshan, T.; Murtada, S.; Hamed, A.; Mohamed, M.; Dhafer, A. Data-Driven Acid Fracture Conductivity Correlations Honoring Different Mineralogy and Etching Patterns. ACS Omega 2020, 5, 16919–16931. [Google Scholar]
- Zhu, Z.; Hsu, M.; Kun, D. A Data-Driven Workflow for Prediction of Fracturing Parameters with Machine Learning. Therm. Sci. 2024, 28, 1085–1090. [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, B.; Liu, Y. Dynamic prediction of fracture propagation in horizontal well hydraulic fracturing: A data-driven approach for geo-energy exploitation. Geoenergy Sci. Eng. 2024, 241, 213182. [Google Scholar] [CrossRef]
- Hou, L.; Ren, J.; Fang, Y. Data-driven optimization of brittleness index for hydraulic fracturing. Int. J. Rock Mech. Min. Sci. 2022, 159, 105207. [Google Scholar] [CrossRef]
- Amro, O.; Zeeshan, T.; Murtada, S. Enhancing Fracturing Fluid Viscosity in High Salinity Water: A Data-Driven Approach for Prediction and Optimization. Energy Fuels 2023, 37, 13065–13079. [Google Scholar]
- Morozov, A.; Popkov, D.; Duplyakov, V. Data-driven model for hydraulic fracturing design optimization: Focus on building digital database and production forecast. J. Pet. Sci. Eng. 2020, 194, 107504. [Google Scholar] [CrossRef]
- Zeng, F.; Hu, D.; Zhang, Y. Research on data-driven intelligent optimization of fracturing treatment parameters for shale oil horizontal wells. Pet. Drill. Tech. 2023, 51, 78–87. [Google Scholar]
- Yang, J.; Wang, Q.; Zhou, Q. Evaluating staged acid fracturing of horizontal wells in carbonate gas reservoirs based on GBDT algorithm. Nat. Gas Explor. Dev. 2023, 46, 84–91. [Google Scholar]
- Sun, F.; Yao, Y.; Li, G.; Qu, S.; Zhang, S.; Shi, Y.; Xu, Z.; Li, X. Effect of Pressure and Temperature of Steam in Parallel Vertical Injection Wells on Productivity of a Horizontal Well During the SAGD Process: A Numerical Case Study. In Proceedings of the SPE International Heavy Oil Conference and Exhibition, Kuwait City, Kuwait, 10–12 December 2018. [Google Scholar]
- Carolina, S.; Garfias, D.; Mario, F. Acid dissolution of ultrathin glass-ceramic and its correlation with flexural strength. J. Prosthet. Dent. 2022, 128, 1084–1088. [Google Scholar]
- Mardani-Fard, H.A. Principal simple linear regression. Hacet. J. Math. Stat. 2024, 53, 524–536. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Q.; Yao, Z.; Zhang, Y. On a class of linear regression methods. J. Complex. 2024, 82, 101826. [Google Scholar] [CrossRef]
- Li, H.; Niu, C. Optimal subsampling for high-dimensional ridge regression. Knowl.-Based Syst. 2024, 286, 111426. [Google Scholar] [CrossRef]
- Nadeem, A.; Muteb, F.; Muhammad, S. Mitigating Multicollinearity in Regression: A Study on Improved Ridge Estimators. Mathematics 2024, 12, 3027. [Google Scholar] [CrossRef]
- Mei, Z.; Shi, Z. On LASSO for high dimensional predictive regression. J. Econom. 2024, 242, 105809. [Google Scholar] [CrossRef]
- Mayur, V.; Joab, R. Numerical properties of solutions of LASSO regression. Appl. Numer. Math. 2024, 208, 297–309. [Google Scholar]
- Hu, S.; Sheng, M.; Qin, S. An unsupervised cluster model of formation fracability based on drill-log data and its application to fracture optimization. Pet. Sci. Bull. 2023, 8, 767–774. [Google Scholar]
- Sheng, M.; Zhang, J.; Zhang, Y. A new data-driven effectiveness evaluation model of temporary plugging fracturing for horizontal wells. Nat. Gas Ind. 2023, 43, 132–140. [Google Scholar]
- Trung, T.; Truong, T.; Tran, V.; Ngo, H.; Dao, Q.; Nguyen, T.; Hoang, K. Virtual Multiphase Flowmetering Using Adaptive Neuro-Fuzzy Inference System (ANFIS): A Case Study of Hai Thach-Moc Tinh Field, Offshore Vietnam. SPE J. 2022, 27, 504–518. [Google Scholar] [CrossRef]
- Padmakar, A.S. Geomechanics Coupled Reservoir Flow Simulation for Diagnostic Fracture Injection Test Design and Interpretation in Shale Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 29 September–2 October 2013. [Google Scholar]



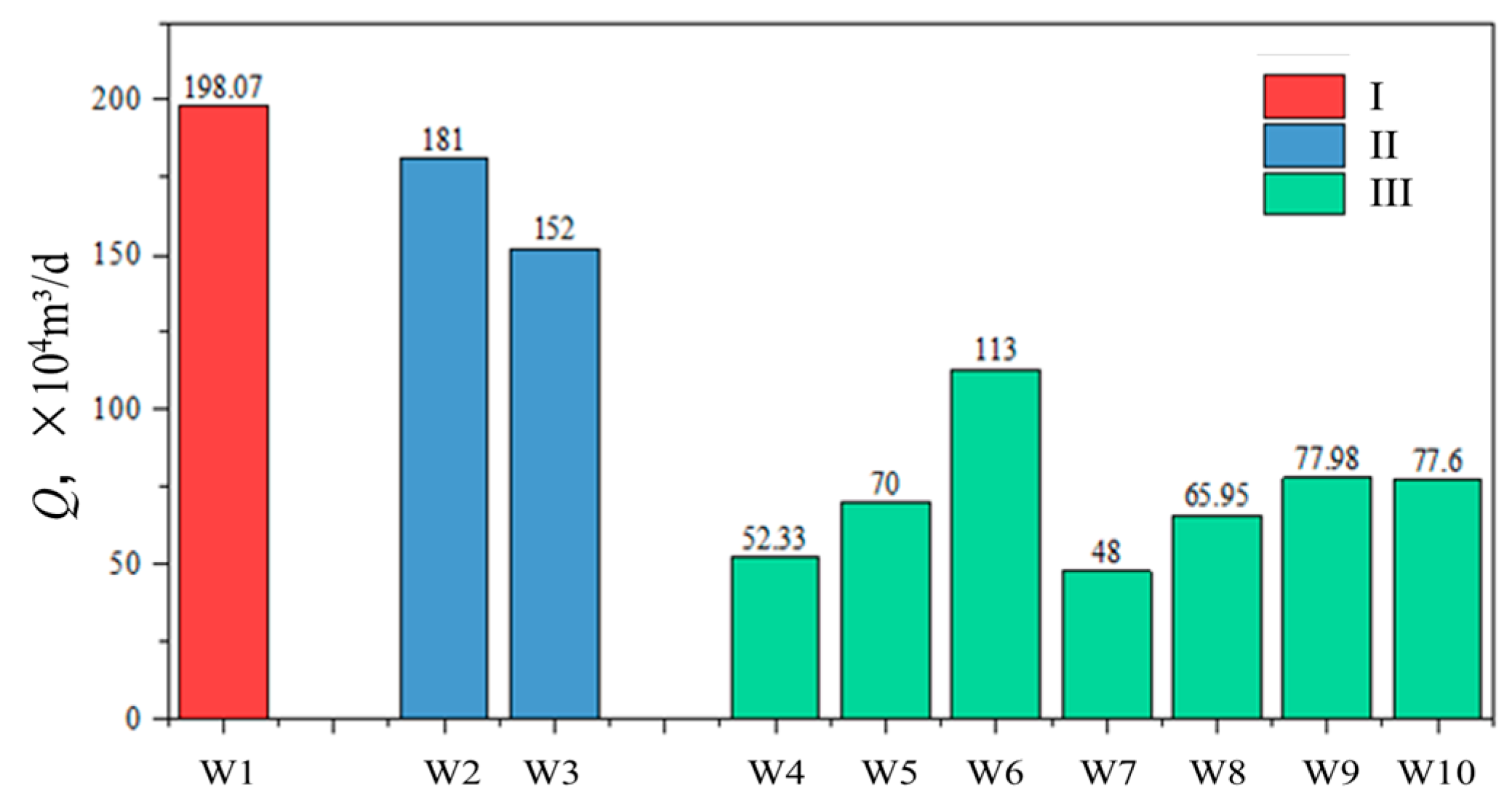
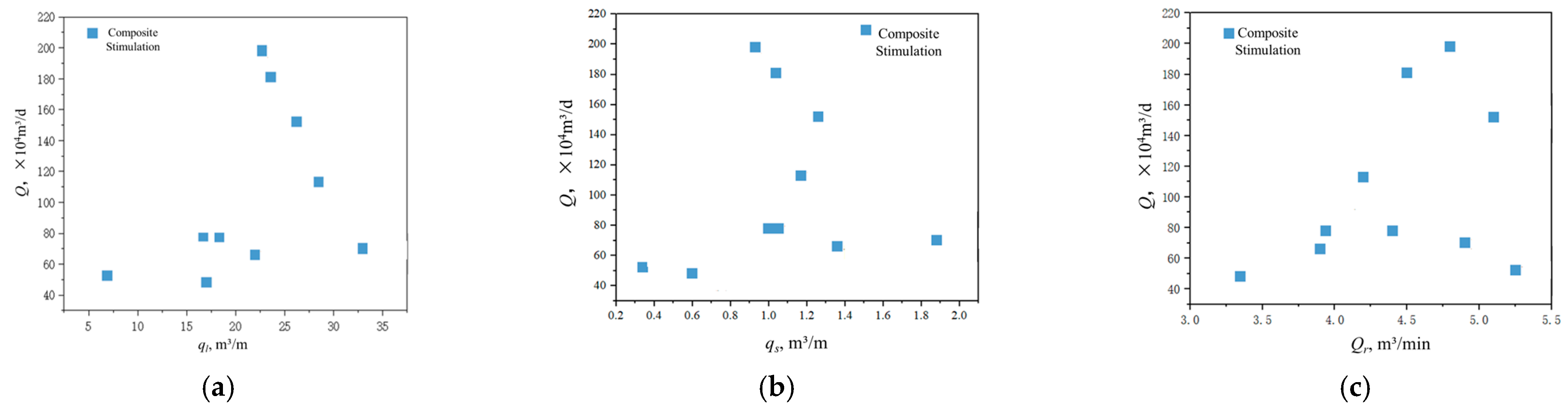
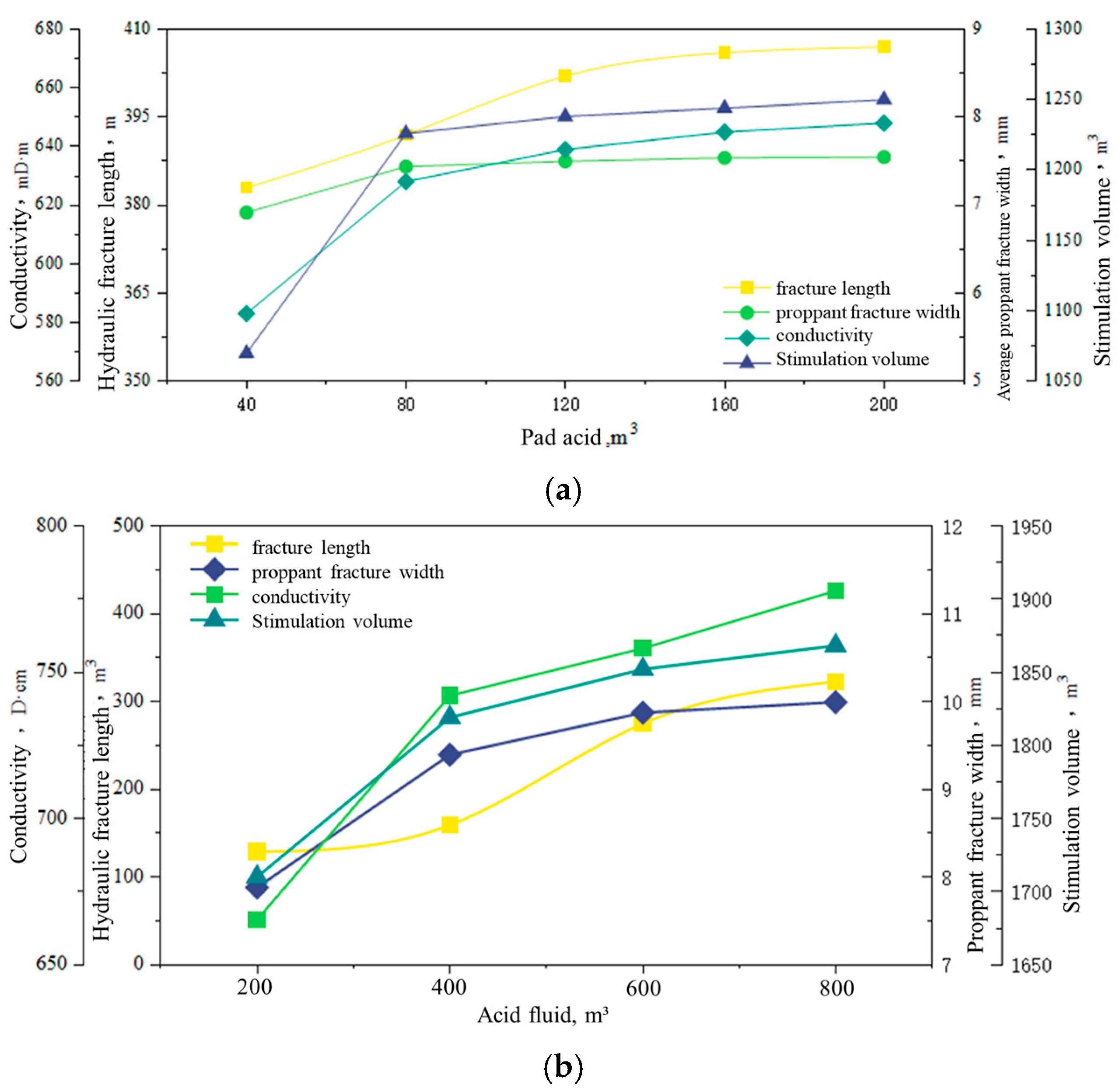
| Reservoir (L) | I | II | III |
|---|---|---|---|
| Fracture characteristics | The longitudinal penetration of reservoirs on a large scale; semi-filled or unfilled tensile fractures are mainly developed, and the fracture aperture is large. | Fractures are rarely developed and well filled. | |
| Imaging logging | Fracture density: >0.4 m−1 Standard deviation of θ: >25° | Fracture density: >0.3 m−1 Standard deviation of θ: 20–25° | Fracture density: <0.3 m−1 Standard deviation of θ: <20° |
| Leak-off characteristics | Fluid density: 0.1–0.2 g/cm3 Leak-off volume: 100–1200 m3 5–15 points uniformly distributed along the wellbore | Fluid density: 0.15–0.25 g/cm3 Leak-off volume: 100–300 m3 3–5 points uniformly distributed along the wellbore | Fluid density: 0.2–0.3 g/cm3 Leak-off volume: <500 m3 Single-point leak-off or no leak-off |
| Stimulation technology | Small-scale acidizing | Large-scale acid fracturing or proppant fracturing | Proppant fracturing |
| Stimulation mechanism | Removing damage in the natural fracture | Activating the natural fracture | Forming artificial fractures |
| Well | L | Q | α | φ | Sg | h | Vl | ρm | Cn | ρn | θ | ql | qs | Qr | Pd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 104 m3/d | / | % | % | m | m3 | g/cm3 | % | m−1 | ° | m3/m | m3/m | m3/min | MPa/min | ||
| W1 | III | 107.8 | 1.79 | 6.0 | 64.9 | 307 | 65.9 | 1.85 | 2.4 | 0.72 | 25 | 8.80 | 0.38 | 3.6 | 0.22 |
| W2 | I | 201.0 | 1.80 | 7.9 | 68.1 | 285 | 221.1 | 1.91 | 4.2 | 0.79 | 25 | 6.78 | 0.29 | 4.2 | 0.33 |
| W3 | III | 67.8 | 1.79 | 6.2 | 65.0 | 100 | 8.5 | 1.90 | 63.5 | 0.68 | 30 | 14.58 | 0.31 | 3.3 | 0.18 |
| W4 | II | 128.0 | 1.76 | 6.1 | 68.7 | 103 | 104.3 | 1.92 | 5.4 | 0.51 | 10 | 13.29 | 0.68 | 4.1 | 0.20 |
| W5 | III | 12.8 | 1.74 | 6.3 | 66.2 | 46 | 0.0 | 0.00 | 1.8 | 0.05 | 25 | 7.70 | 0.34 | 3.3 | 0.47 |
| W6 | III | 192.6 | 1.70 | 7.3 | 66.4 | 114 | 18.0 | 1.88 | 3.1 | 0.41 | 30 | 11.54 | 0.68 | 4.5 | 0.29 |
| W7 | III | 189.1 | 1.71 | 7.4 | 67.0 | 128 | 14.9 | 1.88 | 5.2 | 0.59 | 25 | 14.84 | 0.88 | 4.1 | 0.32 |
| W8 | III | 232.0 | 1.79 | 4.1 | 69.5 | 91 | 9.7 | 1.88 | 19.5 | 0.79 | 30 | 20.35 | 1.17 | 3.7 | 0.48 |
| W9 | I | 200.6 | 1.49 | 7.2 | 67.1 | 82 | 148.0 | 1.78 | 25.1 | 0.85 | 30 | 19.96 | 1.28 | 5.0 | 0.56 |
| W10 | I | 201.4 | 1.79 | 7.3 | 68.3 | 115 | 117.4 | 1.90 | 7.8 | 0.35 | 25 | 15.03 | 1.11 | 3.9 | 0.34 |
| W11 | III | 69.3 | 1.78 | 6.6 | 64.2 | 119 | 0.0 | 1.88 | 11.5 | 0.52 | 12 | 13.15 | 0.43 | 2.9 | 0.78 |
| W12 | II | 66.8 | 1.24 | 7.3 | 68.6 | 43 | 85.6 | 1.72 | 2.4 | 2.70 | 20 | 31.81 | 1.70 | 4.4 | 0.49 |
| W13 | III | 52.3 | 1.34 | 6.0 | 67.1 | 84 | 298.0 | 1.63 | 4.5 | 0.53 | 50 | 6.93 | 0.34 | 5.2 | 0.50 |
| W14 | III | 271.9 | 1.96 | 6.9 | 61.9 | 13 | 0.0 | 1.97 | 10.9 | 0.64 | 30 | 36.99 | 2.14 | 4.8 | 0.24 |
| W15 | II | 165.4 | 1.96 | 8.1 | 71.7 | 40 | 18.4 | 2.03 | 8.4 | 0.70 | 30 | 36.99 | 1.25 | 4.7 | 0.40 |
| W16 | I | 202.9 | 1.88 | 7.0 | 67.8 | 92 | 117.2 | 2.00 | 7.2 | 0.50 | 15 | 7.68 | 0.50 | 4.1 | 0.50 |
| W17 | I | 198.1 | 1.56 | 6.2 | 64.2 | 75 | 178.7 | 1.54 | 38.8 | 0.66 | 68 | 22.73 | 0.93 | 4.8 | 0.29 |
| W18 | II | 182.5 | 1.52 | 6.0 | 64.0 | 87 | 74.2 | 1.61 | 10.1 | 0.88 | 40 | 22.33 | 1.12 | 5.2 | 0.25 |
| W19 | III | 81.1 | 1.73 | 6.5 | 61.2 | 132 | 0.0 | 1.85 | 1.9 | 0.40 | 43 | 6.08 | 0.25 | 3.5 | 0.38 |
| W20 | III | 47.9 | 1.67 | 4.7 | 55.0 | 97 | 7.2 | 1.80 | 4.5 | 0.14 | 25 | 9.66 | 0.39 | 3.7 | 0.39 |
| W21 | II | 330.0 | 1.71 | 6.8 | 64.9 | 77 | 38.2 | 1.84 | 7.9 | 0.25 | 45 | 5.86 | 0.33 | 4.0 | 0.6 |
| W22 | III | 126.8 | 1.58 | 7.2 | 64.8 | 103 | 10.9 | 2.20 | 26.5 | 0.16 | 25 | 12.55 | 0.79 | 4.5 | 0.54 |
| W23 | III | 22.6 | 1.56 | 5.2 | 64.7 | 56 | 2.9 | 2.20 | 5.2 | 0.07 | 20 | 20.04 | 1.22 | 4.0 | 0.41 |
| W24 | III | 66.9 | 1.95 | 7.5 | 64.6 | 17 | 0.0 | 1.97 | 3.3 | 1.51 | 15 | 45.71 | 3.14 | 5.4 | 0.18 |
| W25 | II | 181.9 | 1.82 | 6.3 | 65.5 | 21 | 78.9 | 1.85 | 9.2 | 0.65 | 25 | 34.41 | 2.19 | 4.3 | 0.33 |
| W26 | III | 88.3 | 1.58 | 7.1 | 65.5 | 239 | 1.2 | 1.68 | 5.2 | 0.51 | 25 | 4.12 | 0.15 | 3.8 | 0.42 |
| Well | L | Q | α | φ | Sg | h | Vl | ρm | ρn | θ | Stimulation Technique | ql | qs | Qr | Pd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| / | 104 m3/d | / | % | % | m | m3 | g/cm3 | m−1 | ° | / | m3/m | m3/m | m3/min | MPa/min | |
| W1 | III | 22.6 | 1.56 | 5.3 | 64.7 | 56 | 2.9 | 2.2 | 0.07 | 20 | Mechanical staged fracturing | 20.03 | 1.22 | 4.0 | 0.41 |
| W2 | III | 235.8 | 1.67 | 6.6 | 64.5 | 63 | 1.2 | 1.7 | 0.32 | 15 | Mechanical staged fracturing | 28.08 | 1.49 | 4.4 | 0.82 |
| Well | L | Q | α | φ | Sg | h | Vl | ρm | ρn | θ | Stimulation Technique | ql | qs | Qr | Pd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| / | 104 m3/d | / | % | % | m | m3 | g/cm3 | m−1 | ° | / | m3/m | m3/m | m3/min | MPa/min | |
| W3 | III | 67.8 | 1.79 | 6.4 | 65 | 100 | 8.5 | 1.9 | 0.68 | 45 | Mechanical staged fracturing | 11.57 | 0.51 | 4.3 | 0.18 |
| W4 | III | 192.6 | 1.71 | 7.2 | 66 | 114 | 18.0 | 1.9 | 0.41 | 30 | Mechanical staged fracturing | 14.53 | 0.65 | 4.5 | 0.30 |
| Well | L | Q | α | φ | Sg | h | Vl | ρm | ρn | θ | Stimulation Technique | ql | qs | Qr | Pd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| / | 104 m3/d | / | % | % | m | m3 | g/cm3 | m−1 | ° | / | m3/m | m3/m | m3/min | MPa/min | |
| W5 | III | 103.0 | 1.56 | 5.5 | 64.7 | 56 | 0 | 1.8 | 0.20 | 20 | Mechanical staged fracturing | 20.03 | 1.22 | 4.0 | 0.41 |
| W6 | III | 77.6 | 1.67 | 5.1 | 64.5 | 63 | 0 | 1.7 | 0.23 | 15 | Mechanical staged fracturing | 28.08 | 1.49 | 4.4 | 0.82 |
| Well | L | Q | α | φ | Sg | h | Vl | ρm | ρn | θ | Stimulation Technique | ql | qs | Qr | Pd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| / | 104 m3/d | / | % | % | m | m3 | g/cm3 | m−1 | ° | / | m3/m | m3/m | m3/min | MPa/min | |
| W7 | III | 330.0 | 1.71 | 6.8 | 64.9 | 77 | 38.2 | 1.8 | 0.25 | 45 | Pad acid + diversion fracturing | 5.85 | 0.33 | 4.0 | 0.60 |
| W8 | III | 52.3 | 1.34 | 6.0 | 67.1 | 84 | 298.0 | 1.6 | 0.53 | 50 | Pad acid + diversion fracturing | 6.94 | 0.34 | 5.2 | 0.51 |
| Well | L | Q | α | φ | Sg | h | Vl | ρm | ρn | θ | Stimulation Technique | ql | qs | Qr | Pd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| / | 104 m3/d | / | % | % | m | m3 | g/cm3 | m−1 | ° | / | m3/m | m3/m | m3/min | MPa/min | |
| W9 | III | 113.0 | 1.78 | 7.3 | 62.3 | 88 | 0.0 | 1.8 | 0.76 | 25 | Mechanical multi-stage composite stimulation | 23.50 | 0.96 | 4.2 | 0.59 |
| W10 | III | 67.8 | 1.79 | 6.2 | 65.0 | 100 | 8.5 | 1.9 | 0.70 | 30 | Mechanical multi-stage proppant fracturing | 21.73 | 0.87 | 3.9 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, F.; Zhou, J.; Peng, J.; Liu, J.; Deng, D.; Liu, Z.; Gou, B. Assessment of Reasons for Low Productivity in Ultra-Deep Fractured Tight Sandstone Reservoirs Using Data-Driven Analysis. Processes 2025, 13, 1793. https://doi.org/10.3390/pr13061793
Peng F, Zhou J, Peng J, Liu J, Deng D, Liu Z, Gou B. Assessment of Reasons for Low Productivity in Ultra-Deep Fractured Tight Sandstone Reservoirs Using Data-Driven Analysis. Processes. 2025; 13(6):1793. https://doi.org/10.3390/pr13061793
Chicago/Turabian StylePeng, Fen, Jianping Zhou, Jianxin Peng, Junyan Liu, Dehai Deng, Zihao Liu, and Bo Gou. 2025. "Assessment of Reasons for Low Productivity in Ultra-Deep Fractured Tight Sandstone Reservoirs Using Data-Driven Analysis" Processes 13, no. 6: 1793. https://doi.org/10.3390/pr13061793
APA StylePeng, F., Zhou, J., Peng, J., Liu, J., Deng, D., Liu, Z., & Gou, B. (2025). Assessment of Reasons for Low Productivity in Ultra-Deep Fractured Tight Sandstone Reservoirs Using Data-Driven Analysis. Processes, 13(6), 1793. https://doi.org/10.3390/pr13061793





