Integrating Stochastic Geological Modeling and Injection–Production Optimization in Aquifer Underground Gas Storage: A Case Study of the Qianjiang Basin
Abstract
1. Introduction
2. Methods and Results
2.1. Geomodelling Methods of Aquifer Reservoir
2.2. Establishment of Numerical Model
2.2.1. Establishment of Grid System
- (1)
- Principles for establishing grid system
- (2)
- Numerical simulation grid direction
- (3)
- Establishment of grid system
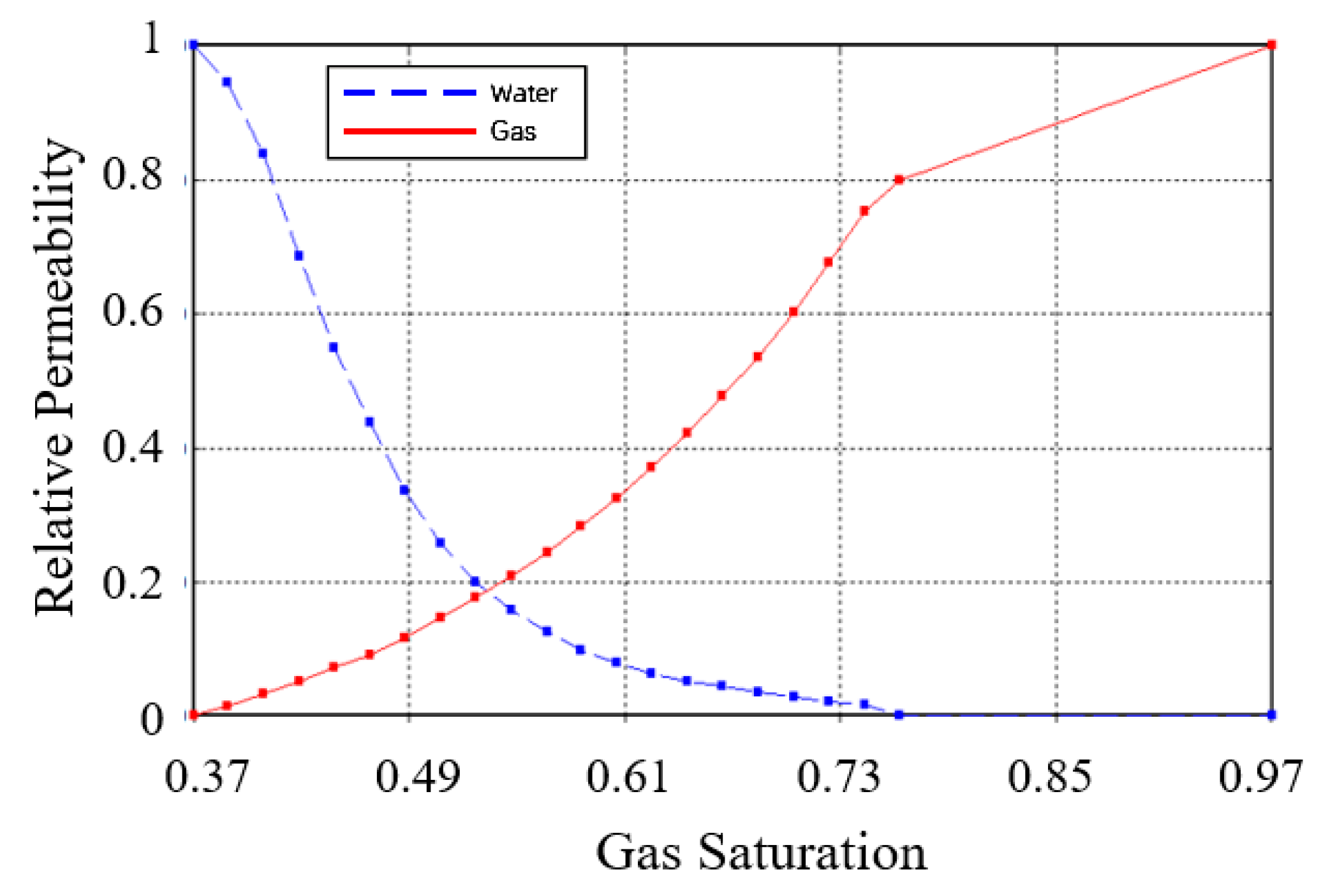
2.2.2. Gas–Water Relative Permeability in Pore Scale
2.2.3. Model Data Processing
- (1)
- Dynamic data processing
- (2)
- Collection and use of well history data
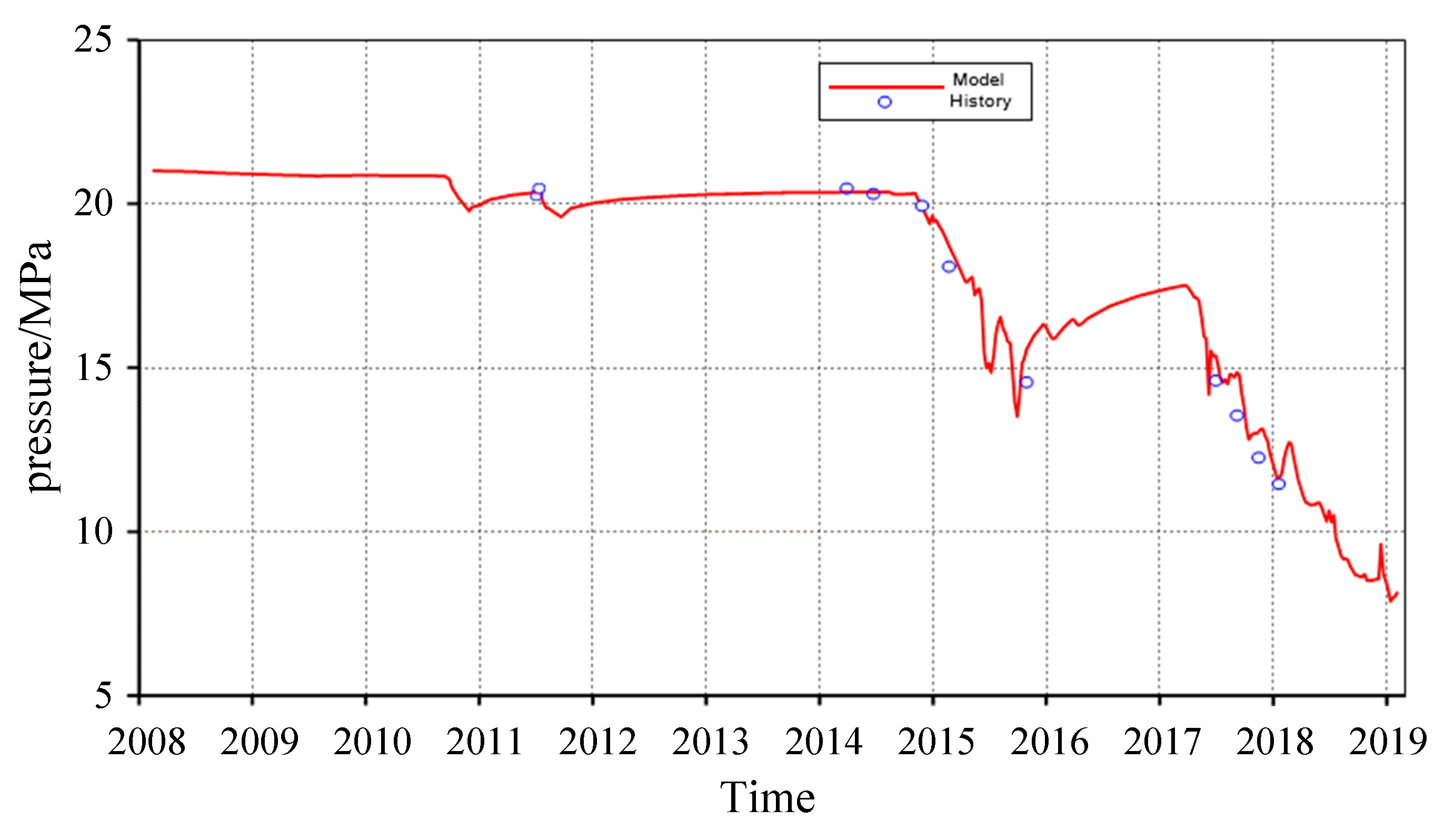
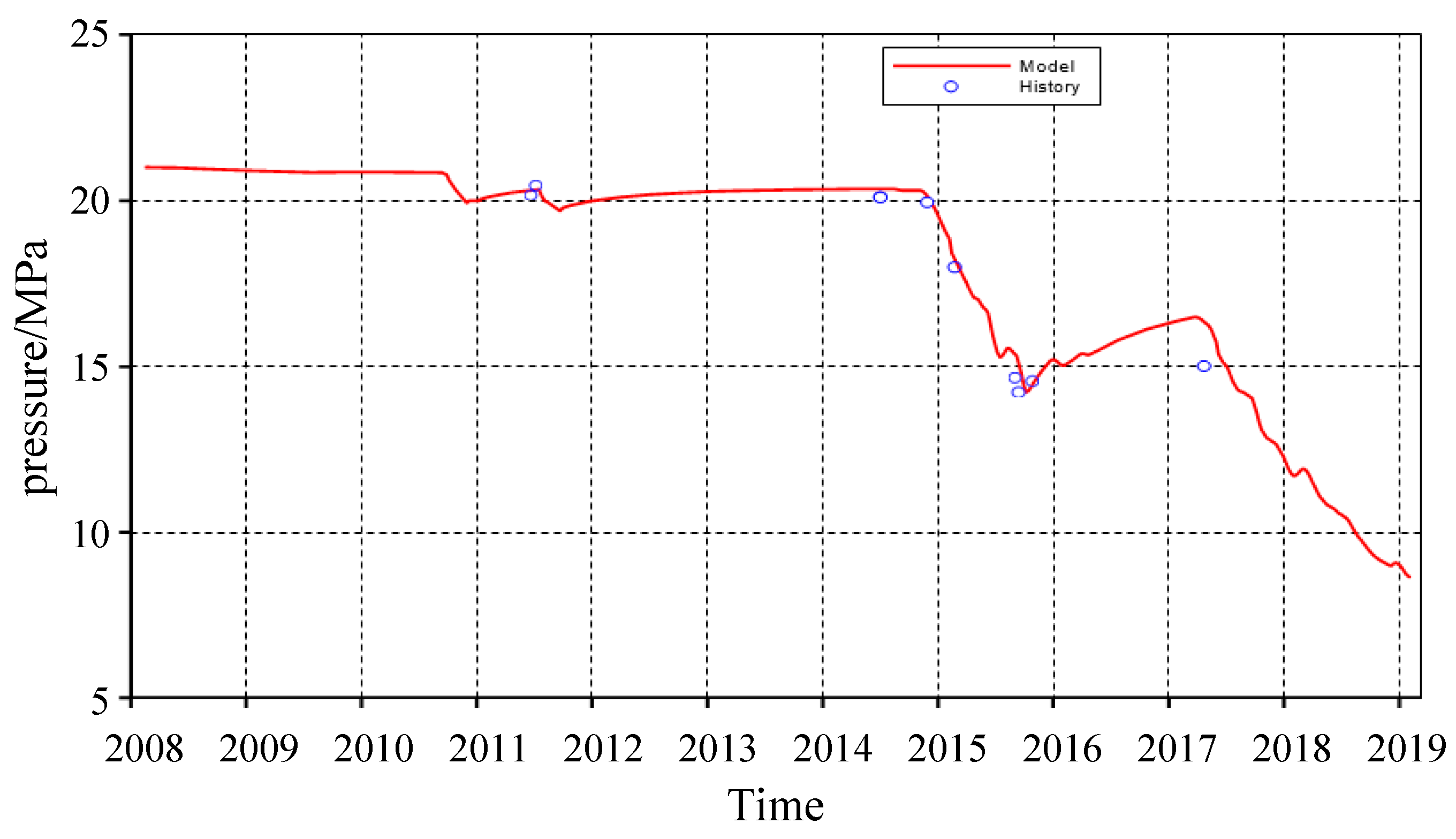
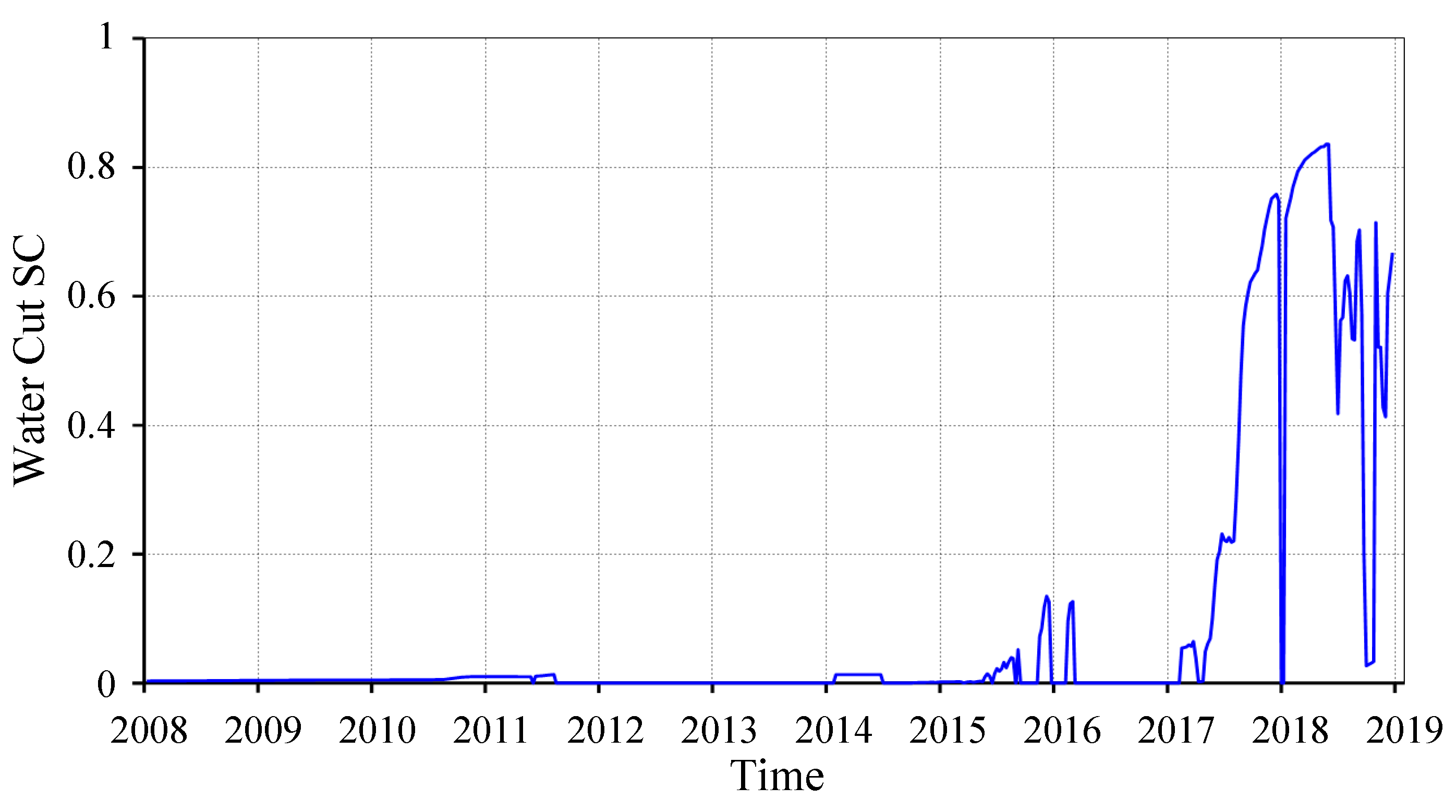
2.3. Production History Matching
2.3.1. Determine the Reservoir Production Working System
2.3.2. Region-Wide History Matching
2.3.3. Single-Well Index Fitting
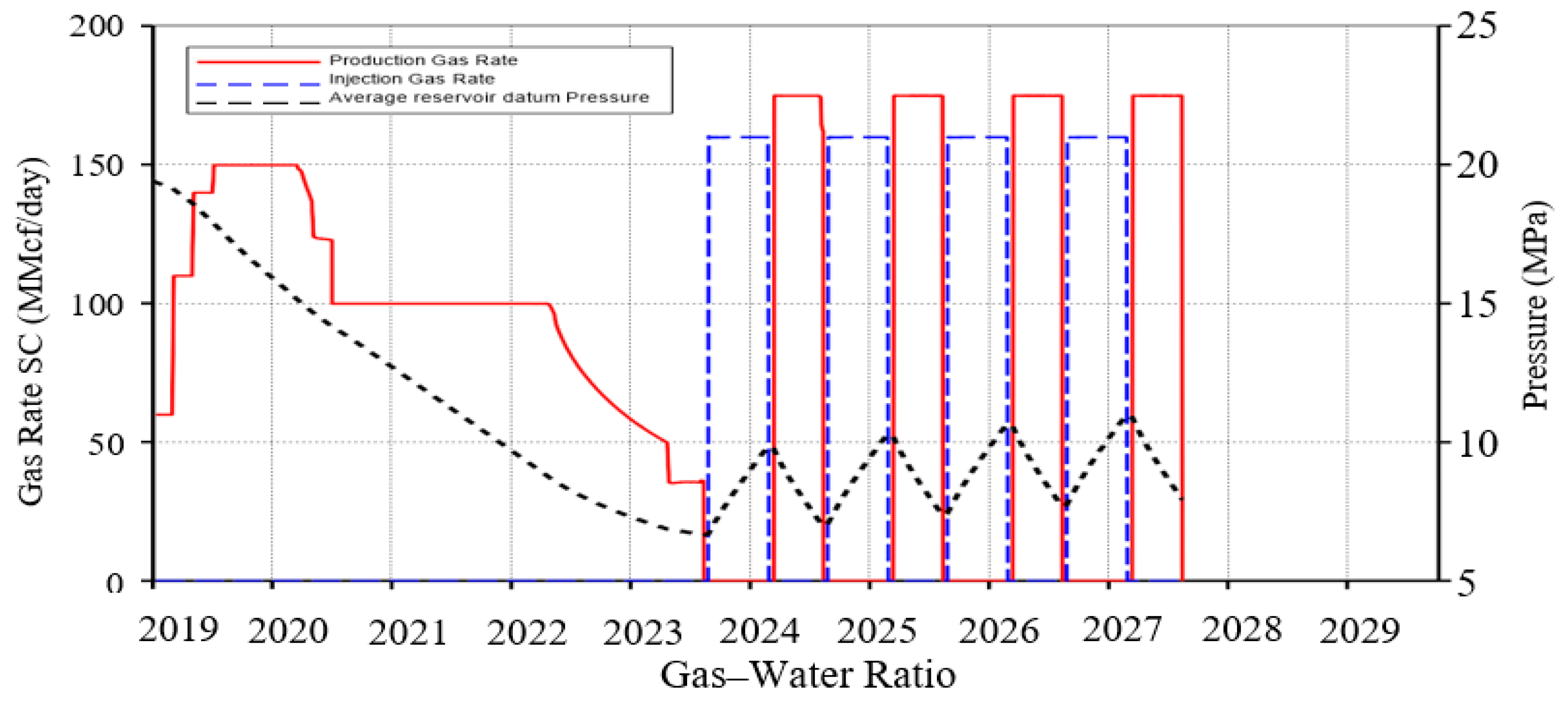
2.4. Injection and Production Cycles
2.5. Analysis of Cap Rock Safety and Reliability Engineering
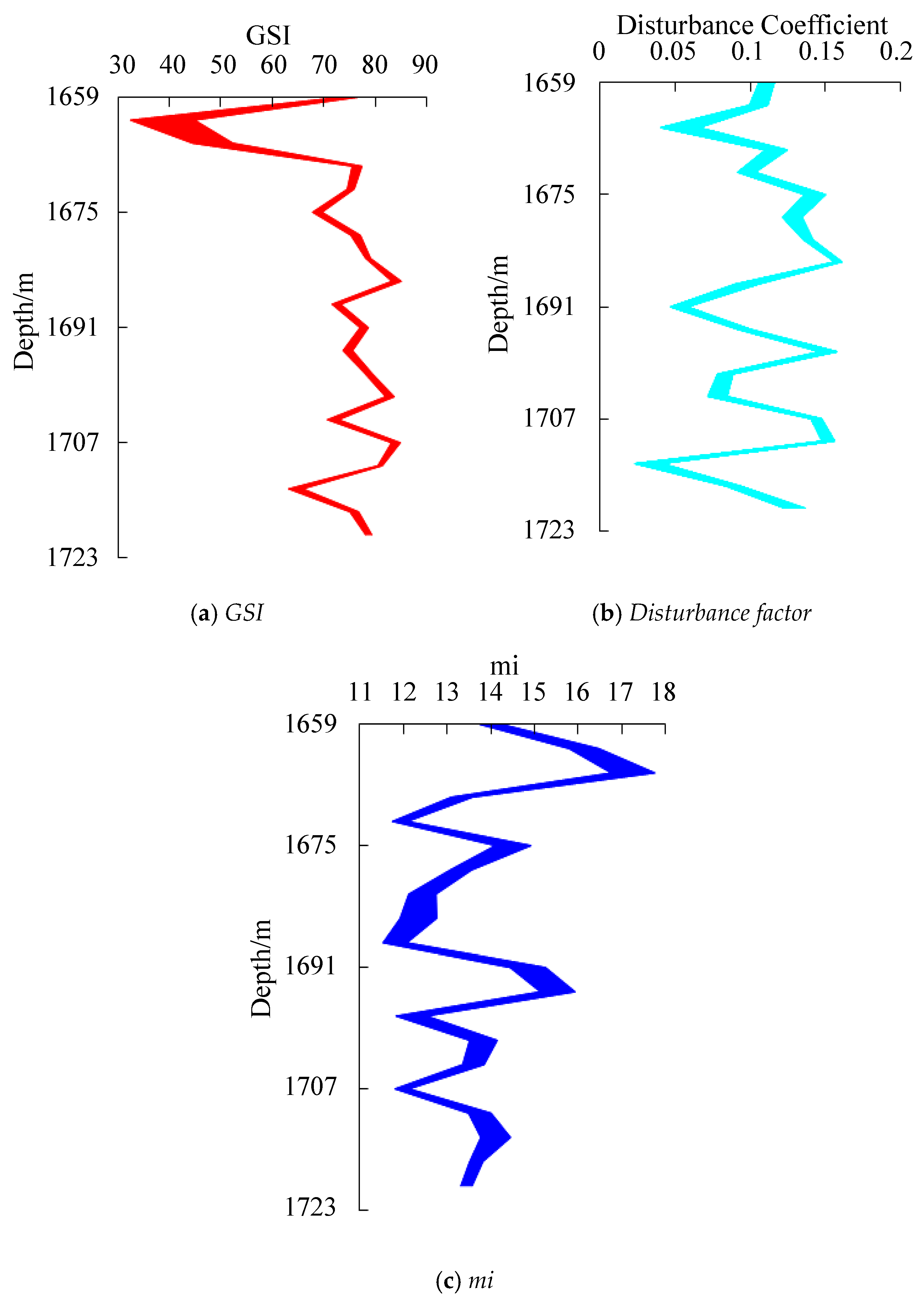
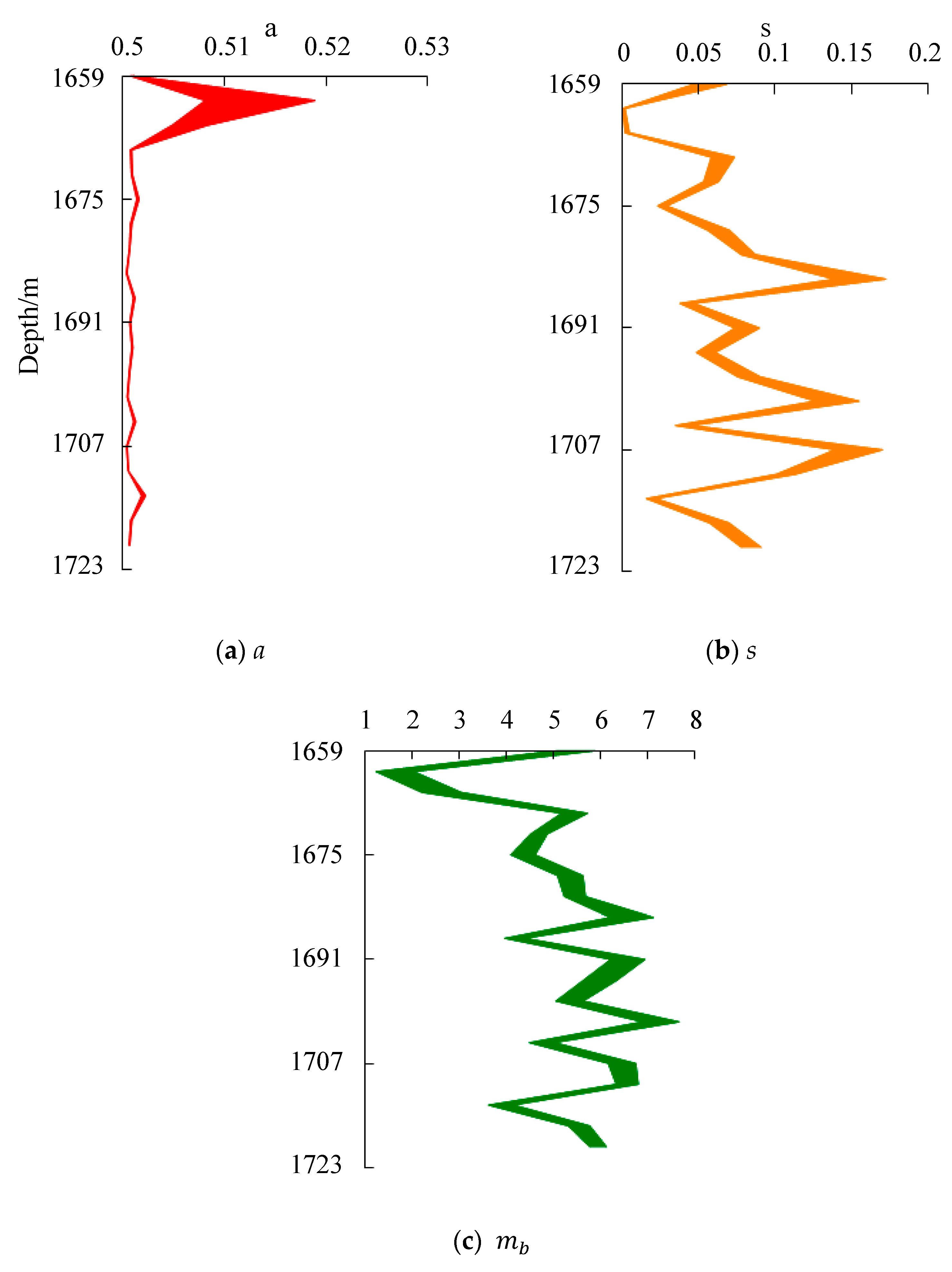
2.5.1. Determination of Confidence Interval of Formation Parameters
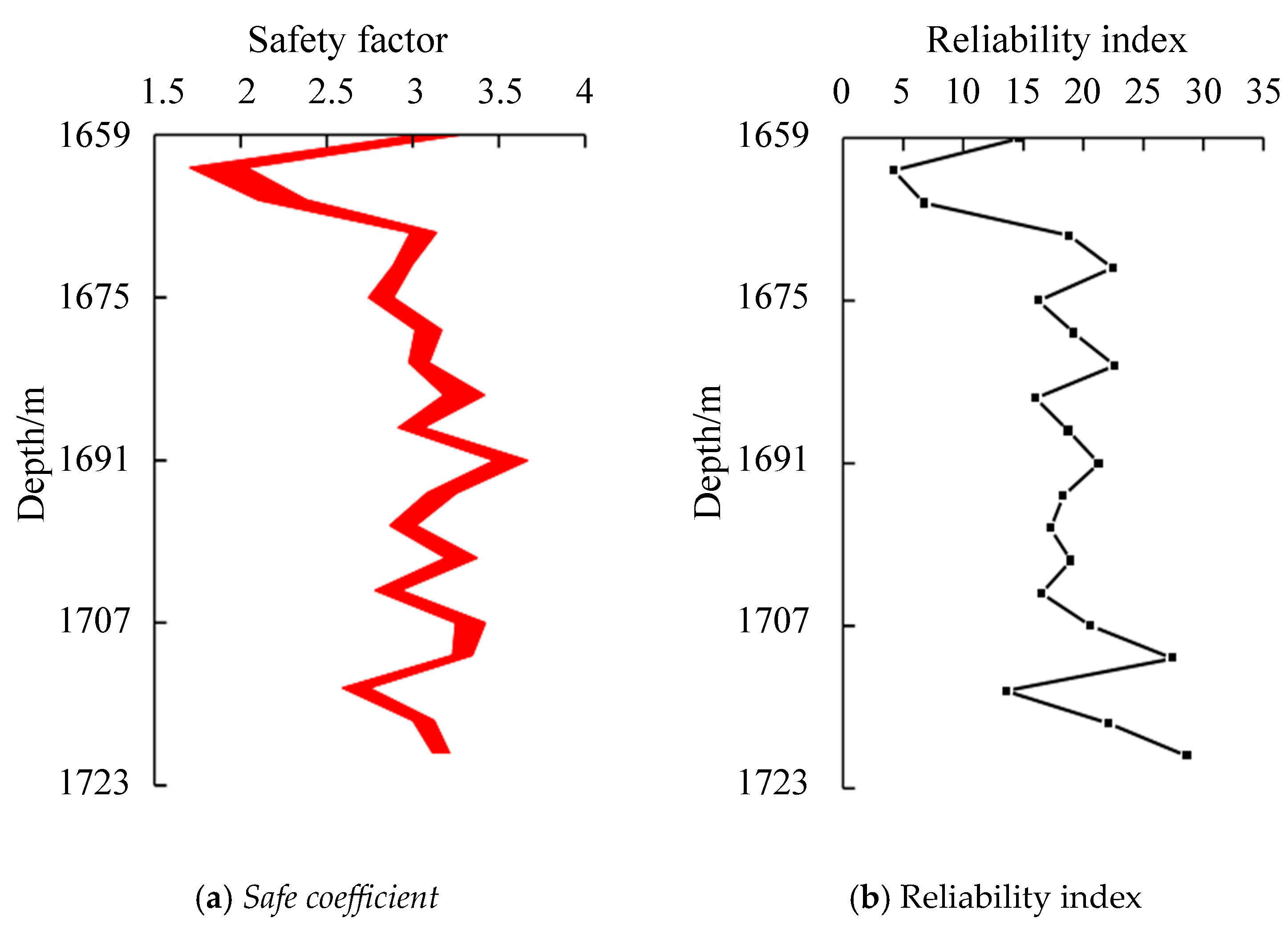
2.5.2. Analysis of Safety and Reliability of Capping Layer After Gas Injection
2.5.3. Example Analysis
2.6. Analysis of Maximum Operating Pressure of Gas Storage
2.6.1. Uncertainty Analysis of Rock Mass Parameters
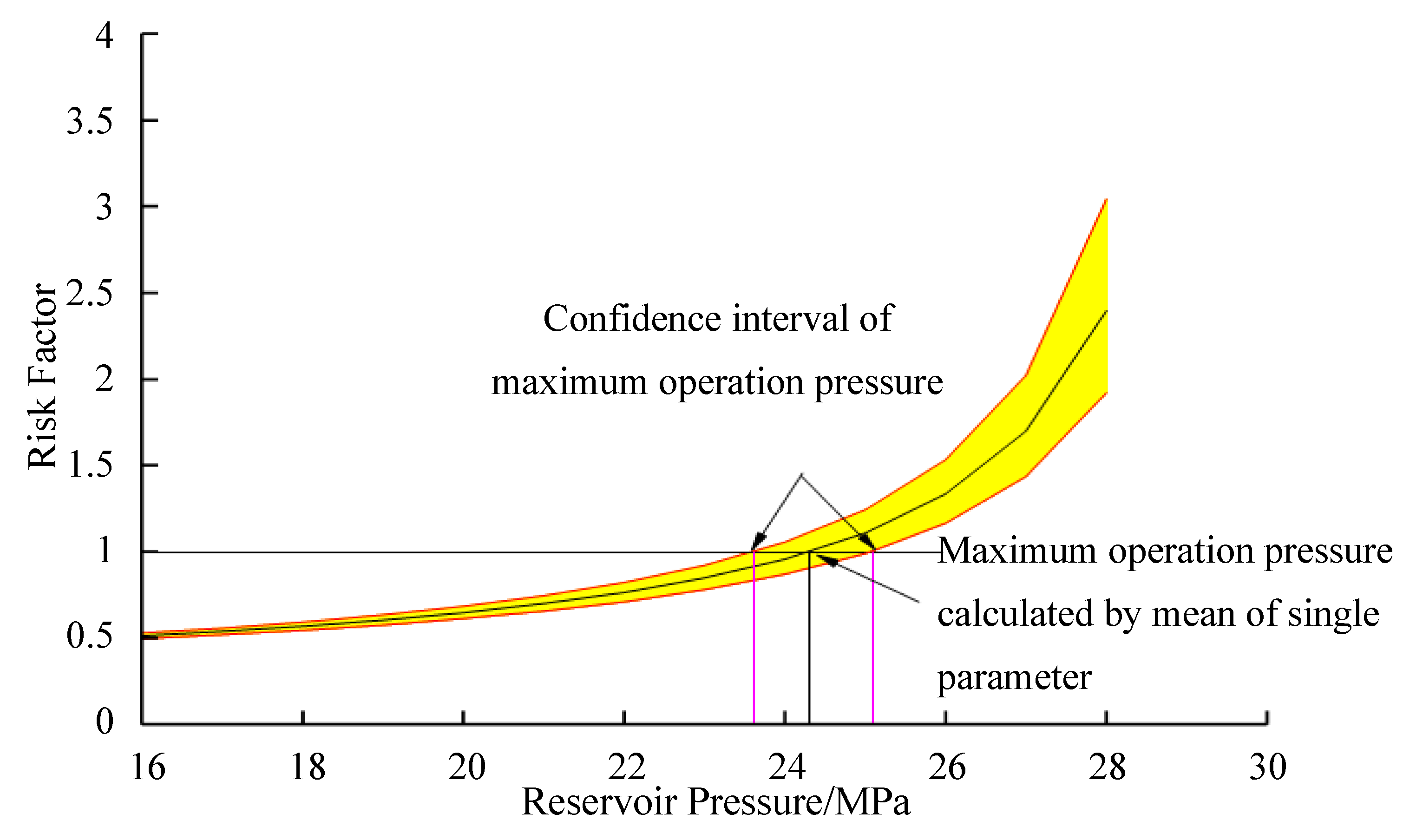
2.6.2. Determination of Maximum Operating Pressure
3. Conclusions
- (1)
- Modeling of Aquifer Type Trap and Seepage Mechanism
- (2)
- Prediction of Maximum Operating Pressure of Aquifer Gas Storage Reservoirs
- (3)
- Non-Probabilistic Reliability Analysis of Aquifer Reservoir Cover and Faults
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Chen, X.X.; Yang, Q.Y. The Fundamentality of Construction Underground Gas Storage to Solve the Imbalance of Gas Consumption. Oil Gas Storage Transp. 2013, 22, 7–10. [Google Scholar] [CrossRef]
- Wang, Y. Application and Development of Natural Gas Underground Storage Facilities. Pet. Storage Gas Stn. 2008, 4, 23–26. [Google Scholar]
- He, C.; Xia, H.N.; Xia, W. The Current Situation of China’s Underground Gas Storage. Equip. Manuf. Technol. 2013, 8, 246–247. [Google Scholar]
- Ding, G.S.; Xie, P. Current Situation and Prospect of Chinese Underground Natural Gas Storage. Nat. Gas. Ind. 2006, 6, 111–113. [Google Scholar]
- Tarkowski, R.; Uliasz-Misiak, B.; Tarkowski, P. Storage of hydrogen, natural gas, and carbon dioxide—Geological and legal conditions. Int. J. Hydrogen Energy 2021, 46, 20010–20022. [Google Scholar] [CrossRef]
- Fan, Z.W. Global natural gas development pattern and the analysis of development direction of natural gas in China. China Min. 2018, 27, 11–16. [Google Scholar]
- Zhang, G.X.; Li, B.; Zheng, D.W. Challenges to and proposals for underground gas storage (UGS) business in China. Nat. Gas Ind. 2017, 37, 153–159. [Google Scholar] [CrossRef]
- Tan, Y.F.; Lian, L.M.; Yan, M.Q. The Technology and Development of Foreign Underground Natural Gas Storage. Oil Gas Storage Transp. 1997, 16, 17–19. [Google Scholar]
- Zhan, C.H.; Jiao, W.L.; Lian, L.M. Underground Gas Storage Reservoir Constructed in Water-Beating Formation. Nat. Gas Ind. 2001, 21, 88–91. [Google Scholar]
- Ding, G.S. Developing trend and motives for global underground gas storage. Nat. Gas Ind. 2010, 30, 59–61. [Google Scholar] [CrossRef]
- Wei, H.; Tian, J.; Li, J.Z. The current situation and development trend of underground natural gas storage facilities in China. Int. Pet. Econ. 2015, 23, 57–62. [Google Scholar]
- Zhang, F.Q.; Zeng, P.; Zhou, L.J. Underground Gas Storage Research Status Quo and Application Expectations at Home and Abroad. China Coal Geol. 2021, 33, 39–42+52. [Google Scholar] [CrossRef]
- Liu, H.Y. Opportunities and challenges of underground natural gas storage based on carbon peak and carbon neutrality goals. Pet. Nat. Gas Chem. Ind. 2022, 51, 70–76. [Google Scholar] [CrossRef]
- Zeng, D.Q.; Zhang, J.F.; Zhang, G.Q. Research progress of Sinopec’s key underground gas storage construction technologies. Nat. Gas Ind. 2020, 40, 115–123. [Google Scholar]
- Xu, J.J.; Wang, Q.J.; Xu, M. Dynamic characteristics of underground gas storage rebuilt from carbonate gas reservoir with bottom water and the water flooding mechanism of its well. Oil Gas Storage Transp. 2019, 38, 5227. [Google Scholar] [CrossRef]
- Wang, Y.F. The Development Prospects of Aquifer Gas Storage Construction in China. Pet. Knowl. 2023, 3, 38–39. [Google Scholar]
- Li, J.C.; Shen, R.C.; Yuan, G.J.; Qu, P.; Gao, Y.B. Research of Relative Construction Technology about Aquifer Gas Storage. Oil Gas Storage Transp. 2009, 28, 9–12. [Google Scholar] [CrossRef]
- Yekta, A.E.; Manceau, J.C.; Gaboreau, S.; Pichavant, M.; Audigane, P. Determination of hydrogen–water relative permeability and capillary pressure in sandstone: Application to underground hydrogen injection in sedimentary formations. Porous Media 2018, 122, 333–356. [Google Scholar] [CrossRef]
- Basso, O.; Lascourreges, J.F.; Le, B.F. Characterization by culture and molecular analysis of the microbial diversity of a deep subsurface gas storage aquifer. Res. Microbiol. 2017, 160, 107–116. [Google Scholar] [CrossRef]
- Rutqvist, J.; Birkholzer, J.; Cappa, F. Estimating maximum sustainable injection pressure during geological sequestration of CO2 using coupled fluid flow and geomechanical fault-slip analysis. Energy Convers. Manag. 2019, 48, 1798–1807. [Google Scholar] [CrossRef]
- Xu, H.C.; Zhang, S.J.; Li, X. A new design method of minimum storage pressure of underground gas storage rebuilt from gas reservoir. Nat. Gas Geosci. 2020, 31, 1648–1653. [Google Scholar]
- Zheng, Y.L.; Sun, J.C.; Qiu, X.S. Connotation and evaluation technique of geological integrity of UGSs in oil-gas fields. Nat. Gas Ind. 2020, 40, 4103. [Google Scholar] [CrossRef]
- Ding, G.S.; Wei, H. Review on 20 years’ UGS construction in China and the prospect. Oil Gas Storage Transp. 2020, 39, 2531. [Google Scholar] [CrossRef]
- Wang, T.T. Research on the Deformation Rules and Safety of Surrounding Rock of Gas Storage in Multi-Layered Salt Rock Mass; China University of Petroleum: Beijing, China, 2016. [Google Scholar]
- Ding, G.S.; Li, X.B.; Jiang, F.G. Discussion on Emergency Gas Supply and Peak Shaving of the Second West to East Gas Pipeline. Nat. Gas Ind. 2008, 12, 92–94. [Google Scholar]
- Yu, B.F.; Yan, X.Z.; Yang, H.L. Non-probabilistic reliability analysis of dead fault slip in underground gas storage based on convex model. J. Pet. Sin. 2014, 35, 577–583. [Google Scholar]
- Zhao, G.F. Engineering Structure Reliability Theory and Application; Dalian University of Technology Press: Dalian, China, 1996. [Google Scholar]
- You, L.J.; Sha, J.X.; Gao, X.P. Simulation Tests of Effective Stress Changes in Gas Storage during Injection and Production. Pet. Drill. Tech. 2020, 48, 1048. [Google Scholar]
- Wang, C.H.; Gao, G.Y.; Jia, J. Variation of stress field and fault slip tendency induced by injection and production in the H underground gas storage. Nat. Gas Ind. 2020, 40, 7685. [Google Scholar] [CrossRef]
- Federico, G. The Spanish Gas and Electricity Sector: Regulation, Markets and Environmental Policies; IESE Business School, Universidad de Navarra: Barcelona, Spain, 2018. [Google Scholar] [CrossRef]
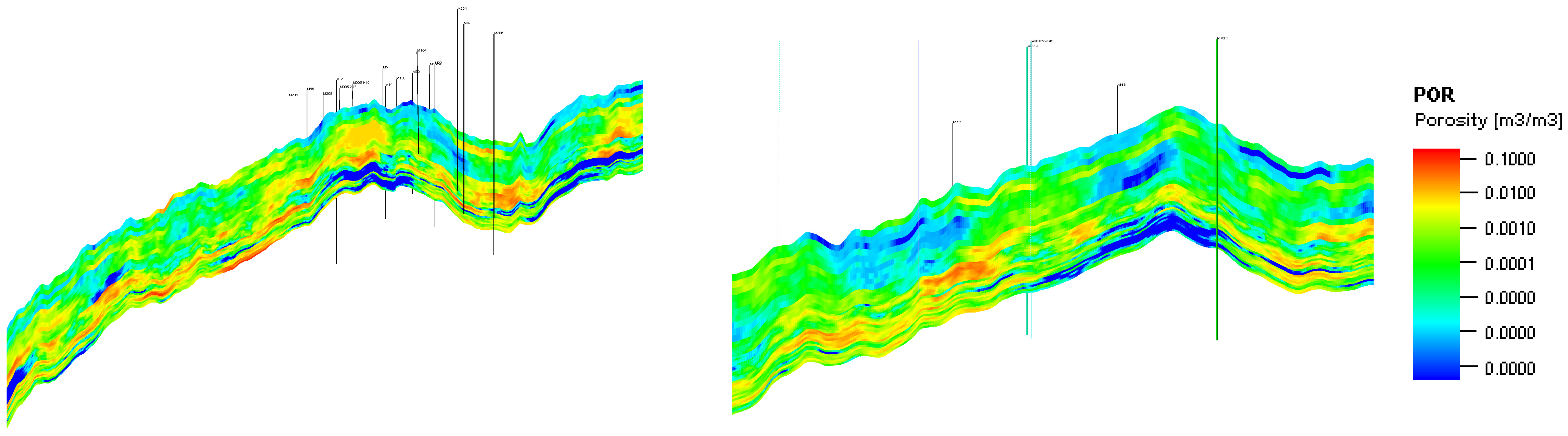

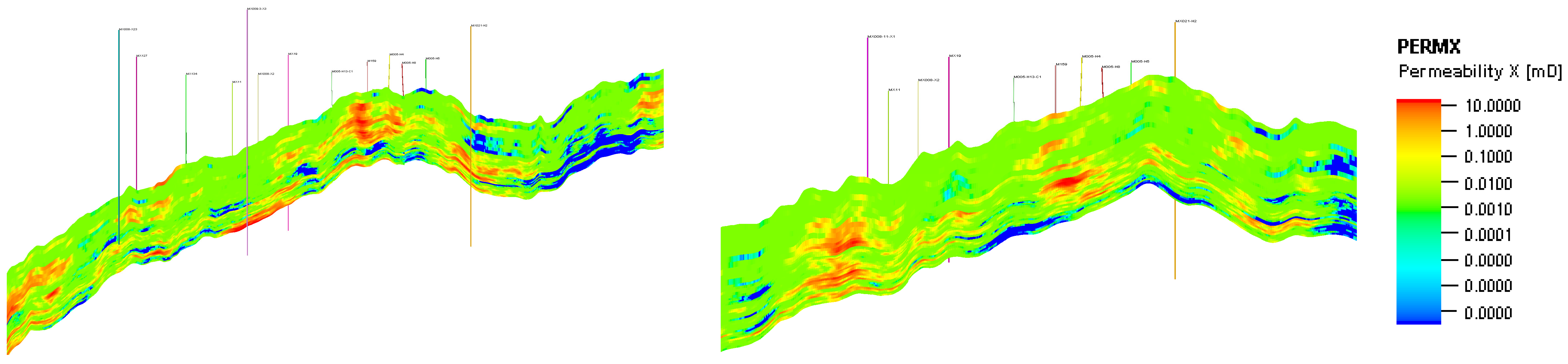
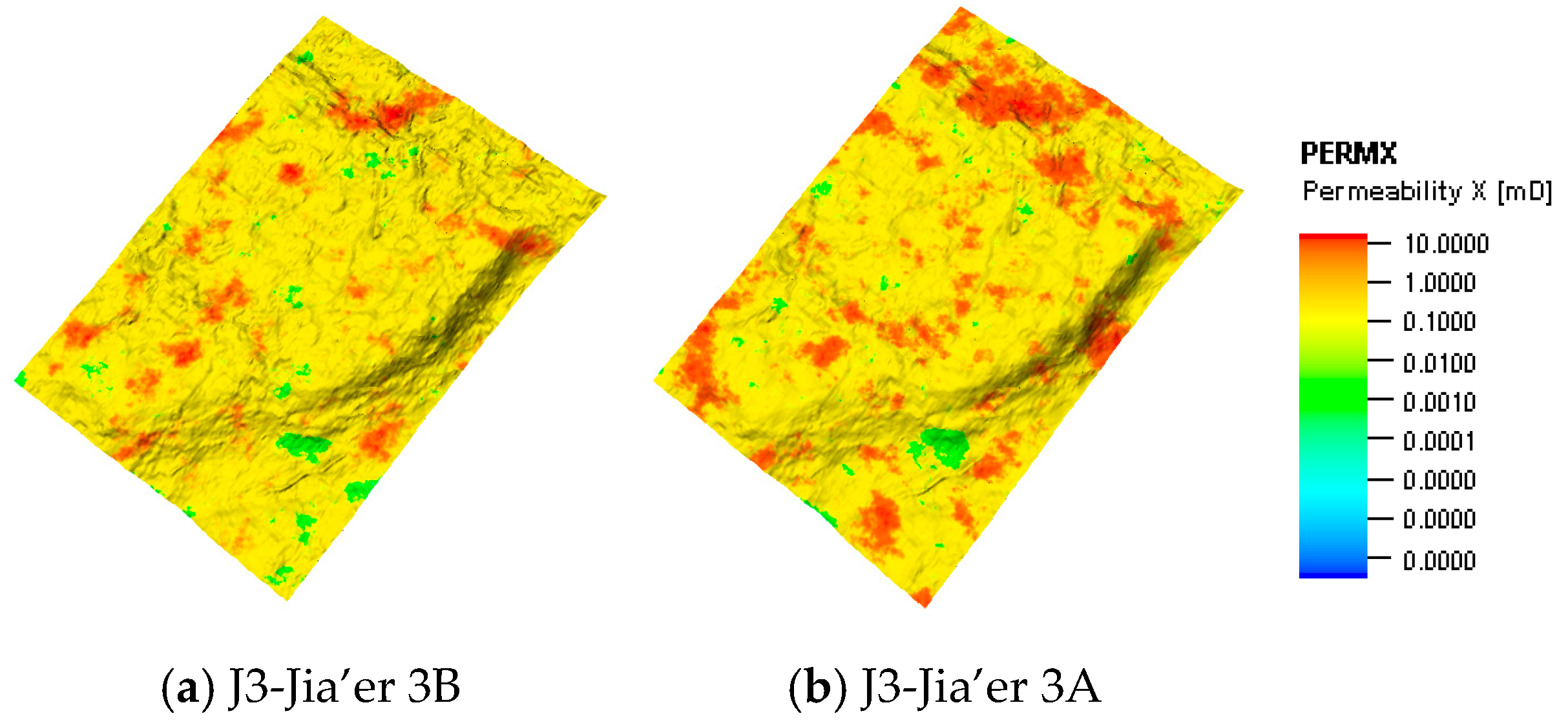


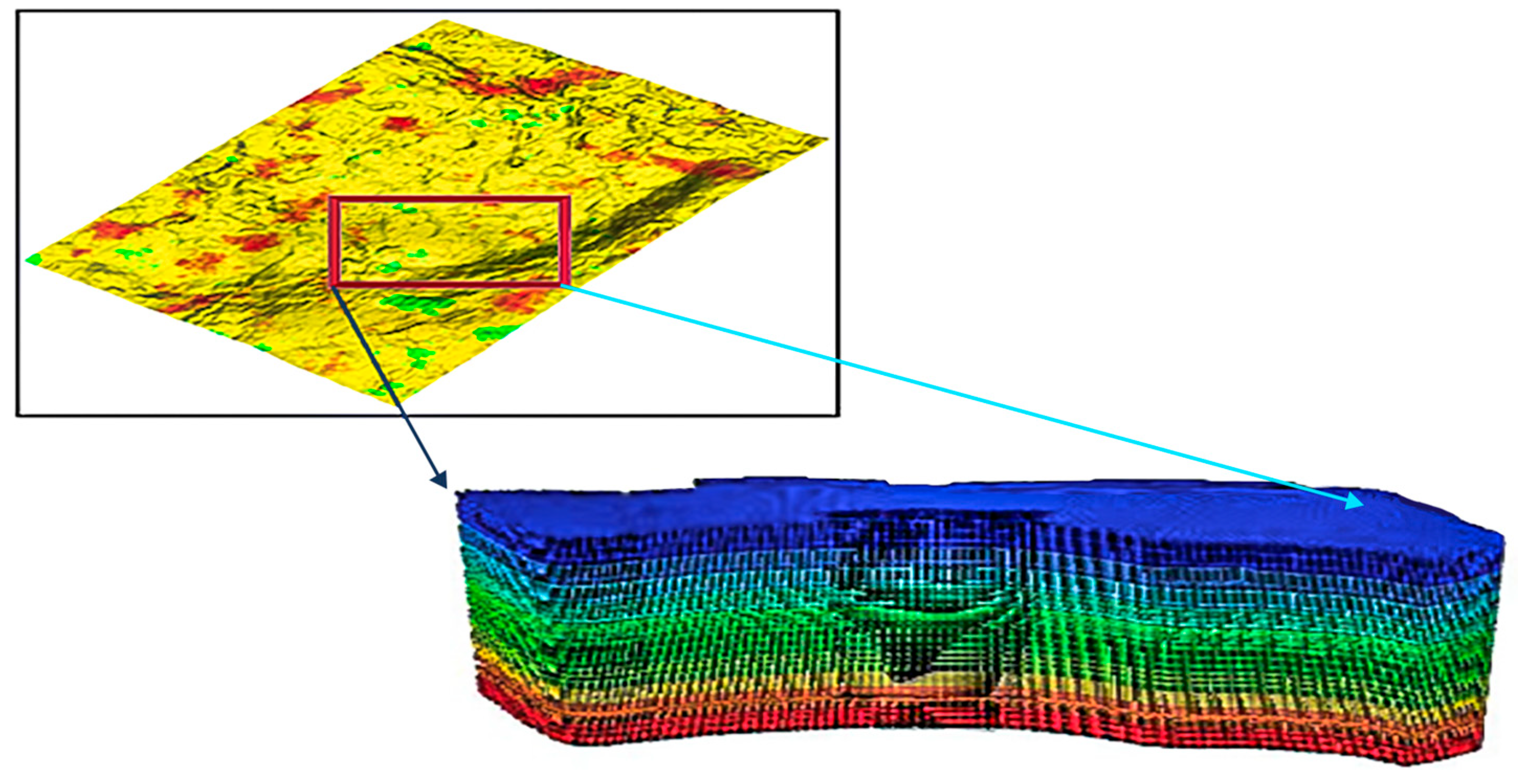










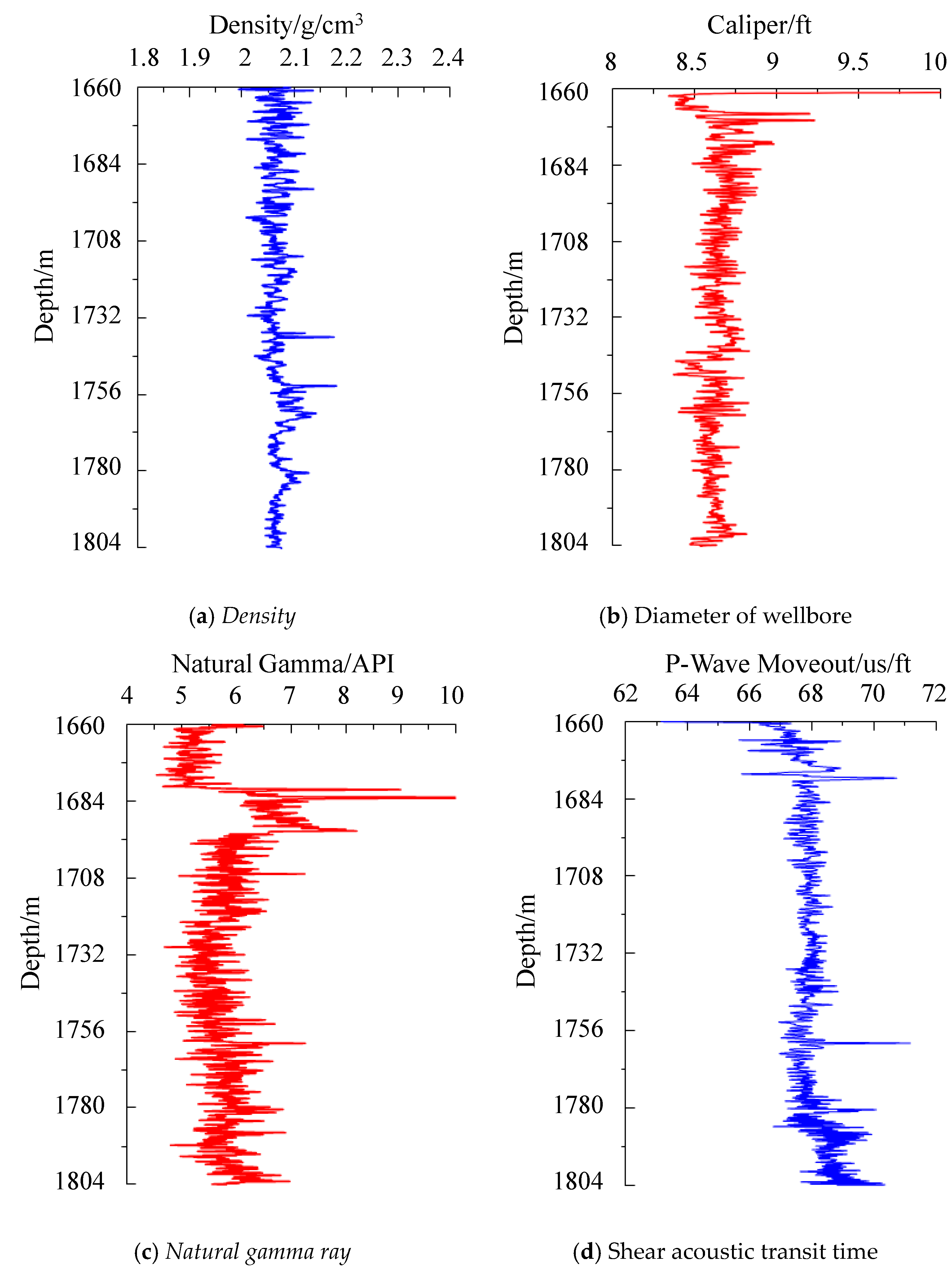
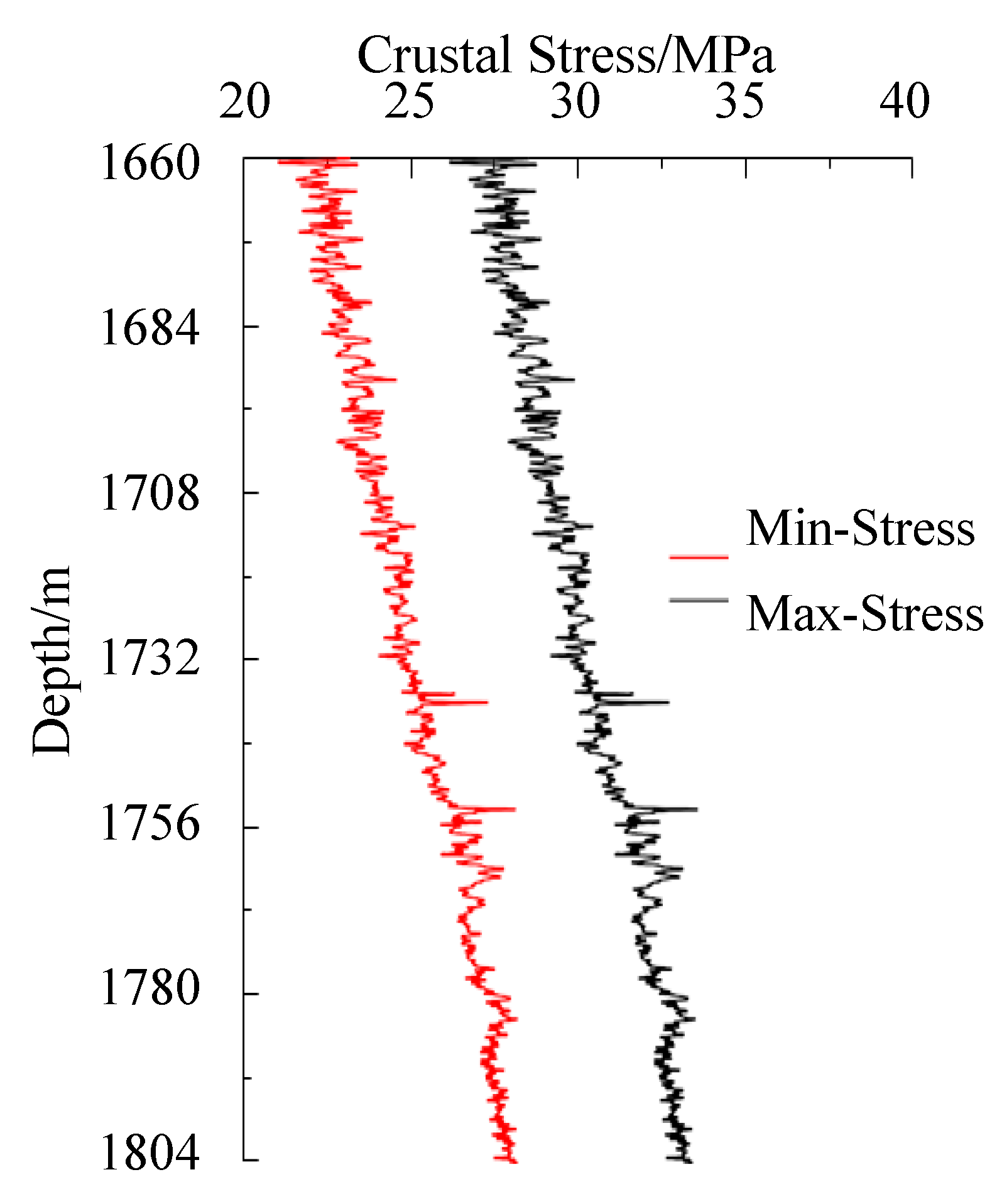
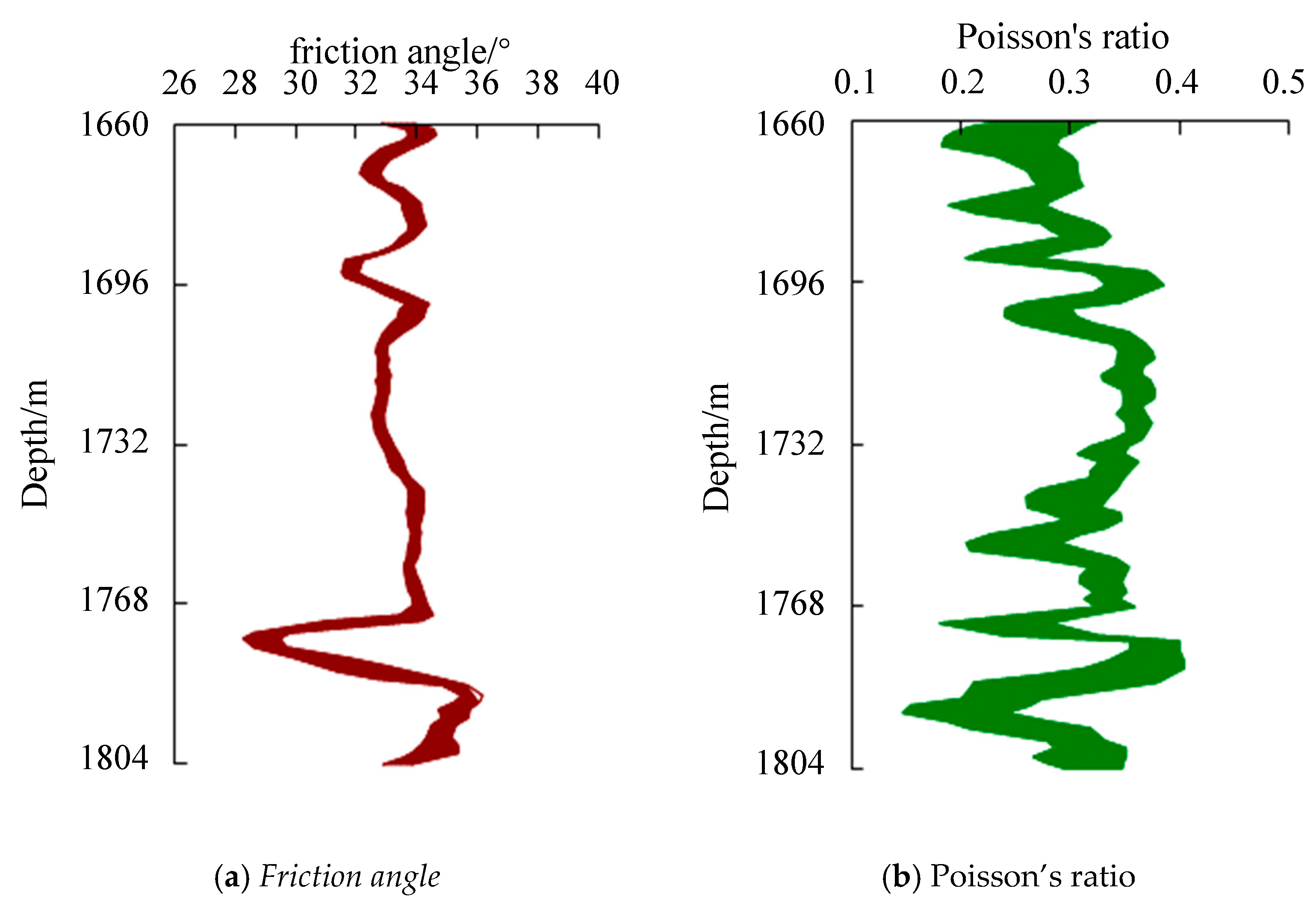
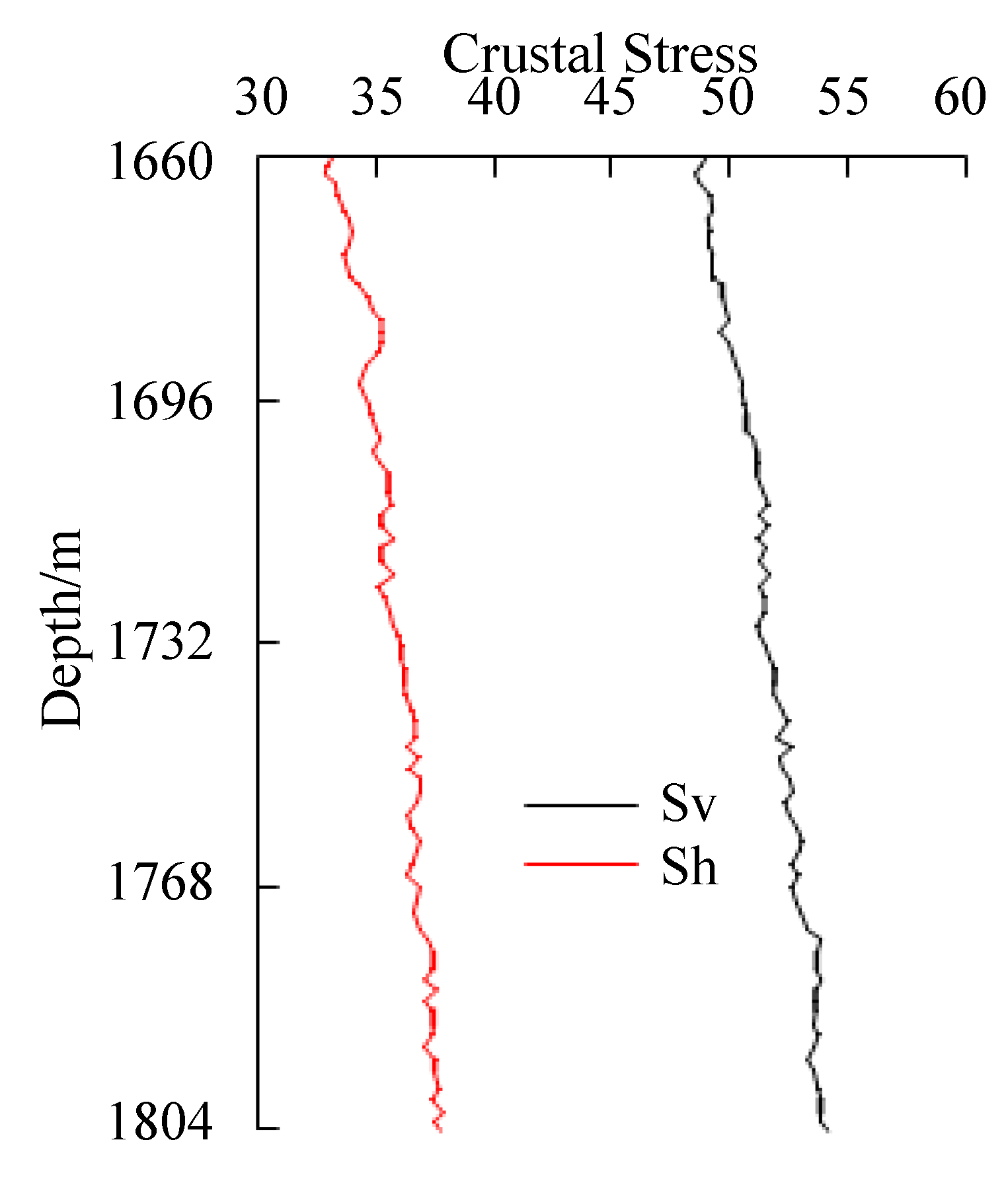

| Layer Number | Analog Layer Number | Oil Layer Thickness (m) | Porosity | Permeability (×103 μm2) |
|---|---|---|---|---|
| qn1-1 | 1 | 11.94 | 0.14 | 4.12 |
| qn1-2 | 2 | 3.96 | 0.12 | 3.52 |
| qn1-3 | 3 | 5.78 | 0.15 | 3.97 |
| qn1-4 | 4 | 6.03 | 0.11 | 1.43 |
| qn1-5 | 5 | 4.71 | 0.1 | 0.99 |
| qn1-6 | 6 | 4.73 | 0.13 | 4.87 |
| qn1-7-1 | 7 | 0.65 | 0.13 | 4.78 |
| qn1-7-n1 | 8 | 1.45 | 0 | 0 |
| qn1-7-2 | 9 | 5.78 | 0.1 | 1.25 |
| qn1-8 | 10 | 7.11 | 0.11 | 1.55 |
| qn1-9 | 11 | 7.86 | 0.12 | 2.93 |
| qn1-10 | 12 | 5.05 | 0.11 | 4.37 |
| qn1-11 | 13 | 5.54 | 0.11 | 2.64 |
| qn1-12-1 | 14 | 4.82 | 0.11 | 7.63 |
| qn1-12-n1 | 15 | 1.45 | 0 | 0 |
| qn1-12-2 | 16 | 3.06 | 0.13 | 6.67 |
| qn1-12-n2 | 17 | 1.44 | 0 | 0 |
| qn1-12-3 | 18 | 5.21 | 0.12 | 1.71 |
| qn1-13 | 19 | 3.82 | 0.11 | 1.52 |
| qn1-14-1 | 20 | 7.86 | 0.11 | 1.95 |
| qn1-14-n1 | 21 | 1.43 | 0 | 0 |
| qn1-14-2 | 22 | 4.91 | 0.11 | 2.82 |
| qn1-15 | 23 | 5.12 | 0.11 | 1.64 |
| qn1-16 | 24 | 5.78 | 0.13 | 2.52 |
| q4-1 | 25 | 3.53 | 0.11 | 2.16 |
| q4-2 | 26 | 3.63 | 0.11 | 2.24 |
| q4-3 | 27 | 2.91 | 0.11 | 2.43 |
| q4-4 | 28 | 5.62 | 0.13 | 2.26 |
| q4-5 | 29 | 6.33 | 0.11 | 2.18 |
| q4-6 | 30 | 7.98 | 0.12 | 2.39 |
| q4-7 | 31 | 4.05 | 0.13 | 2.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Sun, Z.; Chen, W.; Yu, B.; Liu, J.; Ren, Z.; Wang, Y.; Guo, C.; Wu, R.; Jiang, Y. Integrating Stochastic Geological Modeling and Injection–Production Optimization in Aquifer Underground Gas Storage: A Case Study of the Qianjiang Basin. Processes 2025, 13, 1728. https://doi.org/10.3390/pr13061728
Xu Y, Sun Z, Chen W, Yu B, Liu J, Ren Z, Wang Y, Guo C, Wu R, Jiang Y. Integrating Stochastic Geological Modeling and Injection–Production Optimization in Aquifer Underground Gas Storage: A Case Study of the Qianjiang Basin. Processes. 2025; 13(6):1728. https://doi.org/10.3390/pr13061728
Chicago/Turabian StyleXu, Yifan, Zhixue Sun, Wei Chen, Beibei Yu, Jiqin Liu, Zhongxin Ren, Yueying Wang, Chenyao Guo, Ruidong Wu, and Yufeng Jiang. 2025. "Integrating Stochastic Geological Modeling and Injection–Production Optimization in Aquifer Underground Gas Storage: A Case Study of the Qianjiang Basin" Processes 13, no. 6: 1728. https://doi.org/10.3390/pr13061728
APA StyleXu, Y., Sun, Z., Chen, W., Yu, B., Liu, J., Ren, Z., Wang, Y., Guo, C., Wu, R., & Jiang, Y. (2025). Integrating Stochastic Geological Modeling and Injection–Production Optimization in Aquifer Underground Gas Storage: A Case Study of the Qianjiang Basin. Processes, 13(6), 1728. https://doi.org/10.3390/pr13061728







