Evolutionary Process of Worker Behavior Risk in Nuclear Power Plants Under Construction Based on Multi-Source Fusion Algorithm: A Case Study of BN–Game–SD

Abstract

Nuclear power plants (NPPs) under construction are required to meet the stringent safety standards of operational facilities while also facing the heightened risk characteristics of construction projects. The combination of dense worker populations and generally low safety awareness presents serious challenges for ensuring construction safety. To address this, the present study proposes a BN–Game–SD multi-algorithm fusion model that systematically examines the evolution of behavioral risks from both group and individual perspectives. First, a behavioral indicator system was constructed using Bayesian Networks (BNs) to identify key risk factors. Then, a dynamic payoff matrix game model was introduced to analyze the incentive mechanisms between individuals and groups. Finally, a BN–Game–SD model was developed to capture the dynamic evolution of worker behaviors in NPP construction. Simulation results reveal that, under fixed probabilities of safety strategy selection, clear thresholds exist in group resistance to individual behavioral deviation and vice versa. Applied to a real NPP construction site, the model helped achieve a 10.39% reduction in safety violations. This study provides a theoretical foundation for promoting self-organized safety behavior evolution in nuclear enterprises and presents an innovative methodological framework for safety management in nuclear engineering.

1. Introduction

Nuclear power plants (NPPs) under construction face stringent safety requirements and complex risks due to multidisciplinary processes and dense workforces, making safety management a critical concern.

1.1. Research Status of Safety Management in Nuclear Power Plants Under Construction

Some scholars have introduced an evaluation method for nuclear safety culture based on Schein’s three-level organizational culture model, which analyzes artifacts, espoused values, and underlying assumptions. The approach places particular emphasis on understanding deep-seated cultural assumptions that influence safety behavior [1]. Other researchers have identified six key categories for evaluating control rooms in nuclear power plants: system performance, task performance, teamwork, resource utilization, user experience, and design discrepancies. These categories offer a structured framework for improving human factors in control room environments [2]. To enhance the usability of safety cases in practical operations, some scholars have integrated bowtie risk management techniques into their development process. By conducting participatory workshops with frontline personnel and visually mapping accident scenarios and safety barriers, the resulting safety cases became more aligned with real-world operational contexts [3]. In another study, scholars applied systemic thinking in the Finnish nuclear sector and proposed a comprehensive safety framework that integrates systemic methodologies, socio-technical models, and resilient safety principles, thereby offering both theoretical depth and practical guidance [4]. The Delphi method and expert judgment were also employed to revise and quantify safety resilience indicators, with relative importance evaluated via the analytic hierarchy process (AHP) [5].

Artificial intelligence has also been increasingly applied in NPP safety modeling. For example, feedforward artificial neural networks (ANNs) have been used to simulate the coupled dynamics between pressurized water reactor cores and their primary and secondary cooling systems [6]. A recent review highlighted limitations in deep learning applications, such as interpretability and uncertainty, and introduced tools like SHAP and LIME to enhance transparency [7]. In handling high-dimensional data from numerous monitoring variables, CNN-based models have been proposed to support real-time fault diagnosis in nuclear systems [8]. Other researchers developed an open set recognition (OSR) framework using convolutional prototype learning (CPL) to detect faults in simulated NPP data with high accuracy and feature visualization [9]. Additionally, a study employed timed Petri nets and Markov chains to assess the performance of digital safety-critical systems, validated on a shutdown system case [10].

Some investigations have focused on localized safety scenarios. For example, in assessing hydrogen combustion risks, the MAAP code was employed to estimate hydrogen parameters during small-break loss-of-coolant accidents (LOCAs), followed by GASFLOW simulations to enhance the accuracy of hydrogen distribution and deflagration-to-detonation transition (DDT) probability estimates [11]. From a systemic safety perspective, the overall safety concept (ORSAC) framework has been used to incorporate both technical and organizational dimensions into transparent safety assessments [12]. In rotating equipment fault diagnosis, researchers combined ADASYN for class balancing, EEMD and CWT for feature extraction, and deep residual networks for classification based on imbalanced datasets [13].

Although existing studies have advanced system-level safety assessments, few have focused specifically on the dynamic evolution of behavioral risks during NPP construction. Most current models treat safety behavior as a static factor, lacking the integration of causal mechanisms, strategic interactions, and systemic feedback processes [14]. To address this gap, some scholars have expanded defense-in-depth concepts to organizational levels and emphasized bidirectional interactions between technical and organizational mechanisms [15]. Another study identified key aggravating factors in severe accidents, such as containment venting failures and inadequate integration of meteorological and radiological data in evacuation planning, and proposed resilience-enhancing measures, including proactive venting and adaptive evacuation zoning via machine learning [16]. A recent study inspired by the HFACS framework combined it with system dynamics to identify four safety archetypes in human factors, modeling an S-shaped risk accumulation curve to support long-term behavioral reliability assessments [17]. Another review underscored the need for explainable AI in nuclear applications, highlighting SHAP and LIME as tools to improve transparency and trustworthiness [18].

1.2. Research Status of Safety Behavior and Safety Management

Research on safety behavior and safety management is essential for minimizing workplace accidents and strengthening organizational safety capabilities. Safety behavior research centers on individuals’ and teams’ compliance with established safety protocols, whereas safety management focuses on the structured implementation of systems and resource allocation to mitigate risks. In recent years, a variety of modeling approaches, particularly Bayesian networks (BNs), game theory, and system dynamics (SD), have been widely applied in this field.

Bayesian networks (BNs) effectively model probabilistic relationships between risk factors, supporting applications such as behavioral prediction and accident analysis. One study used Bayesian inference to calibrate microscopic crowd models based on flow data from bottleneck conditions [19]. Another constructed a Bayesian network using 7265 aviation safety incidents and applied the MMHC algorithm to learn its structure, identifying high-impact causal factors through mutual information analysis [20]. In cases of incomplete data, researchers combined BN with fuzzy set theory and expert elicitation to handle imprecision and uncertainty in complex risk assessments [21]. Other work integrated BNs with the N-K model and cumulative risk theory to quantify the risk coupling among miners’ unsafe behaviors, identifying key influencing factors [22].

Game theory has been used to study behavioral incentives and decision strategies in multi-agent systems. One study combined prospect theory and mental accounting to model the evolutionary game behavior of firms in safety collaboration contexts, showing how government reward–punishment mechanisms can influence strategic choices [23]. Another applied non-cooperative stochastic games to model reliable decision making, providing Pareto-optimal solutions without requiring precise weights or complete data [24]. Researchers also proposed a resilience risk assessment model that integrates game theory with extension cloud theory and uses the Best Worst Method for more objective indicator weighting [25]. In the field of urban safety, game-theoretic combination weighting (AHP-CRITIC) was used for flood risk assessment, improving indicator robustness and spatial accuracy when mapped through GIS [26].

SD has also gained traction as a method for analyzing complex feedback mechanisms in safety systems. One study developed a system dynamics model to explore how social influences and individual hazard perception affect accident probabilities, demonstrating diminishing returns from safety supervision investments and the greater effectiveness of simple, frequent training sessions [27]. Another model simulated near-miss reporting behavior by capturing interactions between organizational policies and individual attributes [28]. In Peru’s mining sector, SD was combined with a dynamic balanced scorecard to improve safety learning and planning, showing that leadership commitment and continuous training are key to reducing occupational risks [29]. SD has also been applied to evaluate the interaction of management policies in cross-border transport infrastructure projects, using causal-loop diagrams and empirical data from the Hong Kong–Zhuhai–Macao Bridge [30].

Despite the advantages of these methodologies, each exhibits certain limitations. Agent-based modeling (ABM) effectively captures individual heterogeneity and multi-agent interactions but often lacks empirical verifiability and causal transparency. Bayesian networks (BNs) are well-suited for managing uncertainty but depend heavily on expert input, which may introduce subjective bias. Game theory is adept at modeling strategic behavior evolution but has difficulty incorporating complex feedback mechanisms. System dynamics (SD) excels in representing feedback loops and temporal system behavior but is less effective in capturing individual decision making and behavioral strategy changes. To address these gaps, this study proposes an integrated BN–Game–SD framework that combines the strengths of each approach. The goal is to establish a holistic model that unifies causal inference, behavioral dynamics, and system-level feedback to better characterize the evolving risk landscape of worker behavior in nuclear construction environments.

2. Materials and Methods

2.1. Analysis of Behavioral Risk Assessment Index System Based on BN

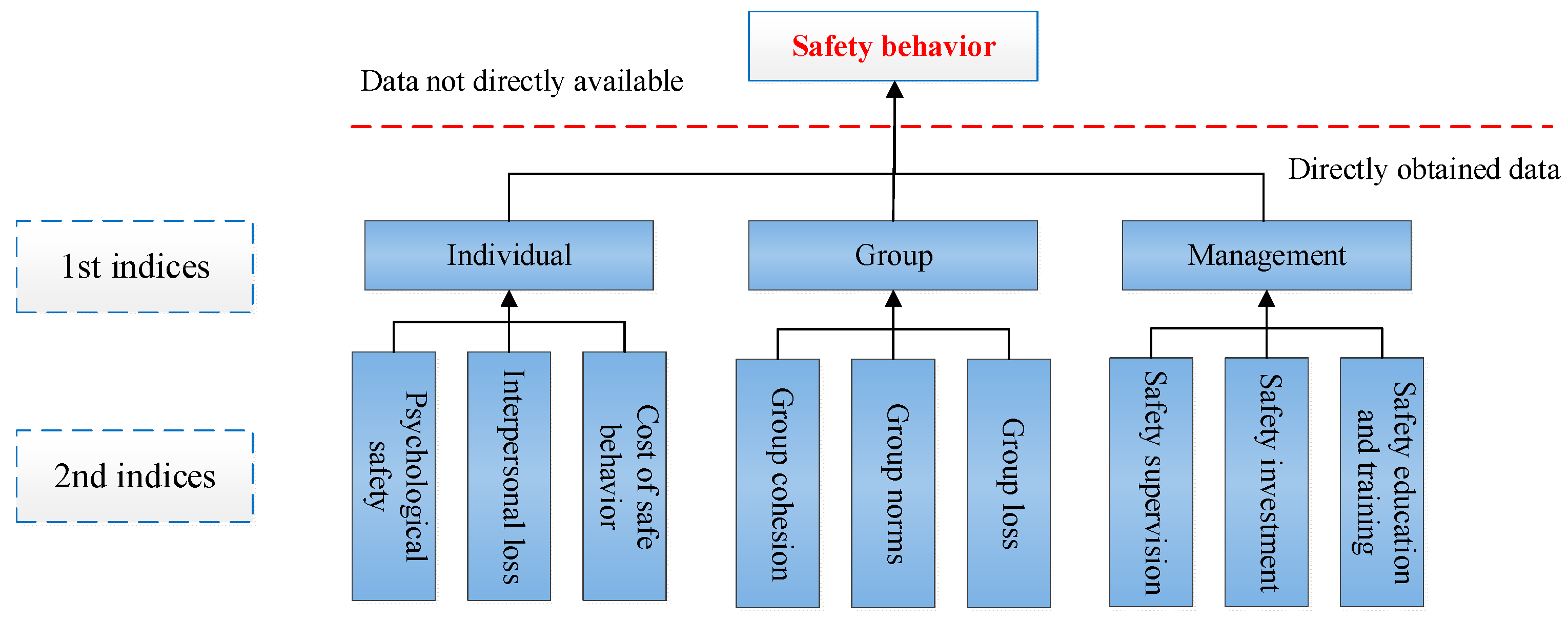
This paper investigates the key factors influencing worker safety behavior in nuclear power plants (NPPs) under construction. We categorized, synthesized, and integrated safety-related data to construct a Bayesian network (BN) model. A BN is a mathematical framework commonly used to represent probabilistic dependencies among random variables. It can be defined as follows:

BN = (G,θ).

$$P(X_1,X_2,X_3,\dots ,X_{\mathrm{n}})={\displaystyle \prod _{i=1}^{n}P(X_i}|X_1,X_2,X_3,\dots ,X_{\mathrm{n}-1})$$

(1)

In the formula, Xi represents the i-th node. When the prior probability of the nodes and the conditional probabilities of each node are known, the joint probability of all nodes can be calculated.

This paper analyzes employee injury and fatality incidents reported internally by the China Nuclear Engineering Group between 2015 and 2024. Drawing on this dataset, a Bayesian network model was developed to assess behavioral risks among workers in nuclear power plants (NPPs) under construction, as illustrated in Figure 1.

To determine the model parameters, a two-stage approach was adopted. First, structured data from incident reports were analyzed to extract relevant behavioral factors, environmental contexts, and accident outcomes. Causal relationships among these variables were identified using co-occurrence frequencies and time-sequenced incident chains. These data-driven correlations informed the initial structure of the Bayesian network (BN) and provided quantitative inputs for many conditional probability tables (CPTs), particularly for intermediate and leaf nodes with sufficient data records.

Second, for nodes with limited or unavailable empirical data, such as prior probabilities of root causes or rare conditional scenarios, expert elicitation was employed to supplement the model. A panel of ten senior experts was convened, each with over 15 years of experience in nuclear construction safety, representing areas such as structural design, field operations, and regulatory oversight. The Delphi method guided two rounds of independent assessments, during which experts evaluated the importance and interdependencies of uncertain variables. Their responses were normalized and averaged to generate probability estimates for the corresponding CPT entries.

To mitigate subjectivity and enhance model robustness, the following measures were implemented: (i) standardized guidance materials ensured consistent interpretation of variables; (ii) logical coherence of expert inputs was cross-verified; and (iii) extreme outlier scores were smoothed using statistical adjustment techniques. A final expert validation session was conducted to confirm the model’s structural logic and its practical applicability to real-world scenarios.

This dual-source methodology, integrating empirical construction data with structured expert input, ensures that the resulting BN model is both data-driven and operationally relevant, enabling accurate analysis of behavioral risk dynamics in the context of nuclear power plant construction.

The key indicators selected for constructing the Bayesian network nodes are summarized in

Table 1. Indicators of BN of safety behavior.

First Indices	Symbol	Second Indices	Symbol
Individual	A1	Psychological safety	p
		Interpersonal loss	l
		Cost of safe behavior	ci
Group	A2	Group cohesion	n
		Group norms	g
		Group loss	s
Management	A3	Safety supervision	j
		Safety investment	cs
		Safety education and training	e

. These variables were identified based on their frequency in incident reports and expert evaluation of behavioral relevance.

To obtain objective and reasonable indicator scoring results, a data preprocessing method was applied, proceeding from parent nodes to child nodes. The target node Z has n primary network nodes A, B, …, N, with scores K1, K2, …, Kn. The score of Z is expressed as follows:

$$\mathrm{Z}={\displaystyle \frac{{\mathrm{K}}_1+{\mathrm{K}}_2+{\mathrm{K}}_3}{\mathrm{n}}}$$

(2)

For a primary network node A, if A has m secondary network nodes A1, A2, …, Am, the score of the primary network node A is expressed as follows:

$$\mathrm{X}=\overline{\mathrm{X}}={\displaystyle \frac{\sum _{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{X}}_{\mathrm{i}}}{\mathrm{m}}}$$

(3)

The specific data obtained through the calculation are shown in

Table 2. Weight values of level II indicators.

Level II Indicators	Weight Value WB	Level II Indicators	Weight Value WB
p	0.18	s	0.34
l	0.21	j	0.10
ci	0.15	cs	0.38
n	0.40	e	0.31
g	0.16

.

2.2. Game Simulation Analysis of Individual and Group Behaviors

2.2.1. Analysis of Evolutional Rules of Individual and Group Safety Behavior

The psychological force field theory posits that human behavior arises from the interaction between an individual’s internal psychological field, shaped by personal needs, and the external force field, determined by environmental influences. Consequently, individual behavior can be viewed as a dynamic interplay or “game” between internal psychological drivers and the behavioral tendencies of the group to which the individual belongs.

The choice of individual behavior is strongly influenced by the perceived sense of psychological safety within the group. When individuals feel psychologically safe, they are more inclined to collaborate with the group and continuously adjust their actions to align with collective behavioral norms. This, in turn, reinforces group cohesion and helps unify behavioral standards. Over time, the accumulation and convergence of individual behaviors according to shared patterns leads to the formation of coherent group behavior.

However, when individuals possess greater self-confidence and perceive that their personal gains outweigh those associated with group conformity, their behaviors tend to diverge from group norms. In such cases, personal objectives take precedence, and individual actions may disrupt group cohesion. This can reduce group size or even lead to group fragmentation and the emergence of new subgroups.

Figure 2 illustrates the evolution model of individual and group behaviors based on the psychological force field theory. On the left side of the diagram, environmental and managerial factors shape group behavior and generate an implicit group-level force field that encourages individuals to conform. On the right side, an individual’s psychological safety, shaped by personal traits and goal-oriented motivations, affects their perception of the benefits of aligning with group behavior. These two opposing forces interact to influence the individual’s behavioral decisions. The bidirectional arrows indicate mutual influence: while group norms shape individual actions, deviations at the individual level can, in turn, alter group norms or lead to group fragmentation.

Individuals are inherently members of one or more social groups. When an individual’s opinions deviate from the majority within a group, they often experience social pressure. To avoid isolation, individuals may compromise on their own viewpoints and conform to the group’s dominant stance. In this context, an individual’s behavior can be conceptualized as a strategic interaction with the group. Each individual continuously evaluates the relative benefits of aligning with or diverging from group behavior and chooses the strategy that maximizes personal gain.

2.2.2. Game Theory Model

Based on the elements of group dynamics and game theory, the following assumptions were first made.

(1)

In the game process, the group and individuals are two parties. Each party has two strategies: safe and unsafe behaviors.

(2)

The effect of the group on individuals is mainly reflected in the interaction between various elements in the group dynamics and their influence on individuals. When individuals and the group adopt safe behaviors, the individual’s benefit is a sense of psychological security, p. The benefits for the group members are the changes in various elements in the group dynamics, mainly including group cohesion, n, and group standard consistency, g. Both group cohesion, n, and group standard consistency, g, increase with the increase in the probability of group safety behavior (denoted as x).

(3)

When the individual behaviors are inconsistent with the group behaviors, the individual suffers from interpersonal loss, denoted as l. However, after the adoption of unsafe behaviors, accidents may occur. The proportion of the occurrence of accidents and the caused loss are denoted as f and s, respectively.

(4)

Everyone in a group is independent and chooses a safe behavior or unsafe behavior strategy at the same time. In this study, c denotes the extra cost when the individual chooses safe behaviors; the individual does not need to pay the cost when choosing unsafe behaviors. The gain coefficient is denoted as r.

In this study, individual behavior was modeled using a dual-strategy framework, namely the choice between safe and unsafe behavior. This formulation reflects the prevailing behavioral orientations typically observed in high-risk construction settings, where decisions tend to polarize under pressure. To facilitate tractable modeling of group–individual interactions, the framework adopts consistent behavioral parameters and deterministic payoff values across agents. This approach helps clarify the core dynamic relationships and supports the analysis of behavioral evolution.

Based on the above assumptions, the payoff matrix of both sides of the game was obtained, as listed in

Table 3. The payoff matrix of both sides of the game.

Individual	Group
	Safe Behavior x	Unsafe Behavior 1 − x
Safe Behavior y	0.18 × p + 0.15 × rxc − 0.15 × c, 0.4 × n + 0.16 × g + rc − 0.15 × c	−0.21 × l − 0.15 × c − 0.34 × fs, −0.34 × fs
Unsafe Behavior 1 − y	0.15 × rxc − 0.21 × l − 0.34 × fs, rc − 0.34 × fs	0.18 × p − 0.34 × fs, 0.4 × n + 0.16 × g − 0.34 × fs

.

In this study, the probability when the group chooses safe behaviors is denoted as x, the probability when the group chooses unsafe behaviors is denoted as 1 − x, the probability when individuals choose safe behaviors is denoted as y, and the probability when the individual chooses unsafe behaviors is denoted as 1 − y. Both x and y are functions of time t.

According to Table 3, the expected benefits of individuals choosing safe behaviors, u1, can be calculated as follows:

$$u_1=x\ast (0.18\ast p+0.15\ast rxc-0.15\ast c)+(1-x)\ast (-1-0.15\ast c-0.34\ast fs)$$

(4)

The expected benefits of individuals choosing unsafe behaviors, u2, can be calculated as follows:

$$u_2=x\ast (0.15\ast rxc-1-0.34\ast fs)+(1-x)\ast (0.18\ast p-0.34\ast fs)$$

(5)

Therefore, the average expected benefits of individuals choosing safe and unsafe behaviors can be calculated as follows:

$$u=y\ast u_1+(1-y)\ast u_2$$

(6)

The rate of change in the proportion of individuals choosing safe behaviors over time is represented by dy/dt. The replication dynamic equation for individuals choosing safe behaviors can be written as follows:

$$G(y)={\displaystyle \raisebox{1ex}{$dy$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.}=y(u_1-u)=y(1-y)(u_1-u_2)=y(1-y)[(0.36\ast p+0.3\ast c+0.34\ast fs)x-1-0.15\ast c]$$

(7)

Similarly, the average expected benefit when the group chooses safe and unsafe behaviors can be calculated as follows:

$$v_1=y(0.4\ast n+0.16\ast g+rc-0.15\ast c)+(1-y)(rc-0.34\ast fs)$$

(8)

$$v_2=-0.34\ast yfs+(1-y)(0.4\ast n+0.16\ast g-0.34\ast fs)$$

(9)

$$v=x\ast v_1+(1-x)\ast v_2$$

(10)

The replication dynamic equation for the group choosing safe behaviors can be written as follows:

$$F(x)={\displaystyle \raisebox{1ex}{$dx$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.}=x(1-x)[(0.8\ast n+0.32\ast g-0.15\ast c+0.34\ast fs)y+rc-0.4\ast n-0.16\ast g]$$

(11)

Equations (7) and (11) constitute a replication dynamic system, and 5 local equilibrium points of the system, (0, 0), (0, 1), (1, 0), (1, 1), ((0.15c + l)/(0.36p + 0.3c + 0.34fs), and (0.4n + 0.16g − rc)/(0.8n + 0.32g − 0.15c + 0.34fs)), can be acquired, which each correspond to an evolutionary game equilibrium. The evolution stability strategy of the system can be obtained by the local stability of its corresponding Jacobian matrix at an equilibrium point. The Jacobian matrix J, Determinant Det(J), and Trace Tr(J) of the system can be written as follows:

$$J=\left[\begin{array}{cc}(1-2x) [(0.8\ast n+0.32\ast g-0.15\ast c+0.34\ast fs)y+rc -0.4\ast n-0.16\ast g]& \left(0.8\ast n+0.32\ast g-0.15\ast c+0.34\ast fs\right)x(1-x)\\ (0.36\ast p+0.3\ast c+0.34\ast fs)y(1-y)& (1-2y)[(0.36\ast p+0.3\ast c+0.34\ast fs)x-0.21\ast l-0.15\ast c] \end{array}\right]$$

(12)

$$\begin{array}{l}Det(J)=\left\{(1-2x) [(0.8\ast n+0.32\ast g-0.15\ast c+0.34\ast fs)y+rc-0.4\ast n-0.16\ast g]\right\}\left\{(1-2y)[(0.36\ast p+0.3\ast c+0.34\ast fs)x-0.21\ast l-0.15\ast c\left.]\right\}\right.\\ +\left(0.8\ast n+0.32\ast g-0.15\ast c+0.34\ast fs\right)x(1-x)(0.36\ast p+0.3\ast c+0.34\ast fs)y(1-y)\end{array}$$

(13)

$$\begin{array}{ll}Tr(J)& =(1-2x) [(0.8\ast n+0.32\ast g-0.15\ast c+0.34\ast fs)y+rc-0.4\ast n-0.16\ast g]\\ & +(1-2y)[(0.36\ast p+0.3\ast c+0.34\ast fs)x-0.21\ast l-0.15\ast c] \end{array}$$

(14)

By substituting the local equilibrium points into the above matrices, the sign of the Determinant Det(J) and Trace Tr(J) can be determined. If the Determinant Det(J) of the matrix corresponding to the equilibrium point is greater than 0, and the Trace Tr(J) of the matrix is less than 0, it can be regarded as an evolutionary stable strategy. If the Trace Tr(J) equals 0, it is a saddle point.

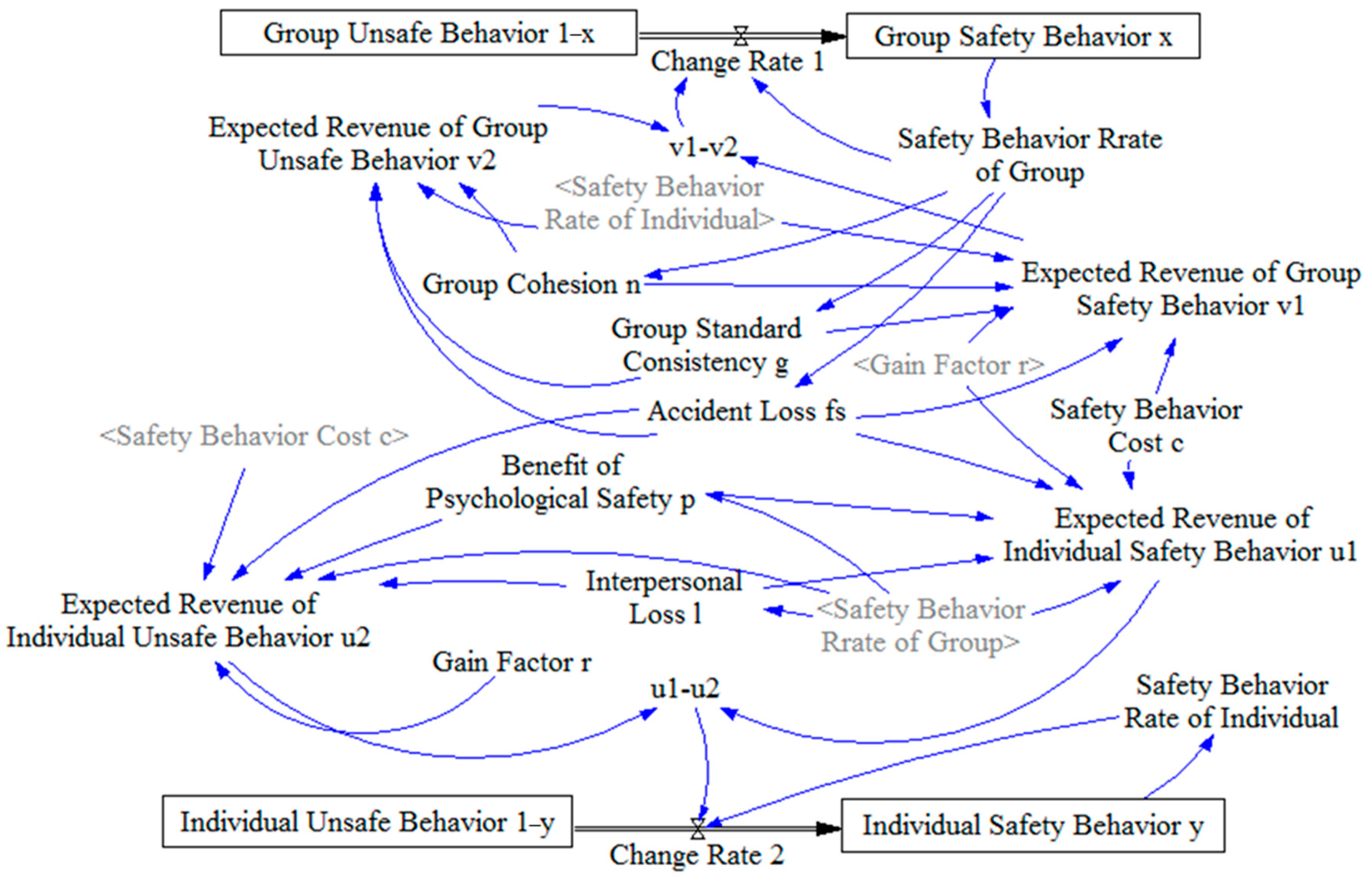
2.3. Establishment and Simulation Analysis of SD Model Under Dynamic Structure

The system dynamics (SD) model constructed in this study consists of 4 state variables, 2 rate variables, 13 auxiliary variables, and 2 external variables. As shown in Figure 3, the core state variables represent the proportions of individual and group safe and unsafe behaviors. The rate variables (Change Rate 1 and Change Rate 2) define the behavioral transition speeds for groups and individuals, respectively. Auxiliary variables, such as psychological safety, group cohesion, gain factor, and expected payoffs, serve as intermediaries that reflect causal relationships and feedback mechanisms within the system. These relationships are quantified through Equations (3) to (12). External variables, including safety behavior cost and accident loss, act as exogenous influences that shape individual decision making. This model captures the dynamic interplay between group-level influence and individual behavioral choices over time and provides a basis for analyzing the threshold effects and behavior stabilization patterns observed in the simulation.

3. Results

3.1. Establishment of SD Model Under Dynamic Structure

According to evolutionary game theory, whether individuals within a group adjust their strategies in response to cost–benefit changes depends primarily on two factors. The first is the number of reference individuals available for imitation; this reflects a behavioral threshold. A higher threshold indicates that individuals find more behavioral patterns to emulate. The second factor is the net gain resulting from successful imitation; greater expected benefits increase both the motivation to imitate and the likelihood of behavioral change.

As the number of individuals engaging in group-level safe behavior increases, the perceived benefit of adopting safe behaviors also rises. This is due to the influence of group dynamic elements, which make individuals more inclined to conform to group safety norms. Accordingly, this study explored the evolution of individual and group safety behavior under various group-state conditions. Special attention was given to identifying the threshold values that prompt behavioral shifts among individuals.

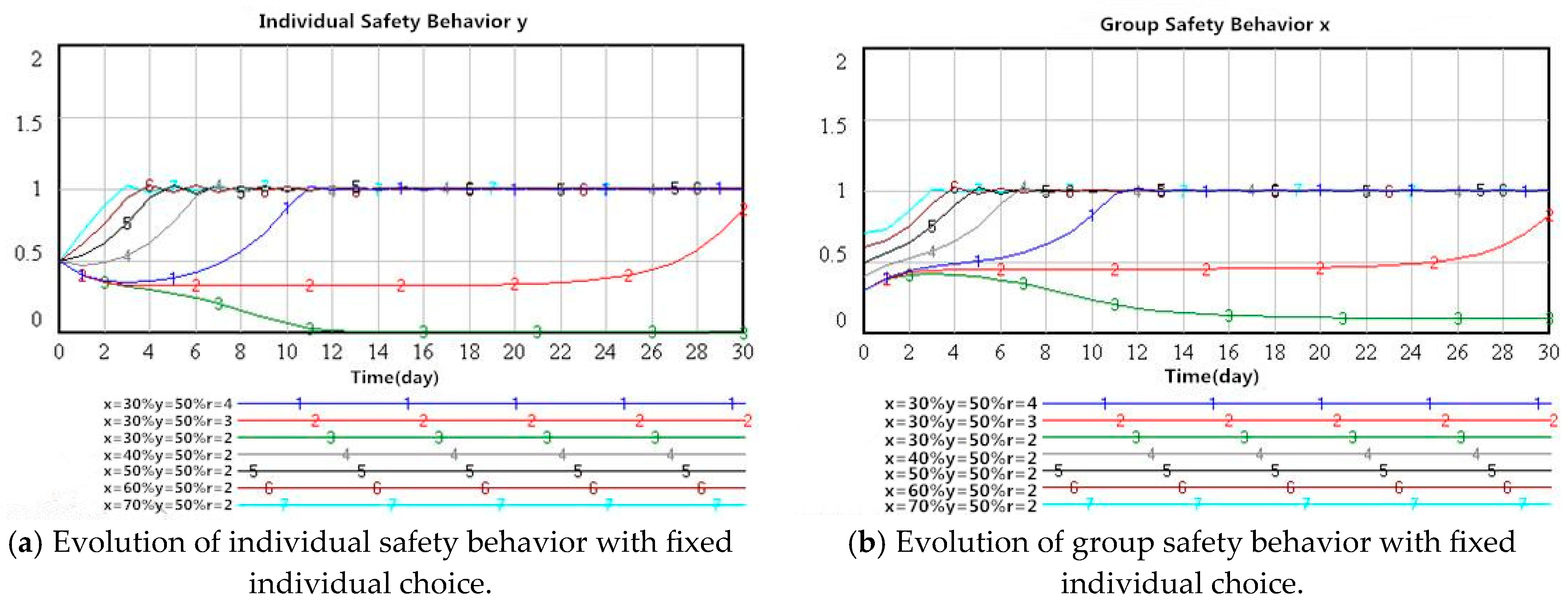
This study assumed that the probability of individuals selecting safe behaviors, denoted as y, was 50%, and the initial probabilities of group safety behavior, x, were 30%, 40%, 50%, 60%, and 70%, respectively. The evolutionary rules of individual and group safety behavior were observed, as shown in Figure 4. In the figure, the horizontal axis represents the simulation time, and the vertical axis indicates the behavioral probability. Each curve corresponds to a different combination of x and the individual gain coefficient r, with the parameter settings labeled below the graphs.

It can be observed in Figure 4 that when the probability of individuals selecting safe behaviors (y) was 50%, both individual and group behaviors evolved in a consistent direction. The evolution of individual behavior was influenced by the group’s initial safety behavior probability (x). In groups with a high initial safety behavior probability (x > 50%), individuals received higher payoffs when choosing safe behaviors and were, therefore, more likely to adopt them (Lines 5–7 in Figure 4). In contrast, in groups with moderate or low initial safety behavior probabilities (40% < x < 50%), individuals initially tended to choose unsafe behaviors (Lines 4 and 5 in Figure 4). However, as the simulation progressed, the payoff from unsafe behaviors became lower than that from safe behaviors, prompting individuals to gradually shift toward choosing safe behaviors. Nevertheless, the rate of transition to safety behavior in these groups was slower than that observed in groups with higher initial safety probabilities.

When the group’s initial safety behavior probability was below 30%, the payoff from unsafe behaviors exceeded that from safe behaviors, leading individuals to prefer unsafe strategies (Line 3 in Figure 4). The value of 30% thus emerged as a critical behavioral threshold in the simulation. When less than 30% of the group members engaged in safe behaviors, the expected utility of aligning with the group diminished. Under these conditions, individuals perceived greater short-term benefits in deviating from weak group norms. As a result, group influence was weakened, and risk-oriented incentives dominated, pushing the behavioral dynamic toward unsafe outcomes. This 30% threshold represents a tipping point, below which group cohesion failed to stabilize behavior, and the overall trend shifted away from collective safety adherence.

It can also be seen in Lines 1–3 in Figure 3 that the larger the cost gain coefficient r (indicating greater economic benefits when individuals choose safe behaviors), the lower the threshold of group safety behavior probability that individuals are willing to accept. Therefore, under the same level of individual quality, for groups with relatively low safety behavior probabilities, leaders can promote both individual and group adoption of safety behavior by increasing incentives, specifically, by raising the gain coefficient r.

In practice, individuals are heterogeneous and display varying levels of quality and behavioral characteristics. Due to differences in personal traits and goals, employees adopt distinct behavior strategies and exhibit varying propensities toward safety behavior. In the game process, such individual differences lead to diverse influences on group behavior. To investigate this, the probability of group safety behavior (x) was held constant, and interactions between individuals with varying probabilities of selecting safe behaviors and a group with a fixed safety level were simulated. The results are shown in Figure 5.

It can also be observed in Lines 3–6 in Figure 5 that when the probability of group safety behavior was 50%, and the probability of individual safety behavior, determined by individual quality, was below 30%, group behaviors tended to shift toward unsafe actions. Conversely, when the individual safety behavior probability exceeded 40%, both individual and group behaviors gradually evolved toward safer outcomes as the game progressed. Moreover, the higher the individual’s initial safety behavior probability, the stronger its influence on overall group behavior. From Lines 1–3, it is also evident that when the probability of group safety behavior exceeded 50%, a higher gain coefficient r corresponded to a lower threshold of acceptable group safety behavior probability for individuals, making both parties more inclined to adopt safety strategies.

Based on group and individual conditions, the threshold values for safety behavior probabilities were identified. These can serve as practical references for managers when making personnel adjustments, helping to reasonably assign individuals and promote the self-organizing evolution of safety behavior within teams. This insight underscores the importance of group leaders and safety managers taking proactive measures. External incentives, such as increasing the gain coefficient for safety behavior, can encourage both groups and individuals to adopt safer practices. Accordingly, managers should consider implementing behavioral interventions or introducing reference groups to rapidly elevate the proportion of safe behaviors within the group and enhance individual safety awareness.

3.2. Case Application

The proposed methodology was piloted in a large-scale nuclear power construction project characterized by high safety demands and complex on-site risks. With over 20,000 workers and numerous construction teams operating simultaneously across dispersed risk zones, the project site presents both the rigorous standards of nuclear operations and the dynamic hazards typical of large construction enterprises. To meet these challenges, a safety supervision grid system was established across multiple critical areas, requiring constant personnel presence for monitoring and inspection.

To support real-time risk control, a dedicated behavioral risk management platform was deployed. This platform enabled continuous tracking of safety behavior across the workforce and identified potential hazards throughout the construction area. In January 2024, the platform began operational use on site, integrating the behavioral risk modeling framework developed in this research.

Figure 6 and Figure 7 present a comparative analysis of violation incidents before and after implementation. The data reveal a consistent decline in the monthly number of employee violations throughout the year following the platform’s introduction. Compared to the same months of the previous year, the reduction ranged from 7.28% to a maximum of 10.39%. This trend suggests that the integrated model and monitoring system contributed to enhanced behavioral compliance and safety awareness on site, demonstrating the practical effectiveness of the proposed approach in a high-risk, real-world setting.

4. Discussion

This study provides valuable insights into the safety behavior of employees in nuclear power plants (NPPs) under construction, particularly with regard to the interaction between individual decision making and group dynamics. The simulation results indicate that group-level safety behavior exerted a significant influence on individual strategic choices. When the proportion of safe behaviors within a group surpassed a certain threshold, individuals were more likely to conform to collective norms, thereby enhancing overall behavioral consistency. This finding highlights the critical role of group cohesion and psychological safety in shaping safety-related behavioral outcomes.

The observed threshold effects further emphasize the need to maintain a baseline level of safety behavior to sustain positive group dynamics. These outcomes are consistent with foundational concepts in game theory and system dynamics, reinforcing the validity of the integrated modeling approach. Compared with earlier research, this study adopts a unified framework that combines Bayesian networks (BNs), game theory, and system dynamics (SD), enabling a more comprehensive view of behavioral risk evolution in complex construction environments. Unlike traditional predictive models, such as AI classifiers or deep neural networks, the BN–Game–SD model emphasizes explainability and captures causal interactions and feedback mechanisms that are often overlooked in purely data-driven approaches.

Rather than relying on static risk indicators, this approach captures behavioral change over time, offering a dynamic perspective better suited to high-risk construction contexts. BNs allow for probabilistic reasoning under uncertainty, game theory models strategic interactions, and SD reveals systemic feedback patterns. Together, these methods provide a more holistic understanding of how safe behaviors emerge, interact, and evolve in practice. The insights derived from this study may also be extended to other high-risk industries. By identifying behavioral thresholds and risk transmission pathways, the model offers practical value for safety planning and decision making.

Several limitations deserve attention. The Bayesian network relies partially on historical incident reports and expert judgment, which may introduce subjective bias and limit generalizability. To address this, future work will incorporate more empirical data from automated on-site monitoring systems and refine parameter estimation through expert-assisted calibration. This will enhance the robustness and adaptability of the model’s causal structure. Additionally, future research will introduce formal statistical inference methods, such as significance testing and confidence intervals, to systematically evaluate the reliability of intervention results across different application contexts. Sensitivity analysis will also be performed to assess the impact of key parameter variations on simulation outcomes, thereby improving transparency and predictive credibility.

Furthermore, individual behaviors in the current game-theoretic model are represented through a dual-strategy framework, “safe” versus “unsafe”, with deterministic payoffs. While this setup facilitates the modeling of key dynamics between group influence and personal decisions, it does not fully reflect the heterogeneity and uncertainty often present in real-world settings. Future efforts will explore agent-based extensions and probabilistic payoff mechanisms to improve behavioral realism and model flexibility.

Beyond nuclear power construction, the integrated BN–Game–SD modeling approach holds promise for broader applications in safety-critical domains. Industries such as chemical processing, aerospace assembly, large-scale infrastructure construction, and offshore oil platforms often involve complex worker interactions, high accident sensitivity, and dynamic behavioral patterns under risk pressure. The framework presented in this study can be adapted to model behavioral risks in these settings, especially where group norms and decision feedback loops strongly influence individual safety choices.

Future research could also integrate this modeling system into real-time decision support tools. By linking the model to live monitoring platforms, such as wearable sensors, on-site surveillance systems, or smart safety helmets, managers can identify emerging behavior risks early and adjust interventions accordingly. Additionally, combining this approach with digital twin technologies may enable proactive simulations and scenario testing in virtual construction environments before implementation on site.

Finally, interdisciplinary collaboration among behavioral psychology, data science, and safety engineering will be essential to expand the explanatory power and practical relevance of the model. As emerging AI technologies advance real-time perception and adaptive learning, future safety management systems may incorporate AI-enhanced BN–Game–SD models that autonomously evolve with the working environment.

5. Conclusions

To enhance safety management and reduce accident rates during the construction of nuclear power plants (NPPs), this study proposes an integrated modeling approach that combines Bayesian networks (BNs), game theory, and system dynamics (SD) to simulate the dynamic interactions between individual and group safety behaviors. The key findings are summarized as follows:

(1)

A Bayesian network was constructed to identify and analyze the key influencing factors of employee safety behavior at NPP construction sites. The index system was categorized into individual, group, and management dimensions, and the relative weights of each indicator were determined using a combination of data analysis and expert input.

(2)

Based on behavioral game theory, an evolutionary game model was established to explore strategic interactions between individuals and groups. Five local equilibrium points were preliminarily identified. The SD model was then developed to capture the temporal evolution of behavior under different initial conditions (e.g., safety behavior probabilities of 30%, 40%, 50%, etc.). The simulation results reveal threshold effects and behavioral trends, providing practical guidance for improving safety interventions.

(3)

The integrated model was applied to a real NPP construction project. Behavioral monitoring data show a consistent reduction in safety violations after model implementation, with the maximum monthly reduction reaching 10.39%.

Overall, the proposed BN–Game–SD framework reflects both theoretical consistency with organizational behavior theories and alignment with real-world construction safety practices. This study offers a structured and practical approach for enhancing worker safety awareness and improving enterprise-level safety performance in high-risk construction environments.