Building Integrated Photovoltaic Systems: Characteristics and Power Management
Abstract
1. Introduction
1.1. Motivation and Research Gap
- The PV array circuit configuration.
- Maximum Power Point Tracking (MPPT) algorithms.
- Partial shading mitigation strategies concentrating on distributed and centralized architectures.
- System bus selection, DC or AC.
- Panel modeling for converter design and control purposes.
1.2. Critical Analysis of BIPV’s Reviews
1.3. Synthesis of Contributions: Advances and Recommendations for BIPV Systems
2. Characteristics of BIPV Systems
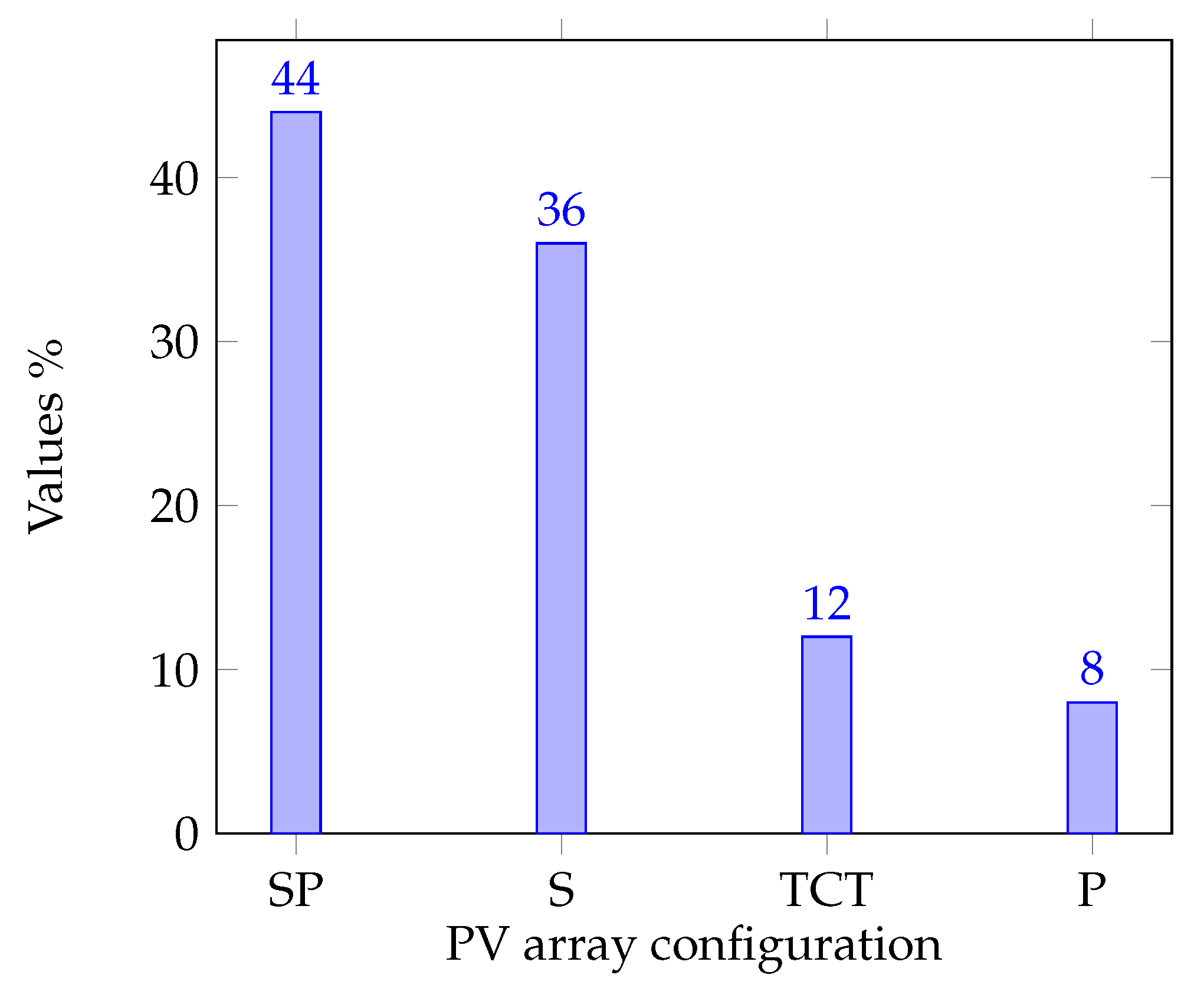
2.1. Panel Arrangement Within the Array
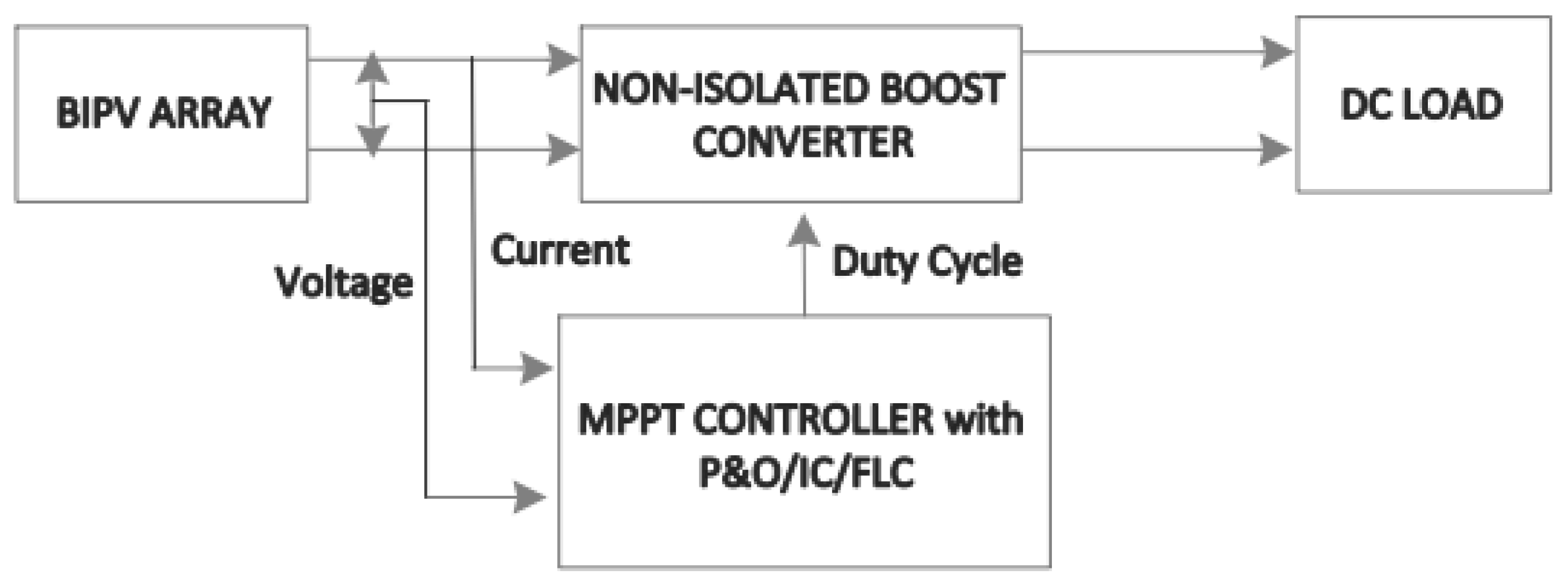
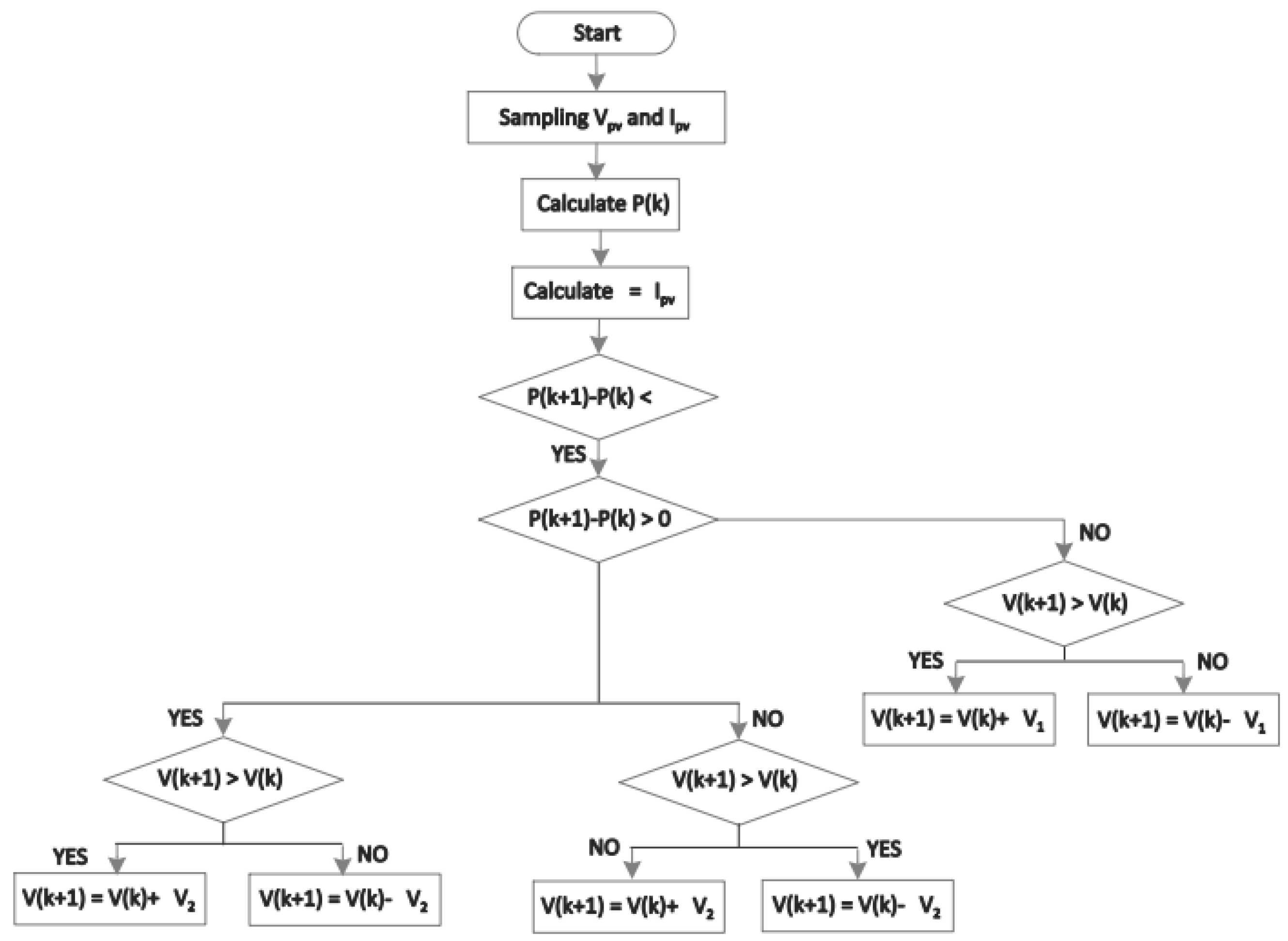
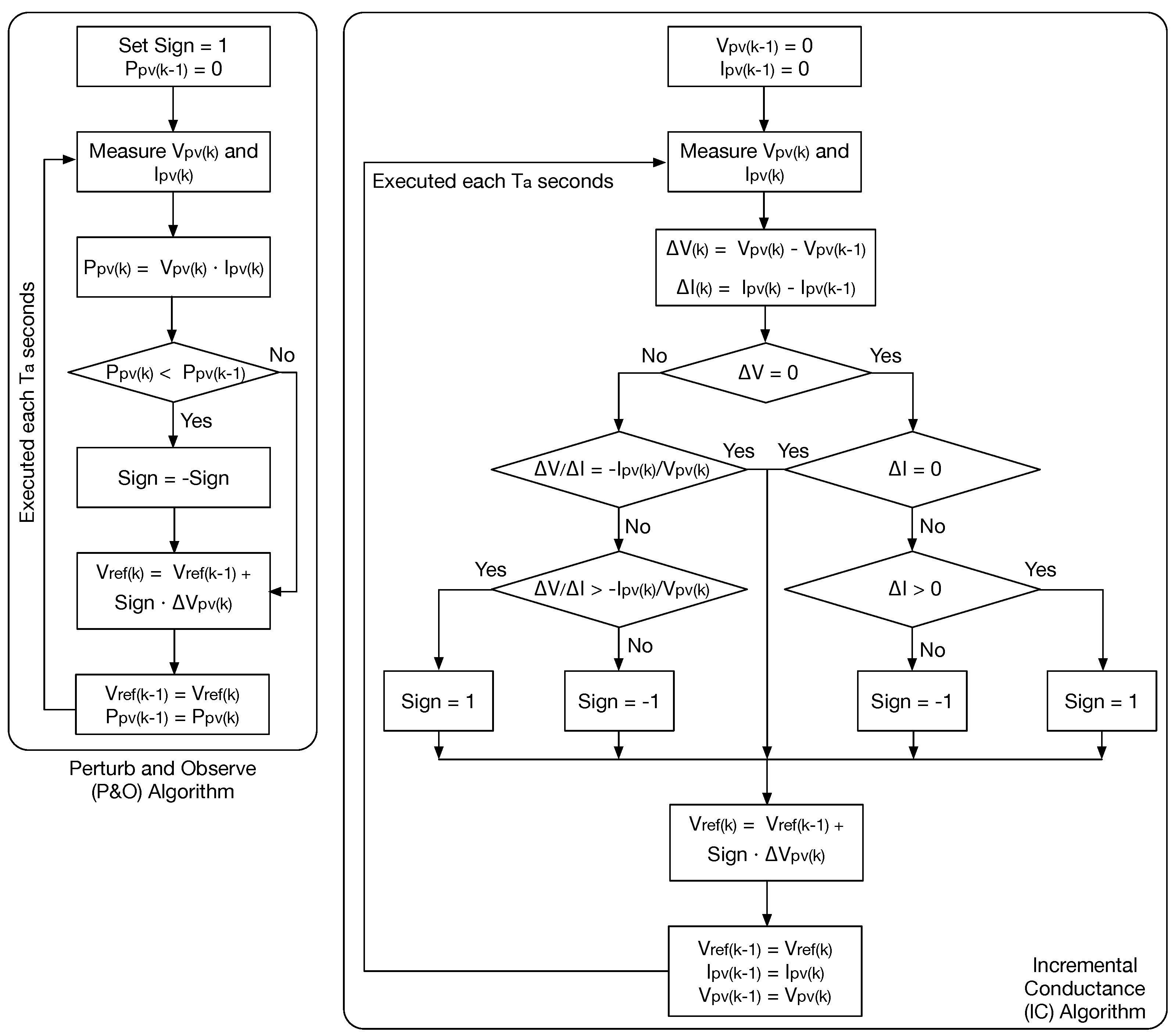
2.2. Maximum Power Point Tracking (MPPT) Algorithms
2.3. Partial Shading Mitigation Strategies
2.4. Voltage Bus Selection
- Standardization of DC buses: The lack of unified regulations for Direct Current (DC) distribution systems limits interoperability between BIPV, V2G, and smart grids. Future studies should propose regulatory and technical frameworks that facilitate safe and efficient integration.
- Bidirectional inverter design: Electric vehicles require power converters with high dynamic responsiveness, low harmonic distortion, and bidirectional capability. Research into advanced inverter topologies, such as multilevel or Wide Band Gap (WBG) semiconductor-based structures, could improve performance and reliability.
- Conversion and distribution efficiency: To maximize the economic viability of BIPV-V2G systems, ultra-high efficiency conversion devices and optimized distribution architectures that minimize losses are required, especially in environments with intermittent generation.
- Availability in adverse conditions: It is crucial to develop energy management strategies that ensure the availability of charging stations, even during periods of low PV generation or reduced demand. Solutions such as hybrid storage (batteries + supercapacitors) or AI-based load prioritization schemes could be explored.
2.5. Electrical Models of Photovoltaic Panels
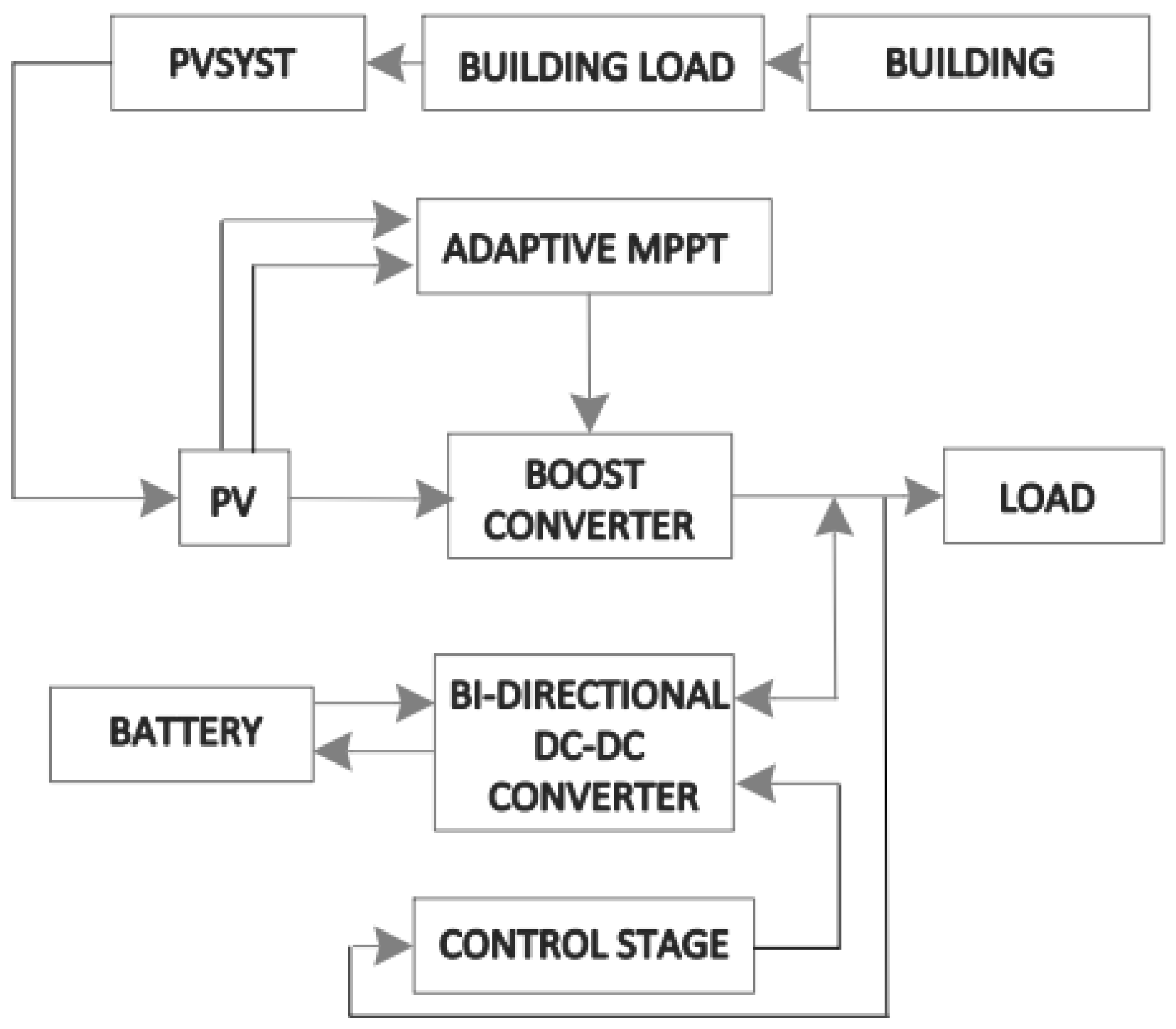
3. Maximum Power Point Tracking Methods in BIPV Applications
- In the first stage, the proposed model considers the dependence on solar irradiation, module temperature, and curve angle and provides the position and width of a scanning window in which the global maximum can be found.
- In the second stage, the global maximum is tracked within the scanning window by using the P&O method.
- The mean value of the scanning window width, and hence its position, is calculated for the given conditions of irradiation and curve angles.
- The information obtained in the previous step serves as the starting point for the scanning of the power–voltage curve and takes the operating point close to the global MPP (with no other peaks expected). The MPPT control is now transferred to the P&O scheme.
- The works presented in refs. [29,32,86] integrate PV modules in facades and proposed the use of P&O algorithms, achieving good performances according to the authors. However, validations are not clear concerning the behavior of the MPPT algorithm under partial shading conditions, which could be a very common issue for facades. It would be useful to go deeper into the study of the potential PV generation in facades by using the information of those works as background.
- Another aspect identified in this section was the use of the boost converter in all reviewed papers, which is also very common for conventional PV systems.
- Concerning the PV module or cell modeling, there was no detailed information. However, most of reviewed works used the one-diode model. Two of the works discussed in this section use the double-diode model, which is suitable for low irradiance levels. Such a condition is very likely in BIPV systems that include facades or other structure elements installed perpendicularly to the ground. In this way, it would be useful to perform a comparison of the analysis proposed in refs. [31,32] using the one-diode model or other models to evaluate the effect of the low irradiation levels and the performance of the MPPT strategies proposed in those works.
- The work reported in ref. [43] presents an interesting approach for modeling curved PV modules used in roofs. The proposed method can be useful to analyze similar structures that could be present in buildings. In the same was, the proposed methodology can be used for modeling other types of PV module technologies, such as bifacial panels and PV windows.
- The approaches presented in refs. [29,86] proposed the use of perovskite solar cells as a suitable options for PV elements to apply to facades. However, the authors did not discuss details concerning the model of the PV cell, which could be very helpful in order to analyze the impact in the design of the MPPT strategy but also in the study of the partial shading condition impact on PV generation.
4. Granularity Level of the MPPT Action
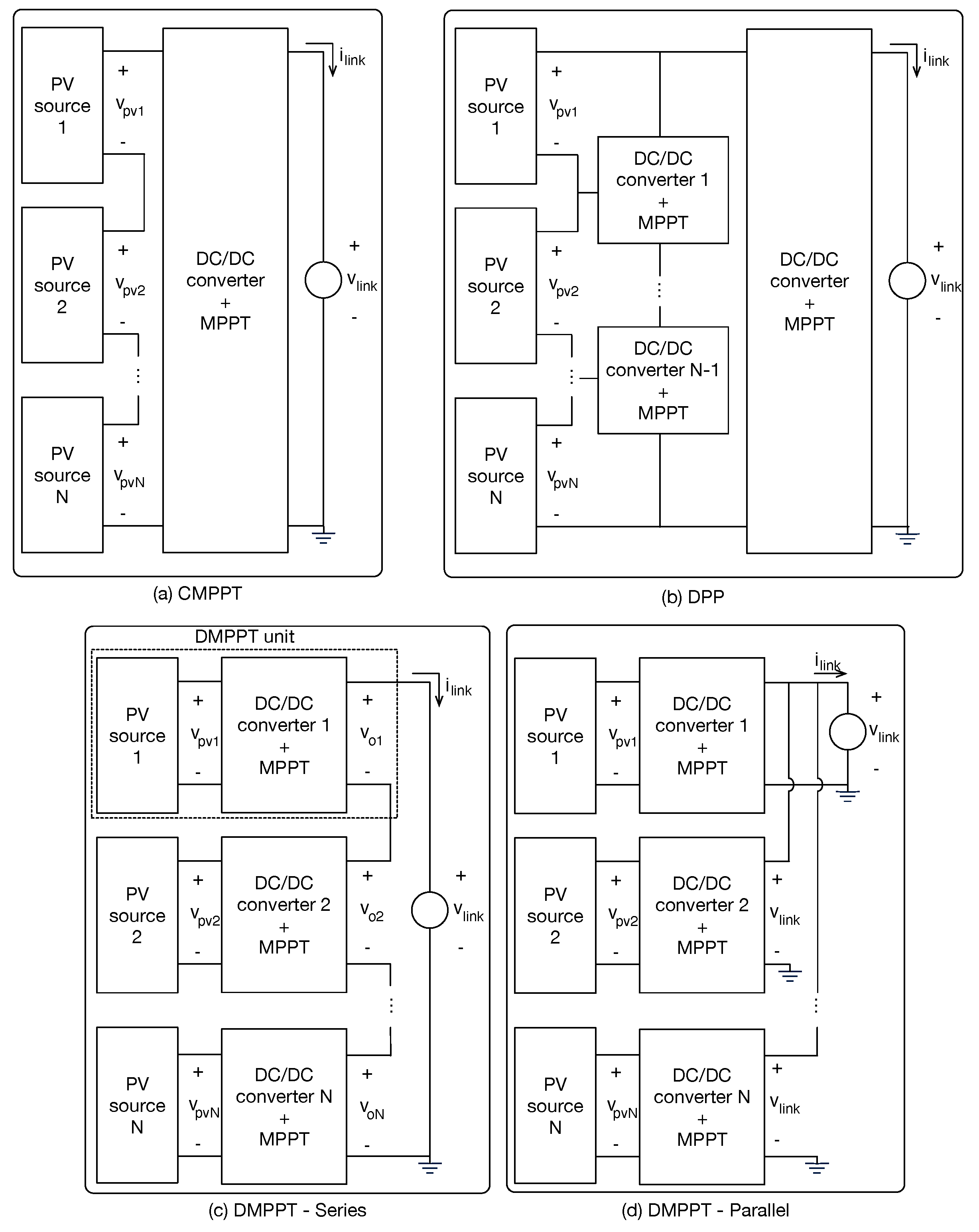
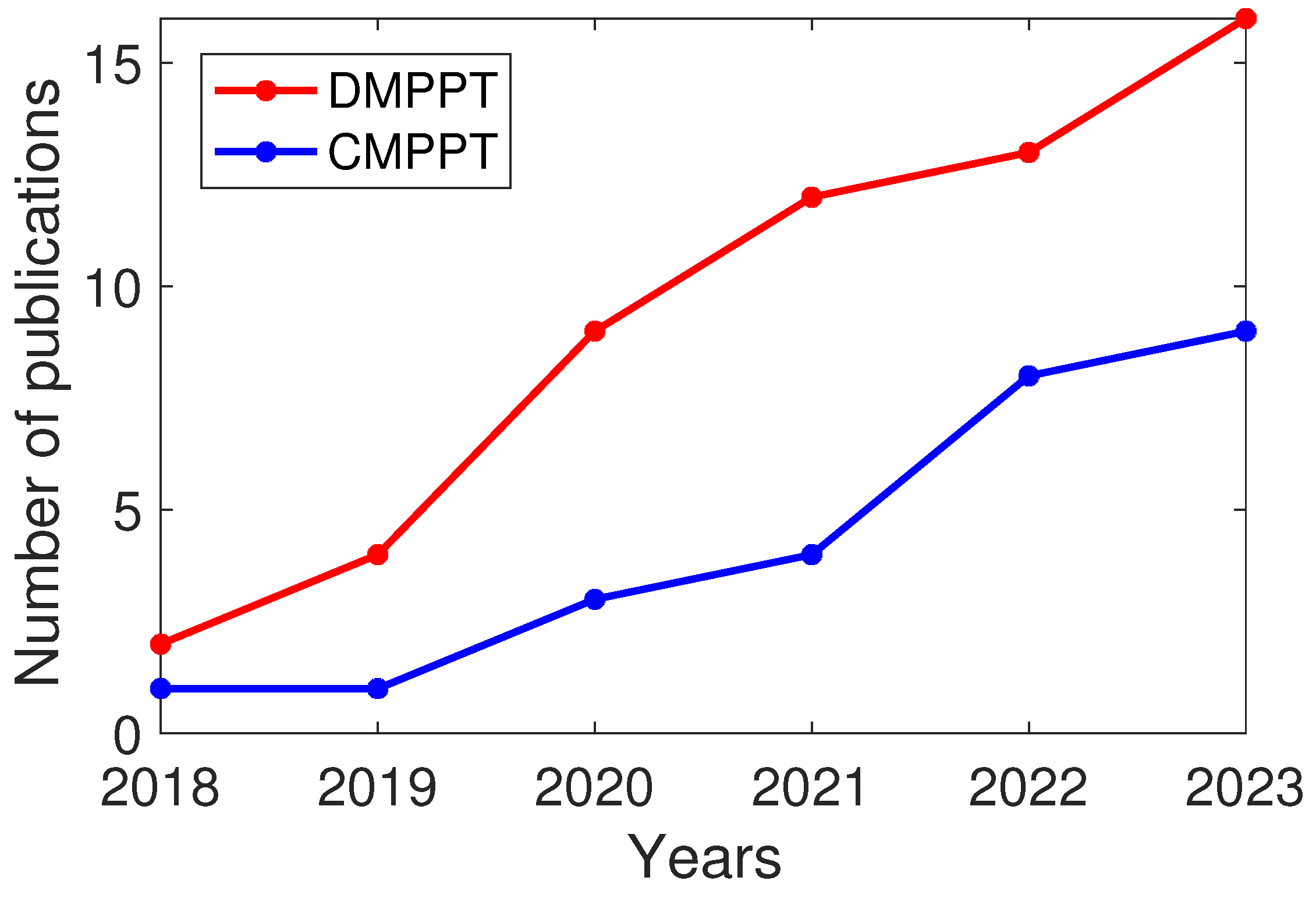
4.1. CMPPT Solutions for BIPV Systems
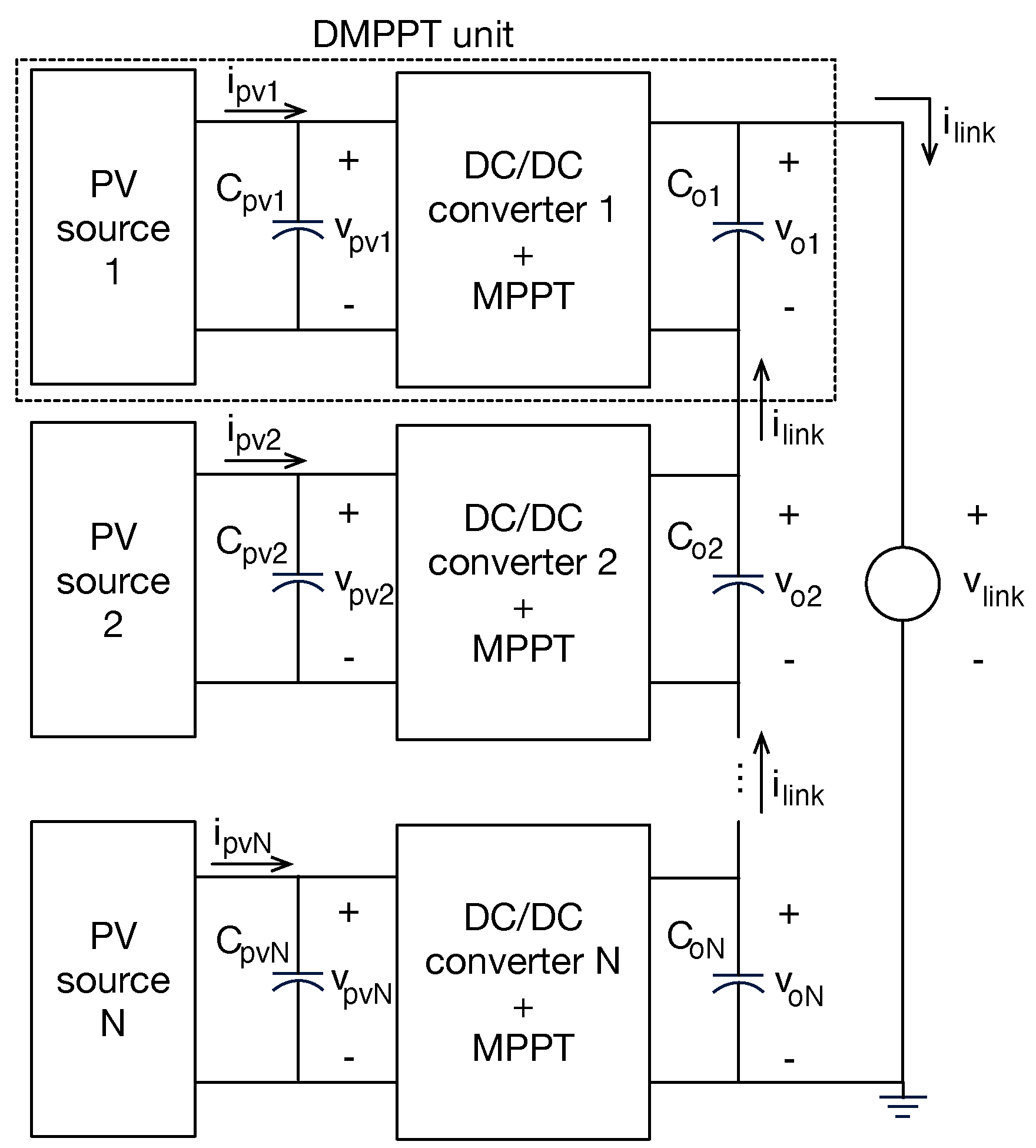
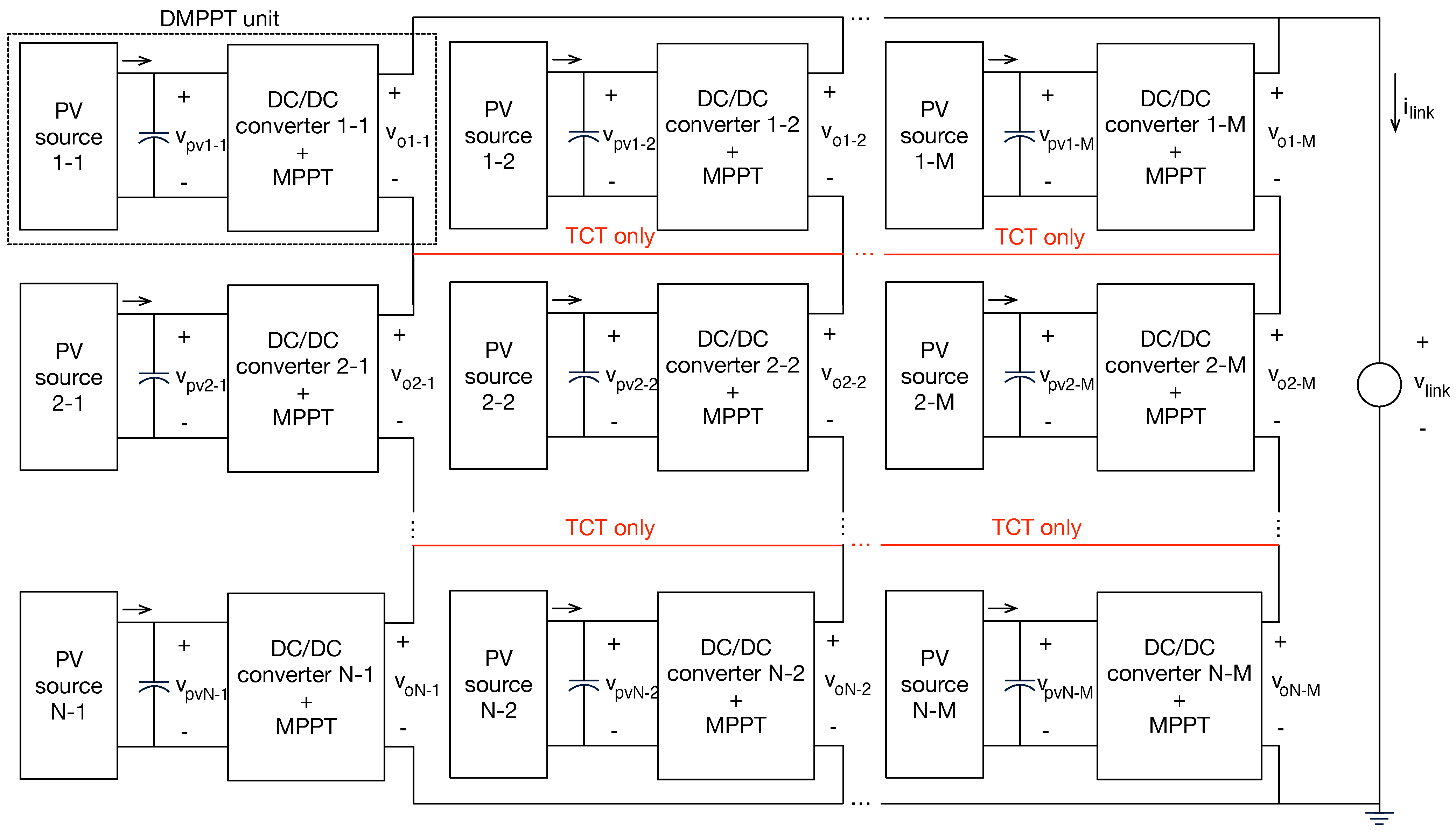
4.2. DMPPT Solutions for BIPV Systems
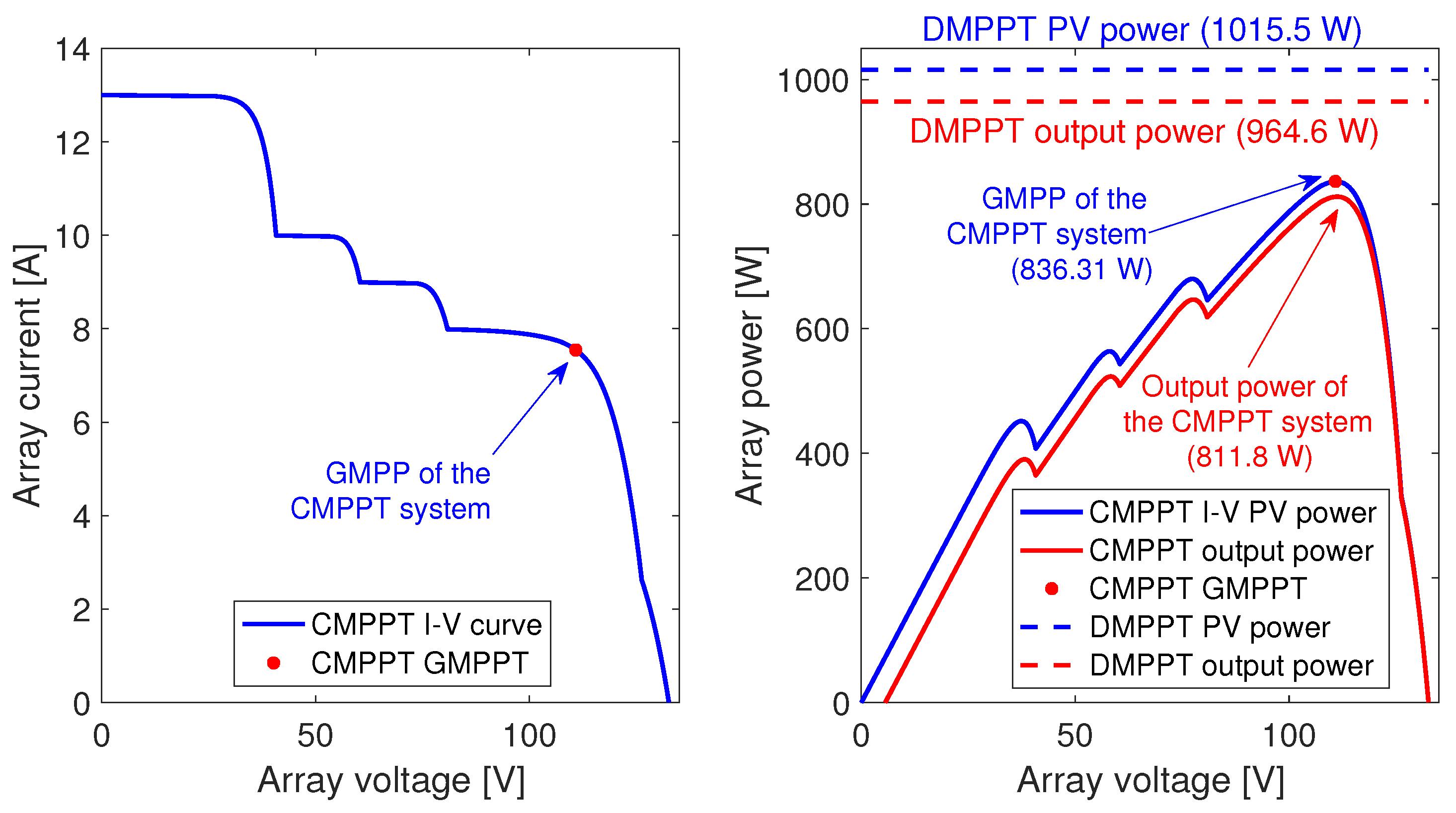
4.3. Synthesis and Discussion of the BIPV Approaches
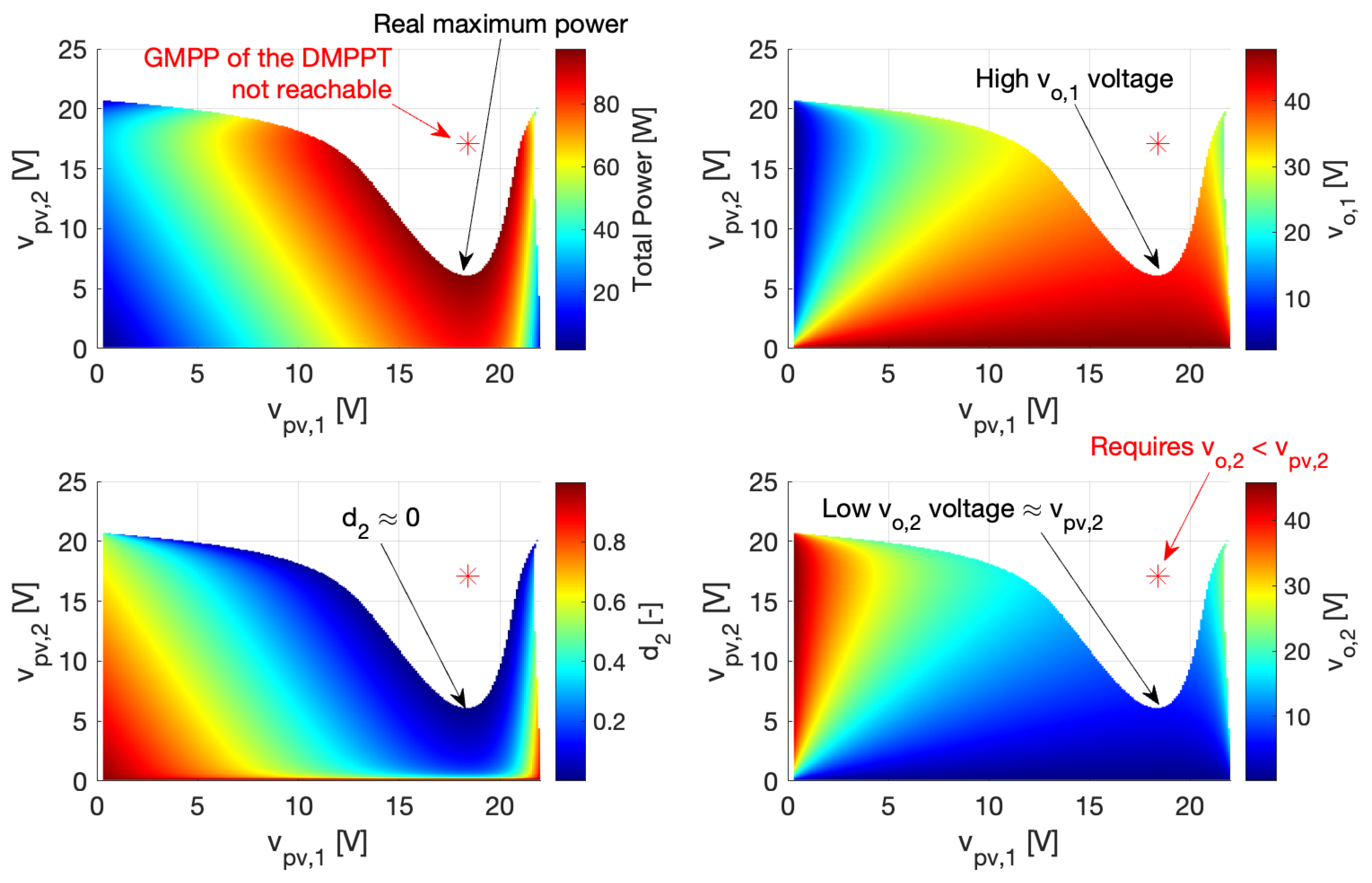
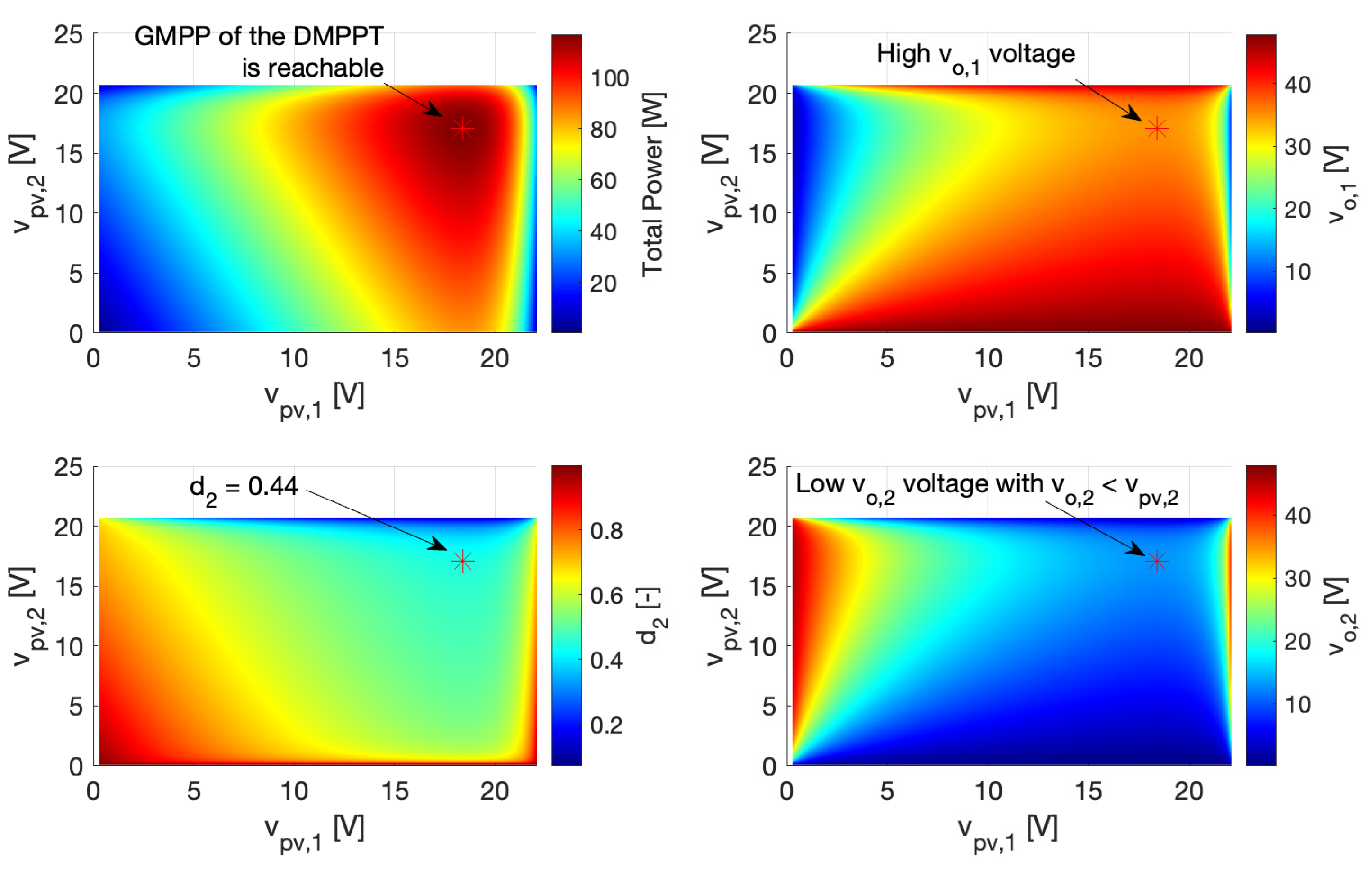
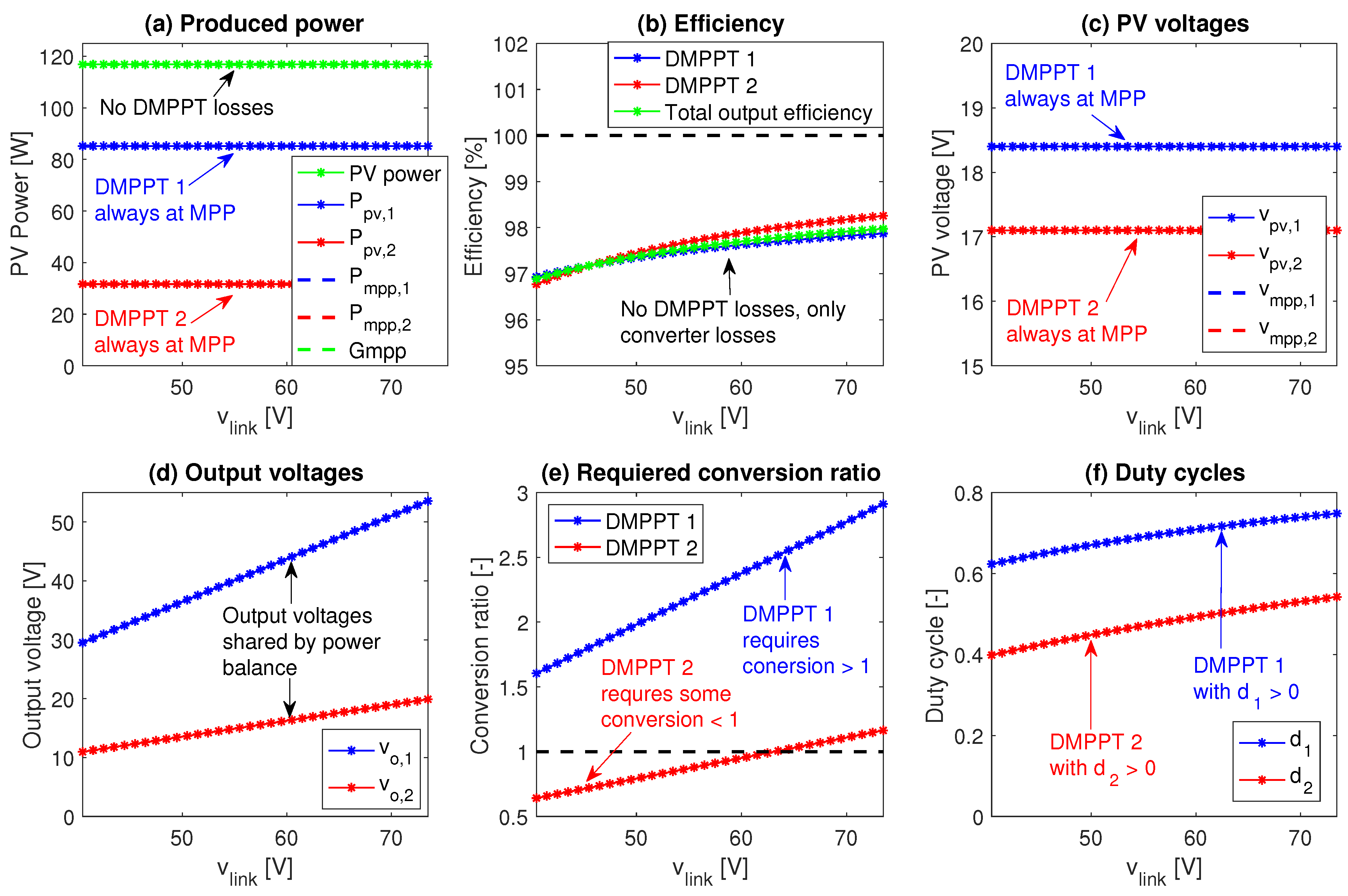
4.4. Discussion of the Cross-Coupling Problem in DMPPT Solutions
- The output voltage of a DMPPT unit depends on the power balance between all the DMPPT units; hence, it could be changed by irradiance perturbations on the other DMPPT units.
- Depending on the power balance between all the DMPPT units, a partially-shaded DMPPT unit could have an output voltage lower than the PV voltage.
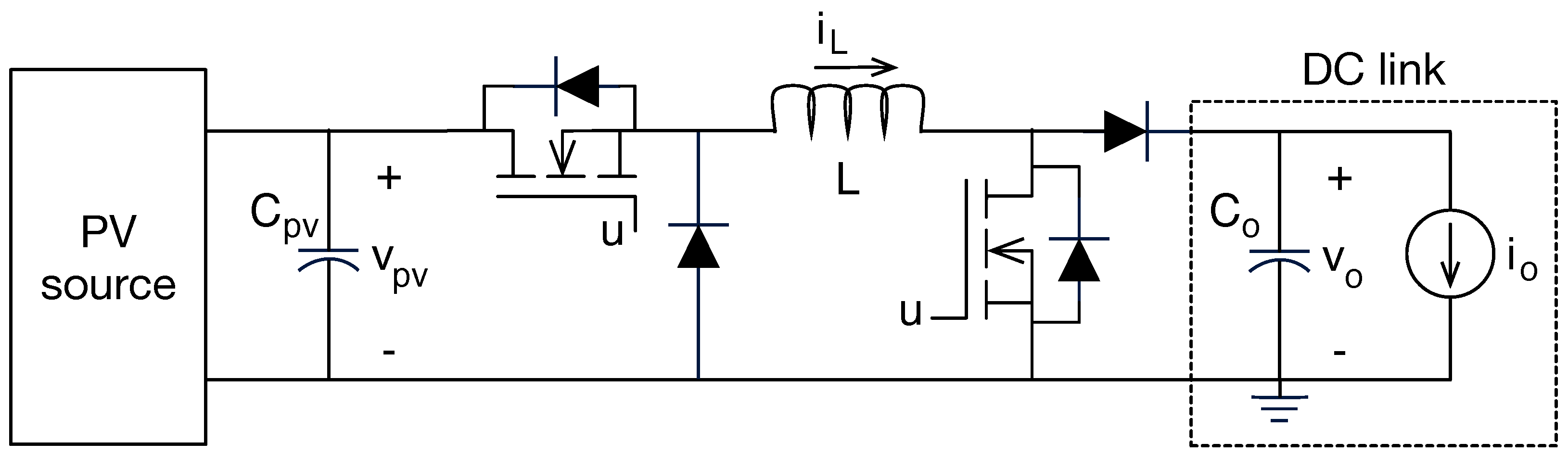
4.4.1. Boost-Based DMPPT Units
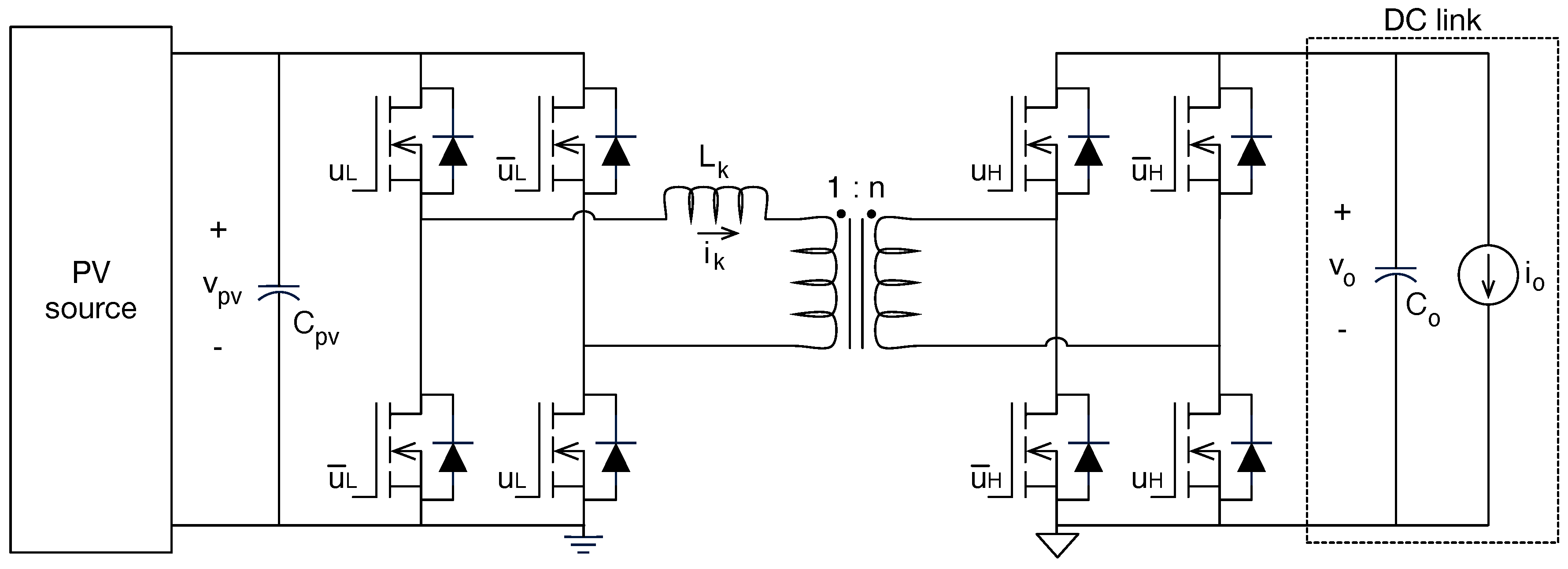
4.4.2. Buck-Boost and Flyback-Based DMPPT Units
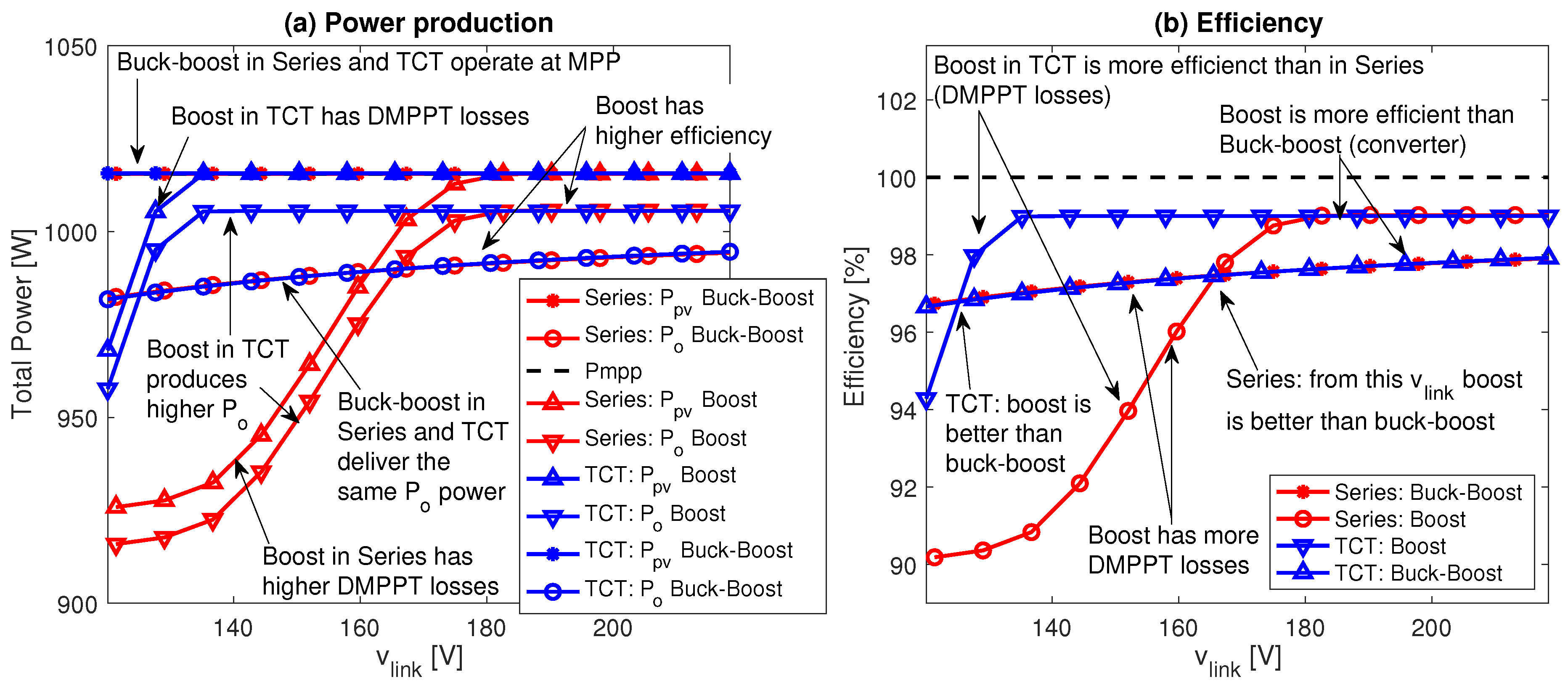
4.4.3. Comparison of Large DMPPT Systems with Series and TCT Connections
- Series connection is unavoidable for small DMPPT systems if a boosting factor is needed.
- For large DMPPT systems, the TCT connection is a viable option to be combined with boost converters.
- For small DC-link voltages, it is better to adopt Series connection with buck-boost (or flyback) converters, since those topologies are not subjected to cross-coupling (DMPPT) losses.
- Flyback DMPPT units are useful to introduce galvanic isolation, but increasing the turn-ratio of the transformer also reduces the system efficiency.
5. Conclusions
- Mixed PV array configuration combines the advantages of series–parallel connections, improving resilience to partial shading.
- MPPT algorithms should be selected considering their ability to handle both dynamic shading conditions and progressive degradation of the panels.
- Distributed architecture (DMPPT) demonstrates superiority over centralized systems, particularly in urban environments with complex shading patterns.
- Implementing a DC bus complementary to the conventional AC system optimizes energy efficiency by reducing conversion losses.
- The panel’s electrical model selection (1 or 2 diodes) should correspond to the specific PV technology used in the architectural integration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SDG | Sustainable Development Goals |
| NZEB | Net Zero Energy Buildings |
| BIPV | Building Integrated Photovoltaic |
| MPP | Maximum Power Point |
| GMPP | Global MPP |
| MPPT | MPP Tracking |
| LMPPT | Local MPPT |
| DMPPT | Distributed MPPT |
| CMPPT | Centralized MPPT |
| ESS | Energy Storage Systems |
| PHESS | Pumped Hydro ESS |
| CAESS | Compressed Air ESS |
| FESS | Flywheel ESS |
| BESS | Battery ESS |
| WWR | Window-to-Wall-Ratio |
| HVAC | Heating, Ventilation, and Air Conditioning |
| BSC | Bifacial Solar Cell |
| DPP | Differential Power Processing |
| DC | Direct Current |
| AC | Alternating Current |
| S | Series |
| P | Parallel |
| SP | Series–Parallel |
| TCT | Total-Cross-Tied |
| P&O | Perturb and Observe |
| IC | Incremental Conductance |
| AI | Artificial Intelligence |
| PV | Photovoltaic |
| EV | Electric Vehicle |
| V2G | Vehicle-to-Grid |
| WBG | Wide BandGap |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| PI | Proportional Integral |
| FLC | Fuzzy Logic Controller |
| 3SVSS | Three-Stage Variable Step Size |
| 2SVSS | Two-Stage Variable Step Size |
| DCL | Double Closed-Loop |
| CCM | Continuous Conduction Mode |
| DCM | Discontinuous Conduction Mode |
| PSC | Perovskite Solar Cell |
| S&H | Sample and Hold |
| BBSM | Buck-Boost Single stage Microinverter |
| SWT | Scanning Window Technique |
| L-M | Lavenberg-Marquardt |
| FF | Fill Factor |
| ESA | Estimation Solar Angle |
| DAB | Dual Active Bridge |
| IIBC | Isolated-Interleaved Boost Converter |
| RGA | Reserve Generation Algorithm |
| SMC | Sliding-Mode Controller |
References
- Ross, J. (Ed.) The Sustainable Development Goals Report: Special Edition Towards a Rescue Plan for People and Planet; United Nations, Department of Economic and Social Affairs Statistics Division: New York, NY, USA, 2023. [Google Scholar]
- Ahmed, V.; Saboor, S.; Ahmed Alshamsi, H.; Ahmed Almarzooqi, F.; Abdalla Alketbi, M.; Ahmed Al Marei, F. Net-zero energy buildings and the sustainable development goals. In The Elgar Companion to the Built Environment and the Sustainable Development Goals; Opoku, A., Ed.; Edward Elgar Publishing: Cheltenham, UK, 2024; pp. 196–216. [Google Scholar] [CrossRef]
- Razzaq, I.; Amjad, M.; Qamar, A.; Asim, M.; Ishfaq, K.; Razzaq, A.; Mawra, K. Reduction in energy consumption and CO2 emissions by retrofitting an existing building to a net zero energy building for the implementation of SDGs 7 and 13. Front. Environ. Sci. 2023, 10, 1028793. [Google Scholar] [CrossRef]
- Scherz, M.; Passer, A.; Kreiner, H. Challenges in the achievement of a Net Zero Carbon Built Environment—A systemic approach to support the decision-aiding process in the design stage of buildings. IOP Conf. Ser. Earth Environ. Sci. 2020, 588, 032034. [Google Scholar] [CrossRef]
- Martín Chivelet, N.; Kapsis, C.; Frontini, F. (Eds.) Building-Integrated Photovoltaics: A Technical Guidebook; Routledge: New York, NY, USA, 2025. [Google Scholar]
- Awuku, S.A.; Bennadji, A.; Muhammad-Sukki, F.; Sellami, N. Myth or gold? The power of aesthetics in the adoption of building integrated photovoltaics (BIPVs). Energy Nexus 2021, 4, 100021. [Google Scholar] [CrossRef]
- Alshareef, R.S.; Maghrabie, H.M. Building-Integrated Photovoltaics with Energy Storage Systems—A Comprehensive Review. J. Energy Storage 2025, 116, 115916. [Google Scholar] [CrossRef]
- Chen, L.; Baghoolizadeh, M.; Basem, A.; Ali, S.H.; Ruhani, B.; Sultan, A.J.; Salahshour, S.; Alizadeh, A. A Comprehensive Review of a Building-Integrated Photovoltaic System (BIPV). Int. Commun. Heat Mass Transf. 2024, 159, 108056. [Google Scholar] [CrossRef]
- Belloni, E.; Bianchini, G.; Casini, M.; Faba, A.; Intravaia, M.; Laudani, A.; Lozito, G.M. An Overview on Building-Integrated Photovoltaics: Technological Solutions, Modeling, and Control. Energy Build. 2024, 324, 114867. [Google Scholar] [CrossRef]
- Constantinou, S.; Al-naemi, F.; Alrashidi, H.; Mallick, T.; Issa, W. A Review on Technological and Urban Sustainability Perspectives of Advanced Building-integrated Photovoltaics. Energy Sci. Eng. 2024, 12, 1265–1293. [Google Scholar] [CrossRef]
- Pelle, M.; Causone, F.; Maturi, L.; Moser, D. Opaque Coloured Building Integrated Photovoltaic (BIPV): A Review of Models and Simulation Frameworks for Performance Optimisation. Energies 2023, 16, 1991. [Google Scholar] [CrossRef]
- Martín-Chivelet, N.; Kapsis, K.; Wilson, H.R.; Delisle, V.; Yang, R.; Olivieri, L.; Polo, J.; Eisenlohr, J.; Ray, B.; Maturi, L.; et al. Building-Integrated Photovoltaic (BIPV) Products and Systems: A Review of Energy-Related Behavior. Energy Build. 2022, 262, 111998. [Google Scholar] [CrossRef]
- Kuhn, T.E.; Erban, C.; Heinrich, M.; Eisenlohr, J.; Ensslen, F.; Neuhaus, D.H. Review of Technological Design Options for Building Integrated Photovoltaics (BIPV). Energy Build. 2021, 231, 110381. [Google Scholar] [CrossRef]
- Abdullahi, M.M.; Mas’ud, A.A.; Mas’ud, I.A.; Ardila-Rey, J.A.; Muhammad-Sukki, F.; Karim, R.; Saudi, A.S.M.; Bani, N.A.; Wirba, A.V. A Review of Building Integrated Photovoltaic: Case Study of Tropical Climatic Regions. Int. J. Power Electron. Drive Syst. (IJPEDS) 2021, 12, 474. [Google Scholar] [CrossRef]
- Spiliotis, K.; Gonçalves, J.E.; Saelens, D.; Baert, K.; Driesen, J. Electrical System Architectures for Building-Integrated Photovoltaics: A Comparative Analysis Using a Modelling Framework in Modelica. Appl. Energy 2020, 261, 114247. [Google Scholar] [CrossRef]
- Ravyts, S.; Vecchia, M.D.; Broeck, G.V.D.; Driesen, J. Review on Building-Integrated Photovoltaics Electrical System Requirements and Module-Integrated Converter Recommendations. Energies 2020, 12, 1532. [Google Scholar] [CrossRef]
- Biyik, E.; Araz, M.; Hepbasli, A.; Shahrestani, M.; Yao, R.; Shao, L.; Essah, E.; Oliviera, A.C.; del Caño, T.; Rico, E.; et al. A Key Review of Building Integrated Photovoltaic (BIPV) Systems. Eng. Sci. Technol. Int. J. 2017, 20, 833–858. [Google Scholar] [CrossRef]
- Heinstein, P.; Ballif, C.; Perret-Aebi, L.-E. Building Integrated Photovoltaics (BIPV): Review, Potentials, Barriers and Myths. Green 2013, 3, 125–156. [Google Scholar] [CrossRef]
- Lee, K.H.; Song, Y.H. Analysis of Energy Reduction and Energy Self-Sufficiency Improvement Effects by Applying a Bidirectional Reflectance PV Array with Integrated External Shading at a School Building. Buildings 2023, 13, 2915. [Google Scholar] [CrossRef]
- Mehedi, I.; Salam, Z.; Ramli, M.; Chin, V.; Bassi, H.; Rawa, M.; Abdullah, M. Critical evaluation and review of partial shading mitigation methods for grid-connected PV system using hardware solutions: The module-level and array-level approaches. Renew. Sustain. Energy Rev. 2021, 146, 111138. [Google Scholar] [CrossRef]
- Al-Janahi, S.A.; Ellabban, O.; Al-Ghamdi, S.G. A Novel BIPV Reconfiguration Algorithm for Maximum Power Generation under Partial Shading. Energies 2020, 13, 4470. [Google Scholar] [CrossRef]
- Başoğlu, M.E. Analysis of The Performance Of The Distributed Maximum Power Point Tracking In Building Integrated Photovoltaic Systems. In Proceedings of the 2023 8th International Symposium on Electrical and Electronics Engineering (ISEEE), Galati, Romania, 26–28 October 2023; pp. 187–192. [Google Scholar] [CrossRef]
- Başoğlu, M.E. Comprehensive review on distributed maximum power point tracking: Submodule level and module level MPPT strategies. Sol. Energy 2022, 241, 85–108. [Google Scholar] [CrossRef]
- Kumar Yadav, V.; Yadav, R.; Singh, R.; Mishra, I.; Ganvir, I.; Manish. Reconfiguration of PV array through recursive addition approach for optimal power extraction under PSC. Energy Convers. Manag. 2023, 292, 117412. [Google Scholar] [CrossRef]
- Bonthagorla, P.K.; Mikkili, S. A Combined Adaptive Coefficient Particle Swarm Optimization MPPT approach and TT configured PV Array to Enhance Maximum Power under PSC. In Proceedings of the 2022 IEEE 1st Industrial Electronics Society Annual On-Line Conference (ONCON), Kharagpur, India, 9–11 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Varma, G.H.K.; Barry, V.R.; Jain, R.K. A Total-Cross-Tied-Based Dynamic Photovoltaic Array Reconfiguration for Water Pumping System. IEEE Access 2022, 10, 4832–4843. [Google Scholar] [CrossRef]
- Appelbaum, J.; Aronescu, A.; Maor, T. Shading by Overhang PV Collectors. Appl. Sci. 2019, 9, 4280. [Google Scholar] [CrossRef]
- Yang, S.; Fiorito, F.; Sproul, A.; Prasad, D. Optimising Design Parameters of a Building-Integrated Photovoltaic Double-Skin Facade in Different Climate Zones in Australia. Buildings 2023, 13, 1096. [Google Scholar] [CrossRef]
- Olatunji, S.I.; Marzki, A.; Ng, A.; Ukeagbu, I.A. Perovskite PV MPPT Design for BIPV Application. In Proceedings of the 2023 IEEE 3rd International Conference in Power Engineering Applications (ICPEA), Putrajaya, Malaysia, 6–7 March 2023; pp. 323–327. [Google Scholar] [CrossRef]
- Zekorn, T.; Weihs, L.; Vohl, K.; Hanhart, M.; Rolff, L.; Wunderlich, R.; Heinen, S. Long Term Evaluation of a Pantile-based Maximum Power Point Tracking DC-DC Power Converter for Solar Roof Tiles. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Pendem, S.R.; Mikkili, S. Assessment of Cross-coupling Effects in PV String-integrated-converters with P&O MPPT Algorithm Under Various Partial Shading Patterns. CSEE J. Power Energy Syst. 2022, 8, 1013–1028. [Google Scholar] [CrossRef]
- Sarkar, D.; Sahoo, R.K.; Kumar, A.; Sadhu, P.K. Comprehensive performance analysis of different MPPT algorithms for Building Integrated Photovoltaic system. In Proceedings of the 2021 IEEE Mysore Sub Section International Conference (MysuruCon), Hassan, India, 24–25 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mathew, D.; Farrag, M.E.; Naidu, R.C.; Muthu, R.K.; Sivaprakasam, A.; Somasundaram, P. Buck-Boost Single-Stage Microinverter for Building Integrated Photovoltaic Systems. Energies 2021, 14, 7854. [Google Scholar] [CrossRef]
- Pendem, S.R.; Mikkili, S.; Bonthagorla, P.K. PV Distributed-MPP Tracking: Total-Cross-Tied Configuration of String-Integrated-Converters to Extract the Maximum Power Under Various PSCs. IEEE Syst. J. 2020, 14, 1046–1057. [Google Scholar] [CrossRef]
- Wang, Y.H.; Liu, W.C.; Kuo, T.H. A 200W MPPT Boost Converter for BIPV Applications with Integrated Controller. In Proceedings of the 2014 International Symposium on Computer, Consumer and Control, Taichung, Taiwan, 10–12 June 2014; pp. 288–291. [Google Scholar] [CrossRef]
- Mazumdar, P.; Enjeti, P.N.; Balog, R.S. Analysis and Design of Smart PV Modules. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 451–459. [Google Scholar] [CrossRef]
- Elmakawi, A.; Bayındır, K. A High-Gain Non-Isolated Three-Port Converter for Building-Integrated PV Systems. Electronics 2022, 11, 387. [Google Scholar] [CrossRef]
- Kolhe, M.L.; Rasul, M. 3-Phase grid-connected building integrated photovoltaic system with reactive power control capability. Renew. Energy 2020, 154, 1065–1075. [Google Scholar] [CrossRef]
- Jois, S.; Bhosale, R.; Ramamritham, K.; Agarwal, V. Novel Scheme For Extracting Maximum Power From Façade Based Building Integrated Photovoltaics. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019; pp. 2053–2059. [Google Scholar] [CrossRef]
- Demir, Y.C.; Aktacir, M.A. Experimental Investigation of the BIPV System under Şanlıurfa Meteorological Conditions. Appl. Sci. 2023, 13, 11286. [Google Scholar] [CrossRef]
- Pradhan, C.; Senapati, M.K.; Ntiakoh, N.K.; Calay, R.K. Roach Infestation Optimization MPPT Algorithm for Solar Photovoltaic System. Electronics 2022, 11, 927. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Zhang, J.; Zhang, Y.; Zhu, Z. A Novel Maximum Power Point Tracking Control Strategy for the Building Integrated Photovoltaic System. Energies 2020, 13, 2679. [Google Scholar] [CrossRef]
- Sharma, P.; Duttagupta, S.P.; Agarwal, V. A Novel Approach for Maximum Power Tracking From Curved Thin-Film Solar Photovoltaic Arrays Under Changing Environmental Conditions. IEEE Trans. Ind. Appl. 2014, 50, 4142–4151. [Google Scholar] [CrossRef]
- Eum, J.; Park, S.; Choi, H.J. Effects of Power Optimizer Application in a Building-Integrated Photovoltaic System According to Shade Conditions. Buildings 2023, 14, 53. [Google Scholar] [CrossRef]
- Kalogerakis, C.; Koutroulis, E.; Lagoudakis, M.G. Global MPPT Based on Machine-Learning for PV Arrays Operating under Partial Shading Conditions. Appl. Sci. 2020, 10, 700. [Google Scholar] [CrossRef]
- Kumar T.M., S.; Sharma, S.; Kurian, C.P.; Varghese S., M.; George, A.M. Adaptive Neuro-fuzzy Control of Solar-Powered Building Integrated with Daylight-Artificial Light System. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Kerala, India, 2–4 January 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Iam, I.W.; Ding, Z.; Huang, Z.; Lam, C.S.; Martins, R.P.; Mak, P.I. A Flexible Rooftop Photovoltaic-Inductive Wireless Power Transfer System for Low-Voltage DC Grid. IEEE Access 2023, 11, 51117–51132. [Google Scholar] [CrossRef]
- Kumari, P.; Kumar, N.; Panigrahi, B.K. A Framework of Reduced Sensor Rooftop SPV System Using Parabolic Curve Fitting MPPT Technology for Household Consumers. IEEE Trans. Consum. Electron. 2023, 69, 29–37. [Google Scholar] [CrossRef]
- Yadav, V.K.; Yadav, A.; Yadav, R.; Mittal, A.; Wazir, N.H.; Gupta, S.; Pachauri, R.K.; Ghosh, S. A novel reconfiguration technique for improvement of PV reliability. Renew. Energy 2022, 182, 508–520. [Google Scholar] [CrossRef]
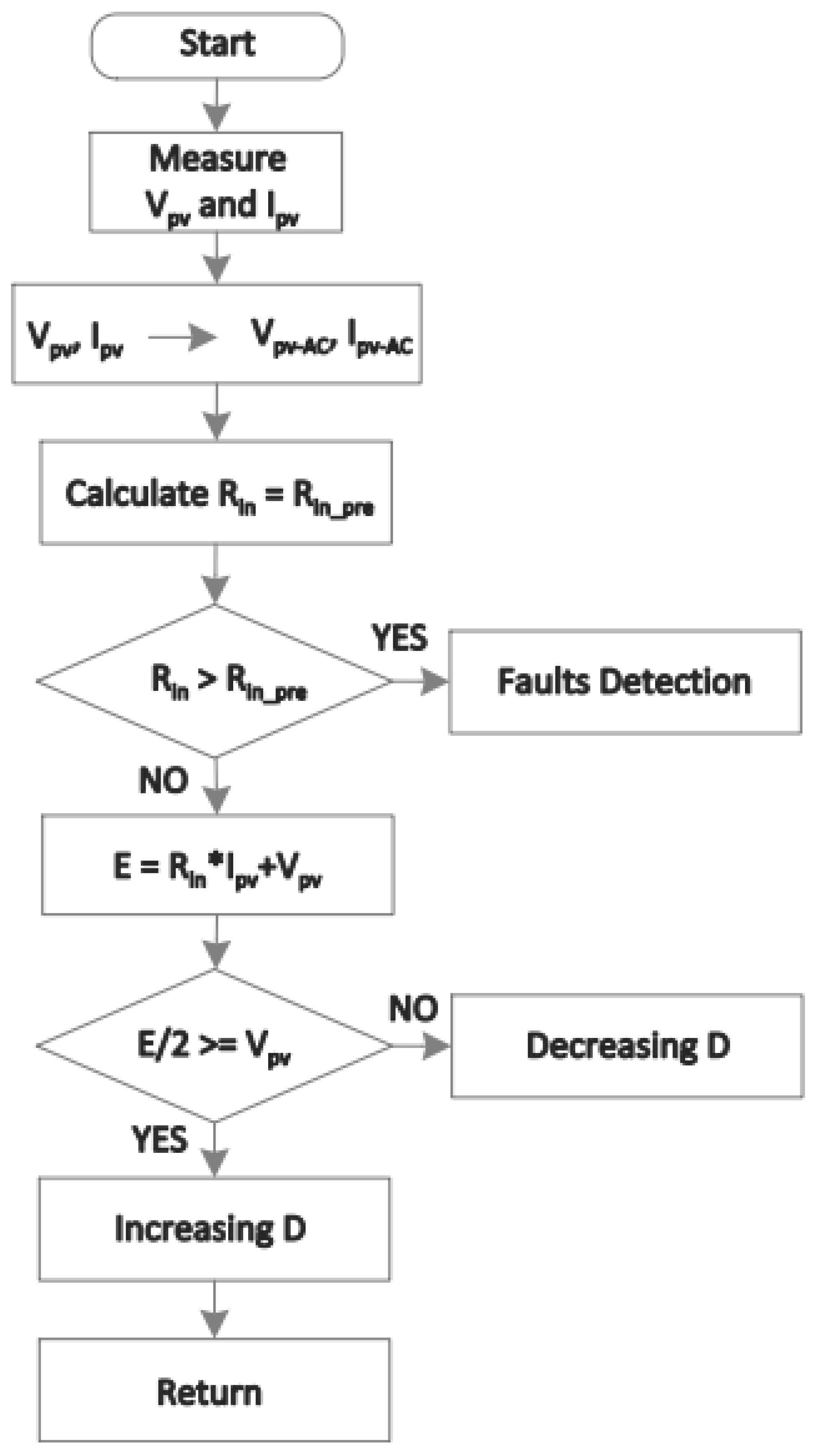
- Zheng, Z.; Nakajima, A.; Masukawa, S. A simple MPPT-Based Fault Detection Technique for a Photovoltaic Array System using Input Current and Voltage Ripples. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 309–313. [Google Scholar] [CrossRef]
- Chub, A.; Vinnikov, D.; Korkh, O.; Malinowski, M.; Kouro, S. Ultrawide Voltage Gain Range Microconverter for Integration of Silicon and Thin-Film Photovoltaic Modules in DC Microgrids. IEEE Trans. Power Electron. 2021, 36, 13763–13778. [Google Scholar] [CrossRef]
- Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. Photovoltaic Sources Modeling, 1st ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Al-Samawi, A.A.; Alkhafaji, A.S.; Atiyah, A.S.; Trabelsi, H. Review Mitigation Methods of Partial Shading Condition for PV System. In Proceedings of the 2024 21st International Multi-Conference on Systems, Signals & Devices (SSD), Erbil, Iraq, 22–25 April 2024; pp. 401–410. [Google Scholar] [CrossRef]
- Niazi, K.A.K.; Kerekes, T.; Dolara, A.; Yang, Y.; Leva, S. Performance Assessment of Mismatch Mitigation Methodologies Using Field Data in Solar Photovoltaic Systems. Electronics 2022, 11, 1938. [Google Scholar] [CrossRef]
- Alves, T.; N. Torres, J.P.; Marques Lameirinhas, R.A.; F. Fernandes, C.A. Different Techniques to Mitigate Partial Shading in Photovoltaic Panels. Energies 2021, 14, 3863. [Google Scholar] [CrossRef]
- Zeeshan, M.; Islam, N.U.; Faizullah, F.; Khalil, I.U.; Park, J. A Novel Row Index Mathematical Procedure for the Mitigation of PV Output Power Losses during Partial Shading Conditions. Symmetry 2023, 15, 768. [Google Scholar] [CrossRef]
- Osmani, K.; Haddad, A.; Jaber, H.; Lemenand, T.; Castanier, B.; Ramadan, M. Mitigating the effects of partial shading on PV system’s performance through PV array reconfiguration: A review. Therm. Sci. Eng. Prog. 2022, 31, 101280. [Google Scholar] [CrossRef]
- Yang, B.; Ye, H.; Wang, J.; Li, J.; Wu, S.; Li, Y.; Shu, H.; Ren, Y.; Ye, H. PV arrays reconfiguration for partial shading mitigation: Recent advances, challenges and perspectives. Energy Convers. Manag. 2021, 247, 114738. [Google Scholar] [CrossRef]
- Youssef, A.R.; Hefny, M.M.; Ali, A.I.M. Partial Shading Mitigation Approaches for PV Generation Systems: A Review. In Proceedings of the 2023 24th International Middle East Power System Conference (MEPCON), Mansoura, Egypt, 19–21 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Belhachat, F.; Larbes, C. Photovoltaic Array Reconfiguration Strategies for Mitigating Partial Shading Effects: Recent Advances and Perspectives. Energy Convers. Manag. 2024, 313, 118547. [Google Scholar] [CrossRef]
- Santos De Araújo, J.V.; De Lucena, M.P.; Da Silva Netto, A.V.; Da Silva Vitorino Gomes, F.; De Oliveira, K.C.; De Souza Neto, J.M.R.; Cavalcante, S.L.; Valer Morales, L.R.; Villanueva, J.M.M.; Tavares De Macedo, E.C. Solar Tracking Control Algorithm Based on Artificial Intelligence Applied to Large-Scale Bifacial Photovoltaic Power Plants. Sensors 2024, 24, 3890. [Google Scholar] [CrossRef]
- Yan, H.W.; Liang, G.; Farivar, G.G.; Tafti, H.D.; Beniwal, N.; Pou, J. Enhanced Energy Storage Utilization Under Partial Shading Conditions in a Microgrid with Flexible Photovoltaic Power Control. In Proceedings of the 2024 International Conference on Electrical, Computer and Energy Technologies (ICECET), Sydney, Australia, 25–27 July 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar] [CrossRef]
- Rao, M.N.; Chaitanya, V.S.N.K. Experimental Analysis of Partial Shading on Solar Panels With Theuse of Aluminium Reflectors. In Proceedings of the 2020 IEEE International Conference on Advances and Developments in Electrical and Electronics Engineering (ICADEE), Coimbatore, India, 10–11 December 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Mohamed Hariri, M.H.; Mat Desa, M.K.; Masri, S.; Mohd Zainuri, M.A.A. Grid-Connected PV Generation System—Components and Challenges: A Review. Energies 2020, 13, 4279. [Google Scholar] [CrossRef]
- Kabalcı, E. Review on novel single-phase grid-connected solar inverters: Circuits and control methods. Sol. Energy 2020, 198, 247–274. [Google Scholar] [CrossRef]
- Chub, A.; Korkh, O.; Kosenko, R.; Vinnikov, D. Novel Approach Immune to Partial Shading for Photovoltaic Energy Harvesting from Building Integrated PV (BIPV) Solar Roofs. In Proceedings of the 2018 20th European Conference on Power Electronics and Applications (EPE’18 ECCE Europe), Riga, Latvia, 17–21 September 2018; pp. P.1–P.10. [Google Scholar]
- Wang, X.; Wen, H.; Chu, G.; Zhou, J. Cost-effective and extensible LLC-resonant voltage-multiplier-based differential power processing optimizer for mismatched photovoltaic systems. Sol. Energy 2021, 225, 501–516. [Google Scholar] [CrossRef]
- Bastidas-Rodríguez, J.; Trejos-Grisales, A.; González-Montoya, D.; Ramos-Paja, C.A.; Petrone, G.; Spagnuolo, G. General modeling procedure for photovoltaic arrays. Electr. Power Syst. Res. 2018, 155, 67–79. [Google Scholar] [CrossRef]
- Gelani, H.E.; Dastgeer, F.; Nasir, M.; Khan, S.; Guerrero, J.M. AC vs. DC Distribution Efficiency: Are We on the Right Path? Energies 2021, 14, 4039. [Google Scholar] [CrossRef]
- Dastgeer, F.; Gelani, H.E. A Comparative analysis of system efficiency for AC and DC residential power distribution paradigms. Energy Build. 2017, 138, 648–654. [Google Scholar] [CrossRef]
- Starke, M.; Tolbert, L.M.; Ozpineci, B. AC vs. DC distribution: A loss comparison. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Hassan, S.J.U.; Mehdi, A.; Haider, Z.; Song, J.S.; Abraham, A.D.; Shin, G.S.; Kim, C.H. Towards medium voltage hybrid AC/DC distribution Systems: Architectural Topologies, planning and operation. Int. J. Electr. Power Energy Syst. 2024, 159, 110003. [Google Scholar] [CrossRef]
- Charadi, S.; Chaibi, Y.; Redouane, A.; Allouhi, A.; El Hasnaoui, A.; Mahmoudi, H. Efficiency and energy-loss analysis for hybrid AC/DC distribution systems and microgrids: A review. Int. Trans. Electr. Energy Syst. 2021, 31, e13203. [Google Scholar] [CrossRef]
- Alshammari, M.; Duffy, M. Bidirectional Synchronous H6 Inverter for Hybrid AC/DC Distribution System With Improved Light Load Efficiency. IEEE Access 2023, 11, 13138–13151. [Google Scholar] [CrossRef]
- Yang, L.; Peng, J.; Yang, F.; Zhang, Y.; Wu, H. Single-Phase High-Gain Bidirectional DC/AC Converter Based on High Step-up/Step-down DC/DC Converter and Dual-Input DC/AC Converter. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 554–559. [Google Scholar] [CrossRef]
- Mohamed, A.; Elshaer, M.; Mohammed, O. Bi-Directional AC-DC/DC-AC Converter for Power Sharing of Hybrid AC/DC Systems. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Advantics. ADM-PC-BP25 User Manual. ADVANTICS Eurl. 2017. Available online: https://advantics.github.io/documentation/#/power-modules/ADM-PC-BP25/servicing (accessed on 10 January 2025).
- Ekici, E.; Koroglu, T.; Çelik, Ö. Design and Analysis of Two-Stage Bidirectional Power Converter for Vehicle-to-Grid Technology with Fuel Cell-Battery Electric Vehicle. J. Energy Storage 2025, 106, 114792. [Google Scholar] [CrossRef]
- Pouresmaeil, K.; Duarte, J.; Wijnands, K. Single-Phase Bidirectional ZVZCS AC-DC Converter for MV-Connected Ultra-Fast Chargers. In Proceedings of the PCIM Europe 2022; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2022; VDE Verlag GMBH: Berlin, Germany, 2022. [Google Scholar] [CrossRef]
- Peng, T.; Yang, P.; Dan, H.; Wang, H.; Han, H.; Yang, J.; Wang, H.; Dong, H.; Wheeler, P. A Single-Phase Bidirectional AC/DC Converter for V2G Applications. Energies 2017, 10, 881. [Google Scholar] [CrossRef]
- Robledo, C.B.; Oldenbroek, V.; Abbruzzese, F.; Van Wijk, A.J.M. Integrating a Hydrogen Fuel Cell Electric Vehicle with Vehicle-to-Grid Technology, Photovoltaic Power and a Residential Building. Appl. Energy 2018, 215, 615–629. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Khaligh, A. A Single Stage Integrated Bidirectional AC/DC and DC/DC Converter for Plug-in Hybrid Electric Vehicles. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Valinejadshoubi, M.; Athienitis, A.K.; Bagchi, A.; Abtahi, M. Integrated Dynamic Photovoltaic Facade for Enhanced Building Comfort and Energy Efficiency. Biomimetics 2024, 9, 463. [Google Scholar] [CrossRef]
- Maghrabie, H.M.; Abdelkareem, M.A.; Al-Alami, A.H.; Ramadan, M.; Mushtaha, E.; Wilberforce, T.; Olabi, A.G. State-of-the-Art Technologies for Building-Integrated Photovoltaic Systems. Buildings 2021, 11, 383. [Google Scholar] [CrossRef]
- Olzhabay, Y.; Hamidi, M.N.; Ishak, D.; Marzuki, A.; Ng, A.; Ukaegbu, I.A. Performance Evaluation of Emerging Perovskite Photovoltaic Energy-Harvesting System for BIPV Applications. Smart Cities 2023, 6, 2430–2446. [Google Scholar] [CrossRef]
- Verma, P.; Kaur, T.; Kaur, R. Power control strategy of PV system for active power reserve under partial shading conditions. Int. J. Electr. Power Energy Syst. 2021, 130, 106951. [Google Scholar] [CrossRef]
- Hasan, M.M.; Jaman, S.; Geury, T.; Hegazy, O. Design and Simulation of a Grid-Connected Two-Stage Bidirectional Converter for a Combined PV-Stationary Energy Storage System. In Proceedings of the 2022 2nd International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Cassino, Italy, 23–25 November 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Hasan, M.M.; Jaman, S.; Geury, T.; Hegazy, O. Performance Assessment of a Grid-Connected Two-Stage Bidirectional Converter for a Combined PV–Battery Energy Storage System. Energies 2023, 16, 4486. [Google Scholar] [CrossRef]
- Sunddararaj, S.P.; Rangarajan, S.S.; Nallusamy, S.; Subramaniam, U.; Collins, E.R.; Senjyu, T. Design of Novel HG-SIQBC-Fed Multilevel Inverter for Standalone Microgrid Applications. Appl. Sci. 2022, 12, 9347. [Google Scholar] [CrossRef]
- Ismail, A.A.; Eldodor, M.; El-Deib, A.A. Development of a High Frequency Current Controlled Grid-connected Microinverter for PV Applications. In Proceedings of the 2022 23rd International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 13–15 December 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Ravyts, S.; Vecchia, M.D.; Van den Broeck, G.; Driesen, J. Experimental Comparison of the Efficiency, Power Density and Thermal Performance of Two BIPV Converter Prototypes. In Proceedings of the 2018 IEEE 6th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Atlanta, GA, USA, 31 October–2 November 2018; pp. 7–13. [Google Scholar] [CrossRef]
- Jain, P.; Singh, J.P.; Kumar Panda, S. Fault remediation for distributed photovoltaic (PV) system. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1057–1064. [Google Scholar] [CrossRef]
- Ravyts, S.; Van De Sande, W.; Vecchia, M.D.; Broeck, G.V.d.; Duraij, M.; Martinez, W.; Daenen, M.; Driesen, J. Practical Considerations for Designing Reliable DC/DC Converters, Applied to a BIPV Case. Energies 2020, 13, 834. [Google Scholar] [CrossRef]
- Ravyts, S.; Moschner, J.D.; Yordanov, G.H.; Van den Broeck, G.; Dalla Vecchia, M.; Manganiello, P.; Meuris, M.; Driesen, J. Impact of photovoltaic technology and feeder voltage level on the efficiency of façade building-integrated photovoltaic systems. Appl. Energy 2020, 269, 115039. [Google Scholar] [CrossRef]
- Fernández-Bustamante, P.; Calvo, I.; Villar, E.; Barambones, O. Centralized MPPT based on Sliding Mode Control and XBee 900 MHz for PV systems. Int. J. Electr. Power Energy Syst. 2023, 153, 109350. [Google Scholar] [CrossRef]



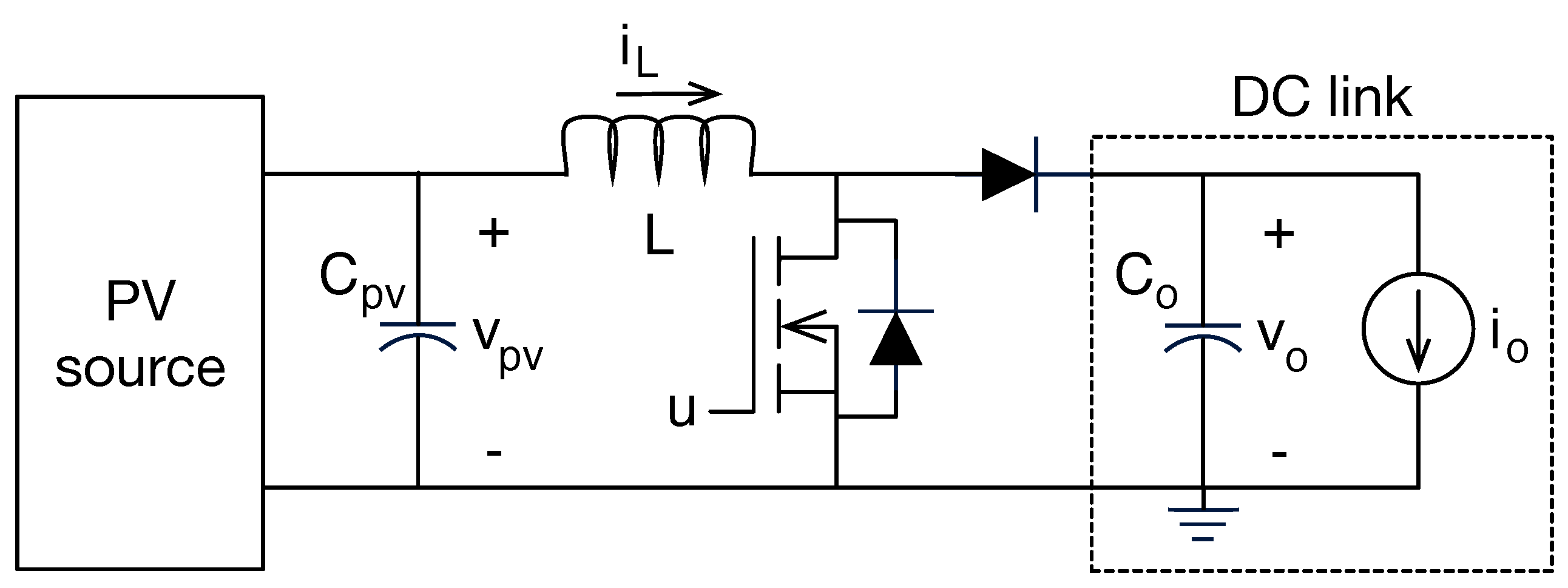
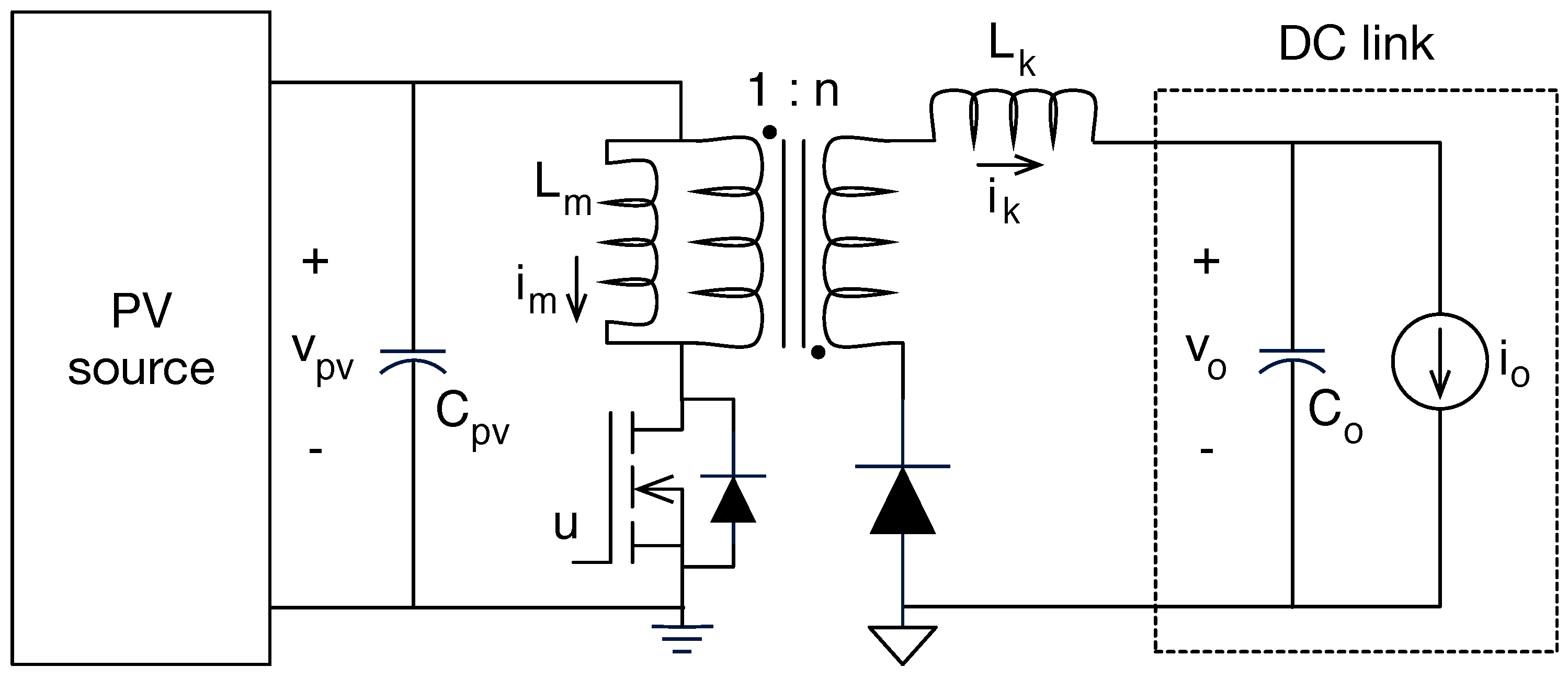
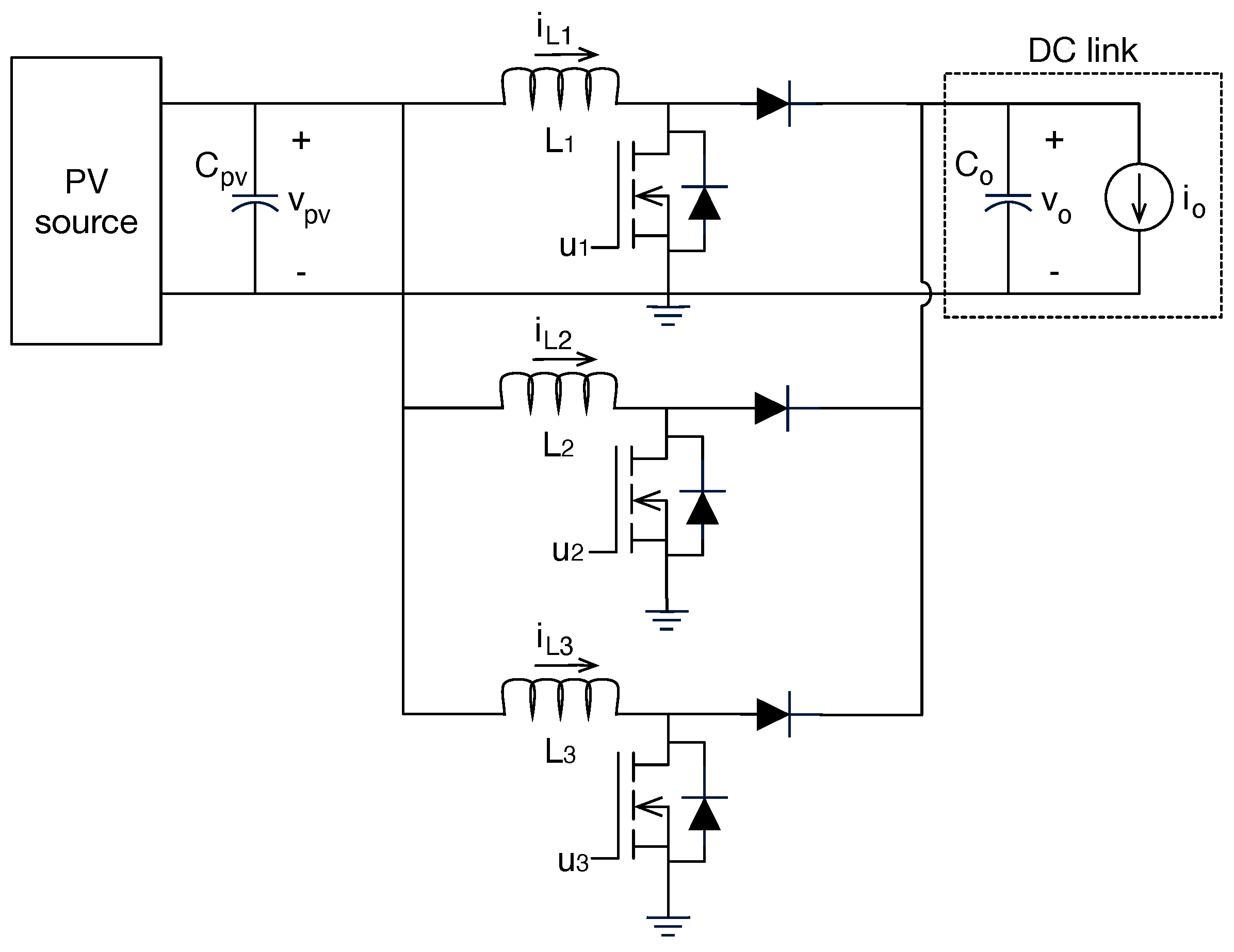
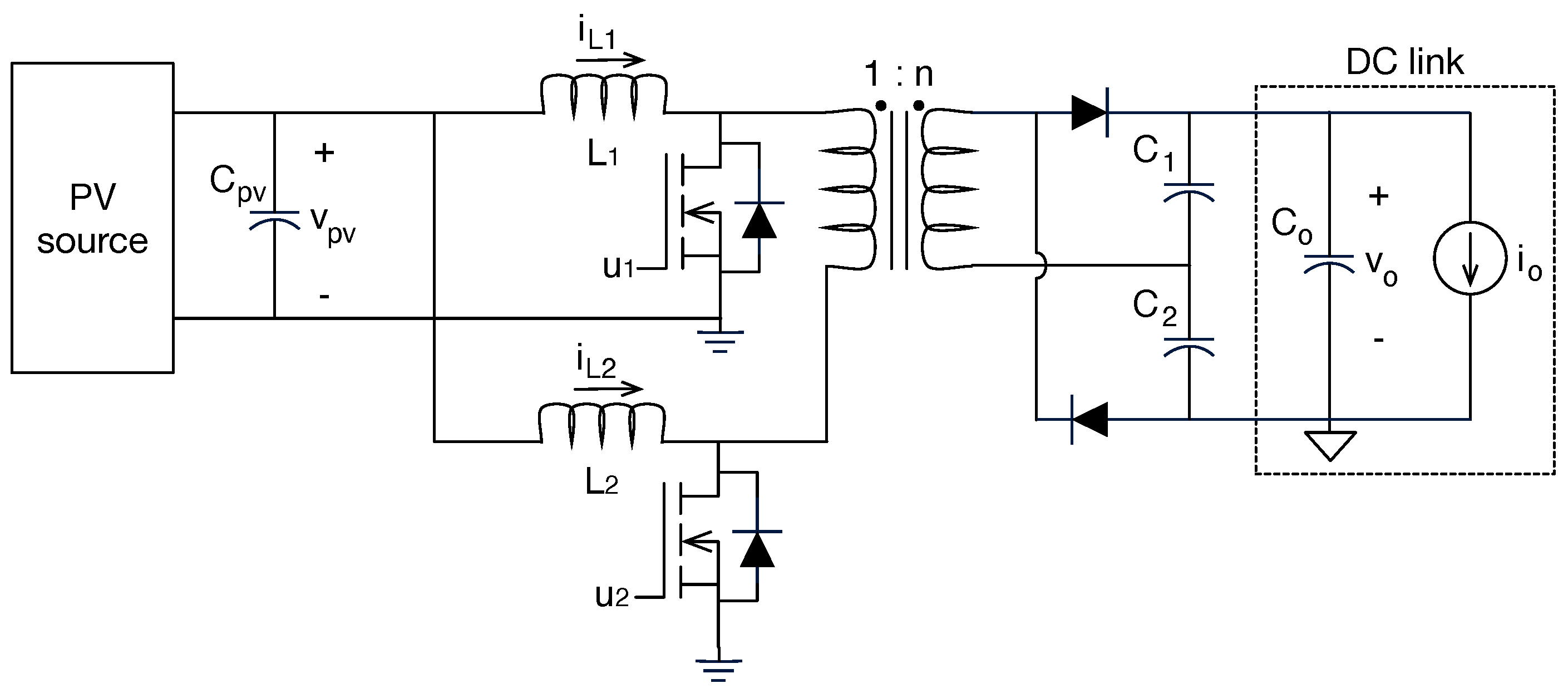

| Electrical Connection | Advantages | Disadvantages |
|---|---|---|
| Series (S) [15,19,20] | Increases system voltage; simplifies inverter design. | Failure of one panel significantly affects the others; panels with similar characteristics are required. |
| Parallel (P) [19] | Failure or shading of one panel does not affect the others; more tolerant of panels with different electrical characteristics. | Handles higher current levels than series; not useful for high voltage systems. |
| Mixed (SP) [13,15,19,20,21,22,23] | Combines the advantages of S and P systems; voltage and current adjustment; high fault tolerance. | More complex; requires balancing; can also be severely affected by partial shading. |
| Total-Cross-Tied (TCT) [19,20,21,24,25,26,27] | High energy efficiency; increased robustness; adaptability. | High complexity; high cost; high maintenance. |
| Algorithm | Advantages | Disadvantages |
|---|---|---|
| P&O [22,28,29,30,31,32,33,34,35,36] | Simple; low cost; quick response. | Oscillations; sensitive to partial shading. |
| IC [26,32,37,38,39] | High precision; less oscillations; better performance before partial shading. | Complexity; higher cost; sensitivity to noise. |
| Optimization [25,27,40,41,42,43] | High efficiency if partial shading is present; robustness; flexibility. | Computational complexity; high cost; slow convergence. |
| AI [32,44,45,46] | Adaptability; it is efficient with partial shading; high precision. | Complexity; high cost; data dependence. |
| Hybrids [47,48,49,50,51] | Improved efficiency; robustness; flexibility. | Complexity; high cost; difficulty of adjustment. |
| Partial Shading Mitigation Technique | Description |
|---|---|
| DMPPT [20,54,55] | Energy production is optimized, which is achieved by installing a DC/DC converter and its MPPT algorithm in each module; there are conditions under which it may not be possible to find the MPP; complex solution since it requires more elements than the CMPPT architecture. |
| CMPPT [55] | A single converter per string or substring and tries to optimize the power extraction of the entire panel group. It is generally less efficient than the system with DMPPT architecture. |
| Electrical configuration [55,56,57,58] | Multiple strings in parallel or with intermediate connections reduce the impact of shading on the overall system performance. |
| Bypass diode [54,55] | They are integrated into the solar panels, allowing the current to flow around the shaded cells. This avoids hot spots and improves performance, without completely eliminating losses. |
| Reconfiguration [20,56,57,58,59,60] | Seeking to match the electrical characteristics of the arrangements, losses in partial shading conditions are reduced. |
| Solar tracking systems [61] | Moving the panels to follow the trajectory of the sun throughout the day and reduce the angle of incidence minimizes shading caused by obstacles. |
| Storage systems [62] | Storing excess energy and releasing it during partial shading helps minimize power fluctuations. |
| Reflectors [63] | With fixed obstacles, the use of reflectors increases the irradiation on the panels. |
| Cleaning and maintenance | A periodic inspection to correct shading due to dirt, dust, and other obstacles can be very useful. |
| Characteristics | DMPPT | CMPPT |
|---|---|---|
| Granularity | Panel or small group of panels | Complete Panel Array |
| Complexity | High—multiple converters | Low—single converter |
| Cost | High—more hardware | Low—less hardware |
| Efficiency in partial shading | High | Low |
| Scalability | Flexible | Limited—requires redesign for expansion |
| Typical applications | Residential, commercial, buildings, dynamic environments | Large solar plants, uniform conditions |
| Dynamic response | Quick—independent adjustment by panel | Slow—centralized adjustment |
| String 1 | String 2 | String 3 | |
|---|---|---|---|
| Row 1 | 800 W/m2 | 800 W/m2 | 1000 W/m2 |
| Row 2 | 800 W/m2 | 800 W/m2 | 1000 W/m2 |
| Row 3 | 500 W/m2 | 500 W/m2 | 1000 W/m2 |
| Row 4 | 400 W/m2 | 400 W/m2 | 1000 W/m2 |
| Row 5 | 300 W/m2 | 300 W/m2 | 1000 W/m2 |
| Row 6 | 300 W/m2 | 300 W/m2 | 1000 W/m2 |
| Bus | Advantages | Disadvantages |
|---|---|---|
| DC [69,70,71] | Transmission losses are lower than in an AC bus; simpler, less costs, less losses since the generation is DC. | It is not easily integrated into existing facilities; it requires DC–AC conversion to feed traditional AC loads (more costs, more losses); it has no standards. |
| AC [69,71] | Wide availability of equipment; compatible with available infrastructure; easy analysis of PF; supported by standards. | Requires AC–DC conversion to feed DC loads (more complex, more costs, more losses); transmission losses are greater than those of the DC bus; requires synchronization with the grid. |
| Hybrid [72,73] | Better cost-benefit ratio; system with the lowest losses because it has both buses. | There are no standards; the control and analysis of the PF is more complex. |
| Technology | Electric Model | Efficiency | Cost | Typical Applications |
|---|---|---|---|---|
| Monocrystalline silicon [83] | 1 or 2 diodes | 18–22% | High | Residential, commercial, industrial |
| Polycrystalline silicon [83,84] | 1 or 2 diodes | 15–18% | Moderate | Residential, commercial |
| Thin-Film (a-Si) [40,42,84,85,86] | 1 diode | 6–10% | Low | BIPV, mobile devices |
| Thin-Film (CdTe) [84] | 1 diode | 10–12% | Low | Large solar plants |
| Thin-Film (CIGS) [40,85,86] | 1 diode | 12–14% | Low | BIPV, mobile devices |
| Perovskita [9,86] | 1 diode | Up to 25% | Low | Research, emerging applications |
| MPPT | Irradiance (W/m2) | Maximum Power from BIPV (kW) | Maximum Power Tracked by MPPT (kW) | Efficiency (%) |
|---|---|---|---|---|
| IC | 600 | 16.2 | 15.81 | 97.59 |
| P&O | 15.91 | 98.20 | ||
| FLC | 15.94 | 98.39 | ||
| IC | 800 | 21.7 | 20.98 | 96.68 |
| P&O | 21.02 | 96.86 | ||
| FLC | 21.16 | 97.51 | ||
| IC | 1000 | 26.89 | 26.15 | 97.26 |
| P&O | 26.18 | 97.37 | ||
| FLC | 26.25 | 97.63 |
| Ref. | MPPT | Converter | PV Model | PV Structure | Integration | Partial Shading |
|---|---|---|---|---|---|---|
| [46] | FLC ANFIS | Boost | Not given | Not given | Roof | Not given |
| [22] | P&O | Boost | Not given | String | Not given | Yes |
| [32] | P&O IC FLC | Boost | Double diode model | Not given | Facade | Not given |
| [29] | P&O | Boost | Not given | Cell | Facade | Not given |
| [33] | P&O | Buck-Boost | One diode model | Panel | Not given | Not given |
| [42] | 3SVSS | Boost | One diode model | Not given | Not given | No |
| [43] | P&O | Boost | Nonlinear regression analysis | Not given | Roof curved | Not given |
| [31] | P&O | Boost | Double diode model | String | Not given | Yes |
| [50] | Internal impedance | Boost | One diode model | Parallel | Facade | Not given |
| [86] | P&O | Boost | One diode model | SP | Roof facade | No |
| Ref. | Type | Sub-Type | MPPT Converter | Controller | MPPT Algorithm |
|---|---|---|---|---|---|
| [64] | CMPPT | - | Boost | N/A | P&O |
| [65] | CMPPT | - | Boost, DAB | N/A | N/A |
| [87] | CMPPT | - | Boost | PI, voltage | RGA |
| [37] | CMPPT | - | Boost | N/A | IC |
| [88] | CMPPT | - | Boost | PI, voltage | N/A |
| [89] | CMPPT | - | Boost | PI, voltage | N/A |
| [90] | CMPPT | - | Boost | N/A | N/A |
| [91] | CMPPT | - | Flyback, boost-flyback | N/A | N/A |
| [92] | CMPPT | - | Interleaved Boost | N/A | N/A |
| [65] | DMPPT | Microinverter | Boost, Flyback | N/A | N/A |
| [36] | DMPPT | Series | Flyback | PI, cascade voltage-current | P&O |
| [34] | DMPPT | TCT | Boost | N/A | P&O |
| [31] | DMPPT | Series | Boost | N/A | P&O |
| [30] | DMPPT | String semi-DMPPT | Boost | P | N/A |
| [29] | DMPPT | General | Boost | N/A | P&O |
| [66] | DMPPT | String semi-DMPPT | Flyback, Quasi-Z source | N/A | Voltage sweep and LMPPT |
| [93] | DMPPT | Series | Non-inverting buck-boost | N/A | N/A |
| [39] | DMPPT | Parallel | Boost | N/A | IC |
| [94] | DMPPT | General | IIBC | N/A | IC |
| [95] | DMPPT | Parallel | Boost, IIBC | N/A | N/A |
| [33] | DMPPT | Microinverter | Buck-boost inverter | N/A | P&O |
| [67] | DMPPT | DPP | LLC inverter | N/A | P&O |
| [20] | DMPPT | Series, Parallel, DPP | Boost, Flyback | N/A | P&O |
| [42] | DMPPT | General | Boost | PI, cascade voltage-current | 3-stage variable step |
| [96] | DMPPT | Parallel | Boost | SMC | Polynomial expressions |
| STC Characteristic of the PV Module | |
|---|---|
| Parameter | Value |
| Short-circuit current | 5 A |
| Maximum power point voltage | 18 V |
| Maximum power point current | 4.72 A |
| Maximum power | 85 W |
| Converter parameters | |
| Parameter | value |
| Inductor | H, maximum current 10 A, series resistance of 40 m (e.g., inductor PA4349.104ANLT, H) |
| Semiconductors series resistances | 3.2 m (e.g., MOSFET AOB290L) |
| Losses in the input/output connectors | 1 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Paja, C.A.; Trejos-Grisales, L.A.; Serna-Garcés, S.I. Building Integrated Photovoltaic Systems: Characteristics and Power Management. Processes 2025, 13, 1650. https://doi.org/10.3390/pr13061650
Ramos-Paja CA, Trejos-Grisales LA, Serna-Garcés SI. Building Integrated Photovoltaic Systems: Characteristics and Power Management. Processes. 2025; 13(6):1650. https://doi.org/10.3390/pr13061650
Chicago/Turabian StyleRamos-Paja, Carlos Andrés, Luz Adriana Trejos-Grisales, and Sergio Ignacio Serna-Garcés. 2025. "Building Integrated Photovoltaic Systems: Characteristics and Power Management" Processes 13, no. 6: 1650. https://doi.org/10.3390/pr13061650
APA StyleRamos-Paja, C. A., Trejos-Grisales, L. A., & Serna-Garcés, S. I. (2025). Building Integrated Photovoltaic Systems: Characteristics and Power Management. Processes, 13(6), 1650. https://doi.org/10.3390/pr13061650










