Application of Blasingame’s Modern Production-Decline Analysis Method in Production Performance Analysis of Buried Hill Condensate Gas Reservoir
Abstract
1. Introduction
2. Principle of the Blasingame Method
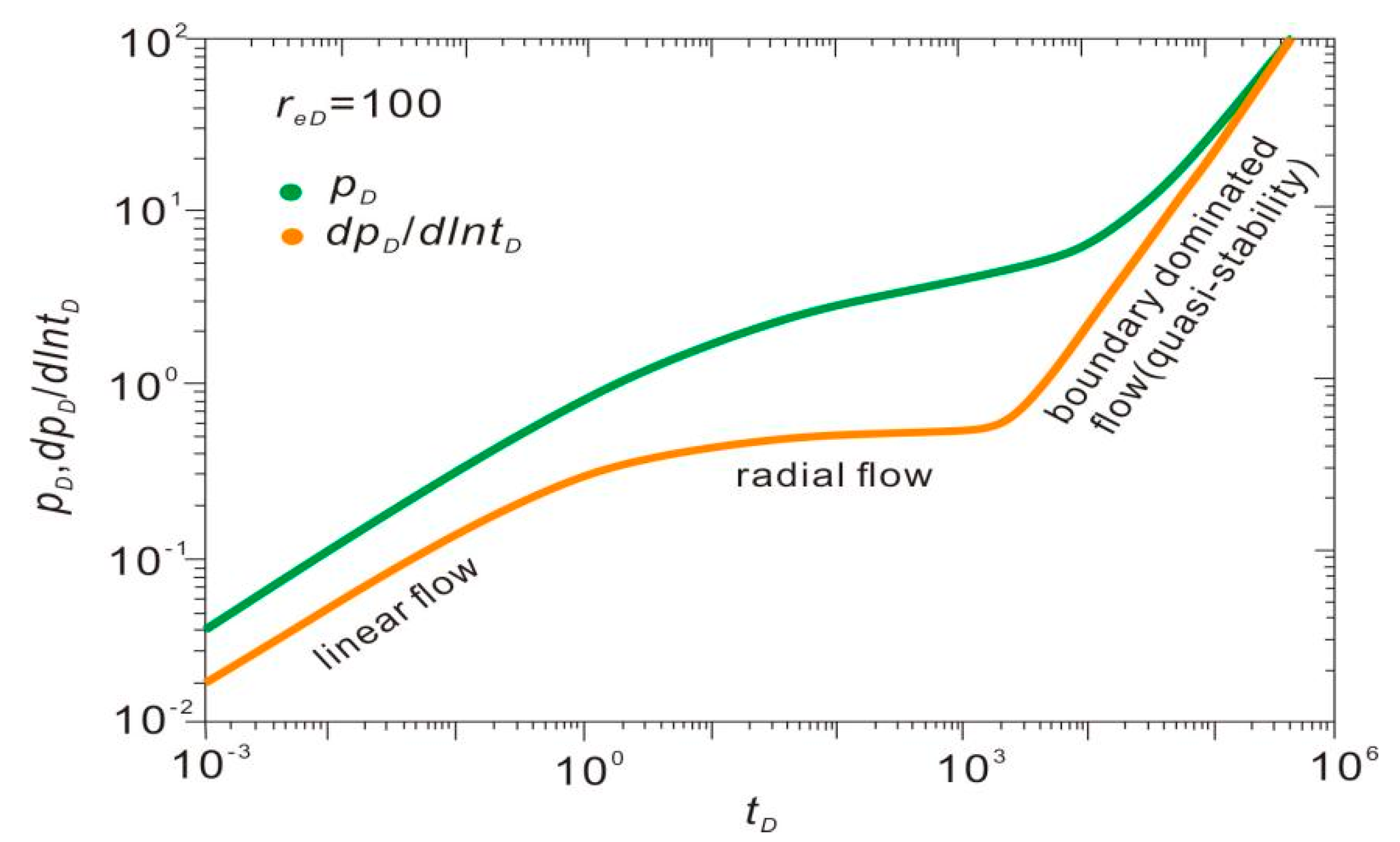
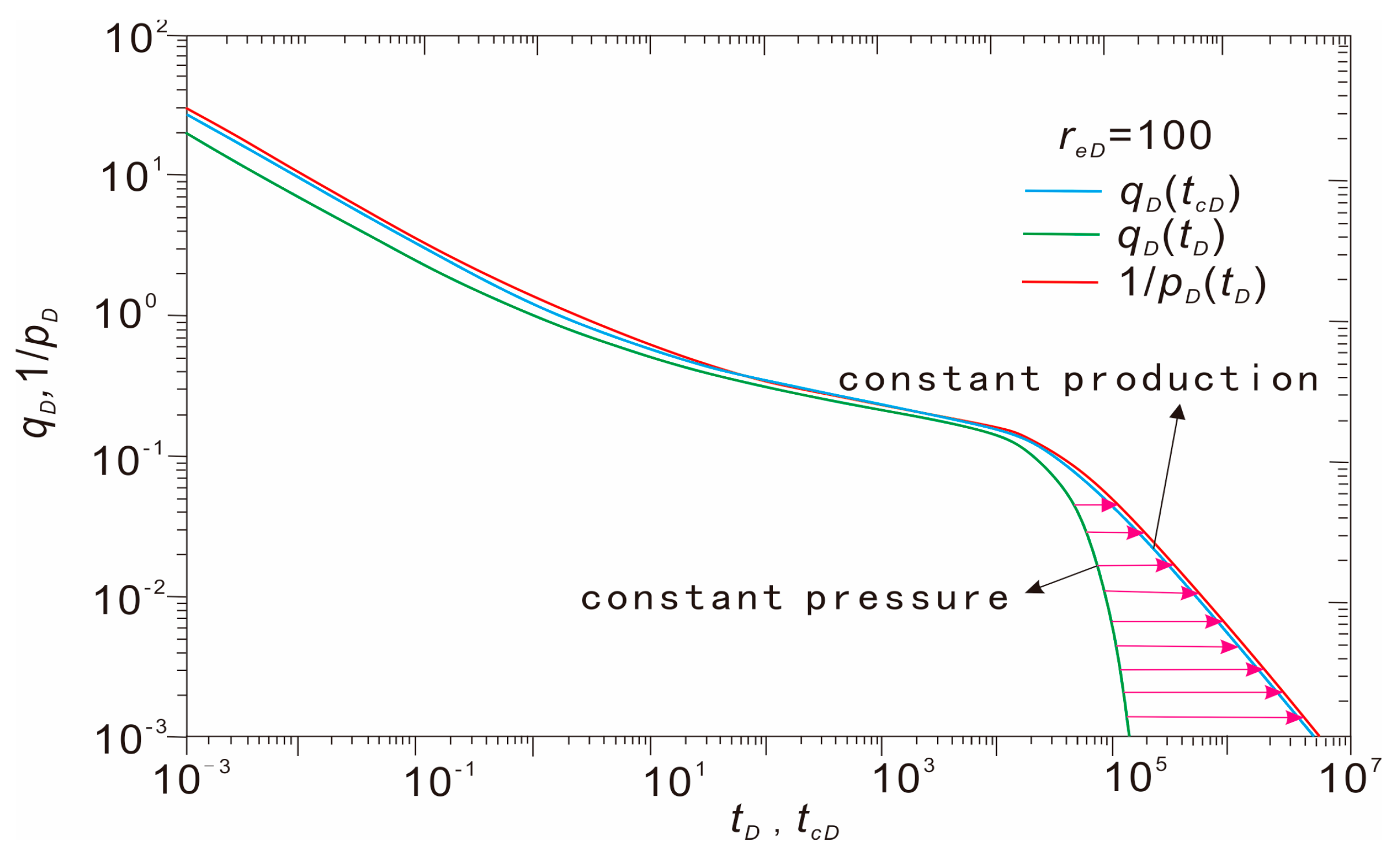
2.1. Unsteady Flow and Boundary Flow
2.2. Material Balance Equivalent Time and Pseudo−Time
2.3. Condensate Gas Reservoir Retrograde Condensation Phenomenon
2.4. Well-Test Interpretation Model of the Condensate Gas Pool
- (1)
- Variable well storage model: The variable well storage model takes into account the change in wellbore storage coefficient with time, which is suitable for the complex wellbore conditions or the change in fluid-phase state.
- (2)
- Dual-porosity medium model: For condensate gas reservoirs with fractures, this model can describe the flow of fluids in the matrix and fractures and the fluid exchange between the two.
- (3)
- Composite model: This model is used to describe multi-layer reservoirs with different fluid flow characteristics. Each layer can have different porosity, permeability, and saturation.
- (4)
- Vertical and horizontal fracture model: This model is suitable for reservoirs with vertical or horizontal fractures. It can also be used to describe the effect of fractures on fluid flow.
- (5)
- Component model: The fluid in the condensate gas reservoir is multi-component. The component model can simulate the migration and phase change in components, especially when the pressure and temperature change.
- (6)
- Pseudo-pressure model: Because the flow characteristics of condensate gas are different from those of conventional gas, the pseudo-pressure model adapts to the characteristics of condensate gas reservoirs by modifying the definition of pressure.
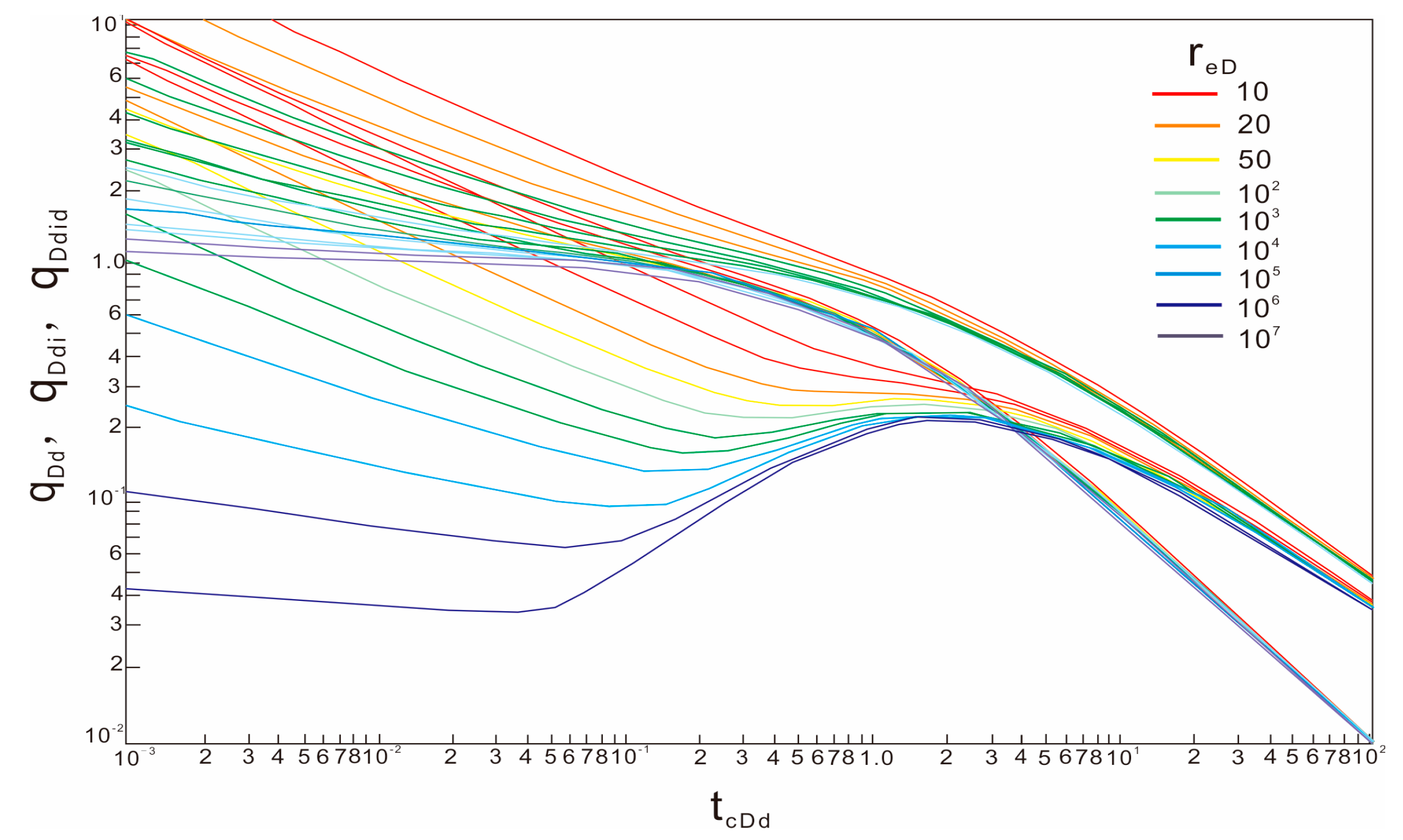
2.5. Blasingame Composite Plate
3. Blasingame Method Fitting Analysis
- (1)
- According to the geological parameters, such as the range of the well control area, an original geological reserve G is assumed.
- (2)
- According to the production of different mining times and the material balance equation, the formation pressure pp of different mining times is calculated.
- (3)
- The material balance time under each production point is calculated:
- (4)
- Using to the production data of gas wells, combined with the proposed production pressure difference, the normalized production of each production point is calculated as follows:
- (5)
- Based on the material balance time and the normalized yield, the integral calculation of the normalized yield is realized:
- (6)
- The derivative of the normalized cumulative yield integral is obtained by the derivative of the normalized yield integral to the material balance time, and the judgment of the change speed of the normalized yield integral is realized:
- (7)
- A (ppi−pp)/q—tca rectangular coordinate curve is drawn and the geological reserves G are calculated according to the slope of the regression line:
- (8)
- The double logarithmic curves of q/∆pp, (q/∆pp)i, and (q/∆pp)id—tca are drawn in the rectangular coordinate system on the semi-transparent paper, and the drawn curves are fitted with the Blasingame typical chart curve (Figure 3) to obtain better curve-fitting results. According to the fitting results, the dimensionless well control radius reD is recorded.
- (9)
- A better-fitting point is chosen, and the actual fitting point (tca, q/∆pp)m and the corresponding theoretical fitting point (tcaDd, qDd)m are recorded. The evaluation parameters such as reservoir permeability, skin factor, well control radius, and well control reserves can be calculated according to the actual fitting point, theoretical fitting point, and dimensionless well control radius.In the above formulae,tca—material balance pseudo-time;Ct—composite compressibility;P—pressure (MPa);q—daily production (104 m3/d);K—permeability (mD);s—skin coefficient;re—well control radius (m);G—original geological reserves (108 m3);Pi—original formation pressure (MPa);Pwf—bottom hole flowing pressure (MPa);B—volumetric coefficient;h—strata thickness (m);Φ—formation porosity;reD—dimensionless well control radius;rw—wellbore radius (m);rwa—effective wellbore radius (m);i—integral;D—differential coefficient.
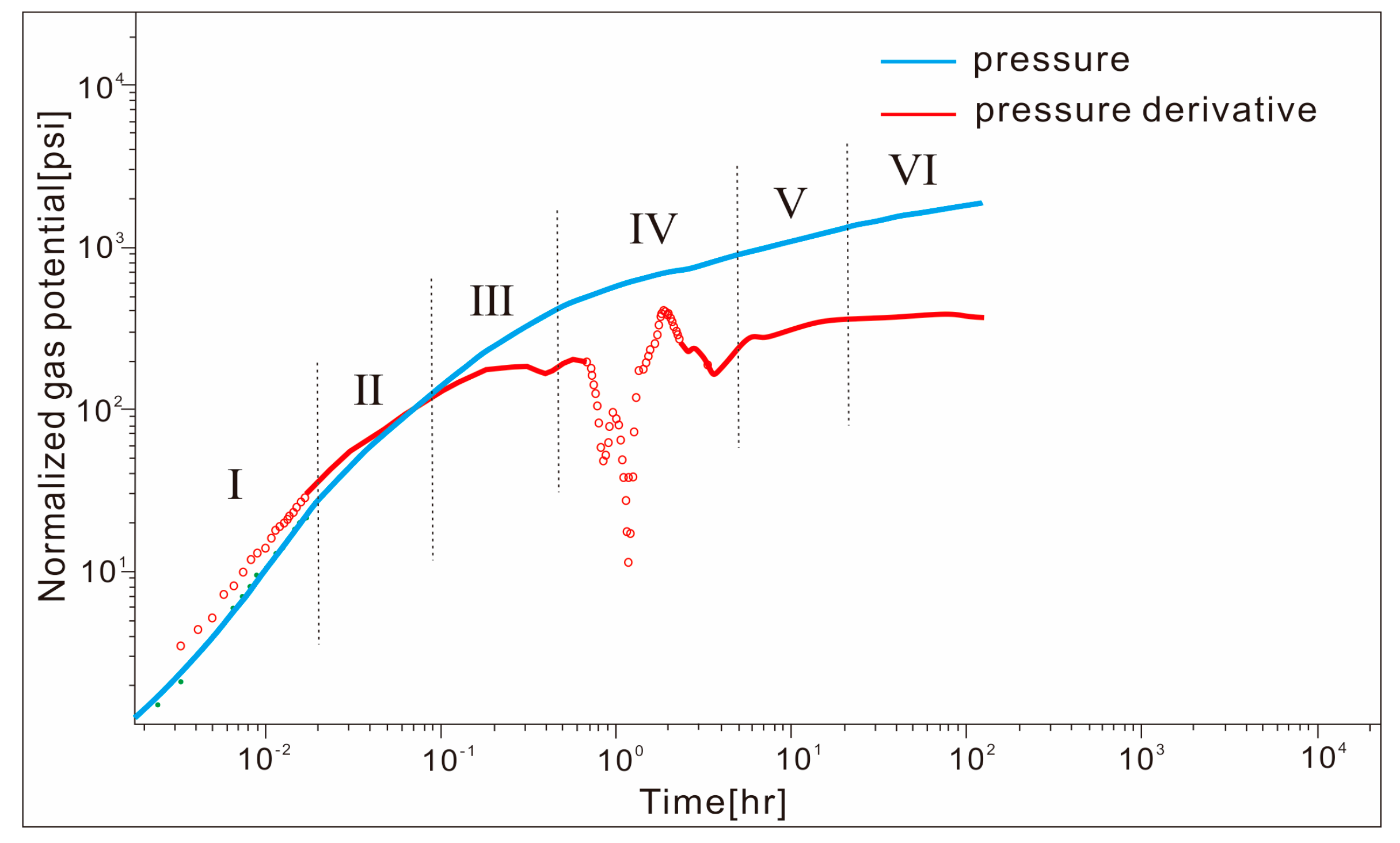
4. Blasingame Method Instance Application
5. Conclusions
- (1)
- The modern production-decline method of Blasingame introduces the equivalent time and pseudo-time of material balance and draws the curve of the production function and material balance time. The typical chart-fitting analysis method was used to calculate the permeability, well control radius, skin factor, well control reserves, and other parameters, which significantly improved the estimation accuracy of dynamic reserves of buried hill condensate gas reservoirs.
- (2)
- The model obtained by well-test interpretation was used to establish a more accurate Blasingame modern production-decline analysis model, and the reservoir physical property evaluation and reserve calculation were realized after fitting with the production dynamics data. Compared with the pressure-recovery unstable-well test method, it has the advantages of low cost, small operation volume, and accurate calculation parameters and can obtain the single well control boundary.
- (3)
- Well A was a low porosity and low permeability reservoir with a permeability of 0.0316 mD, a skin factor of −2.35, a well control radius of 253.5 m, and dynamic reserves of 1.211 × 108 m3.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| qD | The output solution of constant pressure production; |
| tcD | Dimensionless material equilibrium time; |
| tD | Dimensionless time; |
| pD | Dimensionless production; |
| μ | Fluid viscosity; |
| Z | Gas compressibility factor; |
| tca | Material balance pseudo-time; |
| Ct | Composite compressibility; |
| p | Pressure (MPa); |
| q | Daily production (104 m3/d); |
| K | Permeability (mD); |
| s | Skin coefficient; |
| re | Well control radius (m); |
| G | Original geological reserves (108 m3); |
| pi | Original formation pressure (MPa); |
| pp | Regularized pseudo-pressure; |
| pwf | Bottom hole flowing pressure (MPa); |
| B | Volumetric coefficient; |
| h | Strata thickness (m); |
| Φ | Formation porosity; |
| reD | Dimensionless well control radius; |
| rw | Wellbore radius (m); |
| rwa | Effective wellbore radius (m); |
| i | Integral; |
| D | Differential coefficient. |
References
- Li, S.; Sun, L.; Du, J.; Tang, Y.; Zhou, S.; Guo, P.; Liu, J. Difficulties and countermeasures in the development of low permeability tight gas reservoirs and condensate gas reservoirs. Xinjiang Pet. Geol. 2004, 25, 156–159. [Google Scholar]
- China Petroleum Exploration and Production Branch. Natural Gas Exploration and Development Technology Papers; Petroleum Industry Press: Beijing, China, 2000; pp. 7–127. [Google Scholar]
- Anderson, D.M.; Stotts, G.W.; Mattar, L.; Ilk, D.; Blasingame, T.A. Production data analysis challenges, pitfalls, diagnostics. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006; SPE 102048. [Google Scholar]
- Borch, C. Applied Multisource Pressure Data Integration for Dynamic Reservoir Characterization, Reservoir, and Production Management: A Case History from the SiriField, Offshore Denmark. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–3 October 2001; SPE 71629. [Google Scholar]
- Ma, C.; Wu, Y.; Liang, S.; Yang, H. Single well dynamic description of carbonate condensate gas reservoir. Inn. Mong. Petrochem. 2014, 40, 49–50. [Google Scholar]
- Guo, P.; Li, S.; Du, Z.; Sun, L.; Sun, L.; Li, M. Present Situation and Problems of Condensate Gas Reservoir Development Technology. Xinjiang Pet. Geol. 2002, 23, 262–264. [Google Scholar]
- Fraim, M.J. Gas reservoir decline—Curve analysis using type curves with real gas pseudo pressure and normalized time. SPE Form. Eval. 1989, 2, 671–682. [Google Scholar] [CrossRef]
- Hu, Y.; Li, M.; Wu, M. A simple method for production decline analysis of gas wells in low permeability gas reservoirs. Pet. Explor. Dev. 1999, 26, 60–62. [Google Scholar]
- Xu, L. Study on the Production Decline Analysis Method of Multi—Well Waterflooding Reservoir. Master’s Thesis, Xi’an University of Petroleum, Xi’an, China, 2013. [Google Scholar]
- Cao, Y. Application of Modern Production Decline Method in Pre-Fracturing Evaluation of Repeated Fracturing. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2016. [Google Scholar]
- Mattar, L.; Anderson, D.M. A Systematic and Comprehensive Methodology for Advanced Analysis of Production Data. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003; SPE 84472. [Google Scholar]
- Ahmed, T.; McKinney, P. Advanced Reservoir Engineering; Gulf Professional Publishing: Houston, TX, USA, 2011. [Google Scholar]
- Xie, W. Dynamic Analysis of Gas Well Production in Low Permeability Gas Reservoir. Master’s Thesis, Daqing Petroleum Institute: Daqing, China, 2009. [Google Scholar]
- Kabir, C.S.; Izgec, B. Diagnosis of Reservoir Behavior From Measured Pressure/Rate date. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006; SPE 100384. [Google Scholar]
- Hager, C.J.; Jones, J.R. Analyzing Flowing Production Data with Standard Pressure Transient Methods. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference, Keystone, CO, USA, 21–23 May 2001; SPE 71033. [Google Scholar]
- Zuo, Q. Dynamic Analysis of Gas Well Production in Water Gas Reservoir. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2018. [Google Scholar]
- Chen, J.; Wei, M.; Duan, Y. comparative analysis of different gas well production dynamic analysis methods. Nat. Gas Explor. Dev. 2012, 35, 56–59. [Google Scholar]
- Xu, X.; Mei, Q.; Chen, Y.; Han, Y.; Tang, H.; Jiao, C.; Guo, C. Comprehensive analysis method of gas reservoir water invasion and development dynamic experiment. Nat. Gas Geosci. 2020, 31, 1355–1366. [Google Scholar]
- Blasingame, T.A.; Johnston, J.L.; Lee, W.J. Type—Curve Analysis Using the Pressure Integral Method. In Proceedings of the SPE California Regional Meeting, Bakersfield, CA, USA, 5–7 April 1989; SPE 18799-MS. [Google Scholar]
- Yang, M.; Yu, Y.; Ma, D.; He, F. Condensate gas well productivity prediction method research. In Proceedings of the 2015 International Conference on Oil and Gas Field Exploration and Development, Xi’an, China, 20 September 2015; pp. 280–287. [Google Scholar]
- Yan, T.; Li, J. Determination of reasonable productivity of condensate gas wells in the East China Sea. Ocean. Oil 2007, 27, 70–76. [Google Scholar]
- Wang, Z.; Yao, J.; Wu, M. A New Well Test Interpretation Method for Fractured Condensate Gas Reservoirs. China Foreign Energy 2007, 12, 37–42. [Google Scholar]
- Jones, J.R.; Raghavan, R. Interpretation of Flowing Well Response in Gas-Condensate Wells. SPE Form Eval 1988, 3, 578–594. [Google Scholar] [CrossRef]
- Mazlcom, J.; Kelly, R.T.; Mahani, H. A New Two—Phase Pseudo Pressure Approach for the Interpretation of Gas Condensate Well Test in the Naturally Fractured Reservoir. In Proceedings of the SPE Europec/EAGE Annual Conference, Madrid, Spain, 13–16 June 2005; SPE 94189. [Google Scholar]
- Yang, Y.; Ou, J.; Li, J.; Xu, Q.; Lu, Y. A calculation method of gas well productivity based on production performance analysis. In Proceedings of the 33rd National Natural Gas Academic Annual Conference (2023) Proceedings (02 Gas Reservoir Development), Nanning, China, 31 May–2 June 2023; pp. 290–297. [Google Scholar]
- Sun, H.; Zhu, Z.; Shi, Y.; Yang, L.; Jiang, J. Error correction of Blasingame plate making in modern production decline analysis. Nat. Gas Ind. 2015, 35, 71–77. [Google Scholar]
- Palacio, J.C.; Blasingame, T.A. Decline curve analysis using type curves—Analysis of gas well production data. In Proceedings of the SPE Joint Rocky Mountain Regional and Low Permeability Reservoirs Symposium, Denver, CO, USA, 26–28 April 1993; SPE 25909. [Google Scholar]
- Liu, X.; Zou, C.; Jiang, Y.; Yang, X. Basic Principles and Applications of Modern Production Decline Analysis. Nat. Gas Ind. 2010, 30, 50–54+139–140. [Google Scholar]
- Liu, X. Discussion on several key parameters in the calculation of dynamic reserves of gas reservoirs. Nat. Gas Ind. 2009, 29, 71–74. [Google Scholar]
- Poston, S.W.; Poe, B.D., Jr. Analysis of Production Decline Curves; Society of Petroleum Engineers: Richardson, TX, USA, 2008. [Google Scholar]
- Li, X.; Cheng, Y.; Wang, R.; Cao, P.; Chang, S.; Liu, Y. Discussion on the application of the Blasingame production decline analysis method in the Sudong block. In Proceedings of the 14th Ningxia Young Scientists Forum Petrochemical Thematic, Yinchuan, China, 24 July 2018; Petrochemical Applications; pp. 463–464. [Google Scholar]
- Zareenjad, M.H.; Ghanavati, M.; Asl, A.K. Production data analysis of horizontal wells using vertical well decline models, a field case study of an oil field. Pet. Sci. Technol. 2014, 32, 418–425. [Google Scholar] [CrossRef]
- Nobakht, M.; Clarison, C.R.; Kaviani, D. New type curves for analyzing horizontal wells with multiple fractures in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2013, 10, 99–112. [Google Scholar] [CrossRef]
- Ali, A.J.; Siddiqui, S.; Dehghanpour, H. Analyzing the production data of fractured horizontal wells by a linear triple porosity model: Development of analysis equations. J. Pet. Sci. Eng. 2013, 112, 117–128. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Wang, Y.; Zhang, D.; Gu, F. An Integrated Machine Learning-Based Approach to Identifying Controlling Factors of Unconventional Shale Productivity. Energy 2023, 266, 126512. [Google Scholar] [CrossRef]
- Bai, W.; Cheng, S.; Wang, Y.; Cai, D.; Guo, X.; Guo, Q. A transient production prediction method for tight condensate gas wells with multiphase flow. Pet. Explor. Dev. 2024, 51, 1–7. [Google Scholar] [CrossRef]
- Han, J.; Wu, G.; Yang, H.; Dai, L.; Su, Z.; Tang, H.; Xiong, C. Type and genesis of condensate gas reservoir in the Tazhong uplift of the Tarim basin. Nat. Gas Ind. 2021, 41, 24–32. [Google Scholar]
- Du, P. Study on Mechanism of Enhanced Oil Recovery by Gas Injection in the Middle and Late Phases of Condensate Gas Reservoir with High Condensate Oil Content Development. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2018. [Google Scholar]
- Fevang, Ø.; Whitson, C.H. Modeling gas-condensate well deliverability. SPE Reserv. Eng. 1996, 11, 221–230. [Google Scholar] [CrossRef]
- Liu, X.; Zou, C.; Jiang, Y.; Yang, X. Theory and application of modern production decline analysis. Nat. Gas Ind. 2010, 30, 50–54. [Google Scholar]
- Jiang, R.; He, J.; Jiang, Y.; Fan, H. Establishment and application of Blasingame production decline analysis method for fractured horizontal well in shale gas reservoirs. Acta Pet. Sin. 2019, 40, 1503–1510. [Google Scholar]
- Guo, P.; Ou, Z. Material balance equation of a condensate gas reservoir considering water soluble gas. Nat. Gas Ind. 2013, 33, 70–74. [Google Scholar]
- Chen, Y.; Ma, F.; Wang, X.; Li, J.; Jiang, H. New calculation method of material equilibrium equation for condensate reservoirs. Nat. Gas Ind. 2005, 25, 104–106. [Google Scholar]
- Wang, J.; Guo, P.; Wang, F.; Liang, C.; Bo, Z. Calculation of dynamic reserves in fracture-cavity gas condensate reservoirs with material balance method. Spec. Oil Gas Reserv. 2015, 22, 75–77. [Google Scholar]

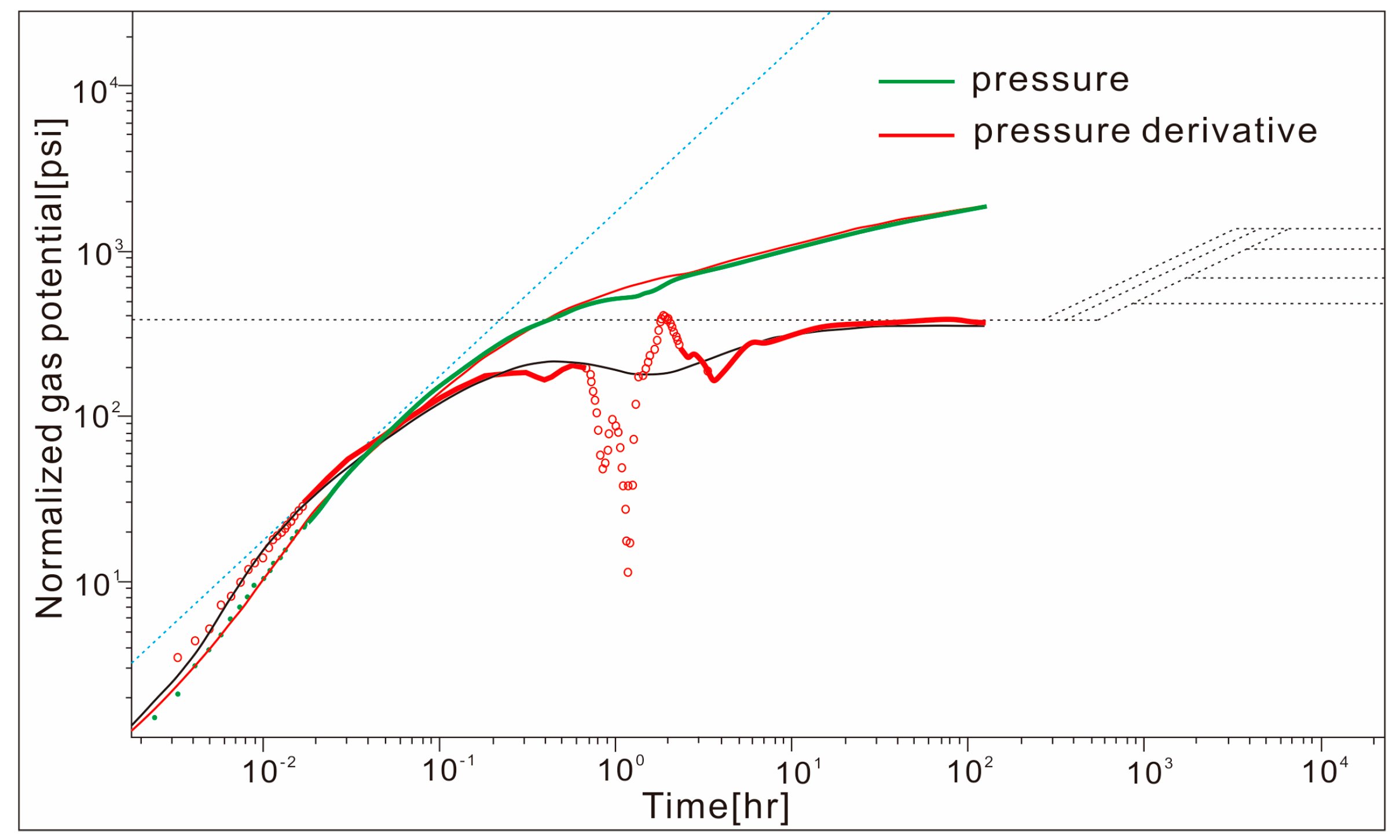
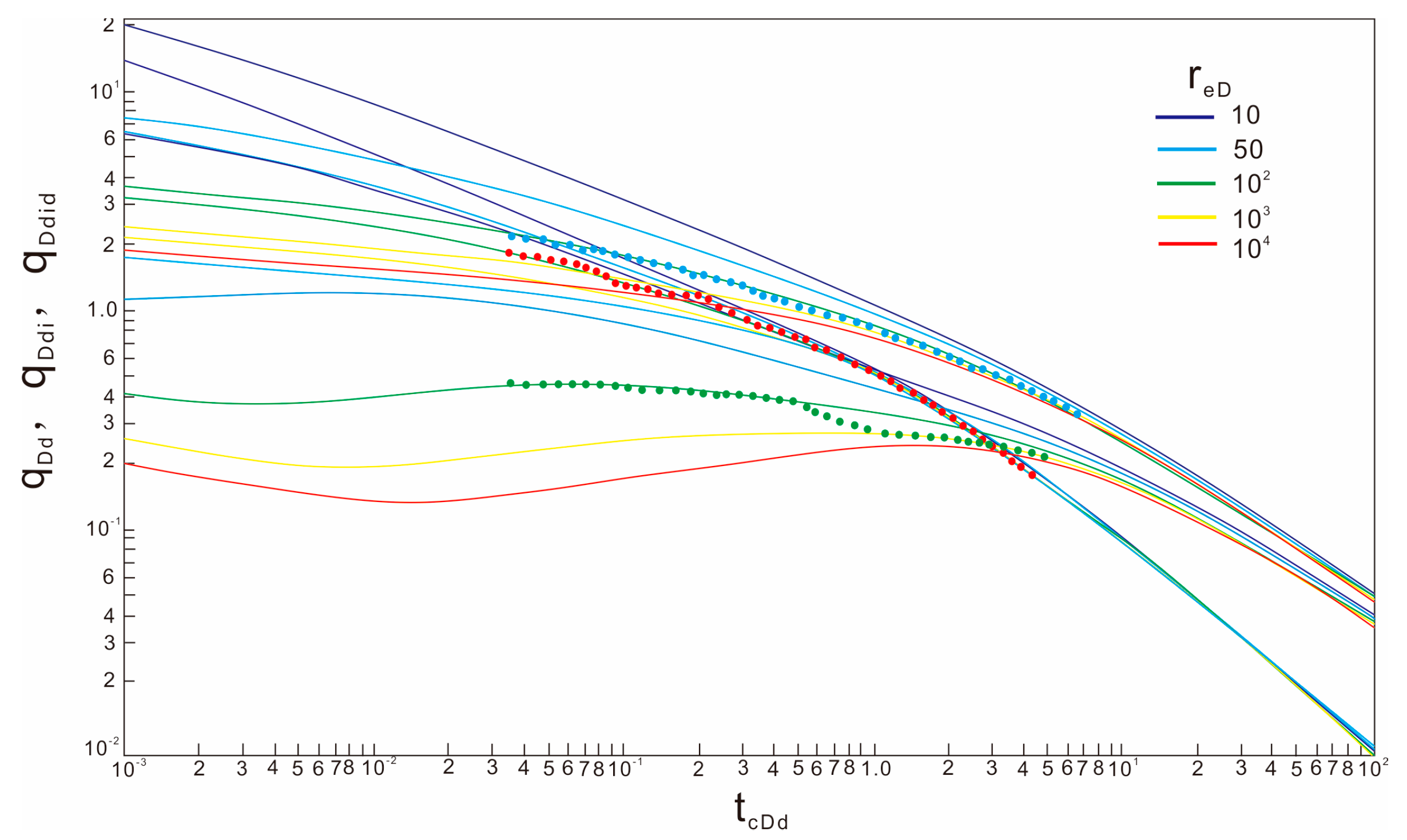
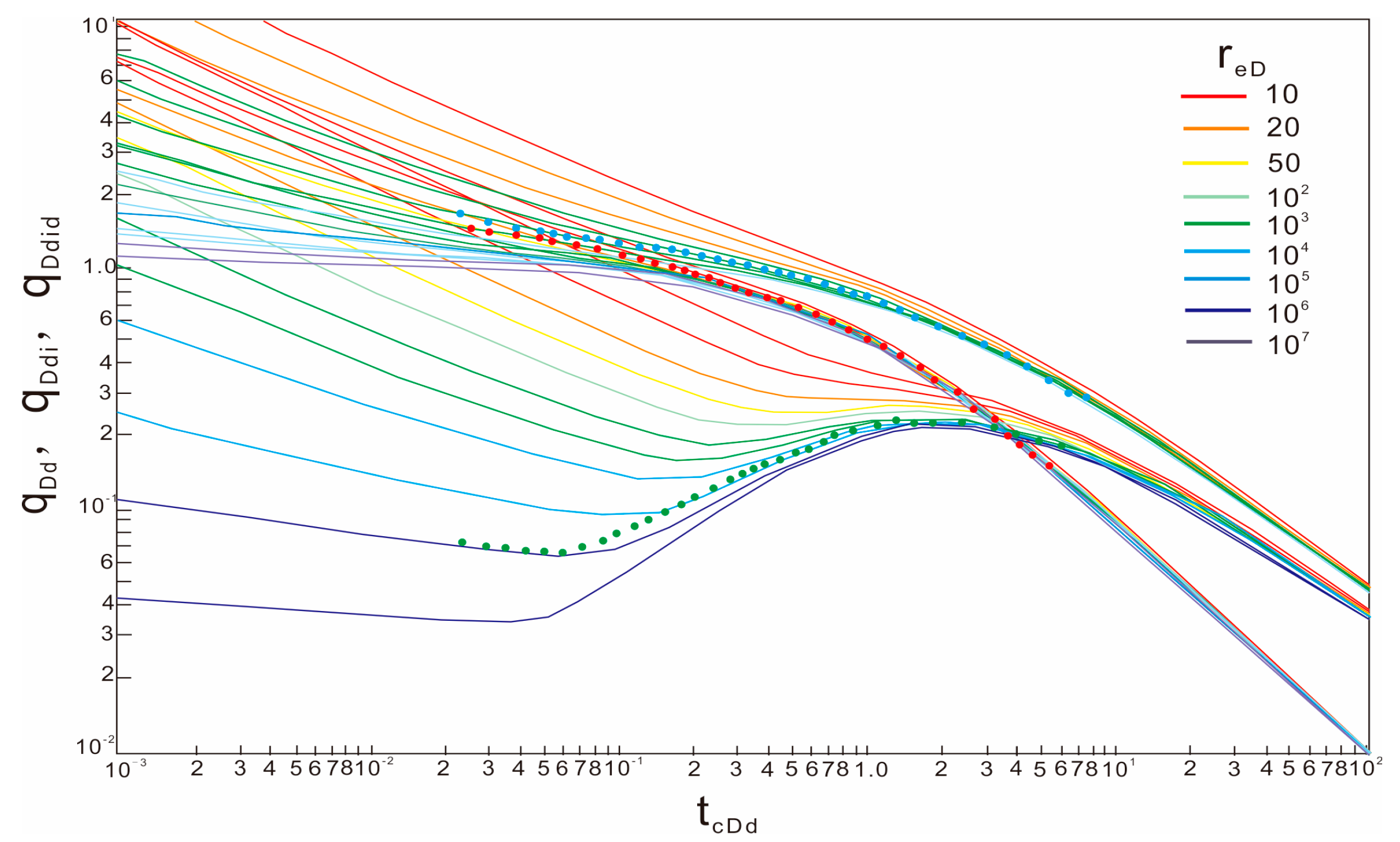
| Parameter | Numerical Value |
|---|---|
| Wellbore storage coefficient | 1.16 m3/MPa |
| Stratigraphic coefficient | 1.014~2.734 mD·m |
| Skin coefficient | −2.51~−0.76 |
| Permeability | 0.023~0.062 mD |
| Parameter | Blasingame Model 1 | Blasingame Model 2 | A-G | NPI | Well-Test Interpretation |
|---|---|---|---|---|---|
| Skin coefficient | −2.44 | −2.26 | −2.88 | −2.45 | −2.51~−0.76 |
| Permeability | 0.0297 mD | 0.0335 mD | 0.047 mD | 0.039 mD | 0.023~0.062 mD |
| Well control radius | 245.8 m | 261.1 m | 308.6 m | 281.3 m | |
| Well control reserves | 1.197 × 108 m3 | 1.224 × 108 m3 | 1.267 × 108 m3 | 1.119 × 108 m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, L.; Chen, P.; Lai, H. Application of Blasingame’s Modern Production-Decline Analysis Method in Production Performance Analysis of Buried Hill Condensate Gas Reservoir. Processes 2025, 13, 1645. https://doi.org/10.3390/pr13061645
Lv L, Chen P, Lai H. Application of Blasingame’s Modern Production-Decline Analysis Method in Production Performance Analysis of Buried Hill Condensate Gas Reservoir. Processes. 2025; 13(6):1645. https://doi.org/10.3390/pr13061645
Chicago/Turabian StyleLv, Lingang, Peng Chen, and Hang Lai. 2025. "Application of Blasingame’s Modern Production-Decline Analysis Method in Production Performance Analysis of Buried Hill Condensate Gas Reservoir" Processes 13, no. 6: 1645. https://doi.org/10.3390/pr13061645
APA StyleLv, L., Chen, P., & Lai, H. (2025). Application of Blasingame’s Modern Production-Decline Analysis Method in Production Performance Analysis of Buried Hill Condensate Gas Reservoir. Processes, 13(6), 1645. https://doi.org/10.3390/pr13061645





