A Hierarchical Distributed and Local Voltage Control Strategy for Photovoltaic Clusters in Distribution Networks
Abstract
1. Introduction
- (1)
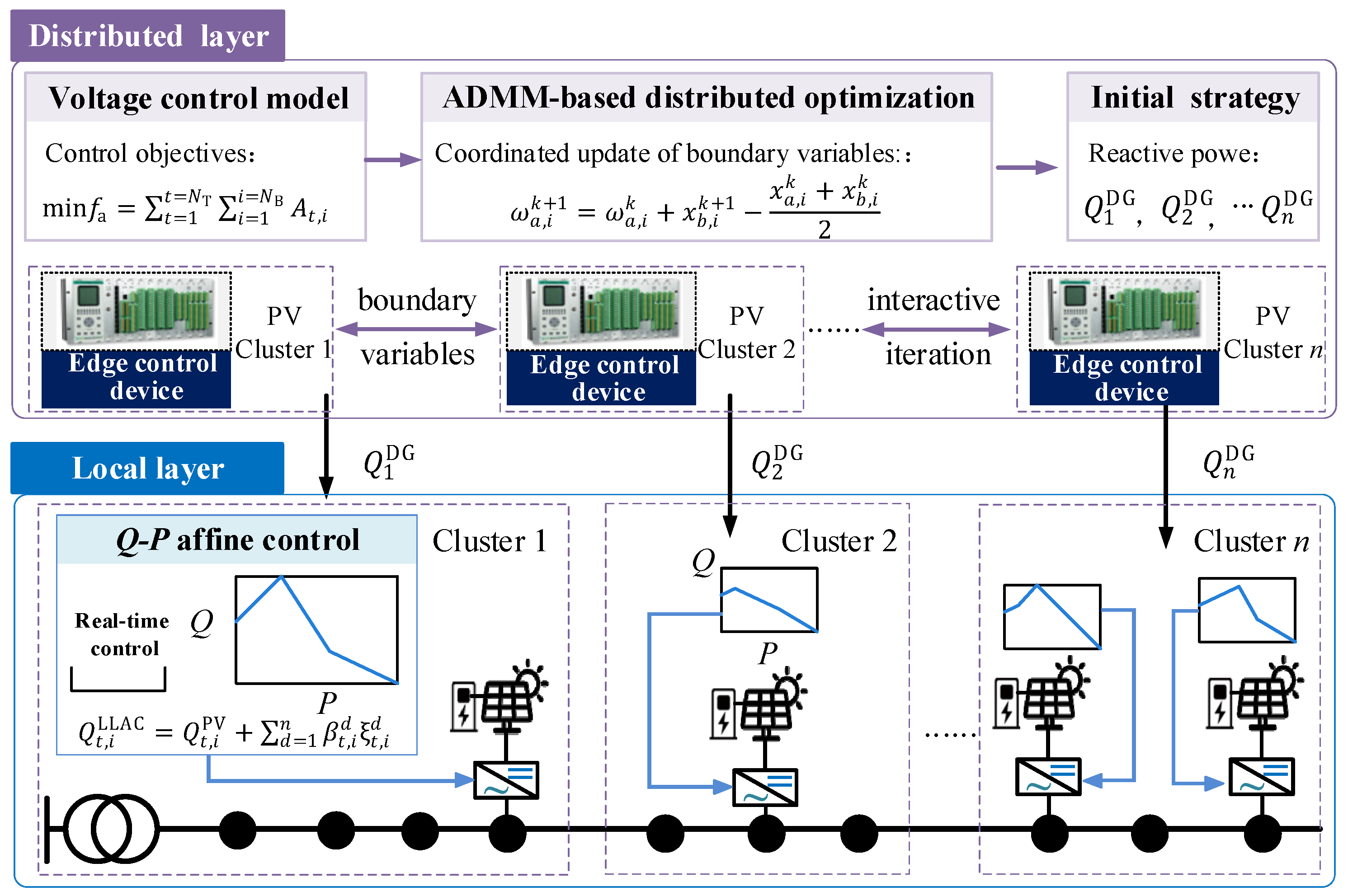
- A hierarchical distributed and local voltage regulation architecture for PV clusters is proposed. The distributed optimization method is employed to coordinate reactive power across different PV clusters, serving as the reference for local control. The local control layer utilizes the Q-P affine control strategy as the complement to address real-time PV fluctuations.
- (2)
- A lifted linear affine control method is proposed for the local control of PV inverters, which segments the Q-P affine control curve to accommodate various PV fluctuation scenarios. The proposed method eliminates the integer variables introduced by traditional piecewise linearization while enhancing the flexibility of the local control strategy. Considering the uncertainty of PV, a robust optimization model is developed, and a dual transformation is performed to facilitate the solution of the proposed local control strategy.
2. Hierarchical Distributed and Local Voltage Control Architecture
3. Decentralized Coordination Based on ADMM
3.1. Voltage Control Model for PV Clusters
- (1)
- Objective function:where is the total voltage deviation in cluster ; represents the remaining time intervals in the optimization horizon; denotes the total nodes in cluster ; represents the proxy variable introduced by cone relaxation; denotes the voltage at node ; and and represent the permissible lower and upper bounds for voltage.
- (2)
- System power flow constraints:where and represent the sets of branches and nodes in cluster , respectively; and denote the reactive and active power flowing from node to ; and indicate the reactance and resistance of branch ; and refer to the net reactive and active power at node ; and represent the reactive power and active power of load at node ; and and represent the reactive power and active power generated by distributed PV at node .
- (3)
- System operation security constraints:where and represent the maximum and minimum allowable voltage levels for safe operation; represents the maximum current that can be tolerated by the branch; is the variable introduced through the cone transformation; and represents the current magnitude between nodes and .
- (4)
- PV operation constraints:where denotes the maximum reactive power output of the PV inverter at node , and is its installed capacity.
3.2. ADMM-Based Distributed Interactive Solution
4. Local Affine Control Strategy Based on Lifted Linear Decision Rule
4.1. Lifted Linear Affine Q-P Control
4.2. Robust Control Model
5. Case Studies and Analysis
5.1. The Modified IEEE 33-Node Distribution System
- (1)
- Evaluation of voltage regulation effectiveness
- (2)
- Performance analysis of distributed algorithms
5.2. Practical Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jian, J.; Zhao, J.; Ji, H.; Bai, L.; Xu, J.; Li, P.; Wu, J.; Wang, C. Supply Restoration of Data Centers in Flexible Distribution Networks with Spatial-Temporal Regulation. IEEE Trans. Smart Grid 2023, 15, 340–354. [Google Scholar] [CrossRef]
- Zhang, K.; Zou, G.; Zhang, J.; Li, H.; Sun, Y.; Li, G. Microgrid Energy Management Strategy Considering Source-Load Forecast Error. Int. J. Electr. Power Energy Syst. 2025, 164, 110372. [Google Scholar] [CrossRef]
- Chamana, M.; Chowdhury, B. Optimal Voltage Regulation of Distribution Networks with Cascaded Voltage Regulators in the Presence of High PV Penetration. IEEE Trans. Sustain. Energy 2018, 9, 1427–1436. [Google Scholar] [CrossRef]
- Tewari, T.; Mohapatra, A.; Anand, S. Coordinated Control of OLTC and Energy Storage for Voltage Regulation in Distribution Network with High PV Penetration. IEEE Trans. Sustain. Energy 2020, 12, 262–272. [Google Scholar] [CrossRef]
- Hua, Y.; Xie, Q.; Hui, H.; Ding, Y.; Cui, J.; Shao, L. Use of Inverter-based Air Conditioners to Provide Voltage Regulation Services in Unbalanced Distribution Networks. IEEE Trans. Power Deliv. 2022, 38, 1569–1579. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, P.; Ji, H.; Yu, H.; Zhao, J.; Xi, W.; Wu, J. Adaptive Voltage Control of Inverter-based DG in Active Distribution Networks with Measurement-strategy Mapping Matrix. IEEE Trans. Sustain. Energy 2025, 16, 1238–1252. [Google Scholar] [CrossRef]
- Xiao, J.; Zu, G.; Zhou, H.; Zhang, X. Total Quadrant Security Region for Active Distribution Network with High Penetration of Distributed Generation. J. Mod. Power Syst. Clean Energy 2020, 9, 128–137. [Google Scholar] [CrossRef]
- Antoniadou-Plytaria, K.; Kouveliotis-Lysikatos, I.; Georgilakis, P.; Hatziargyriou, N. Distributed and Decentralized Voltage Control of Smart Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Smart Grid 2017, 8, 2999–3008. [Google Scholar] [CrossRef]
- Li, J.; Guo, D.; Liu, C.; Gu, Y.; Duan, Y.; Li, Y. Collaborative Control of Reactive Power and Voltage in A Coupled System Considering the Available Reactive Power Margin. Sustainability 2024, 16, 2627. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Niu, Z. Distributed Optimization for Active Distribution Network Considering the Balance of Multi-stakeholder. Processes 2020, 8, 987. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Q.; Chen, J.; Huang, S.; Shen, F. Double-time-scale Distributed Voltage Control for Unbalanced Distribution Networks Based on MPC and ADMM. Int. J. Electr. Power Energy Syst. 2023, 145, 108665. [Google Scholar] [CrossRef]
- Xu, Z.; Chu, B.; Geng, H.; Nian, X. Distributed Power Optimization of Large Wind Farms Using ADMM for Real-time Control. IEEE Trans. Power Syst. 2022, 37, 4832–4845. [Google Scholar] [CrossRef]
- Rahman, T.; Xu, Y.; Qu, Z. Continuous-domain Real-time Distributed ADMM Algorithm for Aggregator Scheduling and Voltage Stability in Distribution Network. IEEE Trans. Autom. Sci. Eng. 2022, 19, 60–69. [Google Scholar] [CrossRef]
- Lin, S.; Chu, C. Optimal Distributed ADMM-based Control for Frequency Synchronization in Isolated AC Microgrids. IEEE Trans. Ind. Appl. 2023, 59, 2458–2472. [Google Scholar] [CrossRef]
- Li, P.; Ji, J.; Ji, H.; Jian, J.; Ding, F.; Wu, J.; Wang, C. MPC-based Local Voltage Control Strategy of DGs in Active Distribution Networks. IEEE Trans. Sustain. Energy 2020, 11, 2911–2921. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Z.; Yu, H.; Ji, H.; Li, P.; Xi, W.; Yan, J.; Wang, C. Cloud-edge Collaboration-based Local Voltage Control for DGs with Privacy Preservation. IEEE Trans. Ind. Inform. 2023, 19, 98–108. [Google Scholar] [CrossRef]
- Abadi, S.; Attarha, A.; Scott, P.; Thiebaux, S. Affinely Adjustable Robust Volt/Var Control for Distribution Systems with High PV Penetration. IEEE Trans. Power Syst. 2021, 36, 3238–3247. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, R.; Yang, L. Optimization of Local Voltage Control with Coordinating Droop Functions Under High PV Penetration. IEEE Trans. Power Syst. 2024, 39, 6776–6779. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, X.; Yan, Z.; Shahidehpour, M.; Wang, H.; Ping, J. Robust Parametric Programming for Adaptive Piecewise Linear Control of Photovoltaic Inverters to Regulate Voltages in Power Distribution Systems. IEEE Trans. Power Syst. 2024, 39, 3685–3700. [Google Scholar] [CrossRef]
- Jabr, R.A. Linear Decision Rules for Control of Reactive Power by Distributed Photovoltaic Generators. IEEE Trans. Power Syst. 2017, 33, 2165–2174. [Google Scholar] [CrossRef]
- Xu, X.; Li, Y.; Yan, Z.; Ma, H.; Shahidehpour, M. Hierarchical Central-local Inverter-based Voltage Control in Distribution Networks Considering Stochastic PV Power Admissible Range. IEEE Trans. Smart Grid 2022, 14, 1868–1879. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, X.; Yan, Z.; Shahidehpour, M. Equitable Active-Reactive Power Envelopes for Distributed Energy Resources in Power Distribution Systems. IEEE Trans. Smart Grid 2025, 16, 1480–1494. [Google Scholar] [CrossRef]
- Nazir, F.U.; Pal, B.C.; Jabr, R.A. Affinely Adjustable Robust Volt/Var Control without Centralized Computations. IEEE Trans. Power Syst. 2022, 38, 656–667. [Google Scholar] [CrossRef]
- Xu, X.; Gao, Y.; Wang, H.; Yan, Z.; Shahidehpour, M.; Tan, Z. Distributionally Robust Optimization of Photovoltaic Power with Lifted Linear Decision Rule for Distribution System Voltage Regulation. IEEE Trans. Sustain. Energy 2024, 15, 758–772. [Google Scholar] [CrossRef]
- Godoy, P.; Almeida, A.; Souza, A.; Marujo, D.; Souza, J. Unified Centralized/Decentralized Voltage and Frequency Control Structure for Microgrids. Sustain. Energy Grids Netw. 2024, 38, 101366. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, P.; Ji, H.; Zhao, J.; Xi, W.; Wang, C. Combined Central-local Voltage Control of Inverter-based DG in Active Distribution Networks. Appl. Energy 2024, 372, 123813. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Jie, G.; Ren, Q.; Yu, H.; Zhao, Y.; Zhang, H. A Cooperative Operation Optimization Method for Medium-and Low-Voltage Distribution Networks Considering Flexible Interconnected Distribution Substation Areas. Processes 2025, 13, 1123. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, D.; Liao, W.; Fan, Q. A Continuous-time Voltage Control Method Based on Hierarchical Coordination for High PV-penetrated Distribution Networks. Appl. Energy 2023, 347, 121274. [Google Scholar] [CrossRef]
- Tang, W.; Huang, Y.; Qian, T.; Wei, C.; Wu, J. Coordinated Central-local Control Strategy for Voltage Management in PV-integrated Distribution Networks Considering Energy Storage Degradation. Appl. Energy 2025, 389, 125684. [Google Scholar] [CrossRef]
- Hou, Q.; Dai, N.; Huang, Y. Voltage Regulation Enhanced Hierarchical Coordinated Volt/var and Volt/watt Control for Active Distribution Networks with Soft Open Points. IEEE Trans. Sustain. Energy 2024, 15, 2021–2037. [Google Scholar] [CrossRef]
- Maharjan, S.; Khambadkone, A.; Peng, J. Robust Constrained Model Predictive Voltage Control in Active Distribution Networks. IEEE Trans. Sustain. Energy 2020, 12, 400–411. [Google Scholar] [CrossRef]
- Georghiou, A.; Kuhn, D.; Wiesemann, W. The decision rule approach to optimization under uncertainty: Methodology and applications. Comput. Manag. Sci. 2019, 16, 545–576. [Google Scholar] [CrossRef]














| Reference | Coordination of Different PV Units | Rapid Response to PV Fluctuations | Consider Improving Control Flexibility | Consider Uncertainty |
|---|---|---|---|---|
| [10,14] | √ | - | - | - |
| [15,17,20] | - | √ | - | √ |
| [16,23] | √ | √ | - | - |
| [21,26,27] | √ | √ | - | √ |
| [19,24] | - | √ | √ | √ |
| This paper | √ | √ | √ | √ |
| Node | Maximum Active Power Output (kW) | Capacity (kWp) |
|---|---|---|
| 12,17,21,24,30,31,32 | 200 | 200 |
| 16 | 300 | 300 |
| 18,22,25,33 | 600 | 600 |
| Scenario | Minimum Voltage Across the System (p.u.) | Maximum Voltage Across the System (p.u.) | AVD (p.u.) |
|---|---|---|---|
| I | 0.9382 | 1.0531 | 0.9886 |
| II | 0.9751 | 1.0308 | 0.5683 |
| III | 0.9712 | 1.0495 | 0.4960 |
| IV | 0.9794 | 1.0212 | 0.4555 |
| V | 0.9815 | 1.0195 | 0.4182 |
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 | Cluster 5 | |
|---|---|---|---|---|---|
| Maximum time for a single iteration (s) | 0.8927 | 0.6132 | 1.9239 | 0.7005 | 0.6699 |
| Node | Maximum Active Power Output (kW) | Capacity (kWp) |
|---|---|---|
| 6,9,16,46 | 300 | 300 |
| 7,14,15,17,40,43,47,50,51 | 400 | 400 |
| 20,21,22,26,27,31,32 | 600 | 600 |
| 28,29,52,53 | 800 | 800 |
| Scenario | Minimum Voltage Across the System (p.u.) | Maximum Voltage Across the System (p.u.) | AVD (p.u.) |
|---|---|---|---|
| I | 0.9482 | 1.0547 | 2.0409 |
| II | 0.9799 | 1.0364 | 1.1824 |
| III | 0.9800 | 1.0202 | 1.1280 |
| IV | 0.9839 | 1.0200 | 0.6923 |
| V | 0.9876 | 1.0199 | 0.4765 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, Z.; Chen, Y.; Ren, Q.; Zhao, J.; Qiu, S.; Zhao, Y.; Zhang, H. A Hierarchical Distributed and Local Voltage Control Strategy for Photovoltaic Clusters in Distribution Networks. Processes 2025, 13, 1633. https://doi.org/10.3390/pr13061633
Liu Z, Wang Z, Chen Y, Ren Q, Zhao J, Qiu S, Zhao Y, Zhang H. A Hierarchical Distributed and Local Voltage Control Strategy for Photovoltaic Clusters in Distribution Networks. Processes. 2025; 13(6):1633. https://doi.org/10.3390/pr13061633
Chicago/Turabian StyleLiu, Zhiwei, Zhe Wang, Yuzhe Chen, Qirui Ren, Jinli Zhao, Sihai Qiu, Yuxiao Zhao, and Hao Zhang. 2025. "A Hierarchical Distributed and Local Voltage Control Strategy for Photovoltaic Clusters in Distribution Networks" Processes 13, no. 6: 1633. https://doi.org/10.3390/pr13061633
APA StyleLiu, Z., Wang, Z., Chen, Y., Ren, Q., Zhao, J., Qiu, S., Zhao, Y., & Zhang, H. (2025). A Hierarchical Distributed and Local Voltage Control Strategy for Photovoltaic Clusters in Distribution Networks. Processes, 13(6), 1633. https://doi.org/10.3390/pr13061633





