An Operational Optimization Model for Micro Energy Grids in Photovoltaic-Storage Agricultural Greenhouses Based on Operation Mode Selection
Abstract
1. Introduction
2. Photovoltaic-Storage Agricultural Greenhouse Micro Energy Grid Model
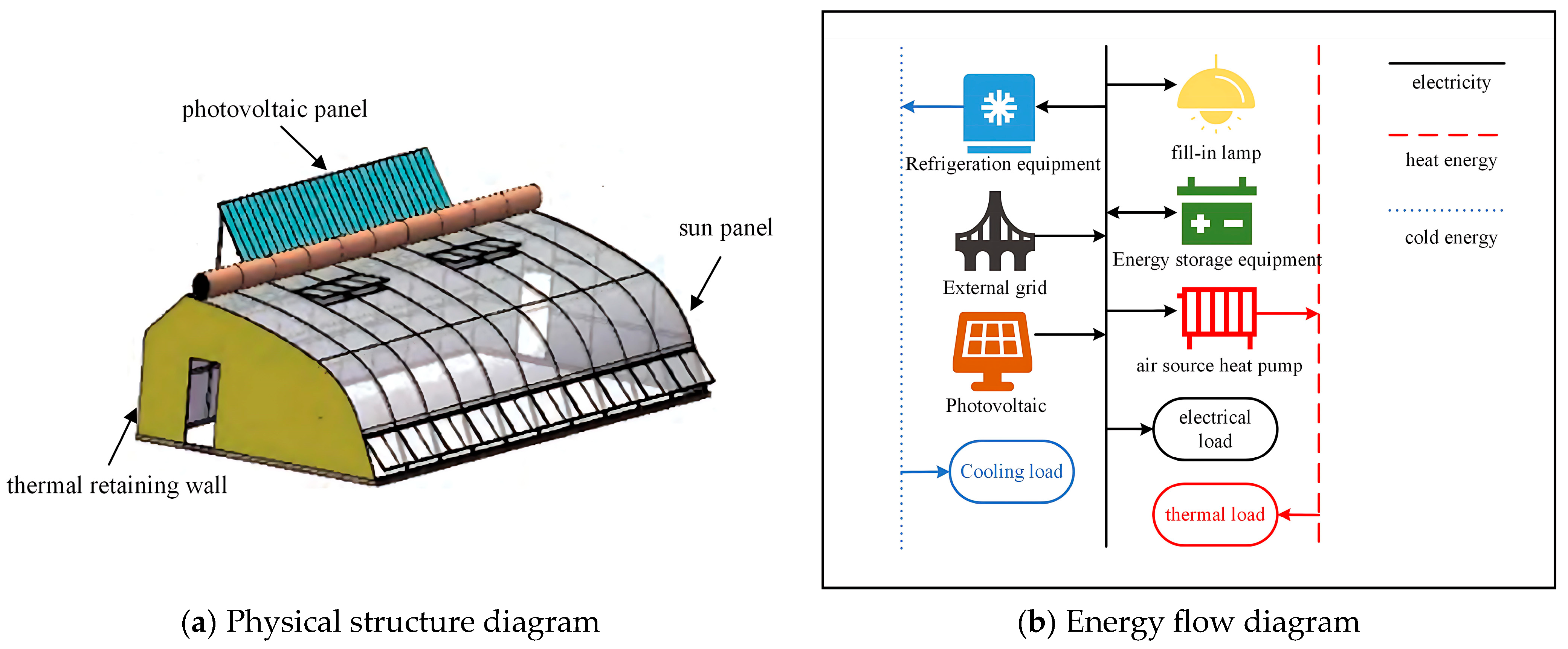
2.1. Physical Structure of Photovoltaic-Storage Agricultural Greenhouses
2.2. Photovoltaic Power Generation System Model
2.3. Energy Storage System Model
2.4. Agricultural Greenhouse Heating Model
2.5. Agricultural Greenhouse Cooling Model
2.6. Robust Optimization Model for Photovoltaic Output Uncertainty
2.7. Load Model of Micro Energy Grids for PSAG
2.8. Carbon Emission Model
2.8.1. Carbon Emission Reduction Model for PV Power Generation
2.8.2. Grid Carbon Model
3. Operational Optimization Model Based on the Selection of Project Operating Mode
3.1. Analysis of Different Project Operation Modes
3.2. Cost–Benefit Analysis of Different Project Operating Modes
3.2.1. Cost–Benefit Analysis Under the SIC Mode
3.2.2. Cost–Benefit Analysis Under the EPC Mode
3.3. Operational Optimization Models Under Different Project Operating Modes
3.3.1. Operational Optimization Model in SIC Mode
3.3.2. Operational Optimization Model in EPC Mode
4. Example Analysis
4.1. Data
4.2. Results and Discussion
4.2.1. Comparison of Total Annual Costs for Different Modes
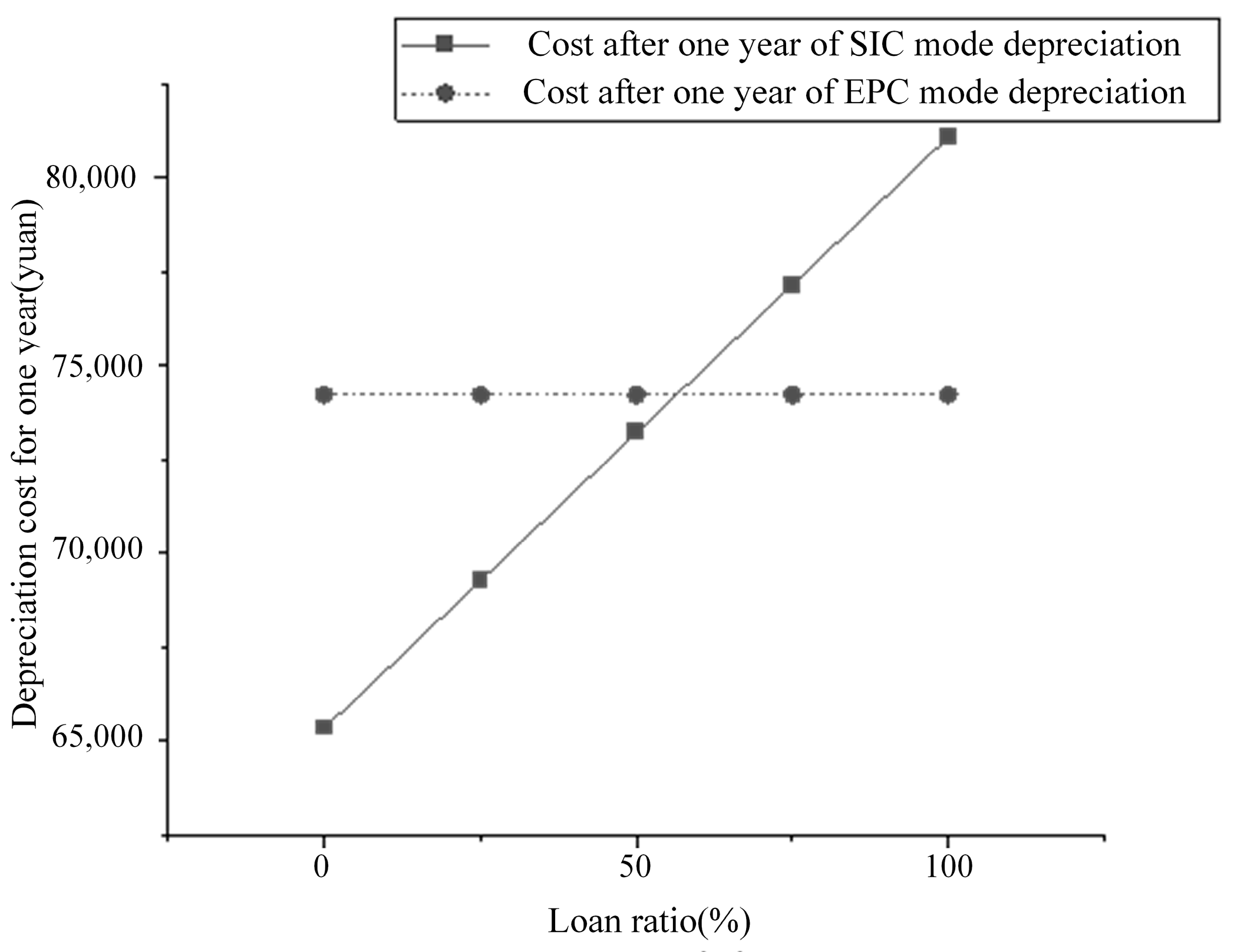
4.2.2. Comparison of Costs for Different Loan Ratios
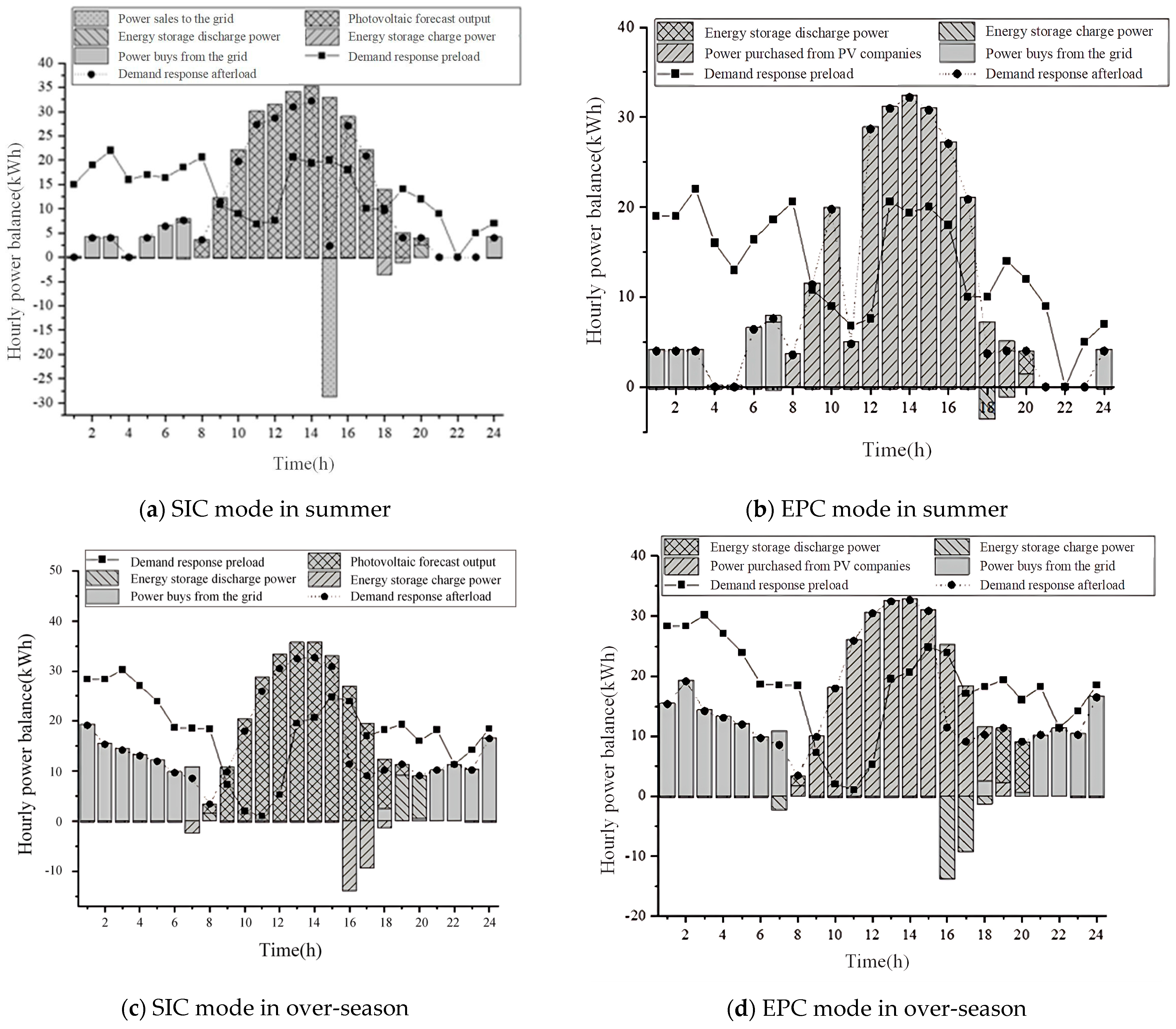
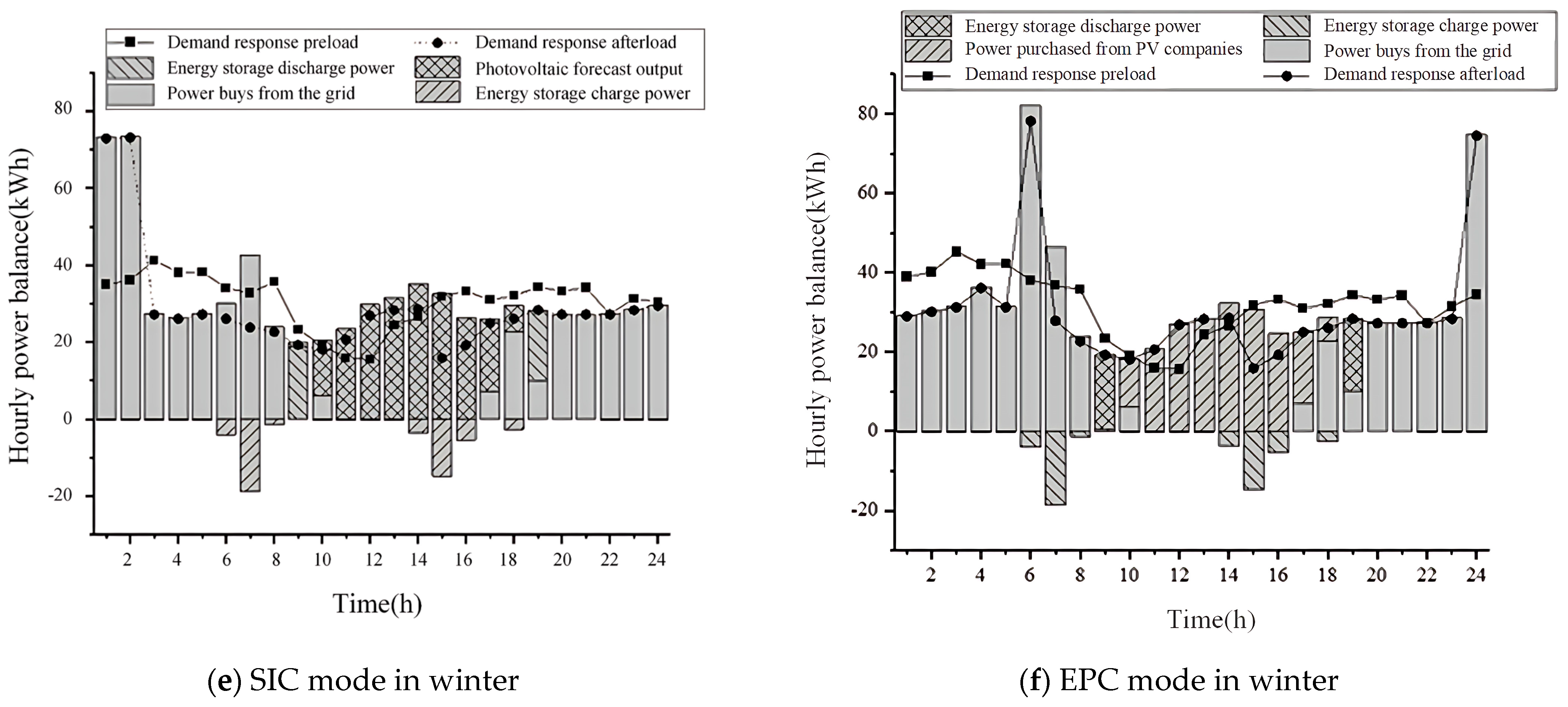
4.2.3. Optimization Analysis of Electricity Supply and Demand Strategies
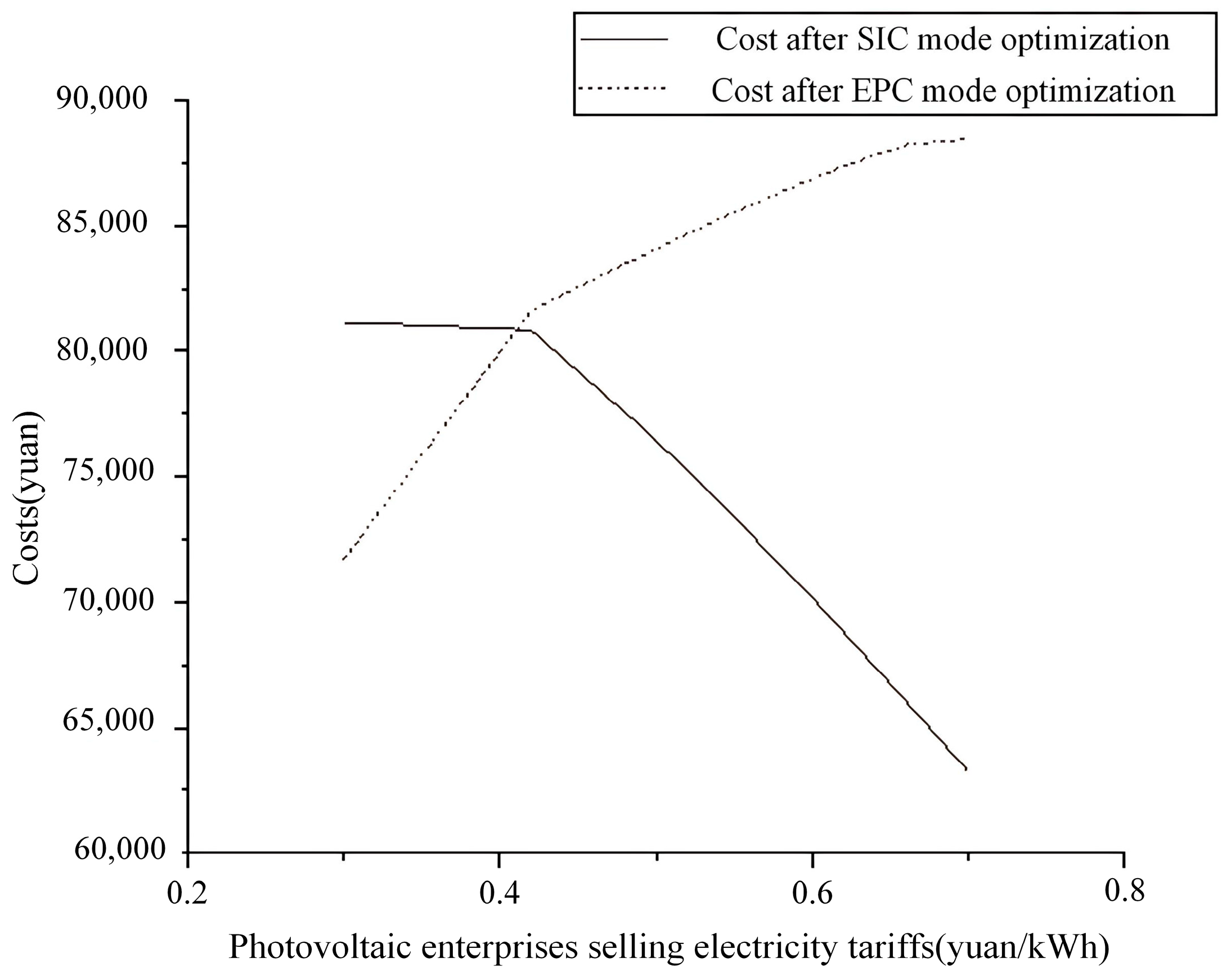
4.2.4. Sensitivity Analysis of Electricity Sales Tariffs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Pan, J.; Xiong, R.; Xiong, Z.; Chen, Y. Study on the Problems and Paths of Cleaner Rural Energy Consumption in Hubei Province under the Target of “Double Carbon”. Rural Econ. Sci.-Technol. 2023, 34, 227–230. [Google Scholar]
- Li, W. Research on Capacity Allocation Optimization and Operation Scheduling of New Household Energy System in Rural Qinghai. Bachelor’s Thesis, Xi’an University of Architecture & Technology, Xi’an, China, 2023. [Google Scholar]
- Cong, H.; Zhao, L.; Wang, J.; Yao, Z. Current situation and development demand analysis of rural energy in China. Trans. Chin. Soc. Agric. Eng. 2017, 33, 224–231. [Google Scholar]
- Bardi, U.; Asmar, T.E.; Lavacchi, A. Turning electricity into food: The role of renewable energy in the future of agriculture. J. Clean. Prod. 2013, 53, 224–231. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Z. Development direction of distribution network in agricultural areas in China. Electr. Supply 2011, 28, 5–6+11. [Google Scholar]
- Li, J.; Chen, S.; Wu, Y.; Wang, Q.; Liu, X.; Qi, L.; Lu, X.; Gao, L. How to make better use of intermittent and variable energy? A review of wind and photovoltaic power consumption in China. Renew. Sustain. Energy Rev. 2021, 137, 110626. [Google Scholar] [CrossRef]
- Fernández, E.F.; Villar-Fernández, A.; Montes-Romero, J.; Ruiz-Torres, L.; Rodrigo, P.M.; Manzaneda, A.J.; Almonacid, F. Global energy assessment of the potential of photovoltaics for greenhouse farming. Appl. Energy 2022, 309, 118474. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, Y.; Wei, W.; Xie, P.; Chen, Y. Day-ahead-real-time cooperative scheduling of wind-fire-storage large bases based on consumption intervals. J. Shanghai Jiao Tong Univ. 2024, 1–24. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, X.; Tong, Q. Optimal Design of Distributed Energy Systems in Rural Area of Developing Country: A Case Study of Guanzhong Area, China. IOP Conf. Ser. Earth Environ. Sci. 2018, 192, 012049. [Google Scholar] [CrossRef]
- Yang, S.; Fang, J.; Zhang, Z.; Lv, S.; Lin, H.; Ju, L. Two-stage coordinated optimal dispatching model and benefit allocation strategy for rural new energy microgrid. Energy 2024, 292, 130274. [Google Scholar] [CrossRef]
- Güven, A.F.; Mengi, O.Ö. Assessing metaheuristic algorithms in determining dimensions of hybrid energy systems for isolated rural environments: Exploring renewable energy systems with hydrogen storage features. J. Clean. Prod. 2023, 428, 139339. [Google Scholar] [CrossRef]
- Kamal, M.; Ashraf, I.; Fernández, E. Optimal sizing of standalone rural microgrid for sustainable electrification with renewable energy resources. Sustain. Cities Soc. 2023, 88, 104298. [Google Scholar] [CrossRef]
- Kamal, M.; Ashraf, I.; Fernández, E. Optimal renewable integrated rural energy planning for sustainable energy development. Sustain. Energy Technol. 2022, 53, 102581. [Google Scholar]
- Suman, G.K.; Guerrero, J.M.; Roy, O.P. Optimisation of Solar/Wind/Bio-Generator/Diesel/Battery Based Microgrids for Rural Areas: A PSO-GWO Approach. Sustain. Cities Soc. 2021, 67, 102723. [Google Scholar] [CrossRef]
- Chen, C.; Xing, J.; Li, Q.; Liu, S.; Ma, J.; Chen, J.; Han, L.; Qiu, W.; Lin, Z.; Yang, L. Wasserstein Distance-Based Distributionally Robust Optimal Scheduling in Rural Microgrid Considering the Coordinated Interaction among Source-Grid-Load-Storage. Energy Rep. 2021, 7, 60–66. [Google Scholar] [CrossRef]
- Yadav, S.; Kumar, P.; Kumar, A. Hybrid Renewable Energy Systems Design and Techno-Economic Analysis for Isolated Rural Microgrid Using HOMER. Energy 2025, 327, 136442. [Google Scholar] [CrossRef]
- Boccalatte, A.; Fossa, M.; Sacile, R. Modeling, design and construction of a zero-energy PV greenhouse for applications in mediterranean climates. Therm. Sci. Eng. Prog. 2021, 25, 101046. [Google Scholar] [CrossRef]
- Azam, M.; Eltawil, M.; Amer, B. Thermal analysis of PV system and solar collector integrated with greenhouse dryer for drying tomatoes. Energy 2020, 212, 118764. [Google Scholar] [CrossRef]
- Ghaffarpour, Z.; Fakhroleslam, M.; Amidpour, M. Calculation of Energy Consumption, Tomato Yield, and Electricity Generation in a PV-Integrated Greenhouse with Different Solar Panels Configuration. Renew. Energy 2024, 229, 120723. [Google Scholar] [CrossRef]
- Haoyi, Y.; Yunfeng, W.; Xun, M.; Ming, L.; Fangling, F. An investigation on daylight in PV greenhouse for mushroom vertical cultivation in Kunming, China. Sol. Energy 2025, 291, 113414. [Google Scholar] [CrossRef]
- Ghiasi, M.; Wang, Z.; Mehrandezh, M.; Paranjape, R. Enhancing Efficiency through Integration of Geothermal and Photovoltaic in Heating Systems of a Greenhouse for Sustainable Agriculture. Sustain. Cities Soc. 2025, 118, 106040. [Google Scholar] [CrossRef]
- Wang, L.; Mao, Y.; Li, Z.; Yi, X.; Ma, Y.; Zhang, Y.; Li, M. Life Cycle Carbon Emission Intensity Assessment for Photovoltaic Greenhouses: A Case Study of Beijing City, China. Renew. Energy 2024, 230, 120775. [Google Scholar] [CrossRef]
- Jamshidi, F.; Ghiasi, M.; Mehrandezh, M.; Wang, Z.; Paranjape, R. Optimizing Energy Consumption in Agricultural Greenhouses: A Smart Energy Management Approach. Smart Cities 2024, 7, 859–879. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, M.; Ma, X.; Wang, Y.; Li, G.; Zhang, Y.; Liu, Y.; Hassanien, R.H.E. Solar irradiance prediction with variable time lengths and multi-parameters in full climate conditions based on photovoltaic greenhouse. Energy Convers. Manag. 2024, 315, 118758. [Google Scholar] [CrossRef]
- Attia, A.M.; Al Hanbali, A.; Saleh, H.H.; Alsawafy, O.G.; Ghaithan, A.M.; Mohammed, A. A Multi-Objective Optimization Model for Sizing Decisions of a Grid-Connected Photovoltaic System. Energy 2021, 229, 120730. [Google Scholar] [CrossRef]
- Sun, T.; Jin, S.; Liu, G.; Hu, Y.; Qu, Y. Robust optimal allocation of photovoltaic town considering source-load uncertainty. Power Eng. Technol. 2023, 42, 42–51. [Google Scholar]
- Cui, Y. Research on Home Energy Management Strategy Based on Robust Optimization. Bachelor’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
- Wang, W.; Liu, F.; Yang, J.; Zheng, J.; Yang, Y.; Zhang, J. Optimal dispatch of micro-energy grid of photovoltaic smart agricultural greenhouse based on time-shiftable agricultural load. J. China Agric. Univ. 2018, 23, 160–168. [Google Scholar]
- Wei, W.; Zhang, P.; Yao, M.; Xue, M.; Miao, J.; Liu, B.; Wang, F. Multi-Scope Electricity-Related Carbon Emissions Accounting: A Case Study of Shanghai. J. Clean. Prod. 2020, 252, 119789. [Google Scholar] [CrossRef]
| Reference | Key Focus | Methodology | Economic Optimization | Operational Mode Analysis |
|---|---|---|---|---|
| Boccalatte et al. [17] | NZEB design | PV–heat pump integration | Energy efficiency metrics | no |
| Azam et al. [18] | Post-harvest drying | Hybrid PV–thermal system | Thermal efficiency analysis | no |
| Zahra et al. [19] | Structural-energy balance | Energy–growth–PV coupling | Yield–energy trade-offs | no |
| Yao et al. [20] | Lighting optimization | RADIANCE lighting simulation | Spatial efficiency metrics | no |
| Ghiasi et al. [21] | Geothermal–PV hybrid | Hybrid heating system Design | Sustainability assessment | no |
| Wang et al. [22] | Lifecycle energy management | LCA framework | Resource utilization efficiency | no |
| Zhu et al. [24] | PV forecasting | Solar irradiance time series | Prediction accuracy improvement | no |
| This study | Operational economics | Dual-mode robust optimization (SIC/EPC) | Cost–benefit trade-offs under financial models | yes |
| Components | Values |
|---|---|
| Benchmark power | 67.8 kW |
| Inverter power | 4.6 kW |
| Number of inverters | 14 |
| PV module rated power | 440 W |
| Number of PV modules | 154 |
| System power generation | 92.2 mWh/yr |
| Annual unit power generation | 1361 kWh/kW/yr |
| System efficiency | 0.904 |
| Array loss | 0.35 kWh/kW/day |
| Systemic loss | 0.05 kWh/kW/day |
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 h–1 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 h–2 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 h–3 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 h–4 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 h–5 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 h–6 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 h–7 h | 0 | 0 | 0 | 0 | 0.7 | 1.4 | 0.7 | 0 | 0 | 0 | 0 | 0 |
| 7 h–8 h | 0 | 0 | 0.2 | 3.2 | 4.3 | 4.1 | 3.9 | 3.1 | 2.6 | 0.2 | 0 | 0 |
| 8 h–9 h | 0 | 3.7 | 8.9 | 12.6 | 13.7 | 12.5 | 11.9 | 12.5 | 10.9 | 10.2 | 8.4 | 0.2 |
| 9 h–10 h | 13.4 | 16.1 | 20.8 | 23.2 | 24.5 | 22.5 | 21.7 | 22.3 | 19.1 | 18.3 | 16.6 | 13.8 |
| 10 h–11 h | 22.2 | 27.1 | 29.7 | 30.9 | 33 | 30.5 | 30.5 | 29.4 | 27.4 | 25.8 | 25.5 | 20.9 |
| 11 h–12 h | 27.9 | 35.3 | 36.1 | 36.1 | 36.4 | 32.3 | 29 | 33.5 | 31.5 | 31.3 | 29.1 | 26.1 |
| 12 h–13 h | 31 | 37.9 | 36.7 | 39.3 | 38.3 | 35.1 | 31.4 | 36 | 33.4 | 34.4 | 32.1 | 25.6 |
| 13 h–14 h | 31.9 | 41.6 | 38.2 | 38.9 | 35.9 | 36.5 | 33.4 | 35.9 | 33.8 | 33.4 | 34.4 | 31.8 |
| 14 h–15 h | 30.9 | 38.4 | 36.1 | 36.4 | 33.9 | 33 | 30.8 | 34.9 | 31 | 29.8 | 31.1 | 28.2 |
| 15 h–16 h | 26.5 | 30 | 30.7 | 30.7 | 27.9 | 28.8 | 27.8 | 30.3 | 26.1 | 23 | 23.6 | 22.7 |
| 16 h–17 h | 19.1 | 22.5 | 22.8 | 23.5 | 19.5 | 21.7 | 21.2 | 23.6 | 19.9 | 15.6 | 15.6 | 15.1 |
| 17 h–18 h | 7.4 | 12.6 | 14.2 | 13.2 | 11.2 | 13.5 | 13.8 | 14.8 | 11.1 | 6.8 | 2 | 0.2 |
| 18 h–19 h | 0 | 0.2 | 3 | 4.1 | 3.9 | 4.9 | 5.5 | 4.9 | 2 | 0 | 0 | 0 |
| 19 h–20 h | 0 | 0 | 0 | 0 | 0.7 | 1.9 | 1.9 | 0.4 | 0 | 0 | 0 | 0 |
| 20 h–21 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 21 h–22 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 22 h–23 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 h–24 h | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Parameters | Values | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||||
| Values | 0 | 0 | 0 | 0 | 0 | 0.1 | 0.67 | 1.11 | 1.72 | 2.23 | 2.57 | 2.69 | |||||
| Time | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |||||
| Values | 3.01 | 2.89 | 1.89 | 1.72 | 1.12 | 0.82 | 0.27 | 0 | 0 | 0 | 0 | 0 | |||||
| Values | 0.9 | 0.7 | 0.5 | 0.3 | 0.1 | ||||||||||||
| Probability | 0.973 | 0.947 | 0.836 | 0.743 | 0.674 | ||||||||||||
| Costs | SIC Mode Costs (yuan) | EPC Mode Costs (yuan) | EPC vs. SIC (%) |
|---|---|---|---|
| Energy storage system costs | 23,077.42 | 23,077.42 | 0 |
| Energy storage system capacity costs | 12,701.20 | 12,701.20 | 0 |
| Energy storage system power cost | 10,376.22 | 10,376.22 | 0 |
| Annual maintenance cost of energy storage systems | 932.21 | 932.21 | 0 |
| Replacement cost of energy storage systems | 25,123.25 | 25,123.25 | 0 |
| Photovoltaic installation costs | 330,520 | 0 | / |
| Annual maintenance costs for photovoltaics | 2775 | 0 | / |
| Rents | 0 | −70,000 | / |
| Annual carbon trading costs | 1.53 | 2383.75 | 155,700 |
| Annual interest on loans | 16,526 | 0 | / |
| Summer solstice day costs | 7.29 | 90.02 | 1134 |
| Costs of a day in excess of seasonal days | 78.77 | 156.17 | 98.26 |
| Winter solstice day costs | 280.59 | 359.0 | 27.94 |
| Total annual running costs | 41,825.65 | 70,730.73 | 69.11 |
| Costs for one year after depreciation | 81,083.69 | 74,216.22 | −8.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhao, M.; Zhang, H.; Zhang, O.; Li, N.; Yue, X.; Tan, Z. An Operational Optimization Model for Micro Energy Grids in Photovoltaic-Storage Agricultural Greenhouses Based on Operation Mode Selection. Processes 2025, 13, 1622. https://doi.org/10.3390/pr13061622
Li P, Zhao M, Zhang H, Zhang O, Li N, Yue X, Tan Z. An Operational Optimization Model for Micro Energy Grids in Photovoltaic-Storage Agricultural Greenhouses Based on Operation Mode Selection. Processes. 2025; 13(6):1622. https://doi.org/10.3390/pr13061622
Chicago/Turabian StyleLi, Peng, Mengen Zhao, Hongkai Zhang, Outing Zhang, Naixun Li, Xianyu Yue, and Zhongfu Tan. 2025. "An Operational Optimization Model for Micro Energy Grids in Photovoltaic-Storage Agricultural Greenhouses Based on Operation Mode Selection" Processes 13, no. 6: 1622. https://doi.org/10.3390/pr13061622
APA StyleLi, P., Zhao, M., Zhang, H., Zhang, O., Li, N., Yue, X., & Tan, Z. (2025). An Operational Optimization Model for Micro Energy Grids in Photovoltaic-Storage Agricultural Greenhouses Based on Operation Mode Selection. Processes, 13(6), 1622. https://doi.org/10.3390/pr13061622






