Evaluation of Ultrasonic Cleaning Characteristics of Filter Cloth in Filter Press Cleaning System
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Materials
2.2. Experimental Conditions and Apparatus
2.3. Sample Analysis
2.4. RSM (Response Surface Methodology)
3. Results
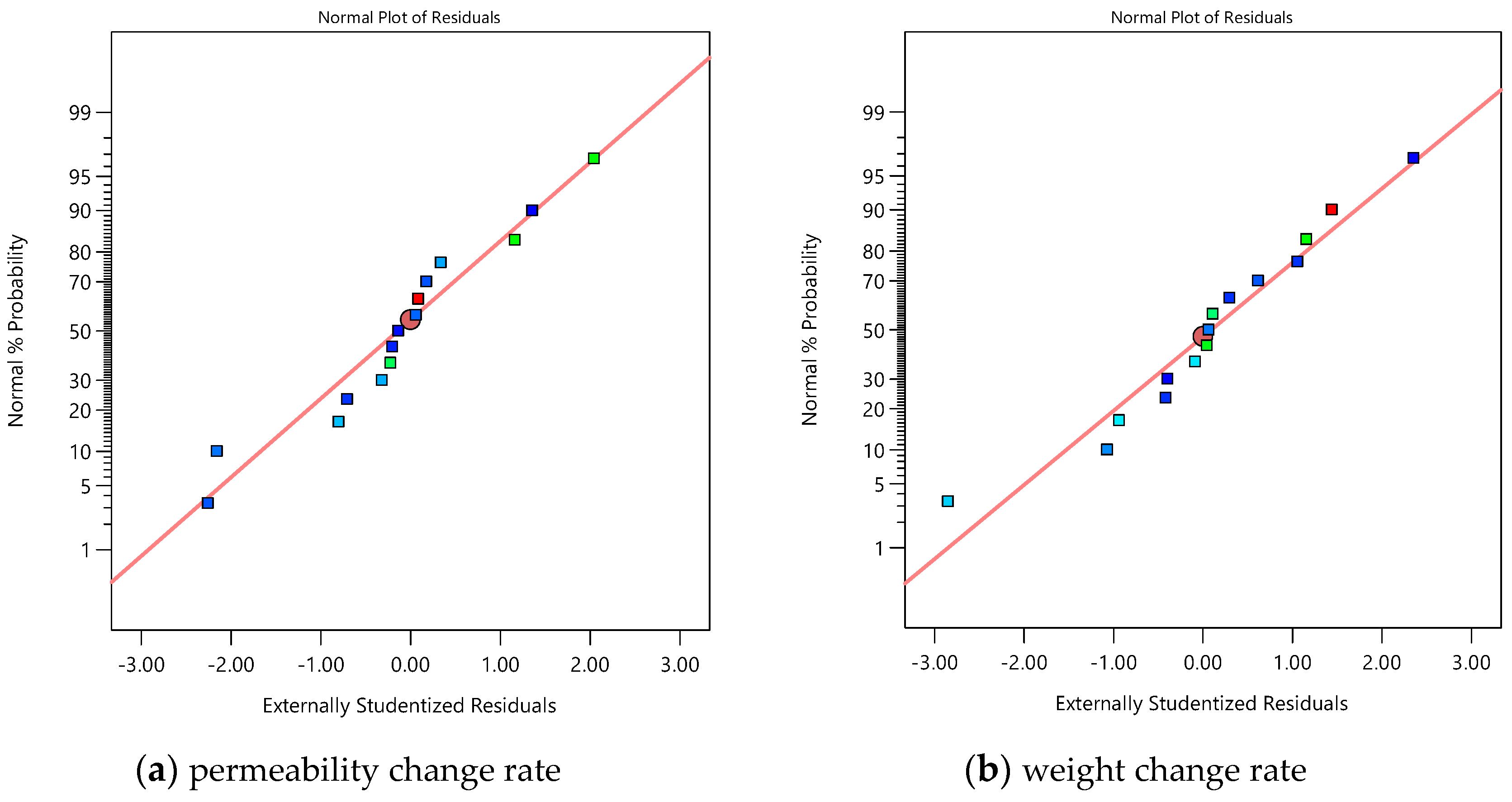
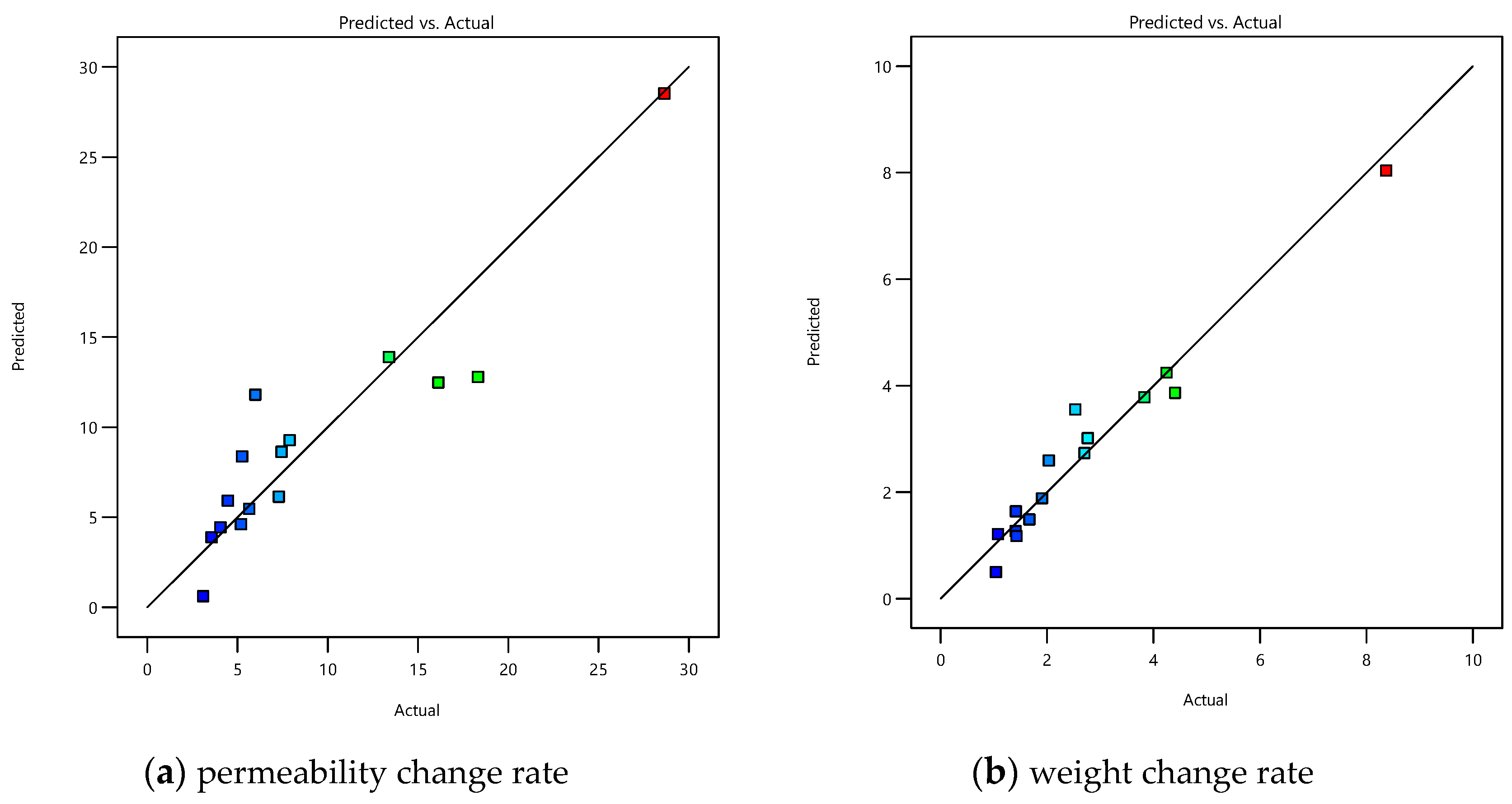
3.1. Analysis of Statics
Analysis of Models (ANOVA)
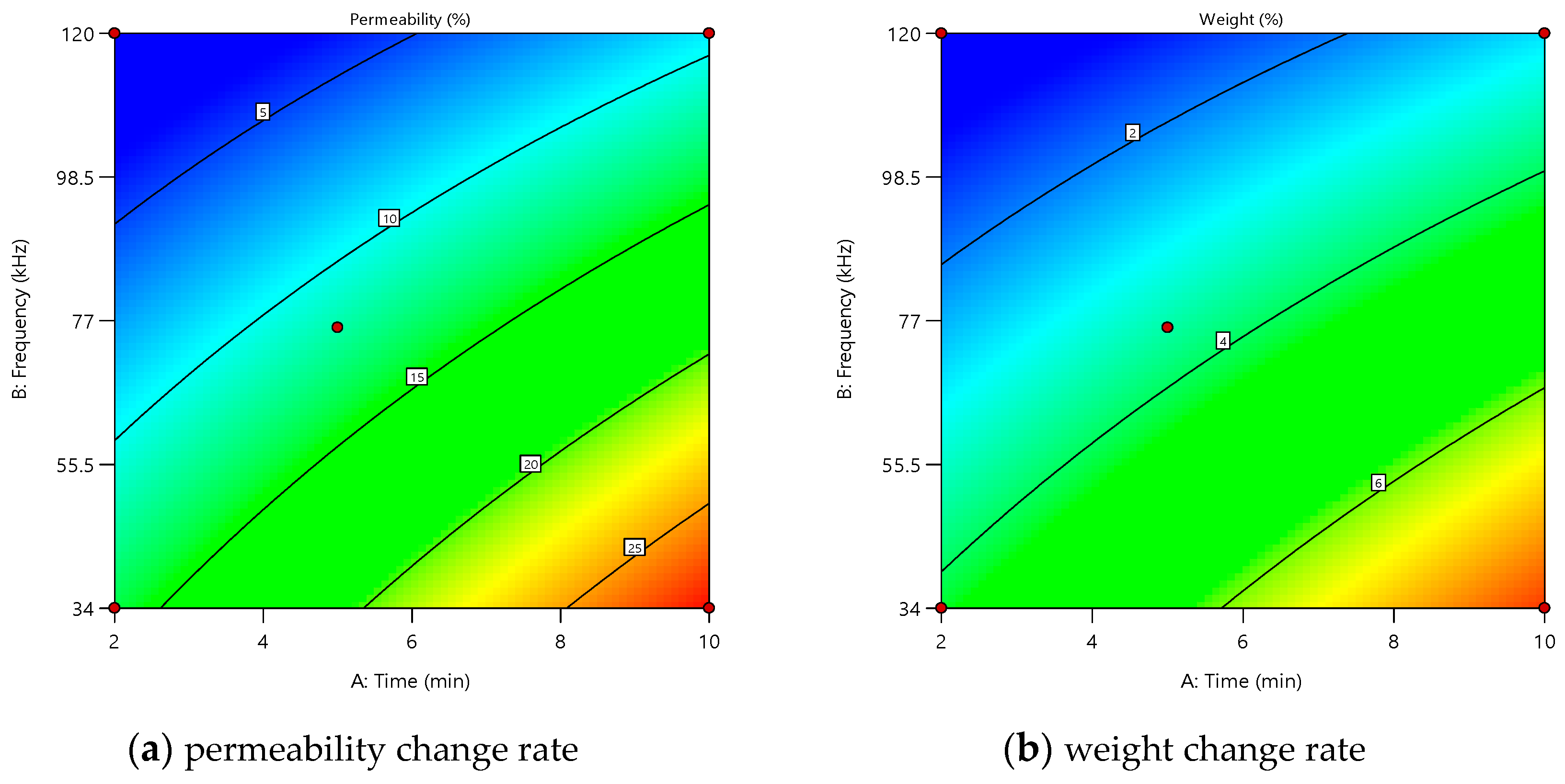
3.2. Optimization of Statistics (RSM)
3.3. Analysis of SEM
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOE | Design of Experiments |
| RSM | Response Surface Methodology |
| CCD | Central composite design |
| BBD | Box–Behnken design |
| DO | Dissolved oxygen |
| ANOVA | Analysis of Variance |
| AP | Adequate precision |
| CI | Confidence Interval |
| TI | Test Interval |
| SE | Standard Error |
| SEM | Scanning electron microscopy |
| p-value | Probability value |
| Dev | Deviation |
| kHz | Kilohertz |
| W | Watt |
| P0 | Air permeability before cleaning (m3·m−2·h−1) |
| Pc | Air permeability after cleaning (m3·m−2·h−1) |
| W0 | Weight before cleaning (g) |
| Wc | Weight after cleaning (g) |
| ε | Error |
| 2FI | Two-Factor Interaction |
References
- Bernd, F.; Patrick, M.; Hermann, N. Regeneration assessments of filter fabrics of filter presses in the mining sector. Miner. Eng. 2021, 168, 106922. [Google Scholar]
- Gunson, A.J.; Klein, B.; Veiga, M.; Dunbar, S. Reducing mine water requirements. J. Clean. Prod. 2012, 21, 71–82. [Google Scholar] [CrossRef]
- Amir, H.M.; Ali, H. Filter press optimisation for black mulberry juice extraction. Biosyst. Eng. 2022, 215, 80–103. [Google Scholar]
- Qasim, M.; Darwish, N.N.; Mhiyo, S. The use of ultrasound to mitigate membrane fouling in desalination and water treatment. Desalination 2018, 443, 143–164. [Google Scholar] [CrossRef]
- Alventosa-deLara, E.; Barredo-Damas, S.; Alcaina-Miranda, M.I.; Iborra-Clar, M.I. Study and optimization of the ultrasound-enhanced cleaning of an ultrafiltration ceramic membrane through a combined experimentale statistical approach. Ultrason. Sonochem. 2014, 21, 1222–1234. [Google Scholar] [CrossRef]
- Gonzalez-Avila, S.R.; Prabowo, F.; Kumar, A.; Ohl, C.D. Improved ultrasonic cleaning of membranes with tandem frequency excitation. J. Membr. Sci. 2012, 415, 776–783. [Google Scholar] [CrossRef]
- Jin, W.; Guo, W.; Lu, X.; Han, P.; Wang, Y. Effect of the ultrasound generated by flat plate transducer cleaning on polluted polyvinylidene fluoride hollow fiber ultrafiltration membrane. Chin. J. Chem. Eng. 2008, 16, 801–804. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kobayashi, T.; Hosaka, Y.; Fujii, N. Ultrasound enhance membrane cleaning processes applied water treatments: Influence of sonic frequency on filtration treatments. Ultrasonics 2003, 41, 185–190. [Google Scholar] [CrossRef]
- Lamminen, M.O.; Walker, H.W.; Weavers, K. Mechanisms and factors influencing the ultrasonic cleaning of particle-fouled ceramic membranes. J. Membr. Sci. 2004, 237, 213–223. [Google Scholar] [CrossRef]
- Lujan-Facundo, M.J.; Mendoza-Roca, J.A.; Cuartas-Uribe, B.; Alvarez-Blanco, S. Ultrasonic cleaning of ultrafiltration membranes fouled with BSA solution. Sep. Purif. Technol. 2013, 120, 275–281. [Google Scholar] [CrossRef]
- Muthukumaran, S.; Yang, K.; Seuren, A.; Kentish, S.; Ashokkumar, M.; Stevens, G.W.; Grieser, F. The use of ultrasonic cleaning for ultrafiltration membranes in the dairy industry. Sep. Purif. Technol. 2004, 39, 99–107. [Google Scholar] [CrossRef]
- Li, J.; Sanderson, R.D.; Jacobs, E.P. Ultrasonic cleaning of nylon microfiltration membranes fouled by Kraft paper mill effluent. J. Membr. Sci. 2002, 205, 247–257. [Google Scholar] [CrossRef]
- Masselin, I.; Chasseray, X.; Laurence, D.B.; Laine, J.M.; Syzaret, P.-Y.; Lemordant, D. Effect of sonication on polymeric membranes. J. Membr. Sci. 2001, 181, 213–220. [Google Scholar] [CrossRef]
- Vergara-Araya, M.; Oeltze, H.; Radeva, J.; Roth, A.G.; Göbbert, C. Operation of Hybrid Membranes for the Removal of Pharmaceuticals and Pollutants from Water and Wastewater. Membranes 2022, 12, 502. [Google Scholar] [CrossRef]
- Abdullayev, A.; Bekheet, M.F.; Hanaor, D.A.H.; Gurlo, A. Materials and Applications for Low-Cost Ceramic Membranes. Membranes 2019, 9, 105. [Google Scholar] [CrossRef]
- Sewerin, T.; Elshof, M.G.; Matencio, S.; Boerrigter, M.; Yu, J.; de Grooth, J. Advances and Applications of Hollow Fiber Nanofiltration Membranes: A Review. Membranes 2021, 11, 890. [Google Scholar] [CrossRef]
- Luo, H.; Wang, Z. A new ultrasonic cleaning model for predicting the flux recovery of the UF membrane fouled with humic acid. J. Environ. Chem. Eng. 2022, 10, 107156. [Google Scholar] [CrossRef]
- Shi, X.; Tal, G.; Hankins, N.P.; Gitis, V. Fouling and cleaning of ultrafiltration membranes: A review. J. Water Process Eng. 2014, 1, 121–138. [Google Scholar] [CrossRef]
- Lujan-Facundo, M.J.; Mendoza-Roca, J.A.; Cuartas-Uribe, B.; Alvarez-Blanco, S. Membrane fouling in whey processing and subsequent cleaning with ultrasounds for a more sustainable process. J. Clean. Prod. 2017, 143, 804–813. [Google Scholar] [CrossRef]
- Arefi-Oskoui, S.; Khataee, A.; Safarpour, M.; Orooji, Y.; Vatanpour, V. A review on the applications of ultrasonic technology in membrane bioreactors. Ultrason. Sonochem. 2019, 58, 104633. [Google Scholar] [CrossRef]
- Ge, H.; Zhan, W.; Xi, W. Ultrasonic cleaning in the membrane process: From phenomenon to mechanism and mathematical model. Chem. Eng. Sci. 2023, 282, 119267. [Google Scholar]
- Hauptmann, M.; Frederickx, F.; Struyf, H.; Mertens, P.; Heyns, M.; De Gendt, S.; Glorieux, C.; Brems, S. Enhancement of cavitation activity and particle removal with pulsed high frequency ultrasound and supersaturation. Ultrason. Sonochem. 2013, 20, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Verhaagen, B.; Fernandez Rivas, D. Measuring cavitation and its cleaning effect. Ultrason. Sonochem. 2016, 29, 619–628. [Google Scholar] [CrossRef] [PubMed]
- Chahine, G.L.; Kapahi, A.; Choi, J.K.; Hsiao, C.T. Modeling of surface cleaning by cavitation bubble dynamics and collapse. Ultrason. Sonochem. 2016, 29, 528–549. [Google Scholar] [CrossRef]
- Park, S.H. Modern Design of Experiments; Minyoug Pub.: Seoul, Republic of Korea, 2011; pp. 521–571. [Google Scholar]
- Raymond, H.M.; Douglas, C.M.; Christine, M.A. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 1–58. [Google Scholar]
- Yuan, J.; Huang, J.; Wu, G.; Tong, J.; Xie, G.; Duan, J.; Qin, M. Multiple responses optimization of ultrasonic-assisted extraction by response surface methodology (RSM) for rapid analysis of bioactive compounds in the flower head of Chrysanthemum morifolium Ramat. Ind. Crops Prod. 2015, 74, 192–199. [Google Scholar] [CrossRef]
- KS K ISO9237; Detemination of the permeability of fabrics to air. Korean Agency for Technology and Standards: Eumseong, Republic of Korea, 1995.
- Pooralhossini, J.; Zanjanchi, M.A.; Ghaedi, M.; Asfaram, A.; Ahmadi Azqhandi, M.H. Statistical optimization and modeling approach for azo dye decolorization: Combined effects of ultrasound waves and nanomaterial-based adsorbent. Appl. Organometal. Chem. 2018, 32, e4205. [Google Scholar] [CrossRef]
- Azqhandi, M.H.A.; Foroughi, M.; Yazdankish, E. A highly effective, recyclable, and novel host-guest nanocomposite for Triclosan removal: A comprehensive modeling and optimization-based adsorption study. J. Colloid Interface Sci. 2019, 551, 195–207. [Google Scholar] [CrossRef]
- O’Brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Malika, M.; Sonawane, S.S. Statistical modelling for the Ultrasonic photodegradation of Rhodamine B dye using aqueous based Bi-metal doped TiO2 supported montmorillonite hybrid nanofluid via RSM. Sustain. Energy Technol. Assess. 2021, 44, 100980. [Google Scholar] [CrossRef]
- Banerjee, P.; Barman, S.R.; Mukhopadhayay, A.; Das, P. Ultrasound assisted mixed azo dye adsorption by chitosan-graphene oxide nanocomposite. Chem. Eng. Res. Des. 2017, 117, 43–56. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Banerjee, P.; Das, P.; Bhowal, A.; Majumdar, S.K.; Ghosh, P. Removal of aqueous carbamazepine using graphene oxide nanoplatelets: Process modelling and optimization. Sustain. Environ. Res. 2020, 30, 17. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Das, P.; Bhowal, A.; Saha, A. Thermal, Chemical and ultrasonic assisted synthesis of carbonized Biochar and its application for reducing Naproxen: Batch and Fixed bed study and subsequent optimization with response surface methodology (RSM) and artificial neural network (ANN). Surf. Interfaces 2021, 26, 101378. [Google Scholar] [CrossRef]
- Noorani Khomeyrani, S.F.; Ahmadi Azqhandi, M.H.; Ghalami-Choobar, B. Rapid and efficient ultrasonic assisted adsorption of PNP onto LDH-GO-CNTs: ANFIS, GRNN and RSM modeling, optimization, isotherm, kinetic, and thermodynamic study. J. Mol. Liq. 2021, 333, 115917. [Google Scholar] [CrossRef]
- Costa, N.R.; Lourenço, J.; Pereira, Z.L. Desirability function approach: A review and performance evaluation in adverse condition. Chemom. Intell. Lab. Syst. 2011, 107, 234–244. [Google Scholar] [CrossRef]
- Nair, A.T.; Ahammed, M.M. The reuse of water treatment sludge as a coagulant for post-treatment of UASB reactor treating urban wastewater. J. Clean. Prod. 2015, 96, 272–281. [Google Scholar] [CrossRef]
- Pandey, A.; Belwala, T.; Sekara, K.C.; Bhatta, I.D.; Rawal, R.S. Optimization of ultrasonic-assisted extraction (UAE) of phenolics and antioxidant compounds from rhizomes of Rheum moorcroftianum using response surface methodology (RSM). Ind. Crops Prod. 2018, 119, 218–225. [Google Scholar] [CrossRef]
- Vivek, K.; Subbarao, K.V.; Srivastava, B. Optimization of postharvest ultrasonic treatment of kiwifruit using RSM. Ultrason. Sonochemistry 2016, 32, 328–335. [Google Scholar] [CrossRef]
- Bai, H.; Tian, J.; Talifu, D.; Okitsu, K.; Abulizi, A. Process optimization of esterification for deacidification in waste cooking oil: RSM approach and for biodiesel production assisted with ultrasonic and solvent. Fuel 2022, 318, 123697. [Google Scholar] [CrossRef]
- Ealias, A.M.; Saravanakumar, M.P. Facile synthesis and characterisation of AlNs using Protein Rich Solution extracted from sewage sludge and its application for ultrasonic assisted dye adsorption: Isotherms, kinetics, mechanism and RSM design. J. Environ. Manag. 2018, 206, 215–227. [Google Scholar] [CrossRef]
- Vedaramana, N.; Sandhyaa, K.V.; Charukeshb, N.R.B.; Venkatakrishnana, B.; Haribabub, K.; Sridharana, M.R.; Nagarajanc, R. Ultrasonic extraction of natural dye from Rubia Cordifolia, optimisation using response surface methodology (RSM) & comparison with artificial neural network (ANN) model and its dyeing properties on different substrates. Chem. Eng. Process. 2017, 114, 46–54. [Google Scholar]
- Vyas, N.; Dehghani, H.; Sammons, R.L.; Wang, Q.X.; Leppinen, D.M.; Walmsley, A.D. Imaging and analysis of individual cavitation microbubbles around dental ultrasonic scalers. Ultrasonics 2017, 81, 66–72. [Google Scholar] [CrossRef] [PubMed]





| Component Parts | Parameter | Value |
|---|---|---|
| Tank | Volume | 191 L |
| Transducers (BLT) | Length | 0.40 m |
| Interval | 0.05–0.15 m | |
| Ultrasonic Generators | Frequency | 34 kHz, 76 kHz, 120 kHz |
| Power | 100 W, 200 W, 300 W |
| Independent Variable | Symbol | Levels | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| Time (min) | A | 2 | 5 | 10 |
| Frequency (kHz) | B | 34 | 76 | 120 |
| Power (W) | C | 100 | 200 | 300 |
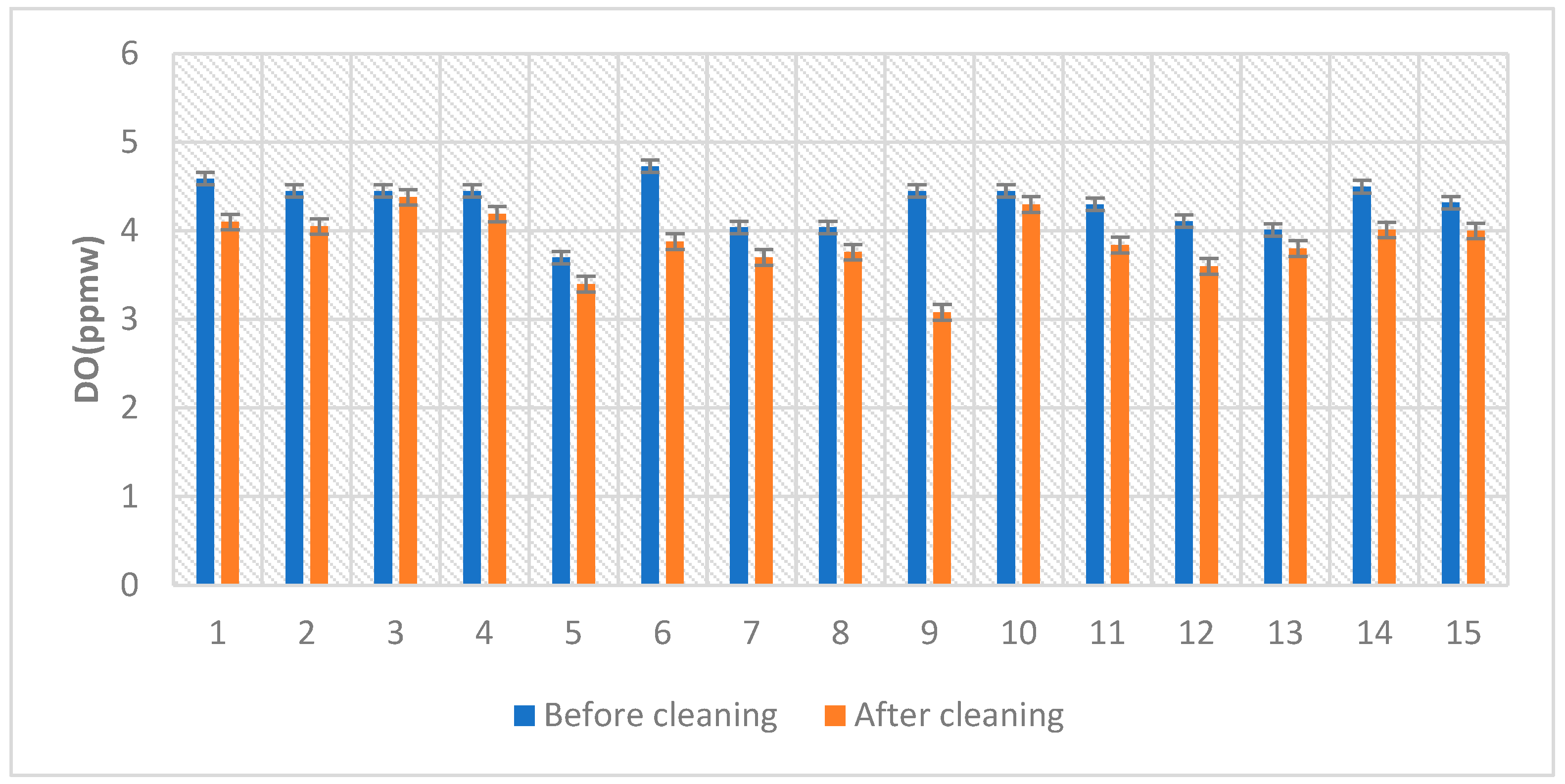
| A: Time | B: Frequency | C: Power | Before | After | |
|---|---|---|---|---|---|
| min | kHz | W | DO (ppmw) | ||
| 1 | 2 | 34 | 300 | 4.59 | 4.10 |
| 2 | 5 | 34 | 200 | 4.45 | 4.05 |
| 3 | 2 | 76 | 200 | 4.45 | 4.38 |
| 4 | 10 | 34 | 100 | 4.45 | 4.19 |
| 5 | 2 | 120 | 100 | 3.70 | 3.40 |
| 6 | 10 | 120 | 300 | 4.73 | 3.88 |
| 7 | 10 | 34 | 300 | 4.04 | 3.70 |
| 8 | 2 | 34 | 100 | 4.04 | 3.76 |
| 9 | 5 | 76 | 100 | 4.45 | 3.08 |
| 10 | 10 | 120 | 100 | 4.45 | 4.30 |
| 11 | 5 | 76 | 200 | 4.30 | 3.84 |
| 12 | 5 | 76 | 300 | 4.11 | 3.60 |
| 13 | 5 | 120 | 200 | 4.01 | 3.80 |
| 14 | 10 | 76 | 200 | 4.50 | 4.01 |
| 15 | 2 | 120 | 300 | 4.32 | 4.00 |
| Factor 1 | Factor 2 | Factor 3 | Response 1 | Response 2 | ||
|---|---|---|---|---|---|---|
| Std | Run | A: Time | B: Frequency | C: Power | Permeability | Weight |
| min | kHz | W | % | % | ||
| 4 | 1 | 2 | 34 | 300 | 13.40 | 4.25 |
| 5 | 2 | 5 | 34 | 200 | 16.14 | 4.41 |
| 12 | 3 | 2 | 76 | 200 | 7.29 | 1.91 |
| 10 | 4 | 10 | 34 | 100 | 5.26 | 2.77 |
| 1 | 5 | 2 | 120 | 100 | 4.47 | 1.08 |
| 13 | 6 | 10 | 120 | 300 | 7.90 | 2.70 |
| 9 | 7 | 10 | 34 | 300 | 28.66 | 8.37 |
| 3 | 8 | 2 | 34 | 100 | 3.58 | 1.67 |
| 11 | 9 | 5 | 76 | 100 | 5.66 | 1.41 |
| 6 | 10 | 10 | 120 | 100 | 4.06 | 1.43 |
| 8 | 11 | 5 | 76 | 200 | 7.45 | 2.04 |
| 15 | 12 | 5 | 76 | 300 | 6.00 | 2.53 |
| 2 | 13 | 5 | 120 | 200 | 5.20 | 1.41 |
| 7 | 14 | 10 | 76 | 200 | 18.34 | 3.83 |
| 14 | 15 | 2 | 120 | 300 | 3.10 | 1.04 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 606.68 | 6 | 101.11 | 7.98 | 0.0049 | significant |
| A—Time | 110.49 | 1 | 110.49 | 8.72 | 0.0183 | |
| B—Frequency | 184.76 | 1 | 184.76 | 14.58 | 0.0051 | |
| C—Power | 137.41 | 1 | 137.41 | 10.84 | 0.0110 | |
| AB | 18.03 | 1 | 18.03 | 1.42 | 0.2671 | |
| AC | 52.11 | 1 | 52.11 | 4.11 | 0.0771 | |
| BC | 117.14 | 1 | 117.14 | 9.24 | 0.0161 | |
| Residual | 101.37 | 8 | 12.67 | |||
| Cor Total | 708.05 | 14 | ||||
| R² | 0.85 | Predicted R² | 0.36 | |||
| Adjusted R² | 0.74 | Adeq Precision | 11.47 | |||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 48.92 | 6 | 8.15 | 28.36 | <0.0001 | significant |
| A—Time | 9.02 | 1 | 9.02 | 31.39 | 0.0005 | |
| B—Frequency | 19.41 | 1 | 19.41 | 67.52 | <0.0001 | |
| C—Power | 11.59 | 1 | 11.59 | 40.33 | 0.0002 | |
| AB | 1.23 | 1 | 1.23 | 4.29 | 0.0720 | |
| AC | 2.61 | 1 | 2.61 | 9.08 | 0.0167 | |
| BC | 6.00 | 1 | 6.00 | 20.88 | 0.0018 | |
| Residual | 2.30 | 8 | 0.29 | |||
| Cor Total | 51.22 | 14 | ||||
| R² | 0.95 | Predicted R² | 0.77 | |||
| Adjusted R² | 0.92 | Adeq Precision | 20.58 | |||
| Solution 1 of 44 Responses | Predicted Mean | Predicted Median | Std Dev | SE Mean | 95% CI Low for Mean | 95% CI High for Mean | 95% TI Low for 99% Pop | 95% TI High for 99% Pop |
|---|---|---|---|---|---|---|---|---|
| Permeability | 19.79 | 19.79 | 3.55 | 2.23 | 14.63 | 24.95 | 0.05 | 39.64 |
| Weight | 5.77 | 5.77 | 0.53 | 0.33 | 4.99 | 6.55 | 2.78 | 8.76 |
| Time min | Frequency kHz | Power W | Permeability % | Weight % | |
|---|---|---|---|---|---|
| Predicted | 5.2 | 34 | 300 | 19.8 | 5.8 |
| Experimental | 5.0 | 34 | 300 | 19.4 | 5.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, C.; Kim, E.; Han, S. Evaluation of Ultrasonic Cleaning Characteristics of Filter Cloth in Filter Press Cleaning System. Processes 2025, 13, 1574. https://doi.org/10.3390/pr13051574
Jeong C, Kim E, Han S. Evaluation of Ultrasonic Cleaning Characteristics of Filter Cloth in Filter Press Cleaning System. Processes. 2025; 13(5):1574. https://doi.org/10.3390/pr13051574
Chicago/Turabian StyleJeong, Cheoljin, Eunju Kim, and Sueongkuk Han. 2025. "Evaluation of Ultrasonic Cleaning Characteristics of Filter Cloth in Filter Press Cleaning System" Processes 13, no. 5: 1574. https://doi.org/10.3390/pr13051574
APA StyleJeong, C., Kim, E., & Han, S. (2025). Evaluation of Ultrasonic Cleaning Characteristics of Filter Cloth in Filter Press Cleaning System. Processes, 13(5), 1574. https://doi.org/10.3390/pr13051574






