Study on the Dissolution Mechanism of Aviation Hydraulic Oil–Nitrogen Gas Based on Molecular Dynamics
Abstract
:1. Introduction
2. Simulation Systems and Models
2.1. Simulation System
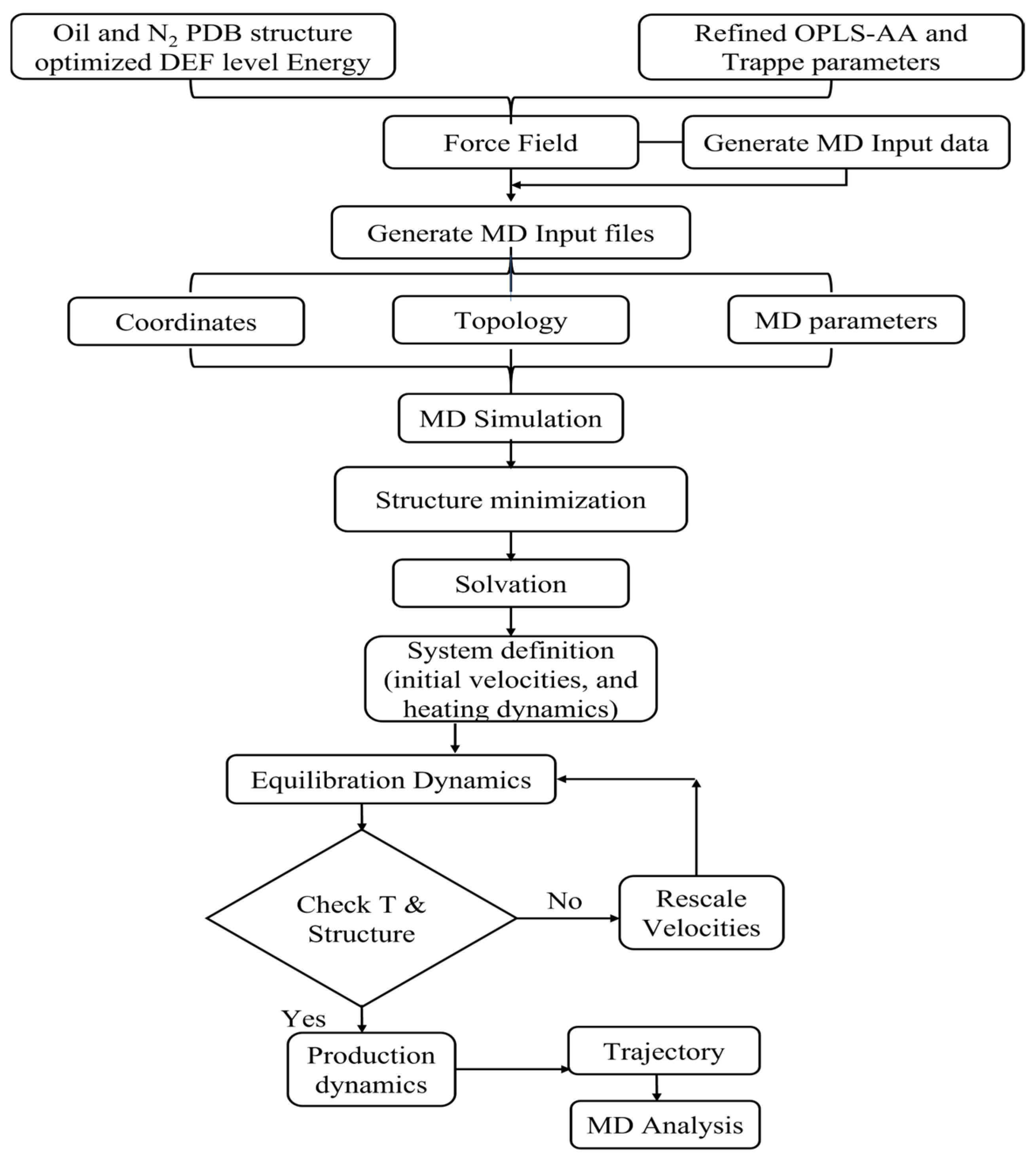
2.2. Simulation Details
3. Results and Discussion
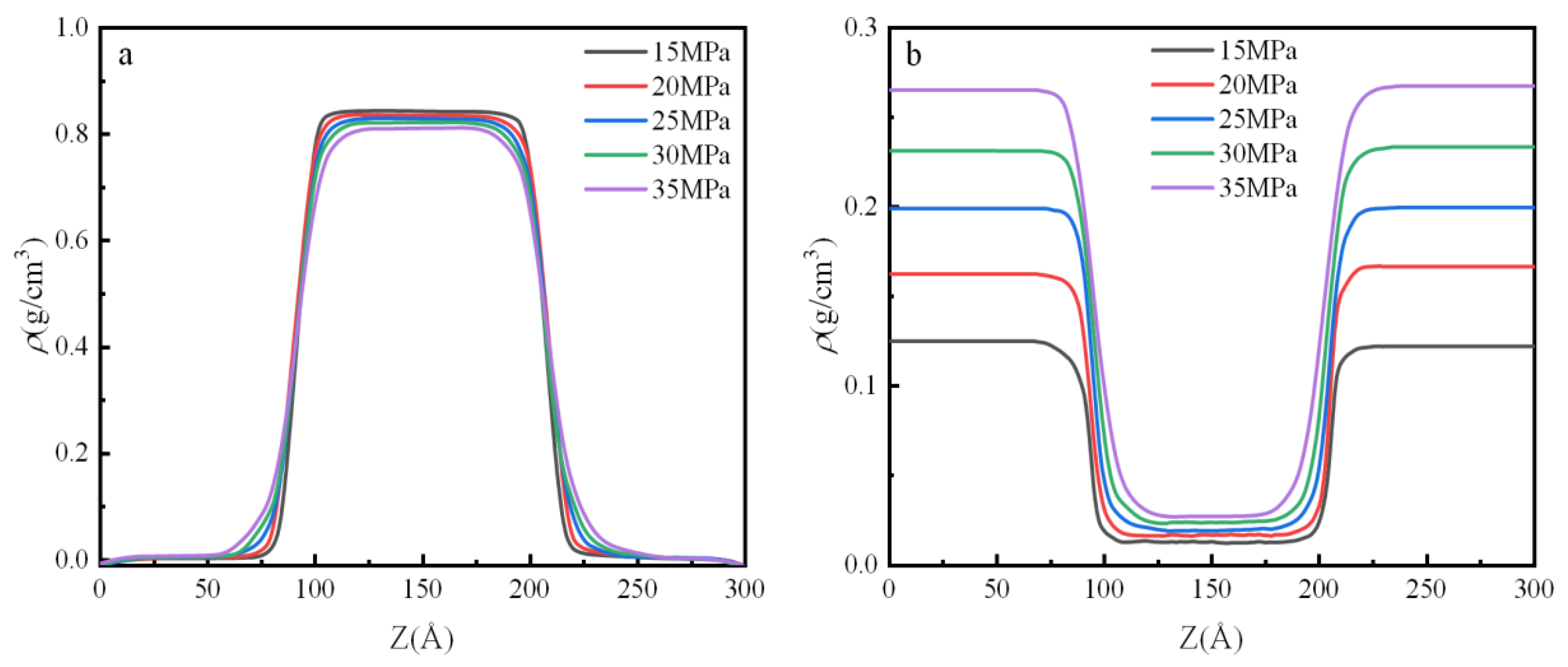
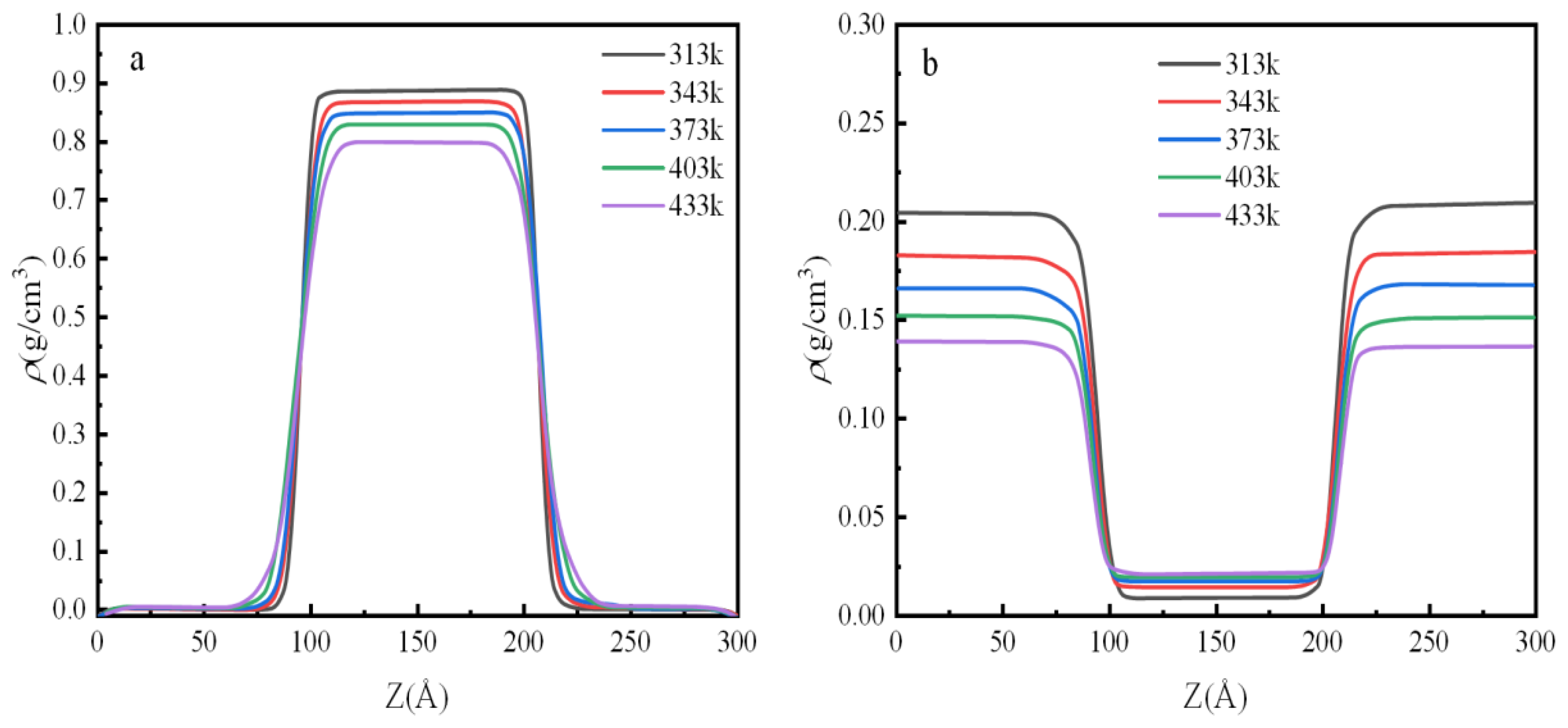
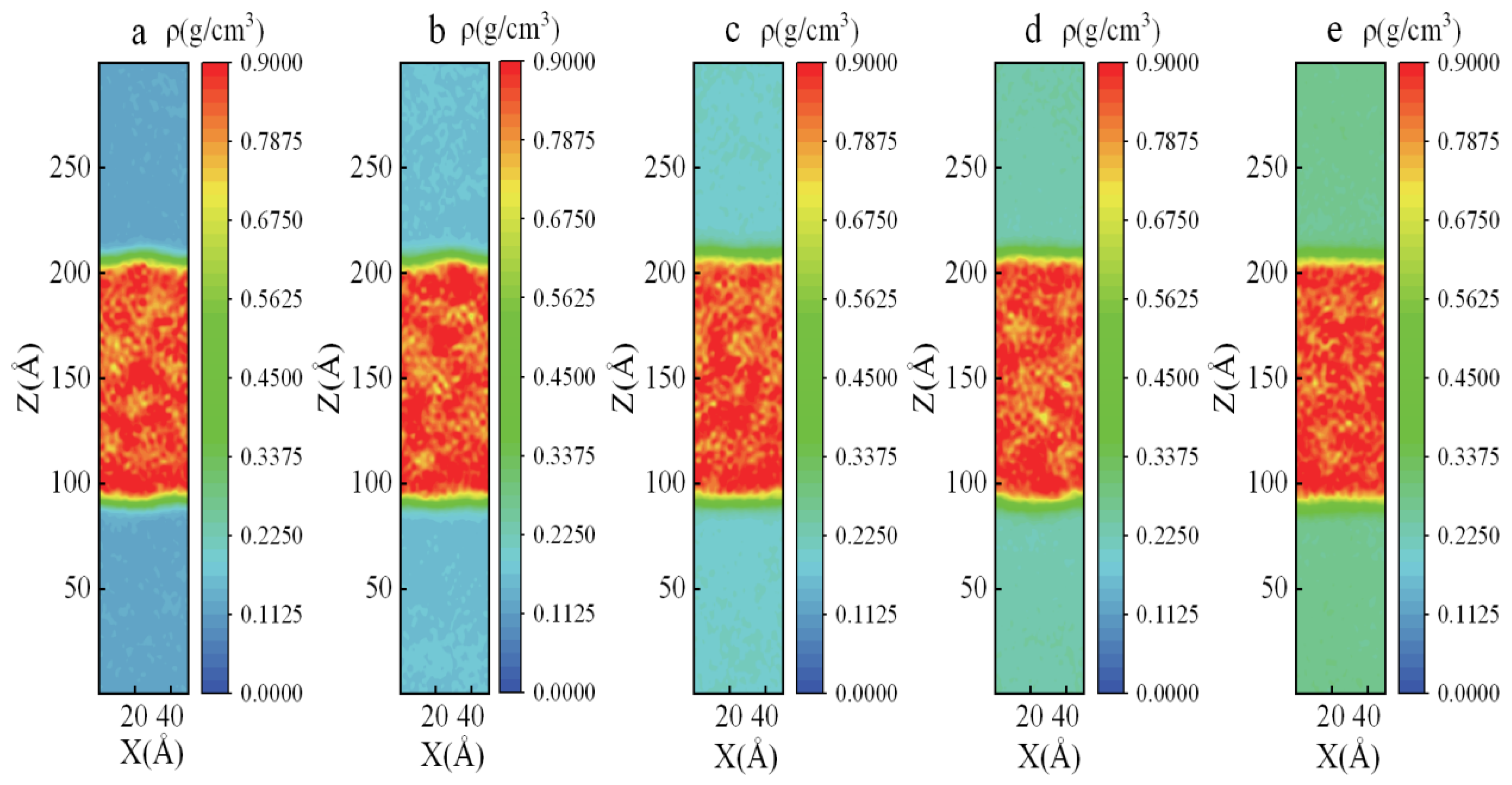
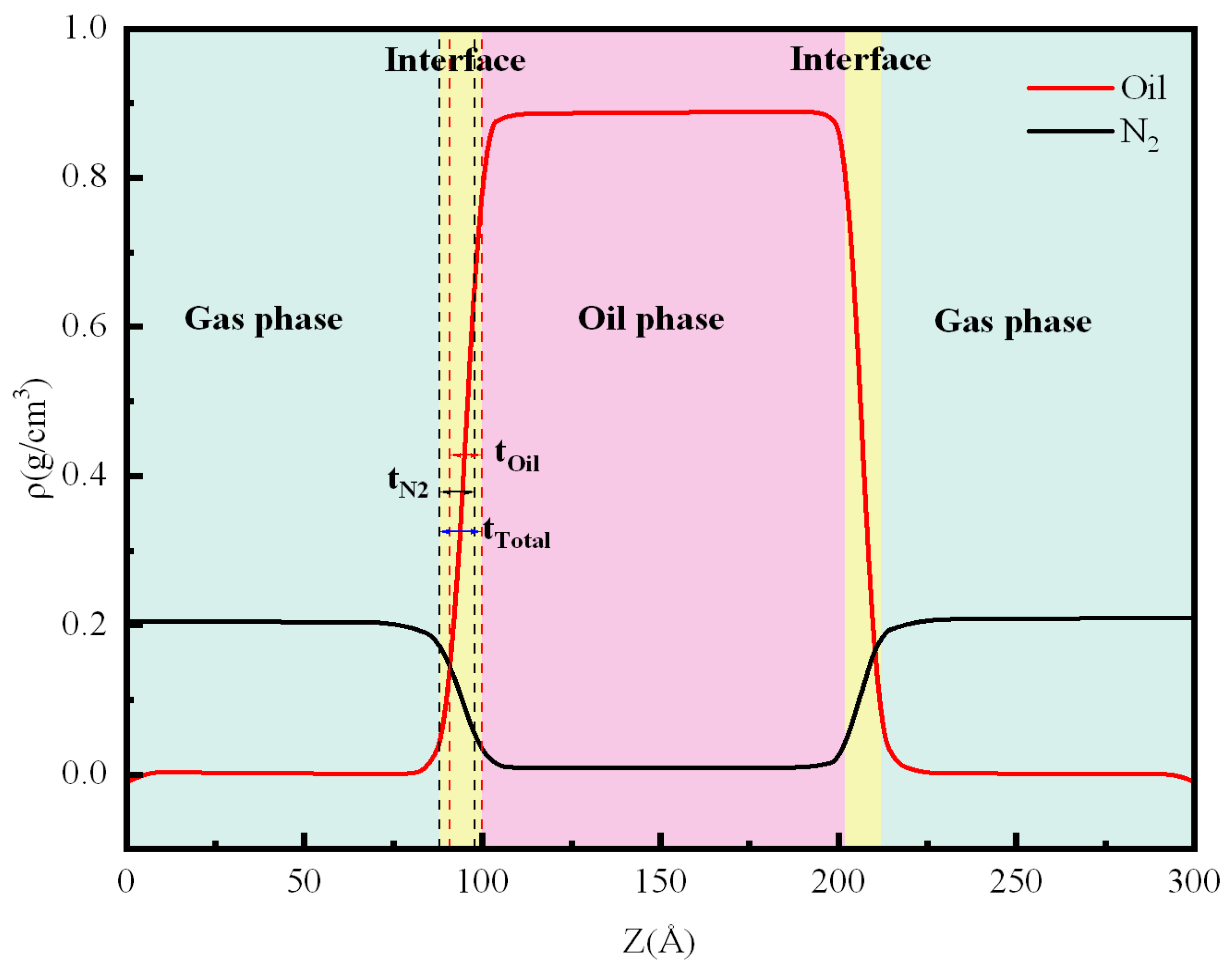
3.1. Density Distribution
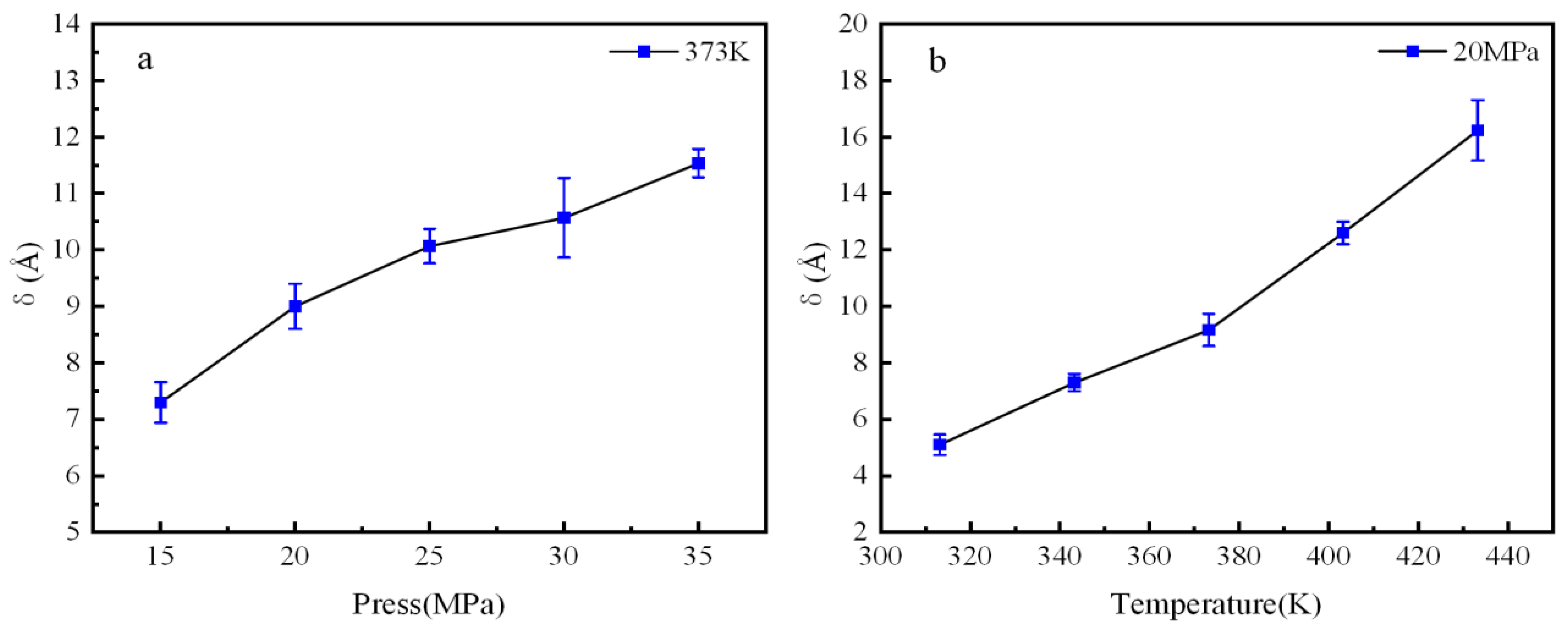
3.2. Interface Thickness
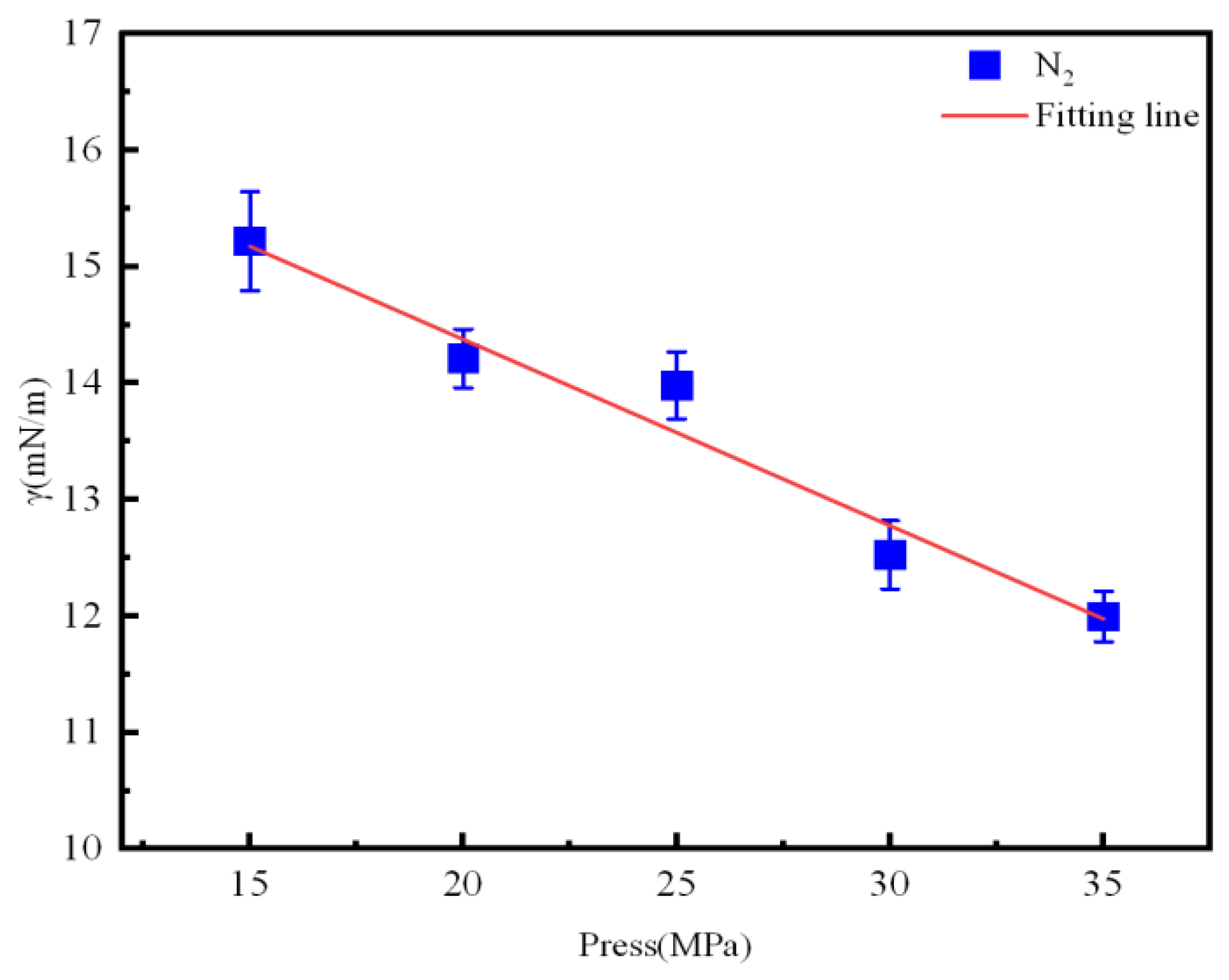
3.3. Interfacial Tension and MMP
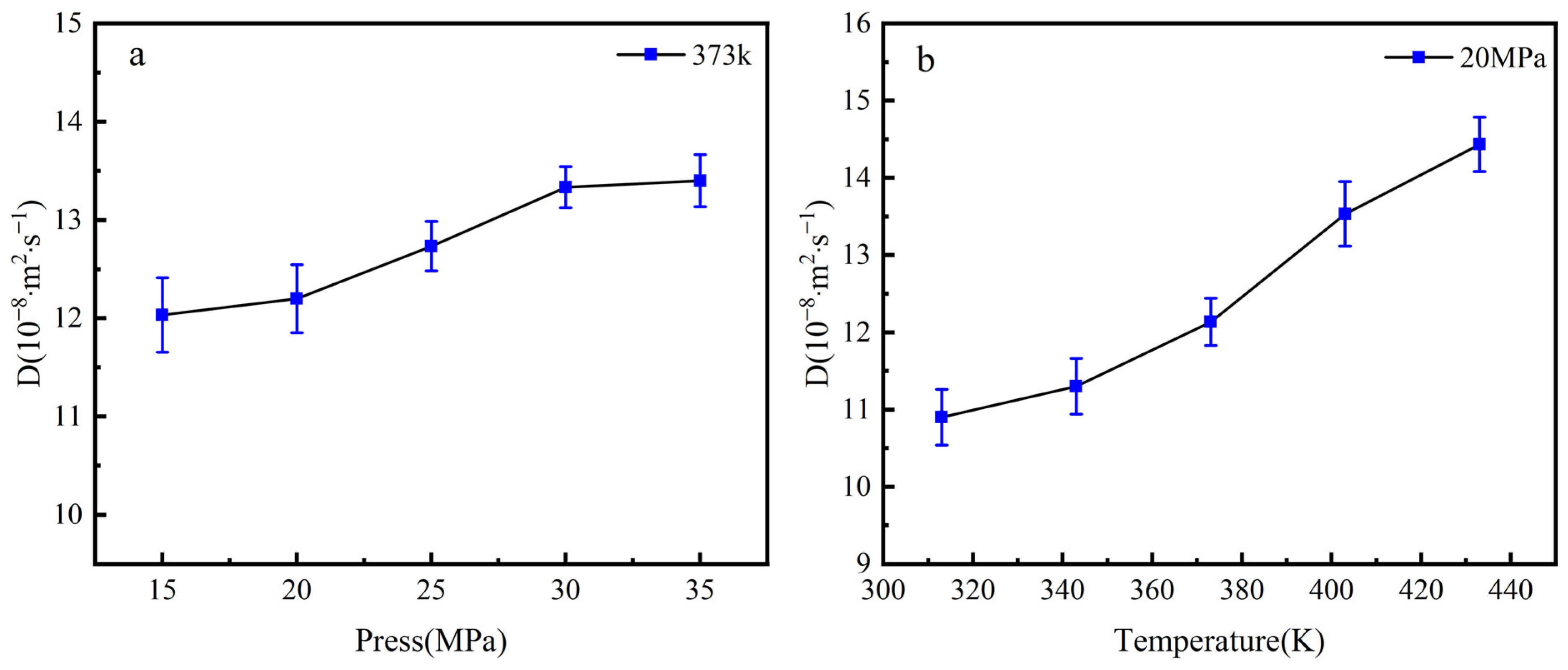
3.4. Diffusion Coefficient
3.5. Influence of System Energy on Oil–Gas Miscibility
3.6. Dissolution of N2 in Aviation Hydraulic Oil
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MD | molecular dynamics |
| MMP | minimum miscibility pressure |
References
- Ahmad, M.A.; Shah, S.I.A.; Shams, T.A.; Javed, A.; Rizvi, S.T.U.I. Comprehensive design of an oleo-pneumatic nose landing gear strut. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 1605–1622. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, C.; Peng, W.; Xuan, C.; Zhan, G. Analysis of Taxiing Performance of Single Strut Landing Gear Based on ISD. Mechanics 2023, 29, 486–493. [Google Scholar] [CrossRef]
- Pecora, R. A Rational Numerical Method for Simulation of Drop-Impact Dynamics of Oleo-Pneumatic Landing Gear. Appl. Sci. 2021, 11, 4136. [Google Scholar] [CrossRef]
- Jiao, F. Oil damping energy loss analysis of landing gear shock absorber. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 3096–3106. [Google Scholar] [CrossRef]
- Fang, X.; Chen, H.; Han, Y.; Xie, X.; Wei, X.; Nie, H. Crashworthiness performance simulation and analysis of combined-type landing gear buffer. J. Aerosp. Eng. 2022, 35, 04022049. [Google Scholar] [CrossRef]
- Du, S.; Zhang, C.; Zhou, K.; Zhao, Z. Study of the two-phase flow characteristics of a damping orifice in an oleo-pneumatic shock absorber. Fluids 2022, 7, 360. [Google Scholar] [CrossRef]
- Yin, Y.; Rakheja, S.; Yang, J.; Boileau, P.-E. Characterization of a hydro-pneumatic suspension strut with gas-oil emulsion. Mech. Syst. Signal Process. 2018, 106, 319–333. [Google Scholar] [CrossRef]
- Yin, Y.; Rakheja, S.; Yang, J.; Boileau, P. Effects of entrapped gas within the fluid on the stiffness and damping characteristics of a hydro-pneumatic suspension strut. SAE Int. J. Commer. Veh. 2017, 10, 204–209. [Google Scholar] [CrossRef]
- Seyyedattar, M.; Ghamartale, A.; Zendehboudi, S.; Butt, S. Assessment of CO2-Oil swelling behavior using molecular dynamics simulation: CO2 utilization and storage implication. J. Mol. Liq. 2023, 379, 121582. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular Dynamics Simulation for All. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Rezaei, N.; Lohi, A. Applications of hybrid models in chemical, petroleum, and energy systems: A systematic review. Appl. Energy 2018, 228, 2539–2566. [Google Scholar] [CrossRef]
- Feng, P.; Zhu, Y.; Zhao, K.; Gao, Y.; Liao, H.; Dai, Q.; Tang, Y.; Gou, K.; Zhu, X. Molecular dynamics simulation on the displacement behaviour of crude oil by CO2/CH4 mixtures on a silica surface. RSC Adv. 2024, 14, 6508–6520. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Li, X.; Hou, C.; Wang, L.; Zhou, G.; Ge, W.; Li, J. Engineering molecular dynamics simulation in chemical engineering. Chem. Eng. Sci. 2015, 121, 200–216. [Google Scholar] [CrossRef]
- Ungerer, P.; Nieto-Draghi, C.; Lachet, V.; Wender, A.; di Lella, A.; Boutin, A.; Fuchs, A.H. Molecular simulation applied to fluid properties in the oil and gas industry. Mol. Simulat. 2007, 33, 287–304. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, S.; Li, X.; Ma, D.; Sun, X.; Wang, H.-Z.; Yan, Y.; Xu, J.; Yang, C. Molecular Dynamics Simulation Reveals Unique Rheological and Viscosity–Temperature Properties of Karamay Heavy Crude Oil. Energy Fuels 2021, 35, 7956–7966. [Google Scholar] [CrossRef]
- Zhang, W.; Feng, Q.; Wang, S.; Xing, X. Oil diffusion in shale nanopores: Insight of molecular dynamics simulation. J. Mol. Liq. 2019, 290, 111183. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Sun, S.; Yao, J.; Kou, J. Flow behaviors of shale oil in kerogen slit by molecular dynamics simulation. Chem. Eng. J. 2022, 434, 134682. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, Z.; Liu, K.; Burke, N. Molecular Simulation of CO2 Solubility and Its Effect on Octane Swelling. Energy Fuels 2013, 27, 2741–2747. [Google Scholar] [CrossRef]
- Li, C.; Pu, H.; Zhong, X.; Li, Y.; Zhao, J.X. Interfacial interactions between Bakken crude oil and injected gases at reservoir temperature: A molecular dynamics simulation study. Fuel 2020, 276, 118058. [Google Scholar] [CrossRef]
- Li, B.; Liu, G.; Xing, X.; Chen, L.; Lu, X.; Teng, H.; Wang, J. Molecular dynamics simulation of CO2 dissolution in heavy oil resin-asphaltene. J. CO2 Util. 2019, 33, 303–310. [Google Scholar] [CrossRef]
- Huang, T.; Cheng, L.; Cao, R.; Wang, X.; Jia, P.; Cao, C. Molecular simulation of the dynamic distribution of complex oil components in shale nanopores during CO2-EOR. Chem. Eng. J. 2024, 479, 147743. [Google Scholar] [CrossRef]
- Wang, P.; Li, X.; Tao, Z.; Wang, S.; Fan, J.; Feng, Q.; Xue, Q. The miscible behaviors and mechanism of CO2/CH4/C3H8/N2 and crude oil in nanoslits: A molecular dynamics simulation study. Fuel 2021, 304, 121461. [Google Scholar] [CrossRef]
- Yan, Y.; Jia, Z.; Geng, X.; Liang, D.; Hao, X.; Yang, Z.; Ding, B. Insight into miscibility mechanism of multiple components crude oil in CO2/CH4 by molecular dynamic simulation. J. Mol. Liq. 2024, 398, 124283. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, Q.; Li, Z.; Qi, Y.; Liu, Y. Molecular Dynamics Study on the Diffusion Mass Transfer Behaviour of CO2 and Crude Oil in Fluids Produced via CO2 Flooding. Molecules 2023, 28, 7948. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, D.; Tian, C.; Ma, W.; Xia, Z. A virtual parallel model for the buffer landing of multi-legged landing gear. Mech. Mach. Theory 2024, 200, 105724. [Google Scholar] [CrossRef]
- Shi, X.; Yu, A.; Nie, H.; Zhang, M.; Gui, X.; Yang, S.; Zheng, Y.; Liu, T. Effects of Pitch Stabilization Buffer on the Dynamic Performance of Frame-Type Landing Gear. Aerospace 2024, 11, 288. [Google Scholar] [CrossRef]
- Yan, S.; Xue, P.; Liu, L.; Zahran, M.S. Optimization of landing gear under consideration of vibration comfort for civil aircraft. Aircr. Eng. Aerosp. Technol. 2024, 96, 378–386. [Google Scholar] [CrossRef]
- Chao, C.; Botao, H.; Xiangming, C.; Yanan, C.; Chun, Z. Variable stroke fatigue test for aircraft landing gears. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 239, 2117–2128. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, N.; Cui, B.; Guo, Q. Failure analysis and structural improvement of helicopter landing gear seals based on experiments and three-dimensional numerical simulation. Eng. Failure Anal. 2024, 163, 108596. [Google Scholar] [CrossRef]
- Bhattacherjee, R.; Botchway, K.; Pashin, J.C.; Chakraborty, G.; Bikkina, P. Developing statistical and machine learning models for predicting CO2 solubility in live crude oils. Fuel 2024, 368, 131577. [Google Scholar] [CrossRef]
- Zhang, J.; Guan, Y.; Li, T.; Yin, G. Solubility Variation and Prediction Model of CO2 in Water-Bearing Crude Oil. ACS Omega 2022, 7, 44420–44427. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Jin, Z.; Kim, Y.-G.; Fan, C. Development of machine learning-based solubility models for estimation of Hydrogen solubility in oil: Models assessment and validation. Case Stud. Therm. Eng. 2023, 51, 103622. [Google Scholar] [CrossRef]
- Saajanlehto, M.; Uusi-Kyyny, P.; Alopaeus, V. Hydrogen solubility in heavy oil systems: Experiments and modeling. Fuel 2014, 137, 393–404. [Google Scholar] [CrossRef]
- Su, H.; Wang, H.; Li, D.; Zhang, D. Diffusion and Dissolution Behaviors of CO2, CH4, and N2 in Heavy Oil under High-Temperature and -Pressure Conditions: Insights into Heavy Oil Production via Multithermal Fluid Stimulation. Energy Fuels 2023, 37, 15753–15767. [Google Scholar] [CrossRef]
- Ding, C.; Fan, Y. Measurement of Diffusion Coefficients of Air in Silicone Oil and in Hydraulic Oil. Chin. J. Chem. Eng. 2011, 19, 205–211. [Google Scholar] [CrossRef]
- de Lara, L.S.; Michelon, M.F.; Miranda, C.R. Molecular dynamics studies of fluid/oil interfaces for improved oil recovery processes. J. Phys. Chem. B 2012, 116, 14667–14676. [Google Scholar] [CrossRef]
- Liu, F.; Gao, X.; Du, J.; Lin, L.; Hou, D.; Luo, J.; Zhao, J. Microscopic mechanism of enhancing shale oil recovery through CO2 flooding-insights from molecular dynamics simulations. J. Mol. Liq. 2024, 410, 125593. [Google Scholar] [CrossRef]
- Li, J.; Chen, D.; Sun, K.; Pan, R.; Tang, Y. Molecular dynamics simulation and experimental study of the rheological performance of graphene lubricant oil. Diam. Relat. Mater. 2024, 141, 110721. [Google Scholar] [CrossRef]
- Gong, H.; Lv, W.; Zhang, H.; Zhang, M.; Sun, H.; Xu, L.; Dong, M. The influence and mechanism of alkyl block polyethers on the interfacial tension and minimum miscibility pressure of CO2 and shale oil. Fuel 2024, 356, 129568. [Google Scholar] [CrossRef]
- Adam, A.M.; Bahamon, D.; Al Kobaisi, M.; Vega, L.F. Molecular dynamics simulations of the interfacial tension and the solubility of brine/H2/CO2 systems: Implications for underground hydrogen storage. Int. J. Hydrogen Energy 2024, 78, 1344–1354. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, M.; Xin, G.; Li, D. Microscopic insights on the effects of flue gas components on CH4–CO2 replacement in natural gas hydrate. Gas Sci. Eng. 2023, 112, 204947. [Google Scholar] [CrossRef]
- Yan, S.; Zang, H.; Yang, S.; Liu, Z.; Li, Y.; Du, D. Exploration of the interfacial tension variation behavior in different CO2/oil systems based on experimental and molecular dynamics simulation studies. J. Mol. Liq. 2024, 415, 126312. [Google Scholar] [CrossRef]
- Mohammed, S.; Mansoori, G.A. Effect of CO2 on the Interfacial and Transport Properties of Water/Binary and Asphaltenic Oils: Insights from Molecular Dynamics. Energy Fuels 2018, 32, 5409–5417. [Google Scholar] [CrossRef]
- Van Rooijen, W.; Habibi, P.; Xu, K.; Dey, P.; Vlugt, T.; Hajibeygi, H.; Moultos, O. Interfacial tensions, solubilities, and transport properties of the H2/H2O/NaCl system: A molecular simulation study. J. Chem. Eng. Data 2023, 69, 307–319. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Chen, H.; Wang, P.; Xie, Z.; Yao, Y.; Yan, Y.; Zhang, J. Effect of surfactant headgroups on the oil/water interface: An interfacial tension measurement and simulation study. J. Mol. Struct. 2013, 1052, 50–56. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 10 January 2025).
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Potoff, J.J.; Siepmann, J.I. Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE J. 2001, 47, 1676–1682. [Google Scholar] [CrossRef]
- Khalaf, M.H.; Mansoori, G.A. Asphaltenes aggregation during petroleum reservoir air and nitrogen flooding. J. Petrol. Sci. Eng. 2019, 173, 1121–1129. [Google Scholar] [CrossRef]
- Ramirez Hincapie, M.L.; Narayanan Nair, A.K.; Che Ruslan, M.F.A.; Yang, Y.; Sun, S. Bulk and Interfacial Properties of the Alkane+ Nitrogen System. J. Chem. Eng. Data 2022, 67, 3138–3145. [Google Scholar] [CrossRef]
- Morrow, B.H.; Harrison, J.A. Interfacial Properties of Linear Alkane/Nitrogen Binary Mixtures: Molecular Dynamics Vapor–Liquid Equilibrium Simulations. J. Phys. Chem. B 2022, 126, 4379–4388. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Liu, H.; Liu, F. Impacts of polar molecules of crude oil on spontaneous imbibition in calcite nanoslit: A molecular dynamics simulation study. Energy Fuels 2021, 35, 13671–13686. [Google Scholar] [CrossRef]
- Sen, W.; Qihong, F.; Ming, Z.; Shuangfang, L.; Yong, Q.; Tian, X. Molecular dynamics simulation of liquid alkane occurrence state in pores and slits of shale organic matter. Pet. Explor. Dev. 2015, 42, 844–851. [Google Scholar] [CrossRef]
- Hong, X.; Yu, H.; Xu, H.; Wang, X.; Jin, X.; Wu, H.; Wang, F. Competitive adsorption of asphaltene and n-heptane on quartz surfaces and its effect on crude oil transport through nanopores. J. Mol. Liq. 2022, 359, 119312. [Google Scholar] [CrossRef]
- Guo, L.; Tang, G.; Kumar, S. Droplet morphology and mobility on lubricant-impregnated surfaces: A molecular dynamics study. Langmuir 2019, 35, 16377–16387. [Google Scholar] [CrossRef]
- Chen, J.; Mi, J.-G.; Chan, K.-Y. Comparison of different mixing rules for prediction of density and residual internal energy of binary and ternary Lennard–Jones mixtures. Fluid Phase Equilibria 2001, 178, 87–95. [Google Scholar] [CrossRef]
- Liu, Z.-Y.; Wang, C.; Zhou, H.; Wang, Y.; Zhang, L.; Zhang, L.; Zhao, S. Characterizing the impact of surfactant structure on interfacial tension: A molecular dynamics study. J. Mol. Model 2017, 23, 112. [Google Scholar] [CrossRef]
- Li, J.; Peng, B.; Xiong, J.; Luo, D.; Li, X.; He, J.; Zhang, H. Molecular dynamics simulation of BS12 and SDS mixed adsorption at the CO2-water interface: Evaluation of interfacial elasticity and permeability. Fuel 2025, 393, 135005. [Google Scholar] [CrossRef]
- Lou, R.; Zhe, S.; Lu, D.; Huang, L. Oleo-pneumatic mixed shock absorber landing pressure analysis of landing Gear. Adv. Aeronaut. Sci. Eng. 2020, 11, 380–386. [Google Scholar] [CrossRef]
- Huang, H.; Mang, Y.; Sun, Y.; Pei, X. Test and Analysis of YH-15 Aviation hydraulic oil viscosity-temperature characteristics. Ord. Ind. Autom. 2015, 34, 42–43. [Google Scholar] [CrossRef]
- Filipe, H.A.; Loura, L.M. Molecular dynamics simulations: Advances and applications. Molecules 2022, 27, 2105. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Gao, S.; Bao, X.; Yu, L.; Wang, H.; Li, J.; Chen, X. Molecular dynamics study of “quasi-gemini” surfactant at n-decane/water interface: The synergistic effect of hydrophilic headgroups and hydrophobic tails of surfactants on the interface properties. Colloids Surf. A Physicochem. Eng. Asp. 2022, 634, 127899. [Google Scholar] [CrossRef]
- Xiao, H.; Zhen, Z.; Sun, H.; Cao, X.; Li, Z.; Song, X.; Cui, X.; Liu, X. Molecular dynamics study of the water/n-alkane interface. Sci. China Chem. 2010, 53, 945–949. [Google Scholar] [CrossRef]
- Orr, F.M.; Jessen, K. An analysis of the vanishing interfacial tension technique for determination of minimum miscibility pressure. Fluid Phase Equilibria 2007, 255, 99–109. [Google Scholar] [CrossRef]
- Nobakht, M.; Moghadam, S.; Gu, Y. Determination of CO2 Minimum Miscibility Pressure from Measured and Predicted Equilibrium Interfacial Tensions. Ind. Eng. Chem. Res. 2008, 47, 8918–8925. [Google Scholar] [CrossRef]
- Yu, H.; Li, S.; Li, J.; Zhu, S.; Sun, C. Interfacial mass transfer characteristics and molecular mechanism of the gas-oil miscibility process in gas flooding. Acta Phys.-Chim. Sin 2020, 38, 2006061. [Google Scholar] [CrossRef]
- Wen, B.; Sun, C.; Bai, B.; Gatapova, E.Y.; Kabov, O.A. Ionic hydration-induced evolution of decane–water interfacial tension. Phys. Chem. Chem. Phys. 2017, 19, 14606–14614. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, C.; Qiu, Q.; Yang, L. Effect of water on the diffusion of small molecular weight acids in nano-SiO2 modified insulating oil. J. Mol. Liq. 2020, 314, 113670. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, Z.; Liu, J.; Chen, X.; Guo, H. Study on Dissolution Characteristics of Nitrogen in Oil-gas Mixed Buffer. Technol. Dev. Chem. Ind. 2022, 51, 35–40. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Wilhelm, E.; Battino, R.; Wilcock, R.J. Low-pressure solubility of gases in liquid water. Chem. Rev. 1977, 77, 219–262. [Google Scholar] [CrossRef]
- Frolich, P.K.; Tauch, E.; Hogan, J.; Peer, A. Solubilities of gases in liquids at high pressure. Ind. Eng. Chem. 1931, 23, 548–550. [Google Scholar] [CrossRef]
- Tileuberdi, N.; Mashrapova, M.; Toktarbay, Z. A review on nitrogen flooding for enhanced oil recovery. ES Mater. Manuf. 2023, 22, 968. [Google Scholar] [CrossRef]
- Zhang, X.; Li, L.; Su, Y.; Da, Q.; Fu, J.; Wang, R.; Chen, F. Microfluidic investigation on asphaltene interfaces attempts to carbon sequestration and leakage: Oil-CO2 phase interaction characteristics at ultrahigh temperature and pressure. Appl. Energy 2023, 348, 121518. [Google Scholar] [CrossRef]
- Hao, H.; Xian, B.; Peng, M.; Deng, S.; Cheng, L.; Wu, H.; Gao, X.; Qu, M.; Zhao, K. Study of Different Gas Floodings on Minimum Miscibility Pressure and Oil Recovery in a Low-Permeability Reservoir with Medium Viscous Oil. ACS Omega 2025, 10, 9426–9440. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, Q.; Gan, Y.; Li, Q.; Liu, C.; Sun, W. Effect of wax composition and shear force on wax aggregation behavior in crude oil: A molecular dynamics simulation study. Molecules 2022, 27, 4432. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhang, Y.; Wang, H. Gas Solubility Measurement for Waxy Crude Oil Saturated with Nitrogen and Natural Gas. Adv. Mater. Res. 2011, 339, 603–606. [Google Scholar] [CrossRef]
- Madani, S.A.; Mohammadi, M.-R.; Atashrouz, S.; Abedi, A.; Hemmati-Sarapardeh, A.; Mohaddespour, A. Modeling of nitrogen solubility in normal alkanes using machine learning methods compared with cubic and PC-SAFT equations of state. Sci. Rep. 2021, 11, 24403. [Google Scholar] [CrossRef]
- Wu, H. Study on Rheological Property of Oil and Gas System Under High Pressure and Gas Solubility in Crude Oil. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2024. [Google Scholar]






| Chemical Compound | Molecular Formula | Percentage/% |
|---|---|---|
| 2-Dodecen-1-ylsuccinic anhydride | C16H26O3 | 25.09 |
| Undec-10-ynoic acid, tetradecyl ester | C25H46O2 | 11.77 |
| 2-Hexyl-1-decanol | C16H34O | 11.36 |
| phytol | C20H40O | 10.67 |
| Tetradecyl chloroacetate | C16H31ClO2 | 8.63 |
| Decyl methacrylate | C17H32O2 | 8 |
| Eicosyl vinyl carbonate | C23H44O3 | 6.92 |
| 2-Methyldecyl acrylate | C14H26O | 5.44 |
| Pentadecyl 2-chloroacetate | C17H33CLO2 | 5.09 |
| 2(1H)-Benzocyclooctenone, decahydro-4a-methyl | C13H22O | 4.53 |
| Butylated Hydroxytoluene | C15H24O | 2.49 |
| Pressure (MPa) | Temperature (K) | Neg − Neg (Number) | SMD (nd) | SEXP (nd) | Error (%) |
|---|---|---|---|---|---|
| 15 | 373 | 45 | 0.0812 | 0.0795 | 2.1 |
| 20 | 98 | 0.1615 | 0.1583 | 2.0 | |
| 25 | 146 | 0.2219 | 0.2119 | 4.7 | |
| 30 | 192 | 0.2723 | 0.2890 | 5.8 | |
| 35 | 244 | 0.3211 | 0.3111 | 3.2 | |
| 20 | 313 | 53 | 0.0899 | 0.0872 | 3.1 |
| 343 | 77 | 0.1285 | 0.1327 | 3.2 | |
| 373 | 98 | 0.1615 | 0.1583 | 2.0 | |
| 403 | 129 | 0.2051 | 0.1988 | 3.2 | |
| 433 | 162 | 0.2500 | 0.2611 | 4.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Zhang, C.; Zhang, H.; Zhang, T.; Meng, D. Study on the Dissolution Mechanism of Aviation Hydraulic Oil–Nitrogen Gas Based on Molecular Dynamics. Processes 2025, 13, 1564. https://doi.org/10.3390/pr13051564
Guo Q, Zhang C, Zhang H, Zhang T, Meng D. Study on the Dissolution Mechanism of Aviation Hydraulic Oil–Nitrogen Gas Based on Molecular Dynamics. Processes. 2025; 13(5):1564. https://doi.org/10.3390/pr13051564
Chicago/Turabian StyleGuo, Qingtai, Changming Zhang, Hui Zhang, Tianlei Zhang, and Dehai Meng. 2025. "Study on the Dissolution Mechanism of Aviation Hydraulic Oil–Nitrogen Gas Based on Molecular Dynamics" Processes 13, no. 5: 1564. https://doi.org/10.3390/pr13051564
APA StyleGuo, Q., Zhang, C., Zhang, H., Zhang, T., & Meng, D. (2025). Study on the Dissolution Mechanism of Aviation Hydraulic Oil–Nitrogen Gas Based on Molecular Dynamics. Processes, 13(5), 1564. https://doi.org/10.3390/pr13051564





