Study on the Influence of Pump Performance Curve Fitting and Seal Ring Wear on Pump Intelligent Monitoring
Abstract
1. Introduction
2. Pump Test System and Characteristic Curve Fitting Method
2.1. Pump Test Object and System
2.2. Characteristic Curve Fitting Method
3. Results and Discussion
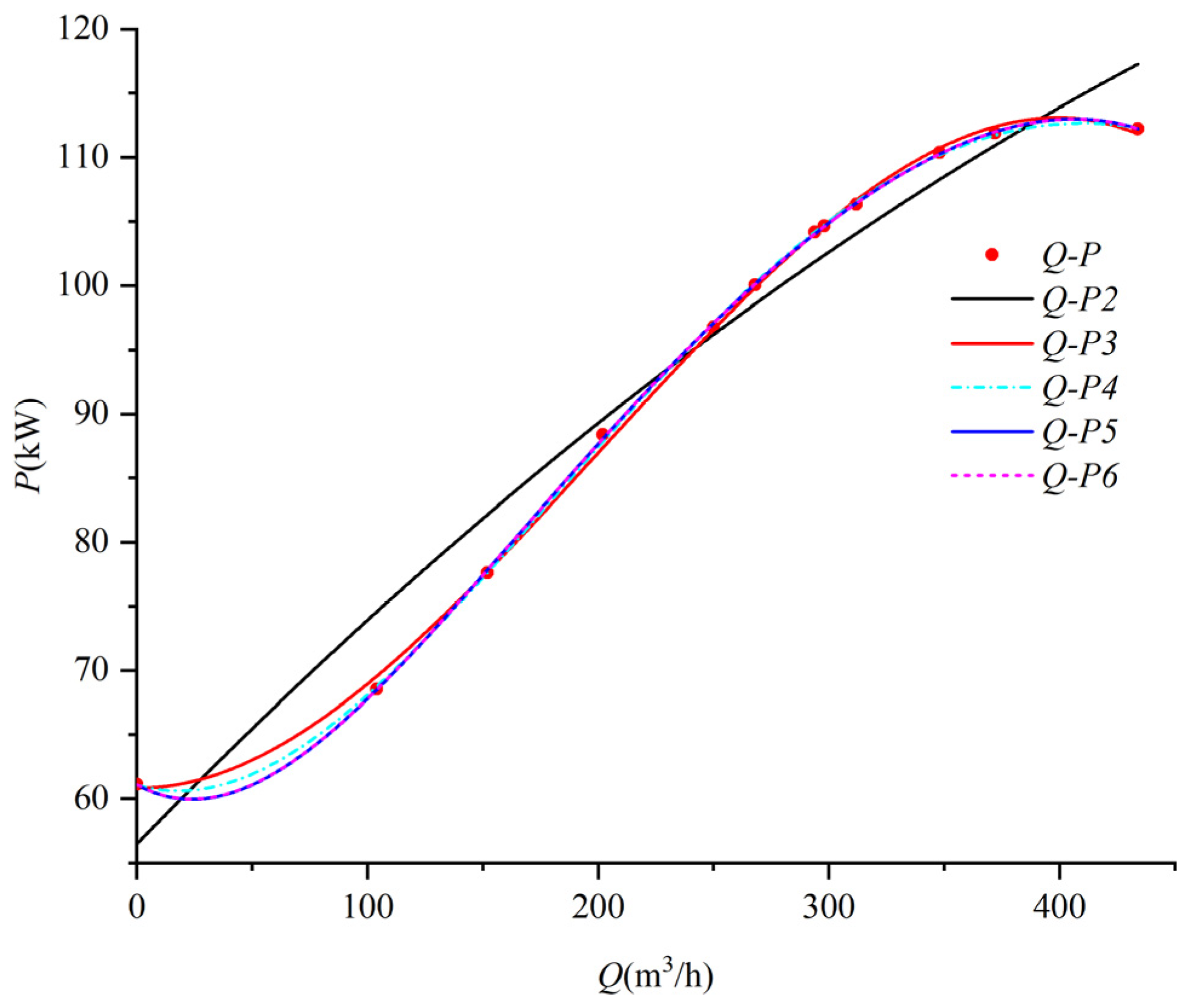
3.1. Pump Performance Curve Fitting
3.1.1. Centrifugal Pump External Characteristic Curve Fitting
3.1.2. Axial Flow Pump External Characteristic Curve Fitting
3.1.3. Mixed-Flow Pump External Characteristic Curve
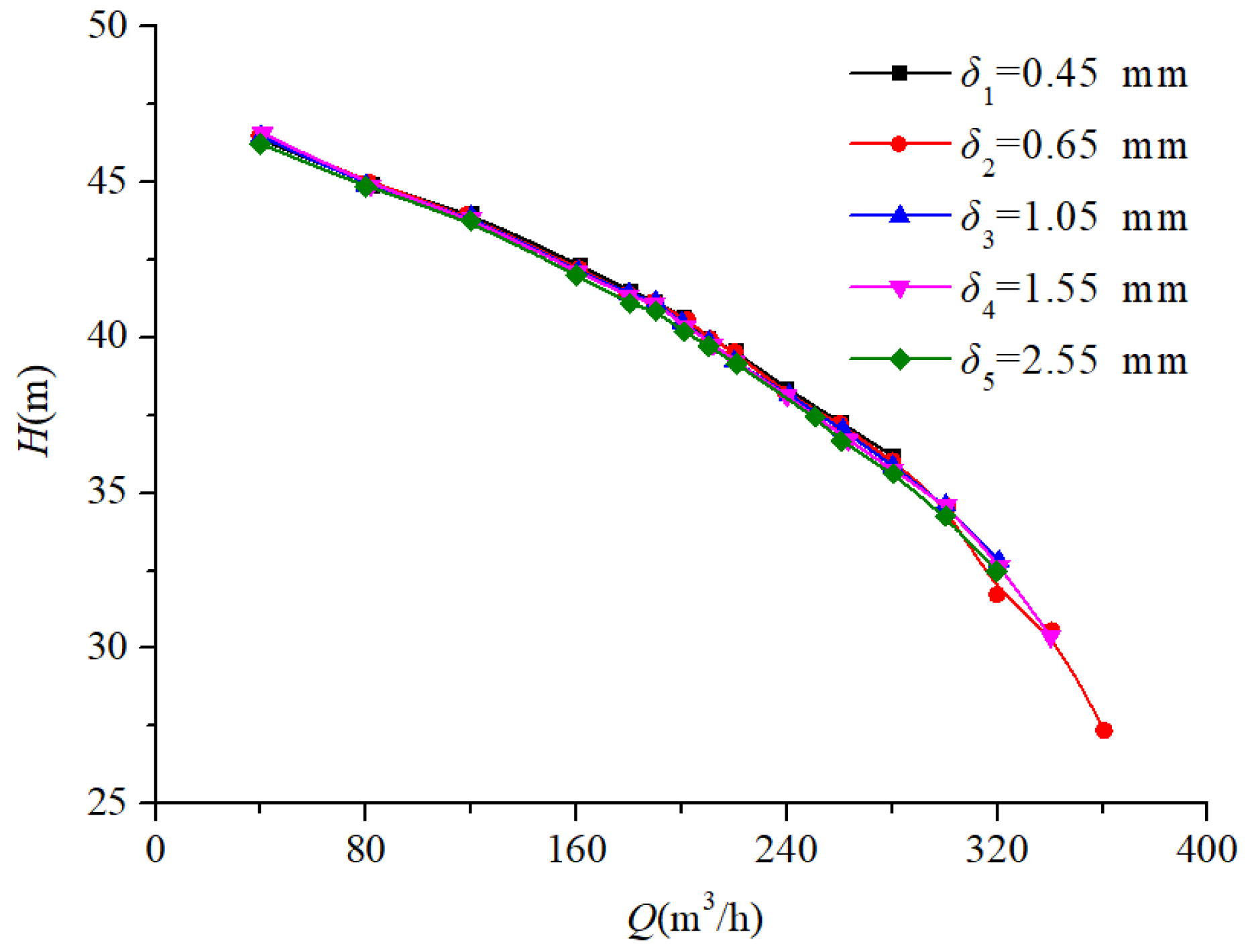
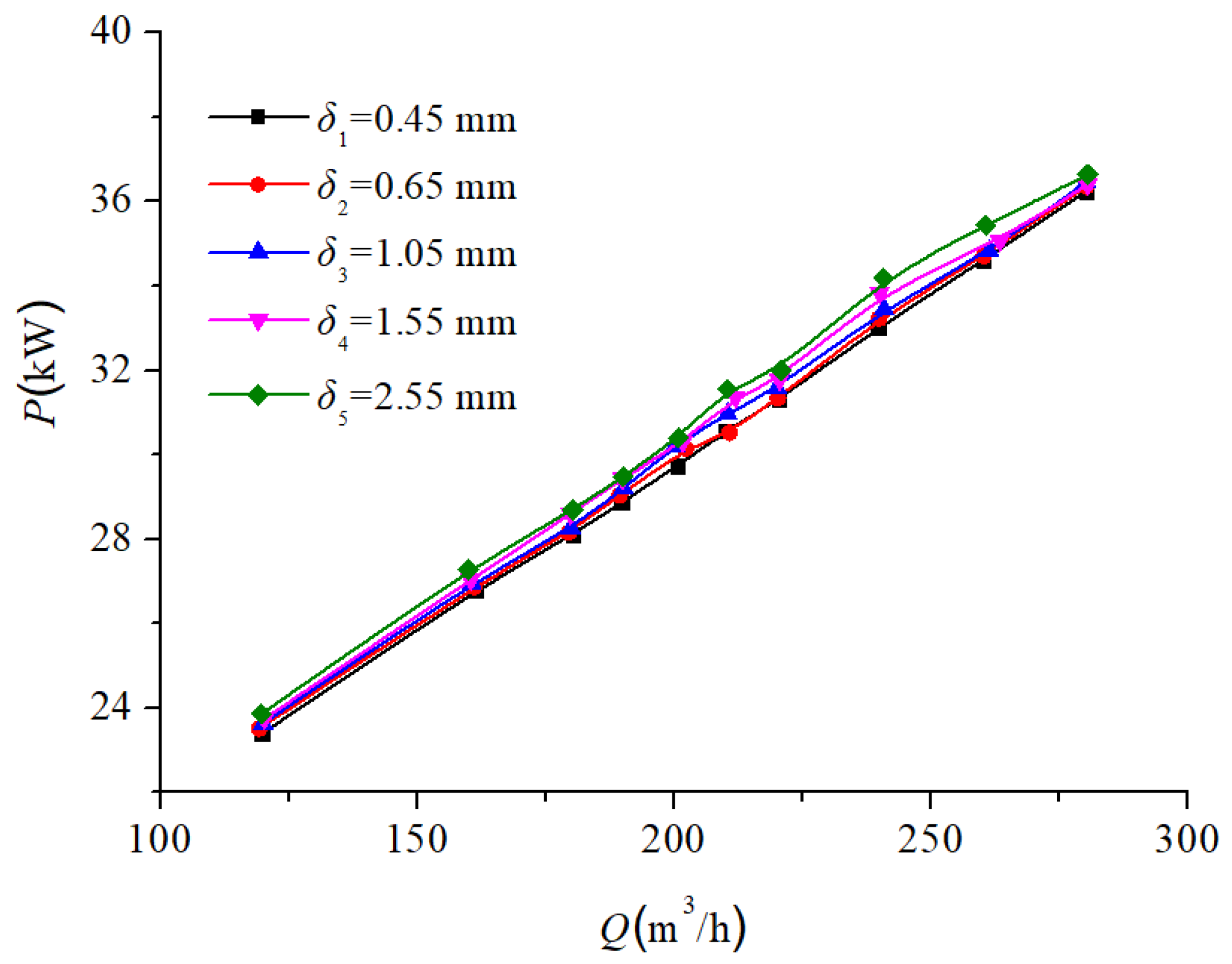
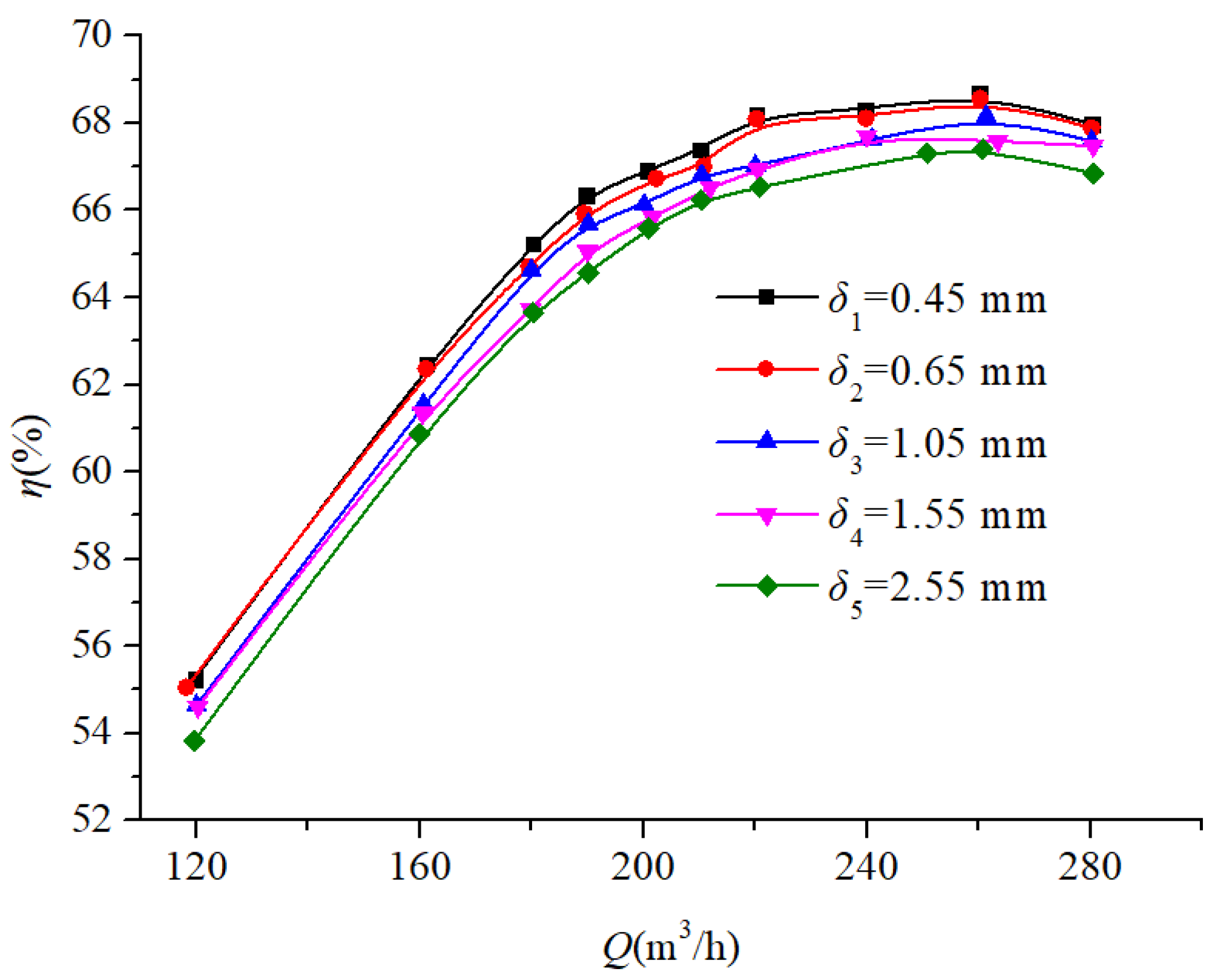
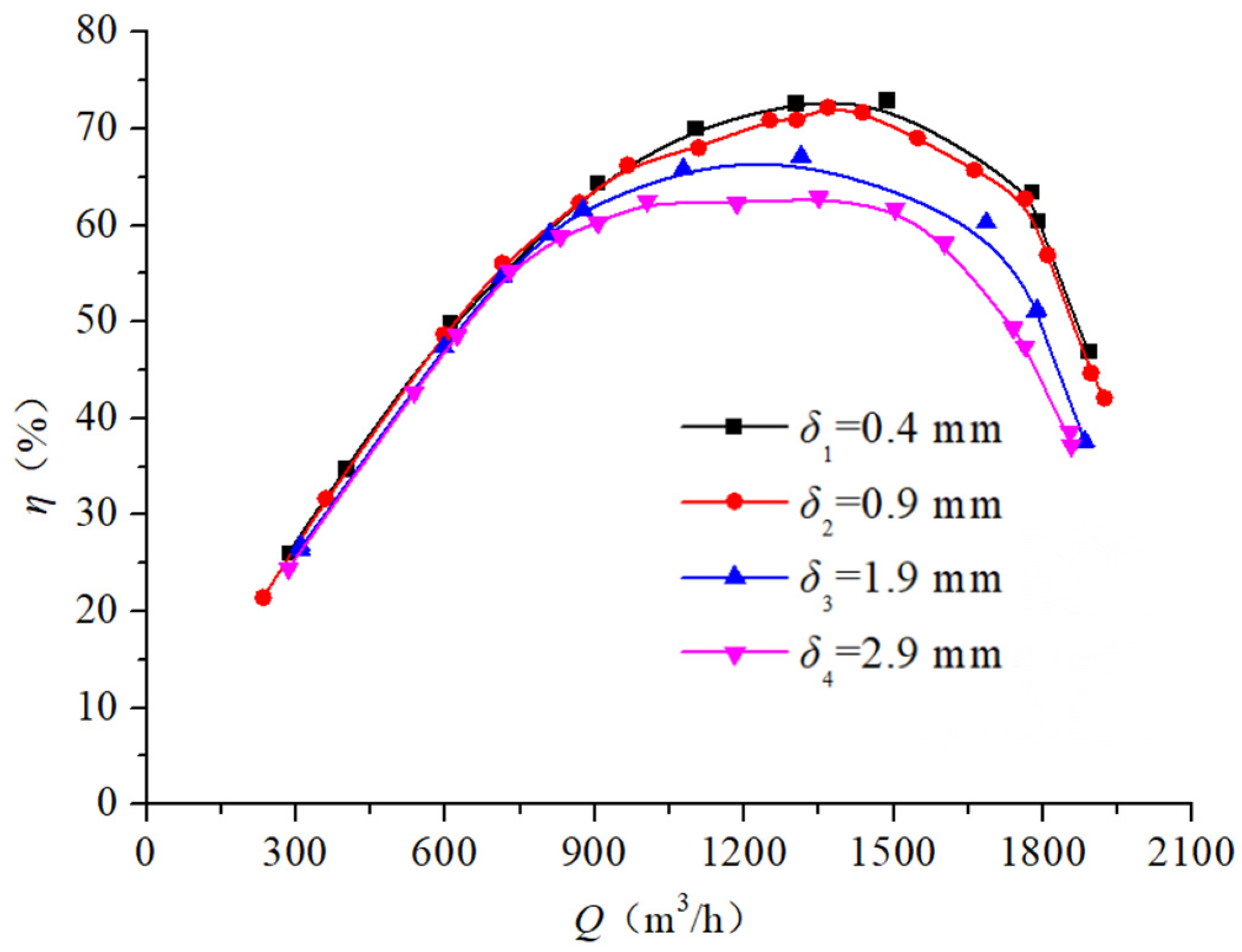
3.2. Experimental Research of the Effect of Different Seal Ring Clearances on the External Characteristics of the Pump
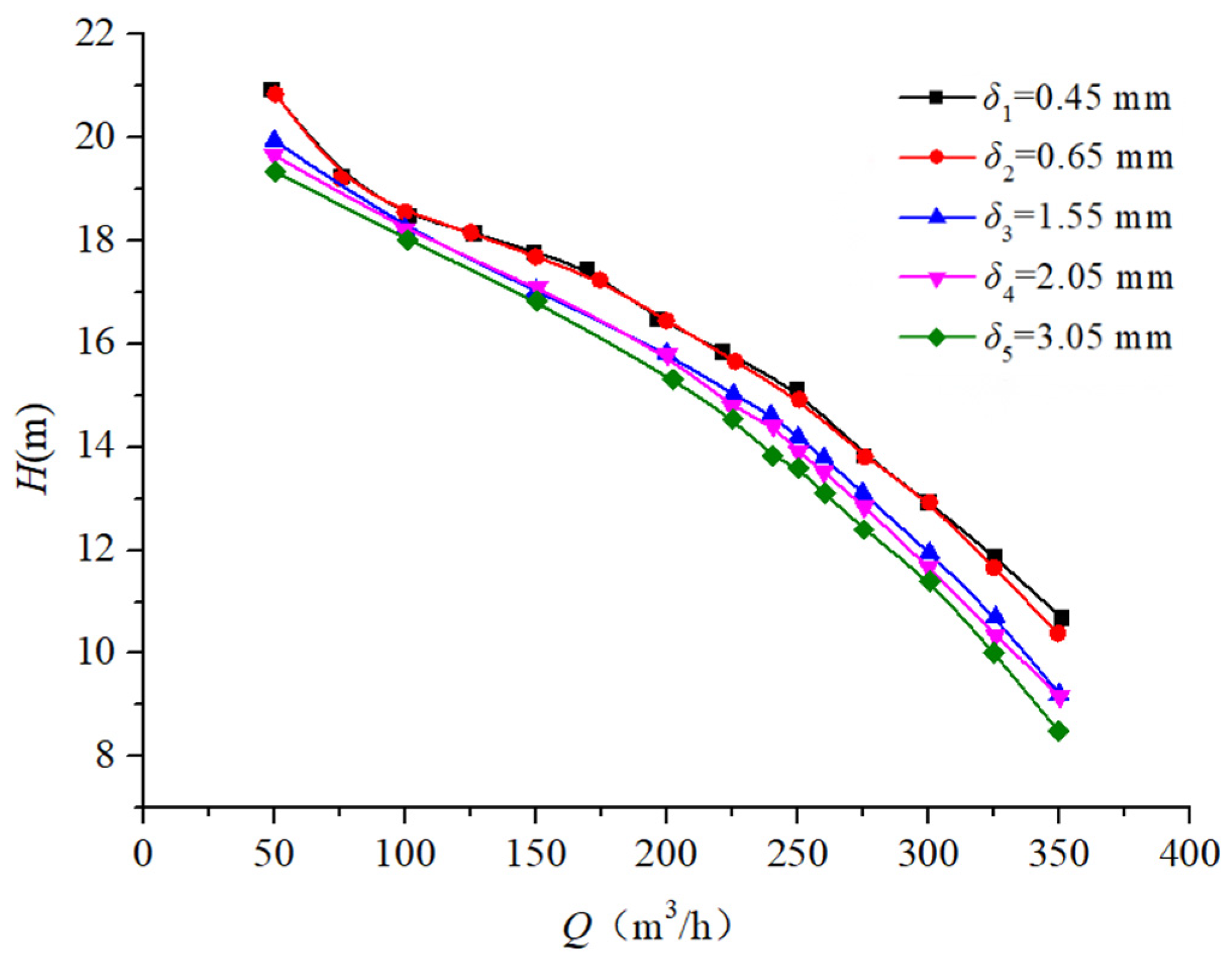
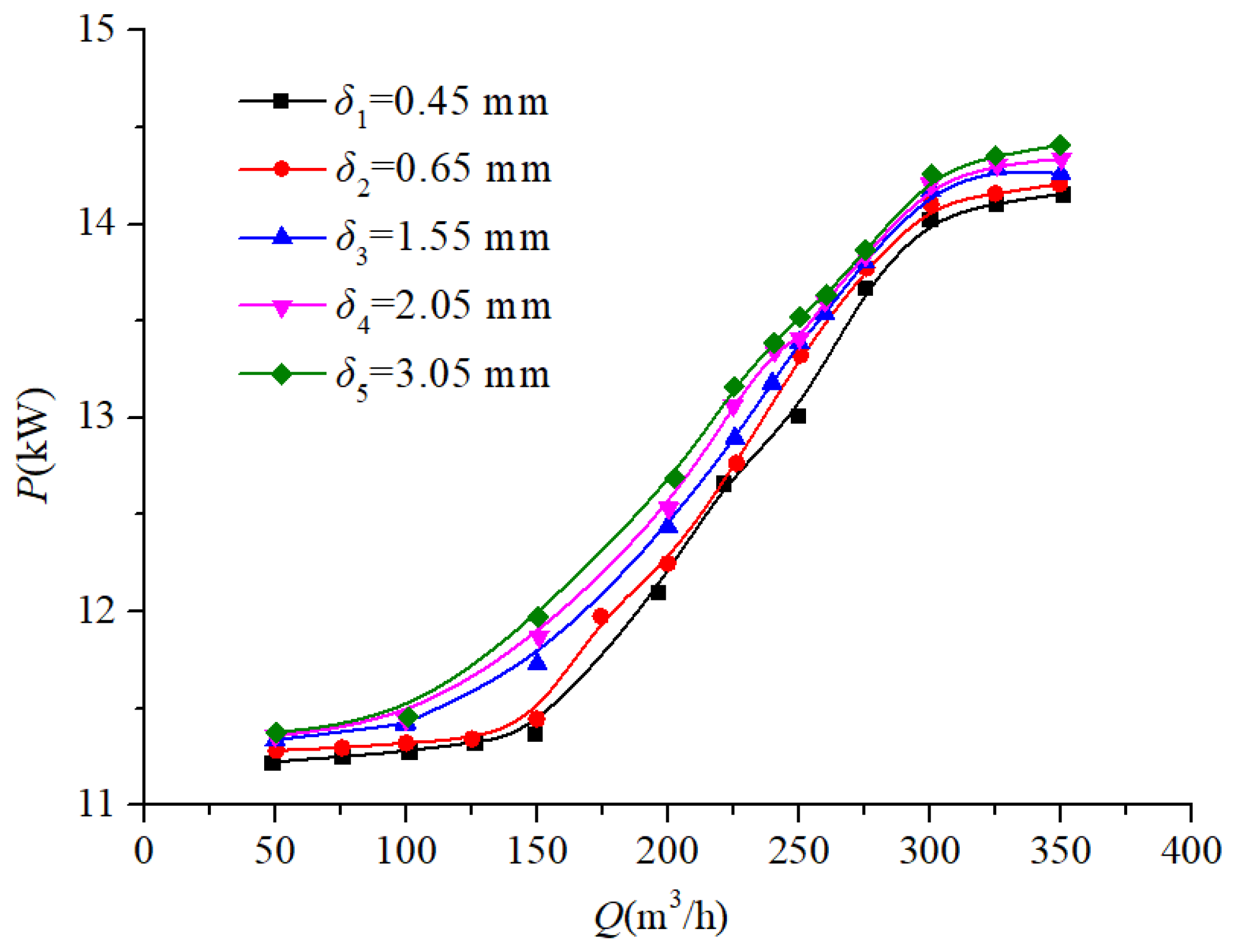
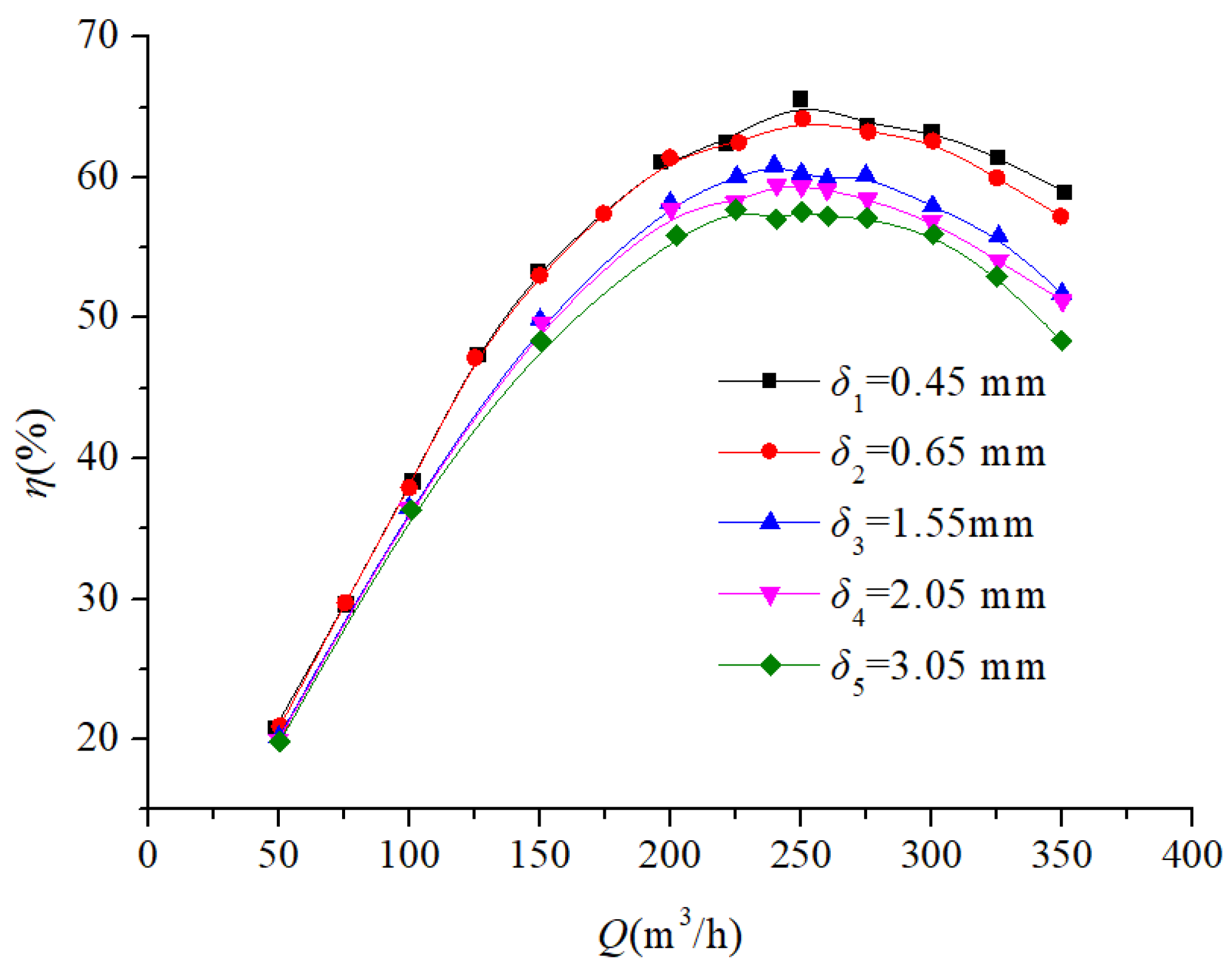
3.2.1. Effect of Different Seal Ring Clearances on Pump External Characteristics at a Speed of ns = 96.2
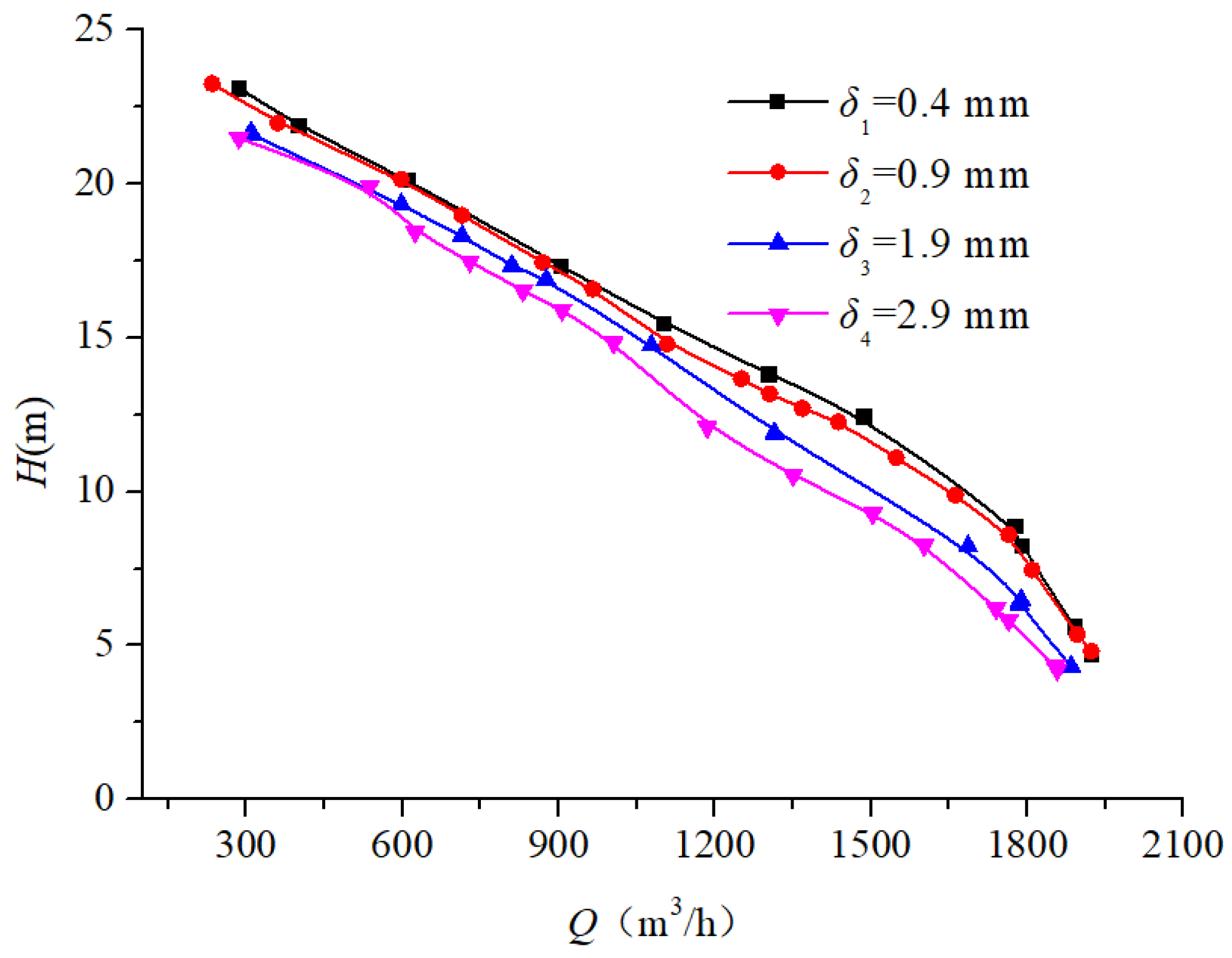
3.2.2. Effect of Different Seal Ring Clearances on Pump External Characteristics at a Speed of ns = 185.5
3.2.3. Effect of Different Clearances on Pump External Characteristics at a Speed of ns = 493.3
3.3. Intelligent Monitoring System for Pumps Based on Soft Measurement
3.3.1. Functional Requirements of the Monitoring System
- Data acquisition—collect the pump’s operating parameters, including current, voltage, frequency, power, and liquid level. Data processing—calculate derived parameters through processing, including the flow, head, etc. Data storage—temporarily retains processed and raw data for monitoring and analysis.
- Status display and parameter setting functions, which can collect the parameters, and set the control thresholds (including start/stop levels).
- Alarm function, which analyzes the collected data in real time; if the liquid level exceeds predefined thresholds, it will cause alarm events with timestamped records.
- Remote monitoring function, in which all collected data can be displayed visually in real time through a mobile application and industrial cloud platform.
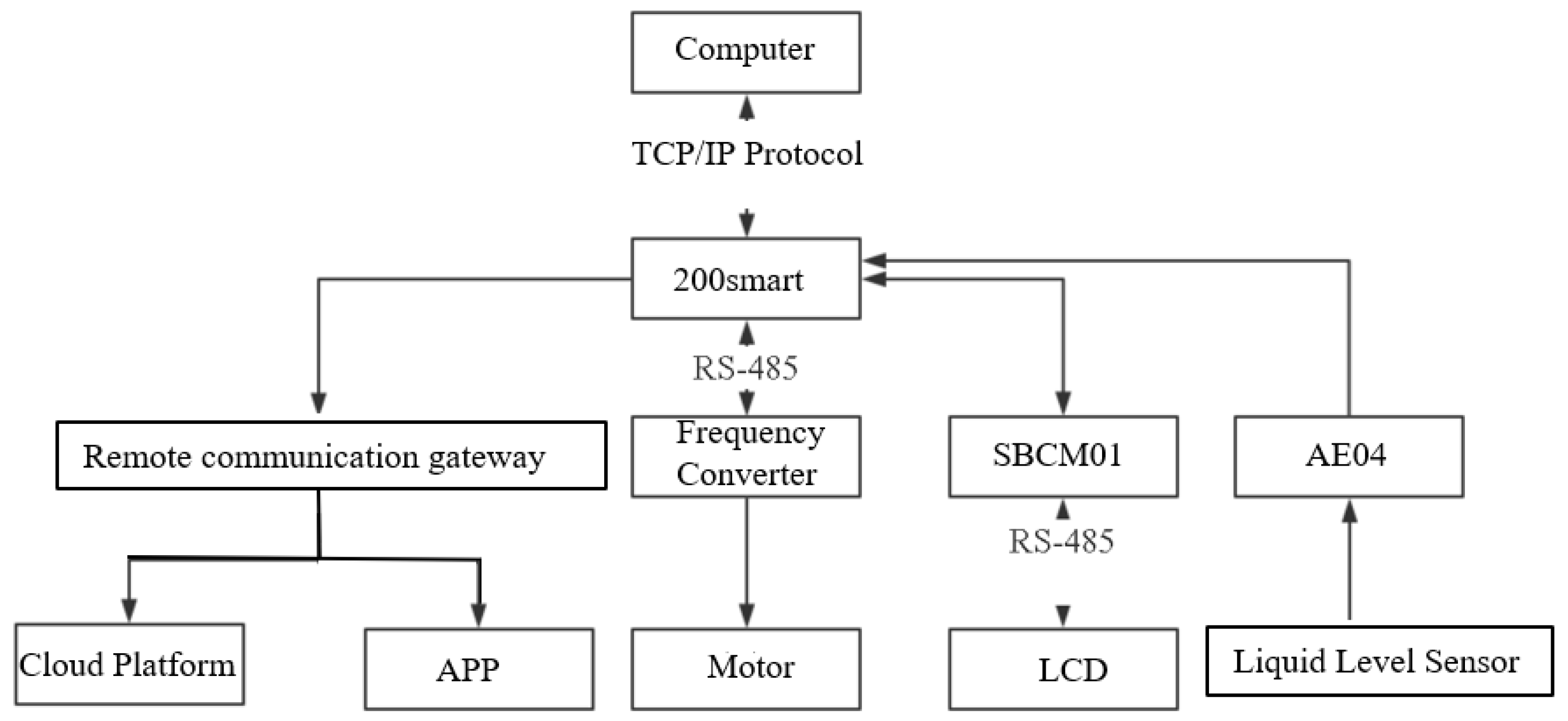
3.3.2. Hardware System in the Monitoring System
- The power switch of the control cabinet, which is responsible for the power switch of the whole cabinet.
- A transformer, which is used to convert the input 240 V voltage into 24 V voltage to supply power to the CPU.
- A 200smart CPU. When the indicator light is green, it means that the CPU is running normally.
- The AE04 analog module. When the indicator light is green, the module is running normally.
- The SBCM01 communication expansion board.
- The remote communication gateway. When the display light is blue, the gateway communication is normal.
- An analog input port.
- The power output interface.
- The power input interface.
- The inverter.
- A liquid crystal display.
3.3.3. Monitoring System Software
4. Conclusions
- (1)
- Compared with the centrifugal pump flow Q-H and Q-P curves with a speed lower than 300, the Q-η curve displays third-order polynomial fitting. The Q-H and Q-P curves of the axial flow pump with a rotational speed higher than 500 are fitted by a piecewise interpolation polynomial; the first segment is a second-order polynomial and the remaining segments are third-order polynomials. However, the Q-η curve retains third-order polynomial fitting. In the mixed-flow pump with speeds between 300 and 500, the Q-H curve adopts the same fitting method as the centrifugal pump. The Q-P curve uses the same fitting method as the axial pump. The Q-η curve is fitted with a third-order polynomial.
- (2)
- The characteristic curves (Q-H, Q-P, and Q-η) are typically fitted using third- to fourth-order polynomials. The maximum polynomial order without inflection points is 3, the maximum polynomial order of inflection points is 4, and the two inflection points are fitted by segmentation.
- (3)
- This study investigates pumps with specific speeds of 96.2, 185.5, and 493.3, systematically analyzing the impact of seal ring clearance variations on the pump performance through external characteristic testing. Progressive decreases in both the head and efficiency occur with increasing seal ring clearance, while the shaft power of the pump presents different variation trends with the increase in the specific speed. When the specific speed is low–medium, the shaft power of the pump gradually increases. However, when the specific speed is relatively high (ns > 300), the shaft power initially decreases, then increases, and finally decreases again.
- (4)
- This paper presents a remote monitoring system and utilizes motor power as the auxiliary variable, using the soft measurement method to ensure that the relative measurement error is <0.5%. All parameters can be displayed via an LCD screen, computer, mobile application, and industrial cloud platform, comprising an integrated alarm system for abnormal conditions. Programmable liquid level thresholds (start/stop) are presented via the LCD interface.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Olszewski, P. Genetic optimization and experimental verification of complex parallel pumping station with centrifugal pumps. Appl. Energy 2016, 178, 527–539. [Google Scholar] [CrossRef]
- Fetyan, K.; El_Gazzar, D. Effect of motor vibration problem on the power quality of water pumping stations. Water Sci. 2014, 28, 31–41. [Google Scholar] [CrossRef]
- Mohamed, M.M.A.; Abdellatif, M.M. Flow Improvement at Pump Intake by the Use of Baffle Posts. Beni-Suef Univ. J. Basic Appl. Sci. 2017, 6, 127–137. [Google Scholar] [CrossRef]
- Joo, J.G.; Jeong, I.S.; Kang, S.H. Deep Reinforcement Learning for Multi-Objective Real-Time Pump Operation in Rainwater Pumping Stations. Water 2024, 16, 3398. [Google Scholar] [CrossRef]
- Moreno-Rodenas, A.M.; Duinmeijer, A.; Clemens, F.H. Deep-learning based monitoring of FOG layer dynamics in wastewater pumping stations. Water Res. 2021, 117482. [Google Scholar] [CrossRef]
- Shaazizov, F. Accounting for the energy efficiency of the operation of pumping equipment in the monitoring system of large pumping stations of the Republic of Uzbekistan. E3S Web of Conf. 2023, 410, 8. [Google Scholar] [CrossRef]
- Yang, W. Checking the Characteristics of Centrifugal Pump Working Condition by Using Motor Running Current. Equip. Manag. Maint. 1997, 4, 28–29. [Google Scholar]
- Guo, L.; Hao, B.; Liu, Y. Research and Application of the Remote Data Monitoring for GSHP(Ground Source Heat Pump) based on MODBUS and TCP/IP Protocol. In Proceedings of the International Conference on Management Science and Intelligent Control(ICMSIC 2011), Hefei, China, 24–26 August 2011; pp. 24–34. [Google Scholar]
- Niu, G. Working Condition Detection System Based on Vibration Signal Analysis; Harbin Institute of Technology: Harbin, China, 2016. [Google Scholar]
- Song, M.; Wang, T.; Dang, B. Intelligent Calibration of Submersible Electric Pump Monitoring System Based on LabVIEW. Mech. Eng. Autom. 2016, 147–149. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=9b1d8c9f0279ca147b59c3fe13c97fec&site=xueshu_se (accessed on 7 May 2025).
- Panaras, G.; Mathioulakis, E.; Belessiotis, V. A method for the dynamic testing and evaluation of the performance of combined solar thermal heat pump hot water systems. Appl. Energy 2014, 114, 124–134. [Google Scholar] [CrossRef]
- Chen, C. Design and Implementation of Intelligent Monitoring System for Sewage Pumping Station. Archit. Eng. Technol. Des. 2018, 12, 959. [Google Scholar]
- Bian, Y.; Yang, Y.; Guo, Z. Design of Computer Monitoring System for Pumping Stations in Water Conservancy Irrigation District. J. Autom. 2018, 39, 94–96. [Google Scholar]
- Schleer, M.; Abhari, R.S. Clearance Effects on the Evolution of the Flow in the Vaneless Diffuser of a Centrifugal Compressor at Part Load Condition. J. Turbo Mach. 2008, 130, 79–87. [Google Scholar] [CrossRef]
- Langthjem, M.A.; Olhoff, N. A numerical study of flow-induced noise in a two-dimensional centrifugal pump. Part I. Hydrodynamics. J. Fluids Struct. 2004, 19, 349–368. [Google Scholar] [CrossRef]
- Dular, M.; Bachert, R.; Stoffel, B.; Širok, B. Experimental evaluation of numerical simulation of cavitating flow around hydrofoil. Eur. J. Mech.-B Fluids 2005, 24, 522–538. [Google Scholar] [CrossRef]
- Choi, C.-H.; Noh, J.-G.; Kim, D.-J.; Hong, S.S.; Kim, J. Effects of floating-ring seal clearance on the pump performance for turbopumps. J. Propuls. Power 2009, 25, 191–195. [Google Scholar] [CrossRef]
- Lomakin, A. Calculation of critical speed and securing of dynamic stability of hydraulic high-pressure pumps with reference to the forces arising in the gap seals. Energomashinostroenie 1958, 4, 1158. [Google Scholar]
- Ayad, A.F.; Abdalla, H.M.; Aly, E.A. Effect of semi-open impeller side clearance on the centrifugal pump performance using CFD. Aerosp. Sci. Technol. 2015, 47, 247–255. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, H.; Wang, Y.; Li, X.; Lin, Q. Influence of ring clearance on the performance of two-stage high-speed centrifugal pumps. J. Rocket Propuls. 2023, 49, 66–72. [Google Scholar]
- Zhao, C.; Han, X.; Cui, Z. Numerical simulations of flow characteristics of wear-ring clearance in the centrifugal pump. Chin. J. Ship Res. 2020, 15, 159–167. [Google Scholar]
- Gao, B.; Wang, Z.; Yang, L.; Du, W.; Li, C. Effect of wear-ring clearance on performance and flow characteristics of centrifugal pump. J. Drain. Irrig. Mach. Eng. (JDIME) 2017, 35, 13–17. [Google Scholar]
- Zhao, W.; Wu, G.; Li, Y.; Wang, Y. Study on effects of wear-rings clearance modifications on performance of centrifugal pump. J. Hydroelectr. Eng. 2014, 33, 211–215. [Google Scholar]
- Chen, Y.; Fei, Z.; Cai, Y.; Yang, R.; Li, W. Effect of the clearance of wear-rings on the performance of centrifugal oil pump while handling water. Fluid Mach. 2006, 34, 1–5. [Google Scholar]
- Fu, Q.; Chen, Y.; Huang, Q.; Zhu, R.; Wang, X. Influence of front ring clearance on internal flow characteristics of centrifugal pump. J. Chongqing Univ. Technol. Nat. Sci. 2022, 36, 203–209. [Google Scholar]
- ISO 9906; Rotodynamic Pump-Hydraulic Performance Acceptance Tests-Grades 1 and 2. International Standardization Orgnization: Geneva, Switzerland, 1999.
- Guan, X. The Hydraulic Design of Centrifugal Pumps and Mixed-Flow Pumps. In Modern Pumps Theory and Design; China Astronautic Publishing House: Beijing, China, 2011; pp. 241–265. [Google Scholar]
- Wu, X.; Ding, D.; Hu, S. Fitting and Mapping of Characteristic Curve of Centrifugal Pump Based on MATLAB. China Rural. Water Hydropower 2010, 144–146. Available online: https://irrigate.whu.edu.cn/EN/Y2010/V0/I11/144 (accessed on 7 May 2025).
- Liu, H.; Sun, T.; Liu, W.; Wang, L.; Wei, J. Fitting of Centrifugal Pump Performance Curve Based on Visual Basic Programming. Contemp. Chem. Ind. 2014, 43, 648–651. [Google Scholar]
- Du, D.; Liu, Q.; Fang, G.; Wang, Y. Performance Curve Fitting of Pump Based on Polynomial-Markov. J. Hydroelectr. Eng. 2014, 7, 144–146. [Google Scholar]
- Tang, Y.; Xiao, M.; Tang, L. Piecewise least squares polynomial fitting algorithm for pump performance curve. J. Drain. Irrig. Mach. Eng.(JDIME) 2017, 35, 744–748. [Google Scholar]
- Dharmarajan, R.; Rowley, P.; Stein, J.; Scott, S. Performance Validation and Curve Fit Generation of Natural Gas and Electric Heat Pump VRF Systems. ASHRAE Trans. 2024, 130, 466–474. [Google Scholar]










| Pump Parameters | 150 QW-260-38-45 | 200 QW-250-15-15 | 350 QW-1388-13-90 |
|---|---|---|---|
| Rotational speed (r/min) | 1480 | 1480 | 1480 |
| Flow rate (m3/h) | 260 | 250 | 1388 |
| Head (m) | 37.28 | 15 | 12.88 |
| Power (kW) | 45 | 15 | 90 |
| Specific speed | 96.2 | 185.5 | 493.3 |
| Pipe diameter (mm) | 150 | 150 | 350 |
| Flow m3/h | Head m | Power kW | Efficiency % |
|---|---|---|---|
| 0 | 137.56 | 61.11931 | 0 |
| 104 | 124.42 | 68.53595 | 51.43 |
| 152 | 120.46 | 77.62387 | 62.45 |
| 202 | 115.93 | 88.39608 | 72.17 |
| 250 | 109.15 | 96.78278 | 76.8 |
| 268 | 106.16 | 100.05306 | 77.46 |
| 294 | 101.85 | 104.15136 | 78.32 |
| 298 | 100.69 | 104.65 | 78.1 |
| 312 | 98.16 | 106.35476 | 78.45 |
| 348 | 89.82 | 110.3911 | 77.14 |
| 372 | 83.92 | 111.89776 | 76 |
| 434 | 64.35 | 112.23356 | 67.79 |
| 2nd Order | 3rd Order | 4th Order | 5th Order | 6th Order | ||
|---|---|---|---|---|---|---|
| Correlation coefficient | Q-H | 0.99483 | 0.99976 | 0.99993 | 0.99997 | 0.99997 |
| Q-P | 0.98061 | 0.99957 | 0.99991 | 0.99996 | 0.99996 | |
| Root mean square | Q-H | 1.9019 | 0.40961 | 0.22201 | 0.14179 | 0.13811 |
| Q-P | 3.273 | 0.49089 | 0.22298 | 0.15686 | 0.15685 | |
| Absolute error maximum | Q-H | 3.7196 | 0.85492 | 0.48282 | 0.23489 | 0.23047 |
| Q-P | 6.0145 | 1.0507 | 0.57996 | 0.34796 | 0.34713 | |
| Relative error maximum | Q-H | 1.5177% | 0.296% | 0.1544% | 0.11364% | 0.10696% |
| Q-P | 2.6647% | 0.3645% | 0.16915% | 0.11867% | 0.l1802% |
| Flow m3/h | Head m | Power kW | Efficiency % |
|---|---|---|---|
| 420.39 | 9.62 | 32.17184 | 34.25 |
| 479.23 | 8.88 | 30.22327 | 38.37 |
| 498.88 | 8.14 | 28.30621 | 39.1 |
| 524.64 | 7.69 | 27.10528 | 40.52 |
| 586.26 | 8.03 | 29.44253 | 43.54 |
| 646.63 | 8.24 | 28.99558 | 50.06 |
| 696.55 | 8.15 | 28.79607 | 53.72 |
| 748.22 | 7.92 | 28.66844 | 56.28 |
| 780.48 | 7.39 | 27.69211 | 56.71 |
| 862.06 | 7.15 | 27.47178 | 61.08 |
| 910.22 | 7 | 26.9138 | 64.45 |
| 999.18 | 6.34 | 25.58673 | 67.47 |
| Actual Power (kW) | Solving Flow (m3/h) | Solving Head (m) | Solving Efficiency | Actual Flow (m3/h) |
| 61.11931 | 39.2048 | 131.5045 | 22.963% | 0 |
| 68.53595 | 103.2173 | 124.7269 | 51.135% | 104 |
| 77.62387 | 151.9494 | 120.4152 | 64.167% | 152 |
| 88.39608 | 204.5221 | 115.1353 | 72.517% | 202 |
| 96.78278 | 248.0516 | 109.5016 | 76.399% | 250 |
| 100.05306 | 267.0092 | 106.5585 | 77.412% | 268 |
| 104.15136 | 293.9204 | 101.7919 | 78.199% | 294 |
| 104.650 | 297.5546 | 101.0923 | 78.247% | 298 |
| 106.35476 | 310.8551 | 98.414 | 78.304% | 312 |
| 110.3911 | 352.6431 | 88.7593 | 77.186% | 348 |
| 111.89776 | 380.5035 | 81.2585 | 75.219% | 372.01 |
| Actual Head (m) | Actual Efficiency | Relative Error of Flow | Relative Error of Head | Relative Error of Efficiency |
| 137.56 | 0 | −inf | −4.402% | inf |
| 124.42 | 51.43% | 0.75263% | 0.24605% | −0.57376% |
| 120.46 | 64.25% | 0.033315% | −0.03716% | −0.12991% |
| 115.93 | 72.17% | −1.2486% | −0.68554% | 0.48067% |
| 109.15 | 76.8% | 0.77937% | 0.32214% | −0.52206% |
| 106.16 | 77.46% | 0.36969% | 0.37538% | −0.06212% |
| 101.85 | 78.32% | 0.027088% | −0.05705% | −0.15443% |
| 100.69 | 78.1% | 0.14947% | 0.3995% | 0.18849% |
| 98.16 | 78.45% | 0.36696% | 0.25876% | −0.18667% |
| 89.82 | 77.14% | −1.3342% | −1.11809% | 0.05966% |
| 83.92 | 76% | −2.2831% | −3.1715% | −1.0272% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, P.; Zheng, Y.; Long, Y.; Qiu, W.; Zhu, R. Study on the Influence of Pump Performance Curve Fitting and Seal Ring Wear on Pump Intelligent Monitoring. Processes 2025, 13, 1529. https://doi.org/10.3390/pr13051529
Lin P, Zheng Y, Long Y, Qiu W, Zhu R. Study on the Influence of Pump Performance Curve Fitting and Seal Ring Wear on Pump Intelligent Monitoring. Processes. 2025; 13(5):1529. https://doi.org/10.3390/pr13051529
Chicago/Turabian StyleLin, Peng, Yingying Zheng, Yun Long, Weifeng Qiu, and Rongsheng Zhu. 2025. "Study on the Influence of Pump Performance Curve Fitting and Seal Ring Wear on Pump Intelligent Monitoring" Processes 13, no. 5: 1529. https://doi.org/10.3390/pr13051529
APA StyleLin, P., Zheng, Y., Long, Y., Qiu, W., & Zhu, R. (2025). Study on the Influence of Pump Performance Curve Fitting and Seal Ring Wear on Pump Intelligent Monitoring. Processes, 13(5), 1529. https://doi.org/10.3390/pr13051529







