Long Short-Term Memory Networks for State of Charge and Average Temperature State Estimation of SPMeT Lithium–Ion Battery Model
Abstract
1. Introduction
2. Problem Formulation
2.1. Literature Review
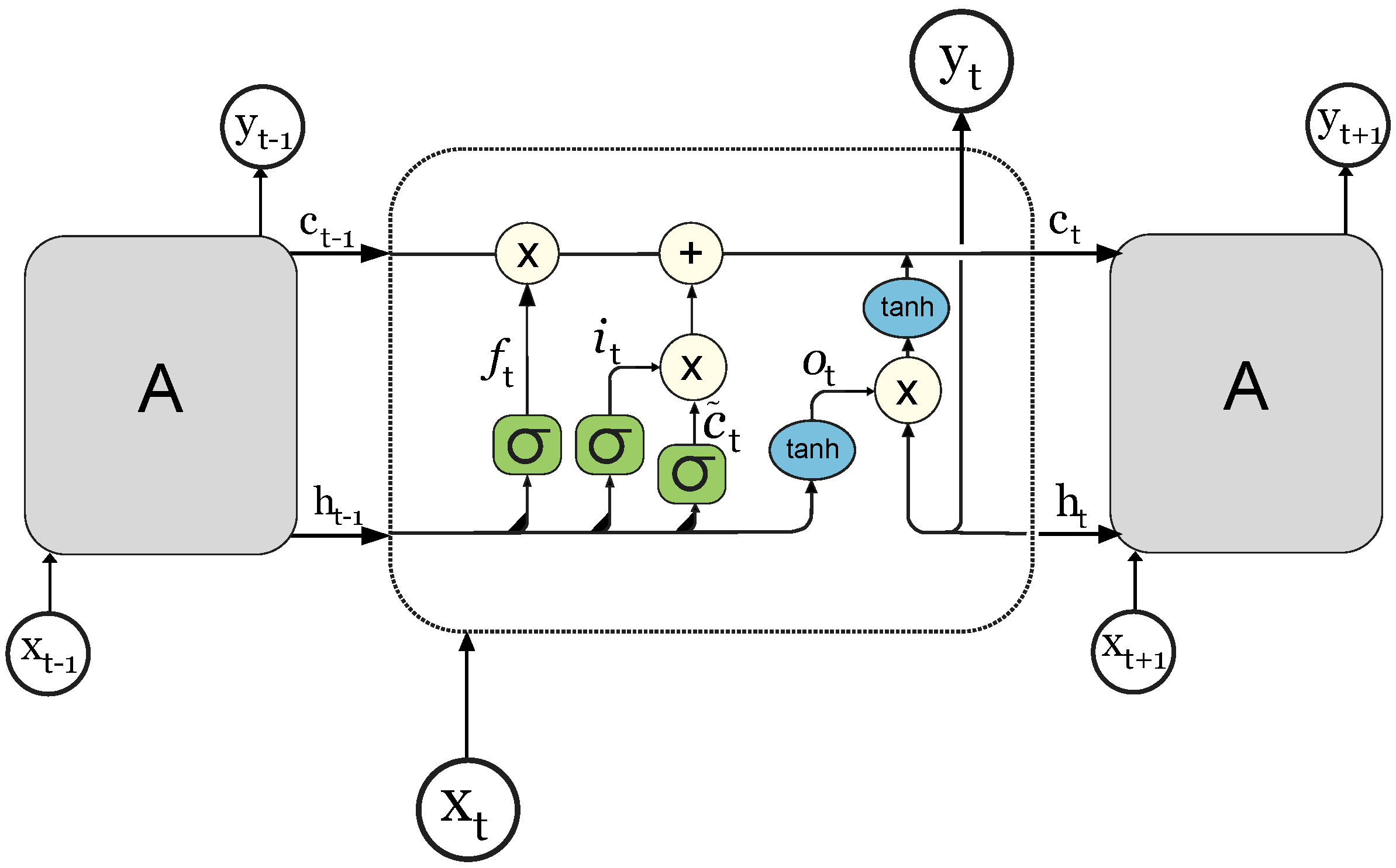
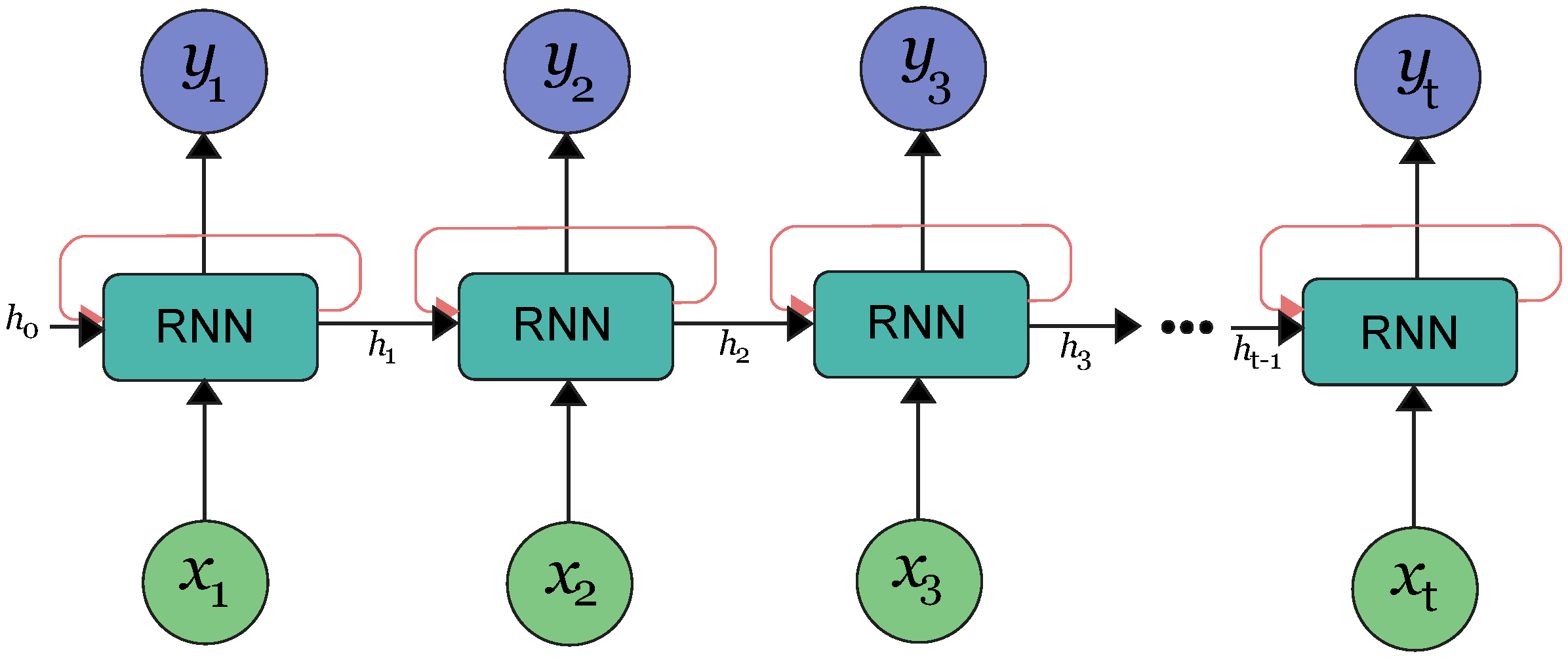
2.2. LSTM Architecture
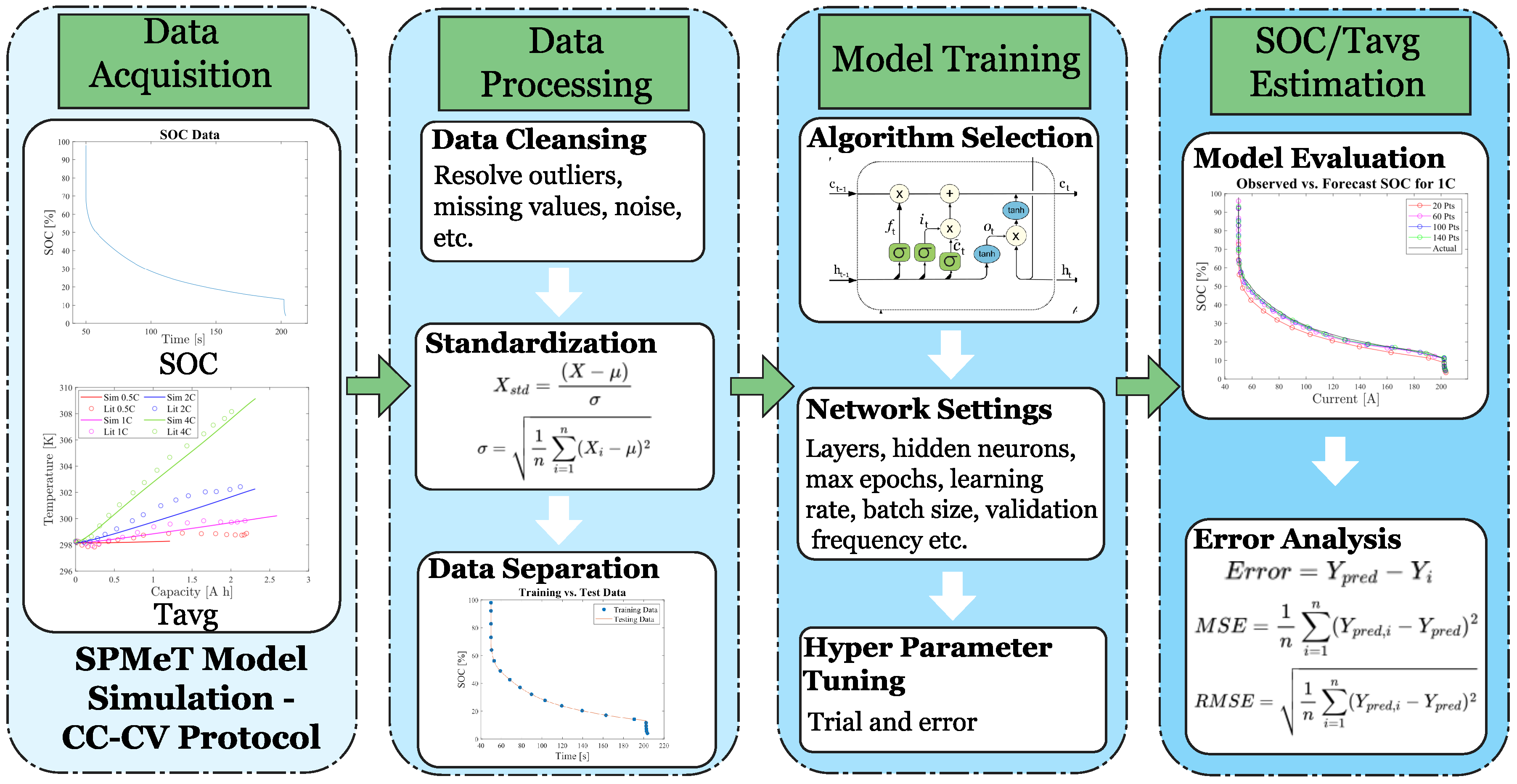
2.3. The Proposed LSTM-Based State-Estimation Method
3. Results
3.1. Data Generation
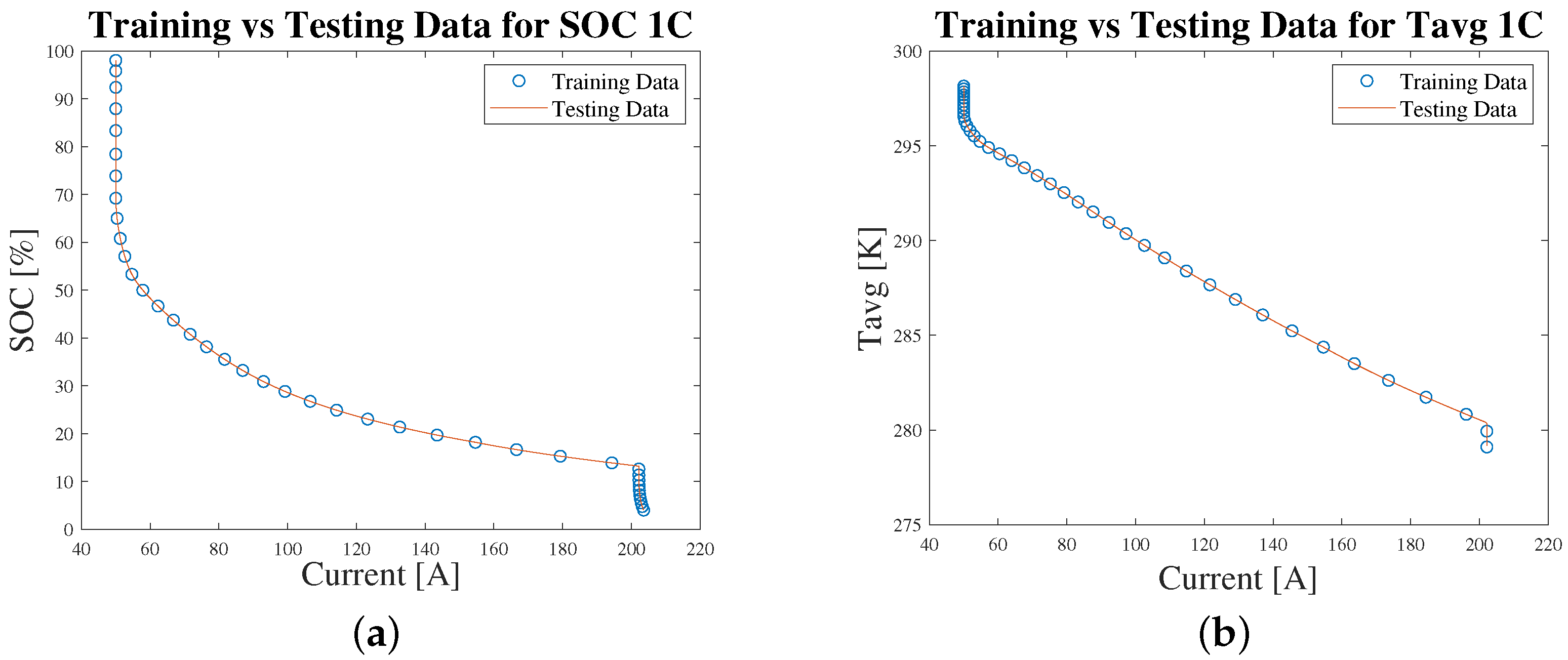
3.2. Data Separation
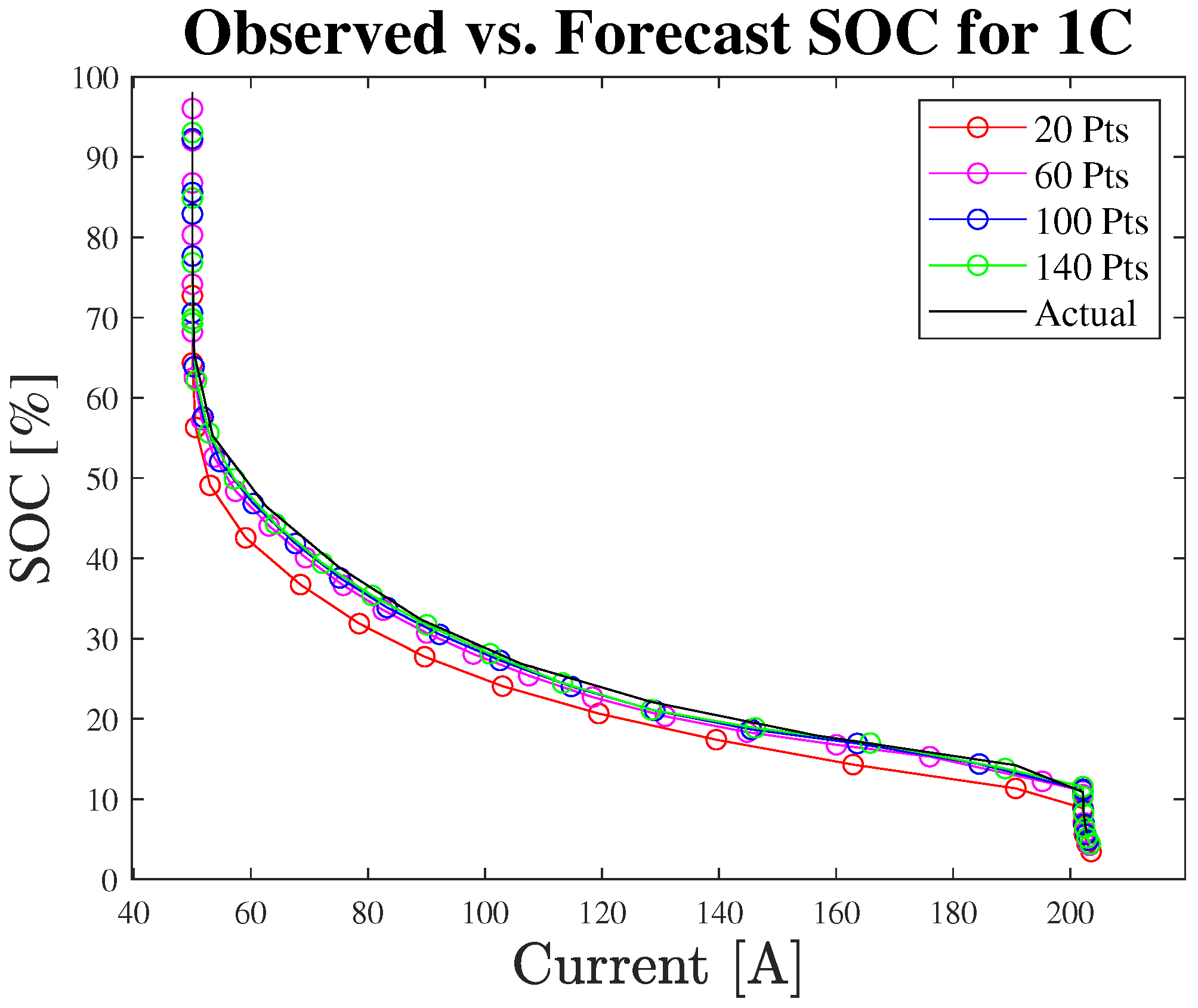
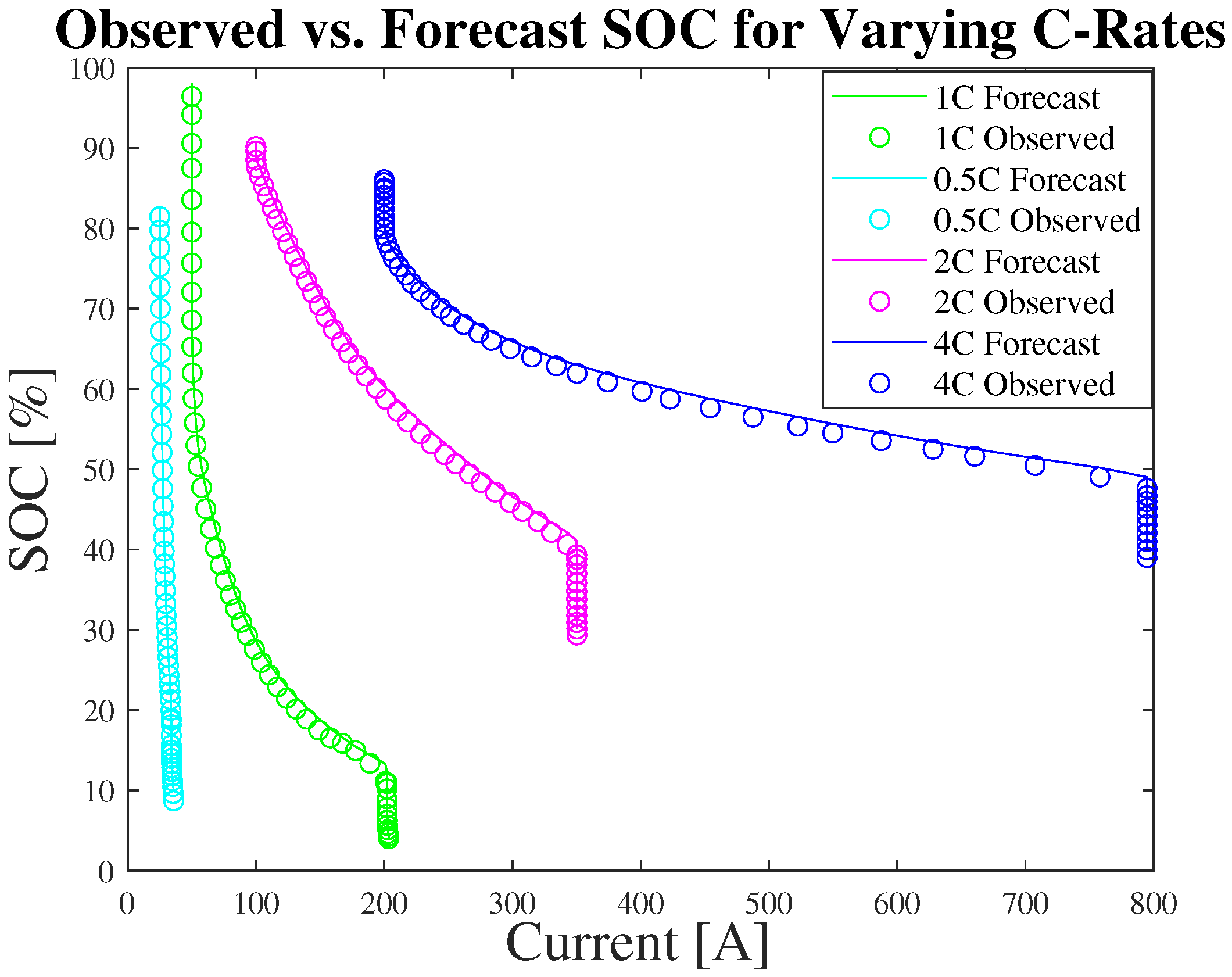
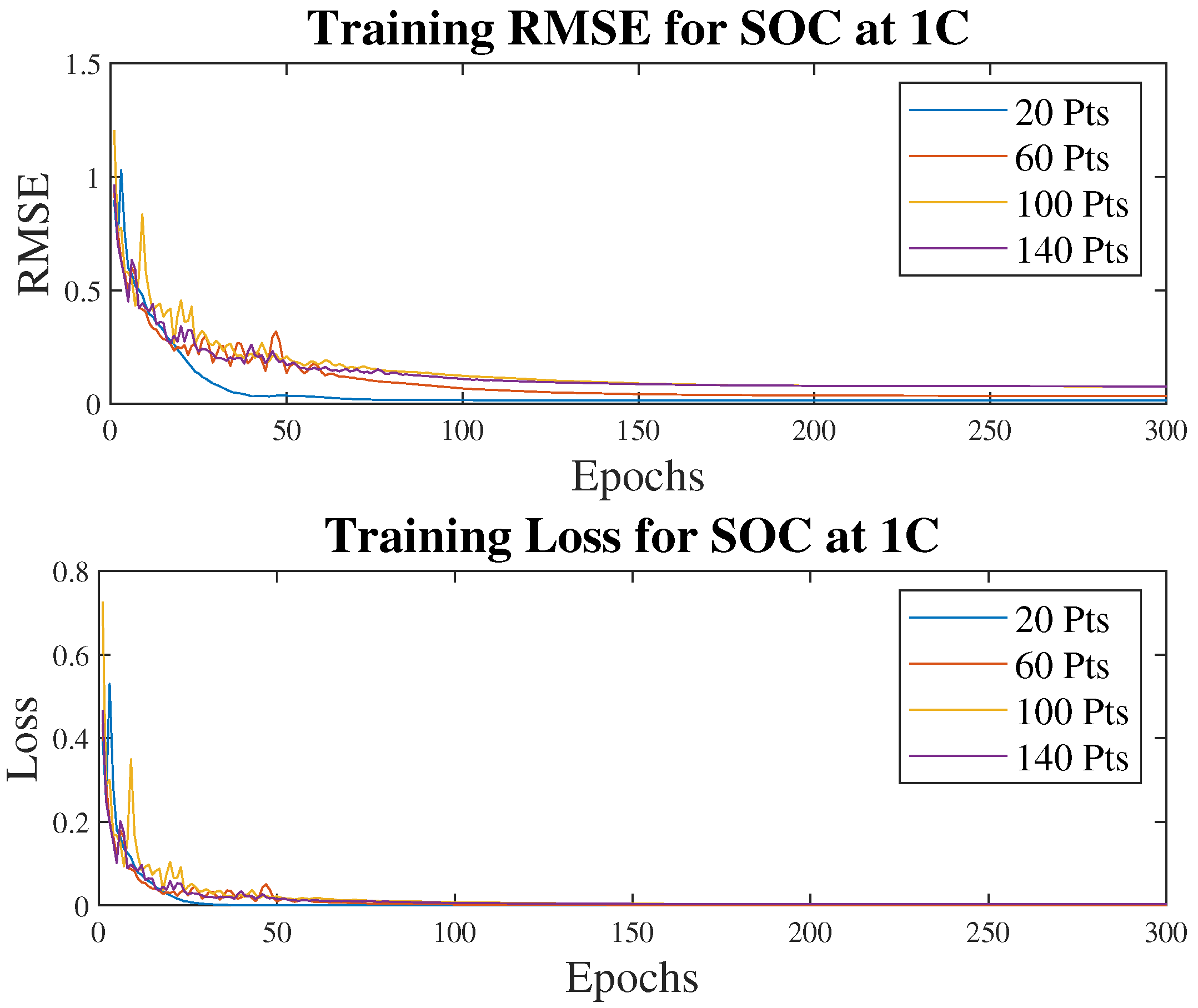
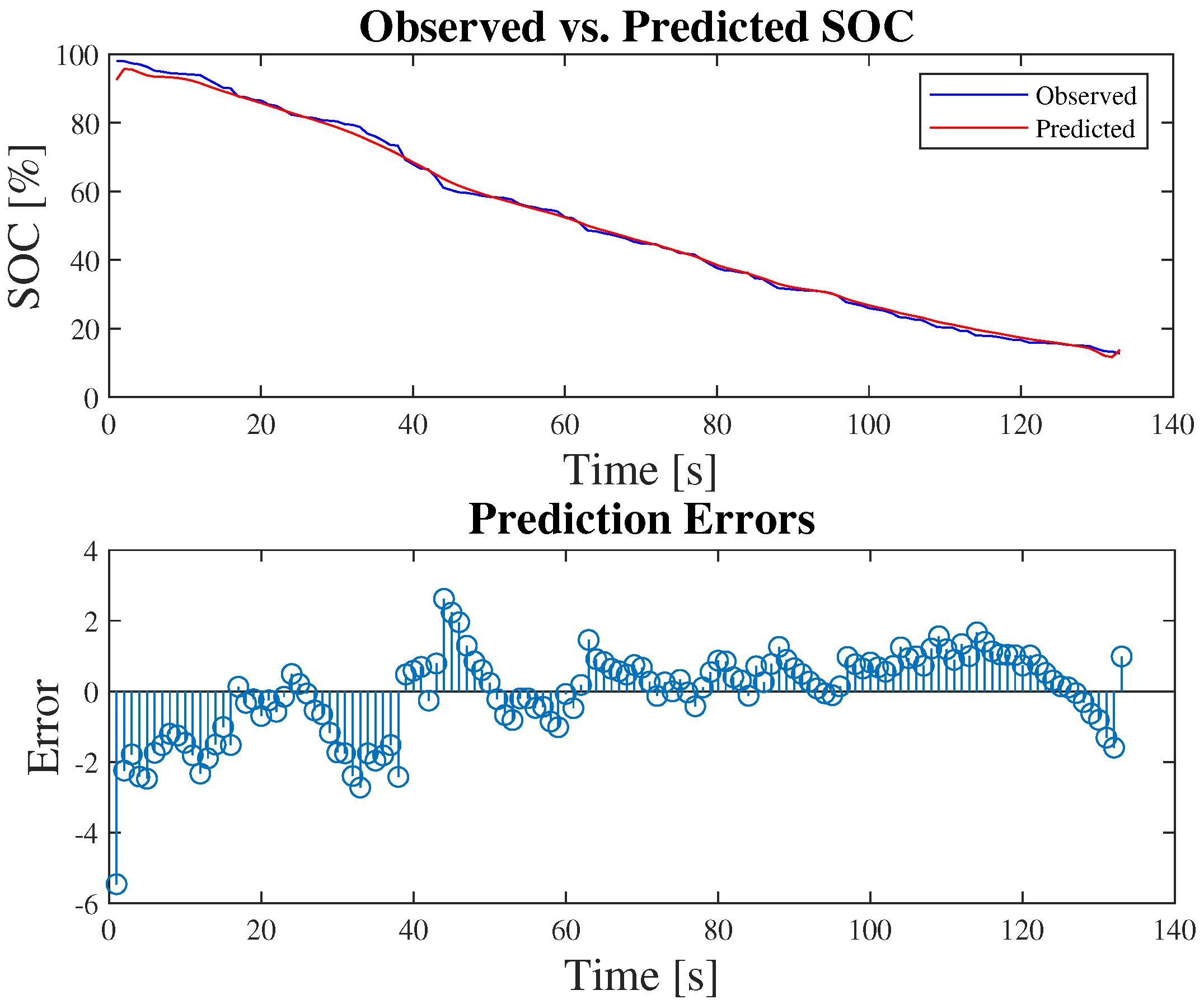
3.3. SOC Estimation
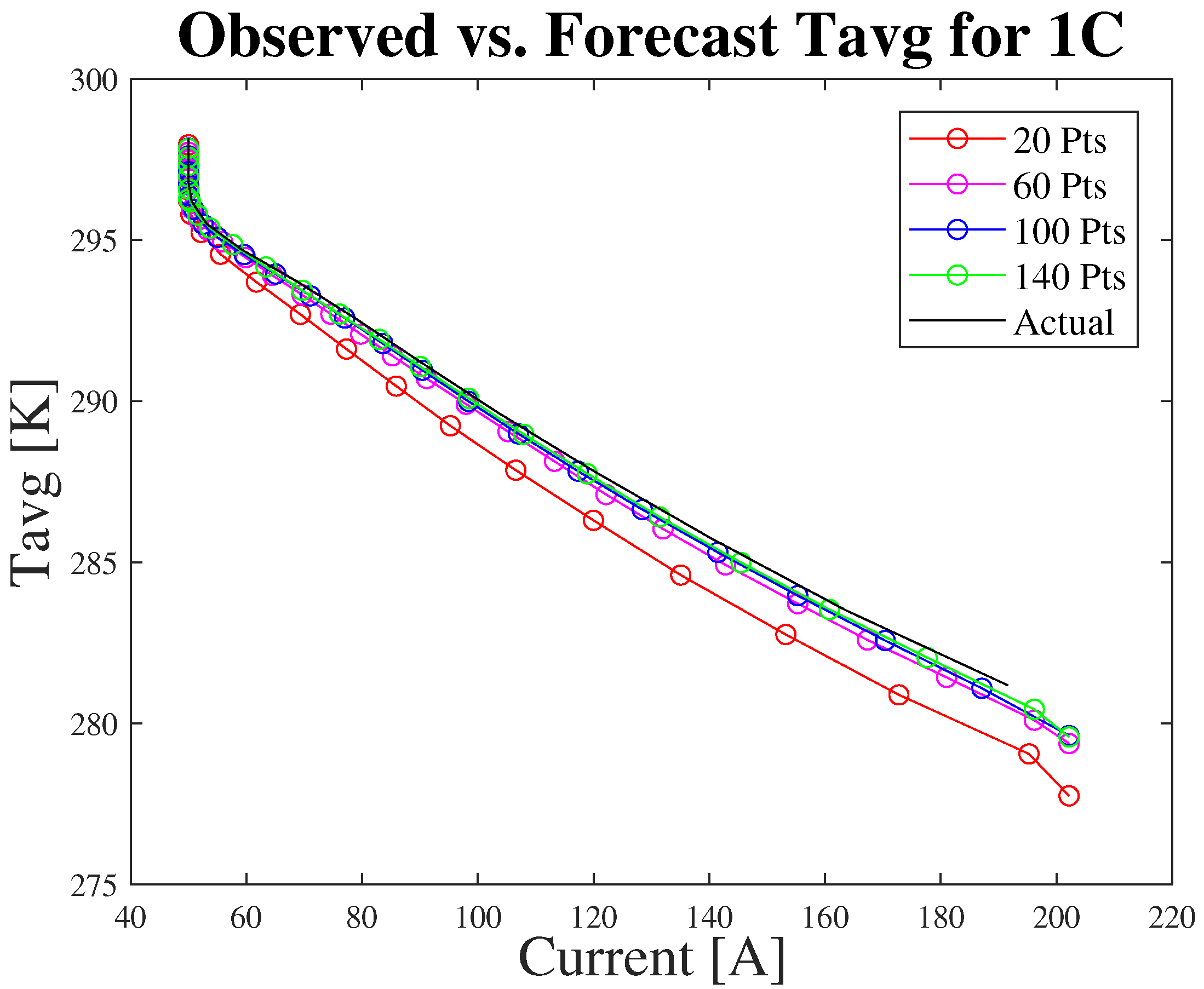
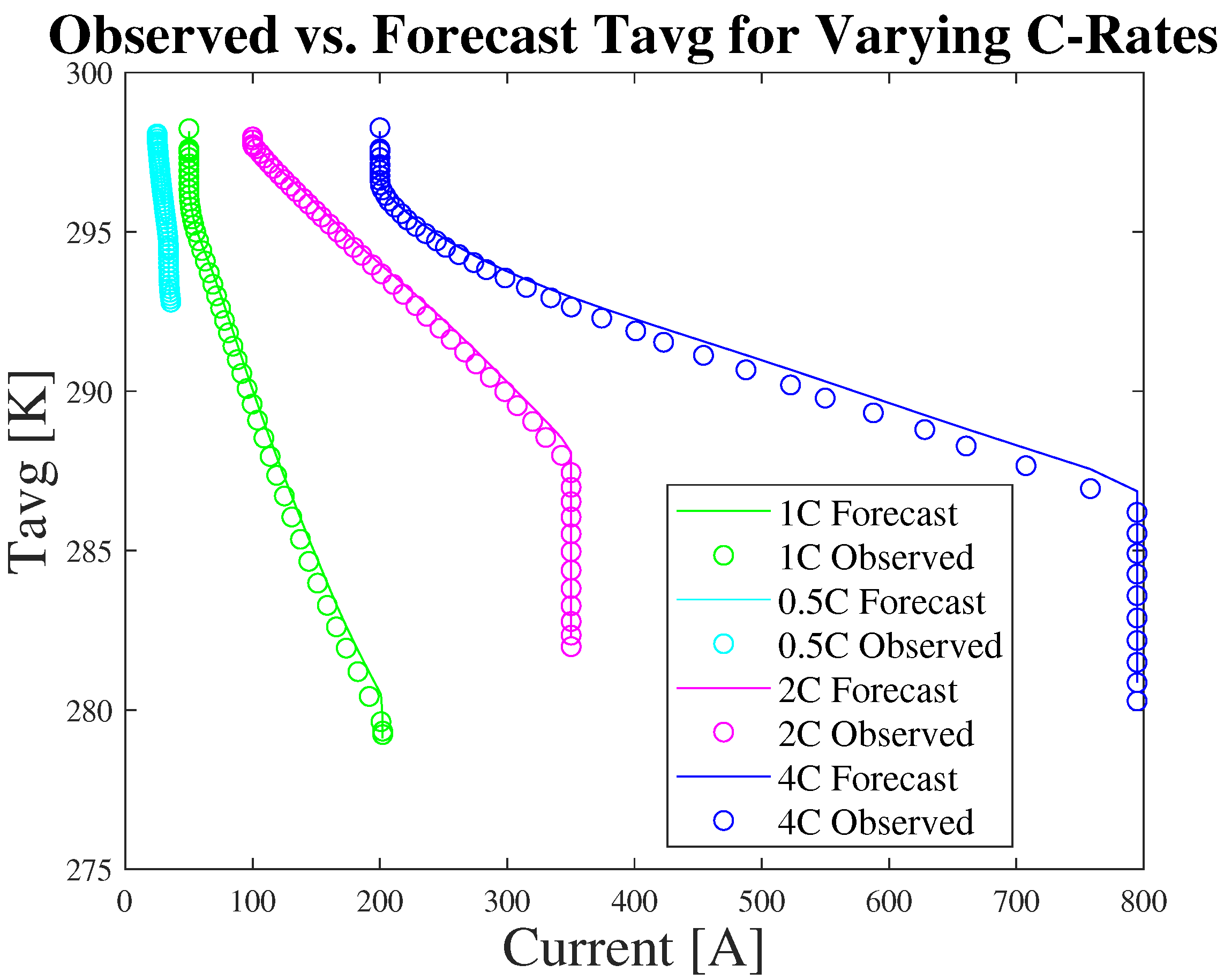
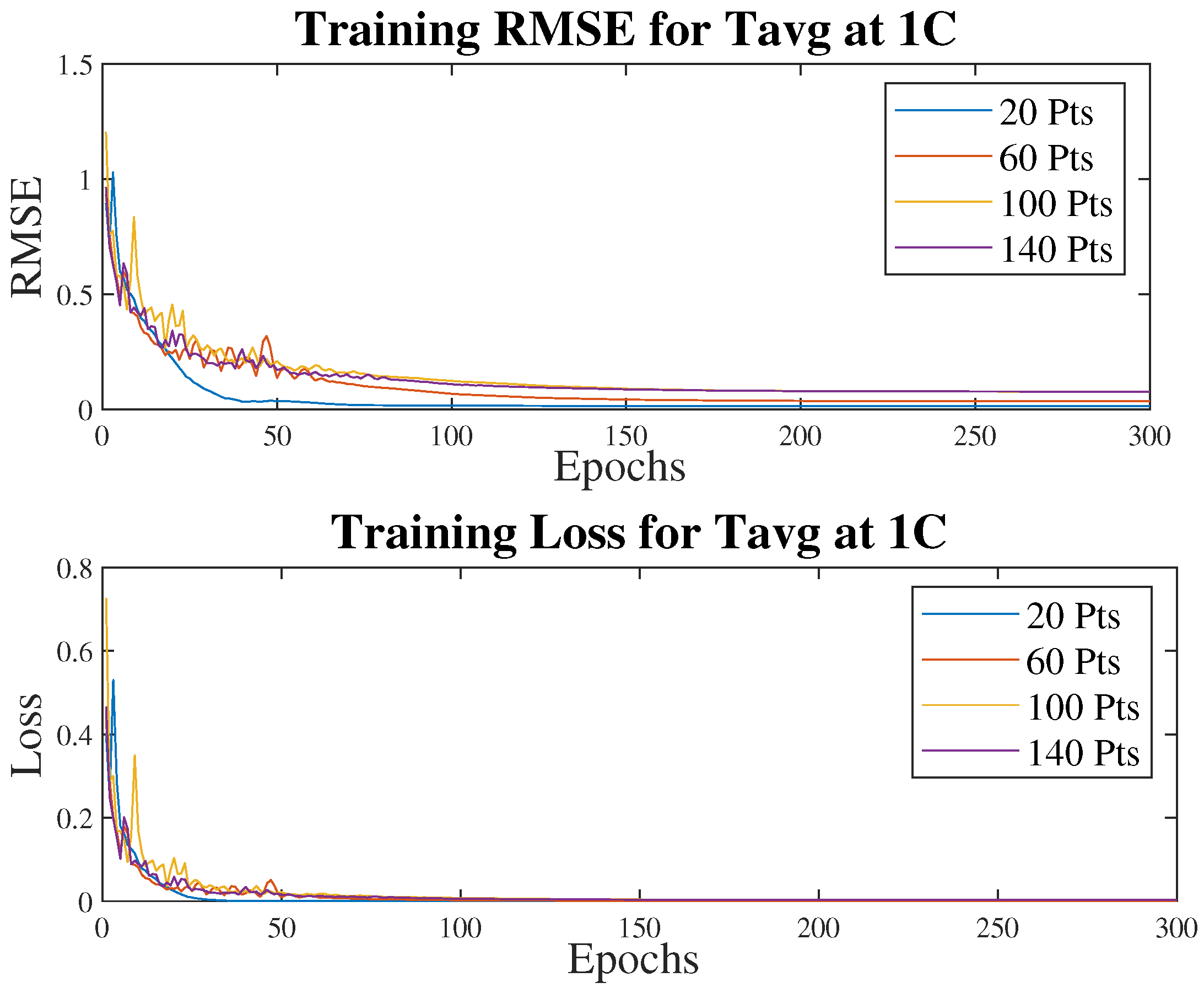
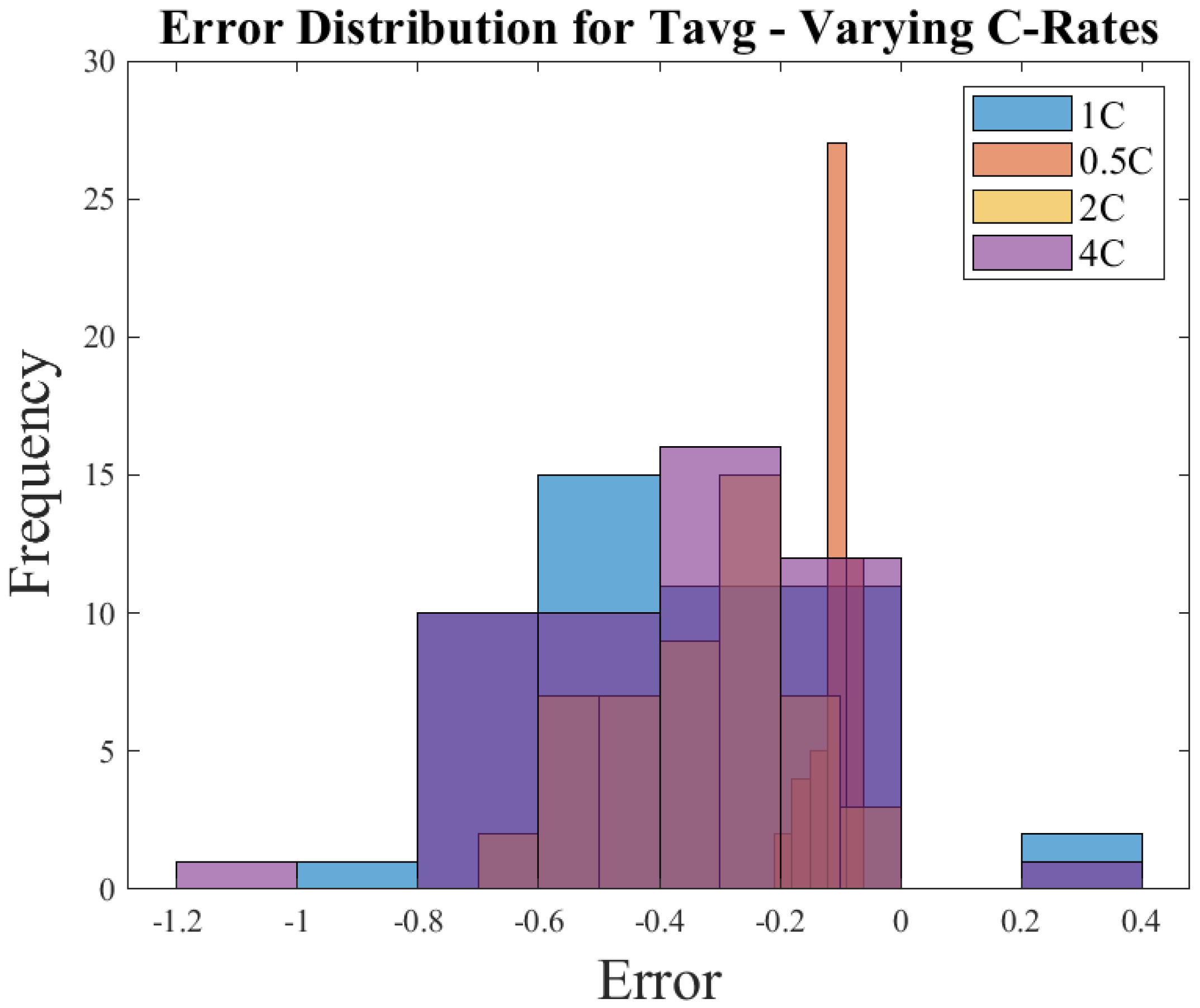
3.4. Temperature Estimation
3.5. Estimation Using Multiple Inputs
- RMSE = 1.54
- MSE = 2.370
- MAE = 0.257
- PCC = 0.994
- RMSE = 0.346
- MSE = 0.120
- MAE = 0.148
- PCC = 0.9984
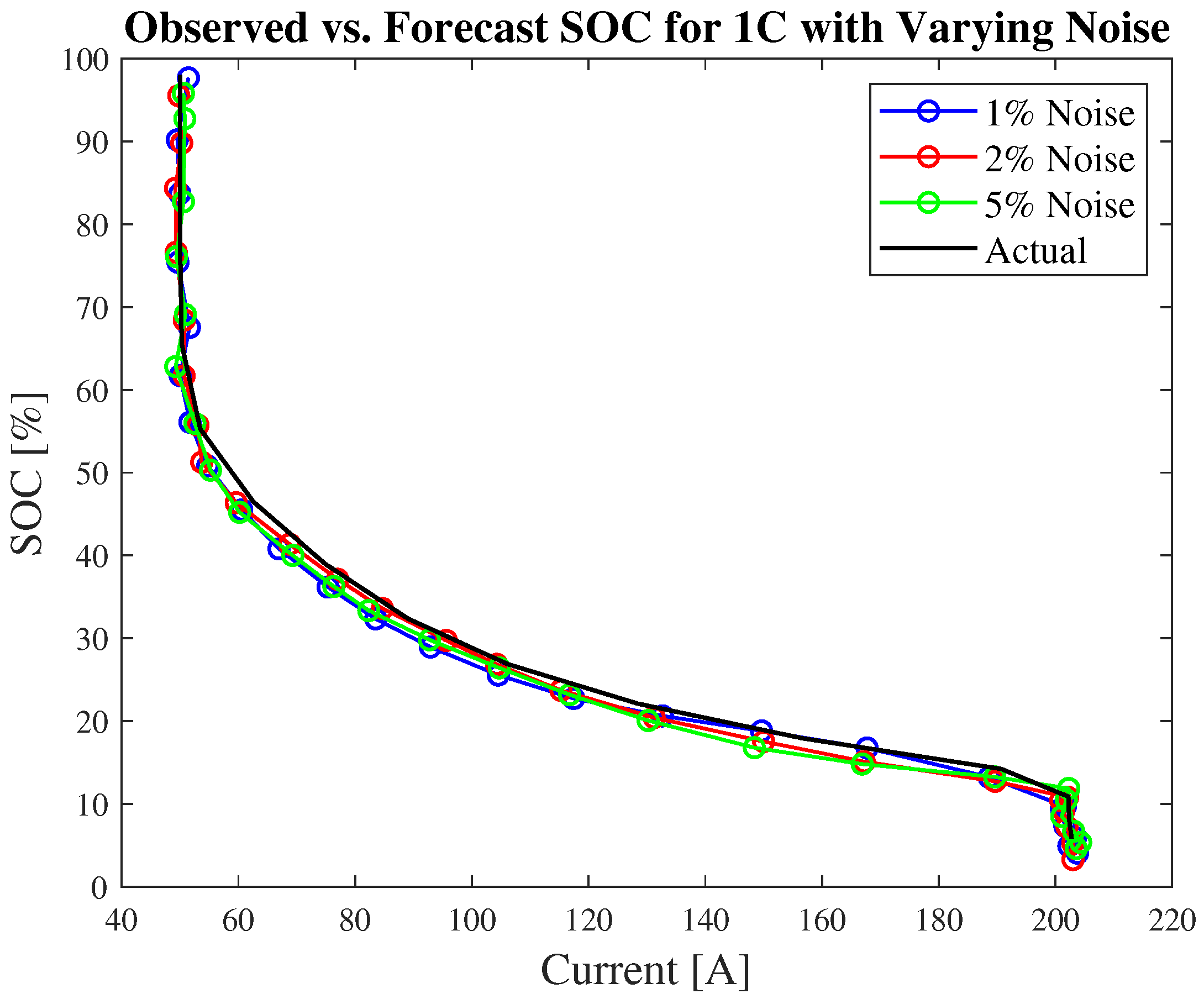
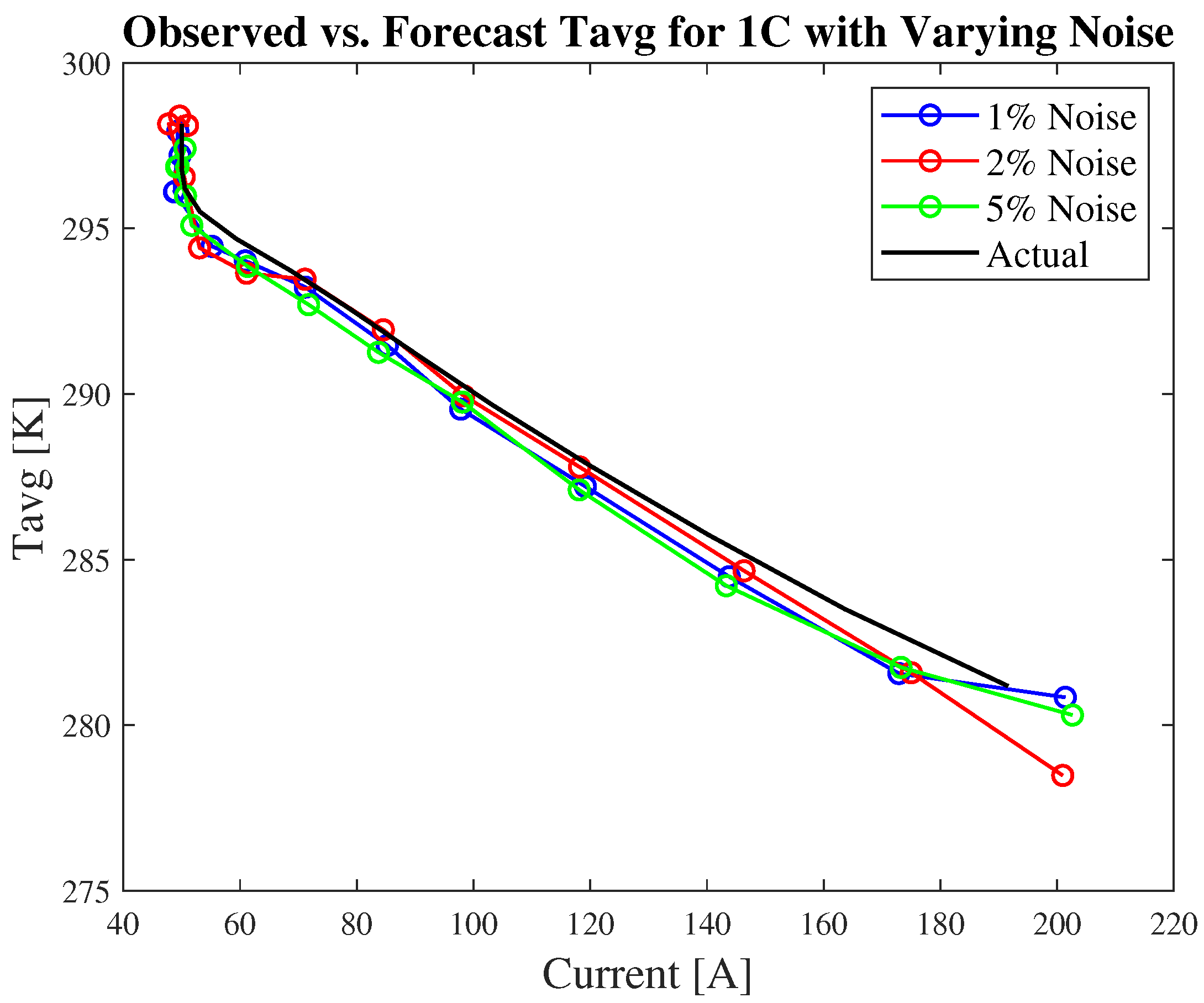
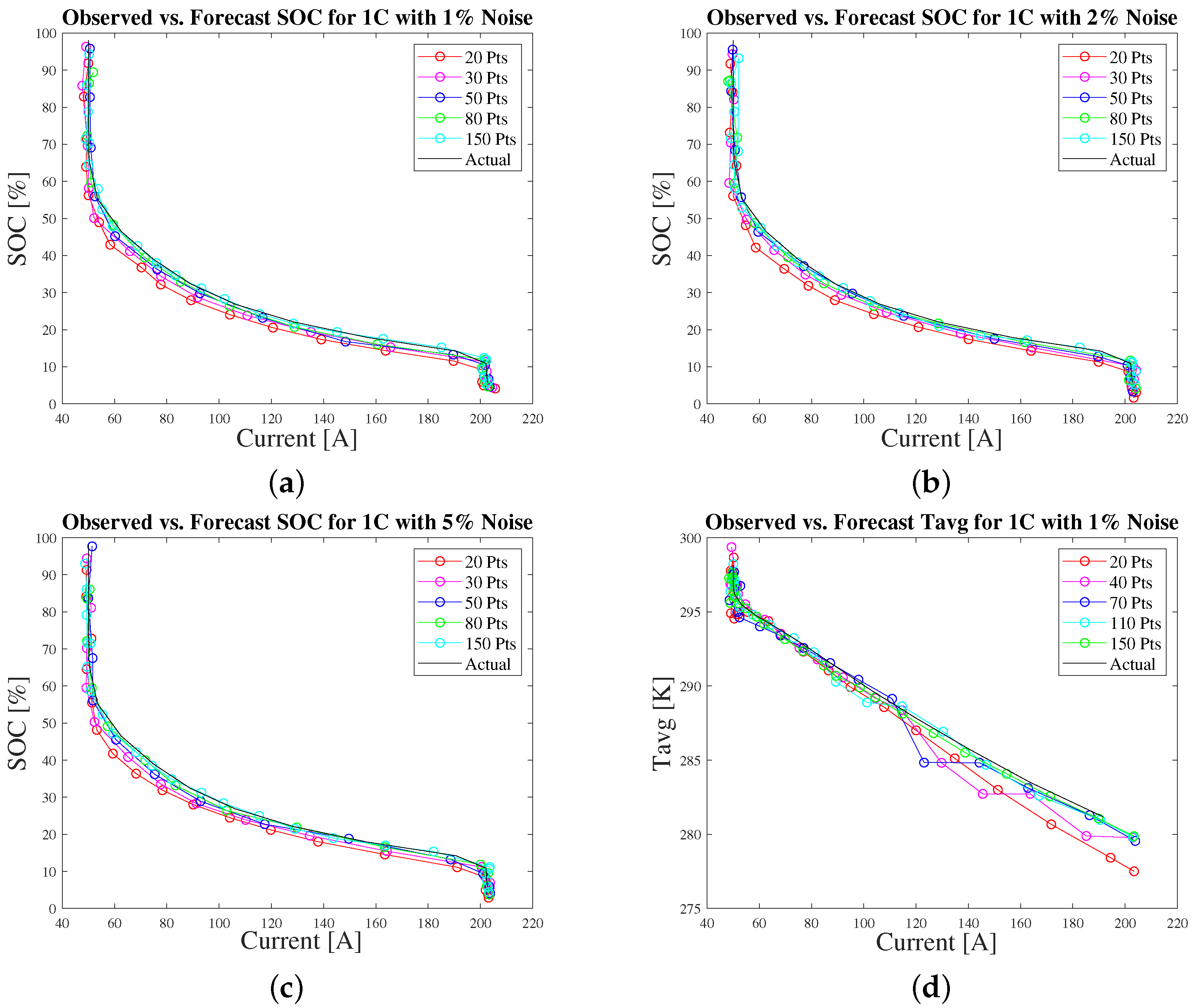
3.6. Estimation Using Noisy Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Abbreviations
| Abbreviations | |
| Symbol | Meaning |
| BMS | Battery management system |
| ML | Machine learning |
| CNN | Convolutional neural network |
| MSE | Mean square error |
| DT | Digital twin |
| NN | Neural network |
| ECM | Equivalent circuit model |
| OCV | Open-circuit voltage |
| GRU | Gated recurrent; form of RNN |
| PCC | Pearson correlation coefficient |
| LFP | Lithium-iron-phosphate |
| PINN | Physics-informed neural network |
| LIB | Lithium–ion battery |
| RMSE | Root mean square error |
| LSTM | Long-short-term-memory; form of multi-layer RNN |
| RNN | Recurrent neural network |
| MAE | Mean absolute error |
| SISO | Single-input single-output |
| MISO | Multi-input single-output |
| SOC | State of charge; measure of difference between a fully charged battery versus a battery in use. |
Appendix B. Nomenclature
| Nomenclature | |
| Symbol | Meaning |
| ; set of biases, different for each associated gate | |
| Cell state at time step t | |
| Candidate cell state values; dictated by the gate gate | |
| Function with parameters w, where w is a set of weights | |
| Hidden state at time step t | |
| Input gate | |
| Output gate | |
| Standard deviation for normalization of data; sigmoid activation function in neural networks | |
| ; set of weight matrices, different for each associated gate | |
| General variable at step i | |
| Standardized/normalized general variable X | |
| Input variable at time step t | |
| Y | Testing value from input dataset |
| Predicted value from the network | |
Appendix C. Hyperparameter Definitions
| Hyperparameter Definitions [36] | |
| Name | Definition |
| Max Epochs | Maximum number of epochs (full passes of the data) to use for training, specified as a positive integer. |
| Initial Learning Rate | Initial learning rate used for training, specified as a positive scalar. If the learning rate is too low, then training can take a long time. If the learning rate is too high, then training might reach a suboptimal result or diverge. |
| Learning Rate Drop Period | Number of epochs for dropping the learning rate, specified as a positive integer. This option is valid only when the LearnRateSchedule training option is “piecewise”. |
| Learning Rate Drop Factor | Factor for dropping the learning rate, specified as a scalar from 0 to 1. This option is valid only when the LearnRateSchedule training option is “piecewise”. |
| Minibatches | Size of the mini-batch to use for each training iteration, specified as a positive integer. A mini-batch is a subset of the training set that is used to evaluate the gradient of the loss function and update the weights. |
| Gradient Threshold | Gradient threshold, specified as Inf or a positive scalar. If the gradient exceeds the value of GradientThreshold, then the gradient is clipped according to the GradientThresholdMethod training option. |
| Validation Frequency | Frequency of neural network validation in number of iterations, specified as a positive integer. The validation frequency value is the number of iterations between evaluations of validation metrics. |
| Validation Patience | Patience of validation stopping of neural network training, specified as a positive integer or Inf. This specifies the number of times the objective metric on the validation set can be worse or equal to the previous best value before training stops. |
| ADAM | Adaptive moment estimation (ADAM). ADAM is a stochastic solver. |
References
- Planella, F.B.; Ai, W.; Boyce, A.M.; Ghosh, A.; Korotkin, I.; Sahu, S.; Sulzer, V.; Timms, R.; Tranter, T.G.; Zyskin, M.; et al. A continuum of physics-based lithium–ion battery models reviewed. Prog. Energy 2022, 4, 042003. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-charge estimation of lithium–ion batteries using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Yi, Y.; Xia, C.; Feng, C.; Zhang, W.; Fu, C.; Qian, L.; Chen, S. Digital twin-long short-term memory (LSTM) neural network based real-time temperature prediction and degradation model analysis for lithium–ion battery. J. Energy Storage 2023, 64, 107203. [Google Scholar] [CrossRef]
- Khah, M.V.; Zahedi, R.; Eskandarpanah, R.; Mirzaei, A.M.; Farahani, O.N.; Malek, I.; Rezaei, N. Optimal sizing of residential photovoltaic and battery system connected to the power grid based on the cost of energy and peak load. Heliyon 2023, 9, e14414. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium–ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium–ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Chung, D.; Ko, J.; Yoon, K. State-of-Charge Estimation of Lithium–ion Batteries Using LSTM Deep Learning Method. J. Electr. Eng. Technol. 2022, 17, 1931–1945. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Deng, J. Real-time estimation of battery internal temperature based on a simplified thermoelectric model. J. Power Sources 2016, 302, 146–154. [Google Scholar] [CrossRef]
- Zhao, F.; Guo, Y.; Chen, B. A Review of Lithium–Ion Battery State of Charge Estimation Methods Based on Machine Learning. World Electr. Veh. J 2024, 15, 131. [Google Scholar] [CrossRef]
- Cho, G.; Zhu, D.; Campbell, J.J.; Wang, M. An LSTM-PINN Hybrid Method to Estimate Lithium–Ion Battery Pack Temperature. IEEE Access 2022, 10, 100594–100604. [Google Scholar] [CrossRef]
- Yao, Q.; Lu, D.D.; Lei, G. A Surface Temperature Estimation Method for Lithium–Ion Battery Using Enhanced GRU-RNN. IEEE Trans. Transp. Electrif. 2023, 9, 1103–1112. [Google Scholar] [CrossRef]
- Li, F.; Krishna, R.; Xu, D. Lecture 10: Recurrent Neural Networks. 2021. Available online: https://cs231n.stanford.edu/2021/slides/2021/lecture_10.pdf (accessed on 7 January 2025).
- Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative Study of CNN and RNN for Natural Language Processing. arXiv 2017, arXiv:1702.01923. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Jiang, Y.; Yu, Y.; Huang, J.; Cai, W.; Marco, J. Li–ion battery temperature estimation based on recurrent neural networks. Sci. China Technol. Sci. 2021, 64, 1335–1344. [Google Scholar] [CrossRef]
- Wang, L.; Luo, F.; Xu, Y.; Gao, K.; Zhao, X.; Wang, R.; Pan, C.; Liu, L. Analysis and estimation of internal temperature characteristics of Lithium–ion batteries in electric vehicles. Ind. Eng. Chem. Res. 2023, 62, 7657–7670. [Google Scholar] [CrossRef]
- Chevalier, B.; Xie, J.; Dubljevic, S. Enhanced Dynamic Modeling and Analysis of a Lithium–Ion Battery: Coupling Extended Single Particle Model with Thermal Dynamics. 2024; under review. [Google Scholar]
- Xie, J.; Dubljevic, S. Discrete-time Kalman filter design for linear infinite-dimensional systems. Processes 2019, 7, 451. [Google Scholar] [CrossRef]
- Perez, H.E.; Dey, S.; Hu, X.; Moura, S.J. Optimal Charging of Li-Ion Batteries via a Single Particle Model with Electrolyte and Thermal Dynamics. J. Electrochem. Soc. 2017, 164, A1679. [Google Scholar] [CrossRef]
- Roman, D.; Saxena, S.; Robu, V.; Pecht, M.; Flynn, D. Machine learning pipeline for battery state-of-health estimation. Nat. Mach. Intell. 2021, 3, 447–456. [Google Scholar] [CrossRef]
- Danko, M.; Adamec, J.; Taraba, M.; Drgona, P. Overview of batteries State of Charge estimation methods. Transp. Res. Proc. 2019, 40, 186–192. [Google Scholar] [CrossRef]
- Richardson, R.; Ireland, P.; Howey, D.; Richardson, R.; Ireland, P.; Howey, D. Battery internal temperature estimation by combined impedance and surface temperature measurement. J. Power Sources 2014, 265, 254–261. [Google Scholar] [CrossRef]
- Bhadriraju, B.; Kwon, J.S.I.; Khan, F. An adaptive data-driven approach for two-timescale dynamics prediction and remaining useful life estimation of Li–ion batteries. Comput. Chem. Eng. 2023, 175, 108275. [Google Scholar] [CrossRef]
- Hwang, G.; Sitapure, N.; Moon, J.; Lee, H.; Hwang, S.; Sang-Il Kwon, J. Model predictive control of Lithium–ion batteries: Development of optimal charging profile for reduced intracycle capacity fade using an enhanced single particle model (SPM) with first-principled chemical/mechanical degradation mechanisms. Chem. Eng. J. 2022, 435, 134768. [Google Scholar] [CrossRef]
- Lee, H.; Sitapure, N.; Hwang, S.; Kwon, J.S.I. Multiscale modeling of dendrite formation in lithium–ion batteries. Comput. Chem. Eng. 2021, 153, 107415. [Google Scholar] [CrossRef]
- Sitapure, N.; Kwon, J.S.I. Exploring the potential of time-series transformers for process modeling and control in chemical systems: An inevitable paradigm shift? Chem. Eng. Res. Des. 2023, 194, 461–477. [Google Scholar] [CrossRef]
- Shi, Y.; Ahmad, S.; Tong, Q.; Lim, T.M.; Wei, Z.; Ji, D.; Eze, C.M.; Zhao, J. The optimization of state of charge and state of health estimation for lithium-ions battery using combined deep learning and Kalman filter methods. Int. J. Energy Res. 2021, 45, 11206–11230. [Google Scholar] [CrossRef]
- Li, M.; Li, C.; Zhang, Q.; Liao, W.; Rao, Z. State of charge estimation of Li–ion batteries based on deep learning methods and particle-swarm-optimized Kalman filter. J. Energy Storage 2023, 64, 107191. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A review of lithium–ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Naguib, M.; Kollmeyer, P.; Vidal, C.; Emadi, A. Accurate Surface Temperature Estimation of Lithium–Ion Batteries Using Feedforward and Recurrent Artificial Neural Networks. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; pp. 52–57. [Google Scholar] [CrossRef]
- Marmarelis, V.Z. Appendix II: Gaussian White Noise. In Nonlinear Dynamic Modeling of Physiological Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004; pp. 499–501. [Google Scholar]
- Du, X.; Meng, J.; Liu, K.; Zhang, Y.; Wang, S.; Peng, J.; Liu, T. Online Identification of Lithium–ion Battery Model Parameters with Initial Value Uncertainty and Measurement Noise. Chin. J. Mech. Eng. 2023, 36, 7. [Google Scholar] [CrossRef]
- Lin, L.; Kawarabayashi, N.; Fukui, M.; Tsukiyama, S.; Shirakawa, I. A Practical and Accurate SOC Estimation System for Lithium-Ion Batteries by EKF. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Su, X.; Sun, B.; Wang, J.; Zhang, W.; Ma, S.; He, X.; Ruan, H. Fast capacity estimation for lithium–ion battery based on online identification of low-frequency electrochemical impedance spectroscopy and Gaussian process regression. Appl. Energy 2022, 322, 119516. [Google Scholar] [CrossRef]
- Sitapure, N.; Kwon, J.S.I. Machine learning meets process control: Unveiling the potential of LSTMc. AIChE J. 2024, 70, e18356. [Google Scholar] [CrossRef]
- The MathWorks Inc. Statistics and Machine Learning Toolbox; The MathWorks Inc.: Natick, MA, USA, 2022; Available online: https://www.mathworks.com/help/stats/index.html (accessed on 7 January 2025).




| Hyperparameters (SOC Estimation) | |||||
|---|---|---|---|---|---|
| Parameter | This Paper | Paper [9] | Paper [2] | Paper [5] | Paper [6] |
| Epochs | 150 | 3000 | 150 | 2000 | |
| Initial Learning Rate | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| Learning Rate Drop Period | 25 | ||||
| Minibatches | 32 | 89 | 60 | 64 | 60 |
| Loss Function Optimizer | ADAM | ADAM | ADAM | ADAM | |
| Hyperparameters (Temperature Estimation) | |||||
|---|---|---|---|---|---|
| Parameter | This Paper | Paper [9] | Paper [2] | Paper [5] | Paper [6] |
| Epochs | 300 | 8 | 1000 | 5000 | |
| Initial Learning Rate | 0.01 | 5 | 0.01 | 0.00001 | |
| Learning Rate Drop Factor | 0.5 | 0.9999 | 0.2 | 0.1 | 0.1 |
| Learning Rate Drop Period | 25 | 200 | 1000 | ||
| Minibatches | 32 | 256 | |||
| Loss Function Optimizer | ADAM | ADAM | ADAM | ||
| Methods | Applications | Advantages | Disadvantages |
|---|---|---|---|
| LSTM [6,9,12,13] | SOC estimation | Accurate, model-free | Sufficient data, high compute cost |
| LSTM + UKF [2] | SOC estimation | Noise filtering, better dynamic performance | High complexity and compute cost |
| GRU/LSTM [15] | Temperature estimation | Accurate tracking | Sufficient data, high compute cost |
| LSTM+PINN [10] | Temperature estimation | Incorporates physics, better accuracy | No electrochem. included, complex to train |
| Digital Twin + LSTM [3] | Temperature prediction, degradation analysis | Real-time prediction | High compute cost |
| OASIS [23] | SOC and voltage prediction | Interpretable, captures degradation | Model integration complexity |
| Enhanced SPM + degradation [24] | Intra-cycle capacity fade prediction | Physically grounded, better control input | Electrochem. knowledge needed |
| kMC + SPM [25] | Demonstrates the effect of major variables | Links micro–macro behavior, interpretable | High computation, complex modelling |
| Transformers [26] | Battery modelling and MPC | Parallelizable training | Needs large data |
| DL + Kalman Filter [27,28] | SOC estimation | Suppresses transient oscillations, improves accuracy | High compute cost, real-time implementation limits |
| Evaluation Metrics—SOC | |||||
|---|---|---|---|---|---|
| C-Rate | Training Points | RMSE (K) | MSE (K) | MAE (%) | PCC |
| 0.5 | 20 | 4.166 | 17.356 | 3.732 | 0.9991 |
| 60 | 1.372 | 1.881 | 1.226 | 0.9999 | |
| 100 | 0.835 | 0.696 | 0.735 | 0.9999 | |
| 140 | 0.894 | 0.800 | 0.561 | 0.9996 | |
| 1 | 20 | 5.461 | 29.817 | 4.728 | 0.9991 |
| 60 | 1.826 | 3.334 | 1.581 | 0.9999 | |
| 100 | 1.913 | 3.658 | 1.050 | 0.9986 | |
| 140 | 2.564 | 6.576 | 0.857 | 0.9965 | |
| 2 | 20 | 3.206 | 10.276 | 3.136 | 0.9995 |
| 60 | 1.054 | 1.110 | 1.022 | 0.9999 | |
| 100 | 0.669 | 0.447 | 0.617 | 0.9999 | |
| 140 | 0.950 | 0.903 | 0.480 | 0.9991 | |
| 4 | 20 | 2.473 | 6.117 | 2.435 | 0.9997 |
| 60 | 1.118 | 1.251 | 0.854 | 0.9987 | |
| 100 | 1.017 | 1.035 | 0.544 | 0.9982 | |
| 140 | 0.995 | 0.989 | 0.405 | 0.9980 | |
| Evaluation Metrics—Tavg | |||||
|---|---|---|---|---|---|
| C-Rate | Training Points | RMSE (K) | MSE (K) | MAE (%) | PCC |
| 0.5 | 20 | 0.311 | 0.097 | 0.296 | 0.9993 |
| 60 | 0.092 | 0.009 | 0.090 | 0.9999 | |
| 100 | 0.059 | 0.004 | 0.055 | 0.9999 | |
| 140 | 0.063 | 0.004 | 0.041 | 0.9995 | |
| 1 | 20 | 1.174 | 1.377 | 1.038 | 0.9990 |
| 60 | 0.383 | 0.147 | 0.315 | 0.9995 | |
| 100 | 0.257 | 0.066 | 0.192 | 0.9996 | |
| 140 | 0.238 | 0.057 | 0.143 | 0.9995 | |
| 2 | 20 | 0.963 | 0.927 | 0.872 | 0.9998 |
| 60 | 0.301 | 0.091 | 0.269 | 0.9999 | |
| 100 | 0.259 | 0.067 | 0.170 | 0.9992 | |
| 140 | 0.239 | 0.057 | 0.119 | 0.9990 | |
| 4 | 20 | 1.136 | 1.292 | 0.982 | 0.9995 |
| 60 | 0.380 | 0.144 | 0.307 | 0.9994 | |
| 100 | 0.317 | 0.100 | 0.195 | 0.9989 | |
| 140 | 0.298 | 0.089 | 0.144 | 0.9987 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chevalier, B.; Xie, J.; Dubljevic, S. Long Short-Term Memory Networks for State of Charge and Average Temperature State Estimation of SPMeT Lithium–Ion Battery Model. Processes 2025, 13, 1528. https://doi.org/10.3390/pr13051528
Chevalier B, Xie J, Dubljevic S. Long Short-Term Memory Networks for State of Charge and Average Temperature State Estimation of SPMeT Lithium–Ion Battery Model. Processes. 2025; 13(5):1528. https://doi.org/10.3390/pr13051528
Chicago/Turabian StyleChevalier, Brianna, Junyao Xie, and Stevan Dubljevic. 2025. "Long Short-Term Memory Networks for State of Charge and Average Temperature State Estimation of SPMeT Lithium–Ion Battery Model" Processes 13, no. 5: 1528. https://doi.org/10.3390/pr13051528
APA StyleChevalier, B., Xie, J., & Dubljevic, S. (2025). Long Short-Term Memory Networks for State of Charge and Average Temperature State Estimation of SPMeT Lithium–Ion Battery Model. Processes, 13(5), 1528. https://doi.org/10.3390/pr13051528