Thermodynamic Method for Evaluating the Gas Adsorption-Induced Swelling of Confined Coal: Implication for CO2 Geological Sequestration
Abstract
1. Introduction
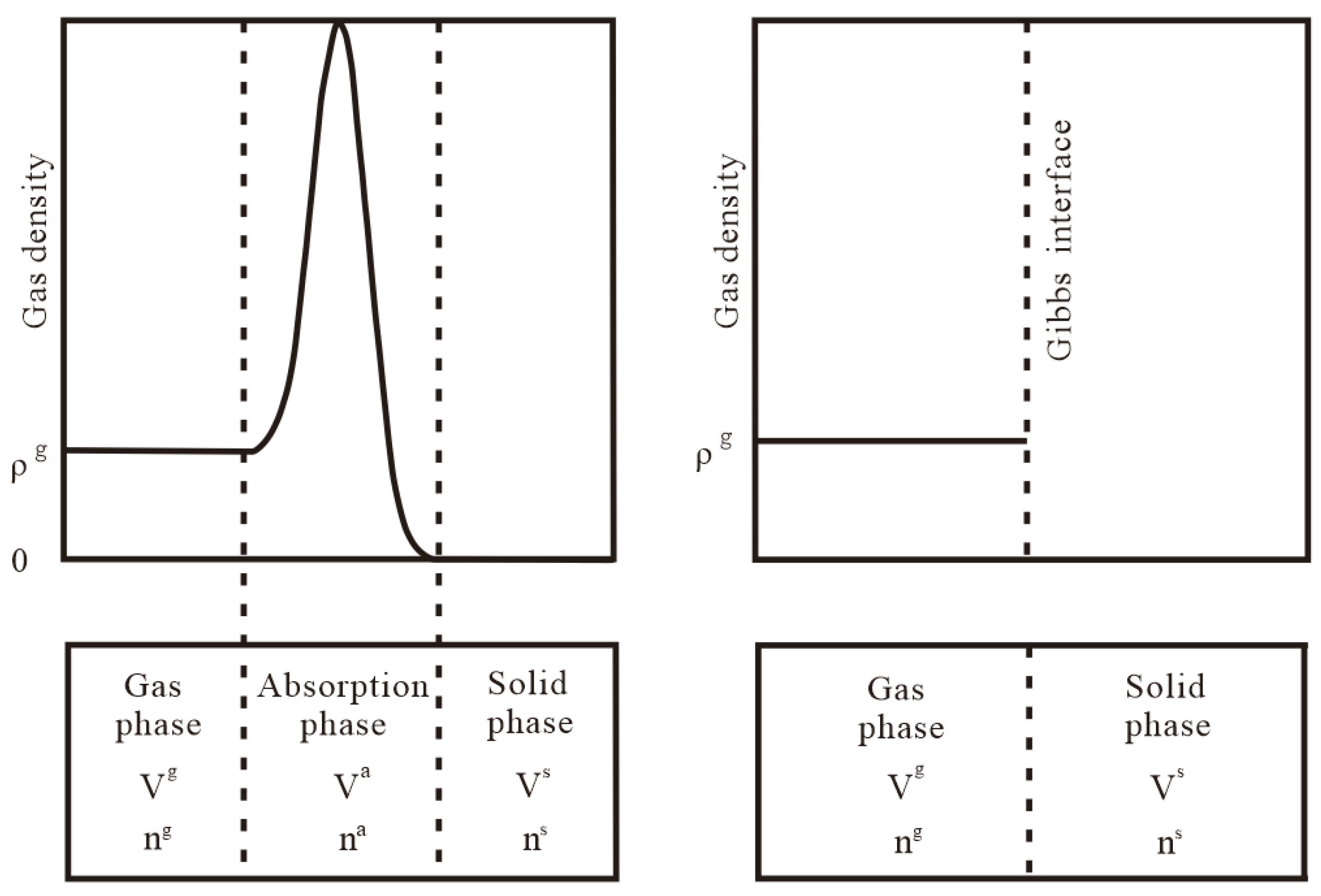
2. Establishment of the Thermodynamic Method
3. Experimental Method
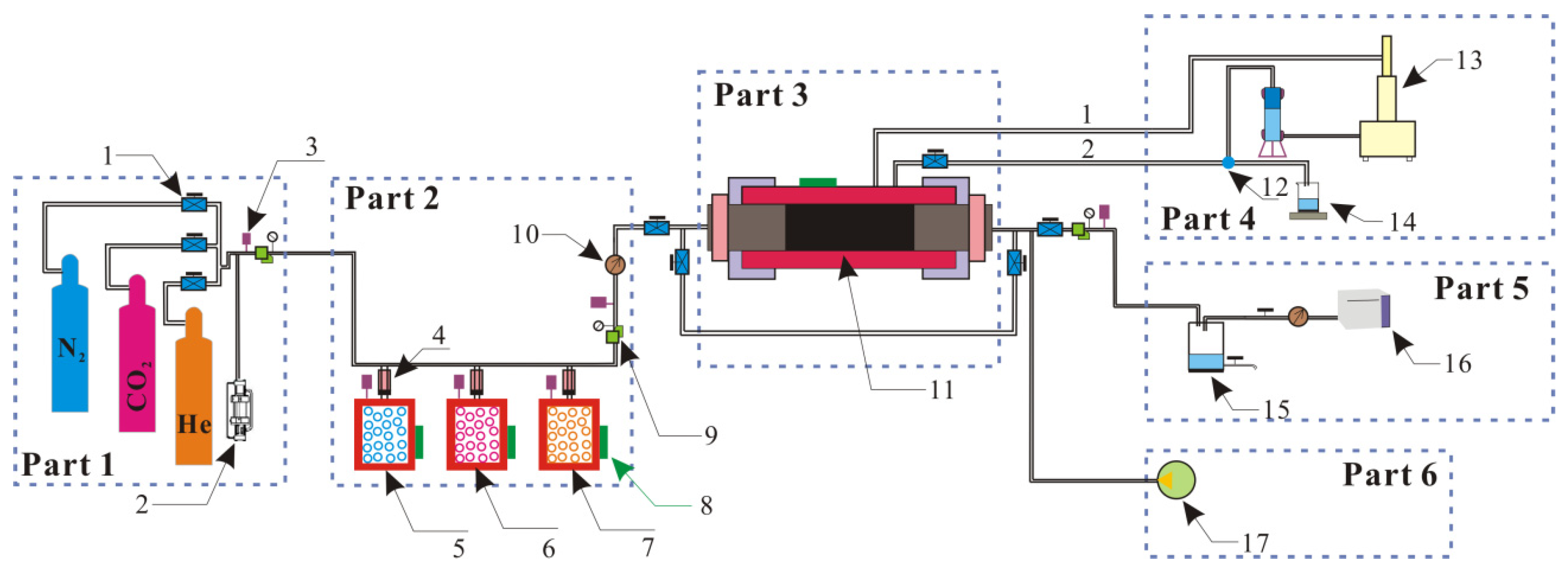
3.1. Measurement of Gas Adsorption Capacity
3.2. Strain Measurement of the Confined Coal
4. Results and Discussions
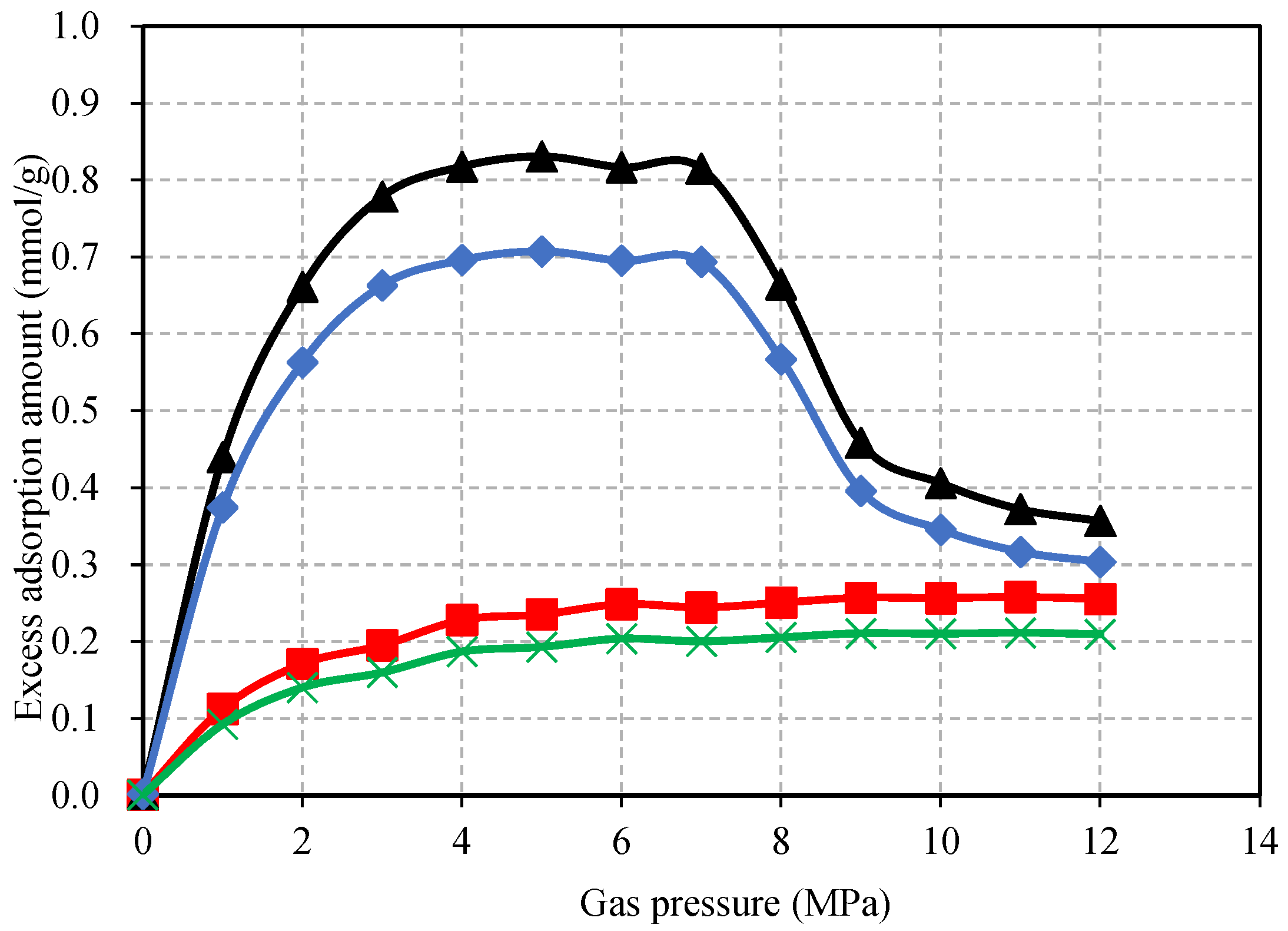
4.1. Gas Adsorption Content of the Confined Coal
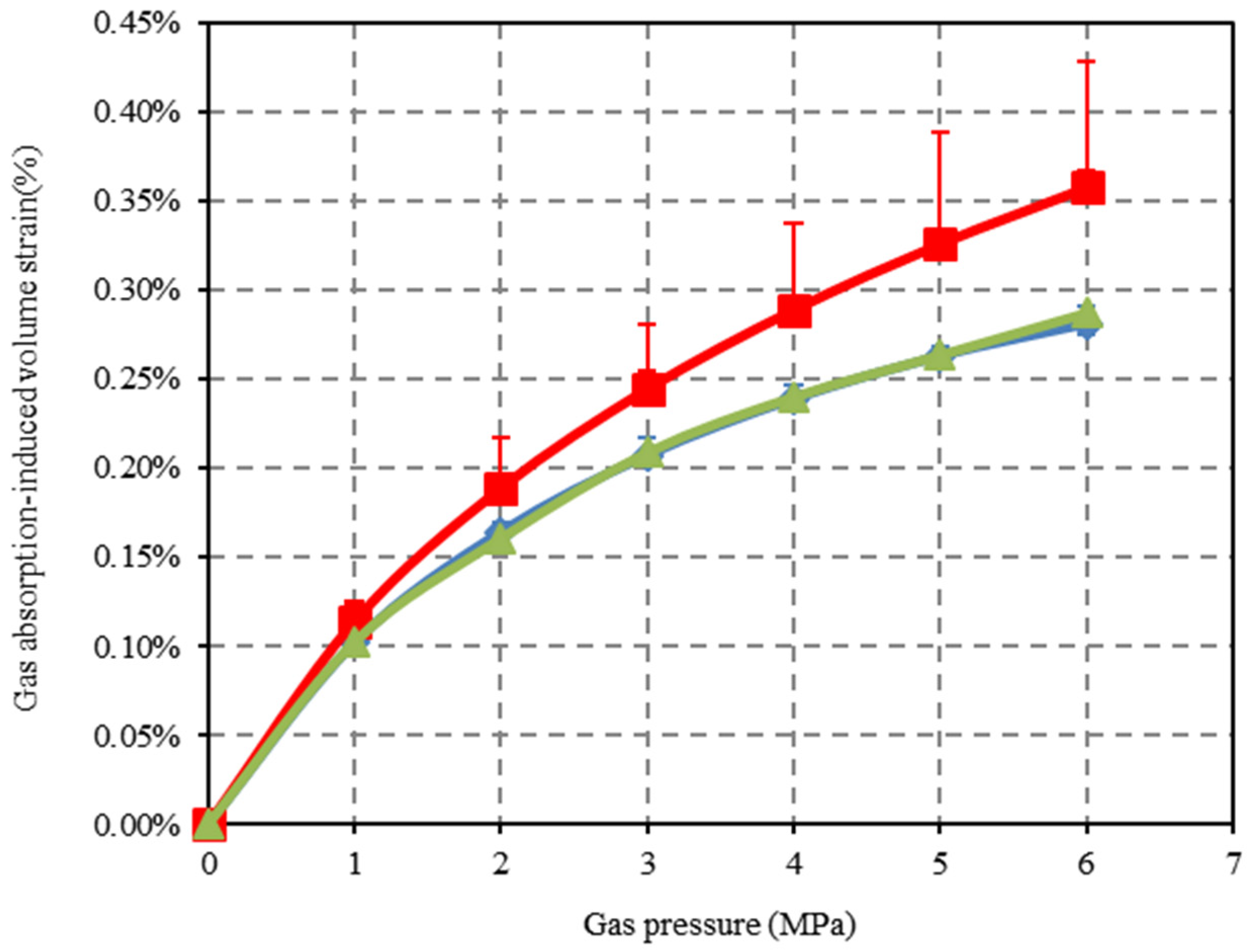
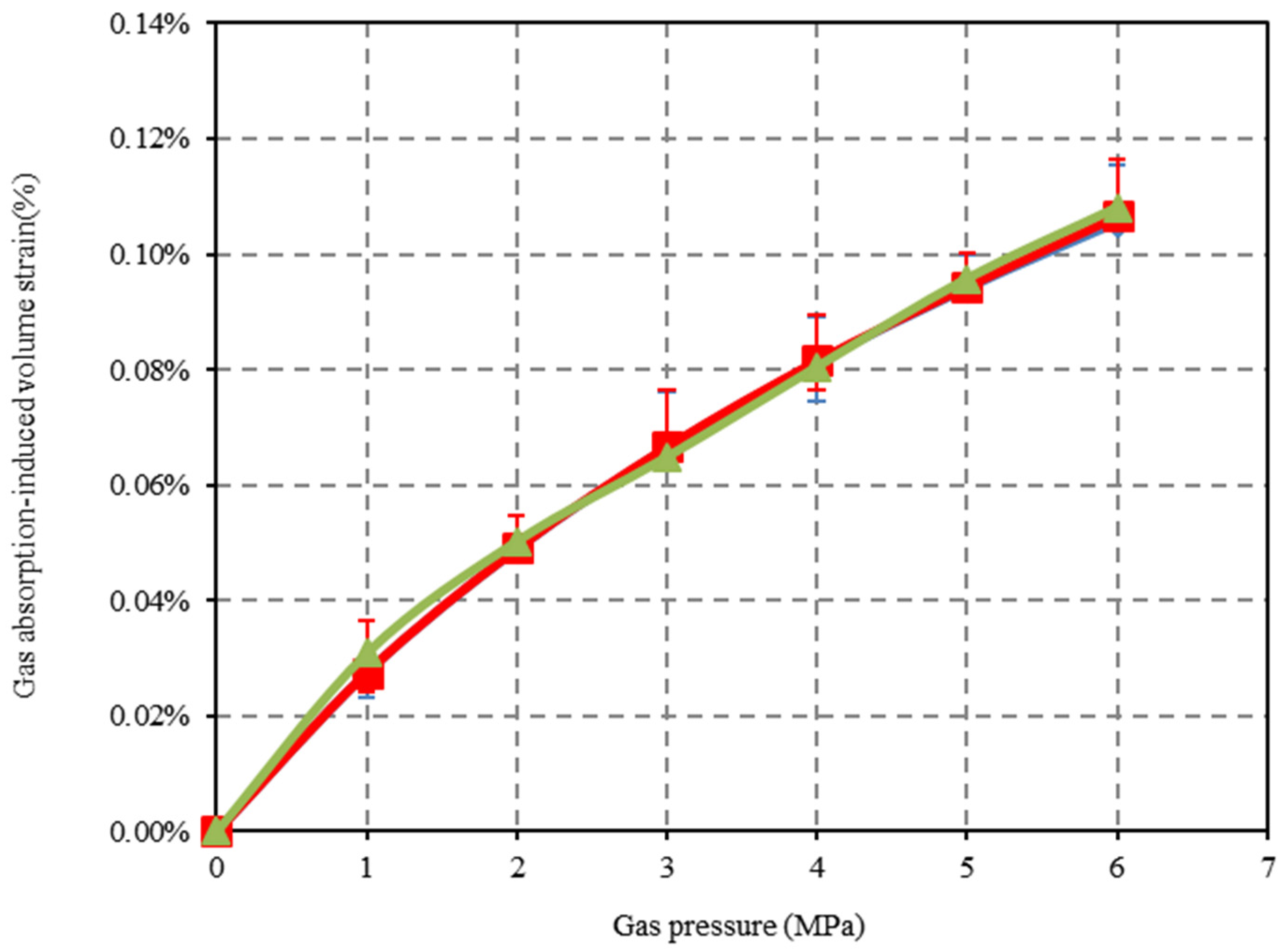
4.2. Gas Adsorption-Induced Deformation of the Confined Coal Under Applied Stress Condition
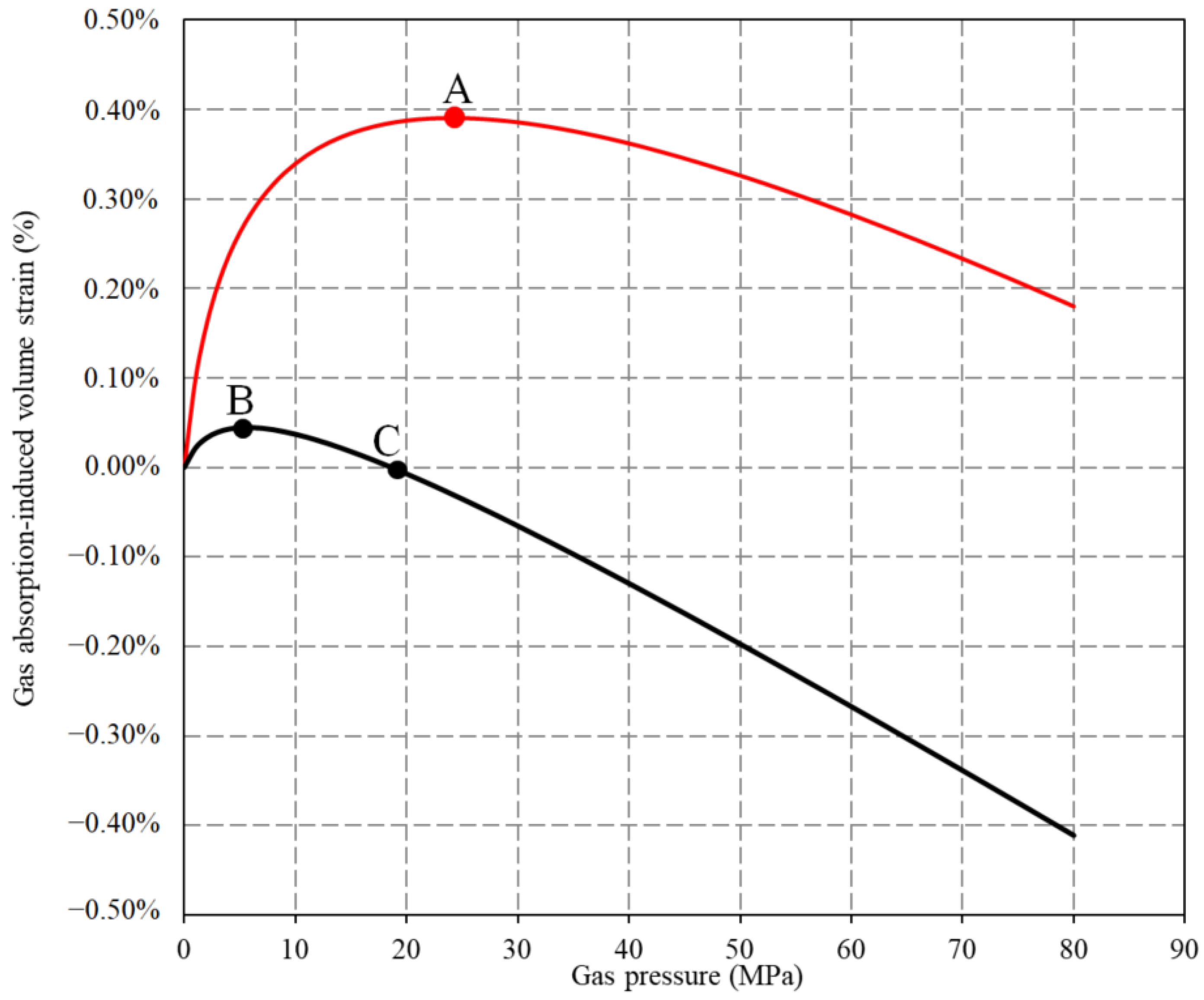
4.3. Gas Adsorption-Induced Deformation of the Confined Coal Under Ultra-High-Pressure Condition
4.4. Implication for CO2 Geological Storage
5. Conclusions
- (1)
- In the process of CO2 adsorption by the confined coal, when the gas pressure is close to its critical pressure, the capillary condensation of CO2 will occur on the coal pore surface. This will result in an excessive adsorption of CO2. With the increase in the applied stress, the porosity and fracture aperture decrease. The applied stress has a negative effect on the adsorption capacity and the adsorption-induced swelling behavior of the confined coal. Compared with N2, the applied stress has a more obvious negative effect on CO2 for the adsorption-induced swelling behavior of the confined coal.
- (2)
- The prediction results of the established mathematical method based on the ideal gas hypothesis is consistent with the experimental result under the low-pressure condition for CO2 (<2 MPa). It is higher than the experimental result under the high-pressure condition (>2 MPa). However, the prediction model of the established mathematical method based on the real gas state has better prediction results under both low- and high-pressure conditions. If the real gas is regarded as an ideal gas, the prediction result of the adsorption-induced swelling deformation of the confined coal will be increased.
- (3)
- In the process of geological storage of CO2 in coal seam, it is necessary to take the real gas state to predict the adsorption-induced swelling strain of the coal seam. Otherwise, the permeability damage degree of the coal seam by CO2 injection will be overestimated. The injectivity of CO2 to the targeted coal seam will be misjudged. For CO2 geological storage in the coal seam, the structural parts with low stress such as fold wing, tectonic slope zone, and tectonic flexural end should be preferred in consideration. Intermittent injection of CO2 to the coal seam can be carried out under high-pressure condition with mixed N2.
- (4)
- In this paper, the model assumes a simplified geo-stress environment and does not account for factors like coal seam heterogeneity, varying porosity, and fracture distribution. In addition, the research focuses mainly on the short-term adsorption-induced swelling behavior under specific pressure and stress conditions. Long-term changes in permeability, fracture propagation, and gas storage potential over extended periods of CO2 injection are not considered. In the next study, these limitations will be considered.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Enobong, H.; Chukwuebuka, N.; Victor, O.H. Carbon capture, utilization, and storage (CCUS) technologies: Evaluating the effectiveness of advanced CCUS solutions for reducing CO2 emissions. Results Surf. Interfaces 2025, 18, 100381. [Google Scholar]
- Mwakipunda, G.C.; Wang, Y.; Mgimba, M.M.; Ngata, M.R.; Alhassan, J.; Mkono, C.N.; Yu, L. Recent advances in carbon dioxide sequestration in deep unmineable coal seams using CO2-ECBM technology: Experimental studies, simulation, and field applications. Energy Fuels 2023, 37, 17161–17186. [Google Scholar] [CrossRef]
- Fang, H.H.; Li, A.; Sang, S.X.; Gu, C.C.; Yang, J.; Li, L.L.; Liu, H.H.; Xu, H.J.; Huang, Y.H. Numerical analysis of permeability rebound and recovery evolution with THM multi-physical field models during CBM extraction in crushed soft coal with low permeability and its indicative significance to CO2 geological sequestration. Energy 2023, 262, 125395. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Haghighi, M.; Salmachi, A.; Shokrollahi, A. Carbon dioxide storage within coal reservoirs: A comprehensive review. Geoenergy Sci. Eng. 2024, 241, 213198. [Google Scholar] [CrossRef]
- Karacan, C.Ö. Swelling-induced volumetric strains internal to a stressed coal associated with CO2 Sorption. Int. J. Coal Geol. 2007, 72, 209–220. [Google Scholar] [CrossRef]
- Day, S.; Fry, R.; Sakurovs, R.; Weir, S. Swelling of coals by supercritical gases and its relationship to sorption. Energy Fuels 2010, 24, 2777–2783. [Google Scholar] [CrossRef]
- Meng, Y.Y.; Yu, L.Y.; Yuan, L. Effects of bedding angle and confining pressure on the mechanical behavior, energy dissipation and micro damage evolution mechanism of layered rock mass under triaxial compression conditions. J. Mater. Res. Technol. 2025, 36, 1259–1272. [Google Scholar] [CrossRef]
- Karacan, C.Ö. Heterogeneous sorption and swelling in a confined and stressed coal during CO2 injection. Energy Fuels 2003, 17, 1595–1608. [Google Scholar] [CrossRef]
- Niu, Q.H.; Cao, L.W.; Sang, S.X.; Zhou, X.Z.; Wang, Z.Z.; Wu, Z.Y. The adsorption-swelling and permeability characteristics of natural and reconstituted anthracite coals. Energy 2017, 141, 2206–2217. [Google Scholar] [CrossRef]
- Ranathunga, A.S.; Perera, M.S.A.; Ranjith, P.G.; Rathnaweera, T.D.; Zhang, X.G. Effect of coal rank on CO2 adsorption induced coal matrix swelling with different CO2 properties and reservoir depths. Energy Fuels 2017, 31, 5297–5305. [Google Scholar] [CrossRef]
- Liu, Z.D.; Cheng, Y.P.; Wang, Y.K.; Wang, L.; Li, W. Experimental investigation of CO2 injection into coal seam reservoir at in-situ stress conditions for enhanced coalbed methane recovery. Fuel 2019, 236, 709–716. [Google Scholar] [CrossRef]
- Wu, S.Y.; Zhao, W.; Guo, Y.Y. Parametric correlation between expansion deformation of coal mass and adsorption thermodynamics. J. Northeast. Univ. Nat. Sci. 2005, 26, 683–686. [Google Scholar]
- Pan, Z.J.; Luke, D.C. A theoretical model for gas adsorption-induced coal swelling. Int. J. Coal Geol. 2007, 69, 243–252. [Google Scholar] [CrossRef]
- Zhou, J.P.; Xian, X.F.; Jiang, Y.D.; Gu, D.S.; Wang, C. A model of adsorption induced coal deformation based on thermodynamics approach. J. Chin. Coal Soc. 2011, 36, 468–472. [Google Scholar]
- Hol, S.; Spiers, C.J. Competition between adsorption-induced swelling and elastic compression of coal at CO2 pressures up to 100 MPa. J. Mech. Phys. Solids 2012, 60, 1862–1882. [Google Scholar] [CrossRef]
- Kang, J.Q.; Elsworth, D.; Fu, X.H.; Liang, S.; Chen, H. Contribution of thermal expansion on gas adsorption to coal sorption-induced swelling. Chem. Eng. J. 2022, 432, 134427. [Google Scholar] [CrossRef]
- Li, L.W.; Liu, X.F.; Nie, B.S.; Sun, H.T.; Jia, X.Q.; Zhang, C.P. Microstructural alterations of coal induced by interaction with sequestered supercritical carbon dioxide. Energy 2024, 304, 131912. [Google Scholar] [CrossRef]
- Shi, F.R.; Xie, H.P.; Li, M.H.; Deng, B.Z.; Shang, D.L.; Lu, J. Heterogeneous mechanical and sorption characteristics induced interaction among different components in coal: Experiment and simulation. Int. J. Rock Mech. Min. Sci. 2025, 188, 106064. [Google Scholar] [CrossRef]
- Tóth, J. Adsorption: Theory, modeling, and analysis. Am. Inst. Phys. Conf. Ser. 2002, 107, 206–213. [Google Scholar]
- Myers, A.L. Thermodynamics of adsorption in porous materials. AIChE J. 2002, 48, 145–160. [Google Scholar] [CrossRef]
- Scherer, G.W. Dilation of porous glass. J. Am. Ceram. Soc. 1986, 69, 473–480. [Google Scholar] [CrossRef]
- Levine, J.R. Model Study of the Influence of Matrix Shrinkage on Absolute Permeability of Coal Bed Reservoirs. Geol. Soc. Lond. Spec. Publ. 1996, 109, 197–212. [Google Scholar] [CrossRef]
- Khudaida, K.J.; Das, D.B. A numerical analysis of the effectsof supercritical CO2 injection on CO2 storage capacities of geological formations. Clean Technol. 2020, 2, 333–364. [Google Scholar] [CrossRef]
- Ren, B.; Sun, Y.H.; Bryant, S. Maximizing local capillary trapping during CO2 injection. Energy Procedia 2014, 63, 5562–5576. [Google Scholar] [CrossRef]
- Walter, P.L.; Verma, S.K.; Riverautrilla, J.; Davis, A. Densities, porosities and surface areas of coal macerals as measured by their interaction with gases, vapours and liquids. Fuel 1988, 67, 1615–1623. [Google Scholar]
- Du, Z.G.; Huang, Q.; Guo, J.J.; Gao, F.Q.; Du, Y.Q. The occurrence of nano- and micro-scale pores and their controls on the selective migration of gases in the coals of different ranks. Fuel 2020, 264, 116748. [Google Scholar] [CrossRef]
- Nie, B.; Liu, X.; Yang, L.; Meng, J.; Li, X. Pore structure characterization of different rank coals using gas adsorption and scanning electron microscopy. Fuel 2015, 158, 908–917. [Google Scholar] [CrossRef]
- Yao, S.P.; Jiao, K.; Zhang, K.; Hu, W.X.; Hai, D.; Li, M.C.; Pei, W.M. An atomic force microscopy study of coal nanopore structure. Chin. Sci. Bull. 2011, 56, 2706–2712. [Google Scholar] [CrossRef]
- Pini, R.; Ottiger, S.; Burlini, L.; Storti, G.; Mazzotti, M. Sorption of carbon dioxide, methane and nitrogen in dry coals at high pressure and moderate temperature. Int. J. Greenh. Gas Control 2010, 4, 90–101. [Google Scholar] [CrossRef]
- Cohan, L.H. Hysteresis and the capillary theory of adsorption of vapors. J. Am. Chem. Soc. 2002, 66, 98–105. [Google Scholar] [CrossRef]
- Perera, M.S.A.; Ranjith, P.G.; Choi, S.K.; Airey, D.; Weniger, P. Estimation of gas adsorption capacity in coal: A review and an analytical study. Int. J. Coal Prep. Util. 2012, 32, 25–55. [Google Scholar] [CrossRef]



| Fitting Model | Applied Stress (MPa) | Gas Type | Adsorption Capacity nmax (mmol/g) | Adsorption Constant B (MPa−1) |
|---|---|---|---|---|
| 8 | CO2 | 1.08 | 0.6830 | |
| 10 | 0.86 | 0.6842 | ||
| 8 | N2 | 0.45 | 0.3234 | |
| 10 | 0.38 | 0.3289 |
| Temperature (K) | Gas Pressure (MPa) | Gas Density (kg/m3) | Enthalpy (KJ/Kg) | Entropy (KJ/Kg/K) | Fugacity | Fugacity Coefficient | Chemical Potential (KJ/Kg) | Molar Mass (g/mol) |
|---|---|---|---|---|---|---|---|---|
| 303.2 | 0 | 0.000 | 511.01 | Infinite | 0.0000 | 1.0000 | 0.00 | 44 |
| 303.2 | 1 | 18.352 | 501.74 | 2.299 | 0.9533 | 0.9534 | −195.20 | 44 |
| 303.2 | 2 | 38.837 | 491.57 | 2.1438 | 1.8147 | 0.9074 | −158.33 | 44 |
| 303.2 | 3 | 62.211 | 480.2 | 2.0395 | 2.5854 | 0.8618 | −138.06 | 44 |
| 303.2 | 4 | 89.759 | 467.15 | 1.9523 | 3.266 | 0.8165 | −124.68 | 44 |
| 303.2 | 5 | 124.02 | 451.44 | 1.8691 | 3.8554 | 0.7711 | −115.18 | 44 |
| 303.2 | 6 | 171.44 | 430.71 | 1.7779 | 4.3493 | 0.7249 | −108.27 | 44 |
| 303.2 | 7 | 266.56 | 392.71 | 1.6367 | 4.732 | 0.676 | −103.44 | 44 |
| 303.2 | 8 | 701.72 | 284.04 | 1.2719 | 4.8924 | 0.6116 | −101.53 | 44 |
| 303.2 | 9 | 744.31 | 276.32 | 1.2419 | 5.0116 | 0.5569 | −100.15 | 44 |
| 303.2 | 10 | 771.5 | 271.62 | 1.222 | 5.1283 | 0.5128 | −98.837 | 44 |
| 303.2 | 11 | 791.67 | 268.36 | 1.2071 | 5.2478 | 0.47707 | −97.618 | 44 |
| 303.2 | 12 | 808.54 | 265.70 | 1.1942 | 5.3635 | 0.44696 | −96.369 | 44 |
| Temperature (K) | Gas Pressure (MPa) | Gas Density (kg/m3) | Enthalpy (KJ/Kg) | Entropy (KJ/Kg/K) | Fugacity | Fugacity Coefficient | Chemical Potential (KJ/Kg) | Molar Mass (g/mol) |
|---|---|---|---|---|---|---|---|---|
| 303.20 | 0.0000 | 0.0000 | 314.74 | Infinite | 0.0000 | 1.0000 | 0.0000 | 28.013 |
| 303.20 | 1.0000 | 11.127 | 312.61 | 6.1673 | 0.9985 | 0.9985 | −1557.3 | 28.013 |
| 303.20 | 2.0000 | 22.275 | 310.51 | 5.9551 | 1.9946 | 0.9973 | −1495.1 | 28.013 |
| 303.20 | 3.0000 | 33.427 | 308.47 | 5.8283 | 2.9889 | 0.9963 | −1458.7 | 28.013 |
| 303.20 | 4.0000 | 44.569 | 306.47 | 5.7365 | 3.9821 | 0.9955 | −1432.8 | 28.013 |
| 303.20 | 5.0000 | 55.686 | 304.53 | 5.6641 | 4.9748 | 0.9950 | −1412.8 | 28.013 |
| 303.20 | 6.0000 | 66.761 | 302.65 | 5.6039 | 5.9677 | 0.9946 | −1396.4 | 28.013 |
| 303.20 | 7.0000 | 77.778 | 300.83 | 5.5521 | 6.9617 | 0.9945 | −1382.6 | 28.013 |
| 303.20 | 8.0000 | 88.723 | 299.07 | 5.5067 | 7.9572 | 0.9947 | −1370.5 | 28.013 |
| 303.20 | 9.0000 | 99.580 | 297.38 | 5.4660 | 8.9551 | 0.9950 | −1359.9 | 28.013 |
| 303.20 | 10.000 | 110.34 | 295.75 | 5.4292 | 9.9561 | 0.9956 | −1350.4 | 28.013 |
| 303.20 | 11.000 | 120.98 | 294.19 | 5.3955 | 10.961 | 0.9964 | −1341.7 | 28.013 |
| 303.20 | 12.000 | 131.49 | 292.70 | 5.3645 | 11.970 | 0.99750 | −1333.8 | 28.013 |
| Gas Pressure (MPa) | Applied Stress (MPa) | Gas Type | Absolute Adsorption Content (mol/g) | (g/cm3) | Adsorption Constant (MPa−1) | Modulus of Elasticity (GPa) | Effective Stress Coefficient | |
|---|---|---|---|---|---|---|---|---|
| 6 | 8 | CO2 | 1.01 | 1.5 | 0.68 | 4.5 | 0.32 | 0.92 |
| 10 | CO2 | 0.86 | 0.68 | |||||
| 8 | N2 | 0.29 | 0.45 | |||||
| 10 | N2 | 0.24 | 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Z.; Chen, T.; Hu, S.; Du, Y.; Gao, F.; He, P.; Huang, Q.; Yan, S.; Li, N. Thermodynamic Method for Evaluating the Gas Adsorption-Induced Swelling of Confined Coal: Implication for CO2 Geological Sequestration. Processes 2025, 13, 1504. https://doi.org/10.3390/pr13051504
Du Z, Chen T, Hu S, Du Y, Gao F, He P, Huang Q, Yan S, Li N. Thermodynamic Method for Evaluating the Gas Adsorption-Induced Swelling of Confined Coal: Implication for CO2 Geological Sequestration. Processes. 2025; 13(5):1504. https://doi.org/10.3390/pr13051504
Chicago/Turabian StyleDu, Zhigang, Tianxiang Chen, Shuigen Hu, Yanqiang Du, Fuqiang Gao, Pengli He, Qiang Huang, Shaoyang Yan, and Ning Li. 2025. "Thermodynamic Method for Evaluating the Gas Adsorption-Induced Swelling of Confined Coal: Implication for CO2 Geological Sequestration" Processes 13, no. 5: 1504. https://doi.org/10.3390/pr13051504
APA StyleDu, Z., Chen, T., Hu, S., Du, Y., Gao, F., He, P., Huang, Q., Yan, S., & Li, N. (2025). Thermodynamic Method for Evaluating the Gas Adsorption-Induced Swelling of Confined Coal: Implication for CO2 Geological Sequestration. Processes, 13(5), 1504. https://doi.org/10.3390/pr13051504





