Load Restoration Based on Improved Girvan–Newman and QTRAN-Alt in Distribution Networks
Abstract
1. Introduction
- A community discovery-based decentralized partially observable Markov decision process (Dec-POMDP) model is proposed, thereby significantly expanding the application capability of MARL in complex distribution network load restoration scenarios.
- A distribution network restoration structure based on the QTRAN-alt algorithm is proposed, where counterfactual analysis is employed to rapidly identify optimal actions during MARL training. This approach effectively accelerates the convergence of MARL in large-scale distribution networks while ensuring the correctness of actions.
- The effectiveness of our approach is demonstrated through practical applications. In terms of key performance indicators such as convergence speed and recovery success rate, our approach surpasses comparison methods.
2. Proposed Load Restoration Method
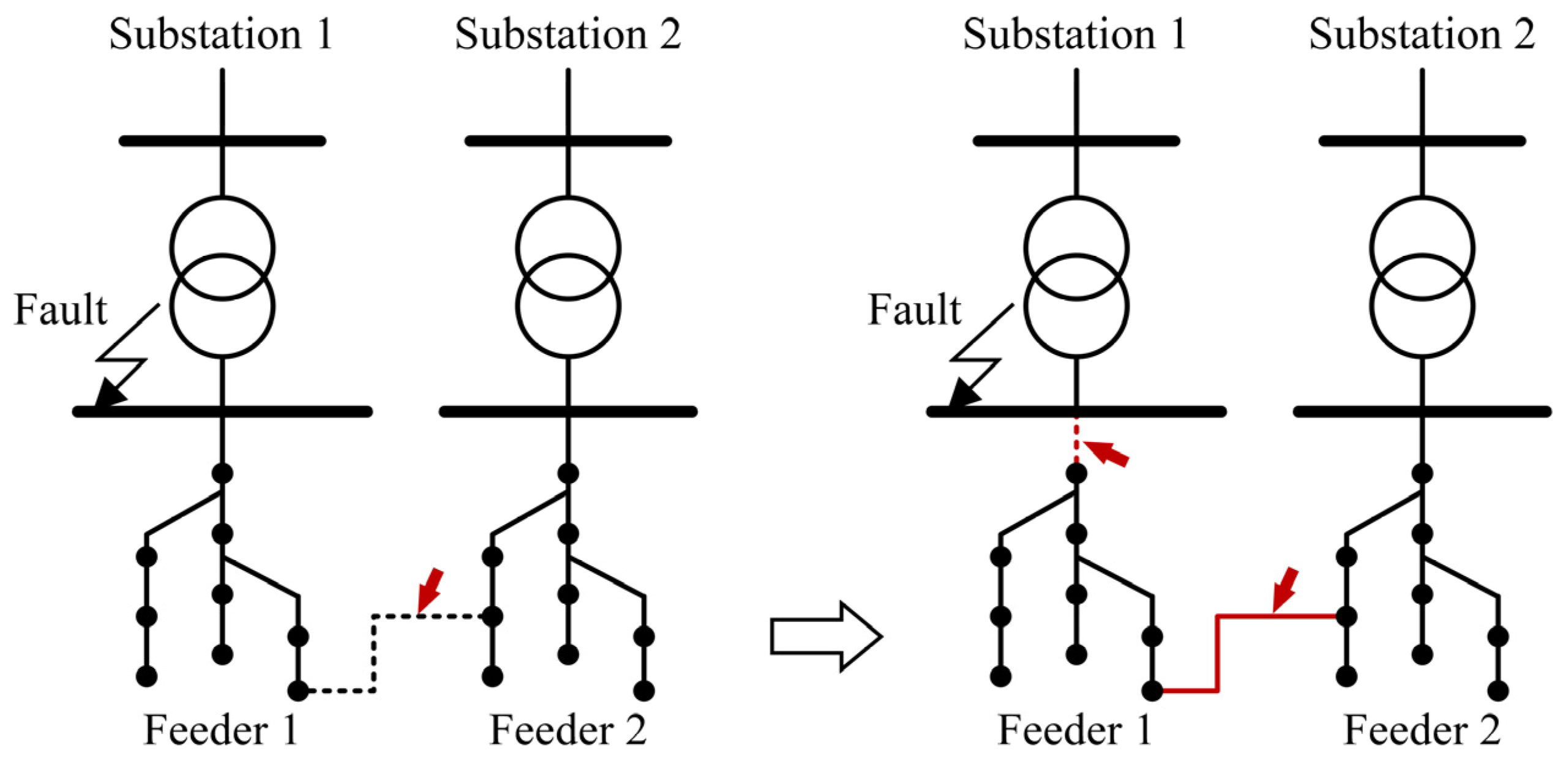
2.1. Load Restoration Model
2.2. Improved Girvan–Newman Community Detection Method
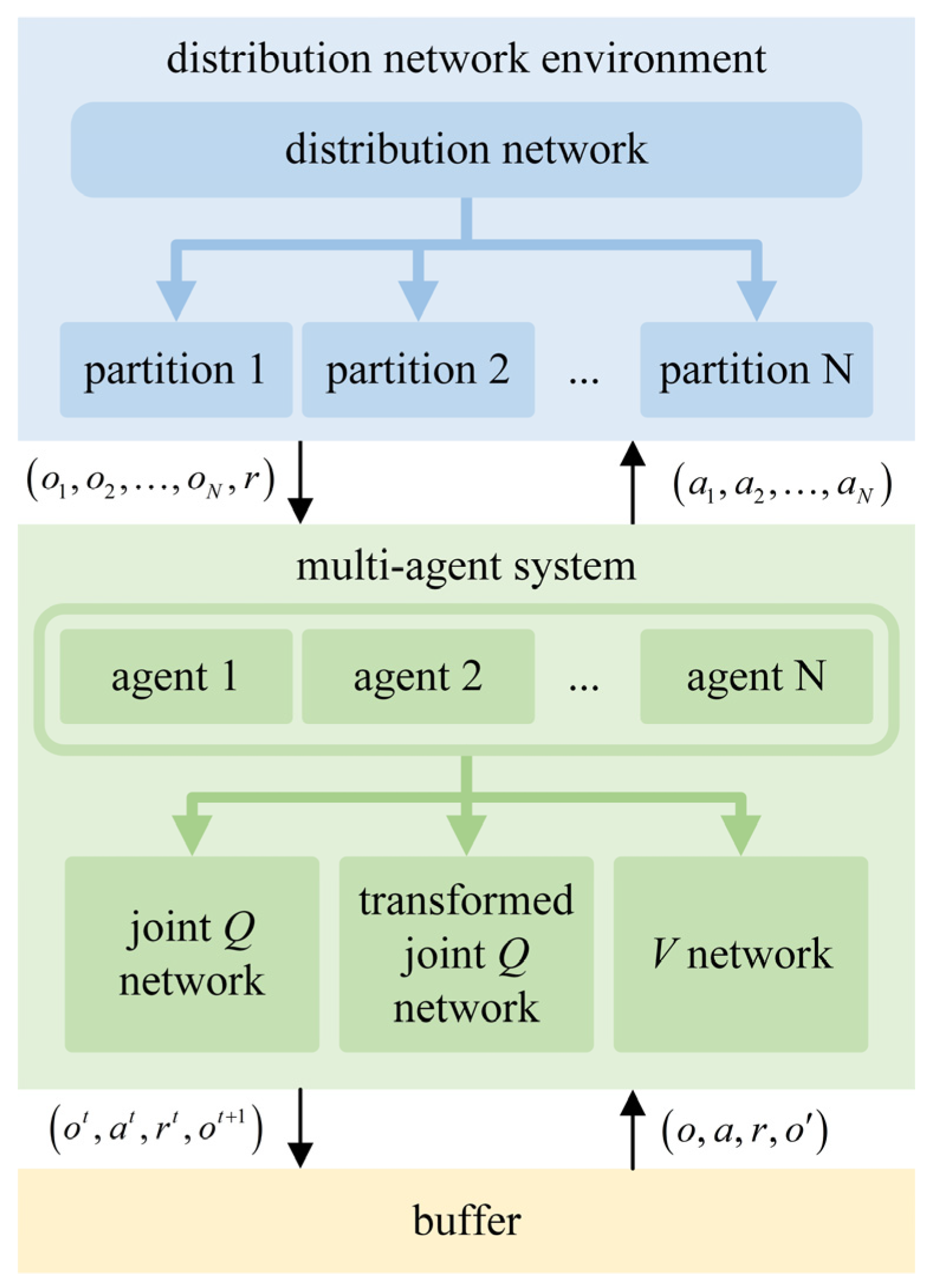
2.3. Dec-POMDP Model for Load Restoration
- 1.
- State space : the state space must fully represent the information of the environment, which is defined as follows:
- 2.
- Joint action space : with the action space of each agent denoted as , the joint action space can be defined as . In the distribution network load restoration scenario, the action space for each agent is defined as follows:
- 3.
- State transition probability distribution : the probability of the environment transitioning from state to state under the joint action is denoted by . In the distribution network load restoration problem, the next state after applying a given action to the grid is deterministic, so it is fixed as .
- 4.
- Reward function : at time , the reward value can be calculated by the state at time , the joint action at time and the state at time . According to the Equation (1) in Section 2.1, the reward function can be defined as follows:
- 5.
- Joint observation space : with the observation space of each agent denoted as , then the joint observation space can be defined as . The observation space for each agent depends on the state space and joint action space and is represented as . Thus, the observation space for each agent can be defined as follows:
3. Load Restoration Structure Based on QTRAN-Alt
3.1. MARL Value Functions Decomposition
3.2. QTRAN-Alt Loss Function
3.3. Load Restoration Structure
4. Experimental Study
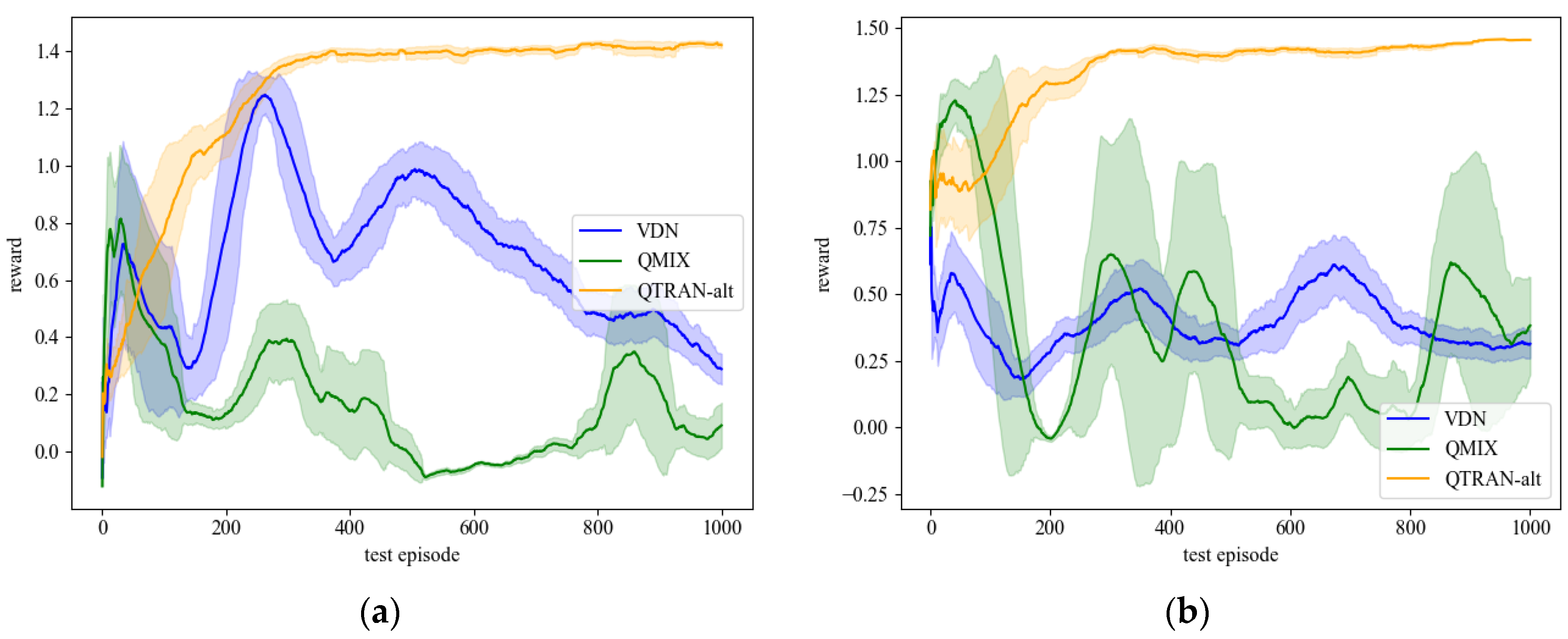
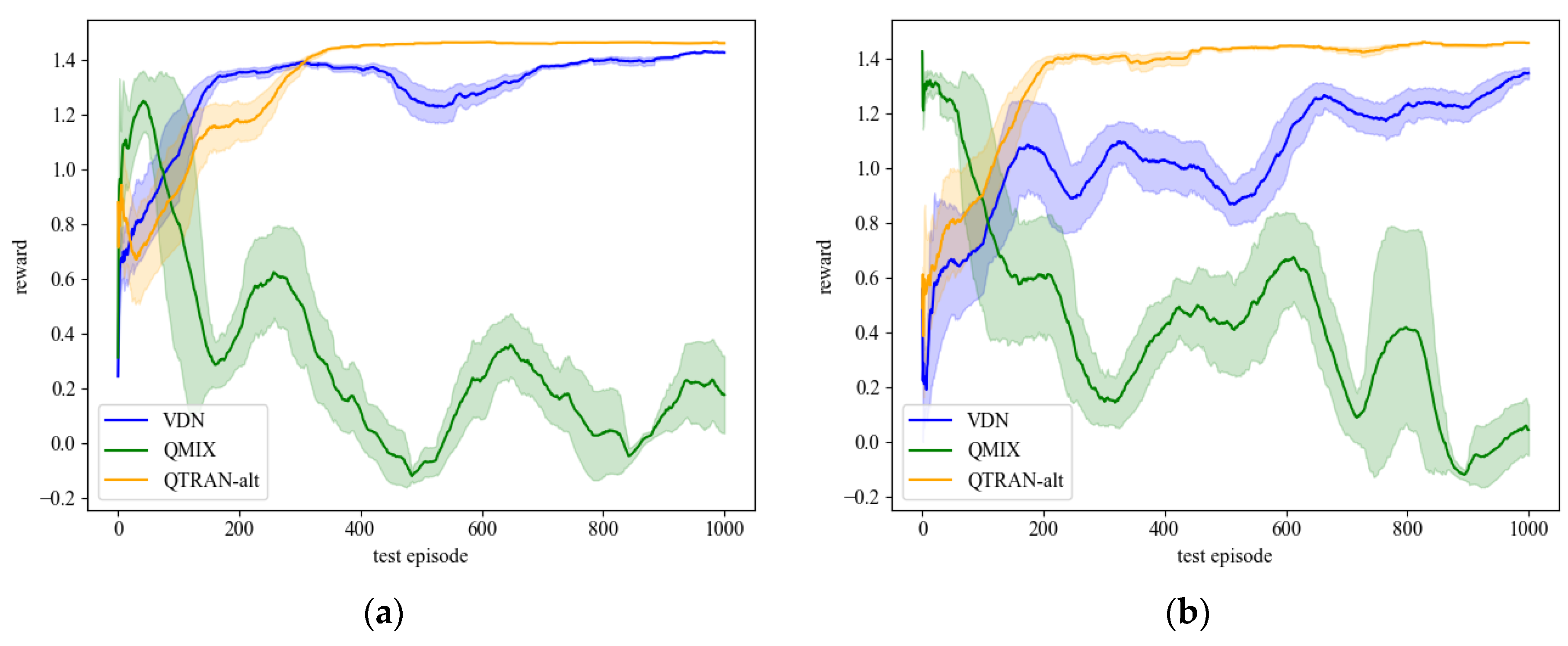
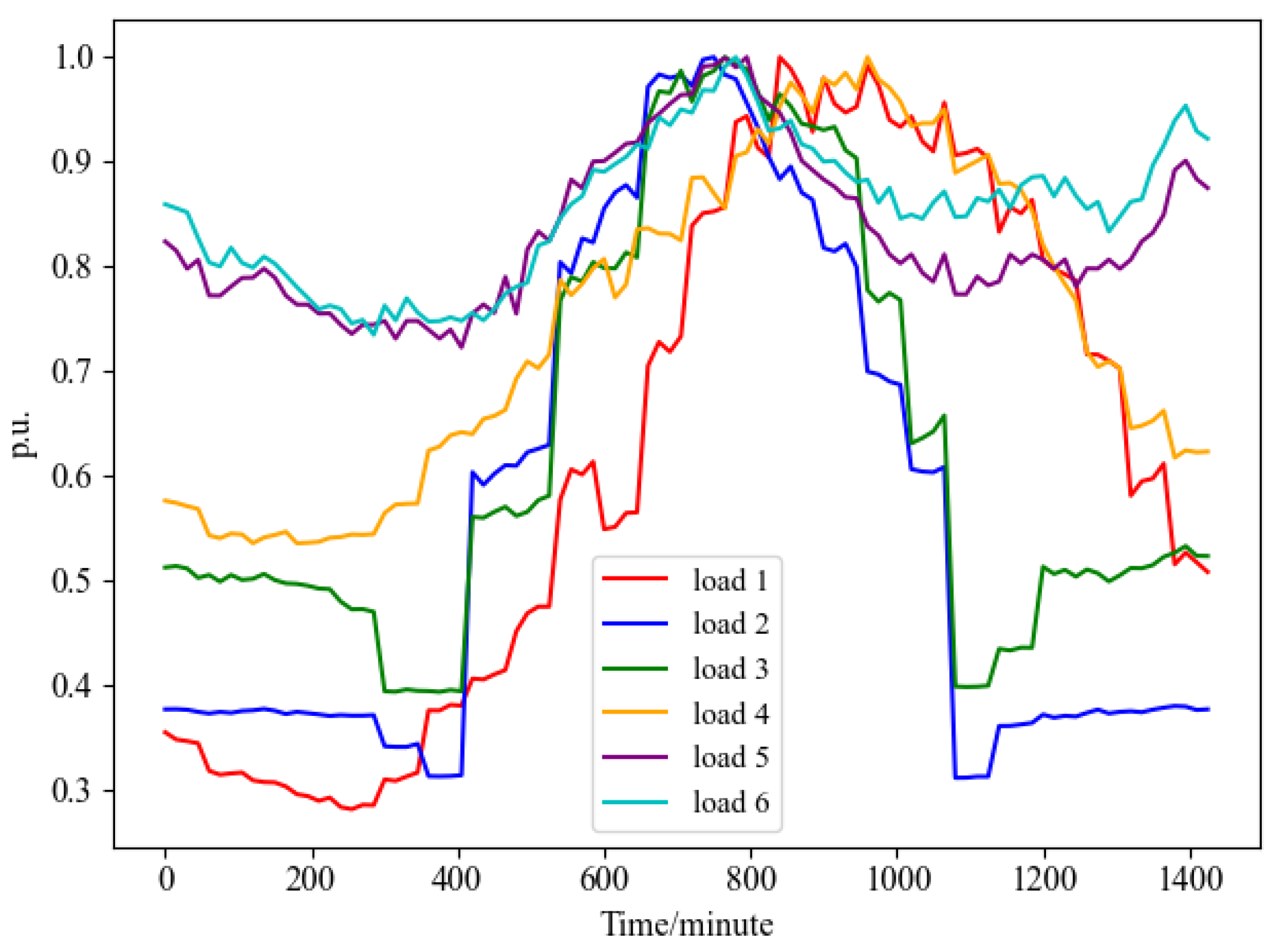
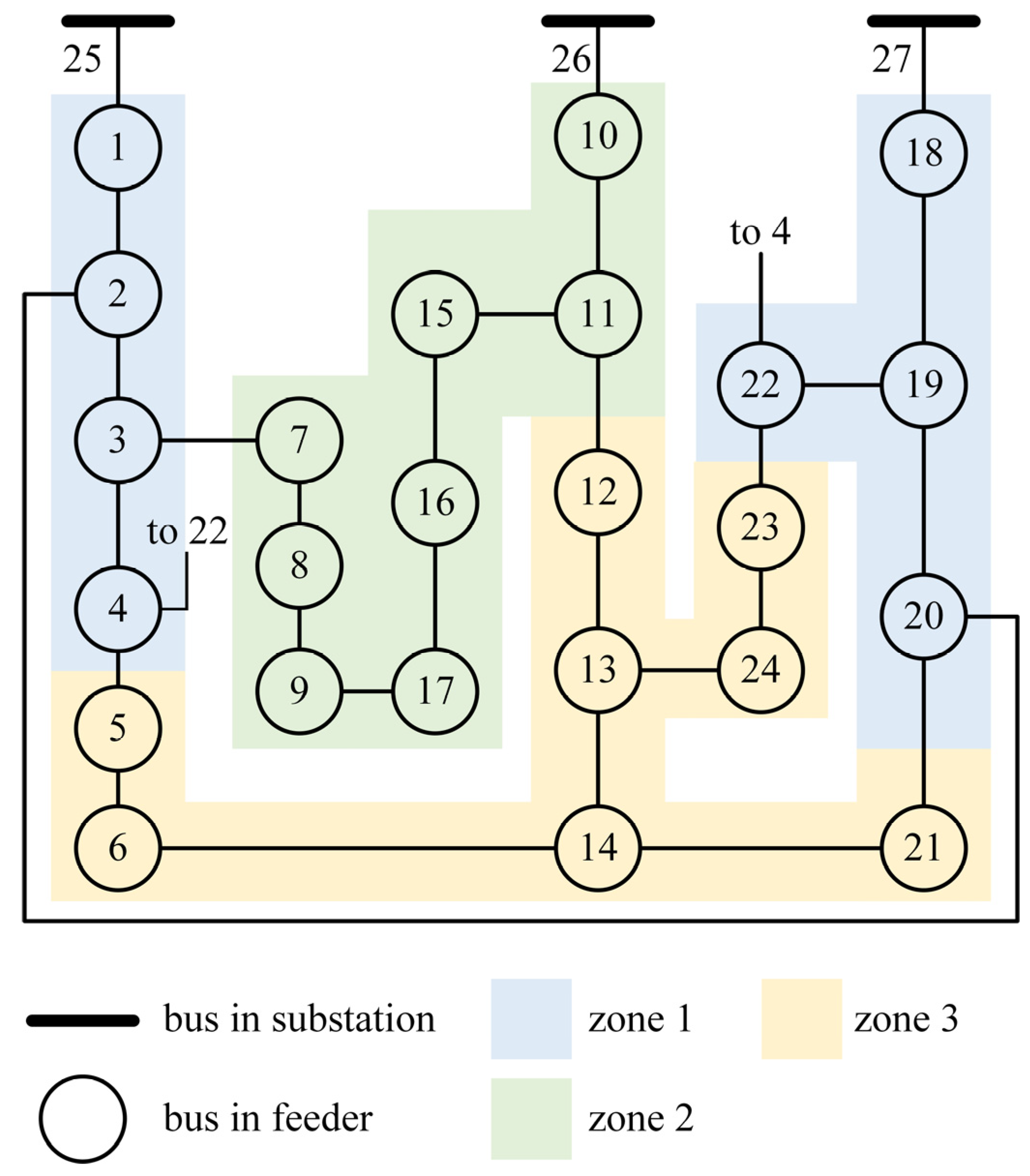
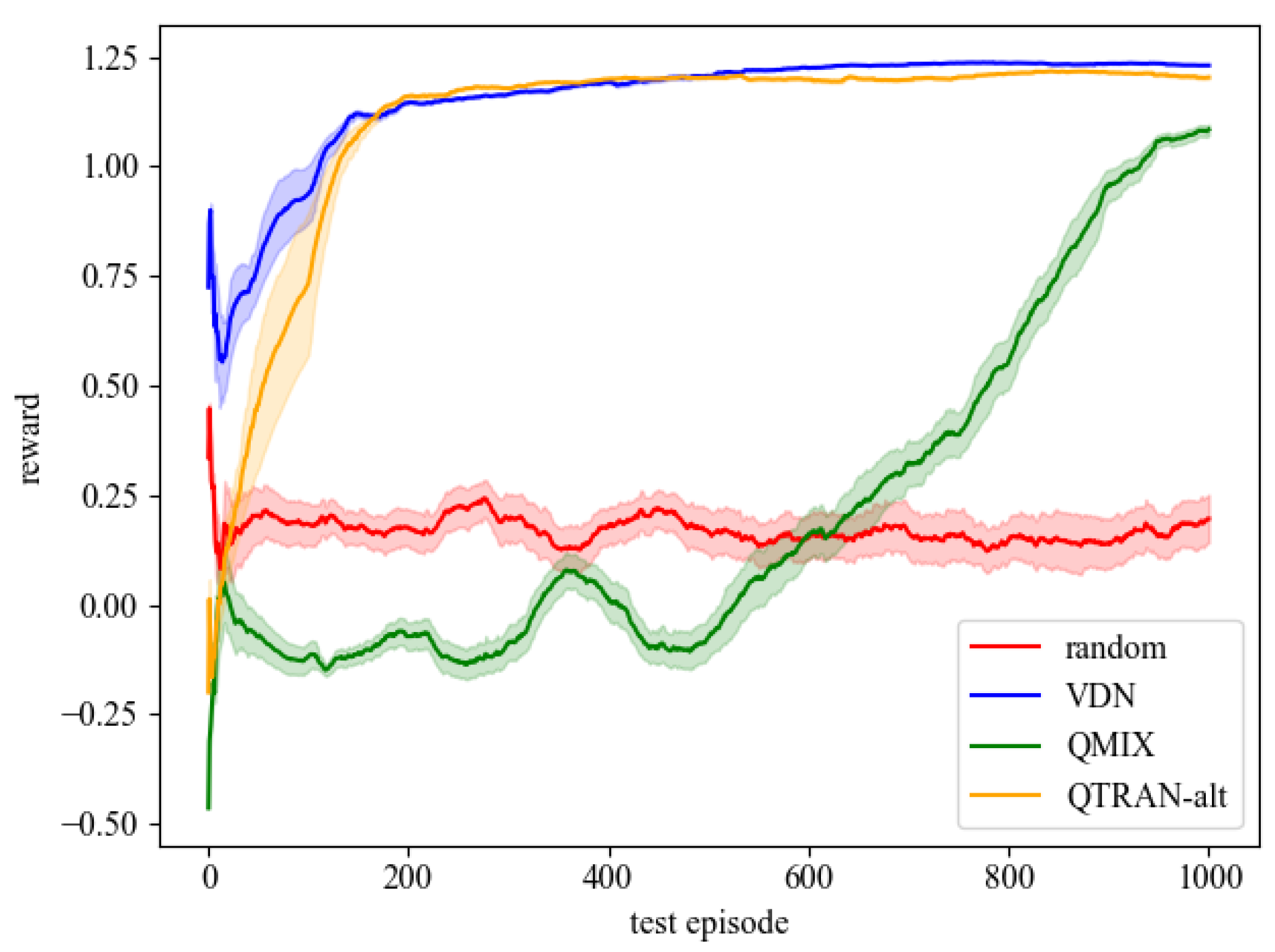
4.1. Load Restoration Experiments in the 27-Bus System
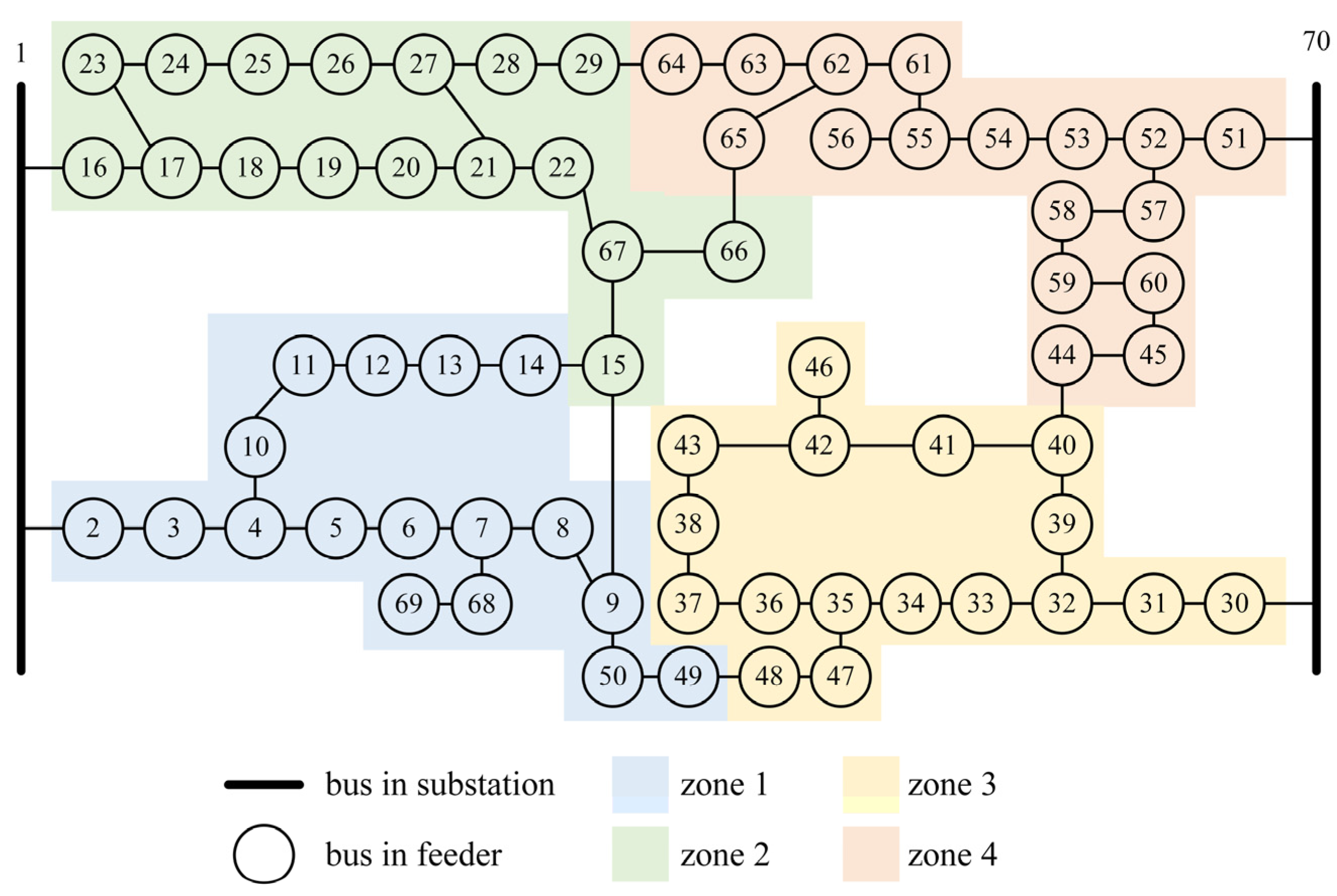
4.2. Load Restoration Experiments in the 70-Bus System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Tong, H.; Zeng, X.; Yu, K.; Zhou, Z. A Fault Identification Method for Animal Electric Shocks Considering Unstable Contact Situations in Low-Voltage Distribution Grids. In IEEE Transactions on Industrial Informatics; IEEE: New York, NY, USA, 2025; pp. 1–12. [Google Scholar] [CrossRef]
- Arif, A.; Cui, B.; Wang, Z. Switching Device-Cognizant Sequential Distribution System Restoration. IEEE Trans. Power Syst. 2022, 37, 317–329. [Google Scholar] [CrossRef]
- Heydt, G.T. The Next Generation of Power Distribution Systems. IEEE Trans. Smart Grid 2010, 1, 225–235. [Google Scholar] [CrossRef]
- Li, X.; Hu, C.; Luo, S.; Lu, H.; Piao, Z.; Jing, L. Distributed Hybrid-Triggered Observer-Based Secondary Control of Multi-Bus DC Microgrids Over Directed Networks. IEEE Trans. Circuits Syst. Regul. Pap. 2025, 1–14. [Google Scholar] [CrossRef]
- Li, J.; Ma, X.-Y.; Liu, C.-C.; Schneider, K.P. Distribution System Restoration with Microgrids Using Spanning Tree Search. IEEE Trans. Power Syst. 2014, 29, 3021–3029. [Google Scholar] [CrossRef]
- Xia, Y.; Li, Z.; Xi, Y.; Wu, G.; Peng, W.; Mu, L. Accurate Fault Location Method for Multiple Faults in Transmission Networks Using Travelling Waves. IEEE Trans. Ind. Inform. 2024, 20, 8717–8728. [Google Scholar] [CrossRef]
- Arif, A.; Wang, Z. Service Restoration in Resilient Power Distribution Systems with Networked Microgrid. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Poudel, S.; Dubey, A. A Graph-Theoretic Framework for Electric Power Distribution System Service Restoration. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Momen, H.; Jadid, S. Resilience Enhancement of Power Distribution System Using Fixed and Mobile Emergency Generators Based on Deep Reinforcement Learning. Eng. Appl. Artif. Intell. 2024, 137, 109118. [Google Scholar] [CrossRef]
- Xie, H.; Tang, L.; Zhu, H.; Cheng, X.; Bie, Z. Robustness Assessment and Enhancement of Deep Reinforcement Learning-Enabled Load Restoration for Distribution Systems. Reliab. Eng. Syst. Saf. 2023, 237, 109340. [Google Scholar] [CrossRef]
- Jo, S.; Oh, J.-Y.; Yoon, Y.T.; Jin, Y.G. Self-Healing Radial Distribution Network Reconfiguration Based on Deep Reinforcement Learning. Results Eng. 2024, 22, 102026. [Google Scholar] [CrossRef]
- Mohammed, N. Mathematics of Reinforcement Learning and Handling of the Curse of Dimensionality. In Proceedings of the Mathematical Sciences Conference, African Institute for Mathematical Science, Cape Town, South Africa, 11–12 June 2019. [Google Scholar]
- Wang, Y.; Qiu, D.; Teng, F.; Strbac, G. Towards Microgrid Resilience Enhancement via Mobile Power Sources and Repair Crews: A Multi-Agent Reinforcement Learning Approach. IEEE Trans. Power Syst. 2024, 39, 1329–1345. [Google Scholar] [CrossRef]
- Vu, L.; Vu, T.; Vu, T.L.; Srivastava, A. Multi-Agent Deep Reinforcement Learning for Distributed Load Restoration. IEEE Trans. Smart Grid 2024, 15, 1749–1760. [Google Scholar] [CrossRef]
- Fan, B.; Liu, X.; Xiao, G.; Kang, Y.; Wang, D.; Wang, P. Attention-Based Multiagent Graph Reinforcement Learning for Service Restoration. IEEE Trans. Artif. Intell. 2024, 5, 2163–2178. [Google Scholar] [CrossRef]
- Si, R.; Chen, S.; Zhang, J.; Xu, J.; Zhang, L. A Multi-Agent Reinforcement Learning Method for Distribution System Restoration Considering Dynamic Network Reconfiguration. Appl. Energy 2024, 372, 123625. [Google Scholar] [CrossRef]
- Correia, A.F.M.; Cavaleiro, M.; Neves, M.; Coimbra, A.P.; Almeida, T.R.O.; Moura, P.; De Almeida, A.T. Architecture and Operational Control for Resilient Microgrids. In Proceedings of the 2024 IEEE/IAS 60th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, USA, 19 May 2024; pp. 1–12. [Google Scholar]
- Hamidieh, M.; Ghassemi, M. Microgrids and Resilience: A Review. IEEE Access 2022, 10, 106059–106080. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Son, K.; Kim, D.; Kang, W.J.; Hostallero, D.E.; Yi, Y. QTRAN: Learning to Factorize with Transformation for Cooperative Multi-Agent Reinforcement Learning. International conference on machine learning. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 1–10 May 2019. [Google Scholar]
- Das, D. Reconfiguration of Distribution System Using Fuzzy Multi-Objective Approach. Int. J. Electr. Power Energy Syst. 2006, 28, 331–338. [Google Scholar] [CrossRef]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-Decomposition Networks for Cooperative Multi-Agent Learning. arXiv 2017, arXiv:1706.05296. [Google Scholar]
- Rashid, T.; Samvelyan, M.; Witt, C.S.; de Farquhar, G.; Foerster, J.; Whiteson, S. Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. J. Mach. Learn. Res. 2020, 21, 1–51. [Google Scholar]
- Thurner, L.; Scheidler, A.; Schafer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An Open-Source Python Tool for Convenient Modeling, Analysis, and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]




| Case No. | Bus | Feeder | Line | Load | Generator |
|---|---|---|---|---|---|
| 1 | 27 | 3 | 30 | 24 | 3 |
| 2 | 70 | 4 | 76 | 68 | 2 |
| Parameter | Value |
|---|---|
| 0.99 | |
| hidden size for each agent | 64 |
| hidden size for mixing network | 32 |
| hidden size for state value network | 64 |
| learning rate | 5 × 10−4 |
| epsilon | 0.5 |
| decreased epsilon every episode | 0.00064 |
| minimum epsilon | 0.02 |
| batch size | 32 |
| buffer size | 5 × 103 |
| 1 | |
| 1 |
| Partitioning Method | Algorithm | Rate (%) |
|---|---|---|
| Random | random | 35.08 |
| VDN | 98.34 | |
| QMIX | 39.41 | |
| QTRAN-alt | 96.87 | |
| Improved Girvan–Newman | random | 83.58 |
| VDN | 97.85 | |
| QMIX | 77.91 | |
| QTRAN-alt | 99.73 |
| Partitioning Method | Algorithm | Rate (%) |
|---|---|---|
| Random | random | 1.40 |
| VDN | 6.23 | |
| QMIX | 1.04 | |
| QTRAN-alt | 23.95 | |
| Improved Girvan–Newman | random | 31.96 |
| VDN | 58.01 | |
| QMIX | 64.57 | |
| QTRAN-alt | 96.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Sun, Q.; Huang, J.; Ma, S.; Wang, Y.; Chen, H.; Mi, H.; Chen, J.; Gao, T. Load Restoration Based on Improved Girvan–Newman and QTRAN-Alt in Distribution Networks. Processes 2025, 13, 1473. https://doi.org/10.3390/pr13051473
Zhang C, Sun Q, Huang J, Ma S, Wang Y, Chen H, Mi H, Chen J, Gao T. Load Restoration Based on Improved Girvan–Newman and QTRAN-Alt in Distribution Networks. Processes. 2025; 13(5):1473. https://doi.org/10.3390/pr13051473
Chicago/Turabian StyleZhang, Chao, Qiao Sun, Jiakai Huang, Shiqian Ma, Yan Wang, Hao Chen, Hanning Mi, Jiuxiang Chen, and Tianlu Gao. 2025. "Load Restoration Based on Improved Girvan–Newman and QTRAN-Alt in Distribution Networks" Processes 13, no. 5: 1473. https://doi.org/10.3390/pr13051473
APA StyleZhang, C., Sun, Q., Huang, J., Ma, S., Wang, Y., Chen, H., Mi, H., Chen, J., & Gao, T. (2025). Load Restoration Based on Improved Girvan–Newman and QTRAN-Alt in Distribution Networks. Processes, 13(5), 1473. https://doi.org/10.3390/pr13051473





