Machine Learning-Based Impact of Rotational Speed on Mixing, Mass Transfer, and Flow Parameter Prediction in Solid–Liquid Stirred Tanks
Abstract
1. Introduction
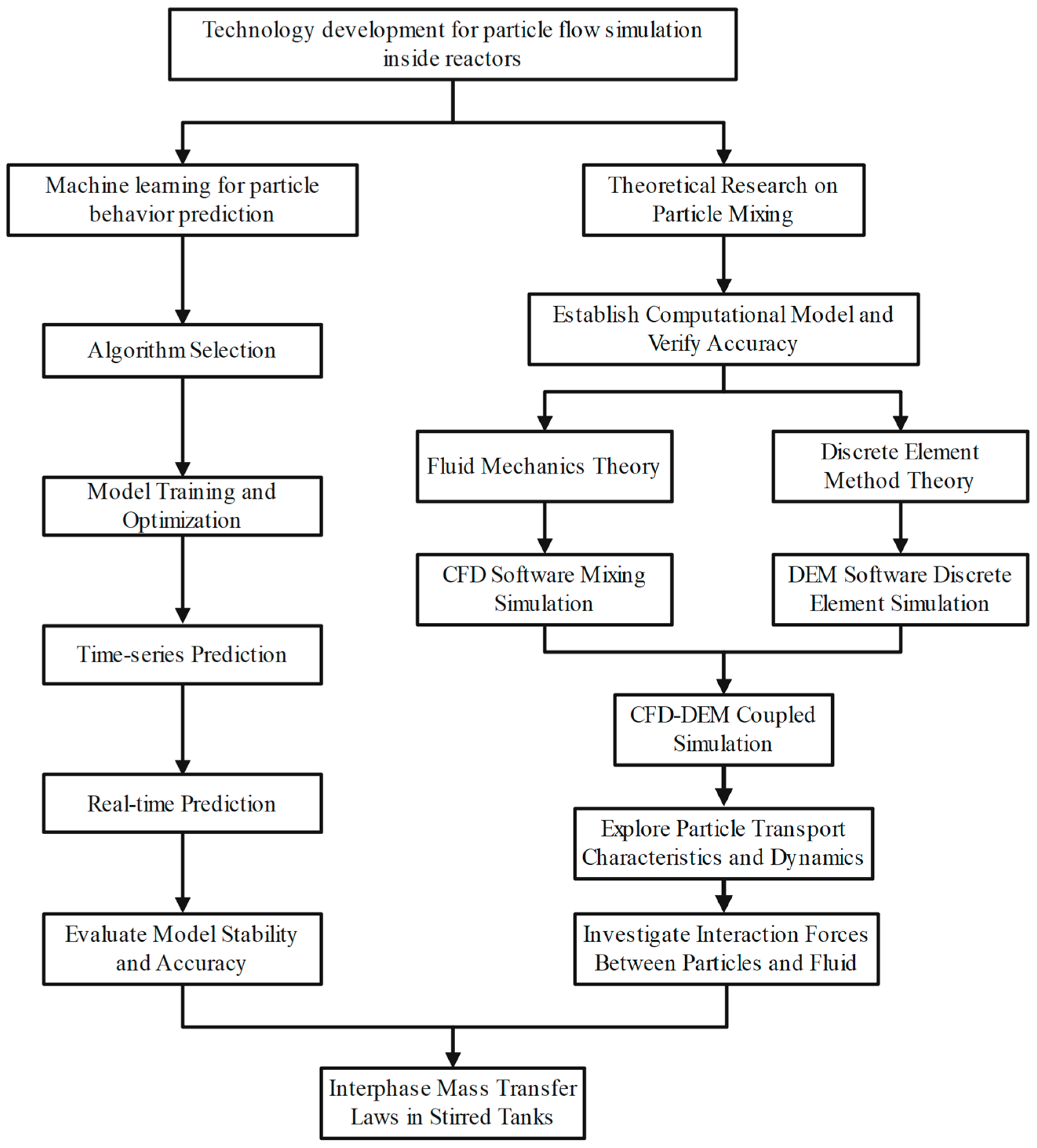
2. Materials and Methods
2.1. Numerical Model
2.1.1. Governing Equations
2.1.2. CFD-DEM Coupling
2.2. Analysis Methods
2.2.1. Particle Dynamics
2.2.2. Mass Transfer Characteristics
2.2.3. Prediction Performance Metrics
2.3. Model Validation
2.4. Prediction Models
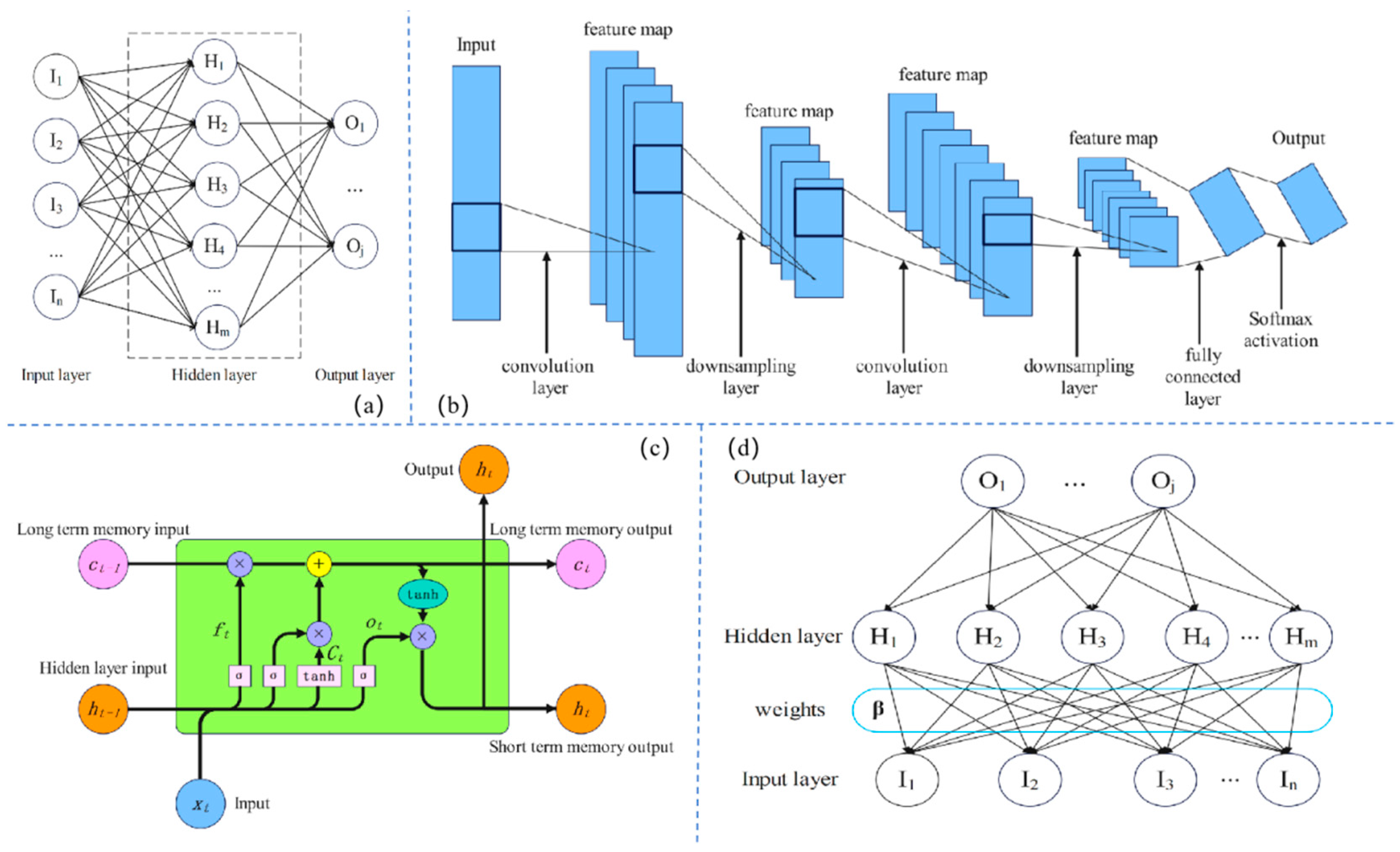
2.4.1. ML Algorithms for Stirred Tanks
2.4.2. Genetic Algorithm
2.4.3. Training Algorithms
2.4.4. PINN Method
3. Results
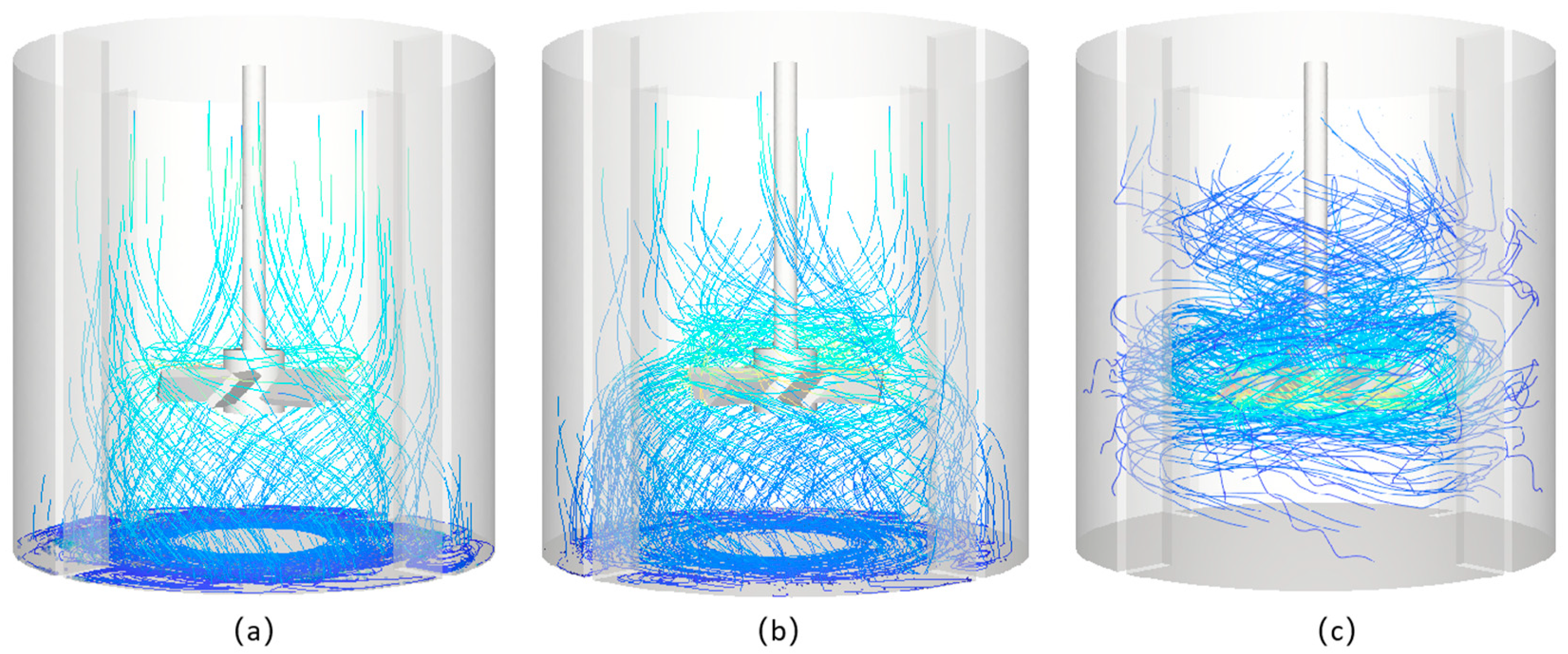
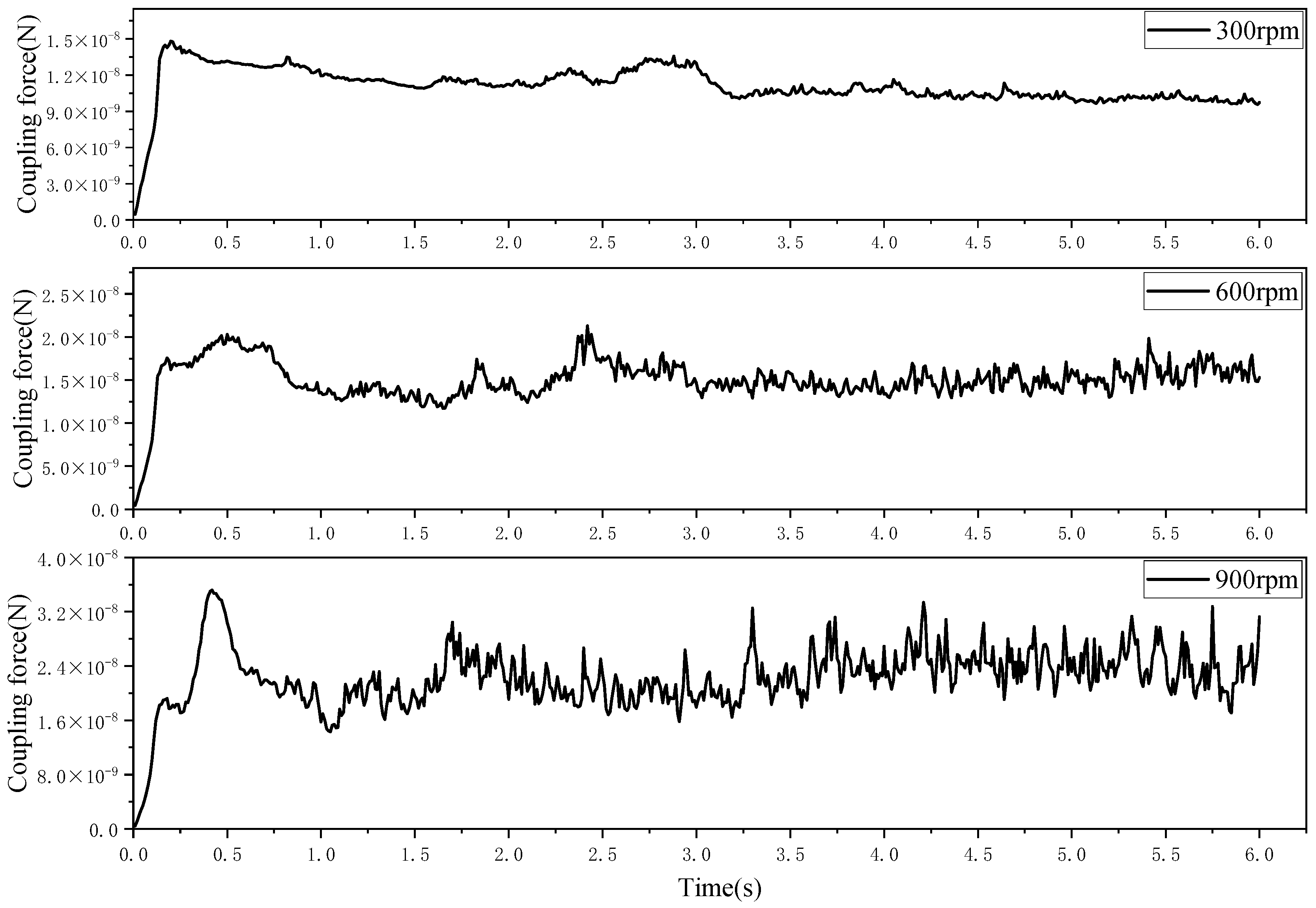
3.1. Particle Dynamics
3.1.1. Particle Size Effects
3.1.2. Impeller Speed Effects
3.1.3. Time-Series Prediction
3.2. Mass Transfer
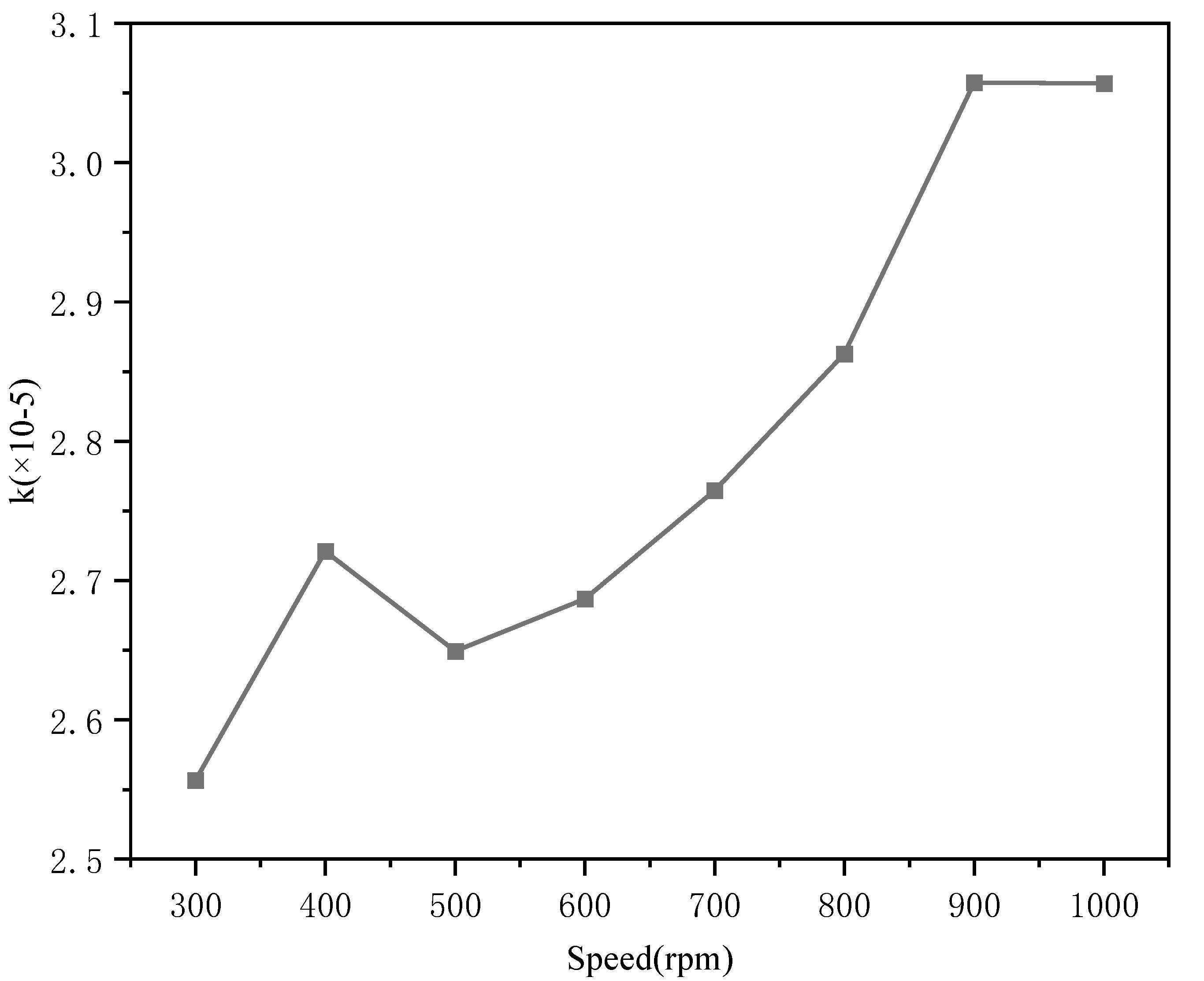
3.2.1. Speed Dependency
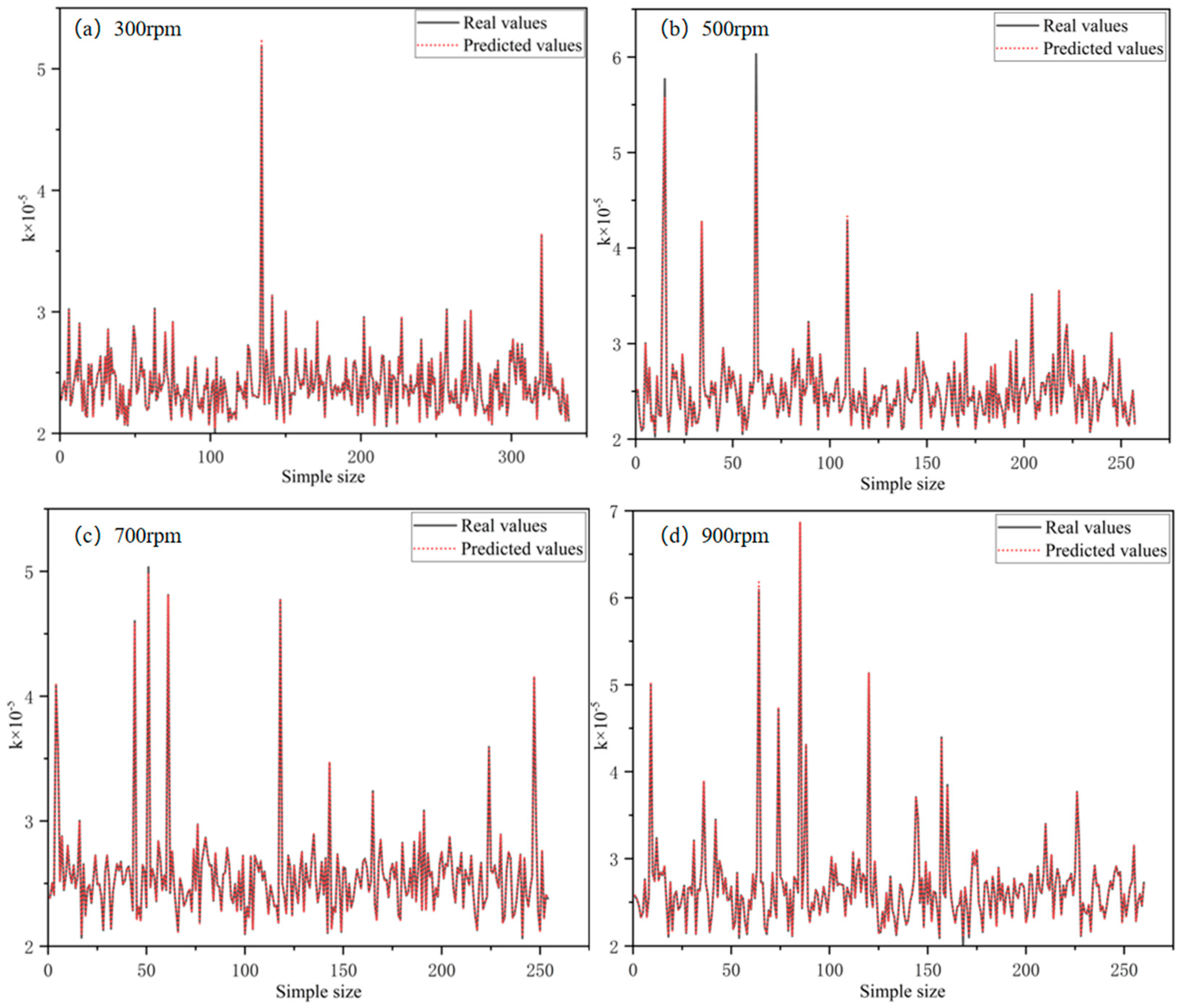
3.2.2. ML Prediction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| mass of the particle (g) | |
| gravitational acceleration (m·s−2) | |
| interparticle contact force (N) | |
| angular velocity (rad·s−1) | |
| moment of inertia tensor of the particle (kg·m2) | |
| net torque on the particle (N·m) | |
| fluid-phase interaction force (N) | |
| additional fluid-phase torque (N·m) | |
| drag force (N) | |
| non-drag forces (N) | |
| pressure gradient force (N) | |
| added (virtual) mass force (N) | |
| lift force (N) | |
| relative particle Reynolds number | |
| T | stirred tank height (mm) |
| H | stirred tank width (mm) |
| D | impeller diameter (mm) |
| d | hub diameter (mm) |
| C | impeller off-bottom clearance (mm) |
| w | blade width (mm) |
| b | blade length (mm) |
| kSL | mass transfer coefficient |
| Sherwood number | |
| diffusivity (m2·s−1) | |
| characteristic length (m) | |
| dynamic viscosity (N·s·m−2) | |
| density (kg·m−2) |
References
- Peng, H.; Zhou, Q.; Liu, H.P.; Huang, X.Y.; Liu, Y.L.; Ran, C.E.; Pan, W.J. Research Progress on Vanadium Extraction Technology from Vanadium Slag. Acta. Petrol. Mineral. 2025, 44, 216–226. [Google Scholar]
- Gharabaghi, M.; Azadmehr, A.; Aghazadeh, S.; Pourabdoli, M. Clean Practical Method for Cadmium Recycling from Toxic Material and Optimization of Recycling Process. JOM 2022, 74, 1945–1957. [Google Scholar] [CrossRef]
- Karacahan, M.K. Optimization and Kinetic Study of Manganese Leaching from Pyrolusite Ore in Hydrochloric Acid Solutions with Oxalic Acid. J. Sustain. Met. 2024, 10, 1717–1732. [Google Scholar] [CrossRef]
- Ismail, N.I.; Kuang, S.; Yu, A. CFD-DEM study of particle-fluid flow and retention performance of sand screen. Powder Technol. 2021, 378, 410–420. [Google Scholar] [CrossRef]
- Gu, D.; Ye, M.; Liu, Z. Computational fluid dynamics simulation of solid-liquid suspension characteristics in a stirred tank with punched circle package impellers. Int. J. Chem. React. Eng. 2020, 18, 20200026. [Google Scholar] [CrossRef]
- Xia, D.; Mao, Z.J.; Zhou, S.Q.; He, X.; Wang, Y.X. Optimized Design of Solid-Liquid Dual-Impeller Mixing Systems for Enhanced Efficiency. ACS Omega 2023, 8, 47635–47645. [Google Scholar] [CrossRef]
- Kohnen, C.; Bohnet, M. Measurement and simulation of fluid flow in agitated solid/liquid suspensions. Chem. Eng. Technol. 2001, 24, 639–643. [Google Scholar] [CrossRef]
- Gu, D.; Li, C.; Gu, X.; Wang, J. Solid-liquid mixing characteristics in a fractal cut impeller stirred reactor with dense solid loading. Chem. Eng. Process.-Process. Intensif. 2024, 196, 109655. [Google Scholar] [CrossRef]
- Sommer, A.E.; Rox, H.; Shi, P.; Eckert, K.; Rzehak, R. Solid-liquid flow in stirred tanks: “CFD-grade” experimental investigation. Chem. Eng. Sci. 2021, 245, 116743. [Google Scholar] [CrossRef]
- Gu, D.; Xu, H.; Ye, M.; Wen, L. Design of impeller blades for intensification on fluid mixing process in a stirred tank. J. Taiwan Inst. Chem. Eng. 2022, 138, 104475. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Y.M.; Xue, N.N.; Zheng, Q. Numerical Simulation of Solid-Liquid Mixing Characteristics of Vanadium Shale with Stirring Tank Shape. Nonferrous Met. (Extr. Metall.) 2022, 11, 68–77. [Google Scholar]
- Basheer, A.A.; Bharathesh, K. Effect of baffle configuration on hydrodynamics and solid suspension in a continuous stirred vessel. Chem. Eng. Commun. 2021, 209, 1413–1422. [Google Scholar] [CrossRef]
- Li, S.; Yang, R.; Wang, C.; Shen, Y.; Wang, H. Simulation of the solid particles behavior in 3D stirred tank using CFD-DEM coupling approach. Part. Sci. Technol. 2022, 40, 911–921. [Google Scholar] [CrossRef]
- Luo, X.; Yu, J.; Wang, B.; Wang, J. Heat Transfer and Hydrodynamics in Stirred Tanks with Liquid-Solid Flow Studied by CFD–DEM Method. Processes 2021, 9, 849. [Google Scholar] [CrossRef]
- Wu, Y.K.; Li, Z.Q.; Wang, Y.; Xu, Z.; Li, K.; Shi, H. Research on Stirring Process Based on Artificial Neural Network and Multi-Phase Flow Simulation Technology. Nonferrous Met. Sci. Eng. 2024, 15, 801–813. [Google Scholar]
- Choong, C.E.; Ibrahim, S.; El-Shafie, A. Artificial Neural Network (ANN) model development for predicting just suspension speed in solid-liquid mixing system. Flow Meas. Instrum. 2020, 71, 101689. [Google Scholar] [CrossRef]
- Moya, J.D.; Molina, A.E.; Belmonte, J.F.; Córcoles-Tendero, J.I.; Almendros-Ibáñez, J.A. Characterization of a triple concentric-tube heat exchanger with corrugated tubes using Artificial Neural Networks (ANN). Appl. Therm. Eng. 2019, 147, 1036–1046. [Google Scholar] [CrossRef]
- Joshi, S.S.; Dalvi, V.H.; Vitankar, V.S.; Joshi, A.J.; Joshi, J.B. Novel Correlation for the Solid–Liquid Mass Transfer Coefficient in Stirred Tanks Developed by Interpreting Machine Learning Models Trained on Literature Data. Ind. Eng. Chem. Res. 2023, 62, 19920–19935. [Google Scholar] [CrossRef]
- Zhao, X.; Fan, H.; Lin, G.; Fang, Z.; Yang, W.; Li, M.; Wang, J.; Lu, X.; Li, B.; Wu, K.; et al. Multi-objective optimization of radially stirred tank based on CFD and machine learning. AIChE J. 2023, 70, 18324. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Z.; Li, S.; Du, Y. Machine learning analysis of pressure fluctuations in a gas-solid fluidized bed. Powder Technol. 2024, 444, 120065. [Google Scholar] [CrossRef]
- Song, Z.; Zou, S.; Zhou, W.; Huang, Y.; Shao, L.; Yuan, J.; Gou, X.; Jin, W.; Wang, Z.; Chen, X.; et al. Clinically applicable histopathological diagnosis system for gastric cancer detection using deep learning. Nat. Commun. 2020, 11, 4294. [Google Scholar] [CrossRef]
- Kabir, H.; Wu, J.; Dahal, S.; Joo, T.; Garg, N. Automated estimation of cementitious sorptivity via computer vision. Nat. Commun. 2024, 15, 9935. [Google Scholar] [CrossRef]
- Puderbach, V.; Schmidt, K.; Antonyuk, S. A Coupled CFD-DEM Model for Resolved Simulation of Filter Cake Formation during Solid-Liquid Separation. Processes 2021, 9, 826. [Google Scholar] [CrossRef]
- Jovanović, A.; Pezo, M.; Pezo, L.; Lević, L. DEM/CFD analysis of granular flow in static mixers. Powder Technol. 2014, 266, 240–248. [Google Scholar] [CrossRef]
- Jiang, H.; Yuan, S.; Liu, H.; Li, W.; Zhou, X. Numerical analysis and optimization of key parts in the stirred tank based on solid-liquid flow field. Sci. Prog. 2022, 105, 1–26. [Google Scholar] [CrossRef]
- Trinh, C.; Meimaroglou, D.; Hoppe, S. Machine Learning in Chemical Product Engineering: The State of the Art and a Guide for Newcomers. Processes 2021, 9, 1456. [Google Scholar] [CrossRef]
- Wu, Y.; Li, Z.; Zhang, B.; Chen, H.; Sun, Y. Multi-objective optimization of key parameters of stirred tank based on ANN-CFD. Powder Technol. 2024, 441, 119832. [Google Scholar] [CrossRef]
- Raikov, A.N.; Panfilov, S.A. Convergent Decision Support System with Genetic Algorithms and Cognitive Simulation. IFAC Proc. Vol. 2013, 46, 1108–1113. [Google Scholar] [CrossRef]
- Zhang, J.; Qu, S.; Lv, Z. Optimization of Backpropagation Neural Network under the Adaptive Genetic Algorithm. Complexity 2021, 2021, 1718234. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Kang, Q.; Feng, X.; Yang, C.; Wang, J. DEM-VOF simulations on the drawdown mechanisms of floating particles at free surface in turbulent stirred tanks. Chem. Eng. J. 2022, 431, 133275. [Google Scholar] [CrossRef]
- Li, M.; Zhang, L.; Li, C.; Wu, G.; An, X.; Zhang, H.; Fu, H.; Yang, X.; Zou, Q. Discrete Element Method–Volume of Fluid Simulation of Drawdown and Dispersion for Floating Particles in Stirred Tanks: Influences of Impeller Parameters. Ind. Eng. Chem. Res. 2024, 63, 10353–10372. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, C.; Sun, H.; Liu, W. Solid-liquid suspension in a stirred tank driven by an eccentric-shaft: Electrical resistance tomography measurement. Powder Technol. 2022, 411, 117943. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Wang, Q.Q.; An, A.M.; Tang, M.A.; Liu, J. Distributed nonlinear model predictive control for cobalt removal process in zinc hydrometallurgy considering error compensation modelling. Can. J. Chem. Eng. 2024, 102, 307–323. [Google Scholar] [CrossRef]
- Christudas, F.; Dhanraj, A.V. System Identification Using Long Short Term Memory Recurrent Neural Networks for Real Time Conical Tank System. Rom. J. Inf. Sci. Technol. 2020, 23, T57–T77. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Hoseini, S.; Rundquist, E.; Poux, M.; Aubin, J. Foam detection in a stirred tank using deep learning neural networks. Chem. Eng. Res. Des. 2024, 209, 346–357. [Google Scholar] [CrossRef]
- Zhong, W.M.; He, G.L.; Pi, D.Y.; Sun, Y.X. SVM with quadratic polynomial kernel function based nonlinear model one-step-ahead predictive control. Chin. J. Chem. Eng. 2005, 13, 373–379. [Google Scholar]
- Carletti, C.; Bikić, S.; Montante, G.; Paglianti, A. Mass Transfer in Dilute Solid-Liquid Stirred Tanks. Ind. Eng. Chem. Res. 2018, 57, 6505–6515. [Google Scholar] [CrossRef]
- Liu, B.; Dong, K.; Chen, R.-J.; Chang, S.-T.; Chu, G.-W.; Zhang, L.-L.; Zou, H.-K.; Sun, B.-C. Study on the Solid–Liquid Mass-Transfer Performance of Suspension in a Rotating Packed Bed. Ind. Eng. Chem. Res. 2023, 62, 8063–8070. [Google Scholar] [CrossRef]
- Moholkar, C.D.; Vala, S.V.; Mathpati, C.S.; Joshi, A.J.; Vitankar, V.S.; Joshi, J.B. Artificial intelligence-based correlation: Process side heat transfer coefficient for helical coils in stirred tank reactors. Heat Transf. 2022, 51, 3099–3125. [Google Scholar] [CrossRef]
- Zhang, Z.F.; Huang, Y.M.; Qin, R.; Ren, W.; Wen, G. XGBoost-based on-line prediction of seam tensile strength for Al-Li alloy in laser welding: Experiment study and modelling. J. Manuf. Process. 2021, 64, 30–44. [Google Scholar] [CrossRef]









| Material | Parameter | Unit | Value |
|---|---|---|---|
| Particles | Density | kg/m3 | 2500 |
| Young’s modulus | Dimensionless | 2 × 108 | |
| Poisson’s ratio | Dimensionless | 0.3 | |
| Fluid | Water density | kg/m3 | 992.8 |
| Water viscosity | Pa∙s | 0.001003 | |
| Air density | kg/m3 | 1.225 | |
| Air viscosity | Pa∙s | 1.7894 × 10−5 | |
| Particle–wall interaction | Static friction coefficient | Dimensionless | 0.3 |
| Rolling friction coefficient | Dimensionless | 0.3 | |
| Tangential stiffness ratio | Dimensionless | 1 | |
| Coefficient of restitution | Dimensionless | 0.3 | |
| Particle–particle interaction | Static friction coefficient | Dimensionless | 0.7 |
| Rolling friction coefficient | Dimensionless | 0.7 | |
| Tangential stiffness ratio | Dimensionless | 1 | |
| Coefficient of restitution | Dimensionless | 0.3 |
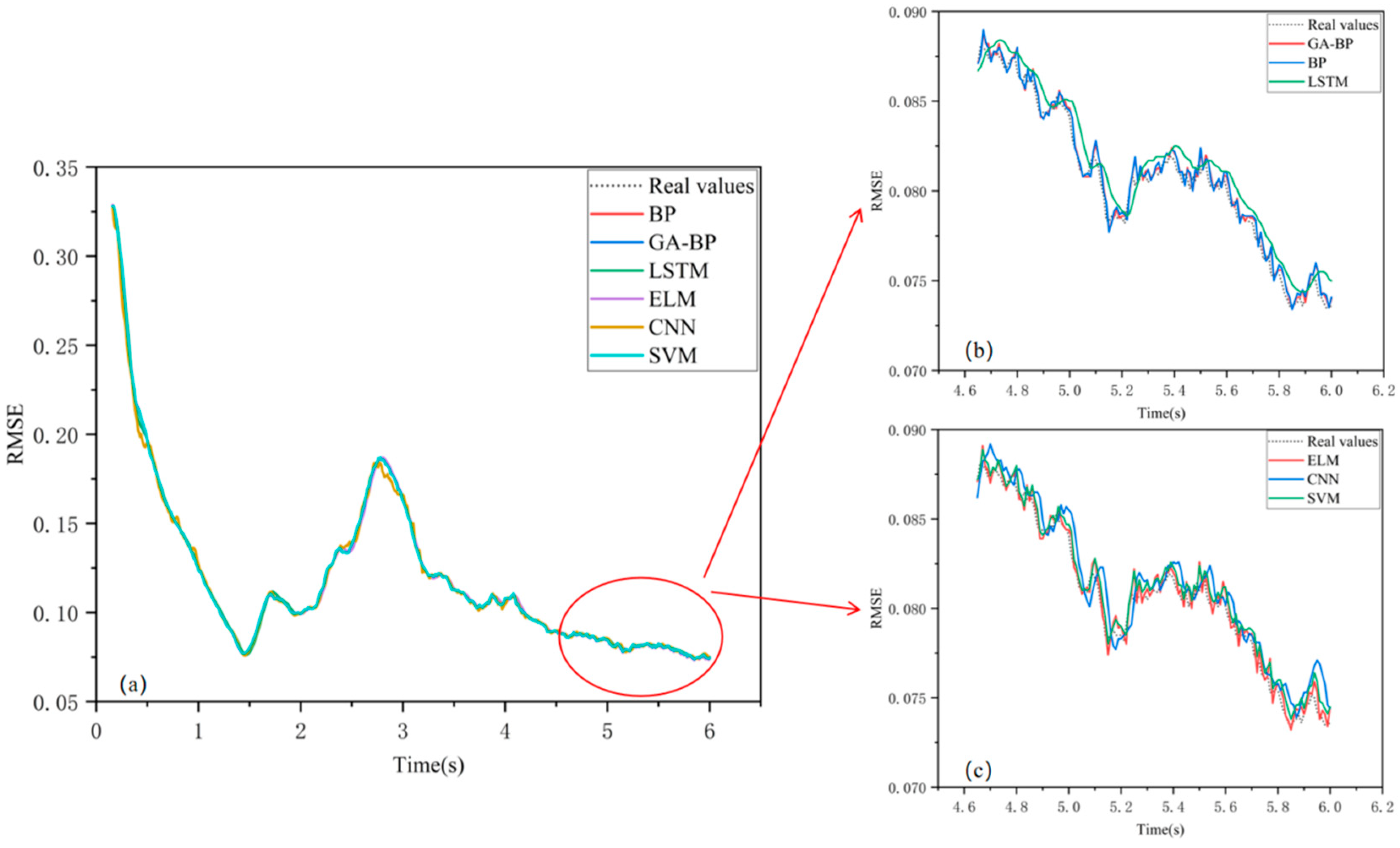
| Algorithm | R2 | R | MAE | MBE | RMSE | |
|---|---|---|---|---|---|---|
| BP | Training | 0.99986 | 0.99993 | 0.00041121 | 9.7225 × 10−6 | 0.00055297 |
| Test | 0.98006 | 0.98998 | 0.00046321 | 0.0002731 | 0.00058149 | |
| GA-BP | Training | 0.99985 | 0.99992 | 0.00042824 | 4.2143 × 10−6 | 0.00056754 |
| Test | 0.98223 | 0.99108 | 0.00043053 | 0.00024306 | 0.00054896 | |
| LSTM | Training | 0.99838 | 0.99919 | 0.0014657 | −2.604 × 10−5 | 0.001896 |
| Test | 0.93115 | 0.96496 | 0.00092888 | 0.00080094 | 0.0010804 | |
| ELM | Training | 0.99988 | 0.99994 | 0.00039456 | 9.5328 × 10−11 | 0.00051279 |
| Test | 0.97688 | 0.98837 | 0.00050124 | 0.00022597 | 0.00062618 | |
| CNN | Training | 0.99489 | 0.99744 | 0.0020812 | −0.00086056 | 0.003366 |
| Test | 0.92587 | 0.96222 | 0.00088106 | 0.00066994 | 0.0011212 | |
| SVM | Training | 0.99986 | 0.99993 | 0.00041974 | −3.8306 × 10−5 | 0.00055695 |
| Test | 0.97067 | 0.98523 | 0.00057967 | 0.00048397 | 0.0007052 |
| Algorithm | Core Mechanism | Difference in R | Advantages | Disadvantages | Applicable Scenarios |
|---|---|---|---|---|---|
| BP | Optimizing weights through backpropagation [36] | 0.00995 | Strong non-linear fitting ability and low error | Prone to getting stuck in local optima | Complex non-linear modeling |
| GA-BP | Optimizing initial weights using genetic algorithms [37] | 0.00884 | High fitting accuracy and strong generalization ability | High computational cost and requires GA optimization | Scenarios with high-precision requirements |
| LSTM | Capturing time-series dependencies via gating mechanisms [38] | 0.03423 | Good at capturing long-term dependencies in time-series data | Relatively large actual error | Short-term time-series prediction |
| ELM | Randomly initializing weights [39] | 0.01157 | No need for iterative parameter tuning and fast training speed | Limited generalization ability | Real-time response for condition monitoring |
| CNN | Handling spatial features [40] | 0.03522 | Good at processing spatial features | Poorest fitting degree | Edge detection in flow field graphics |
| SVM | Minimizing risk [41] | 0.0147 | Balancing accuracy and efficiency | Increasing computational complexity | Data evaluation for dynamic response |
| Rotational Speed (rpm) | Fluid Velocity (m/s) | Particle Velocity (m/s) | Relative Velocity (m/s) | Re | k (×10−5) |
|---|---|---|---|---|---|
| 300 | 0.0847 | 0.0738 | 0.0110 | 1.0913 | 2.5565 |
| 400 | 0.1058 | 0.0874 | 0.0184 | 1.8309 | 2.7209 |
| 500 | 0.1433 | 0.1283 | 0.0149 | 1.4854 | 2.6493 |
| 600 | 0.1733 | 0.1900 | 0.0167 | 1.6616 | 2.6867 |
| 700 | 0.1985 | 0.2192 | 0.0207 | 2.0510 | 2.7645 |
| 800 | 0.2318 | 0.2581 | 0.0263 | 2.6219 | 2.8626 |
| 900 | 0.2526 | 0.2922 | 0.0396 | 3.9400 | 3.0575 |
| 1000 | 0.2593 | 0.2989 | 0.0395 | 3.9345 | 3.0567 |
| Algorithms | R2 | R | MAE | MBE | RMSE | |
|---|---|---|---|---|---|---|
| BP | Training | 0.99973 | 0.99986 | 0.0014704 | −7.6856 × 10−5 | 0.0034852 |
| Test | 0.98416 | 0.99205 | 0.0033053 | 0.0014924 | 0.032499 | |
| GA-BP | Training | 0.99987 | 0.99993 | 0.0013553 | 5.9696 × 10−5 | 0.0023766 |
| Test | 0.99987 | 0.99993 | 0.001514 | −6.8653 × 10−5 | 0.0029763 | |
| RF | Training | 0.99564 | 0.99782 | 0.0031699 | −0.00037206 | 0.013898 |
| Test | 0.88701 | 0.94181 | 0.01091 | −0.0058259 | 0.08679 | |
| XGBoost | Training | 0.99996 | 0.99998 | 0.001001 | 2.2163 × 10−7 | 0.0013082 |
| Test | 0.95656 | 0.97804 | 0.0047947 | −0.0035598 | 0.053812 | |
| LSTM | Training | 0.94695 | 0.97311 | 0.037583 | −7.5798 × 10−5 | 0.048483 |
| Test | 0.91935 | 0.95883 | 0.041425 | −0.0017029 | 0.073324 | |
| ELM | Training | 0.93725 | 0.96812 | 0.038562 | −4.274 × 10−7 | 0.052728 |
| Test | 0.93885 | 0.96894 | 0.041769 | −0.0012613 | 0.063845 | |
| CNN | Training | 0.97488 | 0.98736 | 0.022713 | 0.017768 | 0.033362 |
| Test | 0.97206 | 0.98593 | 0.024634 | 0.018 | 0.043157 | |
| SVM | Training | 0.96065 | 0.98013 | 0.0295 | 0.0046757 | 0.041754 |
| Test | 0.95176 | 0.97558 | 0.034408 | 0.0046691 | 0.056709 |
| Algorithm | Core Mechanism | Difference in R | Advantages | Disadvantages | Applicable Scenarios |
|---|---|---|---|---|---|
| BP | Multivariate non-linear mapping | 0.00781 | Stable error control | Slow training | Modeling of complex mass transfer processes |
| GA-BP | Enhanced generalization ability after optimization | 0 | Strong fitting and generalization ability | High computational cost | High-precision prediction of mass transfer coefficients |
| RF | Ensemble of decision trees for feature selection [44] | 0.05601 | Parallel processing of high-dimensional data | Severe overfitting | Rapid response for feature selection |
| XGBoost | Gradient boosting for anti-overfitting [45] | 0.02194 | Strong anti-overfitting ability | Requires fine-tuning of parameters | Rapid data deployment |
| LSTM | Gating mechanism to capture time-series dependencies | 0.01428 | Alleviates gradient vanishing | Large prediction error | Analysis of mass transfer fluctuations |
| ELM | Random weights for rapid solution | 0.00082 | Fast training speed | Weak generalization ability | Rapid mass transfer prediction |
| CNN | Incorporating particle spatial distribution for auxiliary prediction | 0.00143 | Extracts spatial features and non-linear relationships | High demand for computational resources | Mass transfer prediction with spatial features |
| SVM | Risk minimization | 0.00455 | Balances accuracy and efficiency | Difficult to select kernel functions | Evaluation of mass transfer efficiency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liu, A.; Chen, J.; Wang, J.; Wang, D.; Gao, L.; Chen, C.; Zhu, R.; Raikov, A.; Guo, Y. Machine Learning-Based Impact of Rotational Speed on Mixing, Mass Transfer, and Flow Parameter Prediction in Solid–Liquid Stirred Tanks. Processes 2025, 13, 1423. https://doi.org/10.3390/pr13051423
Zhang X, Liu A, Chen J, Wang J, Wang D, Gao L, Chen C, Zhu R, Raikov A, Guo Y. Machine Learning-Based Impact of Rotational Speed on Mixing, Mass Transfer, and Flow Parameter Prediction in Solid–Liquid Stirred Tanks. Processes. 2025; 13(5):1423. https://doi.org/10.3390/pr13051423
Chicago/Turabian StyleZhang, Xinrui, Anjun Liu, Jie Chen, Juan Wang, Dong Wang, Liang Gao, Chengmin Chen, Rongkai Zhu, Aleksandr Raikov, and Ying Guo. 2025. "Machine Learning-Based Impact of Rotational Speed on Mixing, Mass Transfer, and Flow Parameter Prediction in Solid–Liquid Stirred Tanks" Processes 13, no. 5: 1423. https://doi.org/10.3390/pr13051423
APA StyleZhang, X., Liu, A., Chen, J., Wang, J., Wang, D., Gao, L., Chen, C., Zhu, R., Raikov, A., & Guo, Y. (2025). Machine Learning-Based Impact of Rotational Speed on Mixing, Mass Transfer, and Flow Parameter Prediction in Solid–Liquid Stirred Tanks. Processes, 13(5), 1423. https://doi.org/10.3390/pr13051423







